算法详解及应用
动态规划算法难点详解及应用技巧介绍

动态规划算法难点详解及应用技巧介绍动态规划算法(Dynamic Programming)是一种常用的算法思想,主要用于解决具有重叠子问题和最优子结构性质的问题。
在解决一些复杂的问题时,动态规划算法可以将问题分解成若干个子问题,并通过求解子问题的最优解来求解原始问题的最优解。
本文将详细介绍动态规划算法的难点以及应用技巧。
一、动态规划算法的难点1. 难点一:状态的定义在动态规划算法中,首先需要明确问题的状态。
状态是指问题在某一阶段的具体表现形式。
在进行状态定义时,需要考虑到问题的最优子结构性质。
状态的定义直接影响到问题的子问题划分和状态转移方程的建立。
2. 难点二:状态转移方程的建立动态规划算法是基于状态转移的思想,即通过求解子问题的最优解来求解原始问题的最优解。
因此,建立合理的状态转移方程是动态规划算法的关键。
在进行状态转移方程的建立时,需要考虑问题的最优子结构性质和状态之间的关系。
3. 难点三:边界条件的处理在动态规划算法中,边界条件是指问题的最简单情况,用于终止递归过程并给出递归基。
边界条件的处理需要考虑问题的具体要求和实际情况,确保问题能够得到正确的解。
二、动态规划算法的应用技巧1. 应用技巧一:最长递增子序列最长递增子序列是一类经典的动态规划问题。
其求解思路是通过定义状态和建立状态转移方程,找到问题的最优解。
在应用最长递增子序列问题时,可以使用一维数组来存储状态和记录中间结果,通过迭代计算来求解最优解。
2. 应用技巧二:背包问题背包问题是另一类常见的动态规划问题。
其求解思路是通过定义状态和建立状态转移方程,将问题转化为子问题的最优解。
在应用背包问题时,可以使用二维数组来存储状态和记录中间结果,通过迭代计算来求解最优解。
3. 应用技巧三:最短路径问题最短路径问题是动态规划算法的经典应用之一。
其求解思路是通过定义状态和建立状态转移方程,利用动态规划的思想来求解最优解。
在应用最短路径问题时,可以使用二维数组来存储状态和记录中间结果,通过迭代计算来求解最优解。
前缀和算法详解及应用

前缀和算法详解及应用1.前缀和的定义和计算方法前缀和的定义是指数组中从第一个元素开始到当前位置的所有元素的和。
用数学表达式表示为:prefix_sum[i] = sum(arr[0] + arr[1] + ... + arr[i])。
前缀和的计算方法是通过遍历数组,将当前元素与前一个元素的前缀和相加,得到当前位置的前缀和。
换句话说,prefix_sum[i] =prefix_sum[i - 1] + arr[i]。
通过这种计算方法,可以在O(n)的时间复杂度内得到整个数组的前缀和。
2.前缀和的性质和应用- prefix_sum[0] = 0,即前缀和数组的第一个元素为0。
- 如果要求解数组arr[i]到arr[j]的区间和,可以通过计算prefix_sum[j] - prefix_sum[i - 1]获得。
-子数组和的问题:通过计算前缀和数组,可以在O(1)的时间复杂度内求解数组中任意区间的和,例如最大子数组和、区间和等问题。
-寻找满足特定条件的子数组:通过计算前缀和数组,可以在O(n)的时间复杂度内找到满足其中一特定条件的子数组,例如和为k的子数组、最长连续和为0的子数组等。
3.前缀和算法的具体实现- 构建前缀和数组:首先创建一个长度为n+1的前缀和数组prefix_sum,将第一个元素设为0。
- 计算前缀和:通过遍历数组arr,将当前元素与前一个元素的前缀和相加,得到当前位置的前缀和,并将其存入prefix_sum数组中。
以下是使用前缀和算法求解最大子数组和的Python代码示例:```def max_subarray_sum(arr):n = len(arr)prefix_sum = [0] * (n + 1)for i in range(1, n + 1):prefix_sum[i] = prefix_sum[i - 1] + arr[i - 1]max_sum = float('-inf')for i in range(1, n + 1):for j in range(i, n + 1):curr_sum = prefix_sum[j] - prefix_sum[i - 1]max_sum = max(max_sum, curr_sum)return max_sum```通过使用前缀和算法,可以将最大子数组和问题的时间复杂度从O(n^2)降低到O(n),提升算法的运行效率。
弱监督学习算法详解及应用技巧

弱监督学习算法详解及应用技巧在机器学习领域,监督学习是一种常见的学习方法,它通过已知的标签来训练模型。
但是在实际应用中,很多数据并没有完整的标签信息,这就需要使用一种更加灵活的学习算法来处理这种情况。
弱监督学习算法就是这样一种算法,它不需要完整的标签信息,而是能够利用部分标签或者弱标签来进行学习。
本文将对弱监督学习算法进行详细的介绍,并探讨其应用技巧。
一、弱监督学习算法简介弱监督学习算法是一种能够利用不完整标签信息进行学习的算法。
在传统的监督学习中,训练数据通常包括输入特征和对应的标签,模型通过学习这些标签来进行预测。
而在弱监督学习中,标签信息可能是不完整的,只有部分标签信息或者弱标签信息。
这就需要算法能够从这些不完整的标签信息中学习到有效的知识。
常见的弱监督学习算法包括多示例学习(MIL)、半监督学习、迁移学习等。
这些算法都能够有效地利用不完整标签信息进行学习,并在实际应用中取得了很好的效果。
二、弱监督学习算法原理弱监督学习算法的原理主要是通过利用不完整的标签信息来进行模型训练。
在多示例学习中,训练数据被分为多个示例,每个示例可能包含多个样本,但只有一个标签。
模型需要通过学习这些示例来进行预测。
在半监督学习中,只有部分数据有标签信息,而其他数据则没有标签信息,模型需要通过利用有标签数据来进行学习,并将学到的知识应用到无标签数据上。
在迁移学习中,模型需要利用从一个领域学到的知识来进行另一个领域的学习。
这些算法都能够有效地利用不完整标签信息来进行学习,并取得良好的效果。
三、弱监督学习算法应用技巧1. 数据增强在应用弱监督学习算法时,数据增强是一种常用的技巧。
通过对训练数据进行扩充,可以增加数据的多样性,提高模型的泛化能力。
数据增强的方法包括图像旋转、翻转、缩放等操作,能够有效地提高模型的性能。
2. 标签传播在半监督学习中,标签传播是一种常用的技巧。
通过利用有标签数据和无标签数据之间的相似性来进行标签传播,可以有效地利用不完整标签信息进行学习。
动态规划算法详解及经典例题

动态规划算法详解及经典例题⼀、基本概念(1)⼀种使⽤多阶段决策过程最优的通⽤⽅法。
(2)动态规划过程是:每次决策依赖于当前状态,⼜随即引起状态的转移。
⼀个决策序列就是在变化的状态中产⽣出来的,所以,这种多阶段最优化决策解决问题的过程就称为动态规划。
假设问题是由交叠的⼦问题所构成,我们就能够⽤动态规划技术来解决它。
⼀般来说,这种⼦问题出⾃对给定问题求解的递推关系中,这个递推关系包括了同样问题的更⼩⼦问题的解。
动态规划法建议,与其对交叠⼦问题⼀次重新的求解,不如把每⼀个较⼩⼦问题仅仅求解⼀次并把结果记录在表中(动态规划也是空间换时间的)。
这样就能够从表中得到原始问题的解。
(3)动态规划经常常使⽤于解决最优化问题,这些问题多表现为多阶段决策。
关于多阶段决策:在实际中,⼈们经常遇到这样⼀类决策问题,即因为过程的特殊性,能够将决策的全过程根据时间或空间划分若⼲个联系的阶段。
⽽在各阶段中。
⼈们都须要作出⽅案的选择。
我们称之为决策。
⽽且当⼀个阶段的决策之后,经常影响到下⼀个阶段的决策,从⽽影响整个过程的活动。
这样,各个阶段所确定的决策就构成⼀个决策序列,常称之为策略。
因为各个阶段可供选择的决策往往不⽌⼀个。
因⽽就可能有很多决策以供选择,这些可供选择的策略构成⼀个集合,我们称之为同意策略集合(简称策略集合)。
每⼀个策略都对应地确定⼀种活动的效果。
我们假定这个效果能够⽤数量来衡量。
因为不同的策略经常导致不同的效果,因此,怎样在同意策略集合中选择⼀个策略,使其在预定的标准下达到最好的效果。
经常是⼈们所关⼼的问题。
我们称这种策略为最优策略,这类问题就称为多阶段决策问题。
(4)多阶段决策问题举例:机器负荷分配问题某种机器能够在⾼低两种不同的负荷下进⾏⽣产。
在⾼负荷下⽣产时。
产品的年产量g和投⼊⽣产的机器数量x的关系为g=g(x),这时的年完善率为a,即假设年初完善机器数为x,到年终时完善的机器数为a*x(0<a<1);在低负荷下⽣产时,产品的年产量h和投⼊⽣产的机器数量y 的关系为h=h(y)。
SIFT算法详解及应用

SIFT算法详解及应用SIFT(Scale-Invariant Feature Transform)是一种图像处理算法,它能够在不同尺度、旋转、光照条件下进行特征点匹配。
SIFT算法是计算机视觉领域的一个重要算法,广泛应用于目标识别、图像拼接、图像检索等方面。
首先,尺度空间极值检测是指在不同尺度上检测图像中的极值点,即图像中的局部最大值或最小值。
这样可以使特征点能够对应不同尺度的目标,使算法对尺度变化有鲁棒性。
为了实现这一步骤,SIFT算法使用了高斯差分金字塔来检测尺度空间中的极值点。
接下来是关键点定位,即确定在尺度空间极值点的位置以及对应的尺度。
SIFT算法通过比较每个极值点与其周围点的响应值大小来判断其是否为关键点。
同时,为了提高关键点的稳定性和准确性,算法还会对关键点位置进行亚像素精确化。
然后是关键点方向的确定,即为每个关键点分配一个主方向。
SIFT算法使用图像梯度方向的直方图来确定关键点的方向。
这样可以使得特征描述子具有旋转不变性,使算法在目标旋转的情况下仍能进行匹配。
最后是关键点的描述。
SIFT算法使用局部图像的梯度信息来描述关键点,即构建关键点的特征向量。
特征向量的构建过程主要包括将关键点周围的图像划分为若干个子区域,计算每个子区域的梯度直方图,并将所有子区域的直方图拼接成一个特征向量。
这样可以使得特征向量具有局部不变性和对光照变化的鲁棒性。
SIFT算法的应用非常广泛。
首先,在目标识别领域,SIFT算法能够检测和匹配图像中的关键点,从而实现目标的识别和定位。
其次,在图像拼接方面,SIFT算法能够提取图像中的特征点,并通过匹配这些特征点来完成图像的拼接。
此外,SIFT算法还可以应用于图像检索、三维重建、行人检测等领域。
总结起来,SIFT算法是一种具有尺度不变性和旋转不变性的图像处理算法。
它通过提取图像中的关键点,并构建关键点的描述子,实现了对不同尺度、旋转、光照条件下的目标识别和图像匹配。
机器学习10大经典算法详解

机器学习10⼤经典算法详解本⽂为⼤家分享了机器学习10⼤经典算法,供⼤家参考,具体内容如下1、C4.5C4.5算法是机器学习算法中的⼀种分类决策树算法,其核⼼算法是ID3算法. C4.5算法继承了ID3算法的优点,并在以下⼏⽅⾯对ID3算法进⾏了改进:1)⽤信息增益率来选择属性,克服了⽤信息增益选择属性时偏向选择取值多的属性的不⾜;2)在树构造过程中进⾏剪枝;3)能够完成对连续属性的离散化处理;4)能够对不完整数据进⾏处理。
C4.5算法有如下优点:产⽣的分类规则易于理解,准确率较⾼。
其缺点是:在构造树的过程中,需要对数据集进⾏多次的顺序扫描和排序,因⽽导致算法的低效。
2、The k-means algorithm即K-Means算法k-means algorithm算法是⼀个聚类算法,把n的对象根据他们的属性分为k个分割,k < n。
它与处理混合正态分布的最⼤期望算法很相似,因为他们都试图找到数据中⾃然聚类的中⼼。
它假设对象属性来⾃于空间向量,并且⽬标是使各个群组内部的均⽅误差总和最⼩。
3、Support vector machines⽀持向量机⽀持向量机(Support Vector Machine),简称SV机(论⽂中⼀般简称SVM)。
它是⼀种监督式学习的⽅法,它⼴泛的应⽤于统计分类以及回归分析中。
⽀持向量机将向量映射到⼀个更⾼维的空间⾥,在这个空间⾥建⽴有⼀个最⼤间隔超平⾯。
在分开数据的超平⾯的两边建有两个互相平⾏的超平⾯。
分隔超平⾯使两个平⾏超平⾯的距离最⼤化。
假定平⾏超平⾯间的距离或差距越⼤,分类器的总误差越⼩。
⼀个极好的指南是C.J.C Burges的《模式识别⽀持向量机指南》。
van der Walt和Barnard 将⽀持向量机和其他分类器进⾏了⽐较。
4、The Apriori algorithmApriori算法是⼀种最有影响的挖掘布尔关联规则频繁项集的算法。
其核⼼是基于两阶段频集思想的递推算法。
计算机算法设计五大常用算法的分析及实例

计算机算法设计五⼤常⽤算法的分析及实例摘要算法(Algorithm)是指解题⽅案的准确⽽完整的描述,是⼀系列解决问题的清晰指令,算法代表着⽤系统的⽅法描述解决问题的策略机制。
也就是说,能够对⼀定规范的输⼊,在有限时间内获得所要求的输出。
如果⼀个算法有缺陷,或不适合于某个问题,执⾏这个算法将不会解决这个问题。
不同的算法可能⽤不同的时间、空间或效率来完成同样的任务。
其中最常见的五中基本算法是递归与分治法、动态规划、贪⼼算法、回溯法、分⽀限界法。
本⽂通过这种算法的分析以及实例的讲解,让读者对算法有更深刻的认识,同时对这五种算法有更清楚认识关键词:算法,递归与分治法、动态规划、贪⼼算法、回溯法、分⽀限界法AbstractAlgorithm is the description to the problem solving scheme ,a set of clear instructions to solve the problem and represents the describe the strategy to solve the problem using the method of system mechanism . That is to say, given some confirm import,the Algorithm will find result In a limited time。
If an algorithm is defective or is not suitable for a certain job, it is invalid to execute it. Different algorithms have different need of time or space, and it's efficiency are different.There are most common algorithms: the recursive and divide and conquer、dynamic programming method、greedy algorithm、backtracking、branch and bound method.According to analyze the five algorithms and explain examples, make readers know more about algorithm , and understand the five algorithms more deeply.Keywords: Algorithm, the recursive and divide and conquer, dynamic programming method, greedy algorithm、backtracking, branch and bound method⽬录1. 前⾔ (4)1.1 论⽂背景 (4)2. 算法详解 (5)2.1 算法与程序 (5)2.2 表达算法的抽象机制 (5)2.3 算法复杂性分析 (5)3.五中常⽤算法的详解及实例 (6)3.1 递归与分治策略 (6)3.1.1 递归与分治策略基本思想 (6)3.1.2 实例——棋盘覆盖 (7)3.2 动态规划 (8)3.2.1 动态规划基本思想 (8)3.2.2 动态规划算法的基本步骤 (9)3.2.3 实例——矩阵连乘 (9)3.3 贪⼼算法 (11)3.3.1 贪⼼算法基本思想 (11)3.3.2 贪⼼算法和动态规划的区别 (12)3.3.3 ⽤贪⼼算法解背包问题的基本步骤: (12)3.4 回溯发 (13)3.4.1 回溯法基本思想 (13)3.3.2 回溯发解题基本步骤 (13)3.3.3 实例——0-1背包问题 (14)3.5 分⽀限界法 (15)3.5.1 分⽀限界法思想 (15)3.5.2 实例——装载问题 (16)总结 (18)参考⽂献 (18)1. 前⾔1.1 论⽂背景算法(Algorithm)是指解题⽅案的准确⽽完整的描述,是⼀系列解决问题的清晰指令,算法代表着⽤系统的⽅法描述解决问题的策略机制。
递归算法及经典例题详解
递归算法及经典例题详解大部分人在学习编程时接触的第一个算法应该就是递归了,递归的思想其实很好理解,就是将一个问题拆分为若干个与本身相似的子问题,通过不断调用自身来求解。
但很多新手在实际操作中却很难正确使用到递归,有时面对问题还会有种无从下手的感觉,在此,我总结了一些解决递归问题的方法和思路,希望对你能有所帮助。
1.什么是递归递归简单来说就是在运行过程中不断调用自己,直到碰到终止条件,返回结果的过程。
递归可以看作两个过程,分别是递和归。
递就是原问题把要计算的结果传给子问题;归则是子问题求出结果后,把结果层层返回原问题的过程。
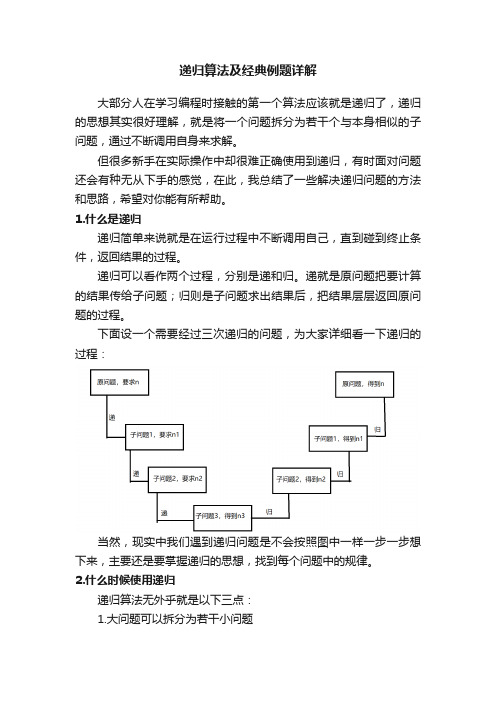
下面设一个需要经过三次递归的问题,为大家详细看一下递归的过程:当然,现实中我们遇到递归问题是不会按照图中一样一步一步想下来,主要还是要掌握递归的思想,找到每个问题中的规律。
2.什么时候使用递归递归算法无外乎就是以下三点:1.大问题可以拆分为若干小问题2.原问题与子问题除数据规模不同,求解思路完全相同3.存在递归终止条件而在实际面对递归问题时,我们还需要考虑第四点:当不满足终止条件时,要如何缩小函数值并让其进入下一层循环中3.递归的实际运用(阶层计算)了解了大概的思路,现在就要开始实战了。
下面我们来看一道经典例题:求N的阶层。
首先按照思路分析是否可以使用递归算法:1.N!可以拆分为(N-1)!*N2.(N-1)!与N!只有数字规模不同,求解思路相同3.当N=1时,结果为1,递归终止满足条件,可以递归:public static int Factorial(int num){if(num==1){return num;}return num*Factorial(num-1);}而最后的return,便是第四步,缩小参数num的值,让递归进入下一层。
一般来说,第四步往往是最难的,需要弄清该如何缩小范围,如何操作返回的数值,这一步只能通过不断地练习提高了(当然如果你知道问题的数学规律也是可以试出来的)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
尺度不变特征变换匹配算法 Scale Invariant Feature Transform (SIFT)
宋丹 10905056
2011/2/18 1/60
提纲
1. SIFT简介 2. SIFT算法实现细节 3. SIFT算法的应用领域
•
目标的旋转、缩放、平移(RST) 目标的旋转、缩放、平移(RST) viewpoint) 图像仿射/投影变换(视点viewpoint 图像仿射/投影变换(视点viewpoint) 光照影响(illumination) 光照影响(illumination) 目标遮挡(occlusion) 目标遮挡(occlusion) 杂物场景(clutter) 杂物场景(clutter) 噪声
2011/2/18
4
SIFT简介 SIFT简介
SIFT
Scale Invariant Feature Transform
Original image courtesy of David Lowe
将一幅图像映射(变换)为一个局部特征向量集; 将一幅图像映射(变换)为一个局部特征向量集;特征向量具有 平移、缩放、旋转不变性,同时对光照变化、 平移、缩放、旋转不变性,同时对光照变化、仿射及投影变换也有一定 不变性。 不变性。
2011/2/18
13
关键点检测的相关概念 关键点检测的相关概念
r2 G (r) = exp − 2 2 2πσ 2σ 1
2 2 r为模糊半径, r= x + y 为模糊半径,
SIFT
Scale Invariant Feature Transform
在减小图像尺寸的场合经常使用高斯模糊。在进行欠采样的时, 在减小图像尺寸的场合经常使用高斯模糊。在进行欠采样的时, 通常在采样之前对图像进行低通滤波处理。 通常在采样之前对图像进行低通滤波处理。这样就可以保证在采样 图像中不会出现虚假的高频信息。 图像中不会出现虚假的高频信息。
SIFT算法实现物体识别主要有三大工序, SIFT算法实现物体识别主要有三大工序,1、提取关键点;2、对关键点附加 算法实现物体识别主要有三大工序 提取关键点; 详细的信息(局部特征)也就是所谓的描述器; 详细的信息(局部特征)也就是所谓的描述器;3、通过两方特征点(附带 通过两方特征点( 上特征向量的关键点)的两两比较找出相互匹配的若干对特征点, 上特征向量的关键点)的两两比较找出相互匹配的若干对特征点,也就建立
•
1999年 Columbia大学大卫 劳伊( 大学大卫. G.Lowe) 1999年British Columbia大学大卫.劳伊(David G.Lowe)教授总结了现有 的基于不变量技术的特征检测方法,并正式提出了一种基于尺度空间的、 的基于不变量技术的特征检测方法,并正式提出了一种基于尺度空间的、对 图像缩放、旋转甚至仿射变换保持不变性的图像局部特征描述算子- 图像缩放、旋转甚至仿射变换保持不变性的图像局部特征描述算子-SIFT (尺度不变特征变换),这种算法在2004年被加以完善。 尺度不变特征变换),这种算法在2004年被加以完善。 ),这种算法在2004年被加以完善
分辨率、不同光照、不同位姿情况下所成的像相对应。 分辨率、不同光照、不同位姿情况下所成的像相对应。 传统的匹配算法往往是直接提取角点或边缘, 传统的匹配算法往往是直接提取角点或边缘,对环境的 适应能力较差,急需提出一种鲁棒性强、能够适应不同 适应能力较差,急需提出一种鲁棒性强、 光照、不同位姿等情况下能够有效识别目标的方法。 光照、不同位姿等情况下能够有效识别目标的方法。
2011/2/18
12
关键点检测的相关概念 关键点检测的相关概念
3. 高斯模糊
SIFT
Scale Invariant Feature Transform
高斯模糊是在Adobe Photoshop等图像处理软件中广泛使用的处理 高斯模糊是在Adobe Photoshop等图像处理软件中广泛使用的处理 效果,通常用它来减小图像噪声以及降低细节层次。 效果,通常用它来减小图像噪声以及降低细节层次。这种模糊技术生成 的图像的视觉效果是好像经过一个半透明的屏幕观察图像。 的图像的视觉效果是好像经过一个半透明的屏幕观察图像。
2011/2/18
3
SIFT简介 SIFT简介
SIFT提出的目的和意义 SIFT提出的目的和意义
SIFT
Scale Invariant Feature Transform
David G. Lowe Computer Science Department 2366 Main Mall University of British Columbia Vancouver, B.C., V6T 1Z4, Canada E-mail: lowe@cs.ubc.ca
2011/2/18 11
关键点检测的相关概念 关键点检测的相关概念
SIFT
Scale Invariant Feature Transform
根据文献《Scale根据文献《Scale-space theory: A basic tool for analysing scales》我们可知, structures at different scales》我们可知,高斯核是唯一可以产生 多尺度空间的核,一个图像的尺度空间, ,定义为原始图像 多尺度空间的核,一个图像的尺度空间,L(x,y,σ) ,定义为原始图像 I(x,y)与一个可变尺度的 维高斯函数G(x,y,σ) 卷积运算。 与一个可变尺度的2 I(x,y)与一个可变尺度的2维高斯函数G(x,y,σ) 卷积运算。
9
关键点检测的相关概念 关键点检测的相关概念
SIFT
Scale Invariant Feature Transform
哪些点是SIFT中要查找的关键点(特征点)? SIFT中要查找的关键点 1. 哪些点是SIFT中要查找的关键点(特征点)?
这些点是一些十分突出的点不会因光照条件的改变而消失,比如角点、 这些点是一些十分突出的点不会因光照条件的改变而消失,比如角点、 边缘点、暗区域的亮点以及亮区域的暗点,既然两幅图像中有相同的景物, 边缘点、暗区域的亮点以及亮区域的暗点,既然两幅图像中有相同的景物, 那么使用某种方法分别提取各自的稳定点, 那么使用某种方法分别提取各自的稳定点,这些点之间会有相互对应的匹配 点。 所谓关键点,就是在不同尺度空间的图像下检测出的具有方向 所谓关键点,就是在不同尺度空间的图像下检测出的具有方向 尺度空间 信息的局部极值点。 信息的局部极值点。 根据归纳,我们可以看出特征点具有的三个特征: 根据归纳,我们可以看出特征点具有的三个特征: 尺度 方向 大小
Back
7
• • • • •
2011/2/18
SIFT算法实现细节 SIFT算法实现细节
SIFT算法实现步骤简述 SIFT算法实现步骤简述
SIFT
Scale Invariant Feature Transform
SIFT算法的实质可以归为在不同尺度空间上查找特征点(关键点)的问题。 SIFT算法的实质可以归为在不同尺度空间上查找特征点(关键点)的问题。 算法的实质可以归为在不同尺度空间上查找特征点
SIFT
Scale Invariant Feature Transform
4. SIFT算法的扩展与改进
2011/2/18
2
SIFT简介 SIFT简介
传统的特征提取方法
•
SIFT
Scale Invariant Feature Transform
成像匹配的核心问题是将同一目标在不同时间、 成像匹配的核心问题是将同一目标在不同时间、不同
2011/2/18 5
SIFT简介 SIFT简介
SIFT算法特点 SIFvariant Feature Transform
• SIFT特征是图像的局部特征,其对旋转、尺度缩放、亮度变化 SIFT特征是图像的局部特征,其对旋转、尺度缩放、 特征是图像的局部特征 保持不变性,对视角变化、仿射变换、 保持不变性,对视角变化、仿射变换、噪声也保持一定程度的稳 定性。 定性。 • 独特性(Distinctiveness)好,信息量丰富,适用于在海量特征 独特性(Distinctiveness)好 信息量丰富, (Distinctiveness) 数据库中进行快速、准确的匹配。 数据库中进行快速、准确的匹配。 • 多量性,即使少数的几个物体也可以产生大量SIFT特征向量。 多量性,即使少数的几个物体也可以产生大量SIFT特征向量。 SIFT特征向量 • 经过优化的SIFT算法可满足一定的速度需求。 经过优化的SIFT算法可满足一定的速度需求。 SIFT算法可满足一定的速度需求
高斯函数
( x − xi )2 + ( y − yi ) 2 G ( xi , yi , σ ) = exp − 2 2πσ 2σ 2 1
L ( x, y , σ ) = G ( x, y , σ ) * I ( x, y )
尺度是自然存在的,不是人为创造的! 尺度是自然存在的,不是人为创造的!高斯卷 积只是表现尺度空间的一种形式… 积只是表现尺度空间的一种形式
2011/2/18
10
关键点检测的相关概念 关键点检测的 关键点检测的 的相关概念
什么是尺度空间( 2. 什么是尺度空间(scale space )?
SIFT
Scale Invariant Feature Transform
我们要精确表示的物体都是通过一定的尺度来反映的。现实世界的 我们要精确表示的物体都是通过一定的尺度来反映的。 物体也总是通过不同尺度的观察而得到不同的变化。 物体也总是通过不同尺度的观察而得到不同的变化。 尺度空间理论最早在1962年提出,其主要思想是通过对原始图像进 尺度空间理论最早在1962年提出, 1962年提出 行尺度变换,获得图像多尺度下的尺度空间表示序列, 行尺度变换,获得图像多尺度下的尺度空间表示序列,对这些序列进行 尺度空间主轮廓的提取,并以该主轮廓作为一种特征向量,实现边缘、 尺度空间主轮廓的提取,并以该主轮廓作为一种特征向量,实现边缘、 角点检测和不同分辨率上的特征提取等。 角点检测和不同分辨率上的特征提取等。 尺度空间中各尺度图像的模糊程度逐渐变大, 尺度空间中各尺度图像的模糊程度逐渐变大,能够模拟人在距离目 标由近到远时目标在视网膜上的形成过程。 标由近到远时目标在视网膜上的形成过程。 尺度越大图像越模糊。 尺度越大图像越模糊。
