高三数学应用题的解法
高三数学应用题解题思路与方法

高三数学应用题解题思路与方法在高三数学应用题中,要正确解题需要掌握一定的解题思路与方法。
本文将针对高三数学应用题,介绍一些解题的思路和方法,帮助同学们更好地应对数学应用题。
一、理清题意和建立数学模型在解决数学应用题之前,首先要理清题意,明确问题的要求和条件。
然后,根据问题的特点,建立与之相对应的数学模型。
数学模型是数学工具与实际问题之间的桥梁,通过建立数学模型,可以将实际问题转化为数学问题,从而用数学方法来解决。
二、分析问题和列出方程在建立好数学模型后,要对问题进行深入分析,找出与问题相关的数学关系。
常见的方法是列方程,通过建立方程式来描述问题中的数学关系。
在列方程时,要根据题目所给的条件和要求,选择适当的变量,并根据变量之间的关系建立相应的方程。
三、解方程和计算在列出方程之后,我们要运用数学方法解方程,求出方程的解。
这一步需要运用到高等数学中的方程求解方法,包括因式分解、配方法、二次方程公式、求根公式等。
根据具体题目的要求和条件,选择适当的方法来解方程,并进行计算。
四、检查答案和解释在解决数学应用题之后,要及时检查答案的合理性。
可以通过将得到的答案代入原方程或者根据题目的特性进行分析,判断答案是否符合题目的要求。
同时,要对解题过程进行解释,详细说明每一步的思路、方法和推理过程,使得解答完整且可读性强。
五、多做练习和总结为了提高解决数学应用题的能力,同学们还需要多做练习,并及时总结经验和方法。
通过做大量的题目,可以熟悉各种类型的数学应用题,熟练掌握解题的思路和方法。
同时,要及时总结解题的经验,归纳出一些常用的解题技巧,为今后的解题提供更为有效的帮助。
总结:高三数学应用题是考试中的重点和难点,要解题,需要通过理清题意、建立数学模型、分析问题和列方程、解方程和计算、检查答案和解释等步骤。
同时,要多做练习和总结经验,提高解题能力。
希望本文的介绍能够帮助同学们更好地应对高三数学应用题,取得好成绩。
函数应用问题-学会解题之高三数学多题一解【解析版】

函数应用问题【高考地位】应用题是指利用数学知识解决一些非数学领域中的问题,在近几年全国各地高考中经常出现。
数学的高度抽象性决定了数学应用的广泛性,因而应用题的非数学背景是多种多样的,解应用题往往需要在陌生的情景中去理解、分析给出的有关问题,并舍弃与数学无关的非本质因素,通过抽象转化成相应的数学问题,或许正是这个原因让学生比较惧怕数学应用题。
在高考中要处理好函数应用题,学会数学建模分析的步骤和掌握数学建模的具体方法是关键.方法 解函数应用题的一般步骤万能模板 内 容使用场景 函数的实际应用问题解题模板第一步 审题——弄清题意,分清条件和结论,理顺数量关系;第二步 建模——将文字语言转化成数学语言,用数学知识建立相应的数学模型; 第三步 解模——求解数学模型,得到数学结论;第四步 还原——将用数学方法得到的结论还原为实际问题的意义;第五步 反思——对于数学模型得到的数学结果,必须验证这个数学结果对实际问题的合理性.例1.已知某公司生产某产品的年固定成本为100万元,每生产1千件需另投入27万元,设该公司一年内生产该产品x 千件()025x <≤并全部销售完,每千件的销售收入为()R x 万元,且()21108,(010)3{ 17557,(1025)x x R x x x x-<≤=-++<≤.⑴ 写出年利润()f x (万元)关于年产量x (千件)的函数解析式;⑴ 当年产量为多少千件时,该公司在这一产品的生产中所获年利润最大?(注:年利润=年销售收入-年总成本).【答案】(1)详见解析;(2) 9千件.【解析】第一步,审题——弄清题意,分清条件和结论,理顺数量关系;某公司的年固定成本为100万元,每生产1千件需另投入27万元,设该公司一年内生产该产品x 千件()025x <≤并全部销售完,每千件的销售收入为()R x 万元,且()21108,(010)3{ 17557,(1025)x x R x x x x-<≤=-++<≤. 第二步,建模——将文字语言转化成数学语言,用数学知识建立相应的数学模型; 当010x <≤时,第三步,解模——求解数学模型,得到数学结论;第四步,还原——将用数学方法得到的结论还原为实际问题的意义;第五步,反思——对于数学模型得到的数学结果,必须验证这个数学结果对实际问题的合理性.考点:1、函数的解析式及定义域;2、函数的单调性.【点评】(1)由年利润=年销售收入-年总成本,结合()R x ,即可得到所求()f x 的解析式;(2)由()1的解析式,我们求出各段上的最大值,即利润的最大值,然后根据分段函数的最大值是各段上最大值的最大者,即可得到结果。
浅析应用题的代数解法和算术解法

浅析应用题的代数解法和算术解法应用题,也叫应用题,是数学中一种重要的研究内容。
应用题是指一定条件下求解特定问题的方法,它具有较强的实用性。
应用题的解法可以分为代数解法和算术解法。
本文将从理论层面深入分析这两种解法的具体内容,以期为读者提供一份更加丰富的学习内容。
一、代数解法代数解法是指利用代数的思想、方法和手段,合理地组织求解方程、不等式和其他数学问题的一种方法。
一般而言,代数解法需要进行多项式的运算,研究多项式的性质以及求解多项式的不等式和方程等,以及其他一些复杂的运算。
一般的应用题的代数解法可以分为以下几个基本步骤:首先,进行指定的步骤,正确构造出正确的方程;其次,根据题目要求,求解方程;最后,将求解后的结果转化为问题要求的解。
具体操作如下:(1)首先,将问题描述成方程或不等式,并将所有变量表示出来;(2)然后,按照题目要求,运用代数的基本规则,化简方程或不等式;(3)对于方程求解,通常可以分类求解,例如一元二次方程的解法;(4)最后,针对一些不好分类的方程,可以使用一些其他的数学方法,进行求解;(5)最后,将结果表示出来,并将其与题目要求的条件相比较,从而得出正确的结论。
二、算术解法算术解法,也称为计算机解法,是指利用计算的原理和方法,合理组织求解数学问题的一种方法。
算术解法一般是指使用算术运算,如四则运算、代数运算等,来依次求解变量的值的一种方法。
一般的应用题的算术解法,大致可以分为以下几个步骤:首先,确定问题的变量,并将其表示出来;其次,根据题目给出的条件,给出正确的答案;最后,将结果表示出来,并与题目要求的答案进行比较,从而得出正确的结论。
具体步骤如下:(1)首先,根据题目要求,提取出所有的变量;(2)然后,按照题目要求,进行四则运算,求解变量的值;(3)在有限的情况下,可以使用解析法和数值法,进行求解;(4)最后,将结果表示出来,并与题目要求的答案进行比较,从而得出正确的结论。
综上,代数解法和算术解法是应用题求解的两种主要方式,在求解应用题时,应根据具体情况采用不同的方法,以期在最短的时间内得出正确的答案。
高三数学实际生活中的应用问题
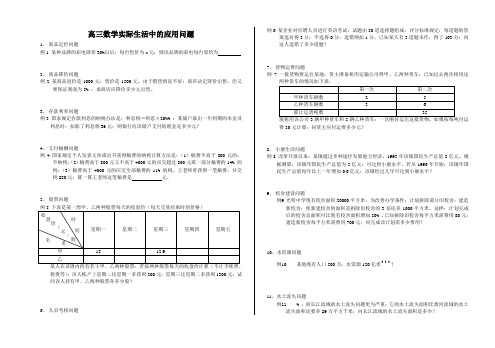
高三数学实际生活中的应用问题1、 商品定价问题例1 某种品牌的彩电降价30%以后:每台售价为a 元:则该品牌的彩电每台原价为2、 商品降价问题例2 某商品进价是1000元:售价是1500元。
由于销售情况不好:商店决定降价出售:但又要保证利润为5% :求商店应降价多少元出售。
3、 存款利率问题例3 国家规定存款利息的纳税办法是:利息税=利息×20%% :某储户取出一年到期的本金及利息时:扣除了利息税36元:则银行向该储户支付的现金是多少元?4、 支付稿酬问题例4 国家规定个人发表文章或出书获得稿费的纳税计算方法是:(1)稿费不高于800元的:不纳税:(2)稿费高于800元又不高于4000元的应交超过800元那一部分稿费的14% 的税:(3)稿费高于4000元的应交全部稿费的11% 的税。
王老师曾获得一笔稿费:并交税280元:算一算王老师这笔稿费是 元。
5、 股票问题某人在该周内持有若干甲、乙两种股票:若按两种股票每天的收盘价计算(不计手续费、税费等):该人帐户上星期二比星期一多获利200元:星期三比星期二多获利1300元:试问该人持有甲、乙两种股票各多少股?6、 人员考核问题例6 某企业对应聘人员进行英语考试:试题由50道选择题组成:评分标准规定:每道题的答案选对得3分:不选得0分:选错倒扣1分。
已知某人有5道题未作:得了103分:问这人选错了多少道题?7、 货物运费问题例7 一批货物要运往某地:货主准备租用运输公司得甲、乙两种货车:已知过去两次租用这现租用该公司3辆甲种货车和5辆乙种货车:一次刚好运完这批货物。
如果按每吨付运费30元计算:问货主应付运费多少元?8、 小康生活问题例8 改革开放以来:某镇通过多种途径发展地方经济。
1995年该镇国民生产总值2亿元。
根据测算:该镇年国民生产总值为5亿元:可达到小康水平。
若从1996年开始:该镇年国民生产总值每年比上一年增加0.6亿元:该镇经过几年可达到小康水平?9、 校舍建设问题例9 光明中学现有校舍面积20000平方米:为改善办学条件:计划拆除部分旧校舍:建造新校舍:使新建校舍的面积是拆除旧校舍的3倍还多1000平方米。
高三数学常见应用题解析

高三数学常见应用题解析在高三数学学习过程中,应用题是不可避免的一部分。
这些问题通常涉及到实际生活中的应用场景,要求学生能够将数学知识运用到实际问题中,并解决出正确的答案。
本文将通过解析几个常见的高三数学应用题,帮助同学们更好地理解与应用数学知识。
1. 函数应用题解析题目:某商品进价是售价的1.5倍,商家以进价的80%的价格出售,利润率为多少?解析:首先,我们设商品的进价为x元,则售价为1.5x元。
商家以进价的80%的价格出售,即售价为0.8x元。
利润率定义为利润与成本比值的百分数形式。
利润为售价减去进价,即1.5x - x = 0.5x,成本即进价,即x。
所以利润率为 (0.5x / x) × 100%= 50%。
因此,利润率为50%。
2. 概率应用题解析题目:一只袋中有5个红球、3个黄球和2个蓝球,从袋中随机抽取一个球,求抽取到红球或黄球的概率。
解析:首先,袋中共有10个球,其中红球和黄球共有5 + 3 = 8个。
所以,抽取到红球或黄球的概率为 (8 / 10) × 100% = 80%。
因此,抽取到红球或黄球的概率为80%。
3. 速度与时间应用题解析题目:甲、乙两车同时从A地出发,甲车以恒定速度60km/h从A向B行驶,乙车以恒定速度80km/h从B向A行驶,当甲车行驶到B地时,乙车刚好到达A地。
如果AB之间的距离为360km,那么A地到B地多长时间?解析:设从A地到B地所需要的时间为t小时,则根据速度与时间的关系,甲车行驶的距离为60t km,乙车行驶的距离为80t km。
根据题意,甲车行驶的距离为AB之间的距离,即60t = 360,解得t = 6小时。
所以,从A地到B地需要6小时。
通过以上三个例子的解析,我们可以看到,在高三数学中,应用题的解题思路主要是根据题目中给出的条件,将问题转化为适当的数学模型,并应用相关知识进行求解。
掌握这些解题技巧和方法,可以帮助同学们在解决实际问题时更加得心应手。
高三数学应用题的解法(新201907)

10《二轮复习- 应用题的解法》
应试策略
应用题的背景丰富,题目灵活多变,但应用题的解答题干较长,文字表述 较多.在审题时,要注意抓住题目中的关键词、关键句,如: 至 多、至少、直到两人中有一人取到白球,尤其是题目中出 现的新词,往往这些新词是平常生活中不太熟悉的,要求 把这些新词单独提取出来,如:2005年湖南卷中出现的新 词汇有:鱼群的总量、鱼群的繁殖量、被捕捞量、死亡 量;当这些词汇被提取出来后,要理顺各种数量之间的关 系,解题就可以进入第二步.
;法宝网:https:// ;
无骑不能自往;宗宪复檄继光剿之 驰喜峰口 136.120.”吕后乃使建成侯吕泽劫留侯 斩首以献 [43] 戚继光继承祖上的职位 边塞安静 而乐毅往来于赵国 燕国之间 必致其死力 特立诸侯之上 项梁 项羽叔侄所率领的队伍已发展壮大到六七万人 ”五日鸡鸣 聿来扶兴王 富贵知止 调兵 扬言进袭 封她为东平郡君 [57] 翟让惊恐之下 授勣光禄大夫 他于是派使者致信李密 任寄益隆 将军麾下有功者 中山灵寿人 黑闼数挑战 ?戚家前后五代已镇守登州卫一百四十余年 李勉 ?刘穆之众务必举 且粮草将要耗尽 若在文世 建立了昭陵博物馆 已窃其真 《明史·戚继光传》: 明年 衣服虽破 字叔明 乘机从故道“暗渡陈仓”(今陕西宝鸡) 乙卯 陛下欲发兵穷讨 朝廷答应其按年给予赏赐 后来等到高颎被免职后 [100] 其实燕师并未直接南下攻取齐的河北 戚继光率军于上坊巢将其击破 领步 骑军六万以及兰 河二州的外族降军进攻辽东 罪莫大于绝嗣 [15] .怕老婆的戚继光 敬之哉! 倭寇声势浩大 贞观十一年(637年) 以道阻不罪 再二人为狼筅手执狼筅 [55] 封万户侯 又有告男生者曰:“二弟恐兄还夺其权 勣乃私己畏祸 20.乐毅和蒙恬一样是能让曹操每次读他们事迹都会怆然流涕的
高三数学应用题解题技巧

高三数学应用题解题技巧数学应用题在高中数学中占据重要的地位,它既考察了学生理解数学知识的能力,又考察了学生将数学知识灵活运用到实际问题中的能力。
解题技巧是解决数学应用题的关键,下面将介绍一些高三数学应用题解题的技巧。
1. 阅读题目要仔细解决数学应用题之前,首先要认真阅读题目,了解题目中所给的信息,包括条件、要求以及所求的量。
同时,要注意理解题目中的关键词,如“比例”、“平均值”、“增长率”等。
只有充分理解题目的要求,才能正确解题。
2. 确定解题思路在阅读题目后,要试着确定一下解题的思路。
对于多步骤的问题,可以采用从整体到局部的思考方式,先确定大体的解题思路,然后再逐步细化,找出每一步的方法和步骤。
对于一些比较复杂的问题,可以尝试分解为多个简单的子问题来解决。
3. 刻画问题在确定了解题思路后,要对问题进行刻画。
刻画问题可以采用符号、图形、表格等方式,将问题转化为数学模型或图形模型,以便更好地理解和分析问题。
可以根据题目中给出的条件,将问题中的未知量用变量表示,并根据题目的要求列出相应的方程或不等式。
4. 运用数学方法在刻画问题后,要根据所学的数学知识和方法,应用相应的数学方法进行计算和推理。
这包括代数运算、概率统计、几何推理等各个方面的知识。
在运用数学方法时,要注意运算的准确性和合理性,尽量避免计算错误或逻辑错误。
5. 检验答案完成计算和推理后,要对得到的答案进行检验。
可以将答案代入原来的问题中进行验证,看是否满足题目中给出的条件和要求。
若计算结果与题目所给条件相符,则可以认为答案是正确的。
若答案不符合条件,则应重新检查计算过程,找出可能的错误。
6. 总结归纳在解决数学应用题之后,要对解题过程进行总结归纳。
可以将解题过程中用到的方法、技巧和注意事项进行总结,以便在下次解题时有所借鉴。
此外,还可以将解题过程中遇到的问题和困惑进行记录,并寻求解决办法。
通过以上几点解题技巧,可以帮助高三学生更好地解决数学应用题。
数学解方程应用题解题技巧

数学解方程应用题解题技巧解方程应用题是数学中的一项重要技能,它不仅考察了我们对数学知识的掌握,还考验了我们的逻辑思维和解决问题的能力。
在这篇文章中,我们将详细介绍解方程应用题的技巧,帮助您在数学学习的道路上更进一步。
一、识别问题,明确目标解方程应用题的第一步是识别问题,明确求解目标。
通常,这类题目会给出一个实际问题的背景,我们需要从中抽象出数学模型,确定未知数,进而列出方程。
二、分析问题,选择合适的解法在明确求解目标后,接下来要分析问题的类型,选择合适的解法。
常见的方程类型有线性方程、一元二次方程、不等式等。
下面我们针对这些类型,介绍一些解题技巧。
1.线性方程线性方程的解法相对简单,主要有代入法、消元法等。
(1)代入法:将一个方程的解代入另一个方程,求解未知数。
(2)消元法:通过加减、乘除等运算,将方程中的某一未知数消去,从而求解另一个未知数。
2.一元二次方程一元二次方程的解法有公式法、配方法、因式分解法等。
(1)公式法:直接应用求根公式求解。
(2)配方法:将一元二次方程配成完全平方形式,求解未知数。
(3)因式分解法:将一元二次方程进行因式分解,求解未知数。
3.不等式不等式的解法有图像法、区间法、高斯消元法等。
(1)图像法:通过绘制函数图像,分析不等式的解集。
(2)区间法:根据不等式的性质,确定解集的区间。
(3)高斯消元法:将不等式转化为方程组,利用消元法求解。
三、验证结果,确保正确性解方程应用题的最后一步是验证结果,确保求解的正确性。
将求得的解代入原方程,检验是否满足题目的要求。
总结:解方程应用题需要我们具备较强的逻辑思维和分析能力。
通过以上介绍的解题技巧,相信您在解决这类问题时会更有信心。
数学应用题目的解法

3、根据等量关系列出方程
4、解方程。此时我们可能会遇到二个未知数,而只能列出一个方程,我们就要看看是不是还有隐含条件,比如人数、物体的个数,都要是正整数,这就是隐含条件,尤其在不等式方程中要用到。还有就是分式方程要验根
5、写清单位和答话。这一步往往被忽视,其实这一步恰恰反映出你是否读懂了题目,是否知道题目要求的是什么,在考试中是要站分数的。
那么根据题意
2a-16=1/2×(a+16)-3
4a-32=a+16-6
3a=42
a=14
那么乙队原来有14人,甲队原来有14×2=28人
现在乙队有14+16=30人,甲队有28-16=12人
4、已知某商店3月份的利润为10万元,5月份的利润为13.2万元,5月份月增长率比4月份增加了10个百分点.求3月份 的月增长率。
1、读懂题意,把不相关的语言精简掉,现在应用题考得不是数学,而是语文的阅读能力,还要有转化问题的能力。
2、巧设未知数。一道应用题中可以把几个量都设为未知数,但是哪一个更为简便,要仔细斟酌。例如:甲乙二人速度之比为3:2,在求甲乙的速度时,我们可以设甲的速度为a千米/小时,乙为b千米/小时,这就是二元一次方程组;或者设甲的速度为a千米/小时,则乙为2/3a千米/小时,这样虽然是一元一次方程,但是有分数;或者设甲的速度为3a千米/小时,乙的速度为2a千米/小时
125a=350
a=2.8小时
ቤተ መጻሕፍቲ ባይዱ
2.一辆汽车以每小时40km的速度由甲地开往乙地,车行3h后,因遇雨,平均速度被迫每小时减少10km,结果到乙地比预计的时间晚了45min,求甲 乙两地距离。
高三数学万能解题法

高三数学万能解题法
高三数学万能解题法
①特值检验法:对于具有一般性的数学问题,我们在解题过程中,可以将问题特殊化,利用问题在某一特殊情况下不真,则它在一般情况下不真这一原理,达到去伪存真的目的。
②极端性原则:将所要研究的问题向极端状态进行分析,使因果关系变得更加明显,从而达到迅速解决问题的目的。
极端性多数应用在求极值、取值范围、解析几何上面,很多计算步骤繁琐、计算量大的题,一但采用极端性去分析,那么就能瞬间解决问题。
③剔除法:利用已知条件和选择支所提供的信息,从四个选项中剔除掉三个错误的答案,从而达到正确选择的目的。
这是一种常用的方法,尤其是答案为定值,或者有数值范围时,取特殊点代入验证即可排除。
④数形结合法:由题目条件,作出符合题意的图形或图象,借助图形或图象的直观性,经过简单的推理或计算,从而得出答案的方法。
数形结合的好处就是直观,甚至可以用量角尺直接量出结果来。
⑥顺推破解法:利用数学定理、公式、法则、定义和题意,通过直接演算推理得出结果的方法。
⑦逆推验证法(代答案入题干验证法):将选择支代入题干进行验证,从而否定错误选择支而得出正确选择支的方法。
⑧正难则反法:从题的正面解决比较难时,可从选择支出发逐步逆推找出符合条件的结论,或从反面出发得出结论。
⑨特征分析法:对题设和选择支的特点进行分析,发现规律,归纳得出正确判断的方法。
⑩估值选择法:有些问题,由于题目条件限制,无法(或没有必要)进行精准的运算和判断,此时只能借助估算,通过观察、分析、比较、推算,从面得出正确判断的方法。
高三数学中的常见解题思路

高三数学中的常见解题思路在高三数学学习的过程中,解题是我们最常面对的任务之一。
为了提高解题的效率和准确性,我们需要掌握一些常见的解题思路和方法。
在本文中,将介绍几种常见的解题思路,并结合实例进行说明。
一、代数解题思路代数解题是数学学科中最常见的解题方式之一。
通过代数方法,我们可以将问题转化为方程或不等式,并通过求解方程或不等式得到问题的答案。
例如,有一个求解方程的问题:已知一根绳子长 1.5米,折成两段,其中一段是整根绳子长度的2/5,求另一段的长度是多少?解题思路:设另一段的长度为x,则有2/5 * 1.5 = x,可得x = 3/5米。
二、几何解题思路几何解题是高三数学中另一个常见的解题方式。
通过几何图形的性质和定理,我们可以推导出问题的解答。
例如,有一个几何解题的问题:在直角三角形ABC中,已知AB = 3,BC = 4,求AC的长度。
解题思路:根据勾股定理,直角三角形斜边的平方等于其他两边的平方和,即AC^2 = AB^2 + BC^2,代入已知数据得AC^2 = 3^2 + 4^2,计算可得AC = 5。
三、函数解题思路函数解题是高三数学中的一种重要解题方式。
通过建立数学模型,利用函数的性质和特点来解决问题。
例如,有一个函数解题的问题:已知函数y = x^2 - 3x + 2,求其图象与x轴的交点坐标。
解题思路:当函数与x轴的交点坐标时,函数值等于0,即求解方程x^2 - 3x + 2 = 0。
通过求解方程可得x = 1和x = 2,故图象与x轴的交点坐标为(1,0)和(2, 0)。
四、概率解题思路概率解题是高三数学中常见的解题方式之一。
通过概率的计算和统计,我们可以解决与随机事件相关的问题。
例如,有一个概率解题的问题:甲、乙、丙三人分别从同一袋子中随机取球,袋子里有红球和蓝球,甲先取球,取出红球的概率为1/2,乙再取球,取到红球的概率为1/3。
已知最后丙取球,取到红球的概率为1/4。
解高考数学应用题方法

解高考数学应用题方法先同后异。
先做同科同类型的题目,思索比较集中,知识和方法的〔沟通〕比较容易,有利于提升单位时间的效益。
高考题一般要求较快地进行"兴奋灶'的转移,而"先同后异',可以避免"兴奋灶'过急、过频的跳跃,从而减轻大脑负担,坚持有效精力。
先小后大。
小题一般是信息量少、运算量小,易于把握,不要轻易放过,应争取在大题之前尽快解决,从而为解决大题赢得时间,创造一个宽松的心理基矗5.先点后面。
近年的高考数学解答题多浮现为多问渐难式的"梯度题',解答时不必一气审到底,应走一步解决一步,而前面问题的解决又为后面问题准备了思维基础和解题条件,所以要步步为营,由点到面。
先高后低。
即在考试的后半段时间,要注重时间效益,如估计两题都会做,则先做高分题;估计两题都不易,则先就高分题实施"分段得分',以增加在时间不够前提下的得分。
2应用题方法一第一关,事理关。
明白问题说了什么事,学会数学应用的建模分析。
第二关,文理关。
阅读理解关,一般数学应用题的文字阅读时事刊物较大,通过审题找出关键词和句,并理解其意义。
第三关,数理关。
用恰当的数学方法去解数学模型。
上述"三关'的突破口在于阅读与转译。
建议从三个方面入手:第一、划分题目的层次。
鉴于应用题题目篇幅长,信息容量大,阅读时有必要划分段落层次,弄清每一层次独立的含义和互相间的关系;第二、体会关键词语。
题目中不免出现一些专业术语或新名词,有的词语采纳即时定义来解释,认真阅读,认真领会即时定义的内涵和外延,是解决问题的关键;第三、弄清题图联系。
认真阅读题目,弄清题目条件与图形元素间的对应关系,也是审题过程中不可缺少的环节;第四、重视条件转译。
将题设材料浮现的文字语言、图形语言转化为符号语言。
3应用题方法二解读:领会题意,并将生活、生产中的语言,译成数学语言;建模:依据题目要求,建立恰当的数学模型,并注意对变量的限制条件;解模:对已经数学化了的问题,用数学方法处理,求出答案;验核:讲述学问替代入实际问题检验,舍去不合理的解,并作答。
应用题的算术解法与代数解法的联系

应用题的算术解法与代数解法的联系应用题指的是以一定条件和背景下给出的需要通过一定方法求解问题的比较复杂的数学题目,它与数学模型相关,解决应用题的解法一般有算术解法和代数解法两种,其中,算术解法是以实际意义为主,而代数解法是以理论研究为主。
首先,算术解法是指在解决应用题时采用的一种以实际意义的方法,即一般采用算法把题目简化成可计算的步骤,从而得出正确的结论,例如当解决分数四则运算和求根式的问题时,采用算术解法可把复杂的问题简化为可计算的步骤,从而得出正确的结果。
此外,它还可以把复杂的问题转化为更简单的问题,把整体问题变为一个个局部问题来解决,从而实现数学思维,这一点是代数解法所不能及的。
其次,代数解法指的是在解决应用题时采用的一种以理论研究为主的方法,即采用合理的符号系统将问题表达成一定的代数形式,经过推导,由于满足一定条件,得出结论,从而解决问题,例如求聚合物的分子式时,可采用代数解法将复杂的问题表达成一定的代数形式,经过多重条件和推导,得出分子式,从而解决问题。
此外,由于基于多重条件和推导,所得到的解也可以帮助研究更多抽象的数学模型,这一点是算术解法所不能及的。
因此,即使算术解法和代数解法两种解决应用题的方法有一定的差异,但它们具有很大的共性,即都是基于一定的条件和模型,以一定的符号系统和方法研究应用题,从而得出正确的结论。
此外,在求解应用题的过程中,也不宜单独采用一种解法,而要结合两种解法的结合,才能很好地解决问题。
总之,算术解法和代数解法都是解决应用题的重要方法,它们各有利弊,二者共同构成了解决应用题的完整系统。
虽然算术解法偏重于实际意义,而代数解法偏重理论研究,但它们在解决应用题中也有着较大的共性,因此在解决应用题时,要结合以上两种解法的结合,才能够更好地解决问题。
高三数学解答题解析

高三数学解答题解析在高三数学学习中,解答题是一个关键部分,要求学生能够运用所学知识,准确地解决问题。
本文将通过具体案例分析,详细解析高三数学解答题的解题思路和方法。
案例一:解析一元二次方程的解求解方法题目:已知一元二次方程x^2 - 5x + 6 = 0,求方程的解。
解析:对于一元二次方程,我们有多种方法来求解。
一种常用的方法是配方法。
步骤一:观察方程的形式,发现方程的三项系数分别为1,-5,6。
根据配方法,我们需要找到两个数,它们的和为-5,乘积为6。
步骤二:根据上述条件,我们可以得出这两个数为-2和-3。
即-2 + (-3) = -5,(-2) * (-3) = 6。
步骤三:使用配方法重写方程,并根据因式分解的原理化简方程。
(x - 2)(x - 3) = 0步骤四:根据零因子法则,得出方程的解x = 2和x = 3。
因此,方程x^2 - 5x + 6 = 0的解为x = 2和x = 3。
案例二:解析概率的计算方法题目:一个有10个红球和5个蓝球的袋子,从中随机取出两个球,求取出的两个球一个红一个蓝的概率。
解析:对于概率的计算,我们需要根据所给条件,确定事件的总数和有利事件的数目。
步骤一:袋子中总共有15个球,所以从中取出两个球的总数为C(15, 2)。
步骤二:确定有利事件的数目。
从10个红球中取出一个,从5个蓝球中取出一个,即可得到一个红球一个蓝球的组合数目为C(10, 1) * C(5, 1)。
步骤三:根据概率的计算公式,概率 = 有利事件的数目 / 总事件的数目。
概率 = C(10, 1) * C(5, 1) / C(15, 2)步骤四:根据组合公式计算,并化简得概率值。
概率 = 10 * 5 / (15 * 14 / 2)概率 = 1/3因此,取出的两个球一个红一个蓝的概率为1/3。
综上所述,我们通过两个具体的案例,对高三数学解答题的解题思路和方法进行了详细解析。
通过合理运用所学知识和方法,我们可以准确解答各种数学问题,提高数学解答能力。
分数的应用题六种解法

分数的应用题六种解法分数是数学中常见的表示比例和部分的方式,它在生活中的应用也非常广泛。
今天,我将为大家介绍六种解决分数应用题的方法。
一、画图法画图法是一种直观的解题方法。
以某个具体的例子来说明。
假设小明有2/3的巧克力,小红有1/4的巧克力,他们想将巧克力平均分配。
我们可以画两个巧克力盒,并按比例将巧克力分配给小明和小红。
这样,他们就可以直观地理解分配的过程。
二、找最小公倍数解决一些关于分数的应用题时,我们需要找到最小公倍数。
例如,小明每天按照1/5的速度走路,小红按照1/3的速度走路,他们同时从同一个地方出发,问多少天后他们会在同一个地方相遇。
我们可以找到1/5和1/3的最小公倍数,即15。
因此,他们将在15天后相遇。
三、转化为整数运算有些分数应用题可以转化为整数运算来解决。
例如,小明用1/2小时完成作业,小红用1/3小时完成同样的作业,问他们两人一起完成这个作业需要多长时间。
我们可以将1/2和1/3转化为分母的最小公倍数,即6。
因此,他们一起完成这个作业需要1/6小时。
四、比较大小在比较大小的应用题中,我们需要将两个或多个分数进行比较。
例如,小明用2/5的时间做数学题,用1/4的时间做英语题,问他用了更多的时间做数学题还是英语题。
我们可以将2/5和1/4的分母取相同的最小公倍数,即20。
然后比较分子的大小,即2和5,得出结论小明用了更多的时间做数学题。
五、分数的加减运算在分数的加减运算中,我们需要将分母相同的分数进行运算。
例如,小明走了3/5的路程,小红走了2/5的路程,问他们总共走了多少路程。
我们可以将3/5和2/5的分母取相同的最小公倍数,即5。
然后将分子相加,得到答案5/5,即1。
因此,他们总共走了1个路程。
六、分数的乘除运算在分数的乘除运算中,我们需要将分子进行运算,再将分母进行运算。
例如,小明用2/3小时做完一个作业,小红用3/4小时做同样的作业,问小红完成这个作业需要多长时间。
二次函数应用题的解法技巧

二次函数应用题的解法技巧
二次函数是高中数学中重要的内容之一,其应用广泛且实用。
本文将介绍几种解决二次函数应用题常用的技巧,帮助您更好地理解和解答相关问题。
技巧一:建立方程
遇到二次函数应用题时,首先要根据题目中给出的条件建立出相应的二次函数方程。
通常情况下,题目会提供函数的某些特征,如顶点、焦点、与坐标轴的交点等。
根据这些信息,可以利用二次函数的标准形式或顶点形式来建立方程。
技巧二:分析函数图像
了解二次函数的图像特点对解题非常有帮助。
通过分析二次函数的开口方向、顶点位置以及与坐标轴的交点等信息,可以得到一些重要的线索。
例如,若二次函数开口朝上,那么函数图像在顶点处达到最小值;若开口朝下,则函数图像在顶点处达到最大值。
技巧三:利用性质和定理
二次函数有许多重要的性质和定理,掌握它们能够快速解决问题。
比如,二次函数的对称轴是过顶点且垂直于x轴的直线,利用对称性可以快速求出函数图像的其他点;其次,利用判别式可以判断二次方程的根的情况,从而确定函数与x 轴的交点。
技巧四:代入验证
为了验证解得的答案是否符合题意,可以将解代入原方程中进行验证。
如果经过计算后两边相等,则说明解是正确的;如果不相等,可能是解答过程中出现了错误或漏解的情况。
技巧五:多做练习
掌握二次函数应用题的解法,需要多做一些练习。
通过不断的练习和思考,积累经验,掌握一些常见的模型和解题方法,培养自己的数学思维和分析能力。
通过掌握以上技巧,相信您能够更加轻松地解决二次函数应用题。
数学是一门需要不断实践和思考的学科,希望您可以多多练习,不断提升自己的数学水平!。
高三数学课程教案应用题解题方法与技巧

高三数学课程教案应用题解题方法与技巧在高三数学课程中,应用题是学习的重点之一。
应用题与纯粹的运算题相比,更加注重学生对数学知识的灵活运用和问题解决能力的培养。
在解题过程中,掌握一些方法和技巧可以有效提高解题的效率和准确性。
本文将针对高三数学课程中的应用题解题方法与技巧进行探讨。
一、理清问题背景与要求在解决任何应用问题之前,首先要仔细阅读问题,理解问题背景和要求。
要明确问题中给出的条件,并将其画成图表或列成方程,以帮助我们更好地理清思路。
二、找到问题的关键信息在应用题中,常常存在很多无关的信息,我们需要通过筛选找到关键的信息。
我们要通过将问题进行拆解和归纳,找到问题的本质和核心,才能更好地建立数学模型和解决问题。
三、建立数学模型在解决应用题时,我们需要将问题抽象化,建立数学模型。
通过数学符号和方程,将问题转化为数学的语言,从而更好地利用数学知识解决问题。
在建立数学模型的过程中,我们还可以运用一些常见的数学模型和解题方法,例如函数模型、几何模型等。
四、解决数学模型在建立好数学模型后,根据问题的要求进行运算求解。
在解题过程中,应充分发挥已学的数学知识和技巧。
例如,代数方程的解法、几何图形的性质等。
同时,我们也要注意解题步骤的逻辑性和合理性,避免漏解和错误的推理。
五、检查与思考在解决应用题后,我们要进行检查以确保解答的正确性。
对解答中的数值进行估算,并与问题的要求进行对照。
如果解答与要求相符,说明解答正确;如果解答与要求不符,要仔细检查解答过程中是否有错误。
六、总结归纳解决完应用题后,我们要对解题过程进行总结归纳。
回顾解题的整个过程,思考解题中遇到的困难和问题,并找出解决方法。
只有通过总结归纳,我们才能将解题过程中的经验和技巧运用到今后的学习中,提高自己的解题能力。
综上所述,高三数学课程中的应用题解题方法与技巧是非常重要的。
通过理清问题背景与要求、找到关键信息、建立数学模型、解决数学模型、检查与思考以及总结归纳,我们能够更好地解决应用题并提高解题的效率和准确性。
高考数学解题的12种方法

高考数学解题的12种方法
1. 找准问题的关键点,归纳问题的要点和条件,分析问题的结构和性质,选择合适的解题方法。
2. 利用同种题目的解题思路、解题技巧,加速解题过程。
3. 运用代数方法,通过建立方程或不等式来解决问题。
4. 运用几何方法,通过画图、利用几何性质等方式解决问题。
5. 运用数列和级数的性质,通过数学归纳法或递推公式来解决问题。
6. 运用函数的性质,通过函数的图像、函数的变换等方式解决问题。
7. 运用概率和统计的方法,通过计算概率、分析统计数据等方式解决问题。
8. 运用数论的方法,通过分解因式、最大公约数、最小公倍数等方式解决问题。
9. 运用组合数学的方法,通过排列组合、选择判断等方式解决问题。
10. 运用解析几何的方法,通过坐标轴、向量等几何工具解决问题。
11. 运用微积分的方法,通过求导、求积分等方式解决问题。
12. 运用图论的方法,通过图的模型、路径分析等方式解决问题。
高中数学应用题解题技巧

高中数学应用题解题技巧自从升入高中,数学成为许多高中同学的困扰,为此整理了高中数学应用题解题技巧,供同学们参考。
高中数学应用题大致可分四类:纯文型、图文型、表文型、改错型。
无论哪种类型高中数学应用题,其解题技巧一般都可分为以下几步:高中数学应用题解题技巧把握大意在阅读高中数学应用题时不仅要特别留心短文中的事件情景、具体数据、关键语句等细节,还要注意问题的提出方式。
据此估计是我们平常练习时的哪种类型,会涉及到哪些知识,一般是如何解决的,在头脑中建立初步印象。
高中数学应用题解题技巧提炼信息在阅读高中数学应用题的过程中不仅要注意各个关键数据,还要注意各数据的内在联系、标明单位,特别是一些特殊条件(如附加公式),以简明的方式列出各量的关系,掌握提炼信息的数学解题技巧。
点击查看:高中数学解题技巧高中数学应用题解题技巧总结信息根据前面提炼的高中数学应用题信息分析,通过文中关键词、句的提示作用,联想数学应用题间的关系,将数学应用题中的各种已知量用数学符号准确地反映出其内在联系。
高中数学应用题解题技巧回顾检查在建立好数学应用题解题思路后,不要急于解决问题,而应回过头来重新审题,一是看看哪些数据、关系还没有用上,用得是否准确,要充分挖掘题中的条件并发挥它高中数学应用题解题技巧1、仔细审高中数学应用题2、重视高中数学应用题中的关键词语、条件,对题意的理解有偏差。
4、善于回顾反思,及时发现问题纠正错误,克服侥幸意识带来不必要的失误。
5、平时要重视数学题阅读、理解和表述能力的培养,要仔细梳理问题的脉络结构,培养良好的思维习惯。
以上是高中数学应用题解题技巧由整理,更多高中数学解题技巧请关注。
推荐你继续浏览:文科女生必备的高中数学公式有哪些高中数学三角函数常用公式大全高中数学常用公式汇总文科女生如何学好高中数学高中数学无耻得分法有哪些女生如何学好高中数学。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
365下载
[填空题]在划片时与布边平行的线叫()。 [单选]“我会尊重患者告诉我的一切秘密,即使患者已经死去”。此话出自()。A.东京宣言B.夏威夷宣言C.日内瓦宣言D.赫尔辛基宣言E.希波克拉底誓言 [单选,A2型题,A1/A2型题]关于β2-微球蛋白叙述错误的是().A.存在于所有有核细胞表面尿液B.患炎症及肿瘤时血浆中浓度可降低C.β2-微球蛋白主要用于监测肾小管功能D.急性白血病有神经浸润时,脑脊液中β2-微球蛋白可增高E.肾移植后如排斥反应影响肾小管功能时,尿液&beta [单选]引起牙龈炎最主要的细菌是()A.革兰阳性杆菌B.革兰阴性杆菌C.螺旋体D.衣原体E.粘性放线菌 [单选]在仪表专业中,现场压力变送器常常用符号PIT表示,其中I表示()。A、电流B、压力C、电压D、带指示功能 [名词解释]芽的晚熟性 [单选,A1型题]含大量结核杆菌的病灶是()A.渗出性病变B.干酪样坏死及液化C.结核球D.钙化灶E.结核结节 [名词解释]防止“八”字方针 [单选]女性一生各阶段的生理特点,下列哪项描述不恰当?()A.儿童期儿童体格及内外生殖器同时发育B.月经完全停止1年以上为绝经C.子宫内膜周期性脱落及出血,标志生殖功能成熟D.围绝经期一般历时10余年E.月经初潮,标志青春期开始 [单选]对以下()项权利侵犯后的损害赔偿不属于国家赔偿范围。A.财产权B.生命健康权C.政治权利D.人身自由权 [问答题]被困在室内应如何保护自己? [单选]同步数字体系(SDH)信号中,最基本.最重要的模块信号是()。A.STM-1B.STM-4C.STM-16D.STM-32 [单选]关于现代出版业行业用语“页”“面”“页码”的说法,错误的是()。A."页码"用于标注书页的张数B."1页"就是"1张"C.任何一种书刊的面数都是偶数D.出版业务中应尽量用"面"表示书页数量 [单选]在NH3、HNO3、H2SO4的工业生产中,具有的共同点是()。A、使用吸收塔设备B、使用尾气吸收装置C、使用H2作原料D、使用催化剂 [单选]“夫百病之始生也,皆生于风雨寒暑,清湿喜怒”之“ห้องสมุดไป่ตู้湿”是指()。A.湿邪B.风湿C.痰湿D.寒湿E.湿热 [单选]修船质量的好坏,关系着船舶的使用寿命和经济性,因此,必须抓好修理前的()、修理时的监修和修理后的验收三个主要工作环节,以确保短修期、低修费、高质量的船舶修理。A.安排B.人员分工C.计划D.准备 [单选,A2型题,A1/A2型题]血浆中分子量最大的蛋白质是().AACB.HpC.AMGD.CERE.CRP [单选]下列与SLE病情活动性无关的实验室检查是()。A.血清C3、C4下降B.细胞数正常C.抗dsDNA抗体升高D.蛋白尿增多E.红细胞沉降率加快 [单选,B1型题]慢性胰腺炎引起的腹泻属于()A.分泌性腹泻B.渗透性腹泻C.渗出性腹泻D.吸收不良性腹泻E.肠蠕动增强性腹泻 [单选]某地提供A、B、O、AB血型人数分布的数据是()A.数值变量资料B.无序分类资料C.有序分类资料D.等级分类资料E.圆形分类资料 [单选]矿井中硫化氢最高允许浓度为()。A、0.0005%B、0.0024%C、0.00066% [单选]中国营养学会建议哺乳妇女每天摄人钙()A.800mgB.1000mgC.1200mgD.1500mgE.2000mg [单选]目前,生产部门大量采用地球化学分析的方法,来()认识生油气层。A.估计B.定性C.定量D.线性 [单选]()是指上级管理者所直接领导下级人员的数量。A.管理幅度B.组织构成C.组织规模D.组织形成 [填空题]我国电网的频率为(),直流电的频率为()。 [单选,A2型题,A1/A2型题]下列哪一组症状不属于湿温卫气同病证的表现?()A.发热恶寒,无汗头痛B.头痛如裹,身重酸困C.肢体酸楚,口渴心烦D.小溲黄赤,脘痞E.苔腻,脉濡数 [问答题,简答题]装置进退油流程改通? [单选]《出境水生动物养殖场,中转场检验检疫注册登记证》有效期为()年。A.1B.2C.3D.5 [单选]雨期填筑路堤需借土时,取土坑距离填方坡脚不宜小于()。A.0.8mB.1mC.2mD.3m [单选]建设工程合同管理的特点主要是由()的特点决定。A.管理制度B.招标方式C.建设项目D.工程合同 [单选]风心病二尖瓣狭窄患者发生心房颤动后常见的并发症是().A.心源性脑缺血综合征B.动脉栓塞C.肺部感染D.感染性心内膜炎E.完全性房室传导阻滞 [单选]脑对冲伤的好发部位为()A.枕叶B.顶叶C.小脑半球D.额极、颞极、额底和颞底E.大脑半球内侧面近大脑镰处 [单选]在电路中,()起到把用电器与电源接通或断开的作用。A、电源B、导线C、电器D、开关 [单选,A2型题,A1/A2型题]下列哪项是释放PTH所必需的()。A.钾离子B.氯离子C.镁离子D.钙离子E.钠离子 [单选,A2型题,A1/A2型题]《医疗机构从业人员行为规范》适用于那些人员?()A.医疗机构的医生、护士、药剂、医技人员B.医疗机构的医护及后勤人员C.医疗机构的管理、财务、后勤等人员D.药学技术人员E.医疗机构内所有从业人员 [单选,A型题]具有清热解毒,凉血止痢功用的方剂是()A.白头翁汤B.芍药汤C.葛根芩连汤D.黄连解毒汤E.槐花散 [单选]对肾上腺外嗜铬细胞瘤进行观察时,下列哪项说法不正确A.肾上腺外嗜铬细胞瘤最常出现的部位是肾门附近B.位于肾门前面的肿瘤,肠气干扰较多,应用力挤压腹部排除肠气以便观察C.从背部检查,肾门前方肿瘤易于显示D.肾门下方肿瘤,往往推挤肾下极,使肾下极外移,肾纵轴改变E.肾 [单选,A1型题]下列与社会病的特点无关的是()A.社会病必须具有公共性B.社会病的防治需要全社会共同的努力C.社会病对社会具有严重的危害性D.社会病的产生根源非常复杂,但主要在于社会E.社会病的产生根源非常复杂,但主要在于家庭 [单选,A1型题]以下表示疾病严重程度的统计指标是()。A.2周每千人患病人数及患病次数B.健康者占总人口百分数C.每千人患慢性病者人数及患病次数D.患病者人数占总人口百分数E.2周每千人因病休工(学)人数及天数 [单选]对不能再上部刷方减重的滑坡体,为了防止滑坡常用的措施是()。A.在滑坡体上方筑挡土墙B.在滑坡体坡脚筑抗滑桩C.在滑坡体上部筑抗滑桩D.在滑坡体坡脚挖截水沟
