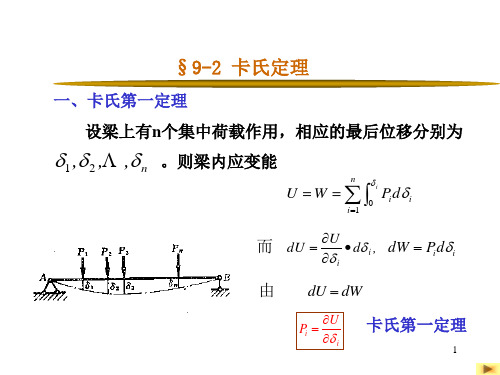
卡氏第一定理
合集下载
材料力学能量法第3节 卡式定理
q 2 M ( x) (l x) M e 2
M 1 M e
（2）计算 B 截面转角 B
M q 2 1 M ( x) (l x) M e M e 2 M ( x) M ( x) Bq M e dx EI M e 1 l q 2 [ ( l x ) M ] ( 1 ) d x e EI 0 2 3 l ql 顺时针转向 Me EI 6 ql 3 顺时针转向 B 令 Me 0 6 EI
2
1 dFi dyi U dFi yi 2
(3)
比较(2)(3)式
1 dFi dyi U dFi yi (3) 2 U ( F1 , F2 , Fn ) yi i 1,2,3,... Fi
U U dFi Fi
(Hale Waihona Puke 2)梁的变形能对某一载荷 Fi 的偏导数，等于 在该载荷处沿载荷方向的位移，这就是卡氏定理， 也称卡氏第二定理。由意大利工程师 A 卡斯蒂利亚 诺（1847-1884）于1873年提出的。卡氏定理对其他 线弹性结构也是适用的。
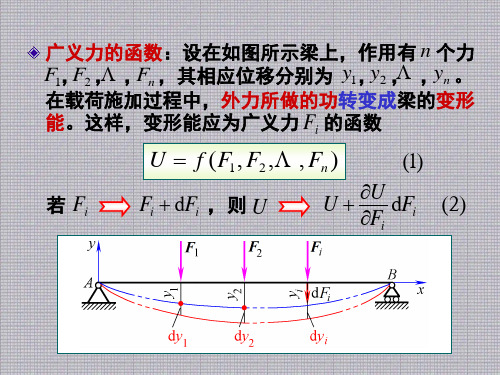
广义力的函数：设在如图所示梁上，作用有 n 个力 y2 ， ， yn 。 F1， F2 ， ， Fn ，其相应位移分别为 y1， 在载荷施加过程中，外力所做的功转变成梁的变形 能。这样，变形能应为广义力 Fi 的函数
U f ( F1, F2 ,, Fn )
若 Fi
(1) ( 2)
Fi dFi ， 则 U
U U dFi Fi
卡式定理的推导 —— 改变加力的次序 (1)先施加 dFi ：在施加 dFi 时，其作用点沿 dFi 方向的 1 dF dy 位移为 dyi ，梁的变形能为 i i；
能量法
1
3Eh2 10GL2
It is therefore customary in engineering practice to neglect the effect of shear in computing the strain energy of slender beams.
F 广义力
1
广义位移
基本变形下杆的应变能：（线弹性范围内）
F
V
1 2
Fl
FN2l 2EA
l
FN2 x dx
2EA
Me
V
1 2
M e
T 2l 2GI P
T 2 xdx
l 2GIP
M
V
1 M
2
M 2l 2EI
横力弯曲
M 2 x dx
2EI 0
2GI p 0
4EI 4GI p
外力功
V
W
1 2
P
A
A
PR3
2EI
3PR3
2GI p
互等定理 (Reciprocal theorems)
1. 功的互等定理
设有两组外力F1和F2分别作用于同一线弹性结构上，如 图所示，(a)、(b)分别称为结构的第一状态和第二状态。
F1 Δ11 1
F1 dF
0
线弹性范围内：
1
1
Vc
V
F 2
➢ 余能仅具有与应变能相同的量纲，无具体 的物理意义。线弹性材料，余能数值上等 于应变能，应区分两者的概念。
应变能的普遍表达式
材料力学卡式定理
l
(2)
于是(1)式改写为
y / l
(3)
3
梁内任一点处的比能
u
1 2
E 2
1 2
E 2
l2
y2
(4)
梁的应变能
l
U VudV 0 (AudA)dx
l 1 E 2
( 02
l2
y2dA)dx 1 EI 2
A
2l
(5)
由卡氏第一定理
m U 1 EI (2 ) EIθ
(6)
2 lx)
2
dx
1 ( 5PL3 RC L3 ) 0
EI 48
3
RC
5P 16
能量法求解超静定结构，适 用任意荷载作用下、线性或 非线性弹性杆系、刚架或曲 杆等超静定系统。
14
2.求 wB
① 求内力
M
AB ( x)
5P 16
(L
x)
P(0.5L
x)
M BC ( x)
5P 16
Px L EI Px
1 EI
x 0
P(L
x1 ) ( x1
x)dx1
P
x3 [
(L
x)x2
Lx 2 ]
EI 3
2
12
例6 等截面梁如图，用卡氏定理求B 点的挠度。
P 0.5 L
B
A
L
解：1.依 wC 0 求多余反力，
卡氏定理解 ① 取静定基如图 C 超静定结构
② 求内力
M AB ( x) RC (L x) P(0.5L x)
L x1
O
x
w
①求内力 M AB ( x1) P(L x1) Px ( x x1) M BC ( x1) P(L x1)
材料力学第三章 能量法
三、卡氏第二定理（线弹性体）
Di
Vc Fi
在线弹性范围内
余能定理 Vc V
Di
V Fi
卡氏第二定理： 线弹性杆件或杆系的应变能对于 作用在该杆件或杆系上的某一荷 载的变化率，就等于与该荷载相 应的位移。
卡氏第二定理适用于一切受力状态下的线弹性体。
卡氏第二定理公式D及i 含义VF：i
若结构的应变能 V 表示为F1、F2 …Fi …的函数，则应变 能对任一载荷Fi的偏导数等于Fi作用点沿Fi方向位移。
C
与需求位移相应的虚设外力
F。求偏导后令其为零。
（2）列弯矩方程
M
x
F 2
ql 2
x
qx 2 2
0
x
l 2
M
x
F 2
ql 2
x
qx 2 2
0
x
l 2
（3）求梁的应变能
M 2 l/2
x
1
V 2 0
dx
2EI
EI
l/2
0
F 2
ql 2
x
qx 2 2
2 dx
1 EI 1 EI
V W
一、杆件基本变形的应变能
(一)轴向拉伸(压缩)
1、杆的应变能
轴力沿轴线不变的情况:
dW Fd(Dl) W Dl1 Fd(Dl) 0
线弹性范围内 W 1 FDl
1
2
V
F
W
FN
2
F Dl Dl
FNl EA
应变能
V
FN2l 2EA
F
l
Dl
F
Dl d (Dl)
Dl1
Dl
(一)轴向拉伸(压缩)
华中科技大学工程力学(841)2001-2005年考研真题
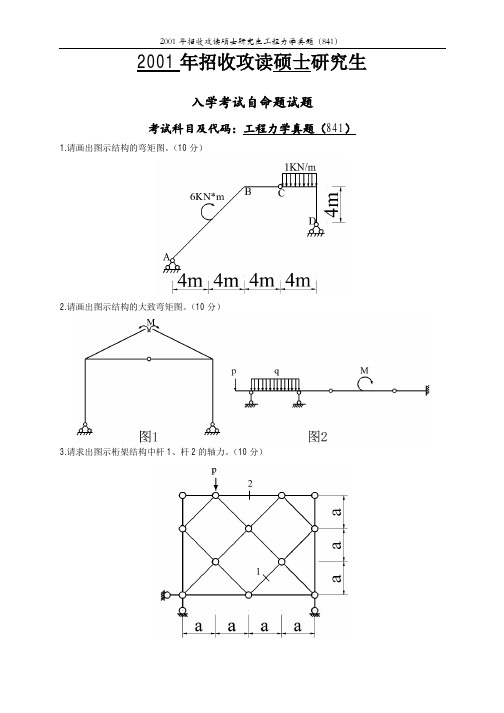
2001年招收攻读硕士研究生入学考试自命题试题考试科目及代码：工程力学真题（841）1.请画出图示结构的弯矩图。
（10分）2.请画出图示结构的大致弯矩图。
（10分）3.请求出图示桁架结构中杆1、杆2的轴力。
（10分）4.请求出图示结构C点的竖向位移。
（10分）5.请求出图示结构D点的竖向位移。
（10分）6.请用力法画出图式结构的弯矩图。
（10分）7.请用位移法计算图示结构并画出弯矩图。
(10分)8.请求出图示结构、的影响线。
（10分）9.请求出图示结构的等效荷载列阵。
（10分）10.请求出图示结构的整体刚度矩阵。
（10分）2002年招收攻读硕士研究生入学考试自命题试题考试科目及代码：工程力学真题（841）第一部分：材料力学（150分）一、填空题。
（每小题4分，共20分。
）1.两端受拉力P的等直杆，截面积为A，长为L,弹性模量为E，其应变能为_______。
2.长为L、抗弯刚度为EI的两端铰支的等截面细长中心受压直杆临界力的欧拉公式为______。
3.某点处的三个主应力分别为、和，材料的弹性模量和泊松比分别为E和,则该点处的体积应变为_________。
4.受扭矩T的薄壁圆筒（壁厚为t，平均半径为），其横截面上的应力为__________。
5.外径为2d,内径为d的圆环的横面惯性矩为_____________。
二、简答题。
（每小题4分，共20分）。
1.何谓温度应力？何种情形下会产生温度应力？2.试述弯曲的概念。
何谓对称轴弯曲？3试述剪应力互等定理。
4.为什么脆性材料的安全系数取值比塑料性材料的安全系数取值大？5.试述第三强度理论。
三计算题。
（４小题，共８０分）。
１.（１５分）试求长为Ｌ，截面积为A的杆在拉力P作用下的余能。
材料在单轴拉伸时的应力——应变关系为σ=K√。
2.（15分）矩形基础长为L，宽为B，受单向偏心荷载P作用，作用点在矩形的长轴线上，偏心距为e，试求基础对地基土的最大压力和最小压力（忽略基础及其上土重）。
卡氏定理材料力学
2Ma 3EI
（
）
DF FD
CD段:
M (x)
Mx , 2a
M (x) F
x,
MC
CB段: M (x) M ,
M (x) 2a x, a F
2a
C
M
AB段: M (x) 0,
M (x) x, F
a
B
A FAx
（4）带入卡氏定理求解。
Dx
l
M (x) M (x) d x EI F
FAy
2a
MC, 在D截面虚设一水平力F 。 MC
DF
C
（2）取刚架为研究对象， a
受力图如图所示。
M
FD
FAx F
B
a
A FAx
FAy
FD
F
1 2a
(M
MC)
FAy
（3）分段列出弯矩方程及偏导方程。
2a
CD段:
MC
M
( x1 )
[F
1 2a
(M
MC
)]x1
Cx aM 2
x
1
DF FD
M (x1) F
新位移 i 上也做功，系统的总的应变能为
V
Fi
i
1 2
Fi
i
（2）
由（1）＝（2），并忽略二阶小量，得
V Fi
i
V Fi
i
若将结构的应变能表示为载荷F1，F2， ，Fn 的 函数，则应变能对任一载荷Fi的偏导数，等于Fi作用
点沿Fi作用方向的位移 i ,称为卡氏第二定理。
说明 （1）卡氏定理只适用线弹性结构。
i
V Fi
FN (x) FN (x) d x L EA Fi
材料力学期末考试总复习
F c r =
p
E I ( m l ) 2
2
压杆的稳定性条件
l = ml
i i = I A
s
c r
s =
F £ j A
[s ]
第十三章 能量法 变形能
Ve =
外力功(线弹性)
ò
l
2 F N ( x ) dx + 2 E A (x )
ò
l
T 2 (x ) dx + 2 G I p ( x )
图解法 内力图 应力圆
实验法 机械性质 电测
单元体应力 组合变形应力
五、基本公式
应力= 内力 截面几何量
内力×杆长 变形= 截面刚度
F s = N A FN l D L = EA
T t = r I p Tl j = GI p
M s = y I z
Ml q = EI z
A C D B
3、图示悬臂梁弯曲时，靠近固定端的一段与大半径刚性圆柱 面贴合，从此以后，随着F力增大，梁内的最大弯矩 (C) 。 (A)线性增大； (B)非线性增大； (C)保持不变； (D)开始减小。
F
4、T形截面铸铁梁，设各个截面的弯矩均为正值， 则将其截面按图 (A) 所示的方式布置，梁的强度最 高。
直线等加速
K d a = 1 + g
匀速旋转
s
d
落体冲击
2 h Kd = 1 + 1 + D st
水平冲击
K d = v 2 g D st
=
g w 2 D 2
g
轴向拉伸与压缩
1 (C)
2、已知材料的比例极限s P =200MPa,弹性模量E=200Gpa, 屈服极限 s s =240 MPa,强度极限s =400 MPa,则下列
第10章 能量法
M n ( x) = − Px
EI L x
2
P A O
U =
∫
[M n ( x)]
L
2 EI
P 2 L2 dx = 6 EI
∂U PL3 = ③求位移 δ A = ∂P 3EI
例5(续): 求 A点的转角 解： ①求弯矩 M n ( x) = −(M 0 + Px) ②求变形能
U =
EI L x
P A O
N1 = N 2 cos α = Pctgα , N 2 =
对每个杆内能
2 2
P sin α
2
L
A N1 α
2
P
U =∫
L
[ N ( x)] dx + [ M T ( x)] dx + [ M n ( x)] dx = N
2 EA
∫
L
2GI p
∫
L
2 EI
L 2 EA
C
对整个杆系内能 N 12 l1 N 22 l 2 1 U = + = W = P yc 2 E A1 2 E A2 2 1 ( Pctg α ) 2 l1 l2 P 2 Py c = + ( ) 2 2 EA 1 2 EA 2 sin α
δ1 δi δn
δ2
Fi
Fn
1 n U = ∑ Fiδ i 2 i =1
二. 互等定理
1.功互等定理 Fi δ′ = Fjδ′ji ij
i 力在 j 力引起的位移δ’ij上 做的功等于j 力在 i 力引起 的位移δ’ji上做的功。
Fi
δ i′
i
0 Fj j
δ i′
i Fi
0
δ ij ′
δ j′
EI L x
2
P A O
U =
∫
[M n ( x)]
L
2 EI
P 2 L2 dx = 6 EI
∂U PL3 = ③求位移 δ A = ∂P 3EI
例5(续): 求 A点的转角 解： ①求弯矩 M n ( x) = −(M 0 + Px) ②求变形能
U =
EI L x
P A O
N1 = N 2 cos α = Pctgα , N 2 =
对每个杆内能
2 2
P sin α
2
L
A N1 α
2
P
U =∫
L
[ N ( x)] dx + [ M T ( x)] dx + [ M n ( x)] dx = N
2 EA
∫
L
2GI p
∫
L
2 EI
L 2 EA
C
对整个杆系内能 N 12 l1 N 22 l 2 1 U = + = W = P yc 2 E A1 2 E A2 2 1 ( Pctg α ) 2 l1 l2 P 2 Py c = + ( ) 2 2 EA 1 2 EA 2 sin α
δ1 δi δn
δ2
Fi
Fn
1 n U = ∑ Fiδ i 2 i =1
二. 互等定理
1.功互等定理 Fi δ′ = Fjδ′ji ij
i 力在 j 力引起的位移δ’ij上 做的功等于j 力在 i 力引起 的位移δ’ji上做的功。
Fi
δ i′
i
0 Fj j
δ i′
i Fi
0
δ ij ′
δ j′
材料力学第8章-能量法3-1
d
FN dx d(l) = EA
0 N
Mdx d EI
0
Tdx d GI p
0 S 0
1 F d l M d F d T d
F FN T T M M dx dx dx EA EI GI p
0 N 0 0
2.力和位移应理解为广义力和广义位移。
能量法/虚功原理 单位力法 图乘法
上节回顾
1、可能内力,可能位移,虚位移 2、虚功原理
在外力作用下处于平衡的结构，任意给它一个虚位移， 则外力在虚位移上所做的虚功，等于结构内力在虚变形上所 作的功。
W Wi
* e
e
*
外力虚功
内力虚功
l
W
Fi
5 M a 3
0 1c
2 Fa a
M
0 2c
3 a 2
Fa a 3 2 2 0 M 3c a 3
能量法/虚功原理 单位力法 图乘法
A
EI1
a
C
EI 2
a
F B
1
2Fa Fa
1
2a 5a/3
2
3a/2
-
2a/3
3
根据图乘法，自由端的挠度为：
1 1 0 0 yB 1M1c 2 M 2c EI 3M 30c EI1 2 1 Fa a 5 3 1 Fa a 2a a Fa a a EI1 2 3 2 EI 2 2 3
能量法/超静定问题 力法 例 如图超静定梁, EI为常数,试求B点的约束反力。
第八章
一、杆件的应变能
卡氏第二定理
F3
F1
3 1
1 , 2 , , i ,
结构的变形能
11 1 V ε W 2 F 1 δ 1 2 F 2 δ 2 2 F 3 δ 3
只给 Fi 一个增量 Fi .
引起所有力的作用点沿力方向的位
移增量为 Δ1,δ Δ2,δ Δ3,δ
在作用Fi 的过程中, Fi 完成 F1
的功为
1 2
ΔFi
氏定理）（Castigliano’s Theorem）
说明 (Directions)：
（1）卡氏第二定理只适用于线性弹性体( Applying only to linearly elastic bodies）
δi
Vε Fi
（2）Fi 为广义力（generalized force） i为相应的位移
（displacement corresponding to force Fi )
一个力
一个力偶
一对力
一对力偶
一个线位移
一个角位移
相对线位移 相对角位移
（3）卡氏第二定理的应用 ( Application of castigliano’s second theorem ) （a） 轴向拉,压（Axial tension and compression）
δ i V F ε i F i F N 2 2 ( E x )x d A F E N (x )A F N F ( ix )d x
Δδi
原有的所有力完成的功为
2
F2
F3
3 1
F 1 Δ 1 F 2 δ Δ 2 δ F iΔ i δ
结构应变能的增量为
Δ ε 1 2 V Δ iΔ i F F δ 1 Δ 1 F δ 2 Δ 2 δ F iΔ i δ
12能量法_1应变能卡式定理互等定理
Vε CB FN 2 a q 2l 2 a 2EA 8EA
1 FN ql 2
2）由截面法，得梁的弯矩方程为 1 1 M x qlx qx 2 2 2 梁的应变能
Vε AB M 2 x dx l 2 EI l
1 1 qlx qx 2 2 2 5 2 dx q l 2 EI
再令Me =0，即得转角
ql 3 B 6 EI
[例5] 图示平面刚架，若各段杆的抗弯刚度均为EI，试求其自由端 C 截面的竖直位移ΔC V 与水平位移ΔC H 。
解：在这种情况下，可分别记竖直方向 的力F 为F1、水平方向的力F 为F2，在 符号上将两者区分开来。
在替换力的符号后，BC 段、AB 段的弯矩 方程及其偏导数分别为
1 EI
2 π M e R2 M e R 2 1 cos d 0 2 EI
π/2
第四节 互等定理
一、功的互等定理
对于线弹性结构，第一组外力在第二组外力所引起的位移上所作
的功等于第二组外力在第一组外力所引起的位移上所作的功，即
F112 F2 21
l
dx1
M x2 M x2 EI F1
l
dx2
1 l F1x1 x1 dx1 l F1l F2 x2 l dx2 EI
l3 4 1 F1 F2 EI 3 2
3. 梁和刚架
只考虑弯曲变形能
M2 Vε dx l 2 EI z
4. 组合变形杆
FN 2 T2 M2 Vε dx dx dx l 2 EA l 2GI l 2 EI p z
[例1] 试求下图所示结构的应变能。已知梁的抗弯刚度为EI，杆 的抗拉刚度为EA。 解：1）CB 杆的轴力 CB 杆的应变能
1 FN ql 2
2）由截面法，得梁的弯矩方程为 1 1 M x qlx qx 2 2 2 梁的应变能
Vε AB M 2 x dx l 2 EI l
1 1 qlx qx 2 2 2 5 2 dx q l 2 EI
再令Me =0，即得转角
ql 3 B 6 EI
[例5] 图示平面刚架，若各段杆的抗弯刚度均为EI，试求其自由端 C 截面的竖直位移ΔC V 与水平位移ΔC H 。
解：在这种情况下，可分别记竖直方向 的力F 为F1、水平方向的力F 为F2，在 符号上将两者区分开来。
在替换力的符号后，BC 段、AB 段的弯矩 方程及其偏导数分别为
1 EI
2 π M e R2 M e R 2 1 cos d 0 2 EI
π/2
第四节 互等定理
一、功的互等定理
对于线弹性结构，第一组外力在第二组外力所引起的位移上所作
的功等于第二组外力在第一组外力所引起的位移上所作的功，即
F112 F2 21
l
dx1
M x2 M x2 EI F1
l
dx2
1 l F1x1 x1 dx1 l F1l F2 x2 l dx2 EI
l3 4 1 F1 F2 EI 3 2
3. 梁和刚架
只考虑弯曲变形能
M2 Vε dx l 2 EI z
4. 组合变形杆
FN 2 T2 M2 Vε dx dx dx l 2 EA l 2GI l 2 EI p z
[例1] 试求下图所示结构的应变能。已知梁的抗弯刚度为EI，杆 的抗拉刚度为EA。 解：1）CB 杆的轴力 CB 杆的应变能
Weierstrass第一逼近定理与第二逼近定理
对一切 x ∈ (−∞ , ∞ ) 成立。
4
Weierstrass 第一逼近定理与第二逼近定理
Karl Weierstrass （1815—1897）是 19 世纪德国数学家，他在数 学的许多领域都作出了重要的工作， 其中不少成果是在他做中学教师 时取得的。由于他对数学科学的重大贡献，他后来被聘为柏林大学教 授和法国巴黎科学院院士。 Weierstrass 是数学分析基础的主要奠基者之一，是把严格的数学 论证引进分析学的一位大师。Weierstrass 利用单调有界的有理数数列 来定义无理数，从而在严格的逻辑基础上建立了实数理论；他提出的 关于极限定义的 ε − δ 语言， 被数学界公认为是关于极限概念的最准确 的描述，并被一直使用至今。
Weierstrass 第二逼近定理
设 f ( x) 是以 2π 为周期的连续函数，
则存在三角多项式序列一致收敛于 f ( x) 。也就是对任意给定的 ε > 0 ， 存在三角多项式 T ( x ) ，使得
T ( x) − f ( x) < ε
对一切 x ∈ (−∞, +∞) 成立。 先证明一个引理： 引理 设 g ( x ) 在 [0, π ] 上连续，则对任意给定的 ε > 0 ，存在余弦三
ε
⎤ ，当 n > N 时, 取N = ⎡ ⎢ δ 2ε ⎥ ⎦ ⎣ M
2
k =0
∑ f⎜
n
⎛k⎞ k k n−k − f ( x) < ε ⎟C n x (1 − x) ⎝n⎠
对一切 x ∈[0, 1]成立。
连续周期函数的三角多项式逼近
形如 Tn ( x) =
a0 n + ∑ ( ak cos kx + bk sin kx ) 的三角函数式称为三角多项式。 2 k =1
材料力学第27讲 Chapter3-2第三章 能量法(卡氏定理)
1
Ax
450
2
l2
l1 Ay
变形协调关系
Ax l1; A ysin4 5 0 A xco s4 5 0 l2
450
V
FN21l1 FN22l2 2EA 2EA
E2lA1 l12 E2lA2 l22
l FNl EA
E 2 lA 1 A x2 E 2 lA 2 A ysin 4 5 0 A xc o s4 5 02
变能V数值上等于余能Vc，则余能定理此时可改写为： Nhomakorabeai
V
(F1,F2 Fi
Fn)
卡氏第二定理
卡氏第二定理只适用于线性弹性情况。
19
例2 求简支梁中点作用集中力F作用时中点处的挠度。
（梁的弯曲刚度为EI，长为l）。
EI
F
A
C
l
2
l
解: 先求应变能
B
V
l M 2(x) d x 2
l 2
(
F 2
x)2 dx
Fn
1 2 i
n
图示梁（材料为线性，也可为非线性）
作用n个集中载荷Fi (i=1,2…n)，
相应位移为i (i=1, 2…n)
5
F1 F2 Fi
Fn
1 2 i
n
梁内的应变能： V W
n
i 0
fid i
i 1
可见，最终梁内的应变能应是关于i (i=1,2…n)的函数，即
V V (1,2 n)
15
F1 F2 Fi
Fn
1 2 i 梁内的余能：Vc Wc
n
n
F i
0
id
fi
i 1
可见，最终梁内的余能应是关于Fi (i=1,2…n)的函数，即
材料力学2--能量法
因仅与第i个荷载相应的位移有一微小增量, 而与其余各荷载相应 的位移保持不变，因此，对于位移的微小增量d i ，仅Fi 作了外 力功，外力功的变化为：
d W Fi di
注意到上式与下式在数值上相等
V d V d i i
从而有：
V Fi i
（卡氏第一定理 ）22l l 2 l l 2 FN EA
F F F Fl FN 2 sin 2 tan 2 l 2
F 代入前一式得： l EA
3
F F= ( /l )3 EA
或： F EA
l
3
（几何非线性弹性问题）
O
其F-间的非线性关系曲线为： 应变能为：
所以有
V vV v Al
应变能的特征：
（1）应变能恒为正的标量，与坐标系的选取无关； （2）由能量守恒原理可以证明：应变能仅与荷载的 最终值有关，而与加载的顺序无关； （3）在线弹性范围之内，应变能为内力（或位移） 的二次函数，因此力的叠加原理不再适用；
例1：弯曲刚度为 EI 的简支梁受均布荷载 q 作用，如图所 示。 试求梁内的应变能 。
由于外力余功在数值上等于余能，得
d V c d Wc
V c 解得： i Fi
（称为“余能定理”）
特别：对线弹性体，由于力与位移成正比，应变能 V 在数值上等于余能V c ， 此时上式变为：
V i Fi
（称为“卡氏第二定理”）
式中的Fi 和i分别为广义力和广义位移。
应用卡氏第一定理得
V EA 4 2 2 ( 1 2) 0 1 2l 2 2 V EA 2 ( 1 2) F 2 2l 2
《材料力学》11-1能量法
F1 dF
0
与外力功
W
1 0
Fd之和等于矩形面积
F1 1
线弹性范围内外力功等
F
F
于余功，能等于余能。
F1
F1
o
1
o
1
例题
试计算图示结构在荷载 F1 作用下的余能，结构中两杆的 长度均为 l，横截面面积均为A材料在单轴拉伸时的应力
—应变曲线如图所示。
B
D
K1nn1 1
C
F1
解：由结点C的平衡方程，可得两杆的轴力为
例题
xy平面内，由k根杆组成的杆系，在结点A处用铰链结 在一起，受到水平荷载和铅垂荷载作用，截面分别 为 A1,A2,Ai,Ak ，试用卡氏第一定理求各杆的轴力。
1
2
i
k
F1 A
F2
这种以位移为基本未知量，把它的求解当作关键性问题的方法称为位移法
本章作业
(II)3－2，
(II)3－4，
(II)3－10，
例题
图示在线弹性范围内工作的一端固定、另一端自由的圆轴，在自由端截面
上承受扭转力偶矩M1。材料的切变模量G和轴的长度 l 以及直径 d 均已知。 试计算轴两端的相对扭转角。
M1
d
A
B
l
四 余功、余能及卡氏第二定理
Wc
F1 dF
0
与余功相应的能称为余能
Vc V vcdV
vc
1 d
0
Vc
Wc
V cvc2Al2A nK lnn1 cF 1 o sn1
卡氏第二定理
F1
F2
F3
Fn
A
B
1
2
3
n
材料力学2.3卡氏第2定理
ds
= —PR—3— Pa=0 2EI
例 求A点位移A和B点位移B
解
• 先求A点位移
由卡氏定理
因为 所以
求B点位移
加入虚载荷P’ AB段
BC段
所以
事实上并无P’,因此令P’=0有 其实可在进行以下积分前令P’=0
（4） 平面桁架 (Plane truss)
δi
Vε Fi
n FNjl j FNj j1 EA Fi
（5） 组合变形(Combined deformation)
δi
Vε Fi
[ FN2( x)dx
T 2( x)dx
M 2( x)dx ]
Fi l 2EA
l 2GIp
l 2EI
FN( x) FN( x)dx T ( x) T ( x)dx M ( x) M ( x)dx
卡氏定理
卡氏定理(Castigliano's Theorem),是意大利工 程师卡斯蒂利亚诺(A.Castigliano )于1873年提出 的,故得其名.
卡氏第二定理
卡氏第一定理
卡氏定理的证明
设弹性结构在支座的约束下无 任何刚性位移.
作用有外力:
F1 ,F2 , ,Fi ,
相应的位移为：
2
F2
RAy=
—m—+m—2 2a
RD=
—m—+m—2 2a
aa
2a
C
m2
B
m
A
RAy
D
RD
RAy=
—m—+m—2 2a
RD=
—m—+m—2 2a
求AB,BC,CD各段的弯 矩方程,并对m2求偏导, 最后由卡氏定理求得C 截面的转角qC。
第九讲-卡氏定理知识交流
D ij
引起位移的载荷 发生位移的部位
线性弹性体的两种加载方式与外力功：
总功与加载次序无关
W1W2
先加 F1，后加 F2
D D D W 1F 1 211 F 2222 F 112
先加 F2，后加 F1
D D D W 2F 2 222 F 1 211 F 221
D D F 1 12 F2 21
D D F 1 12 F2 21
线弹性体受n个载荷
外力功
n
V0 W0
i1
FiDi 2
给载荷增量 d F k 考虑两个加载过程
1)先 Fi,后 dFk
V1 V0
V Fk
dFk
线弹性体外力功 与加载次序无关
2)先 dFk,后 Fi
dd d V 1 W 1 F k 2 D k W 0 D kF k
Dk
V Fk
例题
例 3-1 用卡氏定理求DBy
Crotti-Engesser’s theorem
卡氏定理
对于线性弹性体： Vc Vε
Dk
Vc Fk
Dk
Vε Fk
A. Castigliano (18471884)，意大利工程师。
线性弹性体的应变能，对载1870年入都灵工业学院，
荷
Fk
的偏导数，等于该载荷的1873年提出工程师学位 论文。
相V ε 应 －位l－F 移N 2 2 卡( E Dx 氏) k x 第d 二A l定T 2 2 理( G x ) tx d I lM 卡2 y 2 氏E ( x 第) yx 一d I 定l理M 2 z 2 ( E x ) zx d I
问题：弹性结构受n个载荷作用， 求指定载荷Fk的相应位移Δk
给载荷增量 d F k
引起位移的载荷 发生位移的部位
线性弹性体的两种加载方式与外力功：
总功与加载次序无关
W1W2
先加 F1，后加 F2
D D D W 1F 1 211 F 2222 F 112
先加 F2，后加 F1
D D D W 2F 2 222 F 1 211 F 221
D D F 1 12 F2 21
D D F 1 12 F2 21
线弹性体受n个载荷
外力功
n
V0 W0
i1
FiDi 2
给载荷增量 d F k 考虑两个加载过程
1)先 Fi,后 dFk
V1 V0
V Fk
dFk
线弹性体外力功 与加载次序无关
2)先 dFk,后 Fi
dd d V 1 W 1 F k 2 D k W 0 D kF k
Dk
V Fk
例题
例 3-1 用卡氏定理求DBy
Crotti-Engesser’s theorem
卡氏定理
对于线性弹性体： Vc Vε
Dk
Vc Fk
Dk
Vε Fk
A. Castigliano (18471884)，意大利工程师。
线性弹性体的应变能，对载1870年入都灵工业学院，
荷
Fk
的偏导数，等于该载荷的1873年提出工程师学位 论文。
相V ε 应 －位l－F 移N 2 2 卡( E Dx 氏) k x 第d 二A l定T 2 2 理( G x ) tx d I lM 卡2 y 2 氏E ( x 第) yx 一d I 定l理M 2 z 2 ( E x ) zx d I
问题：弹性结构受n个载荷作用， 求指定载荷Fk的相应位移Δk
给载荷增量 d F k
结构力学主要定理
§11-1概述1．变形功与变形能弹性杆受拉力P作用（图11-1），当P从零开始到终值缓慢加载时，力P在其作用方向上的相应位移也由零增至而做功，称为变形功。
（11-1）与此同时弹性杆被拉长而具有做功的能力，表明杆件内储存了变形能。
单位体积储存的应变能称为应变比能（11-2）整个杆件的变形能为（11-3）如果略去拉伸过程中的动能及其它能量的变化与损失，由能量守恒原理，杆件的变形能U在数值上应等于外力做的功W，即有U=W （11-4）这是一个对变形体都适用的普遍原理称为功能原理，弹性固体变形是可逆的，即当外力解除后，弹性体将恢复其原来形状，释放出变形能而做功。
但当超出了弹性范围，具有塑性变形的固体，变形能不能全部转变为功，因为变形体产生塑性变形时要消耗一部分能量，留下残余变形。
2．应变余功与余能变形体受外力作用时的余功定义为其中P1是外力从零增加到的终值，仿照功与变形能相等的关系，将余功相应的能称为余能，用U c表示。
余功与余能相等，即可仿照前面，定义单位体积余应变能（或应变余能），称为余应变比能由此整个结构余应变能可写成应指出：余功、余应变能、余应变比能具有功的量纲，是变形体的另一能量参数，但都没有具体的物理概念，只是常力所做的功减去变力所做功余下的那部分功。
3．能量原理固体力学中运用功与能有关的基本原理统称为能量原理，由此发展出来的方法称为能量法。
能量原理是在总体上从功与能的角度考察变形体系统的受力、应力与变形的原理与方法，是进一步学习固体力学的基础，也是当今应用甚广的有限元法求解力学问题的重要基础。
4．本章内容本章只涉及能量原理在材料力学中常用的部分内容，如：变形能、互等定理、卡氏定理、虚功原理、单位载荷法及图乘法，更为深入的，如最小势能原理，最小余能原理等变分原理，可参考其它专著。
§11-2 杆件变形能计算杆件不同受力情况下的变形能。
1．轴向拉伸或压缩线弹性杆件（图11-3）拉、压杆应变比能则整个杆的变形能或（11-5）（11-6）其中，N是内力（轴力），A是截面面积，l是杆长。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
卡氏第一定理
卡氏第一定理，也叫罗素-卡氏定理，是把代数学中不可被表示为一阶多项式
的定秩多项式表示成一个特殊的乘积式的定理。
这个定理曾几经变动，不断进行化简、完善，追求更高的表达效率，最终在1882年由英国数学家罗素以及卡氏完善
成现在的形式。
卡氏第一定理以一种解释数学定理的抽象表达方式对多项式进行定义。
就是说，把给定的不可被表示为一阶多项式的定秩多项式表示带出a≠0，当且仅当这个多项式可以被表示成由数学定义的相互互斥的两个多项式的乘积形式。
这个定义帮助数学家们利用特殊的乘积表示形式，给了表达多项式的整体性优势，显著的提高了表达效率和对多项式的理解。
卡氏第一定理是高等代数数学学科中不可缺少的重要定理，理论上可用来证明几乎所有高等代数里的多项式，无论是什么次元多项式，高次元多项式，几乎都能够利用卡氏第一定理做出某种形式的简写和成分分解。
此外，卡氏第一定理还是许多数学定理的出发点和依据，如罗素-卡氏定理的复形式，图灵的模糊式和厄尔森
中的统计学断言等等，它们源于或建立在这一定理之上。
由此可见，卡氏第一定理不仅是数学的一门经典定理，对后人的数学研究有着重要的影响和意义，更是科学研究中不可或缺的重要理论工具之一。