§11-4卡氏定理
材料力学能量法第3节 卡式定理
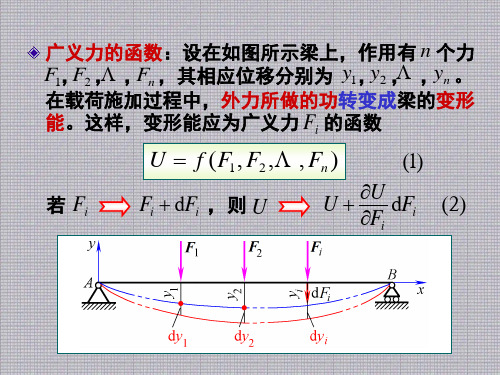
q 2 M ( x) (l x) M e 2
M 1 M e
(2)计算 B 截面转角 B
M q 2 1 M ( x) (l x) M e M e 2 M ( x) M ( x) Bq M e dx EI M e 1 l q 2 [ ( l x ) M ] ( 1 ) d x e EI 0 2 3 l ql 顺时针转向 Me EI 6 ql 3 顺时针转向 B 令 Me 0 6 EI
2
1 dFi dyi U dFi yi 2
(3)
比较(2)(3)式
1 dFi dyi U dFi yi (3) 2 U ( F1 , F2 , Fn ) yi i 1,2,3,... Fi
U U dFi Fi
(Hale Waihona Puke 2)梁的变形能对某一载荷 Fi 的偏导数,等于 在该载荷处沿载荷方向的位移,这就是卡氏定理, 也称卡氏第二定理。由意大利工程师 A 卡斯蒂利亚 诺(1847-1884)于1873年提出的。卡氏定理对其他 线弹性结构也是适用的。
广义力的函数:设在如图所示梁上,作用有 n 个力 y2 , , yn 。 F1, F2 , , Fn ,其相应位移分别为 y1, 在载荷施加过程中,外力所做的功转变成梁的变形 能。这样,变形能应为广义力 Fi 的函数
U f ( F1, F2 ,, Fn )
若 Fi
(1) ( 2)
Fi dFi , 则 U
U U dFi Fi
卡式定理的推导 —— 改变加力的次序 (1)先施加 dFi :在施加 dFi 时,其作用点沿 dFi 方向的 1 dF dy 位移为 dyi ,梁的变形能为 i i;
材料力学卡式定理
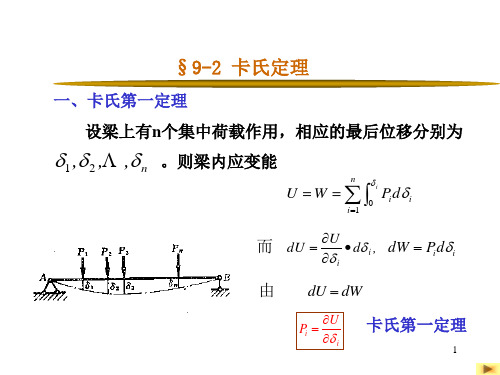
l
(2)
于是(1)式改写为
y / l
(3)
3
梁内任一点处的比能
u
1 2
E 2
1 2
E 2
l2
y2
(4)
梁的应变能
l
U VudV 0 (AudA)dx
l 1 E 2
( 02
l2
y2dA)dx 1 EI 2
A
2l
(5)
由卡氏第一定理
m U 1 EI (2 ) EIθ
(6)
2 lx)
2
dx
1 ( 5PL3 RC L3 ) 0
EI 48
3
RC
5P 16
能量法求解超静定结构,适 用任意荷载作用下、线性或 非线性弹性杆系、刚架或曲 杆等超静定系统。
14
2.求 wB
① 求内力
M
AB ( x)
5P 16
(L
x)
P(0.5L
x)
M BC ( x)
5P 16
Px L EI Px
1 EI
x 0
P(L
x1 ) ( x1
x)dx1
P
x3 [
(L
x)x2
Lx 2 ]
EI 3
2
12
例6 等截面梁如图,用卡氏定理求B 点的挠度。
P 0.5 L
B
A
L
解:1.依 wC 0 求多余反力,
卡氏定理解 ① 取静定基如图 C 超静定结构
② 求内力
M AB ( x) RC (L x) P(0.5L x)
L x1
O
x
w
①求内力 M AB ( x1) P(L x1) Px ( x x1) M BC ( x1) P(L x1)
第九讲-卡氏定理

基本公式
一般物体 载荷 f : 0 → F 相应位移 δ : 0 → ∆ 线性弹性体
dW= fdδ =
W = ∫ fdδ
0
∆
f ∝δ f =kδ
k - 线弹体在载荷作
用点、 用点、沿其作用方向 产生单位位移所需之 力,称为刚度系数 称为刚度系数
W = ∫ kδdδ
0
∆
k∆2 = 2
F∆ W= = 2
施加矩为 Me的力偶 -附加力偶
θB(q) = [θB(q, Me )]M =0
e
θB (q) =
∫
e
2. 位移计算
ql Me FAy = − 2 l x ∂M qlx Me x qx2 =− M( x) = − − l ∂Me 2 l 2 M( x) ∂M( x) θB (q) = dx l EI ∂Me M =0
∆A
A1 A′
B
B
合力的相应位移
∆A =
2 ∆A = (∆A + fA ) 2
2 ∂U 2 ∂U ∂U = = = (∆A + fA ) 2 ∂F 2 ∂F ∂ 2 F
(
)
FN2 = −F
2F ⋅ 2l (-F)l ⋅ 2+ ⋅ (-1) EA EA (2 2 + 1)Fl EA
∆By =
∆By =
(↓ )
例 3-2 利用卡氏定理计算θB
EI EI
-附加力法
解:1. 分析方法
转角θ 所对应的载荷? 转角θB所对应的载荷?
M( x) ∂M( x) dx l EI ∂Me M =0
∂Vc ∵ ∆k = ∂Fk
My ( x) ∂My Mz ( x) ∂Mz FN ( x) ∂FN ( x) T( x) ∂T( x) ∆k = ∫ dx+∫ dx+∫ dx+∫ dx l EA l GI l EI l EI ∂Fk ∂Fk t y ∂F k z ∂F k
卡氏定理材料力学

2Ma 3EI
(
)
DF FD
CD段:
M (x)
Mx , 2a
M (x) F
x,
MC
CB段: M (x) M ,
M (x) 2a x, a F
2a
C
M
AB段: M (x) 0,
M (x) x, F
a
B
A FAx
(4)带入卡氏定理求解。
Dx
l
M (x) M (x) d x EI F
FAy
2a
MC, 在D截面虚设一水平力F 。 MC
DF
C
(2)取刚架为研究对象, a
受力图如图所示。
M
FD
FAx F
B
a
A FAx
FAy
FD
F
1 2a
(M
MC)
FAy
(3)分段列出弯矩方程及偏导方程。
2a
CD段:
MC
M
( x1 )
[F
1 2a
(M
MC
)]x1
Cx aM 2
x
1
DF FD
M (x1) F
新位移 i 上也做功,系统的总的应变能为
V
Fi
i
1 2
Fi
i
(2)
由(1)=(2),并忽略二阶小量,得
V Fi
i
V Fi
i
若将结构的应变能表示为载荷F1,F2, ,Fn 的 函数,则应变能对任一载荷Fi的偏导数,等于Fi作用
点沿Fi作用方向的位移 i ,称为卡氏第二定理。
说明 (1)卡氏定理只适用线弹性结构。
i
V Fi
FN (x) FN (x) d x L EA Fi
04-12.2 卡式定理

M1 dx F1
l l
M2 EI
M2 dx F1
2
1 EI
l l
Fx F1x源自l 2xl 2
dx
F1=0
2
说明: 1,结果为正,表明B点位移方向与虚
力F1一致,即向下 2,虚力F1应在求导以后再令其为零 3,虚力的符号应与其他力的符号有所
1 EI
l
l
Fx
x
l 2
dx
5Fl 3 48EI
大连鲇鱼湾油码头栈桥
胡海昌 钱令希 钟万勰
例题
F
A
B
x l/2
C l/2
线弹性材料悬臂梁受力如图,
若F,EI(常数),l 等均为
已知,试用卡氏定理求: 1. 加力点 A 处的挠度 2. 梁中点 B 处的挠度
解:1. 求 A 点挠度
梁的弯矩方程为 M =-Fx (0≤x<l)
wA
Vε F
Δ1
Δ2
Δi
此时 Vc= Vc( F1, F2, …, Fi , … )
dVc = dWc
Δi
Vc Fi
Crotti-Engesser定理
弹性体的余能对某个载荷的一阶导数,等于 该载荷作用点的相应位移。
三、卡氏定理 Castigliano Second Theorem
线弹性体
Vε = Vc
Δi
Vε Fi
材料力学
大连理工大学 王博
卡氏定理
卡氏定理 (Castigliano’s second theorem)
一、余功、余能
定义
余功Wc (Complementary work)
F
F dF Wc
余能Vc (Complementary energy) ——应力能
卡氏第二定理

F3
F1
3 1
1 , 2 , , i ,
结构的变形能
11 1 V ε W 2 F 1 δ 1 2 F 2 δ 2 2 F 3 δ 3
只给 Fi 一个增量 Fi .
引起所有力的作用点沿力方向的位
移增量为 Δ1,δ Δ2,δ Δ3,δ
在作用Fi 的过程中, Fi 完成 F1
的功为
1 2
ΔFi
氏定理)(Castigliano’s Theorem)
说明 (Directions):
(1)卡氏第二定理只适用于线性弹性体( Applying only to linearly elastic bodies)
δi
Vε Fi
(2)Fi 为广义力(generalized force) i为相应的位移
(displacement corresponding to force Fi )
一个力
一个力偶
一对力
一对力偶
一个线位移
一个角位移
相对线位移 相对角位移
(3)卡氏第二定理的应用 ( Application of castigliano’s second theorem ) (a) 轴向拉,压(Axial tension and compression)
δ i V F ε i F i F N 2 2 ( E x )x d A F E N (x )A F N F ( ix )d x
Δδi
原有的所有力完成的功为
2
F2
F3
3 1
F 1 Δ 1 F 2 δ Δ 2 δ F iΔ i δ
结构应变能的增量为
Δ ε 1 2 V Δ iΔ i F F δ 1 Δ 1 F δ 2 Δ 2 δ F iΔ i δ
12能量法_1应变能卡式定理互等定理

1 FN ql 2
2)由截面法,得梁的弯矩方程为 1 1 M x qlx qx 2 2 2 梁的应变能
Vε AB M 2 x dx l 2 EI l
1 1 qlx qx 2 2 2 5 2 dx q l 2 EI
再令Me =0,即得转角
ql 3 B 6 EI
[例5] 图示平面刚架,若各段杆的抗弯刚度均为EI,试求其自由端 C 截面的竖直位移ΔC V 与水平位移ΔC H 。
解:在这种情况下,可分别记竖直方向 的力F 为F1、水平方向的力F 为F2,在 符号上将两者区分开来。
在替换力的符号后,BC 段、AB 段的弯矩 方程及其偏导数分别为
1 EI
2 π M e R2 M e R 2 1 cos d 0 2 EI
π/2
第四节 互等定理
一、功的互等定理
对于线弹性结构,第一组外力在第二组外力所引起的位移上所作
的功等于第二组外力在第一组外力所引起的位移上所作的功,即
F112 F2 21
l
dx1
M x2 M x2 EI F1
l
dx2
1 l F1x1 x1 dx1 l F1l F2 x2 l dx2 EI
l3 4 1 F1 F2 EI 3 2
3. 梁和刚架
只考虑弯曲变形能
M2 Vε dx l 2 EI z
4. 组合变形杆
FN 2 T2 M2 Vε dx dx dx l 2 EA l 2GI l 2 EI p z
[例1] 试求下图所示结构的应变能。已知梁的抗弯刚度为EI,杆 的抗拉刚度为EA。 解:1)CB 杆的轴力 CB 杆的应变能
卡氏定理求解力

卡氏定理求解力卡氏定理是力学中的一项重要定理,用于计算物体所受合力的大小。
它是根据牛顿第二定律推导出来的,能够帮助我们更好地理解和解决力学问题。
卡氏定理的表述是:“当一个物体受到多个力的作用时,这些力的矢量和等于物体的质量乘以加速度的矢量。
”简单来说,就是物体所受合力等于物体质量乘以加速度。
为了更好地理解卡氏定理,我们可以通过一个具体的例子来说明。
假设有一个质量为2千克的物体,在水平方向上受到两个力的作用:一个是10牛的向右的力,另一个是5牛的向左的力。
我们需要求解物体的加速度。
根据卡氏定理,我们可以将这个问题转化为一个简单的数学方程。
首先,我们需要计算合力。
由于两个力的方向相反,所以合力的大小等于10牛减去5牛,即5牛。
然后,我们需要计算物体的加速度。
根据卡氏定理,合力等于物体质量乘以加速度,所以加速度等于合力除以物体质量,即5牛除以2千克,得到2.5米每平方秒。
通过这个例子,我们可以看出卡氏定理的应用和价值。
它可以帮助我们计算物体所受合力的大小,并进一步求解物体的加速度。
在力学问题中,卡氏定理是一个非常重要的工具,可以帮助我们分析和解决各种力学问题。
除了上述例子中的计算方法,我们还可以通过向量的方法来应用卡氏定理。
在向量法中,我们可以将力和加速度用向量表示,然后利用向量的运算规则来求解问题。
这种方法在处理复杂的力学问题时更加方便和直观。
卡氏定理还可以用于解决一些实际问题。
例如,在工程中,我们经常需要计算物体所受的合力和加速度,以确定结构的强度和稳定性。
在运动学和动力学的研究中,卡氏定理也是一个重要的工具,可以帮助我们理解和描述物体的运动规律。
卡氏定理是力学中一项重要的定理,可以帮助我们计算物体所受的合力和加速度。
它是根据牛顿第二定律推导出来的,具有广泛的应用价值。
通过应用卡氏定理,我们可以更好地理解和解决力学问题,在工程和科学研究中发挥重要作用。
希望通过本文的介绍,读者能够对卡氏定理有一个更清晰的认识,并能够灵活运用它解决实际问题。
材料力学卡氏第二定理

卡氏第二定理的重要性
总结词
卡氏第二定理在材料力学中具有重要意义,它为分析和预测材料的应力分布提供了理论基础。
详细描述
卡氏第二定理是材料力学中一个重要的基本定理,它为解决复杂弹性体的应力分析问题提供了重要的理论依据。 通过卡氏第二定理,可以推导出许多其他的弹性力学公式和定理,从而更好地理解和预测材料的力学行为。
多学科交叉
加强与其他学科的交叉融合, 如物理学、化学、生物学等, 拓展卡氏第二定理在跨学科 领域的应用价值。
THANKS FOR WATCHING
感谢您的观看
04 卡氏第二定理的扩展与应 用
卡氏第二定理在弹性力学中的应用
总结词
卡氏第二定理在弹性力学中具有广泛的应用,它为解决复杂的弹性问题提供了重要的理 论支持。
详细描述
卡氏第二定理在弹性力学中主要用于求解弹性体的位移、应力和应变分布。通过应用卡 氏第二定理,可以建立各种弹性问题的基本方程,如弹性力学中的平衡方程、应变-位
02 卡氏第二定理的公式与推 导
公式展示
公式
(W = DeltaOmega + Delta K)
描述
该公式表示外力功((W))等于变形能((DeltaOmega))和动能((Delta K))之和。
公式推导过程
第一步
根据牛顿第二定律,外力对物体所做的功等 于物体动能的增量,即 (W = Delta K)。
弯曲梁的实例
总结词
卡氏第二定理在弯曲梁分析中起到关 键作用。
详细描述
弯曲梁在受到外力作用时会产生弯曲 变形,卡氏第二定理可以用来计算梁 内部的应力分布,确保梁的稳定性与 安全性。
扭转轴的实例
总结词
卡氏第二定理在分析扭转轴时具有重 要应用。
第九讲-卡氏定理

位移互等定理 位移互等定理
F1D12 F2D21
当F1= F2时
D12 D21
当F1与F2的数值相等时, F2在点1沿F1方位引起 的位移D12,等于F1在点2沿F2方位引起的位移D21
§3 余能与卡氏第二定理
余能概念
克罗第-恩格塞定理 卡氏定理 例题
余能概念 余功与余能
第 11 章 能量法(一)
讲授内容
§1 §2 §3 §4 §5
外力功与应变能 互等定理 余能与卡氏第二定理 变形体虚功原理 单位载荷法
上讲回顾
上讲回顾
相应位移 载荷 F 作用点处 沿载荷作用方向的位移 D. 由所有载荷共同引起 外力功 载荷 F 在其相应 位移 D 上所作之功 应变能 构件因变形而储 存的能量(变形能) 广义载荷 力,力偶,一对大小相等、方向相反 的力或力偶等 广义位移 线位移,角位移,相对线位移,相 对角位移等
克罗第-恩格塞定理
dWc D k dFk
dVc Vc dFk Fk
d Wc d Vc
Vc Dk Fk
弹性体的余能对载荷 Fk 的偏导数,等于该载 荷的相应位移 Dk- 克罗第-恩格塞定理 Crotti-Engesser’s theorem
卡氏定理
对于线性弹性体:
施加矩为 Me的力偶 -附加力偶
B ( q) B ( q , M e )M 0
e
B (q)
e
2. 位移计算
ql M e 2 l M x qlx M e x qx 2 M ( x) M e l 2 l 2 M ( x ) M ( x ) B (q) dx l EI M e M 0 FAy
卡氏第二定理

m+m2 RD= ——— 2a
x1
C D
x2
m2
B
RD
m
2a qC= ——(m+m2) 3EI
x3
A
RAy
实际上并无m2 ,所以令m2 =0得
2am qC= —— 3EI
通常在积分前即令m2 =0,可使积分简单
2
F2
3
1
F3
1 ΔFi Δδi 2
原有的所有力完成的功为
F1 Δδ1 F2 Δδ2 Fi Δδi
结构应变能的增量为
1 ΔVε ΔFi Δδi F1 Δδ1 F2 Δδ2 Fi Δδi 2
略去高阶微量
1 ΔFi Δδi 2 ΔVε F1 Δδ1 F2 Δδ2 Fi Δδi
一个线位移
一个角位移
相对线位移
相对角位移
(3)卡氏第二定理的应用 ( Application of castigliano’s second theorem )
(a) 轴向拉,压(Axial tension and compression)
2 Vε FN ( x )dx FN ( x ) FN ( x ) δi 2 EA EA Fi dx Fi Fi
B P
A f
M ——=Rcosf P
MM PR3p y= S ——— ds = ——— 4EI EI P
再在B点施加水平力Pa
M=PrcosfPaR(1-sinf)
B Pa P
M ——=R(1- sinf) Pa
A
§11-4卡氏定理

M (x) 1 qlx 1 qx 2 M f x
22
l
M(x) x
Mf l
M(x) M(x)
b
l
Pn
dx EI
q
Mf
A
B
x
l
M(x) M(x) M f
1 qx 2 2
1 2l
qx 3
b
l 0
M (x) EI
M (x) Mf
dx
1 l (1 qx2 1 qx3)dx ql3
Pl 4EI
2
(
0
l 2
x2
)dx2
Pl 3 Pl 3 (1 1) 48EI 4EI 4 8
5Pl 3 () 96 EI
U dU Pn dPn
(1)dPn
1
2 dPn (dn )
U
(2)P1, P2 ,...,Pn ,...,Pm
U dU U Pn dPn
U( P1, P2 ,..., Pn ,..., Pm ) dPnn
1
U ( P1 , P2 ,..., Pn ,..., Pm ) dPnn 2 dPn (dn )
M 2 (x2 )
P
1 2
(
l 2
x2
)
M 2 (x2 )
M 2 (x2 )
P
Pl 4
(l 2
x2 )
l
l
fc
1 EI
2
M 1 ( x1 )
0
M 1 ( x1 )
卡氏第二定理

解:
❖ 根据卡氏定理,有
AB段
BC段
例2.7
❖图示刚架EI为常 量,B截面受m作 用。求C截面转角
qC及D点的水平 位移x。轴力及
剪力不计。
a
a
2a
C
D
B
m
A
C点施以附加力偶矩m2,支 反力为
m+m2 RAy= ———
2a
m+m2 RD= ———
2a
a
a
2a
C
m2
B
m
A
RAy
D
RD
m+m2 RAy= ———
卡氏定理
卡氏定理(Castigliano's Theorem),是意大利工程师卡斯蒂利亚诺 (A.Castigliano )于1873年提出的,故得其名.
卡氏第二定理
卡氏第一定理
卡氏定理的证明
设弹性结构在支座的约束下无任何刚性位移.
作用有外力: F1 ,F2 , ,Fi ,
相应的位移为:
2
F2
F3
M
ds =
———
EI P
3
PR p
4EI
再在B点施加水平力Pa
M=PrcosfPaR(1-sinf)
M
——=R(1- sinf)
Pa
A
f
3
x=[ S ———M dsM]Pa=0 = ——— PR
EI Pa
2EI
B Pa
P
例 求A点位移A和B点位移B
解
❖ 先求A点位移
由卡氏定理
因为 所以
求B点位移
F3
F1
3 1
F1Δδ1 F2 Δδ2 Fi Δδi
第九讲-卡氏定理知识交流

引起位移的载荷 发生位移的部位
线性弹性体的两种加载方式与外力功:
总功与加载次序无关
W1W2
先加 F1,后加 F2
D D D W 1F 1 211 F 2222 F 112
先加 F2,后加 F1
D D D W 2F 2 222 F 1 211 F 221
D D F 1 12 F2 21
D D F 1 12 F2 21
线弹性体受n个载荷
外力功
n
V0 W0
i1
FiDi 2
给载荷增量 d F k 考虑两个加载过程
1)先 Fi,后 dFk
V1 V0
V Fk
dFk
线弹性体外力功 与加载次序无关
2)先 dFk,后 Fi
dd d V 1 W 1 F k 2 D k W 0 D kF k
Dk
V Fk
例题
例 3-1 用卡氏定理求DBy
Crotti-Engesser’s theorem
卡氏定理
对于线性弹性体: Vc Vε
Dk
Vc Fk
Dk
Vε Fk
A. Castigliano (18471884),意大利工程师。
线性弹性体的应变能,对载1870年入都灵工业学院,
荷
Fk
的偏导数,等于该载荷的1873年提出工程师学位 论文。
相V ε 应 -位l-F 移N 2 2 卡( E Dx 氏) k x 第d 二A l定T 2 2 理( G x ) tx d I lM 卡2 y 2 氏E ( x 第) yx 一d I 定l理M 2 z 2 ( E x ) zx d I
问题:弹性结构受n个载荷作用, 求指定载荷Fk的相应位移Δk
给载荷增量 d F k
卡氏法原理

卡氏法原理卡氏法,又称为卡尔·弗里德里希·高斯法,是一种用于解决线性方程组的数值方法。
它是由德国数学家卡尔·弗里德里希·高斯在19世纪提出的,被认为是解决线性代数问题中最重要的算法之一。
卡氏法原理的核心思想是通过迭代的方式,逐步逼近线性方程组的解,直至达到一定的精度要求。
在实际应用中,线性方程组的解往往是非常复杂的,特别是当方程组的规模较大时,传统的直接求解方法往往效率较低。
而卡氏法通过迭代的方式,可以在有限的步骤内得到近似解,从而提高了解决线性方程组的效率。
卡氏法的原理可以简单概括为以下几个步骤:1. 初始化,选择一个初始解向量作为迭代的起点。
2. 迭代计算,根据一定的迭代公式,不断更新解向量,直至满足一定的收敛条件。
3. 收敛判据,通常使用残差或者误差的范数来判断迭代是否收敛,当误差小于一定的阈值时,迭代结束。
4. 输出结果,得到满足精度要求的解向量,作为线性方程组的近似解。
卡氏法的优点在于,它不需要对整个线性方程组进行直接求解,而是通过迭代的方式,逐步逼近精确解。
这种迭代的方式使得卡氏法在解决大规模线性方程组时具有较高的效率和稳定性。
同时,卡氏法还可以应用于稀疏矩阵和特殊结构矩阵的求解,具有很强的通用性和适用性。
然而,卡氏法也存在一些局限性,比如对于某些特殊结构的线性方程组,可能需要较多的迭代步骤才能达到精度要求,从而导致计算量较大。
此外,在实际应用中,需要根据具体的线性方程组的特点来选择合适的迭代公式和收敛判据,这需要一定的经验和技巧。
总的来说,卡氏法作为解决线性方程组的重要数值方法,具有较高的实用价值和理论意义。
在实际应用中,我们需要充分理解其原理和特点,结合具体问题选择合适的参数和策略,以达到高效、稳定、精确的求解效果。
同时,也需要不断地进行算法优化和改进,以满足不断增长的科学计算需求。
结构力学主要定理

§11-1概述1.变形功与变形能弹性杆受拉力P作用(图11-1),当P从零开始到终值缓慢加载时,力P在其作用方向上的相应位移也由零增至而做功,称为变形功。
(11-1)与此同时弹性杆被拉长而具有做功的能力,表明杆件内储存了变形能。
单位体积储存的应变能称为应变比能(11-2)整个杆件的变形能为(11-3)如果略去拉伸过程中的动能及其它能量的变化与损失,由能量守恒原理,杆件的变形能U在数值上应等于外力做的功W,即有U=W (11-4)这是一个对变形体都适用的普遍原理称为功能原理,弹性固体变形是可逆的,即当外力解除后,弹性体将恢复其原来形状,释放出变形能而做功。
但当超出了弹性范围,具有塑性变形的固体,变形能不能全部转变为功,因为变形体产生塑性变形时要消耗一部分能量,留下残余变形。
2.应变余功与余能变形体受外力作用时的余功定义为其中P1是外力从零增加到的终值,仿照功与变形能相等的关系,将余功相应的能称为余能,用U c表示。
余功与余能相等,即可仿照前面,定义单位体积余应变能(或应变余能),称为余应变比能由此整个结构余应变能可写成应指出:余功、余应变能、余应变比能具有功的量纲,是变形体的另一能量参数,但都没有具体的物理概念,只是常力所做的功减去变力所做功余下的那部分功。
3.能量原理固体力学中运用功与能有关的基本原理统称为能量原理,由此发展出来的方法称为能量法。
能量原理是在总体上从功与能的角度考察变形体系统的受力、应力与变形的原理与方法,是进一步学习固体力学的基础,也是当今应用甚广的有限元法求解力学问题的重要基础。
4.本章内容本章只涉及能量原理在材料力学中常用的部分内容,如:变形能、互等定理、卡氏定理、虚功原理、单位载荷法及图乘法,更为深入的,如最小势能原理,最小余能原理等变分原理,可参考其它专著。
§11-2 杆件变形能计算杆件不同受力情况下的变形能。
1.轴向拉伸或压缩线弹性杆件(图11-3)拉、压杆应变比能则整个杆的变形能或(11-5)(11-6)其中,N是内力(轴力),A是截面面积,l是杆长。
卡氏定理概述
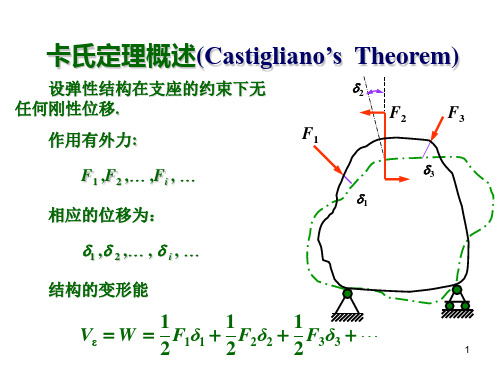
Vε Fi
Fi
FN2( x)dx 2EA
FN ( x) FN ( x)dx EA Fi
(b) 扭转
δi
Vε Fi
Fi
T 2( x)dx 2GIp
T ( x) T ( x)dx GIp Fi
(c) 弯曲
δi
Vε Fi
Fi
M 2( x)dx 2EI
M ( x) M ( x)dx EI Fi
响. 用卡氏第二定理求截面 D 的水平位移 D 和转角 D .
解:在D点虚设一力偶矩 Ma CD:弯曲变形
F1
A
B
C
M ( x) Fx Ma
l
M ( x) x M ( x) 1
F
Ma
l
2l x
F Ma
D
16
将力 F 向C 简化得:
力 F(产生拉伸变形)
A
力偶矩 2Fl(产生弯曲变形)
l
将Ma向C简化得:
氏定理)(Castigliano’s Theorem)
3
说明(Directions): (1)卡氏第二定理只适用于线性弹性体
δi
Vε Fi
(2)Fi 为广义力,i为相应的位移
一个力
一个力偶
一对力
一对力偶
一个线位移
一个角位移
相对线位移
相对角位移
4
(3)卡氏第二定理的应用
(a) 轴向拉伸与压缩
δi
12ΔFiΔδi
ΔVε F1Δδ1 F2Δδ2 FiΔδi
如果把原来的力看作第一组力,而把 Fi 看作第二组力.
根椐互等定理
F1Δδ1 F2Δδ2 FiΔδi ΔFi δi
ΔVε
l4-111 cassels方程

L4-111 Cassels方程是数论中的一个重要问题,由原先的Diophantine方程演化而来,其研究涉及到代数数论和解析数论等多个数学领域。
本文将从多个角度对该方程进行深入的探讨和分析,希望能够为读者提供清晰的理解和全面的知识。
一、Cassels方程的定义和历史Cassels方程最早由约翰·哈理斯·西尔维斯特·卡塞尔斯于20世纪50年代提出,它是一种特殊的临界指数方程。
其一般形式如下所示:\[a_1x_1^n + a_2x_2^n + \cdots + a_kx_k^n = 0\]其中,\(a_1, a_2, \cdots, a_k\)为给定的整数,\(x_1, x_2, \cdots,x_k\)为未知整数,\(n\)为给定的正整数。
Cassels方程的研究涉及到整数解的存在性和性质等问题,对于数论研究具有重要意义。
二、Cassles方程的基本性质1.方程的整数解Cassels方程的解空间包含着一些奇特的整数解,这些解对于数论的研究有着重要的作用。
对于给定的系数和指数,我们希望能够找到满足条件的整数解,因此方程的整数解性质是Cassels方程研究的基本问题之一。
2.方程的临界指数Cassels方程中的临界指数是一个重要的参数,它直接影响着方程解的性质。
在数学研究中,临界指数往往与方程解的存在性和非存在性密切相关,因此对于Cassels方程的临界指数进行深入的研究具有重要意义。
三、Cassles方程的研究方法和进展1.线性递归法线性递归法是Cassels方程研究的一种重要方法,通过构造适当的线性递归序列,可以得到方程解的一些性质和结构。
线性递归法在Cassels方程的研究中有着广泛的应用,为分析解的性质提供了重要的工具。
2.解的存在性和非存在性Cassels方程的解的存在性和非存在性是其研究的一个核心问题。
通过对方程的系数、临界指数和解的结构等进行综合分析,可以得到解的存在性和非存在性的一些判定条件,从而深入理解Cassels方程的性质。
卡氏第一定理推荐优秀PPT
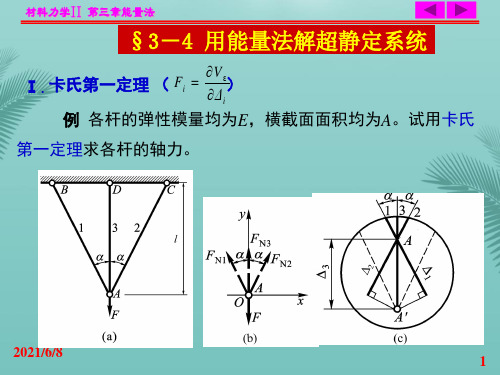
将(4)式代入(1)得
将X 值代入(1),得 与X1,X2 相应的位移条件分别为两截面的相对线位移和相对角位移为零,即
解:该题为一次超静定。
CB, AB段的弯矩方程及其对X 的偏导数分别为
以D3为基本未知量,该题为一次超静定。
F 例 图 a中 k≥3。 F F (4)式包含了平衡方程和物理方程N ,1 而
D1=D2。由图c可知:
Δ1 Δ3cos
(1)
若求出D3,可由(1)求出D1(D2)。再 由胡克定律求出轴力。以D3为基本未知
量,该题为一次超静定。
结构的应变能为
Vε22(l/E coA )sΔ12E 2l A Δ32 E2lAΔ32(2co3s1) (2)
2021/6/8
2
由 F Vε , 得 Δ3
2021/6/8
8
解:以铰链 D 的支反力X 为多余未知力,基本静定系 如图b 所示,F,X 看作基本静定系上独立的外力,
所以
Vc = Vc (F,X )
(不能含有其它未知力)
因为铰链 D 处沿铅垂方向的位移 为零,应有
Vc 0 X 由该式求出X 后,再利用平衡方程求各杆的轴力。
2021/6/8
2cos(co)s 试用卡氏第一定理求各杆的轴力。
N2 ,表示变形的几何关系。
2 1/n
把Dx和Dy代入(2)可得
卡氏第二定理(
)
以力为基本未知量解超静定问题的方法,称为力法。 用余能定理求各杆的轴力。
但由于结构与荷载均是对称的,内力也应该是对称的,但X3是反对称的,故X3=0,问题简化为二次超静定。
因为铰链 D 处沿铅垂方向的位移为零,应有
V 若求出D3,可由(1)求出D1(D2)。 (4)式包含了平衡方程和物理方ቤተ መጻሕፍቲ ባይዱ,而 0 将X 值代入(1),得
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Pl 4EI
2
(
0
l 2
x2
)dx2
Pl 3 Pl 3 (1 1) 48EI 4EI 4 8
5Pl 3 () 96 EI
两种加载过程的变形能应该一样
U
U
Pn
dPn
=
U ( P1 , P2 ,..., Pn ,..., Pm ) dPnn
1
2 dPn (dn )
略去二阶微量
U
U Pn dPn = U ( P1 , P2 ,..., Pn ,..., Pm ) dPnn
U Pn
P1
)
dx2
l
l
1
EI
2
Px12 dx1
0
1 EI
2P 04
(8 x22
6lx2
l 2 )dx2
Pl 3 Pl 3 1 3 1
( )
24 EI 4EI 3 4 2
7 Pl 3 () 16 EI
简支梁跨中挠度 fc
P A
l 2
P
Pl
2
C
B
l
2
M(x) M(x)
dPn
dPn n
U Pn
n
运用卡氏定理应该注意的两点 运用卡氏定理的正负
1) Pn与n对应性 2) 正负
Pn与n同向, n为正; Pn与n异向, n为负。
拉伸、弯曲、扭转和组合变形的卡氏定理
n
U Pn
Pn
l
N 2(x)dx 2EA
n
M (x) 1 qlx 1 qx 2 M f x
22
l
M(x) x
Mf l
M(x) M(x)
b
l
Pn
dx EI
q
Mf
A
B
x
l
M(x) M(x) M f
1 qx 2 2
1 2l
qx 3
b
l 0
M (x) EI
M (x) Mf
dx
1 l (1 qx2 1 qx3)dx ql3
M 2 (x2 )
P
1 2
(
l 2
x2
)
M 2 (x2 )
M 2 (x2 )
P
Pl 4
(l 2
x2 )
l
l
fc
1 EI2Βιβλιοθήκη M 1 ( x1 )0
M 1 ( x1 )
P
dx1
1 EI
2
M
0
2
( x2
)
M 2 (x2
P
)
dx2
l
l
P
2EI
2
x12 dx1
0
l
T 2 (x) dx
2GI p
n
l
T (x) T (x)dx Pn GI p
n
l
N(x) Pn
N (x)dx EA
l
M (x) Pn
M (x)dx EI
l
T (x) Pn
T (x)dx GI p
简支梁的 b
q
A
B
EI
解:
EI 0 2
2l
24EI
悬臂梁自由端的挠度 fa
P
P
M1( x1) P1x1
M1( x1)
P1
x1
A
l
l
2
2
M 1 ( x1 )
M 1 ( x1 )
P1
Px12
解:
fa
l
M(x) P1
M (x) dx
EI
M
2
(
x2
)
P2
x2
P1 ( x2
l 2
)
P 1
P 2
P =P =P
1
2
M 2 (x2
P1
)
( x2
l) 2
A x
1
x 2
M 2 (x2 )
M 2 (x2 )
P1
P 4
(8x22
6lx2
l2)
l
l
1
fa EI
2
M 1 ( x1 )
0
M1( x1)
P1
dx1
1 EI
2 0
M
2
(
x2
)
M 2 (x2
§11-4卡氏定理
卡氏定理的描述 运用卡氏定理应该注意的两点
简支梁的 b
悬臂梁自由端的挠度 fa 简支梁跨中挠度 fc
卡氏定理的描述
U M 2 (x) dx l P2 x2 dx P2l 3
L 2EI
0 2EI
6EI
U P
Pl3 3EI
fa
U对P的偏导数等于P方向的位移。
从一个例子得到的结果不能作为一般结论使用。
从一般情况来证明它。
P2 P1
δ2
δ1
Pn δn
Pm δm
•线弹性体的变形能和加载过程
P1 , P2 ,..., Pn ,..., Pm
无关,只决定于载荷的最后值。 •换一种加载过程。
U U( P1, P2 ,..., Pn ,..., Pm )
dPn P1 , P2 ,..., Pn ,..., Pm
解:f c
l
P
dx
EI
A x1
P
C x2
Mk B
Pl
M
k
2
M 1 ( x1 )
1 2
Px1
M l
k
x1
M 1 ( x1 )
P
1 2
x1
M 1 ( x1 )
M 1 ( x1 )
P
1 2
Px12
M 2 (x2 )
Px2
P 2
(x2
l) 2
Mk l
(x2
l) 2
l
N(x) Pn
N (x)dx EA
n
m
N
2 i
li
m
Ni Ni li
Pn i1 2EAi i1 Pn EAi
n
U Pn
Pn
l
M 2(x) dx
2EI
n
l
M (x) Pn
M (x)dx EI
n
U Pn Pn
U dU Pn dPn
(1)dPn
1
2 dPn (dn )
U
(2)P1, P2 ,...,Pn ,...,Pm
U dU U Pn dPn
U( P1, P2 ,..., Pn ,..., Pm ) dPnn
1
U ( P1 , P2 ,..., Pn ,..., Pm ) dPnn 2 dPn (dn )
