浙江省高数竞赛6历届高等数学竞赛真题
历届全国大学生数学竞赛真题及答案非数学类

高数竞赛预赛试题(非数学类)(参加高等数学竞赛的同学最重要的是好好复习高等数学知识,适当看一些辅导书及相关题目,主要是一些各大高校的试题。
)2009年 第一届全国大学生数学竞赛预赛试卷一、填空题(每小题5分,共20分)1.计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(____________,其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解: 令v x u y x ==+,,则v u y v x -==,,v u v u y x d d d d 1110det d d =⎪⎪⎭⎫ ⎝⎛-=, v u u v u u u y x y x x yy x D D d d 1ln ln d d 1)1ln()(⎰⎰⎰⎰--=--++⎰⎰⎰⎰----=---=1021000d 1)ln (1ln d )d ln 1d 1ln (u uu u u u u u u u v v uuv u u u u u ⎰-=12d 1u uu (*) 令u t -=1,则21t u -=dt 2d t u -=,42221t t u +-=,)1)(1()1(2t t t u u +-=-,⎰+--=0142d )21(2(*)tt t⎰+-=1042d )21(2t t t 1516513221053=⎥⎦⎤⎢⎣⎡+-=t t t 2.设)(x f 是连续函数,且满足⎰--=2022d )(3)(x x f x x f , 则=)(x f ____________.解: 令⎰=20d )(x x f A ,则23)(2--=A x x f ,A A x A x A 24)2(28d )23(202-=+-=--=⎰,解得34=A 。
因此3103)(2-=x x f 。
3.曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是__________.解: 因平面022=-+z y x 的法向量为)1,2,2(-,而曲面2222-+=y x z 在),(00y x 处的法向量为)1),,(),,((0000-y x z y x z y x ,故)1),,(),,((0000-y x z y x z y x 与)1,2,2(-平行,因此,由x z x =,y z y 2=知0000002),(2,),(2y y x z x y x z y x ====,即1,200==y x ,又5)1,2(),(00==z y x z ,于是曲面022=-+z y x 在)),(,,(0000y x z y x 处的切平面方程是0)5()1(2)2(2=---+-z y x ,即曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是0122=--+z y x 。
数学竞赛高数试题及答案

数学竞赛高数试题及答案试题一:极限的计算问题:计算极限 \(\lim_{x \to 0} \frac{\sin x}{x}\)。
解答:根据洛必达法则,我们可以将原式转换为 \(\lim_{x \to 0} \frac{\cos x}{1}\),由于 \(\cos 0 = 1\),所以极限的值为 1。
试题二:导数的应用问题:若函数 \( f(x) = 3x^2 - 2x + 1 \),求其在 \( x = 1 \) 处的导数值。
解答:首先求导数 \( f'(x) = 6x - 2 \),然后将 \( x = 1 \) 代入得到 \( f'(1) = 6 \times 1 - 2 = 4 \)。
试题三:不定积分的求解问题:求不定积分 \(\int \frac{1}{x^2 + 1} dx\)。
解答:这是一个基本的积分形式,可以直接应用反正切函数的积分公式,得到 \(\int \frac{1}{x^2 + 1} dx = \arctan(x) + C\),其中\( C \) 是积分常数。
试题四:级数的收敛性判断问题:判断级数 \(\sum_{n=1}^{\infty} \frac{1}{n^2} \) 是否收敛。
解答:根据比值测试,我们有 \(\lim_{n \to \infty}\frac{1}{(n+1)^2} / \frac{1}{n^2} = \lim_{n \to \infty}\frac{n^2}{(n+1)^2} = 1\),由于极限值为 1,小于 1,所以级数收敛。
试题五:多元函数的偏导数问题:设函数 \( z = f(x, y) = x^2y + y^3 \),求 \( f \) 关于\( x \) 和 \( y \) 的偏导数。
解答:对 \( x \) 求偏导,保持 \( y \) 为常数,得到 \( f_x =2xy \)。
对 \( y \) 求偏导,保持 \( x \) 为常数,得到 \( f_y = x^2 + 3y^2 \)。
高数竞赛试题及答案

高数竞赛试题及答案在高等数学领域中,竞赛试题的编写与解答一直是学生们提高自己数学水平的重要方式之一。
本文将提供一些高等数学竞赛试题,并附上详细的解答过程,以帮助读者更好地理解和应用数学知识。
1. 竞赛试题一考虑函数f(x) = |x^2 - 4x + 3|,其中x为实数。
(1)求函数f(x)的定义域。
(2)求函数f(x)的最大值和最小值。
解答过程:(1)为了求函数f(x)的定义域,我们需要确定使函数的值有意义的x 的范围。
由于函数f(x)中包含了一个绝对值,我们可以将其拆分成两种情况讨论:当x^2 - 4x + 3 ≥ 0时,函数f(x) = x^2 - 4x + 3;当x^2 - 4x + 3 < 0时,函数f(x) = -(x^2 - 4x + 3)。
对于第一种情况,我们需要求解不等式x^2 - 4x + 3 ≥ 0。
通过因式分解或配方法,我们可以得到(x-1)(x-3) ≥ 0。
解这个不等式可以得到x ≤ 1或x ≥ 3。
对于第二种情况,我们需要求解不等式x^2 - 4x + 3 < 0。
同样通过因式分解或配方法,可以得到(x-1)(x-3) < 0。
解这个不等式可以得到1< x < 3。
综上所述,函数f(x)的定义域为x ≤ 1或x ≥ 3,且1 < x < 3。
(2)为了求函数f(x)的最大值和最小值,我们可以分别考虑函数f(x)在定义域的两个区间内的取值情况。
当x ≤ 1时,函数f(x) = x^2 - 4x + 3。
通过求导可以知道,函数f(x)在x = 2处取得最小值。
代入可得最小值为f(2) = 1。
当x ≥ 3时,函数f(x) = -(x^2 - 4x + 3)。
同样通过求导可以知道,函数f(x)在x = 2处取得最大值。
代入可得最大值为f(2) = -1。
综上所述,函数f(x)的最大值为-1,最小值为1。
2. 竞赛试题二已知函数f(x) = 2^(x+1) - 3^(x-2),其中x为实数。
2010年浙江省高等数学竞赛试题与答案(共4份)

试题共四套:数学类、工科类、经管类、文专类2010浙江省大学生高等数学(微积分)竞赛试题(数学类)一、计算题(每小题14分,满分70分)1.求极限1lim 2n →+∞+⎦2.计算()22222exp 21R x xy y dxdy ρρ⎡⎤-+⎢⎥--⎢⎥⎣⎦⎰⎰. 其中01ρ≤< 3.请用,a b 描述圆 222x y y +≤ 落在椭圆 22221x y a b+= 内的充分必要条件,并求此时椭圆的最小面积。
4.已知分段光滑的简单闭曲线Γ(约当曲线)落在平面π:10ax by cz +++=上,设Γ在π上围成的面积为A ,求()()()bz cy dx cx az dy ay bx dz ax by czΓ-+-+-++⎰其中n Γ与的方向成右手系。
5.设f 连续,满足()()() 22 02exp xf x x x t f t dt =--⎰且()11/f e =,求()()1n f 的值。
二、(满分20)定义数列{}n a 如下:{},,max ,211011dx x a a a n n ⎰-==,4,3,2=n ,求n n a ∞→lim 。
三、(满分20分)设函数)(2R C f ∈,且0)(lim =∞→x f x ,1)(≤''x f ,证明:0)(lim ='∞→x f x 。
四、(满分20分)设非负函数f 在[0,1]上满足)()()(,,y f x f y x f y x +≥+∀且1)1(=f ,证明:(1)]1,0[,2)(∈≤x x x f (2)21)(1≤⎰dx x f 五、(满分20分)设全体正整数集合为+N ,若集合+⊂N G 对加法封闭(即G y x G y x ∈+⇒∈∀,),且G 内所有元素的最大公约数为1,证明:存在正整数N ,当正整数n >N 时,G n ∈(工科类)一、计算题(每小题14分,满分70分)1.求极限1lim 2n →+∞+⎦2.计算()() +22 122dxx x x ∞-∞+-+⎰3.设ABC ∆为锐角三角形,求sin sin sin cos cos cos A B C A B C ++---的最大值和最小值。
浙江省《高等数学》竞赛“连续、导数及其应用专题”历年真题汇总

浙江省《高等数学》竞赛“连续、导数及其应用专题”历年真题汇总第一部分:连续、导数定义,函数导数求解1、 (03 经) xe + y + sin x = 0 ,求 y (0) .x '2、 (04)设 f ( x) = arctan1− x (n ) ,求 f (0) . 1+ x 1 x 3、(04 文)求曲线 y = (1 + ) 在 x = 1 处的切线方程. xf ( x) 求 = 1 , f (0) , f ′(0) 和 f ′′(0) x →0 1 − cos x4、 (05 经) f ( x) 在 x = 0 点二阶可导, lim 设 且的值。
⎧ ln(1 + x) , x>0 ⎪ 5、(05 文)设 f ( x) = ⎨ 可导,求常数 a, b 的值. x ⎪ax + b, x ≤ 0 ⎩6、 (06 文)求曲线 ⎨⎧ x = t 2 − 2t ⎪ 在 t = 0 处的切线方程. ⎪ y arctan t + e y = e 2 ⎩⎧ x = cos(t 2 ) d2y ⎪ 2 7、 (07 经)设 ⎨ ,求 . t −u 2 dx 2 sin udu ⎪y = ∫ 0 e ⎩8、 (07 文)设 f ( x) =3x3 (n) ,求 f ( x) . 2 x − 2x − 3( 2008 )9、 (08)设 f ( x) = x arcsin x ,求 f(0) .10、 (08 经)求曲线 ⎨⎧ x = ln t ⎪ 在 t = 1 处的切线方程. t 2 y = 2t + ∫ e −( ts ) ds ⎪ 1 ⎩2 (2009)11、(09 经) 设 f ( x) = x sin x ,求 f(0) .⎧ x = cot t ⎪ 12、(09 经) 设 ⎨ cos 2t , t ∈ (0,π ) ,求此曲线的拐点. ⎪ y = sin t ⎩13、(10 经) 设 f 连续,满足 f ( x ) = x +2∫x0e x −t f ′(t )dt ,求 f ′(0) 。
2006年浙江省大学高等数学(微积分)竞赛试题及解答

2006年浙江省高等数学(微积分)竞赛试题及解答一.计算题1. 求()1lim 2xx x e x →∞⎡⎤-+⎢⎥⎣⎦.解法一 令1t x =,原式011lim 2t t e t t →⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦()0211limtt t e t→-+=()0lim 211tt t e →=+=;解法二 原式112lim 1x x x e x e x -→∞⎛⎫=-+ ⎪⎝⎭121lim1xx e x x-→∞-+=122221lim1xx e xxx-→∞-+=-1lim 21x x e -→∞⎛⎫=-= ⎪⎝⎭.2. 求()()2ln 2ln 132x x dx x x +-+++⎰.解:原式()()()11ln 2ln 112x x dx x x ⎛⎫=+-+-⎪++⎝⎭⎰ ()()()()()()ln 2ln 1ln 2ln 1x x d x x =-+-++-+⎰()()21ln 2ln 12x x C =-+-++⎡⎤⎣⎦.3. 求曲线222,arctan ,y x t t y t e e ⎧=-⎪⎨+=⎪⎩在0t =处的切线方程.解:当0t =时,()00x =,()02y =,由22x t t =-,22dx t dt=-,2t dx dt==-,由2arctan yy t e e +=,21arctan 01yy t y e y t''+⋅+=+,该式中令0t =,2y =, 解出()220t dy y dt e='==-,因此201t dy dxe==,所求曲线()y fx =在0t =处的切线方程为()2120y x e-=-,即212y x e=+.4. 设()1x fx x=+,求()()10fx .解:()()()112211111x fx x x x-+-==+-++()()12f x f x =+,()()1121112f x x -'=+,()()1221111122f x x -⎛⎫''=-+ ⎪⎝⎭,,()()()1101021111191222f x x -⎛⎫⎛⎫=--+ ⎪ ⎪⎝⎭⎝⎭,()()1122112f x x --'=-+,()()1222111122f x x --⎛⎫''=---+ ⎪⎝⎭,,()()()1101022111191222f x x --⎛⎫⎛⎫=-----+ ⎪ ⎪⎝⎭⎝⎭,()()()()()()10101012fx f x f x =+()()()()()()91019212210101113171131719122x x ----=⋅+-⋅⋅+()192101317191121x x -⋅⎛⎫=-++ ⎪+⎝⎭ .二.设()36xxfx e=-,问()0fx =有几个实根?并说明理由.解:()22xxf x e '=-,()xf x e x ''=-,显然()0x f x e x ''=->,(),x ∈-∞+∞,()f x '在(),-∞+∞上严格递增; ()11102f e '-=-<,()010f '=>,由零点定理,存在唯一()01,0x ∈-,使得()00f x '=,即0x 为()f x 的唯一的驻点.同时,0x 为()fx 在(),-∞+∞内唯一的极小值点,也是最小值点, 又在()1,0-,()306xxf x e=->,故方程()0fx =在(),-∞+∞内无实根.三.已知()323lim1x x x ax b →∞++-=,求a ,b 的解.解:由条件,可得()32310lim1x x x ax b x→∞=++--3211lim 1x a x x →∞⎛⎫=++- ⎪⎝⎭1a =-, 于是1a =,从而()323lim1x b x x x →∞=++-3211lim 11x x x x →∞⎛⎫=++- ⎪⎝⎭221332211lim 1111111x x xx x x x x →∞⎛⎫+ ⎪⎝⎭=⎛⎫⎛⎫++++++ ⎪ ⎪⎝⎭⎝⎭13=.四.求由0y =,1y x e=,ln y x =围成的平面图形D 的面积及D 绕x 轴旋转一周所得旋转体体积. 解:1y x e=与ln y x =的交点坐标为2x e =,1y =,在()20,e内,1lnx x e>,所以D 的面积221ln e ex A dx x dx e=-⎰⎰()22321121ln 132ee x x x e =⋅--()2136e=-;或者()1222yA ee ydy =-⎰122301123yeey ⎛⎫=-⎪⎝⎭ ()2136e=-;D 绕x 轴旋转一周所得的旋转体体积222211ln 4e ex V dx xdx eππ=-⎰⎰()221l n l n2224e e x x x x ππ=--+⎡⎤⎣⎦2π=;或者()12222yV y ee ydy π=-⎰1222yydee ππ=-⎰1221222y y e e πππ⎛⎫=--=⎪⎝⎭.五.设()f x 有连续的二阶导数,证明:()()()()000x f x f f x tf x t dt '''=++-⎰.证明:因为()0xtf x t dt ''-⎰()()0x td f x t '=--⎰()()00x xf f x t dt ''=-+-⎰()()()00xd xf f x t dt dt'=-+--⎰()()()00xf f f x '=--+,所以()()()()000x f x f f x tf x t dt '''=++-⎰.六.证明:(),x ∀∈-∞+∞,sin sin 2sin a x b x x +≤的充分必要条件为21a b +≤. 证明:必要性设sin sin 2sin a x b x x +≤,两边分别约去sin 0x ≠, 由此,得2cos 1a b x +≤,令0x →,取极限,得21a b +≤,在2cos 1a b x +≤中,令x π→,取极限得21a b -+≤, 当a ,b 同号时,221a b a b +=+≤, 当a ,b 异号时,221a b a b +=-≤. 充分性设21a b +≤,因为2cos 21a b x a b +≤+≤, 两边同时乘以sin x ,所以sin sin 2sin a x b x x +≤.。
浙江省高等数学竞赛试题与答案

(2)式乘 2 减(1)得 4 2( y3 − 2 2x3 ) = 0 ,即 y = 2x ,因此再由(1)式,得
fx (x,
y)
= 16x(x2
−
1) 2
=
0
,即
x1
=
0,
x2
=
2 2
,
x3
=
−
2 ,解得 2
⎧ ⎨ ⎩
x1 y1
= =
0 0
,
⎧ ⎪ ⎨ ⎩⎪
x2 y2
= =
2 2 1
,
⎧ ⎪ ⎨ ⎪⎩
( ) ∑ 解
设
1− x2
−1 2
=
∞
bn x2n ,
则因
n=0
1
(1
−
t
)−
1 2
=1−
1
t
+
−
1 2
(−
1 2
−1)
t2
+ L+ (−1)m
−
1 2
(−
1 2
−1)L(−
1 2
− m +1)
tm
+L
2
2!
m!
( ) 1− x2
−1 2
=
1−
1
x2
+
−
1 2
(−
1 2
−1)
x4
+L+
(−1)m
−
− x2 2ax
−
y2
(a
>
0
)在
yoz
平面上的投影曲线为 Γ yz
,计算
∫ ⎛ 4a2 − z2
⎜ ⎝ Γ yz
历届全国大学生高等数学竞赛真题及答案非数学类

前三届高数竞赛预赛试题(非数学类)(参加高等数学竞赛的同学最重要的是好好复习高等数学知识,适当看一些辅导书及相关题目,主要是一些各大高校的试题。
)2009年 第一届全国大学生数学竞赛预赛试卷一、填空题(每小题5分,共20分)1.计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(____________,其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解: 令v x u y x ==+,,则v u y v x -==,,v u v u y x d d d d 1110det d d =⎪⎪⎭⎫ ⎝⎛-=, v u u v u u u y x y x x yy x D D d d 1ln ln d d 1)1ln()(⎰⎰⎰⎰--=--++⎰⎰⎰⎰----=---=1021000d 1)ln (1ln d )d ln 1d 1ln (u uu u u u u u u u v v uuv u u u u u ⎰-=12d 1u uu (*) 令u t -=1,则21t u -=dt 2d t u -=,42221t t u +-=,)1)(1()1(2t t t u u +-=-,⎰+--=0142d )21(2(*)tt t⎰+-=1042d )21(2t t t 1516513221053=⎥⎦⎤⎢⎣⎡+-=t t t2.设)(x f 是连续函数,且满足⎰--=2022d )(3)(x x f x x f , 则=)(x f ____________.解: 令⎰=20d )(x x f A ,则23)(2--=A x x f ,A A x A x A 24)2(28d )23(202-=+-=--=⎰,解得34=A 。
因此3103)(2-=x x f 。
3.曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是__________. 解: 因平面022=-+z y x 的法向量为)1,2,2(-,而曲面2222-+=y x z 在),(00y x 处的法向量为)1),,(),,((0000-y x z y x z y x ,故)1),,(),,((0000-y x z y x z y x 与)1,2,2(-平行,因此,由x z x =,y z y 2=知0000002),(2,),(2y y x z x y x z y x ====,即1,200==y x ,又5)1,2(),(00==z y x z ,于是曲面022=-+z y x 在)),(,,(0000y x z y x 处的切平面方程是0)5()1(2)2(2=---+-z y x ,即曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是0122=--+z y x 。
历届全国大学生数学竞赛真题及答案非数学类

高数竞赛预赛试题〔非数学类〕〔参加高等数学竞赛的同学最重要的是好好复习高等数学知识,适当看一些辅导书及相关题目,主要是一些各大高校的试题。
〕2021年 第一届全国大学生数学竞赛预赛试卷 一、填空题〔每题5分,共20分〕1.计算=--++⎰⎰y x yx x yy x D d d 1)1ln()(,其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解:令vx u y x ==+,,那么vu y v x -==,,v u v u y x d d d d 1110det d d =⎪⎪⎭⎫⎝⎛-=,v u u v u u u y x y x x yy x D D d d 1ln ln d d 1)1ln()(⎰⎰⎰⎰--=--++⎰⎰⎰⎰----=---=1021000d 1)ln (1ln d )d ln 1d 1ln (u uu u u u u u u u v v u uv u u u u u〔*〕令u t -=1,那么21t u -=dt 2d t u -=,42221t t u +-=,)1)(1()1(2t t t u u +-=-,⎰+--=0142d )21(2(*)t t t⎰+-=1042d )21(2t t t 151651322153=⎥⎦⎤⎢⎣⎡+-=t t t 2.设)(x f 是连续函数,且满足⎰--=2022d )(3)(x x f x x f , 那么=)(x f .解:令⎰=20d )(x x f A ,那么23)(2--=A x x f ,A A x A x A 24)2(28d )23(202-=+-=--=⎰,解得。
因此。
3.曲面平行平面022=-+z y x 的切平面方程是.解:因平面022=-+z y x 的法向量为)1,2,2(-,而曲面在),(00y x 处的法向量为)1),,(),,((0000-y x z y x z y x ,故)1),,(),,((0000-y x z y x z y x 与)1,2,2(-平行,因此,由x z x =,y z y 2=知0000002),(2,),(2y y x z x y x z y x ====,即1,200==y x ,又5)1,2(),(00==z y x z ,于是曲面22=-+z y x 在)),(,,(0000y x z y x 处的切平面方程是0)5()1(2)2(2=---+-z y x ,即曲面 平行平面022=-+z y x 的切平面方程是0122=--+z y x 。
历届全国大学生数学竞赛真题及答案非数学类

高数竞赛预赛试题(非数学类)(参加高等数学竞赛的同学最重要的是好好复习高等数学知识,适当看一些辅导书及相关题目,主要是一些各大高校的试题。
)2009年第一届全国大学生数学竞赛预赛试卷一、填空题(每小题5分,共20分)1.计算____________,其中区域由直线与两坐标轴所围成三角形区域.解: 令,则,,(*)令,则,,,2.设是连续函数,且满足, 则____________.解: 令,则,,解得。
因此。
3.曲面平行平面的切平面方程是__________.解: 因平面的法向量为,而曲面在处的法向量为,故与平行,因此,由,知,即,又,于是曲面在处的切平面方程是,即曲面平行平面的切平面方程是。
4.设函数由方程确定,其中具有二阶导数,且,则________________.解: 方程的两边对求导,得因,故,即,因此二、(5分)求极限,其中是给定的正整数.解 :因故因此三、(15分)设函数连续,,且,为常数,求并讨论在处的连续性.解 : 由和函数连续知,因,故,因此,当时,,故当时,,这表明在处连续.四、(15分)已知平面区域,为的正向边界,试证:(1);(2).证 :因被积函数的偏导数连续在上连续,故由格林公式知(1)而关于和是对称的,即知因此(2)因故由知即五、(10分)已知,,是某二阶常系数线性非齐次微分方程的三个解,试求此微分方程.解设,,是二阶常系数线性非齐次微分方程的三个解,则和都是二阶常系数线性齐次微分方程的解,因此的特征多项式是,而的特征多项式是因此二阶常系数线性齐次微分方程为,由和,知,二阶常系数线性非齐次微分方程为六、(10分)设抛物线过原点.当时,,又已知该抛物线与轴及直线所围图形的面积为.试确定,使此图形绕轴旋转一周而成的旋转体的体积最小.解因抛物线过原点,故,于是即而此图形绕轴旋转一周而成的旋转体的体积即令,得即因此,,.七、(15分)已知满足, 且, 求函数项级数之和.解,即由一阶线性非齐次微分方程公式知即因此由知,,于是下面求级数的和:令则即由一阶线性非齐次微分方程公式知令,得,因此级数的和八、(10分)求时, 与等价的无穷大量.解令,则因当,时,,故在上严格单调减。
06至浙江省高等数学竞赛工科类试题
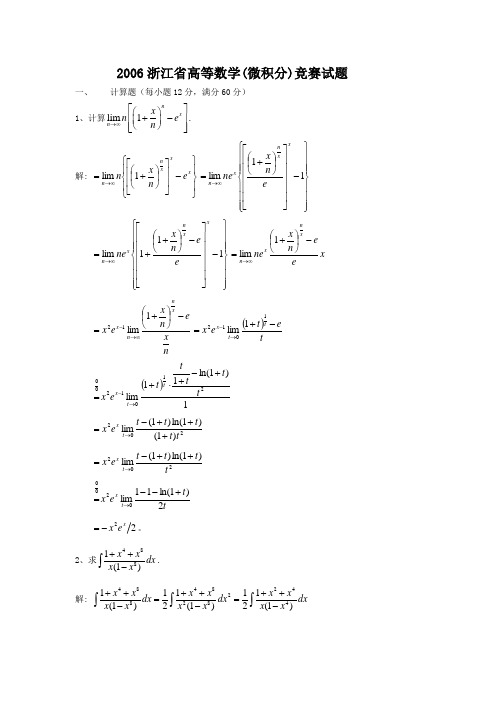
2006浙江省高等数学(微积分)竞赛试题一、计算题(每小题12分,满分60分)1、计算lim 1n x n x n e n →∞⎡⎤⎛⎫+-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦.解: ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+=∞→x x x n n e n x n 1lim ⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧-⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+=∞→11lim x x n x n e n x ne ⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧-⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛++=∞→111lim x x n x n e e n x ne x ee n x ne xnx n -⎪⎭⎫ ⎝⎛+=∞→1limnx en x e x xnn x -⎪⎭⎫ ⎝⎛+=∞→-1lim 12()te t e x t t x -+=→-10121lim()1)1ln(11lim2101200t t t tt e x t t x +-+⋅+=→- 202)1()1ln()1(limt t t t t e x t x +++-=→202)1ln()1(limtt t t e x t x ++-=→ tt e x t x 2)1ln(11lim020+--=→22x e x -=。
2、求4881(1)x x dx x x ++-⎰. 解: 4848242828411111(1)2(1)2(1)x x x x x x dx dx dx x x x x x x ++++++==---⎰⎰⎰242224211114(1)4(1)x x x x dx dx x x x x ++++==--⎰⎰ 3111122411411A B C dx dx x x x x x x ⎛⎫-- ⎪⎛⎫=++=++⎪ ⎪-+-+⎝⎭ ⎪⎝⎭⎰⎰ 131ln(1)ln ln(1)422x x x C ⎡⎤=--+-++⎢⎥⎣⎦311ln(1)ln ln(1)848x x x C =--+-++.3、求22110x y y e dy e dx x ⎡⎤-⎢⎥⎢⎥⎣⎦⎰⎰. 解: 2222111111000x x y y y y ye e dy e dx dy dx dy e dx x x ⎡⎤-=-⎢⎥⎢⎥⎣⎦⎰⎰⎰⎰⎰⎰ 2211100x xy y edx dy dy e dx x =-⎰⎰⎰⎰2221111(1)2x y x e e dx y e dy xe dx -=--==⎰⎰⎰. 4、求过(1,2,3)且与曲面3()z x y z =+-的所有切平面皆垂直的平面方程.解:令3(,,)()F x y z x y z z =+--则(,,)1x F x y z '=,2(,,)3()y F x y z y z '=-,2(,,)3()1z F x y z y z '=---令所求平面方程为: (1)(2)(3)0A x B y C z -+-+-=,在曲面3()z x y z =+-上取一点(1,1,1),则切平面的法向量为{1,0,1}-, 则0A C -=在曲面3()z x y z =+-上取一点(0,2,1),则切平面的法向量为{1,3,4}-, 则340A B C +-=. 解得: A B C ==即所求平面方程为: 6x y z ++=.二、(15分)设3()6xx f x e =-,问()0f x =有几个实根?并说明理由.解: 当0x ≤, 306xx e >≥当0x >, 00e >且xe 的增长速度要比36x 来得快!所以()0f x =无实根.三、(满分20分)求31n n x ∞=⎛⎫ ⎪⎝⎭∑中20x 的系数.解: 当1x <时, 33331111n n x x x x x ∞=⎛⎫⎛⎫⎛⎫==⋅ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭∑3301122n n x x x x ∞=''''⎛⎫⎛⎫=⋅=⋅ ⎪ ⎪-⎝⎭⎝⎭∑ 322(1)2n n x n n x ∞-==-∑ 故31n n x ∞=⎛⎫ ⎪⎝⎭∑中20x 的系数为171.四、(20分) 计算Cxyds ⎰,其中C 是球面2222x y z R ++=与平面0x y z ++=的交线.解: 2222()()2()CCCx y z ds x y z ds xy yz zx ds ++=+++++⎰⎰⎰而2()0Cx y z ds ++=⎰,22223()2CCx y z ds R ds R π++==⎰⎰, CCCxyds yzds zxds ==⎰⎰⎰,故33CR xyds π=-⎰.五、(20分)设12,,,n a a a 为非负实数,试证:1sin sin nkk akx x =≤∑的充分必要条件为11nkk ka=≤∑.证明:必要性 由于1sin sin n k k a kx x =≤∑,则1sin sin nkk kx xa x x=≤∑, 0x ≠0011sin sin lim lim 1nnk k x x k k kx xa ka x x →→==⇒=≤=∑∑. 充分性;要证明1sin sin nkk akx x =≤∑,只需证明:1sin 1sin nkk akxx=≤∑,这里sin 0x ≠,若sin 0x =,不等式显然成立;即只需证明:1sin 1sin nkk kxa x=≤∑, 而11sin sin sin sin nnk kk k kx kx a a x x ==≤∑∑,11nk k ka =≤∑ 故只要说明:sin sin kxk x≤,即sin sin kx k x ≤, 当1k =时,显然成立;假设当k n =时,也成立,即sin sin nx n x ≤;当1k n =+时, sin(1)sin()sin cos sin cos n x nx x nx x x nx +=+=+sin sin (1)sin nx x n x ≤+≤+六、(15分)求最小的实数c ,使得满足1()1f x d x =⎰的连续函数()f x 都有1f dx c ≤⎰.解:1111)2()2()2f dx f dx t f t dx f t dx ≤=≤=⎰⎰⎰⎰,取2y x =,显然1()1f x dx =⎰,而1124233f dx ==⋅=⎰⎰, 取(1)ny n x =+,显然1()1f x dx =⎰,而111(1)22,2nn f dx n dx n n +=+=⋅→→∞+⎰⎰, 故最小的实数2c =.2007浙江省高等数学(微积分)竞赛试题(解答)一.计算题(每小题12分,满分60分) 1、求9.解:9551155==1111555u t du =+==-312222155u u C =-+ C x x ++-+215235)1(52)1(152。
历届全国大学生数学竞赛真题及答案非数学类

高数竞赛预赛试题〔非数学类〕〔参加高等数学竞赛的同学最重要的是好好复习高等数学知识,适当看一些辅导书及相关题目,主要是一些各大高校的试题。
〕2021年 第一届全国大学生数学竞赛预赛试卷 一、填空题〔每题5分,共20分〕1.计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(,其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解:令v x u y x ==+,,那么v u y v x -==,,v u v u y x d d d d 1110det d d =⎪⎪⎭⎫⎝⎛-=,令u t -=1,那么21t u -=2.设)(x f 是连续函数,且满足⎰--=2022d )(3)(x x f x x f , 那么=)(x f .解:令⎰=20d )(x x f A ,那么23)(2--=A x x f , 解得。
因此。
3.曲面平行平面022=-+z y x 的切平面方程是.解:因平面022=-+z y x 的法向量为)1,2,2(-,而曲面在),(00y x 处的法向量为)1),,(),,((0000-y x z y x z y x ,故)1),,(),,((0000-y x z y x z y x 与)1,2,2(-平行,因此,由x z x =,y z y 2=知0000002),(2,),(2y y x z x y x z y x ====,即1,200==y x ,又5)1,2(),(00==z y x z ,于是曲面022=-+z y x 在)),(,,(0000y x z y x 处的切平面方程是0)5()1(2)2(2=---+-z y x ,即曲面 平行平面 022=-+z y x 的切平面方程是0122=--+z y x 。
4.设函数)(x y y =由方程29ln )(y y f e xe =确定,其中f 具有二阶导数,且1≠'f ,那么.解:方程29ln )(y y f e xe =的两边对x 求导,得 因)(29ln y f y xe e =,故,即,因此二、〔5分〕求极限x enx x x x ne e e )(lim 20+++→ ,其中n 是给定的正整数. 解:因 故 因此三、〔15分〕设函数)(x f 连续,⎰=10d )()(t xt f x g ,且,A 为常数,求)(x g '并讨论)(x g '在0=x 处的连续性.解:由与函数)(x f 连续知,0)(limlim )(lim )0(000===→→→xx f x x f f x x x 因⎰=10d )()(t xt f x g ,故0)0(d )0()0(10===⎰f t f g , 因此,当0≠x 时,,故 当0≠x 时,这说明)(x g '在0=x 处连续.四、〔15分〕平面区域}0,0|),{(ππ≤≤≤≤=y x y x D ,L 为D 的正向边界,试证:〔1〕⎰⎰-=---Lx y Lx y x ye y xe x ye y xe d d d d sin sin sin sin ;〔2〕2sin sin 25d d π⎰≥--Ly y x ye y xe .证:因被积函数的偏导数连续在D 上连续,故由格林公式知 〔1〕y x ye y xe x x ye y xe Dx y Lx y d d )()(d d sin sin sin sin ⎰⎰⎰⎥⎦⎤⎢⎣⎡-∂∂-∂∂=---而D 关于x 与y 是对称的,即知 因此 〔2〕因 故 由知即 2sin sin 25d d π⎰≥--Ly y x ye y xe五、〔10分〕x x e xe y 21+=,x x e xe y -+=2,x x x e e xe y --+=23是某二阶常系数线性非齐次微分方程的三个解,试求此微分方程.解设x x e xe y 21+=,x x e xe y -+=2,x x x e e xe y --+=23是二阶常系数线性非齐次微分方程的三个解,那么x x e e y y 212-=--与x e y y -=-13都是二阶常系数线性齐次微分方程的解,因此0=+'+''cy y b y 的特征多项式是0)1)(2(=+-λλ,而0=+'+''cy y b y 的特征多项式是因此二阶常系数线性齐次微分方程为02=-'-''y y y ,由)(2111x f y y y =-'-''与 知,1112)(y y y x f -'-''=)(2)2(42222x x x x x x x x e xe e e xe e e xe +-++-++= 二阶常系数线性非齐次微分方程为六、〔10分〕设抛物线c bx ax y ln 22++=过原点.当10≤≤x 时,0≥y ,又该抛物线与x 轴及直线1=x 所围图形的面积为31.试确定c b a ,,,使此图形绕x 轴旋转一周而成的旋转体的体积最小.解因抛物线c bx ax y ln 22++=过原点,故1=c ,于是 即而此图形绕x 轴旋转一周而成的旋转体的体积 即 令 得 即 因此七、〔15分〕)(x u n 满足),2,1()()(1 =+='-n e x x u x u x n n n, 且, 求函数项级数之与.解 即由一阶线性非齐次微分方程公式知 即 因此 由知,0=C , 于是下面求级数的与:令 那么 即由一阶线性非齐次微分方程公式知 令0=x ,得C S ==)0(0,因此级数的与 八、〔10分〕求-→1x 时, 与等价的无穷大量.解令2)(t x t f =,那么因当10<<x ,(0,)t ∈+∞时,2()2ln 0t f t tx x '=<,故xt t ex t f 1ln22)(-==在(0,)+∞上严格单调减。
2002年—2010年浙江省(经管类)高等数学竞赛试题

2002.12.7年浙江省大学生高等数学(微积分)竞赛试题(经管类)题 号 一二三四五六总分得 分 评卷人一.计算题(每小题5分,满分30分)1. 1.1.求极限01cos lim (1)(11)x x xe x →--+-。
2.求积分|1|Dxy dxdy -⎰⎰,11{(,)2,2}22D x y x y =≤≤≤≤。
3.设2x y x e =是方程hx y ay by ce '''++=的一个解,求常数,,,a b c h 。
学校姓名准考证号 专业装订线4.设()f x 连续,且当1x >-时,2()[()1]2(1)xxxe f x f t dt x +=+⎰,求()f x 。
5.设211arctan 2nn k S k ==∑,求lim n n S →∞。
6.求积分12121(1)x xx e dx x++-⎰。
学校姓名准考证号专业装订线二.(本题满分15分)求平面221x y z +-=含在椭圆柱体22149x y +=内的面积。
三.(本题满分20分)证明:220sin()0x dx π>⎰。
四.(本题满分20分)设二元函数(,)f x y 有一阶连续偏导数,且(0,1)(1,0)f f =.证明:单位圆周上至少存在两点满足方程(,)(,)0yf x y x f x y x y∂∂-=∂∂。
学校姓名准考证号 专业装订线五.(本题满分15分)(非数学类做)设{},{}n n a b 为满足1,1n na b n ea e n +=+≥的两个实数列,已知0(1),n a n >≥且1n n a ∞=∑收敛.证明:1n nn b a ∞=∑也收敛。
六.(本题满分15分)已知函数)(x f 在[ 0, 1 ]上三阶可导,且1)0(-=f ,0)1(=f ,0)0(='f ,试证至少存在一点)1,0(∈ξ,使设11=a ,12=a ,n n n a a a 3212+=++,1≥n ,求n n n x a ∞=∑1的收敛半径、收敛域和函数。
浙江省历年高数竞赛试题及解答

浙江省首届数学分析竞赛试题(2002.12.7)一.计算题(每小题5分,共30分)1.求极限limx →。
2.求积分|1|Dxy dxdy -⎰⎰,11{(,)2,2}22D x y x y =≤≤≤≤。
3.设2x y x e =是方程hx y ay by ce '''++=的一个解,求常数,,,a b c h 。
4.设()f x 连续,且当1x >-时,2()[()1]2(1)xx xe f x f t dt x +=+⎰,求()f x 。
5.设211arctan2nnk S k ==∑,求lim n n S →∞。
6.求积分12121(1)x x x e dx x++-⎰。
二. (15分)求平面221x y z +-=含在椭圆柱体22149x y +=内的面积。
三. (20分)证明:20)0x dx >。
四.(20分)设二元函数(,)f x y 有一阶连续的偏导数,且(0,1)(1,0)f f =。
证明:单位圆周上至少存在两点满足方程(,)(,)0yf x y x f x y x y∂∂-=∂∂。
五.(15分)设11a =,21a =,2123n n n a a a ++=+,1n ≥,求1nn n a x ∞=∑的收敛半径,收敛域及和函数。
2002年浙江省高等数学竞赛试题及解答一、计算题 1. 求极限x →解:原式())()01cos 1lim1xx x ex→-+=-()201cos 2lim1x x x x xe →-=-12112=⋅⋅=. 2. 求积分1D I xy dxdy =-⎰⎰,()11,:2,222D x y x y ⎧⎫=≤≤≤≤⎨⎬⎩⎭.解:记(){}1,:,1D x y xy D xy =∈≥,(){}2,:,1D x y xy D xy =∈≤,()()1211D D I xy dxdy xy dxdy =-+-⎰⎰⎰⎰()()1222111122211x xdx xy dy dx xy dy =-+-⎰⎰⎰⎰222112222211111111222222x dx x dx x x x x ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=---+--- ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎰⎰2211221111222822x dx x dx x x ⎛⎫⎛⎫=+-++- ⎪ ⎪⎝⎭⎝⎭⎰⎰212171582x dx x ⎛⎫=+- ⎪⎝⎭⎰2217111512l n 2l n 2822222⎛⎫⎛⎫⎛⎫=⋅-+--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭152ln 264=+. 3. 设2xy x e =是方程hxy ay by ce '''++=的一个解,求常数a ,b ,c ,h .解:()22x y x x e '=+,()242x y x x e ''=++,代入方程,得()()21422x hxa b x a x e ce ⎡⎤+++++=⎣⎦, 于是 1242010h c a a b =⎧⎪=⎪⎨+=⎪⎪++=⎩,故2a =-,1b =,2c =,1h =.4. 设()f x 连续,且当1x >-时,()()()20121xxxe f x f t dt x ⎡⎤+=⎢⎥⎣⎦+⎰,求()f x . 解:由条件可知()00f =,()()()2211xx f t dt xe x -'⎡⎤+=+⎢⎥⎣⎦⎰,()()()()21111x xt f t dt te d t -+-=-+⎰⎰()11xxt xe x e dt -=-++⎰()111xxxe x e -=-++-11x e x=-+, ()()211xxe f t dt x +=+⎰,()01x f t dt +=⎰()()23221xxef x x =±+.5、 设211arctan2nnk S k==∑,求lim n n S →∞. 解:利用公式arctan arctan arctan1x yx y xy--=+,2111arctan arctan arctan 22121k k k =--+,211arctan 2nn k S k ==∑111arctan arctan 2121nk k k =⎛⎫=- ⎪-+⎝⎭∑1a r c t a n 1a r c t a n 21n =-+,lim 4n n S π→∞=;211arctan 24k k π∞==∑. 由2211arctanarctan arctan 441222k k k k=--+-, 得2221arctan arctan 4412k k k ∞==-+∑. 6. 计算积分121211x x I x e dx x +⎛⎫=+- ⎪⎝⎭⎰.解法一 因为111x x x e x +⎛⎫+- ⎪⎝⎭111x x x x e x e x ++⎛⎫=+- ⎪⎝⎭1x x xe +'⎛⎫= ⎪⎝⎭,所以1212x xI xedx +'⎛⎫= ⎪⎝⎭⎰ 21521232x x xe e +⎛⎫== ⎪⎝⎭. 解法二112211221x x xx I edx x e dx x ++⎛⎫=+- ⎪⎝⎭⎰⎰11221122x x xxedx xde++=+⎰⎰211122111222x x x xxx edx xee dx +++⎛⎫=+- ⎪⎝⎭⎰⎰5232e =.解法三 分析:观察被积函数的特点,令1u x=做代换,利用定积分的“递推方法”求I , 令1u x=,则11222111u u I u e du u u +⎛⎫⎛⎫=+-- ⎪ ⎪⎝⎭⎝⎭⎰112211u u u e d e u ⎛⎫⎛⎫=+- ⎪ ⎪⎝⎭⎝⎭⎰1111112222222111111u u u u u u u e e u e e du e e du u u u ⎡⎤⎛⎫⎛⎫⎛⎫=+--+----⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎣⎦⎰⎰1111522222211311u u u u e u e du e du u u ++⎛⎫⎛⎫=--+--- ⎪ ⎪⎝⎭⎝⎭⎰⎰11152221221131u u u u e u e du e d u u u ++⎛⎫⎛⎫=--+-+ ⎪ ⎪⎝⎭⎝⎭⎰⎰1152223u u e I e +⎛⎫=-- ⎪⎝⎭523e I =-,所以5232I e =.二、求平面221x y z +-=含在椭圆柱体22149x y +=内的面积.解:112z x y =+-,()22,:149x y D x y ⎧⎫=+≤⎨⎬⎩⎭,DS =D=32D d x d y =⎰⎰ 32392ππ=⋅⋅⋅=.三、证明:()200x dx >.证明:令2xu =,则()22sin x dx u π=⎰2012πππ⎛⎫=+ ⎪⎝⎭⎰⎰00sin 12t πππ+⎛⎫=+ ⎪⎝⎭⎰⎰0012ππ⎛⎫=+ ⎪⎝⎭⎰⎰01sin 2u du π=-⎰ 0>. 同理可证20sin 0xdx xπ>⎰. 四、设二元函数(),f x y 有一阶连续的偏导数,且()()0,11,0f f =,证明:在单位圆周上至少存在两点满足方程()(),,0y f x y x f x y x y∂∂-=∂∂. 证明:令cos x θ=,sin y θ=,()()cos ,sin F f θθθ=,()02θπ≤≤;因为(),f x y 有一阶连续的偏导数,所以()F θ可导.()()sin cos f f f fF y x x y x yθθθ∂∂∂∂'=-+=-+∂∂∂∂, 由条件,得()()01,0Ff =,()0,12F f π⎛⎫= ⎪⎝⎭,()()21,0F f π=, ()02F F π⎛⎫= ⎪⎝⎭,()22F F ππ⎛⎫= ⎪⎝⎭,利用罗尔中值定理,得 存在10,2πθ⎛⎫∈ ⎪⎝⎭,使得()10F θ'=, 存在2,22πθπ⎛⎫∈ ⎪⎝⎭,使得()20F θ'=,即得在单位圆周上至少存在两点满足方程()(),,0y f x y x f x y x y∂∂-=∂∂. 五、设11a =,21a =,2123n n n a a a ++=+,()1,2,n =,求1nn n a x ∞=∑的收敛半径,收敛域及和函数. 解:由条件可知, ()2113n n n n a a a a ++++=+,()21133n n n n a a a a +++-=--,于是()2121332n n n n a a a a +++=+=,()()()212131321nnn n a a a a ++-=--=--,从而()()14231nn n a +=+-,()()11312nnn a +=+-,()1,2,n = 因此()()111312n n n a --=+-,()1,2,n =.因为()111133lim lim3113nn n n n n naa -+-→∞→∞-+==⎛⎫+- ⎪⎝⎭,所以收敛半径13r=; ()111111312n nn n n n n n n a x x x ∞∞∞--===⎛⎫=+- ⎪⎝⎭∑∑∑的收敛域为11,33⎛⎫- ⎪⎝⎭; ()11111111312n nn n n n n n n a x x x x ∞∞∞----===⎛⎫=+- ⎪⎝⎭∑∑∑ 1112131x x x ⎛⎫=+ ⎪-+⎝⎭.(五)、设{}n a ,{}n b 为满足1n n ab n e a e +=+,()1,2,n =的两个实数列,已知0na >,()1,2,n =,且1n n a ∞=∑收敛. 证明:1n n b ∞=∑也收敛.证明:由1nn a∞=∑收敛,得lim 0nn a →∞=,由1nn b a n e e a +=-,得 lim 0n n b →∞=,由1n n n a b b n e a e e +=+>,得 1n n a b +>,显然()111n na b nn n eea+∞∞==-=∑∑收敛,因为111lim lim 1n n n n n a b n n a b e e eξ++→∞→∞-==-,所以()11n n n ab ∞+=-∑收敛,()11n n n n b a a b ++=--,11n n n n b a b a ++≤-+,于是1nn b∞=∑收敛,1nn b∞=∑收敛.或者()()1ln ln 1n nb b n n n n a e a b a e -+=+=++,()1ln 1limlim 1nb n n n n n nna e ab a a -+→∞→∞+-==,()11n n n a b ∞+=-∑收敛,从而1n n b ∞=∑收敛.(五)、设0na >,()1,2,n =,且nna b n ea e=+,()1,2,n =,若1n n a ∞=∑收敛.,试证1nn nb a ∞=∑收敛.证明:由1nn a∞=∑收敛,得lim 0nn a →∞=,由nn b a n ee a =-,得 lim 0n n b →∞=,因为()22ln lim lim lim n na n n nn n n n n nb e a a b a a a →∞→∞→∞-==()20ln 1lim 2x x e x x +→-==, 又1n n a ∞=∑收敛,所以1nn nb a ∞=∑收敛.(五) 、设0na >,()1,2,n =,1n n a ∞=∑收敛,且nn n aa b n e a e +=+,()1,2,n =,证明:1nn b∞=∑也收敛.证明:由1nn a∞=∑收敛,得lim 0nn a →∞=,再由nn n a a b n e a e +=+,得 lim 0n n b →∞=,()ln n a n n na b e a +=-,()ln n a n n n b e a a =--,()()10ln ln limlim 0n a xnn x ne a ex a x++→∞→--==,()1ln na nn ea ∞=-∑收敛,所以1nn b∞=∑收敛,1nn b∞=∑收敛.()ln n a n n na b e a +=-,因为2limlim n nn n n n n n na b a a ba a →∞→∞++=()()220ln ln 1limlim 2n a xnn x ne a ex a x +→∞→--===,所以1nnn n a b a ∞=+∑收敛,1nn nb a ∞=∑发散.2004年浙江省大学生高等数学(微积分)竞赛试题(工科类) 一. 计算题(每小题15分,满分60分)1. 计算:()()200cos 2lim tan 1x tx x e tdt x x x →----⎰。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
15、 ,则 。
16、设函数 是由 ( )确定,则 。
17、设 在区间 连续, ,
试解答下列问题:(1)用 表示 ;(2)求 ;(3)求证: ;
(4)设 在 内的最大值和最小值分别是 ,求证: .
18、设 为 在 上应用拉格朗日中值定理的“中值”,则
19、设 ,求 。
历届高等数学竞赛真题
一、极限
1、 2、
3、 4、
5、 6、
7、
8、设 ,且 ,求常数
9、设 ,求 、 的值,使 都存在.
10、 ,其中 为常数。
11、 12、
13、设 ,求
14、 15、
16、 17、 ,求
18、设 在 邻域内可导, , ,求
19、设 ,求
20、设函数 在 处连续,求
21、设 ,求
22、 23、
20、已知函数 在 上三阶可导,且 , , ,试证至少存在一点 ,使 ,
21、已知 在 上二次连续可微, ,证明
其中 .
22、求证方程 有且只有一个实数根,其中常数 满足 .
23、设 为实数, ,在 处可导,求 的范围
24、设 , 是正整数,求
25、设 ,求
26、求方程 有几个实根
27、设 ,求
三、积分
5、设 ( ),则 。
6、设 , ,证明级数 收敛,并求其和。
7、设 在 处收敛,则 在 处(D)
(A)绝对收敛;(B)条件收敛;(C)发散;(D)收敛性与an有关.
8、设幂级数 ,当 时 ,且 ;
(1)求幂级数 的和函数 ;(2)求和函数 的极值..
9、求函数 的定义域,并证明 在定义域内有界.
10、级数 ,问 为何值时级数收敛
8、设函数 在 上连续,在 上可导,且 ,证明
(1)存在 ,使
(2)存在 ,使
9、设函数 在 上可导,且 ,证明存在 ,使
10、求点(0,4)到抛物线 的最短距离
11、设 在 上连续,在 上可导,证明至少存在一点 使得
12、设 具有二阶连续导数,且 , 是曲线 上点 处的切线在 轴的截距,求
13、设 在 内有 ,且 ,证明在 内有 .
40、设 41、 ,求
42、设函数 满足 ,且对 时,有 ,证明:
(1) 存在,(2) 。
四、级数
1、判别级数的敛散性
(1) ; (2)
(3) ,其中 为常数(4)
2、求和函数
(1) (2) (3)
(4) (5)
3、求收敛域
(1) (2)
4、已知级数 的一般项 与前 项的和 有如下关系:
( ),且 ,求级数
28、设 ,计算积分 .
29、以 坐标上的平面曲线段 ( )绕 轴旋转所构成的旋转曲面和 坐标面围成一个无盖容器,已知它的底面积为 ,如果以 的速度把水注入容器内,水表面的面积的 增大,试求曲线 的方程.
30、设 时,有 .
31、设 及 ,求 .
32、求曲线 ( )绕 轴旋转一周延伸到无穷远的旋转体体积
25设非负函数 在 上连续,且单调上升, 与直线 及 围成图形的面积为 , 与直线 及 围成图形的面积为 .⑴ 证明:存在唯一的 ,使得 .⑵ 取何值时两部分面积之和取最小值?
26、设函数 在 连续且非负,证明 .
27、设 是曲线 与 轴围成的平面图形,直线 把 分成 和 两部分,若 的面积 与 的面积 之比 ,求平面图形 的周长以及 绕 轴旋转一周所得旋转体的体积.
五、解析几何
1、求两直线 和 之间的最短的距离
2、设圆锥面的顶点在原点,且三个坐标轴的正半轴都在其上,求圆锥面的方程
24、设 ,求
28、已知数列 ,满足 ,证明:
29、已知 , , ,…, ,….
求证:(1)数列 收敛;(2) 的极限值a是方程 的唯一正根
二、导数和微分
1、求 的 阶导数2、 ,求
3、 ,求
4、设 ,当 时,求
5、设 ,求
6、设 ,求
7、 和 互为连续的反函数, ,求
33、设函数 在 ( )上连续,在 可导,且 .
(1)求证: , ,等式 成立.
(2)求极限 .
34、设 ( 表示不超过 的最大整数),求极限
35、求 ,使 ,其中
36、设函数 在 上连续,且 ,设
(1) (2) 在 内恰有一根
37、设 的一个原函数,且 ,求 .
38、设 ,求
39、设 在 上连续,且 ,求
1、 2、
3、 ( )4、
5、 ( )6、
7、 8、
9、 10、
11、 12、
13、 14、
15、 15、
16、 17、
18、 连续,求
19、设 ,且 ,证明
20、当 满足什么条件时, (1)无反正切函数(2)无对数函数
21、设 为连续函数,且 ,求
22、求证 23、设 ,求
24、设 为连续函数,证明
