22 矩形波导
微波技术第3章1矩形波导

可见前五个导模是 TE10、TE20、TE01、 TE11、TM11。
35
则TE10模 TE20模 TE01模 TE11和TM11模 TE21和TM21模 TE12和TM12模
• 当f0 = 10GHz时,λc=3cm
fcTE10=6.562GHz fcTE20=13.123GHz fcTE01=14.764GHz fcTE11=16.156GHz fcTE21=19.753GHz fcTE12=30.248GHz
传播。
编辑ppt
13
TE20模场结构
TE10 TE20
编辑ppt
14
(2)TE01模与TE0n模
其场分量为
Ex
j n
b H mn sin n b y e
jz
Hy
j n
b
ny
H mn sin b e
jz
Hz
ny H mn cos b e
jz
Ey Ez H x 0
TE01模只有Ex、Hy和Hz三个场分量,它们与x无关,故 沿a边场无变化;
波分布或TM11模场;如 图。
注:TE11与TM11是简并模,这种简并称为模式简并; 同理,TEmn与TMmn (m>0, n>0) 是简并模。
编辑ppt
19
3.管壁电流 Js nˆHtan
主模:TE10模工作下
波导底面 y = 0 ; nˆ yˆ
JSy 0 y ˆ [x ˆHx zˆHz] x ˆHz zˆHx
ZTM
Eu Hv
2
1
k
c
编辑ppt
31
(5)TE10模矩形波导的传输功 率
P Re 1 E H * ds 2S
圆波导与矩形波导比较
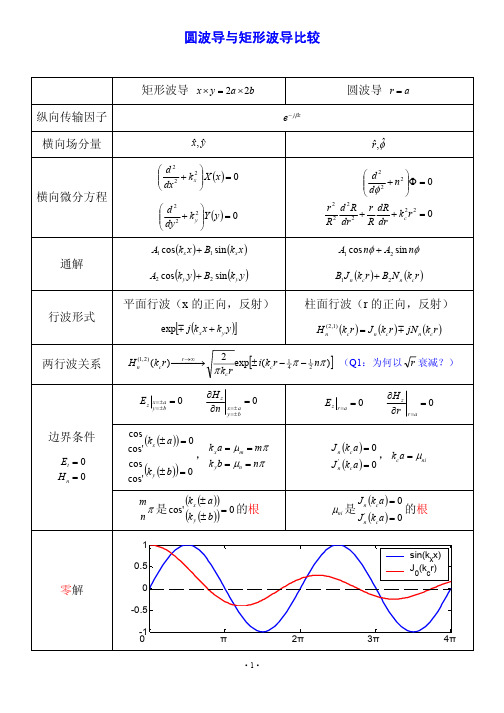
B1 J n (kc r ) + B2 N n (kc r )
平面行波(x 的正向,反射) 行波形式
exp m j (k x x + k y y )
→∞ (1, 2 ) Hn (kc r ) r →
柱面行波(r 的正向,反射)
( 2 ,1) (kc r ) = J n (kc r ) m jN n (kc r ) Hn
驻波波节数: 从中心到边界 的半驻波数
0 0 π 2π 3π 0.5
|sin(kxx)| |J0(kcr)|
4π
相邻波节反相,柱面波周向周期变化 各自周期相等 边界处的函数值取其中一零解上,不同的零点,包含波节数不同 驻波异同 零解从 = 0 开始 等幅驻波 两驻波关系 坐标系/驻波函数的不同仅方便满足边界条件时,函数形式简单 *柱面波的求解方法 3 级数、积分、插值,高阶递推
[
]
两行波关系
2 1 ] (Q1:为何以 r 衰减?) exp[± i(kc r − 1 4 π − 2 nπ ) π kc r
Ez
x=± a y =±b
=0
∂H z ∂n
x=± a y =±b
=0
Ez
r =a
=0
∂H z ∂r
=0
r =a
边界条件
Et = 0 Hn = 0
cos (k x (± a )) = 0 k a = µ m = mπ cos' , x k y b = µ n = nπ cos ( k y (± b )) = 0 cos'
0 -0.5 -1 0 π
·1·
2π
3π
4π
满足边界条件 后的驻波解
cos mπ A cos' a
微波波导型号与详细参数

外截面尺寸(mm) 基本壁厚 内圆角最大 (mm) 直径R1 1.5 1.5 1.5 1.5 1.5 1.2 1.2 1.2 1.2 1.2 1.2 1.2 1.2 0.8 0.8 0.8 0.8 0.8 0.8 0.4 0.4 0.4 0.4 0.4 0.3 0.3 0.2 0.15 0.15 0.15 0.038 6 5 5 3.18 3.18 3.18 3.18 2.03 2.03 2.03 2.03 2.03 1.625 1.625 1.625 1.625 1.625 1.27 1.27 1.015 1.015 1.015 1.015 1.015 1.015 1.015 1.015 1.015 1.015 0.76 0.76 基本宽度 A 待定 待定 待定 待定 待定 待定 待定 169.16 133.6 113.28 90.42 76.2 61.42 50.8 43.64 38.1 31.75 25.4 21.59 17.83 14.99 17.7 10.67 9.14 7.72 6.81 5.79 5.13 4.57 3.556 3.175 基本高度 宽和高的偏 外圆角直径R2 差(±) 最小值 最大值 B 待定 待定 待定 待定 待定 待定 待定 86.61 68.83 58.67 47.24 39.1 32.33 25.4 23.44 19.05 15.88 12.7 12.06 9.93 8.51 6.35 6.35 5.59 4.88 4.42 3.91 3.58 3.3 2.54 2.35 待定 待定 待定 待定 待定 待定 待定 0.2 0.2 0.2 0.17 0.14 0.12 0.1 0.08 0.08 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.025 0.025 待定 待定 待定 待定 待定 待定 待定 1 1 1 1 1 0.8 0.8 0.8 0.8 0.8 0.65 0.65 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 待定 待定 待定 待定 待定 待定 待定 1.5 1.5 1.5 1.5 1.5 1.3 1.3 1.3 1.3 1.3 1.15 1.15 1 1 1 1 1 1 1 1 1 1 0.8 0.8
矩形波导实验

矩形波导实验一.实验目的:1.了解HFSS基本操作,会利用HFSS对波导特性进行仿真。
2.画出电磁场内模式的电磁场分布图。
3.理解并会计算波导中的模式,单模传输,截至频率。
二.实验原理:矩形波导的结构,尺寸a=23mm,b=10mm,内部为真空条件下,在矩形波导内传播的电磁波为TE模。
由截止频率的计算公式由=c/f得,f=c/对于给定的工作频率或波长,只有满足传播条件f>fc的模式才能在波导中传播。
由公式可以看出矩形波导的fc,不仅与波导的尺寸a, b有关,还和模指数m, n 有关。
当a, b一定时,随着f的改变,矩形波导可以处于截止状态。
波导尺寸满足/2<a<2b</2 fc=c/TE10:=2a =46mm fc=6.52GHZTE20=a =23mm fc=13.04GHZTE01=2b=20mm fc=15GHZ波导单模工作频率为a<<2a 2b<工作频率范围为6.52-13GHZ三.实验步骤:1工程设置打开HFSS,出现新的工程窗口(1)设置求解类型Driven Modal(模式激励)(2)设置模型单位毫米(3)保存工程并命名2画波导在屏幕中间模型列表中的Box1为画出的长方体3、设置边界条件(1)选择波导的四个纵向面。
选择多个面(2)将这四个面设置为理想导体边界。
4、设置激励源wave port(1)选中波导的一个端口面(垂直于z轴的平面)建立激励。
5、设置求解频率(1)在菜单栏中点击HFSS>Analysis Setup>Add Solution Setup(2)在求解设置窗口中,设置Solution Frequency:13GHz,其它设为默认值6、计算及后处理在菜单栏中点击HFSS>Analyze all在菜单栏中点击HFSS>Fields>Plot Fields>E,画出电场强度的幅度分布。
在project manager窗口中可以演示电场强度幅度随时间变化情况。
第十章 矩形波导

导波的一般特性 矩形波导
§10.1 导波的一般特性
一、均匀直波导中的电磁场的波动方程 1、几种常见的波导类型及三种基本场型
导 体
内 导 体
外 导 体
2
x
Ex
z y
x Ex Ez
x
Hale Waihona Puke z y Hz
Hx
TE
z y
Hy
TEM
Hy
TM
分别为 TE 波的各分量表达式。 TE 波的波阻抗可由切向分量定义:
ZTE
同时也有:
E0 t H0 t
2 2 E0 x E0 y 2 2 H0 x H0 y
ZTE
E0 y E0 x H0 y H0 x
11
§10.2 矩形波导
一、矩形波导中的TM、TE模 1、矩形波导的结构和模式特点
Er , t AETEM Bn ETMn Cm ETEm
4
2、导波的波动方程
频率为、 沿波导+z 方向传播的电磁波的电场的一 般表达式为:
it i t z E( x, y, z, t ) Ee E0 ( x, y)e
3、TE模式
TE 模式的纵向分量满足的方程为:
H z (k ) H z 0
2 t 2 2
Hz Hz 2 2 (k ) H z 0 2 2 x y
2 2
令 Hz ( x, y) X ( x)Y ( y) ,则上式可用分离变量法求解
1 d X 1dY 2 2 k 2 2 X dx Y dy
矩形波导的模式(3篇)

第1篇一、矩形波导的模式分类矩形波导中的电磁波模式主要分为TE(横电磁波)模式和TM(纵电磁波)模式。
1. TE模式TE模式是指电场只在波导的横向(垂直于传播方向)分量存在,而磁场则在纵向(沿传播方向)分量存在。
根据电场和磁场在波导横截面上的分布,TE模式又可以分为TE10、TE20、TE01等模式。
(1)TE10模式:TE10模式是矩形波导中最基本、最常用的模式。
其电场分布呈矩形,磁场分布呈椭圆。
TE10模式的截止频率最高,适用于高频传输。
(2)TE20模式:TE20模式的电场分布呈矩形,磁场分布呈圆形。
其截止频率低于TE10模式,适用于中频传输。
(3)TE01模式:TE01模式的电场分布呈矩形,磁场分布呈椭圆。
其截止频率最低,适用于低频传输。
2. TM模式TM模式是指磁场只在波导的横向分量存在,而电场则在纵向分量存在。
根据电场和磁场在波导横截面上的分布,TM模式又可以分为TM01、TM11、TM21等模式。
(1)TM01模式:TM01模式的电场分布呈矩形,磁场分布呈圆形。
其截止频率最高,适用于高频传输。
(2)TM11模式:TM11模式的电场分布呈矩形,磁场分布呈椭圆。
其截止频率低于TM01模式,适用于中频传输。
(3)TM21模式:TM21模式的电场分布呈矩形,磁场分布呈圆形。
其截止频率最低,适用于低频传输。
二、矩形波导的模式特性1. 截止频率截止频率是矩形波导中一个重要的参数,它决定了电磁波在波导中能否有效传输。
不同模式的截止频率不同,其中TE10模式的截止频率最高,适用于高频传输。
2. 相速度相速度是指电磁波在波导中传播的速度。
不同模式的相速度不同,TE模式的相速度比TM模式快。
3. 模式损耗模式损耗是指电磁波在波导中传播时,由于波导壁的吸收和辐射等原因,能量逐渐衰减的现象。
不同模式的损耗不同,TE模式的损耗比TM模式小。
4. 传输特性矩形波导中不同模式的传输特性不同,如TE模式的传输特性较好,适用于高频传输;TM模式的传输特性较差,适用于低频传输。
电动力学习题

电动力学复习题一.填空1.a 、k 及0E 为常矢量,则)]sin([0r k E ⋅⋅∇= , )]sin([0r k E ⋅⨯∇= 。
2.真空中一点电荷电量)sin(0t q q ω=,它在空间激发的电磁标势ϕ为 。
3. 电磁场能流密度的意义是 ,其表达式为 。
4.波矢量αβ i k +=,其中相位常数是 ,衰减常数是 。
5.电容率ε'=ε+i ωσ,其中实数部分ε代表 电流的贡献,它不能引起电磁波功率的耗散,而虚数部分是______电流的贡献,它引起能量耗散。
6. 矩形波导中,能够传播的电磁波的截止频率22,,⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=b n a m n m c μεπω,当电磁波的频率ω满足 时,该波不能在其中传播。
若b >a ,则最低截止频率为 。
7.频率为91030⨯Hz 的微波,在0.7cm ⨯0.4cm 的矩形波导管中,能以 波模传播。
8.爱因斯坦质能关系为 。
如果两事件只能用大于光速的信号进行联系,则这两事件 (填:一定不存在/一定存在/可能存在)因果关系,原因是 是一切相互作用传播的极限速度。
9.电荷守恒定律的微分形式为 ,其物理意义为 ;积分形式为 ,其物理意义为 。
10.a 为常矢量,则=⋅∇)(r a , r a )(∇⋅= 。
12. 磁偶极子的矢势)1(A 等于 ;标势)1(ϕ等于 。
13.B =▽⨯A ,若B 确定,则A ____(填确定或不确定),A 的物理意义是 。
14. 变化电磁场的场量E 和B 与势),(ϕA 的关系是E = ,B = 。
15.库仑规范的条件是 ,在此规范下,真空中变化电磁场的标势ϕ满足的微分方程是 。
16.静电场方程的微分形式为 、 _。
电四极矩有 个独立分量。
17. 半径为0R 、电容率为ε的介质球置于均匀外电场中,则球内外电势1ϕ和2ϕ在介质球面上的边界条件可以表示为 和 。
18.金属内电磁波的能量主要是 能量19.良导体条件为 ;它是由 和 两方面决定的。
矩形波导 PPT

m 场量沿x轴[0,a]出现的半周期(半个纯驻波)的数目;
n 场量沿y轴[0,b]出现的半周期的数目。
④j 相位关系 Ey-Hx、Ex-Hy
z轴有功率传输
Ez-Hx、Ez-Hy
x、y轴无功率传输
所以行波状态下,沿波导纵向(z轴)传输有功功率、横向(x、
y轴)无功功率。
2) 场结构
为了能形象和直观的了解场的分布(场结构),可以 利用电力线和磁力线来描绘它。电力线和磁力线遵循 的规律:
力线上某点的切线方向
该点处场的方向
力线的疏密程度
场的强弱
电力线 发自正电荷、止于负电荷,也可以环绕着交变磁场构 成闭合曲线,电力线之间不能相交。在波导壁的内表面(假设为 理想导体)电场的切向分量为零,只有法向分量(垂直分量), 即在波导内壁处电力线垂直边壁。
磁力线 总是闭合曲线,或者围绕载流导体,或者围绕交变电 场而闭合,磁力线之间不能相交,在波导壁的内表面上只能存在 磁场的切向分量,法向分量为零。
3)相速和群速
TMmn和TEmn波型的相速和群速表示式相同:
vp
v
1(/c)2
vg v 1-c2
4)波型阻抗
TMmn和TEmn波型阻抗为:
ZTE
1
1c2
g
ZTM
1c2
g
5)尺寸选择——矩形波导的工作波型图
基于前面的定义,根据波导横截面尺寸、工作波长、 截止波长之间关系,构成矩形波导工作波型图。根据不 同要求,可利用波型图对波导的横截面尺寸和波导波长 作出选择。
TE0n和TEm0是非简并模;其余的TEmn和TMmn都存在简并模: 若a=b, 则TEmn 、TEnm、TMmn和TMnm是简并模;若a=2b,则TE01与TE20,TE02和 TE40,TE50、TE32和TM32是简并模。
标准矩形波导管数据

标 准 型 号 中国-国家 标准 BJ3 BJ4 BJ5 BJ6 BJ8 BJ9 BJ12 BJ14 BJ18 BJ22 BJ26 BJ32 BJ40 BJ48 BJ58 BJ70 BJ84 BJ100 BJ120 BJ140 BJ180 BJ220 BJ260 BJ320 BJ400 BJ500 BJ620 BJ740 BJ900 BJ1200 BJ1400 EIA-国际 标准 WR-2300 WR-2100 WR-1800 WR-1500 WR-1150 WR-975 WR-770 WR-650 WR-510 WR-430 WR-340 WR-284 WR-229 WR-187 WR-159 WR-137 WR-112 WR-90 WR-75 WR-62 WR-51 WR-42 WR-34 WR-28 WR-22 WR-19 WR-15 WR-12 WR-10 WR-8 WR-7 英国-国家 标准 无 无 WG1 WG2 WG3 WG4 WG5 WG6 WG7 WG8 WG9A WG10 WG11A WG12 WG13 WG14 WG15 WG16 WG17 WG18 WG19 WG20 WG21 WG22 WG23 WG24 WG25 WG26 WG27 WG28 WG29 153-IEC 标准 R3 R4 R5 R6 R8 R9 R12 R14 R18 R22 R26 R32 R40 R48 R58 R70 R84 R100 R120 R140 R180 R220 R260 R320 R400 R500 R620 R740 R900 R1200 R1400
矩形波导

仿真分析矩形波导(无探针激励)1.建立三维模型坐标轴 外截面(单位mm)内截面(单位mm)X 轴(a)25.4 22.86 Y 轴(b)12.7 10.16Z 轴 502.设置材料:copper3.设置激励:在Z=0和Z=50mm 的矩形面上设置波端口一、设置频率:fmin 9GHz fmax 11GHz 中心频率10GHz仿真结果与分析理论计算: 工作波长:m m m GHzs mf c 3003.01010100.398==⨯⨯==λ mm mm a cTE 3072.4586.222210>=⨯==λmm mm a cTE 3086.2220<==λmm mm b cTE 3032.2016.102201<=⨯==λ因此,可以判断在工作频率为10GHz 时,只能传输10TE 模。
10TE 模的相位常数m rad a 05.1582122=⎪⎭⎫⎝⎛-=λλπβ 波导波长mm m a g 75.3903975.02122==⎪⎭⎫⎝⎛-==λλβπλ 10TE 模的相速sm a p 8210975.321⨯=⎪⎭⎫ ⎝⎛-==λυβωυ10TE 模的波阻抗Ω=⎪⎭⎫ ⎝⎛-=58.49921120210a Z TE λπ图1.1电场矢量分布图图1.2电场幅度沿Y方向分布图图1.3磁场矢量分布图图1.4磁场幅度沿X方向分布图图1.5磁场幅度沿Z方向分布图S参数图1.6波导仿真11S参数图1.7波导仿真12图1.8回波损耗分析:(1)由图1.1和图1.3可知,电场和磁场沿Z 轴每隔半个波长反向。
电场只有Y 分量,磁场只有X 、Z 分量,且磁场线闭合。
(2)由图1.2、图1.4和图1.5可知,电场幅值Y 分量在宽壁中间最大,磁场幅值X 分量在宽壁中间最大,而磁场幅值Z 分量在宽壁两边最大。
(3)由图 1.1可知,在50mm 的波导中存在大约 1.25个波长,即mm g 4025.150'==λ,在误差允许的范围内,'g g λλ=。
矩形波导尺寸

矩形波导尺寸
矩形波导的尺寸通常由宽度(a)和高度(b)来定义。
这两个尺寸的比例对于波导的模式和特性具有重要影响。
它们的单位可以是米(m)或毫米(mm),具体尺寸取决于所设计的应用和频率范围。
对于一个标准的矩形波导,例如WR90(矩形波导90),其宽度为22.86毫米(0.9英寸),高度为10.16毫米(0.4英寸)。
其他常见的矩形波导尺寸包括:
- WR62:宽度15.88毫米(0.625英寸),高度7.87毫米(0.31英寸);
- WR42:宽度10.16毫米(0.4英寸),高度4.06毫米(0.16英寸);
- WR28:宽度7.11毫米(0.28英寸),高度3.56毫米(0.14英寸)。
需要注意的是,这些尺寸只是一些常见的矩形波导尺寸,并且在实际应用中可能会有其他非标准尺寸的波导。
此外,波导的尺寸还会根据不同的设计要求和频率范围而有所变化。
2.2 矩形波导解析
自 学
§2.2 矩形波导
7.TE10波的波阻抗与等效阻抗
(一) 波阻抗
Z TE 10
1 1 ( / 2 a ) 2
(2-105)
可见TE10波的波阻抗与窄边b的尺寸无关. 因此,如果它完全与传输线的特性阻抗相当,则两个宽边 相等而窄边不等的波导相接时,将无反射存在。 但是实验否定了这一结论。相反这种情况下将发生很大反射。 从而说明:与传输线不同,两个波导的波阻抗并不能保证 它们相匹配。为了寻求波导匹配问题,必须寻求另一个关 于阻抗的量。
§2.2 矩形波导
在y=0宽壁上
J Sz
ˆ (x ˆH x z ˆJ Sx ˆH z ) z ˆJ Sz x J S n H y
a ˆ z H 0 sin( x) cos( t z ) a 2
J Sx
ˆH 0 cos( x
当a=b时,TEmn、TEnm 、TMmn、TMnm是简并波型; 当a=2b时,TE01与TE20 ;TE02与TE40;TE50与TE32;
TEmn、TMmn、是简并波型;等等
唯一的条件:截止波长相等
§2.2 矩形波导
截止频率
f c v / c
1 2
m n a b
ˆE x+y ˆE y+z ˆE z 在直角坐标系中,令 E x
则关于E的矢量波动方程分解为三个标量波动方程,
2 2 其中关于Ez的波动方程为: Ez Ez K 2 E 0 c z 2 2
x
y
(2-62)
同理,Hz所满足的标量形式的波动方程为
2H z x 2 2H z y 2
2 Y '' K y Y 0
第2-5章 矩形波导

Ey Ez Hx
m 1 n 1
j n mx ny j (t z ) E mn sin cos e 2 a b kc b mx ny j (t z ) E mn sin sin e a b j n mx ny j (t z ) E mn sin cos e 2 b a b kc j m mx ny j (t z ) E mn cos sin e 2 a a b kc
如为虚数,令j=a, 则有 EZ=E0Ze-az为衰减波,在波导中为:
2 v c kc f c
2
m / a n / b
2
2
2
则可得截止频率为:
fc v 1 1 m n m n c 2 2 a b 2 a b kc
代入纵横关系式,可得传输型TE模场分量(P52):
Ex Ey
m 0 n 0
j n mx ny j (t z ) H mn cos sin e 2 b a b kc
j m mx ny j (t z ) H mn sin cos e 2 a a b kc m 0 n 0
式中
k
2 c
k
2
2
由于波导中不存在TEM波,故只有TE波和TM波。
1)TE模
E z 0, H z 0
磁场的纵向分量应满足本征值方程:
2 抖H 0 z + 2 抖 x 2
H0z + kc2 H 0 z = 0 y2
对于 H 0 z ( x, y ) 应用分离变量法求解:
H 0 z ( x, y ) X ( x)Y ( y )
chap2 21 22 尺寸选择 波导正规模的特性

三 其他形式的金属柱面波导简介 补充
非对称双脊波导
圆形对称脊波导
应用,如:宽带脊波导滤波器、宽带定向耦合器、双工 器、变频器、移相器、脊波导缝隙天线阵等等。
三 其他形式的金属柱面波导简介
异形波导:椭圆波导、半圆波导、扇形波导
三 其他形式的金属柱面波导简介
林为干 - 微波之父
三 其他形式的金属柱面波导简介
三 其他形式的金属柱面波导简介
微波(通常是指波长为1米至1毫米之间的电磁波) 形成为一门技术科学开始于上世纪30年代,在二次大战期 间得到了全面的发展。当时出于反法西斯战争的需要,微 波的研究集中在雷达方面。在这以后,随着应用研究的不 断扩展,微波理论与技术日趋完善而又不断向纵深及交叉 学科发展。《微波理论与技术汇刊》1994年7月的3位法 国学者认为近代卫星广播通信业所用的多模技术是由拉贡 (Ragan)及林为干提出来的,其发展的基础是根据林为 干及库恩(Cohn)的工作。此项工作至今尚在发展。
2
解得
无量纲
hz AJ n kc r AN n kc r
cos n sin n
cos n sin n
(2.108b) (2.108a)
ez BJ n kc r BN n kc r
一 同轴线中的TE波和TM波 同轴线 圆波导
(2.112a)
代入关系 J 0 J1 ,
N 0 N1 可得
J1 kc a N1 kc b N1 kc a Jkcb 均较大,由大宗量贝塞尔函数的渐近 式(见附录VI)可得
一 同轴线中的TE波和TM波
TM波 由式(2.111b) ,也假定 kc a和kcb 均较大,利用贝塞 尔函数大宗量渐近式可得
第八章矩形波导复习资料0604

第八章 矩形波导1. 波导中的传播条件:f>fc 或λ<λc2. 矩形波导能传输TM 波和TE 波,不能传输TEM 波。
3. 矩形波导中:TEmn 模:m 和n 皆可取0,但又不能同时为0 TMmn 模。
显然,m,n 皆不可能为0,故最低阶模为TM11其中:m 表示电磁场沿波导宽边a 分布的半波数的个数,n 表示电磁场沿波导窄边b 分布的半波数的个数。
当m 和n 取非零值时,TMmn 模和TEmn 模具有相同的截止参数,这种现象称为模式简并,相应的模式称为简并模式。
例如,TM21模和TE21模是简并模式。
4. 波长①工作波长λ:定义:微波振荡源所产生的电磁波的波长。
v f λ==若填充空气,则8310/v c m s ===⨯ 若填充r ε的介质,则v =②波导波长λg :在波导内,合成波沿的等相位面在一个周期内所走过的路程定义为波导波长λg 。
2g πλβ==③截止波长λc :电磁波处于能传输与不能传输的临介状态,此时对应的波长称为截止波长,对应的频率叫截止频率,fc.(或定义为:导行波不能在波导中传输时所对应的最低频率称为截止频率,该频率确定的波长称为截止波长。
)g λλ>c cvf λ==c c v f λ=5.传播速度若填充空气,则8310/v c m s ===⨯ ,若填充r ε的介质,则v =①相速度vp :定义p v ωβ== 或p g v fλ=p v v >②群速度vg :群速度(能速)就是电磁波所携带的能量沿波导纵轴方向(z 轴)的传播速度。
g v =2p g v v v = g v v <6.色散现象:传播速度与频率有关的现象时延失真:波导传输频带内各不同频率的信号传输时间不等,造成信号失真,这种失真称为时延失真。
7. 波阻抗:波导中某种波型的阻抗简称为波阻抗。
定义为波导横截面上该波型的电场强度与磁场强度的比值。
TM波的:x TM y EZ H ==TE 波: TE Z =无界空间中的波阻抗:μηε=空气中:120377ηηπ===Ω介质rε中:0rηηε=8.什么是模式简并?9. 场结构的定义:用电力线(实线)和磁力线(虚线)来表示场强空间变化规律的图形。
波导型号及参数
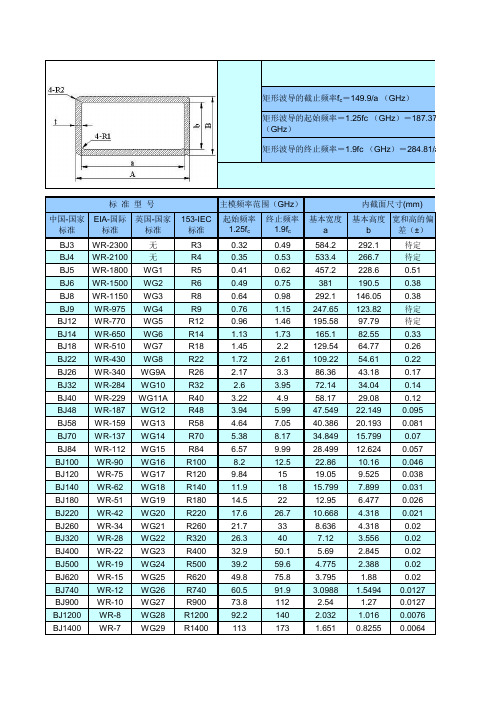
172
BJ2600 WR-3 WG32 R2600
217
220
1.2954 0.6477 0.0064
261
1.0922 0.5461 0.0051
330
0.8636 0.4318 0.0051
GHz) Hz)=187.375/a
z)=284.81/a (GHz)
尺寸(mm)
基本壁厚 内圆角最大 (mm)
R14
1.13
1.73
165.1
R18
1.45
2.2
129.54
R22
1.72
2.61
109.22
R26
2.17
3.3
86.36
R32
2.6
3.95
72.14
R40
3.22
4.9
58.17
R48
3.94
5.99
47.549
R58
4.64
7.05
40.386
R70
5.38
8.17
34.849
R84
6.57
基本宽度 A
待定 待定 待定 待定 待定 待定 待定 169.16 133.6 113.28 90.42 76.2 61.42 50.8 43.64 38.1 31.75 25.4 21.59 17.83 14.99 17.7 10.67 9.14 7.72 6.81 5.79 5.13 4.57 3.556 3.175
0.38 待定 待定
82.55
0.33
64.77
0.26
54.61
0.22
43.18
0.17
34.04
0.14
29.08
《电磁场与微波技术教学课件》2.2 矩形波导

雷达天线
矩形波导可以作为雷达系统的天线, 利用其高方向性和低副瓣特性,提高 雷达的探测精度和距离分辨率。
毫米波雷达
在毫米波雷达中,矩形波导常被用作 发射和接收天线,其宽带宽和低损耗 特性有助于实现高分辨率和高灵敏度 的探测。
测量技术中的应用
微波测量
矩形波导在微波测量技术中常被用作标准测量器件,用于校准和检测微波设备 的性能参数。
100%
军事应用
在二战期间,矩形波导在雷达和 通信系统中得到广泛应用。
80%
技术进步
随着微波技术的不断发展,矩形 波导的性能得到不断提升和优化 。
02
矩形波导的传输特性
传输模式
01
02
03
04
TEM模
在矩形波导中,当工作频率较 低时,只有TM01模可以传输 ,随着频率的升高,会出现 TE11模,TM02模等其他模式 。在某些频率下,可能存在多 个模式同时传输的情况。
矩形波导的应用
雷达系统
矩形波导可用于雷达发射和接收天线,传输高频率 的微波信号。
卫星通信
在卫星通信系统中,矩形波导常用于传输信号,确 保信号的稳定传输。
加热与熔炼
矩形波导的高功率容量使其在工业加热和熔炼中得 到广泛应用。
矩形波导的发展历程
80%
早期研究
20世纪初,科学家开始研究矩形 波导的传输特性。
色散效应
由于色散现象的存在,矩形波导中的信号传输会受到一定的影响。例如,脉冲信号的展宽 、信号畸变等。因此,在设计微波系统时,需要考虑矩形波导的色散效应,以减小其对系 统性能的影响。
பைடு நூலகம் 03
矩形波导的尺寸选择与设计
波导尺寸的选择
01
矩形波导中电磁波截止波长的计算(1)(1)

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载矩形波导中电磁波截止波长的计算(1)(1)地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容矩形波导中电磁波截止波长的计算周和伟物理与电子信息工程学院 07物理学 07234030[摘要]:本文从麦克斯韦方程组出发,从理论上推导了电磁场遵循的波动方程和时谐电磁波遵循的波动方程;根据边值关系从理论上求出了时谐电磁波在矩形波导中的解,并对矩形波导管中传播的电磁波波解进行了讨论;计算了不同尺寸的矩形波导管的截止波长,截止波长大多属于厘米量级,说明波导管只适用于传播微波。
[关键词]:矩形波导电磁波截止波长1 绪言波导是一种用来约束或引导电磁波传输的装置,矩形波导是指横截面是矩形的波导,一般是中空的金属管。
也有其他形式的波导装置,如介质棒或由导电材料和介质材料组成的混合构件[1]。
因此,在广义的定义下,波导不仅是指矩形中空金属管,同时也包括其他波导形式如矩形介质波导等,还包括双导线、同轴线、带状线、微带和镜像线、单根表面波传输线等。
根据波导横截面的形状不同还有其他形状波导,如圆波导等。
尽管已存在很多不同波导形式,且新的形式还不断出现,但直到目前,在实际应用中矩形波导是一种最主要的波导形式。
由于无线信号传输媒介,具有传输频带宽、传输损耗小、可靠性高、抗干扰能力强等特点,因此波导技术在电子技术领域运用非常广泛,主要用于铁氧体结环形器,窄壁缝隙天线阵[2],速调管矩形波导窗,高精度矩形弯铜波导管加工研究【3】等器件设备的制造生产,以及在地铁信号系统中的应用都很广泛。
为了加深对波导传输特性的理解,本文从麦克斯韦方程组出发,推导了电磁场遵循的波动方程和时谐电磁波遵循的波动方程;根据边值关系从理论上求出了时谐电磁波在矩形波导中的解,并对矩形波导管中传播的电磁波波解进行了讨论;计算了不同尺寸的矩形波导管的截止波长,发现其截止波长都在厘米量级,说明波导管只适用于传播微波。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C1、 C2、 C3、 C4、Kx、Ky为待定常数 (6个)
§2.2 矩形波导
则横向场的四个分量表示为
Hx
j
Kc2
H0
m
a
sin
m
a
x
cos
n
b
y e j z
Hy
j
Kc2
H0
n
b
cos
m
a
x
sin
n
b
y e j z
Ex
j
Kc2
H0
n
b
cos
m
a
x
sin
n
b
y e j z
(2-83)
Ez (x, y, z) X (x)Y(y)Z(z) E0 cos(Kxx x )cos(Ky y y )e jz (2-72)
待定常数:E0=ABA+ 、φx、 φy 、Kx、Ky (5个) 同样,磁场可写成 Hz (x, y) H0 cos(Kxx x )cos(K y y y )e jz (2-82)
x e j z
Hz (x,
y)
H0
cos(
a
x)e
j z
Ey
j a
H0
sin
a
x e j z
沿x方向是一个“半驻波” 沿y方向均匀分布,无变化 沿z方向是行波 (2-88)
则
二阶导数
X '' X
Y '' Y
K c2
横向截止波数
K
2 x
K
2 y
K
2 x
K
2 y
Kc2
且 X '' Kx2X 0
X C1 cos(Kxx) C2 sin(Kxx) (2-68)
Y '' K y2Y 0 通解 Y C3 cos(K y y) C4 sin(K y y) (2-69)
则关于E的矢量波动方程分解为三个标量波动方程,
其中关于Ez的波动方程为:
2Ez x2
2Ez y2
K c2 E z
0
同理,Hz所满足的标量形式的波动方程为
2Hz x2
2Hz y2
Kc2H z
0
(2-62)
§2.2 矩形波导
对Ez采用分离变量法求解, 设 Ez (x, y) X (x)Y ( y)e jz
m, n 0
§2.2 矩形波导
分析:
(1) m、n为自然数,分别表示常量沿x轴和y轴出现的 半周期数;
(2) 不同的m、n对应一种波型TEmn,m、n不能同时为零, 但有一个可以取零。 最低次波型为TE10(a>b)或TE01 (a<b)。
(3) 场量沿z轴为行波,沿x轴和y轴为纯驻波
(4) 主模:最低次模
TEm0和TE0n是非简并波型。
举例 当a=b时,TEmn、TEnm 、TMmn、TMnm是简并波型; 当a=2b时,TE01与TE20 ;TE02与TE40;TE50与TE32; TEmn、TMmn、是简并波型;等等
唯一的条件:截止波长相等
§2.2 矩形波导
截止频率
fc
v / c
2
1
m 2 n 2 a b
Kc2
K
2 x
K
2 y
m
a
2
n
b
2
Ey
j
Kc2
H0
m
a
sin m
a
xcos n
b
y e j z
Kc
m
2
n
2
a b
§2.2 矩形波导
通解也可以写成下面的形式
X Acos(Kxx x ) (2-70) Y B cos(K y y y ) (2-71)
A、φx、 B、 φy 、Kx、Ky为待定常数 (6个) 当考虑纵向行波传输规律时,电场强度可写成
为了保证单一的H10波传输,波导尺寸必须满足:
(c ) H20 (c ) H10
a 2a
(c ) H01
2b
§2.2 矩形波导
2.2.4 矩形波导的主模—TE10
1.场表达式
Ez 0
电力线只分布在波导的横截面内
基模:TE10(a>b)
m 1, n 0
Hx
ja
H0
sin
a
截止频率不仅与波型和波导尺寸有关,还与波导中所 填充的介质有关
f>fc的波型可以在波导中传播
波导中截止波长最长的模称为该波导的主模(基模, 最低次模),其它的称为高次模。
矩形波导的主模是TE10(a>b时),其截止波长最长,为2a。
§2.2 矩形波导
因此,矩形波导中可传输的波型为
TE0n、 TEm0、 TEmn、TMmn
§2.2 矩形波导
2.2.3 矩形波导中的波型
1.波型 截止波数的表达式为 分析:
Kc
K
2 x
K
2 y
m
2
n
2
a b
(1)m、n为自然数,分别表示常量沿x轴和y轴出现的半周期 数,也是半驻波数;
(2)不同的m、n对应一种波型TMmn,但不存在TMm0、TM0n、 TM00 (3三)种场波量型沿,z轴最为低行次波波,型沿为xT轴M和11y; 轴为纯驻波;
(4)表达式中,有j的分量和无j的场分量表示相位差90°,
如果是时间相差,就是T/4,如果是空间相差,就是λg/4;
(5)由S E,H在* z向有实功率,传输能量;在横向是虚功率,只存
储能量。
§2.2 矩形波导
2.截止波长和简并波形
截止波数:
Kc2
K
2 x
K
2 y
m
a
2
n
b
2
Kc
m 2 n 2
TE10模
一般来说,用a表示波导宽边,b表示窄边,a>b,K10=π/a是所 有波型中波数最小的,因此TE波型的最低次波型是TE10模。
§2.2 矩形波导
3.传输条件
波导中不同模式的截止波长是不同的,对于特定尺寸的波导,
只有满足 c 的模才能得到传输。
例如:a=2b的矩形波导
c
2
Kc
2
m a
a b
截止波长:
c
2
Kc
2
m a
2
n b
2
(2-84)
Kc、c 是波导横截面尺寸和波型的函数
λ<λc的 波型可以 在波导中 传播
§2.2 矩形波导
简并现象: 截止波长相同的波型,如TEmn和TMmn
具有简并现象的波型,它们的截止频率、相速、群速、 波导波长都是相等的。
哪些情况下无简并现象?
2
nபைடு நூலகம்b
2
TE20 TM11 TE01 TE11
TTEM2211 0.707a a
TE10
截 止 区
2a
当a<λ<2a时,波导中只传 输TE10模,单模工作.
0.894a
a=2b矩形波导截 止波长分布图
§2.2 矩形波导
一般尺寸,截止波长见Page56表格2-1
H10(即TE10)波的截止波长最大,它最容易在波导中传播。
§2.2 矩形波导
本节内容:讨论矩形波导中电磁波的波型、传输特性、 管壁电流,矩形波导的实际应用,以及 等效阻抗的概念。
y
b
x
o
a
z
§2.2 矩形波导
2.2.1(2.2.2) 矩形波导中的TM波和TE波
纵向场法求解
矢量波动方程为
2E
Kc2
E
0
(2-61) 2H Kc2H 0
在直角坐标系中,令 E xˆEx+yˆEy+zˆEz
