(完整版)八年级的上册的三角形相关证明题大全(适用于复习巩固).docx
八年级全等三角形简单证明题及答案(15道)
如图，在△ABC中，D是BC的中点，DE⊥AB， DF⊥AC，垂足分别是E，F，BE=CF． 求证：AD是△ABC的角平分线．
证明：∵DE⊥AB，DF⊥AC， ∴Rt△BDE=Rt△DCF=90°． BD=DC BE=CF ， ∴Rt△BDE≌Rt△DCF（HL）， ∴DE=DF， 又∵DE⊥AB，DF⊥AC， ∴AD是角平分线． 角平分线的性质；全等三角形的判定与性质．
1.已知：如图，AB=AE，∠1=∠2，∠B=∠E．求证： BC=ED．
证明：∵∠1=∠2， ∴∠1+∠BAD=∠2+∠BAD， 即：∠EAD=∠BAC， 在△EAD和△BAC中 ∠B=∠E AB=AE ∠BAC=∠EAD ， ∴△ABC≌△AED（ASA）， ∴BC=ED． 全等三角形的判定与性质．
2.如图，在△ABC中，∠C=90°，点D是AB边上的一点，DM⊥AB，
且DM=AC，过点M作ME∥BC交AB于点E．求证：△ABC≌△MED。
证明：∵MD⊥AB， ∴∠MDE=∠C=90°， ∵ME∥BC， ∴∠B=∠MED， 在△ABC与△MED中， ∠B=∠MED ∠C=∠EDM DM=AC ， ∴△ABC≌△MED（AAS）． 全等三角形的判定．
6.已知：如图，点E，A，C在同一直线上，AB∥CD， AB=CE，AC=CD， ∴∠BAC=∠ECD， 在△BAC和△ECD中 AB=EC ∠BAC=∠ECD AC=CD ， ∴△BAC≌△ECD（SAS）， ∴CB=ED． 全等三角形的判定与性质．
7.如图，D、E分别是AB、AC上的点，且 AB=AC，AD=AE．求证：∠B=∠C．
如图，E、F是四边形ABCD的对角线BD上的两点，AE∥CF， AE=CF，BE=DF．求证：△ADE≌△CBF．
(完整版)八年级上册——全等三角形证明题题型归类训练
(完整版)八年级上册——全等三角形证明题题型归类训练-CAL-FENGHAI.-(YICAI)-Company One1《全等三角形》证明题题型归类训练题型1：全等+等腰性质1、如图，在△ABE 中，AB ＝AE,AD ＝AC,∠BAD ＝∠EAC, BC 、DE 交于点O. 求证：(1) △ABC ≌△AED ； (2) OB ＝OE .2、已知：如图，B 、E 、F 、C 四点在同一条直线上，AB ＝DC ，BE ＝CF ，∠B ＝∠C ．求证：OA ＝OD ．题型2：两次全等1、AB=AC ，DB=DC ，F 是AD 的延长线上的一点。
求证：BF=CFFDCBA2、已知如图，E 、F 在BD 上，且AB ＝CD ，BF ＝DE ，AE ＝CF ，求证：AC 与BD 互相平分O C E BDAABEO FD3、如图，在四边形ABCD 中，AD ∥BC ，∠ABC=90°DE ⊥AC 于点F ，交BC 于点G ，交AB 的延长线于点E ，且AE=AC.求证：BG=FG题型3：直角三角形全等（余角性质）1、如图，在等腰Rt △ABC 中，∠C ＝90°，D 是斜边上AB 上任一点，AE ⊥CD 于E ，BF ⊥CD 交CD 的延长线于F ，CH ⊥AB 于H 点，交AE 于G ． 求证：BD ＝CG ．AFC BDEG2、如图，将等腰直角三角形ABC 的直角顶点置于直线l 上，且过A ，B 两点分别作直线的垂线，垂足分别为D ，E ，请你在图中找出一对全等三角形，并写出证明它们全等的过程．3、如图，∠ABC ＝90°，AB ＝BC ，D 为AC 上一点，分别过A 、C 作BD 的垂线，垂足分别为E 、F 求证：EF ＝CF －AE4、在△ABC 中，︒=∠90ACB ，BC AC =，直线MN 经过点C ，且MN AD ⊥于D ，MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时， 求证： ①ADC ∆≌CEB ∆；②BE AD DE +=；(2)当直线MN 绕点C 旋转到图2的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成立，说明理由.ABC FD E5、如图：BE ⊥AC ，CF ⊥AB ，BM=AC ，CN=AB 。
八年级上册数学全等三角形证明题
八年级上册数学全等三角形证明题一、全等三角形证明题1 20题及解析。
（一）题目1。
1. 题目。
已知：如图，在△ABC中，AD是BC边上的中线，E是AD上一点，且BE = AC，延长BE交AC于F。
求证：AF = EF。
2. 解析。
证明：延长AD到G，使DG = AD，连接BG。
因为AD是BC边上的中线，所以BD = CD。
在△BDG和△CDA中，BD = CD，∠BDG = ∠CDA（对顶角相等），DG = DA。
根据SAS（边角边）全等判定定理，可得△BDG≌△CDA。
所以BG = AC，∠G = ∠CAD。
又因为BE = AC，所以BG = BE。
所以∠G = ∠BEG。
因为∠BEG = ∠AEF（对顶角相等），所以∠AEF = ∠CAD。
所以AF = EF。
（二）题目2。
1. 题目。
如图，在△ABC和△DEF中，AB = DE，BE = CF，∠B = ∠DEF。
求证：AC = DF。
2. 解析。
因为BE = CF，所以BE + EC = CF+EC，即BC = EF。
在△ABC和△DEF中，AB = DE，∠B = ∠DEF，BC = EF。
根据SAS全等判定定理，可得△ABC≌△DEF。
所以AC = DF。
（三）题目3。
1. 题目。
已知：如图，AB = CD，AE = DF，CE = FB。
求证：AF = DE。
2. 解析。
因为CE = FB，所以CE + EF = FB + EF，即CF = BE。
在△AEB和△DFC中，AB = CD，AE = DF，BE = CF。
根据SSS（边边边）全等判定定理，可得△AEB≌△DFC。
所以∠B = ∠C。
在△ABF和△DCE中，AB = CD，∠B = ∠C，BF = CE。
根据SAS全等判定定理，可得△ABF≌△DCE。
所以AF = DE。
（四）题目4。
1. 题目。
如图，在Rt△ABC中，∠ACB = 90°，CA = CB，D是AC上一点，E在BC的延长线上，且AE = BD，BD的延长线与AE交于点F。
人教版八年级数学上册 第12章 全等三角形证明经典50题(含答案)
1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=22. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB延长CD 与P ，使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2AD BC证明：连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ，可得，∠EFD ＝CGDDE ＝DC∠FDE ＝∠GDC （对顶角）∴△EFD ≌△CGDEF ＝CGB ACDF21E∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC为等腰三角形，AC＝CG又EF＝CG∴EF＝AC5.已知：AD平分∠BAC，AC=AB+BD，求证：∠B=2∠CA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C6.已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE 上取F ，使EF ＝EB ，连接CF∵CE ⊥AB∴∠CEB ＝∠CEF ＝90°∵EB ＝EF ，CE ＝CE ，∴△CEB ≌△CEF∴∠B ＝∠CFE∵∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180°∴∠D ＝∠CFA∵AC 平分∠BAD∴∠DAC ＝∠FAC∵AC ＝AC∴△ADC ≌△AFC （SAS ）∴AD ＝AF∴AE ＝AF ＋FE ＝AD ＋BE7. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE＜AE＜AB+BE ∵AB=4即4-2＜2AD＜4+21＜AD＜3∴AD=28.已知：D是AB中点，∠ACB=90°，求证：12 CD AB9.已知：BC=DE，∠B=∠E，∠C=∠D，F是CD中点，求证：∠1=∠2证明：连接BF 和EF 。
八年级三角形的证明题
八年级三角形的证明题一、等腰三角形性质相关证明题（8题）1. 已知：在△ABC中，AB = AC，AD是BC边上的中线。
求证：AD⊥BC。
- 证明：- 因为AB = AC，AD是BC边上的中线，所以BD = DC（中线的定义）。
- 在△ABD和△ACD中，AB = AC（已知），BD = CD（已证），AD = AD（公共边）。
- 所以△ABD≌△ACD（SSS）。
- 则∠ADB=∠ADC（全等三角形对应角相等）。
- 又因为∠ADB + ∠ADC = 180°（平角的定义），所以∠ADB = ∠ADC = 90°，即AD⊥BC。
2. 已知：在等腰△ABC中，AB = AC，∠A = 36°，求证：∠B = 72°。
- 证明：- 因为AB = AC，所以∠B = ∠C（等腰三角形两底角相等）。
- 又因为∠A+∠B + ∠C = 180°（三角形内角和定理），∠A = 36°。
- 设∠B = x，则∠C = x，可得方程36°+x + x = 180°。
- 2x=180° - 36°，2x = 144°，解得x = 72°，即∠B = 72°。
3. 已知：在△ABC中，AB = AC，D是AC上一点，且AD = BD = BC。
求∠A的度数。
- 证明：- 设∠A=x，因为AD = BD，所以∠ABD = ∠A=x（等边对等角）。
- 则∠BDC=∠A + ∠ABD = 2x（三角形外角性质）。
- 因为BD = BC，所以∠C = ∠BDC = 2x。
- 又因为AB = AC，所以∠ABC = ∠C = 2x。
- 根据三角形内角和定理，∠A+∠ABC+∠C = 180°，即x + 2x+2x = 180°。
- 5x = 180°，解得x = 36°，所以∠A = 36°。
初二数学三角形证明练习题
初二数学三角形证明练习题三角形是初中数学中一个重要的几何形状，证明三角形的性质是数学证明中的基本内容之一。
在初二数学中，我们将通过一些练习题来巩固和提高我们对三角形性质的理解和运用。
一、证明角平分线相交于三角形内心已知△ABC 中，∠BAD 和∠CAE 是∠BAC 的两条角平分线，我们要证明 BD 和 CE 的交点 D 是三角形 ABC 的内心。
证明过程如下：1. 过 B 作 BD 的垂线，交 AC 于 F；2. 过 C 作 CE 的垂线，交 AB 于 G；3. 要证明 GD = FD，即证明 D 是△ABC 的内心。
证明过程分析：我们可以利用角平分线的性质以及垂线的性质进行推理。
证明过程：由于∠BAD 是∠BAC 的角平分线，所以∠DAB = ∠DAC。
又因为∠BAD = ∠CAD，所以△ADB ≌△ADC，从而 AD = AD。
同理可证，AE = AE。
根据反身性质可得：△AFB ≌△AGC（共边 AB ≌ AC，∠BAC = ∠CAB = 90°）。
所以 AF = AG。
在△AFG 中，AD 是∠FAG 的角平分线（∠BAD = ∠CAD）。
所以 DF = FG。
因此，从 AF = AG 和 DF = FG，可以推出 D 是 AF 和 DG 的交点，也就是△ABC 的内心。
综上所述，我们证明了角平分线相交于三角形的内心。
二、证明勾股定理已知△ABC 是一个直角三角形，其中∠C = 90°，我们要证明勾股定理，即 a^2 + b^2 = c^2。
证明过程如下：1. 过 C 作 AB 的垂线，交 AB 于 D；2. 连接 CD。
证明过程分析：我们可以利用勾股定理的核心思想，即直角三角形中，两直角边的平方和等于斜边的平方。
证明过程：由于 CD 与 AB 垂直，所以△ABC 和△CBD 相似。
根据相似三角形的性质可得：AB/BC = BC/BD。
进一步推导可得：(AB/BC) ×(BC/BD) = 1。
八年级上册三角形相关证明题大全(适用于复习巩固).doc
三角形证明题1、求证：三角形一边的中线小于其他两边和的一半。
(1)已知ZkABC中,AB=4cm ,BC=6cm ,BD是厶ABC的中线，求BD的取值范围.(2)在厶ABC中,AO5,中线AD=7,则AB边的取值范围是()A. 1<AB<29B. 4<AB<24C. 5<AB<19D. 9<AB<19(3)在AABC 中，AD 是BC±的中线，求证：AD<l/2 (AB+AC)。
2、如图，已知在AABC中，ZB AC为直角，AB二AC, D为AC上一点，CE丄BD于E・(1)若BD 平分ZABC,求证CE^BD；(2)若D为AC上一动点，ZAED如何变化，若变化，求它的变化范围；若不变，求岀它的度数，并说明理由。
3、在AABC屮，，AB二AC,在AB边上取点D,在AC延长线上了収点E ,使CE=BD , 连接DE交BC 于点F,求证DF=EF・4、如图，取一张长方形纸片，用A、B、C、D表示其四个顶点，将其折叠，使点D与点B重合。
图中有没有全等的三角形，如果有，请先用“仝”表示出来，再说明理由。
5、如图所示，AABC 中，ZACB=90° , AC=BC, AE 是BC 边上的中线，过C 作CF 丄AE,垂足为F, 过B 作BD 丄BC 交CF 的延长线于D.求证：(1)AE=CD; (2)若 AC 二 12cm,求 BD 的长.6、在Z\ABC 中，AB=AC, ZBAC=90° , BD 是中线，AF 丄BD, F 是垂足，过点C 作AB 的平行 线交AF 的延长线于点E o 求证：(1) ZABD 二ZFAD ； (2) AB=2CE8、如图，在AABC 中，D 是BC 的中点，E 、F 分别是AB 、AC 上的点，且FD 丄ED ,求证：BE+CF >EF 9、ABCD 为正方形，CE 平分ZDCF, M 为线段BC ±的点，连接AM 、ME, 问:AM 和ME 有何大小关系？当M 点在射线BC 上运动时,AM 和ME 的大小关系改变吗?7、如图所示，AB=AC , AD 丄BC 于D ,且 AB+AC+BC 二50,而 AB+BD+AD=40,则 AD 为多少?B MC F10、如图，在AABC中，AD丄BC , CE丄AB ,垂足分别为D、E , AD、CE交于点H,已知EH=EB=3, AE=4,则CH的长是多少？为什么？11、如图，已知ZXABC中，ZBAC=90°, AB二AC, AE是过A的一条直线，且B、C在A、E 的异侧,BD 丄AE于D, CE丄AE于E系如何？为什么？⑶ 若直线AE绕A点旋转到图⑶位置时(BD>CE),其余条件不变，问BD与DE、CE的关系如何？请直接写出结果，不需说明.12、在AABC中ZBAC是锐角，AB=AC, AD和BE是高，它们交于点且AE二BE；(1)求证:AH=2BD；(2)若将ZBAC改为钝角，其余条件不变，上述的结论还成立？立，请说明理由；13、如图所示，已知D 是等腰AABC 底边BC 上的一点，它到两腰AB 、AC 的距离分别为DE 、DF, CM 丄AB,垂足为请你探索一下线段DE 、DF 、CH 三者之间的数量关系，并给予证明.14、在 RtAABC 中，AB=AC, ZBAC=90° , 0 为 BC 的中点.(1) 写出点0到AABC 的三个顶点A 、B 、C 的距离的大小关系，并说明理由.(2) 若点M 、N 分别是AB 、AC 上的点,且BM=AN,试判断△OMN 形状，并证明你的结论.15、如图22⑴，AB 二CD, AD 二BC, O 为AC 中点，过O 点的直线分别与AD 、BC 相交于 点M 、N,那么Z1与Z2有什么关系？请说明理由。
8上全等三角形证明经典50题(含答案)
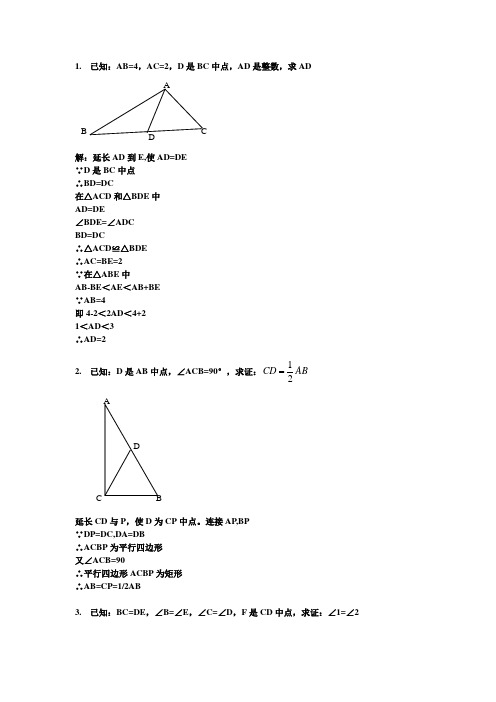
1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=22. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB延长CD 与P ，使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2AD BC证明：连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ，可得，∠EFD ＝CGDDE ＝DC∠FDE ＝∠GDC （对顶角）∴△EFD ≌△CGDEF ＝CGB ACDF21E∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC为等腰三角形，AC＝CG又EF＝CG∴EF＝AC5.已知：AD平分∠BAC，AC=AB+BD，求证：∠B=2∠CA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C6.已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE 上取F ，使EF ＝EB ，连接CF∵CE ⊥AB∴∠CEB ＝∠CEF ＝90°∵EB ＝EF ，CE ＝CE ，∴△CEB ≌△CEF∴∠B ＝∠CFE∵∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180°∴∠D ＝∠CFA∵AC 平分∠BAD∴∠DAC ＝∠FAC∵AC ＝AC∴△ADC ≌△AFC （SAS ）∴AD ＝AF∴AE ＝AF ＋FE ＝AD ＋BE7. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=28. 已知：D 是AB 中点，∠ACB=90°，求证：1CD AB9. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
三角形证明题
1、求证：三角形一边的中线小于其他两边和的一半。
（1 ）已知△ ABC 中， AB=4cm ,BC=6cm ,BD是△ ABC的中线,求BD的取值范围.
（2）在△ ABC中 ,AC=5, 中线 AD=7,则 AB边的取值范围是 ( )
A.1<AB<29
B.4<AB<24
C.5<AB<19
D.9<AB<19
（3）在△ ABC 中， AD 是 BC 上的中线，求证： A D＜ 1/2 （ AB+AC）。
2、如图，已知在△ABC中，∠ BAC为直角， AB=AC， D 为 AC上一点， CE⊥ BD于 E．
1
（1）若 BD平分∠ ABC，求证 CE= BD；
2
（2）若 D为 AC上一动点，∠ AED如何变化，若变化，求它的变化范围；若不变，求出它的度数，并说明理由。
C
DE
B A
3、在△ ABC 中， ,AB=AC ，在 AB 边上取点 D ，在 AC 延长线上了取点 E ，使 CE=BD，连接 DE 交 BC 于点 F，求证 DF=EF .
A
D
F
C
B
E 4、如图，取一张长方形纸片，用 A 、 B 、C 、D 表示其四个顶点，将其折叠，使点 D 与点 B 重合。
图中有没有全等的三角形，如果有，请先用“≌”表示出来，再说明理由。
A Ｅ
D
B
ＦC
Ｃ｀
5、如图所示 , △ ABC中, ∠ ACB=90° ,AC=BC,AE是 BC边上的中线 , 过 C 作 CF⊥ AE, 垂足为 F,
过 B 作 BD⊥ BC交 CF的延长线于 D.
求证 :(1)AE=CD;(2)若AC=12cm,求BD的长.
A
D
F
B E C
C 作AB的平行
6、在△ ABC中， AB=AC，∠ BAC=90°， BD是中线， AF⊥ BD，F 是垂足，过
点
线交 AF 的延长线于点 E 。
求证：（ 1）∠ ABD=∠ FAD；（2）AB=2CE
B
E
F
A D C
7、如图所示， AB=AC，A D⊥ BC于D，且AB+AC+BC=50，而AB+BD+AD=40，则AD为多少？
C
A D
B
8、如图，在△ ABC中，D 是 BC的中点， E、F 分别是 AB、AC上的点，且 FD⊥ED ，求证： BE+CF ﹥E F
A
F
E
B
D C
9、 ABCD 为正方形， CE 平分∠ DCF ， M 为线段 BC 上的点，连接AM 、 ME ，
问：AM 和 ME 有何大小关系？当M 点在射线 BC 上运动时，AM 和 ME 的大小关系改变吗？
D 、 E， AD、C
E 交于点H，已知
10、如图，在△ABC 中， AD⊥ BC ， CE⊥ AB ，垂足分别为
EH=EB=3， AE=4，则 CH的长是多少？为什么？
A
E
H
C
B D
11、如图 , 已知△ ABC 中 , ∠ BAC=90 0, AB=AC,AE 是过 A 的一条直线 , 且 B、C在 A、E
的异侧 , BD ⊥AE 于 D, CE⊥AE 于 E
(1) 试说明 : BD=DE+CE.
(2)若直线 AE 绕 A 点旋转到图 (2) 位置时 (BD<CE), 其余条件不变 , 问 BD 与 DE、 CE 的关系如何 ? 为什么？
(3)若直线 AE 绕 A 点旋转到图 (3)位置时 (BD>CE), 其余条件不变 , 问 BD 与 DE 、CE 的关系如何 ? 请直接写出结果 , 不需说明 .
12、在△ ABC中∠ BAC是锐角， AB=AC， AD和 BE是高，它们交于点H，且 AE=BE；
（1）求证： AH=2BD；
（2）若将∠ BAC改为钝角，其余条件不变，上述的结论还成立？若成立，请证明；若不成
立，请说明理由；A
E
H
C
B D
13、如图所示 , 已知 D是等腰△ ABC底边 BC上的一点 , 它到两腰 AB、AC的距离分别为 DE、DF,CM ⊥AB, 垂足为 M,请你探索一下线段 DE、 DF、 CM三者之间的数量关系 , 并给予证明 .
A
M
F
E
B D C
14、在 Rt△ ABC中， AB=AC，∠ BAC=90°， O为 BC的中点 .
(1) 写出点 O 到△ ABC的三个顶点 A、 B、 C 的距离的大小关系，并说明理由.
(2)若点 M、 N 分别是 AB、 AC上的点，且 BM=AN，试判断△ OMN形状，并证明你的结论 .
15、如图 22⑴， AB=CD ， AD=BC ， O 为 AC 中点，过O 点的直线分别与点 M 、 N，那么∠ 1 与∠ 2 有什么关系？请说明理由。
若过 O 点的直线旋转至图⑵、⑶的情况，其余条件不变，那么图⑴中的∠系成立吗？请说明理由。
AD 、 BC 相交于
1 与∠
2 的关
16、在△ ABC中， AD平分∠ BAC， DE∥ AC， EF⊥ AD交 BC延长线于F，求证：∠ FAC=∠ B
A
E
G
B F
D C
17、（易错题）在△ ABC 中，已知∠ A=1 ∠ B= 1
∠ C ，求∠ A 、∠ B 、∠ C 的度数．
3 5
18、如图 19 所示 , 在△ ABC 中 ,AD 平分∠ BAC,AB+BD=AC,求∠ B: ∠ C 的值 .
A
B
D
C
(19)
19、已知：如图， AF 平分∠ BAC ， BC ⊥ AF ， 垂足为 E ，点 D 与点 A 关于点 E 对称， PB 分别
与线段 CF ， AF 相交于 P ， M ．
(1)求证： AB=CD ；
(2)若∠ BAC=2 ∠MPC ，请你判断∠ F 与∠ MCD
的数量关系，并说明理由．
C
P
A
ED M F
B
20、如图，在△ ABC 中，∠ ABC=45 0，CD ⊥ AB 于 D ，BE 平分
∠相交于点 F ， H 是 BC 边的中点，连结 DH 与 BE 相交于点 G 。
(1) 求证： BF=AC
（ 2）求证 :CE= 1
BF
2
(3)CE 与 BG 的大小关系如何？试证明你的结论。
ABC ，且 BE ⊥AB 于 E,与 CD
A
D
E
F
G
C
B
H
21、如图，已知△ABC的周长是 21， OB，OC 分别平分∠ABC和∠ACB，OD⊥BC于D，且OD＝3，求△ ABC的面积．
A
O
B
C
D
22、已知 :在四边形 ABCD 中,BC>BA,AD=DC,BD平分∠ ABC。
（1）求证：∠ A+∠ C=180 °
（2）作 DH⊥ BC ，求证： BH=1/2（ AB+BC）
A
D
B H C。