四边形综合提高练习题
八年级下册四边形提高练习
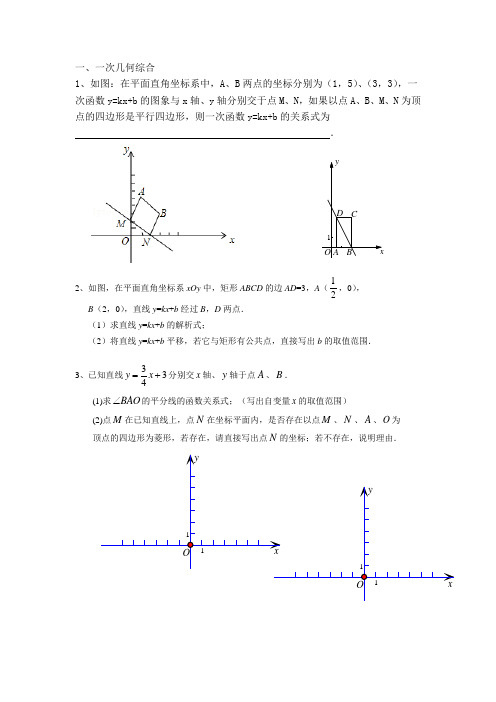
1D CB A xO y 一、一次几何综合1、如图:在平面直角坐标系中,A 、B 两点的坐标分别为(1,5)、(3,3),一次函数y=kx+b 的图象与x 轴、y 轴分别交于点M 、N ,如果以点A 、B 、M 、N 为顶点的四边形是平行四边形,则一次函数y=kx+b 的关系式为 .2、如图,在平面直角坐标系xOy 中,矩形ABCD 的边AD =3,A (12,0), B (2,0),直线y =kx +b 经过B ,D 两点. (1)求直线y =kx +b 的解析式;(2)将直线y =kx +b 平移,若它与矩形有公共点,直接写出b 的取值范围.3、已知直线334y x =+分别交x 轴、y 轴于点A 、B . (1)求BAO ∠的平分线的函数关系式;(写出自变量x 的取值范围)(2)点M 在已知直线上,点N 在坐标平面内,是否存在以点M 、N 、A 、O 为 顶点的四边形为菱形,若存在,请直接写出点N 的坐标;若不存在,说明理由.O11yxO11yx二、勾股定理:1、已知:点P 为正方形ABCD 内一点,连接PA 、PB 、PC ,若AP 2+CP 2=2PB 2, 求证:A 、P 、C 三点共线2、 请阅读下列材料:问题:如图1,点A ,B 在直线l 的同侧,在直线l 上找一点P ,使得BP AP +的值最小.小明的思路是:如图2,作点A 关于直线l 的对称点'A ,连接B A ',则B A '与直线l 的交点P 即为所求.P BAll图2图1AB请你参考小明同学的思路,探究并解决下列问题:(1)如图3,在图2的基础上,设'AA 与直线l 的交点为C ,过点B 作l BD ⊥,垂足为D . 若1=CP ,2=PD ,1=AC ,写出BP AP +的值为 ; (2)将(1)中的条件“1=AC ”去掉,换成“AC BD -=4”,其它条件不变,写出此时BP AP +的值 ;图3lCABPA'D(3)1)32(2+-m +4)28(2+-m 的最小值为.3. 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:222.a b c+=证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a.∵S四边形ADCB=S△ACD+S△ABC=b2+a b.又∵S四边形ADCB=S△ADB+S△DCB=c2+a(b﹣a)∴b2+ab=c2+a(b﹣a)∴222.a b c+=请参照上述证法,利用图2完成下面的证明.将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:222.a b c+=FCDBAE4. 有一块直角三角形纸片,两直角边AC = 6cm ,BC = 8cm .①如图1,现将纸片沿直线AD 折叠,使直角边AC 落在斜边AB 上,则CD = _________ cm .图1 图2②如图2,若将直角∠C 沿MN 折叠,点C 与AB 中点H 重合,点M 、N 分别在AC 、BC 上,则2AM 、2BN 与2MN 之间有怎样的数量关系?并证明你的结论.三、正方形压轴:1.设E 、F 分别在正方形ABCD 的边BC ,CD 上滑动保持且∠EAF =45°.若AB =5,求△ECF的周长.2.如图,P 是正方形ABCD 对角线AC 上一点,点E 在BC 上,且PE=PB .(1)求证:PE=PD ;(2)连接DE ,试判断∠PED 的度数,并证明你的结论.APABHM N AC BD3.如图,正方形ABCD 的边长为6,点O 是对角线AC ,BD 的交点, 点E 在CD 上,且DE =2CE ,连接BE .过点C 作CF ⊥BE ,垂足为点F , 连接OF .求(1)CF 的长; (2)OF 的长.4. (1)如图1,将∠EAF 绕着正方形ABCD 的顶点A 顺时针旋转,∠EAF 的两边交BC 于E ,交CD 于F ,连接EF .若∠EAF=45°,BE 、DF 的长度是方程2560x x -+=的两根,请直接写出EF 的长;(2)如图2,将∠EAF 绕着四边形ABCD 的顶点A 顺时针旋转,∠EAF 的两边交CB 的延长线于E ,交DC 的延长线于F ,连接EF .若AB=AD ,∠ABC 与∠ADC 互补,∠EAF=21∠BAD ,请直接写出EF 与DF 、BE 之间的数量关系,并证明你的结论;(3)在(2)的前提下,若BC=4,DC=7,CF=2,求△CEF 的周长.图1(1)EF 的长为: ; (2)数量关系: ; 证明:EDB DC5、如图,已知正方形ABCD 和正方形AEFG ,连结BE 、DG . (1)求证:BE =DG ,BE ⊥DG ;(2)连接BD 、EG 、DE ,点M 、N 、P 分别是BD 、EG 、DE 的中点,连接MP,PN,MN ,求证:MPN ∆是等腰直角三角形;(3)若AB =4,EF,45DAE ∠=o,直接写出MN = .6、如图,在正方形ABCD 外侧作直线DQ ,点C 关于直线DQ 的对称点为P ,连接DP 、AP ,AP 交直线DQ 于点F ,交BD 于点E . (1)依题意补全图形;(2)若25QDC ∠=︒,求DPA ∠的度数;(3)探究线段AE 、EF 、FP 的等量关系并加以证明.7.已知,如图,正方形ABCD 的边长为6,菱形EFGH 的三个顶点E ,G ,H 分别在正方形ABCD的边AB ,CD ,DA 上,AH=2,连接CF . (1)当DG=2时,求证:菱形EFGH 是正方形; (2)设DG=x ,用含x 的代数式表示FCG △的面积; (3)判断FCG △的面积能否等于1,并说明理由.A DH QDCBAGFEDCBA8、操作,将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线上滑动,直角的一边始终经过B点,另一边与射线DC相交于点Q. 设AP =x.(1)当Q点在CD上时,线段PQ与线段PB的大小关系怎样?并证明你的结论;(2)当Q在CD上时,设四边形PBCQ面积为y,求y与x之间的函数关系,并写出x的取值范围;(3)当点P在线段AC上滑动,且Q在DC延长线上时,△PCQ能否为等腰三角形?若能,求出x的值;若不能,说明理由.(1)结论:PQ_____PB 证明:(2)解:(3)解:图1图2(备用)图3(备用)9.如图,四边形ABCD 是正方形,△ABE 是等边三角形,M 为对角线BD (不含B 点)上任意一点....,连接AM 、CM .其中BN=BM ,∠MB N=60°,连接 EN . (1)证明:△A BM ≌△EBN(2)当M 点在何处时,AM +BM +CM 的值最小,并说明理由;(3)当AM +BM +CM 1时,求正方形的边长.五、涉及中点类:1.在中,∠A =∠DBC , 过点D 作DE =DF , 且∠EDF =∠ABD , 连接EF 、 EC , M 、N 、P 分别为EF 、EC 、BC 的中点,连接NP .请你发现∠ABD 与∠MNP 满足的等量关系,并证明.2.如图1,在△ACB 和△AED 中,AC=BC ,AE=DE ,∠ACB =∠AED =90°,点E 在AB 上,点D 在AC 上.(1)若F 是BD 的中点,求证:CF=EF ;(2) 将图1中的△AED 绕点A 顺时针旋转,使AE 恰好在AC 上(如图2).若F 为BD 上一点,且CF=EF ,求证:BF= DF ;(3)将图1中的△AED 绕点A 顺时针旋转任意的角度(如图3).若F 是BD 的中点.探究CE 与EF 的数量关系,并证明你的结论.附加题(本题10分,每小题5分)26.Rt△ABC 中,∠BAC=90°,AB=AC=2,以AC 为一边,在△ABC 外部作等腰直角三角形 ACD ,则线段BD 的长为 .3. 在△ABC 中,D 为BC 中点,BE 、CF 与射线AE 分别相交于点E 、F (射线AE 不经过点D ). (1)如图①,当BE ∥CF 时,连接ED 并延长交CF 于点H . 求证:四边形BECH 是平行四边形;(2)如图②,当BE ⊥AE 于点E ,CF ⊥AE 于点F 时,分别取AB 、AC 的中点M 、N ,连接ME 、MD 、NF 、ND . 求证:∠EMD =∠FND .图① 图②FHDBEN MFDBE4.如图,在矩形ABCD 中,AB =3,BC =4,点M 、N 、分别在BC 、AB 上,将矩形ABCD 沿MN 折叠,设点B 的对应点是点E . (1)若点E 在AD 边上,BM =27,求AE 的长; (2)若点E 在对角线AC 上,请直接写出AE 的取值范围:_________.5. 阅读下列材料:问题:如图1,在□ABCD 中,E 是AD 上一点,AE =AB ,∠EAB =60°,过点E 作直线EF ,在EF 上取一点G ,使得∠EGB =∠EAB ,连接AG .求证:EG =AG +BG .小明同学的思路是:作∠GAH =∠EAB 交GE 于点H ,构造全等三角形,经过推理解决问题.参考小明同学的思路,探究并解决下列问题: (1)完成上面问题中的证明;(2)如果将原问题中的“∠EAB =60°”改为“∠EAB =90°”,原问题中的其它条件不变(如图2),请探究线段EG 、AG 、BG 之间的数量关系,并证明你的结论. (1)证明:(2)解:线段EG 、AG 、BG 之间的数量关系为____________________________.M NEDCBA 图1图26.若一个四边形的一条对角线把四边形分成两个等腰三角形,我们把这条对角线叫这个四边形的和谐线,这个四边形叫做和谐四边形.如菱形就是和谐四边形.(1)如图1,在四边形ABCD中,AD∥BC,∠BAD=120°,∠C=75°,BD平分∠ABC.求证:BD是四边形ABCD的和谐线;(2)图2和图3中有三点A、B、C,且AB=AC,请分别在图2和图3方框内...作一个点D,使得以A、B、C、D为顶点的四边形的两条对角线都是和谐线,并画出相应的和谐四边形(要求尺规作图,保留作图痕迹,不写作法..................);(3)四边形ABCD中,AB=AD=BC,∠BAD=90°,AC是四边形ABCD的和谐线,求∠BCD 的度数.(1)证明:(2)在方框内用尺规作图,..........保留作图痕迹,不写作法...........(3)解:图1图3图27、如图,菱形ABCD 的对角线长分别为2和5,动点P 在对角线AC 上运动(不与点A 或C 重合),且PE ∥BC 交AB 于点E ,PF ∥CD 交AD 于点F.请问:阴影部分的面积是否随点P 的运动而变化?若变化,说明理由;若不变,求出相应的值。
2022年人教版中考数学一轮复习:四边形综合 专项练习题2(Word版,含答案)

2022年人教版中考数学一轮复习:四边形综合专项练习题21.如图,已知四边形ABCD是平行四边形,从①AB=AD,②AC=BD,③∠ABC=∠ADC中选择一个作为条件,补充后使四边形ABCD成为菱形,则其选择是(限填序号).2.如图1,平行四边形纸片ABCD的面积为120,AD=15.今沿两对角线将四边形ABCD剪成甲、乙.丙、丁四个三角形纸片.若将甲、丙合并(AD、CB重合)形成一个对称图形戊,如图2所示.则图形戊的两条对角线长度之和为.3.如图,菱形ABCD的两条对角线AC,BD交于点O,BE⊥AD于点E,若AC=8,BD=6,则BE的长为.4.如图,在▱ABCD中,∠A=70°,DB=DC,CE⊥BD于E,则∠BCE=.5.如图,在菱形ABCD中,AB=BD,点E、F分别在AB、AD上,且AE=DF,连接BF与DE交于点H,若CG=1,则S=.四边形BCDG6.如图,正方形瓷砖图案是四个全等且顶角为45°的等腰三角形.已知该瓷砖的面积是1m2,则中间小正方形的面积为m2.7.如图所示,在Rt△ABC外作等边△ADE,点E在AB边上,AC=5,∠ABC=30°,AD=3.将△ADE沿AB方向平移,得到△A′D′E′,连接BD′.给出下列结论:①AB=10;②四边形ADD′A′为平行四边形;③AB平分∠D′BC;④当平移的距离为4时,BD′=3.其中正确的是(填上所有正确结论的序号).8.如图,菱形ABCD的对角线AC,BD相交于点O,P为AB边上一动点(不与点A,B重合),PE⊥OA于点E,PF⊥OB于点F,若AB=4,∠BAD=60°,则EF的最小值为.9.如图,在正方形ABCD中,点E为BC边上一点,且CE=2BE,点F为对角线BD上一点,且BF=2DF,连接AE交BD于点G,过点F作FH⊥AE于点H,若HG=2cm,则正方形ABCD 的边长为cm.10.把图1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图2,图3所示的正方形,则图1中菱形的面积为.11.如图,在正方形ABCD内有一点P,若AP=4,BP=7,DP=9,则∠APB的度数为.12.如图是两个边长分别为2a,a的正方形,则△ABC的面积是.13.如图,点P是正方形ABCD内一点,连接AP、BP、DP,若AP=1,PD=,∠APB=135°,则正方形ABCD的面积为.14.如图,正三角形ABC与正方形CDEF的顶点B,C,D三点共线,动点P沿着CA由C向A 运动.连接EP,若AC=10,CF=8.则EP的最小值是.15.如图,正方形ABCD中,H为CD上一动点(不含C、D),连接AH交BD于G,过点G作GE⊥AH交BC于E,过E作EF⊥BD于F,连接AE,EH.下列结论:①AG=EG;②∠EAH=45°;③BD=2GF;④GE平分∠FEC.正确的是(填序号).16.如图,平面内三点A、B、C,AB=4,AC=3,以BC为对角线作正方形BDCE,连接AD,则AD的最大值是.17.如图,在正方形ABCD中,点E在对角线AC上,EF⊥AB于点F,EG⊥BC于点G,连接FG,若AB=8,则FG的最小值为.18.如图,正方形ABCD的边长为2,点E是BC的中点,连接AE与对角线BD交于点G,连接CG并延长,交AB于点F,连接DE交CF于点H,连接AH.以下结论:①CF⊥DE;②=;③GH=;④AD=AH,其中正确结论的序号是.19.如图,矩形ABCD中,对角线AC、BD交于点O,AE⊥BD于E,若∠DAE=3∠BAE.则的值为.20.将矩形ABCD按如图所示的方式折叠,BE、EG、FG为折痕,若顶点A、C、D都落在点O 处,且点B、O、G在同一条直线上,同时点E、O、F在另一条直线上.(1)的值为.(2)若AD=4,则四边形BEGF的面积为.参考答案1.解:①∵四边形ABCD是平行四边形,AB=AD,∴平行四边形ABCD是菱形;②∵四边形ABCD是平行四边形,AC=BD,∴平行四边形ABCD是矩形;③∵四边形ABCD是平行四边形,∴∠ABC=∠ADC,因此∠ABC=∠ADC时,四边形ABCD还是平行四边形;故答案为:①.2.解:如图,连接AD、EF,则可得对角线EF⊥AD,且EF与平行四边形的高相等.∵平行四边形纸片ABCD的面积为120,AD=1520,∴BC=AD=15,EF×AD=×120,∴EF=8,又BC=15,∴则图形戊中的四边形两对角线之和为20+3=23,故答案为23.3.解:∵四边形ABCD是菱形,∴AO=CO=4,BO=DO=3,AC⊥BD,∴AD===5,=AD×BE=×AC×BD,∵S菱形ABCD∴BE=,故答案为:.4.解:∵四边形ABCD是平行四边形,∴∠BCD=∠A=70°,∵DB=DC,∴∠DBC=∠BCD=70°,∵CE⊥BD,∴∠CEB=90°,∴∠BCE=20°.故答案为:20°.5.解:过点C作CM⊥GB于M,CN⊥GD,交GD的延长线于N.∵四边形ABCD为菱形,∴AB=AD=CD=BC,∵AB=BD,∴AB=BD=AD=CD=BC,∴△ABD为等边三角形,△BCD是等边三角形,∴∠A=∠BDF=60°,∠ADC=60°,在△ADE和△DBF中,,∴△ADE≌△DBF(SAS),∴∠ADE=∠DBF,∵∠FBC =60°+∠DBF ,∠NDC =180°﹣(120°﹣∠ADE )=60°+∠ADE ,∴∠NDC =∠FBC ,在△CDN 和△CBM 中,,∴△CDN ≌△CBM (AAS ),∴CM =CN ,在Rt △CBM 与Rt △CDN 中,,∴Rt △CBM ≌Rt △CDN (HL ),∴S 四边形BCDG =S 四边形CMGN .S 四边形CMGN =2S △CMG ,∵∠CGM =60°,∴GM =CG =,CM =CG =,∴S 四边形BCDG =S 四边形CMGN =2S △CMG =2×××=, 故答案为:.6.解:如图,作大正方形的对角线,作小正方形的对角线并延长交大正方形各边于中点, 设小正方形的边长为xm , 则大正方形的边长为x +x x =(1)xm , ∵瓷砖的面积是1m 2,∴大正方形的边长为1m ,即(1)x =1, 解得x =﹣1, ∴中间小正方形的面积为()2=3﹣2, 故答案为:3﹣2.7.解:∵∠ACB=90°,AC=5,∠ABC=30°,∴AB=2AC=10,故①正确;由平移的性质得:A'D'=AD,A'D'∥AD,∴四边形ADD′A′为平行四边形,故②正确;当平移的距离为4时,EE'=4,∴BE'=AB﹣AE﹣EE'=10﹣3﹣4=3,由平移的性质得:∠A'D'E'=∠A'E'D'=∠AED=60°,A'D'=D'E'=DE=AD=3,∴BE'=D'E',∴∠E'BD'=∠E'D'B=∠A'E'D'=30°,∴∠A'D'B=60°+30°=90°,∴BD'=A'D'=3,故④正确;由④得:当平移的距离为4时,∠E'BD'=∠ABC=30°,故③错误;故答案为:①②④.8.解:连接OP,∵四边形ABCD是菱形,∴AC⊥BD,∠CAB=DAB=30°,∵PE⊥OA于点E,PF⊥OB于点F,∴∠EOF=∠OEP=∠OFP=90°,∴四边形OEPF是矩形,∴EF=OP,∵当OP取最小值时,EF的值最小,∴当OP⊥AB时,OP最小,∵AB=4,∴OB=AB=2,OA=AB=2,∴S=OA•OB=AB•OP,△ABO∴OP==,∴EF的最小值为,故答案为:.9.解:如图,过F作FI⊥BC于I,连接FE,FA,∴FI∥CD,∵CE=2BE,BF=2DF,∴设BE=EI=IC=a,CE=FI=2a,AB=3a,∴则FE=FC=FA=a,∴H为AE的中点,∴AH=HE=AE=a,∴AG=AH+GH=a+2,∵四边形ABCD是正方形,∴BE∥AD,∴==,∴GE=AG=(a+2),∵GE=HE﹣GH=a﹣2,∴(a+2)=a﹣2,解得,a=,∴AB=3a=.故答案为:.10.解:设图1中分成的直角三角形的长直角边为a,短直角边为b,,得,∴图1中菱形的面积为:×4=48,故答案为48.11.解:∵四边形ABCD为正方形,∴∠ABC=90°,BA=BC,∴△BAP绕点A逆时针旋转90°可得△ADE,连接PE,由旋转的性质得,ED=BP=7,AE=AP=4,∠PBE=90°,∠AED=∠APB,∴△APE为等腰直角三角形,∴PE=AP=4,∠AEP=45°,在△PED中,∵PD=9,ED=7,PE=4,∴DE2+PE2=DP2,∴△PED为直角三角形,∠PED=90°,∴∠AED=90°+45°=135°,∴∠APB=135°,故答案为:135°.12.解:∵两个正方形的边长分别为2a,a,∴△ABC的的高为:2a+a,底边为:BC=a,∴△ABC的面积是:(2a+a)•a=a2.故答案为:a2.13.解:如图,将△APB绕点A逆时针旋转90°得到△AHD,连接PH,过点A作AE⊥DH交DH的延长线于E,∴△APB≌△AHD,∠PAH=90°,∴PB=DH,AP=AH=1,∠APB=∠AHD=135°,∴PH=AP=,∠APH=∠AHP=45°,∴∠PHD=90°,∴DH===2,∵∠AHD=135°,∴∠AHE=45°,∵AE⊥DH,∴∠AHE=∠HAE=45°,∴AE=EH,AH=AE,∴AE=EH=,∴DE=,∵AD2=AE2+DE2=13,∴正方形的面积为13,故答案为:13.14.解:如图,过点E作EP⊥AC,交FC于点G,当EP⊥AC时,EP取得最小值,∵正三角形ABC与正方形CDEF的顶点B,C,D三点共线,∴∠ACB=60°,∠FCD=90°,∴∠ACF=30°,∴∠CGP=∠EGF=60°,∵∠F=90°,∴∠FEG=30°,设PG=x,则CG=2x,∴FG=CF﹣CG=8﹣2x,∴EG=2FG=2(8﹣2x),∵FG=EF,∴8﹣2x=8×,∴x=4﹣,∴EP=EG+PG=2(8﹣2x)+x=16﹣3x=4+4.故答案为:4+4.15.解:连接GC,延长EG交AD于点L,∵四边形ABCD为正方形,∴AD∥CB,AD=CD,∠ADG=∠CDG=45°,∵DG=DG,∴△ADG≌△CDG(SAS),∴AG=GC,∠HCG=∠DAG,∵∠HCG+∠GCB=90°,∴∠DAG+∠GCB=90°,∵GE⊥AH,∴∠AGL=90°,∴∠ALG+∠LAG=90°,∵AD∥CB,∴∠ALG=∠GEC,∴∠GEC+∠LAG=90°,∴∠GEC=∠GCE,∴GE=GC,∴AG=EG,故①正确;∵GE⊥AH,∴∠AGE=90°,∵AG=EG,∴∠EAH=45°,故②正确;连接AC交BD于点O,则BD=2OA,∵∠AGF+∠FGE=∠GEF+∠EGF=90°,∴∠AGF=∠GEF,∵AG=GE,∠AOG=∠EFG=90°,∴△AOG≌△GFE(AAS),∴OA=GF,∵BD=2OA,∴BD=2GF,故③正确.过点G作MN⊥BC于点N,交AD于点M,交BC于点N,∵G是动点,∴GN的长度不确定,而FG=OA是定值,∴GE不一定平分∠FEC,故④错误;故答案为:①②③.16.解:将△ABD绕点D顺时针旋转90°,得△MCD,如图:由旋转不变性可得:CM=AB=4,AD=MD,且∠ADM=90°,∴△ADM是等腰直角三角形,∴AD=AM,AD最大,只需AM最大,而在△ACM中,AM<AC+CM,∴当且仅当A、C、M在一条直线上,即不能构成△ACM时,AM最大,且最大值为AC+CM =AC+AB=7,此时AD=AM=,故答案为:.17.解:连接BE,如图:∵四边形ABCD是正方形,∴∠ABC=90°,又EF⊥AB于点F,EG⊥BC,∴四边形FBGE是矩形,∴FG=BE,所以当BE最小时,FG就最小,根据垂线段最短,可知当BE⊥AC时,BE最小,当BE⊥AC时,在正方形ABCD中,△AEB是等腰直角三角形,在Rt△ABE中,根据勾股定理可得2BE2=AB2=64,解得BE=4,∴FG最小为4;故答案为4.18.解:∵四边形ABCD是边长为2的正方形,点E是BC的中点,∴AB=AD=BC=CD=2,BE=CE=,∠DCE=∠ABE=90°,∠ABD=∠CBD=45°,∴△ABE≌△DCE(SAS),∴∠CDE=∠BAE,DE=AE,∵AB=BC,∠ABG=∠CBG,BG=BG,∴△ABG≌△CBG(SAS),∴∠BAE=∠BCF,∴∠BCF=∠CDE,又∵∠CDE+∠CED=90°,∴∠BCF+∠CED=90°,∴∠CHE=90°,∴CF⊥DE,故①正确;∵CD=2,CE=,由勾股定理得,DE===5,=CD×CE=DE×CH,∵S△DCE∴CH=2,∵∠CHE=∠CBF,∠BCF=∠ECH,∴△ECH∽△FCB,∴=,∴=,∴CF=5,∴HF=CF﹣CH=3,∴=,故②正确;如图,过点A作AM⊥DE于点M,∵DC=2,CH=2,由勾股定理得,DH===4,∵∠CDH+∠ADM=90°,∠DAM+∠ADM=90°,∴∠CDH=∠DAM,又∵AD=CD,∠CHD=∠AMD=90°,∴△ADM≌△DCH(AAS),∴CH=DM=2,AM=DH=4,∴MH=DM=2,又∵AM⊥DH,∴AD=AH,故④正确;∵DE=5,DH=4,∴HE=1,∴ME=HE+MH=3,∵AM⊥DE,CF⊥DE,∴∠AME=∠GHE,∵∠HEG=∠MEA,∴△MEA∽△HEG,∴=,∴=,∴HG=,故③错误.综上,正确的有:①②④.故答案为:①②④.19.解:∵四边形ABCD是矩形,∴∠BAD=90°,OA=AC,OB=BD,AC=BD,∴OA=OB,∴∠OAB=∠OBA,∵∠DAE=3∠BAE,∴∠BAE=×90°=22.5°,∵AE⊥BD,∴∠OAB=∠OBA=90°﹣22.5°=67.5°,∴∠OAE=67.5°﹣22.5°=45°,∴△AOE是等腰直角三角形,∴OA=OE,设OE=a,则OB=OA=a,∴BE=OB﹣OE=(﹣1)a,BD=2OB=2a,∴DE=BD﹣BE=2a﹣(﹣1)a=(+1)a,∴==,故答案为:.20.解:(1)由折叠可得,AE=OE=DE,CG=OG=DG,∴E,G分别为AD,CD的中点,设CD=2a,AD=2b,则AB=OB=2a,DG=OG=CG=a,BG=3a,BC=AD=2b,∵∠C=90°,在Rt△BCG中,CG2+BC2=BG2,∴a2+(2b)2=(3a)2,∴b=a,∴===,由折叠可得:∠ABE=∠EBG,∠AEB=∠BEO,∠DEG=∠GEO,∵∠AEB=∠BEO+∠DEG=∠GEO=180°,∴∠BEG=90°,∵∠A=∠BEG=90°,∠ABE=∠EBG,∴△ABE∽△EBG,∴==,故答案为:;(2)∵AD=BC=2b=4,∴b=2,a=2,∴AB=OB=4,CG=2,AE=OE=2,∴BG=6,∵∠OBF =∠CBG ,由折叠可得∠BOF =∠BCG =90°, ∴△BOF ∽△BCG , ∴=, 即=,∴OF =,∴S 四边形EBFG =S △BEG +S △BFG =×6×2+×6×=9. 故答案为:9.。
2021年中考复习数学压轴题:四边形 综合专题练习

2021年中考数学压轴题专题练习:四边形综合复习1、如图,在△ABC中,AB=AC,点D、E分别是线段BC、AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.(1)求证:△BDE≌△FAE;(2)求证:四边形ADCF为矩形.2、如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:(1)EA是∠QED的平分线;(2)EF2=BE2+DF2.3、如图,点E是正方形ABCD的边BC延长线上一点,连结DE,过顶点B作BF⊥DE,垂足为F,BF分别交AC于H,交BC于G.(1)求证:BG=DE;(2)若点G为CD的中点,求的值.4、已知:在平行四边形ABCD中,点E、F分别在AD和BC上,点G、H在对角线AC上,且BF=DE,AH=CG,连接FH 、HE 、BG 、FG .(1)求证:FG=EH .(2)若EG 平分∠AEH ,FH 平分∠CFG ,FG//AB ,∠ACD=68°,∠GFH=35°,求∠GHF 的度数.5、如图,点E 是正方形ABCD 的边BC 上一点,连接DE ,将DE 绕着点E 逆时针旋转90°,得到EG ,过点G 作GF ⊥CB ,垂足为F ,GH ⊥AB ,垂足为H ,连接DG ,交AB 于I .(1)求证:四边形BFGH 是正方形;(2)求证:ED 平分∠CEI ;(3)连接IE ,若正方形ABCD 的边长为,则△BEI 的周长为 .6、如图,正方形CD AB 的边长为1,点E 为边AB 上一动点,连结C E 并将其绕点C 顺时针旋转90得到CF ,连结DF ,以C E 、CF 为邻边作矩形CFG E ,G E 与D A 、C A 分别交于点H 、M ,GF 交CD 延长线于点N .(1)证明:点A 、D 、F 在同一条直线上;(2)随着点E 的移动,线段D H 是否有最小值?若有,求出最小值;若没有,请说明理由;(3)连结F E 、MN ,当//F MN E 时,求AE 的长.7、定义:有一个内角为90°,且对角线相等的四边形称为准矩形.(1)如图1,准矩形ABCD中,∠ABC=90°,若AB=2,BC=3,则BD=_____;(2)如图2,正方形ABCD中,点E、F分别是边AD、AB上的点,且CF⊥BE,求证:四边形BCEF是准矩形;(3)已知,准矩形ABCD中,∠ABC=90°,∠BAC=60°,AB=2,当△ADC为等腰三角形时,求这个准矩形的面积.8、【性质探究】如图,在矩形ABCD中,对角线AC,BD相交于点O,AE平分∠BAC,交BC于点E.作DF⊥AE于点H,分别交AB,AC于点F,G.(1)判断△AFG的形状并说明理由.(2)求证:BF=2OG.【迁移应用】(3)记△DGO的面积为S1,△DBF的面积为S2,当时,求的值.【拓展延伸】(4)若DF交射线AB于点F,【性质探究】中的其余条件不变,连结EF,当△BEF的面积为矩形ABCD 面积的时,请直接写出tan∠BAE的值.9、若边长为6的正方形ABCD绕点A顺时针旋转,得正方形AB′C′D′,记旋转角为a.(I)如图1,当a=60°时,求点C经过的弧CC 的长度和线段AC扫过的扇形面积;(Ⅱ)如图2,当a=45°时,BC与D′C′的交点为E,求线段D′E的长度;(Ⅲ)如图3,在旋转过程中,若F为线段CB′的中点,求线段DF长度的取值范围.10、△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.(1)观察猜想如图1,当点D在线段BC上时,①BC与CF的位置关系为:.②BC,CD,CF之间的数量关系为:;(将结论直接写在横线上)(2)数学思考如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.(3)拓展延伸如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2,CD=BC,请求出GE的长.11、点P 是平行四边形ABCD 的对角线AC 所在直线上的一个动点(点P 不与点A 、C 重合),分别过点A 、C 向直线BP 作垂线,垂足分别为点E 、F .点O 为AC 的中点.(1)如图1,当点P 与点O 重合时,线段OE 和OF 的关系是 ;(2)当点P 运动到如图2所示的位置时,请在图中补全图形并通过证明判断(1)中的结论是否仍然成立?(3)如图3,点P 在线段OA 的延长线上运动,当∠OEF =30°时,试探究线段CF 、AE 、OE 之间的关系.12、如图(1),在矩形ABCD 中,8,6AB AD ==,点,E F 分别是边,DC DA 的中点,四边形DFGE 为矩形,连接BG .(1)问题发现在图(1)中,CE BG=_________; (2)拓展探究将图(1)中的矩形DFGE绕点D旋转一周,在旋转过程中,CEBG的大小有无变化?请仅就图(2)的情形给出证明;(3)问题解决当矩形DFGE旋转至,,B G E三点共线时,请直接写出线段CE的长.13、如图,四边形ABCD是正方形,点O为对角线AC的中点.(1)问题解决:如图①,连接BO,分别取CB,BO的中点P,Q,连接PQ,则PQ与BO的数量关系是,位置关系是;(2)问题探究:如图②,△AO'E是将图①中的△AOB绕点A按顺时针方向旋转45°得到的三角形,连接CE,点P,Q分别为CE,BO'的中点,连接PQ,PB.判断△PQB的形状,并证明你的结论;(3)拓展延伸:如图③,△AO'E是将图①中的△AOB绕点A按逆时针方向旋转45°得到的三角形,连接BO',点P,Q分别为CE,BO'的中点,连接PQ,PB.若正方形ABCD的边长为1,求△PQB的面积.14、已知:Rt△EFP和矩形ABCD如图①摆放(点P与点B重合),点F,B(P),C在同一直线上,AB=EF=6cm,BC=FP=8cm,∠EFP=90°,如图②,△EFP从图①的位置出发,沿BC方向匀速运动,速度为1cm/s,EP与AB交于点G;同时,点Q从点C出发,沿CD方向匀速运动,速度为1cm/s.过点Q作QM⊥BD,垂足为H,交AD于点M,连接AF,FQ,当点Q停止运动时,△EFQ也停止运动.设运动时间为t(s)(0<t<6),解答下列问题:(1)当t为何值时,PQ∥BD?(2)设五边形AFPQM的面积为y(cm2),求y与t之间的函数关系式;(3)在运动过程中,是否存在某一时刻t,使S五边形AFPQM :S矩形ABCD=9:8?若存在,求出t的值;若不存在,请说明理由.(4)在运动过程中,是否存在某一时刻t,使点M在线段PG的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.15、问题背景:如图1,在四边形ABCD中,∠BAD=90°,∠BCD=90°,BA=BC,∠ABC=120°,∠MBN =60°,∠MBN绕B点旋转,它的两边分别交AD、DC于E、F.探究图中线段AE,CF,EF之间的数量关系.小李同学探究此问题的方法是:延长FC到G,使CG=AE,连接BG,先证明△BCG≌△BAE,再证明△BFG≌△BFE,可得出结论,他的结论就是;探究延伸1:如图2,在四边形ABCD中,∠BAD=90°,∠BCD=90°,BA=BC,∠ABC=2∠MBN,∠MBN绕B点旋转.它的两边分别交AD、DC于E、F,上述结论是否仍然成立?请直接写出结论(直接写出“成立”或者“不成立”),不要说明理由;探究延伸2:如图3,在四边形ABCD中,BA=BC,∠BAD+∠BCD=180°,∠ABC=2∠MBN,∠MBN绕B点旋转.它的两边分别交AD、DC于E、F.上述结论是否仍然成立?并说明理由;实际应用:如图4,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处.舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以75海里/小时的速度前进,同时舰艇乙沿北偏东50°的方向以100海里/小时的速度前进,1.2小时后,指挥中心观测到甲、乙两舰艇分别到达E、F处.且指挥中心观测两舰艇视线之间的夹角为70°.试求此时两舰艇之间的距离.。
2021年中考数学第三轮冲刺专题复习:四边形的综合 (含答案)

2021年中考数学第三轮冲刺专题复习:四边形的综合专项练习1、如图,已知正方形ABCD的边长为1,正方形CEFG的面积为S1,点E在DC边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为S2,且S1=S2.(1)求线段CE的长;(2)若点H为BC边的中点,连接HD,求证:HD=HG.2、如图,▱ABCD的对角线AC、BD相交于点O,EF经过O,分别交AB、CD于点E、F,EF的延长线交CB的延长线于M.(1)求证:OE=OF;(2)若AD=4,AB=6,BM=1,求BE的长.3、如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.(1)求证:BG=DE;(2)若E为AD中点,FH=2,求菱形ABCD的周长.4、如图,在平行四边形ABCD中,AE平分∠DAB,已知CE=6,BE=8,DE=10.(1)求证:∠BEC=90°;(2)求cos∠DAE.5、如图,已知平行四边形ABCD中,AB=5,BC=3,AC=2.(1)求平行四边形ABCD的面积;(2)求证:BD⊥BC.6、如图所示,已知正方形OEFG的顶点O为正方形ABCD对角线AC、BD的交点,连接CE、DG.(1)求证:△DOG≌△COE;(2)若DG⊥BD,正方形ABCD的边长为2,线段AD与线段OG相交于点M,AM=,求正方形OEFG 的边长.7、如图,在四边形ABCD中,点E和点F是对角线AC上的两点,AE=CF,DF=BE,且DF∥BE,过点C作CG⊥AB交AB的延长线于点G.(1)求证:四边形ABCD是平行四边形;(2)若tan∠CAB=,∠CBG=45°,BC=4,则▱ABCD的面积是24.8、如图,四边形ABCD是正方形,△EFC是等腰直角三角形,点E在AB上,且∠CEF=90°,FG⊥AD,垂足为点C.(1)试判断AG与FG是否相等?并给出证明;(2)若点H为CF的中点,GH与DH垂直吗?若垂直,给出证明;若不垂直,说明理由.9、定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.(1)如图1,在△ABC中,AB=AC,AD是△ABC的角平分线,E,F分别是BD,AD上的点.求证:四边形ABEF是邻余四边形.(2)如图2,在5×4的方格纸中,A,B在格点上,请画出一个符合条件的邻余四边形ABEF,使AB 是邻余线,E,F在格点上.(3)如图3,在(1)的条件下,取EF中点M,连结DM并延长交AB于点Q,延长EF交AC于点N.若N为AC的中点,DE=2BE,QB=3,求邻余线AB的长.10、如图,在平行四边形ABCD中,点E在边BC上,连结AE,EM⊥AE,垂足为E,交CD于点M,AF⊥BC,垂足为F,BH⊥AE,垂足为H,交AF于点N,点P是AD上一点,连接CP.(1)若DP=2AP=4,CP=,CD=5,求△ACD的面积.(2)若AE=BN,AN=CE,求证:AD=CM+2CE.11、如图,在正方形ABCD中,分别过顶点B,D作BE∥DF交对角线AC所在直线于E,F点,并分别延长EB,FD到点H,G,使BH=DG,连接EG,FH.(1)求证:四边形EHFG是平行四边形;(2)已知:AB=2,EB=4,tan∠GEH=2,求四边形EHFG的周长.12、如图,四边形ABCD是矩形,AB=20,BC=10,以CD为一边向矩形外部作等腰直角△GDC,∠G=90°.点M在线段AB上,且AM=a,点P沿折线AD﹣DG运动,点Q沿折线BC﹣CG运动(与点G 不重合),在运动过程中始终保持线段PQ∥AB.设PQ与AB之间的距离为x.(1)若a=12.①如图1,当点P在线段AD上时,若四边形AMQP的面积为48,则x的值为;②在运动过程中,求四边形AMQP的最大面积;(2)如图2,若点P在线段DG上时,要使四边形AMQP的面积始终不小于50,求a的取值范围.13、在矩形ABCD中,AE⊥BD于点E,点P是边AD上一点.(1)若BP平分∠ABD,交AE于点G,PF⊥BD于点F,如图①,证明四边形AGFP是菱形;(2)若PE⊥EC,如图②,求证:AE•AB=DE•AP;(3)在(2)的条件下,若AB=1,BC=2,求AP的长.14、已知矩形ABCD中,AB=5cm,点P为对角线AC上的一点,且AP=2cm.如图①,动点M从点A出发,在矩形边上沿着A→B→C的方向匀速运动(不包含点C).设动点M的运动时间为t(s),△APM 的面积为S(cm2),S与t的函数关系如图②所示.(1)直接写出动点M的运动速度为cm/s,BC的长度为cm;(2)如图③,动点M重新从点A出发,在矩形边上按原来的速度和方向匀速运动,同时,另一个动点N从点D出发,在矩形边上沿着D→C→B的方向匀速运动,设动点N的运动速度为v(cm/s).已知两动点M,N经过时间x(s)在线段BC上相遇(不包含点C),动点M,N相遇后立即同时停止运动,记此时△APM与△DPN的面积分别为S1(cm2),S2(cm2)①求动点N运动速度v(cm/s)的取值范围;②试探究S1•S2是否存在最大值,若存在,求出S1•S2的最大值并确定运动时间x的值;若不存在,请说明理由.15、如图1,正方形ABDE和BCFG的边AB,BC在同一条直线上,且AB=2BC,取EF的中点M,连接MD,MG,MB.(1)试证明DM⊥MG,并求的值.(2)如图2,将图1中的正方形变为菱形,设∠EAB=2α(0<α<90°),其它条件不变,问(1)中的值有变化吗?若有变化,求出该值(用含α的式子表示);若无变化,说明理由.16、综合与实践动手操作:第一步:如图1,正方形纸片ABCD沿对角线AC所在的直线折叠,展开铺平.在沿过点C的直线折叠,使点B,点D都落在对角线AC上.此时,点B与点D重合,记为点N,且点E,点N,点F三点在同一条直线上,折痕分别为CE,CF.如图2.第二步:再沿AC所在的直线折叠,△ACE与△ACF重合,得到图3.第三步:在图3的基础上继续折叠,使点C与点F重合,如图4,展开铺平,连接EF,FG,GM,ME.如图5,图中的虚线为折痕.问题解决:(1)在图5中,∠BEC的度数是,的值是.(2)在图5中,请判断四边形EMGF的形状,并说明理由;(3)在不增加字母的条件下,请你以图中5中的字母表示的点为顶点,动手画出一个菱形(正方形除外),并写出这个菱形:.17、已知:在矩形ABCD中,E,F分别是边AB,AD上的点,过点F作EF的垂线交DC于点H,以EF为直径作半圆O.(1)填空:点A(填“在”或“不在”)⊙O上;当=时,tan∠AEF的值是;(2)如图1,在△EFH中,当FE=FH时,求证:AD=AE+DH;(3)如图2,当△EFH的顶点F是边AD的中点时,求证:EH=AE+DH;(4)如图3,点M在线段FH的延长线上,若FM=FE,连接EM交DC于点N,连接FN,当AE=AD 时,FN=4,HN=3,求tan∠AEF的值.参考答案2021年中考数学第三轮冲刺专题复习:四边形的综合专项练习1、如图,已知正方形ABCD的边长为1,正方形CEFG的面积为S1,点E在DC边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为S2,且S1=S2.(1)求线段CE的长;(2)若点H为BC边的中点,连接HD,求证:HD=HG.【解答】解:(1)设正方形CEFG的边长为a,∵正方形ABCD的边长为1,∴DE=1﹣a,∵S1=S2,∴a2=1×(1﹣a),解得,(舍去),,即线段CE的长是;(2)证明:∵点H为BC边的中点,BC=1,∴CH=0.5,∴DH==,∵CH=0.5,CG=,∴HG=,∴HD=HG.2、如图,▱ABCD的对角线AC、BD相交于点O,EF经过O,分别交AB、CD于点E、F,EF的延长线交CB的延长线于M.(1)求证:OE=OF;(2)若AD=4,AB=6,BM=1,求BE的长.【解答】(1)证明:∵四边形ABCD是平行四边形,∴OA=OC,AB∥CD,BC=AD,∴∠OAE=∠OVF,在△AOE和△COF中,,∴△AOE≌△COF(ASA),∴OE=OF;(2)解:过点O作ON∥BC交AB于N,则△AON∽△ACB,∵OA=OC,∴ON=BC=2,BN=AB=3,∵ON∥BC,∴△ONE∽△MBE,∴=,即=,解得,BE=1.3、如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.(1)求证:BG=DE;(2)若E为AD中点,FH=2,求菱形ABCD的周长.【解答】解:(1)∵四边形EFGH是矩形,∴EH=FG,EH∥FG,∴∠GFH=∠EHF,∵∠BFG=180°﹣∠GFH,∠DHE=180°﹣∠EHF,∴∠BFG=∠DHE,∵四边形ABCD是菱形,∴AD∥BC,∴∠GBF=∠EDH,∴△BGF≌△DEH(AAS),∴BG=DE;(2)连接EG,∵四边形ABCD是菱形,∴AD=BC,AD∥BC,∵E为AD中点,∴AE=ED,∵BG=DE,∴AE=BG,AE∥BG,∴四边形ABGE是平行四边形,∴AB=EG,∵EG=FH=2,∴AB=2,∴菱形ABCD的周长=8.4、如图,在平行四边形ABCD中,AE平分∠DAB,已知CE=6,BE=8,DE=10.(1)求证:∠BEC=90°;(2)求cos∠DAE.【解答】(1)证明:∵四边形ABCD是平行四边形,∴DC=AB=,AD=BC,DC∥AB,∴∠DEA=∠EAB,∵AE平分∠DAB,∴∠DAE=∠EAB,∴∠DAE=∠DEA∴AD=DE=10,∴BC=10,AB=CD=DE+CE=16,∵CE2+BE2=62+82=100=BC2,∴△BCE是直角三角形,∠BEC=90°;(2)解:∵AB∥CD,∴∠ABE=∠BEC=90°,∴AE===8,∴cos∠DAE=cos∠EAB===.5、如图,已知平行四边形ABCD中,AB=5,BC=3,AC=2.(1)求平行四边形ABCD的面积;(2)求证:BD⊥BC.【解答】解:(1)作CE⊥AB交AB的延长线于点E,如图:设BE=x,CE=h在Rt△CEB中:x2+h2=9①在Rt△CEA中:(5+x)2+h2=52②联立①②解得:x=,h=∴平行四边形ABCD的面积=AB•h=12;(2)作DF⊥AB,垂足为F∴∠DF A=∠CEB=90°∵平行四边形ABCD∴AD=BC,AD∥BC∴∠DAF=∠CBE又∵∠DF A=∠CEB=90°,AD=BC∴△ADF≌△BCE(AAS)∴AF=BE=,BF=5﹣=,DF=CE=在Rt△DFB中:BD2=DF2+BF2=()2+()2=16∴BD=4∵BC=3,DC=5∴CD2=DB2+BC2∴BD⊥BC.6、如图所示,已知正方形OEFG的顶点O为正方形ABCD对角线AC、BD的交点,连接CE、DG.(1)求证:△DOG≌△COE;(2)若DG⊥BD,正方形ABCD的边长为2,线段AD与线段OG相交于点M,AM=,求正方形OEFG 的边长.【解答】解:(1)∵正方形ABCD与正方形OEFG,对角线AC、BD∴DO=OC∵DB⊥AC,∴∠DOA=∠DOC=90°∵∠GOE=90°∴∠GOD+∠DOE=∠DOE+∠COE=90°∴∠GOD=∠COE∵GO=OE∴在△DOG和△COE中∴△DOG≌△COE(SAS)(2)如图,过点M作MH⊥DO交DO于点H∵AM=,DA=2∴DM=∵∠MDB=45°∴MH=DH=sin45°•DM=,DO=cos45°•DA=∴HO=DO﹣DH=﹣=∴在Rt△MHO中,由勾股定理得MO===∵DG⊥BD,MH⊥DO∴MH∥DG∴易证△OHM∽△ODG∴===,得GO=2则正方形OEFG的边长为27、如图,在四边形ABCD中,点E和点F是对角线AC上的两点,AE=CF,DF=BE,且DF∥BE,过点C作CG⊥AB交AB的延长线于点G.(1)求证:四边形ABCD是平行四边形;(2)若tan∠CAB=,∠CBG=45°,BC=4,则▱ABCD的面积是24.【解答】(1)证明:∵AE=CF,∴AE﹣EF=CF﹣EF,即AF=CE,∵DF∥BE,∴∠DF A=∠BEC,∵DF=BE,∴△ADF≌△CBE(SAS),∴AD=CB,∠DAF=∠BCE,∴AD∥CB,∴四边形ABCD是平行四边形;(2)解:∵CG⊥AB,∴∠G=90°,∵∠CBG=45°,∴△BCG是等腰直角三角形,∵BC=4,∴BG=CG=4,∵tan∠CAB=,∴AG=10,∴AB=6,∴▱ABCD的面积=6×4=24,故答案为:24.8、如图,四边形ABCD是正方形,△EFC是等腰直角三角形,点E在AB上,且∠CEF=90°,FG⊥AD,垂足为点C.(1)试判断AG与FG是否相等?并给出证明;(2)若点H为CF的中点,GH与DH垂直吗?若垂直,给出证明;若不垂直,说明理由.【解答】解:(1)AG=FG,理由如下:如图,过点F作FM⊥AB交BA的延长线于点M∵四边形ABCD是正方形∴AB=BC,∠B=90°=∠BAD∵FM⊥AB,∠MAD=90°,FG⊥AD∴四边形AGFM是矩形∴AG=MF,AM=FG,∵∠CEF=90°,∴∠FEM+∠BEC=90°,∠BEC+∠BCE=90°∴∠FEM=∠BCE,且∠M=∠B=90°,EF=EC∴△EFM≌△CEB(AAS)∴BE=MF,ME=BC∴ME=AB=BC∴BE=MA=MF∴AG=FG,(2)DH⊥HG理由如下:如图,延长GH交CD于点N,∵FG⊥AD,CD⊥AD∴FG∥CD∴,且CH=FH,∴GH=HN,NC=FG∴AG=FG=NC又∵AD=CD,∴GD=DN,且GH=HN∴DH⊥GH9、定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.(1)如图1,在△ABC中,AB=AC,AD是△ABC的角平分线,E,F分别是BD,AD上的点.求证:四边形ABEF是邻余四边形.(2)如图2,在5×4的方格纸中,A,B在格点上,请画出一个符合条件的邻余四边形ABEF,使AB 是邻余线,E,F在格点上.(3)如图3,在(1)的条件下,取EF中点M,连结DM并延长交AB于点Q,延长EF交AC于点N.若N为AC的中点,DE=2BE,QB=3,求邻余线AB的长.【解答】解:(1)∵AB=AC,AD是△ABC的角平分线,∴AD⊥BC,∴∠ADB=90°,∴∠DAB+∠DBA=90°,∴∠FBA与∠EBA互余,∴四边形ABEF是邻余四边形;(2)如图所示(答案不唯一),四边形AFEB为所求;(3)∵AB=AC,AD是△ABC的角平分线,∴BD=CD,∵DE=2BE,∴BD=CD=3BE,∴CE=CD+DE=5BE,∵∠EDF=90°,点M是EF的中点,∴DM=ME,∴∠MDE=∠MED,∵AB=AC,∴∠B=∠C,∴△DBQ∽△ECN,∴,∵QB=3,∴NC=5,∵AN=CN,∴AC=2CN=10,∴AB=AC=10.10、如图,在平行四边形ABCD中,点E在边BC上,连结AE,EM⊥AE,垂足为E,交CD于点M,AF⊥BC,垂足为F,BH⊥AE,垂足为H,交AF于点N,点P是AD上一点,连接CP.(1)若DP=2AP=4,CP=,CD=5,求△ACD的面积.(2)若AE=BN,AN=CE,求证:AD=CM+2CE.【解答】(1)解:作CG⊥AD于G,如图1所示:设PG=x,则DG=4﹣x,在Rt△PGC中,GC2=CP2﹣PG2=17﹣x,在Rt△DGC中,GC2=CD2﹣GD2=52﹣(4﹣x)2=9+8x﹣x2,∴17﹣x2=9+8x﹣x2,解得:x=1,即PG=1,∴GC=4,∵DP=2AP=4,∴AD=6,∴S△ACD=×AD×CG=×6×4=12;(2)证明:连接NE,如图2所示:∵AH⊥AE,AF⊥BC,AE⊥EM,∴∠AEB+∠NBF=∠AEB+∠EAF=∠AEB+∠MEC=90°,∴∠NBF=∠EAF=∠MEC,在△NBF和△EAF中,,∴△NBF≌△EAF(AAS),∴BF=AF,NF=EF,∴∠ABC=45°,∠ENF=45°,FC=AF=BF,∴∠ANE=∠BCD=135°,AD=BC=2AF,在△ANE和△ECM中,,∴△ANE≌△ECM(ASA),∴CM=NE,又∵NF=NE=MC,∴AF=MC+EC,∴AD=MC+2EC.11、如图,在正方形ABCD中,分别过顶点B,D作BE∥DF交对角线AC所在直线于E,F点,并分别延长EB,FD到点H,G,使BH=DG,连接EG,FH.(1)求证:四边形EHFG是平行四边形;(2)已知:AB=2,EB=4,tan∠GEH=2,求四边形EHFG的周长.【解答】解:(1)∵四边形ABCD是正方形,∴AB=CD,AB∥CD,∴∠DCA=∠BAC,∵DF∥BE,∴∠CFD=∠BEA,∵∠BAC=∠BEA+∠ABE,∠DCA=∠CFD+∠CDF,∴∠ABE=∠CDF,在△ABE和△CDF中,∵,∴△ABE≌△CDF(AAS),∴BE=DF,∵BH=DG,∴BE+BH=DF+DG,即EH=GF,∵EH∥GF,∴四边形EHFG是平行四边形;(2)如图,连接BD,交EF于O,∵四边形ABCD是正方形,∴BD⊥AC,∴∠AOB=90°,∵AB=2,∴OA=OB=2,Rt△BOE中,EB=4,∴∠OEB=30°,∴EO=2,∵OD=OB,∠EOB=∠DOF,∵DF∥EB,∴∠DFC=∠BEA,∴△DOF≌△BOE(AAS),∴OF=OE=2,∴EF=4,∴FM=2,EM=6,过F作FM⊥EH于M,交EH的延长线于M,∵EG∥FH,∴∠FHM=∠GEH,∵tan∠GEH=tan∠FHM==2,∴,∴HM=1,∴EH=EM﹣HM=6﹣1=5,FH===,∴四边形EHFG的周长=2EH+2FH=2×5+2=10+2.12、如图,四边形ABCD是矩形,AB=20,BC=10,以CD为一边向矩形外部作等腰直角△GDC,∠G=90°.点M在线段AB上,且AM=a,点P沿折线AD﹣DG运动,点Q沿折线BC﹣CG运动(与点G 不重合),在运动过程中始终保持线段PQ∥AB.设PQ与AB之间的距离为x.(1)若a=12.①如图1,当点P在线段AD上时,若四边形AMQP的面积为48,则x的值为3;②在运动过程中,求四边形AMQP的最大面积;(2)如图2,若点P在线段DG上时,要使四边形AMQP的面积始终不小于50,求a的取值范围.【解答】(1)解:①P在线段AD上,PQ=AB=20,AP=x,AM=12,四边形AMQP的面积=(12+20)x=48,解得:x=3;故答案为:3;②当P,在AD上运动时,P到D点时四边形AMQP面积最大,为直角梯形,∴0<x≤10时,四边形AMQP面积的最大值=(12+20)10=160,当P在DG上运动,10<x≤20,四边形AMQP为不规则梯形,作PH⊥AB于M,交CD于N,作GE⊥CD于E,交AB于F,如图2所示:则PM=x,PN=x﹣10,EF=BC=10,∵△GDC是等腰直角三角形,∴DE=CE,GE=CD=10,∴GF=GE+EF=20,∴GH=20﹣x,由题意得:PQ∥CD,∴△GPQ∽△GDC,∴=,即=,解得:PQ=40﹣2x,∴梯形AMQP的面积=(12+40﹣2x)×x=﹣x2+26x=﹣(x﹣13)2+169,∴当x=13时,四边形AMQP的面积最大=169;(2)解:P在DG上,则10≤x≤20,AM=a,PQ=40﹣2x,梯形AMQP的面积S=(a+40﹣2x)×x=﹣x2+x,对称轴为:x=10+,∵0≤x≤20,∴10≤10+≤15,对称轴在10和15之间,∵10≤x≤20,二次函数图象开口向下,∴当x=20时,S最小,∴﹣202+×20≥50,∴a≥5;综上所述,a的取值范围为5≤a≤20.13、在矩形ABCD中,AE⊥BD于点E,点P是边AD上一点.(1)若BP平分∠ABD,交AE于点G,PF⊥BD于点F,如图①,证明四边形AGFP是菱形;(2)若PE⊥EC,如图②,求证:AE•AB=DE•AP;(3)在(2)的条件下,若AB=1,BC=2,求AP的长.【解答】(1)证明:如图①中,∵四边形ABCD是矩形,∴∠BAD=90°,∵AE⊥BD,∴∠AED=90°,∴∠BAE+∠EAD=90°,∠EAD+∠ADE=90°,∴∠BAE=∠ADE,∵∠AGP=∠BAG+∠ABG,∠APD=∠ADE+∠PBD,∠ABG=∠PBD,∴∠AGP=∠APG,∴AP=AG,∵P A⊥AB,PF⊥BD,BP平分∠ABD,∴P A=PF,∴PF=AG,∵AE⊥BD,PF⊥BD,∴PF∥AG,∴四边形AGFP是平行四边形,∵P A=PF,∴四边形AGFP是菱形.(2)证明:如图②中,∵AE⊥BD,PE⊥EC,∴∠AED=∠PEC=90°,∴∠AEP=∠DEC,∵∠EAD+∠ADE=90°,∠ADE+∠CDE=90°,∴∠EAP=∠EDC,∴△AEP∽△DEC,∴=,∵AB=CD,∴AE•AB=DE•AP;(3)解:∵四边形ABCD是矩形,∴BC=AD=2,∠BAD=90°,∴BD==,∵AE⊥BD,∴S△ABD=•BD•AE=•AB•AD,∴AE=,∴DE==,∵AE•AB=DE•AP;∴AP==.14、已知矩形ABCD中,AB=5cm,点P为对角线AC上的一点,且AP=2cm.如图①,动点M从点A出发,在矩形边上沿着A→B→C的方向匀速运动(不包含点C).设动点M的运动时间为t(s),△APM 的面积为S(cm2),S与t的函数关系如图②所示.(1)直接写出动点M的运动速度为2cm/s,BC的长度为10cm;(2)如图③,动点M重新从点A出发,在矩形边上按原来的速度和方向匀速运动,同时,另一个动点N从点D出发,在矩形边上沿着D→C→B的方向匀速运动,设动点N的运动速度为v(cm/s).已知两动点M,N经过时间x(s)在线段BC上相遇(不包含点C),动点M,N相遇后立即同时停止运动,记此时△APM与△DPN的面积分别为S1(cm2),S2(cm2)①求动点N运动速度v(cm/s)的取值范围;②试探究S1•S2是否存在最大值,若存在,求出S1•S2的最大值并确定运动时间x的值;若不存在,请说明理由.【解答】解:(1)∵t=2.5s时,函数图象发生改变,∴t=2.5s时,M运动到点B处,∴动点M的运动速度为:=2cm/s,∵t=7.5s时,S=0,∴t=7.5s时,M运动到点C处,∴BC=(7.5﹣2.5)×2=10(cm),故答案为:2,10;(2)①∵两动点M,N在线段BC上相遇(不包含点C),∴当在点C相遇时,v==(cm/s),当在点B相遇时,v==6(cm/s),∴动点N运动速度v(cm/s)的取值范围为cm/s<v≤6cm/s;②过P作EF⊥AB于F,交CD于E,如图3所示:则EF∥BC,EF=BC=10,∴=,∵AC==5,∴=,解得:AF=2,∴DE=AF=2,CE=BF=3,PF==4,∴EP=EF﹣PF=6,∴S1=S△APM=S△APF+S梯形PFBM﹣S△ABM=×4×2+(4+2x﹣5)×3﹣×5×(2x﹣5)=﹣2x+15,S2=S△DPM=S△DEP+S梯形EPMC﹣S△DCM=×2×6+(6+15﹣2x)×3﹣×5×(15﹣2x)=2x,∴S1•S2=(﹣2x+15)×2x=﹣4x2+30x=﹣4(x﹣)2+,∵2.5<<7.5,在BC边上可取,∴当x=时,S1•S2的最大值为.15、如图1,正方形ABDE和BCFG的边AB,BC在同一条直线上,且AB=2BC,取EF的中点M,连接MD,MG,MB.(1)试证明DM⊥MG,并求的值.(2)如图2,将图1中的正方形变为菱形,设∠EAB=2α(0<α<90°),其它条件不变,问(1)中的值有变化吗?若有变化,求出该值(用含α的式子表示);若无变化,说明理由.【解答】(1)证明:如图1中,延长DM交FG的延长线于H.∵四边形ABCD,四边形BCFG都是正方形,∴DE∥AC∥GF,∴∠EDM=∠FHM,∵∠EMD=∠FMH,EM=FM,∴△EDM≌△FHM(AAS),∴DE=FH,DM=MH,∵DE=2FG,BG=DG,∴HG=DG,∵∠DGH=∠BGF=90°,MH=DM,∴GM⊥DM,DM=MG,连接EB,BF,设BC=a,则AB=2a,BE=2a,BF=a,∵∠EBD=∠DBF=45°,∴∠EBF=90°,∴EF==a,∵EM=MF,∴BM=EF=a,∵HM=DM,GH=FG,∴MG=DF=a,∴==.(2)解:(1)中的值有变化.理由:如图2中,连接BE,AD交于点O,连接OG,CG,BF,CG交BF于O′.∵DO=OA,DG=GB,∴GO∥AB,OG=AB,∵GF∥AC,∴O,G,F共线,∵FG=AB,∴OF=AB=DF,∵DF∥AC,AC∥OF,∴DE∥OF,∴OD与EF互相平分,∵EM=MF,∴点M在直线AD上,∵GD=GB=GO=GF,∴四边形OBFD是矩形,∴∠OBF=∠ODF=∠BOD=90°,∵OM=MD,OG=GF,∴MG=DF,设BC=m,则AB=2m,易知BE=2OB=2•2m•sinα=4m sinα,BF=2BO°=2m•cosα,DF=OB=2m•sinα,∵BM=EF==,GM=DF=m•sinα,∴==.16、综合与实践动手操作:第一步:如图1,正方形纸片ABCD沿对角线AC所在的直线折叠,展开铺平.在沿过点C的直线折叠,使点B,点D都落在对角线AC上.此时,点B与点D重合,记为点N,且点E,点N,点F三点在同一条直线上,折痕分别为CE,CF.如图2.第二步:再沿AC所在的直线折叠,△ACE与△ACF重合,得到图3.第三步:在图3的基础上继续折叠,使点C与点F重合,如图4,展开铺平,连接EF,FG,GM,ME.如图5,图中的虚线为折痕.问题解决:(1)在图5中,∠BEC的度数是67.5°,的值是.(2)在图5中,请判断四边形EMGF的形状,并说明理由;(3)在不增加字母的条件下,请你以图中5中的字母表示的点为顶点,动手画出一个菱形(正方形除外),并写出这个菱形:菱形EMCH或菱形FGCH.【解答】解:(1)由折叠的性质得:BE=EN,AE=AF,∠CEB=∠CEN,∠BAC=∠CAD,∵四边形ABCD是正方形,∴∠EAF=90°,∴∠AEF=∠AFE=45°,∴∠BEN=135°,∴∠BEC=67.5°,∴∠BAC=∠CAD=45°,∵∠AEF=45°,∴△AEN是等腰直角三角形,∴AE=EN,∴==;故答案为:67.5°,;(2)四边形EMGF是矩形;理由如下:∵四边形ABCD是正方形,∴∠B=∠BCD=∠D=90°,由折叠的性质得:∠BCE=∠ECA=∠ACF=∠FCD,CM=CG,∠BEC=∠NEC=∠NFC=∠DFC,∴∠BCE=∠ECA=∠ACF=∠FCD==22.5°,∠BEC=∠NEC=∠NFC=∠DFC=67.5°,由折叠可知:MH、GH分别垂直平分EC、FC,∴MC=ME=CG=GF,∴∠MEC=∠BCE=22.5°,∠GFC=∠FCD=22.5°,∴∠MEF=90°,∠GFE=90°,∵∠MCG=90°,CM=CG,∴∠CMG=45°,∵∠BME=∠BCE+∠MEC=22.5°+22.5°=45°,∴∠EMG=180°﹣∠CMG﹣∠BME=90°,∴四边形EMGF是矩形;(3)连接EH、FH,如图所示:∵由折叠可知:MH、GH分别垂直平分EC、FC,同时EC、FC也分别垂直平分MH、GH,∴四边形EMCH与四边形FGCH是菱形,故答案为:菱形EMCH或菱形FGCH.17、已知:在矩形ABCD中,E,F分别是边AB,AD上的点,过点F作EF的垂线交DC于点H,以EF为直径作半圆O.(1)填空:点A在(填“在”或“不在”)⊙O上;当=时,tan∠AEF的值是;(2)如图1,在△EFH中,当FE=FH时,求证:AD=AE+DH;(3)如图2,当△EFH的顶点F是边AD的中点时,求证:EH=AE+DH;(4)如图3,点M在线段FH的延长线上,若FM=FE,连接EM交DC于点N,连接FN,当AE=AD 时,FN=4,HN=3,求tan∠AEF的值.【解答】解:(1)连接AO,∵∠EAF=90°,O为EF中点,∴AO=EF,∴点A在⊙O上,当=时,∠AEF=45°,∴tan∠AEF=tan45°=1,故答案为:在,1;(2)∵EF⊥FH,∴∠EFH=90°,在矩形ABCD中,∠A=∠D=90°,∴∠AEF+∠AFE=90°,∠AFE+∠DFH=90°,∴∠AEF=∠DFH,又FE=FH,∴△AEF≌△DFH(AAS),∴AF=DH,AE=DF,∴AD=AF+DF=AE+DH;(3)延长EF交HD的延长线于点G,∵F分别是边AD上的中点,∴AF=DF,∵∠A=∠FDG=90°,∠AFE=∠DFG,∴△AEF≌△DGF(ASA),∴AE=DG,EF=FG,∵EF⊥FG,∴EH=GH,∴GH=DH+DG=DH+AE,∴EH=AE+DH;(4)过点M作MQ⊥AD于点Q.设AF=x,AE=a,∵FM=FEEF⊥FH,∴△EFM为等腰直角三角形,∴∠FEM=∠FMN=45°,∵FM=FE,∠A=∠MQF=90°,∠AEF=∠MFQ,∴△AEF≌△QFM(ASA),∴AE=EQ=a,AF=QM,∵AE=AD,∴AF=DQ=QM=x,∵DC∥QM,∴,∵DC∥AB∥QM,∴,∴,∵FE=FM,∴,∠FEM=∠FMN=45°,∴△FEN~△HMN,∴,∴.。
平行四边形、矩形、菱形、正方形提高题
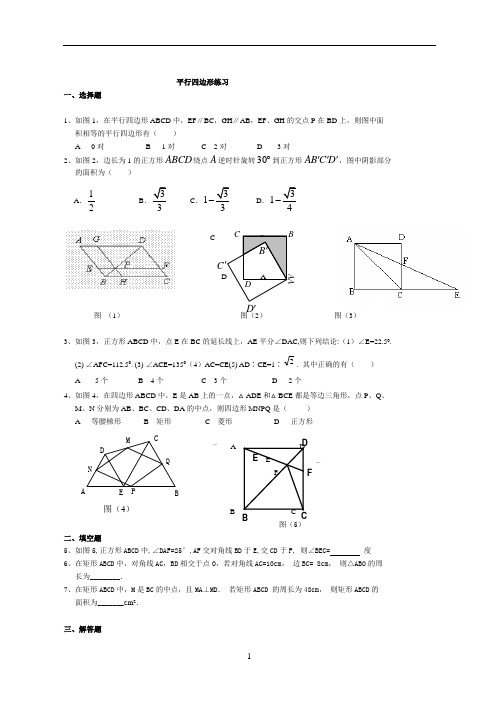
平行四边形练习 一、选择题1、如图1,在平行四边形ABCD 中,EF ∥BC ,GH ∥AB ,EF 、GH 的交点P 在BD 上,则图中面 积相等的平行四边形有( )A 0对B 1对C 2对D 3对 2、如图2,边长为1的正方形ABCD 绕点A 逆时针旋转30︒到正方形AB C D ''',图中阴影部分的面积为( )A .12B .33C .313-D .314-CBD A图 (1) 图(2) 图(3)3、如图3,正方形ABCD 中,点E 在BC 的延长线上,AE 平分∠DAC,则下列结论:(1)∠E=22.50. (2) ∠AFC=112.50. (3) ∠ACE=1350(4)AC=CE(5) AD ∶CE=1∶2. 其中正确的有( ) A 5个 B 4个 C 3个 D 2个4、如图4,在四边形ABCD 中,E 是AB 上的一点,△ADE 和△BCE 都是等边三角形,点P 、Q 、 M 、N 分别为AB 、BC 、CD 、DA 的中点,则四边形MNPQ 是( ) A 等腰梯形 B 矩形 C 菱形 D 正方形A DEFB C图(5)二、填空题5、如图5,正方形ABCD 中,∠DAF=25°,AF 交对角线BD 于E,交CD 于F, 则∠BEC= 度6、在矩形ABCD 中,对角线AC ,BD 相交于点O ,若对角线AC=10cm ,•边BC=•8cm ,•则△ABO 的周 长为________.7、在矩形ABCD 中,M 是BC 的中点,且MA ⊥MD .•若矩形ABCD•的周长为48cm ,•则矩形ABCD 的 面积为_______c m 2.三、解答题C BB '__D C 'D 'DAAQ E PMN DCBA 图(4)_ E _ F_ B_ C8、已知,如图,矩形ABCD 的对角线AC ,BD 相交于点O ,E ,F 分别是OA ,OB 的中点. (1)求证:△ADE ≌△BCF ;(2)若AD=4cm ,AB=8cm ,求OF 的长.10、如图,在正方形ABCD 中,E 是AB 上一点,F 是AD 延长线上一点,且DF =BE . ⑴求证:CE =CF ;⑵在图1中,若G 在AD 上,且∠GCE =45°,则GE =BE +GD 成立吗?为什么? ⑶运用⑴⑵解答中所积累的经验和知识,完成下题:如图2,在直角梯形ABCD 中,AD ∥BC (BC >AD ),∠B =90°,AB =BC =6,E 是AB 上一点, 且∠DCE =45°,BE =2,求DE 的长.6.如图1,在△ABC 中,AB=BC ,P 为AB 边上一点,连接CP ,以PA 、PC 为邻边作□APCD ,AC 与PD 相交于点E ,已知∠ABC=∠AEP=α(0°<α<90°). (1)求证:∠EAP=∠EPA;(2)□APCD 是否为矩形?请说明理由;(3)如图2,F 为BC 中点,连接FP ,将∠AEP 绕点E 顺时针旋转适当的角度,得到∠MEN(点M 、N 分别是∠MEN 的两边与BA 、FP 延长线的交点).猜想线段EM 与EN 之间的数量关系,并证明你的结论.图1ABDCE P 图2ABDCEPM NFB CA G D FEB CA DE图1图2。
2021年九年级中考数学考前强化练习:《四边形综合》(三)

2021年九年级中考数学考前强化练习:《四边形综合》(三)1.在平面直角坐标系中(单位长度为1cm),已知点A(0,m),N(n,0),且+|m+n ﹣10|=0.(1)m=,n=.(2)如图,若点E是第一象限内的一点,且EN⊥x轴,过点E作x轴的平行线a,与y 轴交于点A,点P从点E处出发,以每秒2cm的速度沿直线a向左移动,点Q从原点O 同时出发,以每秒1cm的速度沿x轴向右移动.①经过几秒PQ∥y轴?②若某一时刻以A、O、Q、P为顶点的四边形的面积是10cm2,求此时点P的坐标.2.如图,在▱ABCD,点E为AD的中点,延长BE、CD交于点F,连接AF,BD,CE.(1)求证:四边形ABDF为平行四边形.(2)若BE为∠ABC的角平分线,AB=5,CE=6,求△AEF的面积.3.已知正方形ABCD,点E,F分别在射线BC,射线CD上,BE=CF,AE与BF交于点H.(1)如图1,当点E,F分别在线段BC,CD上时,求证:AE=BF,且AE⊥BF;(2)如图2,当点E在线段BC延长线上时,将线段BE沿BF平移至FG,连接AG.①依题意将图2补全;②用等式表示线段AG,FG和AD之间的数量关系,并证明.4.如图,正方形ABCD中,点E在AB上,点F在BC的延长线上,DF⊥DE,EG平分∠BEF 交BD于点G.(1)求证:DE=DF;(2)请写出线段DG和DF的数量关系并证明;(3)作GH⊥EF于点H,请直接写出线段AB、GH与EF的数量关系.5.在菱形ABCD中,∠ABC=60°,点K是线段AB延长线上一点,点E是∠CBK的平分线上一点,连接DE,取DE的中点F,连接BF.(1)依照题意补全图形.(2)求证:∠FDA=∠FBA.(3)若点G是线段BE延长线上任意一点,连接CG,点H为CG中点,连接FH,用等式表达EG,DA,FH的数量关系,并证明.6.如图,在正方形ABCD中,E是边AB上的一动点,点F在边BC的延长线上,且CF=AE,连接DE、DF.(1)求证:DE⊥DF;(2)连接EF,取EF中点G,连接DG并延长交BC于H,连接BG.①依题意,补全图形;②求证:BG=DG;③若∠EGB=45°,用等式表示线段BG、HG与AE之间的数量关系,并证明.7.在△ABC中,BC=AC,∠C=90°,D是BC边上一个动点(不与点B,C重合),连接AD,以AD为边作正方形ADEF(点E,F都在直线BC的上方),连接BE.(1)根据题意补全图形,并证明∠CAD=∠BDE;(2)用等式表示线段CD与BE的数量关系,并证明;(3)用等式表示线段AD,AB,BE之间的数量关系(直接写出).8.如图,平行四边形ABCD中,BC=BD.点F是线段AB的中点.过点C作CG⊥DB交BD于点G,CG延长线交DF于点H.且CH=DB.(1)如图1,若DH=1.求FH的值;(2)如图2,连接FG.求证:DB=FG+HG.9.如图,在正方形ABCD中,E为边CD上一点(不与点C,D重合),垂直于BE的一条直线MN分别交BC,BE,AD于点M,P,N,正方形ABCD的边长为6.(1)如图1,当点M和点C重合时,若AN=4,求△CDN的面积为.(2)在(1)的条件下求线段PM的长度;(3)如图2,当点M在BC边上时,判断线段AN,MB,EC之间的数量关系,并说明理由.10.如图,在边长为6的正方形ABCD中,点M为对角线BD上任意一点(可与B,D重合),连接AM,将线段AM绕点A逆时针旋转90°得到线段AN,连接MN,DN,设BM=x.(1)求证:△ABM≌△ADN;(2)当时,求MN的长;(3)嘉淇同学在完成(1)后有个想法:“△ABM与△MND也会存在全等的情况”,请判断嘉淇的想法是否正确,若正确,请直接写出△ABM与△MND全等时x的值;若不正确,请说明理由.11.在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴、y轴上,点B的坐标为,将矩形OABC 绕点A 顺时针旋转α,得到矩形O 1AB 1C 1,点O ,B ,C 的对应点分别为O 1,B 1,C 1.(Ⅰ)如图①,当α=45°时,O 1C 1与AB 相交于点E ,求点E 的坐标;(Ⅱ)如图②,当点O 1落在对角线OB 上时,连接BC 1,四边形OAC 1B 是何特殊的四边形?并说明理由;(Ⅲ)连接BC 1,当BC 1取得最小值和最大值时,分别求出点B 1的坐标(直接写出结果即可).12.如图,在平面直角坐标系中,已知菱形ABCD ,A (﹣3,0),B (2,0),D 在y 轴上.直线l 从BC 出发,以每秒1个单位长度的速度沿CD 向左平移,分别与CD 、BD 交于E 、F .设△DEF 的面积为S ,直线l 平移时间为t (s )(0<t <5). (1)求点C 的坐标; (2)求S 与t 的函数表达式;(3)过点B 作BG ⊥l ,垂足为G ,连接AF 、AG ,设△AFG 的面积为S 1,△BFG 的面积为S 2,当S 1+S 2=S 时,若点P (1﹣a ,a +3)在△DEF 内部(不包括边),求a 的取值范围.13.如图,A (0,3)是直角坐标系y 轴上一点,动点P 从原点O 出发,沿x 轴正半轴运动,速度为每秒2个单位长度,以P 为直角顶点在第一象限内作等腰Rt △APB .设P 点的运动时间为t秒.(1)若AB∥x轴,求t的值;(2)如图2,当t=2时,坐标平面内有一点M(不与A重合)使得以M、P、B为顶点的三角形和△ABP全等,请直接写出点M的坐标.14.如图1,对角线互相垂直的四边形叫做垂美四边形.(1)概念理解:给出下列图形:①平行四边形;②矩形;③菱形;④正方形.其中一定是“垂美四边形”的是(填序号);(2)性质探究:如图1,四边形ABCD的对角线AC、BD交于点O,AC⊥BD.求证:AB2+CD2=AD2+BC2;(3)解决问题:如图2,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE,连接CE,BG,GE.已知AC=,AB=3.①请问四边形CGEB是垂美四边形吗?并说明理由;②求GE的长.15.如图,四边形ABCD为正方形,点E为正方形ABCD外一点,且AD=AE,连接BE,∠DAE 的角平分线交BE于点P,连接CP,设∠DAE=α.(1)当α=60°,求∠APB的大小;(2)在(1)的条件下,当PE=2时,求AB的长;(3)当0°<α<60°时,求PA,PB,PC三条线段满足的等量关系.参考答案1.解:(1)依题意,得,解得;故答案为:4,6;(2)①设经过x秒PQ平行于y轴,依题意,得6﹣2x=x,解得x=2,∴经过2秒PQ∥y轴;②当点P在y轴右侧时,依题意,得,解得x=1,此时点P的坐标为(4,4),当点P在y轴左侧时,依题意,得,解得x=,此时点P的坐标为(﹣,4).综合以上可得点P的坐标为(4,4)或(﹣,4).2.解:(1)证明:由题意得,AB∥CF,∴∠ABE=∠DFE,又∵点E为AD的中点,∴AE=DE,在△ABE和△DFE中,,∴△ABE≌△DFE(AAS)∴AB =DF , 又∵AB ∥DF ,∴四边形ABDF 为平行四边形(一组对边平行且相等的四边形是平行四边形); (2)过点F 作AD 的垂线交AD 延长线于点K ,过点D 作DH ⊥EC ,过点E 作EG ⊥CD ,∵S △AEF =;,∴S △AEF =S △EDF ,又∵BE 为∠ABC 的角平分线, ∴∠ABE =∠EBC , 又∵AD ∥BC , ∴∠EBC =∠FED , 而∠ABE =∠DFE , ∴∠FED =∠DFE , ∴ED =FD ,由(1)可知AB =DC =FD =5, ∴ED =FD =DC =5, 又∵S △EFD =,S △EDC =,∴S △AEF =S △EDF =S △ECD ,在等腰△EDC 中,ED =CD =5,EC =6, ∵DH ⊥EC , ∴EH ===3,在Rt △EHD 中,ED =5,EH =3, ∴DH ===4,∴S △ECD ==12,∴S△AEF =S△EDF=S△ECD=12,故S△AEF=12.3.解:(1)如图1,∵四边形ABCD是正方形,∴AB=BC,∠ABE=∠BCF=90°,在△ABE和△BCF中,,∴△ABE≌△BCF(SAS),∴AE=BF,∠BAE=∠CBF,∵∠CBF+∠ABH=90°,∴∠BAE+∠ABH=90°,∴∠AHB=90°,∴AE⊥BF,故AE=BF,且AE⊥BF;(2)①补全图如图2所示;②AG2=2AD2+2FG2.理由如下:如图3,连接EG,∵线段BE沿BF平移至FG,∴四边形BEGF是平行四边形,∴EG=BF,EG∥BF,在△ABE和△BCF中,,∴△ABE≌△BCF(SAS),∴AE=BF,∠BFC=∠AEB,∴EG=BF=AE,∵∠BFC+∠CBF=90°,∴∠AEB+∠CBF=90°,∴∠BHE=90°,∵EG∥BF,∴∠AEG=∠BHE=90°,∴AG2=AE2+EG2=2AE2,∵AE2=AB2+BE2=AD2+FG2,∴AG2=2AD2+2FG2.4.(1)证明:∵四边形ABCD是正方形,∴AD=CD,∠BAD=∠BCD=90°,∴∠CDE+∠EDA=90°,∠FCD=∠EAD=90°,∵DE⊥DF,∴∠FDC+∠CDE=90°,∴∠FDC=∠EDA,∴△EDA≌△FDC(ASA),∴DE=DF;(2)解:DG=DF,证明如下:由(1)得:DE=DF,∵∠FDE=90°,∴∠DEF是等腰直角三角形,∴∠DFE=∠DEF=45°,∴∠DEG=45°+∠FEG,∵四边形ABCD是正方形,∴∠ABG=45°,∴∠DGE=∠ABG+∠BEG=45°+∠BEG,∵EG平分∠BEF,∴∠FEG=∠BEG,∴∠DEG=∠DGE,∴DE=DG,∴DG=DF;(3)解:AB﹣GH=EF,理由如下:过点G作GM⊥AB于M,如图所示:∵EG平分∠BEF,GM⊥AB,GH⊥EF,∴GM=GH,∵∠ABG=45°,∴△BGM、△ABD是等腰直角三角形,∴BG=GM=GH,BD=AB,由(2)可知,DG=DE,△DEF是等腰直角三角形,∴EF=DE,∵DE=DG,∴DG=EF,∵BD﹣BG=DG,∴AB﹣GH=EF,∴AB﹣GH=EF.5.解(1)如图所示.(2)如图所示,连接DB,∵四边形ABCD是菱形,∴BD平分∠ABC,∴∠DBC=∠ABC=30°,同理∠CBE=∠CBK=60°,∴∠DBE=∠DBC+∠CBE=90°,在Rt△DBE中,F为BE中点,∴BF=DE=DF,∴∠FDB=∠FBD,∵DA=AB,∴∠ADB=∠ABD,∴∠FDA=∠FBA.(3)4FH2=EG2+DA2+EG•DA.如图1所示,连接CE,取CE中点为点M,连接FM,HM,延长HM交AB于点N,不妨设EG=a,DA=b,FH=c,∵H,M分别为CG,CE的中点,∴HM∥GE,且HM=EG=a,同理FM∥DC,且FM=DC=DA=b.∴∠HMF=∠MNA=∠ABG=120°;如图2所示,过点H作HP⊥FP交FM延长线于点P,在Rt△HMP中,∠HMP=60°,HM=a,∴MP=a,HP=a.∴FP=b+a.在Rt△HMP中,∠HPM=90°,∴HP2+MP2=HM2,即(a)2+(b+a)2=c2,化简得:4c2=a2+b2+ab.即4FH2=EG2+DA2+EG•DA.6.(1)证明:∵四边形ABCD是正方形,∴AD=CD,∠A=∠B=∠BCD=∠ADC=90°,∴∠DCF=90°,又∵AE=CF,∴△ADE≌△CDF(SAS),∴∠ADE=∠CDF,∵∠ADE+∠CDE=90°,∴∠CDF+∠CDE=90°,即∠EDF=90°,∴DE⊥DF;(2)①解:依题意,补全图形如图所示:②证明:由(1)可知,△DEF和△BEF都是直角三角形,∵G是EF的中点,∴DG=EF,BG=EF,∴BG=DG;③解:BG2+HG2=4AE2,证明如下:由(1)可知,△ADE≌△CDF,DE⊥DF,∴DE=DF,∴△DEF是等腰直角三角形,∴∠DEG=45°,∵G为EF的中点,∴DG⊥EF,DG=EF=EG,BG=EF=EG=FG,∴∠EGD=∠HGF=∠DGF=90°,∠GDF=45°,∠EDG=∠DEG=45°,∠GBF=∠GFB,∵∠EGB=45°,∴∠GBF=∠GFB=22.5°,∵∠DHF+∠HFG=∠DHF+∠CDH=90°,∴∠HFG=∠CDH=22.5°,∴∠CDF=∠GDF﹣∠HDC=22.5°=∠CDH,又∵∠DCH=∠DCF=90°,CD=CD,∴△CDH≌△CDF(ASA),∴CH=CF,在Rt△GHF中,由勾股定理得:GF2+HG2=HF2,∵HF=2CF=2AE,GF=BG,∴BG2+HG2=(2AE)2,∴BG2+HG2=4AE2.7.解:(1)补全图形如下:∵正方形ADEF,∴∠ADE=90°,∴∠BDE=180°﹣∠ADE﹣∠ADC=90°﹣∠ADC,∵∠C=90°,∴∠CAD=90°﹣∠ADC,∴∠CAD=∠BDE;(2)CD与BE的数量关系为:BE=CD,证明如下:过E作EG⊥CB于G,如图:∵四边形ADEF是正方形,∴AD=DE,∵EG⊥CB,∴∠G=90°=∠C,在△ACD和△DGE中,,∴△ACD≌△DGE(AAS),∴CD=EG,AC=DG,∵AC=BC,∴DG=BC,∴DG﹣DB=BC﹣DB,即BG=CD,∴BG=EG,∴△BGE是等腰直角三角形,∴BE=BG,∴BE=CD;(3)AD,AB,BE之间的数量关系为:AB2=2AD2﹣BE2,理由如下:∵∠C=90°,AC=BC,∴AB2=AC2+BC2=2AC2,AC2=AD2﹣CD2,∴AB2=2(AD2﹣CD2),而BE=CD,∴CD2=BE2,∴AB2=2(AD2﹣BE2),即AB2=2AD2﹣BE2.8.(1)证明:如图1中,∵四边形ABCD是平行四边形,∴AD=BC,AB=CD,AB∥CD,∵BD=BC,∴AD=BD,∵AF=FB,∴DF⊥AB,∴DF⊥DC,∵CG⊥BD,∴∠CDH=∠CGD=∠DFB=90°,∴∠BDF+∠CDG=90°,∠CDG+∠DCH=90°,∴∠BDF=∠DCH,∵CH=DB,∴△DFB≌△CDH(AAS),∴DH=BF,CD=DF,∴AB=DF,∵AB=2BF,∴DF=2DH=2,∴FH=DH=1;(2)解:如图1中,过点F作FJ⊥BD于J,FK⊥CH交CH的延长线于K.过点D作DT⊥DF交FG的延长线于T,连接CT,设FT交CD于N.∵∠K=∠FJG=∠KGJ=90°,∴四边形FKGJ是矩形,∴∠FKJ=90°,∵∠DFB=90°,∴∠KFH=∠BFJ,∵∠K=∠FJB=90°,FH=FB,∴△FKH≌△FJB(AAS),∴FK=FJ,∵FK⊥GK,FJ⊥GJ,∴FG平分∠KGJ,∴∠FGH=∠FGJ=45°,∵∠DGT=∠FGJ=45°,∠GDT=90°,∴DG=DT,∵∠FDC=∠GDT=90°,∴∠FDG=∠CDT,∵DF=DC,∴△FDG≌△CDT(SAS),∴FG=CT,∠DFN=∠TCN,∵∠DNF=∠CNF,∴∠FDN=∠CTN=90°,∵∠TGC=∠FGK=45°,∴TG=TC,CG=CT=FG,∴BD=CH=GH+CG=GH+FG,∴DB=FG+HG.9.解:(1)∵四边形ABD是正方形,∴AD=CD=6,∠D=90°,∵AN=4,∴DN=AD﹣AN=2,∴△CDN的面积=CD×DN=×6×2=6,故答案为:6;(2)∵四边形ABCD是正方形,∴AB=BC=CD=AD=6,∠D=∠BCE=90°,∵BE⊥MN,点M和点C重合,∴MD=BC=6,∠DMN+∠BCP=90°,∠CBE+∠BCP=90°,∴∠DMN=∠CBE,在△DMN和△CBE中,,∴△DMN≌△CBE(AAS),∴MN=BE,DN=CE,∵AN=4,∴CE=DN=AD﹣AN=6﹣4=2,由勾股定理得:MN===2,∴BE=2,∵MN⊥BE,∴△BME的面积=BE×PM=BC×CE,∴PM===;(3)线段AN、MB、EC之间的数量关系为:AN+EC=MB,理由如下:过点N作NF⊥BC于N,如图2所示:则四边形ANFB为矩形,∴AN=BF,NF=AB=BC,∵MN⊥BE,∴∠EBC+∠PMB=90°,∠MNF+∠NMF=90°,∴∠EBC=∠MNF,在△EBC和△MNF中,,∴△EBC≌△MNF(ASA),∴FM=EC,∴MB=BF+FM=AN+EC,即AN+EC=MB.10.(1)证明:在正方形ABCD中,AB=AD,由旋转的性质知:AM=AN,∵∠BAD=∠MAN=90°,∴∠BAM=∠DAN,在△ABM和△ADN中,,∴△ABM≌△ADN(SAS).解:(2)∵BD是正方形ABCD的对角线,且AB=6,∴,∠ADB=45°,∴,由△ABM≌△AND得:,∠ADN=∠ABM=45°,∴∠MDN=∠ADB+∠AND=45°+45°=90°,在Rt△MDN中,.(3)正确;.理由如下:如图:当AM⊥BD,易得△ABM和△ADN是全等的等腰直角三角形,∴∠NDA=∠ABM=45°,AN=AM,∵正方形ABCD中,∠ADB=∠ABD=45°,∴∠NDM =90°,∵∠NAM =∠AMD =∠∠NDM =90°,∴四边形AMDN 为矩形,又∵AN =AM ,∴矩形AMDN 为正方形,∴△NMD ≌△DAN (SAS ),∴△NMD ≌△ABM (全等传递性),此时AM ===3.当△ABM 与△MND 全等时x =3.11.解:(Ⅰ)∵矩形OABC ,∴∠OAB =90°.∵∠OAO 1=45°,∴∠O 1AE =45°,∵∠AO 1E =90°,O 1A =OA =2, ∴, ∴E ;(Ⅱ)四边形OAC 1B 是平行四边形,在Rt△AOB中,,∴∠BOA=60°,同理,∠O1AC1=60°.∵OA=O1A,∴△OAO1是等边三角形,∴∠OAO1=60°,∴AC1与x轴的夹角=180﹣∠O1AO﹣∠C1AO1=180﹣60﹣60=60°,∴BO∥AC1,又BO=AC1,∴四边形OAC1B为平行四边形;(Ⅲ)点C1的运动路径是以A为圆心,AC1为半径的圆,当点C1在AB延长线上时,BC1为最小值,过点B1为作B1G⊥x轴A于点G,在Rt△B1AG中,∠B1AG=180﹣90﹣30=60°,∴,,当BC1取得最小值时点B1的坐标为;当点C1在A延A长线上时,BC1为最大值,过点B1为作B1H⊥x轴A于点H,在Rt△B1AH中,∠B1AH=180﹣90﹣30=60°,∴,,当BC1取得最大值时点B1的坐标为(,﹣3),综上所述当BC1取得最小值和最大值时点B1的坐标分别为,.12.解:(1)∵AB=2﹣(﹣3)=5=AD=CD,则OD==4,故点C的坐标为(5,4);=CD×OD=5×4=10,(2)S△DBC∵l∥BC,∴△DEF∽△DCB,则S:S△DBC=(DE:CD)2=(5﹣t)2:52,∴S=10×=t2﹣4t+10;(3)设直线l与x轴交于点K,则BK=CE=t,∵l∥AD,故∠GKB=∠ADO,则tan∠GKB=tan∠ADO=,则sin∠GKB=,则sin∠GBK=,则KG=BK sin∠GBK=t,则GF=5﹣(5﹣t)﹣t=t,则EF=DE=5﹣t,设点B到AD的距离为h,则S△ABD=×AB×OD=AD×h,则h=OD=4,∴S1+S2=GF×h=t××4=t=S,而S=10×=t2﹣4t+10;故点E(2.5,4);由点A、D的坐标得,直线AD表达式为y=x+4,故设直线l的表达式为y=x+t,将点E的坐标代入上式得:4=×+t,解得t=,故直线l的表达式为y=x+①,令y=x+=0,解得x=﹣,故点K的坐标为(﹣,0),由点P的坐标知,点P在直线y=﹣x+4②上,联立①②并解得,两个函数的交点坐标为(,),则0<x P<,则0<1﹣a<,解得﹣<a<1.13.解:(1)过点B作BC⊥x轴于点C,如图所示.∵AO⊥x轴,BC⊥x轴,且AB∥x轴,∴四边形ABCO为矩形,∴AO=BC=3,∵△APB为等腰直角三角形,∴AP=BP,∠PAB=∠PBA=45°,∴∠OAP=90°﹣∠PAB=45°,∴△AOP为等腰直角三角形,∴OA=OP=3,∴t=3÷2=1.5(秒),故t的值为1.5;(2)当t=2时,M、P、B为顶点的三角形和△ABP全等,①如图3,若△ABP≌△MBP,则AP=PM,过点M作MD⊥OP于点D,∵∠AOP=∠PDM,∠APO=∠DPM,∴△AOP≌△MDP(AAS),∴OA=DM=3,OP=PD=4,∴M(8,﹣3).②如图4,若△ABP≌△MPB,同理可求得M(3,7),③如图5,若△ABP≌△MPB,同理可求得M(7,﹣1).综合以上可得点M的坐标为(3,7),(8,﹣3),(11,﹣1).14.解:(1)∵菱形、正方形的对角线垂直,∴菱形、正方形都是垂美四边形.故答案为:③④.(2)证明:∵AC⊥BD,∴∠AOD=∠AOB=∠BOC=∠COD=90°,由勾股定理,得AD2+BC2=AO2+DO2+BO2+CO2,AB2+CD2=AO2+BO2+CO2+DO2,∴AB2+CD2=AD2+BC2;(3)①连接CG、BE,AB与CE交于点O,BG与CE交于点N,如图2,∵∠CAG=∠BAE=90°,∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,在△GAB和△CAE中,,∴△GAB≌△CAE(SAS),∴∠ABG=∠AEC,又∠AEC+∠AOE=90°,∴∠ABG+∠AOE=90°,即CE⊥BG,∴四边形CGEB是垂美四边形;②由(2)得,CG2+BE2=CB2+GE2,∵AC=,AB=3,∴BC===2,CG=AC=,BE=AB=3,∴GE2=CG2+BE2﹣CB2==24,∴GE=2.15.解:(1)∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD,∵AD=AE,∠DAE=60°,∴AB=AE,∠BAE=∠BAD+∠DAE=150°,∴∠ABE=AEB=(180°﹣∠BAE)=×(180°﹣∠BAE)=15°,∵AP平分∠DAE,∴∠PAE=∠DAE=30°,∴∠APB=∠PAE+∠AEP=30°+15°=45°;(2)连接PD,∵AD=AE,∠DAE=60°,∴△ADE为等边三角形,∴∠AED=∠ADE=60°,DE=AD,∵∠DAP=∠EAP,AP=AP,∴△DAP≌△EAP(SAS),∴PD=PE,∴∠PED=∠PDE,∵∠AEP=15°,∴∠PED=45°,∴∠DPE=90°,∵PE=2,∴DE=PE=2,∴AB=AD=DE=2;(3)PC+PA=PB.如图2,过点B作BH⊥BE交PA延长线于点H,∴∠HBE=90°,∵∠APB=45°,∴∠BHP=180°﹣∠HBE﹣∠APB=45°,∴∠BHP=∠APB,∴BH=BP,∵四边形ABCD是正方形,∴AB=BC,∠ABC=90°,∴∠HBE=∠ABC,∴∠HBE﹣∠ABE=∠ABC﹣∠ABE,即∠HBA=∠EBC,在△PBC与△HBA中,,∴△PBC≌△HBA(SAS),∴∠BPC=∠BHP=45°,BP=BH,CP=AH,∴∠HBE=90°,∴PH2=BH2+BP2=2BP2,即PH=BP,∴PC+PA=AH+AP=PH=BP.。
平行四边形综合练习附答案

平行四边形综合练习学校:___________姓名:___________班级:___________考号:___________一、单选题1.下列判断错误的是()A.两组对边分别相等的四边形是平行四边形B.四个内角都相等的四边形是矩形C.四条边都相等的四边形是菱形D.两条对角线垂直且平分的四边形是正方形【答案】D【解析】【分析】分别利用平行四边形、矩形、菱形和正方形的判定定理,对选项逐一分析即可做出判断.【详解】解:A、两组对边分别相等的四边形是平行四边形,符合平行四边形的判定,故本选项正确,不符合题意;B、∵四边形的内角和为360°,四边形的四个内角都相等,∴四边形的每个内角都等于90°,则这个四边形有三个角是90°,∴这个四边形是矩形,故四个内角都相等的四边形是矩形,本选项正确,不符合题意;C、四条边都相等的四边形是菱形,符合菱形的判定,故本选项正确,不符合题意;D、两条对角线垂直且平分的四边形是菱形,不一定是正方形,故本选项错误,符合题意;故选:D.【点睛】本题考查了平行四边形、矩形、菱形和正方形的判定定理,解题的关键是正确理解并掌握判定定理.2.如图,平行四边形ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE ,则AB的长为()6cm【答案】D【解析】【分析】根据平行四边形的性质,可得出点O 平分AC ,则OE 是三角形ABC 的中位线,则AB =2OE ,继而求出答案.【详解】解:∵四边形ABCD 为平行四边形,∴AO =CO ,∵点E 是CB 的中点,∴OE 为△ABC 的中位线,∴AB =2OE ,∵OE =6cm ,∴AB =12cm .故选:D .【点睛】本题考查了平行四边形的性质和三角形的中位线定理,关键是根据平行四边形的性质得出OE 为△ABC 的中位线.3.如图,点P 是矩形ABCD 的对角线上一点,过点P 作EF //BC ,分别交,AB CD 于,E F ,连接,PB PD ,若1,3AE PF ==,则图中阴影部分的面积为( )A .3B .6C .9D .12 【答案】A【解析】【分析】先根据矩形的性质证得DFP PBE SS =,然后求解即可.【详解】∴四边形AEPM 、四边形DFPM 、四边形CFPN 和四边形BEPN 都是矩形,∵ADC ABC S S =△△,AMP AEP S S =,PBE PBN S S =,PFD PDM S S =,PFC PCN S S =, ∴S 矩形DFPM =S 矩形BEPN ,∵PM =AE =1,PF =NC =3, ∴131322DFP PBE S S ==⨯⨯=△△, ∴S 阴=33+=322, 故选:A .【点睛】本题主要考查矩形的性质、三角形的面积等知识,证得DFP PBE S S =是解答本题的关键. 4.在四边形ABCD 中,O 是对角线的交点,能判定这个四边形是正方形的条件是( ) A .AC =BD ,AB ∥CD ,AB =CDB .AD ∥BC ,∠A =∠C C .AO =BO =CO =DO ,AC ⊥BDD .AO =CO ,BO =DO ,AB =BC【答案】C【解析】【详解】试题分析:根据正方形的判定:对角线互相垂直平分且相等的四边形是正方形进行分析从而得到最后的答案.解:A ,不能,只能判定为矩形;B ,不能,只能判定为平行四边形;C ,能;D ,不能,只能判定为菱形.故选C .5.如图,ABC ∆中,DE BC ∥,EF AB ∥,要判定四边形DBFE 是菱形,还需要添加的条件是( )A .BE 平分ABC ∠B .AD BD =C .BE AC ⊥D .AB AC =【答案】A【解析】【分析】 当BE 平分∠ABC 时,四边形DBFE 是菱形,可知先证明四边形BDEF 是平行四边形,再证明BD=DE 即可解决问题.【详解】解:当BE 平分ABC ∠时,四边形DBFE 是菱形,理由:∵DE BC ∥,∴DEB EBC ∠=∠,∵EBC EBD ∠=∠,∴EBD DEB ∠=∠,∴BD DE =,∵DE BC ∥,EF AB ∥,∴四边形DBFE 是平行四边形,∵BD DE =,∴四边形DBFE 是菱形.其余选项均无法判断四边形DBFE 是菱形,故选A.【点睛】本题考查菱形的判定、平行四边形的判定和性质、角平分线的定义、等腰三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型. 6.若一个菱形的边长为2,则这个菱形两条对角线长的平方和为( )A .16B .8C .4D .1【答案】A根据菱形的对角线互相垂直平分,即菱形被对角线平分成四个全等的直角三角形,根据勾股定理,即可求解.【详解】解:设两对角线长分别是:a ,b . 则(12a )2+(12b )2=22,故有a 2+b 2=16.故选:A .【点睛】本题主要考查了菱形的性质和勾股定理,菱形被两个对角线平分成四个全等的直角三角形,因为菱形的这个性质,使得菱形的题目一般都会和勾股定理结合起来,同学们要注意掌握.7.如图,把一张矩形纸片ABCD 按所示方法进行两次折叠,得到等腰直角三角形BEF ,若BC =1,则AB 的长度为( )A 2B 21+C 51+D .43【答案】A【解析】 【分析】 先判断出∠ADE =45°,进而判断出AE =AD ,利用勾股定理即可得出结论.【详解】解:由折叠补全图形如图所示,∵四边形ABCD 是矩形,∴∠ADA '=∠B =∠C =∠A =90°,AD =BC =1,CD =AB ,由第一次折叠得:∠DAE =∠A =90°,∠ADE =12∠ADC =45°,∴∠AED =∠ADE =45°,∴AE =AD =1,在Rt △ADE 中,根据勾股定理得,DE 2AD 2,由第二次折叠可知,DC DE =【点睛】本题考查了图形的折叠和勾股定理,搞清楚折叠中线段的数量关系是解决此类题的关键.8.如图,矩形ABCD 的对角线相交于点O ,过点O 作OG AC ⊥,交AB 于点G ,连接CG ,若15BOG ∠=,则BCG ∠的度数是( )A .15B .15.5C .20D .37.5【答案】A【解析】【分析】 根据矩形的性质求出OCB ∠的度数,从而得到GAC ∠的度数,再根据垂直平分线的性质得到GCA GAC ∠=∠,最后求出BCG ∠的度数.【详解】解:∵OG AC ⊥,∴90COG ∠=︒,∵15BOG ∠=︒,∴901575COB COG BOG ∠=∠-∠=︒-︒=︒,∵四边形ABCD 是矩形,∴AC BD =,12OC OA AC ==,12OB OD BD ==,//AB DC ,90BCD ∠=︒, ∴OC OB =, ∴1801807552.522COB OCB OBC ︒-∠︒-︒∠=∠===︒, ∴37.5ACD BCD OCB ∠=∠-∠=︒,∵//AB CD ,∴37.5GAC ACD ∠=∠=︒,∴GO 是AC 的垂直平分线,∴AG CG =,∴37.5GCA GAC ∠=∠=︒,∴52.537.515BCG OCB GCA ∠=∠-∠=︒-︒=︒.故选:A .【点睛】本题考查矩形的性质,垂直平分线的性质,解题的关键是熟练掌握这些性质定理,并结合题目条件进行证明.二、填空题9.正方形是有一组邻边_______,并且有一个角是_______的平行四边形,因此它既是______又是________.【答案】 相等 直角 矩形 菱形【解析】【分析】根据正方形的定义和性质填空即可.【详解】 正方形是有一组邻边相等,并且有一个角是直角的平行四边形,因此它既是矩形又是菱形.故答案为:相等,直角,矩形,菱形【点睛】本题考查了正方形的定义,解题关键是明确正方形的定义:正方形是有一组邻边相等,并且有一个角是直角的平行四边形,因此它既是矩形又是菱形.10.如图,在矩形ABCD 中,5AB =,4BC =,将矩形ABCD 翻折,使得点B 落在CD 边上的点E 处,折痕AF 交BC 于点F ,则FC =______【答案】32【分析】在Rt△ADE中,AD2+DE2=AE2,可得DE=3,CE=CD-DE=2,设FC=x,则EF=BC-FC=4-x,在Rt△ECF中,EF2=EC2+FC2,可得(4-x)2=22+x2,解方程即可.【详解】解∵△ABF≌△AEF,∴AE=AB=5,在矩形ABCD中,AD=BC=4,在Rt△ADE中,AD2+DE2=AE2,∴DE=3,CE=CD-DE=2,设FC=x,则EF=BC-FC=4-x,在Rt△ECF中,EF2=EC2+FC2,即(4-x)2=22+x2,8x=12,x=32,∴FC=32.故此答案为32.【点睛】本题考查翻折变换、矩形的性质、勾股定理等知识,解题的关键是学会利用参数构建方程解决问题.11.如图所示,在Rt△ABC中,∠C=90°,AC=4,将△ABC沿CB向右平移得到△DEF,若平移距离为2,则四边形ABED的面积等于_______.【答案】8【解析】【分析】形ABED 是平行四边形,最后根据平行四边形的面积公式即可得.【详解】由平移的性质得2AD BE ==,4DF AC ==,90C DFE ∠=∠=︒∴四边形ACFD 是矩形//AD CF ∴//AD BE ∴∴四边形ABED 是平行四边形(一组对边平行且相等的四边形是平行四边形) 则四边形ABED 的面积为428DF BE ⋅=⨯=故答案为:8.【点睛】本题考查了平移的性质、平行四边形的判定、矩形的判定与性质等知识点,掌握平移的性质是解题关键.12.如图,ACE ∆是以ABCD 的对角线AC 为边的等边三角形,点C 与点E 关于x 轴对称.若E 点的坐标是(7,33)-,则D 点的坐标是_____.【答案】(5,0)【解析】【分析】设CE 和x 轴交于H ,由对称性可知63CE =63AC CE ==根据勾股定理即可求出AH 的长,进而求出AO 和DH 的长,所以OD 可求,又因为D 在x 轴上,纵坐标为0,问题得解.【详解】解:点C 与点E 关于x 轴对称,E 点的坐标是(7,33)-, C ∴的坐标为(7,33),33CH ∴=3CE =63AC ∴=,9AH ∴=,7OH =,2AO DH ∴==,5OD ∴=,D ∴点的坐标是(5,0),故答案为:(5,0).【点睛】本题考查了平行四边形的性质、等边三角形的性质、点关于x 轴对称的特点以及勾股定理的运用,解题的关键是综合应用以上知识点.13.如图,在矩形ABCD 中,6AB =,8AD =,P 是AD 上不与A 和D 重合的一个动点,过点P 分别作AC 和BD 的垂线,垂足为E ,F ,则PE PF +的值为______.【答案】245【解析】【分析】连接OP ,利用勾股定理列式求出BD ,再根据矩形的对角线相等且互相平分求出OA 、OD ,然后根据S △AOD =S △AOP +S △DOP 列方程求解即可.【详解】解:如图,连接OP ,∵AB=6,AD=8,∴2222.6810BD AB AD ++=,∵四边形ABCD 是矩形,∵S△AOD=S△AOP+S△DOP,∴12×12×6×8=12×5•PE+12×5•PF,解得PE+PF=245.故答案为:245.【点睛】本题考查了矩形的性质,三角形的面积,熟记性质并利用三角形的面积列出方程是解题的关键.14.如图,在平面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为_____.【答案】(2,6)【解析】【分析】此题涉及的知识点是平面直角坐标系图像性质的综合应用.过点M作MF⊥CD于F,过C作CE⊥OA于E,在Rt△CMF中,根据勾股定理即可求得MF与EM,进而就可求得OE,CE的长,从而求得C的坐标.【详解】∵四边形OCDB是平行四边形,点B的坐标为(16,0),CD∥OA,CD=OB=16,过点M作MF⊥CD于F,则182CF CD,==过C作CE⊥OA于E,∵A(20,0),∴OA=20,OM=10,∴OE=OM−ME=OM−CF=10−8=2,连接MC,110,2MC OA==∴在Rt△CMF中,2222108 6.MF MC CF=-=-=∴点C的坐标为(2,6).故答案为(2,6).【点睛】此题重点考察学生对坐标与图形性质的实际应用,勾股定理,注意数形结合思想在解题的关键.三、解答题15.如图是某区部分街道示意图,其中AB AF⊥,E、D分别是FA和FG的中点,点C、D、E在一条直线上,点A、G、B在一条直线上,//BC FG.从B站乘车到E站只有两条路线有直接到达的公交车,路线1是B D A E⇒⇒⇒,且长度为5公里,路线2是B C F E⇒⇒⇒,求路线2的长度.【答案】5公里【解析】【分析】证明四边形BCDG是平行四边形,得到DG=CB,再证四边形BCFD是平行四边形,根据平行四边形的性质计算,得到答案.【详解】解:∵E、D分别是FA和FG的中点,∴AB∥DE,∵BC∥GF,∴四边形BCDG是平行四边形,∴DG=CB.∵FD=DG,∴CB=FD.又∵BC ∥DF ,∴四边形BCFD 是平行四边形,∴CF =BD ,∵AB ∥DE ,AB AF ⊥,FE =AE ,∴CE 垂直平分AF ,∴AE =FE ,FD =DA ,∴BC =DA ,∴路线2的长度:BC +CF +FE =AD +BD +AE =5(公里).【点睛】本题考查的是平行四边形的判定和性质、线段垂直平分线的性质,掌握平行四边形的判定定理和性质定理是解题的关键.16.已知:如图,ABCD 中,5AB =,3BC =.(1)作DAB ∠的角平分线,交CD 于点E (用直尺和圆规作图,不写作法,保留作图痕迹);(2)求CE 的长.【答案】(1)见解析;(2)CE 的长为2【解析】【分析】(1)根据尺规作图作DAB ∠的平分线即可;(2)根据平行四边形的性质和角平分线的定义,求出DE =DA =BC =3,再求出CE 即可.【详解】解:如图,(1)AE 即为∠DAB 的角平分线;(2)∵AE 为∠DAB 的角平分线,∴∠DAE =∠BAE ,在▱ABCD中,CD∥AB,∴∠BAE=∠DEA,∴∠DAE=∠DEA,∴DE=DA=BC=3,∵DC=AB=5,∴CE=CD﹣DE=2.答:CE的长为2.【点睛】当平行线遇上角平分线时,通过角的转化,可以得到等腰三角形,这是初中几何一个很重要的数学模型,要深刻领会.17.如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF,(1)求证:AF=DC;(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.【答案】(1)见解析(2)见解析【解析】【分析】(1)根据AAS证△AFE≌△DBE,推出AF=BD,即可得出答案.(2)得出四边形ADCF是平行四边形,根据直角三角形斜边上中线性质得出CD=AD,根据菱形的判定推出即可.【详解】解:(1)证明:∵AF∥BC,∴∠AFE=∠DBE.∵E是AD的中点,AD是BC边上的中线,∴AE=DE,BD=CD.在△AFE和△DBE中,∵∠AFE=∠DBE,∠FEA=∠BED,AE=DE,∴△AFE≌△DBE(AAS)∴AF =BD .∴AF =DC .(2)四边形ADCF 是菱形,证明如下:∵AF ∥BC ,AF =DC ,∴四边形ADCF 是平行四边形.∵AC ⊥AB ,AD 是斜边BC 的中线,∴AD =DC .∴平行四边形ADCF 是菱形.18.如图,四边形ABCD 是边长为13cm 的菱形,其中对角线BD 长10cm .求:(1)对角线AC 的长度;(2)菱形ABCD 的面积.【答案】(1)24cm AC =;(2)2120cm【解析】【分析】(1)根据菱形的对角线互相垂直平分,可利用勾股定理求出AE 的长,从而求出AC 的长;(2)根据菱形的面积公式:两条对角线乘积的一半即可求得面积.【详解】解:(1)∵四边形ABCD 是菱形,AC 与BD 相交于点E ,∴90AED ∠=︒(菱形的对角线互相垂直),11105(cm)22DE BD ==⨯=(菱形的对角线互相平分). ∴222213512(cm)AE AD DE =--=.∴221224(cm)AC AE ==⨯=(菱形的对角线互相平分);(2)ABD BDC ABCD S S S =+菱形1122BD AE BD CE =⋅+⋅ 1()2BD AE CE =⋅+ 12BD AC =⋅ 110242=⨯⨯ 2120(cm )=.【点睛】本题主要考查了菱形的性质、菱形的面积公式、勾股定理,熟知菱形的性质是解本题的关键.19.如图,E 是▱ABCD 的边CD 的中点,延长AE 交BC 的延长线于点F .(1)求证:△ADE ≌△FCE .(2)若∠BAF =90°,BC =5,EF =3,求CD 的长.【答案】(1)证明过程见解析;(2)8【解析】【分析】(1)由平行四边形的性质得出AD ∥BC ,AB ∥CD ,证出∠DAE =∠F ,∠D =∠ECF ,由AAS 证明△ADE ≌△FCE 即可;(2)由全等三角形的性质得出AE =EF =3,由平行线的性质证出∠AED =∠BAF =90°,由勾股定理求出DE ,即可得出CD 的长.【详解】(1)∵四边形ABCD 是平行四边形, ∴AD ∥BC ,AB ∥CD ,∴∠DAE =∠F ,∠D =∠ECF ,∵E 是▱ABCD 的边CD 的中点, ∴DE =CE ,在△ADE 和△FCE 中,DAE F D ECF DE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△ADE ≌△FCE (AAS );(2)∵ADE≌△FCE,∴AE=EF=3,∵AB∥CD,∴∠AED=∠BAF=90°,在▱ABCD中,AD=BC=5,∴DE=2222-=-=4,AD AE53∴CD=2DE=8【点睛】考点:(1)平行四边形的性质;(2)全等三角形的判定与性质20.(1)如图,纸片▱ABCD中,AD=5,S▱ABCD=15.过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为() A.平行四边形B.菱形C.矩形D.正方形(2)如图,在(1)中的四边形纸片AEE/D中,在EE/上取一点F,使EF=4,剪下△AEF,将它平移至△DE/F/的位置,拼成四边形AFF/D.①求证:四边形AFF'D是菱形;②求四边形AFF'D的两条对角线的长.图1图2【答案】(1)C;(2)①证明见解析;1010【解析】【详解】试题分析:(1)如图1,纸片▱ABCD中,AD=5,S▱ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AE E′D的形状为矩形,故选C;(2)①证明:∵纸片▱ABCD中,AD=5,S▱ABCD=15,过点A作AE⊥BC,垂足为E,∴AE=3.如图2:∵△AEF ,将它平移至△DE′F′,∴AF ∥DF′,AF=DF′,∴四边形AFF′D 是平行四边形.在Rt △AEF 中,由勾股定理,得AF=2222=34++AE EF =5,∴AF=AD=5,∴四边形AFF′D 是菱形;②连接AF′,DF ,如图3:在Rt △DE′F 中E′F=FF′﹣E′F′=5﹣4=1,DE′=3,∴DF=2222=13=10''++E D E F ,在Rt △AEF′中EF′=EF+FF′=4+5=9,AE=3,∴AF′=2222=39'++AE F E =310. 考点:①图形的剪拼;②平行四边形的性质;③菱形的判定与性质;④矩形的判定;⑤平移的性质.21.如图,在正方形ABCD 中,E 、F 分别为边AD 和CD 上的点,且AE=CF ,连接AF 、CE 交于点G .求证:AG=CG .【答案】证明见解析.【解析】【分析】先用SAS 证明△ADF ≌△CDE ,得∠DAF=∠DCE ,再用AAS 证明△AGE ≌△CGF 即可.【详解】∵四边形ABCD 是正方形,∴∠ADF=∠CDE=90°,AD=CD .∵AE=CF ,∴DE=DF ,在△ADF 和△CDE 中,AD AD ADF CDE DF DE =⎧⎪∠=∠⎨⎪=⎩, ∴△ADF ≌△CDE (SAS ),∴∠DAF=∠DCE ,在△AGE 和△CGF 中,GAE GCF AGE CGF AE CF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AGE ≌△CGF (AAS ),∴AG=CG .22.如图,△ABC 中,AB =AC =1,∠BAC =45°,△AEF 是由△ABC 绕点A 按顺时针方向旋转得到的,连接BE ,CF 相交于点D,(1)求证:BE =CF ;(2)当四边形ACDE 为菱形时,求BD 的长.【答案】(1)证明见解析(22【解析】【分析】(1)先由旋转的性质得AE=AB ,AF=AC ,∠EAF=∠BAC ,则∠EAF+∠BAF=∠BAC+∠BAF ,即∠EAB=∠FAC ,利用AB=AC 可得AE=AF ,得出△ACF ≌△ABE ,从而得出BE=CF ;(2)由菱形的性质得到DE=AE=AC=AB=1,AC ∥DE ,根据等腰三角形的性质得∠AEB=∠ABE ,根据平行线得性质得∠ABE=∠BAC=45°,所以∠AEB=∠ABE=45°,于是可判断△ABE 为等腰直角三角形,所以22BD=BE ﹣DE 求解.【详解】(1)∵△AEF 是由△ABC 绕点A 按顺时针方向旋转得到的,∴AE=AB ,AF=AC ,∠EAF=∠BAC ,∴∠EAF+∠BAF=∠BAC+∠BAF ,即∠EAB=∠FAC ,在△ACF 和△ABE 中,AC AB CAF BAE AF AE =⎧⎪∠=∠⎨⎪=⎩∴△ACF ≌△ABE∴BE=CF.(2)∵四边形ACDE 为菱形,AB=AC=1,∴DE=AE=AC=AB=1,AC ∥DE ,∴∠AEB=∠ABE ,∠ABE=∠BAC=45°,∴∠AEB=∠ABE=45°,∴△ABE 为等腰直角三角形,∴BE=2AC=2,∴BD=BE ﹣DE=21-.考点:1.旋转的性质;2.勾股定理;3.菱形的性质. 23.如图,AD 是ABC 的中线,//AE BC ,且12AE BC =,连接DE ,CE .(1)求证:AB DE =;(2)当ABC 满足条件__________时,四边形ADCE 是矩形.【答案】(1)见解析;(2)AB =AC 或 ABC ACB ∠=∠【解析】【分析】(1)根据三角形中位线定理和平行四边形的判定和性质解答即可; (2)根据矩形的判定解答即可.【详解】(1)∵AD 是ABC 的中线,∴12BD BC =, ∵12AE BC =, ∴AE BD =,∵//AE BC ,∴四边形ABDE 是平行四边形,∴AB DE =(2)当△ABC 满足AB =AC 或ABC ACB ∠=∠时,四边形ADCE 是矩形, 11,,22BC BD AE CD BC =∴== ∴AE =CD ,∵AE ∥BC ,∴四边形ADCE 是平行四边形,∵AB =DE ,∴当AB =AC 或ABC ACB ∠=∠时,AC =DE ,∴四边形ADCE 是矩形.【点睛】此题考查了平行四边形的判定与性质、等腰三角形的性质以及矩形的判定.此题难度适中,注意掌握数形结合思想的应用.24.在边长为5的正方形ABCD 中,点E 在边CD 所在直线上,连接BE ,以BE 为边,在BE 的下方作正方形BEFG ,并连接AG .(1)如图1,当点E 与点D 重合时,AG = ;(2)如图2,当点E 在线段CD 上时,DE =2,求AG 的长;(3)若AG =5172,请直接写出此时DE 的长.【答案】(1)5(2109(3)52或152. 【解析】【分析】 (1)如图1,连接CG ,证明△CBD ≌△CBG (SAS ),可得G ,C ,D 三点共线,利用勾股定理可得AG 的长;(2)如图2,作辅助线,构建全等三角形,证明△BCE ≌△BKG ,可得AK 和KG 的长,利用勾股定理计算AG 的长;(3)分三种情况:①当点E在边CD的延长线上时,如图3,同(2)知△BCE≌△BKG (AAS),BC=BK=5,根据勾股定理可得KG的长,即可CE的长,此种情况不成立;②当点E在边CD上;③当点E在DC的延长线上时,同理可得结论.【详解】(1)如图1,连接CG,∵四边形ABCD和四边形EBGF是正方形,∴∠CDB=∠CBD=45°,∠DBG=90°,BD=BG,∴∠CBG=45°,∴∠CBG=∠CBD,∵BC=BC,∴△CBD≌△CBG(SAS),∴∠DCB=∠BCG=90°,DC=CG=5,∴G,C,D三点共线,∴AG=22+=22AD DG+=55,510故答案为:55;(2)如图2,过点G作GK⊥AB,交AB的延长线于K,∵DE=2,DC=5,∴CE=3,∵∠EBG=∠EBC+∠CBG=90°,∠CBG+∠GBK=90°,∵BE=BG,∠K=∠BCE=90°,∴△BCE≌△BKG(AAS),∴CE=KG=3,BC=BK=5,∴AK=10,由勾股定理得:AG=22103+=109;(3)分三种情况:①当点E在CD的延长线上时,如图3,由(2)知△BCE≌△BKG(AAS),∴BC=BK=5,∵AG=5172,由勾股定理得:KG=22517102⎛⎫-⎪⎪⎝⎭=52,∴CE=KG=52,此种情况不成立;②当点E在边CD上时,如图4,由(2)知△BCE≌△BKG(AAS),∵AG=5172,由勾股定理得:KG=22517102⎛⎫-⎪⎪⎝⎭=52,∴CE=KG=52,∴DE=CD-CE=52;③当点E在DC的延长线上时,如图5,同理得CE=KG=52,∴DE=5+52=152;综上,DE的长是52或152.【点睛】本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、勾股定理等知识,本题综合性强,有一定难度,证明三角形全等是解决问题的关键.。
平行四边形和特殊四边形提高练习常考题和培优题(供参考)

平行四边形和特殊四边形提高练习常考题和培优题一.选择题(共5小题)1.如图,把大小相同的两个矩形拼成如下形状,则△FBD是()A.等边三角形B.等腰直角三角形C.一般三角形D.等腰三角形2.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=,CE=3,H 是AF的中点,那么CH的长是()A.3.5 B.C. D.23.如图,在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O 作OE垂直AC交AD于点E,则AE的长是()A.3 B.5 C.2.4 D.2.54.如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,EF=7,BC=10,则△EFM的周长是()A.17 B.21 C.24 D.275.如图,在矩形ABCD中,AB=6,AD=8,P是AD上不与A和D重合的一个动点,过点P分别作AC和BD的垂线,垂足为E、F,则PE+PF的值为()A.10 B.4.8 C.6 D.5二.填空题(共4小题)6.如图,在矩形ABCD中,对角线AC与BD相交于点O,AE平分∠BAD交BC 于点E,若∠CAE=15°,则∠BOE的度数等于.7.如图,将平行四边形ABCD的边DC延长到E,使CE=CD,连接AE交BC于F,∠AFC=n∠D,当n=时,四边形ABEC是矩形.8.如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,则线段AC、BF、CD之间的关系式是.9.如图,在平面直角坐标系中,O为原点,四边形OABC是矩形,A(﹣10,0),C(0,3),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标是.三.解答题(共31小题)10.如图,正方形ABCD中,AE=AB,直线DE交BC于点F,求∠BEF的度数.11.如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC、BD交于点O,AC⊥BD,E、F、G、H分别为AB、BC、CD、DA的中点.(1)求证:四边形EFGH为正方形;(2)若AD=1,BC=3,求正方形EFGH的边长.12.如图,点E、F分别是正方形ABCD的边CD和AD的中点,BE和CF交于点P.求证:AP=AB.13.如图,点P为正方形ABCD对角线BD上一点,PE⊥BC于E,PF⊥DC于F.(1)求证:PA=EF;(2)若正方形ABCD的边长为a,求四边形PFCE的周长.14.如图1,在正方形ABCD中,点E为BC上一点,连接DE,把△DEC沿DE折叠得到△DEF,延长EF交AB于G,连接DG.(1)求∠EDG的度数.(2)如图2,E为BC的中点,连接BF.①求证:BF∥DE;②若正方形边长为6,求线段AG的长.15.如图①,在正方形ABCD中,F是对角线AC上的一点,点E在BC的延长线上,且BF=EF.(1)求证:BF=DF;(2)求证:∠DFE=90°;(3)如果把正方形ABCD改为菱形,其他条件不变(如图②),当∠ABC=50°时,∠DFE=度.16.已知正方形ABCD中,对角线AC、BD相交于O.①如图1,若E是AC上的点,过A 作AG⊥BE于G,AG、BD交于F,求证:OE=OF②如图2,若点E在AC的延长线上,AG⊥EB交EB的延长线于G,AG延长DB 延长线于点F,其它条件不变,OE=OF还成立吗?17.如图,点P是菱形ABCD中对角线AC上的一点,且PE=PB.(1)求证:PE=PD;(2)求证:∠PDC=∠PEB;(3)若∠BAD=80°,连接DE,试求∠PDE的度数,并说明理由.18.如图,正方形ABCD中,AB=1,点P是BC边上的任意一点(异于端点B、C),连接AP,过B、D两点作BE⊥AP于点E,DF⊥AP于点F.(1)求证:EF=DF﹣BE;(2)若△ADF的周长为,求EF的长.19.如图,正方形ABCD的对角线AC、BD的交点为O,以O为端点引两条互相垂直的射线OM、ON,分别交边AB、BC于点E、F.(1)求证:0E=OF;(2)若正方形的边长为4,求EF的最小值.20.如图,在正方形ABCD中,点E是边AD上任意一点,BE的垂直平分线FG 交对角AC于点F.求证:(1)BF=DF;(2)BF⊥FE.21.已知:如图所示,四边形ABCD中,∠ABC=∠ADC=90°,M是AC上任一点,O是BD的中点,连接MO,并延长MO到N,使NO=MO,连接BN与ND.(1)判断四边形BNDM的形状,并证明;(2)若M是AC的中点,则四边形BNDM的形状又如何?说明理由.22.如图,在△ABC中,O是边AC上的一动点,过点O作直线MN∥BC,设MN 交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.(1)求证:OE=OF;(2)当点O运动到何处时,四边形AECF是矩形?23.(1)如图矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且DP=OC,连接CP,判断四边形CODP的形状并说明理由.(2)如果题目中的矩形变为菱形,结论应变为什么?说明理由.(3)如果题目中的矩形变为正方形,结论又应变为什么?说明理由.24.如图1,已知AB∥CD,AB=CD,∠A=∠D.(1)求证:四边形ABCD为矩形;(2)E是AB边的中点,F为AD边上一点,∠DFC=2∠BCE.①如图2,若F为AD中点,DF=1.6,求CF的长度:②如图2,若CE=4,CF=5,则AF+BC=,AF=.25.如图,直线a、b相交于点A,C、E分别是直线b、a上两点且BC⊥a,DE ⊥b,点M、N是EC、DB的中点.求证:MN⊥BD.26.如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.(1)经过多长时间,四边形PQCD是平行四边形?(2)经过多长时间,四边形PQBA是矩形?(3)经过多长时间,当PQ不平行于CD时,有PQ=CD.27.如图,E、F是正方形ABCD的边AD上的两个动点,满足AE=DF.连接CF 交BD于G,连接BE交AG于H.已知正方形ABCD的边长为4cm,解决下列问题:(1)求证:BE⊥AG;(2)求线段DH的长度的最小值.28.如图,点M是矩形ABCD的边AD的中点,点P是BC边上一动点,PE⊥MC,PF⊥BM,垂足为E、F.(1)当矩形ABCD的长与宽满足什么条件时,四边形PEMF为矩形?猜想并证明你的结论.(2)在(1)中,当点P运动到什么位置时,矩形PEMF变为正方形,为什么?29.某校数学兴趣小组开展了一次课外活动,过程如下:如图①,正方形ABCD 中,AB=4,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.(1)求证:AP=CQ;(2)如图②,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;(3)在(2)的条件下,若AP=1,求PE的长.30.如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,求t的值.31.如图,在Rt△ABC中,∠ABC=90°,点D是AC的中点,作∠ADB的角平分线DE交AB于点E,(1)求证:DE∥BC;(2)若AE=3,AD=5,点P为BC上的一动点,当BP为何值时,△DEP为等腰三角形.请直接写出所有BP的值.32.已知:如图,BF、BE分别是∠ABC及其邻补角的角平分线,AE⊥BE,垂足为点E,AF⊥BF,垂足为点F.EF分别交边AB、AC于点M、N.求证:(1)四边形AFBE是矩形;(2)BC=2MN.33.如图,在边长为5的菱形ABCD中,对角线BD=8,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.(1)对角线AC的长是,菱形ABCD的面积是;(2)如图1,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由;(3)如图2,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变请说明理由,若变化,请直接写出OE、OF之间的数量关系,不用明理由.34.如图,已知Rt△ABD≌Rt△FEC,且B、D、C、E在同一直线上,连接BF、AE.(1)求证:四边形ABFE是平行四边形.(2)若∠ABD=60°,AB=2cm,DC=4cm,将△ABD沿着BE方向以1cm/s的速度运动,设△ABD运动的时间为t,在△ABD运动过程中,试解决以下问题:(1)当四边形ABEF是菱形时,求t的值;(2)是否存在四边形ABFE是矩形的情形?如果存在,求出t的值,如果不存在,请说明理由.35.已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.(1)如图1,连接AF、CE.求证:四边形AFCE为菱形.(2)如图1,求AF的长.(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P的速度为每秒1cm,设运动时间为t秒.①问在运动的过程中,以A、P、C、Q四点为顶点的四边形有可能是矩形吗?若有可能,请求出运动时间t和点Q的速度;若不可能,请说明理由.②若点Q的速度为每秒0.8cm,当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.36.如图1,E,F是正方形ABCD的边上两个动点,满足AE=DF,连接CF交BD 于G,连接BE交AG于点H(1)求证:AG⊥BE;(2)如图2,连DH,若正方形的边长为4,则线段DH长度的最小值是.37.如图,在菱形ABCD中,AB=2,∠DAB=60°,点E时AD边的中点,点M时AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.(1)求证:四边形AMDN是平行四边形.(2)填空:①当AM的值为时,四边形AMDN是矩形;②当AM的值为时,四边形AMDN是菱形.38.如图,已知正方形OABC的边长为4,顶点A、C分别在x、y轴的正半轴上,M是BC的中点,点P(0,m)是线段oc上的一动点9点P不与点O、C重合0,直线PM交AB的延长线于点D.(1)求点D的坐标;(用含m的代数式表示)(2)若△APD是以AP边为一腰的等腰三角形,求m的值.39.如图,在△ABC中,∠ABC=90°,点D为AC的中点,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.(1)证明:四边形BDFG是菱形;(2)若AC=10,CF=6,求线段AG的长度.40.如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连接EF与边CD相交于点G,连接BE与对角线AC相交于点H,AE=CF,BE=EG.(1)求证:EF∥AC;(2)求∠BEF大小;(3)若EB=4,则△BAE的面积为.初二数学平行四边形和特殊四边形提高练习常考题和培优题参考答案与试题解析一.选择题(共5小题)1.(2012春•炎陵县校级期中)如图,把大小相同的两个矩形拼成如下形状,则△FBD是()A.等边三角形B.等腰直角三角形C.一般三角形D.等腰三角形【分析】根据正方形性质得出FG=BC,∠G=∠C=90°,GB=CD,根据SAS证△FGB ≌△BCD,推出∠FBG=∠BDC,BF=BD,求出∠DBC+∠FBG=90°,求出∠FBD的度数即可.【解答】解:∵大小相同的两个矩形GFEB、ABCD,∴FG=BE=AD=BC,GB=EF=AB=CD,∠G=∠C=∠ABG=∠ABC=90°,∵在△FGB和△BCD中,∴△FGB≌△BCD,∴∠FBG=∠BDC,BF=BD,∵∠BDC+∠DBC=90°,∴∠DBC+∠FBG=90°,∴∠FBD=180°﹣90°=90°,即△FBD是等腰直角三角形,故选B.【点评】本题考查了等腰直角三角形,全等三角形的性质和判定,正方形性质的应用,关键是证出△FGB≌△BCD,主要考查学生运用性质进行推理的能力.2.(2015春•江阴市期中)如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=,CE=3,H是AF的中点,那么CH的长是()A.3.5 B.C. D.2【分析】根据正方形的性质求出AB=BC=,CE=EF=3,∠E=90°,延长AD交EF于M,连接AC、CF,求出AM=4,FM=2,∠AMF=90°,根据正方形性质求出∠ACF=90°,根据直角三角形斜边上的中线性质求出CH=AF,根据勾股定理求出AF即可.【解答】解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=,CE=3,∴AB=BC=,CE=EF=3,∠E=90°,延长AD交EF于M,连接AC、CF,则AM=BC+CE=4,FM=EF﹣AB=2,∠AMF=90°,∵四边形ABCD和四边形GCEF是正方形,∴∠ACD=∠GCF=45°,∴∠ACF=90°,∵H为AF的中点,∴CH=AF,在Rt△AMF中,由勾股定理得:AF==2,∴CH=,故选:C.【点评】本题考查了勾股定理,正方形的性质,直角三角形斜边上的中线的应用,解此题的关键是能正确作出辅助线,并求出AF的长和得出CH=AF,有一定的难度.3.(2015春•泗洪县校级期中)如图,在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是()A.3 B.5 C.2.4 D.2.5【分析】根据矩形的性质得出∠CDE=90°,AD=BC=8,AB=DC=4,AO=OC,根据线段垂直平分线性质得出AE=CE,在Rt△CDE中,由勾股定理得出CE2=CD2+DE2,代入求出即可.【解答】解:∵在矩形ABCD中,AB=4,BC=8,∴∠CDE=90°,AD=BC=8,AB=DC=4,AO=OC,∵OE⊥AC,∴AE=CE,在Rt△CDE中,由勾股定理得:CE2=CD2+DE2,即AE2=42+(8﹣AE)2,解得:AE=5,故选B.【点评】本题考查了矩形的性质,勾股定理,线段垂直平分线性质的应用,解此题的关键是得出关于AE的方程.4.(2015秋•无锡期中)如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,EF=7,BC=10,则△EFM的周长是()A.17 B.21 C.24 D.27【分析】根据CF⊥AB于F,BE⊥AC于E,M为BC的中点,利用直角三角形斜边上的中线等于斜边的一半,求出FM和ME的长,即可求解.【解答】解:∵CF⊥AB,M为BC的中点,∴MF是Rt△BFC斜边上的中线,∴FM=BC=×10=5,同理可得,ME=BC=×10=5,又∵EF=7,∴△EFM 的周长=EF +ME +FM=7+5+5=17.故选A .【点评】此题主要考查学生对直角三角形斜边上的中线这个知识点的理解和掌握,解答此题的关键是利用直角三角形斜边上的中线等于斜边的一半,求出FM 和ME 的长.5.(2015春•乌兰察布校级期中)如图,在矩形ABCD 中,AB=6,AD=8,P 是AD 上不与A 和D 重合的一个动点,过点P 分别作AC 和BD 的垂线,垂足为E 、F ,则PE +PF 的值为( )A .10B .4.8C .6D .5【分析】连接OP ,利用勾股定理列式求出BD ,再根据矩形的对角线相等且互相平分求出OA 、OD ,然后根据S △AOD =S △AOP +S △DOP 列方程求解即可.【解答】解:如图,连接OP ,∵AB=6,AD=8,∴BD===10,∵四边形ABCD 是矩形,∴OA=OD=×10=5,∵S △AOD =S △AOP +S △DOP , ∴××6×8=×5•PE +×5•PF ,解得PE +PF=4.8.故选B .【点评】本题考查了矩形的性质,三角形的面积,熟记性质并利用三角形的面积列出方程是解题的关键.二.填空题(共4小题)6.(2016春•东平县期中)如图,在矩形ABCD 中,对角线AC 与BD 相交于点O ,AE 平分∠BAD 交BC 于点E ,若∠CAE=15°,则∠BOE 的度数等于 75° .【分析】由矩形ABCD ,得到OA=OB ,根据AE 平分∠BAD ,得到等边三角形OAB ,推出AB=OB ,求出∠OAB 、∠OBC 的度数,根据平行线的性质和等角对等边得到OB=BE ,根据三角形的内角和定理即可求出答案.【解答】解:∵四边形ABCD是矩形,∴AD∥BC,AC=BD,OA=OC,OB=OD,∠BAD=90°,∴OA=OB,∠DAE=∠AEB,∵AE平分∠BAD,∴∠BAE=∠DAE=45°=∠AEB,∴AB=BE,∵∠CAE=15°,∴∠DAC=45°﹣15°=30°,∠BAC=60°,∴△BAO是等边三角形,∴AB=OB,∠ABO=60°,∴∠OBC=90°﹣60°=30°,∵AB=OB=BE,∴∠BOE=∠BEO=(180°﹣30°)=75°.故答案为75°.【点评】本题主要考查了三角形的内角和定理,矩形的性质,等边三角形的性质和判定,平行线的性质,角平分线的性质,等腰三角形的判定等知识点,解此题的关键是求出∠OBC的度数和求OB=BE.7.(2014春•武昌区期中)如图,将平行四边形ABCD的边DC延长到E,使CE=CD,连接AE交BC于F,∠AFC=n∠D,当n=2时,四边形ABEC是矩形.【分析】首先根据四边形ABCD是平行四边形,得到四边形ABEC是平行四边形,然后证得FC=FE,利用对角线互相相等的四边形是矩形判定四边形ABEC是矩形.【解答】解:当∠AFC=2∠D时,四边形ABEC是矩形.∵四边形ABCD是平行四边形,∴BC∥AD,∠BCE=∠D,由题意易得AB∥EC,AB∥EC,∴四边形ABEC是平行四边形.∵∠AFC=∠FEC+∠BCE,∴当∠AFC=2∠D时,则有∠FEC=∠FCE,∴FC=FE,∴四边形ABEC是矩形,故答案为:2.【点评】此题考查了平行四边形的性质以及矩形的判定.此题难度适中,注意掌握数形结合思想的应用,解题的关键是了解矩形的判定定理.8.(2015春•南长区期中)如图,在正五边形ABCDE中,连接AC、AD、CE,CE 交AD于点F,连接BF,则线段AC、BF、CD之间的关系式是AC2+BF2=4CD2.【分析】首先根据菱形的判定方法,判断出四边形ABCF是菱形,再根据菱形的性质,即可判断出AC⊥BF;然后根据勾股定理,可得OB2+OC2=BC2,据此推得AC2+BF2=4CD2即可.【解答】解:∵五边形ABCDE是正五边形,∴AB∥CE,AD∥BC,∴四边形ABCF是平行四边形,又∵AB=BC=CD=DE=EA,∴四边形ABCF是菱形,∴AC⊥BF,∴OB2+OC2=BC2,∵AC=2OC,BF=2OB,∴AC2+BF2=(2OC)2+(2OB)2=4OC2+4OB2=4BC2,又∵BC=CD,∴AC2+BF2=4CD2.故答案为:AC2+BF2=4CD2.【点评】(1)此题主要考查了菱形的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:菱形是在平行四边形的前提下定义的,首先它是平行四边形,但它是特殊的平行四边形,特殊之处就是“有一组邻边相等”,因而就增加了一些特殊的性质和不同于平行四边形的判定方法.(2)此题还考查了勾股定理的应用:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方,要熟练掌握.9.(2015春•株洲校级期中)如图,在平面直角坐标系中,O为原点,四边形OABC是矩形,A(﹣10,0),C(0,3),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标是(﹣4,3),或(﹣1,3),或(﹣9,3).【分析】先由矩形的性质求出OD=5,分情况讨论:(1)当OP=OD=5时;根据勾股定理求出PC,即可得出结果;(2)当PD=OD=5时;①作PE⊥OA于E,根据勾股定理求出DE,得出PC,即可得出结果;②作PF⊥OA于F,根据勾股定理求出DF,得出PC,即可得出结果.【解答】解:∵A(﹣10,0),C(0,3),∴OA=10,OC=3,∵四边形OABC是矩形,∴BC=OA=10,AB=OC=3,∵D是OA的中点,∴AD=OD=5,分情况讨论:(1)当OP=OD=5时,根据勾股定理得:PC==4,∴点P的坐标为:(﹣4,3);(2)当PD=OD=5时,分两种情况讨论:①如图1所示:作PE⊥OA于E,则∠PED=90°,DE==4,∴PC=OE=5﹣4=1,∴点P的坐标为:(﹣1,3);②如图2所示:作PF⊥OA于F,则DF==4,∴PC=OF=5+4=9,∴点P的坐标为:(﹣9,3);综上所述:点P的坐标为:(﹣4,3),或(﹣1,3),或(﹣9,3);故答案为:(﹣4,3),或(﹣1,3),或(﹣9,3).【点评】本题考查了矩形的性质、坐标与图形性质、等腰三角形的性质、勾股定理;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.三.解答题(共31小题)10.(2012春•西城区校级期中)如图,正方形ABCD中,AE=AB,直线DE交BC 于点F,求∠BEF的度数.【分析】设∠BAE=x°,根据正方形性质推出AB=AE=AD,根据等腰三角形性质和三角形的内角和定理求出∠AEB和∠AED的度数,根据平角定义求出即可.【解答】解:设∠BAE=x°,∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD,∵AE=AB,∴AB=AE=AD,∴∠ABE=∠AEB=(180°﹣∠BAE)=90°﹣x°,∠DAE=90°﹣x°,∠AED=∠ADE=(180°﹣∠DAE)=[180°﹣(90°﹣x°)]=45°+x°,∴∠BEF=180°﹣∠AEB﹣∠AED,=180°﹣(90°﹣x°)﹣(45°+x°),=45°,答:∠BEF的度数是45°.【点评】本题考查了三角形的内角和定理,等腰三角形性质,正方形性质的应用,解此题的关键是如何把已知角的未知角结合起来,题目比较典型,但是有一定的难度.11.(2012秋•高淳县期中)如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC、BD交于点O,AC⊥BD,E、F、G、H分别为AB、BC、CD、DA的中点.(1)求证:四边形EFGH为正方形;(2)若AD=1,BC=3,求正方形EFGH的边长.【分析】(1)先由三角形的中位线定理求出四边相等,然后由AC⊥BD入手,进行正方形的判断.(2)连接EG,利用梯形的中位线定理求出EG的长,然后结合(1)的结论求出EH2=2,也即得出了正方形EHGF的边长.【解答】(1)证明:在△ABC中,∵E、F分别是AB、BC的中点,∴EF=同理FG=,GH=,HE=在梯形ABCD中,∵AB=DC,∴AC=BD,∴EF=FG=GH=HE∴四边形EFGH为菱形.设AC与EH交于点M在△ABD中,∵E、H分别是AB、AD的中点,∴EH∥BD,同理GH∥AC又∵AC⊥BD,∴∠BOC=90°.∴∠EHG=∠EMC=∠BOC=90°∴四边形EFGH为正方形.(2)解:连接EG,在梯形ABCD中,∵E、G分别是AB、DC的中点,∴EG=(AD+BC)=(1+3)=2,在Rt△HEG中,EG2=EH2+HG2,4=2EH2,EH2=2,则EH=.即四边形EFGH的边长为.【点评】此题考查了等腰梯形的性质及三角形、梯形的中位线定理,解答本题的关键是根据三角形的中位线定理得出EH=HG=GF=FE,这是本题的突破口.12.(2013秋•青岛期中)如图,点E、F分别是正方形ABCD的边CD和AD的中点,BE和CF交于点P.求证:AP=AB.【分析】延长CF、BA交于点M,先证△BCE≌△CDF,再证△CDF≌△AMF得BA=MA 由直角三角形中斜边中线等于斜边的一半,可得Rt△MBP中AP=BM,即AP=AB.【解答】证明:延长CF、BA交于点M,∵点E、F分别是正方形ABCD的边CD和AD的中点,∴BC=CD,∠BCE=∠CDF,CE=DF,∴△BCE≌△CDF,∴∠CBE=∠DCF.∵∠DCF+∠BCP=90°,∴∠CBE+∠BCP=90°,∴∠BPM=∠CBE+∠BCP=90°.又∵FD=FA,∠CDF=∠MAF,∠CFD=∠MFA,∴△CDF≌△AMF,∴CD=AM.∵CD=AB,∴AB=AM.∴PA是直角△BPM斜边BM上的中线,∴AP=BM,即AP=AB.【点评】本题考查了正方形各边长相等、各内角为直角的性质,全等三角形的判定和对应边相等的性质,直角三角形斜边中线长为斜边长一半的性质,本题中求证△CDF≌△AMF是解题的关键.13.(2015春•禹州市期中)如图,点P为正方形ABCD对角线BD上一点,PE⊥BC于E,PF⊥DC于F.(1)求证:PA=EF;(2)若正方形ABCD的边长为a,求四边形PFCE的周长.【分析】(1)连接PC,证四边形PFCE是矩形,求出EF=PC,证△ABP≌△CBP,推出AP=PC即可;(2)证△CBD是等腰直角三角形,求出BF、PF,求出周长即可.【解答】解:证明:(1)连接PC,∵四边形ABCD是正方形,∴AB=CB,∠ABD=∠CBD=45°,∠C=90°,在△ABP与△CBP中,,∴△ABP≌△CBP(SAS),∴PA=PC,∵PE⊥BC,PF⊥CD,∴∠PFC=90°,∠PEC=90°.又∵∠C=90°,∴四边形PFCE是矩形,∴EF=PC,∴PA=EF.(2)由(1)知四边形PFCE是矩形,∴PE=CF,PF=CE,又∵∠CBD=45°,∠PEB=90°,∴BE=PE,又BC=a,∴矩形PFCE的周长为2(PE+EC)=2(BE+EC)=2BC=2a.【点评】本题主要考查正方形的性质,全等三角形的性质和判定等知识点的连接和掌握,能证出AP=PC是解此题的关键.14.(2015秋•福建校级期中)如图1,在正方形ABCD中,点E为BC上一点,连接DE,把△DEC沿DE折叠得到△DEF,延长EF交AB于G,连接DG.(1)求∠EDG的度数.(2)如图2,E为BC的中点,连接BF.①求证:BF∥DE;②若正方形边长为6,求线段AG的长.【分析】(1)由正方形的性质可得DC=DA.∠A=∠B=∠C=∠ADC=90°,由折叠的性质得出∠DFE=∠C,DC=DF,∠1=∠2,再求出∠DFG=∠A,DA=DF,然后由“HL”证明Rt△DGA≌Rt△DGF,由全等三角形对应角相等得出∠3=∠4,得出∠2+∠3=45°即可;(2)①由折叠的性质和线段中点的定义可得CE=EF=BE,∠DEF=∠DEC,再由三角形的外角性质得出∠5=∠DEC,然后利用同位角相等,两直线平行证明即可;②设AG=x,表示出GF、BG,根据点E是BC的中点求出BE、EF,从而得到GE 的长度,再利用勾股定理列出方程求解即可;【解答】(1)解:如图1所示:∵四边形ABCD是正方形,∴DC=DA.∠A=∠B=∠C=∠ADC=90°,∵△DEC沿DE折叠得到△DEF,∴∠DFE=∠C,DC=DF,∠1=∠2,∴∠DFG=∠A=90°,DA=DF,在Rt△DGA和Rt△DGF中,,∴Rt△DGA≌Rt△DGF(HL),∴∠3=∠4,∴∠EDG=∠3+∠2=∠ADF+∠FDC,=(∠ADF+∠FDC),=×90°,=45°;(2)①证明:如图2所示:∵△DEC沿DE折叠得到△DEF,E为BC的中点,∴CE=EF=BE,∠DEF=∠DEC,∴∠5=∠6,∵∠FEC=∠5+∠6,∴∠DEF+∠DEC=∠5+∠6,∴2∠5=2∠DEC,即∠5=∠DEC,∴BF∥DE;②解:设AG=x,则GF=x,BG=6﹣x,∵正方形边长为6,E为BC的中点,∴CE=EF=BE=×6=3,∴GE=EF+GF=3+x,在Rt△GBE中,根据勾股定理得:(6﹣x)2+32=(3+x)2,解得:x=2,即线段AG的长为2.【点评】本题考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理、翻折变换的性质;熟练掌握正方形的性质,并能进行推理论证与计算是解决问题的关键.15.(2016春•召陵区期中)如图①,在正方形ABCD中,F是对角线AC上的一点,点E在BC的延长线上,且BF=EF.(1)求证:BF=DF;(2)求证:∠DFE=90°;(3)如果把正方形ABCD改为菱形,其他条件不变(如图②),当∠ABC=50°时,∠DFE=50度.【分析】(1)根据正方形的四条边都相等可得BC=DC,对角线平分一组对角可得∠BCF=∠DCF,然后利用“边角边”证明即可;(2)易证∠FBE=∠FEB,又因为∠FBE=∠FDC,所以可证明∠FEB=∠FDC,进而可证明∠DFE=90°;(3)根据全等三角形对应角相等可得∠CBF=∠CDF,根据等边对等角可得∠CBF=∠E,然后求出∠DFE=∠DCE,再根据两直线平行,同位角相等可得∠DCE=∠ABC,从而得解.【解答】(1)证明:在正方形ABCD中,BC=DC,∠BCF=∠DCF=45°,∵在△BCF和△DCF中,,∴△BCF≌△DCF(SAS);∴BF=DF;(2)证明:∵BF=EF,∴∠FBE=∠FEB,又∵∠FBE=∠FDC,∴∠FEB=∠FDC,又∵∠DGF=∠EGC,∴∠DFG=∠ECG=90°,即∠DFE=90°;(3)证明:由(1)知,△BCF≌△DCF,∴∠CBF=∠CDF,∵EE=FB,∴∠CBF=∠E,∵∠DGF=∠EGC(对顶角相等),∴180°﹣∠DGF﹣∠CDF=180°﹣∠EGC﹣∠E,即∠DFE=∠DCE,∵AB∥CD,∴∠DCE=∠ABC,∴∠DFE=∠ABC=50°,故答案为:50.【点评】本题考查了正方形的性质,全等三角形的判定与性质,菱形的性质,等边对等角的性质,熟记正方形的性质确定出∠BCF=∠DCF是解题的关键.16.(2015秋•泗县期中)已知正方形ABCD中,对角线AC、BD相交于O.①如图1,若E是AC上的点,过A 作AG⊥BE于G,AG、BD交于F,求证:OE=OF②如图2,若点E在AC的延长线上,AG⊥EB交EB的延长线于G,AG延长DB 延长线于点F,其它条件不变,OE=OF还成立吗?【分析】①由正方形的性质得出OA=OB,AC⊥BD,得出∠BOE=∠AOF=90°,由角的互余关系得出∠OBE=∠OAF,由ASA证明△BOE≌△AOF,得出对应边相等即可;②由正方形的性质得出OA=OB,AC⊥BD,得出∠BOE=∠AOF=90°,由角的互余关系得出∠OBE=∠OAF,由ASA证明△BOE≌△AOF,得出对应边相等即可.【解答】①证明:∵四边形ABCD是正方形,∴OA=OB,AC⊥BD,∴∠BOE=∠AOF=90°,∴∠OEB+∠OBE=90°,∵AG⊥BE,∴∠AGE=90°,∴∠OEB+∠OAF=90°,∴∠OBE=∠OAF,在△BOE和△AOF中,,∴△BOE≌△AOF(ASA),∴OE=OF;②解:OE=OF还成立;理由如下:∵四边形ABCD是正方形,∴OA=OB,AC⊥BD,∴∠BOE=∠AOF=90°,∴∠OEB+∠OBE=90°,∵AG⊥BE,∴∠AGE=90°,∴∠OEB+∠OAF=90°,∴∠OBE=∠OAF,在△BOE和△AOF中,,∴△BOE≌△AOF(ASA),∴OE=OF.【点评】本题考查了正方形的性质、全等三角形的判定与性质;熟练掌握正方形的性质,并能进行推理论证是解决问题的关键.17.(2016春•邳州市期中)如图,点P是菱形ABCD中对角线AC上的一点,且PE=PB.(1)求证:PE=PD;(2)求证:∠PDC=∠PEB;(3)若∠BAD=80°,连接DE,试求∠PDE的度数,并说明理由.【分析】(1)由菱形的性质得出AB=BC=CD=AD,AB∥CD,∠DCP=∠BCP,由SAS 证明△CDP≌△CBP,得出PB=PD,再由PE=PB,即可得出结论;(2)由等腰三角形的性质得出∠PBC=∠PEB,由全等三角形的性质得出∠PDC=∠PBC,即可得出∠PDC=∠PEB;(3)由四边形内角和定理得出∠DPE=100°,由等腰三角形的性质和三角形内角和定理即可得出结果.【解答】(1)解:∵四边形ABCD是菱形,∴AB=BC=CD=AD,AB∥CD,∠DCP=∠BCP,在△DCP和△BCP中,,∴△CDP≌△CBP(SAS),∴PB=PD,∵PE=PB,∴PE=PD;(2)证明:∵PE=PB,∴∠PBC=∠PEB,∵△CDP≌△CBP,∴∠PDC=∠PBC,∴∠PDC=∠PEB;(3)解:如图所示:∠PDE=40°;理由如下:在四边形DPEC中,∵∠DPE=360°﹣(∠PDC+∠PEC+∠DCB)=360°﹣(∠PEB+∠PEC+∠DCB)=360°﹣(180°+80°)=100°,∵PE=PD∴∠PDE=∠PED=40°.【点评】本题考查了菱形的性质、全等三角形的判定与性质、等腰三角形的性质;熟练掌握菱形的性质,证明三角形全等是解决问题的关键.18.(2016春•昆山市期中)如图,正方形ABCD中,AB=1,点P是BC边上的任意一点(异于端点B、C),连接AP,过B、D两点作BE⊥AP于点E,DF⊥AP于点F.(1)求证:EF=DF﹣BE;(2)若△ADF的周长为,求EF的长.【分析】(1)由正方形的性质得出AD=AB,证出∠DAF=∠ABE,由AAS证明△ADF ≌△BAE,得出AF=BE,DF=AE,即可得出结论;(2)设DF=a,AF=b,EF=DF﹣AF=a﹣b>0,由已知条件得出DF+AF=,即a+b=,由勾股定理得出a2+b2=1,再由完全平方公式得出a﹣b即可.【解答】(1)证明:∵BE⊥AP,DF⊥AP,∴∠DFA=∠AEB=90°,∠ABE+∠BAE=90°,∵四边形ABCD为正方形,∴AD=AB,∠DAB=90°=∠DAF+∠BAE,∴∠DAF=∠ABE,在△ADF和△BAE中,,∴△ADF≌△BAE(AAS),∴AF=BE,DF=AE,∴EF=AE﹣AF=DF﹣BE;(2)解:设DF=a,AF=b,EF=DF﹣AF=a﹣b>0,∵△ADF的周长为,AD=1,∴DF+AF=,即a+b=,由勾股定理得:DF2+AF2=AD2,即a2+b2=1,∴(a﹣b)2=2(a2+b2)﹣(a+b)2=2﹣=,∴a﹣b=,即EF=.【点评】本题考查了正方形的性质、全等三角形的判定与性质、勾股定理等知识;熟练掌握正方形的性质,由勾股定理得出a与b的关系式是解决问题(2)的关键.19.(2015春•繁昌县期中)如图,正方形ABCD的对角线AC、BD的交点为O,以O为端点引两条互相垂直的射线OM、ON,分别交边AB、BC于点E、F.(1)求证:0E=OF;(2)若正方形的边长为4,求EF的最小值.【分析】(1)根据正方形的性质可得∠EAO=∠FBO=45°,OA=OB,再根据同角的余角相等可得∠AOE=∠BOE,然后利用“角边角”证明△AOE和△BOF全等,根据全等三角形对应边相等即可得证;(2)根据等腰直角三角形△EOF,当OE最小时,再根据勾股定理得出EF的最小值.【解答】解:(1)∵四边形ABCD是正方形,∴OA=OB,∠AOB=90°,∠EAO=∠FBO=45°,∴∠AOE+∠BOE=90°,∵OE⊥OF,∴∠BOF+∠BOE=90°,∴∠AOE=∠BOF,在△AOE与△BOF中,,∴△AOE≌△BOF(ASA),∴OE=OF;(2)由(1)可知,△EOF是等腰直角三角形,∠EOF是直角,当OE最小时,EF的值最小,∵OA=OB,OE⊥AB,∴点E是AB的中点,∴OE=AB,∵AB=4,∴OE=2,∴EF=,即EF的最小值是2.【点评】本题考查了正方形的性质,解决此类问题的关键是正确的利用旋转不变量.正确作出辅助线是关键.20.(2016春•江宁区期中)如图,在正方形ABCD中,点E是边AD上任意一点,BE的垂直平分线FG交对角AC于点F.求证:(1)BF=DF;(2)BF⊥FE.【分析】(1)由正方形的性质得出AB=AD,∠BAF=∠DAF=45°,由SAS证明△BAF ≌△DAF,得出对应边相等即可;(2)由线段垂直平分线的性质得出BF=EF,证出EF=DF,得出∠FDE=∠FED,再由全等三角形的性质证出∠ABF=∠FED,由邻补角关系得出∠FED+∠FEA=180°,证出∠ABF+∠FEA=180°,由四边形内角和得出∠BAE+∠BFE=180°,求出∠BFE=90°即可.【解答】证明:如图所示:(1)∵四边形ABCD是正方形,∴AB=AD,∠BAF=∠DAF=45°,∠BAE=90°,在△BAF和△DAF中,,∴△BAF≌△DAF(SAS),∴BF=DF;(2)∵BE的垂直平分线FG交对角AC于点F,∴BF=EF,∵BF=DF,∴EF=DF,∴∠FDE=∠FED,∵△BAF≌△DAF,∴∠ABF=∠FDE,∴∠ABF=∠FED,∵∠FED+∠FEA=180°,∴∠ABF+∠FEA=180°,∴∠BAE+∠BFE=180°,∴∠BFE=90°,∴BF⊥FE.【点评】本题考查了正方形的性质、全等三角形的判定与性质、等腰三角形的判定与性质、四边形内角和定理等知识;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.21.(2015春•台州校级期中)已知:如图所示,四边形ABCD中,∠ABC=∠ADC=90°,M是AC上任一点,O是BD的中点,连接MO,并延长MO到N,使NO=MO,连接BN与ND.(1)判断四边形BNDM的形状,并证明;(2)若M是AC的中点,则四边形BNDM的形状又如何?说明理由.【分析】(1)由对角线互相平分的四边形是平行四边形即可得出结论;(2)由直角三角形斜边上1的中线性质得出BM=AC,DM=AC,得出BM=DM,即可得出结论.【解答】(1)解:四边形BNDM是平行四边形,理由如下:。
数学思维训练营认识平行四边形的综合算式练习题

数学思维训练营认识平行四边形的综合算式练习题数学思维训练营是为了提升学生的数学思维能力而设立的培训机构。
在这里,我们将探索平行四边形的特性,并通过一系列综合算式练习题来巩固我们对平行四边形的认识和运用。
1. 已知平行四边形ABCD,AB = 8cm,AD = 5cm,BC = 6cm,求平行四边形的周长和面积。
解析:根据平行四边形的性质,可知AD || BC,AB || DC,AD = BC。
由此,我们可以得到平行四边形的周长和面积。
周长 = AB + BC + CD + DA = 8cm + 6cm + 8cm + 5cm = 27cm面积 = 底 ×高 = BC × AD = 6cm × 5cm = 30cm²因此,这个平行四边形的周长为27cm,面积为30cm²。
2. 若两个平行四边形的面积分别为12cm²和18cm²,其中一个平行四边形的底长是另一个平行四边形底长的2倍,高是另一个平行四边形高的3倍,求这两个平行四边形的周长之和。
解析:假设较小的平行四边形底长为x,高为y,则较大的平行四边形底长为2x,高为3y。
根据平行四边形的面积公式,我们可以得到以下两个方程:1) x * y = 122) 2x * 3y = 18解方程组,可得 x = 2,y = 6。
因此,较小的平行四边形的底长为2cm,高为6cm;较大的平行四边形的底长为4cm,高为18cm。
两个平行四边形的周长分别为:较小平行四边形的周长 = 2 * (2cm + 6cm) = 16cm较大平行四边形的周长 = 2 * (4cm + 18cm) = 44cm所以,这两个平行四边形的周长之和为 16cm + 44cm = 60cm。
综上所述,这两个平行四边形的周长之和为60cm。
3. 平行四边形ABCD中,AB = 10cm,BC = 6cm,∠BAD = 60°,求平行四边形的面积。
中考数学一轮复习《四边形》综合复习练习题(含答案)

中考数学一轮复习《四边形》综合复习练习题(含答案)一、单选题1.一个多边形的内角和为900°,则这个多边形是( )A .七边形B .八边形C .九边形D .十边形 2.如图,将三角形纸片剪掉一角得四边形,设△ABC 与四边形BCDE 的外角和的度数分别为α,β,则正确的是( )A .0αβ-=B .0αβ-<C .0αβ->D .无法比较α与β的大小3.如图,把一个长方形纸片沿EF 折叠后,点D 、C 分别落在D ′、C ′的位置,若∠EFB =65°,则∠AED ′等于( )A .50°B .55°C .60°D .65°4.若一个正多边形的一个外角是60°,则这个正多边形的边数是( )A .10B .9C .8D .65.如图,四边形ABCD 是平行四边形,下列结论中正确的是( )A .当ABCD 是矩形时,90BAC ∠=︒B .当ABCD 是菱形时,AB BC ⊥ C .当ABCD 是正方形时,AC BD = D .当ABCD 是菱形时,AB AC =6.如图,在正方形ABCD 中,AE 平分BAC ∠交BC 于点E ,点F 是边AB 上一点,连接DF ,若BE AF =,则CDF ∠的度数为( )A .45︒B .60︒C .67.5︒D .775︒.7.如图,要拧开一个边长为()=6mm a a 的正六边形,扳手张开的开口b 至少为( )A .43mmB .63mmC . 42mmD . 12mm8.如图,菱形ABCD 中,∠BAD = 60°,AB = 6,点E ,F 分别在边AB ,AD 上,将△AEF 沿EF 翻折得到△GEF ,若点G 恰好为CD 边的中点,则AE 的长为( )A .34B .214C 3154D .39.以下说法不正确的是( )A .平行四边形是抽对称图形B .矩形对角线相等C .正方形对角线互相垂直平分D .菱形四条边相等10.陈师傅应客户要求加工4个长为4cm 、宽为3cm 的矩形零件.在交付客户之前,陈师傅需要对4个零件进行检测.根据零件的检测结果,图中有可能不合格的零件是( )A.B.C.D.11.如图,AB是半圆O的直径,以弦AC为折痕折叠AC后,恰好经过点O,则AOC∠等于()A.120°B.125°C.130°D.145°12.如图,在平面直角坐标系中,矩形ABCD的对角线AC经过坐标原点O,矩形的边分别平行于坐标轴,点B在函数kyx=(k≠0,x>0)的图像上,点D的坐标为(﹣3,1),则k的值为()A.53B.3-C.3D.53-二、填空题13.如果一个多边形的每一个外角都是60︒,那么这个多边形的边数是_______.14.如图,在矩形ABCD中,E是AD边上一点,且2AE DE=,BD与CE相交于点F,若DEF 的面积是3,则BCF △的面积是______.15.如果正多边形的一个外角是45︒,则这个正多边形的内角和是________︒.16.巧板是我国古代劳动人民的一项发明,被誉为“东方魔板”,它由五块等腰直角三角形、一块正方形和一块平行四边形组成.如图是利用七巧板拼成的正方形,随机向该图形内抛一枚小针,则针尖落在阴影部分的概率为 _____.17.如图,四边形ABCD 是菱形,42BD =,26AD =,点E 是CD 边上的一动点,过点E 作EF ⊥OC 于点F ,EG ⊥OD 于点G ,连接FG ,则FG 的最小值为_________.18.如图,矩形ABCD 的对角线AC 、BD 相交于点O ,过点O 作OE AC ⊥交AD 于点E ,若4AB =,8BC =,则DE 的长为______.19.已知ABC 中,65A ∠=︒,将B C ∠∠、按照如图所示折叠,若35ADB '∠=︒,则123∠+∠+∠=_____︒.CE ,F 20.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,5为DE的中点.若CEF△的周长为18,则OF的长为______.三、解答题21.如图,一组正多边形,观察每个正多边形中a的变化情况,解答下列问题.(1)将表格补充完整.正多边形的边数 3 4 5 6α的度数(2)观察上面表格中α的变化规律,角α与边数n的关系为.(3)根据规律,当α=18°时,多边形边数n=.22.如图,在ABCD中,AC=BC,M、N分别是AB和CD的中点.(1)求证:四边形AMCN是矩形;(2)若∠B=60°,BC=8,求ABCD的面积.23.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD 的中点,延长AE至G,使EG=AE,连接CG.(1)求证:△ABE≌△CDF;(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.24.如图,矩形ABCD中,点E在边CD上,将△BCE沿BE折叠,点C落在AD边上的点F处,过点F作FG∥CD交BE于点G,连接CG.(1)求证:四边形CEFG是菱形;(2)若AB=6,AD=10,求四边形CEFG的面积.25.如图,点E为矩形ABCD外一点,AE = DE.求证:△ABE≌△DCE26.如图,已知四边形ABCD为正方形,AB=2,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)求证:矩形DEFG是正方形;(2)探究:①CE与CG有怎样的位置关系?请说明理由.②CE+CG的值为.27.某数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段做了如下探究:【现察与猜想】(1)如图1,在正方形ABCD中,点E,F分别是AB,AD上的两点,连接DE,CF,DE⊥CF,则DECF的值为______.(2)如图2,在矩形ABCD中,AD=7,CD=4,点E是AD上的一点,连接CE,BD,且CE⊥BD,则CEBD的值______.【类比探究】(3)如图3,在四边形ABCD中,∠A=∠B=90°,点E为AB上一点,连接DE,过点C作DE 的垂线交ED的延长线于点G,交AD的延长线于点F,求证:DE•AB=CF•AD.28.在矩形ABCD中,AB=6,AD=4,点M为AB边上一个动点,连接DM,过点M作MN⊥DM,且MN=32DM,连接DN.(1)如图1,连接BD与BN,BD交MN于点E.①求证:△ABD∽△MND;②求证:∠CBN=∠DNM.(2)如图2,当AM=4BM时,求证:A,C,N三点在同一条直线上.参考答案1.A2.A3.A4.D5.C6.C7.B8.B9.A10.C11.A12.B13.614.2715.108016.381718.319.265︒20.7221.(1)正多边形每个内角的度数为180(2)n n -. 1803,603n α===; 904,452n α===; 正五边形的内角180(52)1085-=,1801085,362n α-===; 正五边形的内角180(62)1206-=,1801206,302n α-===.(2)观察(1)中结论,1803,603n == 1804,454n == 1805,365n == 1806,306n == 总结规律,则有180n α=. (3)借助(2)中公式,有180n α=,即18018n= 解得10n =.22.(1)证明:∵四边形ABCD 是平行四边形, ∴AB ∥CD ,AB =CD ,∵M 、N 分别是AB 和CD 的中点, ∴AM =BM ,AM ∥CN ,AM =CN , ∴四边形AMCN 是平行四边形,又∵AC =BC ,AM =BM ,∴CM ⊥AB ,∴∠CMA =90°,∴四边形AMCN 是矩形;(2)解:∵∠B =60°,BC =8,∠BMC =90°, ∴∠BCM =30°,∴Rt △BCM 中,BM =12BC =4,CM∵AC =BC ,CM ⊥AB ,∴AB =2BM =8,∴ABCD 的面积为AB ×CM23.(1)证明:∵四边形ABCD 是平行四边形, ∴AB =CD ,AB ∥CD ,OB =OD ,OA =OC , ∴∠ABE =∠CDF ,∵点E ,F 分别为OB ,OD 的中点, ∴BE =12OB ,DF =12OD ,∴BE =DF ,在△ABE 和△CDF 中,AB CD ABE CDF BE DF ⎧⎪∠∠⎨⎪⎩===,∴△ABE ≌△CDF (SAS ) .(2)当AB =12AC 时,四边形EGCF 是矩形;理由如下: 当AB =12AC 时,∵AC =2OA ,AC =2AB ,∴AB =OA ,∵E 是OB 的中点,∴AG⊥OB,∴∠OEG=90°,同理:CF⊥OD,∴AG∥CF,∴EG∥CF,由(1)得:△ABE≌△CDF,∴AE=CF,∵EG=AE,∴EG=CF,∴四边形EGCF是平行四边形,∵∠OEG=90°,∴四边形EGCF是矩形.24.(1)证明:由题意可得,△BCE≌△BFE,∴∠BEC=∠BEF,FE=CE,∵FG∥CE,∴∠FGE=∠CEB,∴∠FGE=∠FEG,∴FG=FE,∴FG=EC,∴四边形CEFG是平行四边形,又∵CE=FE,∴四边形CEFG是菱形;(2)解:∵矩形ABCD 中,AB =6,AD =10,BC =BF ,∴∠BAF =90°,AD =BC =BF =10,∴AF =8,∴DF =2,设EF =x ,则CE =x ,DE =6-x ,∵∠FDE =90°,∴22+(6-x )2=x 2,解得,x =103, ∴CE =103, ∴四边形CEFG 的面积是:CE •DF =103×2=203. 25.解:四边形ABCD 是矩形,AB DC ∴=,90BAD CDA ∠=∠=︒,AE DE =,EAD EDA ∴∠=∠,EAB BAD EAD CDA EDA EDC ∴∠=∠+∠=∠+=∠, 在ABE ∆和DCE ∆中,AE DE EAB EDC AB DC =⎧⎪∠=∠⎨⎪=⎩()ABE DCE SAS ∴∆∆≌.26.(1)如图,作EM ⊥BC 于M ,EN ⊥CD 于N ,又∠BCD =90°,∴∠MEN =90°,∵点E 是正方形ABCD 对角线上的点,∴EM =EN ,∵∠DEF =90°,∴∠DEN =∠MEF =90°﹣∠FEN ,∵∠DNE =∠FME =90°,在△DEN 和△FEM 中,DNE FME EN EMDEN FEM ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△DEN ≌△FEM (ASA ),∴EF =DE ,∵四边形DEFG 是矩形,∴矩形DEFG 是正方形;(2)①CE ⊥CG ,理由如下:∵正方形DEFG 和正方形ABCD ,∴DE =DG ,AD =DC ,∵∠CDG +∠CDE =∠ADE +∠CDE =90°,∴∠CDG =∠ADE ,在△ADE 和△CDG 中,AD CD ADE CDG DE DG =⎧⎪∠=∠⎨⎪=⎩,∴△ADE ≌△CDG (SAS ),∴∠DAE =∠DCG ,∵∠ACD +∠CAD +∠ADC =180°,∠ADC =90°,∴∠ACG =∠ACD +∠DCG =∠ACD +∠CAD =90°, ∴CE ⊥CG ;②由①知,△ADE ≌△CDG ,∴AE =CG ,∴CE +CG =CE +AE =ACAB=2,故答案为:2.27.(1)解:设DE与CF的交点为G,∵四边形ABCD是正方形,∴∠A=∠FDC=90°,AD=CD,∵DE⊥CF,∴∠DGF=90°,∴∠ADE+∠CFD=90°,∠ADE+∠AED=90°,∴∠CFD=∠AED,在△AED与△DFC中,A FDCCFD AEDAD CD∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AED≌△DFC(AAS),∴DE=CF,∴DECF=1,故答案为:1;(2)解:如图,设DB与CE交于点G,∵四边形ABCD是矩形,∴∠A=∠EDC=90°,∵CE⊥BD,∴∠DGC=90°,∴∠CDG +∠ECD =90°,∠ADB +∠CDG =90°,∴∠ECD =∠ADB ,∵∠CDE =∠A ,∴△DEC ∽△ABD , ∴47CE DC BD AD ==, 故答案为:47; (3)证明:如图,过点C 作CH ⊥AF 交AF 的延长线于点H ,∵CG ⊥EG ,∴∠G =∠H =∠A =∠B =90°,∴四边形ABCH 为矩形,∴AB =CH ,∠FCH +∠CFH =∠DFG +∠FDG =90°,∴∠FCH =∠FDG =∠ADE ,∠A =∠H =90°,∴△AED ∽△HFC ,∴DE AD CF CH =, ∴DE AD CF AB=, ∴DE •AB =CF •AD .28.(1)①证明:∵四边形ABCD 是矩形,DM ⊥MN ∴∠A =∠DMN =90°∵AB =6,AD =4,MN =32DM ∴23AD DM AB MN == ∴△ABD ∽△MND .②证明:∵四边形ABCD 是矩形,DM ⊥MN ∴∠ABC =∠DMN =90°∴∠ABD +∠CBD =90°由①得△ABD ∽△MND∴∠ABD =∠DNM又∵∠MEB =∠DEN∴△MBE ∽△DNE ∴ME BE DE NE = ∴ME DE BE NE= 又∠MED =∠BEN∴△DME ∽△NBE∴∠NBE =∠DME =90°∴∠CBN +∠CBD =90°又∠ABD +∠CBD =90°,∠ABD =∠DNM ∴∠CBN =∠DNM .(2) 如图②,过点N 作NF ⊥AB 于点F ,连接AC ,AN ∴∠NF A =90°∵四边形ABCD 是矩形,AD =4,AB =6 ∴∠A =∠ABC =90°,BC =AD =4∴23BC AB =,∠ADM +∠AMD =90° ∵AM =4BM ,AB =6∴42455AM AB ==又DM ⊥MN∴∠AMD +∠FMN =90° ∴∠ADM =∠FMN∴△ADM ∽△FMN ∴AD AM DM MF FN MN== 又MN =32DM ∴24425=3DM MF FN MN == ∴MF =6,FN =365∴AF =AM +MF =2454655+= ∴23NF AF = ∴NF BC AF AB = ∵∠ABC =∠AFN =90° ∴△ABC ∽△AFN∴∠BAC =∠F AN∴A ,C ,N 三点在同一条直线.。
2023届中考数学专项练习 四边形综合训练(A)

四边形综合训练(A )1.两个矩形的位置如图所示,若1α∠=,则2∠=( )A.90α-︒B.45α-︒C.180α︒-D.270α︒-2.在四边形ABCD 中,AB CD =,AD BC =,80B ∠=︒,则C ∠的度数为( )A.10°B.40°C.80°D.100°3.下列说法正确的是( )A.有一个角是直角的平行四边形是正方形B.对角线相等的四边形是正方形C.四边都相等的四边形是菱形D.对角线互相垂直的四边形是矩形4.如图,在Rt ABC 中,90ACB ∠=︒,点D ,E 分别是边AB ,AC 的中点,延长BC 到点F ,使12CF BC =.若10AB =,则EF 的长是( )A.6B.5C.3D.525.如图,在矩形ABCD 中,对角线AC 与BD 相交于点,O CE BD ⊥,垂足为点,5E CE =,且2EO DE =,则AD 的长为( )A. B. C.10 D.6.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH AB⊥于点H,连接OH,OH=,若菱形ABCD的面积为,则CD的长为( )4A.4B.C.8D.7.如图,在ABC△中,点D,E分别是AB,BC边的中点,点F在DE的延长线上.添加一个条件,使得四边形ADFC为平行四边形,则这个条件可以是( )A.B F= C.AC CF∠=∠ B.DE EF= D.AD CF=8.如图,在正方形ABCD中,3DM=,AEM与ADM关AB=,点M在CD边上,且1于AM所在的直线对称.将ADM按顺时针方向绕点A旋转90°得到ABF,连接EF,则线段EF的长为( )A.3B.9.如图,在ABC△和ABC△关于直线BC对称,连接AD,与BC=,DBC△中,AB AC相交于点O,过点C作CE CDBC=,则AD=,6⊥,垂足为C,与AD相交于点E.若8 +的值为( )2OE AEBDA.43B.34C.53D.5410.如图,在边长为2的等边三角形ABC的外侧作正方形ABED,过点D作DF BC⊥,垂足为F,则DF的长为( )A.2+ B.5- C.3111.如图,已知正方形ABCD的边长为4cm,则图中阴影部分的面积为________2cm.12.如图,点A的坐标为(1,3),点B在x轴上,把OAB△沿x轴向右平移得到ECD△,若四边形ABDC的面积为9,则点C的坐标为___________________.13.菱形ABCD的边长为2,45ABC∠=︒,点P、Q分别是BC、BD上的动点,CQ PQ+的最小值为_____________.14.如图,长方形纸片ABCD中,E为BC上一点,将纸片沿AE对折,点B落在AC上F处,若F恰好为AC中点,则ACB=∠_______.15.如图,将矩形纸片ABCD折叠,使点B与点D重台,点A落在点P处,折痕为EF,(1)求证:PDE CDF△△;≅(2)若4EF=cm,求BC的长.CD=cm,5答案以及解析1.答案:C解析:如图.1903∠=︒+∠,3902∠=︒-∠,190902∴∠=︒+︒-∠,21801180α∴∠=︒-∠=︒-.2.答案:D解析:如图,AB CD=,AD BC=,∴四边形ABCD是平行四边形,//AB CD∴,180B C∴∠+∠=︒,180********C B∴∠=︒-∠=︒-︒=︒,故选:D.3.答案:C解析:A.有一个角是直角的平行四边形是矩形,故本选项不正确,不符合题意;B.两条对角线相等的菱形才是正方形,故本选项不正确,不符合题意;C.四边都相等的四边形是菱形,故本选项正确,符合题意;D.两条对角线互相垂直的四边形不一定是矩形,故本选项不正确,不符合题意;故选:C.4.答案:B解析:由题意知,DE是ABC的中位线,//DE BC∴,12DE BC=,又12CF BC=,DE CF ∴=.又AE EC =,90AED ECF ∠=∠=︒,ADE EFC ∴≌,EF AD ∴=,152AD AB ==,5EF ∴=.故选B. 5.答案:A解析:∵四边形ABCD 是矩形,90,.2ADC OC OD EO DE ∴∠===,∴设DE x =,则2,3,6.EO x OD OC x AC x CE BD =∴===⊥,90DEC OEC ∴∠=∠=︒.在Rt OCE △中,222EO CE OC +=,222(2)5(3)x x ∴+=,解得xx =(舍去).DE AC ∴==CD AD ∴==6.答案:C解析:DH AB ⊥,90BHD ∴∠=︒,四边形ABCD 是菱形,OB OD ∴=,12OC OA AC ==,AC BD ⊥,12OH OB OD BD ∴===(直角三角形斜边上中线等于斜边的一半),4OD ∴=,8BD =,由12AC BD ⋅=得,182AC ⨯⋅=AC ∴=12OC AC ∴==,28CD OD ∴=,故答案为:C. 7.答案:B解析:D ,E 分别是AB ,BC 的中点,∴DE 是ABC △的中位线,//DE AC ∴,12DE AC =, A 、当B F ∠=∠,不能判定//AD CF ,即不能判定四边形ADFC 为平行四边形,故本选项不符合题意; B 、DE EF =,12DE DF ∴=,AC DF ∴=,//AC DF ,∴四边形ADFC 为平行四边形,故本选项符合题意;C 、根据AC CF =,不能判定AC DF =,即不能判定四边形ADFC 为平行四边形,故本选项不符合题意;D 、AD CF =,AD BD =,BD CF ∴=,由BD CF =,BED CEF ∠=∠,BE CE =,不能判定BED CEF ≅△△,不能判定//CF AB ,即不能判定四边形ADFC 为平行四边形,故本选项不符合题意;故选:B.8.答案:C解析:如图,连接BM .由题意可知,AE AD =,MAD MAE ∠=∠,AF AM =,FAB MAD ∠=∠.FAB MAE ∴∠=∠.FAB BAE BAE MAE ∴∠+∠=∠+∠.即FAE MAB ∠=∠.FAE MAB ∴≌.EF BM ∴=.四边形ABCD 是正方形,3BC CD AB ∴===.1DM =,2CM ∴=.∴在Rt BCM 中,BM =EF ∴=故选C.9.答案:D解析:DBC △和ABC △关于直线BC 对称,AC CD ∴=,AB BD =,AB AC =,AC CD AB BD ∴===,∴四边形ABDC 是菱形,AD BC ∴⊥,4AO DO ==,3BO CO ==,ACO DCO ∠=∠,5BD ∴==,CE CD ⊥,90DCO ECO CAO ACO DCO CAO ∴∠+∠=︒=∠+∠=∠+∠,CAO ECO ∴∠=∠,tan EO CO ECO CO AO∠∴==, 334EO ∴=, 94EO ∴=, 74AE ∴=,972254454OE AE BD ⨯++∴==, 故选D.10.答案:D解析:如图,过点E 作EG DF ⊥于点G ,作EH BC ⊥于点H ,则90BHE DGE ∠=∠=︒,ABC △是边长为2的等边三角形,2AB ∴=,60ABC ∠=︒,四边形ABED 是正方形,2BE DE ∴==,90ABE BED ∠=∠=︒,180180609030EBH ABC ABE ∴∠=︒-∠-∠=︒-︒-︒=︒,1sin 2sin30212EH BE EBH ∴=⋅∠=⋅︒=⨯=,cos 2cos30BH BE EBH =⋅∠=︒,EG DF ⊥,EH BC ⊥,DF BC ⊥,90EGF EHB DFH ∴∠=∠=∠=︒,∴四边形EGFH 是矩形,1FG EH ∴==,90BEH BEG GEH ∠+∠=∠=︒,90DEG BEG ∠+∠=︒,BEH DEG ∴∠=∠,在BEH △和DEG △中,BHE DGEBEH DEG BE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩,(AAS)BEH DEG ∴≅△△,DG BH ∴=,1DF DG FG ∴=+=,故选:D.11.答案:8 解析:图中阴影部分的面积之和正好等于正方形面积的一半,且正方形的边长为4cm ,∴图中阴影部分的面积为:()22148cm 2S =⨯=. 故答案为:8.12.答案:(4,3)解析:由平移的性质易得//AC BD 且AC BD =,∴四边形ABDC 是平行四边形.过点A 作AH x ⊥轴于点H ,则3AH =.ABDC 的面积为9,9BD AH ∴⋅=,3BD AC ∴==.(1,3)A ,(4,3)C ∴.13.解析:连接AQ ,作AH BC ⊥于H ,四边形ABCD 是菱形,AB CB ∴=,ABQ CBQ ∠=∠,BQ BQ =,(SAS)ABQ CBQ ∴≅△△,AQ CQ ∴=,∴当点A 、Q 、P 共线,AQ PQ +的最小值为AH 的长,2AB =,45ABC ∠=︒,AH ∴=CQ PQ ∴+.14.答案:30° 解析:在长方形纸片ABCD 中,90B ∴∠=︒,将纸片沿AE 对折,点B 落在AC 上F 处, BAE FAE ∴∠=∠,90AFE B ∠=∠=︒,即EF AC ⊥, F 恰好为AC 中点,∴EF 是AC 的中垂线,AE CE ∴=,EAF ECA ∴∠=∠,90BAC ACB ∠+∠=︒,30EAF ECA BAE ∴∠=∠=∠=︒,即:30ACB ︒=∠. 故答案是:30°.15.答案:(1)证明见解析(2)163BC = 解析:(1)四边形ABCD 是矩形,AB CD ∴=,90A B ADC C ∠=∠=∠=∠=︒, 由折叠知,AB PD =,A P ∠=∠,90B PDF ∠=∠=︒,PD CD ∴=,P C ∠=∠,PDF ADC ∠=∠, PDF EDF ADC EDF ∴∠-∠=∠-∠, PDE CDF ∴∠=∠,在PDE △和CDF △中,P C PD CD PDE CDF ∠=∠⎧⎪=⎨⎪∠=∠⎩, (ASA)PDE CDF ∴≅△△;(2)如图,过点E 作EG BC ⊥交于点G ,四边形ABCD 是矩形,4AB CD EG ∴===cm ,又5EF =cm,3GF ==∴, 设AE x =,EP x ∴=,由PDE CDF ≅△△知,EP CF x ==, 3DE GC GF FC x ∴==+=+, 在Rt PED △中,222PE PD DE +=, 即()22243x x +=+, 解得,76x =,77163663BC BG GC ∴=+=++=cm.。
《四边形的认识》综合练习题

《四边形的认识》综合练习题
四边形的认识综合练题
问题一
请问以下哪些图形是四边形?
a) 正方形
b) 圆形
c) 梯形
d) 三角形
答案:a) 正方形, c) 梯形
问题二
四边形具有哪些特点?
答案:四边形是一个有四条边的几何图形。
它的特点包括:
- 有四个角
- 相邻两边不共线
- 相邻两边不重叠
- 对角线相交于一点
- 对角线长度相等
问题三
下面哪些陈述是关于平行四边形的?
a) 对角线相等
b) 对边平行
c) 有一个直角
d) 有两条边相等
答案:b) 对边平行
问题四
计算下面平行四边形的面积:
________________
/ /
/ /
/______________/
已知底边长度为 10cm,高度为 5cm。
答案:面积 = 底边长度 ×高度 = 10cm × 5cm = 50cm²
问题五
请问矩形和正方形是什么关系?
答案:矩形是一种特殊的四边形,它的特点是拥有四个直角。
正方形是一种特殊的矩形,它的特点是拥有四个相等的边和四个直角。
问题六
如果一个四边形有两个相等的边,这个四边形是什么形状?答案:如果一个四边形有两个相等的边,它是一个梯形。
八年级数学下《四边形》培优练习卷

八年级数学下《四边形》培优练习卷一、选择题1.若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是()A.矩形B.菱形C.对角线互相垂直的四边形D.对角线相等的四边形2.如图,在△ABC,∠ACB=90°中,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,CE=4,求四边形A CEB的周长。
A.4 B.10+ 4 C. 10+2 D. 23.在矩形ABCD中,AB=2AD,E是CD上一点,且AE=AB,则∠CBE= ( )A.30° B.22.5° C.15° D.以上都不对4.如图,将矩形ABCD沿AE折叠,若∠BAD'=30°,则∠AED' 等于 ( )A.30° B.45° C.60° D.75°第6题5.如图,矩形ABCD中,AB=3,BC=5.过对角线交点O作OE⊥AC交AD于E,则AE的长是 ( ) A.1.6 B.2.5 C.3 D.3.46.平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别是AB和CD五等分点,点B1,B2和D1,D2分别是BC和DA三等分点,若四边形A4B2C4D2面积为1.则平行四边形ABCD面积为 ( )A.2 B.35C.53D.157.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EB的长为()A.1 B.4C.4﹣2D.4﹣4第7题二、填空题8.在□ABCD中,一角的平分线把一条边分成3 cm和4 cm两部分,则□ABCD的周长为______.9.矩形的两条对角线的夹角为60°,一条对角线与较短边的和为15,则较长边的长为_______.10.已经△ABC中,∠C=90°,C=10,a:b=3:4 ,则a= b=11.如图,在△ABC中,AB=AC,将△ABC绕点C旋转180°得到△FEC,连接AE、BF.当∠ACB为度时,四边形ABFE为矩形.第11题第12题第13题第14题12.如图,矩形ABCD中,AB=2,BC=3,对角线AC的垂直平分线分别交AD,BC于点E、F.连接CE,则CE的长是_______.13.如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3厘米,EF=4厘米,则边AD的长是_______厘米.14.如图,△ABC中,∠A的平分线交BC于点D,过点D作DE⊥AC,DF⊥AB,垂足分别为E,F,下面四个结论:①∠AFE=∠AEF;②AD垂直平分EF;③CEBFSSCEDBFD=∆∆;④EF∥BC.其中正确的是_______.15.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,7=∆ABCS,DE=2,AB=4,则AC长为.三、解答题16.如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A,D不重合),G,F,H分别是BE,BC,CE的中点.(1)证明:四边形EGFH是平行四边形;(2)在(1)的条件下,若EF⊥BC,且EF=BC,证明:平行四边形EGFH是正方形.17.已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D为BC边上一点.(1)求证:△ACE≌△ABD;(2)若AC=8,CD=1,求ED的长.18.如图,四边形ABCD中,AB=CD,M、N分别是AD、BC的中点,延长BA、NM、CD分别交于点E、F.求证:∠BEN=∠NFC. (提示:连结AC并取中点)19.如图,在Rt⊿ABC中,∠B=90°,AC=100cm,BC=80cm,点P从点A开始沿边AB向点B以1cm/s的速度运动,同时,另一点Q由点B开始沿边BC向点C以1.5cm/s的速度运动.(1)20s后,点P与点Q相距 cm.(2)在(1)的条件下,若P、Q两点同时在直线PQ上相向而行,多少秒后,两点相遇?(3)多少秒后,AP=CQ?20.△ABC中,∠ACB=90°,AC=BC,AB=2.现将一块三角板的直角顶点放在AB的中点D处,两直角边分别与直线..AC、直线..BC相交于点E、F.我们把DE⊥AC时的位置定为起始位置(如图1),将三角板绕点D顺时针方向旋转一个角度α (0°<α<90°).(1)在旋转过程中,当点E在线段AC上,点F在线段BC上时(如图2),①试判别△DEF的形状,并说明理由;②判断四边形ECFD的面积是否发生变化,并说明理由.(2)设直线..ED交直线..BC于点G,在旋转过程中,是否存在点G,使得△EFG为等腰三角形?若存在,求出CG的长,若不存在,说明理由;D DEADEDA。
中考数学总复习《四边形的综合题》练习题附带答案

中考数学总复习《四边形的综合题》练习题附带答案一、单选题1.如图,两个平行四边形的面积分别为18、12,两阴影部分的面积分别为a、b (a>b),则(a−b)等于()A.3B.4C.5D.6 2.如图,在矩形ABCD中,对角线AC、BD相交于点O,∠ABD=60°,则∠BOC的大小为()A.30°B.60°C.90°D.120°3.若一个多边形的内角和是外角和的2.5倍,则该多边形为()A.五边形B.六边形C.七边形D.八边形4.如图,矩形ABCD对角线相交于点O,∠AOB=60°,AB=4,则矩形的对角线AC 为()A.4 B.8 C.4√3D.10 5.一个长方形的周长为28厘米,长的2倍比宽的3倍多3厘米,则这个长方形的面积是()A.45平方厘米B.35平方厘米C.25平方厘米D.20平方厘米6.如图,在矩形ABCD中,对角线AC,BD相交于点O,AE垂直平分BO,AE=√3cm,则OD=()A.1cm B.1.5cm C.2cm D.3cm 7.如图,矩形纸片ABCD中,AB=4,AD=8 ,将纸片沿EF折叠使点B与点D 重合,折痕EF与BD相交于点O,则DF的长为()A.3B.4C.5D.6 8.如图,⊙O的半径为4,点P是⊙O外的一点PO=10,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时PA的长度为()A.10B.212C.11D.434 9.已知平行四边形一边长为8,一条对角线长为6,则另一条对角线α满足()A.10<α<22B.4<α<20C.4<α<28D.2<α<1410.如图,两张等宽的纸条交又重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为()A.a2B.5cm C.2√7cm D.6cm 11.如图,E、F分别是正方形ABCD的边AB、BC上的点,BE=CF,连接CE、DF,将∠BCE绕着正方形的中心O按逆时针方向旋转到∠CDF的位置,则旋转角是( )A .45°B .60°C .90°D .120°12.Rt∠ABC 两直角边的长分别为6cm 和8cm ,则连接这两条直角边中点的线段长为( ) A .10cmB .3cmC .4cmD .5cm二、填空题13.如图,点E 在边长为2的正方形ABCD 内,满足∠AEB =90°,若∠DAE =30°,则图中阴影部分的面积为 .14.把一把直尺和一块三角板如图放置,若∠1=42°,则∠2的度数为 °.15.已知 ▱ABCD 中一条对角线分 ∠A 为35°和45°,则 ∠B = 度. 16.如图,在一块长AB =26m ,宽BC =18m 的长方形草地上,修建三条宽均为3m 的长方形小路,则这块草地的绿地面积(图中空白部分)为 m 217.如图,在∠ABC 中,∠ABC =90°,E 为AC 的中点,AD∠BE 交BC 于D ,若AD=152,BE =5,则BD = .18.如图,在四边形ABCD中,∠A=90°,AB=12,AD=5.点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF长度的最大值是.三、综合题19.如果抛物线C1:y=ax2+bx+c与抛物线C2:y=−ax2+dx+e的开口方向相反,顶点相同,我们称抛物线C2是C1的“对顶”抛物线.(1)求抛物线y=x2−4x+7的“对顶”抛物线的表达式;(2)将抛物线y=x2−4x+7的“对顶”抛物线沿其对称轴平移,使所得抛物线与原抛物线y=x2−4x+7形成两个交点M、N,记平移前后两抛物线的顶点分别为A、B,当四边形AMBN是正方形时求正方形AMBN的面积.(3)某同学在探究“对顶”抛物线时发现:如果抛物线C1与C2的顶点位于x轴上,那么系数b与d,c与e之间的关系是确定的,请写出它们之间的关系.20.解答题(1)如图1,在平行四边形ABCD 中,已知点E 在AB 上,点F 在CD 上,且AE=CF .求证:DE=BF ;(2)如图2,AB 是∠O 的直径,点C 在AB 的延长线上,CD 与∠O 相切于点D ,若∠C=20°,求∠CDA 的度数.21.如图,▱ABCD 放置在平面直角坐标系申,已知点A (-2,0)、B (-6,0)、D(0,3).点C 在反比例函数y=k x的图象上。
2021年九年级中考数学复习强化练习——正方形及四边形综合问题

正方形及四边形综合问题一、选择题1. 下列条件不能判断▱ABCD是正方形的是()A.∠ABC=90°且AB=ADB.AB=BC且AC⊥BDC.AC⊥BD且AC=BDD.AC=BD且AB=BC2. 下列说法,正确的个数有 ()①正方形既是菱形又是矩形;②有两个角是直角的四边形是矩形;③菱形的对角线相等;④对角线互相垂直平分且相等的四边形是正方形.A.1个B.2个C.3个D.4个3. 如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边的正方形EFGH的周长为()A. 2B. 2 2C. 2+1D. 22+14. 如图正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于点O,则∠DOC的度数为()A.60°B.67.5°C.75°D.54°5. (2020·威海)如图,在▱ABCD中,对角线BD⊥AD,AB=10,AD=6,O为BD的中点,E为边AB上一点,直线EO交CD于点F,连结DE,BF.下列结论不成立的是()A.四边形DEBF为平行四边形B.若AE=3.6,则四边形DEBF为矩形C.若AE=5,则四边形DEBF为菱形D.若AE=4.8,则四边形DEBF为正方形6. 如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为()A. 2B. 3C. 2D. 17. 已知在平面直角坐标系中放置了5个如图X3-1-10所示的正方形(用阴影表示),点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3在x轴上.若正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则点A3到x轴的距离是()A.3+318 B.3+118C.3+36 D.3+168. (2020·东营)如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC 、BD 相交于点O ,过点P 分别作AC 、BD 的垂线,分别交AC 、BD 于点E 、F ,交AD 、BC 于点M 、N ,下列结论:①△APE ≌△AME ;②PM+PN=AC ;③222PE PF PO ;④△POF ∽△BNF ;⑤点O 在M 、N 两点的连线上.其中正确的是( )A. ①②③④B. ①②③⑤C. ①②③④⑤D. ③④⑤A BCDEFMNOP二、填空题9. 如图,在正方形ABCD 中,AC 为对角线,点E 在AB 边上,EF ⊥AC 于点F ,连接EC ,AF=3,若△EFC 的周长为12,则EC 的长为 .10. 如图,E ,F是正方形ABCD 的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF 的周长是 .11. ▱ABCD的对角线AC 与BD 相交于点O ,且AC ⊥BD ,请添加一个条件:________,使得▱ABCD 为正方形.12. 如图,正方形ABCO 的顶点C ,A 分别在x 轴,y 轴上,BC 是菱形BDCE 的对角线,若∠D =60°,BC =2,则点D 的坐标是________.13. 如图,在正方形ABCD 中,点E ,N ,P ,G 分别在边AB ,BC ,CD ,DA 上,点M ,F ,Q 都在对角线BD 上,且四边形MNPQ 和AEFG 均为正方形,则S 正方形MNPQS 正方形AEFG的值等于________.14. 如图,正方形ABCD的边长为22,对角线AC,BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F,则FM的长为________.15. 如图,有一个边长不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组平行的对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是________.16. 如图,正方形ABCD的面积为3 cm2,E为BC边上一点,∠BAE=30°,F 为AE的中点,过点F作直线分别与AB,DC相交于点M,N.若MN=AE,则AM的长等于________cm.三、解答题17. 如图,在正方形ABCD中,E是DC边上一点(与D,C不重合),连接AE,将△ADE沿AE所在的直线折叠得到△AFE,延长EF交BC于点G,连接AG,作GH⊥AG,与AE的延长线交于点H,连接CH.显然AE是∠DAF的平分线,EA是∠DEF的平分线.仔细观察,请逐一找出图中其他的角平分线(仅限于小于180°的角的平分线),并说明理由.18. 如图①,在四边形ABCD中,点P是AB上一点,点E在射线DP上,且∠BED=∠BAD,连接AE.(1)若AB=AD,在DP上截取点F,使得DF=BE,连接AF,求证:△ABE≌△ADF;(2)如图②,若四边形ABCD是正方形,点P在AB的延长线上,BE=1,AE=32,求DE的长;(3)如图③,若四边形ABCD是矩形,AD=2AB,点P在AB的延长线上,AE=5 BE,若AE=nDE,求n的值.图①图②图③19. 已知正方形ABCD中,点E在BC上,连接AE,过点B作BF⊥AE于点G,交CD于点F.(1)如图①,连接AF,若AB=4,BE=1,求证:△BCF≌△ABE;(2)如图②,连接BD,交AE于点N,连接AC,分别交BD、BF于点O、M,连接GO,求证:GO平分∠AGF;(3)如图③,在第(2)问的条件下,连接CG,若CG⊥GO,AG=nCG,求n的值.20. (2020·河南)将正方形ABCD的边AB绕点A逆时针旋转至AB′,记旋转角为.连接BB′,过点D作DE垂直于直线BB′,垂足为点E,连接DB′,CE.(1)如图1,当=60°时,△DEB′的形状为,连接BD,可求出BBCE′的值为;(2)当0°<<360°且≠90°时,①(1)中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;②当以点B′、E、C、D为顶点的四边形是平行四边形时,请直接写出BEB E′的值.正方形及四边形综合问题-答案一、选择题1. 【答案】B[解析]A.▱ABCD中,若∠ABC=90°,则▱ABCD是矩形,再由AB=AD 可得是正方形,故此选项错误;B.▱ABCD中,若AB=BC,则▱ABCD是菱形,再由AC⊥BD仍可得是菱形,不能判定为正方形,故此选项正确;C.▱ABCD中,若AC⊥BD,则▱ABCD是菱形,再由AC=BD可得是正方形,故此选项错误;D.▱ABCD中,若AC=BD,则▱ABCD是矩形,再由AB=BC可得是正方形,故此选项错误.故选B.2. 【答案】B3. 【答案】B【解析】∵正方形ABCD的面积为1,∴BC=CD=1,∵E、F是边的中点,∴CE=CF=12,∴EF=(12)2+(12)2=22,则正方形EFGH的周长为4×22=2 2.4. 【答案】A[解析]连接BF,∵E为AB中点,FE⊥AB,∴EF垂直平分AB,∴AF=BF.∵AF=2AE,∴AF=AB,∴AF=BF=AB,∴△ABF为等边三角形,∴∠FBA=60°,BF=BC,∴∠FCB=∠BFC=15°,∵四边形ABCD为正方形,∴∠DBC=45°,根据三角形的外角等于与它不相邻的两个内角的和得∠DOC=15°+45°=60°.5. 【答案】:∵O为BD的中点,∴OB=OD,∵四边形ABCD为平行四边形,∴DC∥AB,∴∠CDO=∠EBO,∠DFO=∠OEB,∴△FDO≌△EBO(AAS),∴OE=OF,∴四边形DEBF为平行四边形,故A选顶结论正确,若AE=3.6,AD=6,∴,又∵,∴,∵∠DAE=∠BAD,∴△DAE∽△BAD,∴AED=∠ADB=90°.故B选项结论正确,∵AB=10,AE=5,∴BE=5,又∵∠ADB=90°,∴DE AB =5,∴DE =BE ,∴四边形DEBF 为菱形. 故C 选项结论正确,∵AE =3.6时,四边形DEBF 为矩形,AE =5时,四边形DEBF 为菱形, ∴AE =4.8时,四边形DEBF 不可能是正方形. 故D 不正确. 故选:D .6. 【答案】B【解析】∵AB =2,∴BF =2,又∵BM =12BC =1,由勾股定理得FM =FB 2-BM 2= 3.7. 【答案】⎝⎛⎭⎪⎫72,0D 解析:过小正方形的一个顶点D 3作FQ ⊥x 轴于点Q ,过点A 3作A 3F ⊥FQ 于点F .∵正方形A 1B 1C 1D 1的边长为1,∠B 1C 1O =60°,B 1C 1∥B 2C 2∥B 3C 3, ∴∠B 3C 3E 4=60°,∠D 1C 1E 1=30°,∠E 2B 2C 2=30°, ∴D 1E 1=12D 1C 1=12,∴D 1E 1=B 2E 2=12, ∴cos30°=B 2E 2B 2C 2=12B 2C 2,解得:B 2C 2=33.∴B 3E 4=36,cos30°=B 3E 4B 3C 3.解得:B 3C 3=13. 则D 3C 3=13. 根据题意得出:∠D 3C 3Q =30°,∠C 3D 3Q =60°,∠A 3D 3F =30°, ∴D 3Q =12×13=16,FD 3=D 3A 3·cos30°=13×32=36.则点A3到x轴的距离FQ=D3Q+FD3=16+36=3+16.8. 【答案】B【解析】本题考查了垂线、平行线和正方形的性质,全等三角形的判定与性质、等腰直角三角形的判断和性质、相似三角形的判定和性质,是常见问题的综合,灵活的运用所学知识是解答本题的关键.综合应用垂线、平行线和正方形的性质,全等三角形的判定与性质、等腰直角三角形的判断和性质、相似三角形的判定和性质等知识,逐个判断5个结论的正确性,得出结论.①∵正方形ABCD,∴∠APE=∠AME=45°,∵PM⊥AE,∴∠AEP=∠AEM=90°,∵AE=AE,∴△APE≌△AME(ASA);②过点N作NQ⊥AC于点Q,则四边形PNQE是矩形,∴PN=EQ,∵正方形ABCD,∴∠P AE=∠MAE=45°,∵PM⊥AE,∴∠PEA=45°,∴∠P AE=∠APE,PE=NQ,∴△APE等腰直角三角形,∴AE=PE,同理得:△NQC等腰直角三角形,∴NQ=CQ,∵△APE≌△AME,∴PE=ME,∴PE=ME= NQ=CQ,∴PM=AE+CQ,∴PM+PN=AE+CQ+EQ=AC,即PM+PN=AC成立;③∵正方形ABCD,∴AC⊥BD,∴∠EOF是直角,∵过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,∴∠PEO和∠PFO是直角,∴四边形PFOE 是矩形,∴PF=OE,在R t△PEO中,有PE2+OE2=PO2,∴PE2+PF2=PO2,即PE2+PF2=PO2成立;④△BNF是等腰直角三角形,点P不在AB的中点时,△POF不是等腰直角三角形,所以△POF与△BNF不一定相似,即△POF∽△BNF不一定成立;⑤∵△AMP是等腰直角三角形,△PMN∽△AMP,∴△PMN是等腰直角三角形,∵∠MPN=90°,∴PM=PN,∵AP=22PM,BP=22PN,∴AP=BP,∴点P是AB的中点,又∵O为正方形的对称中点,∴点O在M、N两点的连线上.综上,①②③⑤成立,即正确的结论有4个,答案选B.二、填空题9. 【答案】5[解析]∵四边形ABCD是正方形,AC为对角线,∴∠F AE=45°,又∵EF⊥AC,∴∠AFE=90°,∴∠AEF=45°,∴EF=AF=3,∵△EFC的周长为12,∴FC=12-3-EC=9-EC,在Rt△EFC中,EC2=EF2+FC2,∴EC2=9+(9-EC)2,解得EC=5.10. 【答案】8 [解析]如图,连接BD 交AC 于点O ,∵四边形ABCD 为正方形,∴BD ⊥AC ,OD=OB=OA=OC , ∵AE=CF=2,∴OA -AE=OC -CF ,即OE=OF ,∴四边形BEDF 为平行四边形,且BD ⊥EF , ∴四边形BEDF 为菱形, ∴DE=DF=BE=BF , ∵AC=BD=8,OE=OF==2,∴由勾股定理得:DE===2,∴四边形BEDF 的周长=4DE=4×2=8,故答案为:8.11. 【答案】∠BAD =90°(答案不唯一)【解析】∵▱ABCD 的对角线AC 与BD 相交于点O ,且AC ⊥BD ,∴▱ABCD 是菱形,当∠BAD =90°时,菱形ABCD 为正方形.故可添加条件:∠BAD =90°.12. 【答案】(3+2,1) 【解析】如解图,过点D 作DG ⊥BC 于G ,DF ⊥x 轴于F ,∵在菱形BDCE 中,BD =CD ,∠BDC =60°,∴△BCD 是等边三角形,∴DF =CG =12BC =1,CF =DG =3,∴OF =3+2,∴D(3+2,1).解图13. 【答案】89 【解析】设BD =3a ,∠CDB =∠CBD =45°,且四边形PQMN 为正方形,∴DQ =PQ =QM =NM =MB ,∴正方形MNPQ 的边长为a ,正方形AEFG的对角线AF =12BD =32a ,∵正方形对角线互相垂直,∴S 正方形AEFG =12×32a×32a =98a 2,∴S 正方形MNPQ S 正方形AEFG =a 298a2=89.14. 【答案】55【解析】∵四边形ABCD 为正方形,∴AO =BO ,∠AOF =∠BOE=90°,∵AM ⊥BE ,∠AFO =∠BFM ,∴∠FAO =∠EBO ,在△AFO 和△BEO中,⎩⎨⎧∠AOF =∠BOE AO =BO ∠FAO =∠EBO,∴△AFO ≌△BEO(ASA ),∴FO =EO ,∵正方形ABCD的边长为22,E 是OC 的中点,∴FO =EO =1=BF ,BO =2,∴在Rt △BOE 中,BE =12+22=5,由∠FBM =∠EBO ,∠FMB =∠EOB ,可得△BFM ∽△BEO ,∴FM EO =BF BE ,即FM 1=15,∴FM =55.15. 【答案】62≤a ≤3-3 【解析】∵ABCD 是正方形,∴AB =a =22AC ,∴a的取值范围与AC 的长度直接相关.如解图①,当A ,C 两点恰好是正六边形一组对边中点时,a 的值最小,∵正六边形的边长为1,∴AC =3,∴AB =a =22AC =62;如解图②,连接MN ,延长AE ,BF 交于点G ,∵正六边形和正方形ABCD ,∴△MNG 、△ABG 、△EFG 为正三角形,设AE =BF =x ,则AM =BN =1-x ,AG =BG =AB =1+x =a ,∵GM =MN =2,∠BNM =60°,∴sin ∠BNM =sin 60°=BC 2BN =a 21-x,∴3()1-x =a ,∴3()2-a =a ,解得,a=233+1=3- 3.∴正方形边长a 的取值范围是62≤a ≤3- 3.16. 【答案】233或33【解析】如解图,过N 作NG ⊥AB ,交AB 于点G ,∵四边形ABCD 为正方形,∴AB =AD =NG = 3 cm ,在Rt △ABE 中,∠BAE =30°,AB = 3 cm ,∴BE =1 cm ,AE =2 cm ,∵F 为AE 的中点,∴AF =12AE =1 cm ,在Rt △ABE 和Rt △NGM 中,⎩⎨⎧AB =NGAE =NM ,∴Rt △ABE ≌Rt △NGM(HL ),∴BE =GM ,∠BAE =∠MNG =30°,∠AEB =∠NMG =60°,∴∠AFM =90°,即MN ⊥AE ,在Rt △AMF 中,∠FAM =30°,AF =1 cm ,∴AM =AF cos 30°=132=233cm ,由对称性得到AM′=BM =AB -AM =3-233=33 cm ,综上,AM 的长等于233或33 cm .解图三、解答题17. 【答案】[解析]过点H 作HN ⊥BM 于N ,利用正方形的性质及轴对称的性质,证明△ABG ≌△AFG ,可推出AG 是∠BAF 的平分线,GA 是∠BGF 的平分线;证明△ABG ≌△GNH ,推出HN=CN ,得到∠DCH=∠NCH ,推出CH 是∠DCM 的平分线;再证∠HGN=∠EGH ,可知GH 是∠EGM 的平分线. 解:过点H 作HN ⊥BM 于N ,则∠HNC=90°,∵四边形ABCD 为正方形,∴AD=AB=BC ,∠D=∠DAB=∠B=∠DCB=∠DCM=90°. ①∵将△ADE 沿AE 所在的直线折叠得到△AFE , ∴△ADE ≌△AFE ,∴∠D=∠AFE=∠AFG=90°,AD=AF ,∠DAE=∠F AE ,∴AF=AB. 又∵AG=AG ,∴Rt △ABG ≌Rt △AFG (HL), ∴∠BAG=∠F AG ,∠AGB=∠AGF ,∴AG 是∠BAF 的平分线,GA 是∠BGF 的平分线. ②由①知,∠DAE=∠F AE ,∠BAG=∠F AG ,又∵∠BAD=90°,∴∠GAF+∠EAF=×90°=45°,即∠GAH=45°.∵GH⊥AG,∴∠GHA=90°-∠GAH=45°,∴△AGH为等腰直角三角形,∴AG=GH.∵∠AGB+∠BAG=90°,∠AGB+∠HGN=90°,∴∠BAG=∠NGH.又∵∠B=∠HNG=90°,AG=GH,∴△ABG≌△GNH(AAS),∴BG=NH,AB=GN,∴BC=GN.∴BC-CG=GN-CG,∴BG=CN,∴CN=HN.∵∠HNC=90°,∴∠NCH=∠NHC=×90°=45°,∴∠DCH=∠DCM-∠NCH=45°,∴∠DCH=∠NCH,∴CH是∠DCM的平分线.③∵∠AGB+∠HGN=90°,∠AGF+∠EGH=90°,由①知,∠AGB=∠AGF,∴∠HGN=∠EGH,∴GH是∠EGM的平分线.综上所述,AG是∠BAF的平分线,GA是∠BGF的平分线,CH是∠DCM的平分线,GH是∠EGM的平分线.18. 【答案】(1)证明:∵∠BED=∠BAD,∠BPE=∠DP A,∴∠ABE=∠ADF,又∵AB=AD,BE=DF,∴△ABE≌△ADF;(2)解:如解图①,延长ED到点F,使得DF=BE,连接AF,解图①∵四边形ABCD 是正方形, ∴∠BAD =∠BED =∠BEP ,∵∠P =∠P ,∴∠PBE =∠ADP , ∴∠ABE =∠ADF , ∵BE =DF ,AB =AD , ∴△ABE ≌△ADF ,∴AE =AF ,∠BAE =∠F AD ,∴∠F AD +∠EAD =∠BAE +∠EAD =90°, ∴EF =2AE =32×2=6,∴DE =EF -DF =EF -BE =6-1=5;(3)解:如解图②,过点A 作AF ⊥AE 交ED 的延长线于点F ,解图②∵四边形ABCD 是矩形,∴∠BAD =∠BED =∠BEP =90°, ∵AF ⊥AE ,∠P =∠P ,∴∠PBE =∠ADP ,∠EAB =90°-∠EAD =∠F AD , ∴∠ABE =180°-∠PBE =180°-∠ADP =∠ADF , ∴△ABE ∽△ADF , ∴,21===AFAE DFBE ADAB∴AF =2AE ,DF =2BE ,在Rt △AEF 中,由勾股定理得EF 22AE AF +=5AE , ∵AE =5BE ,∴EF =5AE =5·5BE =5BE , ∴AE DE =53,∴n =53. 19. 【答案】(1)证明:∵四边形ABCD 是正方形,∴BC =CD =AD =AB =4,∠ABE =∠C =∠D =90°, ∴∠ABG +∠CBF =90°, ∵BF ⊥AE ,∴∠ABG +∠BAE =90°, ∴∠BAE =∠CBF , 在△BCF 和△ABE 中,⎩⎨⎧∠C =∠ABEBC =AB∠CBF =∠BAE, ∴△BCF ≌△ABE (ASA);(2)证明:∵AC ⊥BD ,BF ⊥AE , ∴∠AOB =∠AGB =∠AGF =90°, ∴A 、B 、G 、O 四点共圆, ∴∠AGO =∠ABO =45°,∴∠FGO =90°-45°=45°=∠AGO , ∴GO 平分∠AGF ;(3)解:如解图,连接EF ,解图∵CG ⊥GO ,∴∠OGC =90°,∵∠EGF =∠BCD =90°, ∴∠EGF +∠BCD =180°, ∴C 、E 、G 、F 四点共圆,∴∠EFC =∠EGC =180°-90°-45°=45°, ∴△CEF 是等腰直角三角形, ∴CE =CF ,同(1)得△BCF ≌△ABE , ∴CF =BE ,∴CE =BE =12 BC ,∴OA =12 AC = 22BC = 2CE , 由(2)得A 、B 、G 、O 四点共圆, ∴∠BOG =∠BAE ,∵∠GEC =90°+∠BAE ,∠GOA =90°+∠BOG , ∴∠GOA =∠GEC ,又∵∠EGC =∠AGO =45°,∴△AOG ∽△CEG , ∴AG CG =OACE =2, ∴AG = 2 CG , ∴n = 2 .20. 【答案】解: (1)等腰直角三角形,2. (2)①两个结论仍成立.证明:连接BD.∵AB=AB′,∠BAB′=,∴∠AB′B=90°-2a,∵∠B′AD=a -90°,AD=AB′,∴∠AB′D=135-2a,∴∠EB′D=∠AB′D -∠AB′B=45°.∵DE ⊥BB′,∴∠EDB′=∠EB′D=45°,∴△DEB′是等腰直角三角形,∴DB DE′=2. ∵四边形ABCD 为正方形,∴BD CD =2,∠BDC=45°.∴DB DE′=BDCD , ∵∠EDB′=∠BDC ,∴∠EDB′+∠EDB=∠BDC+∠EDB ,即∠BDB′=∠CDE.∴△B′DB ∽△EDC ,∴2BB BDCE CD′; ②3或1.思路提示:分两种情况.情形一,如图,当点B′在BE 上时,由BB CE′=2,设BB′=2m ,CE=2m . ∵CE ∥B′D ,CE=B′D ,∴B′D=2m ,在等腰直角三角形DEB′中,斜边B′D=2m ,∴B′E=DE=m ,于是得到BE B E ′2=3m mm. 情形二,如图,当点B′在BE 延长线上时,由BB CE′=2,设BB′=2m ,CE=2m .∵CE ∥B′D ,CE=B′D ,∴B′D=2m ,在等腰直角三角形DEB′中,斜边B′D=2m ,∴B′E=DE=m 。
2020年八年级数学下册四边形综合题重难点培优练习(含答案)

第 1 页 共 26 页 1.如图,在矩形ABCD 中,中,AB=4cm AB=4cm AB=4cm,,BC=8cm BC=8cm,点,点P 从点D 出发向点A 运动,运动到点A 即停止;同时点Q 从点B 出发向点C 运动,运动到点C 即停止.点P 、Q 的速度的速度都是1cm/s 1cm/s,连结,连结PQ PQ,,AQ AQ,,CP CP,设点,设点P 、Q 运动的时间为t (s ).).(1)当t 为何值时,四边形ABQP 是矩形?是矩形?(2)当t 为何值时,四边形AQCP 是菱形?是菱形? (3)分别求出()分别求出(22)中菱形AQCP 的周长和面积.的周长和面积.2.如图,在Rt Rt△△ABC 中,∠中,∠ACB=90ACB=90ACB=90°,过点°,过点C 的直线m ∥AB AB,,D 为AB 边上一点,过点D 作DE DE⊥⊥BC BC,交直线,交直线m 于点E ,垂足为点F ,连接CD CD,,BE BE..(1)求证:)求证:CE=AD CE=AD CE=AD;; (2)当点D 是AB 中点时,四边形BECD 是什么特殊四边形?说明你的理由;(3)当∠)当∠A A 的大小满足什么条件时,四边形BECD 是正方形?(不需要证明)3.如图1,在矩形,在矩形ABCD ABCD ABCD中,动点中,动点中,动点P P 从点从点A A 出发,沿出发,沿A A →D →C →B 的路径运动.设点的路径运动.设点P P 运动的路程为运动的路程为x x ,△PAB PAB的面积为的面积为的面积为y y .图2反映的是点反映的是点P P 在A →D →C 运动过程中,运动过程中,y y 与x 的函数关系.请根据图象回答以下问题:以下问题:(1)矩形)矩形ABCD ABCD ABCD的边的边的边AD= AD=,AB= ; (2)写出点)写出点P P 在C →B 运动过程中运动过程中y y 与x 的函数关系式,并在图2中补全函数图象.中补全函数图象.4.在图1,2,3中,已知▱ABCD ABCD,∠,∠,∠ABC=120ABC=120ABC=120°,点°,点E 为线段BC 上的动点,连接AE AE,以,以AE 为边向上作菱形AEFG AEFG,且∠,且∠,且∠EAG=120EAG=120EAG=120°.°.°.(1)(1)如图如图1,当点E 与点B 重合时,∠重合时,∠CEF= CEF= CEF= °;°;(2)(2)如图如图2,连接AF AF..①填空:∠①填空:∠FAD FAD FAD ∠EAB(EAB(填“>”,“<“,“填“>”,“<“,“填“>”,“<“,“==”);②求证:点F 在∠在∠ABC ABC 的平分线上;的平分线上;(3)(3)如图如图3,连接EG EG,,DG DG,并延长,并延长DG 交BA 的延长线于点H ,当四边形AEGH 是平行四边形时,是平行四边形时, 求的值.的值.5.如图,两个全等的△如图,两个全等的△ABC ABC 和△和△DEF DEF 重叠在一起,固定△重叠在一起,固定△ABC ABC ABC,将△,将△,将△DEF DEF 进行如下变换:进行如下变换:(1)如图1,△,△DEF DEF 沿直线CB 向右平移(即点F 在线段CB 上移动),连接AF AF、、AD AD、、BD BD,请直,请直接写出S △ABC 与S 四边形AFBD 的关系的关系(2)如图2,当点F 平移到线段BC 的中点时,若四边形AFBD 为正方形,那么△为正方形,那么△ABC ABC 应满足什么条件:请给出证明;么条件:请给出证明;(3)在()在(22)的条件下,将△)的条件下,将△DEF DEF 沿DF 折叠,点E 落在FA 的延长线上的点G 处,连接CG CG,请,请你画出图形,此时CG 与CF 有何数量关系有何数量关系. .6.菱形ABCD 中,点P 为CD 上一点,连接BP.(1)如图1,若BP BP⊥⊥CD CD,菱形,菱形ABCD 边长为1010,,PD=4PD=4,连接,连接AP AP,求,求AP 的长的长. .(2)如图2,连接对角线AC AC、、BD 相交于点O ,点N 为BP 的中点,过P 作PM PM⊥⊥AC 于M ,连接ON ON、、MN.MN.试判断△试判断△试判断△MON MON 的形状,并说明理由的形状,并说明理由. .7.如图,在Rt Rt△△ABC 中,∠ACB=90°,过点C 的直线MN∥AB,D 为AB 边上一点,过点D 作DE⊥BC,交直线MN 于E ,垂足为F ,连接CD CD、、BE.(1)求证:)求证:CE=AD CE=AD CE=AD;;(2)当D 在AB 中点时,四边形BECD 是什么特殊四边形?说明你的理由;是什么特殊四边形?说明你的理由;(3)若D 为AB 中点,则当∠A 的大小满足什么条件时,四边形BECD 是正方形?请说明你的理由.8.如图,在在四边形ABCD 中,中,AD AD AD∥∥BC BC,∠,∠,∠B=90B=90B=90°,且°,且AD=12cm AD=12cm,,AB=8cm AB=8cm,,DC=10cm DC=10cm,若动点,若动点P 从A 点出发,以每秒2cm 的速度沿线段AD 向点D 运动;动点Q 从C 点出发以每秒3cm 的速度沿CB 向B 点运动,当P 点到达D 点时,动点P 、Q 同时停止运动,设点P 、Q 同时出发,并运动了t 秒,回答下列问题:秒,回答下列问题:(1)BC= BC= cm cm;;(2)当t= t= 秒时,四边形PQBA 成为矩形.成为矩形.(3)当t 为多少时,为多少时,PQ=CD PQ=CD PQ=CD??(4)是否存在t ,使得△,使得△DQC DQC 是等腰三角形?若存在,请求出t 的值;若不存在,说明理由.的值;若不存在,说明理由.9.如图1,已知正方形已知正方形ABCD ABCD ABCD,,点E 、F 、G 、H 分别在边分别在边AB AB AB、、BC BC、、CD CD、、DA DA上,上,若EG EG⊥⊥FH FH,,则易证:EG=FH EG=FH..(1)如果把条件中的“正方形”改为“长方形”,并设,并设AB=2AB=2AB=2,,BC=3BC=3(如图(如图2),试探究,试探究EG EG EG、、FH FH之之间有怎样的数量关系,并证明你的结论;间有怎样的数量关系,并证明你的结论; (2)如果把条件中的“)如果把条件中的“EG EG EG⊥⊥FH FH”改为“”改为“”改为“EG EG EG与与FH FH的夹角为的夹角为4545°”°”,并假设正方形,并假设正方形ABCD ABCD ABCD的边长为的边长为1,FH FH的长为的长为(如图3),试求,试求EG EG EG的长度.的长度.的长度.10.如图,如图,P P 为正方形为正方形ABCD ABCD ABCD的边的边的边BC BC BC上一动点(上一动点(上一动点(P P 与B 、C 不重合),连接不重合),连接AP AP AP,过点,过点,过点B B 作BQ BQ⊥⊥AP AP交交CD CD于于点Q ,将△,将△BQC BQC BQC沿沿BQ BQ所在的直线对折得到△所在的直线对折得到△所在的直线对折得到△BQC BQC BQC′,延长′,延长′,延长QC QC QC′交′交′交BA BA BA的延长线于点的延长线于点的延长线于点M M . (1)试探究)试探究AP AP AP与与BQ BQ的数量关系,并证明你的结论;的数量关系,并证明你的结论;的数量关系,并证明你的结论;(2)当)当AB=3AB=3AB=3,,BP=2PC BP=2PC,求,求,求QM QM QM的长;的长;的长;(3)当)当BP=m BP=m BP=m,,PC=n PC=n时,求时,求时,求AM AM AM的长.的长.的长.11.11.如图,在矩形如图,在矩形如图,在矩形ABCD ABCD ABCD中,点中,点中,点E E 为CD CD上一点,将△上一点,将△上一点,将△BCE BCE BCE沿沿BE BE翻折后点翻折后点翻折后点C C 恰好落在恰好落在AD AD AD边上的点边上的点边上的点F F 处,将线段线段EF EF EF绕点绕点绕点F F 旋转,使点旋转,使点E E 落在落在BE BE BE上的点上的点上的点G G 处,连接处,连接CG. CG.(1)(1)证明:四边形证明:四边形证明:四边形CEFG CEFG CEFG是菱形;是菱形;是菱形;(2)(2)若若AB=8AB=8,,BC=10BC=10,求四边形,求四边形,求四边形CEFG CEFG CEFG的面积;的面积;的面积;(3)(3)试探究当线段试探究当线段试探究当线段AB AB AB与与BC BC满足什么数量关系时,满足什么数量关系时,满足什么数量关系时,BG=CG BG=CG BG=CG,请写出你的探究过程.,请写出你的探究过程.,请写出你的探究过程.12.四边形ABCD是正方形,点E在边BC上(不与端点B、C重合),点F在对角线AC上,且EFDF、、FG,点G是AE的中点,连接DF,连接AE⊥ACAC,连接AE,点(1)若AB=7,的长;BE=,求FG的长;FG;DF=FG;)求证:DF=(2)求证:中的△CEFCEF绕点C按顺时针旋转,使边CF的顶点F恰好在正方形ABCD的边BC上(如(3)将图1中的△之间的数量关系,并证明你的猜想. AE、点图2),连接AE、点G仍是AE的中点,猜想BF与FG之间的数量关系,并证明你的猜想.13.△ABC 和△和△DEF DEF 都是边长为6cm 的等边三角形,且A 、D 、B 、F 在同一直线上,连接CD CD、、BF BF..(1)求证:四边形BCDE 是平行四边形;是平行四边形;(2)若AD=2cm AD=2cm,△,△,△ABC ABC 沿着AF 的方向以每秒1cm 的速度运动,设△的速度运动,设△ABC ABC 运动的时间为t 秒.秒. (a )当t 为何值时,平行四边形BCDE 是菱形?说明理由;是菱形?说明理由;(b )平行四边形BCDE 有可能是矩形吗?若有可能,求出t 的值,并求出矩形的面积;若不可能,说明理由.能,说明理由.14.14.已知已知E,F 分别为正方形ABCD 的边BC,CD 上的点上的点,AF,DE ,AF,DE 相交于点G,G,当当E,F 分别为边BC,CD 的中点时中点时,,有AF=DE,AF AF=DE,AF⊥⊥DE 成立成立. . 试探究下列问题试探究下列问题: : (1)(1)如图①如图①如图①,,若点E 不是边BC 的中点的中点,F ,F 不是边CD 的中点的中点,,且CE=DF,CE=DF,上述结论是否仍然成立上述结论是否仍然成立上述结论是否仍然成立?(?(?(请请直接回答“成立”或“不成立”直接回答“成立”或“不成立”,,不需要证明不需要证明) ) (2)(2)如图②如图②如图②,,若点E,F 分别在CB 的延长线和DC 的延长线上的延长线上,,且CE=DF,CE=DF,此时此时此时,,上述结论是否仍然成立?若成立若成立,,请写出证明过程请写出证明过程,,若不成立若不成立,,请说明理由请说明理由; ; (3)(3)如图③如图③如图③,,在(2)(2)的基础上的基础上的基础上,,连接AE 和EF,EF,若点若点M,N,P,Q 分别为AE,EF,FD,AD 的中点的中点,,请判断四边形MNPQ 是“矩形、菱形、正方形”中的哪一种是“矩形、菱形、正方形”中的哪一种,,并证明你的结论并证明你的结论. .15.如图,在如图,在Rt Rt Rt△△ABC ABC中,∠中,∠中,∠B=90B=90B=90°,°,°,AC=60cm AC=60cm AC=60cm,∠,∠,∠A=60A=60A=60°,点°,点°,点D D 从点从点C C 出发沿出发沿CA CA CA方向以方向以4cm/s 4cm/s的速的速度向点度向点A A 匀速运动,同时点同时点E E 从点从点A A 出发沿出发沿AB AB AB方向以方向以2cm/s 2cm/s的速度向点的速度向点的速度向点B B 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点达终点时,另一个点也随之停止运动.设点D D 、E 运动的时间是运动的时间是ts ts ts.过点.过点.过点D D 作DF DF⊥⊥BC BC于点于点于点F F ,连接DE DE、、EF EF.. (1)用)用t t 的代数式表示:的代数式表示:AE= AE= ;DF= ; (2)四边形)四边形AEFD AEFD AEFD能够成为菱形吗?如果能,求出相应的能够成为菱形吗?如果能,求出相应的能够成为菱形吗?如果能,求出相应的t t 值;如果不能,请说明理由;值;如果不能,请说明理由; (3)当)当t t 为何值时,△为何值时,△DEF DEF DEF为直角三角形?请说明理由.为直角三角形?请说明理由.为直角三角形?请说明理由.参考答案1.解:解:(1)当四边形ABQP 是矩形时,是矩形时,BQ=AP BQ=AP BQ=AP,即:,即:,即:t=8t=8t=8﹣﹣t ,解得t=4t=4.. 答:当t=4时,四边形ABQP 是矩形;是矩形; (2)设t 秒后,四边形AQCP 是菱形是菱形 当AQ=CQ AQ=CQ,即,即=8=8﹣﹣t 时,四边形AQCP 为菱形.解得:为菱形.解得:t=3t=3t=3..答:当t=3时,四边形AQCP 是菱形;是菱形;(3)当t=3时,时,CQ=5CQ=5CQ=5,则周长为:,则周长为:,则周长为:4CQ=20cm 4CQ=20cm 4CQ=20cm,面积为:,面积为:,面积为:44×8﹣2××3×4=204=20((cm 22).).2.(1)证明:∵直线m ∥AB AB,∴,∴,∴EC EC EC∥∥AD AD..又∵∠又∵∠ACB=90ACB=90ACB=90°,∴°,∴°,∴BC BC BC⊥⊥AC AC.又∵.又∵.又∵DE DE DE⊥⊥BC BC,∴,∴,∴DE DE DE∥∥AC AC.. ∵EC EC∥∥AD AD,,DE DE∥∥AC AC,∴四边形,∴四边形ADEC 是平行四边形.∴是平行四边形.∴CE=AD CE=AD CE=AD.. (2)当点D 是AB 中点时,四边形BECD 是菱形. 证明:∵证明:∵D D 是AB 中点,中点,DE DE DE∥∥AC AC(已证)(已证),∴,∴F F 为BC 中点,∴中点,∴BF=CF BF=CF BF=CF.. ∵直线m ∥AB AB,∴∠,∴∠,∴∠ECF=ECF=ECF=∠∠DBF DBF.∵∠.∵∠.∵∠BFD=BFD=BFD=∠∠CFE CFE,∴△,∴△,∴△BFD BFD BFD≌△≌△≌△CFE CFE CFE.∴.∴.∴DF=EF DF=EF DF=EF.. ∵DE DE⊥⊥BC BC,∴,∴,∴BC BC 和DE 垂直且互相平分.∴四边形BECD 是菱形. (3)当∠)当∠A A 的大小是4545°时,四边形°时,四边形BECD 是正方形. 理由是:∵∠理由是:∵∠ACB=90ACB=90ACB=90°,∠°,∠°,∠A=45A=45A=45°,∴∠°,∴∠°,∴∠ABC=ABC=ABC=∠∠A=45A=45°,∴°,∴°,∴AC=BC AC=BC AC=BC,, ∵D 为BA 中点,∴中点,∴CD CD CD⊥⊥AB AB,∴∠,∴∠,∴∠CDB=90CDB=90CDB=90°,°,∵四边形BECD 是菱形,∴四边形BECD 是正方形, 即当∠即当∠A=45A=45A=45°时,四边形°时,四边形BECD 是正方形.3.解:(解:(11)根据题意得:矩形)根据题意得:矩形ABCD ABCD ABCD的边的边的边AD=2AD=2AD=2,,AB=4AB=4;故答案为:;故答案为:;故答案为:22;4; (2)当点)当点P P 在C →B 运动过程中,运动过程中,PB=8PB=8PB=8﹣﹣x ,∴,∴y=S y=S △APB=×4×(×(88﹣x ),即),即y=y=y=﹣﹣2x+162x+16((6≤x ≤8),正确作出图象,如图所示:正确作出图象,如图所示:4.解:解:(1)(1)∵四边形∵四边形AEFG 是菱形,∴∠是菱形,∴∠AEF=180AEF=180AEF=180°﹣∠°﹣∠°﹣∠EAG=60EAG=60EAG=60°,°,°, ∴∠∴∠CEF=CEF=CEF=∠∠AEC AEC﹣∠﹣∠﹣∠AEF=60AEF=60AEF=60°,°,°, 故答案为:故答案为:606060°;°;°; (2)(2)①∵四边形①∵四边形ABCD 是平行四边形,∴∠是平行四边形,∴∠DAB=180DAB=180DAB=180°﹣∠°﹣∠°﹣∠ABC=60ABC=60ABC=60°,°,°, ∵四边形AEFG 是菱形,∠是菱形,∠EAG=120EAG=120EAG=120°,∴∠°,∴∠°,∴∠FAE=60FAE=60FAE=60°,°,°, ∴∠∴∠FAD=FAD=FAD=∠∠EAB EAB,, ②作FM FM⊥⊥BC 于M ,FN FN⊥⊥BA 交BA 的延长线于N ,则∠,则∠FNB=FNB=FNB=∠∠FMB=90FMB=90°,°,°, ∴∠∴∠NFM=60NFM=60NFM=60°,°,°, 又∠又∠AFE=60AFE=60AFE=60°,∴∠°,∴∠°,∴∠AFN=AFN=AFN=∠∠EFM EFM,, ∵EF=EA EF=EA,∠,∠,∠FAE=60FAE=60FAE=60°,∴△°,∴△°,∴△AEF AEF 为等边三角形,∴为等边三角形,∴FA=FE FA=FE FA=FE,, 在△在△AFN AFN 和△和△EFM EFM 中,,∴△,∴△AFN AFN AFN≌△≌△≌△EFM(AAS) EFM(AAS)∴FN=FM FN=FM,又,又FM FM⊥⊥BC BC,,FN FN⊥⊥BA BA,, ∴点F 在∠在∠ABC ABC 的平分线上;的平分线上; (3)(3)∵四边形∵四边形AEFG 是菱形,∠是菱形,∠EAG=120EAG=120EAG=120°,°,°, ∴∠∴∠AGF=60AGF=60AGF=60°,∴∠°,∴∠°,∴∠FGE=FGE=FGE=∠∠AGE=30AGE=30°,°,°,∵四边形AEGH 为平行四边形,∴为平行四边形,∴GE GE GE∥∥AH AH,, ∴∠∴∠GAH=GAH=GAH=∠∠AGE=30AGE=30°,∠°,∠°,∠H=H=H=∠∠FGE=30FGE=30°,°,°, ∴∠∴∠GAN=90GAN=90GAN=90°,又∠°,又∠°,又∠AGE=30AGE=30AGE=30°,∴°,∴°,∴GN=2AN GN=2AN GN=2AN,, ∵∠∵∠DAB=60DAB=60DAB=60°,∠°,∠°,∠H=30H=30H=30°,∴∠°,∴∠°,∴∠ADH=30ADH=30ADH=30°,∴°,∴°,∴AD=AH=GE AD=AH=GE AD=AH=GE,, ∵四边形ABCD 为平行四边形,∴为平行四边形,∴BC=AD BC=AD BC=AD,∴,∴,∴BC=GE BC=GE BC=GE,, ∵四边形ABEH 为平行四边形,∠为平行四边形,∠HAE=HAE=HAE=∠∠EAB=30EAB=30°,°,°, ∴平行四边形ABEN 为菱形,∴为菱形,∴AB=AN=NE AB=AN=NE AB=AN=NE,∴,∴,∴GE=3AB GE=3AB GE=3AB,, ∴=3=3..5.解:(解:(11)S △ABC =S 四边形AFBD ,理由:由题意可得:理由:由题意可得:AD AD AD∥∥EC EC,则,则S △ADF =S △ABD , 故S △ACF =S △ADF =S △ABD ,则S △ABC =S 四边形AFBD ; (2)△)△ABC ABC 为等腰直角三角形,即:为等腰直角三角形,即:AB=AC AB=AC AB=AC,∠,∠,∠BAC=90BAC=90BAC=90°,°,°, 理由如下:理由如下:∵F 为BC 的中点,∴的中点,∴CF=BF CF=BF CF=BF,∵,∵,∵CF=AD CF=AD CF=AD,∴,∴,∴AD=BF AD=BF AD=BF,, 又∵又∵AD AD AD∥∥BF BF,∴四边形,∴四边形AFBD 为平行四边形,为平行四边形, ∵AB=AC AB=AC,,F 为BC 的中点,∴的中点,∴AF AF AF⊥⊥BC BC,∴平行四边形,∴平行四边形AFBD 为矩形为矩形∵∠∵∠BAC=90BAC=90BAC=90°,°,°,F F 为BC 的中点,∴的中点,∴AF=AF=BC=BF BC=BF,,∴四边形AFBD 为正方形;为正方形; (3)如图3所示:所示: 由(由(22)知,△)知,△ABC ABC 为等腰直角三角形,为等腰直角三角形,AF AF AF⊥⊥BC BC,,设CF=k CF=k,,则GF=EF=CB=2k GF=EF=CB=2k,,由勾股定理得:CG=k ,∴CG=CF.6.6.解:解:(1)如图1中,∵四边形ABCD 是菱形,∴是菱形,∴AB=BC=CD=AD=10AB=BC=CD=AD=10AB=BC=CD=AD=10,,AB AB∥∥CD∵PD=4PD=4,∴,∴,∴PC=6PC=6PC=6,∵,∵,∵PB PB PB⊥⊥CD CD,∴,∴,∴PB PB PB⊥⊥AB AB,∴∠,∴∠,∴∠CPB=CPB=CPB=∠ABP=90°,∠ABP=90°,∠ABP=90°, 在RT RT△△PCB 中,∵∠CPB=90°P 中,∵∠CPB=90°PC=6C=6C=6,,BC=10BC=10,∴,∴,∴PB=PB===8=8,, 在RT RT△△ABP 中,∵∠ABP=90°,中,∵∠ABP=90°,AB=10AB=10AB=10,,PB=8PB=8,∴,∴,∴PA=PA===2.(2)△)△OMN OMN 是等腰三角形是等腰三角形..理由:如图2中,延长PM 交BC 于E. ∵四边形ABCD 是菱形,∴是菱形,∴AC AC AC⊥⊥BD BD,,CB=CD CB=CD,, ∵PE PE⊥⊥AC AC,∴,∴,∴PE PE PE∥∥BD BD,∴,∴=,∴,∴CP=CE CP=CE CP=CE,∴,∴,∴PD=BE PD=BE PD=BE,,∵CP=CE CP=CE,,CM CM⊥⊥PE PE,∴,∴,∴PM=ME PM=ME PM=ME,∵,∵,∵PN=NB PN=NB PN=NB,∴,∴,∴MN=MN=BE BE,,∵BO=OD BO=OD,,BN=NP BN=NP,∴,∴,∴ON=ON=PD PD,∴,∴,∴ON=MN ON=MN ON=MN,∴△,∴△,∴△OMN OMN 是等腰三角形是等腰三角形. .7.(1)证明:∵DE⊥BC,∴∠DFB=90°,)证明:∵DE⊥BC,∴∠DFB=90°,∵∠ACB=90°,∴∠ACB=∠DFB,∴AC∥DE,∵∠ACB=90°,∴∠ACB=∠DFB,∴AC∥DE,∵MN∥AB,即CE∥AD,∴四边形ADEC 是平行四边形,∴是平行四边形,∴CE=AD CE=AD CE=AD;; (2)解:四边形BECD 是菱形,理由是:∵是菱形,理由是:∵D D 为AB 中点,∴中点,∴AD=BD AD=BD AD=BD,, ∵CE=AD CE=AD,∴,∴,∴BD=CE BD=CE BD=CE,∵BD∥CE,∴四边形,∵BD∥CE,∴四边形BECD 是平行四边形,是平行四边形, ∵∠ACB=90°,∵∠ACB=90°,D D 为AB 中点,∴中点,∴CD=BD CD=BD CD=BD,∴,∴▱四边形BECD 是菱形;是菱形; (3)当∠A=45°时,四边形BECD 是正方形,理由是:是正方形,理由是: 解:∵∠ACB=90°,∠A=45°,∴∠ABC=∠A=45°,∴解:∵∠ACB=90°,∠A=45°,∴∠ABC=∠A=45°,∴AC=BC AC=BC AC=BC,, ∵D 为BA 中点,∴CD⊥AB,∴∠CDB=90°,中点,∴CD⊥AB,∴∠CDB=90°, ∵四边形BECD 是菱形,∴菱形BECD 是正方形,是正方形, 即当∠A=45°时,四边形BECD 是正方形是正方形. . 8.解:解:9.(1)结论:)结论:EG EG EG::FH=3FH=3::2证明:过点证明:过点A A 作AM AM∥∥HF HF交交BC BC于点于点于点M M ,作,作AN AN AN∥∥EG EG交交CD CD的延长线于点的延长线于点的延长线于点N N ,如图1: ∴AM=HF AM=HF,,AN=EG AN=EG,∵长方形,∵长方形,∵长方形ABCD ABCD ABCD,∴∠,∴∠,∴∠BAD=BAD=BAD=∠∠ADN=90ADN=90°,°,°, ∵EG EG⊥⊥FH FH,∴∠,∴∠,∴∠NAM=90NAM=90NAM=90°,∴∠°,∴∠°,∴∠BAM=BAM=BAM=∠∠DAN DAN,∴△,∴△,∴△ABM ABM ABM∽△∽△∽△ADN ADN ADN,, ∴AM:AN=AB:AD AM:AN=AB:AD,∵,∵,∵AB=2BC=AD=3AB=2BC=AD=3AB=2BC=AD=3,∴,∴,∴EG:FH=1.5EG:FH=1.5EG:FH=1.5;; (2)解:过点)解:过点A A 作AM AM∥∥HF HF交交BC BC于点于点于点M M ,过点,过点A A 作AN AN∥∥EG EG交交CD CD于点于点于点N N ,如图2:∵AB=1AB=1,,AM=FH=,∴在,∴在Rt Rt Rt△△ABM ABM中,中,中,BM=0.5BM=0.5将△AND AND绕点绕点绕点A A 旋转到△旋转到△APB APB APB,, ∵EG EG与与FH FH的夹角为的夹角为4545°,∴∠°,∴∠°,∴∠MAN=45MAN=45MAN=45°,∴∠°,∴∠°,∴∠DAN+DAN+DAN+∠∠MAB=45 即∠即∠PAM=PAM=PAM=∠∠MAN=45MAN=45°,从而△°,从而△°,从而△APM APM APM≌△≌△≌△ANM ANM ANM,∴,∴,∴PM=NM PM=NM PM=NM,,设DN=x DN=x,则,则,则NC=1NC=1NC=1﹣﹣x ,NM=PM=0.5+x NM=PM=0.5+x在在Rt Rt△△CMN CMN中,中,中,(0.5 +x)(0.5 +x)2=0.25+(1=0.25+(1﹣﹣x)2,解得,解得x=1/3x=1/3x=1/3,,∴EG=AN=,答:,答:EG EG EG的长为的长为.10.11. (1)证明:证明:根据翻折的方法可得根据翻折的方法可得EF=EC EF=EC EF=EC,,∠FEG=FEG=∠∠CEG.CEG.又∵又∵又∵GE=GE GE=GE GE=GE,,∴△∴△EFG EFG EFG≌△≌△≌△ECG.ECG.ECG.∴∴FG=GC. ∵线段∵线段FG FG FG是由是由是由EF EF EF绕绕F 旋转得到的,∴旋转得到的,∴EF=FG.EF=FG.EF=FG.∴∴EF=EC=FG=GC.EF=EC=FG=GC.∴四边形∴四边形∴四边形FGCE FGCE FGCE是菱形.是菱形.是菱形. (2)连接)连接FC FC FC交交GE GE于于O 点.根据折叠可得点.根据折叠可得BF=BC=10.BF=BC=10.BF=BC=10.∵∵AB=8 ∴在∴在Rt Rt Rt△△ABF ABF中,根据勾股定理得中,根据勾股定理得中,根据勾股定理得AF=6.AF=6.AF=6.∴∴FD=AD FD=AD--AF=10AF=10--6=4.设EC=x EC=x,则,则,则DE=8DE=8DE=8--x ,EF=x EF=x,在,在,在Rt Rt Rt△△FDE FDE中,中,中,FD FD 2+DE 2=EF 2,即42+(8-x)2=x 2.解得解得x=5.x=5.x=5.即即CE=5.S 菱形菱形CEFG CEFG =CE =CE··FD=5FD=5××4=20.(3)当=时,时,BG=CG BG=CG BG=CG,理由:由折叠可得,理由:由折叠可得,理由:由折叠可得BF=BC BF=BC BF=BC,∠,∠,∠FBE=FBE=FBE=∠∠CBE CBE,,∵在∵在Rt Rt Rt△△ABF ABF中,中,=,∴,∴BF=2AF.BF=2AF.BF=2AF.∴∠∴∠∴∠ABF=30ABF=30ABF=30°°.又∵∠又∵∠ABC=90ABC=90ABC=90°,∴∠°,∴∠°,∴∠FBE=FBE=FBE=∠∠CBE=30CBE=30°,°,°,EC=0.5BE. EC=0.5BE.∵∠∵∠BCE=90BCE=90BCE=90°,∴∠°,∴∠°,∴∠BEC=60BEC=60BEC=60°°.又∵又∵GC=CE GC=CE GC=CE,∴△,∴△,∴△GCE GCE GCE为等边三角形.为等边三角形.为等边三角形. ∴GE=CG=CE=0.5BE.GE=CG=CE=0.5BE.∴∴G 为BE BE的中点.∴的中点.∴的中点.∴CG=BG=0.5BE. CG=BG=0.5BE. 12.13.(1)证明:∵△)证明:∵△ABC ABC 和△和△DEF DEF 是两个边长为6cm 的等边三角形,的等边三角形,∴BC=DE BC=DE,∠,∠,∠ABC=ABC=ABC=∠∠FDE=60FDE=60°,∴°,∴°,∴BC BC BC∥∥DE DE,∴四边形,∴四边形BCDE 是平行四边形;是平行四边形; (2)解:(a )当t=2秒时,▱BCDE 是菱形,此时A 与D 重合,∴重合,∴CD=DE CD=DE CD=DE,∴,∴▱ADEC 是菱形;是菱形; (b )若平行四边形BCDE 是矩形,则∠是矩形,则∠CDE=90CDE=90CDE=90°,如图所示:∴∠°,如图所示:∴∠°,如图所示:∴∠CDB=90CDB=90CDB=90°﹣°﹣°﹣606060°°=30=30°° 同理∠同理∠DCA=30DCA=30DCA=30°°=∠CDB CDB,∴,∴,∴AC=AD AC=AD AC=AD,同理,同理FB=EF FB=EF,∴,∴,∴F F 与B 重合,重合, ∴t=t=((6+26+2)÷)÷)÷1=81=8秒,∴当t=8秒时,平行四边形BCDE 是矩形.是矩形.14.14.解:解:解:(1)(1)(1)成立成立成立. .(2)(2)成立成立理由理由::∵四边形ABCD 为正方形为正方形,,∴AD=DC,AD=DC,∠∠BCD=BCD=∠∠ADC=90ADC=90°°. 在△在△ADF ADF 和△和△DCE DCE 中,DF=CE,,DF=CE,∠∠ADC=ADC=∠∠BCD,AD=CD BCD,AD=CD∴△∴△∴△ADF ADF ADF≌△≌△≌△DCE(SAS), DCE(SAS), ∴AF=DE,AF=DE,∠∠DAF=DAF=∠∠CDE. ∵∠∵∠ADG+ADG+ADG+∠∠EDC=90EDC=90°°,∴∠∴∠ADG+ADG+ADG+∠∠DAF=90DAF=90°°,∴∠∴∠AGD=90AGD=90AGD=90°°,即AF AF⊥⊥DE. (3)(3)四边形四边形MNPQ 是正方形是正方形. . 理由理由::如图如图,,设MQ 交AF 于点O,PQ 交DE 于点H, ∵点M,N,P,Q 分别为AE,EF,FD,AD 的中点的中点, ,∴MQ=PN=错误!未找到引用源。
(完整版)平行四边形提高题练习
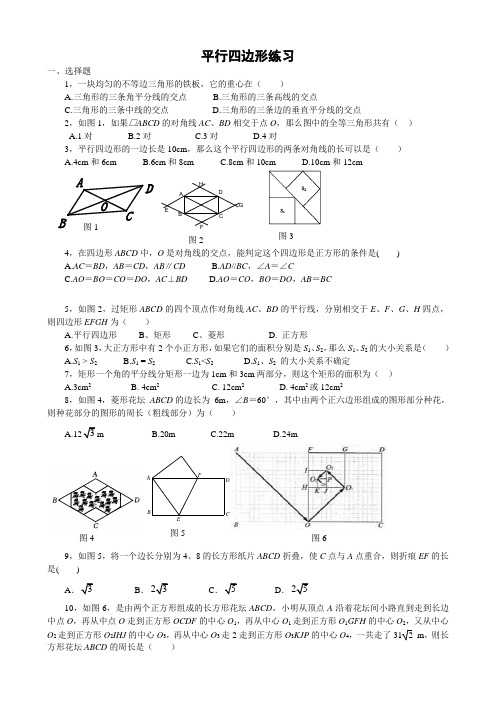
平行四边形练习一、选择题1,一块均匀的不等边三角形的铁板,它的重心在( )A.三角形的三条角平分线的交点B.三角形的三条高线的交点C.三角形的三条中线的交点D.三角形的三条边的垂直平分线的交点2,如图1,如果□ABCD 的对角线AC 、BD 相交于点O ,那么图中的全等三角形共有( )A.1对B.2对C.3对D.4对3,平行四边形的一边长是10cm ,那么这个平行四边形的两条对角线的长可以是( )A.4cm 和6cmB.6cm 和8cmC.8cm 和10cmD.10cm 和12cm4,在四边形ABCD 中,O 是对角线的交点,能判定这个四边形是正方形的条件是( )A.AC =BD ,AB =CD ,AB ∥CDB.AD //BC ,∠A =∠CC.AO =BO =CO =DO ,AC ⊥BDD.AO =CO ,BO =DO ,AB =BC5,如图2,过矩形ABCD 的四个顶点作对角线AC 、BD 的平行线,分别相交于E 、F 、G 、H 四点,则四边形EFGH 为( )A.平行四边形 B 、矩形 C 、菱形 D. 正方形6,如图3,大正方形中有2个小正方形,如果它们的面积分别是S 1、S 2,那么S 1、S 2的大小关系是( )A.S 1 > S 2B.S 1 = S 2C.S 1<S 2D.S 1、S 2 的大小关系不确定7,矩形一个角的平分线分矩形一边为1cm 和3cm 两部分,则这个矩形的面积为( )A.3cm 2B. 4cm 2C. 12cm 2D. 4cm 2或12cm 28,如图4,菱形花坛 ABCD 的边长为 6m ,∠B =60°,其中由两个正六边形组成的图形部分种花,则种花部分的图形的周长(粗线部分)为( )A.123mB.20mC.22mD.24m9,如图5,将一个边长分别为4、8的长方形纸片ABCD 折叠,使C 点与A 点重合,则折痕EF 的长是( )A .3B .23C .5D .2510,如图6,是由两个正方形组成的长方形花坛ABCD ,小明从顶点A 沿着花坛间小路直到走到长边中点O ,再从中点O 走到正方形OCDF 的中心O 1,再从中心O 1走到正方形O 1GFH 的中心O 2,又从中心O 2走到正方形O 2IHJ 的中心O 3,再从中心O 3走2走到正方形O 3KJP 的中心O 4,一共走了31 2 m ,则长方形花坛ABCD 的周长是( )图6 图4 F EDC B A 图5 图3 AD C B HE FG 图2O A B D C 图1A.36 mB.48 mC.96 mD.60 m二、填空题(每题3分,共30分)11,如图7, 若将四根木条钉成的矩形木框变形为平行四边形ABCD 的形状,并使其面积为矩形面积的一半,则这个平行四边形的一个最小内角的值等于___.12,如图8,过矩形ABCD 的对角线BD 上一点K 分别作矩形两边的平行线MN 与PQ ,那么图中矩形AMKP 的面积S 1与矩形QCNK 的面积S 2的大小关系是S 1 S 2(填“>”或“<”或“=”).13,如图9,四边形ABCD 是正方形,P 在CD 上,△ADP 旋转后能够与△ABP ′重合,若AB =3,DP =1,则PP ′=___.14,已知菱形有一个锐角为60°,一条对角线长为6cm ,则其面积为___cm 2.15,如图10,在梯形ABCD 中,已知AB ∥CD ,点E 为BC 的中点, 设△DEA 的面积为S 1,梯形ABCD 的面积为S 2,则S 1与S 2的关系为___.16,如图11,四边形ABCD 的两条对角线AC 、BD 互相垂直,A 1B 1C 1D 1四边形ABCD 的中点四边形.如果AC =8,BD =10,那么四边形A 1B 1C 1D 1的面积为___.17,如图12,□ABCD 中,点E 在边AD 上,以BE 为折痕,将△ABE 向上翻折,点A 正好落在CD 上的点F ,若△FDE 的周长为8,△FCB 的周长为22,则FC 的长为___.18,将一张长方形的纸对折,如图13所示,可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折四次可以得到 条折痕,如果对折n 次,可以得到 条折痕.三、解答题(共40分)19,如图1,4,等腰梯形ABCD 中,AD ∥BC ,∠DBC =45°,翻折梯形ABCD ,使点B 重合于D ,折痕分别交边AB 、BC 于点F 、E ,若AD =2,BC =8.求BE 的长.…… 第一次对折 第二次对折 第三次对折图13图11A 1B 1C 1D 1 D A B C D A B C EF 图12 D C BA 图7 图9 图8K NM Q C BF E D C B A 图14图10 E D C B A20,在一次数学实践探究活动中,小强用两条直线把平行四边形ABCD 分割成四个部分,使含有一组对顶角的两个图形全等;(1)根据小强的分割方法,你认为把平行四边形分割成满足以上全等关系的直线有___组;(2)请在图15的三个平行四边形中画出满足小强分割方法的直线;(3)由上述实验操作过程,你发现所画的饿两条直线有什么规律?21,如图16,已知四边形ABCD 是平行四边形,∠BCD 的平分线CF 交边AB 于F ,∠ADC 的平分线DG 交边AB 于G .(1)线段AF 与GB 相等吗?(2)请你在已知条件的基础上再添加一个条件,使得△EFG 为等腰直角三角形,并说明理由.1.七巧板是我们祖先的一项创造,被誉为“东方魔板”,如图是一副七巧板,若已知S △BIC =1,请你根据七巧板制作过程的认识,解决下列问题: A B C D A B C D D CB A 图15 A BCDEF 图17图16 O F D B E C A· 图18(1)求一只蚂蚁从点A 沿A →B →C →H →E 所走的路线的总长。
2021年中考一轮复习数学综合题复习:四边形 强化训练练习

2021年中考一轮复习九年级数学综合题复习:四边形强化训练练习1、如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作BH AE⊥,垂足为点H,延长BH交CD于点F,连接AF.(1)求证:AE BF=.BE=,求AF的长.(2)若正方形边长是5,22、如图,在平行四边形ABCD中,P是对角线BD上的一点,过点C作CQ∥DB,且CQ=DP,连接AP、BQ、PQ.(1)求证:△APD≌△BQC;(2)若∠ABP+∠BQC=180°,求证:四边形ABQP为菱形。
3、如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.(1)求证:四边形BCFD为平行四边形;(2)若AB=6,求平行四边形BCFD的面积.4、如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.(1)BD与CD有什么数量关系,并说明理由;(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.5、把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG。
(1)求证:△BHE≌△DGF;(2)若AB=6cm,BC=8cm,求线段FG的长。
6、如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于E,BF∥DE,交AG于F.(1)求证:AF﹣BF=EF;(2)将△ABF绕点A逆时针旋转,使得AB与AD重合,记此时点F的对应点为点F′,若正方形边长为3,求点F′与旋转前的图中点E之间的距离.7、如图所示,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.(1)求证:D是BC的中点;(2)若AB=AC,试判断四边形AFBD的形状,并证明你的结论.8、如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.(1)求证:△AGE≌△BGF;(2)试判断四边形AFBE的形状,并说明理由.9、如图,□ABCD中,点E是BC的中点,连接AE并延长交DC延长线于点F.(1)求证:CF=AB;(2)连接BD、BF,当∠BCD=90°时,求证:BD=BF.10、已知点E为正方形ABCD的边AD上一点,连接BE,过点C作CN⊥BE,垂足为M,交AB于点N.(1)求证:△ABE≌△BCN;(2)若N为AB的中点,求tan∠ABE.11、如图,等腰梯形MNPQ的上底长为2,腰长为3,一个底角为60°.正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD 在梯形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动.(1)请在所给的图中,用尺规画出点A在正方形整个翻滚过程中所经过的路线图;(2)求正方形在整个翻滚过程中点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S.12、如图,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四边形综合提高练习题
1、十二边形的内角和为( ) A.1080° B.1360° C 、1620° D 、1800°
2、能判定四边形ABCD 为平行四边形的题设是( ).
(A )AB ∥CD ,AD=BC; (B )∠A=∠B ,∠C=∠D; (C )AB=CD ,AD=BC; (D )AB=AD ,CB=CD
(D)
3、菱形ABCD 的对角线长分别为6cm 和8cm ,则菱形的面积为( ) A.12, B.24 C.36 D.48 4.下列说法不正确的是( )
(A )对角线相等且互相平分的四边形是矩形;(B )对角线互相垂直平分的四边形是菱形; (C )对角线垂直的菱形是正方形;(D )底边上的两角相等的梯形是等腰梯形 5、如图1,在平行四边形ABCD 中,CE AB ⊥,E 为垂足.如果
125A =∠,则BCE =∠( )
A.55
B.35
C.
25
D.30
6、顺次连结任意四边形各边中点所得到的四边形一定是__ ___.
7、如图4,把一张矩形纸片ABCD 沿EF 折叠后,点C D ,分别落在C D '',的位置上,EC '交AD 于点G .则△EFG 形状为 8、如图5,在梯形ABCD 中,AD BC ∥,419045==︒=∠︒=∠BC AD C B ,,, 则AB=
9.如图6,AC 是正方形ABCD 的对角线,AE 平分∠BAC ,EF ⊥AC 交AC 于点F ,若BE=2,则CF 长为
1.如图,在Rt △ABC 中,∠B=90°,BC=53,∠C=30°.点D 从点C 出发沿CA 方向以每秒2个单位长的速度向点A 匀速运动,同时点E 从点A 出发沿AB 方向以每秒1个单位长的速度向点B 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D 、E 运动的时间是t 秒(t >0).过点D 作DF ⊥BC 于点F ,连接DE 、EF . (1)求AB,AC 的长;(2)求证:AE=DF ;
(3)四边形AEFD 能够成为菱形吗?如果能,求出相应的t 值;如果不能,说明理由. (4)当t 为何值时,△DEF 为直角三角形?请说明理由.
2.如图,已知菱形ABCD 的对角线AC 、BD 相交于点O ,延长AB 至点E ,使BE =AB ,连接CE . (1)求证:四边形BECD 是平行四边形;
(2)若∠E =60°,AC =43,求菱形ABCD 的面积.
3.在△ABC 中,AB =AC =2,∠BAC =45º.△AEF 是由△ABC 绕点A 按逆时针方向旋转得到,连接BE ,CF 相交于点D . (1)求证:BE =CF ;
(2)当四边形ABDF 是菱形时,求CD 的长.
4.如图,四边形ABCD 是正方形,点E ,F 分别在BC ,AB 上,点M 在BA 的延长线上,且CE=BF=AM ,过点M ,E 分别作NM ⊥DM ,NE ⊥DE 交于N ,连接NF . (1)求证:DE ⊥DM ;
(2)猜想并写出四边形CENF 是怎样的特殊四边形,并证明你的猜想.
5.如图,正方形ABCD的面积为4,对角线交于点O,点O是正方形A1B1C1O的一个顶点,如果这两个正方形全等,正方形A1B1C1O绕点O旋转.
(1)求两个正方形重叠部分的面积;
(2)若正方形A1B1C1O旋转到B1在DB的延长线时,求A与C1的距离.
6.在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.(备注:在直角三角形中30度角所对的边是斜边的一半)
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,
如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
7.如图1,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.
(1)求证:AE=EF.
(2)如图2,若把条件“点E是边BC的中点”改为“点E是边BC上
的任意一点”其余条件不变,那么结论AE=EF是否成立呢?若成立,
请你证明这一结论,若不成立,请你说明理由.8.已知□OABC的顶点A、C分别在直线x=2和x=4上, O为坐标原点,直线x=2分别与x轴和OC边交于D、E,直线x=4分别与x轴和AB边的交于点F、G.
(1)如图,在点A、C移动的过程中,若点B在x轴上,
①直线 AC是否会经过一个定点,若是,请直接写出定点的坐标;若否,请说明理由.
②□OABC是否可以形成矩形?如果可以,请求出矩形OABC的面积;若否,请说明理由.
③四边形AECG是否可以形成菱形?如果可以,请求出菱形AECG的面积;若否,请说明理由.(2)在点A、C移动的过程中,若点B不在x轴上,且当□OABC为正方形时,直接写出点C的坐标.
9.如图,矩形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6.点P从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为t秒.
(1)求AE的长;
(2)当t为何值时,△PAE为直角三角形?
(3)是否存在这样的t,使EA恰好平分∠PED,若存在,求出t的值;若不存在,请说明理由.。
