椭圆抛物面画法

4.6抛物面

x 2 2a 2 z，抛物线 C y 0： y 0.
③用x = 0 截曲面
O
Cx＝0
y
y 2 2b 2 z，抛物线x Cx 0： x 0.
Cy＝0
ⅱ）用平行于坐标面的平面截割
①用z = h (h>0)截曲面
x2 y2 1, 椭圆 Cz h： 2a 2 h 2b 2 h z h.
z
结论：椭圆抛物面可看作由一个椭圆的变动（大小位置都改变）而产生，该椭圆在变动中，保持所在平面与xOy 面平行，且两对顶点分别在两主抛物线上滑动
y O
x
ⅱ）用平行于坐标面的平面截割
2 y2 2 x 2a z 2 ， 2b 抛物线 ②用y = k截曲面 C y k： z y k. 结论：取这样两个抛物线，它们所在的平面互相垂直，它们的顶点和轴都重合，且两抛物线有相同的开口方向，让其中一条抛物线平行于自己（即与抛物线所在的平面平行），且使其顶点在另一个抛物线上 O 滑动，那么前一抛物线的运动轨迹是一个椭圆 x 抛物面.
2
z
绕它的对称轴旋转
o
y
例
y 2 pz : 将抛物线 x 0
2
z
绕它的对称轴旋转
.
o
y
x
旋转抛物面 z
例
y 2 pz : 将抛物线 x 0
2
x2 y 2 2 pz
绕它的对称轴旋转
.
.
o
y
x
Back
二、椭圆抛物面的性质
1 对称性
关于 z 轴，xOz 、yOz 坐标平面对称;

《椭球双曲抛物面》PPT课件

微分几何
微分几何课程建设组
1
微分几何
§4.4 椭球面
§4.5 双曲曲
§4.6 抛物面
微分几何课程建设组
2
4.4 椭球面
x2 y2 z2 1
a2 b2 c2
平行截割法
用z = h截曲面用y = m截曲面用x = n截曲面
z
c
o a
x
by
3
4.6 椭圆抛物面
x2 y2
p2
q2
2z
z
平行截割法
q2
z
z
平行截割法
用z = a截曲面
x
用y = 0截曲面
0
用x = b截曲面
y
7
4.6双曲抛物面（马鞍面）
x2 y2
p2
q2
z
z
平行截割法
用z = a截曲面
x
用y = 0截曲面
0
用x = b截曲面
y
8 .
4.6 双曲抛物面（马鞍面）
x2 y2
p2
q2
z
z
平行截割法
用z = a截曲面
x
用y = 0截曲面
截口椭圆任意接近，即：
x
双曲面和锥面任意接近。
z
o
y
10
2.开关按键和塑胶按键设计间隙建议留0.05~0.1mm，以防按键死键。 3.要考虑成型工艺，合理计算累积公差，以防按键手感不良。
4.6 椭圆抛物面
x2 y2
p2
q2
2z
z
平行截割法
用z = a截曲面
用y = b截曲面
用x = c截曲面
y
0
.
x

椭圆抛物面

z
简图
a
.
0
a
y
a
x
o y
三个坐标平面
第一卦限
x
2x y 4
z 4 x
顶点
2
z
S (0,0,4)
S (0,0,4)
平面
2x y 4
o y
三个坐标平面
第一卦限
x
z 4 x
顶点
2
z
S (0,0,4)
S (0,0,4)
平面
2x y 4
o y
三个坐标平面
第一卦限
x
z 4 x
0
(1)
y x
2 2 t 2 x 2a ( z 2 ) 2b y t
（4）
此外，抛物线（4）的顶点
z
t (0, t , 2 ) 2b
位于主抛物线（2）上，
2
y 2 2b 2 z x 0
0
(2) x
y
因此我们得到下面得结论：
如果取两个这样的抛物线，它们所在的平面互相垂直，它们的顶点和轴都重合，而且两抛物线有相同的开口方向，让其中一条抛物线平行于自己（即与抛物线所在的平面平行）且使其顶点在另一个抛物线上滑走，那么这一抛物线的运动轨迹便是一个椭圆抛物面.
顶点
2
z
S (0,0,4)
S (0,0,4)
平面
2x y 4
o
Q
y
三个坐标平面 P
第一卦限
x
我们设想用一平行于yoz面的平面来截割它们，
那么截得一矩形ABCD
z 4 x
顶点
2
z
S (0,0,4)

04-2.抛物面PPT

g = Zi
与平面z = Z1 (z1 v 0)不相
交.
+ 2q =z
二、椭圆抛物面
(2 )用坐标面xoz (y = 0)与曲面相截截得抛物线［X2 = 2P' I y = o
与平面y =凹的交线为抛物线.
[2 ( y2)
X2 = 2 p z
一丄
I 2q
丿
它的轴平行于z轴
顶点(。，诚)
22
xy
+ =z
x2 — y2 = z 2 x2 — 3 y2 = z
2 p 2q
用截痕法讨论：
设>
p 0
>
0, q
图形如下：
y
截痕法研究抛物面:
用平行于坐标面的平面去截抛物面，观察截痕的形状大小，然后综合考察曲面的形状特征。
常见的抛物面方程： z = x 2 + 2 y 2 z = —2 x2 — 3 y2
z = x 2 + y 2 2 — z = 2 x 2 + 3 y2
二次曲面的定义：三元二次方程所表示的曲面称之. 相应地平面被称为一次曲面.
讨论二次曲面性状的截痕法：用坐标面和平行于坐标面的平面与曲面相截,
考察其交线（即截痕）的形状，然后加以综合, 从而了解曲面的全貌.
椭圆抛物面
x2 y 2 每+ 2q =」「与q同号）
椭圆抛物面
用截痕法讨论：设p > 0, q > 0
2 p 2q
二、椭圆抛物面
(3 )用坐标面 yoz (x = 0), X = X］与曲面相
截均可得抛物线.
同理当p V 0, q V 0时可类似讨论.
22

§4.6 抛物面

§4.6 抛物面一、椭圆抛物面1．在直角坐标系下,由方程+＝2z所表示的曲面叫做椭圆抛物面, 该方程叫做椭圆抛物面的标准方程, 其中a, b为任意正常数.2. 椭圆抛物面的图形（如图4-7）.(1) 曲面的对称性：椭圆抛物面关于yOz, zOx坐标面以及z轴对称, 但它没有对称中心, 它与对称轴交于点(0, 0, 0), 这点叫做椭圆抛物面的顶点.(2) 曲面与坐标轴的交点：椭圆抛物面通过坐标原点, 且除原点外, 曲面与三坐标轴没有别的交点.(3) 曲面的存在范围：椭圆抛物面全部在xOy坐标面的一侧, 即在z≥0的一侧.(4) 被坐标面截得的曲线①②③①表示一点(0, 0, 0), 而②与③分别为xOz与yOz坐标面上的抛物线, 它们有着相同的顶点和相同的对称轴即z轴, 开口都向着z轴的正向,都叫做椭圆抛物面的主抛物线.(5) 被坐标平面的平行平面所截得的曲线：用平行于xOy坐标面的平行平面z＝h(h>0)来截椭圆抛物面, 得截线方程为+＝1. ④椭圆抛物面可看成是由椭圆族④所生成, 这族椭圆中的每一个椭圆所在的平面与xOy坐标面平行, 两顶点分别在双曲线②与③上.用平行于xOz坐标面的平面y＝k来截割椭圆抛物面,所截得的曲线为抛物线用平行于yOz坐标面的平面来截椭圆抛物面所得的截线也是抛物线.若a＝b, 则椭圆抛物面就是旋转抛物面.3. 椭圆抛物面的参数方程为(u, v是参数)二、双曲抛物面1. 在直角坐标系下, 由方程－＝2z所表示的曲面叫做双曲抛物面, 如图5-8, 该方程叫做双曲抛物面的标准方程, 其中a, b为任意正常数.2. 双曲抛物面的图形（如图4-8）.(1) 曲面的对称性：双曲抛物面关于xOz坐标面, yOz坐标面以及z轴都对称, 但它没有对称中心.(2) 曲面与坐标轴的交点：双曲抛物面通过原点, 且除原点外与三坐标轴没有其它交点.(3) 被坐标面所截得的曲线：双曲抛物面被xOy坐标面截得的曲线方程为⑤这是一对相交于原点的直线与被xOz与yOz坐标面截得的曲线方程分别为⑥⑦这两抛物线叫做双曲抛物面的主抛物线, 它们有着相同的顶点与相同的对称轴, 即z轴, 但开口方向相反.(4) 被坐标面的平行平面所截得的曲线：用平行于xOy坐标面的平面z＝h来截割双曲抛物面, 得截线方程为⑧这是双曲线, 当h>0时, 双曲线⑧的实轴与x轴平行, 虚轴与y轴平行, 顶点(±a, 0, h)在主抛物线⑥上; 当h<0时,双曲线⑧的实轴与y轴平行, 虚轴与x轴平行, 顶点(0, ±b,h)在主抛物线⑦上.用分别平行于xOz与yOz坐标面的平面y＝k与x＝t来截曲面,其截线都是抛物线, 方程分别为⑨⑩抛物线⑨的对称轴平行于z轴, 且开口方向与z轴正向相同, 顶点(0, k, －)在主抛物线⑦上; 抛物线⑩的对称轴也平行于z轴, 但开口方向与z轴的正向相反, 顶点(t, 0,)在主抛物线⑥上.双曲抛物面也叫做马鞍曲面.椭圆抛物面与双曲抛物面统称为抛物面, 它们都没有对称中心,所以又都叫做无心二次曲面.3. 双曲抛物面的参数方程为(u, v为参数)例1. 在空间直角坐标系中, 求与直线l1：＝＝和l2：＝＝共面且与平面：x－y－5＝0平行的直线所组成的轨迹.解：设满足条件的直线方程为＝＝，由直线与l1共面得＝0,或 (4y0＋z0－4)X＋(－4x0＋z0＋4)Y＋(－x0－y0＋z)Z=0. ①由直线与l2共面得＝0,或z0X＋z0Y＋(―x0―y0)Z＝0. ②由直线平行于平面π得X－Y＝0. ③因为X, Y, Z不全为零, 所以由上面①、②、③构成的齐次线性方程组应有非零解, 因而＝0,化简得x02－y02＝z0.其中 (x0, y0, z0) 表示所求直线上的点, 从而满足条件的直线所组成的轨迹是双曲抛物面x2－y2＝z.例2. 适当选取坐标系, 求下列轨迹的方程：(1) 到一定点和一定平面距离之比等于常数的点的轨迹;(2) 与两给定异面直线等距离的点的轨迹,已知两异面直线之间的距离为2a, 夹角为2α.解:(1) 设定点到定平面的距离为h>0, 常数c>0. 取定平面为xOy平面, z轴垂直于定平面并通过定点建立直角坐标系, 设定点坐标为(0, 0, h), 动点坐标为(x, y, z), 依题意有，化简整理得x2+y2+(1－c2)z2－2hz＋h2＝0.讨论：当h＝0时, 方程为x2+y2+(1－c2)z2＝0,(i) c>1时为圆锥面;(ii) c＝1时为z轴;(iii) c<1时为一点(0, 0, 0).当h≠0时,(i) c>1时为旋转双叶双曲面;(ii) c＝1时为旋转抛物面;(iii) c<1时为旋转椭球面.(2) 取两异面直线的公垂线为z轴, 公垂线中点为原点, 并取轴与两异面直线成等角建立空间直角坐标系, 设公垂线与两异面直线的交点分别为E (0, 0, a), F (0, 0, －a).则两异面直线的方向矢量分别为＝{cosα, sinα, 0}, ＝{cosα, －sinα,0}.设动点为P(x, y, z), 依题意有＝,即 |{cosα, sinα, 0}×{x, y, z－a}|＝|{ cosα, －sinα, 0}×{x, y, z+a}|,化简整理得2az＋xy sin2α＝0.该曲面表示一个双曲抛物面.例3.画出下列各组曲面所围成的立体的图形：(1) y＝0, z＝0, 3x＋y＝6, 3x＋2y＝12, x＋y＋z＝6；(2) x2+y2＝z, 三坐标面, x＋y＝1;(3) x＝, ＝x, y＝1；(4) x2＋y2＝1, y2＋z2＝1.解：如下图作业题：1. 判断下列方程表示什么曲面, 并画出草图.(1) 4y2＋z2＝4x；(2) 3x2－5y2+15z＝0 .2. 方程＋＝z (a>b>0, k为参数)表示一族无心二次曲，问k取何值时，二次曲面为椭圆抛物面、双曲抛物面？。

4.4-4.6 椭球面、双曲面、抛物面(课堂PPT)

对称.
26
(3) 截痕
x2 y2 z , （ p 与 q 同号）
2 p 2q
用平面 z = z0 (z0 0) 截曲面所得截痕为双曲线 x2 y2 1 2 pz0 2qz0 z z0
z
o
y
x
27
截痕 z x2 y2 , （ p 与 q 同号） 2 p 2q
用平面 x = x0与 y = y0 截曲面所得截痕为抛物线
7
例已知椭球面
x2 y2 z2 1(cab)
a2 b2 c2
求过x轴且与椭球面的交线是圆的平面.
解设所求平面方程为 z ky,
它与椭球面的交线是
x2 a2
c2 b2k2
b2c2
y2
1,
z ky
(1)
8
它与椭球面的交线是
x2 a2
c2 b2k2
b2c2
y2
1,
z ky
(1)
如果交线是圆，则圆心是椭球面的对称中心(0,0,0)，且圆通过椭球面的顶点(a,0,0)，(-a,0,0)，故其方程为
x2 a2
y2 b2
1
z0 2 c2
z z0
z
用平面 y = y0 截曲面所得截痕为：
x2 a2
z2 c2
1
y0 2 b2
y y0
这是一条双曲线（或两条直线）. x
o
y
12
截痕
x2 a2
y2 b2
z2 c2
1
用平面 x = x 0 截曲面所得截痕为：
y2 b2
z2 c2
1
x0 2 a2
x x0
椭球面与平面 z z1 （ | z1 | c）的交线为椭圆

椭圆抛物面方程

椭圆抛物面方程椭圆抛物面方程，是描述椭圆抛物面的数学方程。

椭圆抛物面是一种三维几何体，具有特殊的形状和性质。

在本文中，我们将介绍椭圆抛物面的定义、特征以及一些相关的应用。

我们来看一下椭圆抛物面的定义。

椭圆抛物面可以通过以下方程来描述：(x^2)/a^2 + (y^2)/b^2 = 2z其中，a和b分别为椭圆抛物面在x轴和y轴上的半径。

可以看出，椭圆抛物面在z轴上的形状是一个抛物线。

而在平面上，椭圆抛物面的截面是一个椭圆。

椭圆抛物面具有一些特殊的性质。

首先，它是一个二次曲面，形状对称。

其次，椭圆抛物面在三个坐标轴上的截面分别是一个抛物线、一个椭圆和一个双曲线。

此外，椭圆抛物面还具有焦点和准线等重要概念。

椭圆抛物面在几何学中有广泛的应用。

首先，它可以用来描述物体的形状。

例如，在建筑设计中，椭圆抛物面常被用来设计拱门和穹顶。

其次，椭圆抛物面还可以用来求解一些物理问题。

例如，在光学中，椭圆抛物面可以用来描述光线在曲面上的反射或折射行为。

此外，在机械工程中，椭圆抛物面可以用来设计一些特殊形状的零件，如齿轮和摆线轮。

除了几何学和物理学应用外，椭圆抛物面还在数学分析中有重要的地位。

例如，在微积分中，椭圆抛物面可以用来求解一些曲线的长度、曲率和曲率半径等问题。

此外，在微分方程中，椭圆抛物面的方程也常常出现。

椭圆抛物面方程是描述椭圆抛物面的数学方程，它具有特殊的形状和性质。

椭圆抛物面在几何学、物理学和数学分析中有广泛的应用。

通过研究和应用椭圆抛物面方程，我们可以更好地理解和利用这一特殊的几何体。

椭球面双曲面抛物面

椭球面双曲面抛物面§7.9 二次曲面三元二次方程所表示的曲面称着二次曲面。

相应地，将平面叫做一次曲面。

一般的三元方程F x y z(,,)=0所表示的曲面形状，已难以用描点法得到，那未怎样了解它的形状呢?利用坐标面或用平行于坐标面的平面与曲面相截，考察其交线( 即截痕 )的形状，然后加以综合，从而了解曲面的全貌，这种方法叫做截痕法。

下面，我们用截痕法来讨论几个特殊的二次曲面。

一、椭球面由方程x aybzc2222221++=(1)所表示的曲面叫做椭球面。

1、由(1)可知：x a y b z c≤≤≤,,这表明：椭球面(1)完全包含在以原点为中心的长方体内，这长方体的六个面的方程为x a y b z c=±=±=±,,其中常数a b c,,叫做椭球面的半轴。

2、为了进一步了解这一曲面的形状，先求出它与三个坐标面的交线x a y bzybzcxxazcy222222222222111+==⎧⎨⎪⎩⎪+==⎧⎨⎪⎩⎪+==⎧⎨⎪⎩⎪这些交线都是椭圆。

3、用平行于xoy坐标面的平面z z z c=≤11()去截椭球面，其截痕(即交线)为x a cc z y b c c z z z 222122221211()()-+-==⎧⎨⎪⎪⎩⎪⎪这是位于平面 z z =1内的椭圆，它的两个半轴分别等于 a c c z 212-与b c c z 212-，其椭圆中心均在z 轴上，当z 1由0渐增大到c 时，椭圆的截面由大到小，最后缩成一点。

4、以平面y y y b =≤11()或 x x x a =≤11()去截椭球面分别可得与上述类似的结果。

综上讨论知：椭球面(1)的形状如图所示。

5、特别地，若ab =，而ac ≠，则 (1) 变为x a y a z c 2222221++=这一曲面是xoz 坐标面上的椭圆 x a z c 22221+=绕z 轴旋转而成的旋转曲面，因此，称此曲面为旋转椭球面。

ch4-4椭球面双曲面抛物面

椭圆抛物面的图形如下：
z o x y z
x
o
y
p 0, q 0
p 0, q 0
特殊地：当 p q 时，方程变为
x y z 2p 2p
2
2
( p 0)
旋转抛物面
2 xoz x （由面上的抛物线 2 pz 绕它的轴旋转而成的）与平面 z z1 ( z1 0) 的交线为圆.
2 x2 y 1 2 pz1 2qz1 z z 1
当 z1 变动时，这种椭圆的中心都在 z 轴上.
与平面 z z1 ( z1 0) 不相交. （2）用坐标面 xoz ( y 0)与曲面相截
x 2 pz 截得抛物线 y 0
2
与平面 y y1 的交线为抛物线.
2 2 2
z
o
y
上一页
返回
§4.5 抛物面
x y z （ p 与 q 同号） 2 p 2q
椭圆抛物面
2 2
用截痕法讨论：设 p 0, q 0
（1）用坐标面 xoy ( z 0) 与曲面相截
截得一点，即坐标原点 O (0,0,0)
原点也叫椭圆抛物面的顶点.
与平面 z z1 ( z1 0) 的交线为椭圆.
上一页下一页
实轴与 x 轴相合，虚轴与 z 轴相合.
返回
（3）用坐标面 yoz ( x 0)，与曲面相截
均可得双曲线.
单叶双曲面图形
z
o x
y
上一页
下一页
返回
二、双叶双曲面
x2 y2 z2 2 2 1 2 a b c
双叶双曲面 z
o x
y

表面变形计算的椭圆抛物面法

表面变形计算的椭圆抛物面法AbstractIn the field of surface deformation calculation, the ellipsoid-paraboloid method has gained increasing attention over the last few years. In this paper, a thorough investigation of this method will be presented, including principles, implementation, and performance evaluation.The ellipsoid-paraboloid method calculates surface deformation by fitting an ellipsoid and a paraboloid to the pre- and post-displacement data, respectively. The displacement vector at each point is then determined by the intersection of the two surfaces. The method offers several advantages over other methods, including its ability to model complex deformation patterns and its robustness to outliers.Implementation of the method involves a few key steps, such as data preprocessing, determining the ellipsoid and paraboloid parameters, and calculating the intersection. The optimization process for determining the surface parameters is critical to achieving accurate results, and various techniques can be employed to ensure convergence.Performance evaluation of the method was conducted using both synthetic and real-world data. The results demonstrate that the method is capable of accurately modeling a variety of deformation patterns, and is particularly useful for monitoring subsidence, landslides, and volcano deformation. Comparisons to other methods show that the ellipsoid-paraboloid method outperformstraditional methods such as the least squares method and the Okada model.Overall, the ellipsoid-paraboloid method has proven to be a reliable and effective approach for surface deformation calculation. Its ability to accurately capture complex deformation patterns and its robustness to outliers make it a valuable tool in geodetic and remote sensing applications.Keywords: surface deformation, ellipsoid-paraboloid method, optimization, performance evaluation.IntroductionSurface deformation calculation has become an important research topic in the fields of geodetic and remote sensing applications. Understanding deformation patterns is critical for assessing potential natural hazards such as subsidence, landslides, and volcanic activity. Many different methods have been developed for surface deformation calculation, such as the least squares method, the Okada model, and the finite-element method.In recent years, the ellipsoid-paraboloid method has gained increasing attention as a robust and effective approach for surface deformation calculation. The method fits an ellipsoid and a paraboloid to pre- and post-displacement data, respectively, and calculates the displacement vector at each point as the intersection of the two surfaces. The method offers several advantages over other methods, such as its ability to model complex deformation patterns and its robustness to outliers.This paper presents a thorough investigation of the ellipsoid-paraboloid method, including principles, implementation, and performance evaluation. The following section introduces the principles of the method.PrinciplesThe ellipsoid-paraboloid method uses two surfaces to model surface deformation: an ellipsoid to represent the pre-displacement surface and a paraboloid to represent the post-displacement surface. The displacement vector at each point is then calculated as the intersection of the two surfaces.The ellipsoid has the general form:(x^2/a^2) + (y^2/b^2) + (z^2/c^2) = 1 (1)where a, b, and c are the semi-axes of the ellipsoid, and x, y, and z are the Cartesian coordinates of a given point.The paraboloid has the general form:z = Ax^2 + By^2 + Cx + Dy + E (2)where A, B, C, D, and E are the parameters of the paraboloid.To determine the displacement vector at each point, the intersection of the ellipsoid and paraboloid is calculated. This is a non-linear problem, which can be solved through an optimizationprocess.ImplementationThe implementation of the ellipsoid-paraboloid method involves several key steps, including data preprocessing, determination of the ellipsoid and paraboloid parameters, and calculation of the intersection.Data preprocessing involves removing any systematic errors or biases in the data. This can be accomplished through various techniques such as atmospheric correction, phase unwrapping, and filtering.The determination of the ellipsoid and paraboloid parameters involves an optimization process to minimize the difference between the observed data and the model. Various techniques can be employed for this process, such as the Levenberg-Marquardt algorithm or the Gauss-Newton algorithm.Once the parameters of the ellipsoid and paraboloid are determined, the intersection of the two surfaces can be calculated. This is done by solving the system of equations formed by the ellipsoid and paraboloid.Performance EvaluationTo evaluate the performance of the ellipsoid-paraboloid method, both synthetic and real-world data were used. The synthetic data was generated using a known deformation pattern, and the real-world data was acquired from GPS and InSAR measurements.The results show that the ellipsoid-paraboloid method is capable of accurately modeling a variety of deformation patterns, including subsidence, uplift, and horizontal displacement. The method is particularly useful for monitoring subsidence, landslides, and volcano deformation.Comparisons to other methods, such as the least squares method and the Okada model, show that the ellipsoid-paraboloid method outperforms traditional methods. The method is able to handle non-linear deformation patterns more effectively, and is more robust to outliers.ConclusionThe ellipsoid-paraboloid method is a reliable and effective approach for surface deformation calculation. Its ability to accurately capture complex deformation patterns and its robustness to outliers make it a valuable tool in geodetic and remote sensing applications. The method offers several advantages over traditional methods, such as the least squares method and the Okada model. Further research should focus on refining the optimization process and exploring the method's potential for other applications.In addition to its advantages over traditional methods, the ellipsoid-paraboloid method has several other benefits. The method is computationally efficient, requiring only a few iterations of the optimization process to achieve accurate results. This is particularly advantageous for large datasets or real-time monitoring applications.Another benefit of the method is its flexibility in modeling different types of deformation patterns. The ellipsoid and paraboloid surfaces can be adjusted to fit different shapes and magnitudes of deformation, allowing for customized models for specific applications.The ellipsoid-paraboloid method also offers improved accuracy compared to traditional methods. The method reduces the effects of noise and measurement errors through its robustness to outliers, resulting in more accurate displacement estimates.Moreover, the method can be applied to different types of measurement data, such as GPS, InSAR, or optical imagery. This versatility makes it applicable to a wide range of geodetic and remote sensing applications.Despite its advantages, the ellipsoid-paraboloid method has some limitations. The method requires precise knowledge of the location of the pre-displacement surface, which may not be available in all cases. The optimization process also requires some manual intervention or initial guess for the parameters, which can affect the accuracy of the results.In conclusion, the ellipsoid-paraboloid method has emerged as a valuable tool for surface deformation calculation. Its ability to accurately model complex deformation patterns, robustness to outliers, and computational efficiency make it a promising method for a wide range of geodetic and remote sensing applications.A significant advantage of the ellipsoid-paraboloid method is itsability to estimate the magnitude and direction of surface deformation. The method calculates the three principal strains and their corresponding directions along the ellipsoid, providing a comprehensive analysis of the deformation pattern. This information can be used to understand the geophysical processes behind the deformation, such as tectonic plate movements, volcanic activity, or ground subsidence.Furthermore, the ellipsoid-paraboloid method can also detect and quantify spatially varying deformation patterns within a study area. This is particularly useful for studying the behavior of localized deformation phenomena, such as landslides, sinkholes, or fault zones. The method can be applied to multi-temporal data to observe the temporal evolution of these phenomena and provide insights into their mechanisms and hazards.Another potential application of the ellipsoid-paraboloid method is in deformation monitoring and early warning systems. The method's computational efficiency and accuracy make it suitable for real-time or near-real-time analysis of geodetic data. This can help detect and alert authorities to potential hazards, such as earthquakes or volcanic eruptions, before they cause significant damage.In conclusion, the ellipsoid-paraboloid method has several advantages over traditional surface deformation methods, including its accuracy, flexibility, and efficiency. The method can provide valuable insights into the geophysical processes behind deformation patterns and is a promising tool for a range of geodetic and remote sensing applications. Its potential benefits inhazard monitoring and early warning systems also make it a significant contribution to the field of geodesy and geophysics.Another advantage of the ellipsoid-paraboloid method is its ability to detect and quantify surface deformation at different spatial scales. The method is suitable for analyzing data from a variety of sources, including GPS, InSAR, and terrestrial measurements. This enables researchers to study deformation at local, regional, and global scales, providing a more comprehensive understanding of geophysical processes.One prominent application of the ellipsoid-paraboloid method is in the study of volcanic deformation. The method can help researchers to monitor and analyze surface deformation associated with volcanic activity, providing critical information on the behavior of active volcanoes. By understanding how volcanoes deform over time, researchers can forecast volcanic eruptions and assess the associated hazards. The method has been used to study deformation at several volcanoes worldwide, including Mount St. Helens in the United States and Mount Etna in Italy. Moreover, the ellipsoid-paraboloid method can also be used to study the behavior of fault zones and earthquakes. The method can detect and quantify surface deformation associated with seismic activity, providing insights into the mechanisms behind earthquakes and fault movements. This information is crucial for understanding the risks associated with earthquakes and improving seismic hazard assessments. The method has been used to study deformation associated with several earthquakes worldwide, including the 2010 M8.8 earthquake in Chile and the 2011 M9.0 earthquake in Japan.In summary, the ellipsoid-paraboloid method is a powerful tool for analyzing surface deformation associated with geophysical processes. Its ability to detect and quantify deformation at different spatial scales and sources make it suitable for a wide range of geodetic and remote sensing applications. The method's potentialto improve hazard monitoring and early warning systems further highlights its significance in the field of geodesy and geophysics.Yes, that is correct. The ellipsoid-paraboloid method has many significant applications in geodesy and geophysics, particularly in the study of volcanic deformation, seismic activity, and fault movement. Its ability to analyze data from multiple sources at different spatial scales makes it a valuable tool for monitoring and understanding the behavior of various geophysical processes. The method's potential to improve hazard monitoring and early warning systems is also a critical contribution to the field.。

抛物面

3 a 2
a
0
a
3 a 2
y
3 a 2
a
x
3 平面x a, y a, z a, x y z a 在第一卦限所围立体图 2
z
3 a 2
a
0
.
a
3 a 2
y
3 a 2
a
x
平面x a, y a, z a, x y z
z
3 a 2
3 a 在第一卦限所围立体图 2
4.主截线
1°用z = 0 截曲面
z
Cz 0： 0,0,0 顶点
2°用y = 0 截曲面
两条主抛物线具有相同的顶点,对称轴和开口方向
x 2 2a 2 z，抛物线 C y 0： y 0.
3°用x = 0 截曲面
y 2 2b 2 z，抛物线 Cx 0： x 0.
x2 y2 当a b 时, 2 2 2 z x 2 y 2 2a 2 z , a b
课程《几何学》
例将抛物线
y 2 2 pz : x 0
z
绕它的对称轴旋转
o
y

课程《几何学》
例将抛物线
y 2 2 pz : x 0
z
绕它的对称轴旋转
o
y
x
Cx＝0
y O
Cy＝0
主抛物线
x2 y2 2 2 0 b a z 0
————其为点（0，0，0）
x 2 2a 2 z ————xoz 面上的抛物线 y 0
y 2 2b2 z ———— yoz 面上的抛物线 x 0
有相同的定点（0，0，0）相同的对称轴 z 轴，开口均向z轴正方向

一椭圆抛物面

§6 抛物面例：yoz 面上抛物线()0022>⎩⎨⎧==p x pzy 绕z 轴旋转，所得旋转面为()pz y x 2222=+±，即 ()()z py p x 22222=+。

此曲面称为旋转抛物面，将该曲面推广便有：一椭圆抛物面：1、定义：在直角系下，由方程 z by a x 22222=+ （a,b>0）（1）所表示的图形称为椭圆抛物面；而（1）称为椭圆抛物面的标准方程。

注：在直角系下，由方程y c z a x 22222=+或x cz b y 22222=+所表示的图形也是椭圆抛物面。

2、性质和形状：（i ）对称性：椭圆抛物面（1）关于z 轴，z y 面，z x 面对称，在ch6中，我们将会知道椭圆抛物面无对称中心。

（ii ）有界性：由（1）知z=⎪⎪⎭⎫⎝⎛+222221b y a x ≧0，∴椭圆抛物面（1）位于y x 面的上方，且为无界的。

（iii ）与坐标轴的交点及与坐标面的交线（1）与三坐标轴均交于原点——顶点；（1）与三坐标面交于 ⎩⎨⎧=0)1(x ，⎩⎨⎧=0)1(y ，⎩⎨⎧=0)1(z ，亦即⎩⎨⎧==0222x z b y （2），⎩⎨⎧==0222y z a x （3），⎪⎩⎪⎨⎧==+02222z b y a x （4）（2），（3）均为抛物线，其顶点均为原点，其开口方向均指z 轴正向。

对称轴均为z轴；而（4）为原点。

（iv ）与平行于坐标面平面的交线：首先，（1）与平行于y x 面的平面交于⎩⎨⎧=kz )1( ，即⎪⎩⎪⎨⎧==+k z k b y a x 22222 （()0≥k ）（5）当0=k 时，（5）为原点；当0>k 时，（5）为椭圆，其顶点为（0，±b k 2，k ）∈（2）, （±a k 2，0，k ）∈（3）.可见，椭圆抛物面（1）是由y x 面上方的一系列“平行”椭圆构成，这些椭圆的顶点在抛物线（2）和（3）上变化。

椭圆抛物面的参数方程

椭圆抛物面的参数方程
椭圆抛物面是一种经典三维几何图形，从数学的角度来看，它可以用参数方程来表示，它可以用于许多不同的应用场景，包括在解释某些物理学问题以及计算空间中实体的位置和几何信息。

本文将介绍椭圆抛物面的参数方程，以及它在建模和解释物理学问题中的应用。

椭圆抛物面是一种单个轴对称几何体，它具有两个主要轴由中心点单个点穿过，它可以平面截2个抛物线。

因此，它可以用参数方程来表示，其形式为：
z = ax2 + by2 + cxy + dx + ey + f
在这里，a，b，c，d，e，f是实数系数，x，y，z是空间坐标。

其中，a，b和c是椭圆抛物面的形式系数，它们可以决定椭圆抛物面的几何形状，它们必须满足以下条件：
在实际应用中，椭圆抛物面可以用来建模和解释物理学问题。

例如，当物体处于容易受到反作用力的状态时，它的运动轨迹可以用椭圆抛物面的参数方程来表示，例如一个位于重力场中的固体物体的运动轨迹可以用椭圆抛物面的参数方程来表示。

此外，椭圆抛物面的参数方程还可以用来计算空间中的实体的位置和几何信息。

例如，可以使用椭圆抛物面的参数方程来计算一个物体在某些定义好的空间中的位置，这可以使用微分几何中的参数方程组来实现。

另外，椭圆抛物面的参数方程也可以用于计算多维几何体的表面积、体积以及法向量。

例如，可以使用椭圆抛物面的参数方程来计算
一个球体的表面积，这可以使用勒让德积分来实现。

总之，椭圆抛物面的参数方程可以用来描述和建模某种特定几何体，也可以用来计算几何图形的位置、表面积、体积、以及向量。

它可以用于许多不同的应用场景，例如计算物体在受到反作用力时的运动轨迹，计算空间中的实体的位置等等。

椭圆抛物面

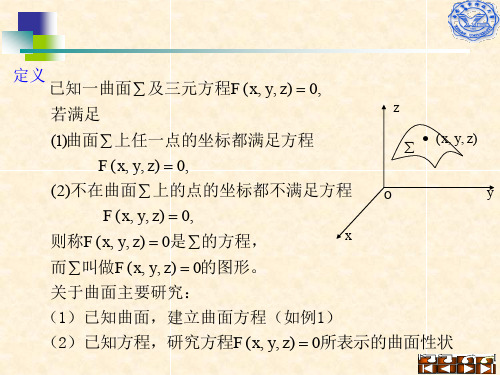
三、柱面例7 在空间直角坐标系中，方程x2 y2 R2表示怎样的曲面？
解：在xoy面上,x2 y2 R2表示圆。显然直线L上点M (x, y, z)满足
x2 y2 R2 故曲面:x2 y2 R2称为圆柱面圆x2 y2 R2 ---准线， L 母线（平行于z轴）定义平行于定直线，并沿定曲线C移动的直线L形成的轨迹叫做柱面定曲线C 准线, 动直线L 母线
绕z轴旋转的曲面方程为 f ( x2 y2 , z) 0
曲线C : f (x, y) 0绕x轴旋转的曲面方程为 f (x, y2 z2 ) 0
绕y轴旋转的曲面方程为 f ( x2 z2 , y) 0
例5 yoz平面上直线L : z cot y绕z旋转的曲面方程：
| OM | 1 | AM | 2
x2 y2 z2 1 (x 2）2 （y - 3）2 (z 4)2
2
所求方程为 x2 y2 z2 4 x 2 y 8 z 29 0
3
3
即 (x 2）2 （y 1）2 (z 4)2 ( 2 39)2
解决方法：采用截痕法，即用坐标面及平行于坐标面的平面去截曲面，观察所的截线的形状，从而确定曲面图形。
下面讨论几个特殊的二次曲面
一、椭球面
方程
：x 2
a2

y2 b2

z2 c2
1,
(a 0,b 0, c 0)
首先： x a,
y b, z c
其次：与 xoy 坐标面的交线（截痕）
z
0
x
z y
0
x-y=0 x

椭球面双曲面抛物面

椭球面双曲面抛物面§7.9 二次曲面三元二次方程所表示的曲面称着二次曲面。

相应地，将平面叫做一次曲面。

一般的三元方程F x y z(,,)=0所表示的曲面形状，已难以用描点法得到，那未怎样了解它的形状呢?利用坐标面或用平行于坐标面的平面与曲面相截，考察其交线( 即截痕)的形状，然后加以综合，从而了解曲面的全貌，这种方法叫做截痕法。

下面，我们用截痕法来讨论几个特殊的二次曲面。

一、椭球面由方程x aybzc2222221++=(1)所表示的曲面叫做椭球面。

1、由(1)可知：这表明：椭球面(1)完全包含在以原点为中心的长方体内，这长方体的六个面的方程为其中常数a b c,,叫做椭球面的半轴。

2、为了进一步了解这一曲面的形状，先求出它与三个坐标面的交线这些交线都是椭圆。

3、用平行于xoy 坐标面的平面z z z c =≤11()去截椭球面，其截痕(即交线)为这是位于平面 z z =1内的椭圆，它的两个半轴分别等于 a c c z 212-与b c c z 212-，其椭圆中心均在z 轴上，当z 1由0渐增大到c 时，椭圆的截面由大到小，最后缩成一点。

4、以平面 y y y b =≤11()或 x x x a =≤11()去截椭球面分别可得与上述类似的结果。

综上讨论知：椭球面(1)的形状如图所示。

5、特别地，若a b =，而a c ≠，则 (1) 变为这一曲面是xoz 坐标面上的椭圆 x a z c 22221+=绕z 轴旋转而成的旋转曲面，因此，称此曲面为旋转椭球面。

它与一般椭球面不同之处在于如用平面z z z c =≤11()与旋转椭球面相截时，所得的截痕是圆心在z 轴上的圆其半径为a c c z 212-。

6、若 a b c ==，那未(1)变成这是球心在原点，半径为a 的球面。

二、抛物面由方程x p y q z p q 2222+=()与同号 (2) 所表示的曲面叫做椭圆抛物面。

设p q >>00,，用截痕法来考察它的形状1、用坐标面xoy z ()=0与该曲面相截，其截痕为2、用平行于xoy 坐标面的平面z z z =>110()与该曲面相截，所得截痕为这是中心在z 轴，半轴分别为21pz 与 21qz 的椭圆。

4.6抛物面

《椭球双曲抛物面》PPT课件

椭圆抛物面

04-2.抛物面PPT

最新46抛物面汇总

§4.6 抛物面

4.4-4.6 椭球面、双曲面、抛物面(课堂PPT)

椭圆抛物面方程

椭球面 双曲面 抛物面

ch4-4椭球面双曲面抛物面

表面变形计算的椭圆抛物面法

抛物面

一椭圆抛物面

椭圆抛物面的参数方程

椭圆抛物面

椭球面双曲面抛物面

椭球面双曲面抛物面