自动控制原理稳态误差PPT课件
合集下载
自动控制原理--控制系统的稳态误差

不能采用拉氏变换终值定理的缘故。因此,利用式(356)来计算稳态误差是普遍成立的,而利用拉氏变换终 值定理的式(3-60)求稳态误差时,应注意使用条件。
二、给定作用下的稳态误差
设系统开环传递函数为:
其中K为开环增益,v为系统中含有的积分环节数 对应于v=0,1,2的系统分别称为0型,Ⅰ型和Ⅱ型系统。
稳态误差的定义
• 误差定义为输入量与反馈量的差值
• 稳态误差为误差的稳态值 • 如果需要可以将误差转换成输出量的量纲
• 稳态误差不仅与其传递函数有关,而且与输入 信号的形式和大小有关。其终值为:
稳态误差计算
误差的定义:
E(s) R(s) B(s)
lim ess ()
( L1[ E ( s )])
(1)系统是稳定的; (2)所求信号的终值要存在。
例27 已知系统如图3-36所示。当输入信号 rt ,1干t扰信 号 n时t,求1t系 统的总的稳态误差。
Ns
Rs
Es
K1
K2 s
Y s
Bs
图3-36 例3-15系统结构图
解:⑴对于本例,只要参数 K1, K均2大于零,则系统一定是稳 定的。
⑵在r t 信1t号 作用下(此时令 n)t 0
s0
s0
1 s K1K2
K2 s K1K2
1 s
1 K1
由以上的分析和例题看出,稳态误差不仅与系统本身
的结构和参数有关,而且与外作用有关。利用拉氏变换
的终值定理求得的稳态误差值或者是零,或者是常数,
或者是无穷大,反映不出它随时间的变化过程。另外,
对于有些输入信号,例如正弦函数,是不能应用终值定
最后由终值定理求得稳态误差 ess
ess
二、给定作用下的稳态误差
设系统开环传递函数为:
其中K为开环增益,v为系统中含有的积分环节数 对应于v=0,1,2的系统分别称为0型,Ⅰ型和Ⅱ型系统。
稳态误差的定义
• 误差定义为输入量与反馈量的差值
• 稳态误差为误差的稳态值 • 如果需要可以将误差转换成输出量的量纲
• 稳态误差不仅与其传递函数有关,而且与输入 信号的形式和大小有关。其终值为:
稳态误差计算
误差的定义:
E(s) R(s) B(s)
lim ess ()
( L1[ E ( s )])
(1)系统是稳定的; (2)所求信号的终值要存在。
例27 已知系统如图3-36所示。当输入信号 rt ,1干t扰信 号 n时t,求1t系 统的总的稳态误差。
Ns
Rs
Es
K1
K2 s
Y s
Bs
图3-36 例3-15系统结构图
解:⑴对于本例,只要参数 K1, K均2大于零,则系统一定是稳 定的。
⑵在r t 信1t号 作用下(此时令 n)t 0
s0
s0
1 s K1K2
K2 s K1K2
1 s
1 K1
由以上的分析和例题看出,稳态误差不仅与系统本身
的结构和参数有关,而且与外作用有关。利用拉氏变换
的终值定理求得的稳态误差值或者是零,或者是常数,
或者是无穷大,反映不出它随时间的变化过程。另外,
对于有些输入信号,例如正弦函数,是不能应用终值定
最后由终值定理求得稳态误差 ess
ess
自动控制原理课件第三章PPT课件

第31页/共66页
研究输出曲线的变化速 率对(: 3-2-3)式求导:
dy(t ) dt
—1
T
t
eT
t 0, y(t) 1 / T
y(t ) 1 et /T (3-2-3)
斜率 y(t) =1/T
1
0.632
0
B
A86.5% 98.2% 63.2 95% 99.3% %
T 2T 3T 4T 5T t
2、调节时间反映了系统的整体快速性。
3、最大偏差、超调量和衰减比反映了系 统的平稳性。
4、稳态误差反映了系统的调节精度。 第21页/共66页
动态性能指标定义1
h(t)
A
超调量σ% =
A B
100%
峰值时间tp B
上升 时间tr
调节时间ts
t
第22页/共66页
动c t 态性能指标定义1
Step Response
第5页/共66页
一、典型输入信号
R
1.阶跃输入信号
t
阶跃输入信号可表示为:
R
x(t
)
0
t0 t0
R为阶跃信号的幅值,是一常数。R=1时叫做单位阶跃信号,记做1(t),否则记为 R·1(t)。
表示在t=0时刻出现了幅值为R的跳变,是最不利的外作用。常用阶跃函数作为评 价系统动态性能的典型外作用。所以阶跃函数在自动控制系统的分析中起着特别重 要的作用。
总结:
=1/T 1
B
一阶系统单位阶跃响应的02重.63要63性.A28%质6.59:5%9%8.299.3%
%
0 T 2T 3T 4T 5T t
1、经过一倍时间常数,即t=T时,系统从0
上升到稳态值的63.2%。
研究输出曲线的变化速 率对(: 3-2-3)式求导:
dy(t ) dt
—1
T
t
eT
t 0, y(t) 1 / T
y(t ) 1 et /T (3-2-3)
斜率 y(t) =1/T
1
0.632
0
B
A86.5% 98.2% 63.2 95% 99.3% %
T 2T 3T 4T 5T t
2、调节时间反映了系统的整体快速性。
3、最大偏差、超调量和衰减比反映了系 统的平稳性。
4、稳态误差反映了系统的调节精度。 第21页/共66页
动态性能指标定义1
h(t)
A
超调量σ% =
A B
100%
峰值时间tp B
上升 时间tr
调节时间ts
t
第22页/共66页
动c t 态性能指标定义1
Step Response
第5页/共66页
一、典型输入信号
R
1.阶跃输入信号
t
阶跃输入信号可表示为:
R
x(t
)
0
t0 t0
R为阶跃信号的幅值,是一常数。R=1时叫做单位阶跃信号,记做1(t),否则记为 R·1(t)。
表示在t=0时刻出现了幅值为R的跳变,是最不利的外作用。常用阶跃函数作为评 价系统动态性能的典型外作用。所以阶跃函数在自动控制系统的分析中起着特别重 要的作用。
总结:
=1/T 1
B
一阶系统单位阶跃响应的02重.63要63性.A28%质6.59:5%9%8.299.3%
%
0 T 2T 3T 4T 5T t
1、经过一倍时间常数,即t=T时,系统从0
上升到稳态值的63.2%。
自动控制理论ppt3
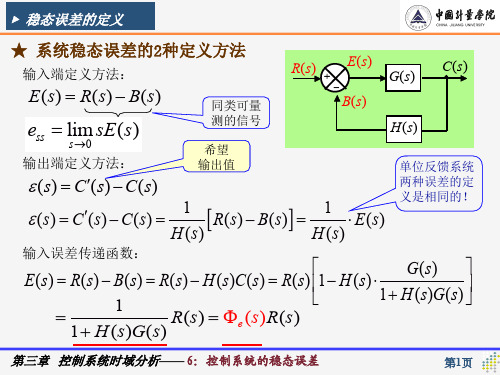
r(t) Rr 1(t)
-
G2 (s)
G2 (s) K2 s(1 T2 s)
C ( s)
G1 (s)
essr lim sER ( s) lim
s Rr s lim s 0 K1 K2 1 (1 T1s) s(1 T2 s )
②
sR( s) s 0 1 G ( s )G ( s ) 1 2
G(s) H (s)
K ( j s 1) s
☆ 按积分环节来区分的系统结构:
(T s 1)
i 1 i
j 1 n
0 型: 0 型: 1 型: 2
开环系统串连 积分环节的个 数
第 4页
第三章 控制系统时域分析—— 6:控制系统的稳态误差
▶ 稳态误差与系统结构的关系
第三章 控制系统时域分析—— 6:控制系统的稳态误差
第 2页
▶ 误差传递函数
☆ 例:求右图系统稳态误差
解:①
令 n(t ) 0 ER ( s) er ( s) R( s)
s 0
R(s)
E E N R E ( s( ) s)
+
N (s) n(t) Rn 1(t)
G1 (s)
+ +
按泰勒级数展开
s 0邻域
分别对应 位置、速度、加速度 误差系数
d er (s) 1 er (s) er (0) 1 G( s) ds
2 1 d er (s) s 0 s 2! ds 2
s 0
s
2
1 1 1 2 s s k1 k2 k3
0 0 ess K 1/ K
自动控制原理 第三章 控制系统的时域分析—5稳态误差

2020年9月6日6时59分
2
一、稳态误差的定义
系统的误差e(t)一般定义为输出量的希望值与 实际值之差。系统误差的定义有两种形式: (1)系统误差(从输出端定义) (s) Cr (s) C(s)
Cr(s)为系统输出量的希望值,其定义为E(s)=0时系 统的输出,C(s)为输出量的实际值。
(2)作用误差(从输入端定义)E(s) R(s) B(s) 作用误差就是给定输入R(s)与主反馈信号B(s)之差。
§ 3-6 控制系统的稳态误差
系统的稳态分量反映系统跟踪输入信号的准 确度或抑制扰动信号的能力,用稳态误差描述。在 系统的分析、设计中,稳态误差是一项重要的性能 指标,它与系统本身的结构、参数及外作用的形式 有关,也与元件的不灵敏、零点漂移、老化及各种 传动机械的间隙、摩擦等因素有关。
本章只讨论由于系统结构、参数及外作用等因 素所引起的稳态误差。 ➢ 给定稳态误差(由给定输入引起的稳态误差) ➢ 扰动稳态误差(由扰动输入引起的稳态误差)
式中
1 er (s) 1 G(s)H (s)
称为给定输入作用下系统的误差传递函数。
应用拉氏变换的终值定理可以方便地求出系 统的稳态误差。
2020年9月6日6时59分
9
ess
lim
t
e(t)
lim
s0
sE(s)
lim
s0
s
1
1 G(s)H(s)
R(s)
1
lim s
R(s)
s0 1 G开 (s)
稳态误差可表示为ess1 1 Kp因此,在单位阶跃输入下,给定稳态误差取决于
系统的稳态位置误差系数。
2020年9月6日6时59分
12
对于0型系统,v=0
自动控制原理第9讲(稳态误差)

§3.6
线性系统的稳态误差(2)
§3.6.1 误差与稳态误差
按输入端定义的误差
E ( s ) R( s ) H ( s )C ( s )
按输出端定义的误差
E ( s ) R( s ) C ( s) H ( s)
稳态误差
e ss lim e( t ) e( )
t
§3.6.2 计算稳态误差的一般方法
K 1 (Ts 1) K K1 a s 2 ( s a) v 2 K1 ( s ) 2 s ( s a ) K 1 (Ts 1)
D( s) s 3 as2 K1Ts K1 0
r1 (t ) 2t
1 r2 ( t ) 4t 8 t 2 2
K G 0(s )H 0(s ) v s 1 lim s e(s ) R(s ) lim s R(s ) s 0 s 0 K 1 v G 0(s )H 0(s ) s
1
E(s ) 1 R(s ) 1 G 1(s )H (s )
1
§3.6.3
s 0
静态误差系数法(2)
2
ess 1 0
ess 2 A 8a K K1
ess ess 1 ess 2
8a K1
§3.6.3
静态误差系数法(6)
K s(Ts 1)
例 4 系统结构图如图所示,已知输入 r (t ) At ,求 Gc ( s) ,使稳态误差为零。
G( s ) 解.
K K v 1
s0
A Ka
K a lim s 2 G1 ( s ) H ( s ) lim
s0 s0
K sv2
第8讲控制系统的稳态误差ppt课件

1 2
1 essa Ka
例:某控制系统的结构图为
r(t) 51(t)
10
C(s)
- s2 2s 1
H (s)
试分别求出H(s)=1和H(s)=0.5时,系统的稳态误 差(定义在输出端)。
解:当H(s)=1时,系统的开环传递函数为
G(s)
s2
10 , k 2s 1
10,
0
则系统稳态误差 当H(s)=0.5时,
G(s)H (s)
K1
P(s) Q(s)
1
Q(s) K1P(s) 0
K1
Q(s) P(s)
由于根轨迹上的分离点与特征方程式的重根相对应,
即满足: D(s) Q(s) K1P(s) 0
D(s) Q(s) K1P(s) 0
利用上两式消去K1,可得
P(s)Q(s) P(s)Q(s) 0 以上分析没有考虑K10(且
2、0<K1<0.25 时,两个互异负实根 3、K1=0.25时,s1=s2=-0.5 4、0.25<K1<∞时,s1,2=-0.5±0.5j√4k-1
K1
j
K1=0 -1
K1=0.25 K1=0 -0.5 0
K1
所谓根轨迹图,即以系统根轨 迹0→增∞益时K,1为系参统变闭量环,极当点K在1s由平 面上变化的轨迹。
如果实轴上相邻的开环极点、零点之间存在 根轨迹,则或者无分离点,或者存在成对的分 离点。
m
G(s)H (s)
K1
n
(s
i 1
(s
p
zi ) j)
K1
P(s) Q(s)
,
其中P(s)
m
(s zi ),Q(s)
i 1
《自动控制原理》第三章稳态误差计算(共28张PPT)优秀

kp
K
位置误差
ess
R 1 kp
R
1 K
I
0
II
0
III
0
7
第七页,共28页。
3. 输入作用下稳态误差计算…
(2)斜坡作用下的稳态误差
R
r(t)R,tR(s)s 非过主阻导 尼极点>1:响除应主直导接极收点敛外,的系其统他有闭两环个极不点等2的负实根
速度误差不是速度上存在稳态误差 误差与稳态误差的定义
)
1
R Lims R 输入作用下稳态误差计算…
s0
第二十三页,共28页。 LimsG(s)H(s) K Lims 临界稳定:若系统的响应随时间的推移而趋于常值或等幅正弦振荡
开环系统的静态误差s系0数Kp,Kv,Ka;
s0
输入作用下稳态误差计算…
kvL s 0ism G (s)H(s), essk R v
(1)阶跃作用下的稳态误差
r(t)R1(t),R(s)R s
ess
Lim sR(s) s0 1G(s)H(s)
Lims1R(s)
s0
K Lims
s0
1
R LimG(s)H(s)
Lims R
s0
K Lims
s0
s0
kpL s 0iG m (s)H (s), ess1 R kp
系统 型别
0
静态位置 误差系数
18
第十八页,共28页。
19
第十九页,共28页。
主导极点: 如果在所有的闭环极点中,距虚轴
最近的极点周围没有闭环零点,而其他闭环极点 又远离虚轴,那么距虚轴最近的极点在系统响应 过程中起主导作用,这样的闭环极点称为主导极 点 非主导极点:除主导极点外的其他闭环极点
K
位置误差
ess
R 1 kp
R
1 K
I
0
II
0
III
0
7
第七页,共28页。
3. 输入作用下稳态误差计算…
(2)斜坡作用下的稳态误差
R
r(t)R,tR(s)s 非过主阻导 尼极点>1:响除应主直导接极收点敛外,的系其统他有闭两环个极不点等2的负实根
速度误差不是速度上存在稳态误差 误差与稳态误差的定义
)
1
R Lims R 输入作用下稳态误差计算…
s0
第二十三页,共28页。 LimsG(s)H(s) K Lims 临界稳定:若系统的响应随时间的推移而趋于常值或等幅正弦振荡
开环系统的静态误差s系0数Kp,Kv,Ka;
s0
输入作用下稳态误差计算…
kvL s 0ism G (s)H(s), essk R v
(1)阶跃作用下的稳态误差
r(t)R1(t),R(s)R s
ess
Lim sR(s) s0 1G(s)H(s)
Lims1R(s)
s0
K Lims
s0
1
R LimG(s)H(s)
Lims R
s0
K Lims
s0
s0
kpL s 0iG m (s)H (s), ess1 R kp
系统 型别
0
静态位置 误差系数
18
第十八页,共28页。
19
第十九页,共28页。
主导极点: 如果在所有的闭环极点中,距虚轴
最近的极点周围没有闭环零点,而其他闭环极点 又远离虚轴,那么距虚轴最近的极点在系统响应 过程中起主导作用,这样的闭环极点称为主导极 点 非主导极点:除主导极点外的其他闭环极点
第9讲-控制系统的稳态误差

sE(s)的极点不全部分布在[S]平面的左半部
终值定理
六、动态误差系数方法
前面研究的稳态误差主要讨论的是典型输入信号下的稳 态误差,对于部分非典型信号(如正弦信号)下,求稳态误 差的极限计算方法可能不能用。另外,我们可能还需要了解 输出响应在进入稳态(t>ts)后变化的规律如何。这些问题用 前面介绍的方法都不方便。因此,下面再介绍一种适应范围 更广泛的方法:动态误差系数法(又称广义误差系数法)。
它零、极点对分类没有影响。下面分析系统在不同典
型输入信号作用下的稳态误差。
1、单位阶跃输入时的稳态误差
对于单位阶跃输入,R(s)=1/s,系统的稳态误差为
令
称 Kp为稳态位置误差系数。
稳态误差可表示为
因此,在单位阶跃输入下,给定稳态误差决定于 系统的位置误差系数。
(1)对于0型系统, (2)对于1型系统(或高于1型的系统)
一
从系统输出端定义的稳态误差,概念清晰,物
理意义明确,也符合基本定义,但在实际系统中
无法测量,因而,一般只有数学意义。而从系统
输入端定义的稳态误差,它在系统中是可以测量
的,因而具有实用性。对于单位反馈系统,要求
输出量C(t)的变化规律与给定输入r(t)的变化规
律一致,所以给定输入r(t)也就是输出量的希望
当 差又是多少?
时,上例的稳态误
因为0型系统在速度输入和加速度输入下的稳态误差 为无穷大,根据叠加原理,ess=∞
稳态误差小结: 1.公式小结
(1)基本公式
(1)
(2)
给
定
输
(3) 入
单
独
作
(4)
用 时
(5)
扰动单独作用时
终值定理
六、动态误差系数方法
前面研究的稳态误差主要讨论的是典型输入信号下的稳 态误差,对于部分非典型信号(如正弦信号)下,求稳态误 差的极限计算方法可能不能用。另外,我们可能还需要了解 输出响应在进入稳态(t>ts)后变化的规律如何。这些问题用 前面介绍的方法都不方便。因此,下面再介绍一种适应范围 更广泛的方法:动态误差系数法(又称广义误差系数法)。
它零、极点对分类没有影响。下面分析系统在不同典
型输入信号作用下的稳态误差。
1、单位阶跃输入时的稳态误差
对于单位阶跃输入,R(s)=1/s,系统的稳态误差为
令
称 Kp为稳态位置误差系数。
稳态误差可表示为
因此,在单位阶跃输入下,给定稳态误差决定于 系统的位置误差系数。
(1)对于0型系统, (2)对于1型系统(或高于1型的系统)
一
从系统输出端定义的稳态误差,概念清晰,物
理意义明确,也符合基本定义,但在实际系统中
无法测量,因而,一般只有数学意义。而从系统
输入端定义的稳态误差,它在系统中是可以测量
的,因而具有实用性。对于单位反馈系统,要求
输出量C(t)的变化规律与给定输入r(t)的变化规
律一致,所以给定输入r(t)也就是输出量的希望
当 差又是多少?
时,上例的稳态误
因为0型系统在速度输入和加速度输入下的稳态误差 为无穷大,根据叠加原理,ess=∞
稳态误差小结: 1.公式小结
(1)基本公式
(1)
(2)
给
定
输
(3) 入
单
独
作
(4)
用 时
(5)
扰动单独作用时
北京科技大学《自动控制原理》课件-稳定性与稳态误差

1)当平衡态的任意小邻域内不存在系统的别的平 衡态时,称此平衡态为孤立的平衡态。 2) 对于线性定常系统当A为非奇异矩阵式,平衡 状态唯一,当A为奇异时,则会有无穷多个。
3) 稳定性问题都是相对于某个平衡状态而言的。
4) 如果一个系统有多个平衡点。由于每个平衡
a
点处系统的稳定性可能是不同的。
4.2 线性系统稳定性的基本概念
行。从而完成劳斯表的排列。
①关于原点对称的根可以通过求解这个辅助方程式得到, 而且其根的数目总是偶数的。
②若劳斯表第一列中系数的符号有变化,其变化的次数就 论 结 等于该方程在S右半平面上根的数目,相应的系统为不稳定。
③如果第一列上的元素没有符号变化,则表示该方程中有 共轭纯虚根存在,相应的系统为临界稳定。
系统稳态 误差定义
第一 方法
第二 方法
线性 非线性
系统稳态 误差计算
4.1 引子
A.Lyapunov(1857-1918),俄国 数学家(Chebyshev 的学生, Markov的同学),在他的博 士论文中,Lyapunov系统地研 究了由微分方程描述的一般运 动的稳定性问题,建立了著名 的Laypunov方法,他的工作 为现代控制及非线性控制奠定 基础。
如果第一列上面的系数与下面的系数符号相同,则表
示该方程中有一对共轭虚根存在,相应的系统为临界稳 定。
4.3线性定常系统稳定性的代数判据
例4.3-2 已知系统的闭环特征方程式为
S 3 2S 2 S 2 0
试判别相应系统的稳定性。
解: 列劳斯表 S 3
1
1
S2
2
2
S1
0( )
S0
2
由于表中第一列 上面元素的符号与其下面元素的符号相同,
3) 稳定性问题都是相对于某个平衡状态而言的。
4) 如果一个系统有多个平衡点。由于每个平衡
a
点处系统的稳定性可能是不同的。
4.2 线性系统稳定性的基本概念
行。从而完成劳斯表的排列。
①关于原点对称的根可以通过求解这个辅助方程式得到, 而且其根的数目总是偶数的。
②若劳斯表第一列中系数的符号有变化,其变化的次数就 论 结 等于该方程在S右半平面上根的数目,相应的系统为不稳定。
③如果第一列上的元素没有符号变化,则表示该方程中有 共轭纯虚根存在,相应的系统为临界稳定。
系统稳态 误差定义
第一 方法
第二 方法
线性 非线性
系统稳态 误差计算
4.1 引子
A.Lyapunov(1857-1918),俄国 数学家(Chebyshev 的学生, Markov的同学),在他的博 士论文中,Lyapunov系统地研 究了由微分方程描述的一般运 动的稳定性问题,建立了著名 的Laypunov方法,他的工作 为现代控制及非线性控制奠定 基础。
如果第一列上面的系数与下面的系数符号相同,则表
示该方程中有一对共轭虚根存在,相应的系统为临界稳 定。
4.3线性定常系统稳定性的代数判据
例4.3-2 已知系统的闭环特征方程式为
S 3 2S 2 S 2 0
试判别相应系统的稳定性。
解: 列劳斯表 S 3
1
1
S2
2
2
S1
0( )
S0
2
由于表中第一列 上面元素的符号与其下面元素的符号相同,
自动控制原理:3-3 控制系统的稳态误差

ans=
2.0000
-2.0000
-0.0000+1.0000i
-0.0000-1.0000i -0.5000+0.8660i -0.5000-0.8660i
由于有1个正实部根的特征根, 所以,系统不稳定。
《自动控制原理》国家精品课程 浙江工业大学自动化研究所 14
3.4.2 MATLAB求控制系统的单位阶跃响应
有差系统 无差系统
准确跟踪 系统
§3-3 控制系统的稳态误差
2.单位斜坡输入 xr (t) t
Xr
(s)
1 s2
e lim s0
sE
(s)
lim
s0
s 1
Xr (s)
WK s
lim
s0
1
s WK
s
1 s2
1
lim
s0
sWK
s
若令
Kv
lim
s0
sWK
s
则 e 1
Kv
速度 误差系数
0型系统 Ⅰ型系统 Ⅱ型以上系统
当输入r(t) 为单位加速度信号时,为使系统的 静态误差为零,试确定前馈环节的参数a 和b 。
lim
s0
sN1X r s
sN K
稳态误差取决于Kk与N,而N越高稳态精度(准 确性)越高,稳定性越差。
二、典型输入情况下系统的给定稳态误差及误差系数
1.单位阶跃输入
xr
t
1 0
t0 t0
1 X r (s) s
§3-3 控制系统的稳态误差
e
lim
s0
sE
(s)
lim
s0
s 1
Xr (s)
WK s
自动控制原理第8章 误差分析

在一般情况下,分子阶次为m,分母阶 次为n的开环传递函数可表示为
G( s)H (s)
K ( i s 1) s (T j s 1)
j 1 i 1 n
m
式中,K为开环增益;τi和Tj为时间常数 ;υ为开环系统在s平面坐标原点上的极 点的重数。也是系统积分环节的个数。
2017/6/16
第8章 误差分析
3
引 言
误差的分类 给定稳态误差(由给定输入引起的稳态 误差) 对于随动系统,给定输入变化,要 求系统输出量以一定的精度跟随输入量的 变化,因而用给定稳态误差来衡量系统的 稳态性能。 扰动稳态误差(由扰动输入引起的稳态 误差) 对恒值系统,给定输入通常是不变 的,需要分析输出量在扰动作用下所受到 的影响,因而用扰动稳态误差来衡量系统 的稳态性能。
2 t /T e ( t ) T e 其中, ts
随时间增长逐渐衰减至 ess (t) T( t T) 表明稳态误差 ess 零; (2)当 r(t ) sin t 时, R( s) / ( s2 2 ) s T 1 由于 E(s)
1 ( s )( s 2 2 ) T T 2 2 1 s 1 T
s T 2 3 1 2 2 T 1 s2 2 T 2 2 1 )
T T 2 2 cos t 2 2 sin t 2 2 T 1 T 1
2017/6/16
第8章 误差分析
11
8.1 稳态误差的基本概念
2017/6/16
第8章 误差分析
9
8.1 稳态误差的基本概念
【例8-1】设单位反馈系统的开环传递函 数为 G( s) 1 / Ts ,输入信号分别为 r(t ) t 2 / 2以及 r (t ) sin t ,试求控制 系统的稳态误差。 2 r ( t ) t / 2 时, R( s) 1/ s3 ,求得 解:(1)当
G( s)H (s)
K ( i s 1) s (T j s 1)
j 1 i 1 n
m
式中,K为开环增益;τi和Tj为时间常数 ;υ为开环系统在s平面坐标原点上的极 点的重数。也是系统积分环节的个数。
2017/6/16
第8章 误差分析
3
引 言
误差的分类 给定稳态误差(由给定输入引起的稳态 误差) 对于随动系统,给定输入变化,要 求系统输出量以一定的精度跟随输入量的 变化,因而用给定稳态误差来衡量系统的 稳态性能。 扰动稳态误差(由扰动输入引起的稳态 误差) 对恒值系统,给定输入通常是不变 的,需要分析输出量在扰动作用下所受到 的影响,因而用扰动稳态误差来衡量系统 的稳态性能。
2 t /T e ( t ) T e 其中, ts
随时间增长逐渐衰减至 ess (t) T( t T) 表明稳态误差 ess 零; (2)当 r(t ) sin t 时, R( s) / ( s2 2 ) s T 1 由于 E(s)
1 ( s )( s 2 2 ) T T 2 2 1 s 1 T
s T 2 3 1 2 2 T 1 s2 2 T 2 2 1 )
T T 2 2 cos t 2 2 sin t 2 2 T 1 T 1
2017/6/16
第8章 误差分析
11
8.1 稳态误差的基本概念
2017/6/16
第8章 误差分析
9
8.1 稳态误差的基本概念
【例8-1】设单位反馈系统的开环传递函 数为 G( s) 1 / Ts ,输入信号分别为 r(t ) t 2 / 2以及 r (t ) sin t ,试求控制 系统的稳态误差。 2 r ( t ) t / 2 时, R( s) 1/ s3 ,求得 解:(1)当
自动控制原理稳定性和误差PPT课件

1
s11 0.5
s10 1
劳斯表中第一列元素不全为正,且第一列元素符号 改变了一次,故系统在s1 右半平面有一个根。因此,系 统在垂直线 s = 1的右边有一个根。
14
第14页/共30页
3.6 稳态误差的定义及一般计算公式
3.6.1 误差的基本概念
1. 误差的定义
R(s)
E(s)
C(s)
误差的定义有两种:
共轭复数根)。对此情况,可作如下处理:
10
第10页/共30页
用全为零上一行的系数构成一个辅助方程,对辅助 方程求导,用所得方程的系数代替全零行,继续劳斯表。
s4 1
3
2
s3 1
1
s2 2
2 F(s) = 2s2+ 2
s1 4
F(s)= 4s
s0 2
由于劳斯表中第一列元素的符号改变了两次,∴系
统有两个正根,系统不稳定。关于对原点对称的根,
可解辅助方程求出。得 s1=1 和 s2= 1 。 对本例题,可用长除法求出另二个根,分别为
s3=1 和 s4= 2 。
11
第11页/共30页
(2)分析参数变化对稳定性的影响
例3-8 已知系统结构图如下,试确定使系统稳定时K 的取值范围。
R(s)
+﹣
K
C(s)
s(s+1)(s+2)
解:系统特征方程式 s3 + 3s2 + 2s + K = 0
解:劳斯表 s4 1
35
s3
2
4
s2 1 5
s1 6
s0
5
第一列元素 符号改变了2次,∴系统不稳定,且s 右半平 面有2个根。
3.6 控制系统的稳态误差.ppt

time
10
单位抛物线响应曲线
er(t)→∞
r(t) y(t)
time
11
不同G2时的单位阶跃响应曲线
r(t)
G2
0.5s 1 s2 s 1
G2
2 2s
1
y(t)
G2
s
1
(原模型) 1
稳态误差都为零
time
12
系统的类型与误差系数
m
K(is 1)
设 Gk ( s )
i1 n
s ( Ti s 1 )
esr
lim
s0
sEr (
s
)
lim
s0
A s2Gk (
s
)
K(is 1)
Gk ( s )
i1 n
s ( Ti s 1 )
i1
加速度(或抛物线)误差系数:K a
lim
s0
s 2Gk (s
)
系统型 1 Ka 0
系统为2 型 Ka K
系统型 3 Ka
R(s) Er(s)
Y(s)
G1(s)
3s s( s
4 1)
s2 4s 4 闭环稳定。
R(s) Er(s)
Y(s)
G1(s)
G 2(s)
-
H(s)
该系统为1型 情况(1)无稳态误差
情况(2):R
1 ,
s2
Er ( s )
1 1 Gk(s)
R( s )
s( s 1 ) s2 4s 4
•
1 s2
esr(t)
lim
Y(s)
G1(s)
G 2(s)
-
H(s)
j 稳定 不稳定 区域 区域
10
单位抛物线响应曲线
er(t)→∞
r(t) y(t)
time
11
不同G2时的单位阶跃响应曲线
r(t)
G2
0.5s 1 s2 s 1
G2
2 2s
1
y(t)
G2
s
1
(原模型) 1
稳态误差都为零
time
12
系统的类型与误差系数
m
K(is 1)
设 Gk ( s )
i1 n
s ( Ti s 1 )
esr
lim
s0
sEr (
s
)
lim
s0
A s2Gk (
s
)
K(is 1)
Gk ( s )
i1 n
s ( Ti s 1 )
i1
加速度(或抛物线)误差系数:K a
lim
s0
s 2Gk (s
)
系统型 1 Ka 0
系统为2 型 Ka K
系统型 3 Ka
R(s) Er(s)
Y(s)
G1(s)
3s s( s
4 1)
s2 4s 4 闭环稳定。
R(s) Er(s)
Y(s)
G1(s)
G 2(s)
-
H(s)
该系统为1型 情况(1)无稳态误差
情况(2):R
1 ,
s2
Er ( s )
1 1 Gk(s)
R( s )
s( s 1 ) s2 4s 4
•
1 s2
esr(t)
lim
Y(s)
G1(s)
G 2(s)
-
H(s)
j 稳定 不稳定 区域 区域
6控制系统的稳态误差ppt课件

r(t) 1(t) t 1 t 2 2
作稳定性分析及误差分析。
R(s) +-
K1(s 1)
Km C(s) s2 (Tms 1)
32
解: (1) 稳定性分析
当 K1 0, Km 0, Tm
系统稳定
33
解: (1) 稳定性分析
当 K1 0, Km 0, Tm
系统稳定
(2) 稳态误差
m
i1
K(is 1)
G(s)H(s)
i1 nv
sv (Tis 1)
V=0
e ssp
1 1 Kp
1 1 K
i1
m
K(is 1)
Kv
lim sG(s)H(s)
s0
lim s
s0
i1 n
0
(Tis 1)
i1
e ssv
1 Kv
m
K(is 1)
Ka
lim s2G(s)H(s) lim s2
s0
s0
e
(0)
' e
(0)s
1 2!
'' e
(0)s 2
E(s)
e
(s)R(s)
e
(0)R(s)
' e
(0)sR(s)
1 2!
'' e
(0)s 2 R (s)
•在s=0的邻域t的邻域
e ss
lim e(t)
t
e
(0)r(t
)
' e
(0)r'
(t)
1 2!
'' e
(0)r'
'
(t
)
1 r(t) 1 r'(t) 1 r''(t)
作稳定性分析及误差分析。
R(s) +-
K1(s 1)
Km C(s) s2 (Tms 1)
32
解: (1) 稳定性分析
当 K1 0, Km 0, Tm
系统稳定
33
解: (1) 稳定性分析
当 K1 0, Km 0, Tm
系统稳定
(2) 稳态误差
m
i1
K(is 1)
G(s)H(s)
i1 nv
sv (Tis 1)
V=0
e ssp
1 1 Kp
1 1 K
i1
m
K(is 1)
Kv
lim sG(s)H(s)
s0
lim s
s0
i1 n
0
(Tis 1)
i1
e ssv
1 Kv
m
K(is 1)
Ka
lim s2G(s)H(s) lim s2
s0
s0
e
(0)
' e
(0)s
1 2!
'' e
(0)s 2
E(s)
e
(s)R(s)
e
(0)R(s)
' e
(0)sR(s)
1 2!
'' e
(0)s 2 R (s)
•在s=0的邻域t的邻域
e ss
lim e(t)
t
e
(0)r(t
)
' e
(0)r'
(t)
1 2!
'' e
(0)r'
'
(t
)
1 r(t) 1 r'(t) 1 r''(t)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例 2 系统结构图如图所示,求 r(t)分别为A·1(t), At, At2/2时系统的稳态误差。
解. e(s)E R((ss))s(T s(T s1 s)1 )K s(T s1) A
r(t)A1(t) es1 sls i0m ss(T s1)Ks0
r(t)At
s(T s1) A A es2 sls i0m ss(T s1)Ks2K
(1)判定系统的稳定性 (2)求误差传递函数
E(s)
E(s)
e(s)R(s), en(s)N(s)
(3)用终值定理求稳态误差 e s s l s 0 i s m e ( s ) R ( s ) e ( s n ) N ( s )
§3.6.2
计算稳态误差的一般方法 (1)
例1 系统结构图如图所示,已知 r(t)=n(t)=t,求系统的稳态误差。
(1)判定稳定的必要条件 ai 0
(2)劳斯判据 (3)劳斯判据特殊情况的处理 (4)劳斯判据的应用(判定稳定性,确定稳定的参数范围)
3
劳斯判据的应用
(1)、判断稳定性,确定正根的个数 (2)、确定使系统稳定的参数的范围 (3)、判断系统的相对稳定性
例1 某单位反馈系统的开环零、极点分布如图所示,判定系 统能否稳定,若能稳定,试确定相应增益K的范围。 解 依题意有
s(T s1)
e ss l s n 0 is m e( s n )N ( s ) l s 0 is m ( T n s 1 K ) n s s ( ( T T 1 1 ) ) s s K s 1 2 K K n
essessressn1KKn
§3.6.2
计算稳态误差的一般方法 (2)
§3.6
线性系统的稳态误差(2)
§3.6.1 误差与稳态误差
按输入端定义的误差 E (s) R (s) H (s)C (s)
按输出端定义的误差
E(s) R(s) C(s) H(s)
稳态误差
静态误差:esslt i m e(t)e()
动态误差:误差中的稳态分量 e s ( t )
§3.6.2 计算稳态误差的一般方法
s3
1
23
s2
37 10K061
s1
91210K0 37
0
K9.12
s 0 10K061
K0.61
§3.5
线性系统的稳定性分析
问题讨论:
(1) 系统的稳定性是其自身的属性,与输入类型,形式无关。 (2) 闭环稳定与否,只取决于闭环极点,与闭环零点无关。
( s ) K ( * s ( s 1 z ) 1 s ) s ( ( 2 z ) 2 ) ( s ( s n z ) m ) s C 1 1 s C 2 2 s C n n
k ( t) C 1 e 1 t C 2 e 2 t C n e n t
闭环零点影响系数Ci ,只会改变动态性能。 闭环极点决定稳定性,也决定模态,同时影响稳定性和动态性能。
(3) 闭环系统的稳定性与开环系统稳定与否无直接关系。
自动控制原理 态误差(1)
概述
稳态误差是系统的稳态性能指标, 是对系统控制精度的度量。 对稳定的系统研究稳态误差才有意义, 所以计算稳态误差应以系统稳定为前提。
本讲只讨论系统的原理性误差, 不考虑由于非线性因素引起的误差。
通常把在阶跃输入作用下没有原理性稳态误 差的系统称为无差系统; 而把有原理性稳态误差的系统称为有差系统。
解.
E(s) e(s)R(s)1
1 K
s(T s1) s(T s1)K
s(T s1)
D (s)T2s sK0
s (T 1 s ) 1 1 e ss r ls 0 ism e (s )R (s ) ls 0 ism s (T 1 s ) K s2 K
Kn
en (s)N E((ss))1TnsK 1 (Tns 1 K )nss((T T ss11))K
r(t) A t2 2
s(T s1) A es3 sls i0m ss(T s1)Ks3
影响 ess 的因素:
系统自身的结构参数 外作用的类型(控制量,扰动量及作用点) 外作用的形式(阶跃、斜坡或加速度等)
§3.6.3
静态误差系数法(1)
静态误差系数法 —— r(t)作用时ess的计算规律
G ( s ) G 1 ( s ) H ( s ) s K v ( ( T 1 1 s s 1 1 ) ) ( ( T n m s v s 1 1 ) ) s K v G 0 ( s )
G (s)K s3s 1 129K s(s3 2 1)
D ( s ) s 3 2 9 K s 1 s 2 9 K 6 s 9 1 K 0
9K 6 0
1
K
0
2 K 1 3
系统闭环稳定与开环稳定之间没有直接关系
例2 系统结构图如右,
(1)确定使系统稳定的参数(K,x 的范围;
令ssa,代入系统特征方程,若对 s 稳定,则全部极点 sa 之左
(2)当 x2 时,确定使全部极点均位于s=-1之左的K值范围。 当 x2 时,进行平移变换:ss1 D (s ) s 3 2 2 0 s 2 1s 0 1 0 K 0 0 0 ss1
D ( s ) ( s 1 ) 3 4 ( s 1 ) 2 0 1 ( s 1 ) 0 1 K 0 0 00 s 3 3 s s 2 2 7 s ( 1 3 K 0 6 ) 0 0 1
自动控制原理
吉 林 化 工 学 院 自动化系
自动控制原理教学组
课程回顾
一 稳定性的概念
l i mk(t) 0
t
二 稳定的充要条件
系统闭环特征方程的所有根都具有负的实部 或所有闭环特征根均位于左半s平面
三 劳斯判据
D ( s ) a n s n a n 1 s n 1 a 1 s a 0 0
(2)当x2时,确定使全部极点均位于s=-1之左的K值范围。
解.
(1)
G(s)s(s2
Ka
20xs10)0
K Ka 100
x D (s ) s3 20 s2 1s 0 1 0K 0 0 0
s3
1
100
s2
2x0 10K0 x0
s1
200x010K0 20x
0
s0
100K
K2x0
K0
判断系统的相对稳定性
