七年级培优试题(新可)
七年级下培优生测试卷3.docx

七年级下生物培优生专项测试卷(血液、血管、心脏)姓名:一、选择题1.下而是邻居张叔叔去医院做血常规检查的摘录结果。
下列说法正确的是 ()A 显微镜观察张叔叔的血液涂片可发现血小板最多B 张叔叔皮肤受伤出血后,其伤口会流血不止C 根据检测结果口J 推测张叔叔口J 能身体有炎症 I )如杲给张叔叔输液,针丿应该刺人他的动脉血管项冃测定结果 参考值 备注 单位红细胞(RBC ) 2.3 4.0 〜5.5 ♦1012个 /L 血红蛋口 (Hb ) 90 120〜160 igL 口细胞(WBC ) 37 4〜10 1()9 个/L 血小板(PLT ) 180100〜300109 个/L2A.血流方向是:乙->丙一甲血流最慢的是血管丙,有利于物质交换 C.血管乙为动脉,管壁薄、血压高D.血管甲有瓣膜,能防止血液倒流3.下列选项表示血液、血浆、血细胞三个概念Z 间的关系,」E 确的是()A B CD4•关于血液中各种成份功能的说法,错误的是()A 红细胞可以运输氧气和养料B 口细胞可以吞噬病菌,有防御保护功能C 血小板有止血和加速凝血的作用D 血浆主要功能是运载血细胞,运输养料和废物5•今年3月,我市7名教师赴疆支教.他们刚到高海拔地区时,红细胞的数量变化趋势是()6•你一定有过手指被划出小伤口的经历,但你会发现伤口即便不包扎血液也会慢慢凝固,这与下列哪种细胞的作用冇关()A.吞噬细胞B.血小板C.红细胞D. £1细胞7.右图是用显微镜观察到的人血涂片视野,下列表述正确的是() A. ①个体最小,能穿透血管壁B.②数量最多,能够呑噬病菌C.③的数量最多,具冇运输氧的功能D.①②③三种细胞中,只冇③没冇细胞核&下图为人体内某结构的血流情况示意图,乙代表某结构,甲、丙代表与其相连的血管,箭头代表血流方向。
下列说法正确的是()A. 若乙表示毛细血管网,则丙内流静脉血B. 若乙表示小肠,则丙内含氧量增加C. 若乙表示肾小球,则丙是静脉血管血细胞血浆血浆血液血液血细胞血细胞血细胞血液血浆D班级:D.若乙是胰岛,当血糖增多丙内胰岛素会增加9•某人因车祸大腿受伤(如图所示),鲜红的血液喷射而出。
七年级数学培优试题
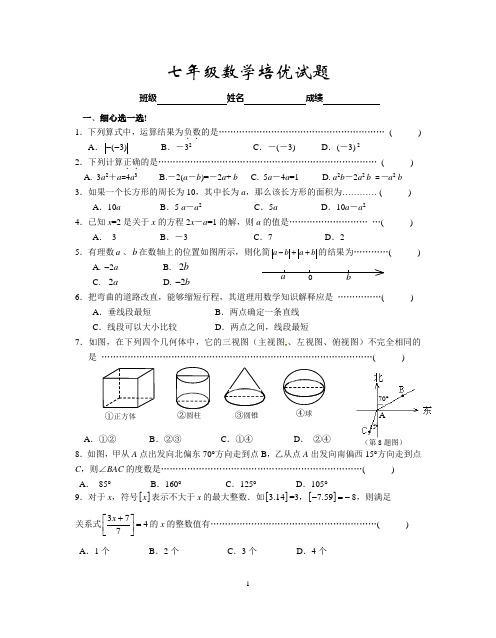
ba七年级数学培优试题班级 姓名 成绩一、细心选一选!1.下列算式中,运算结果为负数..的是………………………………………………… ( ) A .(3)-- B .-32 C .-(-3) D .(-3) 22.下列计算正确..的是………………………………………………………………… ( ) A . 3a 2+a =4a 3 B.-2(a -b )=-2a + b C . 5a -4a =1 D .a 2b -2a 2 b =-a 2 b 3.如果一个长方形的周长为10,其中长为a ,那么该长方形的面积为………… ( )A .10aB .5 a -a 2C .5aD .10a -a 24.已知x =2是关于x 的方程2x -a =1的解,则a 的值是……………………… …( )A . 3B .-3C .7D .25.有理数a 、b 在数轴上的位置如图所示,则化简a b a b -++的结果为…………( )A .2a -B . b 2C . 2aD .2b - 6.把弯曲的道路改直,能够缩短行程,其道理用数学知识解释应是 ……………( )A .垂线段最短B .两点确定一条直线C .线段可以大小比较D .两点之间,线段最短7.如图,在下列四个几何体中,它的三视图(主视图、左视图、俯视图)不完全相同的是 …………………………………………………………………………………( )A .①②B .②③C .①④ D . ②④8.如图,甲从A 点出发向北偏东70°方向走到点B ,乙从点A 出发向南偏西15°方向走到点C ,则∠BAC 的度数是……………………………………………………………( ) A . 85° B .160° C .125° D .105°9.对于x ,符号[]x 表示不大于x 的最大整数.如[]3.14=3,[]7.59-=-8,则满足关系式3747x +⎡⎤=⎢⎥⎣⎦的x 的整数值有…………………………………………………( ) A .1个 B .2个 C .3个 D .4个①正方体圆柱③圆锥④球A70°15°︶ ︵(第8题图)二、细心填一填11.-3的相反数为 ;绝对值等于3的数有 .12.1cm 2的手机上约有细菌120 000个,120 000用科学记数法表示为 . 13.如果单项式13a x y +与132-b y x 是同类项,那么a b= .14.如果一个角的度数是77°53′24" ,那么这个角的余角度数....为 °. 15.小华的爸爸现在的年龄比小华大25岁,8年后小华爸爸的年龄将是小华的3倍多1岁,则小华现在的年龄是 岁.16.如图,要使图中平面展开图按虚线折叠成正方体后,相对面上两个数之和.为0, 则x -2y = .17. 如图,直线AB 、CD 相交于点O ,∠DOF =90°,OF 平分∠AOE ,若∠BOD =28°,则∠EOF的度数为 .19.大于1的正整数的三次方都可以分解为若干个连续奇数的和.如 23=3+5,33=7+9+11,43=13+15+17+19.按此规律,若m 3分解后,最后一个奇数为109,则m 的值为 . 三、认真答一答(写出必要的解题步骤和过程)20.计算:(1)231(1)2(4)22-⨯--÷⨯(-); (2)31136(36)36()424⨯--⨯+⨯-.21.解方程:(1)6745x x -=-; (2)2151136x x +--=.(第16题图)(第17题图)22.先化简,后求值:21(428)(2)4a a b a b -+----, 其中1,2a b ==2014.23.如图,所有小正方形的边长都为1,A 、B 、C 都在格点上. (1)过点C 画直线AB 的平行线(不写画法,下同); (2)过点A 画直线BC 的垂线,并注明垂足..为 G ;过点A 画直线AB 的垂线,交BC 于点H . (3)线段 的长度是点A 到直线BC的距离;(4)线段AG 、AH 的大小..关系为 AG AH .(填写下列符号>,<,≥≤,之一 )24.已知关于a 的方程2(24a a -=+)的解也是关于x 的方程2(3x b -)-=7的解. (1)求a 、b 的值;(2)若线段AB =a ,在直线..AB 上取一点P ,恰好使b PBAP=,点Q 为PB 的中点,求线段AQ 的长.25.某超市用6800元购进A 、B 两种计算器共120只,这两种计算器的进价、标价如下表.(1)这两种计算器各购进多少只?(2)若A 型计算器按标价的9折出售,B 型计算器按标价的8折出售,那么这批计算器全部售出后,超市共获利多少元?26.如图,是由若干个完全相同的小正方体组成的一个几何体. (1)请画出这个几何体的三视图;(正视图) (左视图) (俯视图)(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的正视图和俯视图不变,那么最多可以再添加______个小正方体.27.如图1,已知∠AOB =150°,∠AOC =40°,OE 是∠AOB 内部的一条射线,且OF 平分∠AOE . (1)若∠EOB =10°,则∠COF=________; (2) 若∠COF =20°,则∠EOB =____________;(3) 若∠COF =n °,则∠EOB =_____(用含n 的式子表示).初一数学期末试卷参考答案及评分标准(答案) 2014.1(图1)FECBOA一、精心选一选(每小题3分,共30分)1.B 2.D 3.B 4.A 5.B 6.D 7.B 8.C 9.C 10.B二、细心填一填(每空2分,共20分)11.3 ;±3 12.1.2×105 13.16 14.12.11 15.4 16.6 17.62° 18.63π 19. 10 (备注:有两个答案的,对一个,得1分) 三、认真答一答(本大题共9小题,满分60分.) 20、计算:(每题4分)(1)原式=111(8)422⨯-+⨯⨯……2分 (2)原式= 31136424⨯+-()…………2分 =—8+1………………………3分 = 36 ×1 ………………………3分 =—7 ………………………4分 =36 ……………………………4分 21. 解方程 (1)2x =2…………………2分 (2) 2(2x +1) -(5x -1)=6 ……1分 x =1……………………4分 4x +2-5x +1=6………………2分 x =-3 ……………………4分 22.(本题6分)先化简,后求值:解:原式= 21222a a b a b -+-++ …………………………………………………1分= 232a a -+ …………………………………………………………………3分当12a =时原式= 2131222+⨯-()=12………………………………………………………………………………5分23.(1)画对……………………………1分 (2)画对 ……………………………3分 (3)AG ……………………………4分 (4) < …………………………………5分 24.(1) a=8……………………………1分; b =3………………………………………2分(2)点P 在线段AB 上,AQ =7 …………………………………………………………4分; 点P 在线段AB 的延长线上,AQ =10………………………………………………6分. 25.(1)设A 种计算器购进x 台.由题意列方程:30x+70(120-x)=6800 ………………………………………1分x=40 …………………………………………3分120-x=80 …………………………………………4分答:略(2)列出算式:(50×90%-30)×40+(100×80%-70)×80……………………5分=1400 ………………………………………………………………6分答:略26.(1)图略:三视图画对每个1分,共3分(2)2 ………………………………………………………………………………5分27.(1)30°………………………………………………………………………………1分(2)30°………………………………………………………………………………2分(3)70°—2n°…………………………………………………………………………3分(4)画图1分∠EOB=70°+2∠COF…………………………………………………………………5分证明:设∠COF=n°,则∠AOF=∠AOC—∠COF=40°—n°………………………7分又因OF平分∠AOE,所以∠AOE=2∠AOF=80°—2 n°.∠EOB=∠AOB-∠AOE =150°—(80°—2 n°)=(70+2n)°即∠EOB=70°+2∠COF.28.(1)①2,4………(每个结果1分)………………………………………………2分②13或1 (每个结果2分)……………………………………………………6分(2)65或103(每个结果2分)……………………………………………………10分。
七年级培优试题及答案

1.如图1,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B;(1)求证:CD⊥AB,并指出你在证明过程中应用了哪两个互逆的真命题;(2)如图2,若AE平分∠BAC,交CD于点F,交BC于E.求证:∠AEC=∠CFE;(3)如图3,若E为BC上一点,AE交CD于点F,BC=3CE,AB=4AD,△ABC、△CEF、△ADF的面积分别为S△ABC、S△CEF、S△ADF,且S△ABC=36,则S△CEF﹣S△ADF=3.(仅填结果)【考点】命题与定理;三角形的面积;直角三角形的性质.【分析】(1)根据直角三角形两锐角互余可得∠A+∠B=90°,然后求出∠A+∠ACD=90°,从而得到∠ADC=90°,再根据垂直的定义证明即可;(2)根据角平分线的定义可得∠CAE=∠BAE,再根据直角三角形两锐角互余可得∠CAE+∠AEC=90°,∠BAE+∠AFD=90°,从而得到∠AEC=∠AFD,再根据对顶角相等可得∠AFD=∠CFE,然后等量代换即可得证;(3)根据等高的三角形的面积的比等于底边的比求出S△ACD和S△ACE,然后根据S△CEF ﹣S△ADF=S△ACE﹣S△ACD计算即可得解.【解答】(1)证明:∵∠ACB=90°,∴∠A+∠B=90°,∵∠ACD=∠B,∴∠A+∠ACD=90°,∴∠ADC=90°,即CD⊥AB,证明时应用了“直角三角形两锐角互余”和“有两个锐角互余的三角形是直角三角形”;(2)证明:∵AE平分∠BAC,∴∠CAE=∠BAE,∵∠CAE+∠AEC=90°,∠BAE+∠AFD=90°,∴∠AEC=∠AFD,∵∠AFD=∠CFE(对顶角相等),∴∠AEC=∠CFE;(3)解:∵BC=3CE,AB=4AD,∴S△ACD=S△ABC=×36=9,S△ACE=S△ABC=×36=12,∴S△CEF﹣S△ADF=S△ACE﹣S△ACD=12﹣9=3.故答案为:3.【点评】本题考查了命题与定理,三角形的面积,直角三角形两锐角互余的性质,有两个锐角互余的三角形是直角三角形,(3)利用等高的三角形的面积的比等于底边的比求出S△ACD 和S△ACE是解题的关键.2. Rt△ABC中,∠C=90°,点D,E分别是边AC,BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.(1)若点P在线段AB上,如图①,且∠α=50°,则∠1+∠2=140°;(2)若点P在斜边AB上运动,如图②,则∠α、∠1、∠2之间的关系为∠1+∠2=90°+∠α;(3)如图③,若点P在斜边BA的延长线上运动(CE<CD),请直接写出∠α、∠1、∠2之间的关系:∠2﹣∠1=90°+∠α;∠2=∠1+90°;∠1﹣∠2=∠α﹣90°;(4)若点P运动到△ABC形外(只需研究图④情形),则∠α、∠1、∠2之间有何关系?并说明理由.【考点】三角形内角和定理;三角形的外角性质.【专题】探究型.【分析】(1)连接PC,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠1=∠PCD+∠CPD,∠2=∠PCE+∠CPE,再表示出∠1+∠2即可;(2)利用(1)中所求得出答案即可;(3)利用三角外角的性质分三种情况讨论即可;(4)利用三角形内角和定理以及邻补角的性质可得出.【解答】解:(1)如图,连接PC,∵∠1=∠PCD+∠CPD,∠2=∠PCE+∠CPE,∴∠1+∠2=∠PCD+∠CPD+∠PCE+∠CPE=∠DPE+∠C,∵∠DPE=∠α=50°,∠C=90°,∴∠1+∠2=50°+90°=140°,故答案为:140°;(2)连接PC,∵∠1=∠PCD+∠CPD,∠2=∠PCE+∠CPE,∴∠1+∠2=∠PCD+∠CPD+∠PCE+∠CPE=∠DPE+∠C,∵∠C=90°,∠DPE=∠α,∴∠1+∠2=90°+∠α;故答案为:∠1+∠2=90°+∠α;(3)如图1,∵∠2=∠C+∠1+∠α,∴∠2﹣∠1=90°+∠α;如图2,∠α=0°,∠2=∠1+90°;如图3,∵∠2=∠1﹣∠α+∠C,∴∠1﹣∠2=∠α﹣90°.故答案为;∠2﹣∠1=90°+∠α;∠2=∠1+90°;∠1﹣∠2=∠α﹣90°.(4)∵∠PFD=∠EFC,∴180°﹣∠PFD=180°﹣∠EFC,∴∠α+180°﹣∠1=∠C+180°﹣∠2,∴∠2=90°+∠1﹣α.故答案为:∠2=90°+∠1﹣α.【点评】本题考查了三角形内角和定理和外角的性质、对顶角相等的性质,熟练利用三角形外角的性质是解题的关键.3.阅读下面的材料:如图①,在ABC ∆中,试说明180A B C ∠+∠+∠=︒.分析:通过画平行线,将A ∠、B ∠、C ∠作等量代换,使各角之和恰为一个平角,依辅助线不同而得多种方法.第24题解:如图②,延长BC 到点D ,过点C 作CE //BA . 因为BA //CE (作图所知),所以2B ∠=∠,1A ∠=∠(两直线平行,同位角、内错角相等). 又因为21180BCD BCA ∠=∠+∠+∠=︒(平角的定义), 所以180A B ACB ∠+∠+∠=︒(等量代换).如图③,过BC 上任一点F ,作FH //AC , FG //AB ,这种添加辅助线的方法能说明180A B C ∠+∠+∠=︒吗?并说明理由.. 能 理由:因为FH ∥AC ,所以1,2C CGF ∠=∠∠=∠,因为FG ∥AB ,所以3,B CGF A ∠=∠∠=∠,所以2A ∠=∠,因为180BFC ∠=︒,所以180A B C ∠+∠+∠=︒.4.如图,在△ABC 中(BC >AC ),∠ACB =90°,点D 在AB 边上,DE ⊥AC 于点E .设点F 在线段EC 上,点G 在射线CB 上,以F ,C ,G 为顶点的三角形与△EDC 有一个锐角相等,FG 交CD 于点P ,问:线段CP 可能是△CFG 的高线还是中线?或两者都有可能?请说明理由. .①若1CFG ECD ∠=∠,此时线段CP 1为△CFG 1的斜边FG 1上的中线.证明如下: ∵1CFG ECD ∠=∠,∴11CFG FCP ∠=∠.又∵1190CFG CG F ∠+∠=︒,∴11190FCP PCG ∠+∠=︒. ∴111CG F PCG ∠=∠. ∴111CP G P =.又∵11CFG FCP ∠=∠,∴11CP FP =. ∴1111CP FP G P ==. ∴线段CP 1为△CFG 1的斜边FG 1上的中线.②若2CFG EDC ∠=∠,此时线段CP 2为△CFG 2的斜边FG 2上的高线.证明如下:∵2CFG EDC ∠=∠,又∵DE ⊥AC ,∴90DEC ∠=︒. ∴90ECD EDC ∠+∠=︒. ∴290ECD CFG ECD EDC ∠+∠=∠+∠=︒. ∴CP 2⊥FG 2. ∴线段CP 2为△CFG 2的斜边FG 2上的高线.③当CD 为∠ACB 的平分线时,CP 既是△CFG 的FG 边上的高线又是中线.E ADBC5.如图,D 是ABC ∆的边BC 上任意一点,E 、F 分别是线段AD 、CE 的中点,且ABC∆的面积为20 cm 2,求BEF ∆的面积.. 因为E 是AD 的中点,所以BE 是ABD ∆的中线,CE 是ACD ∆的中线,所以BF 是BCE ∆的中线,所以12BEF BEC S S ∆∆==5(cm 2) 6.在ABC ∆中,C B ∠>∠.如图①,AD BC ⊥于点D ,AE 平分BAC ∠,则易知1()2EAD C B ∠=∠-∠.(1)如图②,AE 平分BAC ∠, F 为AE 上的一点,且FD BC ⊥于点D ,这时EFD ∠与B ∠、C ∠有何数量关系?请说明理由;(2)如图③,AE 平分BAC ∠,F 为AE 延长线上的一点,FD BC ⊥于点D ,请你写出这时AFD ∠与B ∠、C ∠之间的数量关系(只写结论,不必说明理由)..(1)如图辅助线:作AG BC ⊥,1()2EFD C B ∠=∠-∠. (2)1()2AFD C B ∠=∠-∠7. BC ∥OA ,∠B=∠A=100︒,试回答下列问题:(1)如图,求证:OB ∥AC ;(2)如图,若点E 、F 在BC 上,且满足∠FOC=∠AOC ,并且OE 平分∠BOF①∠EOC 的度数;②求∠OCB :∠0FB 的值;③如图,若∠OEB=∠OCA ,此时∠OCA= (在横线上填上答案即可).(1)证明:∵BC ∥OA ∴∠B+∠0=180°.∵∠A=∠B .∴∠A+∠O=180°.∴OB ∥AC . (2)①∠A=∠B=:100°,由(1)得∠BOA=180°-∠B=80°. ∵∠FOC=∠AOC ,并且OE 平分∠BOF ,BC ∥OA ,∴∠FOC=12∠FOA ,∠EOF=12∠BOF . ∴∠EOC=∠EOF+∠FOC=12 (∠BOF+∠FOA)= 12∠BOA=40°.②∵BC ∥OA ,∴∠FCO=∠COA .又∵∠FOC=,∠AOC ,.∴∠FOC=∠FCO .∵∠FOC+∠FCO=180°-∠OFC ,且∠BFO=180°-∠0FC , ∴∠OFB=∠FOC+∠FCO=2∠OCB . ∴∠0CB :∠0FB=1:2.③由(1)知OB ∥AC ,∴∠OCA=∠BOC .由(2)可以设∠B0E=∠E0F=a ,∠FOC=∠COA=β,∴∠OCA=∠BOC=2a +β ∵∠ECO+∠EOC=180°-∠OEC ,且∠OEB=180°-∠OEC , 即∠OEB=∠EOC+∠ECO=a +β+β=a +2β ∵∠OEB=∠OCA .∴2a +β=a +2β·即a =β ∵∠AOB=80°,∴a =β=20°. ∴∠OCA=2a +β=40°+20°=60°9.阅读下列材料:一般地,n 个相同的因数a 相乘, 记为n a .如2×2×2=32=8,此时,3叫做以2为底8的对数,记为log 8a (即log 8a =3).一般地,若n a =6(a >0且a ≠1,6>0),则n 叫做以a 为底b 的对数,记为log a b (即log a b =n).如34=81,则4叫做以3为底81的对数,记为3log 81 (即3log 81=4). (1)计算以下各对数的值:2log 4= ;2log 16= ;2log 64= . (2)观察(1)中三数4、16、64之间满足怎样的关系式,2log 4、2log 16、2log 64之间又满足怎样的关系式;(3)由(2)的结果,你能归纳出一个一般性的结论吗?8.如图7所示,直线a ∥b ,则∠A =_______. .如图8所示,∠A+∠B+∠C+∠D+∠E =______.log log a a M N += (a>0且a≠1,M>0,N>0); (4)根据幂的运算法则:n m a a =n m a +以及对数的含义证明上述结论.10.(1)阅读材料:求l+2+22+32+42+…+22013的值. 解:设S= l+2+22+32+42+…+ 20122+22013 ,将等式两边同时乘2, 得2S=2+22+32+42+52+…+22013+22014. 将下式减去上式,得2S-S=22014一l 即S=22014一l ,即1+2+ 22+32+42+…+22013= 22014一l 仿照此法计算:(1)1+3+2333++…+1003 (2) 231111222+++…+1001211.阅读下列一段话,并解决后面的问题.观察下面一列数:l ,2,4,8,…我们发现,这列数从第二项起,每一项与它前一项的比值都是2.我们把这样的一列数叫做等比数列,这个共同的比值叫做等比数列的公比.(1)等比数列5,一15,45,…的第4项是_______;(2)如果一列数a 1,a 2,a 3,…是等比数列,且公比是q ,那么根据上述规定有21a q a =32a q a =,43aq a =,…所以a 2=a 1q,a 3=a 2q=a 1q ·q=a 1q 2,a 4=a 3q=a 1q 2·q=a 1q 3, … 则a n =______;(用a 1与q 的代数式表示)(3)一个等比数列的第2项是10,第3项是20,求它的第1项和第4项.12.如图1,△ABC中,两条角平分线BD,CE交于点M,MN⊥BC于点N,将∠MBN 记为∠1,∠MCN记为∠2.∠CMN记为∠3.(1)若∠A=98°,∠BEC=124°,则∠2=26°,∠3﹣∠1=49°;(2)猜想∠3﹣∠1与∠A的数量关系,并证明你的结论;(3)若∠BEC=α,∠BDC=β,如图2所示,用含α和β的代数式表示∠3﹣∠1的度数.(直接写出结果即可)【考点】三角形内角和定理;三角形的外角性质.【专题】计算题.【分析】(1)利用三角形外角性质得到∠BEC=∠A+∠ACE,则可计算出∠ACE=26°,再根据角平分线定义得到∠2=∠ACE=26°,接着在△BCE中计算出∠EBC,从而得到∠1的度数,然后利用互余求∠3=64°,最后计算∠3﹣∠1;(2)利用三角形外角性质得∠BMC=∠MDC+∠DCM,∠MDC=∠A+∠ABD,即∠BMC=∠2+∠A+∠1,再利用三角形内角和得到180°﹣∠1﹣∠2=∠2+∠A+∠1,然后把∠2=90°﹣∠3代入后整理得到∠3﹣∠1=∠A;(3)利用三角形外角性质得∠BEC=∠A+∠ACE,∠BDC=∠A+∠ABD,加上∠1=∠EBM,∠2=∠DCM,则α=∠A+∠2,β=∠A+∠1,把两式相加后把∠A=∠3﹣∠1代入得到α+β=2(∠3﹣∠1)+90°﹣∠3+∠1,整理即可得到∠3﹣∠1=α+β﹣90°.【解答】解:(1)∵∠BEC=∠A+∠ACE,∴∠ACE=124°﹣98°=26°,∵CE平分∠ACB,∴∠2=∠ACE=26°,∴∠EBC=180°﹣∠2﹣∠BEC=30°,而BD平分∠ABC,∴∠1=×30°=15°,∵MN⊥BC,∴∠3=90°﹣∠2=90°﹣26°=64°;∴∠3﹣∠1=49°,故答案为26,49;(2)∠3﹣∠1=∠A.理由如下:∵∠BMC=∠MDC+∠DCM,而∠MDC=∠A+∠ABD,∠DCM=∠2,∴∠BMC=∠2+∠A+∠ABD,∵BD平分∠ABC,∴∠1=∠ABD,∴∠BMC=∠2+∠A+∠1,∴180°﹣∠1﹣∠2=∠2+∠A+∠1,∴2∠2+2∠1=180°﹣∠A,而∠2=90°﹣∠3,∴2(90°﹣∠3)+2∠1=180°﹣∠A,∴∠3﹣∠1=∠A;(3)∵∠BEC=∠A+∠ACE,∠BDC=∠A+∠ABD,而∠1=∠EBM,∠2=∠DCM,∴α=∠A+∠2,β=∠A+∠1,∴α+β=2∠A+∠2+∠1,而∠A=∠3﹣∠1,∴α+β=2(∠3﹣∠1)+90°﹣∠3+∠1,∴∠3﹣∠1=α+β﹣90°.【点评】本题考查了三角形内角和定理:三角形内角和是180°.正确运用角平分线和三角形外角性质是解题的关键.13.已知:如图①,直线MN⊥直线PQ,垂足为O,点A在射线OP上,点B在射线OQ 上(A、B不与O点重合),点C在射线ON上且OC=2,过点C作直线l∥PQ,点D在点C的左边且CD=3.(1)直接写出△BCD的面积.(2)如图②,若AC⊥BC,作∠CBA的平分线交OC于E,交AC于F,求证:∠CEF=∠CFE.(3)如图③,若∠ADC=∠DAC,点B在射线OQ上运动,∠ACB的平分线交DA的延长线于点H,在点B运动过程中的值是否变化?若不变,求出其值;若变化,求出变化范围.考点:坐标与图形性质;垂线;三角形的面积.分析:(1)因为△BCD的高为OC,所以S△BCD=CD•OC,(2)利用∠CFE+∠CBF=90°,∠OBE+∠OEB=90°,求出∠CEF=∠CFE.(3)由∠ABC+∠ACB=2∠DAC,∠H+∠HCA=∠DAC,∠ACB=2∠HCA,求出∠ABC=2∠H,即可得答案.解答:解:(1)S△BCD=CD•OC=×3×2=3.(2)如图②,∵AC⊥BC,∴∠BCF=90°,∴∠CFE+∠CBF=90°,∵直线MN⊥直线PQ,∴∠BOC=∠OBE+∠OEB=90°,∵BF是∠CBA的平分线,∴∠CBF=∠OBE,∵∠CEF=∠OBE,∴∠CFE+∠CBF=∠CEF+∠OBE,∴∠CEF=∠CFE.(3)如图③,∵直线l∥PQ,∴∠ADC=∠PAD,∵∠ADC=∠DAC∴∠CAP=2∠DAC,∵∠ABC+∠ACB=∠CAP,∴∠ABC+∠ACB=2∠DAC,∵∠H+∠HCA=∠DAC,∴∠ABC+∠ACB=2∠H+2∠HCA∵CH是,∠ACB的平分线,∴∠ACB=2∠HCA,∴∠ABC=2∠H,∴=.点评:本题主要考查垂线,角平分线和三角形面积,解题的关键是找准相等的角求解.14.如图,四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,∠ABC、∠BCD的角平分线交于点F.(1)若∠F=80,则∠ABC+∠BCD=200°;∠E=100°;(2)探索∠E与∠F有怎样的数量关系,并说明理由;(3)给四边形ABCD添加一个条件,使得∠E=∠F所添加的条件为AB∥CD.【考点】多边形内角与外角;三角形内角和定理.【分析】(1)先根据三角形内角和定理求出∠FBC+∠BCF=180°﹣∠F=100°,再由角平分线定义得出∠ABC=2∠FBC,∠BCD=2∠BCF,那么∠ABC+∠BCD=2∠FBC+2∠BCF=2(∠FBC+∠BCF)=200°;由四边形ABCD的内角和为360°,得出∠BAD+∠CDA=360°﹣(∠ABC+∠BCD)=160°.由角平分线定义得出∠DAE=∠BAD,∠ADE=∠CDA,那么∠DAE+∠ADE=∠BAD+∠CDA=(∠BAD+∠CDA)=80°,然后根据三角形内角和定理求出∠E=180°﹣(∠DAE+∠ADE)=100°;(2)由四边形ABCD的内角和为360°得到∠BAD+∠CDA+∠ABC+∠BCD=360°,由角平分线定义得出∠DAE+∠ADE+∠FBC+∠BCF=180°,又根据三角形内角和定理有∠DAE+∠ADE+∠E=180°,∠FBC+∠BCF+∠F=180°,那么∠DAE+∠ADE+∠E+∠FBC+∠BCF+∠F=360°,于是∠E+∠F=360°﹣(∠DAE+∠ADE+∠FBC+∠BCF)=180°;(3)由(2)可知∠E+∠F=180°,如果∠E=∠F,那么可以求出∠E=∠F=90°,根据三角形内角和定理求出∠DAE+∠ADE=90°,再利用角平分线定义得到∠BAD+∠CDA=180°,于是AB∥CD.【解答】解:(1)∵∠F=80,∴∠FBC+∠BCF=180°﹣∠F=100°.∵∠ABC、∠BCD的角平分线交于点F,∴∠ABC=2∠FBC,∠BCD=2∠BCF,∴∠ABC+∠BCD=2∠FBC+2∠BCF=2(∠FBC+∠BCF)=200°;∵四边形ABCD的内角和为360°,∴∠BAD+∠CDA=360°﹣(∠ABC+∠BCD)=160°.∵四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,∴∠DAE=∠BAD,∠ADE=∠CDA,∴∠DAE+∠ADE=∠BAD+∠CDA=(∠BAD+∠CDA)=80°,∴∠E=180°﹣(∠DAE+∠ADE)=100°;(2)∠E+∠F=180°.理由如下:∵∠BAD+∠CDA+∠ABC+∠BCD=360°,∵四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,∠ABC、∠BCD的角平分线交于点F,∴∠DAE+∠ADE+∠FBC+∠BCF=180°,∵∠DAE+∠ADE+∠E=180°,∠FBC+∠BCF+∠F=180°,∴∠DAE+∠ADE+∠E+∠FBC+∠BCF+∠F=360°,∴∠E+∠F=360°﹣(∠DAE+∠ADE+∠FBC+∠BCF)=180°;(3)AB∥CD.故答案为200°;100°;AB∥CD.【点评】本题考查了三角形、四边形内角和定理,角平分线定义,平行线的判定,等式的性质,利用数形结合,理清角度之间的关系是解题的关键.15.已知:在△ABC和△DEF中,∠A=40°,∠E+∠F=100°,将△DEF如图摆放,使得∠D 的两条边分别经过点B和点C.(1)当将△DEF如图1摆放时,则∠ABD+∠ACD=240度(2)当将△DEF如图2摆放时,请求出∠ABD+∠ACD的度数,并说明理由;(3)能否将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB?直接写出结论不能.(填“能”或“不能”)考点:多边形内角与外角;三角形内角和定理;三角形的外角性质.分析:(1)要求∠ABD+∠ACD的度数,只要求出∠ABC+∠CBD+∠ACB+∠BCD,利用三角形内角和定理得出∠ABC+∠ACB=180°﹣∠A=180°﹣40°=140°;根据三角形内角和定理,∠CBD+∠BCD=∠E+∠F=100°,∴∠ABD+∠ACD=∠ABC+∠CBD+∠ACB+∠BCD=140°+100°=240°;(2)要求∠ABD+∠ACD的度数,只要求出∠ABC+∠ACB﹣(∠BCD+∠CBD)的度数.根据三角形内角和定理,∠CBD+∠BCD=∠E+∠F=100°;根据三角形内角和定理得,∠ABC+∠ACB=180°﹣∠A=140°,∴∠ABD+∠ACD=∠ABC+∠ACB﹣(∠BCD+∠CBD)=140°﹣100°=40°;(3)不能.假设能将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB.则∠CBD+∠BCD=∠ABD+∠ACD=100°,那么∠ABC+∠ACB=200°,与三角形内角和定理矛盾,所以不能.解答:解:(1)在△ABC中,∠A+∠ABC+∠ACB=180°,∠A=40°∴∠ABC+∠ACB=180°﹣40°=140°在△BCD中,∠D+∠BCD+∠CBD=180°∴∠BCD+∠CBD=180°﹣∠D在△DEF中,∠D+∠E+∠F=180°∴∠E+∠F=180°﹣∠D∴∠CBD+∠BCD=∠E+∠F=100°∴∠ABD+∠ACD=∠ABC+∠CBD+∠ACB+∠BCD=140°+100°=240°.故答案为:240°;(2)∠ABD+∠ACD=40°;理由如下:∵∠E+∠F=100°∴∠D=180°﹣(∠E+∠F)=80°∴∠ABD+∠ACD=180°﹣∠A﹣∠DBC﹣∠DCB=180°﹣40°﹣(180°﹣80°)=40°;(3)不能.假设能将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB.则∠CBD+∠BCD=∠ABD+∠ACD=100°,那么∠ABC+∠ACB=200°,与三角形内角和定理矛盾,所以不能.故答案为:不能.点评:考查三角形内角和定理,外角性质.熟练掌握这些性质是解题的关键.16.已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.(1)如图1,若AB∥ON,则①∠ABO的度数是20°;②当∠BAD=∠ABD时,x=120°;当∠BAD=∠BDA时,x=60°.(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.考点:三角形的角平分线、中线和高;平行线的性质;三角形内角和定理.专题:计算题.分析:利用角平分线的性质求出∠ABO的度数是关键,分类讨论的思想.解答:解:(1)①∵∠MON=40°,OE平分∠MON∴∠AOB=∠BON=20°∵AB∥ON∴∠ABO=20°②∵∠BAD=∠ABD∴∠BAD=20°∵∠AOB+∠ABO+∠OAB=180°∴∠OAC=120°∵∠BAD=∠BDA,∠ABO=20°∴∠BA D=80°∵∠AOB+∠ABO+∠OAB=180°∴∠OAC=60°故答案为:①20 ②120,60(2)①当点D在线段OB上时,若∠BAD=∠ABD,则x=20若∠BAD=∠BDA,则x=35若∠ADB=∠ABD,则x=50②当点D在射线BE上时,因为∠ABE=110°,且三角形的内角和为180°,所以只有∠BAD=∠BDA,此时x=125.综上可知,存在这样的x的值,使得△ADB中有两个相等的角,且x=20、35、50、125.点评:本题考查了三角形的内角和定理和三角形的外角性质的应用,注意:三角形的内角和等于180°,三角形的一个外角等于和它不相邻的两个内角之和.17.如图,在△ABC中,A D⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.(1)求∠BAE的度数;(2)求∠DAE的度数;(3)探究:小明认为如果只知道∠B﹣∠C=40°,也能得出∠DAE的度数?你认为可以吗?若能,请你写出求解过程;若不能,请说明理由.考点:三角形内角和定理;角平分线的定义;三角形的外角性质.专题:探究型.分析:(1)利用三角形的内角和定理求出∠BAC,再利用角平分线定义求∠BAE.(2)先求出∠BAD,就可知道∠DAE的度数.(3)用∠B,∠C表示∠DAE即可.解答:解:(1)∵∠B=70°,∠C=30°,∴∠BAC=180°﹣70°﹣30°=80°,因为AE平分∠BAC,所以∠BAE=40°;(2)∵AD⊥BC,∠B=70°,∴∠BAD=90°﹣∠B=90°﹣70°=20°,而∠BAE=40°,∴∠DAE=20°;(3)可以.理由如下:∵AE为角平分线,∴∠BAE=,∵∠BAD=90°﹣∠B,∴∠DAE=∠BAE﹣∠BAD=﹣(90°﹣∠B)=,若∠B﹣∠C=40°,则∠DAE=20°.点评:熟练运用角平分线定义和三角形的内角和定理.同时也要熟练掌握角与角之间的代换.18.如图,(1)在图1中,猜想:∠A1+∠B1+∠C1+∠A2+∠B2+∠C2=360度.并试说明你猜想的理由.(2)如果把图1称为2环三角形,它的内角和为:∠A1+∠B1+∠C1+∠A2+∠B2+∠C2;图2称为2环四边形,它的内角和为∠A1+∠B1+∠C1+∠D1+∠A2+∠B2+∠C2+∠D2;图3称为2环5五边形,它的内角和为∠A1+∠B1+∠C1+∠D1+∠E1++∠A2+∠B2+∠C2+∠D2+∠E2请你猜一猜,2环n边形的内角和为360(n﹣2)度(只要求直接写出结论).考点:多边形内角与外角;三角形内角和定理.专题:规律型.分析:(1)连结B1B2,可得∠A2+∠C1=∠B1B2A2+∠B2B1C1,再根据四边形的内角和公式即可求解;(2)A1A2之间添加两条边,可得B2+∠C2+∠D2=∠EA1D+∠A1EA2+∠EA2B2,再根据边形的内角和公式即可求解;2环n边形添加(n﹣2)条边,再根据边形的内角和公式即可求解.解答:解:(1)连结B1B2,则∠A2+∠C1=∠B1B2A2+∠B2B1C1,∠A1+∠B1+∠C1+∠A2+∠B2+∠C2=∠A1+∠B1+∠B1B2A2+∠B2B1C1+∠B2+∠C2=360度;(2)如图,A1A2之间添加两条边,可得B2+∠C2+∠D2=∠EA1D+∠A1EA2+∠EA2B2则∠A1+∠B1+∠C1+∠D1+∠A2+∠B2+∠C2+∠D2=∠A1+∠B1+∠C1+∠D1+∠A2+∠EA1D+∠A1EA2+∠EA2B2=720°;2环n边形添加(n﹣2)条边,2环n边形的内角和成为(2n﹣2)边形的内角和.其内角和为180(2n﹣4)=360(n﹣2)度.故答案为:(1)360;(2)360(n﹣2)点评:考查了多边形内角和定理:(n﹣2)•180°(n≥3)且n为整数).19.已知如图∠xOy=90°,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于点C,当点A,B分别在射线Ox,Oy上移动时,试问∠ACB的大小是否发生变化?如果保持不变,请说明理由;如果随点A,B的移动而变化,请求出变化范围.考点:三角形内角和定理;三角形的外角性质.分析:根据角平分线的定义、三角形的内角和、外角性质求解.解答:解:∠C的大小保持不变.理由:∵∠ABY=90°+∠OAB,AC平分∠OAB,BE平分∠ABY,∴∠ABE=∠ABY=(90°+∠OAB)=45°+∠OAB,即∠ABE=45°+∠CAB,又∵∠ABE=∠C+∠CAB,∴∠C=45°,故∠ACB的大小不发生变化,且始终保持45°.点评:本题考查的是三角形内角与外角的关系,掌握“三角形的内角和是180°”是解决问题的关键.20.某同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②.图①中,∠B=90°,∠A=30°;图②中,∠D=90°,∠F=45°.图③是该同学所做的一个实验:他将△DEF 的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合).(1)在△DEF沿AC方向移动的过程中,该同学发现:F、C两点间的距离逐渐变小;连接FC,∠FCE的度数逐渐变大.(填“不变”、“变大”或“变小”)(2)△DEF在移动的过程中,∠FCE与∠CFE度数之和是否为定值,请加以说明.(3)能否将△DEF移动至某位置,使F、C的连线与AB平行?请求出∠CFE的度数.考点:三角形的外角性质;平行线的判定;三角形内角和定理.分析:(1)利用图形的变化得出F、C两点间的距离变化和,∠FCE的度数变化规律;(2)利用外角的性质得出∠FEC+∠CFE=∠FED=45°,即可得出答案;(3)要使FC∥AB,则需∠FCE=∠A=30°,进而得出∠CFE的度数.解答:解;(1)F、C两点间的距离逐渐变小;连接FC,∠FCE的度数逐渐变大;故答案为:变小,变大;(2)∠FCE与∠CFE度数之和为定值;理由:∵∠D=90°,∠DFE=45°,又∵∠D+∠DFE+∠FED=180°,∴∠FED=45°,∵∠FED是△FEC的外角,∴∠FEC+∠CFE=∠FED=45°,即∠FCE与∠CFE度数之和为定值;(3)要使FC∥AB,则需∠FCE=∠A=30°,又∵∠CFE+∠FCE=45°,∴∠CFE=45°﹣30°=15°.点评:此题主要考查了三角形的外角以及平行线的判定和三角形内角和定理等知识,熟练利用相关定理是解题关键.21.如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,AB=10cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm.设运动的时间为t秒.(1)当t=6秒时,CP把△ABC的周长分成相等的两部分?(2)当t=6.5秒时,CP把△ABC的面积分成相等的两部分?(3)当t为何值时,△BCP的面积为12?考点:一元一次方程的应用;三角形的面积.专题:几何动点问题.分析:(1)先求出△ABC的周长为24cm,所以当CP把△ABC的周长分成相等的两部分时,点P在AB上,此时CA+AP=BP+BC=12cm,再根据时间=路程÷速度即可求解;(2)根据中线的性质可知,点P在AB中点时,CP把△ABC的面积分成相等的两部分,进而求解即可;(3)分两种情况:①P在AC上;②P在AB上.解答:解:(1)△ABC中,∵AC=8cm,BC=6cm,AB=10cm,∴△ABC的周长=8+6+10=24cm,∴当CP把△ABC的周长分成相等的两部分时,点P在AB上,此时CA+AP=BP+BC=12cm,∴2t=12,t=6;(2)当点P在AB中点时,CP把△ABC的面积分成相等的两部分,此时CA+AP=8+5=13(cm),∴2t=13,t=6.5;(3)分两种情况:①当P在AC上时,∵△BCP的面积=12,∴×6×CP=12,∴CP=4,∴2t=4,t=2;②当P在AB上时,∵△BCP的面积=12=△ABC面积的一半,∴P为AB中点,∴2t=13,t=6.5.故答案为6秒;6.5秒.点评:本题考查了一元一次方程的应用,三角形的周长与面积,三角形的中线,难度适中.利用分类讨论的思想是解(3)题的关键.22.如图,已知长方形的每个角都是直角,将长方形ABCD沿EF折叠后点B恰好落在CD边上的点H处,且∠CHE=40°.(1)求∠HFA的度数;(2)若再将△DAF沿DF折叠后点A恰好落在HF上的点G处,请找出线段DF和线段EF 有何位置关系,并证明你的结论.考点:翻折变换(折叠问题).分析:(1)根据余角的定义,可得∠CEH的度数,根据角的和差,可得∠HEB的度数,根据翻折的性质,可得∠EHF的度数,根据四边形内角和,可得∠HFB的度数,根据邻补角的定义,可得答案;(2)根据翻折的性质,可得∠BFE=∠HFE,∠AFD=∠GFD,根据角的和差,等式的性质,可得答案.解答:解:(1)由余角的定义,得∠CEH=90°﹣∠CHE=50°由角的和差,得∠HEB=180°﹣∠CEH=180°﹣50°=130°,由翻折的性质,得∠B=∠EHF=90°,由四边形内角和,得∠HFB=360°﹣∠B﹣∠BEH﹣∠EHF=50°,由邻补角的定义,得∠HFA=180°°﹣∠HFB=130°;(2)DF和线段EF位置关系是DF⊥EF,证明:∵长方形ABCD沿EF折叠后点B恰好落在CD边上的点H处,将△DAF沿DF折叠后点A恰好落在HF上的点G处,∴∠BFE=∠HFE,∠AFD=∠GFD.∵∠BFE+∠HFE+∠AFD+∠GFD=180°,∴∠DFG+∠GFE=90°,即∠DFE=90°,∴DF⊥EF.点评:本题考查了翻折变换,利用了余角的定义,角的和差,翻折的性质,四边形内角和,邻补角的定义,利用知识点较多,题目稍微有点难度..23.在梯形ABCD中,AB∥CD,∠B=90°,AB=BC=3cm,CD=4cm,动点P从点A出发,先以1cm/s的速度沿A→B→C运动,然后以2cm/s的速度沿C→D运动.设点P运动的时间为t秒,是否存在这样的t,使得△BPD的面积S=3cm2?考点:梯形.专题:动点型.分析:分三段考虑,①点P在AB上,②点P在BC上,点P在CD上,分别用含t的式子表示出△BPD的面积,再由S=3cm2建立方程,解出t的值即可.解答:解:①当点P在AB上时,点P的速度为1cm/s,0<t<3,如图①所示:,则BP=AB﹣AP=3﹣t,S△BPD=BP×CB=﹣=3,解得:t=1.②当点P在BC上时,点P的速度为1cm/s,3<t≤6,如图②所示:,则BP=t﹣3,S△BPD=BP×DC=2t﹣6=3,解得:t=4.5.③当点P在CD上时,点P的速度为2cm/s,6<t<8,如图③所示:,则DP=CD﹣CP=4﹣2(t﹣6)=16﹣2t,S△BPD=DP×BC=24﹣3t=3,解得:t=7.综上可得:当t=1秒或4.5秒或7秒时,使得△BPD的面积S=3cm2.点评:本题考查了梯形的知识,解答本题的关键是分段讨论,画出每段的图形,根据△BPD 的面积为3建立方程,注意数形结合思想的运用.24.(1)如图1,已知△ABC,过点A画一条平分三角形面积的直线;(2)如图2,已知l1∥l2,点E,F在l1上,点G,H在l2上,试说明△EGO与△FHO面积相等;(3)如图3,点M在△ABC的边上,过点M画一条平分三角形面积的直线.考点:三角形的面积.分析:(1)根据三角形的面积公式,只需过点A和BC的中点画直线即可;(2)结合平行线间的距离相等和三角形的面积公式即可证明;(3)结合(1)和(2)的结论进行求作.解答:(1)解:取BC的中点D,过A、D画直线,则直线AD为所求;(2)证明:∵l1∥l2,∴点E,F到l2之间的距离都相等,设为h.∴S△EGH=GH•h,S△FGH=GH•h,∴S△EGH=S△FGH,∴S△EGH﹣S△GOH=S△FGH﹣S△GOH,∴△EGO的面积等于△FHO的面积;(3)解:取BC的中点D,连接MD,过点A作AN∥MD交BC于点N,过M、N画直线,则直线MN为所求.点评:此题主要是根据三角形的面积公式,知:三角形的中线把三角形的面积等分成了相等的两部分;同底等高的两个三角形的面积相等.25.已知:如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.试解答下列问题:(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关∠A+∠D=∠B+∠C;(2)仔细观察,在图2中“8字形”的个数:6个;(3)在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.利用(1)的结论,试求∠P的度数;(4)如果图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结论即可)考点:三角形内角和定理.专题:探究型.分析:(1)利用三角形的内角和定理表示出∠AOD与∠BOC,再根据对顶角相等可得∠AOD=∠BOC,然后整理即可得解;(2)根据“8字形”的结构特点,根据交点写出“8字形”的三角形,然后确定即可;(3)根据(1)的关系式求出∠OCB﹣∠OAD,再根据角平分线的定义求出∠DAM﹣∠PCM,然后利用“8字形”的关系式列式整理即可得解;(4)根据“8字形”用∠B、∠D表示出∠OCB﹣∠OAD,再用∠D、∠P表示出∠DAM﹣∠PCM,然后根据角平分线的定义可得∠DAM﹣∠PCM=(∠OCB﹣∠OAD),然后整理即可得证.解答:解:(1)在△AOD中,∠AOD=180°﹣∠A﹣∠D,在△BOC中,∠BOC=180°﹣∠B﹣∠C,∵∠AOD=∠BOC(对顶角相等),∴180°﹣∠A﹣∠D=180°﹣∠B﹣∠C,∴∠A+∠D=∠B+∠C;(2)交点有点M、O、N,以M为交点有1个,为△AMD与△CMP,以O为交点有4个,为△AOD与△COB,△AOM与△CON,△AOM与△COB,△CON 与△AOD,以N为交点有1个,为△ANP与△CNB,所以,“8字形”图形共有6个;(3)∵∠D=40°,∠B=36°,∴∠OAD+40°=∠OCB+36°,∴∠OCB﹣∠OAD=4°,∵AP、CP分别是∠DAB和∠BCD的角平分线,∴∠DAM=∠OAD,∠PCM=∠OCB,又∵∠DAM+∠D=∠PCM+∠P,∴∠P=∠DAM+∠D﹣∠PCM=(∠OAD﹣∠OCB)+∠D=×(﹣4°)+40°=38°;(4)根据“8字形”数量关系,∠OAD+∠D=∠OCB+∠B,∠DAM+∠D=∠PCM+∠P,所以,∠OCB﹣∠OAD=∠D﹣∠B,∠PCM﹣∠DAM=∠D﹣∠P,∵AP、CP分别是∠DAB和∠BCD的角平分线,∴∠DAM=∠OAD,∠PCM=∠OCB,∴(∠D﹣∠B)=∠D﹣∠P,整理得,2∠P=∠B+∠D.点评:本题考查了三角形内角和定理,角平分线的定义,多边形的内角和定理,对顶角相等的性质,整体思想的利用是解题的关键.26.课本拓展旧知新意:我们容易证明,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?1.尝试探究:(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?2.初步应用:(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,∠1=130°,则∠2﹣∠C=50°;(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案∠P=90°﹣∠A.3拓展提升:(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D 有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需说明理由)考点:三角形的外角性质;三角形内角和定理.专题:探究型.分析:(1)根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠DBC+∠ECB,再利用三角形内角和定理整理即可得解;(2)根据(1)的结论整理计算即可得解;(3)表示出∠DBC+∠ECB,再根据角平分线的定义求出∠PBC+∠PCB,然后利用三角形内角和定理列式整理即可得解;(4)延长BA、CD相交于点Q,先用∠Q表示出∠P,再用(1)的结论整理即可得解.解答:解:(1)∠DBC+∠ECB=180°﹣∠ABC+180°﹣∠ACB=360°﹣(∠ABC+∠ACB)=360°﹣(180°﹣∠A)=180°+∠A;(2)∵∠1+∠2=∠180°+∠C,∴130°+∠2=180°+∠C,∴∠2﹣∠C=50°;(3)∠DBC+∠ECB=180°+∠A,∵BP、CP分别平分外角∠DBC、∠ECB,∴∠PBC+∠PCB=(∠DBC+∠ECB)=(180°+∠A),在△PBC中,∠P=180°﹣(180°+∠A)=90°﹣∠A;即∠P=90°﹣∠A;故答案为:50°,∠P=90°﹣∠A;(4)延长BA、CD于Q,则∠P=90°﹣∠Q,∴∠Q=180°﹣2∠P,∴∠BAD+∠CDA=180°+∠Q,=180°+180°﹣2∠P,=360°﹣2∠P.点评:本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的内角和定理,角平分线的定义,熟记性质并读懂题目信息是解题的关键.27.(1)已知:如图1,P为△ADC内一点,DP、CP分别平分DP、CP分别平公∠ADC 和∠ACD,如果∠A=60°,那么∠P=120°;如果∠A=90°,那么∠P=135°;如果∠A=x°,则∠P=90+°;(答案直接填在题中横线上)(2)如图2,P为四边形ABCD内一点,DP、CP分别平分∠ADC和∠BCD,试探究∠P 与∠A+∠B的数量关系,并写出你的探索过程;(3)如图3,P为五边形ABCDE内一点,DP、CP分别平分DP、CP分别平公∠ADC和∠ACD,请直接写出∠P与∠A+∠B+∠E的数量关系:(∠A+∠B+∠E)﹣90°;(4)如图4,P为六边形ABCDEF内一点,DP、CP分别平分DP、CP分别平公∠ADC和∠ACD,请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:(∠A+∠B+∠E+∠F)﹣180°;(5)若P为n边形A1A2A3…A n内一点,PA1平分∠A n A1A2,PA2平分∠A1A2A3,请直接写出∠P与∠A3+A4+A5+…∠A n的数量关系:(∠A3+∠A4+∠A5+…∠A n)﹣(n﹣4)×90°.(用含n的代数式表示)【考点】多边形内角与外角;三角形内角和定理;三角形的外角性质.【专题】探究型.【分析】(1)根据角平分线的定义可得∠PDC=∠ADC,∠PCD=∠ACD,然后根据三角形内角和定理列式整理即可得解;(2)根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理(1)解答即可;(3)根据五边形的内角和公式表示出∠EDC+∠BCD,然后同理(1)解答即可;(4)根据六边形的内角和公式表示出∠EDC+∠BCD,然后同理(1)解答即可;(5)根据n边形的内角和公式表示出∠EDC+∠BCD,然后同理(1)解答即可.【解答】解:(1)∵DP、CP分别平分∠ADC和∠ACD,∴∠PDC=∠ADC,∠PCD=∠ACD,∴∠DPC=180°﹣∠PDC﹣∠PCD=180°﹣∠ADC﹣∠ACD=180°﹣(∠ADC+∠ACD)=180°﹣(180°﹣∠A)=90°+∠A,∴如果∠A=60°,那么∠P=120°;如果∠A=90°,那么∠P=135°;如果∠A=x°,则∠P=(90+)°;(2)∵DP、CP分别平分∠ADC和∠BCD,∴∠PDC=∠ADC,∠PCD=∠BCD,∴∠DPC=180°﹣∠PDC﹣∠PCD=180°﹣∠ADC﹣∠BCD=180°﹣(∠ADC+∠BCD)=180°﹣(360°﹣∠A﹣∠B)=(∠A+∠B);(3)五边形ABCDEF的内角和为:(5﹣2)•180°=540°,∵DP、CP分别平分∠EDC和∠BCD,∴∠P=∠EDC,∠PCD=∠BCD,∴∠P=180°﹣∠PDC﹣∠PCD=180°﹣∠EDC﹣∠BCD=180°﹣(∠EDC+∠BCD)=180°﹣(540°﹣∠A﹣∠B﹣∠E)=(∠A+∠B+∠E)﹣90°,即∠P=(∠A+∠B+∠E)﹣90°.(4)六边形ABCDEF的内角和为:(6﹣2)•180°=720°,∵DP、CP分别平分∠EDC和∠BCD,∴∠PDC=∠EDC,∠PCD=∠BCD,∴∠P=180°﹣∠PDC﹣∠PCD=180°﹣∠EDC﹣∠BCD=180°﹣(∠EDC+∠BCD)=180°﹣(720°﹣∠A﹣∠B﹣∠E﹣∠F)=(∠A+∠B+∠E+∠F)﹣180°,即∠P=(∠A+∠B+∠E+∠F)﹣180°.(5)同(1)可得,∠P=(∠A3+∠A4+∠A5+…∠A n)﹣(n﹣4)×90°.故答案为:120,135,(90+);(∠A+∠B);∠P=(∠A+∠B+∠E)﹣90°;∠P=(∠A+∠B+∠E+∠F)﹣180°;,∠P=(∠A3+∠A4+∠A5+…∠A n)﹣(n﹣4)×90°.【点评】本题考查了三角形的外角性质,三角形的内角和定理,多边形的内角和公式,此类题目根据同一个解答思路求解是解题的关键.28.已知凸四边形ABCD中,∠A=∠C=90°.(1)如图1,若DE平分∠ADC,BF平分∠ABC的邻补角,判断DE与BF位置关系并证明;(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.考点:多边形内角与外角;平行线的判定.分析:(1)DE⊥BF,延长DE交BF于G.易证∠ADC=∠CBM.可得∠CDE=∠EBF.即可得∠EGB=∠C=90゜,则可证得DE⊥BF;(2)DE∥BF,连接BD,易证∠NDC+∠MBC=180゜,则可得∠EDC+∠CBF=90゜,继而可证得∠EDC+∠CDB+∠CBD+∠FBC=180゜,则可得DE∥BF.解答:解:(1)DE⊥BF,延长DE交BF于点G∵∠A+∠ABC+∠C+∠ADC=360°又∵∠A=∠C=90°,∴∠ABC+∠ADC=180°∵∠ABC+∠MBC=180°∴∠ADC=∠MBC,∵DE、BF分别平分∠ADC、∠MBC∴∠EDC=∠ADC,∠EBG=∠MBC,∴∠EDC=∠EBG,∵∠EDC+∠DEC+∠C=180°∠EBG+∠BEG+∠EGB=180°。
七年级数学下学期培优作业15试题(共5页)

七年级下册数学(shùxué)培优作业15一、选择题〔每一小题3分,一共24分〕题号 1 2 3 4 5 6 7 8答案1、以下等式正确的选项是〔▲〕A、 B、C、 D、2、假设,那么以下不等式中成立的是〔▲〕A、 B、 C、 D、3、用平方差公式计算结果正确的选项是〔▲〕A、B、x4-1C、D、4、三角形两边为7和2,其周长为偶数,那么第三边的长为〔▲〕A、3B、6C、7D、85、以下句子中,是命题的是〔▲〕A、三角两边之和大于第三边吗?B、作线段AB∥CDC、连结A、B两点D、正数大于负数6、以下命题的逆命题是真命题的是〔▲〕A、对顶角相等B、两直线平行,同旁内角相等C、假如a2=b2,那么a=bD、三角形的外角和为360度7、关于的方程的解为正实数,那么的取值范围是〔▲〕A、 B、 C、 D、8、如图,AB∥EF,∠C=90°,那么α、β、γ的关系为〔▲〕A、β=α+γB、α+β+γ=180°〔第8C、β+γ-α=90°D、α+β-γ=90°二、填空题〔每空3分,一共(yīgòng) 30分〕9、某种细菌的存活时间是只有0. 000 012秒,假设用科学记数法表示此数据应为。
10、。
11、假设一个多边形的内角和是外角和的2倍,那么这个多边形的边数为。
12、,,那么= 。
13、:a+b=,ab=1,化简〔a-2〕(b-2)的结果是。
14、因式分解: 4a(x-y)-2b(y-x)= 。
15、在方程=5中,用含x的代数式表示为:y=。
16、某种品牌的面粉,外包装标明:净含量为30kg,说明了这袋面粉的净含量x范围是。
17、假设,那么x=,y=。
18、∠A=50°,且∠B的两边与∠A的两边分别垂直,那么∠B的度数为。
三、解答题〔一共46分〕19、计算:〔每一小题3分,一共6分〕〔1〕〔2〕20、因式分解:〔每一小题3分,一共6分〕〔1〕〔2〕21、解方程组、不等式组:〔每一小(yī xiǎo)题3分,一共6分〕〔1〕〔2〕22、〔5分〕如图,: ∠ABC+∠C+∠CDE=360°,GH分别交AB、ED 于点G、H。
(完整版)七年级(下)数学培优试题(九)含答案,推荐文档

七年级(下)数学培优试题(九)含答案(考试时间:120分钟满分:150分)题号一二三四五总分总分人得分一、选择题:(本大题10个小题,每小题4分,共40分)每个小题都给出了代号为 A、B、C、D的四个答案,其中只有一个是正确的,请将正确答案的代号填入题后的括号中.1.数学考试中,每一个选择题都给出了代号为 A、B、C、D的四个答案,但其中只有一个是正确的.如果同学们不加思考就在四个答案中随便选一个,则()A.选对的可能性大 B.选错的可能性大C.选对、选错的可能性一样大 D.说不清楚2.下列几何体属于柱体的个数是()A.3B.4C.5D.63.下列几个事件中,不确定事件的个数是()①抛出的蓝球会下落②掷一枚均匀的骰子,骰子停止转动后偶数点朝上③在正常情况下,将水加热1000C到时,水会沸腾④任意买一张电影票,座位号是奇数A.1 B.2 C.3 D.44.袋中装有4只红球、3只黑球、2只白球、1只黄球,这些球除颜色外都相同.现从袋中任意摸出一球,则摸到可能性最大的是()A.红球B.黑球C.白球D.黄球5.下列说法正确的是()A.若两个数的绝对值相等,则这两个数相等 B.有理数的绝对值一定比0大C.互为相反数的两个数的绝对值相等D.有理数的相反数一定比0小6.下列四个图中,能用∠1、∠AOB、∠O三种方法表示同一个角的图形是()得分评卷人7.某班共有x 个学生,其中女生人数占%45,则男生人数是( )A .x %45B .%45xC .x %)451(-D .%451-x8.下列计算正确的是( )A .x x x 257=-B .xy y x 633=+C .971622=-y yD .1091922=-ab b a9. 信用卡上的号码由14位数字组成,每一位数字写在下面的方格中,如果任何相邻的 三个数字之和都等于20,则x 的值等于( )A.3B.4C.5D.6 10.下列各式一定成立的个数是( )①22)(a a -= ②33)(a a -= ③22a a -=- ④33a a = A. 4 B. 3 C.2 D. 1二、填空题:(本大题6个小题,每小题4分,共24分)请将正确答案直接填写在题中的横线上.11.如果零上5ºC 记作+5ºC ,那么零下3ºC 记作 . 12.已知5=x 是方程a ax +=-208的解,则=a . 13.用科学记数法表示:1300000000= .14.如图,若D 是AB 的中点,E 是BC 的中点,且8=AC ,3=EC ,则AD =_____.15.用火柴棒按如图所示的方式搭图形,按照这样的规律搭下去,填写下表:图形编号 (1)(2)(3)…n火柴根数得分 评卷人14题图EDCB A16.从3-,2-,1-,4,5中任意取出三个不同的数,将其可能得到的最小乘积填在下面的□中,可能得到的最大乘积填在下面的○中,并将下式计算的结果填在等号右边的横线上: .三、解答题:(本大题4个小题,每小题6分,共24分) 下列各题解答时必须给出必要的演算过程或推理步骤.17.计算:)43(27)56(13-++-+ 18.化简:)2()35(b a b a a ---+19.如图,已知A 、B 、C 、D 是平面内四个点,请根据下列要求在所给图中作图. ①画直线AB ; ②画射线AC ; ③画线段AD ; ④画DBC ∠; ⑤线段AD 与DBC ∠的边BC 交于点O ; ⑥过点O 作线段BD OE ⊥于E .20.下图是由几个小立方块所搭几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,请画出这个几何体的主视图和左视图.主视图 左视图四、解答题:(本大题4个小题,每小题10分,共40分) 下列各题解答时必须给出必要的演算过程或推理步骤.21.解下列方程(每小题5分,共10分)(1)3)20(34=--x x ; (2)1615312=--+x x . 得分 评卷人得分 评卷人19题图22.先化简,再求值(每小题5分,共10分) (1))32(36922x x x x --+,其中2-=x ;(2))1(2)1(2)(22222+---+ab b a ab b a ,其中2,2=-=b a .23.一所中学准备搬迁到新校舍,在迁入新校舍之前,同学们就该校300名学生如何到校问题进行了一次调查,并得到以下数据:请根据以上数据在如下指定的图中分别制作条形统计图、折线统计图、扇形统计图,并填写扇形统计图相关数据表.步行 骑自行车 坐公共汽车 其他 60人100人130人10人24.某文艺团体为“希望工程”募捐组织了一场义演,共售出1000张票,其中成人票每张8元,学生票每张5元,筹得票款6950元.求成人票与学生票各售出多少张?(请按下列两种不同的设未知数方法,完成后续解题过程,每种解法5分)解法1:设售出的成人票为x张,则根据题意列方程:解法2:设所得的成人票款为y元,那么所得的学生票款为()元,则根据题意列方程:得分评卷人五、解答题:(本大题2个小题,25题10分,26题12分,共22分)解答时必须给出必要的演算过程或推理步骤.25. 利用正方形、圆、三角形、平行四边形设计一个图案,并说明你想表现什么.(要求:每种图形都要用到,且其中两种及两种以上图形要用到2次及2次以上)3⨯方阵图,每行的三个数、每列的三个数,每斜对角的三个数相加的26.图1是一个3和均相等.的和均相等,是我们祖先早就在研究的问题.古代的“洛书”、汉朝徐岳的“九宫算”就揭示出祖先们得到的神奇填写方法.图1显示出把4-,3-,2-,1-,0,1,2,3,4填入一个33⨯方阵,使每行、每列、每斜对角的三个数相加的和均相等的一种方法.同学们,你能正确填写吗?马上试一试:(1)请观察图1中数字的填写规律,然后将下列各数组中的9个数分别填入图2 、图3、图4所示的9个空格中,使得每行的三个数、每列的三个数,每斜对角的三个数相加的和均相等;(图2、3、4填对一个得2分,共6分) ①6,5,4,3,2,1,0,1-,2- ②9,8,7,6,5,4,3,2,1 ③8-,6-,4-,2-,0,2,4,6,8(2)拓展探究:在图5所示 9个空格中,填入5个2和4个2-,使得每行、每列、每斜对角的三个数的乘积都是8;(3分)(3)拓展再探究:将25,24,23,22,21,20,19,18,17,16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1这25个数分别填入图 6所示25个空格中,使得每行、每列、每斜对角的五个数相加的和均相等.(3分)七年级数学试题参考答案及评分意见一、选择题:BDB A C ,DCABD试题出处:2题(课本P5)、3题(课本P204)、4题(课本P240)、5题(课本P50)、7题(课本P109)、8题(课本P119)、10题(课本P100)二、填空题: 11. C ︒-3(填3-扣1分)12.7=a 13.9103.1⨯ 14.1;15. 7,12,17,25+n 16.-60,30,-2. 试题出处:11题(课本P40)、12题(课本P196)、13题(课本P200)、14题(课本P141改)15题(课本P105) 三、解答题:(共24分)17.(课本P58)解:原式=)]43()56[()2713(-+-++-----------2分 =)99(40-+-----------------------4分 =59-.------------- ----------- ---6分 18.(课本P121)解:原式=b a b a a 235+--+-----------2分=)23()5(b b a a a +-+-+------4分 =b a -5.-----------------------6分19.画对一个得1分,共6分.20.(课本P26)画对主视图和左视图各3分共6分 四、解答题:(本大题4个小题,每小题10分,共40分) 21.解下列方程:20题左视图20题主视图(1)(课本P175)解:去括号得:33604=+-x x .-----------------2分 移项得:60334+=+x x .-----------------3分合并同类项得:637=x .------------------------4分 两边同除以7得:9=x .------------------------5分(2)(课本P178)解:去分母得:6)15()12(2=--+x x .----------1分去括号得:61524=+-+x x .--------------2分移项得:21654--=-x x .-------------3分合并同类项得:3=-x .-----------------------4分 两边同除以1-得:3-=x .--------------------5分22.(1)(课本P130) 解:原式=222369x x x x +-+-----------------1分 =286x x +.--------------------------2分当2-=x 时,原式=2)2(8)2(6-⨯+-⨯----------------3分=3212+--------------------------4分=20.----------------------- -------5分(2)(课本P130) 解:原式=2222222222--+-+ab b a ab b a ------------2分 =)22()22()22(2222-+-+-ab ab b a b a -----3分=0. ---------------------4分 当2,2=-=b a 时,原式=0.--------------------5分 23.(课本P212)图如下.条形统计图3分,折线统计图3分;扇形统计图有关数据表2分,扇形统计图2分. (所作条形统计图、折线统计图、扇形统计图中无“步行、骑自行车、坐公共汽车和其他”说明,每个图扣1分)24.(课本P189)解法1:设售出的成人票为x 张,则根据题意列方程: 了 69508)1000(5=+-x x .------------2分 解这个方程得:650=x .3501000=-x .----------------4分答:售出成人票650张,学生票350张.----------5分解法2:设所得的成人票款为y 元,则根据题意列方程:1000856950=+-yy .--------------2分 解这个方程得:5200=y .6508=y , 35056950=-y.----4分 答:售出成人票650张,学生票350张.----------5分25. (课本P242)本题属于开放性试题,可根据美观程度和与欲表现吻合程度参照以下标准给分:优秀:四种图形都用到,且其中有两种及两种以上图形用到2次及以上,图案与欲表现意图非常吻合,图案漂亮、美观、大气.---------10分良好:四种图形都用到,且其中只有一种图形用到2次及以上,图案与欲表现意图吻合,图案简洁、漂亮、美观.-----------------8分及格:四种图形都用到且只用到1次,图案与欲表现意图吻合,图案简洁、漂亮、美观.-----------------------------6分 不合格:四种图形未用完.-----0分 26.(1)(课本P60、P65、P65)图2填写过程如下:(填法不唯一,图3中只要按由小到大,斜角填写均可)图3、4填写过程如下:(填法不唯一,在图3中只要按由小到大,斜角填写均可)(2)图5填写如图:(3)图6填写过程如下:(填法不唯一,图3中只要按由小到大,斜角填写均可)。
七年级数学上册全册单元试卷培优测试卷

七年级数学上册全册单元试卷培优测试卷一、初一数学上学期期末试卷解答题压轴题精选(难)1.已知,,点E是直线AC上一个动点(不与A,C重合),点F是BC边上一个定点,过点E作,交直线AB于点D,连接BE,过点F作,交直线AC于点G.(1)如图①,当点E在线段AC上时,求证:.(2)在(1)的条件下,判断这三个角的度数和是否为一个定值?如果是,求出这个值,如果不是,说明理由.(3)如图②,当点E在线段AC的延长线上时,(2)中的结论是否仍然成立?如果不成立,请直接写出之间的关系.(4)当点E在线段CA的延长线上时,(2)中的结论是否仍然成立?如果不成立,请直接写出之间的关系.【答案】(1)解:∵∴∵∴∴(2)解:这三个角的度数和为一个定值,是过点G作交BE于点H∴∵∴∴∴即(3)解:过点G作交BE于点H∴∵∴∴∴即故的关系仍成立(4)不成立| ∠EGF-∠DEC+∠BFG=180°【解析】【解答】解:(4)过点G作交BE于点H∴∠DEC=∠EGH∵∴∴∠HGF+∠BFG=180°∵∠HGF=∠EGF-∠EGH∴∠HGF=∠EGF-∠DEC∴∠EGF-∠DEC+∠BFG=180°∴(2)中的关系不成立,∠EGF、∠DEC、∠BFG之间关系为:∠EGF-∠DEC+∠BFG=180°故答案为:不成立,∠EGF-∠DEC+∠BFG=180°【分析】(1)根据两条直线平行,内错角相等,得出;两条直线平行,同位角相等,得出,即可证明.(2)过点G作交BE于点H,根据平行线性质定理,,,即可得到答案.(3)过点G作交BE于点H,得到,因为,所以,得到,即可求解.(4)过点G作交BE于点H,得∠DEC=∠EGH,因为,所以,推得∠HGF+∠BFG=180°,即可求解.2.已知线段AB=6.(1)取线段AB的三等分点,这些点连同线段AB的两个端点可以组成多少条线段?求这些线段长度的和;(2)再在线段AB上取两种点:第一种是线段AB的四等分点;第二种是线段AB的六等分点,这些点连同(1)中的三等分点和线段AB的两个端点可以组成多少条线段?求这些线段长度的和。
七年级培优卷(一)

七年级培优卷(一)1.下列说法:①若a a =,则0a =;②若a ,b 互为相反数,且0ab ≠,则1b a=-;③若22a b =,则a b =;④若0a <,0b <,则ab a ab a -=-.其中正确的个数有(B )A .1个B .2个C .3个D .4个2.等边ABC △在数轴上的位置如图所示,点A 、C 对应的数分别为0和1-,若ABC △绕顶点沿顺时针方向在数轴上连续翻转,翻转1次后,点B 所对应的数为1,则连续翻转2012次后,点B ().不对应任何数B .对应的数是2010C .对应的数是2011D .对应的数是20123.已知a ,b ,c 为非零的实数,则a ab ac bc a ab ac bc +++的可能值的个数为()A .4B .5C .6D .74.若33x x +=-,则x 的取值范围是.5.规定图形表示运算a b c -+,图形表示运算x z w γ+--(直接写出答案).6.已知a ,b,c ,d 分别是一个四位数的千位,百位,十位,个位上的数字,且低位上的数字不小于高位上的数字,当a b b c c d d a -+-+-+-取得最大值时,这个四位数的最小值是.7.(8分)如图,数轴上的三点A 、B 、C 分别表示有理数a 、b 、C .1)填空:a b -0,a c +0,b c -0.(用<或>或=号填空)(2)化简:a b a c b c --++-8.(8分)已知3x =,7y =.(1)若x y <,求x y +的值;(2)若0xy <,求x y -的值.9.(10分)同学们都知道,()52--表示5与2-之差的绝对值,实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离,(1)()52--=.(2)同理52x x ++-表示数轴上有理数x 所对应的点到5-和2所对应的两点距离之和,请你求出所有符合条件的整数x ,使得527x x ++-=.(3)由以上探索猜想对于任何有理数x ,63x x ++-是否有最小值?如果有,写出最小值;如果没有,说明理由.10.已知a 、b 是有理数,满足a <0<b ,a +b >0,则把a 、-a 、b 、-b 按照从小到大的顺序排列,正确的是()A .-b <-a <a <bB .-b <a <-a <bC .-a <-b <a <bD .a <-b <b <-a11.下列各式运用等式的性质变形,错误的是()A .若-a =-b ,则a =bB .若c b c a =,则a =bC .若ac =bc ,则a =bD .若(m 2+1)a =(m 2+1)b ,则a =b12.在数轴上,点A 表示的数为-3,将点A 在数轴上移动4个单位长度到达点B ,则点B 表示的数是__________13.船在静水中的速度为a 千米/时,水流速度为18千米/时,船顺水航行5小时的行程比船逆水航行4小时的行程多(__________)千米14.如图,已知四个有理数m 、n 、p 、q 在数轴上对应的点分别为M 、N 、P 、Q ,且m +p =0,则在m 、n 、p 、q 四个有理数中,绝对值最小的一个是___________15.(本题12分)某校要将一块长为a 米,宽为b 米的长方形空地设计成花园,现有如下两种方案供选择方案一:如图1,在空地上横、竖各铺一条宽为4米的石子路,其余空地种植花草方案二:如图2,在长方形空地中留一个四分之一圆和一个半圆区域种植花草,其余空地铺筑成石子路(1)分别表示这两种方案中石子路(图中阴影部分)的面积(若结果中含有π,则保留)(2)若a =30,b =20,该校希望多种植物美化校园,请通过计算选择其中一种方案(π取3.14)16.实数a 、b 在数轴上对应点的位置如图所示,则下列结论:①a -b >1;①a 2>b 2;①ab >-1;①1->ba ,其中正确结论的序号是___________17.九格幻方有如下规律:处于同一横行、同一竖列、同一斜对角线上的三个数的和都相等(如图1).则图2的九格幻方中的9个数的和为___________(用含a 的式子表示)五、解答题(共3小题,第26题10分,第27题12分,第28题12分共34分)18.(本题10分)已知A =2x 2+3xy -2x -1,B =x 2-xy -1(1)化简:4A -(2B +3A ),将结果用含有x 、y 的式子表示(2)若式子4A -(2B +3A )的值与字母x 的取值无关,求B A y 1251412573-+的值19.(本题12分)观察下面三行数:①2,-4,8,-16,32,-64……;①3,-3,9,-15,33,-63……;①-1,2,﹣4,8,-16,32……;取每一行的第n个数,依次记为x、y、z.如上图中,当n=2时,x=-4,y=-3,z=2(1)当n=7时,请直接写出x、y、z的值,并求这三个数中最大的数与最小的数的差(2)已知n为偶数,且x、y、z这三个数中最大的数与最小的数的差为384,求n的值(3)若m=x+y+z,则x、y、z这三个数中最大的数与最小的数的差为_________(用含m的式子表示)20.(本题12分)如图,在数轴上,点A、B表示的数分别是-4、8(A、B两点间的距离用AB表示),点M、N是数轴上两个动点,分别表示数m、n(1)AB=______个单位长度;若点M在A、B之间,则|m+4|+|m-8|=___________(2)若|m+4|+|m-8|=20,求m的值(3)若点M、点N既满足|m+4|+n=6,也满足|n-8|+m=28,则m=________;n=________21.(8分)我们把分子为1的分数叫做单位分数,如…,任何一个单位分数都可以拆分成两个不同的单位分数的和,如,,…观察上述式子的规律:(1)把写成两个单位分数之和;(2)把表示成两个单位分数之和.22.(8分)如图所示,将面积为a2的小正方形和面积为b2的大正方形放在同一水平面上(b>a>0).(1)用a、b表示阴影部分的面积;(2)计算当a=3,b=5时,阴影部分的面积.23.(8分)阅读下列材料:我们知道|a|的几何意义是在数轴上数a对应的点与原点的距离,即|a|=|a﹣0|,也就是说,|a|表示在数轴上数a与数0对应点之间的距离.这个结论可以推广为:|a﹣b|表示在数轴上数a与b对应点之间的距离.例1已知|a|=2,求a的值.解:在数轴上与原点距离为2的点的对应数为﹣2和2,即a的值为﹣2和2.例2已知|a﹣1|=2,求a的值.解:在数轴上与1的距离为2点的对应数为3和﹣1,即a的值为3和﹣1.仿照阅读材料的解法,解决下列问题:(1)已知|a|=3,求a的值;(2)已知|a+2|=4,求a的值;(3)若数轴上表示a的点在﹣4与2之间,则|a+4|+|a﹣2|的值为;(4)当a满足时,则|a﹣1|+|a﹣2|的值最小,最小值是.24.如图是小明家的楼梯示意图,其水平距离(即:AB的长度)为(2a+b)米,一只蚂蚁从A点沿着楼梯爬到C点,共爬了(3a﹣b)米.问小明家楼梯的竖直高度(即:BC的长度)为米.25.若a是不为1的实数,我们把1﹣称为a的差倒数,设a1=﹣,若a2是a1的差倒数,a3是a2的差倒数,a4是a3是差倒数,…,依此类推,a2017的值是.26.按下面的程序计算:若输入x=100,输出结果是501,若输入x=25,输出结果是631,若开始输入的x值为正整数,最后输出的结果为556,则开始输入的x值可能有()A.1种B.2种C.3种D.4种27.若a,b互为相反数,C,d互为倒数,m为绝对值是2,则+2m2﹣3cd 的值是()A.B.6C.5D.。
七年级数学培优测试

七年级数学培优测试对想进培优班的学生是个能力水平的测试七年级数学培优测试卷一、选择题(每小题4分,共40分)1.在____、____、____这三个数中,质数有()A.1个 B.2个 C.3个 D.4个 2.如图,AB∥CD,AC⊥BC,AC≠BC,则图中与∠BAC互余的角有()A.1个 B.2个 C.3个D.4个3.在数轴上,坐标是整数的点称为“整点”.设数轴的单位长度是1cm,若在这条数轴上随意画出一条长为____cm的线段AB,则线段AB盖住的整点至少有()A.____个 B.____个 C.____个 D.____个4.若_2+_-2=0,则_3+2_2-_+____=()A.____ B.____ C.-____ D.-____5.在△ABC中,2∠A=3∠B,且∠C-30__186;=∠A+∠B,则△ABC是() A.锐角三角形 B.钝角三角形C.有一个角是30__186;的直角三角形 D.等腰直角三角形6.设M=(|_+2|-|_|+2)(|_+2|-|_|-2),则M的取值范围表示在数轴上是()7.The coordinates of the three points A,B,C on the plane are (-5,-5),(-2,-1) and (-1,-2),respectively,the triangle ABC is () A.a right triangle B.an isosceles triangleC.an equilateral triangle D.an obtuse triangle(英汉词典:right 直角的,isosceles 等腰的,equilateral 等边的,obtuse 钝角的)8.用一根长为am的细绳围成一个等边三角形,测得它的面积是bm2.在这个等边三角形内任取一点P,则点P到等边三角形三边的距离的和等于()A 2b 4b 6b 8b m B.m Cm D.m aaaa9.用数字1,2,3,4,5,6组成的没有重复的三位数中,是9的倍数的数有()A.12个 B.18个 C.20个 D.30个10.如图,平面上有A、B、C、D、E五个点,其中B、C、D及A、E、C在同一条直线上,那么以这五个点中的三个点为顶点的三角形有()A.4个 B.6个 C.8个 D.10个 E 二、A组填空题(每小题4分,共40分) a____+b____-c____11.当a=-1,b=0,c=1时,代数式. a-b+c12.《全国土地利用总体规划纲要(____—____)》明确,全国耕地保有量到____年保持在18.18亿亩.用科学记数法表示此数,是. B 13.如图,点E、F、G、H分别是正方形ABCD各边的中点,点I、J、K、L分别是四边形EFGH各边的中点,点M、N分别是IJ、IL的F 中点.若图中阴影部分的面积是10,则AB的长是.14.古代科举考试以四书五经为主要考试内容.据统计,《论语》11705C 字,《孟子》34685字,《易经》24107字,《书经》25700字,《诗经》39234字,《礼记》99010字,《左传》196845字.根据以上数据计算,《论语》字数占这7本书字数的 %(保留两个有效数字).。
七年级培优试卷 一

七年级培优试卷一七年级培优试卷(一)1.下列式子中,正确的是( )A.5-|-5|=10 B.(-1) = -99 C.-10= (-10) ×(-10) D.-(-2)=4 2.下列代数式的值中,一定是正数的是( )A .(x +1) 2B .x +1C .(-x ) 2+1D .-x 2+116.某校开展以“迎新年”为主题的艺术活动,举办了四个项目的比赛. 它们分别是:A 演讲、B 唱歌、C书法、D 绘画。
要求每位同学必须参加且限报一项. 以七(9)班为样本进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给出的信息解答下列问题:(1)这次共调查了_____名学生;求出扇形统计图中参加书法比赛的学生所在的扇形圆心角的度数; (2)补充完整条形统计图;3.已知a -b = -2,则代数式3 (a-b) 2 -b+a的值为( ) 若该校九年级学生共有 (3)500人,请你估计这次活动中参加演讲和绘画的学生共有多少人?A .-12B .-10C .10D . 124.根据2021年第六次全国人口普查公报,成都市常住人口约为1405万人,用科学计数法表示为 ( ) A . 1. 405⨯104 B . 1. 405⨯107 C . 1. 405⨯105 D . 1.405⨯108 5. 某学校楼阶梯教室,第一排有m 个座位,后面每一排都比前面一排多4个座位,则第n 排座位数是( )A .n+4(m -1) B.m+4(n -1) C .m+4n D.m+4 6. 下列方程的变形中正确..的是( ) A .由x +5=6x -7得x -6x =7-5 B .由-2(x -1)=3得-2x -2=3C .由x -310x -300.7=1得7=10D .由12x +9=-32x -3得2x = -12 7.若代数式(m -2) x 2+5y 2+3的值与字母x 的取值无关,则m . 8.某厂第一个月生产机床a 台,第二个月生产的机床数量比第一个月的1.5倍少2台,则这两个月共生产机床台.9. 如果甲、乙两班共有90人,如果从甲班抽调3人到乙班,则甲乙两班的人数相等,则甲班原有人.10. 已知C 点在线段AB 上,线段AB=14cm,BC=3AC ,则BC 的长为. 11.某种电器产品,每件若以原定价的9折销售,可获利150元,若以原定价的7折销售,则亏损50元,该种商品每件的进价为___ ______元.12(1)-23⨯(-8) -⎛ ⎛-1⎛2⎛⎛⨯(-16)+49⨯(-3)2 (2) -32÷(-3) 2+3⨯(-2) +-4+(512+23-34) ⨯(-12)13.解方程:x -1-x x +3=214. 先化简,再求值:2(5a 2-7ab+9b 2)-3(14a 2-2ab+3b2) ,其中a=34, b =-23.15.如图, 已知O 为直线AB 上一点, 过点O 向直线AB 上方引三条射线OC 、OD 、OE , 且OC 平分∠AOD ,∠BOE =3∠DOE ,∠COE =70︒,求A∠BOE 的度数.项目 17.某公司要把240吨白砂糖运往某市的A 、B 两地,用大、小两种货车共20辆,恰好能一次性装完这批白砂糖.已知这两种货车的载重量分别为15吨/辆和10吨/辆,运往A 地的运费为:大车630元/辆,小车420元/辆;运往B 地的运费为:大车750元/辆,小车550元/辆.(1)求两种货车各用多少辆;(2)如果安排10辆货车前往A 地,其中调往A 地的大车有a 辆,其余货车前往B 地,若设总运费为W ,求w 与a 的关系式(用含有a 的代数式表示w ).18.观察上面的一系列等式: 32-12=8×1;52-32=8×2;72-52=8×3;92-72=8×4;……则第n 个等式为. 19.已知,a =-a ,=-1 , c =c , 化简a +b +a -c +b -c =.20.有一些相同的房间需要粉刷,一天3名师傅去粉刷8个房间,结果其中有40m 2墙面未来得及刷;同样的时间内5名徒弟粉刷了9个房间的墙面。
(完整版)七年级(下)数学培优试题(七)含答案,推荐文档

七年级(下)数学培优试题(七)含答案(时间:90分钟,满分:100分)一、选一选,看完四个选项后再做决定呀!(每小题3分,共24分)1.下列计算中,正确的是( )A.()23313a a a a --=--B.()222a b a b -=- C.()()2232394a a a ---=- D.()222242a b a ab b -=-+ 2.在1,2,3,4,5这五个数中,任取三个数作为三角形的边长,能围成几种不同的三角形( )A.1种 B.2种 C.3种 D.4种3.如果多项式29x mx ++是一个完全平方式,则m 的值是( )A.3 B.3± C.6 D.6±4.下列语句正确的是( )A.近似数0.009精确到了百分位B.近似数800精确到个位,有一个有效数字C.近似数56.7万精确到千位,有三个有效数字D.近似数53.67010⨯精确到千分位5.如图1,已知AB AC =,E 是角平分线AD 上任意一点,则图中全等三角形有( ) A.4对 B.3对 C.2对 D.1对6.如果两个角互为补角,那么这两个角( )A.都是锐角 B.都是钝角C.一个锐角一个钝角 D.以上说法都不正确7.下列说法正确的个数有( )(1)两个角和其中一角的对边对应相等的两个三角形全等(2)两条边和其中一边的对角对应相等的两个三角形全等(3)三个角对应相等的两个三角形全等(4)成轴对称的两个图形全等A.1个 B.2个 C.3个 D.4个8.有一游泳池已经注满水,现按一定的速度将水排尽,然后进行清扫,再按相同的速度注满清水,使用一段时间后,又按相同的速度将水排尽,则游泳池的存水量V (立方米)随时间t (小时)变化的大致图象可以是( )二、填一填,要相信自己的能力(每小题3分,共30分)1.请你写出一个只含有字母m n ,的单项式,使它的系数为2,次数为3,______.2.在Rt ABC △中,90C =o ∠,A ∠是B ∠的2倍,则A =∠______.3.生物学校发现一种病毒的长度约为0.0000405 毫米,用科学计数法表示为______.有A. B. C. D.效数字是______.4.完全平方公式有许多变形,如:()2222a b a ab b +=++,可以变形为()2222a b a b ab +=+-.请你再写出一个完全平方公式的变形:______.5.如图2,已知ABC DCB =∠∠,现要说明ABC DCB △≌△A,则还要补加一个条件为______.6.某公路急转弯处设立了一面大镜子,从镜子中看到汽车的车牌号码如图3所示,则该汽车的号码是______.7.如图4,已知DE 是AC 的垂直平分线,10cm AB =,11cm BC =,则ABD △的周长为______.8.如图5,是一个正三角形的靶子,靶心为其三条对称轴的交点,则A 部分面积占靶子面积的______,飞镖随机地掷在靶上,则投到区域A 或区域B 的概率是______.9.已知圆柱的底面半径为3厘米,则圆柱的体积υ(厘米3)与高h (厘米)之间的关系式是______.10.观察下列每组算式,并根据你发现的规律填空: 45203618⨯=⎧⎨⨯=⎩,;56304728⨯=⎧⎨⨯=⎩,;67425840⨯=⎧⎨⨯=⎩,;…… 已知122212231494506⨯=,则12211224⨯=______.三、做一做,要注意认真审题呀!(共66分)1.(12分)已知222x x -=,将下式先化简,再求值: ()()()()()213331x x x x x -++-+--.2.(12分)下面是数学课堂的一个学习片断.阅读后,请回答下面的问题:学习等腰三角形有关内容后,张老师请同学们交流讨论这样一个问题:“已知等腰ABC △的A ∠等于30o ,请你求出其余两角.” 同学们经片刻的思考与交流后,李明同学举手讲:“其余两角是30o 和120o ;王华同学说:”其余两角是75o 和75o .还有一些同学也提示了不同的看法……(1)假如你也在课堂中,你的意见如何,为什么?(2)通过上面数学问题的讨论,你有什么感受?(用一句话表示)3.(10分)如图6是小明用棋子摆成的字母“T”,它的主要特点是轴对称图形.请你再用棋子摆出两个轴对称图形的字母(用○代表棋子).4.(16分)“扫雷”是一个有趣的游戏,下图是此游戏的一部分:图7中数学2表示有以该数字为中心的8个方格中有2个地雷,小旗表示该方格已被探明有,,三个方格未被探明,其它地方为完全区(包括有数字的方格).地雷,现在还剩下A B C(1)现在还剩下几个地雷?,,三个方格中有地雷的概率分别是多大?(2)A B C人数 1 2 4 3 2 每人所作标本数 2 4 6 8 10根据表中提供的信息,回答下列问题:(1)该组共有学生多少人?(2)制作标本数在6个及以上的人数在全组人数中所占比例.七年级第二学期期末综合复习数学水平测试参考答案(一)一、1~4.CCDC 5~8.BDBC二、1.略.答案不惟一 2.60o 3.54.0510-⨯;4,0,54.答案不惟一.如()()224a b a b ab -=+- 5.略.答案不惟一6.B6395 7.21 8.13,239.9πh υ= 10.1494504 三、1.化简为:2365x x --,值为1.2.(1)李明和王华同学的回答均不全面,应该是:“其余两角的大小是75o ,75o 或30o ,120o ”; (2)略.只要表述合理即可,如:“分类讨论的思想很重要”等.3.略.4.(1)2;(2)1,12,12. 5.(1)12人;(2)34.。
七年级数学下学期培优试题 新人教版-新人教版初中七年级全册数学试题

七年级数学培优试题填空题(共25题,满分100)1、有一只手表每小时比准确时间慢3分钟, 若在清晨4:30与准确时间对准, 则当天上午手表指示的时间是10:50, 准确时间应该是。
2、将正方形纸片由下往上对折,再由左向右对折,称为完成一次操作(见下图).按上边规则完成五次操作以后,剪去所得小正方形的左下角. 问:当展开这X正方形纸片后,一共有个小孔3、已知关于x的整系数的二次三项式ax2+bx+c,当x分别取1,3,6,8时,某同学算得这个二次三项式的值分别为1,5,25,50,经过验算,只有一个结果是错误的,这个错误的结果是。
4、下表记录了某次钓鱼比赛中,钓到n条鱼的选手数:n 0 1 2 3 …13 14 15 钓到n条鱼的人数9 5 7 23 … 5 2 1 已知:(1)冠军钓到了15条鱼; (2)钓到3条或更多条鱼的所有选手平均钓到6条鱼; (3)钓到12条或更少鱼的所有选手平均钓到5条鱼;则参加钓鱼比赛的所有选手共钓到条鱼。
5、如图,在一个正方体的两个面上画了两条对角线AB,AC,那么这两条对角线的夹角等于度。
6、一个木制的立方体,棱长为n(n是大于2的整数),表面涂上黑色,用刀片平行于立方体的各面,将它切成3n个棱长为1的小立方体,若恰有一个面涂黑色的小立方体的个数等于没有一个面涂黑色的小立方体的个数,则n= .7、把8X不同的扑克牌交替的分发成左右两叠:左一X,右一X,左一X,右一X,……;然后把左边一叠放在右边一叠上面,称为一次操作。
重复进行这个过程,为了使扑克牌恢复到最初的次序,至少要进行操作的次数是。
8、一台大型计算机中排列着500个外形相同的同一种元件,其中有一只元件已损坏,为了找出这一元件,检验员将这些元件按1-500的顺序编号,第一次先从中取出单数序号的元件,发现其中没有坏元件,他将剩下的元件在原来的位置上又按1-250编号。
(原来的2号变成1号,原来的4号变成2号…)又从中取出单数序号的元件进行检查,仍没有发现…如此下去,检查到最后一个元件,才是坏元件。
期中复习培优训练卷(第9章:整式乘法与因式分解)(B)-2020-2021苏科版七年级数学下学期

期中复习培优训练卷(9章:整式乘法与因式分解)(B )-2020-2021苏科版七年级下学期数学一、选择题1、计算(1)(2)x x -+的结果是( )A .22x x +-B .22x x --C .22x +D .22x - 2、下列计算正确的是( )A .224x x x +=B .222()x y x y -=-C .26()x y x y =3D .532x x x =• 3、下列等式从左到右的变形中,属于因式分解的是( )A .()()244224x x x x x -+=+-+ B .()()23123x x x x +-=+-C .()266x x x x -=-D .623ab a b =4、多项式﹣5mx 3+25mx 2﹣10mx 各项的公因式是( )A .5mx 2B .﹣5mx 3C .mxD .﹣5mx 5、在括号内填上适当的单项式,使()2144y -+成为完全平方式应填( )A .12yB .24C .24y ±D .12 6、(﹣8)2009+(﹣8)2008能被下列数整除的是( )A .3B .5C .7D .97、已知25x x m -+有一个因式为2x -,则另一个因式为( )A .3x +B . 6 x ﹣C . 3 x ﹣D .6x + 8、若3x y -=-,5xy =,则代数式3223242x y x y xy -+的值为( )A .90B .45C .15-D .30-9、若2223a b -=,12a b -=,则+a b 的值为( )A .12- B .43 C .32D .210、若11x x -=,则221x x+的值是( )A .3B .2C .1D .411、已知()()22113(21)a b ab ++=-,则1b a a ⎛⎫-⎪⎝⎭的值是( ) A .0 B .1 C .-2 D .-112、7张如图1的长为a ,宽为b (a >b )的小长方形纸片,按图2的方式不重叠地放在矩形ABCD 内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S ,当BC 的长度变化时,按照同样的放置方式,S 始终保持不变,则a ,b 满足( )A .a=25b B .a=3b C .a=27b D .a=4b二、填空题13、分解因式:2(2)2a b a b --+=_______.14、分解因式()(4)a b a b ab --+的结果是___________.15、如果关于x,y 的多项式()22325256ax axy x bxy x x +-----++不含二次项,那么ab=_________ 16、若()2316m m x --+是一个完全平方式,则m =________.17、已知x 2+9y 2﹣4x+6y+5=0,则x=________, y=________.18、若m 3+m ﹣1=0,则m 4+m 3+m 2﹣2=____.19、已知230b a -+=,则2(2)48a b a b --+=______.20、已知:24x y -=且代数式2214x xy y m -++的值为9,那么x y m -21的值是____________. 21、已知120182019a =+,120192019b =+,120202019c =+, 则代数式222a b c ab bc ac ++---的值为______.22、观察下列等式:()()2111x x x -+=-,()()23111x x x x -++=-,()()324111x x x x x -+++=-,……,利用你发现的规律回答:若()()65432112x x x x x x x -++++++=-,则2021x 的值是三、解答题 23、计算:(1)(﹣2x )2•(2x 2y ﹣4xy 2)+x 4y ; (2)(x ﹣1)(4﹣x )+(﹣2x )2(x ﹣3).(3)(2x ﹣3y )2﹣(y +3x )(3x ﹣y ); (4)(m +2)(m ﹣2)﹣(m ﹣1)2.24、分解因式:(1)36mx my - (2)22125a b - (3)2244ab a b ---25、分解因式(1)ax bx - (2)26348n n x x -+ (3)2221a a b -+- (4)3()a b a b --+26、计算:(1)39×37﹣13×91; (2)29×20.09+72×20.09+13×20.09﹣20.09×14.27、(1)化简求值:2(2)(2)(3)x y x y x y +----,其中1,13x y ==.(2)先因式分解再求值,已知3xy =-,123x y -=,求42332444x y x y x y -+-.28、若x ,y 满足x 2+y 2=8,xy =2,求下列各式的值.(1)(x +y )2; (2)x 4+y 4; (3)x ﹣y .29、阅读材料:若2222440m mn n n -+-+=,求m ,n 的值.解:∵2222440m mn n n -+-+=,∴()()2222440m mn nnn -++-+=,∴()()2220m n n -+-=,∴()20m n -=,()220n -=,∴2n =,2m =.根据你的观察,探究下面的问题:(1)2262100a b a b ++-+=,则a =__________,b =__________.(2)已知22228160x y xy y +-++=,求xy 的值.(3)已知ABC 的三边长a 、b 、c 都是正整数,且满足22248180a b a b +--+=,求ABC 的周长.30、阅读理解以下文字:我们知道,多项式的因式分解就是将一个多项式化成几个整式的积的形式.通过因式分解,我们常常将一个次数比较高的多项式转化成几个次数较低的整式的积,来达到降次化简的目的.这个思想可以引领我们解决很多相对复杂的代数问题. 例如:方程2230x x +=就可以这样来解:解:原方程可化为()230x x += 所以0x =或者230x +=.解方程230x +=,得32x =-所以解为10x =,232x =-. 根据你的理解,结合所学知识,解决以下问题:(1)解方程:250x x -=; (2)解方程:22(3)40x x +-=;(3)已知ABC ∆的三边长为4,x ,y ,请你判断代数式22816y y x -+-的值的符号.31、图1是一个长为2m ,宽为2n 的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.(1)图2中的阴影部分的正方形的边长等于 . (2)观察图2你能写出下列三个代数式(m +n )2,(m ﹣n )2,mn 之间的等量关系 . (3)运用你所得到的公式,计算若mn =﹣2,m ﹣n =4,求:①(m +n )2的值. ②m 4+n 4的值.(4)用完全平方公式和非负数的性质求代数式x 2+2x +y 2﹣4y +7的最小值.32、【知识生成】我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如图1可以得到(a +b )2=a 2+2ab +b 2,基于此,请解答下列问题:(1)根据图2,写出一个代数恒等式: .(2)利用(1)中得到的结论,解决下面的问题:若a +b +c =10,ab +ac +bc =35,则a 2+b 2+c 2= . (3)小明同学用图3中x 张边长为a 的正方形,y 张边长为b 的正方形,z 张宽、长分别为a 、b 的长方形纸片拼出一个面积为(3a +b )(a +3b )长方形,则x +y +z = .【知识迁移】(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为x的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式:.期中复习培优训练卷(9章:整式乘法与因式分解)(B )-2020-2021苏科版七年级下学期数学(解析)一、选择题1、计算(1)(2)x x -+的结果是( )A .22x x +-B .22x x --C .22x +D .22x -【分析】按照多项式乘多项式的法则进行计算即可.【详解】22(1)(2)222x x x x x x x -+=+--=+-故选:A .2、下列计算正确的是( )A .224x x x +=B .222()x y x y -=-C .26()x y x y =3D .532x x x =•【分析】根据整式的加法法则,乘法法则,积的乘方计算法则,完全平方公式分别计算进行判断. 【详解】A 、2222x x x +=,故该项错误;B 、222()2x y x xy y -=-+,故该项错误;C 、2363()x y x y =,故该项错误;D 、532x x x =•,故该项正确;故选:D .3、下列等式从左到右的变形中,属于因式分解的是( )A .()()244224x x x x x -+=+-+ B .()()23123x x x x +-=+-C .()266x x x x -=-D .623ab a b =【分析】根据因式分解的定义逐个判断即可.【详解】解:A 、等式从左到右的变形不属于因式分解,故本选项不符合题意;B 、等式从左到右的变形不属于因式分解,故本选项不符合题意;C 、等式从左到右的变形属于因式分解,故本选项符合题意;D 、等式从左到右的变形不属于因式分解,故本选项不符合题意;故选:C .4、多项式﹣5mx 3+25mx 2﹣10mx 各项的公因式是( )A .5mx 2B .﹣5mx 3C .mxD .﹣5mx【分析】根据公因式是多项式中每项都有的因式,可得答案. 【解答】解:﹣5mx 3+25mx 2﹣10mx 各项的公因式是﹣5mx ,故选:D . 5、在括号内填上适当的单项式,使()2144y -+成为完全平方式应填( )A .12yB .24C .24y ±D .12【分析】利用完全平方公式的结构特征判断即可; 【详解】()()()2222412=24144-±+±-±+y y y y ;故答案选C .6、(﹣8)2009+(﹣8)2008能被下列数整除的是( )A .3B .5C .7D .9【分析】原式变形后,提取公因式即可得到结果.【解答】解:原式=(﹣8)2008×(﹣8+1)=(﹣8)2008×(﹣7)=﹣82008×7,则结果能被7整除. 故选C7、已知25x x m -+有一个因式为2x -,则另一个因式为( )A .3x +B . 6 x ﹣C . 3 x ﹣D .6x + 【分析】所求的式子25x x m -+的二次项系数是1,因式(x−2)的一次项系数是1,则另一个因式的一次项系数一定是1,然后根据25x x m -+中一次项系数为-5,列方程求出另一个因式.【解析】设另一个因式为(x +a ),则x 2−5x +m =(x −2)(x +a ),即x 2−5x +m =x 2+(a −2)x −2a ,∴a −2=−5,解得:a =−3,∴另一个因式为(x −3). 故选:C .8、若3x y -=-,5xy =,则代数式3223242x y x y xy -+的值为( )A .90B .45C .15-D .30-【分析】将多项式提取公因式2xy 后再根据完全平方公式分解因式,再将3x y -=-,5xy =代入计算即可.【详解】解:∵3x y -=-,5xy =,∴3223242x y x y xy -+=22(22)x xy xy y -+=22()x x y y -=225(3)⨯⨯-=90,故选:A . 9、若2223a b -=,12a b -=,则+a b 的值为( )A .12-B .43C .32D .2【分析】已知第一个等式利用平方差公式化简,将第二个等式代入计算即可求出a+b 的值.【详解】解:∵a 2-b 2=(a+b )(a-b )=23,a-b=12,∴a+b=23÷12=43,故选B .10、若11x x -=,则221x x+的值是( ) A .3 B .2 C .1D .4【分析】利用完全平方公式展开,即可得到结果. 【详解】解:∵11x x -=,两边平方得:22121x x +-=,∴221x x+=3,故选A11、已知()()22113(21)a b ab ++=-,则1b a a ⎛⎫-⎪⎝⎭的值是( ) A .0B .1C .-2D .-1【分析】先对()()22113(21)a b ab ++=-进行变形,可以解出a ,b 的关系,然后在对1b a a ⎛⎫-⎪⎝⎭进行因式分解即可.【详解】∵()()22113(21)a b ab ++=-,∴2222163a b a b ab +++=-,22222440a b ab a b ab +-+-+=,()()2220a b ab -+-=, ∴a b =,2ab =,∴1121bb a ab a a⎛⎫-=-=-=- ⎪⎝⎭ 故选:D .12、7张如图1的长为a ,宽为b (a >b )的小长方形纸片,按图2的方式不重叠地放在矩形ABCD 内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S ,当BC 的长度变化时,按照同样的放置方式,S 始终保持不变,则a ,b 满足( )A .a=25b B .a=3b C .a=27b D .a=4b分析:表示出左上角与右下角部分的面积,求出之差,根据之差与BC 无关即可求出a 与b 的关系式. 解答:解:左上角阴影部分的长为AE ,宽为AF=3b ,右下角阴影部分的长为PC ,宽为a ,∵AD=BC ,即AE+ED=AE+a ,BC=BP+PC=4b+PC , ∴AE+a=4b+PC ,即AE-PC=4b-a , ∴阴影部分面积之差S=AE •AF-PC •CG=3b •AE-a •PC=3b (PC+4b-a )-a •PC=(3b-a )PC+12b 2-3ab , 则3b-a=0,即a=3b . 故选B二、填空题13、分解因式:2(2)2a b a b --+=_______.【分析】先添加括号,再提取公因式,即可得出答案. 【详解】解:(2a-b )2-2a+b=(2a-b )2-(2a-b )=(2a-b )(2a-b-1),故答案为:(2a-b )(2a-b-1).14、分解因式()(4)a b a b ab --+的结果是___________.试题分析:()(4)a b a b ab --+=2254a ab b ab -++=2244a ab b -+=2(2)a b -.故答案为2(2)a b -.考点:因式分解-运用公式法.15、如果关于x,y 的多项式()22325256ax axy x bxy x x +-----++不含二次项,那么ab=_________ 【分析】先把多项式进行化简,根据多项式不含二次项,即可求出a 、b 的值,即可得到答案. 【详解】解:∵()22325256ax axy x bxy x x +-----++=22325256ax axy x bxy x x +--++-- =2(2)(3)711a x a b xy x +++--, ∵多项式不含二次项,∴2030a a b +=⎧⎨+=⎩,解得:26a b =-⎧⎨=⎩, ∴2612ab =-⨯=-;故答案为:12-.16、若()2316m m x --+是一个完全平方式,则m =________.【分析】运用完全平方公式求解即可. 【详解】原式()2234x m x =--+,该式是完全平方式,()324m x x -=±⨯⋅∴, 38m -=±, ①当38m -=时,11m =,②当38m -=-时,5m =-,综上,11m =或5-.17、已知x 2+9y 2﹣4x+6y+5=0,则x=________, y=________. 【解析】∵x 2+9y 2﹣4x+6y+5=0,∴x 2+9y 2﹣4x+6y +1+4=0, 即x 2−4x +4+9y 2+6y +1=0, ∴(x −2)2+(3y +1)2=0,∴x =2,y =−1 318、若m 3+m ﹣1=0,则m 4+m 3+m 2﹣2=____.【分析】由已知变形为3=1m m -,然后整体代入,去括号合并同类项即可. 【详解】∵310m m +-=,∴3=1m m -,∴4322m m m ++-()2112m m m m =-+-+-2212m m m m =-+-+-1=-.故答案为:1-.19、已知230b a -+=,则2(2)48a b a b --+=______.【分析】先由题意将式子2b−a+3=0,进行变形,变成a-2b=3的形式,然后再将要求的式子化简,使每一项都含有因式a-2b ,再代入求值即可得出.【详解】∵230b a -+=,∴23a b -=,∴222(2)48(2)4(2)3433a b a b a b a b --+=---=-⨯=-20、已知:24x y -=且代数式2214x xy y m -++的值为9,那么x y m -21的值是____________. 【分析】根据题意可以求得m 的值和12y -x 的值,从而可以解答本题. 【详解】解:∵24x y -=且代数式2214x xy y m -++的值为9, ∴122y x -=-,2222112942x xy y m x y m m ⎛⎫-++=-+=+= ⎪⎝⎭, ∴5m =, ∴1221525y x m --==. 故答案为:125.21、已知120182019a =+,120192019b =+,120202019c =+, 则代数式222a b c ab bc ac ++---的值为______.【分析】把已知的式子化成2221[()()()]2a b a c b c -+-+-的形式,然后代入求解. 【解析】解:120182019a =+,120192019b =+,120202019c =+, 1a b ∴-=-,2a c -=-,1b c -=-,则原式2221(222222)2a b c ab ac bc =++--- 2222221[(2)(2)(2)]2a ab b a ac c b bc c =-++-++-+ 2221[()()()]2a b a c b c =-+-+-1[141]2=⨯++3=,故答案为:3.22、观察下列等式:()()2111x x x -+=-,()()23111x x x x -++=-,()()324111x x x x x -+++=-,……,利用你发现的规律回答:若()()65432112x x x x x x x -++++++=-,则2021x 的值是【分析】先根据已知等式归纳类推出一般规律,再根据()()65432112x x x x x x x -++++++=-求出x的值,然后代入求值即可得.【详解】观察等式:()()2111x x x -+=-,()()23111x x x x -++=-,()()324111x x x x x -+++=-,归纳类推得:()()12111n n n x xx x x --+-+++=-,其中n 为大于1的整数,则()()6547321121x x x x x x x x -++++=-++=-,即71x =-,解得1x =-,则2021x =2021)1(-=-1三、解答题23、计算:(1)(﹣2x )2•(2x 2y ﹣4xy 2)+x 4y ; (2)(x ﹣1)(4﹣x )+(﹣2x )2(x ﹣3).(3)(2x ﹣3y )2﹣(y +3x )(3x ﹣y ); (4)(m +2)(m ﹣2)﹣(m ﹣1)2. 【分析】(1)根据积的乘方和单项式乘多项式可以解答本题;(2)根据多项式乘多项式和级的惩罚可以解答本题. (3)根据完全平方公式和平方差公式可以解答本题; (4)根据平方差公式和完全平方公式可以解答本题. 【解析】(1)(﹣2x )2•(2x 2y ﹣4xy 2)+x 4y =4x 2•(2x 2y ﹣4xy 2)+x 4y=8x 4y ﹣16x 3y 2+x 4y =9x 4y ﹣16x 3y 2;(2)(x ﹣1)(4﹣x )+(﹣2x )2(x ﹣3)=4x ﹣x 2﹣4+x +4x 2(x ﹣3)=4x ﹣x 2﹣4+x +4x 3﹣12x 2=4x 3﹣13x 2+5x ﹣4.(3)(2x ﹣3y )2﹣(y +3x )(3x ﹣y )=4x 2﹣12xy +9y 2﹣(9x 2﹣y 2)=4x 2﹣12xy +9y 2﹣9x 2+y 2=﹣5x 2﹣12xy +10y 2;(4)(m +2)(m ﹣2)﹣(m ﹣1)2=m 2﹣4﹣(m 2﹣2m +1)=m 2﹣4﹣m 2+2m ﹣1=2m ﹣5.24、分解因式:(1)36mx my - (2)22125a b -(3)2244ab a b --- 【分析】(1)根据提取公因式法,即可分解因式;(2)根据平方差公式,即可分解因式; (3)根据完全平方公式,即可分解因式. 【详解】(1)36mx my -=3m(x-2y);(2)22125a b -=1155a b a b ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭;(3)2244ab a b ---=()2244a ab b -++=-(2a+b)225、分解因式(1)ax bx - (2)26348n n x x -+ (3)2221a a b -+- (4)3()a b a b --+ 【分析】(1)提公因式x 即可分解;(2)提公因式23n x -,再逐步利用平方差公式分解;(3)先分组,再利用完全平方公式分解,最后利用平方差公式分解; (4)先提公因式a-b ,再利用平方差公式分解. 【详解】解:(1)ax bx -=()x a b -;(2)26348nnx x -+=()322348nn x x -+=()2223116n n x x ⎡⎤--⎢⎥⎣⎦=()222314n n x x ⎡⎤--⎢⎥⎣⎦ =()()22234141n n n x x x -+-=()()22234121n n n x x x ⎡⎤-+-⎢⎥⎣⎦=()()()23412121n n n nx x x x ++-;(3)2221a a b -+-=221a b =11a b a b ;(4)3()a b a b --+=()()3a b a b ---=()()21a b a b ⎡⎤---⎣⎦=()()()11a b a b a b --+--26、计算:(1)39×37﹣13×91; (2)29×20.09+72×20.09+13×20.09﹣20.09×14.【分析】(1)首先提取公因式13,进而求出即可;(2)首先提取公因式20.09,进而求出即可.【解答】解:(1)39×37﹣13×91=3×13×37﹣13×91=13×(3×37﹣91)=13×20=260;(2)29×20.09+72×20.09+13×20.O9﹣20.O9×14=20.09×(29+72+13﹣14)=2009.27、(1)化简求值:2(2)(2)(3)x y x y x y +----,其中1,13x y ==. (2)先因式分解再求值,已知3xy =-,123x y -=,求42332444x y x y x y -+-. 【分析】(1)原式利用平方差公式及完全平方公式化简,去括号合并得到最简结果,把x 与y 的值代入计算即可求出值. (2)提公因式22x y -,再利用完全平方公式进行因式分解,最后将3xy =-,123x y -=代入计算. 【详解】解:(1)2(2)(2)(3)x y x y x y +----=()2222964x y xy x y +-+- =2222964x y xy x y ----=2136y xy -- 将1,13x y ==代入,原式=21131613-⨯-⨯⨯=15-; (2)42332444x y x y x y -+-=()222244x y x xy y --+=()2222x y x y -- ∵3xy =-,123x y -=, ∴原式=()()222xy x y --=()22133⎛⎫--⨯ ⎪⎝⎭=1-.28、若x ,y 满足x 2+y 2=8,xy =2,求下列各式的值.(1)(x +y )2; (2)x 4+y 4;(3)x ﹣y .【分析】(1)先根据完全平方公式进行变形,再代入求出即可;(2)先根据完全平方公式进行变形,再代入求出即可;(3)先求出(x ﹣y )2的值,再根据完全平方公式求出即可.【解析】解:(1)∵x 2+y 2=8,xy =2,∴(x +y )2=x 2+y 2+2xy =8+2×2=12;(2)∵x 2+y 2=8,xy =2,∴x 4+y 4=(x 2+y 2)2﹣2x 2y 2=82﹣2×22=64﹣8=56;(3)∵x 2+y 2=8,xy =2,∴(x ﹣y )2=x 2+y 2﹣2xy =8﹣2×2=4,∴x ﹣y =±2.29、阅读材料:若2222440m mn n n -+-+=,求m ,n 的值.解:∵2222440m mn n n -+-+=,∴()()2222440m mn nn n -++-+=, ∴()()2220m n n -+-=,∴()20m n -=,()220n -=,∴2n =,2m =. 根据你的观察,探究下面的问题:(1)2262100a b a b ++-+=,则a =__________,b =__________.(2)已知22228160x y xy y +-++=,求xy 的值. (3)已知ABC 的三边长a 、b 、c 都是正整数,且满足22248180a b a b +--+=,求ABC 的周长.【详解】(1)∵2262100a b a b ++-+=,∴()()2269210a a b b ++-+=+,∴()()22310a b ++-=, ∵()230a +≥,()210b -≥,∴30a +=,3a =-,10b -=,1b =; (2)∵22228160x y xy y +-++=,∴()()22228160x xy y y y -++++=,∴()()2240x y y -++=, ∵()20x y -≥,()240y +≥, ∴0x y -=,x y =,40y +=,4y =-,∴4x =-, ∴16xy =;(3)∵22248180a b a b +--+=,∴222428160a a b b -++-+=,∴()()222140a b -+-=,∵()210a -≥,()240b -≥,∴10a -=,1a =,40b -=,4b =, ∵a b c +>,∴5c <,∵b a c -<,∴3c >,∵a 、b 、c 为正整数,∴4c =,∴ABC 周长=1449++=.30、阅读理解以下文字:我们知道,多项式的因式分解就是将一个多项式化成几个整式的积的形式.通过因式分解,我们常常将一个次数比较高的多项式转化成几个次数较低的整式的积,来达到降次化简的目的.这个思想可以引领我们解决很多相对复杂的代数问题.例如:方程2230x x +=就可以这样来解:解:原方程可化为()230x x += 所以0x =或者230x +=.解方程230x +=,得32x =- 所以解为10x =,232x =-. 根据你的理解,结合所学知识,解决以下问题:(1)解方程:250x x -=;(2)解方程:22(3)40x x +-=;(3)已知ABC ∆的三边长为4,x ,y ,请你判断代数式22816y y x -+-的值的符号.【分析】(1)提取公因式分解因式,可得两个一元一次方程,可得方程的解;(2)提取公因式分解因式,可得两个一元一次方程,可得方程的解;(3)将代数式变形后得:(y+4-x )(y+4+x ),根据三角形的三边关系得:x+y-4>0,x-y+4>0,y+4+x >0,则y 2-8y+16-x 2>0 【详解】解:(1)250x x -=,∴()50x x -=,∴x=0或x-5=0,∴x 1=0或x 2=5;(2)(x+3)2-4x 2=0,∴(x+3+2x )(x+3-2x )=0,∴(3x+3)(-x+3)=0,∴3x+3=0或-x+3=0,解方程得:x 1 =-1,x 2=3;(3)∵△ABC 的三边长为4,x ,y ,∴x+y >4,x+4>y ,∴x+y-4>0,x-y+4>0,y+4+x >0,∵y 2-8y+16-x 2=(y-4-x )(y-4+x )<0,即代数式y 2-8y+16-x 2的值的符号为负号.31、图1是一个长为2m ,宽为2n 的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.(1)图2中的阴影部分的正方形的边长等于 .(2)观察图2你能写出下列三个代数式(m +n )2,(m ﹣n )2,mn 之间的等量关系 . (3)运用你所得到的公式,计算若mn =﹣2,m ﹣n =4,求:①(m +n )2的值. ②m 4+n 4的值.(4)用完全平方公式和非负数的性质求代数式x 2+2x +y 2﹣4y +7的最小值.【分析】(1)根据阴影部分正方形的边长等于小长方形的长减去宽解答即可;(2)根据大正方形的面积减去四个长方形的面积等于阴影部分小正方形的面积解答即可;(3)把数据代入(3)的数量关系计算即可得解;(4)根据完全平方公式配方,再根据非负数的性质即可得解.【详解】解:(1)由图可知,阴影部分小正方形的边长为:m﹣n;故答案为:m﹣n;(2)根据正方形的面积公式,阴影部分的面积为(m﹣n)2,还可以表示为(m+n)2﹣4mn,∴(m﹣n)2=(m+n)2﹣4mn,故答案为:(m﹣n)2=(m+n)2﹣4mn;(3)①∵mn=﹣2,m﹣n=4,∴(m+n)2=(m﹣n)2+4mn=42+4×(﹣2)=16﹣8=8,②m2+n2=(m﹣n)2+2mn=42+2×(﹣2)=16﹣4=12,∴m4+n4=(m2+n2)2﹣2 m2·n2=122﹣2×(﹣2)2=136;(4)x2+2x+y2﹣4y+7=x2+2x+1+y2﹣4y+4+2=(x+1)2+(y﹣2)2+2,∵(x+1)2≥0,(y﹣2)2≥0,∴(x+1)2+(y﹣2)2≥0,∴当x=﹣1,y=2时,代数式x2+2x+y2﹣4y+7的最小值是2.32、【知识生成】我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如图1可以得到(a+b)2=a2+2ab+b2,基于此,请解答下列问题:(1)根据图2,写出一个代数恒等式:.(2)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,则a2+b2+c2=.(3)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a、b的长方形纸片拼出一个面积为(3a+b)(a+3b)长方形,则x+y+z=.【知识迁移】(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为x的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式:.【分析】(1)依据正方形的面积=(a+b+c)2;正方形的面积=a2+b2+c2+2ab+2ac+2bc,可得等式;(2)依据a2+b2+c2=(a+b+c)2﹣2ab﹣2ac﹣2bc,进行计算即可;(3)依据所拼图形的面积为:xa2+yb2+zab,而(3a+b)(a+3b)=3a2+9ab+ab+3b2=3a2+3b2+10ab,即可得到x,y,z的值;(4)根据原几何体的体积=新几何体的体积,列式可得结论.【解析】(1)由图2得:正方形的面积=(a+b+c)2;正方形的面积=a2+b2+c2+2ab+2ac+2bc,∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,故答案为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;(2)∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,∵a+b+c=10,ab+ac+bc=35,∴102=a2+b2+c2+2×35,∴a2+b2+c2=100﹣70=30,故答案为:30;(3)由题意得:(3a+b)(a+3b)=xa2+yb2+zab,∴3a2+10ab+3b2=xa2+yb2+zab,∴x=3,y=3,z=10,∴x+y+z=16,故答案为:16;(4)∵原几何体的体积=x3﹣1×1•x=x3﹣x,新几何体的体积=(x+1)(x﹣1)x,∴x3﹣x=(x+1)(x﹣1)x.故答案为:x3﹣x=x(x+1)(x﹣1).。
初一培优数学试题及答案

初一培优数学试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是正数?A. -5B. 0C. 3D. -7答案:C2. 计算下列哪个表达式的结果为负数?A. 5 - 3B. 2 + (-4)C. 6 × 2D. 8 ÷ 2答案:B3. 下列哪个分数是最简分数?A. 4/8B. 3/6C. 5/10D. 7/14答案:A4. 哪个数的绝对值最大?A. 2B. -3C. 0D. 4答案:B5. 哪个数的平方最小?A. 2B. -3C. 0D. 4答案:C6. 下列哪个方程的解是x = 2?A. 2x - 4 = 0B. 3x + 6 = 0C. 4x - 8 = 0D. 5x + 10 = 0答案:A7. 哪个不等式的解集是x > 3?A. x - 3 > 0B. x + 3 > 0C. x - 3 < 0D. x + 3 < 0答案:A8. 下列哪个图形的周长最长?A. 边长为3的正方形B. 长为4,宽为2的长方形C. 直径为5的圆D. 边长为4的等边三角形答案:C9. 哪个数是无理数?A. 2B. 1/2C. πD. 0.7510. 下列哪个图形的面积最大?A. 边长为4的正方形B. 长为5,宽为3的长方形C. 半径为3的圆D. 底为4,高为5的三角形答案:C二、填空题(每题4分,共40分)11. 计算:(-3) × (-2) = ______。
答案:612. 计算:(-4) ÷ 2 = ______。
13. 计算:|-5| = ______。
答案:514. 计算:√9 = ______。
答案:315. 计算:(1/2) + (1/3) = ______。
答案:5/616. 计算:(2/3) × (3/4) = ______。
答案:1/217. 计算:(-2)² = ______。
答案:418. 计算:(-3)³ = ______。
培优初一练习册及答案

培优初一练习册及答案### 培优初一练习册及答案#### 一、语文阅读理解阅读下面的短文,回答问题。
短文:春天来了,万物复苏。
小草从土地里探出头来,好奇地打量着这个崭新的世界。
花儿也不甘示弱,竞相开放,为大地披上了五彩斑斓的衣裳。
问题:1. 短文中描述了哪些春天的景象?2. 短文表达了作者怎样的情感?答案:1. 短文中描述了小草探出头来和花儿竞相开放的春天景象。
2. 短文表达了作者对春天的喜爱和对大自然的赞美之情。
#### 二、数学计算题计算下列表达式的值:1. \( 3x^2 + 2x - 5 \) 当 \( x = 2 \) 时。
2. \( \frac{1}{2} \times 4 + \frac{3}{4} \times 6 \)。
答案:1. \( 3 \times 2^2 + 2 \times 2 - 5 = 12 + 4 - 5 = 11 \)。
2. \( \frac{1}{2} \times 4 + \frac{3}{4} \times 6 = 2 + 4.5 = 6.5 \)。
#### 三、英语完形填空阅读下面的短文,从括号内选择合适的词填空。
In the morning, I usually get up at 6:30. After getting dressed, I brush my teeth and wash my face. Then I have breakfast with my family. After breakfast, I go to school with my friends. We often talk and laugh on the way. School starts at 8:00. I enjoy my classes because I can learn many new things. After school, I usually play soccer with my friends. I think it's a good way to relax. In the evening, I do my homework and then read a book before going to bed.1. I usually get up at 6:30 in the _______. (morning/evening)2. I have breakfast with my _______. (classmates/family)3. School starts at _______. (8:00/9:00)答案:1. morning2. family3. 8:00#### 四、科学实验题描述一个简单的实验来证明水的表面张力。
初一数学上册培优训练题3

.优选文档 .初一数学上册培优训练题3初一数学上册培优训练题3(新人教版带答案)80 元,一件盈利1、某商场有两件进价不相同上衣均卖了60%,另一件亏本20%,此次买卖中商家()A不赔不赚B赚了10 元C赚了8元D赚了32 元2、如图,B是线段AD的中点,C是BD上一点则下列结论中错误的选项是()ABC=AB-CDBBC=(AD-CD)CBC=(AD-CD)DBC=AC-BD3、如图,甲、乙两所学校,其中男女生情况可见以下统计图,甲学校有1000 人,乙有 1250 人,则()A甲校的女生比乙校的女生多B甲校的女生比乙校的女生少C甲校与乙校的女生相同多D甲校与乙校男生共是2250人甲校乙校4、甲从 A 出发向北偏东45 度走到点B,乙从点 A 出发向北偏西30 度走到点,则∠ BA等于()A15 度B75度C105度D135度2016 崭新优选资料 - 崭新公文范文 -全程指导写作–独家原创1 / 55、规定 a○ b = ,则(6○4)○ 3等于()A4B13C15D306 、(-2007)÷2007× (+1)× (2.15-2)=______________.7 、已知(a-3)2+|b+6|=0,则方程ax=b的解为_________________.8、七年级一班部分同学参加全国“希望杯”数学邀请赛,获取了优异成绩,指导教师统计所有参赛同学的成绩(成绩为整数,满分150 分)并绘制了统计图,以以下列图所示(注:图中各组中不包含最高分)请回答:(1)该班参加本次竞赛同学有多少人?(2)若是成绩在 90 分以上同学获奖,那么该班参赛同学获奖率是多少?(3)参赛同学有多少人及格?9、小明想在两种灯中选购一种,其中一种是10 瓦(即0.01 千瓦)的节能灯,售价 50 元,另一种是100 瓦(即 0.1千瓦)的白炽灯,售价 5 元,两种灯的照明收效相同,使用寿命也相同( 3000 小时内)节能灯售价高,但较省电,白炽灯售价低,但用电多,电费0.5 元/ 千瓦 • 时(1)照明时间 50 0 小时选哪一种灯省钱?( 2)照明时间 1500 小时选哪一种灯省钱?2016 崭新优选资料 - 崭新公文范文 -全程指导写作–独家原创2 / 5( 3)照明多少时间用两种灯花销相等?(本大题10分)数学培优增强训练(四)答案1、某商场有两件进价不相同上衣均卖了60%,另一件亏本20%,此次买卖中商家(A不赔不赚B赚了10 元80 元,一件盈利B)C赚了8元D赚了32 元2、如图,B是线段AD的中点,C是BD上一点则下列结论中错误的选项是()ABC=AB-CDBBC=(AD-CD)CBC=(AD-CD)DBC=AC-BD3、如图,甲、乙两所学校,其中男女生情况可见以下统计图,甲学校有1000 人,乙有 1250 人,则()A甲校的女生比乙校的女生多B甲校的女生比乙校的女生少C甲校与乙校的女生相同多D甲校与乙校男生共是2250 人甲校乙校4、甲从 A 出发向北偏东45 度走到点B,乙从点 A 出发向北偏西30 度走到点,则∠ BA等于(B )A15 度B75度C105度D135度2016 崭新优选资料 - 崭新公文范文 -全程指导写作–独家原创3 / 5.优选文档.5、规定a○ b= ,则(6○ 4)○3等于(A)A4B13C15D306 、(-2007)÷2007× (+1)× (2.15-2)=______________.07 、已知(a-3)2+|b+6|=0,则方程ax=b的解为_________________. x=-28、七年级一班部分同学参加全国“希望杯”数学邀请赛,获取了优异成绩,指导教师统计所有参赛同学的成绩(成绩为整数,满分150 分)并绘制了统计图,以以下列图所示(注:图中各组中不包含最高分)请回答:(1)该班参加本次竞赛同学有多少人?(2)若是成绩在 90 分以上同学获奖,那么该班参赛同学获奖率是多少?(3)参赛同学有多少人及格?25. ( 1) 20 人(2) 55% ( 3) 11 人9、小明想在两种灯中选购一种,其中一种是10 瓦(即0.01 千瓦)的节能灯,售价 50 元,另一种是100 瓦(即 0.1千瓦)的白炽灯,售价 5 元,两种灯的照明收效相同,使用寿命也相同( 3000 小时内)节能灯售价高,但较省电,白炽灯售价低,但用电多,电费0.5 元/ 千瓦 • 时(1)照明时间500 小时选哪一种灯省钱?(2)照明时2016 崭新优选资料 - 崭新公文范文 -全程指导写作–独家原创4 / 5.优选文档 .间1500 小时选哪一种灯省钱?(3)照明多少时间用两种灯花销相等?(本大题 10 分)26.( 1)白炽灯( 2)节能灯( 3 )1000 小时2016 崭新优选资料 - 崭新公文范文 -全程指导写作–独家原创5 / 5。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级培优试题一.单项选择(共20小题,计20分)1.My brother plays ______ basketball well but he doesn’t play _______ piano well.A. the, theB. /, /C. the, /D. /, the2.I don’t like fruits. Please take the _______ away.A. broccol iB. eggsC. ice creamD. strawberries3. I want to know your age. ___________A. How are you?B. How old are you?C. What’s your name?D. When is your birthday?4. Ken is Aunt Lucy’s son. _______ birthday is October 3rd.A. HeB. SheC. HisD. Her5. I’m ________ years old and it’s my _______ birthday today.A. fifteen, fifteenB. fifteen, fifteenthC. fifteenth, fifteenD. fifteenth, fifteenth6. We usually have our school trip _______ a morning of April.A. inB. atC. toD. on7. My parents’ friend ________ Beijing Opera very much.A. likesB. likeC. likingD. don’t like8. —______ you speak Chinese?—No, I can’t.A. DoB. AreC. CanD. Does9. The price of the pants ______ ninety yu an.A. isB. amC. areD. be10. —It’s my birthday today!—____________A. Thank you very much!B. You’re welcome!C. Happy birthday to you!D. I’m sorry!11.—What do you usually have ___________ lunch?—Fish _________ vegetables and rice.A. for, withB. in, withC. to, forD. with, for12.— Why not __________ some orange juice? It’s very good.— Good idea.A. drinkingB. hasC. havingD. drink13.—The pink skirt looks very nice __________ you.—OK. I’ll ________ it.A. of, thinkB. in, giveC. on, takeD. at, let14.—Let’s go to Zhongshan Park ________ a picnic __________ Sunday.—That’s a good idea.A. at, atB. at, onC. for, atD. for, on15.—Hello! May I speak to Helen?— Hello! _____________.A. This is HelenB. I’m HelenC. It’s HelenD. She is Helen16.—__________ is the letter ___________?—My pen pal.A. Which, fromB. What, forC. Who, forD. Who, from17. --Let’s play computer games.--Great! That sounds_______.A.boringB.difficultC.interestingD. sad18. Mr Green is _______ father.A. Jim and KateB. Jim’s and Kate’sC. Jim’s and KateD. Jim and Kate’s19.---Do you have a _____?--- Yes, I _____ at a clothes shop.A.work, workB.work, jobC. job, job,D.job, work.20. A:B: He’s tall.A. Is the boy tall or short?B. Is the boy tall?C. Is the boy short?D. How old is he ?二、完形填空(共10小题,计10分)My name is Ann. 36 favorite day of the week is Sunday. 37 Sundays I usually get up late, at about 9 o’clock in the 38 . I have breakfast from 9:10 to 9:40. Then 39 breakfast, I often 40 TV. My parents and I usually go out for a big meal at noon. In the afternoon, I often go to the park(公园) 41 my friends. We play games and have a good time in 42 park. After dinner I play computer games at 43 . Sometimes I go to a movie with my family. We all like44 .We think they’re very exciting.I like Sunday so much because on that day I 45 do things I like to.26. A. My B. Your C. His D. Her27. A. In B. On C. At D. From28. A. morning B. afternoon C. evening D. night29. A. at B. in C. before D. after30. A. look B. see C. watch D. read31. A. for B. with C. and D. to32. A. a B. an C. / D. the33. A. school B. home C. hotel D. park34. A. books B. salad C. documentaries D. action movies35. A. can B. can’t C. don’t D. must三、阅读理解(共10小题,计10分)根据短文内容,选择最佳答案。
AJune is from England. Her family are in Beijing now. She is fourteen years old. The date of her birth is September seventh. Her father, Mr Smith, is an English teacher. And her mother, Mrs Smith, is an English teacher, too. They all like Chinese movies. Mr Smith likes action movies. He thinks they are really exciting. His favorite actor is Jet Li. Mrs Smith likes Beijing Opera. She thinks she can learn much about Chinese history by seeing them. And June herself likes comedies. Herfavorite actor is Zhao Benshan. She thinks he is very funny. She also thinks Zhao Benshan’s movies are better(更好) than Rowan Atkinson’s. Mr Smith and Mrs Smith like Beijing Roast Duck(北京烤鸭). They often go to Quanjude to have it.36. June is __________.A. a Chinese boyB. a Chinese girlC. an American girlD. an English girl37. June is ___________.A. twelveB. thirteenC. fourteenD. fifteen38. June’ s birthday is ________.A. December seventhB. September seventhC. December eleventhD. September eleventh39. ________ likes action movies.A. JuneB. Mr SmithC. Mrs SmithD. Nobody40. ________ like(s) Beijing Roast Duck.BMr Green works in an office(办公室). Every morning he has breakfast with his wife at 7:30, watches TV, drinks tea(喝茶) and then leaves his home at 8:00 and takes a bus to his office.Now he still sits comfortably at the breakfast table and watches his news on TV at 8:05. He doesn’t hurry and asks his wife for another cup of tea.“Another cup?”she says in surprise (吃惊的). “Don’t you need to go to the office today?”“The office?” he says, “I think I’m at the office!”41. Mr Green works in a(an) ______.A. schoolB. hotelC. officeD. hospital42. Mr Green usually goes to work by _______.A. carB. busC. bikeD. train43. Mr Green likes ________ every day.A. runningB. playing basketballC. watching TVD. drinking coffee44. Mrs Green is surprised because Mr Green_________.A. doesn’t drink teaB. doesn’t watch TV newsC. doesn’t go to workD. doesn’t have breakfast45. Mr Green forgets(忘记) that he is _________.A. at homeB. at his officeC. on the busD. in his car( C )One day a Chinese student went to study English in England. His family name is Sun. It is the same as the word “sun”. England is a country with bad weather. It is often cloudy or misty, and it rains now and again. So the people there don’t get much sunshine in the whole year. When the Chinese student went to London, a tall English policeman with a large face opened his passport to examine(检查) it. The policeman was interested to find the Chinese name “sun”in the passport. He thought it was pronounced just like the English word “sun”,so he said to theChinese student, “ I see your name is sun. You are wanted here.”The Chinese student was greatly surprised. But after a moment the policeman began tosmile, “Mr. Sun, you’ve brought sunshine to England! So we don’t want you to go away.”根据短文内容,判断正(T)误(F)。
