计算题1、2、4

合集下载

期货从业考题八：套利交易

期货从业考题八：套利交易期货从业考题八第八章套利交易一、单向选择题1(在进行套利时，交易者主要关注的是合约之间的( )。

A(相对价格关系B(绝对价格关系C(交易品种的差别 D(交割地的差别2(与普通投机交易相比，套利者在一段时间内( )。

A(只进行多头操作 B(只进行空头操作 C(同时进行多头和空头操作D(先进行一种操作再进行另一种操作3(国外交易所规定，套利的佣金支出与一个回合单盘交易的佣金相比( )。

A(是后者两倍 B(大于后者两倍C(小于后者两倍 D(介于后者的一倍到两倍之间 4(正向市场中，发生以下哪类情况时应采取牛市套利决策( )。

A(近期月份合约价格上升幅度大于远期月份和约 B(近期月份合约价格上升幅度等于远期月份和约 C(近期月份合约价格上升幅度小于远期月份和约 D(近期月份合约价格下降幅度大于远期月份和约 5(理论上，在正向市场牛市套利中，如果价差扩大，交易者( )。

A(获利 B(亏损C(保本 D(以上都有可能6(正向市场牛市套利的操作规则为( )。

A(买人近期合约，同时卖出远期合约B(卖出近期合约，同时买入远期合约C(买入近期和约D(卖出远期合约7(反向市场中，发生以下哪类情况时应采取牛市套利决策( )。

A(近期月份合约价格上升幅度大于远期月份和约 B(近期月份合约价格上升幅度等于远期月份和约 C(近期月份合约价格上升幅度小于远期月份和约 D(近期月份合约价格下降幅度大于远期月份和约8(理论上，在反向市场牛市套利中，如果价差缩小，交易者( )。

A(获利 B(亏损C(保本 D(以上都有可能9(反向市场牛市套利的操作规则为( )。

A(买入近期合约，同时卖出远期合约B(卖出近期合约，同时买入远期合约C(买人近期和约D(卖出远期合约10(正向市场中，发生以下哪类情况时应采取熊市套利决策( )。

A(近期月份合约价格上升幅度大于远期月份和约 B(近期月份合约价格上升幅度等于远期月份和约 C(近期月份合约价格上升幅度小于远期月份和约 D(近期月份合约价格下降幅度小于远期月份和约 11(理论上，在正向市场熊市套利中，如果价差扩大，交易者( )。

水力学试题(计算题)

水力学试题（计算题）0.6 如图所示有一0.8×0.2m的平板在油面上作水平运动，已知运动速度μ＝1m/s，平板与固定边界的距离δ＝1mm，油的动力粘滞系数为1.15N.S/m2，由平板所带动的油的速度成直线分布，试求平板所受的阻力。

题0.60.7 （1）容积为4m3的水，当压强增加了5个大气压时容积减少1升，试求该水的体积弹性系数K。

（2）又为使水的体积相对压缩1／1000，需要增大多少压强？1.23 如图示，闸门AB宽1.2m，铰在A点，压力表G的读数为－14700N／m2，在右侧箱中油的容重γ0＝8.33KN/m2，问在B点加多大的水平力才能使闸门AB 平衡？题1.232.21 贮水器内水面保持恒定，底部接一铅垂直管输水，直管直径d1＝100mm，末端收缩管嘴出口直径d2＝50mm，若不计水头损失，求直管中A、B两断面的压强水头。

题2.212.22 设有一股自喷咀以速度V0喷射出来的水流，冲击在一个与水流方向成α角的固定平面壁上，当水流冲击到平面壁后，分成两股水流流出冲击区，若不计重量，（流动在一个水平面上），并忽略水流沿平面壁流动时的摩阻力，试推证沿着射流方向施加于平面壁上的压力P＝ρ.Q.V0sin2α，并求出Q1与Q2各为多少？题2.222.23 水平放置的水电站压力钢管分岔段，用混凝土支座固定，已知主管直径D ＝3.0m，两个分岔管直径d=2.0m，转角α＝1200，主管末断压强p＝294KN/m2，通过总流量Q＝35m3/s，两分岔管的流量相等，动水压强相等，损失不计，试求水对支座的总推力为若干？题2.232.24 射流自喷嘴中水平射出，冲击在一块与射流方向垂直的正方形平板上，平板为等厚度，边长为30cm，平板上缘悬挂在绞上，（绞磨擦力不计），当射流冲击到平板中心上后，平板偏转300，以后平板不再偏转。

设喷嘴直径d＝25mm，喷嘴前渐变流起点处压力表读数为1.96N/cm2，该断面平均流速v=2.76m/s，喷嘴的局部水头损失系数ξ嘴＝0.3，求平板的质量为多少？题2.242.25 如图所示船闸，闸室长l=100m，宽b=10m，上、下游闸门上的充放水孔面积A＝1m2，孔口的流量系数μ＝0.65，上游孔口的作用水头H＝2m，上、下游水位Z＝4m，试求（1）闸室的充水时间T1（充水时下游放水孔全闭，上游充水孔全开）。

固体废物处理计算题

固体废物处理计算题2.1.据统计，某城市2005年的人口数量为20万，生活垃圾产生量平均为200t/d。

根据该城市的经济发展和城市化进程，预计到2010年该城市的人口数量会增加到22万，为控制生活垃圾的过分增加，规划控制垃圾的人均产生量在2010年为1.1kg/d。

请选择合适的计算方法，预测该城市在2006—2015年期间各年的人口规模、生活垃圾产生量及垃圾产率。

（10分）解：（1）人口预测（4分）2005年人口数量为20万，2010年人口数量预计为22万，按几何增加法（也可用其他方法）预测2006—2015年期间的各年人口规模，设未来每年人口增加率为k，则：Pn=Po·exp(k·n) ①式中Pn=22万，Po=20万，n=2010-2005=5,代入求得k=0.01906，则：Pn=20·exp(0.01906·n)（2）垃圾产率预测（4分）设2005—2015年垃圾产率呈几何增长,每年增长率为x，则：Wn=Wo(1+X)n ②式中 Wn=1.1 kg/(d?人)，Wo=200000（kg/d）/200000(人)=1kg/(d?人),n=2010-2005=5,代入求得X=0.0192设2006—2015年每年垃圾产生量为Nn,则:Nn=Pn·Wn·365/1000 ③式中 Nn为2006—2015年每年的生活垃圾产生量；Pn为2006—2015年的每年人口规模；Wn为2006—2015年每年的垃圾产率；n＝2006—2015。

（3）预测结果（2分）分别用式①、②、③求得2006—2015年的Wn、Nn、Pn，如下表：2.10.某城市垃圾的化学组成为C60.0H25.4O37.5N7.8S5.6Cl，其水份含量为45.6％，灰分含量为14.3％。

请估算该废物的高位热值和低位热值。

（12分）(C1为有机碳，C2为无机碳)答：（1）求垃圾的中各元素组分质量含量生活垃圾有机物含量=100%-45.6%-14.3%=40.1% （1分）垃圾中有机物化学组成为C60.0H25.4O37.5N7.8S5.6Cl的垃圾，其分子量为1669.3，（1分）则每kg垃圾中各元素组分含量为：C含量=0.401?720/1669.3=0.173kg/kg，碳（设全部为有机碳，即C2=0）；（1分）H含量=0.401?25.4/1669.3=0.0061kg/kg；（1分）O含量=0.401?600/1669.3=0.144kg/kg；（1分）N含量=0.401?109.2/1669.3=0.026kg/kg；（1分）S含量=0.401?179.2/1669.3=0.043kg/kg；（1分）Cl含量=0.401?35.5/1669.3=0.0085kg/kg；（1分）（2）求H H、H L废物的高位热值H H：（书本32页公式2-22b）H H=7831m C1+35932(m H-m O/8-m Cl/35.5)+2212m s-3546m C2+1187m O-578m N-6 20m Cl（1分）= [7831?0.173+35932(0.0061-0.144/8-0.0085/35.5)+2212?0.043-3546?0+1187?0.144-578?0.026-620?0.0085]=1157.1(kcal/kg)（1分）H L=H H-583?[m H2O+9(m H-m Cl/35.5)] （书本32页公式2-23）（1分）=1157.1-583?[0.173+9(0.006-0.0085/35.5)]=1020.5(kcal/kg) （1分）2.14.对垃圾取样进行有机组分全量分析的结果见下表，请确定垃圾中有机组分的化学组分表达式（考虑C、H、O、N、S）（13分）答：（1）求各组分质量分数将各类垃圾成分中的相同元素质量相加，得到各元素质量及总质量，所有组分质量为58.1kg，（1分）则各组分质量分数为：C质量分数=27.39/58.1=0.471kg/kg（1分）H质量分数=3.62/58.1=0.0623（1分）O质量分数=22.97/58.1=0.395（1分）N质量分数=0.54/58.1=0.0093（1分）S质量分数=0.1/58.1=0.0017（1分）灰分质量分数=3.48/58.1=0.0599（2）求各组分摩尔百分数将各组分质量分数除以各自原子量得到各组分摩尔分数比，结果如下：C摩尔分数比=0.0471/12=0.0393H摩尔分数比=0.0623/1=0.0623O摩尔分数比=0.395/16=0.0247N摩尔分数比=0.0093/14=0.00066S摩尔分数比=0.0017/32=0.000053设最小的S摩尔分数比为1，则其他元素为：C摩尔分数比=0.0393/0.000053=615.4（1分）H摩尔分数比=0.0623/0.000053=1175.4（1分）O摩尔分数比=0.0247/0.000053=466（1分）N摩尔分数比=0.00066/0.000053=12.4（1分）S摩尔分数比=0.000053/0.000053=1（1分）（3）确定分子式所以垃圾中有机组分的化学表达式为C615.4H1175.4O466N12.4S（2分）3.4.在垃圾收集工人和官员之间发生了一场纠纷，争执的中心是关于收集工人非工作时间的问题。

物理化学试题库.doc

物理化学试题库.doc物理化学试题库 1一、单项选择题本题共10小题，满分20分。

1、一个隔离体系的熵（）（A）保持不变（ B）总是减小（C）总是增大（D）永不减小2、某化学反应在300K, p? 于烧杯中进行时，放热60 kJ，若在相同条件下在可逆电池中进行吸热 6 kJ，则该系统的熵变为（）J·K-1(A)–200 (B)200 (C ) –20 (D) 203、下列各量哪个是偏摩尔量( )(A)(B)(C)(D)4、能改变化学反应的平衡常数的因素是（）(A)温度 (B) 压力 (C) 惰性气体 (D) 物质的量5、在水的相图中存在几条两相平衡线（）(A) 0 (B) 1 (C) 2 (D) 36、将两个银电极插入溶液，通以电流共30，则()(A)阴极析出银(B)阳极析出银(C) 阴极质量减轻(D)阴极质量不变7、在电场作用下，正、负离子传输的电量是否相等（）(A)一定相等 (B) 一定不相等 (C) 一般不相等 (D) 无法比较8、天旱时，农民通过锄地可以保持土壤水分，称为锄地保墒，锄地保墒的科学道理可以用下列哪个物理化学原理解释（）(A) 附加压力（B）渗透压（C）毛细管现象（D）液体的润湿与铺展9、以和溶液混合制备溶胶，若制备时过量，则胶核优先吸附（）(A)(B)(C)(D) 没有选择性10、质量作用定律适用于()(A)只适用于基元反应(B) 适用于复合反应(C) 适用于基元反应和简单反应(D) 适用于所有反应二、填空题本题共10 小题，满分22 分。

1、由循环关系式可知=2、 1理想气体始态体积为，温度为℃，经等温恒外压膨胀到终态体积为，气体所做的体积功为3、在下图中，AB 线代表等温可逆过程，AC 线代表绝热可逆过程。

若从 A 点出发经绝热不可逆膨胀到达V2，则终点将在 C 之下、 B 之上。

B 和C 之间：4、已知 373K 时液体 A 的饱和蒸气压为105pa，液体 B 的饱和蒸气压为×105pa。

(仓库管理)仓储管理计算题

1. 某公司经过对某种产品库存的仔细研究，发现其存货持有成本为产品的单位成本的25%，并且由于出现缺货所导致的延期交货的成本为每年产品的单位成本的150%。

这种产品的单位成本为400 元，每次再订货成本为100 元。

针对这种产品的每年的需求是恒定不变的，为300 个产品单位，并且所有的缺货情况都可以通过延期交货的方式来进行弥补。

最佳的订购政策是什么？在一年中有多少比例的时间是通过延期交货来满足需求的？2. 某种产品的需求是每年2000个产品单位，每一个订单的成本是10元，每年的存货持有成本是产品单位成本的40%，而单位成本根据订单批量变化的规律如下：订单批量小于500 个产品单位，单位成本为 1 元；订单批量在500~999 个产品单位之间，单位成本为0.80 元；订单批量大于等于1000个产品单位，单位成本为0.60 元；在这种情况下，最佳的订单批量是多少？3. C公司生产中使用的甲零件，全年共需耗用3600件。

该零件既可自行制造也可外购取得。

如果自制，单位制造成本为l0 元，每次生产准备成本34．375元，每日生产量32 件。

如果外购，购入单价为9．8元，从发出定单到货物到达需要l0 天时间，一次订货成本72 元。

假设该零件的每年单位储存成本为4元，一年按360天计算。

要求通过计算确定C公司自制和外购方案哪个方案更好。

例题1例：某公司发现，针对某种产品的需求呈正态分布，需求的平均值为每年2000个产品单位，标准偏差为400个产品单位。

产胎的单位成本为100欧元，订货至交货周期为3周。

请计算在服务水平为95 %的情况下的安全存货是多少？解：已知条件为6)=400个产品单伐，L=3周查表，对应？5%的服务禾平，Z值等于1.64,故可以得出：妥全库存二Z x b。

x L i/i =1*64 * 400 x (3/52 ) b- =158 (个产品单住)例题2.某公司每年以每个单位30美元的价格采购6 000个单位的某种产品。

第七单元整数四则混合运算测试题1、2、3、4

第七单元整数四则混合运算测试题1姓名分数一、口算题(共 12分 )5×3—2= 5×3+2= 52＋25-52＋25=5×2＋3= 5×2—3= 100+100×0=50+90÷(2×3)= (50+90)÷2×3= 50+90÷2×3=(50+90÷2)×3= 72÷9×48÷8= 64÷64×7=二、填空(5+8=13分)1、将你上期期末各科考试成绩填入（1）中，并回答下列（2）、（3）问题(5 分)．（1）．语文( )分、数学( )分、英语( )分．（2）．数学比英语高( )分．（3）．三科平均( )分．2、把下面几个分步式改写成综合算式．(8 分)（1）960÷15=64 28=36-64 综合算式_____________________________.（2）75×24=1800 1800=7200-9000 综合算式____________________________（3）810-19=791 791×2=1582 1582+216=1798 综合算式___________________（4）96×5=480 480+20=500 500÷4=125 综合算式____________________三、判断(正确的括号中划“√”，错误的在括号中划“×”并改正)(9分)1．720÷(15－3×2) 2．3889－(108－931)×5 3．(800＋200÷50)×3=720÷(12×2) =3889－149×5 =(100÷50)×3=720÷24 =3889－745 =20×3=30 =3144 =60 ( ) ( ) ( )1、改正：2、改正：3、改正：四、计算题(每道小题 3分共 18分 )962÷74-19×96 (59＋66)×64-10000（798-616)-5940÷45 364÷7-15×4012520÷8×(121÷11) 906×(65+15)-2010五、文字题(每道小题 6分共 18分 )1. 25除175的商加上17与13的积,和是多少?2. 从4000除以25的商里减去13与12的积, 差是多少?3. 6000除以59与35的差, 商是多少?六、应用题(第1小题 5分, 共 30分)1. 某化肥厂一月份生产化肥310吨，二月份生产400吨，三月份生产490吨化肥，平均每月生产化肥多少吨？2.工人王师傅和徒弟做机器零件, 王师傅每小时做45个, 徒弟每小时做28个, 王师傅工作6小时, 徒弟工作8小时, 他们共做多少个机器零件?3. 工厂有煤8000千克, 原计划烧25天, 由于改进炉灶, 实际烧了32天, 平均每天比原计划节约多少千克?4. 一个养鸡场四月份卖出12300只鸡, 五月份卖出的比四月份的2倍还少200只, 两个月一共卖出多少只鸡?5.听过猫和老鼠的故事吗？一天，猫发现前面20米的地方有只老鼠，立即去追，同时，老鼠也发现了猫，马上就跑。

一到三章计算题练习

37. [ 2002年4月第37题]资料：假定某厂拟生产一种新产品甲，经过市场调查，提出三种不同的产量方案可供选择，它们能提供的贡献毛益资料如下：要求：分别采用以下方法选择最满意的方案：(1)大中取大法 (2)大中取小法39.[ 2002年4月第39题]设某公司只生产和销售一种产品，盈亏临界点销售额为每月240000元。

当固定成本增加8000元，为了达到保本必须增加销售额32000元。

若该产品的单位售价及单位变动成本均不变。

要求：(1)计算变动成本率(即变动成本占销售收入的比重)； (2)计算未增加8000元以前的固定成本总额；(3)计算固定成本增加的幅度和盈亏临界点销售额增加的幅度。

37．[ 2003年4月第37题]某企业经营一种产品，正常的月销售量为4,000件，销售单价为25元，单位变动成本为15元，固定成本为25,000元。

要求：（1）分别计算达到盈亏临界点作业率、安全边际率和销售利润率；（2）若其他条件不变，当销售利润率达到30％时，销售量为多少？39．[ 2003年4月第39题]设某企业目前只生产一种甲产品，年需耗用零部件乙10,000件，该企业现有剩余生产能力可用于生产乙零部件，也可用于生产丙产品800件，二个方案互相排斥。

如果生产丙产品，每件可获净利80元。

乙零部件既可自制，亦可外购。

如果自制，其单位成本为：直接材料14元，直接人工3元，变动性制造费用7元，固定性制造费用10元；如果外购，其单位价格为30元。

要求：根据上述资料，进行该企业的零部件乙应自制或外购的决策。

37．[ 2004年4月第37题]资料：某厂生产甲半成品，年产销量为20,000件，可销售给其他厂商作为原材料进一步加工，单位售价为40元，其单位制造成本如下：直接材料8元，直接人工12元，变动性制造费用4元，固定性制造费用6元，合计30元。

该厂正考虑利用剩余生产能力将甲半成品继续加工，加工后每单位售价为56元，继续加工20,000件所增加的单位成本：直接人工5元，变动性制造费用3元；所增加的专属固定成本32,000元。

汽车理论计算题

五、计算题11 某汽车的总质量m=4600kg,C D =0.75,A=4m 2, 03.01＝δ,03.02=δ,f=0.015,传动系机械效率ηT =0.82,传动系总传动比100==gi i i ,假想发动机输出转矩为T e =35000N.m , 车轮半径m r 360.0=，道路附着系数为4.0=ϕ,求汽车全速从30km/h 加速至50km/h 所用的时间。

由于ϕ>F F t ,所以，t u u a ∆-=12,即st 42.181.94.06.33050=⨯⨯-=∆2 已知某汽车的总质量m=4600kg,C D =0.75,A=4m 2,旋转质量换算系数δ1=0.03,δ2=0.03,坡度角α=5°,f=0.015, 车轮半径r r =0.367m ，传动系机械效率ηT =0.85,加速度du/dt=0.25m/s 2,u a =30km/h,计算汽车克服各种阻力所需要的发动机输出功率？kwdtdu mu Au C Gu Gfu P a aD a a t e 18.5736001)25.030460006.176********.05sin 3081.946005cos 3081.9015.04600(85.01)3600761403600sin 3600cos (133=⨯⨯⨯+⨯⨯++⨯⨯+⨯⨯⨯=δ++α+αη=3 已知某车总质量为8025kg ,L =4m (轴距),质心离前轴的距离为a =2.5m ,至后轴距离为b =1.5m ,质心高度h g =1.15m ,在纵坡度为i =3.5的良好路面上等速下坡时 ,求轴荷再分配系数(注:再分配系数m f 1=F Z 1/F Z ,m f 2=F Z 2/F Z )。

NiF z 81.9309081.980255.25.115.15.11⨯=⨯⨯+⨯+=NiF z 81.9493581.980255.25.115.15.22⨯=⨯⨯+⨯-=385.08025/30901==f m ,615.0385.012=-=f m4 已知某汽车发动机的外特性曲线回归公式为T t q =19+0.4n e -150×10-6n e 2，传动系机械效率ηT =0.90-1.35×10-4n e ，车轮滚动半径r r =0.367m,汽车总质量4000kg ，汽车整备质量为1900kg ，滚动阻力系数f =0.009+5.0×10-5u a ,空气阻力系数×迎风面积＝2.77m 2,主减速器速比i 0=6.0,飞轮转动惯量I f =0.2kg ·m 2,前轮总转动惯量I w 1=1.8 kg ·m 2, 前轮总转动惯量I w 1=3.6 kg ·m 2,发动机的最高转速n max =4100r/min ,最低转速n min =720r/min ,各档速比为:计算汽车在V 档、车速为70km/h 时汽车传动系机械损失功率，并写出不带具体常数值的公式。

一元二次方程100道计算题练习(附答案)+一元二次方程经典练习题(6套)附带详细答案

一元二次方程100道计算题练习1、)4(5)4(2+=+x x 2、x x 4)1(2=+ 3、22)21()3(x x -=+4、31022=-x x 5、（x+5）2=16 6、2（2x －1）－x （1－2x ）=07、x 2 =64 8、5x 2 - 52=0 9、8（3 -x ）2 –72=010、3x(x+2)=5(x+2) 11、（1－3y ）2+2（3y －1）=0 12、x 2+ 2x + 3=013、x 2+ 6x －5=0 14、x 2－4x+ 3=0 15、x 2－2x －1 =016、2x 2+3x+1=0 17、3x 2+2x －1 =0 18、5x 2－3x+2 =019、7x 2－4x －3 =0 20、 -x 2-x+12 =0 21、x 2－6x+9 =022、22(32)(23)x x -=- 23、x 2-2x-4=0 24、x 2-3=4x25、3x 2＋8 x －3＝0（配方法） 26、(3x ＋2)(x ＋3)＝x ＋14 27、(x+1)(x+8)=-1228、2(x －3) 2＝x 2－9 29、－3x 2＋22x －24＝0 30、（2x-1）2+3（2x-1）+2=031、2x 2－9x ＋8＝0 32、3（x-5）2=x(5-x) 33、(x ＋2) 2＝8x34、(x －2) 2＝(2x ＋3)2 35、2720x x += 36、24410t t -+=37、()()24330x x x -+-= 38、2631350x x -+= 39、()2231210x --=40、2223650x x -+=补充练习：一、利用因式分解法解下列方程(x －2) 2＝(2x-3)2 042=-x x 3(1)33x x x +=+x 2 ()()0165852=+---x x二、利用开平方法解下列方程51)12(212=-y 4（x-3）2=25 24)23(2=+x三、利用配方法解下列方程25220x x -+= 012632=--x x01072=+-x x四、利用公式法解下列方程－3x 2＋22x －24＝0 2x （x －3）=x －3． 3x 2+5(2x+1)=0五、选用适当的方法解下列方程(x ＋1) 2－3 (x ＋1)＋2＝0 22(21)9(3)x x +=- 2230x x --=21302x x ++= 4)2)(1(13)1(+-=-+x x x x--xx x（x＋1）－5x＝0. 3x(x－3) ＝2(x－1) (x＋1).23(=)2)(11应用题：1、某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元，为扩大销售增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价一元，市场每天可多售2件，若商场平均每天盈利1250元，每件衬衫应降价多少元？2、两个正方形，小正方形的边长比大正方形的边长的一半多4 cm，大正方形的面积比小正方形的面积的2倍少32平方厘米，求大小两个正方形的边长.3、如图，有一块梯形铁板ABCD，AB∥CD，∠A=90°，AB=6 m，CD=4 m，AD=2 m，现在梯形中裁出一内接矩形铁板AEFG，使E在AB上，F在BC上，G在AD上，若矩形铁板的面积为5 m2，则矩形的一边EF长为多少？4、如右图，某小在长32米，区规划宽20米的矩形场地ABCD上修建三条同样宽的3条小路，使其中两条与AD平行，一条与AB平行，其余部分种草，若使草坪的面积为566米2，问小路应为多宽？5、某商店经销一种销售成本为每千克40元的水产品，据市场分析，若按每千克50元销售一个月能售出500千克；销售单价每涨1元，月销售量就减少10千克，商店想在月销售成本不超过1万元的情况下，使得月销售利润达到8000元，销售单价应定为多少？6.某工厂1998年初投资100万元生产某种新产品，1998年底将获得的利润与年初的投资的和作为1999年初的投资，到1999年底，两年共获利润56万元，已知1999年的年获利率比1998年的年获利率多10个百分点，求1998年和1999年的年获利率各是多少？思考：1、关于x 的一元二次方程()04222=-++-a x x a 的一个根为0，则a 的值为。

增值税计算题习题(附详细答案)

【例2—4·计算题】某自营出口的生产企业为增值税一般纳税人,出口货物的征税税率为17％，退税税率为13％.2005 年4 月的有关经营业务为:购进原材料一批，取得的增值税专用发票注明的价款200 万元,外购货物准予抵扣的进项税额34万元通过认证.上月末留抵税款3万元,本月内销货物不含税销售额100万元，收款117万元存入银行，本月出口货物的销售额折合人民币200万元。

试计算该企业当期的“免、抵、退”税额。

『正确答案』（1)当期免抵退税不得免征和抵扣税额＝200×（17％－13％）＝8(万元）（2)当期应纳税额＝100×17%－(34－8）－3＝17－26－3＝－12（万元）(3）出口货物“免、抵、退”税额＝200×13％＝26(万元）（4）按规定，如当期末留抵税额≤当期免抵退税额时:当期应退税额＝当期期末留抵税额即该企业当期应退税额＝12(万元)（5）当期免抵税额＝当期免抵退税额－当期应退税额当期免抵税额＝26－12＝14（万元）【例2－5·计算题】某自营出口的生产企业为增值税一般纳税人，出口货物的征税税率为17％，退税税率为13%.2005 年6 月有关经营业务为：购原材料一批，取得的增值税专用发票注明的价款400 万元，外购货物准予抵扣的进项税额68万元通过认证。

上期末留抵税款5 万元。

本月内销货物不含税销售额100 万元，收款117 万元存入银行。

本月出口货物的销售额折合人民币200 万元。

试计算该企业当期的“免、抵、退"税额.【解析】（1）当期免抵退税不得免征和抵扣税额＝200×（17%－13％）＝8（万元）（2）当期应纳税额＝100×17％－（68－8）－5＝17－60－5＝－48(万元）(3）出口货物“免、抵、退"税额＝200×13％＝26（万元）(4）按规定，如当期期末留抵税额>当期免抵退税额时：当期应退税额＝当期免抵退税额即该企业当期应退税额＝26（万元）（5）当期免抵税额＝当期免抵退税额－当期应退税额该企业当期免抵税额＝26－26＝0（万元）（6）6月期末留抵结转下期继续抵扣税额为22（48－26）万元.（2）如果出口企业有进料加工复出口业务,“免、抵、退”办法如下:【例2－6·计算题】某自营出口生产企业是增值税一般纳税人,出口货物的征税税率为17％,退税税率为13％。

国际运输与保险计算题

FOB+I+F =CFR+I =CIF FCA+I+C =CPT+I =CIP 保险金额＝CIF（１＋投保加成率）保险费＝保险金额×保险费率 CIF=CFR/(1－保险费率×投保加成)
练习题
1、出口箱装货物共100箱，报价为每箱4000美元FOB 上海，基本费率为每运费吨32美元或1.5%，以W/M or Ad Val 选择法计算，每箱体积为1.4m × 1.3m × 1.1m,毛重为每箱2公吨，并加收燃油附加费10%，货币贬值附加费20%，转船附加费30%，求总运费。×
W：0.015
M：0.35×0.30×.015=0.01575
F:0.1575×120×(1+10%+20%)=2.பைடு நூலகம்57
FOB=CFR-F=30-2.457=27.54美元
3、我公司出口到海湾国家A商品l00箱，每箱体积 40厘米×30厘米×20厘米，毛重30公斤，应付给船公司运费多少？又知货装外轮，查得《中租表》：A商品安货物分级表规定计算标准为M/W，货物等级为10级；又查“中国一海湾地区航线等级费率表”，10级每运费吨的基本费率为222港元，另收燃料附加费l0%。
一公吨＝220.62磅；
一短吨＝2000磅按短吨计算，每运费吨＝60（美元）
则每运费吨按公吨计算应为
60×2204.62/2000=66.1（美元）
CFR价＝FOB价＋运费＝180+66.1＝246.1（美元）
故我方应改报：每公吨246.1美元CFR东京或将每公吨 180美元，折算为每短吨
保险赔款＝保险金额 ×
货物完好价值－货物受损后价值货物完好价值

（完整版）一年级元角分计算题

（完整版）一年级元角分计算题2角＋2元8角＝（）元9角＋4角＝（）角4元＋5元＝（）元1元○100分4角8分○50分1角1分○9分3元=（）角50角=（）元9元=（）角80角=（）元1元5角=（）角14角=（）元（）角3元8角=（）角16角=（）元（）角3角+5角=（）角4角+6角=（）角40元+5元=（）元20元—2元=（）元1元=（）角1角+3元=（）元（）角8角5分-4分=( )角( )分3元4角=（）角75角=（）角1元5角+2元5角=（）元1元4角+9角=（）角4元5角+4角=（）元（）角1元=（）分8角5分-4分=( )角( )分5分+8分=( )分1元-9角=( )角7角+9角=( )元( )角1角5分-4分=( )角( )分4角+9角=( )元( )角5分+3分=( )分1元-3角=( )角1角2分-6分=( )分9分+5分=( )角( )分1角5分-4分=( )角( )分4角+9角=( )元( )角5分+3分=( )分1元-3角=( )角1角2分-6分=( )分9分+5分=( )角( )分100元=（)角1角8分-6分=( )分6分+5分=( )角( )分2元3角=（）角 5.6元=（）元（）角3元4角-5角=（）元（）角3角+7角=（）角9角－5角=（）角1角=（）分1元－8角=（）角20分－10分=（）分=（）角3元7角－4角=（）元（）角14分+7分=（）分15分－5分=（）角6元5角+6角=（）元（）角30分=（）角20角=（）元30角=（）元5元=（）角70角=（）元 80分=（）角1元1角=（）角2元7角=（）角13角=（）元（）角25角=（）元（）角49分=（）角（）分8角5分=（）分5角4分=（）分90角=（）元80角=（）元3元=（）角50角=（）元20元—2元=（）元9元=（）角80角=（）元1元5角=（）角14角=（）元（）角3元8角=（）角16角=（）元（）角。

资产评估计算题整理

资产评估计算题整理资产评估计算题1 . (8分) 甲企业将一项专利使用权转让给乙公司，拟采用利润分成的方法，该专利系三年前从外部购入，账面成本为100万元，三年间物价累计上升50%，该专利法律保护期10年，已过3年，尚可保护7年。

经专业人士测算，该专利成本利润率为400%，乙企业资产重置成本为5000万元，成本利润率为10%，通过对该专利的分析，技术人员认为该专利剩余使用寿命为5年，另外，通过对市场供求状况及有关会计资料分析得知，乙企业实际生产能力为年产某型号产品20万台，成本费用每年约为400元，未来5年间产量与成本费用变动不大，该产品由于采用了专利技术，性能有较大幅度提高，未来第一、第二年每台售价要达500元，在竞争的作用下，为维护市场占有率，第三、第四年售价将下降到每台450元，第五年下降到每台420元，折现率确定为10%。

要求根据上述资料确定该专利的评估值（不考虑流转税因素，计算结果保留两位小数）答案:（1）确定利润分成率：确定专利的重置成本：100×（1+50%）=150（万元）专利的约当投资量：150×（1+400%）=750（万元）乙企业资产的约当投资量：5000×（1+10%）=5500（万元）利润分成率：750/（5500+750）×100%=12%（2）确定评估值①确定每年利润总额：第一、第二年：（500-400）×20=2000（万元）第三、第四年：（450-400）×20=1000（万元）第五年：（420-400）×20=400（万元）②确定分成额：第一、第二年：2000×12%=240（万元）第三、第四年：1000×12%=120（万元）第五年：600×12%=72（万元）③确定评估值：240/（1+10%）+240/（1+10%）2 +120/（1+10%）3 +120/（1+10%）4+72/（1+10%）5=240×0.9091+240×0.8264+120×0.7513+120×0.6830+72×0. 6209 =218.18+198.34+90.16+81.96+44.71 =633.35（万元）2 . (7分) 甲企业有购买了A企业发行的三年期一次还本付息债券，面值10000元，票面利率为7%，单利计息，评估日距到期日一年，当时国库券利率为6%，据评估人员分析调查，发行企业经营业绩较好，两年后有还本付息的能力，风险不大，取2%的风险报酬率。

财务管理计算题【仅供参考】

书上第二章1、某企业购入国债2500手，每手面值1000元，买入价格1008元，该国债期限为5年，年利率为6.5%（单利），则到期企业可获得本利和共为多少元？Fv =Pv（1+r×n）=2500×1000×(1+6.5%×5)=2500000×1.3250= 3312500(元)单利现值的计算:P=F/(1+rn)2、某投资者将10000元用于购买债券，该债券的年报酬率为10％，按复利计算，到期一次还本付息，第5年末该投资者本利和？(复利终值)F5=P×(1+r)n=10000×（1+10％）5=10000×（F/P 10％，5）=10000×1.6105=16105（元）3、某人计划5年后获得10 000元，用于购卖汽车，假设投资报酬率为8％，按复利计算，他现在应投入多少元？(复利现值)P=10，000×1/（1+8％）5=10，000×（P/F ，8％，5 ）=10，000×0.6806 =6806（元）4、如某人决定从孩子10岁生日到18岁生日止每年年末（不包括第10岁生日）为孩子存入银行200元，以交纳孩子上大学学费。

如银行存款利率为10％，父母在孩子18岁生日时能从银行取出多少钱？F=200·[（1+10％）8-1]/10%=200×（F/A，10％，8）=200×11.436=2287.2（元）（年金终值）5、某技术项目1年建成并投产，投产后每年净利润为50，000元，按10％的利率计算，在3年内刚好能收回全部投资。

问此项目投资多少？（年金现值）P=A×（P/A 10％3）=50 000×（P/A 10％3）=50 000×2.4869=124345（元）偿债基金系数＝1÷普通年金终值系数投资回收系数＝1÷普通年金现值系数6、某人从现在起准备每年年末等额存入银行一笔钱，目的在于5年后从银行提取15 000元，用于购买福利住房。

2018届高考物理高考计算题54分练(1)(2)(3)(4) 分类突破-含答案,60分钟规范答题抓大分!

高考计算题54分练(1)分类突破,60分钟规范答题抓大分!1.如图所示,在倾角θ=37°的粗糙斜面上距离斜面底端s=1m处有一质量m=1kg的物块,受水平恒力作用,由静止开始沿斜面下滑。

到达底端时撤去水平恒力,物块在水平面上滑动一段距离后停止。

不计物块撞击水平面时的能量损失。

物块与各接触面之间的动摩擦因数均为μ=0.2,sin37°=0.6,cos37°=0.8,g=10m/s2。

求:(1)若物块运动过程中的最大速度为1m/s,水平恒力F的大小为多少?(结果保留两位有效数字)(2)若改变水平恒力F的大小,可使物块总的运动时间有一最小值,最小值为多少?【解析】(1)物块到达斜面底端时速度最大,v2=2as对物块,有F N=mgcosθ+Fsinθ;mgsinθ-Fcosθ-f=ma;f=μF N;代入数据得F=4.2N(2)设斜面上物块加速度为a1,运动时间为t1,在水平面上运动时间为t2;则s=错误！未找到引用源。

a1错误！未找到引用源。

;到达底端时速度v′2=2a1s;物块在水平面上时a2=μg;v′=a2t2;总时间t=t1+t2=错误！未找到引用源。

+错误！未找到引用源。

;由数学知识可知,当a1=2m/s2时t min=2s。

答案:(1)4.2N (2)2 s2.一长l=0.80m的轻绳一端固定在O点,另一端连接一质量m=0.10kg 的小球,悬点O距离水平地面的高度H=1.00m。

开始时小球处于A点,此时轻绳拉直处于水平方向上,如图所示。

让小球从静止释放,当小球运动到B点时,轻绳碰到悬点O正下方一个固定的钉子P时立刻断裂。

不计轻绳断裂的能量损失,重力加速度g取10m/s2。

求:(1)当小球运动到B点时的速度大小。

(2)绳断裂后球从B点抛出并落在水平地面的C点,求C点与B点之间的水平距离。

(3)若OP=0.6m,轻绳碰到钉子P时绳中拉力达到所能承受的最大拉力断裂,求轻绳能承受的最大拉力。

矿山测量计算试题50道计算题带答案

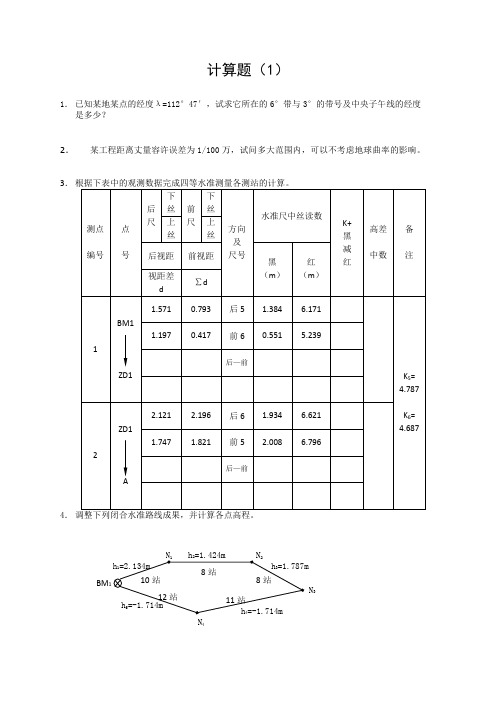
计算题（1）1．已知某地某点的经度λ=112°47′，试求它所在的6°带与3°的带号及中央子午线的经度是多少？2．某工程距离丈量容许误差为1/100万，试问多大范围内，可以不考虑地球曲率的影响。

3．根据下表中的观测数据完成四等水准测量各测站的计算。

测点编号点号后尺下丝前尺下丝方向及尺号水准尺中丝读数K+黑减红高差中数备注上丝上丝后视距前视距黑（m）红（m）视距差d∑d1BM1ZD11.5710.793后5 1.384 6.171K5=4.787K6=4.687 1.1970.417前60.5515.239后—前2ZD1A 2.121 2.196后6 1.934 6.621 1.747 1.821前5 2.008 6.796后—前4．调整下列闭合水准路线成果，并计算各点高程。

BM1h2=1.424mh1=2.134m h3=1.787mh4=-1.714m11站h5=-1.714m10站8站8站12站N1N2N3N4其中：水准点的高程H BM1=44.313m水准测量成果调整表测点测站数高差值高程m备注观测值m 改正数mm 调整值mBM1N1N2N3N4BM1∑实测高差∑h= 已知高差=H终-H始=0高差闭合差f h= 容许闭合差f h容==一个测站的改正数=5．完成下表测回法测角记录的计算。

测站测回数盘位目标水平度盘读数°′″水平角草图半测回值°′″一测回值°′″平均值°′″O 1左A 0 12 00B 91 45 00右A 180 11 30B 271 45 00 2左A 90 11 48B 181 44 54右A 270 12 12B 1 45 126．完成下表竖直角测量记录计算。

测站目标竖盘位置竖盘读数°′″半测回角值°′″一测回角值°′″指标差竖盘形式O M左81 18 42全圆式顺时针注记右278 41 30N左124 03 30右235 56 54n10±=∑-nfhA BO7．丈量两段距离，一段往测为126.78米，返测为126.68米，另一段往测、返测分别为357.23米和357.33米。