流体力学-第四章
流体力学第四章

由连续方程 V2
2
A1 V1 A2
,代入上式,有
A V A h j (1 1 ) 2 1 ,即1 (1 1 ) 2 A2 2 g A2
如以
V1
A2 则有 V2代入,则有 A1
2 A2 2 V2 h j ( 1) , 即 2 ( A2 1) 2 A1 2g A1
4.3.2 混合长度理论
4.3.3 湍流的速度分布 1、粘性底层(层流底层)
dv (1) 很大; dy
(2)粘性底层的厚度δ很小。 2、湍流核心
dv (1) dy
很小;
(2)区域大。 3、 过渡层—有时可将它算在湍流核心的 范围。
速度分布:在粘性底层中速度分布是直 线规律;湍流核心中为对数关系。 粗糙度 Δ 管壁凹凸不平的平均尺寸。 水利光滑管 δ>Δ 粗糙度对湍流核心几乎没有影响。 水利粗糙管 δ<Δ 粗糙度的大小对湍流特性产生直接影响。
《流体力学》
教学课件
第4章 流体在圆管中的流动
1 流体在固体内部的管中流动和缝隙中流动; 2 流体在固体外部的绕流; 3 流体在固体一侧的明渠流动; 4 流体与固体不相接触的孔口出流和射流。
4.1 雷诺实验
雷诺实验
雷诺实验发现 1.用不同的流体在相同直径的管道中进行实验,
所测得的临界速度 vk 是各不相同的;
T
有
W W W ,代入上式,得
T
1 1 W W W dt W W dt T0 T0 T 1 所以 T W dt 0 0
T
即脉动量的时均值
W 0
运用时均统计法就将湍流分为两个组成部分:一部分是用时均值表示 的时均流动;另一部分是用脉动值表示的脉动运动。时均流动代表运动 的主流,脉动反映湍流的本质。
流体力学第四章 流动阻力及能量损失

d
d
d
d1 d2
d
S2
S1
S1
【例】 有一长方形风道长 l 40m,截面积A= 0.5×0.8m2
,管壁绝对粗糙度 K= 0.19mm,输送t=20℃的空气,流
量Q 21600m3/h,试求在此段风道中的沿程损失。
【解】 平均流速
当量直径
V Q 21600 15 A 3600 0.5 0.8
and 2(If λ=0.02) ?
【例 】 圆管直径 d m20m0,管长 l 10m0,0输送运动黏度
cm2/s的石油1,.6流量
m3/h,求沿Q程损 1失44。
【解】 判别流动状态
Vd 1.270.2
Re
1587.5 2000
1.6104
为层流
式中 V
4Q
d 2
4 144 36003.14 0.22
第四章 流动阻力及水头损失
本章主要研究恒定流动时,流动阻力和水 头损失的规律。对于粘性流体的两种流态—— 层流与紊流,通常可用下临界雷诺数来判别, 它在管道与渠道内流动的阻力规律和水头损失 的计算方法是不同的。对于流速,圆管层流为 旋转抛物面分布,而圆管紊流的粘性底层为线 性分布,紊流核心区为对数规律分布或指数规 律分布。对于水头损失的计算,层流不用分区, 而紊流通常需分为水力光滑管区、水力粗糙管 区及过渡区来考虑。
式中: ——沿程阻力系数。 •物理意义:圆管层流中,沿程水头损失与断面平均流速的一次
方成正比,而与管壁粗糙度无关。 •适用范围: 1.只适用于均匀流情况,在管路进口附近无效。 2.推导中引用了层流的流速分布公式,但可扩展到紊流,紊流 时l值不是常数。
四、圆管流的起始段
图中起始段长度l’:从进
流体力学第四章:流体阻力及能量损失

优化物体表面粗糙度、使用润滑剂、改变流体的流速和方 向等。
形状阻力
形状阻力
由于物体形状的不同,流体在绕过物体时产生的阻力。
形状阻力公式
$F_s = frac{1}{2} rho u^2 A C_s$,其中$C_s$为形状阻力系数, 与物体形状、流体性质和流速有关。
减小形状阻力的方法
详细描述
汽车设计中的流体阻力优化主要包括车身形 状设计和空气动力学套件的应用。设计师会 采用流线型设计来减小空气阻力,同时也会 采用导流板、扰流板等空气动力学套件来调 整汽车周围的空气流动,以提高汽车的行驶
稳定性、减小风噪,并降低燃油消耗。
THANKS FOR WATCHING
感谢您的观看
详细描述
船舶航行中的流体阻力主要来自船体与水之间的摩擦力以及水对船体的冲击力。为了减小流体阻力, 船舶设计师通常会采用流线型设计,优化船体表面的光滑度,以及减少不必要的突出物,从而提高航 行效率。
管道流动中的能量损失
总结词
管道中流体流动时,由于流体与管壁之 间的摩擦以及流体内部的湍流等效应, 会产生能量损失。
根据伯努利方程、欧拉方程等计算公式,结合物体的形状、速度和流体密度等 参数进行计算。
02 流体阻力现象
摩擦阻力
摩擦阻力
由于流体与物体表面的相对运动产生摩擦而形成的阻力。
摩擦阻力公式
$F_f = frac{1}{2} rho u^2 A C_f$,其中$rho$为流体密 度,$u$为流速,$A$为流体与物体接触的表面积,$C_f$ 为摩擦阻力系数。
流体力学第四章流体阻力及能量损 失
目录
• 流体阻力的概念 • 流体阻力现象 • 能量损失原理 • 流体阻力的减小方法 • 实际应用案例
流体力学第四章
动量方程16-运动控制体
已知V = 30m/s,U = 10m/s,忽略重力和摩擦力, 已知V = 30m/s,U = 10m/s,忽略重力和摩擦力, 出口截面A11= 0.003m22,求Rxx和 Ryy 出口截面A = 0.003m ,求R 和 R
解:(1) 坐标系 (2) 控制体
r r r Vr = V − U
流体力学
动量方程15-运动控制体
∂ ∂t
∫
CV
r r r r r ρVr dτ + ∫ ρVrVr ⋅ ndS = ΣF
CS
流体仅在控制面的有限个区域流入流出且 ρ,V 在进出口截面均布,定常流动
r r & ∑ F = ∑ mriVri
(
)
out
−∑
(
r & mriVri
)
in
r r r 其中 Vr = V − VCV
φ
流体力学
雷诺输运方程1
欧拉方法描述系统物理量对时间的变化率
CSIII CSI I
t
r V
II
III
dS3
dS1 r n
r n
r V
t +δ t
DN sys Dt
流体力学
= lim
N sys (t + δt ) − N sys (t )
δt → 0
δt
雷诺输运方程2
DN sys Dt
DN sys Dt
流体力学
质点导数与系统导数
质点导数
r Dφ ∂φ = + (V ⋅ ∇ )φ Dt ∂t
流体质点某物理量随时间的变化率同空 间点上物理量之间的关系 系统导数
DN ∂ = Dt ∂t r r φV ⋅ ndS
流体力学第四章 水头损失

P59表4-1为不同形状导管的临界雷诺数(水力半径)。
雷诺数的物理意义: Re = V d/ 粘性大、 Re 小、 易层流
13
§4–5 层流的水头损失---圆管中的层流
在这一章节主要讨论粘性力和沿程水头损失 hf 的规律。
假设流体在等截面水平圆管中作层流运动。取出其中半径 为 r 的圆柱体作为研究对象,写出运动方程式:(因为是定常
因此在计算每一个具体流动的水头损失时,首先须要判 别该流体的流动状态,而雷诺数为判别流体是层流还是湍 流提供了准则。
11
§4-4 雷诺数
管中流体的平均流速不是一个独立不变的量。
由实验知:流体平均流速与流体运动粘性成正比、与管道直 径d成反比;则引入一个无量纲比例常数Re 可写为:
V= Re /d
其中 Re 称为雷诺数。
8
(c)继续增大管内流速,则染色流束剧烈地波动,最后个别部 分出现破裂,并失掉原来的清晰的形状,混杂在很多小旋涡中。 染色液体很快充满整个管,如图c。这表明此时管内的流体向前 流动时处于完全无规则的混乱状态,称其为“湍流”,或“紊 流”。
流体由层流转变为湍流时 的平均流速,称之为“上临 界速度VC `”。
长管、短管
不是由管道的长与短来决定,而是由局部水头损失与沿程水头 损失的比例大小来确定。
长管:沿程损失比局部损失和速度水头的和大,局部损失可忽略;
短管:局部损失和速度水头的和比沿程损失大,考虑局部损失;
§4-3 流体流动两种状态
在不同条件下,流体质点的运动可能表现为两种状态。 一是、流体质点作有规则的运动,在运动过程中质点之间
互不混杂、互不干扰。 二是、流体质点的运动非常混乱。 1883年英国科学家雷诺进行了负有盛名的雷诺实验。
工程流体力学第4章流体在圆管中的流动

流体在圆管中的摩擦系数
定义
表示流体在圆管中流动时, 流体与管壁之间的摩擦力 与压力梯度之间的比值。
影响因素
流体的物理性质、管道的 粗糙度、流动状态等。
测量方法
通过实验测定,常用的实 验设备有摩擦系数计和流 阻仪等。
流体在圆管中的流动效率
定义
表示流体在圆管中流动的能量转 换效率,即流体在流动过程中所 消耗的能量与流体所具有的能量
流速分布受流体粘性和密度的影响, 粘性越大、密度越小,靠近管壁处流 速降低越快。
03
流体在圆管中的流动现象
流体阻力
01
02
03
定义
流体在流动过程中,由于 流体内部以及流体与管壁 之间的摩擦力而产生的阻 力。
影响因素
流体的物理性质、流动状 态、管道的形状和尺寸等。
减小阻力措施
选择适当的流速、优化管 道设计、使用减阻剂等。
之比。
影响因素
流体的物理性质、管道的形状和尺 寸、流动状态等。
提高效率措施
优化管道设计、改善流体物性、降 低流速等。
流体பைடு நூலகம்圆管中的流动稳定性
定义
表示流体在圆管中流动时,流体的速 度和压力等参数随时间的变化情况。
影响因素
流动稳定性控制
通过控制流体物性、流速和管道设计 等措施,保持流体在圆管中的流动稳 定性。
根据输送距离、流量和扬程要求,选择合适的水 泵。
输送效率
优化输送管道布局,降低流体阻力,提高输送效 率。
输送安全性
确保输送过程中不发生泄漏、堵塞等安全问题。
液压系统
液压元件
根据液压系统要求,选择合适的液压元件,如油泵、阀、油缸等。
系统稳定性
确保液压系统在各种工况下稳定运行,避免压力波动和振动。
流體力學第四章伯努利方程

第四章 伯努利方程4.1 伯努利方程4.1.1 理想流体沿流线的伯努利方程1. 伯努利方程的推导将欧拉运动微分方程式积分可以得到流体的压力分布规律,但只能在特殊的条件下,不可能在任何的情况下都可求得其解,故我们需对流场作出如下假设:(1)理想流体(2)定常流动(3)质量力有势(4)不可压缩流体(5)沿流线积分在定常流动的条件下,理想流体的运动微分方程(欧拉运动微分方程)可以写成 ⎪⎪⎪⎩⎪⎪⎪⎨⎧∂∂+∂∂+∂∂=∂∂-∂∂+∂∂+∂∂=∂∂-∂∂+∂∂+∂∂=∂∂-z v v y v v x v v z p f z v v y v v x v v y p f z v v y v v x v v x p f z z z y z x z y z y y y x y x z x y x x x ρρρ111 (4.1) 将这个方程沿流线积分,如图4.1所示,可得到伯努利方程。
为此,将式(4.1)的第一式乘以x d 得x zv v x y v v x x v v x x p x f x z x y x x x d d d d 1d ∂∂+∂∂+∂∂=∂∂-ρ (1) 按照流线方程 zy x v z v y v x d d d == 将有,y v x v x y d d =,z v x v x z d d =故式(1)可写成x x x x x x x x x v v z zv v y y v v x x v v x x p x f d d d d d 1d =∂∂+∂∂+∂∂=∂∂-ρ (2) 式(4.1)的另外两式分别乘y d 、z d 后,作类似的代换,可得y y y v v y yp y f d d 1d =∂∂-ρ (3)z z z v v z zp z f d d 1d =∂∂-ρ (4) 将式(2)、(3)和式(4)相加,得 z z y y x x z y x v v v v v v z zp y y p x x p z f y f x f d d d )d d d (1d d d ++=∂∂+∂∂+∂∂-++ρ (5) p 的全微分可以表示为 dz zp dy y p dx x p dp ∂∂+∂∂+∂∂= 质量力有势,则必存在势函数U ,满足y f y f x f z zU y y U x x U U y y x d d d d d d d ++=∂∂+∂∂+∂∂=而 2/d d d d 2v v v v v v v z z y y x x =++式中等号右端的v 为平均速度。
流体力学课件第四章流动阻力和水头损失

l v hf d 2g
2
r w g J 2
w v 8
定义壁剪切速度(摩擦速度) 则
w v
*
v v
*
8
§4-4 圆管中的层流
层流的流动特征
du dy
du du dy dr
du dr
g J
r 2
r du g J 2 dr
层流 紊流
§4-3 沿程水头损失与剪应力的关系
均匀流动方程式
P G cos P2 T 0 1
P p1 A1 1
P2 p2 A2
T w l
G cos gAl cos gA( z1 z2 )
w l p1 p2 ( z1 ) ( z2 ) g g gA
v2 hj 2g
§4-2 粘性流体的两种流态
两种流态
v小
' c
v小
v > vc
v大 v大
临界流速。 下临界流速 vc ——由紊流转化为层流时的流速称为下 临界流速。
vc' ——由层流转化为紊流时的流速称为上 上临界流速
vv
层流 紊流
' c
紊流 层流
a-b-c-e-f f-e-d-b-a
第四章 流动阻力和水头损失
水头损失产生的原因: 一是流体具有粘滞性, 二是流动边界的影响。
§4-1 流动阻力和水头损失的分类
沿程阻力和沿程水头损失
在边界沿程无变化(边壁形状、尺寸、过 流方向均无变化)的均匀流段上,产生的流动 阻力称为沿程阻力或摩擦阻力。由于沿程阻力 做功而引起的水头损失称为沿程水头损失。均 匀流中只有沿程水头损失 h f 。
工程流体力学-第4章-M

运动学物理量的比例系数都可以表示为尺度比例系数和时间比例系数的不同组合形式。
如:kv=klkt-1 ka=klkt-2 k=kt-1 k=kl2kt-1 kqv=kl3kt-1 的单位是m2/s qV的单位是m3/s
三 动力相似(受力相似)
定义:两流动的对应部位上同名力矢成同一比例。 原型流动中作用有:重力、阻力、表面张力,则模型流动中相应点上也应存在这三种力,并且各同名力的方向相同、比值保持相等。 引入力比例系数 也可写成
[解](1) 对流动起主要作用的力是黏滞力,应满足雷诺准则
流动的压降满足欧拉准则
[例2] 有一直径d=50cm的输油管道,管道长l=200m,油的运动粘滞系数 ,管中通过油的流量 。现用10℃的水和管径dm= 5 cm的管路进行模型试验,试求模型管道的长度和通过的流量。
M: 1= c+d L: 1= a+b-3c-d T: -2= -b -d 上述三个方程中有四个未知数,其中的三个未知数必须以第四个未知数表示: c=1-d; b=2-d; a=2-d 求得各指数值,带入假设式,得到无量纲关系式
(2)根据量纲和谐原理建立联立方程式
上式是一个无量纲方程,与具有四个未知数的原函数方程相比,仅包含一个独立的无量纲变量。在分析试验结果并确定变量之间的关系时,独立变量数的减少是非常方便的,这也是量纲分析的明显好处。
非定常相似准则
由当地惯性力与迁移惯性力的关系,得到 称为斯特罗哈(Strouhal)数,要使两个流动的当地惯性力作用相似,则它们的斯特罗哈数必须相等,这称为惯性力相似准则,也称为非定常相似准则。
流动相似理论是工程模型研究和实验的基础。模型和原型的相似参数的测试与数据处理是工程模型研究的两个核心问题。 一、模型与原型的相似 1、近似相似 1)不是所有的相似准则数都能同时被满足的; 2)甚至,有时连保证几何相似都是困难的。 2、实验方法 根据具体的问题,选择最重要的相似准则,确定模型尺寸及实验条件;得到无量纲准则数之间的关系。
流体力学 第4章
模型与原型的流场动力相似,它们的牛顿数必定相等。
4.2 动力相似准则
4.2.1.重力相似准则
在重力作用下相似的流动,其重力场相似。
kF
Fg Fg
V g Vg
k kl3kg
代入
kF k kl2kv2
kv (kl kg )1/ 2
1
v (gl)1/ 2
v (gl)1/ 2
Fr
Fr——弗劳德数,惯性力与重力的比值。
自模化状态 紊流的阻力有两部分
例如:泵与风机的动力相似是自动满足的
如图为弧形闸门放水时的情形,已知水深h=6m, 模型闸门是按比例尺kl=1/20制作,试验时的开度与 原型相同。试求流动相似时模型闸门前的水深。在模 型 上 测 得 收 缩 截 面 的 平 均 流 速 vˊ=2.0m 流 量 qvˊ=30L/s, 水作用在闸门上的力Fˊ=92N,绕闸门的 力矩Mˊ=110N·m,试求原型上收缩截面的平均流速、 流量、以及作用在闸门上的力。
第4章 相似原理和量纲分析
4.1 流动的力学相似
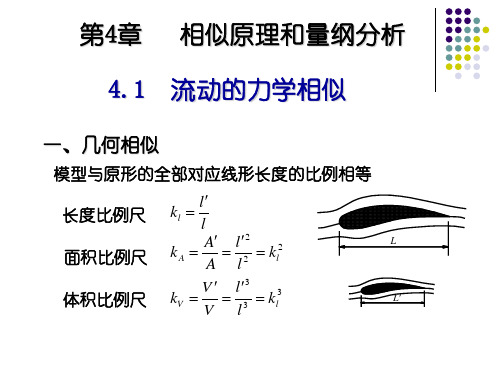
一、几何相似
模型与原形的全部对应线形长度的比例相等
长度比例尺
kl
l l
面积比例尺
kA
A A
l2 l2
kl2
L
体积比例尺
kV
V V
l3 l3
kl3
L
二、运动相似
模型与原形的流场所有对应点上、对应时刻 的流速方向相同而流速大小的比例相等。
速度比例尺 时间比例尺 加速度比例尺 体积流量比例尺 运动粘度比例尺
力的比例尺
kF
FP FP
F F
Fg Fg
Fi Fi
FP ——总压力 F ——切向力 Fg ——重力 Fi ——惯性力
流体力学-第四章-流动阻力和能量损失(章结)

K(mm) 管道材料 K(mm)
表面光滑砖风道
4.0
度锌钢管
0.15
矿渣混凝土板风道 1.5
钢管
0.046
钢丝网抹灰风道 10~15
铸铁管
0.25
胶合板风道
1.0
混凝土管
0.3~3.0
墙内砌砖风道
5~10 木条拼合圆管 0.18~0.9
确定沿程阻力系数的方法:
(1)经验公式 (2)莫迪图 (3)查相关手册
二、等效过程
(1)用实验方法对某种材料的管道进行沿程损 失实验,测出 和 hf ;
(2)再用达西公式计算出λ;
hf
l d
2
2g
(3)用尼古拉兹阻力平方区公式计算出绝对
粗糙度K。
1
(1.74 2 lg d )2
2K
此时的K值在阻力的效果上是与人工粗糙管的管 道粗糙度相当的,故称其为当量粗糙度。
莫迪(Mood渐扩管 (d)减缩管
(e)折弯管
(f)圆弯管
(g)锐角合流三通
(h)圆角分流三通
在局部阻碍范围内损失的能量,只占局部损失中 的一部分,另一部分是在局部阻碍下游一定长度的 管段上损耗掉的,这段长度称为局部阻碍的影响长 度。受局部阻碍干扰的流动,经过影响长度后,流 速分布和紊流脉动才能达到均匀流动的正常状态。
核心问题2 水力半径、湿周、当量直径
以上讨论的都是圆管,圆管是最常用的断面形式。 但工程上也常用到非圆管的情况。例如通风系统 中的风道,有许多就是矩形的。如果设法把非圆 管折合成圆管来计算,那么根据圆管制定的上述 公式和图表,也就适用于非圆管了。这种由非圆 管折合到圆管的方法是从水力半径的概念出发, 通过建立非圆管的当量直径来实现的。
流体力学第四章

1.渐变流及其特性
渐变流过水断面近似为平面,即渐变流是流线接近于
平行直线的流动。均匀流是渐变流的极限。
动压强特性:在渐变流同一过水断面上,各点动压强
按静压强的规律式分布,即
注:上述结论只适用于渐变流或均匀流的同一过水断面上 的 各点,对不同过水断面,其单位势能往往不同。
选取:控制断面一般取在渐变流过水断面或其极限情况均匀 流断面上。
即J=JP。 5.总水头线和测压管水头线之间的距离为相应段
的流速水头。
6.如果测压管水头线在总流中心线以上,压强就 是正职;如相反,则压强为负值,则有真空。
4.总流能量方程在推导过程中的限制条件
(1)不可压缩流体;
(2)恒定流;
(3)质量力只有重力,所研究的流体边界是静止 的(或处于平衡状态);
取管轴0-0为基准面,测压管所在断面
1,2为计算断面(符合渐变流),断面的形
心点为计算点,对断面1,2写能量方程(4-
15),由于断面1,2间的水头损失很小,
可视
,取α1=α2=1,得
由此得:
故可解得:
式中,K对给定管径是常量,称为文丘里流 量计常数。
实际流量 : μ——文丘里流量计系数,随流动情况和管
流体力学
第四章 流体动力学基础
本章是工程流体力学课程中最重要的一 章。本章建立了控制流体运动的微分方程, 即理想流体运动微分方程和实际流体的运 动微分方程;并介绍了求解理想流体运动 微分方程的伯努利积分形式;构建了工程 流体力学中应用最广的恒定总流运动的三 大基本方程:连续性方程、伯努利方程 (即能量方程)和动量方程。通过本章的 学习要培养综合运用三大基本方程分析、 计算实际总流运动问题的能力。
道收缩的几何形状而不同。
流体力学实验_第四章流速与流量测量 [兼容模式]
![流体力学实验_第四章流速与流量测量 [兼容模式]](https://img.taocdn.com/s3/m/a4dd8a0ecc17552707220828.png)
25
King(1914)提出了无限长圆柱和流体之间的强迫对流热交换 理论,得到了著名的king公式:
Nu A B Re
热线 l 1 d
Nu
Q2
l(Tw Te )
Re Ud
(1) 校准的原因
热线热膜探针的性能是随制造工艺、探针尺寸和金属丝、 膜的材料而异的,即使是相同的材料、制造工艺、尺寸, 其性能也不可能完全一样;
探针的性能和流体的温度、密度以及测量时的气压有关; 探针的性能也和实验室环境条件、污染情况有关; 探针使用后会发生老化; 探针的性能和流速范围有关; 探针在测量中是和仪器结合在一起使用的,真正的相应
流体粘性的影响:需满足Re>200,在小雷诺数时, 毕托管的标定系数将随雷诺数的变化而变化
管柄堵塞的影响:毕托管管柄堵塞使流体过流面积 减小,流速增加,静压减小,总压不变。毕托管管柄 直径≤1/50管道直径且插入深度≤管道半径时可忽略
横向流速梯度的影响:毕托管头部与流体之间的相 互作用引起邻近流线的微小位移,使较高流速区的流 线移至总压孔处,总压增大。通过测压位置修正。
8
两种测量方式: 不对向测量
探针固定在某个参考方向,测量两侧孔的 压力差,根据探针校准曲线确定气流方向 和大小
9
对向测量
转动三孔探针,使1、3测压孔的压力平衡;
1 测压孔1、3的
轴心线的平分线 即为气流方向。
V
三孔压力值:
2
P2
P
K2
1 2
V2
P1
流体力学-第四章 流体动力学基础

Dt t CV
CS
单位质量流体的能量 e (u V 2 gz) 流体系统的总能量
2
DE ed eV ndS
Dt t CV
CS
E ed
初始时刻系统与控制体重合
Q WSYS Q WCV
ed eV ndS Q W
t CV
CS
§4.2 对控制体的流体力学积分方程
§4.1 系统和控制体,雷诺输运定理
雷诺输运定理:
举例:动量定理运用于流体系统
F Dk Dt
F 是外界作用系统的合力,K 是系统的动量,
k Vd
由于系统不断改变位置、形状大小,组成系统的流体质点的密度和速度随
时间也是变化的,所以系统的动量也是变化的,求其对时间的变化率,即
求该流体系统体积分的物质导数。
取 N M 单位体积的质量
DM 0 Dt
d V ndS 0
t CV
CS
d V ndS 0
t CV
CS
积分形式的连续性方程
§4.2 对控制体的流体力学积分方程
非定常流动情况下:
d V ndS 0
t CV
CS
即单位时间内控制体内流体质量的增加或减少等于同时间内通过控制面流入 或流出的净流体质量。如果控制体内的流体质量不变,则必然同一时间内流 入与流出控制体的流体质量相等。
左端第一项——是控制体内流体动量随时间变化而产生的力,它反映流体运动的非定常性
左端第二项——是单位时间内流体流入和流出控制体的动量之差,它表示流入动量与流出动量
不等所产生的力。
§4.2 对控制体的流体力学积分方程
定常流动条件:
F
FB FS
VV ndS
CS
VV ndS
第一篇 流体力学第四章 阻力损失与管路计算

上一页
返回
第四节 局部损失的计算
• 局部损失可按下式计算:
• 局部损失的计算可以转化为求局部阻力系数ζ 的问题.对于不同的局部 阻碍,有不同的局部阻力系数ζ 值,其多数通过试验确定,并编制成专用 计算图、表,供计算时查用.表4-1列出了各种常用管件的局部阻力系 数ζ值.应当注意,表4-1中的ζ 值都是针对某一过流断面的平均流速而 言的,查表时必须与指定的断面流速相对应,凡未注明的,均应采用局部 阻碍以后断面的平均流速.
• 根据流体的边界情况,将流动阻力和能量损失分为两种形式:一种是沿 程阻力与沿程能量损失;另一种是局部阻力与局部能量损失.
下一页 返回
第一节 流动阻力与能量损失
• 如图4-1所示,水箱侧壁上连接一根由三段不同直径的管段所组成的 管路.在边壁沿程不变的管段上(1-2、2-3、3-4、4-5段), 阻碍流体流动的阻力沿程基本不变,这类阻力称为沿程阻力.为克服沿 程阻力而产生的能量损失称为沿程能量损失.沿程损失以水柱高度表 示时,称为沿程水头损失,用符号hf 表示.图中的hf12、hf23、hf34、 hf45就是相应1-2、2-3、3-4、4-5各管段的沿程水头 损失.图中整个管路的沿程水头损失等于各管段的沿程水头损失之和, 即
• 人们很早以前就发现沿程损失与流速之间存在着某种关系,但直到1 883年,英国物理学家雷诺在他做的试验中揭示了流体运动存在着 两种流态,这才认识到沿程损失与流速的关系与流态密切相关.
• 雷诺试验的装置如图4-2所示,水箱A 中水位恒定,水流通过玻璃管B 恒定出流,阀门K 用来调节管内流量,容器D 中盛有颜色水,颜色水可以 经过细管E 注入玻璃管B 中.
流体力学第4章流体流动基本原理
mCV qm2 qm1 0 t
28
对稳态流动系统,流体及流动参数均与 时间无关,即
mCV / t 0
因此,质量守恒方程简化为
qm1 qm2
或 1v1 A1 2v2 A2
即稳态流动,输入与输出的质量必然相等。
29
对不可压缩流体的稳态流动,ρ=const,则
v1 A v2 A2 1
CV
vmax
2
R v1R 0
2 2
34
故有
vmax=2v1
例题:一储气罐,罐中空气经管道向外界排出,
已知管道出口处气流密度和压强为均匀分布,而 速度呈抛物线规律分布:
r v vmax (1 2 ) r0
已知排气管r0=0.025m,当储气罐 中p0=0.14MPa,T0=277.8K,测得 管道出口处气流vmax=32m/s,储气 罐和管道的总容积0.32m3。
24
③ 控制体内的质量变化率
对于控制体内密度为ρ的任意微元体积dV,其质 量为ρdV。将ρdV在整个控制体CV积分可得控制体内 的瞬时总质量,再对时间求导得:
控制体内的 质量变化率 =
t
dV
CV
ρ dv
25
④ 质量守恒方程
将上述各式集合在一起即可得到控制体系
统的质量守恒方程:
输出控制体 的质量流量 输入控制体 — 的质量流量
4.2.1 控制体系统的质量守恒方程
根据质量守恒原理,对于质量为m的系统,其质 量守恒方程为
dm ( )系统 0 dt
由输运公式,以控制体为研究对象时质量守恒方程 可表述为
19
输出控制体 的质量流量
—
输入控制体 的质量流量
工程流体力学-第四章
p
p x
dx
dydz
X
dxdydz
dxdydz
dux dt
X 1 p dux
x dt
X 1 p dux
x dt Y 1 p duy
y dt Z 1 p duz
z dt
——Euler运动方程Βιβλιοθήκη f 1 p u (u )u
t
(1)物理意义:作用在单位质量流体上的质量力与表 面力之代数和等于其加速度。 (2)适用条件:理想流体。
z p C
g
急变流:流动参量沿流程急剧变化的总流。
例如:
缓变流断面:
1-1、4-4
急变流断面:
2-2、3-3
这样,即可得到:
1
gQ
A (z
p )gudA g
1
gQ
(z
p
g
)
A
gudA
z
p
g
动能修正系数
引入目的: 解决积分
1,
u 2 gudA
gQ A 2g
代之以 V 表达的关系式。
因为总流有效断面上的速度分布是不均匀的,设各点
2gQ
A
u3A 2gQ
1
3
u
A
2
dA
u2A
u2 2g
1 3
u
A
2
dA
u2A
动能修正
系数
则
1
u 2 gudA u 2
gQ A 2g
2g
令
hw12
1
gQ
A2 A1
hw 12 gudA
则(2)式变成:
z1
p1
g
1
u12 2g
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
dp p p p p u v w dt t x y z
密度变化:
d u v w dt t x y z
温度变化:
dT T T T T u v w dt t x y z
§1
描述方法
描述流体运动方法
随体法 当地法 拉格朗日法 欧拉法 质点轨迹: r r (a,b,c,t ) 参数分布:B = B(x, y, z, t)
x et c1 tet dt et c1 (t 1)e t c1et t 1 y et c2 tet dt et c2 (t 1)e t c2et t 1
(b)
xa 上式中c1 ,c2 为积分常数,由t = 0时刻流体质点位于 ,可确 y b c1 a 1 定 ,代入(b)式,可得参数形式的流体质点轨迹方程为
c 2 b 1
x (a 1)et t 1 y (b 1)et t 1
讨论: 本例说明虽然给出的是速度分布式(欧拉法),即各空间点上速 度分量随时间的变化规律,仍然可由此求出-指定流体质点在不 同时刻经历的空间位置,即运动轨迹(拉格朗日法)。
第四章
§1
§2
d 2 y 2 ya, b, c, t ay 2 a y a, b, c, t dt t 2
dx xa, b, c, t u u a, b, c, t dt t
dy y a, b, c, t v va, b, c, t dt t
§3
流动的分类
为了便于研究流体流动,可将流体流动分类如下:
1、按流体性质分类 理想流体流动和粘性流体流动
可压缩流体流动与不可压缩流体流动
2、按流体运动状态分类 定常流动和非定常流动,有旋流动和无旋流动,层流流动和紊流
流动,亚声速流动和超声速流动
3 、按流动空间的坐标变量数分类 一维流动、二维流动、三维流动
三维速度廓线
u u ( x, y, z , t ) v v( x, y, z, t ) w w( x, y, z, t )
B)一维,二维与三维流动
1. 流动维数的确定:
三维流动: 速度场必须表示为三个方向坐标的函数
二维流动: 速度场简化为二个空间坐标的函数 v=v ( x, y, t) 或 v=v ( r, z, t)
A)速度场
• 速度场是最基本的场
速度分量:
v = v (x, y, z, t )
u u ( x, y, z , t ) v v( x, y, z, t ) w w( x, y, z, t )
• 可用速度廓线(剖面)描述空间线或面上的速度分布
二维速度剖面 u =u ( x, y)
已知: 求: 解:
u xt 已知用欧拉法表示的流场速度分布规律为
在t = 0时刻位于点(a,b)的流体质点的运动轨迹。 对某时刻t位于坐标点上(x,y)的质点
u dx x t dt dy v y t dt
v y t
(a)
求解一阶常微分方程(a)可得
流体运动学
描述流体运动方法
流场的几何描述
§3
§4 §5 §6
流动的分类
流管与流量 连续性方程 流体微团的运动分析
§2
—
流场的几何描述
一、迹线与流线
1、迹线 流体质点的运动轨迹称为迹线。这 在拉格朗日研究法中运用。 2、流线 — 在欧拉法中流线是流场中的瞬时光 滑曲线,曲线上各点的切线方向与 各该点的瞬时速度方向一致。
流体力学
(第四章 流体运动学)
同济大学汽车学院
目
前言 第一章 第二章 第三章 第四章 第五章 第六章 第七章 第八章 第九章
录
绪论 流体的物理性质及作用力 流体静力学 流体运动学 理想流体动力学基础 流体漩涡运动的基本理论 相似原理和量纲分析 粘性流体力学 气体动力学
第四章
§1
§2
流体运动学
描述流体运动方法
讨论:
dN 1、物理量的质点导数 有两部分组成。 dt
N 2、 t 项为当地导数、局部导数或时变导数。它代表质点在没有空 间变位时,物理量 N 对时间的变化率,反映流场的非定常性。
N N N v w 3、 x y z 项为迁移导数或位变导数。它代表质点经过 dt 时间处于不同位置时,物理量 N 对时间的变化率,反映流场的 非均匀性。 u
3)两种描述流动的方法之比较
拉格朗日法 分别描述有限质点的轨迹 欧拉法 同时描述所有质点的瞬时参数
表达式复杂
不能直接反映参数的空间分布 不适合描述流体微元的运动变形特性
表达式简单
直接反映参数的空间分布 适合描述流体微元的运动变形特性
拉格朗日观点是重要的
流体力学最常用的解析方法
[例1] 由速度分布求质点轨迹
dx u dt
dy v dt
dz w dt
DN N N N N u v w Dt t x y z
DN N v N Dt t
i j k x y z
§1
描述流体运动方法
dN N N N N u v w dt t x y z
§2 流场的几何描述
总流:微元流束的总和
在有效截面上取平均值,按一维流动处理 缓变流与急变流:流束内流线间的夹角很小、流线曲率很大,近乎平行 直线的流动为缓变流。不符合上述条件的流动成为急 变流。
第四章
§1
§2
流体运动学
描述流体运动方法
流场的几何描述
§3
§4 §5 §6
流动的分类
流管与流量 连续性方程 流体微团的运动分析
点,由于流场的非定常性和非均匀性,质点 M 所具
有的物理量 N 在运动中不仅经历了 t 时间的 变化,而且也经历了空间 s xi yj zk 的变化。
§1
描述流体运动方法
s 这种空间的变化量即为质点的位移与 t 时间有关,故流体质点 M 所具有的
物理量 N 是
§1
描述流体运动方法
压强变化:
4、各物理量的随体导数
加速度:
du u u u u ax u v w dt t x y z dv v v v v ay u v w dt t x y z
dw w w w w az u v w dt t x y z
v=v ( x, y, z, t)
一维流动: 速度场可表示为一个方向坐标的函数
v=v( x ) 或 v=v ( s )
2. 常用的流动简化形式:
dz z a, b, c, t w wa, b, c, t dt t
流体质点的其它物理量:
d 2 z 2 z a, b, c, t az 2 az a, b, c, t 2 dt t
p pa, b, c, t
a, b, c, t
§1
描述流体运动方法
t
的坐标位置
1)拉格朗日法
拉格朗日法是利用质点在任意时刻
x、 y、 z
来确定
质点的运动轨迹流。要研究整个流体流动就必须着眼于每一个流体质点
的研究,综合所有流体质点的运动后便可得到整个流体的运动规律。 拉格朗日法选取初始时刻 t 0 ,以每一个质点的初 始坐标 a、b、c 作为标记,用 (a、b、c) 的不同值区分不同的质点。流体质点的坐标可以表 示为时间 t 及初始位置 a、b、c 的函数,即:
3)物理量的质点导数
动量、动能等)对时间的变化率为物理量的质点导数(随体导数)。
运动中的流体质点所具有的物理量 N (例如速度、压强、密度、温度、质量、
dN N lim dt t 0 t 流体质点 M 在瞬时 t 从某一空间点 Ax, y, z 以瞬时速 度 v x u(t )i vt j wt k 携带某个物理量 N N x, y, z, t 在流场中流动,经过 t 时间,质点到达 Bx x, y y, z z
x xt
z za, b, c, t
§1
描述流体运动方法
y ya, b, c, t
流体质点的坐标:
x xa, b, c, t
流体质点的速度:
z za, b, c, t
流体质点的加速度:
d 2 x 2 xa, b, c, t ax 2 ax a, b, c, t 2 dt t
T T a, b, c, t
§1
描述流体运动方法
2)欧拉法
欧拉法着眼于研究空间固定点的流动情况,即研究流体质点经过某一空间点的 速度、压强、密度等变化的规律, 将许多空间点在不同时刻的流体质点的运动情况 记录下来,就可以知道整个流体的运动规律。显然,欧拉法不研究个别流体质点的 运动规律,对于流体质点从哪里来,又流到何处去,并不加以研究。因此,欧拉法 不能直接给定流体质点的运动轨迹。
v ds 0
写成投影式,则
dx dy dz u ( x, y, z, t ) v( x, y, z, t ) w( x, y, z, t )
§2
流场的几何描述
4、流线与迹线的性质 a、 流线与迹线的共同点是,它们都是与速度相切的曲线。但流线是同 一瞬时、不同质点所形成的曲线;迹线是同一质点在不同瞬时所 经过的位置的轨迹。 b、在给定瞬时空间一个点只能作一条流线,因为在同一点上不可能同 时有几个流动方向,所以流线不能相交、也不能突然折转。
§2
流场的几何描述
c、定常流动时,流线的形状始终不变,与时间无关。任意流体质点必定
沿某 一 确定的流线运动,其迹线和流线相重合。
