用Hough变换检测二值图像中的圆
hough变换圆拟合
hough变换圆拟合
Hough变换圆拟合（Hough transform circle fitting）是一种用于从图像中检测圆的技术。
它是从Hough变换（Hough transform）算法演变而来的。
Hough变换圆拟合算法使用梯度信息来检测圆，并且它能够检测出各种大小、位置和形状的圆。
算法步骤如下：
1. 首先对图像进行预处理，如灰度化、边缘检测等。
2. 选择一组圆心候选点，可以采用图像中的各种特征点，例如边缘点、角点、中心点等。
3. 对于每个候选点，设定一个半径范围，然后在这个半径范围内搜索圆。
4. 对于每个搜索到的圆，计算出它的梯度值。
如果梯度值大于设定的阈值，则将这个圆作为候选圆。
5. 重复步骤3和步骤4，直到所有的候选点都被搜索完毕。
6. 统计所有候选圆的得票数，并根据得票数高低进行排序。
7. 选取得票数最高的圆作为最终检测结果。
Hough变换圆拟合算法的优点是可以检测出各种大小、位置和形状的圆，它的缺点是计算量大，需要较长的运行时间。
Python下opencv使用hough变换检测直线与圆
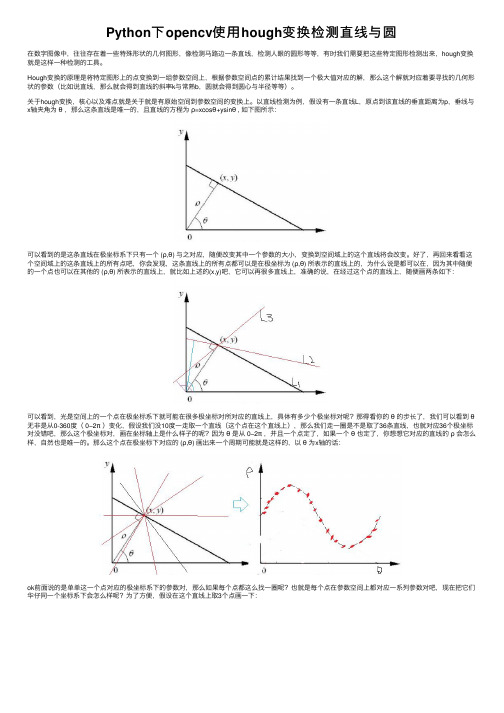
Python下opencv使⽤hough变换检测直线与圆在数字图像中，往往存在着⼀些特殊形状的⼏何图形，像检测马路边⼀条直线，检测⼈眼的圆形等等，有时我们需要把这些特定图形检测出来，hough变换就是这样⼀种检测的⼯具。
Hough变换的原理是将特定图形上的点变换到⼀组参数空间上，根据参数空间点的累计结果找到⼀个极⼤值对应的解，那么这个解就对应着要寻找的⼏何形状的参数（⽐如说直线，那么就会得到直线的斜率k与常熟b，圆就会得到圆⼼与半径等等）。
关于hough变换，核⼼以及难点就是关于就是有原始空间到参数空间的变换上。
以直线检测为例，假设有⼀条直线L，原点到该直线的垂直距离为p，垂线与x轴夹⾓为θ，那么这条直线是唯⼀的，且直线的⽅程为ρ=xcosθ+ysinθ , 如下图所⽰：可以看到的是这条直线在极坐标系下只有⼀个 (ρ,θ) 与之对应，随便改变其中⼀个参数的⼤⼩，变换到空间域上的这个直线将会改变。
好了，再回来看看这个空间域上的这条直线上的所有点吧，你会发现，这条直线上的所有点都可以是在极坐标为 (ρ,θ) 所表⽰的直线上的，为什么说是都可以在，因为其中随便的⼀个点也可以在其他的 (ρ,θ) 所表⽰的直线上，就⽐如上述的(x,y)吧，它可以再很多直线上，准确的说，在经过这个点的直线上，随便画两条如下：可以看到，光是空间上的⼀个点在极坐标系下就可能在很多极坐标对所对应的直线上，具体有多少个极坐标对呢？那得看你的θ的步长了，我们可以看到θ⽆⾮是从0-360度（ 0−2π）变化，假设我们没10度⼀⾛取⼀个直线（这个点在这个直线上），那么我们⾛⼀圈是不是取了36条直线，也就对应36个极坐标对没错吧，那么这个极坐标对，画在坐标轴上是什么样⼦的呢？因为θ是从 0−2π，并且⼀个点定了，如果⼀个θ也定了，你想想它对应的直线的ρ会怎么样，⾃然也是唯⼀的。
那么这个点在极坐标下对应的 (ρ,θ) 画出来⼀个周期可能就是这样的，以θ为x轴的话：ok前⾯说的是单单这⼀个点对应的极坐标系下的参数对，那么如果每个点都这么找⼀圈呢？也就是每个点在参数空间上都对应⼀系列参数对吧，现在把它们华仔同⼀个坐标系下会怎么样呢？为了⽅便，假设在这个直线上取3个点画⼀下：那么可以看到，⾸先对于每⼀个点，在极坐标下，会存在⼀个周期的曲线来表⽰通过这个点，其次，这三个极坐标曲线同时经过⼀个点，要搞清楚的是，极坐标上每⼀个点对 (ρ,θ) 在空间坐标上都是对应⼀条直线的。
hough 变换检测圆的一般步骤
hough 变换检测圆的一般步骤霍夫变换是一种图像处理算法，可用于检测图像中的圆形。
下面是霍夫变换检测圆的一般步骤：1.导入图像：首先，将要检测圆的图像导入到计算机中。
图像可以来自于摄像机、存储设备或是从其他算法的输出中获得。
2.灰度化处理：将彩色图像转换为灰度图像。
这是因为灰度图像只有一个通道，可以简化后续处理步骤。
3. 边缘检测：使用边缘检测算法（如Canny算子）对灰度图像进行处理，提取图像中的边缘。
这一步骤可以帮助找到圆形的边界。
4.霍夫变换：将边缘图像输入到霍夫变换中。
霍夫变换将边缘点从笛卡尔坐标系转换到霍夫空间，形成二维投票器矩阵。
在投票器矩阵中，每个圆形都有一个对应的概率值，用于表示该圆形的可能性。
5.阈值设置：在霍夫变换之后，需要设置一个阈值来确定哪些圆形应被认为是检测到的圆形。
根据应用的需求和图像的噪声程度，可以调整阈值的大小。
较高的阈值会产生较少的圆形，而较低的阈值会产生较多的圆形。
6.圆形检测：根据阈值从投票器矩阵中选择可能的圆形。
这些圆形可能包含噪声或重叠的圆形。
因此，需要进行圆形重叠或去噪的处理。
7.圆形参数提取：从霍夫空间中获取每个候选圆形的参数，如圆心的坐标和半径长度。
8.绘制圆形：根据提取的参数，在原始图像上绘制检测到的圆形。
这样一来，圆形就会在图像中展示出来。
9.输出结果：最后，将包含检测到的圆形的图像保存或显示出来。
可以使用不同的颜色或标记形式来区分不同的圆形。
霍夫变换是一种广泛应用于图像处理和计算机视觉领域的算法。
通过这一变换，我们可以快速准确地检测图像中的圆形，为后续的分析和应用提供基础。
hough变换检测圆原理
hough变换检测圆原理
Hough变换是一种常用的图像处理算法，用于检测图像中的圆形目标。
其原理是将图像中的每个像素点转换为极坐标系下的参数空间，并在该空间中寻找圆心和半径相对应的峰值。
具体实现步骤如下：
1. 对图像进行边缘检测，得到一系列边缘点。
2. 在极坐标系下，将每个边缘点表示为一个三元组(r,θ,a)，
其中r表示边缘点到图像原点的距离，θ表示边缘点与x轴的夹角，a表示圆心坐标在x轴上的投影。
3. 在参数空间中建立一个二维数组，表示每个可能的圆心(a,b)和半径r对应的计数值。
4. 遍历所有的边缘点，在参数空间中对应的位置上增加计数值。
5. 在参数空间中寻找计数值最大的位置，该位置所对应的圆心
和半径即为检测到的圆形目标。
通过Hough变换，我们可以快速高效地检测图像中的圆形目标。
该算法在计算复杂度和空间复杂度上相对较高，但其检测精度和鲁棒性较为优秀，广泛应用于计算机视觉和机器人领域。
- 1 -。
用点Hough变换实现圆检测的方法
用点Hough变换实现圆检测的方法
林金龙;石青云
【期刊名称】《计算机工程》
【年(卷),期】2003(029)011
【摘要】给出了一种新的Hough变换圆检测方法--点Hough变换(PHT).该方法根据圆周上任意两条不平行弦的中垂线相交与圆心的几何性质,同时选取曲线上3点进行计算,将传统Hough变换圆检测时的三维参量统计变成一维参量统计,极大地降低了计算复杂性和对资源的需求.为了克服任意选取组合点可能带来的计算量增加及统计结果的分散程度提高,文中提出了点的选择方法.合成图和实际图像的实验结果表明,该方法用于普通图像中圆检测时快速、稳定、准确.
【总页数】3页(P17-18,160)
【作者】林金龙;石青云
【作者单位】北京大学信息科学中心,北京,100871;北京大学信息科学中心,北京,100871
【正文语种】中文
【中图分类】TP317.4
【相关文献】
1.单参数Hough变换实现圆检测方法的研究 [J], 王敏;李启堂;丁书斌
2.基于TMS320DM642的快速Hough变换圆检测算法的实现 [J], 何富运;罗晓曙;周虹
3.一种简易Hough变换圆检测的原木端面识别方法 [J], 杨泽灿;林耀海;林艺杉
4.改进的Hough变换实现圆检测 [J], 段黎明;汪威;张霞
5.基于改进轮廓提取的Hough变换椭圆检测方法 [J], 翟永立; 丁雷; 裴浩东因版权原因，仅展示原文概要，查看原文内容请购买。
用Hough变换检测直线和圆.
特殊图像变换1、 HoughLines功能：利用 Hough 变换在二值图像中找到直线格式：CvSeq* cvHoughLines2( CvArr* image, void* line_storage, int method, double rho, double theta, int threshold,double param1=0, double param2=0 ;参数：image：输入 8-比特、单通道 (二值图像，其内容可能被函数所改变line_storage：检测到的线段存储仓. 可以是内存存储仓 (此种情况下，一个线段序列在存储仓中被创建，并且由函数返回），或者是包含线段参数的特殊类型（见下面）的具有单行/单列的矩阵(CvMat*。
矩阵头为函数所修改，使得它的cols/rows将包含一组检测到的线段。
如果line_storage是矩阵，而实际线段的数目超过矩阵尺寸，那么最大可能数目的线段被返回(线段没有按照长度、可信度或其它指标排序.method：Hough 变换变量，是下面变量的其中之一：CV_HOUGH_STANDARD - 传统或标准 Hough 变换. 每一个线段由两个浮点数(ρ, θ 表示，其中ρ 是点与原点 (0,0 之间的距离，θ 线段与 x-轴之间的夹角。
因此，矩阵类型必须是CV_32FC2 type.CV_HOUGH_PROBABILISTIC - 概率 Hough 变换(如果图像包含一些长的线性分割，则效率更高. 它返回线段分割而不是整个线段。
每个分割用起点和终点来表示，所以矩阵（或创建的序列）类型是 CV_32SC4.CV_HOUGH_MULTI_SCALE - 传统 Hough 变换的多尺度变种。
线段的编码方式与CV_HOUGH_STANDARD 的一致。
rho:与象素相关单位的距离精度theta:弧度测量的角度精度threshold:阈值参数。
如果相应的累计值大于threshold，则函数返回的这个线段. param1:第一个方法相关的参数:∙对传统 Hough 变换，不使用(0.∙对概率 Hough 变换，它是最小线段长度.∙对多尺度 Hough 变换，它是距离精度rho的分母 (大致的距离精度是rho而精确的应该是rho / param1 .param2:第二个方法相关参数:∙对传统 Hough 变换，不使用 (0.∙对概率 Hough 变换，这个参数表示在同一条直线上进行碎线段连接的最大间隔值(gap, 即当同一条直线上的两条碎线段之间的间隔小于param2时，将其合二为一。
一种基于Hough变换的圆和矩形的快速检测方法
一种基于Hough变换的圆和矩形的快速检测方法一、本文概述随着计算机视觉技术的快速发展，图像中的形状检测成为了许多实际应用领域的核心问题，如机器人导航、工业自动化、医学影像分析、安全监控等。
在这些应用场景中，快速准确地检测出图像中的圆形和矩形对于后续的图像理解和处理至关重要。
本文提出了一种基于Hough变换的圆和矩形的快速检测方法，旨在提高形状检测的效率和准确性，为相关领域的实践应用提供新的思路和技术支持。
Hough变换作为一种经典的图像处理技术，已经在直线检测等领域取得了广泛应用。
然而，将其应用于圆形和矩形的检测时，传统的Hough变换方法面临着计算量大、检测速度慢等问题。
为了解决这些问题，本文在深入研究Hough变换原理的基础上，提出了一种改进的快速检测方法。
该方法结合了图像预处理、形状特征提取和Hough变换等多个步骤，通过优化算法和减少不必要的计算，实现了圆形和矩形的高效检测。
本文首先介绍了Hough变换的基本原理及其在形状检测中的应用背景，然后详细阐述了本文提出的快速检测方法的理论框架和实现步骤。
接着，通过实验验证了该方法的有效性，并与其他经典算法进行了比较。
本文总结了研究成果，指出了方法的优点和局限性，并对未来的研究方向进行了展望。
通过本文的研究，我们期望能够为计算机视觉领域的形状检测问题提供一种更加高效、准确的解决方案，推动相关应用的发展和创新。
二、Hough变换原理及其应用Hough变换是一种在计算机视觉和图像处理中广泛应用的特征检测方法，尤其在形状识别，如直线、圆和矩形检测中，显示出其独特的优势。
Hough变换的基本原理是通过将图像空间中的形状映射到参数空间中的峰值，从而实现对这些形状的检测。
对于直线检测，Hough变换通过将图像中的每个点映射到参数空间的一条线上，从而得到多条线的交点，这些交点即对应图像空间中的直线。
类似地，对于圆和矩形的检测，Hough变换也可以将图像中的形状映射到相应的参数空间，如圆的参数空间包括圆心和半径，矩形的参数空间包括四个顶点的坐标等。
c++ 霍夫变换实现圆弧检测
c++ 霍夫变换实现圆弧检测霍夫变换是一种常用于图像处理中的技术，它可以用于圆弧的检测。
在本文中，我们将介绍如何使用C++语言实现圆弧检测。
1. 图像预处理在进行圆弧检测之前，首先需要对图像进行一些预处理。
这些预处理步骤包括灰度化、高斯滤波、二值化和边缘检测。
这些步骤可以通过使用OpenCV库中的函数来实现。
示例代码：```cppMat srcImage = imread("image.jpg");Mat grayImage, blurImage, binaryImage, edgeImage;cvtColor(srcImage, grayImage, COLOR_BGR2GRAY);GaussianBlur(grayImage, blurImage, Size(5, 5), 0);threshold(blurImage, binaryImage, 0, 255, THRESH_BINARY | THRESH_OTSU);Canny(binaryImage, edgeImage, 50, 150);```2. 霍夫变换在进行霍夫变换之前，需要先定义一些变量来存储检测到的圆弧的信息。
这些变量包括圆心坐标和半径。
在霍夫变换中，我们需要使用HoughCircles函数。
此函数接受一个二值化图像和检测圆的参数。
检测圆的参数包括最小和最大半径以及两个圆之间的最小距离。
函数的返回值是一个向量，其中包含检测到的圆的信息。
```cppvector<Vec3f> circles;HoughCircles(edgeImage, circles, HOUGH_GRADIENT, 1, edgeImage.rows / 8, 100, 30, 0, 0);```3. 绘制圆弧检测到圆弧之后，我们可以使用OpenCV库中的函数来在图像上绘制圆弧。
函数接受一个源图像、圆心坐标、半径和颜色。
完整代码如下：```cpp#include <iostream>#include <opencv2/opencv.hpp>using namespace cv;using namespace std;for (size_t i = 0; i < circles.size(); i++){Point center(cvRound(circles[i][0]), cvRound(circles[i][1]));int radius = cvRound(circles[i][2]);circle(srcImage, center, radius, Scalar(0, 0, 255), 2, LINE_AA);}return 0;}```以上就是使用C++实现圆弧检测的完整代码，运行程序可以看到圆弧已经被成功检测并绘制在了源图像上。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
用Hough变换检测二值图像中的圆Hough 变换简介Hough变换是实现图像边缘检测的一种有效方法，其基本思想是将测量空间的一点变换到参量空间中的一条曲线或一个曲面，而具有同一参量特征的点交换后在参量空间中相交，通过判断交点处的积累程度来完成特征曲线的检测，基于参量性质的不同，Hough变换可以检测直线、圆、椭圆、双曲线、抛物线等。
同时，将概率论、模糊集理论、分层迭代的思想和级联的方法应用于Hough变换的过程中，大大地提高了Hough变换的效率，改善了Hough变换的性能。
实验主要使用的函数MATLAB内部常数pi：圆周率p（=3.1415926...）MATLAB常用基本数学函数:abs(x)：纯量的绝对值或向量的长度；round(x)：四舍五入至最近整数；floor(x)：地板函数，即舍去正小数至最近整数；MATLAB常用三角函数sin(x)：正弦函数cos(x)：余弦函数；向量的常用函数max(x):向量x的元素的最大值。
MATLAB图像类型转换函数：rgb2gray:将一副真彩色图像转换成灰度图像；im2bw:通过设定高度阈值将真彩色，索引色，灰度图转换成二值图像；MATLAB图形图像文件的读取和显示函数imread(filename)；MATLAB二进制图像及其显示imshow（f1）。
用double对二值图像双精度化图形处理：sobel算子检测边缘hough变换检测圆分别显示灰度图像：figure;subplotSobel:算子边缘检测图像hough变换检测后的图像实验相关代码I=imread('*.jpg');f=rgb2gray(I);f1=im2bw(f,200/255);BW1=double(f1);BW=edge(BW1,'sobel',0.4);r_max=50;r_min=10;step_r=10;step_angle=pi/12;p=0.7;[m,n]=size(BW);size_r=round((r_max-r_min)/step_r)+1;size_angle=round(2*pi/step_angle);hough_space=zeros(m,n,size_r);[rows,cols]=find(BW);ecount=size(rows);for i=1:ecountfor r=1:size_rfor k=1:size_anglea=round(rows(i)-(r_min+(r-1)*step_r)*cos(k*step_angle));b=round(cols(i)-(r_min+(r-1)*step_r)*sin(k*step_angle));if(a>0&&a<=m&&b>0&&b<=n)hough_space(a,b,r)=hough_space(a,b,r)+1;endendendendmax_para=max(max(max(hough_space)));index=find(hough_space>=max_para*p);length=size(index);hough_circle=false(m,n);for i=1:ecountfor k=1:lengthpar3=floor(index(k)/(m*n))+1;par2=floor((index(k)-(par3-1)*(m*n))/m)+1;par1=index(k)-(par3-1)*(m*n)-(par2-1)*m;if((rows(i)-par1)^2+(cols(i)-par2)^2<(r_min+(par3-1)*step_r)^2+5&&...(rows(i)-par1)^2+(cols(i)-par2)^2>(r_min+(par3-1)*step_r)^2-5)hough_circle(rows(i),cols(i))=true;endendendfor k=1:lengthpar3=floor(index(k)/(m*n))+1;par2=floor((index(k)-(par3-1)*(m*n))/m)+1;par1=index(k)-(par3-1)*(m*n)-(par2-1)*m;par3=r_min+(par3-1)*step_r;fprintf(1,'Center%d%d radius%d\n',par1,par2,par3);para(:,k)=[par1,par2,par3];endsubplot(221),imshow(f);subplot(222),imshow(BW);subplot(223),imshow(hough_circle)图像读取图像处理的第一步就是对所采集的图像进行读入，本次研究采集的图像是24位真彩色的JPG 格式的图像。
真彩色图像可用双精度存储，亮度值范围是[0,1]；比较符合习惯的存储方法是用无符号整型存储，亮度值范围[0,255]。
在实验中我们开始因为遇到了sobel算子无法识别二值图像的问题，后来用了double解决问题。
MATLAB中图形图像文件的读取利用函数imread（）完成。
图像灰度与二值化处理白色与黑色之间按对数关系分为若干等级，称为灰度。
灰度分为256阶。
用灰度表示的图像称作灰度图。
MATLAB中rgb2gray（）函数可以实现图像灰度化，它是以R、G、B为轴建立空间直角坐标系，则RGB图的每个象素的颜色可以用该三维空间的一个点来表示，而Gray图的每个象素的颜色可以用直线R=G=B上的一个点来表示。
于是rgb转gray图的本质就是寻找一个三维空间到一维空间的映射，最容易想到的就是射影（即过rgb空间的一个点向直线R=G=B做垂线），事实上MATLAB也是这样做的，并且有Gray=0.29900*R+0.58700*G+0.11400*B。
图像的二值化，就是将图像上的像素点的灰度值设置为0或255，也就是将整个图像呈现出明显的只有黑和白的视觉效果。
全局二值化最常用的方法就是设定一个全局的阈值P，用P 将图像的数据分成两部分：大于P的像素群和小于P的像素群。
将大于P的像素群的像素值设定为白色（或者黑色），小于P的像素群的像素值设定为黑色（或者白色）。
MATLAB中使用im2bw函数，f1=im2bw(f,阈值)即将f以阈值分割。
边缘检测图像边缘是一个图像的重要特征，是计算机模式识别，视觉等的基础，边缘检测是图像处理过程中的一个重要环节。
检测物体边缘时,首先粗略检测其轮廓点,然后把原来检测到的轮廓点连接到一起,同时检测、连接遗漏的边界点并去除虚假的边界点。
边缘检测的算法很多，如方向算子，特度算子，canny算子和拉普拉斯算子等。
常用的有Sobel 算子，梯度算子的Roberts算子，Prewitt算子以及Canny边缘检测等。
本文主要涉及的是Sobel算子的边缘检测，Sobel算子是一阶微分算子，包含两组3*3矩阵，分别为横向和纵向，将之与图像作平面卷积，得出横向，纵向的亮度差分近似值。
我们也用过其他算子，sobel效果最好。
具体语法如下：BW=edge(A,'sobel',p);p为[0,1]的阈值hough变换Hough变换本来用于直线检测中,充分体现了Hough变换具有明了的几何解析性、一定的抗干扰能力以及易于实现并行处理等优点。
人们在对图像进行几何特征检测时,感兴趣的往往有直线,圆，椭圆等等。
自然而然地想到应用Hough变换。
这里不再赘述hough变换检测直线。
Hough变换是基于通过提取分布于目标圆周上的参数及点的特征值的来检测圆或圆弧的。
为了检测目标外形,对图像上的每点定义一个参数空间的映射。
Hough变换通过在参数空间找寻特征(峰值或最大值点)得到位于图像空间中的特征(目标形状)来转换问题。
对于已知半径的圆Hough变换可以检测任意已知表达形式的曲线，关键在于选择合适的参数空间。
我们可以根据曲线的表达形式决定其参数空间。
当检测某一已知半径的圆时，可以使用与原图像空间相同的空间作为其参数空间。
则原图像空间中的一个圆对应参数空间中的一个点，参数空间的一个点对应图像空间中一个圆，原图像空间中在同一圆上的点，它们的参数相同即a，b相同，它们在参数空间对应的圆就会过同一点（a，b），因此，将原图像中的所有点变换到参数空间之后，依据参数空间中点的聚集度就可判断出原图像空间中有无近似于圆的图形。
对于未知半径的圆，在一个xy平面图像中确定一个圆至少需要三个元素，即圆心的x轴和y轴坐标，圆的半径，因此Hough变换检测圆的目的就是检测出图像中各个圆的圆心坐标以及圆的半径。
其基本思想是将原图像空间中边缘点映射至参数空间中，再将参数空间中得到的全部坐标点元素所对应的累加值进行统计，并根据此累加值来判断圆的大小和圆心的位置。
例如，在xy平面上的方程为(x-a)2+(y-b)2=r2其中点（a，b）为圆心坐标，r为圆半径，点（x，y）为圆周上的一点，将其转换为参数坐标系（a，b，r），方程为(a-x)2+(b-y)2=r2,可看出次方程为圆锥面，对于原图像中任意确定的一个点在参数空间都有一个三维锥面与其对应。
在Hough变换检测圆时，可以利用梯度信息在很大程度上加快圆检测的速度。
对圆周而言，其梯度方向只有背离圆心或者指向圆心，当梯度指向圆心，圆心就在梯度的延长线上，而当梯度背离圆心，圆心则在梯度的反向延长线上。
所以，边缘梯度信息的加入可以预估圆心的位置，这样可以使算法的运算量明显减少，并且可以有效抑制虚假局部最大值。
圆心位置可以用极坐标方程形式表达:a=x - r•co s(θ (x,y)),a=y - r•sin(θ(x,y))或者a=x+r•co s(θ(x,y)),a=y+r•sin(θ(x,y))，边缘像素（x，y）处的梯度方向为θ(x,y)。
前一组公式是梯度方向背离圆心，后一组为梯度方向指向圆心。
以前一种情况为例，边缘图像中每个边缘像素点（x，y）都可以算出其相应的梯度方向θ(x,y)。
通过前一个公式可算出圆心坐标（a0，b0），对于参数空间可能的半径r0，其相应的参数空间累加器单元加一，最后找到累加器的局部最大值，就得到一个圆。
实验结果通过对图像进行灰度化，二值化，边缘检测，hough变换等过程将图片中柑橘轮廓检测了出来。
以下为圆坐标数据及处理的图像Center157radius10Center168radius10Center179radius10Center967radius10Center968radius10Center7568radius10Center7169radius10Center7270radius10Center7370radius10Center7271radius10Center7272radius10Center7674radius10Center7577radius10Center7677radius10Center17312radius10Center17213radius10Center17413radius10Center17214radius10Center17314radius10Center17115radius10Center17315radius10Center16916radius10Center17316radius10Center125205radius10Center127205radius10Center127206radius10Center122210radius10Center122215radius10Center121216radius10Center122216radius10Center1647radius20Center131214radius20实验分析在试验到最后的时候还是存在一些问题，期终检测时，我发现检测的圆比原图片中的柑橘小，还有左边的图片中有一个柑橘被另一个遮住了一部分，但是我们没有能在最后的检测的圆的图上清楚地看出来。