《递增序列》解题报告

合集下载

2009年清北学堂暑期培训NOIP模拟试题递增序列

2009年清北学堂暑期培训NOIP模拟试题递增序列(inc)解题手记递增序列(inc)【问题描述】蓝猫7号写下了一列非负整数，他看了一下，数乱七八糟的，于是他想改变一些书，使得序列变成一个严格递增的肺腑序列。

然而，蓝猫7号不想把整数序列中的数改得太大。

于是，他希望在改变的数最少的情况下，最后所有书的和最小【输入格式】输入文件inc.in中第一行有一个正整数n，表示序列的长度以下n行，每一行一个非负整数从前往后描述这个序列，序列中的每个数都不超过109.【输出格式】输出到未见inc.out中，仅有两个整数，两个正整数间用空格分开。

第一个整数表示最少需要改变的数的个数，第二个整数表示改编后的序列的所有数的总合。

【输入样例】6813919【输出样例】3 22【样例说明】最后的序列变成了 0 1 3 4 5 9【数据范围】1<=n<=10000好吧我最近考了一次试这道题事后看会做但时间快到了于是交了个骗分程序大致代码如下const f:array[1..8] of longint=(n1,n2,..n8);(即样例输入) ......读入Sum->所有元素的和if 读入与样例输入符合 then 输出样例else 输出0与Sum这样骗到了20分比一个只输出样例的家伙多了10分于是我总分就比他高了-_,-但是事后我看了题目原来这么简单实际上就是与导弹拦截是一样的原理即找出最长上升子序列然后处理一下头和尾就行了于是我直接用导弹拦截程序抄了上去做点处理就测了一下结果是——20分和我用骗分的方法分数和对的点一模一样= =于是我仔细看了一下样例有两点引起了我的注意一、样例中从3到9之间是从3开始递增的即从较小数开始递增而不是从较大数开始递减而题目中"他希望...最后所有数的和最小" 更加印证了我的想法另外我们可以推出处理头的时候必是从0开始递增处理尾的时候必是从最后"拦截"的"导弹"开始递增二、我们注意到拦截导弹问题和这道题有些许不同既是确定了上升序列后每两个临近的元素中间要填充一定数量的数字(依照1的法则填充) 那么有没有可能有无法填充的情况呢?显然是有的那么这样的序列便是无用的序列我们可以舍弃于是我们在进行"导弹拦截"的动规时便需要加个判断如果填充"空间"足够才能将其加入序列中我们仍然可以推出处理头的时候如果以这枚导弹作最后一枚导弹的上升序列为1 那么就同样要判断它的填充"空间"足不足够了尾不用处理三、样例中最后一个"拦截"的"导弹"既可以选择可以"拦截"3枚"导弹"的第四个9 也可以选择同样的第6个9 但是样例选择了后者我们可以简单的认为在相同的情况下最后一枚"拦截"的“导弹”是较后面的“导弹”时比较符合数据但是这样还不够我们经过模拟一下就可知道(依照1 2的法则) 最后拦截的是第四个9的时候整个序列的和比较大就不符合题目中要求的"所有数的和最小"的原则那么我们可以大胆猜想在相同的情况下最后一枚"拦截"的"导弹"是较后面的导弹整个序列的和相同或更小(易证)这个推论貌似和上边的推论没什么两样但是我们可以把它推广开去当第N枚被拦截的导弹能选择k种作为第N-1枚被拦截的导弹其拦截的导弹总数相同应该选择哪枚导弹作为第N-1枚被拦截的导弹?我们很容易就想到根据上面的法则我们应该拦截的是k种里最靠后的导弹还有N的范围是10^5 极限数据看上去用拦截导弹的N^2方法会超时不过数据有些弱我的破电脑一个数据运行最长时间是1.1秒(而且是N=9000的N=10000的0.7秒就过了) 相信好点的电脑1秒内应该能过呃注意了这几点后这道题也就差不多可以AC了另外吐槽下题目明明说每个数不超过109 我估摸着109*10^5 Lonignt还可以承受结果数据里到处都是几亿的东西只能用int64来存所有数的和还有最后一个数据输出错了它第一个数字输出的竟然是最长序列的长度而不是最少需要改变的数的个数我一直错了好久才发现囧源程序代码Program inc;Const MaxN=10000;VarD,F,Up,Ans:Array [1..MaxN] Of Longint;N,i,j,Max,x:Longint;Sum:int64;BeginAssign(Input,'inc.in');Reset(Input);Assign(Output,'inc.out');Rewrite(Output);Readln(N);For i:=1 to N Do Readln(D[i]);//读入数据F[1]:=1;For i:=2 to N Do//导弹拦截动规(稍作修改)BeginF[i]:=1;For j:=1 to i-1 DoIf (F[j]+1>=F[i])And(D[i]>D[j])And(D[i]-D[j]>=i-j) ThenIf (F[j]+1>F[i])or((F[j]+1=F[i]))And(x<j)Then Begin F[i]:=F[j]+1; Up[i]:=j; End;If F[i]=1 ThenBeginUp[i]:=0;If i-1>D[i] Then F[i]:=0;End;End;Max:=0; x:=0;For i:=1 to N DoIf Max<=F[i] Then Begin Max:=F[i]; x:=i; End; //找出最长上升子序列Max:=x;For i:=1 to N-x Do Ans[x+i]:=D[x]+i;//处理头While Up[x]<>0 Do//填充中间BeginAns[x]:=D[x];Ans[Up[x]]:=D[Up[x]];For i:=1 to x-Up[x]-1 DoAns[Up[x]+i]:=D[Up[x]]+i;x:=Up[x];End;Ans[x]:=D[x];For i:=0 to x-2 Do Ans[i+1]:=i;//处理尾Sum:=0;For i:=1 to N Do//累加所有数的总和Sum:=Sum+Ans[i];Write(N-F[Max],' ');//输出Writeln(Sum);Close(Input);Close(Output);End.。

递增数列牛顿-概述说明以及解释

递增数列牛顿-概述说明以及解释1.引言1.1 概述概述递增数列是数学中的一个重要概念，它在很多领域中都有广泛的应用。

牛顿是17世纪最重要的科学家之一，他在自然科学和数学方面的贡献被广泛认可。

本文旨在探讨递增数列与牛顿之间的关系，并总结递增数列的特点，强调牛顿对数学的重要性，并展望递增数列与牛顿的未来研究方向。

在本文的正文部分，我们将首先介绍递增数列的定义。

递增数列是一种数学序列，其中的每个数比前一个数大。

通过研究递增数列，我们可以深入了解数列中的数值规律以及数值之间的关系，这对于数学领域的研究和实际应用具有重要意义。

然后，我们将介绍牛顿在数学领域的贡献。

牛顿是一位杰出的数学家和物理学家，他提出了微积分和自然哲学的新理论，这些理论对于数学和物理学的发展产生了深远的影响。

牛顿的工作为递增数列的研究提供了重要的理论基础和方法。

接下来，我们将讨论递增数列与牛顿之间的关系。

通过研究递增数列，我们可以应用牛顿的方法和理论来解决数学问题，并进一步拓展数学的应用领域。

递增数列与牛顿的关系不仅仅停留在理论上，更体现在实际应用中，为多个领域的研究和发展提供了重要的支持。

最后，在结论部分，我们将总结递增数列的特点，强调牛顿对数学的重要性，以及展望递增数列与牛顿的未来研究方向。

递增数列作为一种重要的数学概念，其研究还有待进一步深入和拓展，而牛顿的方法和理论将为递增数列的未来研究提供宝贵的参考和启示。

通过本文的撰写，我们希望能够对读者更加深入地介绍递增数列的概念，展示牛顿在数学领域的贡献，以及分析递增数列与牛顿之间的关系。

同时，我们也希望能够引起读者对递增数列和牛顿的兴趣，并对未来研究方向有一定的展望。

递增数列和牛顿的研究将会在数学领域继续发展，并产生更多的新的发现和应用。

1.2文章结构文章结构部分的内容可以按照以下方式进行编写：文章结构：本文将分为以下几个部分进行阐述：引言、正文和结论。

- 引言部分将提供一个概述，介绍递增数列和牛顿的基本概念，并阐明本文的目的。

NOI提高组解题报告

第七届（2001）分区联赛复赛解题报告（提高组）俞玮赵爽第一题：一元三次方程求解给出一个三次方程32()0f x ax bx cx d =+++=，试求它所有的三个根。

这里所有的根都在区间[100,100]-中，并保证方程具有三个实根，且它们之间的差不小于1。

分析：如果是一般的求三次方程根的问题，那么只能直接使用求根公式，但这是非常复杂的。

由于题目要求只精确到0.01，故我们考虑一下是否可以应用数值方法进行计算。

由题目给出的方程在区间内存在根的条件可知，我们可以用一个变量i 从-100.000到100.000以步长0.001做循环。

若()(0.001)0f i f i ⋅+<，则可知在区间(,0.001)i i +内存在方程的解。

这样无论这个区间内的解是什么，在取两位小数的精度后都与i 取两位小数的结果是一样的。

故我们就可以把取两位小数精度的i 作为问题的解。

另外还有可能方程的根在区间端点i 的情况，我们可以通过判断()f i 是否为0来获得。

但这种方法由于用到了题目所要求的数值精度小的特殊性，故无法扩展。

而在用数值方法求方程根的时候，我们最常用的方法就是二分法。

该方法的应用在于如果确定了方程()0f x =在区间(,)a b 内如果存在且只存在一个根，那么我们可以用逐次缩小根可能存在范围的方法确定出根的某精度的数值。

该方法主要利用的就是题目所给的若在区间(,)a b 内存在一个方程的根，则()()0f a f b ⋅<这个事实，并重复执行如下的过程： ● 取当前可能存在解的区间(,)a b ； ● 若0.001a b +>或()20a bf +=，则可确定根为2a b+并退出过程； ● 若()2()0a b f a f+⋅<，则由题目给出的定理可知根在区间()2,a b a +中，故对区间()2,a ba +重复该过程；若()2()0a b f a f+⋅>，则必然有()2()0a b f f b +⋅<，也就是说根在()2,a bb +中，应该对此区间重复该过程。

Noip_2013_提高组_Day2_解题报告

第二题:花匠（动态规划）1.令S[i][1]表示以i为结尾，且降序到达a[i]的最长抖动序列长度；令S[i][0]表示以i为结尾，且升序到达a[i]的最长抖动序列长度。

依然设数组S[i][0/1],但考虑如下递推公式：（1）a[i+1]>a[i]:S[i+1][0]=max(S[i][1]+1，S[i][0]);S[i+1][1]=S[i][1];（2）a[i+1]<a[i]:S[i+1][0]=S[i][0];S[i+1][1]=max(S[i][0]+1,S[i][1]);（3）a[i+1]= =a[i]:S[i+1][0]=S[i][0];S[i+1][1]=S[i][1];S[1][0]=S[1][1]=1.算法优化后，再一次编写程序，O(n)的时间复杂度，当然是顺利AC了，代码如下：2.这道题明显可以用类似最长上升子序列的动态规划求解，易得思路如下：用f(i,0)表示以i为结尾的且最后一段上升的子序列最大长度，f(i,1)表示表示以i 为结尾的且最后一段下降的子序列最大长度，那么答案明显就是max{f(i,0),f(i,1)} 方程：f(i,0)=max{f(j,1)}+1 0<=j<i且h[j]<h[i]f(i,1)=max{f(j,0)}+1 0<=j<i且h[j]>h[i]边界：f(0,0)=f(0,1)=0如果直接DP毫无疑问复杂度是O(n^2)，会TLE，但是，考虑到我们每次取最值时候取得都是一个区间里的数，如f(i,0)=max{f(j,1)}+1 0<=j<i且h[j]<h[i]取得就是区间[0,h[i]-1]里的最值，所以可以使用线段树或者是BIT（树状数组）来优化，这样复杂度就是O(n log n)，可以过全部数据。

这道题还有一个解法，直接求拐点数目，然后就可以神奇的做到O(n)了，由于我找不到满意的证明，就不发上来了。

递增数列的通项公式推导

递增数列的通项公式推导数列是数学中的一个重要概念，它是按照一定规律排列的一组数的序列。

其中，递增数列是指数列中的每一项都比前一项大的数列。

在数列中，递增数列是一种常见且有规律的数列形式。

了解递增数列的通项公式对于数列相关问题的解决具有重要意义。

本文将对递增数列的通项公式进行推导，以帮助读者更好地理解递增数列的规律和特点。

假设我们有一个递增数列：$a_1, a_2, a_3, a_4, \cdots$，其中$a_1$表示数列的首项，$a_2$表示数列的第二项，$a_3$表示数列的第三项，依次类推。

由于该数列是递增数列，因此我们可以得出以下关系：$a_1 < a_2 < a_3 < a_4 < \cdots$。

我们可以观察到，递增数列中的每一项与其前一项之间有一个固定的增量，即公差。

假设递增数列的公差为$d$，则有以下关系成立：$a_2 - a_1 = d, a_3 - a_2 = d, a_4 - a_3 = d, \cdots$。

在推导递增数列的通项公式时，我们可以先假设递增数列的通项公式为$a_n = S_n$，其中$n$表示数列中的第$n$项，$S_n$表示递增数列的通项公式。

根据递增数列的定义和性质，我们可以得到以下关系：$S_2 = a_1 + d$$S_3 = a_1 + 2d$$S_4 = a_1 + 3d$$\cdots$$S_n = a_1 + (n-1)d$通过观察以上关系，我们发现递增数列的第$n$项$S_n$与首项$a_1$和公差$d$之间存在一定的数学关系。

通过分析递增数列中各项之间的规律，我们可以得出递增数列的通项公式为：$S_n = a_1 + (n-1)d$其中，$S_n$表示递增数列的第$n$项，$a_1$表示数列的首项，$d$表示数列的公差。

递增数列的通项公式能够准确地表示递增数列中任意一项的数值，使我们能够更加方便和快速地计算数列中各项的数值。

高中递增数列定义

高中递增数列定义全文共四篇示例，供读者参考第一篇示例：高中递增数列定义在高中数学中，递增数列是一种常见的数学概念。

递增数列指的是数列中的每一项都比前一项大的数列。

这意味着数列中的元素随着索引的增加而增大。

在数学中，数列是一组按照一定顺序排列的数的集合。

数列中的每个数称为该数列的项。

数列可以是有限的，也可以是无限的。

递增数列是一种重要的数列，它在数学和实际问题中都有着重要的应用。

递增数列的定义很简单，即数列中的每一项都比前一项大。

1, 2, 3, 4, 5就是一个递增数列。

在这个数列中，每一项都比前一项大1。

递增数列在数学中有着重要的应用。

在数列的求和问题中，递增数列是一个常见的研究对象。

通过对递增数列的性质和规律进行分析和研究，可以推导出数列求和的公式，从而简化数学计算。

在数学建模和实际问题中，递增数列也经常出现。

在经济学和金融学中，递增数列可以用来描述某项指标随时间递增的趋势。

在生物学和医学中，递增数列可以用来描述细胞增殖的规律。

在高中数学教学中，递增数列是一个很重要的概念。

通过对递增数列的学习，可以帮助学生提高数学思维能力和解决问题的能力。

递增数列是数学中的基础知识，掌握了递增数列的概念和性质，可以为学生日后更深入的学习打下坚实的基础。

第二篇示例：高中数学中，递增数列是常见的数列类型之一，递增数列的定义是指数列中每一项都比前一项大的数列。

递增数列在数学领域中有着重要的地位，不仅在数列的研究中起到重要作用，也在实际问题中有广泛的应用。

递增数列可以用数学符号表示为：{a1, a2, a3, ..., an}，其中an>an-1，n为正整数。

也就是说，递增数列中的每一项都比前一项大。

递增数列的性质有很多，这里主要介绍一些常见的性质。

递增数列中的任意相邻项之差都是正数，即an-an-1>0。

递增数列中的任意两项之间的差值也是递增的，即an-an-1<an+1-an。

递增数列是一个有上界的数列，也就是说，递增数列中的任意项都小于等于某个常数M。

Spoj解题报告

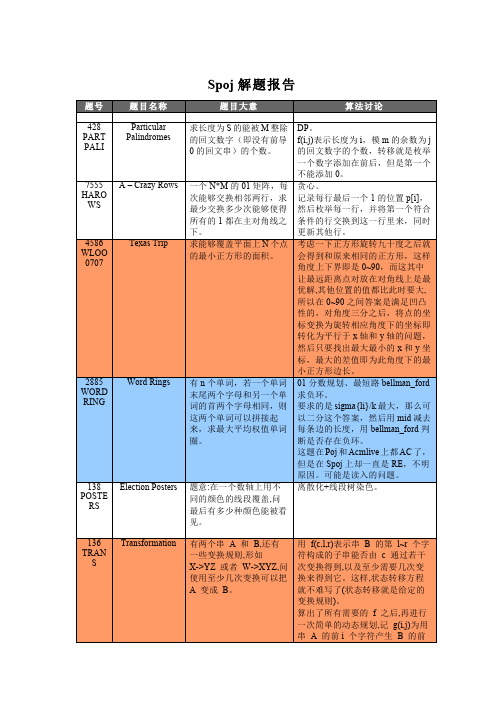
Spoj 解题报告
题号 428 PART PALI 题目名称 Particular Palindromes 题目大意求长度为 S 的能被 M 整除的回文数字（即没有前导 0 的回文串）的个数。算法讨论 DP。 f(i,j)表示长度为 i，模 m 的余数为 j 的回文数字的个数，转移就是枚举一个数字添加在前后，但是第一个不能添加 0。贪心。记录每行最后一个 1 的位置 p[i]，然后枚举每一行，并将第一个符合条件的行交换到这一行里来，同时更新其他行。考虑一下正方形旋转九十度之后就会得到和原来相同的正方形，这样角度上下界即是 0~90，而这其中让最远距离点对放在对角线上是最优解,其他位置的值都比此时要大, 所以在 0~90 之间答案是满足凹凸性的，对角度三分之后，将点的坐标变换为旋转相应角度下的坐标即转化为平行于 x 轴和 y 轴的问题，然后只要找出最大最小的 x 和 y 坐标，最大的差值即为此角度下的最小正方形边长。 01 分数规划、最短路 bellman_ford 求负环。要求的是 sigma{li}/k 最大，那么可以二分这个答案，然后用 mid 减去每条边的长度，用 bellman_ford 判断是否存在负环。这题在 Poj 和 Acmlive 上都 AC 了，但是在 Spoj 上却一直是 RE，不明原因。可能是读入的问题。离散化+线段树染色。
136 TRAN S
Transformation
用 f(c,l,r)表示串 B 的第 l~r 个字符构成的子串能否由 c 通过若干次变换得到,以及至少需要几次变换来得到它。这样,状态转移方程就不难写了(状态转移就是给定的变换规则)。算出了所有需要的 f 之后,再进行一次简单的动态规划,记 g(i,j)为用串 A 的前 i 个字符产生 B 的前

青岛版一下智慧广场“递增(递减)问题”教案

用你喜欢的颜色涂一涂，然后在小组里说一说。

四、课堂小结：师：在这个单元的学习中，大家都有不同的收获，你觉得还有哪些方面做的不够呢？希望我们收获的苹果越来越多，不满意的地方越来越少。

智慧广场——递增递减问题【设计理念】：本智慧广场是在学生已经初步学习过用列举法解决问题的基础上进行教学的，是列举法的进一步深化与应用。

这节课我采用了循序渐进的学习方式，首先让学生自主探索交流出运用画图法来解决问题，然后将问题加深进一步引出列举法，最后学习表格列举法，整个过程通过让学生通过自主观察、对比、交流等学习方式来完成本节课的任务。

【教学目标】：1、在解决实际问题的过程中，巩固画图法，学习表格列举法。

2、学生在对解决简单实际问题过程的反思和交流中，感受表格列举法的特点和价值，进一步发展思维的条理性和严密性。

3、增强解决问题的策略意识，并获得解决问题的成功体验，提高学好数学的信心。

【教学重难点】：引导学生用表格列举法解决递增递减问题，体会表格列举法的优点。

【教学准备】：《递增递减》多媒体课件【教学过程】：一、创设情境，导入新课导入：同学们！由于我们人类乱砍滥伐树木，现在地球上的树木逐年在减少，给人们的生活带来了很大的影响，作为地球小主人应该怎么做啊？有个叫欢欢的小朋友也积极的参与到了保护树木的活动中。

102二、自主探索，解决问题1．情境导入出示信息，抽生读信息。

师导语：请同学们仔细观察情境图，看看图上的小朋友们在干什么？（1）生认真看图思考。

抽生回答交流。

师总结：对！他们通过给树立牌子的方式告诉大家，要爱护树木，勿乱砍滥伐树。

看着长成参天大树的欢欢高兴地说了一句话，同学们仔细看！谁能站起来大声读一读？（点击出示欢欢高兴地说的一句话。

）抽生大声读出信息：我从8岁开始种第一棵树，以后每年比前一年多种1棵树。

（2）小组合作,理解题意。

师导语：在这里老师有个疑问欢欢说以后每年比前一年多种1棵树，这句话是什么意思？生先独立思考。

数量序列的逻辑发展分析

数量序列的逻辑发展分析数量序列是指由数字按照一定规律排列形成的序列，它在数学和逻辑推理中起着重要的作用。

通过对数量序列的逻辑发展进行分析，我们可以揭示出其中的规律和模式，从而帮助我们更好地理解数学和逻辑思维。

一、递增序列递增序列是最简单的数量序列形式，它由一个起始数字开始，每次增加一个固定的差值。

例如，1, 3, 5, 7, 9就是一个递增序列，其中的差值为2。

在递增序列中，我们可以通过计算两个相邻数字之间的差值来找到规律。

如果差值是一个定值，那么这个序列可以被归类为等差数列。

等差数列可以用以下公式来表示：an = a1 + (n-1)d，其中an表示序列的第n个数字，a1表示起始数字，d表示公差。

二、递减序列与递增序列相反，递减序列是由一个起始数字开始，每次减少一个固定的差值。

例如，10, 8, 6, 4, 2就是一个递减序列，其中的差值为2。

递减序列的规律和递增序列相似，我们可以通过计算两个相邻数字之间的差值来找到规律。

如果差值是一个定值，那么这个序列可以被归类为等差数列。

等差数列的公式同样适用于递减序列。

三、递增递减序列递增递减序列是由递增和递减两部分组成的序列。

例如，1, 2, 3, 2, 1就是一个递增递减序列。

在递增递减序列中，无论是递增部分还是递减部分，都可以按照等差数列的规律进行分析。

递增部分的等差数列的公差为正值，递减部分的等差数列的公差为负值。

递增递减序列可以通过设定一个关键点，以该点为分界，分别对递增和递减部分进行分析。

通过找到递增和递减部分的规律，我们可以综合得出整个序列的逻辑发展规律。

四、其他类型序列除了递增、递减和递增递减序列外，数量序列还可以有其他各种形式。

例如，斐波那契数列是一种非常有名的序列，它的每个数字都是前两个数字之和。

斐波那契数列的规律为：1, 1, 2, 3, 5, 8, 13, 21...还有一种常见的序列是乘法序列，它的每个数字都是前一个数字乘以一个固定的因数。

递增排序ppt课件

数据完整性
在数据检索过程中，递增排序有助于确保数据的完整性。有序的数据结构可以避免数据丢失或重复，提高数据质量。
数据库索引
索引结构
数据库索引通常采用递增排序的方式，以便快速定位和检索数据。索引能够显著提高查询速度，减少数据库查询的响应时间。
索引优化
通过优化索引结构，可以实现更高效的查询性能。对索引进行递增排序可以减少磁盘I/O操作，提高数据库的整体性能。
人工智能与机器学习对排序算法的影响
人工智能
人工智能技术可以应用于排序算法中，例如利用神经网络、深度学习等技术对数据进行特征提取和分类，以提高排序算法的准确性和效率。
机器学习
机器学习技术可以通过对大量数据进行学习，自动发现数据中的模式和规律，从而实现对数据的快速分类和排序。机器学习技术可以应用于递增排序算法中，以提高其效率和准确性。
适用场景
数据量较小
当待排序数据量较小，且对排序效率要求不高时，递增排序算法是一个不错的选择。
递增顺序需求
当需要按照从小到大的顺序对数据进行处理或分析时，递增排序算法能够满足需求。
算法复杂度
时间复杂度
O(nlogn)，其中n为待排序元素的数量。
空间复杂度
O(1)，递增排序算法在原地进行排序，不需要额外的存储空间。
THANKS
感谢观看
分布式处理
分布式处理是一种将计算任务分配给多个计算机节点协同完成的方法。在递增排序中，可以使用分布式处理来将待排序数据分布到多个节点上进行处理，从而提高排序效率。例如，可以将待排序数据分布到多个节点上，然后使用并行计算和分布式处理技术来同时处理多个数据元素，最后再将结果汇总。
05
递增排序与其他排序算法的比较

新教材高中数学第一章数列4数列在日常经济生活中的应用课后巩固提升含解析北师大版选择性必修第二册

第一章数列§4 数列在日常经济生活中的应用课后篇巩固提升必备知识基础练1.龙门石窟是中国石刻艺术宝库.某洞窟的浮雕共7层,它们构成一幅优美的图案.若从下往上计算,从第二层开始,每层浮雕像个数依次是下层个数的2倍,该洞窟浮雕像总共有1 016个,则第5层浮雕像的个数为( )A.64B.128C.224D.512a 1,依题意有公比q=2,n=7,S 7=a 1(1-27)1-2=1016,解得a 1=8,则a n =8×2n-1=2n+2(1≤n ≤7,n ∈N+),所以a 5=27=128.2.我国工农业总产值从2001年到2021年的20年间翻了两番,设平均每年的增长率为x ,则有( ) A.(1+x )19=4 B.(1+x )20=3 C.(1+x )20=2 D.(1+x )20=42001年总产值为1,由于我国工农业总产值从2001年到2021年的20年间翻了两番,说明2021年的工农业总产值是2001年工农业总产值的4倍,则(1+x )20=4.3.某市利用省运会的契机,鼓励全民健身,从2021年7月起向全市投放A,B 两种型号的健身器材.已知7月投放A 型健身器材300台、B 型健身器材64台,计划8月起,A 型健身器材每月的投放量均为a 台,B 型健身器材每月的投放量比上一月多50%,若12月底该市A,B 两种健身器材投放总量不少于2 000台,则a 的最小值为( ) A.243 B.172 C.122 D.74B 型健身器材这6个月投放量构成数列{b n },则数列{b n }是首项b 1=64,公比q=32的等比数列,其前6项的和S 6=64×[1-(32) 6]1-32=1330,∴5a+300+1330≥2000,解得a ≥74,故选D .4.公元前5世纪,古希腊哲学家芝诺发表了著名的阿基里斯悖论:他提出让乌龟在阿基里斯前面1 000米处和阿基里斯赛跑,并且假定阿基里斯的速度是乌龟的10倍.当比赛开始后,若阿基里斯跑了1 000米,此时乌龟便领先他100米;当阿基里斯跑完下一个100米时,乌龟领先他10米;当阿基里斯跑完下一个10米时,乌龟仍然领先他1米……所以,阿基里斯永远追不上乌龟.按照这样的规律,若阿基里斯和乌龟的距离恰好为10-2米时,乌龟爬行的总距离为( ) A.104-190米B.105-1900米C.105-990米 D.104-9900米,乌龟每次爬行的距离构成等比数列{a n},且a1=100,q=110,a n=10-2,所以乌龟爬行的总距离为S n=a1-a n q1-q =100-10-2×1101-110=105-1900(米).5.将n个大小不同的正方体形状的积木从上到下、从小到大堆成塔状,平放在桌面上.上面一个正方体积木下底面的四个顶点正好是它下面一个正方体积木的上底面各边的中点,按此规律不断堆放.如果最下面的正方体积木的棱长为1,且这些正方体积木露在外面的面积之和为S n,则S n=()A.8-82n B.9-82nC.10-8n D.10-82n-11,则该正方体除下底面外的表面积为5×12=5;第二个正方体的棱长为1×√22=√22,它的侧面积为4×√222,第3个小正方形的边长为√22×√22=√222,它的侧面积为4×√222×2;第n个小正方形的边长为√22n-1,它的侧面积为4×√222(n-1)=4×12n-1,则它们的表面积为5+4×121+122+123+…+12n-1=5+4×12(1-12n-1)1-12=9-42n-1=9-82n.6.某运动员一脚把球踢到32米高处,从此处开始计算,假设足球每次着地后又弹回到原来高度的一半再落下,则第5次着地时,该球所经过的总路程为米.1次落地经过的路程为32;足球第2次落地经过的路程为32+32×12×2=64;足球第3次落地经过的路程为64+32×122×2=80;足球第4次落地经过的路程为80+32×123×2=88;足球第5次落地经过的路程为88+32×124×2=92.7.有纯酒精a(a>1)升,从中取出1升,再用水加满,然后再取出1升,再用水加满,如此反复进行,则第九次和第十次共取出纯酒精升.答案1-1a 82-1a,取出的纯酒精数量是一个以1为首项,1-1a为公比的等比数列, 即:第一次取出的纯酒精为1升,第二次取出的纯酒精为1-1a升,第三次取出的纯酒精为1-1a2升,……,第n次取出的纯酒精为1-1an-1升,则第九次和第十次共取出的纯酒精数量为a9+a10=1-1a 8+1-1a9=1-1a 82-1a(升).8.小明打算从2018年起,每年的1月1日到银行存入a元的一年期定期储蓄,若年利率为p,且保持不变,并约定每年到期存款本息均自动转为新一年的定期.2019年1月1日小明去银行继续存款a元后,他的账户中一共有元;到2022年的1月1日不再存钱且将所有的存款和利息全部取出,则可取回元.2a ap[(1+p)5-(1+p)],2019年1月1日存款a元后,账户中一共有a(1+p)+a=(ap+2a)元;银行利息为单利计息,故2022年1月1日可取出钱的总数为a(1+p)4+a(1+p)3+a(1+p)2+a(1+p)=a·(1+p)[1-(1+p)4]1-(1+p)=ap[(1+p)5-(1+p)].9.某抗洪指挥部接到预报,24小时后有一洪峰到达,为确保安全,指挥部决定在洪峰到来之前临时筑一道堤坝作为第二道防线.经计算,除现有的参战军民连续奋战外,还需调用20台同型号翻斗车,平均每辆车工作24小时.从各地紧急抽调的同型号翻斗车目前只有一辆投入使用,每隔20分钟能有一辆翻斗车到达,一共可调集25辆,那么在24小时内能否构筑成第二道防线?(单位:小时)依次设为a1,a2,…,a25..由题意可知,此数列为等差数列,且a1=24,公差d=-13=500,25辆翻斗车完成的工作量为a1+a2+…+a25=25×24+25×12×-13而需要完成的工作量为24×20=480.∵500>480,∴在24小时内能构筑成第二道防线.关键能力提升练10.据有关文献记载:我国古代一座9层塔挂了126盏灯,且相邻两层中的下一层灯数比上一层灯数都多d(d为常数)盏,底层的灯数是顶层的13倍,则塔的顶层共有灯()A.2盏B.3盏C.4盏D.5盏d=x,由题意得x盏灯,则最下面有(x+8d)盏,则x+8d=13x,即23+36d=126,解得d=3,x=2,所以顶层x+(x+d)+(x+2d)+…+(x+8d)=126,整理得9x+36d=126,所以9×2d3有2盏灯.故选A.11.某人的月工资由基础工资和绩效工资组成,2010年每月的基础工资为2 100元、绩效工资为2 000元.从2011年起每月基础工资比上一年增加210元、绩效工资为上一年的110%.照此推算,此人2021年的年薪为(结果精确到0.1)()A.9.3万元B.10.4万元C.12.14万元D.14万元,基础工资是以2100元为首项,以210元为公差的等差数列,绩效工资以2000元为首项,以1.1为公比的等比数列,则此人2021年每月的基础工资为2100+210(12-1)=4410(元),每月的绩效工资为2000×1.111≈5706.23(元),则此人2021年的年薪为12(4410+5706.23)≈12.14(万元).12.在我国明代数学家“珠算之父”程大位(1533—1606)所著的《算法统宗》中,有许多用诗歌形式表达的数学问题,如八子分棉歌:“九百九十六斤棉,赠分八子做盘缠,次第每人多十七,要将第八数来言,务要分明依次第,孝和休惹外人传.”此问题(第八数)的答案为(单位:斤)()A.150B.167C.184D.201a1斤棉,则{a n}是公差为17的等差数列,由题意得8a1+8×7×17=996,解得a1=65(斤),2所以a8=65+7×17=184(斤).13.侏罗纪蜘蛛网是一种非常有规则的蜘蛛网,如图,它是由无数个正方形环绕而成,且每一个正方形的四个顶点都恰好在它的外围一层正方形四条边的三等分点上,设外围第一个正方形的边长是m ,有人说,如此下去,蜘蛛网的长度也是无限的增大,那么,试问,侏罗纪蜘蛛网的长度真的是无限长的吗?设侏罗纪蜘蛛网的长度为S n ,则( ) A.S n 无限大 B.S n <3(3+√5) m C.S n =3(3+√5) m D.S n 可以取100 m,从外到内正方形的边长依次为a 1=m ,a 2=√(2m 3) 2+(m3) 2=√5m3, a 3=(2√5m 3×3)(√5m3×3)=5m 9,……则数列{a n }是以m 为首项,以√53为公比的等比数列,所以S n =4·m[1-(√53) n ]-√53,当n →∞时,S n →3(3+√5)m.故选B .14.如图,作边长为3的正三角形的内切圆,在这个圆内作内接正三角形,然后作新三角形的内切圆……如此下去,前n 个内切圆的面积和为 .-14n )π根据题意知第一个内切圆的半径为√36×3=√32,面积为34π,第二个内切圆的半径为√34,面积为316π,……这些内切圆的面积组成一个等比数列,首项为34π,公比为14,故前n 个内切圆的面积之和为34π(1-14n )1-14=(1-14n)π.15.在我国古代著名的数学专著《九章算术》里有一段叙述:今有良马与驽马发长安至齐,齐去长安四百二十里,良马初日行九十七里,日增一十五里;驽马初日行九十二里,日减一里;良马先至齐,复还迎驽马,二马相逢.两匹马在第日相逢.,可知良马第n 日行程记为a n ,则数列{a n }是首项为97,公差为15的等差数列,驽马第n 日行程记为b n ,则数列{b n }是首项为92,公差为-1的等差数列,则a n =97+15(n-1)=15n+82,b n =92-(n-1)=93-n.∵数列{a n }的前n 项和为n (97+15n+82)2=n (179+15n )2,数列{b n }的前n 项和为n (92+93-n )2=n (185-n )2,∴n (179+15n )2+n (185-n )2=840,整理得14n 2+364n-1680=0,即n 2+26n-120=0,解得n=4(n=-30舍去),即两匹马在第4日相逢. 16.某企业2018年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降.若不能进行技术改造,预测从2019年起每年比上一年纯利润减少20万元,2019年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第n 年(2019年为第一年)的利润为5001+12n 万元(n 为正整数).(1)设从2019年起的前n 年,若该企业不进行技术改造的累计纯利润为A n 万元,进行技术改造后的累计纯利润为B n 万元(须扣除技术改造资金),求A n ,B n 的表达式;(2)依上述预测,从2019年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?依题设,A n =(500-20)+(500-40)+…+(500-20n )=490n-10n 2,B n =5001+12+1+122+…+1+12n-600=500n-5002n -100.(2)B n -A n =500n-5002n -100-(490n-10n 2)=10n 2+10n-5002n -100=10n (n+1)-502n -10, 因为数列n (n+1)-502n -10在(0,+∞)上为递增数列, 当1≤n ≤3时,n (n+1)-502n -10≤12-508-10<0; 当n ≥4时,n (n+1)-502n -10≥20-5016-10>0,所以当n ≥4时,B n >A n ,所以至少经过4年,该企业进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润.学科素养创新练17.某工厂为扩大生产规模,今年年初新购置了一条高性能的生产线,该生产线在使用过程中的维护费用会逐年增加,第一年的维护费用是4万元,从第二年到第七年,每年的维护费用均比上年增加2万元,从第八年开始,每年的维护费用比上年增加25%. (1)设第n 年该生产线的维护费用为a n ,求a n 的表达式;(2)若该生产线前n 年每年的平均维护费用大于12万元时,需要更新生产线,求该生产线前n 年每年的平均维护费用,并判断第几年年初需要更新该生产线.当n ≤7时,数列{a n }是首项为4,公差为2的等差数列,a n =4+2(n-1)=2n+2,当n ≥8时,数列{a n }是首项为a 8,公比为54的等比数列,又a 7=16,a 8=16×54,∴a n =16×54n-7,∴a n 的表达式为a n ={2n +2,1≤n ≤7,16×(54) n -7,n ≥8,n ∈N +.(2)设S n 表示数列{a n }的前n 项和,由等差及等比数列的求和公式得,当1≤n ≤7时,S n =n (4+2n+2)2=n 2+3n ,当n ≥8时,由S 7=70,S n =S 7+16×54×1-(54) n -71-54=80·54n-7-10, 该生产线前n 年每年的平均维护费用S n n ={n +3,1≤n ≤7,80·(54) n -7-10n ,n ≥8,n ∈N +, 当1≤n ≤7时,S n n为递增数列,当n ≥8时,∵S n+1n+1−S n n=80·(54) n -7·(n 4-1)+10n (n+1)>0,∴S n n也为递增数列.又S 88>S 77,∴S n n为递增数列.又S77=10<12,S88=11.25<12,S 99=1159>12,则第10年年初需要更新该生产线.。

最长递增序列问题

最长递增序列问题The longest increasing subsequence problem is a classic problem in computer science and mathematics. It involves finding the longest subsequence of an array that is strictly increasing. This problem has applications in various fields such as data compression, genetics, and computer algorithms. It is a challenging problem that requires dynamic programming techniques to solve efficiently.最长递增子序列问题是计算机科学和数学中经典的问题。

它涉及查找数组的最长递增子序列。

这个问题在数据压缩、遗传学和计算机算法等领域都有应用。

这是一个具有挑战性的问题，需要动态规划技术来高效解决。

One way to approach the longest increasing subsequence problem is through dynamic programming. Dynamic programming involves breaking down a complex problem into smaller subproblems, solving each subproblem only once, and storing the solutions to avoid redundant calculations. By using dynamic programming, we can efficiently find the longest increasing subsequence in an array with a time complexity of O(n^2).解决最长递增子序列问题的一种方法是通过动态规划。

最长递增子序列问题---动态规划

最长递增⼦序列问题---动态规划最长递增⼦序列问题是⼀个很基本、较常见的⼩问题，但这个问题的求解⽅法却并不那么显⽽易见，需要较深⼊的思考和较好的算法素养才能得出良好的算法。

由于这个问题能运⽤学过的基本的算法分析和设计的⽅法与思想，能够锻炼设计较复杂算法的思维，我对这个问题进⾏了较深⼊的分析思考，得出了⼏种复杂度不同算法，并给出了分析和证明。

⼀，最长递增⼦序列问题的描述设L=<a1,a2,…,a n>是n个不同的实数的序列，L的递增⼦序列是这样⼀个⼦序列Lin=<a K1,a k2,…,a km>，其中k1<k2<…<k m且a K1<a k2<…<a km。

求最⼤的m值。

⼆，第⼀种算法：转化为LCS问题求解设序列X=<b1,b2,…,b n>是对序列L=<a1,a2,…,a n>按递增排好序的序列。

那么显然X与L的最长公共⼦序列即为L的最长递增⼦序列。

这样就把求最长递增⼦序列的问题转化为求最长公共⼦序列问题LCS了。

最长公共⼦序列问题⽤动态规划的算法可解。

设Li=< a1,a2,…,a i>,Xj=< b1,b2,…,b j>，它们分别为L和X的⼦序列。

令C[i,j]为Li与Xj的最长公共⼦序列的长度。

则有如下的递推⽅程：这可以⽤时间复杂度为O(n2)的算法求解，由于这个算法上课时讲过，所以具体代码在此略去。

求最长递增⼦序列的算法时间复杂度由排序所⽤的O(nlogn)的时间加上求LCS的O(n2)的时间，算法的最坏时间复杂度为O(nlogn)＋O(n2)＝O(n2)。

三，第⼆种算法：动态规划法设f(i)表⽰L中以a i为末元素的最长递增⼦序列的长度。

则有如下的递推⽅程：这个递推⽅程的意思是，在求以a i为末元素的最长递增⼦序列时，找到所有序号在L前⾯且⼩于a i的元素a j，即j<i且a j<a i。

《用列举法解决递增递减问题》(说课稿)青岛版一年级下册数学

用列举法解决递增递减问题一、前言递增和递减问题是小学数学中比较基础的一类问题，如何解决这类问题是一件非常重要的事情。

在这里，我们将介绍一种非常简单易用的方法——列举法，来解决这类问题。

我们将以青岛版一年级下册数学教材为例，来详细说明这种方法的具体应用。

二、递增问题首先我们来看一下递增问题，我们可以定义递增问题为：序列中的每一项都比前一项大的一类问题。

比如：问题：小明身高比小李高5厘米，小李身高比小红高6厘米，那么小明比小红高多少厘米？我们可以用列举法来解决这个问题：人物身高小红0小李6小明11我们可以发现，小明比小红高11厘米，所以答案为11。

接下来我们再来看一个例子：问题：有1个苹果，第一天吃掉一半后剩下的苹果再减去1个，第二天再吃掉一半后剩下的苹果再减去1个，以此类推，第5天会剩下几个苹果？我们可以用列举法来解决这个问题：天数剩下的苹果数0110203-14-35-7我们可以发现，第5天会剩下7个苹果，所以答案为7。

三、递减问题接下来我们再来看一下递减问题，我们可以定义递减问题为：序列中的每一项都比前一项小的一类问题。

比如：问题：小明有20元，他买了一份价值8元的礼物，还剩多少钱？我们可以用列举法来解决这个问题：余下的钱020112我们可以发现，小明还剩12元，所以答案为12。

再来一个例子：问题：小红家里有20个苹果，每天都要吃掉1个，问几天之后，家里的苹果吃完？我们可以用列举法来解决这个问题：剩下的苹果数0201192183174165156147138129111010119128137146155164173182191200我们可以发现，家里的苹果在20天之后被吃完，所以答案为20。

四、总结通过以上列举法的例子，我们可以看出，列举法是一种非常简单易用的方法来解决递增递减问题。

在实际教学中，我们可以通过列举法的实例来培养学生的逻辑思维能力和数学分析能力。

同时，我们也可以适当引导学生自主探索和发现问题，帮助他们建立正确的数学思维方式，提高他们的自学能力和创新能力。

演出队列解题报告

《演出队列》解题报告题目描述今年是镇海中学的百年校庆。

校庆演出时，导演需要一列连续的身高递增的学生来演出一个节目。

现在有一列连续排列的学生，可以从这些学生中筛选掉最多一段连续的几个学生。

然后从剩下的学生中，选出连续的若干个，这些学生的身高依次连续递增。

求可以得到的身高连续递增队列的最大长度？输入输入文件第一行只有一个整数n。

第二行有n个正整数（互相之间以一个空格分隔），表示连续排列的每个学生的身高。

输出输出文件仅有一行，该行只有一个整数，表示符合要求的最长队列的长度。

样例输入13176 171 172 173 179 177 178 175 176 177 170 178 179样例输出6提示【样例说明1】筛选掉第5、6、7三个（179 177 178）后，得到长度最长的连续递增序列：171 172 173 175 176 177【样例输入2】10176 175 171 172 173 175 176 170 168 158【样例输出2】【样例说明2】长度最长的连续递增序列为第3-7个：171 172 173 175 176【数据说明】30%的数据n≤2070%的数据n≤200100%的数据n≤5000,高度不超过10^9。

本题考察点：动态规划、枚举暴力一开始，看到n≤5000，心里一直想着用O（nlogn）的算法，但发现很难实现，于是改用O（n^2)，心慌慌超时，后来发现，其实算法的复杂度不足o（n^2), 准确来讲，大约是n（n-1）/2，思路如下：以样例为例子首先，我们按照没有删去的，算出f[i]，f[i]表示以i结尾的最长上升数列阶段：一个数为一个阶段动归三要素：状态：以i结尾的最长上升数列转移方程：if a[i-1]<a[i] thenf[i]:=f[i-1]+1elsef[i]:=1;最后找出f数组中的最大值，存在ans变量里i，j是两个指针，用来枚举删掉的数列，i从2到n-1，表示要删的数列的最左边的数，j从i到n-1，表示要删的数列的最右边的数，很显然，删去最左，最右两个数是毫无意义的，这样不能使最大长度变大，所以也不用考虑，省点时间for i:=2 to n-1 dofor j:=i to n-1 do紧接着，我们来思考，为什么要删除一段数：很显然，删除一段数，是为了让取的数列变长，怎么样才能变长呢？只有当删除数列的两端的数a[i-1]与a[j+1]满足a[i-1]<a[j+1]时，即左右两边的上升数列可以拼成一个数列时，最长上升数列才可能会变大，所以，当a[i-1]>=a[j+1]时，无需考虑那么，如果满足上述条件，我们应该如何处理呢？这里我们以样例来说明如图：当i,j的位置如图所示时，删除的数列为179,177,178，此时发现，满足条件，则计算拼接后的上升数列的长度。

递增有序顺序表的插入解题思路

递增有序顺序表的插入解题思路全文共四篇示例，供读者参考第一篇示例：递增有序顺表是一种特殊的顺序表，其中存储的元素是按照递增顺序排列的。

在递增有序顺表中插入元素是一个常见的操作，但是需要特别注意保持顺序表的有序性。

下面我将详细介绍关于递增有序顺表的插入解题思路。

我们需要明确递增有序顺表的特点，即表中元素是按照递增顺序排列的。

当插入一个新元素时，需要找到合适的位置将该元素插入进去，同时保持表的有序性。

插入操作可以分为两种情况：一种是插入的元素比表中所有元素都大，此时直接将新元素插入到表的末尾即可；另一种情况是插入的元素需要插入到表中间某个位置，这时需要找到合适的位置将新元素插入进去。

在找到合适的插入位置后，我们需要将插入位置后的元素依次后移，腾出插入位置。

这个过程需要谨慎处理，确保元素的顺序不会被打乱。

在实际的插入操作中，还需要考虑边界情况。

当插入的元素比表中所有元素都小，或者表已满时，需要做出相应的处理，避免出现越界或溢出的情况。

递增有序顺表的插入操作需要注意以下几点：1. 确定插入位置：根据插入元素的大小，找到合适的插入位置。

2. 移动元素：将插入位置后的元素依次后移，腾出插入位置。

3. 处理边界情况：考虑插入元素比表中所有元素都小或大、表已满等情况，做出相应处理。

4. 保持有序性：在插入操作过程中，确保表的有序性不会被打乱。

递增有序顺表的插入操作是一个相对简单但需要细心处理的过程。

通过合理的算法设计和实现，可以确保插入操作的准确性和高效性。

希望以上内容对你理解如何在递增有序顺表中进行插入操作有所帮助。

第二篇示例：递增有序顺表是指表中元素按照升序排列的顺序表，插入操作是在有序表中插入一个新的元素，并保持有序性。

插入元素的操作在实际的程序设计中非常常见，因此掌握递增有序顺表的插入解题思路对于数据结构和算法的学习至关重要。

本文将详细介绍递增有序顺表的插入操作的具体实现思路。

我们需要了解顺序表的基本概念。

java最长递增子序列题解

java最长递增子序列题解
Java最长递增子序列问题是一个经典的算法问题，它要求在一个给定的序列中找到一个最长的递增子序列。

这个问题有多种解法，其中最常用的是动态规划算法。

动态规划算法的基本思想是将一个大问题分解成若干个小问题，然后通过求解小问题的解来推导出整个问题的解。

在Java最长递增子序列问题中，我们可以将问题分解成以每一个元素结尾的最长递增子序列的长度，然后通过求解每一个以元素结尾的最长递增子序列的长度来推导出整个序列的最长递增子序列的长度。

具体来说，我们可以定义一个数组dp，其中dp[i]表示以序列中第i个元素为结尾的最长递增子序列的长度。

对于元素i，我们可以从1到i-1枚举前面的所有元素j，如果j比i小且dp[j]的值加上1大于dp[i]的值，那么dp[i]的值就更新为dp[j]+1。

最终，整个序列的最长递增子序列的长度就是dp数组中的最大值。

在实际的实现中，我们还需要注意一些细节问题。

例如，我们需要在dp数组中初始化每一个元素的值为1，因为每个元素本身也可以构成一个长度为1的递增子序列。

另外，我们还需要记录最长递增子序列的具体内容，可以使用一个数组path来记录每个元素的前驱元素的下标，最后再根据path数组构造出最长递增子序列即可。

总的来说，Java最长递增子序列问题是一个经典的算法问题，它可以帮助我们提高对动态规划算法的理解和应用能力。

如果您感兴趣，可以尝试自己编写实现代码，并进行更深入的研究和探索。

单调递增子序列详解及实现(nlogn)

最长不下降子序列的O(n*logn)算法分析如下：设 A[t]表示序列中的第t个数，F[t]表示从1到t这一段中以t结尾的最长上升子序列的长度，初始时设F [t] = 0(t = 1, 2, ..., len(A))。

则有动态规划方程：F[t] = max{1, F[j] + 1} (j = 1, 2, ..., t - 1, 且A[j] < A[t])。

现在，我们仔细考虑计算F[t]时的情况。

假设有两个元素A[x]和A[y]，满足(1)x < y < t(2)A[x] < A[y] < A[t](3)F[x] = F[y]此时，选择F[x]和选择F[y]都可以得到同样的F[t]值，那么，在最长上升子序列的这个位置中，应该选择A[x]还是应该选择A[y]呢？很明显，选择A[x]比选择A[y]要好。

因为由于条件(2)，在A[x+1] ... A[t-1]这一段中，如果存在A[z]，A[x] < A[z] < a[y]，则与选择A[y]相比，将会得到更长的上升子序列。

再根据条件(3)，我们会得到一个启示：根据F[]的值进行分类。

对于F[]的每一个取值k，我们只需要保留满足F[t] = k的所有A[t]中的最小值。

设D[k]记录这个值，即D[k] = min{A[t]} (F[t] = k)。

注意到D[]的两个特点：(1) D[k]的值是在整个计算过程中是单调不上升的。

(2) D[]的值是有序的，即D[1] < D[2] < D[3] < ... < D[n]。

利用D[]，我们可以得到另外一种计算最长上升子序列长度的方法。

设当前已经求出的最长上升子序列长度为len。

先判断A[t]与D[len]。

若A [t] > D[len]，则将A[t]接在D[len]后将得到一个更长的上升子序列，len = len + 1， D[len] = A [t]；否则，在D[1]..D[len]中，找到最大的j，满足D[j] < A[t]。

几何级递增问题

262144
6710886 4 1717986 9184 4398046 511104 1125899 9068426 24 2882303 7615171 1744
524288
1048576
2097152
5368709 12 1374389 53472 3518437 2088832 9007199 2547409 92 2305843 0092136 93952
……
京级
兆级亿级
万级
个级
3689 3488 1474 1910 3232
2、36893488147419103232粒小麦到底有多重呢？
据调查：如果按每粒小麦0.1克计算，这些小麦的质量是多少千克？ 36893488147419103232×0.1÷10 00 =3689348814741910.3232(千克)
乐清丹霞路小学毛裕长
小课题研究
一、发现问题和提出问题只有善于发现和提出问题的人，才能产生创新的冲动。（爱因斯坦）二、分析问题和解决问题 1、制定研究方案(计划)——准备从哪几个方面第一步先研究什么？第二步再研究什么？第三步还要研究什么？ …… 2、进行探究——根据方案进行探究 3、得出结论 4、应用三、总结——撰写数学小论文、数学日记、报告等
几何级数的现象与应用?101024?201048576第六章为将来预备足够用的金钱几何递增法月份101112人民第六章为将来预备足够用的金钱几何递增法月份1632月份101112人民币6412825651210242048合计4095元你准备如何写小论文题目作者研究背景发现问题和提出问题为什么研究
“微”小课题研究之——几何级数问题
13421772 2684354 8 56 34359738 6871947 368 6736 87960930 1759218 22208 6044416 22517998 4503599 13685248 6273704 96 57646075 1152921 23034234 5046068 88 46976