自平衡车模型分析
平衡车分析报告

平衡车分析报告一、引言平衡车,又称为电动平衡车或者个人平衡车,是一种以电动机和陀螺仪等控制元件为基础,通过感应身体的重心变化来实现平衡的交通工具。
近年来,随着科技的不断进步,平衡车越来越受到人们的关注和喜爱。
本文将通过对平衡车的分析,探讨其原理、应用领域以及未来发展方向。
二、原理分析平衡车的平衡原理主要基于陀螺仪和加速度传感器的配合。
陀螺仪感知车身的倾斜角度,再通过控制系统调整电动机的转速,使车身保持平衡状态。
加速度传感器则用于感知车辆的前后倾斜,从而控制车辆的前进和后退。
这种基于重心倾斜的控制方式,使得平衡车可以有效地实现平稳行驶。
三、应用领域 1. 个人代步工具:平衡车作为一种便携式交通工具,被广泛应用于个人代步。
它的小巧灵活,适合在狭小的空间中使用,例如校园、工厂、商场等场所。
2. 旅游观光:许多旅游景区开始引入平衡车作为旅游观光工具。
游客可以骑着平衡车游览,既方便快捷又环保节能。
3. 物流配送:平衡车在物流配送领域也展现出了巨大潜力。
配备货架的平衡车可以轻松穿梭于仓库之间,完成货物的装载和运输工作。
四、市场现状目前,平衡车市场呈现出快速增长的趋势。
随着人们对便捷出行方式的需求不断增加,平衡车作为一种时尚、环保的交通工具受到了广大消费者的追捧。
同时,技术的不断进步也使得平衡车的性能得到了显著提升,更加安全、稳定。
预计未来几年,平衡车市场将继续保持高速增长。
五、发展趋势 1. 智能化:随着人工智能技术的发展,未来的平衡车将更加智能化。
通过加入智能导航、语音控制等功能,使平衡车更加智能化、人性化。
2. 多样化:平衡车的外观设计将更加多样化,以满足不同消费者的个性化需求。
同时,不同型号的平衡车将针对不同场景和用户需求进行专门设计,提供更多选择。
3.安全性:未来平衡车将更加注重安全性,例如加入碰撞预警、紧急制动等功能,提高车辆的安全性能。
六、结论平衡车作为一种新兴的个人交通工具,具有广阔的市场前景和发展潜力。
自动搜索平衡车的两种数学模型

一、研究背景及意义自动搜索平衡车的两种数学模型。
它是用小车及车上倒置的摆模拟控制火箭垂直起飞的装置。
外力u(t)目的使摆保持与车身垂直。
火箭起飞阶段必须维持与地面垂直,待到达指定速度和高度后才开始转弯。
倘若火箭在起飞阶段受侧风干扰,火箭轴线偏离铅垂线一个小角度,则在重力作用下偏离角度会越来越大最终导致发射失败。
为防止失败.在火箭轴线刚偏离垂直位置时,应启动发动机产生横向力校正火箭位置使其与地面垂直。
为使问题简化,设车与摆只在平面内运动并忽略杆的质量,电机本身的惯性,摩擦,风力等因素,设摆球质量为m ,车质量为M ,摆长为l 。
二、建模机理令H(t)和V(t)分别是小车通过铰链作用于杆也就是作用于摆球的水平分力和垂直分力。
当然杆通过铰链作用于车的反作用力为—H(t)和—V(t)。
应用牛顿定律得到:小车水平方向)()()(y t H t u t M -=。
(2-1) 摆水平方向2......22)(sin cos )sin ()(θθθθθml ml y m l y dt d m t H -+=+= (2-2)摆垂直方向)cos ()(22θl dtd m mg t V =- 2...)(cos sin θθθθml ml --= (2-3)力的分解θθcos sin )()(=t V t H (2-4) 将式(2)带入式(1)得到)()(sin cos )(2.....t u ml ml y m M =-++θθθθ将式(2-2)、(2-3)代入式(2-4)得到θθθθθθθθθθcos sin )(cos sin )(sin cos ..2.....2...=---+l l g l l y 三、模型简化上面两式均系非线性方程。
该系统目的在于控制摆与地面垂直,可以认为θ(t)和)(t 。
θ都接近于零。
在此假设下,取sin θ(t)≈θ(t),cos θ(t)≈l ,同时略去此θ(t),)(t 。
θ更高阶的无穷小量,经过如此线性化后得到)(....t u ml y m M =++θ)( (2-5) 0....=-+θθg l y (2-6)对式(5)和式(6)等号两边分别取拉氏变换并令初始条件为零便求出由u (t )到y(t)的传递函数)(g s yu 和由u(t)到θ(t)的传递函数)(s g uθ分别如下:])([)(222g m M Mls s g ls s g yu +--= (2-7)gm M Mls s g u )(1)(2+--=θ (2-8)或者写为)()()()()(s u s s s s y g g u yu ⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡θθ (2-9)式(9)是系统频域中输入一输出描述式,为了推导它的动态方程式选取相变量作为状态变量,即 y x=1,。
双轮自平衡小车的动力学建模与分析

双轮自平衡小车的动力学建模与分析作者:孙阳辛颂雷荣芳张忠秋胡琴芳来源:《硅谷》2014年第05期摘要双轮自平衡小车本身具有不稳定、非线性等特点,使得对双轮自平衡小车的控制变得相当复杂。
文章从双轮车结构出发,利用牛顿法建立数学模型,归一化处理后得到系统线性化模型,便于之后对双轮自平衡的仿真与控制。
关键词双轮自平衡小车;本质不稳定;数学模型;牛顿法中图分类号:TP242 文献标识码:A 文章编号:1671-7597(2014)05-0170-02近些年来,对移动机器人的研究越来越深入,其应用领域越来越广泛,具有广阔的研究背景。
双轮车是一种本质不稳定的特殊的轮式移动机器人,具有多变量、非线性等特征,对它的控制也比较复杂。
文章从双轮车结构出发,利用牛顿力学建立数学模型,之后进行归一化处理,最终得到了系统的线性化模型,便于进一步对双轮自平衡小车进行控制。
1 系统模型建立1.1 车轮模型以两轮轴线方向为x轴,车体前进方向为y轴,过车轮轴中点竖直向上为z轴,建立坐标系。
以右侧车轮为例,对其进行受力分析,如图1所示。
图1 两轮车右轮受力分析根据牛顿力学方程,我们可以得到:(1)(2)同理,我们可以得到左轮的平衡方程:(3)(4)其中:是车轮的质量,为轮子的半径,是车轮的转动惯量,,分别为左右车轮的线加速度,,为左右轮与地面的摩擦力,,是左右轮水平方向的作用力,,是左右轮的角加速度,,分别为左右轮的转矩。
1.2 车身模型平衡车车身的运动由绕车轴的相对转动和沿y轴方向的平动两部分构成,假设平衡车车身的倾角为,我们建立了平衡车车身的模型图(如图2所示)。
图2 两轮车车身的受力分析我们可以得到车身的平衡方程:(5)其中:(6)(7)车体的和外力矩:(8)其中:是除车轮外车身部分的质量,是车轮的平均位移,分别是左右轮的位移,,是质心的水平位移和线加速度,为车体质心到车轮轴的距离,是车身倾斜的角加速度,是左右轮竖直方向的作用力,是车体的转动惯量。
自平衡独轮车动力学模型的建立

2 自平衡独轮车动力学模型的建立2.1 自平衡的原理动态平衡原理即为自平衡独轮车的工作原理。
通过运动补偿算法,运用加速度传感器和陀螺仪对车体姿态测试,同时借助精密的伺服控制系统高敏地对电机进行驱动,并作适度的调节,从而使整个车体的平衡性以及稳定性得到确保。
由图 2.1能够得出,自平衡独轮车的车体摆动和它的转动是存在一定分离性的,驾驶人员的两腿将车身的两端夹紧,进而和车体产生了一个整体。
一旦其身体倾向后方,那么驱动车轮就会朝后转,从而防止车体倒向后方;反之,若是朝前,那么车轮就会朝钱转;若其身体处于竖直状态,那么则独轮车也就表现为动态平衡。
独轮车控制系统的重中之重就是平衡控制。
就自平衡独轮车加以建模并做深度分析,便能够对系统的特性产生更多的了解,这对于相应控制算法的设计规划甚为有益。
图2.12.2动力学建模2.2.1 物理模型化简自平衡独轮车不是平面机构,需要采用空间坐标的方式对其进行分析,坐标定义可详见图2.2,能够看出其自由度共有6个,其中平移、旋转各为3个。
俯仰角Ψ、横滚角γ、偏航角Φ均为其旋转姿态角。
因为独轮车的左右方向以驾驶者自身的调节为主,只能够控制前方和后方,故而把模型简单化至x o z平面,仅对这两个方向上的平衡控制进行探讨。
图2.2运动学是力学的一个分支,主要是站在几何的视角上来对物体位置伴随时间的波动规律进行阐述及探究的,刚体的运动学以对其自身的运动特性的研究为主,譬如转动经过、位移、角速度及其加速度等。
由于有部分难以测得的因素存在于独轮车的机械零件以及运动经过当中,因而必须对其做简化建模,因此作如下假设:1驾驶者和独轮车运动相同,可将二者看成一个整体,假定是刚体;2行走轮为质心在圆心的空心圆环;3在独轮车行驶期间,车轮和地面从始至终都处于彼此接触的状态,且一直是纯滚动;4忽略其他摩擦和外界干扰。
基于以上条件,我们进行独轮车物理模型化简如图 2.3,Φ为车轮转过的角度,θ为车体的倾角。
两轮自平衡车横向动力学建模与控制研究进展

?执行机构与控制算法
当两轮车前进速度满足 ZJ#Z#Z4时"在外界扰动 下"具有一定的姿态回复能力% 而在两轮车实际行驶 过程中"速度并不能总是满足上述条件"如两轮车启动 时速度 Zb" eZJ% 为了使两轮车在更大的速度范围内 具备保持姿态平衡的能力"需要在两轮车车体上安装 驱动机构"以产生侧倾方向的力矩来维持两轮车姿态 平衡% 目前主要使用重量平衡体(转向控制器和控制 力矩陀螺仪 % 种驱动机构% ?重量平衡体控制
熊宇聪等两轮自平衡车横向动力学建模与控制研究进展
两轮车在加速度作用下达到一定车速时"还需考虑空 气阻力&#< A#8' %
两轮车横向动力学模型除了受到加速度影响外" 还受到轮胎顺应性的影响% 轮胎顺应性主要影响两轮 车的抖动运动(侧滑运动和高速运动&#=' %
@D*)NWD&#&' (L-(D.F 和 VK.*4	' "以及 ?7_),+&#$' 等 人对两轮车轮胎顺应性影响进行了相关研究% 研究表 明轮胎的顺应性导致轮胎受力情况复杂"其受力不仅 取决于轮胎侧滑位移的大小和轮胎的柔性"还取决于 轮胎框架的刚度%
图 ! HD,ID((-AY4/^^()模型特征根 E/J7,)!aH4D,D*+),/M+/*,--+M-GHD,ID((-AY4/^^()Q-F)(
HD,ID((-AY4/^^()模型描述了两轮车匀速直线行 驶过程中"受到外力矩扰动时的姿态动力学性质% 但 是该模型成立的假设条件有一定的局限性"如未考虑 前向加速度与轮胎顺应性对两轮自平衡车姿态动力学 模型的影响等% !&"?7,89,::; < =>?@@:A 扩展模型
平衡车分析报告

平衡车分析报告1. 引言本文旨在对平衡车进行全面的分析和评估,深入探讨其原理、应用以及市场前景。
平衡车,又称为电动平衡车或自平衡车,是一种新型的个人交通工具。
它采用借助陀螺仪、加速度计和控制系统等技术,实现了自平衡行驶。
本文将从技术原理、市场需求和未来发展方向等多个角度进行分析。
2. 技术原理平衡车的核心技术原理是借助陀螺仪和加速度计实现自平衡。
陀螺仪用于检测车身的倾斜角度,而加速度计用于检测车身的加速度。
通过实时监测和分析这些数据,控制系统能够根据车身的倾斜程度和加速度来调整电机的转速,实现平衡行驶。
同时,平衡车还配备了高精度的传感器和执行器,以实现精确的控制和操控。
3. 应用领域平衡车在个人交通、巡逻、物流配送等领域具有广泛的应用前景。
首先,平衡车作为一种便携、环保的交通工具,可以在短距离出行时替代传统的步行、自行车等方式,提高出行效率。
其次,平衡车还可以应用于巡逻和安防领域,搭载摄像头和传感器等设备,实现对于区域内的监控和巡逻。
此外,平衡车还可以用于物流配送,提高效率和降低成本。
4. 市场需求目前,随着城市化进程的加快和个人出行需求的增加,市场对于个人交通工具的需求不断增长。
平衡车作为一种绿色、便携、智能的出行方式,受到了越来越多消费者的青睐。
而且,平衡车的成本也在逐渐降低,使其更加普及化。
在未来,随着技术的进一步发展和成本的进一步降低,市场对平衡车的需求将会进一步增加。
5. 发展趋势随着人们对于便捷出行和智能交通的需求增加,平衡车的发展前景十分广阔。
未来,平衡车有望实现更加智能化和人性化的设计。
例如,可以通过增加自动导航和智能避障功能,使平衡车更加方便、安全地应用于城市道路。
同时,随着电池技术的进步,平衡车的续航能力将会不断提升,进一步增加其可靠性和实用性。
6. 结论综上所述,平衡车作为一种新兴的个人交通工具,具有广阔的市场前景和发展空间。
其核心技术原理以及多种应用领域使其成为了一种受欢迎的出行方式。
两轮平衡小车数学建模

两轮平衡小车数学建模为了实现两轮平衡小车的稳定运动,我们需要进行数学建模和控制算法设计。
本文将从数学模型的角度来探讨如何建立一个能够实现平衡的两轮小车。
两轮平衡小车是一种基于动力学原理实现平衡的机械设备。
它具有广泛的应用前景,如智能运输、仓储管理等。
在该项目中,我们将通过数学建模的方式,研究并实现两轮平衡小车的控制系统。
2. 小车的动力学模型小车的动力学模型是建立控制算法的基础。
我们首先需要考虑小车的运动姿态,它由车身的倾斜角度和角速度来描述。
2.1 车身的倾斜角度小车的倾斜角度决定了小车的平衡状态,通过使用传感器可以测量到倾斜角度。
我们将倾斜角度表示为θ,正值表示小车向前倾斜,负值表示小车向后倾斜。
2.2 角速度角速度是小车旋转的速度,用ω来表示。
正值表示小车顺时针旋转,负值表示小车逆时针旋转。
3. 控制算法设计为了使小车保持平衡,我们需要设计一个有效的控制算法。
基于小车的动力学模型,可以采用PID控制算法进行设计。
3.1 比例控制比例控制是根据小车的倾斜角度进行调整,使小车趋向于平衡状态。
比例控制的输出与倾斜角度成正比,通过调整比例系数可以控制控制器的灵敏度。
3.2 积分控制积分控制主要用于消除比例控制带来的静差。
通过积分小车倾斜角度的累积误差,来调整控制器的输出。
3.3 微分控制微分控制可以预测小车倾斜角度的变化趋势,通过调整微分系数,可以使控制器对倾斜角度变化的响应更加迅速。
4. 仿真实验与实际实现为了验证控制算法的有效性,我们可以进行仿真实验,并将算法运用到实际的两轮平衡小车中。
4.1 仿真实验通过使用MATLAB等数学仿真工具,可以建立小车的动力学模型,并进行控制算法的仿真实验。
通过分析仿真结果,我们可以得出控制算法参数的优化值。
4.2 实际实现将控制算法应用到实际的两轮平衡小车中,需要搭建硬件平台和编写相应的控制程序。
通过实际实现,我们可以验证控制算法在真实环境中的有效性。
本文以两轮平衡小车的数学建模为主题,从小车的动力学模型出发,讨论了控制算法的设计和实现。
平衡车运动方程

平衡车运动方程一、平衡车运动方程平衡车是一种无人驾驶的车辆,它通过电机、传感器和控制器来实现自动平衡和控制。
它的运动方程描述了平衡车的运动规律,是平衡车运动控制的基础。
1、动力学模型平衡车的动力学模型可以表示为:M(θ)*ddθ/dt^2 + C(θ,dθ/dt)*dθ/dt + G(θ) = T(t)其中,M(θ)是平衡车的转动惯量,C(θ,dθ/dt)是惯性阻尼系数,G(θ)是重力力矩,T(t)是电机的输出力矩。
2、状态空间模型由于平衡车的运动是非线性的,因此可以使用状态空间模型来描述它的运动规律:x′ = Ax + Bu其中,x′表示状态变量的导数,A是状态空间矩阵,B是输入矩阵,u是控制量。
3、控制方法控制平衡车的运动可以采用PID控制器,它能够根据设定的参数实现自动控制,从而达到自动平衡的目的。
PID控制器的运动方程为:u = Kp*e + Ki*∫e + Kd*(de/dt)其中,Kp、Ki和Kd是PID控制器的参数,e是误差,de/dt是误差的导数。
4、模型预测控制模型预测控制(Model Predictive Control,MPC)是一种基于模型的控制策略,它能够根据模型预测系统未来的状态,从而实现预测控制。
MPC的运动方程为:u = argmin (Kp*e + Ki*∫e + Kd*(de/dt))其中,Kp、Ki和Kd是MPC控制器的参数,e是误差,de/dt是误差的导数。
5、综合控制综合控制是将PID控制、模型预测控制和其他控制方法结合起来,使用多种控制策略实现自动控制的方法。
综合控制的运动方程为:u = f(Kp*e + Ki*∫e + Kd*(de/dt),A,B)其中,Kp、Ki和Kd是PID控制器的参数,e是误差,de/dt是误差的导数,A和B是状态空间矩阵和输入矩阵。
二、总结以上就是平衡车运动方程的概述,它涉及到动力学模型、状态空间模型、PID控制、模型预测控制和综合控制等控制方法。
平衡车

车模的控制
数学模型: 根据切向加速度守恒:
X(t)为外力干扰引起的角加速度 当角度很小时,简化模型:
在该平衡控制中,与角度成比例的控制量称为比例控制,相当于回复力 与角速度成比例的控制量称为微分控制,其中的微分参数相当于阻尼力。
总结控制平衡车直立的条件: 1、能够精确测量车模倾角和角速度的大小 2、能够控制车轮的加速度
模块篇:
检测模块:
(1)加速度传感器:
通过AD采样的电压信号可以算出倾斜角度
型号:MMA7260三轴速度计 灵敏度:800mv/g
加速度计测量信号值
(2)角速度传感器—陀螺仪:
角速度积分漂移现象
两个传感器进行信息融合
控制模块:
平衡车直立控制的基本框图
电路硬件模块:
(1)单片机最小系统 (2)陀螺仪与加速度计信号放大与滤波电路 (3)电机驱动模块 (4)电源供电模块 (5)其他通信、显示、监控等模块
成本预算:
车模: 两个传感器: 390元 60元
单片机最小系统板+调试器: 80+40=120元 电源模块: 电机驱动模块: 50元 120元
成员分工:
童国川:
郑俊超: 吴志乾: 沈邱红:
计划:
10.1~10.20:资料查找 10.21~10.30:材料购买 11.1~11.15:软件编程、调试
软件编程
软件编程 材料购买 硬件组装
11.15~11.20:报告撰写
徐文丽: 撰写报告
不同阻尼力下的单摆运动
车模受力分析: 通过控制车轮,使它做加速运动, 给车子提供一个额外的惯性力,该 力与车轮的加速方向相反,能够为 车子直立提供回复力。
由于角度较小,这里做了近似处理
双轮自平衡小车的动力学建模与分析

参考 文献
力 争 优 化获 取 来 自于各 级 交 通管 理 部 门 的积 极 支持 , 针对 高速 公 路 通 信 网络 对 应 的 市场 化 运行 可 能 性展 开 深 化研 究 ; 基 于 我 国整 体 利益 的角 度 出发 , 杂牌 高 速 公路 建 设 进程 当 中所 敷设 的 通 信 管 道 隶属 于 社 会基 础 设 施 , 是 我 国重 要 的 战 略性 资 源 , 在 处 理 我 国通信 战 备 、 紧急 事 件 、安全 、灾 害 的 时候 占据着 重 要 的应 用 地位 , 使得 我 国国土 能够 更为 合 理 地 实施 开 发 , 可 将 该 项 工作 实施 作 为一 项 国家政 策提 出 , 结合 实 际 的市场 经济 规律 , 根 据 实 际现 状 , 放 眼未 来 , 构 建 我 国安 全 稳 定 的通 信 走 廊 ; 努 力 强 化 我 国高 速 公路 通 信 网络 技 术 力量 ,旨在 充 分 保 障 高速 公 路 联 网运 行 具 备 有较 高 的 稳 定性 , 结 合 现 今 高速 公 路 通信 联 网 建 设 发展 进 程状 况 , 针对 通 信 专业 人 员 培 训及 配 置 问题 进 行深 化 研 究 并给 予 相应 的解 决方 法 ;紧跟 时 代 潮流 , 充 分借 鉴 来 自 于 国外 先进 的技术 和 实践 经验 , 强 化相 互 问的 技术 交流 。
将 联 网监 控 以及政 务 信 息 、省 内联 网 收费 、应 急管 理 等类 型 的工 作 需 求作 为 关 键 的核 心 内 容 , 进而 推 动 高速 通 信 联 网 建 设, 为 充 分满 足 全 国 组 网需 求 则 需采 用 适合 的光 纤 芯线 ; 将 高
速 公路 通 信作 为 主 要 的通 信 平 台 , 积 极推 动 高 速 公路 信 息化 建 设进程 , 使 其 能够趋 向于信 息共享 整 合 、 综 合化 分析 、 挖 掘数 据 、 服 务 采 集 动态 信 息 等 方面 进 行 良性 发 展 ; 跟 踪 调查 我 国 高速 公 路 涉 及使 用 的通 信 资源 , 将 工作 重 点放 在光 缆线 路 及通 信管 道 、 传 输 系统 级技 术体 制 等方面 ; 深入 调查 研 究高 速公 路联 网需 求 ,
平衡小车设计报告

平衡小车设计报告
简介
平衡小车是一种能够自主保持平衡并在不同地面上移动的智能机器人。
本文将
介绍平衡小车的设计原理、结构、控制系统等方面的内容。
设计原理
平衡小车的设计原理基于控制系统对小车的动态稳定性进行控制。
通过在小车
主体上装配传感器和执行器,实现对小车倾斜角度的感知和控制,从而保持小车的平衡状态。
结构设计
1. 主体结构
平衡小车主体结构采用轻量化材料制作,以减少小车整体重量,提高机动性能。
主体结构通常包括底盘、电池仓、控制器安装板等部分。
2. 传感器部分
平衡小车的传感器部分包括倾斜角度传感器、加速度传感器等,用于感知小车
的倾斜状态并传输数据给控制系统。
3. 控制系统
平衡小车的控制系统采用微控制器作为核心控制单元,通过算法实现对小车的
倾斜角度进行实时调整,保持平衡状态。
控制系统设计
1. 控制算法
平衡小车的控制算法通常采用PID控制算法,通过对目标角度、当前角度和角
速度的比较,实现对小车的平衡控制。
2. 控制器选型
控制器选型考虑到性能、成本和稳定性等因素,选用适合的微控制器作为控制单元,以确保平衡小车的控制效果。
性能测试
平衡小车的性能测试主要包括速度测试、转向灵活性测试和稳定性测试等,以评估小车在不同场景下的运动性能和稳定性。
结论
通过对平衡小车的设计原理、结构、控制系统等方面的介绍和分析,可以看出平衡小车作为一种智能机器人具有广泛的应用前景。
未来可以进一步优化设计,提高性能,拓展应用领域。
以上是对平衡小车设计的报告内容,希望能对您有所帮助。
平衡车模型分析报告

平衡车模型分析报告1. 引言平衡车作为一种人力控制的交通工具,近年来越来越受到人们的关注。
其独特的设计和功能使得它成为了许多人的选择。
本报告旨在对平衡车的模型进行分析,探讨其原理和机制,并提供相关的模型分析结果。
2. 平衡车的原理和机制平衡车的原理和机制基于倒立摆的控制理论。
倒立摆是一个具有两个自由度的非线性动力学系统,通过控制系统使得摆杆保持竖直状态。
平衡车可以在两个轮子上实现这种倒立摆的稳定。
平衡车的控制系统通常由以下几个组成部分组成:2.1 传感器系统传感器系统用于感知平衡车的姿态和环境信息。
常见的传感器包括陀螺仪、加速度计和磁力计。
陀螺仪用于测量平衡车的角速度,加速度计用于测量平衡车的加速度,磁力计用于测量平衡车的方向。
2.2 控制算法控制算法是平衡车实现倒立摆稳定的关键。
常见的控制算法包括PID控制器和模糊控制器。
PID控制器通过调节控制器的比例、积分和微分系数来实现控制。
模糊控制器通过模糊推理和模糊规则来实现控制。
2.3 电机系统电机系统用于控制平衡车的速度和方向。
通常使用直流有刷或无刷电机作为平衡车的驱动电机。
电机系统通过调节电机的电流来实现对平衡车的控制。
3. 模型分析结果我们基于上述原理和机制对平衡车进行了建模和分析,得出以下模型分析结果:3.1 平衡车的动力学模型平衡车可以用一个二自由度倒立摆模型来描述其动力学行为。
该模型由两个非线性微分方程组成,描述了平衡车在不同时间和位置的姿态和速度。
3.2 平衡车的控制算法我们针对平衡车的控制系统设计了一个PID控制器算法。
该算法通过测量平衡车的姿态和速度,并通过调节控制器的参数来实现对平衡车的稳定控制。
3.3 平衡车的性能分析我们对平衡车的性能进行了分析,包括其稳定性、响应速度和能耗。
通过模拟实验和仿真分析,我们得出了平衡车在不同工况下的性能指标。
4. 结论通过对平衡车模型的分析,我们深入理解了平衡车的原理和机制。
我们设计了一个PID控制器算法,并对平衡车的性能进行了评估。
自平衡小车数学模型

自平衡小车数学模型2.3.1两轮自平衡小车受力分析为了准确控制车轮转动,保持小车始终稳定的直立平衡,需要对自平衡车进行运动学分析并建立其数学模型,从而更好的设计控制系统。
为了更加直观的分析系统受力情况,下面将直立小车与单摆模型进行对比说明小车的受力情况。
重力场中使用细线悬挂的重物经抽象化便形成理想化的单摆模型,两轮自平衡车可以看作一级倒立摆模型进行分析,如图2-3所示。
单摆模型一级倒立摆模型图2-3 小车抽象为一级倒立摆模型对普通单摆进行受力分析如图2-4所示。
mg=图2-4 单摆受力分析当物体离开平衡位置后便会受到重力与线的合作用力,驱使物体回复至平衡位置。
这个力称为回复力,其大小为:=F m gθ-s in(式2-1)在偏移角很小情况下,回复力与偏移角之间的大小成正比,方向相反。
在此回复力的作用下,单摆进行周期运动。
由于空气阻力的存在,单摆最终会停止在平衡位置。
空气阻尼力与单摆的速度成正比,方向相反。
阻尼力越大,单摆会越快停止在平衡位置。
可得出,单摆保持平衡的条件有两点:(1) 受到与偏移相反的回复力作用;(2) 受到与运动速度相反的阻尼力作用。
如果没有阻尼力,单摆会在平衡位置左右晃动而无法停止。
如果阻尼力过小(欠阻尼),单摆会在平衡位置震荡。
阻尼力过大(过阻尼)则导致单摆恢复平衡时间加长。
因而存在一个临界阻尼系数,使单摆稳定在平衡位置所需时间最短。
对静止的一级倒立摆模型进行受力分析(不考虑车轮与地面的滚动摩擦力),如图2-5所示。
θsin图2-5一级倒立摆模型受力分析图由一级倒立摆模型静止时的受力分析可知,其回复力大小为:=F m gθsin(式2-2)静止的倒立摆之所以不能像单摆一样可以稳定在平衡位置,是因为在偏离平衡位置时所受回复力与其偏移方向相同,而不是相反,因此不能回复至平衡位置,而是加速偏离垂直位置直至倾倒。
经分析可知,要控制倒立摆使其能够与单摆一样能够回复至平衡位置并保持稳定有两种方案。
自平衡车模型分析
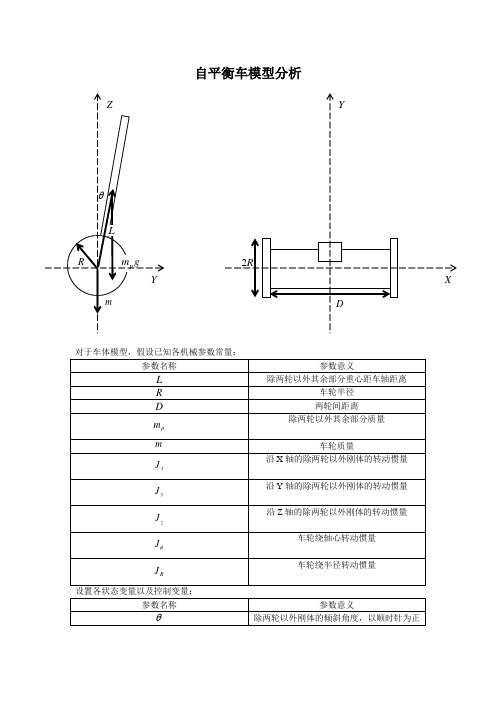
自平衡车模型分析设置各状态变量以及控制变量:一、 求解车体除两轮外部分动能车体沿X 轴方向速度:R L V R L x 2)(cos θθθθ&&&++= 车体沿Y 轴方向速度:R DL V RL y )(sin θθθ&&-=车体沿Z 轴方向速度θθsin &L V z =车体沿过质心的Z 轴的转动惯量为:m yz J J J y z z ⎰⎰⎰++=d sin cos 22θθθ由于假设车体关于ZY 平面对称,因此0d =⎰⎰⎰m yz 因此θθθ22sin cos y z z J J J +=则可以得到车体的平动动能:⎪⎪⎭⎫ ⎝⎛+-+++=2221)sin ())(sin ()2)(cos 21θθθθθθθθθ&&&&&&L R D L R L E R L R L kp ( 车体的转动动能为:⎪⎪⎭⎫ ⎝⎛+-+=22222))()(sin cos (21θθθθθ&&&x R L y z kp J R D J J E 则车体的总动能为:21kp kp kp E E E +=二、 求解车轮动能左车轮平动速度为:R V Lx w L θ&= 右车轮平动速度为R V Rx w R θ&=两轮有同样的绕垂直于半径的转动速度:R DRL w )(θθω&&-=则左车轮的动能为:222)(2121)(21⎪⎪⎭⎫ ⎝⎛-++=D R J J R m E R L R L L kw Lθθθθφ&&&&则右车轮的动能为:222)(2121)(21⎪⎪⎭⎫ ⎝⎛-++=D R J J R m E R L R R R kw Rθθθθφ&&&& 三、 求解车体势能由于在平地上行进,车轮势能不变。
全自主移动双轮平衡车轨迹规划及平衡特性分析

全自主移动双轮平衡车轨迹规划及平衡特性分析全自主移动双轮平衡车是一种动态稳定的轮式移动机器人,其近年来己成为机器人研究的一个热点。
与传统的静态轮式移动机器人相比,其机械本体通常被设计成高重心、小占地面积。
由于全自主移动双轮平衡车以倒立摆原理为基础,故需要不断消耗能量来维持自身平衡。
稳定性是全自主移动双轮平衡车必须具备的首要性能,其不仅表现在前进/后退等简单运动中,还在转向等复杂运动中更为重要。
因为全自主移动双轮平衡车通过两个同轴的电机的协作来控制其运动。
本研究课题以全自主移动双轮平衡车的结构为基础,分析其动力学和运动学特点,创新的利用轨迹规划的方法提高全自主移动双轮平衡车转向运动过程中的稳定性,使其以一较快的速度匀速沿既定轨迹曲线运动且无碰撞。
本课题的主要研究内容分为以下四个部分:1.建立全自主双轮平衡车动力学和运动学数学模型,以动力学模型为基础分析其平衡特性,通过运动学模型分析其在转向过程中临界倾斜情况下曲率与速度的关系,确定其运动轨迹的最大曲率值。
2.根据A*路径搜索算法生成轨迹的不连续性,提出基于A*算法的三次B-spline曲线轨迹规划方法。
在原有A*路径搜索算法生成无碰撞路径的基础上,利用三次B-spline曲线平滑路径,使得轨迹曲线具有C2连续性,避免了全自主移动双轮平衡车不停地在路径点处启动、停止和原地转向。
3.考虑到生成轨迹曲线可能与障碍物发生碰撞,以及曲率并不一定满足全自主移动双轮平衡车运动轨迹曲率的要求,提出基于控制点修正的曲线曲率控制方法。
首先对轨迹曲线进行碰撞分析,然后结合A*路径搜索算法和三次B-spline 曲线的性质,确定控制点移动位置,最终实现对轨迹曲线曲率的控制。
4.验证移动控制点控制轨迹曲线曲率方法可行性。
根据上述分析过程编写算法,并在 matlab 软件上进行仿真。
仿真结果表明,该方法可以有效地控制轨迹曲线曲率,使其满足全自主移动双轮平衡车最大曲率要求。
两轮自平衡车的设计研究

两轮自平衡车的设计研究首先,两轮自平衡车的设计中最重要的组件是姿态感知器和控制系统。
姿态感知器通过加速度计和陀螺仪等传感器来感知车辆的姿态变化,并将数据传递给控制系统。
控制系统根据这些数据来计算出应该施加的力矩,以保持车辆的平衡。
我们需要精确地设计和调整这些组件,以确保车辆能够稳定地保持平衡。
其次,两轮自平衡车的动力系统也至关重要。
目前常用的动力系统是电池供电的电动机。
电动机将电能转化为机械能,驱动车辆前进。
设计动力系统时需要考虑能量效率、稳定性和驱动力的大小。
另外,选择合适的电池类型和容量也是关键,以确保车辆的续航能力。
此外,两轮自平衡车的操控系统也需要设计和研究。
一个简单直观的操控系统可以提高用户体验,并减少操作难度。
常见的操控系统包括使用身体重心移动来控制车辆的前进、后退和转向。
此外,也可以考虑添加智能化的操控功能,如蓝牙连接手机进行远程操控等。
在结构设计方面,两轮自平衡车需要考虑车辆的稳定性和可靠性。
一个好的结构设计能够提高车辆的抗风性和减震性能。
此外,车辆的重心位置也需要合理安排,以减小车辆倾倒的风险。
最后,两轮自平衡车的安全性是设计中不可忽视的因素。
设备应具备紧急停止和防护措施,以防止意外伤害。
例如,可以在车辆上加装限位开关,在发生故障时停止电机的运转。
另外,可以考虑添加LED灯和蜂鸣器等装置,以提高车辆的可见性和警示效果。
总之,两轮自平衡车的设计研究涉及姿态感知器和控制系统、动力系统、操控系统、结构设计和安全性等多个方面。
通过合理设计和研究,可以提高车辆的平衡性、稳定性和安全性,进一步推动两轮自平衡车的发展和广泛应用。
自平衡独轮车动力学模型的建立

2 自平衡独轮车动力学模型的建立2.1 自平衡的原理动态平衡原理即为自平衡独轮车的工作原理。
通过运动补偿算法,运用加速度传感器和陀螺仪对车体姿态测试,同时借助精密的伺服控制系统高敏地对电机进行驱动,并作适度的调节,从而使整个车体的平衡性以及稳定性得到确保。
由图 2.1能够得出,自平衡独轮车的车体摆动和它的转动是存在一定分离性的,驾驶人员的两腿将车身的两端夹紧,进而和车体产生了一个整体。
一旦其身体倾向后方,那么驱动车轮就会朝后转,从而防止车体倒向后方;反之,若是朝前,那么车轮就会朝钱转;若其身体处于竖直状态,那么则独轮车也就表现为动态平衡。
独轮车控制系统的重中之重就是平衡控制。
就自平衡独轮车加以建模并做深度分析,便能够对系统的特性产生更多的了解,这对于相应控制算法的设计规划甚为有益。
图2.12.2动力学建模2.2.1 物理模型化简自平衡独轮车不是平面机构,需要采用空间坐标的方式对其进行分析,坐标定义可详见图2.2,能够看出其自由度共有6个,其中平移、旋转各为3个。
俯仰角Ψ、横滚角γ、偏航角Φ均为其旋转姿态角。
因为独轮车的左右方向以驾驶者自身的调节为主,只能够控制前方和后方,故而把模型简单化至x o z平面,仅对这两个方向上的平衡控制进行探讨。
图2.2运动学是力学的一个分支,主要是站在几何的视角上来对物体位置伴随时间的波动规律进行阐述及探究的,刚体的运动学以对其自身的运动特性的研究为主,譬如转动经过、位移、角速度及其加速度等。
由于有部分难以测得的因素存在于独轮车的机械零件以及运动经过当中,因而必须对其做简化建模,因此作如下假设:1驾驶者和独轮车运动相同,可将二者看成一个整体,假定是刚体;2行走轮为质心在圆心的空心圆环;3在独轮车行驶期间,车轮和地面从始至终都处于彼此接触的状态,且一直是纯滚动;4忽略其他摩擦和外界干扰。
基于以上条件,我们进行独轮车物理模型化简如图 2.3,Φ为车轮转过的角度,θ为车体的倾角。
两轮自平衡小车文档

四、演示算法:极点配置控制方法
Figure. 8
自平衡小车系统极点配置算法的 Simulink 框图
Figure. 9 小车的位移曲线
Figure. 10 小车系统的纵摇角曲线
一、两轮自平衡小车系统的特点
双轮自平衡小车是一种本质上不稳定的轮式机器人, 又称为两轮自平衡机器人。 两轮自 平衡小车模型与倒立摆模型很相似, 倒立摆的原理即为当摆倒向左边的时候, 角度编码器测 得摆杆不是竖直的而是有一定的角度, 把所得的角度反映给控制器, 为了维持摆与小车的相 对位置不变, 即摆的平衡状态, 这时根据现有摆杆角度而计算得到的控制力使小车同时向左 运动,这样就保持了系统的平衡。两轮自平衡机器人与倒立摆相似,也需要驱动电机来完成 两轮自平衡机器人是一类本 质上不稳定的移动机器人,其不稳定性、多耦合性、非线性、参数不确定性等特性,是验证 各种控制算法能力的优良装置。由于其自身体积轻巧,控制电压低,移动性能好,因此我们 可以在两轮自平衡机器人上验证我们所研究的控制算法。
系统二:左右转弯系统。
1 0 0 23.7097 0 0 0 83.7742
0 x 0 0 x 1.8332 C 1 0 0 4.9798
0 1 0 C 0 0 5.1915
Tilted
Figure. 1
Balanced
二、自平衡小车系统的结构和工作原理
Figure. 2
Figure. 3
Figure. 4
Figure. 5 两轮自平衡小车由以下几部分在组成: 带有每个轮子耦合到行星齿轮箱直流电动机的底 座,DSP 板用来实现控制,电动机的电力放大器,测量小车状态必要的传感器,无线电控 制单元接收器和垂直棒。电池固定在机器人内部,它们的重量可以模拟一个驾驶员。小车的 轮子直接连接在齿轮箱的输出轴上。控制软件使用在 Windows98/2000 上运行的 Matlab。使 用 Simulink 作为一个交互式的工具,用来建模,仿真和分析倒立摆系统。它能让你建立图 表,评估系统性能,改善你的设计。Matlab 仿真表明,控制一个两个轮子上各有一个发动 机的系统是确实可行的。为了成功地控制系统,要量化状态空间变量;或者直接测量,或者 通过适当的观测器。 直线位置和速度, 首摇角和速率可以很容易的由两个直流电动机上安装 的增量编码器决定(假定纵摇角和速率已知) 。纵摇速率由速率陀螺仪测量。控制系统是基 于两个不耦合的状态空间控制器:一个控制横轴周围的稳定性(纵摇) ,另一个控制纵轴上 的动态性(首摇) 。每个控制器输出一个转矩应用于它相关的轴线,一个去耦单元把这两个 信号转化为一个转矩分别应用于左边或者右边的发动机。 操作者通过无线电控制单元微系统 导航,对板上控制系统输送希望得到的直线速率和旋转速率。
自平衡车

一、基本原理[url=][/url]本项目机器人是一辆简易型的双轮自主平衡小车,通过一个简单的机械式传感器获取小车的姿态,并通过调节小车前后运动方向,使得小车依靠两轮也能保持一个直立平衡。
1、运动机理[url=][/url]双轮小车的自主平衡原理,其实就是不断的通过改变小车前后运动的方向,使小车的车身在竖直方向上保持一个动态的直立平衡。
就类似杂技演员表演独轮车一样,需要不断的前后踩脚踏板使小车在前进和后退间不断变换,以保持一个平衡。
这个具体的平衡原理如下:1、双轮自平衡小车一般长得都比较“高”,也就是重心位置比较高,位于车身底部的两个车轮是平行安装的,默认静止状态小车是无法保持一个直立的状态的。
2、如果车轮带动小车前进,小车下半身会比上半身先获得前进的加速度,即启动的瞬间小车的下半身前进而上半身静止,则会出现小车趋向后仰的状态。
就类似汽车突然加速,我们身体会感到一个后仰的趋势。
3、如果车轮带动小车后退,小车下半身会比上半身先获得后退的加速度,即启动的瞬间小车的下半身后退而上半身静止,则会出现小车趋向前倾的状态。
就类似汽车突然刹车(后退),我们身体会有一个前倾的趋势。
4、由于小车重心较高,如果小车前进--后仰,或者小车后退--前倾,随着小车的继续运动,这个后仰或者前倾的趋势会越来越大,必须及时纠正,否则小车就会倾倒下去。
5、如果小车前进中,有了后仰的趋势,达到一定程度后,可以让小车变成后退,让小车后退产生的前倾趋势去纠正原来前进时后仰的趋势;如果小车后退中,有了前倾的趋势,达到一定程度后,让小车变成前进,让小车前进产生的后仰趋势去纠正原来后退时前倾的趋势。
如此往复循环,使小车保持一个直立的动态平衡状态。
/0Mz-UObc2fXoMbbfWGoQAA==/28586 59863474816487.gif/0Mz-UObc2fXoMbbfWGoQAA==/28586 59863474816487.gif[/url]2、控制原理[url=][/url]根据以上平衡原理,我们的双轮自平衡小车的具体运动控制过程如下:1、车身后仰,则让小车后退,车身恢复直立;2、小车继续后退,车身又会前倾;3、车身前倾,则让小车前进,车身恢复直立;4、小车继续前进,车身又会后仰;5、重复以上第1步……对于小车后仰或者前倾趋势的纠正,必须及时需要在适当的时刻进行纠正,太早了可能小车过快变成相反状态无法控制;太晚了可能已经错过时机无法纠正最后导致小车倾倒下去了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自平衡车模型分析
一、
求解车体除两轮外部分动能
车体沿X 轴方向速度:
R L V R L x 2
)(cos θθθθ ++= 车体沿Y 轴方向速度:
R D
L V R
L y )(sin θθθ -=
车体沿Z 轴方向速度
θθ
sin L V z = 车体沿过质心的Z 轴的转动惯量为:
m yz J J J y z z ⎰⎰⎰++=d sin cos 22θθθ
由于假设车体关于ZY 平面对称,因此
0d =⎰⎰⎰m yz 因此
θθθ22sin cos y z z J J J +=
则可以得到车体的平动动能:
⎪⎪⎭
⎫ ⎝⎛+-+++=2221)sin ())(sin ()2)(cos 21θθθθθθθθθ L R D L R L E R L R L kp ( 车体的转动动能为:
⎪⎪⎭
⎫ ⎝⎛+-+=22222
))()(sin cos (21θθθθθ x R L y z kp J R D J J E 则车体的总动能为:
21kp kp kp E E E +=
二、
求解车轮动能
左车轮平动速度为:
R V L
x w L θ = 右车轮平动速度为
R V R
x w R θ =
两轮有同样的绕垂直于半径的转动速度:
R D
R
L w )(θθω -=
则左车轮的动能为:
2
22)(2121)(21⎪⎪⎭
⎫ ⎝⎛-++=D R J J R m E R L R L L kw L
θθθθφ
则右车轮的动能为:
222)(2121)(21⎪⎪⎭
⎫ ⎝⎛-++=D R J J R m E R L R R R kw R
θθθθφ 三、
求解车体势能
由于在平地上行进,车轮势能不变。
车体整体势能可变部分表示为:
θcos g m E p p =
四、
拉格朗日函数的求解
得到最终的拉格朗日函数为:
p kw kw kp kp E E E E E L L R -+++=21
依据拉格朗日动力学法求解,进行如下运算:
R L M M L dt L
d
--=∂∂-∂∂θ
θ L L
L
M L dt L
d
=∂∂-∂∂θθ R R
R
M L dt L d
=∂∂-∂∂θθ 得到动力学方程:
方程一:
()
R
L R L z y p p R L p x p M M R D J J L m gL m R L m J L m --=⎪⎪⎭
⎫ ⎝⎛--+--+++222
)(cos sin sin 2)(cos )θθθθθθθθθ (
方程二:
()
()
L
R L R L L R L z y p R L z y p R L p p p M D
R J J mR D R J J L m D
R J J L m R m LR m LR m =-+++--++-+++++-2
222222
2222222)(2)(cos sin 2)(cos sin sin 4)(sin 21cos 21θθθθθθθθθθθθθθθθθθθθφ
方程三:
()
()
R
R L R R R R L z y p R L z y p R L p p p M D
R J J mR D R J J L m D R J J L m R m LR m LR m =--++--+--++-++-2
222222
2222222)(2)(cos sin 2)(cos sin sin 4)(sin 21cos 21θθθθθθθθθθθθ
θθθθθθθθφ 五、
方程中各项的力学意义分析
方程一中:
θ
)2x p J L m +( 表示的是让车体产生θ 的角加速度,应该产生的合力矩为θ
)2
x p J L m +(,其中转轴为车轮中心。
R L m R
L p 2
)(cos θθθ +
是以车底盘为参考系而产生的非惯性力的力矩。
θsin gL m p
是重力产生的力矩。
(
)
2
2)
(cos sin ⎪⎪⎭
⎫ ⎝⎛--+R D J J L m R L z y p θθθθ 是离心力的力矩。
R L M M --
为电机产生的力矩。
方程二中:
对于轮子的受力分析中,由于车体自身有加速度以及角加速度,因此需要从轮轴给予车体一定的力产生加速度。
在轮子上,由于轮轴收到车体的反作用力,为了让轮子产生抵消车轮轴心收到的作用力,需要由地面给予车轮额外的作用力。
因而为了让车轮能够以预计的角加速度运转,力矩不仅要为角加速度提供力矩,还应克服地面产生的作用力的力矩。
θθcos 2
1 LR m p 为使车体产生水平加速度所需要的力对轮子产生的力矩,该加速度为转动速度改变造成
的加速度水平分量
4
)(2R m R
L p θθ +
为使车体产生水平加速度所需要的力对轮子产生的力矩,该加速度为底盘的加速度。
与
之前加起为总的水平加速度。
θθsin 2
12 LR m p 为车体离心力在水平方向产生的力矩
(
)
2
22
2
2
2
)(cos sin sin D
R J J L m R
L z y p θθθθθ -++ 是车体在XY 平面绕Z 轴旋转角加速度所需要的力矩转移到轮上的力矩。
所以在两个轮上方向不相同。
(
)
2
22
)(cos sin 2D R J J L m R
L z y p θθθθθ --+ 为使车体克服摆动造成的柯里奥利力力矩,而由轮子为车体提供力矩时,轮子收到的反作用力造成的力矩。
R
mR θ 2 为让车体产生R R
θ 的加速度所需要的力矩 R
J θφ 为让车体产生R
θ 的角加速度所需要的力矩 2
2)(2D
R J R
L R θθ - 为让车体产生绕半径转动的角加速度所需要的力矩 六、
控制矩阵
令:
(
)
222
222
2222
12cos sin sin 4
D
R J J mR D R J J L m R m K R z y p p ++++++=
φθθθ
(
)
22
222
2222
22cos sin sin 4
D
R J D R J J L m R m K R z y p p -++-=
θθθ
()
223)(cos sin sin ⎪⎪⎭
⎫ ⎝⎛--++=R D J J L m gL m K R
L z y p p θθθθθ
θθsin 2
124 LR m K p =
(
)
22
2
5)(cos sin 2D
R J J L m K R L z y p θθθθθ --+=
则有控制矩阵:
⎥⎦⎤⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+-=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥
⎥⎥⎥⎥⎥⎥⎦
⎤
⎢
⎢⎢⎢⎢⎢⎢⎣
⎡+R L R L p p p p x p M M K K K K K K K LR m K K LR m LR m LR m J L m 1001001100
2cos 02cos 00102cos 2
cos 05454312
212
θθθθθθθθ
此为非线性控制方程,可以用于matlab 仿真 将其在小角度线性化以后,得到:
⎥⎦⎤⎢⎣⎡⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎣⎡--+⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦
⎤
⎢
⎢⎢⎢⎢⎢⎢⎣
⎡+R L R L
p R L p p p p x p M M gL m K K LR m K K LR m LR m LR m J L m 1001001100
00000000100000
2cos 02cos 00102cos 2cos 012
2
12
θθθθθθθθθθθθ
(此文档部分内容来源于网络,如有侵权请告知删除,文档可自行编辑修改内容,
供参考,感谢您的配合和支持)。
