公交车调度方案的优化模型
可变线路式公交车辆调度优化模型

i ∈S
( ) 1
. t . s
∑x ∑x
, i j
/ { } S 1 = 1, j∈S / { S S} = 1, j∈S
( ) 2 ( ) 3 ( ) 4 ( ) 5 ( ) 6 ( ) 7 ( ) 8 ( ) 9 ( ) 1 0
, i j
T S S i∈ S i >A i +T s, e Pk ≤l k ∈ N1 ∪ N3 k ≤T k, T Pk < T Dk , k∈ N T Pk ≥ T Rk , k ∈ N1 ∪ N3 ) ≤C NB( t∈ ( 0, T) t B ,
0 引 言
随着经济的发 展 和 机 动 化 水 平 的 提 高 , 城市 交通拥堵问题也不断加剧 。 公共交通在道路交通 资源的充分利用上具有私人交通无法比拟的优越 性, 已经成为缓解道路交通拥堵的 1 条重要途径 。 ) 可变线路 式 公 交 ( 作为1种新 f l e x r o u t e t r a n s i t - 融合了常规公交运营模式 型公 交 运 营 模 式 , ( 的高成本效益以及需求响应式公交系统 F R T) ( ) 能够提供门到门的公交运输 D R T 的机动灵活 , 是解决城郊 地 区 公 交 服 务 问 题 的 1 条 重 要 服务 , 途径 。 可变线路式公 交 可 以 描 述 为 : 车辆在一定的 服务区域内围绕 基 准 线 路 运 行 , 并在松弛时间内 偏离基准路线行 驶 , 在乘客要求的地点停车上下 客 。 车辆行驶过 程 中 满 足 一 定 的 时 空 限 制 , 即车 辆驶离基 准 路 线 为 乘 客 提 供 站 外 上 下 车 服 务 之 需要返回基准线路继续行驶 , 并且满足线路上 后, 固定站点的时间约束 。 根据可变线路式公交乘客 的上下车位置可 以 将 其 分 为 4 类 : 站外上车站外 、 、 下车 ( 站内 上 车 站 外 下 车 ( 站外上车 I类 ) I I类 ) 。 站内下车 ( 和站内上车站内下车( I I I类 ) I V 类) 其运行模式见图 1, 其中 1 和s 为公交线路的首末 站。
城市公交调度优化模型及算法研究

号,标准容量相 同;
(1)一天当中,乘客因等车所损失 的总费用 :
(2)所有公交车辆均不准许越站和相互超车 ; (3)该线路可调配的公交车数量是一定 的;
K J
r=Cx ∑k=l∑_-l [ l L mk x ‘ ] I |
20t0.10《城市公获交遁》URBAN№ TRANSPORT
1 公 交发车 间隔优化模型的建立
费用 ;[ ]【 仅— — 乘客利益的权重 ;
B— — 运营公司利益的权重 ;
1.1 模型假设
其 中,仪+13=l。
1.3 目标 函数
(1)该公交线路上运行 的公交 车辆均为 同一 型
平均 满 载 率 和全 天 总发 车 次 数 作 为 约束 。所 得优 化 结 果 ,既 减 少 了公 交公 司 的运 营成 本 ,又 节 约 了乘 客 的候 车时 间 , 能较 好 地 兼顾 乘 客及 运 营公 司 的利 益 。
关 键 词 :公交调度 ;公共 交通 ;优化模型;发 车间隔
中图分 类 号 :U492.4 12 文 献 标 识码 :A Study on Optimal Model and Algorithm for Bus Dispatching
注 :北 京 交通 大学 大 学 生创 新性 实验 计 划项 目资 助 项 目编 号 :0950034
但 目前 ,我 国的公共交通事业发展还比较落后 ,
公 交智 能化水平还 比较低 ,绝大部分是 旧的运行体
制。现行 的公交企业运营调度管理工作存 在很多问
题 :调度管理主要依靠人力 ,运营计划主要依靠调
uRBAN PUBLIC TR ̄SPORT《城市公蔌交运 》2010.10
公交车调度方案的优化模型

公交车调度方案的优化模型(一)本文通过对某市某条公交线路的客流调查和运营资料分析,建立公交车调度方案的优化模型,使公交公司在满足一定的社会效益和获得最大经济效益前提下,给出了理想公交车调度方案。
对于问题一,模型Ⅰ中建立了最大客容量,发车车次数的数学模型,运用决策方法给出了各时间段最大客容量数,在满足客车载满率及载完各时段所有乘客情形下,得出每天最少车次数为462次,最少车辆数为60辆;并给出了整分发车时刻表(见附件四)。
模型Ⅱ中,用层次分析法分析乘满意度为mc=w t mc mc ⨯+⨯6165 ,在公交车最大载客量分别为120、100、50时乘客和公交公司的满意度mc 、mg 。
拟合得出乘客及公交公司满意度对应的关系式,建立目标函数max=(mc+mg)-|mc-mg|,使双方满意度之和达到最大,同时双方满意度之差最小,得到上下行的最优满意度(0.8688,0.8688),此时公交车调度为474次50辆。
对于问题二,交待了综合效益目标函数及整数规划法求解流程。
公交调度 层次分析法 满意度 整数规划一、问题的重述公共交通是城市交通的重要组成部分,作好公交车的调度对于完善城市交通环境、改进市民出行状况、提高公交公司的经济和社会效益,都具有重要意义。
公交公司制定一个公交车调度方案需要考虑各方面的因素。
我国一座特大城市某条公交线路情况,一个工作日两个方向各个站上下车的乘客数量统计表如表1、表2所示。
已知运营情况与调度要求如下: (1)公交线路上行方向共14站,下行方向共13站。
(2)公交公司配给该线路同一型号的大客车,每辆载客100 人,据统计客车在该线路上运行的平均速度为20公里/小时,车辆满载率不应超过 120%,一般也不要低于50%。
(3)乘客候车时间一般不要超过10分钟,早高峰时一般不要超过5分钟。
需要解决的问题:(1)试根据这些资料和要求,为该线路设计一个便于操作的全天(工作日)的公交车调度方案,包括两个起点站的发车时刻表;一共需要多少辆车;这个方案以怎样的程度照顾到了乘客和公交公司双方的利益;等等。
公交车调度的优化模型

种 较 好 的解 决方 法 。本 文 以公 交公 司运 营 的 总 车 辆数 最 小 为 目标, 运 营 过 程 中满 足 各 方 需 求 的 车 辆 数 为 约 束 务 件 建 立 了优 化 模 型 模 型 实 以 现 了 对 线路 运 营 进 行 评 估 和 优 化 公 交 车 配 置 、 考 虑 了 乘 客 等 车 的 社 会 成 本 又 兼顾 了公 交 公 司 的 利 益, 法 易 于操 作 , 有 较 大 的 实 际 应 用 价 既 方 具
善城市交 通环境 、 改进市 民出行 状况 、 高公交公 司的经济 和社会 效 提 益, 都具有重要意义 。 下面考虑一条公 交线路上公 交车的调度问题 , 其 数 据 来 自我 国 一 座 特 大 城 市某 条公 交 线 路 的 客 流 调 查 和 运 营 资 料 。 该 条 公 交 线 路 上 行 方 向共 l 4站 , 行 方 向 共 l 下 3站 。 3 4页 给 第 - 出的是典型 的~个工 作 日两个运 行方 向各 站上下车 的乘 客数量统计 ( 数据从略) 。公交公司配给该线路同一型号的大客车 ,每辆标准载客 10人 , 0 据统计 客车在该线路上运行 的平均速度 为 2 0公里 、 运 营 时。 调度要求 , 客候 车时间一般不要超过 1 乘 0分钟 , 早高 峰时一 般不要超 过 5分钟 , 车辆满载率不应超过 10 一般也不要低 于 5 %。 2 %, 0 试根据这些 资料和要求 , 为该线路设计 一个便于 操作 的全天 ( 工 作 日) 的公 交 车 调 度 方 案 , 括 两 个 起 点 站 的 发 车 时 刻 表 : 共 需 要 多 包 一 少 辆 车 ;这 个 方 案 以 怎 样 的程 度 照 顾 封 了乘 客 和 公 交 公 司 双 方 的利 益: 等. 等 . 如何 将 这 个 调 度 问题 抽 象 成 一 个 明 确 、 整 的 数 学 模 型 。 出 求 完 指 解模 型的方法 ; 根据 实际问题 的要求 , 如果要设 计更 好的调度方案 , 应 如何 采集 运 营数 据 。
数学建模-公交车调度问题
第三篇公交车调度方案得优化模型2001年 B题公交车调度Array公共交通就是城市交通得重要组成部分,作好公交车得调度对于完善城市交通环境、改进市民出行状况、提高公交公司得经济与社会效益,都具有重要意义。
下面考虑一条公交线路上公交车得调度问题,其数据来自我国一座特大城市某条公交线路得客流调查与运营资料。
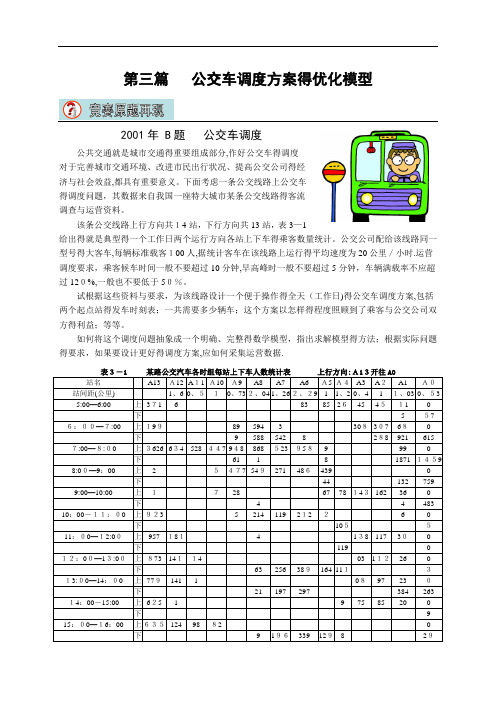
该条公交线路上行方向共14站,下行方向共13站,表3—1给出得就是典型得一个工作日两个运行方向各站上下车得乘客数量统计。
公交公司配给该线路同一型号得大客车,每辆标准载客100人,据统计客车在该线路上运行得平均速度为20公里/小时.运营调度要求,乘客候车时间一般不要超过10分钟,早高峰时一般不要超过5分钟,车辆满载率不应超过120%,一般也不要低于50%。
试根据这些资料与要求,为该线路设计一个便于操作得全天(工作日)得公交车调度方案,包括两个起点站得发车时刻表;一共需要多少辆车;这个方案以怎样得程度照顾到了乘客与公交公司双方得利益;等等。
如何将这个调度问题抽象成一个明确、完整得数学模型,指出求解模型得方法;根据实际问题得要求,如果要设计更好得调度方案,应如何采集运营数据.公交车调度方案得优化模型*摘要:本文建立了公交车调度方案得优化模型,使公交公司在满足一定得社会效益与获得最大经济效益得前提下,给出了理想发车时刻表与最少车辆数。
并提供了关于采集运营数据得较好建议。
在模型Ⅰ中,对问题1建立了求最大客容量、车次数、发车时间间隔等模型,运用决策方法给出了各时段最大客容量数,再与车辆最大载客量比较,得出载完该时组乘客得最少车次数462次,从便于操作与发车密度考虑,给出了整分发车时刻表与需要得最少车辆数61辆。
模型Ⅱ建立模糊分析模型,结合层次分析求得模型Ⅰ带给公司与乘客双方日满意度为(0、941,0、811)根据双方满意度范围与程度,找出同时达到双方最优日满意度(0、8807,0、8807),且此时结果为474次50辆;从日共需车辆最少考虑,结果为484次45辆。
公交车调度优化模型

公交车调度优化模型
何宝泉;吴斯浩;陆文辉;罗世庄
【期刊名称】《暨南大学学报(自然科学与医学版)》
【年(卷),期】2003(024)005
【摘要】提出了制定一条公交线路车辆调度方案的优化数学模型.该模型计算了乘客在车站等候的时间内所可能创造的财富--社会效益,并将乘客因候车而丧失创造该财富的机会看成一种社会成本.对车辆调度方案的评估时,不仅考虑了公司运营成本,而且考虑了相应的社会成本.因此,该模型制定的调度方案兼顾了公司利益和社会效益.最后将实际的统计数据带入模型,给出一个车辆调度发车时刻表的优化方案.【总页数】6页(P65-70)
【作者】何宝泉;吴斯浩;陆文辉;罗世庄
【作者单位】暨南大学统计系,广东,广州,510632;暨南大学统计系,广东,广
州,510632;暨南大学统计系,广东,广州,510632;暨南大学数学系,广东,广州,510632【正文语种】中文
【中图分类】O224
【相关文献】
1.公交车调度的优化模型 [J], 李传伟;叶红
2.基于候车与乘车满意度的公交车调度优化模型 [J], 姜少毅;王博;闫哲
3.公交车调度优化模型 [J], 李成功;脱小伟;郭尚彬;祁忠斌
4.可变线路式公交车辆调度优化模型 [J], 林叶倩;李文权;邱丰;丁钰玲
5.基于NSGA算法的公交车辆调度优化模型 [J], 宋晓鹏;韩印;姚佼
因版权原因,仅展示原文概要,查看原文内容请购买。
公交运营调度优化的评价指标模型研究

项 目( 0 7 A1 Z 0 ) 2 0 A 12 1 、
全 面 、 理 的特 点 。 由于公 共交 通涉 及 的 目标 、 合 因素 很 多 , 要对所 有 因素进行 有效 筛选 , 用定 性 与定 需 利 量 相结合 的方 法建 立一套 完整 的评 价 指标 体 系 。因
1 评价指标的确立的原则和方法
1 1 确 立的原 则 .
行 评价 , 仅 以乘 客 等待 时间为 依据 , 于 片面 。本 但 过
公交 运 营调度 优化 的评价 指标 的构 建是 以乘客
出行利益 并兼 顾公 交企业 效益 最大 为 目标 而建 立 的
线 网优化 模型 。评 价指标 模型 应该 具有 简 单 、 学 、 科
第1 0卷
第 1 期
21 00年 1月
科
学
技
术
与
工
程
Vo. 0 No 1 J n 2 1 11 . a . 0 0
@ 2 0 S i T c . g g 01 c. e h En n .
l 7 — l 1 ( 0 0 10 2 - 6 l 8 5 2 1 ) -3 4 6 0
文献标志码
公共 交通对 于一个 城市 的发展 起 着举 足轻 重 的
文 旨在研 究 出一种 公 交 调 度优 化效 果 的模 型 , 模 该 型将 集合 各种影 响调 度效 果 的因素 , 面 、 观地 对 全 客 优化 效果 进行评 价 。 建立 一套科 学 、 系统 、 有效 的评 价指标 体 系不 仅
作用 , 而公 交运 营调度 是通 过合理 的资 源配置 , 效 有 地 管理 车辆资源 , 使供 需矛 盾得 到解 决 。现 阶段 , 对
公交调度中的数学模型

公交调度 中的数 学模型
武 斌 ( 中国石油大学胜利学院 山东 东营 270) 5 0 0 摘要:建立合理有效 的数 学模 型来模 拟公 交运 营是优 化公交调度 、改善公 交服 务的关键 ,在分析现有模型 的基础 上,建立 以乘客
费用 最 小 ,公 交企 业 运 营 利 润 最 大化 的 多 目标 规 划模 型 。
l. 为第f h} —— 个小时时 间内。以^ 车时间 为发 间隔的 到达
第七站前的公交车已有的乘客数;
— —
公交车的最大载客量;
—
—
第1 个小时时间内在 车站下车的乘客总人数; 第f 个小时时问内到达 车站的乘客总人数; 根据客流量划分的时间段:
—
—
—
—
将 教育 理论知 识具体 应用到 教学 实践 中 去, 新教师在 岗前 培训 中亲 的总 成绩 记入 人事 档案 。 使 身体验 教 学的 各个环 节 ,掌握 教 学 的方 法和 艺术 ,尽快 适应 教 学的 青 年教师从毕业 到走上工 作岗位真正适应 教师角色需 要一个长期 过 程 。 的过程 ,把培训工作作为教师成长和教师队伍建设的重要环节,从 5 .建立有效考核体系 青年教 师 的需要 入手 ,促进 高 校教 师 岗前培 训 向专 业化 、科 学化 发 严格考核是检查督促岗前培训工作的有效手段, 但在授课后即以 展 ,以切 实提 高 青年 教 师 岗前 培 训 的效果 。 闭卷形 式考核却 不利 于新教 师对 所学 理论 的融会 贯通 。 青年 教师 岗前 培训体 系的建立 应本着 科学 性和 可操 作性 的原则 。 闭卷 考试 可用来 考 参考 文献: 察高 等教 育学 、高等 心理 学等 课 堂讲 授 内容 的记 忆情 况 ,督促 受训 【】 海高校教师岗前培训述评 【】 山东省青年管理干部学 1 J. 教师 强化 记忆 , 以指 导 实际教 学 工 作 。同时 ,青年 教 师听 取专题 讲 院学报 ,2 0 , 1 O 3 () 座 、典 型 报 告 、参 加 教 学观 摩 、 交流 讨 论 、参 观访 问和 提 交 论 文 [】赵志鲲 ,陶 勤. 高校青年教师岗前培训制度研究 【】 2 J. 的情况 也都要 以学分 形式记 入 岗前培 训档案 。 在使 用期结束 后 、 并 转 黑龙 江 高教研 究, 2 0 , 1) 7 (0 口 0 正之前 由专家 小组对 教学实 践能 力进 行考核 , 计总分 作为 岗前培 训 合
一种优化的公交车调度模型

乘 客数 … , 则第 时段 发 的 车需 从 A 站 运 送 的 乘
客 数量 N( ,) jk 为 N(, )= k 一(, )+ ( 十1 k jk A(,)一 k J ,)
其 中 A j k 为 第 时段 在 A (,) 站 净 上 车 人 数
( =1 2 …… ,7 1 ; ,, 1 , 8 k=1 , 2 1 , … , ,1 3 1 ,1 … 2 ,
率不 能超 过 l0 , 果发 车次数 < 2% 如 些 则必然 导致该 站 的部分 乘客滞 留.
,
表 1 上 行 方 向
总 共需 要发 车 2 7次 3
由于假设 各 时段发 车 的时间 间隔相 同 , 以 由 所
上述 发车次 数可 得到始 发站 的发 车时刻 表 , 而可 进 求至 少需要 多少 辆车 . 设 D。 A。 必 需 的车 辆 数 , 为 A 站 必 为 , 站 D 。 需 的车 辆数. i i 为 A , d () 。站在 i 刻发 车 前 由 A 时 。
( 平顶 山 学院 , 南 平顶 山 4 7 0 ) 河 600
摘
要: 在尽量 满足 乘客 和公 交车公 司双方利益 的前提 下, 将所给的数据进行转换处理 , 以每个 时段发
出 的公 交 车 将 乘 客 进 行 重 新 划 分 , 然后 由各 时段 内站 间 最 大 运 送 乘 客 数 量 求 出 该 时 段 的 最 少发 车 次 数 , 而 求 进 出需 要 的 最 少车 辆 , 对 所 求 结 果 进 行 评 价 . 并 关 键 词: 时段 ; 间 运 送 乘客 数 量 ; 优 化 ; 站 最 线性 规 划 ; 交 车 调 度 公
第2 5卷第 2期
21 0 0年 4月
公交车调度的规划数学模型

下面给出两种算法模型 : 算法模型 Ⅰ Pi = ρ = Ni i ×C
Qi Hi Hi Hi Qi Hi
算法模型 Ⅱ Pi = max ρ , = max , C N i ×L C i × C ×L 我们对确定发车间隔的模型采用两种不同的间隔确定方法进行求解 , 综合评价后得出综 合算法模型 : ( 假设每小时被调查的上车人数基于均匀的达到率) i) 参数分析
k
L ( bn , k ) =
j =1
∑D ( i
j
, i j +1 - 1 )
( 1)
其中 , i k + 1 = n + 1
3 损失函数值越小 , 分类越合理 。 设 bn , k 为使式 ( 1 ) 达到极小的解 费歇 ( Fisher) 的计算方法使用下面两个递推公式 : 3 L ( b n , 2 ) = min { D ( 1 , j - 1) + D ( j , n ) }
1
j - i +1
j
ቤተ መጻሕፍቲ ባይዱl=i
x ∑
l
3) 计算最小损失函数 。 用 b i3, j 表示用前 i 个样品分成 j 类的最优解 , 它的最优损失函数
为 L ( b i3, j ) 。 当 j ≤i ≤ 18 , 2 ≤j ≤ 8 时 , 利用费歇算法得到上下行方向的最小损失函数值变化曲线图 ( 1)
L : 上行方向 L = 14158 ( km) , 下行方向 L = 14161 ( km)
n
Qi : Qi =
j =1
∑d
ij D ij
方法 Ⅱ 确定公交调度发车间隔 我们通过引入时段配车数的概念 , 来探讨在不同客流状态时如何确定时段配车数和发车 间隔 。 定义 在某一时间段内需求的车辆数称之为时段配车数 。 确定原则是 , 既保证有足够的 服务质量 , 又保证配车数最小 。
城市公交优化模型研究

城市公交优化模型研究城市公交是城市交通中最常用的一种交通方式,每天都有成千上万的人选择乘坐公交车。
如今随着城市化进程的不断深入,城市公交的发展也在不断加快,公交网络的规模和覆盖面都在不断扩大。
然而,在大部分城市中,公交系统面临的问题也越来越显著,通勤时间长、车流混乱拥堵、交通安全隐患大等问题不断出现,给人们出行带来困扰。
如何优化城市公交成为了当下亟待解决的问题之一。
因此,本文将对城市公交优化模型进行研究,探讨如何提高城市公交的效率与质量。
一、公交线路优化公交线路优化是城市公交优化模型中的重要环节之一,它关系到公交网络的规模和覆盖面。
在公交线路优化时,需要考虑到尽可能地提高公交的覆盖率和服务质量。
首先,需要对城市中的交通流量进行分析,通过交通量巨大的区域配置更多的公交车辆。
其次,需要对路网进行细致的划分与研究,使得公交线路能够尽可能满足人们的出行需求。
最后,还需考虑公交线路长短、环线去向、中途换乘、终点站等因素,使得公交线路更加高效,为市民出行提供更好的服务。
二、车辆调度优化车辆调度也是城市公交优化中的重要环节之一,它涉及公交车辆的排班与调度。
如何合理安排车辆的行驶计划,是一个极为复杂的问题。
在车辆调度过程中,需要综合考虑多方面因素,如车辆的数量、发车间隔、路上的车流情况等。
通过科学的调度,可以减少运营成本、提高公交网络服务效率,从而建立更完善的公交网络。
三、信息化建设随着科技的不断发展,信息化技术在城市公交中的应用越来越广泛。
通过信息化建设,可以大幅提高公交服务的效率和便利性。
信息化技术可以用于公交线路规划、公交车辆调度、公交旅行时间预测、客流分析等环节,通过采用智能化技术与大数据分析,可以实现对公交的精细化管理和调度,为市民提供更加舒适、便利的出行环境。
四、环保优化随着全球环保意识的不断提高,城市公交也需要守护好环境。
在城市公交的发展过程中,环保优化是一个必须要考虑的因素。
如何合理运营公交,减少废气排放、降低噪音及其他对环境产生的不良影响,也是城市公交优化的重要一环。
响应动态需求的灵活型公交路径优化调度模型

第47卷第3期2021年3月北京工业大学学报JOURNAL OF BEIJING UNIVERSITY OF TECHNOLOGYVol. 47 No.3Mar. 2021响应动态需求的灵活型公交路径优化调度模型孙继洋1,2,黄建玲3,陈艳艳1,魏攀一1,2,贾建林1,宋程程1收稿日期:2019-10-18基金项目:国家重点研发计划资助项目(2017YFC0803903,2016YFE0206800)作者简介:孙继洋(1980—),男,高级工程师,主要从事智能交通大数据方面研究,E-mail :cdyan@ bjut. edu. cn(1.北京工业大学北京市交通工程重点实验室,北京100124; 2.交通运输部公路科学研究院,北京100088;3.北京市交通信息中心,北京100161)摘要:为解决灵活公交乘客需求差异性大、实时变化性大的问题,提出一种考虑乘客动态需求的灵活公交路径优化调度模型.在已知乘客预约需求量、车辆载客容量、车队规模等条件下,根据乘客需求动态变化特征对接驳行程 时间进行实时迭代更新,将车辆的运营成本(车辆行驶时间)和乘客的时间成本(乘客上车前等待车辆的时间、实际到达时间与期望到达时间之间的差值)最小化作为目标,构建了考虑乘客动态需求的灵活型公交路径优化调度模 型,并采用基于引力模型的启发式算法进行求解.最后,通过实例分析验证了模型和算法的可行性.结果表明:对 随机产生的15个需求点的102个出行需求,全部服务完成所需车辆为17~21辆,平均每辆车的旅行时间为24. 59min,100组数据的求解时间均在25. 00 s 以内,计算耗时平均为12. 04 s.可见该优化模型能够在实时调整接驳规划时间的前提下,更大程度满足乘客动态需求,有效减小规划路径的误差,缩短行车距离和乘客出行时间,相比忽略接驳行程时间变化的灵活公交调度模型结果更优.关键词:交通工程;城市交通;路径优化;启发式算法;灵活型公交;动态需求中图分类号:U121 文献标志码:A 文章编号:0254 -0037(2021)03 -0269 - 11doi : 10.11936/bjutxb2019100011Flexible Bus Route Optimal Scheduling Model in Responseto Dynamic DemandSUN Jiyang 1,2 , HUANG Jianling 3, CHEN Yanyan 1 , WEI Panyi 1,2 , JIA Jianlin 1 , SONG Chengcheng 1(1. Beijing Key Laboratory of Traffic Engineering , Beijing University of Technology , Beijing 100124, China ;2. Research Institute of Highway , the Ministry of Transport , Beijing 100088, China ;3. Beijing Transportation Information Center , Beijing 100161, China )Abstract : To solve the problem that the demand of flexible bus passengers varies significantly and thedemand of flexible bus passengers varies significantly in real time , a flexible bus route optimization scheduling model considering the dynamic demand of passengers was proposed. Under the conditions ofknown passenger reservation demand , vehicle passenger capacity and the team known condition such as size , according to the dynamic changes of passenger demand for real-time iterative update shuttle traveltime , the operating costs of the vehicle ( vehicle ) and time cost for passengers before ( the passengers waiting time of the vehicle , the actual time of arrival and the difference in value between expected time of arrival) minimization as the target , was established considering the passenger dynamic demand type flexible bus route optimization scheduling model , and USES the heuristic algorithm based on gravitymodel. Finally , the feasibility of the model and algorithm was verified by an example. The analysis results show that for the 102 travel demands of 15 randomly generated demand points , the number ofvehicles needed to complete all the services is 17 - 21 , the average travel time of each vehicle is 24. 59270北京工业大学学报2021年minutes,the solution time of100sets of data is all within25.00seconds,and the average calculation time is12.04seconds.It can be seen that under the premise of real-time adjustment of connection planning time,this optimization model can satisfy the dynamic demand of passengers to a greater extent,effectively reduce the error of the planning path,shorten the driving distance and passenger travel time,and achieve better results than the flexible bus scheduling model that ignores the change of connection travel time.Key words:traffic engineering;urban traffic;route optimization;heuristic algorithms;flexible bus;dynamic demand城市公交线路优化调度是提高公交运行效率、降低乘客出行和公交运营成本的主要手段.一个好的公交调度系统能够根据乘客的出行需求,快速优化调整线路运营方案,提高线路服务率,减少运行时间,降低乘客出行时间成本[1-»传统公交路径优化方法主要是通过长期的经验观察或IC卡数据统计分析,对部分线路进行延长、缩短、增删、调整走向等优化,优先满足大客流站点的乘客需求,这类方法主要适用于固定线路的公交路径优化,线路调整周期较长[4-7].灵活型公交的出现,为线路的动态优化调整提供了可能[7-10],目前国内外学者均开展了相关研究.其中,Quadrifoglio等[11-12]通过对灵活公交系统关键参数的分析,建立了公交系统运行效率参数优化调整模型,并针对其前期建立的系统线路设计和调度问题,进行了仿真验证分析,对模型进行了参数修正.付晓等[13]利用超级网络同时模拟用户的活动与出行行为,并根据用户出行行为特征建立了公交路径选择模型.Koffman[14]提出了基于多目标需求的城市公交智能调度算法;Tsubouchi[15]提出了 利用最小生成树寻优公交路径最优算法;熊杰[16]通过对区域内潜在公交用户需求的分析,建立了接驳轨道交通的公交线路优化模型;Li等[17]、Chen 等[18]通过对乘客预期等待时间和线路上客概率的推导,建立了超路径的公交运输路径调整模型;潘述亮[19]重点考虑了长时预约对灵活公交线路调整的影响,并提出了优化调度方法;郭晓俊[20]重点考虑了短时预约对灵活公交线路调整的影响,并提出了优化调度方法.这些研究虽然都是根据乘客的预约需求建立的灵活型公交路径优化算法,但其前提条件均是乘客需提前发出预约或假设乘客需求已知,相对即时预约来说均属于“静态需求”.然而,在乘客出行过程中,往往会根据出行需要发出短时预约或即时预约,灵活型公交需要根据乘客的“动态需求”,计算因动态需求变化导致的车辆接驳行程时间变化,即时调整线路实现路径的动态优化.鉴于此,考虑到乘客需求的动态变化以及由于需求变化导致的车辆接驳行程时间变化,本文提出了一种基于乘客动态需求的灵活公交路径优化调度方法.在已知车辆载客容量、车队规模等条件下,根据乘客需求动态变化特征对接驳行程时间实时迭代更新,将车辆运营成本和乘客出行成本最小化作为主要目标,建立了考虑乘客动态需求的灵活型公交路径优化调度模型.1问题描述与建模1.1问题描述在传统的固定型接驳公交运营中,公交线路规划设计与车辆运营调度是2个独立的过程,一般在线路规划设计完成之后制定车辆运营调度方案,调度方案在相当长一段时间内不发生变化.这就造成了线路设计和车辆调度之间脱节,两者不能有效衔接的问题,且线路设计和车辆调度无法根据乘客需求进行及时调整•但高效的接驳公交系统,应能够根据乘客的实际需求及时调整运营线路,并根据线路和乘客需求实时动态调整车辆调度方案.灵活型公交是一种以需求为基础的交通系统,它能根据乘客发出的需求,以最短路线服务最多乘客为目标,动态调整运营线路,并在线路调整同时,融合分析沿线乘客需求数量、车辆载客容量等因素,实时调整车辆调度方案,最大程度地满足更多乘客需求,解决传统固定型接驳公交的乘客需求与线路规划、车辆调度脱节的问题.本文提出的响应动态需求的灵活公交路径优化调度模型,将乘客即时需求作为公交路径动态优化调整的依据之一,根据乘客出行需求点位、需求量和需求时间,对公交路径和行车方案进行实时优化和调度.为使得本文所建立的模型更合理、得当,本文综合考虑乘客需求、运营成本等各方面的因素,进行如下灵活型公交路径优化模型假设、参数选取和建模.1.2模型假设对灵活型公交路径优化模型的建立提出如下假设,其中1)、2)为动态假设,3)~6)为静态假设.第3期孙继洋,等:响应动态需求的灵活型公交路径优化调度模型2711)每个站点的乘客预约需求量动态变化.2)车辆站点之间的行程时间动态变化.3)每个站点的位置均已知.4)预约后,每个乘客拟到达目标站点的时间已知.5)乘客到站上车的服务时间为常数.6)接驳车辆的载客容量已知.1.3模型参数按照上述模型假设,对各模型变量进行定义,如表1所示.表1模型参数Table1Medol parameter变量定义及说明参数类型Z优化路径的总时间成本因变量H乘客需求站点集合常量D目标站点集合常量K接驳运营车辆集合常量R乘客需求集合常量d”乘客需求r的目标站点d决策变量T t目标站的第t个发车时刻决策变量N乘客需求总量决策变量P r乘客需求r的上车站点p决策变量T”乘客需求r的期望发车时刻决策变量C j站点i和j之间的旅行时间决策变量V接驳车队规模决策变量Q k接驳车辆k的载客容量决策变量M足够大的一个常数常量X kt t时刻时车辆k将需求r接驳至乘客期望的站点,X,”为1;否则为0决策变量如车辆k选择(i,j)路段作为途经路径时,匕*为1;否则为0决策变量a 车辆行驶至需求r所在公交站点的时间决策变量乘客需求r到达目标站的时间决策变量车辆行驶至需求s所在站点的时间决策变量决定车辆k的运行线路不出现闭环U ik 的变量.如果接驳车辆离开站点i,则-=0;如果接驳车辆到达站点则4=1决定车辆k的运行线路不出现闭环辅助变量U k的变量.如果接驳车辆离开站点j,则乞=0;如果接驳车辆到达站点j,则U k=1辅助变量1.4模型表述按照上述模型假设和变量设置情况,采用非线性规划形式对灵活型公交路径优化模型进行表述,即Z=min I移移移c£k+移a+i e H U D j e H U D A e K reR移移移(S-e”)](1)r e R k e K t式(1)为灵活型公交路径优化模型表述的目标方程,由3个部分之和组成,取其最小化值:1)所有车辆的行驶时间,以降低运营成本;2)每个乘客在需求点等候车辆抵达的时间之和,以减少乘客的总出行时间;3)每个乘客等待车辆的实际到达时间与期望到达时间的差值之和,以减少乘客的总出行时间.移移Y jk逸1,VieH(2)j e H U D keK移移Y jk臆V,VieH(3)j e H U D keK约束式(2)(3)表示在任意一个乘客需求点,保证车辆进行服务,且车辆数在1与V之间.移移如臆V,V j e D(4)i e H k e K约束式(4)表示参与服务的车辆总数不超过V辆.移忌-移乙逸0,VieH,keK(5)j e H U D p e H约束式(5)表示对任意一个需求点,任一参与服务的车辆均有到达和离开的过程.4-匕+IHI X Y j臆IHI-1,Vi',eHUD,keK(6)约束式(6)保证了系统规划路径的单向性,即不能产生往返回路.移移如逸1,VkeK(7)i e H j e D移移Y jk臆0,VkeK(8)i e H j e D约束式(7)(8)表示参与服务的任意一辆车必须将乘客运送至目标站点.移移X rkt臆Q k,VkeK(9)r e R t e T约束式(9)保证车辆不能超载运输.移移X rkt=1,VreR(10)k e K t e T约束式(10)表示乘客发出需求后,只能被一辆车服务,不能同时被多辆车服务.移X skm-(1-X rkt)M臆0,Vr,seR,meT/{t}VkeK,VteT (11)272北京工业大学学报2021年约束式(11)表示一辆接驳车辆在单程接驳运送中,只能服务于一个目标站点的一个发车时刻.移移移X kt=N(⑵r沂 R k沂K i沂T约束式(12)表示所有接驳车辆实际服务的需求数量与预约的需求量相等.a+-a+抵严臆必,坌『异沂R,V"K(13)-a r-%+丫”肿MWM,V r,swR,V kwK(14)约束式(13)(14)表示当同一接驳车辆为相邻2个站点提供接驳服务时,后一个站点接受服务的时间应等于前一个站点接受服务的时间与两站点间行程时间之和.a r+%一a s+Y p肿MWM,Vr e R,Vk e K,V/'eD(15)a s一a r一%+岭亦MWM,V r沂R,V k沂K,Vj沂D(16)约束式(15)(16)表示接驳车辆到达目标站点的时间等于为最后一个需求点提供服务的时间与需求点与目标站点之间的行程时间之和.e,臆移移X ki T i,VreR(17)约束式(17)表示接驳车辆应在 目标站点车辆发车之前抵达目标站点.2模型求解本文提出的面向多目标站的灵活性公交路径优化调度问题,是一类典型的非确定性多项式问题都能在多项式时间复杂度内归约到的问题(non-deterministic polynomial hard,NP-hard).在问题规模较大时计算量和复杂程度会急速增加.因此,为了应对复杂问题的快速高效计算问题,通常采用可同时保证计算速度和计算精度的启发式算法进行求解.当在一定区域范围内,多个点位同时发出出行需求时,可看作同时存在的多个引力点.受点位间距离影响,不同点位之间引力大小各有不同,可对应理解为车辆在2个需求点间接驳运送的时间成本各不相同.因此,为使车辆能够快速在需求最多、距离最小的点位间进行接驳服务,受四阶段出行分布预测的引力模型启发,本文提出一种基于引力模型的启发式算法.总体思路是:首先基于引力模型生成较优的初始解,再利用路线间和路线内的优化算法分别改进路线,从而得到最终路线.详细步骤介绍如下.2.1乘客出行预约与需求分配首先,将乘客发出出行预约和进行需求服务分配分为以下4个步骤:步骤1乘客按其出行需求,进行预约出行.每个乘客将其出发站、目标站、期望到达目标站的时间等信息传输到出行预约平台.考虑到乘客需求和接驳车辆站点之间的行程时间的动态变化特征,预约平台的乘客需求和接驳车辆站点之间的行程时间每5min进行一次更新.步骤2出行预约平台根据每个乘客的目标站和期望到达目标站的时间,按照实际到达时间不晚于乘客期望值的原则,对所有乘客进行聚类.步骤3根据2.2,2.3节中路径生成结果,结合接驳车辆到达时间、平均行驶速度、乘客需求点的位置、各需求点乘客数量等因素,初步估算车辆到达的时间.步骤4将初步估计的接驳车辆到达各需求点的时间,发送给对应需求点的乘客,乘客根据接驳车辆到达时间的合理性,选择是否确定乘车.2.2基于引力模型的生成初始车辆路径解基于引力模型的计算方法,以起始需求点为已知站点,根据引力模型的原理遍历所有剩余需求点,查找与已知点之间引力最大的点,并将最新搜索到的站点作为新的已知点,继续遍历剩余需求点确定下一个与已知点之间引力最大的点,按此步骤逐步迭代,直到所有需求点均被查找到,从而可以生成可行的初始车辆路径解.定义两站点间的引力T(18)式中:N,为站点,的上车人数;c.为站点,和站点j 之间的车辆行驶时间.F,.的值越大,说明这2个站点的乘客数越多且旅行花费越小,需要优先服务,应该将站点j设为站点,的下一个站点.在已知车辆载客限定辆Q时,按如下步骤生成初始路径的解:步骤1确定车辆出发站点.初始k=1,从有乘客上车需求的站点中,随机抽取一个作为车辆k 的出发点.步骤2判断是否还有同类乘客未服务.若有,则跳至步骤3;否则,跳至步骤5.步骤3搜索下一站点.在包含同类乘客的上车站点中,找出与当前站点之间吸引力最大的站点第3期孙继洋,等:响应动态需求的灵活型公交路径优化调度模型273X,尝试将站点X加入路径选择链,计算车辆在加入该需求点后车上总人数,以及加入该需求点X后直接行驶至目标站点所需的时长.步骤4判断加入站点X后,车辆路线是否合理.若当前车辆服务的乘客数量未超过车载容量Q k,且到达目标站点的时间未超过乘客需求的时间,则以站点X为新的起点,跳至步骤3;否则,跳至步骤5.步骤5判断是否所有类别的乘客均被安排服务.若还有乘客未被安排服务,则调度下一辆车, k=k+1,跳至步骤1;否则,输出当前全部初始解,结束基于引力模型的初始解计算步骤.2.3基于站点均衡与交换的车辆路径优化介绍路线间和路线内的路径优化算法,使得路径质量和乘客服务水平进一步提升.需要注意的是,算法的步骤1和步骤2均属于车辆路径间的优化,在步骤1和步骤2的路径优化算法执行过程中,可能会搜索出多组可行的路线解.若在搜索时仅保存当前最优的一组解,再执行步骤3,可能搜索到的最终路线结果并不是最优.所以,本算法会保存步骤1和步骤2寻找到的所有可行解组,并对每一组可行解执行步骤3,综合评价所有的路线解组的目标函数,以找到最终的最优解.步骤1首先对服务于目标站点和到达目标站点时间需求相同的车辆之间进行站点数量均衡.检查各接驳车辆是否存在服务需求点过多或过少的现象.如果有,则在确保车辆不超载的条件下,将需经过站点数量较多的车辆路线中的部分站点,转移给经过站点数量较少的车辆路线,并安排合理的站点顺序.步骤2尝试对服务于目标站点和到达目标站点时间需求相同的车辆之间进行路径优化.主要应用两路线间,交换两站点的方式,搜索更优的路线.在交换优化的过程中,保证车辆不超载和按时到达目标站点的需求.步骤3对每一辆车的路线进行内部优化.主要在同一车辆路线内,尝试交换两站点的顺序,评估目标函数值是否减少.若减少,则交换站点顺序;否则舍弃本次交换.在尝试一定次数之后,结束计算流程,生成最终路线结果.步骤4考虑到乘客需求的动态变化特征和站点之间旅行时间的变化特征,每5min进行一次各站点需求的采集和重新计算,重复以上步骤1至步骤3.经过如上4个步骤,可在保证乘客按照预期时间到达目标站点的前提下,使得路径调度模型的目标函数最优,全部服务时间缩短,每一辆车的路线更加合理,车辆的运行成本降低,乘客的等待时间减少,提升服务质量和效率.3案例分析3.1案例假设北京市回龙观地区是通勤人群居住密集区,高峰时段出行需求量大,不同工作性质和通勤距离的出行者出行时间差异较大,因此适合作为需求响应型灵活公交模型验算的案例.为了便于模型分析,本文对回龙观区域公交网络进行了抽象化提取,保留网络拓扑结构.根据实际情况下乘客的出行需求,假设一个乘客出行案例,采用上述模型对案例进行求解,验证本文所提模型的可用性.小型网络常变量的输入参数如表2所示,初始时刻每个站点的乘客需求如表3所示,初始时刻站与站之间的旅行耗时矩阵如表4所示,其中H为需求点,D为目标站.表2案例中的常变量Table2Constant variables in the case变量名称变量值需求点数量/个15目标站点数量/个3车辆额定载客量/人7车队规模/辆18期望到达站点时间/min30/40/50乘客到站上车服务时间/min0.53.2案例计算根据本文提出的计算模型和方法,对上述假设案例进行计算,获取各接驳车辆的行驶路线、接驳乘客的数量、每条路线对应的目标函数如表5所示.之后,随着乘客需求和站点之间旅行时间的动态变化,上述路径规划结果无法满足当前乘客需求和真实状况,需进行新的路径规划.此时,预约平台将汇总的第一个5min后新的乘客需求和接驳车辆站点之间的行程时间并进行更新,如表6所示,再次利用2.2节中所述的方法进行求解.之后,根据乘客需求和站点之间旅行时间的动态变化信息,预约平台汇总第2个5min后新的乘客需求,并更新接驳车辆站点之间的行程时间,如274北京工业大学学报2021年表3初始时刻各站点乘客需求(初始5min)Table3Quantity demanded at the demand point(the first5minutes)乘客出发站目标站期望到站乘客出发站目标站期望到站乘客出发站目标站期望到站编号时间/m in编号时间/m in编号时间/m in 111303112306113302115032125062135031150332230631350421303422506423305215035323065235063130363240663330731403732506733408413038423068433095130395230695330105140405240705340115150415250715350125150426230725350136130436240736330146140446250746340157130457230757330167150467250767350177150478230778330188130488240788340198140498250798350209140509240809340211014051102408110340221015052102508210350231114053112408311340241115054122308412330251213055122508512350261215056122508612350271313057132308713330281414058142408814340291414059152408915340301514060152409015340表7所示,再次利用2.2节中所述的方法进行求解.下,车辆行驶最终路径结果如图1所示,此时,15个以此类推,预约平台继续汇总之后每个5min的乘需求站点发出的102个预约需求全部得以满足(为客需求和更新接驳车辆站点之间的行程时间,并利便于识别,分别以D1、。
城市公交智能调度系统解决方案

城市公交智能调度系统解决方案随着城市化进程的不断加速,城市公交运输成为解决交通问题的重要途径。
然而,由于城市规模扩大和人口增加,公交车的运营和调度变得越来越复杂,传统的调度方法已经难以满足当前的需求。
为了提高公交运营效率和服务质量,引入智能调度系统是提高城市公交运输管理水平的重要手段之一城市公交智能调度系统是一种利用现代信息技术和智能算法,对公交车的调度进行优化的系统。
它通过大量的数据分析,综合考虑路线、时间、客流和交通状况等因素,实时监控和调度公交车的运行。
下面是一些解决方案,可以提高城市公交智能调度系统的效果和效率:1.预测模型:通过建立基于历史数据和实时数据的预测模型,可以预测公交车的客流量和交通状况。
这可以帮助调度员根据需求做出更准确的调度决策,例如增加或减少车辆数量、改变运行路线等。
2.数据共享:通过建立城市交通数据共享平台,不同部门和企业可以共享公共交通数据,包括车辆位置、客流量、交通状况等信息。
这可以提供给调度员更全面的数据基础,使调度决策更为科学和准确。
3.车辆调度算法:通过优化算法,对车辆进行智能调度。
这些算法可以考虑多个因素,例如不同路段的交通拥堵情况、客流量分布等,以减少行车时间和提高服务质量。
例如,可以使用智能路由算法来选择最佳行驶路线,或者使用车辆调度算法来分配最优的车辆资源。
4.实时监控和调度:通过安装GPS设备和监控摄像头等设备,实时监控车辆的位置和运行情况。
调度员可以通过调度中心的终端查看车辆位置、交通状况和客流量等信息,并根据实时情况做出相应的调度决策。
5.客户服务:通过建立公交车APP和智能车站,提供实时公交信息和导航服务。
乘客可以通过手机APP查询公交车的到达时间和实时位置,从而规划自己的出行路线。
智能车站可以提供实时客流量统计和乘客健康码等服务,提高客户满意度和运营效率。
6.大数据分析:通过收集和分析大量的公交运营数据,可以帮助运营者了解公交车运行的状况,并进行绩效评估和优化。
公交车调度优化模型(3)

文章编号:1009-2269(2002)02-0006-05公交车调度优化模型Ξ祁忠斌,李成功,脱小伟,郭尚彬(兰州工业高等专科学校基础学科部,甘肃兰州 730050)摘要:研究了随着时间和空间上客流不均衡性的变化,车辆应如何调度的问题,建立了多目标规划的模型。
实现了“有早出,有晚出”,车辆有多有少的调度计划。
在保证一定效益和顾客满意的情况下,使在岗车辆的总运行时间最短。
所有的计算都在计算机上实现,得出了调度时刻表,最少的车辆数为42,顾客与公交公司的满意程度比为:0.68∶0.46.关 键 词:公交车调度;客流量;目标规划中图分类号:O141.4;U491 文献标识码:A1 已知数据及问题的提出 我们要考虑的是某城市的一条公交线路上的车辆调度问题。
现已知该线路上行的车站总数N 1(=14),下行的车站总数N 2(=13)。
且在问题中给出了某一个工作日(分为m 个时间段,第i 时间段的时间跨度为t i =1h )中第i 时间段第j 站点上行方向上、下车的乘客数量为Q ′u (ij ),Q ″u (ij ),第i 时间段第j 站点下行方向上、下车的乘客数量为Q ′d (ij ),Q ″d(ij ),上、下行站点间的距离分别为L j ,L ′j 。
公交公司供给该线路同一型号的大客车,每辆标准载客量为q 0=100人。
由统计知,该线路上客车运行的平均速度为v =20km/h 。
运营调度要求,乘客候车时间不要超过T 1=10min ,早高峰一般不要超过T 2=5min ,车辆满载率不应超过r =120%,一般也不要底于r =50%。
现要我们根据以上资料和要求,为该线路设计一个便于操作的全天(工作日)的公交车调度方案,包括两个起点的发车时间表;一共需要多少辆车;并给出刻划乘客和公交公司双方利益、满意程度的指标,进行评估等。
2 问题的初步分析及基本假设 制定公交车调度方案需要考虑的因素非常多,且很多因素都是随机的。
城市公交车辆运行计划综合优化模型的研究

enterprise,discussed and a n alysised integrated optim ization m o d el combined with traditional empir ical for m ula,achieved satisfactory results.
Abstract:Reasonable formulating urban bus operation plan Wa s an important means to raise the level of public tra n sport services an d the ef i ciency of vehicle resources.Facing w ith t he complexity of city bus operation plan,it was established an
Key words:f low space-time distlibuf ion;operation pla n ;adjusunent;optimization mo d el
随 着我 国城 市化 的迅 速发 展 ,许 多城市 特 别是
为 了评 价客 流沿 日营 业时 间 内各小 时分 布的 不
K,f= /a^
(1)
式 中 : , 为线 路营 业时 间第 小 时的时 间 不均
匀 系 数 ,z=1,2,… … ,m;
需求响应接驳公交调度优化模型与方法

针对需求响应接驳公交调度的优化模型与方法,以下是一种可能的解决方案:
1. 数据收集与分析:收集并分析公交车站乘客需求数据、公交车运行数据、交通流量数据等。
通过数据分析,可以确定需求高峰时段和路段拥堵情况,为优化调度提供依据。
2. 建立优化模型:基于数据分析结果,建立调度优化模型。
常用的优化模型包括整数规划、动态规划、网络流模型等。
模型的目标是最小化乘客等待时间、减少换乘次数、平衡各线路负载等。
3. 制定调度策略:根据优化模型的结果,制定合理的调度策略。
例如,通过增加或减少车辆数量、优化线路路径、调整发车间隔等方式来提高乘客满意度和运行效率。
4. 实时调度与调整:由于城市交通状况时刻变化,需要实时监测数据,并根据实时情况进行调度与调整。
可以利用实时公交数据、交通导航系统等技术手段来实现实时调度优化。
5. 考虑多因素:除了乘客需求和交通流量外,还应考虑其他因素如环境保护、能源消耗等。
通过综合考虑多个因素,可以制定更加全面和可持续的调度策略。
需要注意的是,优化调度是一个复杂的问题,不同城市和交通网络情况可能存在差异,所以具体的模型和方法需要根据实际情况进行调整和优化。
此外,实施调度优化需要有相关的技术支持和信息系统建设,以确保调度策略的有效实施和监控。
可变线路式公交车辆调度优化模型

停靠点i 的 横 坐 标 ; d x b a c k为 车 辆 在 x 方 向 上 允 许 ; 的最大逆行距 离 固 定 站 点i 的 车 辆 计 划 发 车 时 间用 T 上 一 发 车 班 次 固 定 站 点i 的 发 车 S i 表 示, 时间用 T 且T S ′ S T S ′ T; A S i 表示 , i= i+ i 为计划 分别用t 中车辆到达固定站点i 的时间 ; )、 )( t i a( i d( i 表示车辆到 达 停 靠 点i 的 时 间 和 从 停 靠 点 S) ∈S i 发车的时间 ; T P k 和 TDk 分 别 为 乘 客k 的 上 车 时间 和 下 车 时 间 ; ( T R i k)为 站 外 上 车 乘 客 希 望 在 ( [ 能够上车的时间 ; 为站外 停靠点i i S) e l ∈N k, k] 上车乘客 k( 上 车 时 间 的 时 间 窗; k∈N1 ∪N3 ) T s 为公交车辆在每 个 站 点 的 服 务 时 间 , 文中认为各 个站点的服务时间相同 ; w1 、 w2 和 w3 分别为车辆 乘客候 车 时 间 和 乘 客 在 固 定 站 点 空 闲 运营成本 、 时间的 权 重 系 数 ; α 1 为车辆行驶里程的货币成 本, 为 c m ∈M ) α 2 为乘客时间消耗的 货 币 价 值 ; m( 本文 认 为 同 类 乘 客 第 m 类乘客支付的公交票价 , 的票价相同 ; 车 辆 的 行 驶 速 度 用v 表 示; CB 为 公 交车辆的额定载客数 ; Z 为一个任意大的值 。 1. 3 数学模型 以系统总成本最优为目标建立的可变线路式 公交车辆调度模型为 m i n Z=w α 1[ 1
[] 度模型 ; W e i L u 等 7 针对多车辆可变线路式公 交
浅谈公交优化调度问题

Author: by Fabian Cevallos & Fang Zhao
这篇论文基于遗传算法,提出了解决公交系统内换乘时间最优化问 题的系统性方法。主要是通过调整现有时刻表,找到最优解决方案。 文中所提出的方法用到了现有时刻表和所有换乘站点的乘客资料,并 考虑了车辆到达的随机性。基于Broward County Transit 公交公司所 提供的调度资料,计算了系统目前状况下的总换乘时间,以及用本文 所介绍的方法对系统现有时刻表进行调整,所得推荐系统的总换乘时 间,结果表明该算法可以在很大程度上节约公交系统的总换乘时间。
任传祥,张海,范跃祖在文章《混合遗传-模拟退火算法在公交智能调度中的应 用》中,兼顾企业与乘客的利益建立了公交车辆行车计划模型,将遗传算法与 模拟退火算法相结合,组成混合遗传――模拟退火(GA-SA)算法,对公交行车调 度进行优化。
Ceder Avishai and Ofer Tal.在文章Timetable Synchronization for Buses中, 提出了一种启发式算法,基于同时到达换乘站点的车辆数最多求得最优解,研 究了车辆同步性问题。
4
二、国内外研究情况综述
查阅国内外有关公交优化调度方面的文献,可以看出, 已有众多学 者对公交运营设计中的运行线路、时刻表、以及车辆路径等问题分别 进行过有益的探索,给出了解决复杂运营设计、时刻表优化等问题的 模型、算法等,而且基于不同目标函数、不同约束条件给出了问题的 解决方案,这对于该领域的进一步研究工作提供了极为可贵的借鉴意 义。
公交车调度的数学模型

ma y b s e d d Th n we u e Dae t( o t r)t tt e c r e o h u e f p o l wh n u e n e e . e , s tf a s fwa e o f h u v f t e n mb r o e p e s i i o
维普资讯
第 7 卷
第 4期
哈 尔 滨 理 工 大 学 学 报
J U R N A L H A R BI N I .S I O N U V C .& TEC H
.
V0 . O. 17 N 4 Au . 0 g ,2 02
20 0 2年 8月
GAI Li g— y n,CH EN i n W ANG i n u Ja , Fe
( a e c Ad io o p o a h ma i lM o eig Ac d mi vs rGr u f M te tc a d ln ,Hab n Un v c.T c . r i i .S i e h ,Ha bn 1 0 8 ,Chn ) r i 0 0 5 ia
Ab t a t Fo d s t h n t e u e of pu l t a s r a i n ou e sr c : r i pa c i g h b s s a bi c r n po t to r t of c t , we e eop a iy d v l op i i e o e s wih h e h y a c pr g a m i g tm z d m d l t t e m t od of d n m o r m i n .W e e tm a e t e t e f b s e i g s i t h i s o u e s nd n m s
公交车调度数学模型

公交车调度数学模型编者按:木文依据题意和数据进行分析与抽象,建立了车辆的满载率, 乘客的等待抱怨程度和拥挤抱怨程度三个目标函数的多目标规划数学模型。
基于多目标规划加权分析法,进行数值计算,结果合理。
但加权分析时所取权系数只有一组,最好多取几组权系数进行比较。
虽然, 文中最后提及灵敏度检验,但并没有实质性进行分析,缺乏理论指导。
摘要:本文利用多目标优化方法建立了公交车调度的数学模型。
首先通过数据分析,并考虑到方案的可操作性,将一天划分为早高峰前, 早高峰,早高峰和晚高峰之间,晚高峰及晚高峰后5个时段;引入车辆的平均满载率,乘客的等待抱怨程度及拥挤抱怨程度作为三个目标函数, 建立了三目标优化模型;通过加权,将三个目标函数合并为一个目标函数。
运用MATLAB数学软件计算出了上行、下行各个时段发车的时间间隔:上行各时段时间间隔分别为5、2、4、3、25,下行各时段时间间隔分别为10、2、5、3、&单位:分钟);所需总车辆数为52辆,共发车534次,公交公司的平均满载率为82.094%,抱怨顾客的百分比为0.91%. 通过模型检验得出所求模型较为稳定。
最后,通过对原始数据的分析和处理,得出在进入和离开乘客高峰时期,局部缩短采集数据时间间隔是改善调度方案的有效方法.关键词:公交车调度;数学模型;多目标非线性规划二、正文1模型假设1)假设表上所给数据能反映该段线路上的H常客流量;2)车辆上行或下行到达终点站时,所有的乘客必须全部下车;3)乘客无论是上行还是下行,无论经过几个站,车票价为定值;4)各公交车为同一个型号,公交车会按调度表准时到站和出站;5)在同一个时间段内,相邻两辆车发车时间间隔相等;6)车上标准载客人数为100人,超过此数将会造成乘客抱怨;7)早高峰时乘客等待时间不超过5分钟,正常时不超过10分钟,否则乘客将会抱怨;8)早上5:00上下行起点站必须同时发车;9)不计乘客上下车所花费的时间,公交车在行驶过程中速度保持不变;10)假设每辆车经过各个车站时不会留有乘客。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三篇公交车调度方案的优化模型2001年 B题公交车调度Array公共交通是城市交通的重要组成部分,作好公交车的调度对于完善城市交通环境、改进市民出行状况、提高公交公司的经济和社会效益,都具有重要意义。
下面考虑一条公交线路上公交车的调度问题,其数据来自我国一座特大城市某条公交线路的客流调查和运营资料。
该条公交线路上行方向共14站,下行方向共13站,表3-1给出的是典型的一个工作日两个运行方向各站上下车的乘客数量统计。
公交公司配给该线路同一型号的大客车,每辆标准载客100人,据统计客车在该线路上运行的平均速度为20公里/小时。
运营调度要求,乘客候车时间一般不要超过10分钟,早高峰时一般不要超过5分钟,车辆满载率不应超过120%,一般也不要低于50%。
试根据这些资料和要求,为该线路设计一个便于操作的全天(工作日)的公交车调度方案,包括两个起点站的发车时刻表;一共需要多少辆车;这个方案以怎样的程度照顾到了乘客和公交公司双方的利益;等等。
如何将这个调度问题抽象成一个明确、完整的数学模型,指出求解模型的方法;根据实际问题的要求,如果要设计更好的调度方案,应如何采集运营数据。
公交车调度方案的优化模型*摘要:本文建立了公交车调度方案的优化模型,使公交公司在满足一定的社会效益和获得最大经济效益的前提下,给出了理想发车时刻表和最少车辆数。
并提供了关于采集运营数据的较好建议。
在模型Ⅰ中,对问题1建立了求最大客容量、车次数、发车时间间隔等模型,运用决策方法给出了各时段最大客容量数,再与车辆最大载客量比较,得出载完该时组乘客的最少车次数462次,从便于操作和发车密度考虑,给出了整分发车时刻表和需要的最少车辆数61辆。
模型Ⅱ建立模糊分析模型,结合层次分析求得模型Ⅰ带给公司和乘客双方日满意度为(0.941,0.811)根据双方满意度范围和程度,找出同时达到双方最优日满意度(0.8807,0.8807),且此时结果为474次50辆;从日共需车辆最少考虑,结果为484次45辆。
对问题2,建立了综合效益目标模型及线性规划法求解。
对问题3,数据采集方法是遵照前门进中门出的规律,运用两个自动记录机对上下车乘客数记录和自动报站机(加报时间信息)作录音结合,给出准确的各项数据,返站后结合日期储存到公司总调度室。
关键词:公交调度;模糊优化法;层次分析;满意度3.1 问题的重述3.1.1 问题的基本背景公交公司制定公交车调度方案,要考虑公交车、车站和乘客三方面因素。
我国某特大城市某条公交线路情况,一个工作日两个运营方向各个站上下车的乘客数量统计见表3-1。
3.1.2 运营及调度要求⑴公交线路上行方向共14站,下行方向共13站;⑵公交公司配给该线路同一型号的大客车,每辆标准载客100人,据统计客车在该线路上运营的平均速度为20公里/小时。
车辆满载率不应超过120%,一般也不低于50%;⑶乘客候车时间一般不要超过10分钟,早高峰时一般不要超过5分钟。
3.1.3 要求的具体问题⑴试根据这些资料和要求,为该线路设计一个便于操作的全天(工作日)的公交车调度方案,包括两个起点站的发车时刻表;一共需要多少辆车;这个方案以怎样的程度照顾到了乘客和公交公司双方的利益,等等;⑵如何将这个调度问题抽象成一个明确完整的数学模型,并指出求解方法;⑶据实际问题的要求,如果要设计好更好的调度方案,应如何采集运营数据。
3.2 问题的分析本问题的难点是同时考虑到完善城市交通环境、改进市民出行状况、提高公交公司的经济和社会效益等诸多因素。
如果仅考虑提高公交公司的经济效益,则只要提高公交车的满载率,运用数据分析法可方便地给出它的最佳调度方案;如果仅考虑方便乘客出行,只要增加车辆数的次数,运用统计方法同样可以方便地给出它的最佳调度方案,显然这两种方案是对立的。
于是我们将此题分成两个方面,分别考虑到:⑴公交公司的经济效益,记为公司的满意度;⑵乘客的等待时间和乘车的舒适度,记为乘客的满意度。
显然公交公司的满意度取决于每一趟车的满载率,且满载率越高,公交公司的满意度越高;乘客的满意度取决于乘客等待的时间和乘车的舒适度,而乘客等待时间取决于车辆的班次,班次越多等待时间越少,满意度越高;乘客的舒适度取决于是否超载,超载人数越少,乘客越满意。
很明显可以知道公交公司的满意度与乘客的满意度相互矛盾,所以我们需要在这两个因素中找出一个合理的匹配关系,使得双方的满意度达到最好。
3.3 模型的假设⑴道路:交通情况、路面状况良好,无交通堵塞和车辆损坏等意外情况;⑵公交车:发车间隔取整分钟,行进中彼此赶不上且不超车,到达终点站后调头变为始发车;⑶乘客:在每时段内到达车站的人数可看作是负指数分布,乘客乘车是按照排队的先后有序原则乘车,且不用在两辆车的间隔内等待太久;⑷数据:“人数统计表”中的数据来源准确、可信、稳定、科学;⑸票价:乘车票价为定值,不因乘车远近而改变。
3.4 定义与符号说明序号符号意义1a上或下行第j时段第k站上车人数;ijk2b上或下行第j时段第k站下车人数;ijk3l上或下行第j时段最大客容量;ij4k上或下行时第j时段平均载客量;ij5 C日所需总车次;6c上或下行第j时段的车次;ij7s上或下行第j时段平均发车时差;ij8p上或下行第j时段平均载客量;ij9t上或下行的平均发车时间间隔;ij10m上或下行时公交公司日平均满意度;gi11m上或下行时乘客整体日平均满意度;ci12m上或下行时公交公司各时段的满意度;gij13m上或下行时乘客各时段的满意度;ci*本文获2001年全国一等奖。
队员:叶云,周迎春,齐欢,指导教师:朱家明等。
14 Q日所需车辆数。
注:1=i (表示上行运动(14,,3,2,1 =k ),2=i 表示下行运动(13,,3,2,1 =k ),18,3,2,1 ,=j 。
3.5 模型的建立与求解3.5.1 模型Ⅰ:相关量及车辆数的确定模型对问题1为设计便于操作的公交车调度方案,根据表3-1给出的一个工作日两个运营方向各个站上下车的乘客数量统计,假设各时段车辆平均足够载完在相等时间内到达的乘客,乘客也只能乘坐该路车而没有太大的不满,我们要设计两个起点站的发车时刻表,计算需要的车辆数,首先可建立以下各模型来求相关量。
⑴相关量①上下行各时间段内最大客容量:建立模型如下{}{}⎪⎪⎩⎪⎪⎨⎧==-==-=∑∑==13,2,12m ax 14,2,11m ax 11 ,,n i b am i b a l nk ijkijkmk ijk ijkij运用模型和表3-1中的上下车乘客数,算出上下行各时间段内最大客容量如下:图3-1 (1)上行各时间段内最大客容量 图3-1 (2)下行各时间段内最大客容量②车次数:因为座位数为100的客车满载率在50%和120%之间,即12050≤≤ij k ,在满足客车满载率和载完各时段所有乘客前提下,由模型:∑∑===21181i j ij c C ,⎪⎪⎪⎩⎪⎪⎪⎨⎧∈∉+⎥⎦⎤⎢⎣⎡=++Z l l Z l l c ij ijij ij ij 1201201201120(其中Z +是正整数)可计算每个时段的详细车次数如下:上行:6,25,42,23,13,10,12,10,9,8,8,18,24,8,4,4,3,4 下行:3,9,23,27,16,10,9,7,8,9,11,19,31,21,10,7,7,4求和可得出全工作日可行的最少车次总数:462231231=+=C 。
③安排发车时间间隔:用每个时段60分钟除以车次数,即:ij ij c s /60=,经计算可得出该时段平均发车时间间隔依次如下:上行:10,2.4,1.4,2.6,4.6,6,5,6,6.7,7.5,7.5,3.3,2.5,7.5,15,15,20,20;下行:20,6.7,2.6,2.2,3.8,6,6.7,8.6,7.5,6.7,5.5,3.1,1.9,2.8,6,8.6,20。
由ij s 的值有分数出现,而现实中列车、客车等时刻表的最小单位为分钟,故间隔应取整数。
当ij s 取整数时,可直接安排等时间发车ij c 次。
当某个ij s 取小数时,不妨设][ij s F 和][ij s C 是与ij s 相邻的两个连续整数且][][ij ij ij s C s s F ≤≤,由模型:)18,,2,1;2,1(60][][ ==⎪⎩⎪⎨⎧=+=⨯+⨯j i c n m s C n s F m ijij ij ij ij ij ij可求出以][ij s F 为间隔的班次ij m 和以][ij s C 为间隔的班次ij n ,再分别以发车间隔;为][ij s F 和][ij s C ,兼顾发车密度,将此时间段进行适当划分。
将上述各ij c 与ij s 值代入方程组,可相应地求出具体的发车间隔的次数ij ij n m ,,考虑到公交车调度方案的可操作性和公交公司的利益所在,在同时段线路上的车辆不宜过多,我们对结果进行了分析比较,将相邻时间段内发车间隔相等的班次尽量安排在一起,并且对高峰时期发车的先后顺序作了调整,得出了全天(一个工作日)内的公交车调度方案,见表3-5。
⑵日所需车辆数由汽车平均速度20千米/小时和A0-A13的距离61.14千米、A13-A0的距离58.14千米,可求得车辆从起点站到终点站的时间约为44分钟;又由假设可知车辆到达终点站后立即调头往回开且不跑空车,由于早高峰乘客数最多,故此时车辆实际占用数也应是当日的上限,考虑到8:00之前从A13发出的车次每个时段都多于A0发出的车次,且最大逆差数为3819163)(3121=++=-∑=i j jc c即从A13多发出38辆车;8:00到9:00虽然从A0发来的车辆多于从A13发出的车辆,但从8:00到8:44仍要从A13发出的15辆车,由假设恰在8:44时对方开来的车辆到站并调头再结合动态车辆有8辆赶不上时差。
故早高峰车辆实际占用为61辆,也即当天共需开动的车辆最少为61辆。
3.5.2 模型Ⅱ 最小车次数线性规划模型问题明显可看作是一个排队随机服务系统,我们把汽车看作是“顾客”,将各个车站看作是“服务台”,则此公交系统可看作是一个顾客不消失的、单通道多级服务台串联的排队系统。
因此,这里所遇到的,主要是排队问题。
归纳起来,需要考虑三种活动:①首站发车活动:根据发车时刻表确定;②到达中途站活动:在中途站主要考虑和计算上下车人数、车上的总人数和上下车时间;③到达终点站调头活动:在终点站根据发车时刻表确定。
我们先考上行时乘客在站的逗留时间,即乘客在k A 1站的等待时间,它包括相邻两趟车到达kA 1站的时间间隔jk q 1即发车间隔和乘客上下车的服务时间jk p 1。
