必修二讲义

合集下载

高一数学授课讲义(必修二)

① 讨论：水平放置的平面图形的直观感觉？以六边形为例讨论.
② 给出斜二测画法规则：
建立直角坐标系，在已知水平放置的平面图形中取互相垂直的OX，OY，建立直角坐标系；
画出斜坐标系，在画直观图的纸上（平面上）画出对应的O’X’,O’Y’,使 =450（或1350），它们确定的平面表示水平平面；
画对应图形，在已知图形平行于X轴的线段，在直观图中画成平行于X‘轴，且长度保持不变；在已知图形平行于Y轴的线段，在直观图中画成平行于Y‘轴，且长度变为原来的一半；
④讨论：棱、圆与柱、锥、台的组合得到6个几何体.棱台与棱柱、棱锥有什么关系？圆台与圆柱、圆锥有什么关系？（以台体的上底面变化为线索）
2．教学球体的结构特征：
①定义：以半圆的直径所在直线为旋转轴，半圆面旋转一周形成的几何体，叫球体.结合图形认识：球心、半径、直径.→球的表示.
②讨论：球有一些什么几何性质？
结合图形认识：上下底面、侧面、侧棱（母线）、顶点、高.
讨论：棱台的分类及表示？圆台的表示？圆台可如何旋转而得？
③讨论：棱台、圆台分别具有一些什么几何性质？
★棱台：两底面所在平面互相平行；两底面是对应边互相平行的相似多边形；侧面是梯形；侧棱的延长线相交于一点.
★ 圆台：两底面是两个半径不同的圆；轴截面是等腰梯形；任意两条母线的延长线交于一点；母线长都相等.
→结合图形认识：底面、轴、侧面、母线、高.→表示方法
③讨论：棱柱与圆柱、棱柱与棱锥的共同特征？→柱体、锥体.
④观察书P2若干图形，找出相应几何体；
三、巩固练习：
1.已知圆锥的轴截面等腰三角形的腰长为5cm,,面积为12cm,求圆锥的底面半径.
2.已知圆柱的底面半径为3cm,,轴截面面积为24cm,求圆柱的母线长.

高中物理必修二讲义全

第五章平抛运动§5-1 曲线运动 & 运动的合成与分解一、曲线运动1.定义：物体运动轨迹是曲线的运动。

2.条件：运动物体所受合力的方向跟它的速度方向不在同一直线上。

3.特点：①方向：某点瞬时速度方向就是通过这一点的曲线的切线方向。

②运动类型：变速运动（速度方向不断变化）。

③F 合≠0，一定有加速度a 。

④F 合方向一定指向曲线凹侧。

⑤F 合可以分解成水平和竖直的两个力。

4.运动描述二、运动的合成与分解1.合运动与分运动的关系：等时性、独立性、等效性、矢量性。

2.互成角度的两个分运动的合运动的判断：①两个匀速直线运动的合运动仍然是匀速直线运动。

v v 水 v 船θ 船v d t =m in，θsin d x = 水船v v =θtand ②速度方向不在同一直线上的两个分运动，一个是匀速直线运动，一个是匀变速直线运动，其合运动是匀变速曲线运动，a 合为分运动的加速度。

③两初速度为0的匀加速直线运动的合运动仍然是匀加速直线运动。

④两个初速度不为0的匀加速直线运动的合运动可能是直线运动也可能是曲线运动。

当两个分运动的初速度的和速度方向与这两个分运动的和加速度在同一直线上时，合运动是匀变速直线运动，否则即为曲线运动。

三、有关“曲线运动”的两大题型（一）小船过河问题模型一：过河时间t 最短：模型二：直接位移x 最短：模型三：间接位移x 最短：[触类旁通]1．(2011 年上海卷)如图 5－4 所示，人沿平直的河岸以速度 v 行走，且通过不可伸长的绳拖船，船沿绳的方向行进．此过程中绳始终与水面平行，当绳与河岸的夹角为α时，d vv 水v 船θ当v 水<v 船时，x min =d ， θsin 船v d t =，船v v θ Av 水v 船 θ 当v 水>v 船时，L v v dx 船水==θcos min， θsin 船v d t =，水船v v =θcosθθsin )cos -(min 船船水v L v v s =θv 船 d船的速率为（ C ）。

高中物理必修二讲义

第三章曲线运动1.曲线运动⑴条件：物体所受合外力方向与速度方向不在一条直线上。

合外力指向轨迹的凹侧，轨迹夹在v 与合F 之间，速度方向就是轨迹的切线方向。

⑵曲线运动问题：思想（复杂的问题分解成简单的问题）；方法（运动的合成与分解）。

2.平抛运动（初速水平且只有重力作用的匀变速曲线运动） ⑴基本规律（两个直角△）：任意时刻速度：222022t g v v v v y x t +=+= x y v v =αtan任意时刻位移：222022)2()(gt t v y x s t +=+= x y =βtan运动时间：g h t 2=3.小船过河（水v 、船v 、合v 都是相对于河岸的。

）⑴最短时间：船v 方向垂直于河岸，水流速度不影响靠岸时间（垂直矢量独立原理）。

⑵最短距离：① 水v <船v :合v 垂直于河岸，水v 、船v 、合v 构成直角△，最短距离是河宽d ②水v >船v :合v 偏向水流方向，水v 、船v 、合v 构成直角△，最短距离是河宽αsin /d 。

用矢量圆求解！4.关联问题：确定关联的双方和关联物；确定关联的方向；将关联双方沿关联方向正交分解（还是直角△）；关联方向上速度相等，求解方程。

5.圆周运动 ⑴基本关系线速度：t s v /= 角速度：t /θω= 单位“s rad /”。

周期：ωπ/2=T 单位“s ”。

频率：T f /1= 单位“Hz ”。

转速：πω2/=n 单位“s r /”。

r v ω= r r v a n 22/ω==⑵基本问题：①竖直平面内绳球：最高点速度满足r v g /2=即可②竖直平面内杆球：最高点速度满足0=v 即可，gr v =是杆力发生变化的临界条件③小球沿竖直光滑圆轨道运动不脱离圆轨道的另一种可能是到达半圆位置速度为零，然后往复运动；小球的初速介于过顶点和这个速度之间时，它将从底端冲上上半圆，速度到达某值后作斜抛运动而脱轨④由于圆轨道的凹凸不同，易引起运动物体对轨道的压力不同，从而产生不同的摩擦力，这时要是小球以相同的初速进入圆轨道，从A 到C 所用的时间小于从C 到A 所用的时间，想想为什么？（终于明白了30年前王永良老师给我出的第二个问题了，感谢恩师，是您的鼓励让我始终坚信我是个聪明的孩子，是您使我有了战胜各种挫折的信心！再次跪拜！！）第四章万有引力1.万有引力定律2RMmGF = （注意中心天体质量的变化，一般用密度和体积求解！匀质球壳内各点引力为零！） 2.绕中心天体的圆周运动⑴基本力学关系：①在天体表面：mg F =万（g R GM =2/）②绕天体运动：万向F F =。

高中数学必修二讲义专题4.3 空间直角坐标系

一、空间直角坐标系定义以空间中两两__________且相交于一点O 的三条直线分别为x 轴、y 轴、z 轴，这时就说建立了空间直角坐标系Oxyz ，其中点O 叫做坐标__________，x 轴、y 轴、z 轴叫做__________．通过每两个坐标轴的平面叫做__________，分别称为xOy 平面、yOz 平面、__________平面．画法在平面上画空间直角坐标系Oxyz 时，一般使∠xOy ＝__________，∠yOz ＝90°．图示说明本书建立的坐标系都是右手直角坐标系，即在空间直角坐标系中，让右手拇指指向__________轴的正方向，食指指向__________轴的正方向，如果中指指向__________轴的正方向，则称这个坐标系为右手直角坐标系．二、空间直角坐标系中点的坐标1．空间中的任意点与有序实数组(),,x y z 之间的关系如图所示，设点M 为空间直角坐标系中的一个定点，过点M 分别作垂直于x 轴、y 轴和z 轴的__________，依次交x 轴、y 轴和z 轴于点P 、Q 和R ．设点P 、Q 和R 在x 轴，y 轴和z 轴上的坐标分别是x 、y 和z ，那么点M 就和有序实数组（x ，y ，z ）是__________的关系，有序实数组__________叫做点M 在此空间直角坐标系中的坐标，记作__________，其中x 叫做点M 的__________，y 叫做点M 的__________，z 叫做点M 的__________．2．空间直角坐标系中特殊位置点的坐标点的位置点的坐标形式原点（0，0，0） x 轴上（a ，0，0） y 轴上（0，b ，0） z 轴上（0，0，c ） xOy 平面上（a ，b ，0） yOz 平面上（0，b ，c ） xOz 平面上（a ，0，c ）3．空间直角坐标系中的对称点设点P （a ，b ，c ）为空间直角坐标系中的点，则对称轴（或中心或平面）点P 的对称点坐标原点(),,a b c --- x 轴 (),a b c --,y 轴（－a ，b ，－c ）z 轴),(,a b c -- xOy 平面(,,)a b c -yOz 平面(),,a b c - xOz 平面(,)a b c -，三、空间两点间的距离公式如图，设点11112222(,,),(,,)P x y z P x y z 是空间中任意两点，且点11112222(,,),(,,)P x y z P x y z 在xOy 平面上的射影分别为M ，N ，那么M ，N 的坐标分别为1122(,,0),(,,0)M x y N x y ．在xOy 平面上，221212||()()MN x x y y =-+-．在平面21MNP P 内，过点1P 作2P N 的垂线，垂足为H ，则11122||||,||||,||||PH MN MP z MP z ===，所以221||||HP z z =-．在12Rt △PHP 中，2211212||||()()PH MN x x y y ==-+-，根据勾股定理，得221212||||||PP PH HP =+=____________________________．因此，空间中点P 1（x 1，y 1，z 1）、P 2（x 2，y 2，z 2）之间的距离是12||PP =____________________________．特别地，点P (x ，y ，z )到坐标原点O (0,0,0)的距离为|OP |＝222x y z ++．空间两点间的距离公式可以类比平面上两点间的距离公式，只是增加了对应的竖坐标的运算．空间中点坐标公式：设A (x 1，y 1，z 1)，B (x 2，y 2，z 2)，则AB 中点P ⎝⎛⎭⎫x 1＋x 22，y 1＋y 22，z 1＋z 22．K 知识参考答案：三、222121212()()()x x y y z z-+-+-222121212()()()x x y y z z-+-+-K—重点1．会建立空间直角坐标系（右手直角坐标系），会表示空间中的任意点；2．能在空间直角坐标系中求出点的坐标；3．记住空间两点间的距离公式，并能应用两点间的距离公式解决一些简单的问题．K—难点对空间直角坐标系的理解，空间两点间距离公式的推导．K—易错易混淆平面与空间直角坐标系．1．确定空间任一点的坐标确定空间直角坐标系中任一点P的坐标的步骤是：①过P作PC⊥z轴于点C；②过P作PM⊥平面xOy于点M，过M作MA⊥x轴于点A，过M作MB⊥y轴于点B；③设P（x，y，z），则|x|＝|OA|，|y|＝|OB|，|z|＝|OC|．当点A、B、C分别在x、y、z轴的正半轴上时，则x、y、z的符号为正；当点A、B、C分别在x、y、z轴的负半轴上时，则x、y、z的符号为负；当点A、B、C与原点重合时，则x、y、z的值均为0．空间中点的坐标受空间直角坐标系的制约，同一个点，在不同的空间直角坐标系中，其坐标是不同的．【例1】如图，在长方体ABCD -A1B1C1D1中，E，F分别是棱BC，CC1上的点，|CF|＝|AB|＝2|CE|，|AB|∶|AD|∶|AA1|＝1∶2∶4.试建立适当的坐标系，写出E，F点的坐标．【解析】以A为坐标原点，射线AB，AD，AA1的方向分别为正方向建立空间直角坐标系，如图所示．【名师点睛】空间中点P坐标的确定方法（1）由P点分别作垂直于x轴、y轴、z轴的平面，依次交x轴、y轴、z轴于点P x、P y，P z，这三个点在x轴、y轴、z轴上的坐标分别为x，y，z，那么点P的坐标就是(x，y，z)．（2）若题所给图形中存在垂直于坐标轴的平面，或点P在坐标轴或坐标平面上，则要充分利用这一性质解题．【例2】如图所示，在长方体ABCD-A1B1C1D1中，|AD|=3，|DC|=4，|DD1|=2，E，F分别是BB1，D1B1的中点，求点A，B，C，D，A1，B1，C1，D1，E，F的坐标．【例3】如图，在正方体1111ABCD A B C D -中，,E F 分别是111,BB D B 的中点，棱长为1．试建立适当的空间直角坐标系，写出点,E F 的坐标．【解析】建立如图所示坐标系．方法一：E 点在xDy 面上的射影为,1,()1,0B B ，竖坐标为12．所以1(1,1,)2E ．F 在xDy 面上的射影为BD 的中点G ，竖坐标为1．所以11(,,1)22F ．方法二：11,()1,1B ，10,()0,1D ，()1,1,0B ，E 为1B B 的中点，F 为11B D 的中点．故E 点的坐标为111110(,,)222+++即1(1,1,)2，F 点的坐标为101011(,,)222+++，即11(,,1)22．2．求空间对称点的坐标求对称点的坐标一般依据“关于谁对称，谁保持不变，其余坐标相反”来解决．如关于横轴（x 轴）的对称点，横坐标不变，纵坐标、竖坐标变为原来的相反数；关于xOy 坐标平面的对称点，横坐标、纵坐标不变，竖坐标变为原来的相反数．【例4】设点是直角坐标系中一点，则点关于轴对称的点的坐标为A ．B ．C ．D ．【答案】A 【解析】点关于x 轴对称的点的坐标为．【例5】空间直角坐标系中，点关于点的对称点的坐标为A ．B ．C ．D ．【答案】C【名师点睛】（1）求空间对称点的规律方法空间的对称问题可类比平面直角坐标系中点的对称问题，要掌握对称点的变化规律，才能准确求解．对称点的问题常常采用“关于谁对称，谁保持不变，其余坐标相反”这个结论．（2）空间直角坐标系中，任一点P (x ，y ，z )的几种特殊对称点的坐标如下： ①关于原点对称的点的坐标是P 1（－x ，－y ，－z ）； ②关于x 轴（横轴）对称的点的坐标是P 2（x ，－y ，－z ）； ③关于y 轴（纵轴）对称的点的坐标是P 3（－x ，y ，－z ）； ④关于z 轴（竖轴）对称的点的坐标是P 4（－x ，－y ，z ）； ⑤关于xOy 坐标平面对称的点的坐标是P 5（x ，y ，－z ）； ⑥关于yOz 坐标平面对称的点的坐标是P 6（－x ，y ，z ）； ⑦关于xOz 坐标平面对称的点的坐标是P 7（x ，－y ，z ）．（3）点关于点的对称要用中点坐标公式解决，即已知空间中两点111222(,,),(,,)A x y z B x y z ，则AB 的中点P 的坐标为121212(,,)222x x y y z z +++． 3．空间两点间的距离公式（1）已知空间两点间的距离求点的坐标，是距离公式的逆应用，可直接设出该点坐标，利用待定系数法求解点的坐标．（2）若求满足某一条件的点，要先设出点的坐标，再建立方程或方程组求解．（3）利用空间两点间的距离公式判断三角形的形状时，需分别求出三边长，得到边长相等或者满足勾股定理；判断三点共线时，需分别求出任意两点连线的长度，判断其中两线段长度之和等于另一条线段长度．【例6】已知点()3,2,1M ，()1,0,5N ，求：（1）线段MN 的长度；（2）到,M N 两点的距离相等的点(),,P x y z 的坐标满足的条件．【例7】如图所示，建立空间直角坐标系Dxyz ，已知正方体ABCD-A 1B 1C 1D 1的棱长为1，点P 是正方体的体对角线D 1B 的中点，点Q 在棱CC 1上．当2|C 1Q|=|QC|时，求|PQ|．【例8】如图，在四棱锥P-ABCD 中，底面ABCD 是矩形，PA ⊥平面ABCD ，|AP|=|AB|=2，|BC|=2，E ，F 分别是AD ，PC 的中点．求证：PC ⊥BF ，PC ⊥EF ．【解析】如图，以A 为坐标原点，AB ，AD ，AP 所在直线分别为x 轴，y 轴，z 轴建立空间直角坐标系．∵|AP|=|AB|=2，|BC|=2，四边形ABCD 是矩形，∴A （0，0，0），B （2，0，0），C （2，2，0），D （0，2，0），P （0，0，2），∴|PB|==2，∴|PB|=|BC|，又F 为PC 的中点，∴PC ⊥BF ．∵(0,2,0)E ，∴222||(00)(20)(02)6PE =-+-+-=，222||(02)(222)(00)6CE =-+-+-=，∴||||PE CE =，又F 为PC 的中点，∴PC ⊥EF ．【例9】如图，已知正方体ABCD -A ′B ′C ′D ′的棱长为a ，M 为BD ′的中点，点N 在A ′C ′上，且|A ′N |＝3|NC ′|，试求|MN |的长．因为|A ′N |＝3|NC ′|，所以N 为A ′C ′的四等分点，从而N 为O ′C ′的中点，故N ⎝⎛⎭⎫a 4，34a ，a . 根据空间两点间的距离公式，可得|MN |＝⎝⎛⎭⎫a 2－a 42＋⎝⎛⎭⎫a 2－3a 42＋⎝⎛⎭⎫a 2－a 2＝64a .【名师点睛】求空间两点间的距离时，一般使用空间两点间的距离公式，应用公式的关键在于建立适当的坐标系，确定两点的坐标．确定点的坐标的方法视具体题目而定，一般说来，要转化到平面中求解，有时也利用几何图形的特征，结合平面直角坐标系的知识确定． 4．混淆平面与空间直角坐标系【例10】已知空间中两点(3,1,1)(2,2,3)A B ---、，在z 轴上有一点C ，它到A B 、两点的距离相等，求点C 的坐标．【错解】由已知得，AB 的中点坐标为51(,,2)22-，且AB 所在直线的斜率为3，故AB 的垂直平分线的斜率为13-，则垂直平分线的方程为15112()()3232z x y -=-+--，当0x y ==时，43z =，故点C 的坐标为4(0,0,)3．【错因分析】上面解法照搬平面解析几何中的解题思路而出现错误．由于点C 到A B 、两点的距离相等，故可求AB 的垂直平分线．以目前所学知识只能用两点间的距离公式求解．【正解】设点C 的坐标为(0,0,)z ，则22222231(1)2(2)(3)z z ++-=+-+-，即2210(1)3()8z z +-=+-，解得32z =，所以点C 的坐标为3(0,0,)2．【易错点睛】平面直角坐标系中的性质在空间直角坐标系中并不能全部适用，如平面直角坐标系中的中点公式，可类比到三维空间中，而直线方程及一些判定定理、性质在三维空间中不一定适用．1．在空间直角坐标系中，点P （1，2，3）关于x 轴对称的点的坐标为 A ．（－1，2，3） B ．（1，－2，－3） C ．（－1，－2，3）D ．（－1，2，－3）2．在空间直角坐标系中，点P （3，4，5）关于yOz 平面对称的点的坐标为 A ．（－3，4，5） B ．（－3，－4，5） C ．（3，－4，－5）D ．（－3，4，－5）3．如图，在正方体OABC －O 1A 1B 1C 1中，棱长为2，E 是B 1B 上的点，且|EB |＝2|EB 1|，则点E 的坐标为A ．（2，2，1）B ．（2，2，23）C ．（2，2，13）D ．（2，2，43）4．在长方体ABCD －A 1B 1C 1D 1中，若D （0，0，0）、A （4，0，0）、B （4，2，0）、A 1（4，0，3），则对角线AC 1的长为A．9 B．29C．5 D．2 65．已知点A（1，a，－5），B（2a，－7，－2）（a∈R）则|AB|的最小值是A．3 3 B．3 6C．2 3 D．2 66．点（2，0，3）在空间直角坐标系中的A．y轴上B．xOy面上C．xOz面上D．第一象限内7．在空间直角坐标系中，已知点P（1，2，3），过点P作平面yOz的垂线PQ，则垂足Q的坐标为A．（0，2，0）B．（0，2，3）C．（1，0，3）D．（1，0，0）8．如图所示，在长方体ABCO－A1B1C1O1中，OA＝1，OC＝2，OO1＝3，A1C1与B1O1交于P，分别写出A，B，C，O，A1，B1，C1，O1，P的坐标．9．（1）已知A（1，2，－1），B（2，0，2），①在x轴上求一点P，使|PA|＝|PB|；②在xOz平面内的点M到A点与到B点等距离，求M点轨迹．（2）在xOy平面内的直线x＋y＝1上确定一点M，使它到点N（6，5，1）的距离最小．10．在空间直角坐标系中，一定点P到三个坐标轴的距离都是1，则该点到原点的距离是A．62B． 3C．32D．6311．已知A点坐标为（1，1，1），B（3，3，3），点P在x轴上，且|PA|＝|PB|，则P点坐标为A．（6，0，0）B．（6，0，1）C．（0，0，6）D．（0，6，0）12．已知M（5，3，－2），N（1，－1，0），则点M关于点N的对称点P的坐标为________．13．在空间直角坐标系中，正方体ABCD－A1B1C1D1的顶点A的坐标为（3，－1，2），其中心M的坐标为（0，1，2），则该正方体的棱长等于________．14．如图所示，正方形ABCD，ABEF的边长都是1，并且平面ABCD⊥平面ABEF，点M在AC上移动，点N在BF上移动．若|CM|＝|BN|＝a（0<a<2）．（1）求MN的长度；（2）当a为何值时，MN的长度最短？15．如图，在棱长为1的正方体ABCD－A1B1C1D1中，M在线段BC1上，且|BM|＝2|MC1|，N是线段D1M的中点，求点M，N的坐标．16．如图所示，V-ABCD是正棱锥，O为底面中心，E，F分别为BC，CD的中点．已知|AB|＝2，|VO|＝3，建立如图所示空间直角坐标系，试分别写出各个顶点的坐标．17．如图，在棱长为1的正方体ABCD-A1B1C1D1中，以正方体的三条棱所在直线为轴建立空间直角坐标系Oxyz．（1）若点P在线段BD1上，且满足3|BP|＝|BD1|，试写出点P的坐标，并写出P关于y轴的对称点P′的坐标；（2）在线段C1D上找一点M，使点M到点P的距离最小，求出点M的坐标．18．如图，三棱柱ABC-A1B1C1中，所有棱长都为2，侧棱AA1⊥底面ABC，建立适当坐标系写出各顶点的坐标．19．（2017•上海）如图，以长方体ABCD﹣A1B1C1D1的顶点D为坐标原点，过D的三条棱所在的直线为坐标轴，建立空间直角坐标系，若1DB 的坐标为（4，3，2），则1AC 的坐标是__________．1 2 3 4 5 6 7 10 11 BADBBCBAA1．【答案】B【解析】关于x 轴对称，横坐标不变．故选B ． 2．【答案】A【解析】关于yOz 平面对称，y ，z 不变．故选A ． 3．【答案】D4．【答案】B【解析】由已知求得C 1（0，2，3），∴|AC 1|＝29．故选B ． 5．【答案】B【解析】|AB |2＝（2a －1）2＋（－7－a ）2＋（－2＋5）2＝5a 2＋10a ＋59＝5（a ＋1）2＋54．∴a ＝－1时，|AB |2的最小值为54．∴|AB |min ＝54＝36．故选B ． 6．【答案】C【解析】因为该点的y 坐标为0，根据坐标平面上点的特点可知该点在xOz 面上．故选C ． 7．【答案】B【解析】平面yOz 内点的横坐标为0．故选B ． 8．【答案】详见解析．9．【答案】（1）①P （1，0，0）；②M 点的轨迹是xOz 平面内的一条直线，其方程为x ＋3z －1＝0；（2）M （1，0，0）．【解析】（1）①设P （a ，0，0），则由已知得222(1)(2)1a -+-+2(2)4a -+，即a 2－2a ＋6＝a 2－4a ＋8，解得a ＝1，所以P 点坐标为（1，0，0）． ②设M （x ，0，z ），222(1)(2)(1)x z -+-++22(2)(2)x z -+- 整理得2x ＋6z －2＝0，即x ＋3z －1＝0．故M 点的轨迹是xOz 平面内的一条直线．（2）由已知，可设M （x ，1－x ，0），则|MN |＝222(6)(15)(01)x x -+--+-22(1)51x -+ 所以当x ＝1时，|MN |min ＝51，此时点M （1，0，0）． 10．【答案】A【解析】设P （x ，y ，z ），由题意可知222222111x y y z x z ⎧+=⎪+=⎨⎪+=⎩，∴x 2＋y 2＋z 2＝32．∴222x y z ++＝62．故选A ． 11．【答案】A【解析】设P （x ，0，0），|PA |2(1)11x -++，|PB |2(3)99x -++，由|PA |＝|PB |，得x ＝6．故选A ．12．【答案】（－3，－5，2）13．【答案】2393【解析】设正方体的棱长为a ，由|AM |＝9＋4＋0＝13可知，正方体的体对角线长为3a ＝213，故a ＝2133＝2393．14．【答案】（1221a a -+2）当a ＝22时，MN 的长度最短．【解析】因为平面ABCD ⊥平面ABEF ，且交线为AB ，BE ⊥AB ，所以BE ⊥平面ABCD ，所以BA ，BC ，BE 两两垂直．取B 为坐标原点，过BA ，BE ，BC 的直线分别为x 轴，y 轴和z 轴，建立空间直角坐标系．因为|BC |＝1，|CM |＝a ，点M 在坐标平面xBz 内且在正方形ABCD 的对角线上，所以点M （22a ，0，1－22a ）．因为点N 在坐标平面xBy 内且在正方形ABEF 的对角线上，|BN |＝a ，所以点N （22a ，22a ，0）．（1）由空间两点间的距离公式，得|MN |2222222()(0)(10)2222a a a a -+-+-- 221a a -+MN 221a a -+ （2）由（1），得|MN |＝221a a -+221()22a -+ 当a ＝22（满足0<a <2221()22a -+取得最小值，即MN 的长度最短，最短为22． 15．【答案】M ⎝⎛⎭⎫13，1，23；N ⎝⎛⎭⎫16，12，56．16．【答案】V （0，0，3），A （－1，－1，0），B （1，－1，0），C （1，1，0），D （－1，1，0）．【解析】∵底面是边长为2的正方形，∴|CE |＝|CF |＝1． ∵O 点是坐标原点，∴C （1，1，0），同样的方法可以确定B （1，－1，0），A （－1，－1，0），D （－1，1，0）． ∵V 在z 轴上，∴V （0，0，3）．17．【答案】（1）P ′⎝⎛⎭⎫－23，23，－13；（2）当m ＝12时，|MP |取得最小值22，此时点M 为⎝⎛⎭⎫0，12，12．【解析】（1）由题意知P 的坐标为⎝⎛⎭⎫23，23，13， P 关于y 轴的对称点P ′的坐标为⎝⎛⎭⎫－23，23，－13．（2）设线段C 1D 上一点M 的坐标为（0，m ，m ），则有|MP |＝⎝⎛⎭⎫－232＋⎝⎛⎭⎫m －232＋⎝⎛⎭⎫m －132＝2m 2－2m ＋1＝2⎝⎛⎭⎫m －122＋12．当m ＝12时，|MP |取得最小值22，所以点M 为⎝⎛⎭⎫0，12，12． 18．【答案】详见解析．19．【答案】（﹣4，3，2）【解析】如图，以长方体ABCD ﹣A 1B 1C 1D 1的顶点D 为坐标原点，过D 的三条棱所在的直线为坐标轴，建立空间直角坐标系，∵1DB 的坐标为（4，3，2），∴A （4，0，0），C 1（0，3，2），∴1AC （﹣4，3，2）．故答案为：（﹣4，3，2）．。

高中数学必修第二册讲义

高中数学必修二（人教A 版2019)同步讲义与练习6.1平面向量的概念 1 6.2.1向量的加法运算 9 6.2.2向量的减法运算 15 6.2.3向量的数乘运算 20 6.2.4向量的数量积 25 6.3.1平面向量基本定理 30 6.3.2平面向量加、减运算的坐标表示 35 6.3.3平面向量数乘运算的坐标表示 39 6.3.4平面向量数量积的坐标表示 44 6.4.1平面向量的几何、物理应用 48 6.4.2余弦定理 53 6.4.3正弦定理 57 6.4.4余弦定理、正弦定理应用举例 61微专题:平面向量数量积的综合应用 69第六章章末复习 70第六章章末练习1 73第六章章末练习2 76第六章章末测试卷 787.1.1数系的扩充和复数的概念 82 7.1.2复数的几何意义 87 7.2.1复数的加、减运算及其几何意义 91 7.2.2复数的乘、除运算 95第七章章末复习 99第七章章末测试卷 101期中检测试卷（前两章） 1048.1.1棱柱、棱锥、棱台 107 8.1.2圆柱、圆锥、圆台、球、简单组合体 115 8.2　立体图形的直观图 123 8.3.1　棱柱、棱锥、棱台的表面积和体积 129 8.3.2　圆柱、圆锥、圆台、球的表面积和体积 135 8.4.1平　面 140 8.4.2　空间点、直线、平面之间的位置关系 147 8.5.1　直线与直线平行 153 8.5.2　直线与平面平行 160 8.5.3　平面与平面平行 167 8.6.1　直线与直线垂直 174 8.6.2　直线与平面垂直 181 8.6.3　平面与平面垂直 191第八章微专题1　与球有关的内切、外接问题 199第八章微专题2　求二面角的平面角的常见解法 200第八章章末复习 201第八章章末练习1 207第八章章末练习2 209第八章章末检测试卷 213 9.1.1　简单随机抽样 219 9.1.2分层随机抽样 225 9.2.1总体取值规律的估计 231 9.2.2总体百分位数的估计 240 9.2.3总体集中趋势的估计 249 9.2.4总体离散程度的估计 256第九章章末复习 261第九章章末练习 265第九章测试卷 269 10.1.1有限样本空间与随机事件 276 10.1.2事件的关系和运算 282 10.1.3古典概型 288 10.1.4概率的基本性质 293 10.2事件的相互独立性 298 10.3频率与概率 304第十章微专题：古典概型的应用 311第十章章末复习 312第十章章末练习 316第十章末检测试卷 318期末检测试卷(一) 322期末检测试卷(二) 3276.1平面向量的概念知识点一　向量的概念1.向量：既有大小又有方向的量叫做向量.2.数量：只有大小没有方向的量称为数量.知识点二　向量的几何表示1.有向线段：具有方向的线段叫做有向线段，它包含三个要素：起点、方向、长度，如图所示.以A 为起点、B 为终点的有向线段记作AB ，2.向量的表示(1)几何表示：向量可以用有向线段表示，有向线段的长度表示向量的大小，有向线段的方向表示向量的方向.(2)字母表示：向量可以用字母a ，b ，c ，⋯表示(印刷用黑体a ，b ，c ，书写时用a ，b ，c ).3.模、零向量、单位向量向量AB 的大小，称为向量AB 的长度(或称模)，记作|AB |.长度为0的向量叫做零向量，记作0；长度等于1个单位长度的向量，叫做单位向量.1.思考　“向量就是有向线段，有向线段就是向量”的说法对吗？知识点三　相等向量与共线向量1.平行向量：方向相同或相反的非零向量叫做平行向量.(1)记法：向量a 与b 平行，记作a ∥b .(2)规定：零向量与任意向量平行.2.相等向量：长度相等且方向相同的向量叫做相等向量.3.共线向量：由于任一组平行向量都可以平移到同一直线上，所以平行向量也叫做共线向量.要注意避免向量平行、共线与平面几何中的直线、线段的平行和共线相混淆.2.思考:　(1)平行向量是否一定方向相同？(2)不相等的向量是否一定不平行？(3)与任意向量都平行的向量是什么向量？(4)若两个向量在同一直线上，则这两个向量一定是什么向量？3.如果|AB |>|CD |，那么AB >CD .()4.若a ，b 都是单位向量，则a =b .()5.力、速度和质量都是向量.()6.零向量的大小为0，没有方向.()一、向量的概念【例1】.(多选)下列说法错误的有()A.向量AB 与向量BA 的长度相等B.两个有共同起点，且长度相等的向量，它们的终点相同C.零向量都是相等的D.若两个单位向量平行，则这两个单位向量相等【跟踪训练1.1】.下列说法中正确的是()A.数量可以比较大小，向量也可以比较大小B.方向不同的向量不能比较大小，但同向的向量可以比较大小C.向量的大小与方向有关D.向量的模可以比较大小二、向量的几何表示及应用【例2】.一辆汽车从A 点出发向西行驶了100km 到达B 点，然后又改变方向，向西偏北50°的方向走了200km 到达C 点，最后又改变方向，向东行驶了100km 到达D 点.(1)作出向量AB ，BC ，CD ；(2)求|AD |.【跟踪训练2.1】.在如图的方格纸上，已知向量a ，每个小正方形的边长为1.(1)试以B 为终点画一个向量b ，使b =a ；(2)在图中画一个以A 为起点的向量c ，使|c |=5，并说出向量c 的终点的轨迹是什么？三、相等向量与共线向量【例3】.如图所示，△ABC 的三边均不相等，E ，F ，D 分别是AC ，AB ，BC 的中点.(1)写出与EF 共线的向量；(2)写出模与EF 的模相等的向量；(3)写出与EF 相等的向量.【跟踪训练3.1】.如图所示，O 是正六边形ABCDEF 的中心.(1)与OA 的模相等的向量有多少个？(2)是否存在与OA 长度相等、方向相反的向量？若存在，有几个？(3)与OA 共线的向量有几个？四、特殊向量的作用【例4】.给出下列命题：①若a ∥b ，则a 与b 的方向相同或相反；②若a ∥b ，b ∥c ，则a ∥c ；③若两个模相等的向量互相平行，则这两个向量相等；④若a =b ，b =c ，则a =c ，其中正确的是.(填序号)1.在同一平面内，把所有长度为1的向量的起点固定在同一点，这些向量的终点形成的轨迹是()A.单位圆B.一段弧C.线段D.直线2.(多选)下列说法错误的有()A.共线的两个单位向量相等B.相等向量的起点相同C.若AB ∥CD ，则一定有直线AB ∥CDD.若向量AB ，CD 共线，则点A ，B ，C ，D 必在同一直线上3.若|AB |=|AD |且BA =CD ，则四边形ABCD 的形状为()A.平行四边形 B.矩形 C.菱形 D.等腰梯形4.如图所示，设O 是正方形ABCD 的中心，则下列结论正确的有.(填序号)①AO =OC ；②AO ∥AC ；③AB 与CD 共线；④AO =BO .5.已知A ，B ，C 是不共线的三点，向量m 与向量AB 是平行向量，与BC 是共线向量，则m =________.1.给出下列物理量：①质量；②速度；③位移；④力；⑤路程；⑥功；⑦加速度.其中是向量的有()A.4个 B.5个C.6个D.7个2.(多选)下列命题中错误的有()A.温度含零上和零下温度，所以温度是向量B.向量的模是一个正实数C.向量a 与b 不共线，则a 与b 都是非零向量D.若|a |>|b |，则a >b3.设O 是△ABC 的外心，则AO ，BO ，CO 是()A.相等向量 B.模相等的向量 C.平行向量 D.起点相同的向量4.如图所示，梯形ABCD 为等腰梯形，则两腰上的向量AB 与DC 的关系是()A.AB =DCB.|AB |=|DC |C.AB >DCD.AB <DC5.下列说法正确的是()A.若a ∥b ，则a =b B.若|a |=|b |，则a =b C.若a =b ，则a 与b 共线 D.若a ≠b ，则a 一定不与b 共线6.若A 地位于B 地正西方向5km 处，C 地位于A 地正北方向5km 处，则C 地相对于B 地的位移的大小是km ，方向是.7.已知在边长为2的菱形ABCD 中，∠ABC =60°，则|BD |=.8.如图，在菱形ABCD 中，∠BAD =120°，则以下说法正确的是.(填序号)①与AB 相等的向量只有1个(不含AB )；②与AB 的模相等的向量有9个(不含AB )；③BD 的模恰为DA 的模的3倍；④CB 与DA 不共线.9.如图所示，在四边形ABCD 中，AB =DC ，N ，M 分别是AD ，BC 上的点，且CN =MA ，求证：DN =MB .10.一辆消防车从A 地去B 地执行任务，先从A 地向北偏东30°方向行驶2千米到D 地，然后从D 地沿北偏东60°方向行驶6千米到达C 地，从C 地又向南偏西30°方向行驶2千米才到达B 地.(1)画出AD ，DC ，CB ，AB ；(2)求B 地相对于A 地的位移.11.如图所示，四边形ABCD ，CEFG ，CGHD 是全等的菱形，则下列结论中不一定成立的是()A.|AB |=|EF |B.AB 与FH 共线C.BD 与EH 共线D.CD =FG12.在如图所示的半圆中，AB 为直径，点O 为圆心，C 为半圆上一点，且∠OCB =30°，|AB |=2，则|AC |=.13.已知在四边形ABCD 中，BC =AD 且|AB |=|BD |=|BC |=2，则该四边形内切圆的面积是.14.一艘海上巡逻艇从港口向北航行了30km ，这时接到求救信号，在巡逻艇的正东方向40km 处有一艘渔船抛锚需救助.试求：(1)巡逻艇从港口出发到渔船出事点所航行的路程；(2)巡逻艇从港口出发到出事地点之间的位移.15.设O 是正方形ABCD 对角线的交点，四边形OAED ，OCFB 都是正方形，在如图所示的向量中：(1)分别找出与AO ，BO 相等的向量；(2)找出与AO共线的向量；(3)找出与AO模相等的向量；(4)向量AO 与CO是否相等？16.如图的方格纸由若干个边长为1的小正方形组成，方格纸中有两个定点A ，B .点C 为小正方形的顶点，且|AC|= 5.(1)画出所有的向量AC ；(2)求|BC|的最大值与最小值.6.2.1向量的加法运算知识点一　向量加法的定义及其运算法则1.向量加法的定义求两个向量和的运算，叫做向量的加法.2.向量求和的法则向量求和的法则三角形法则已知非零向量a ，b ，在平面内任取一点A ，作AB=a ，BC=b ，则向量AC 叫做a 与b 的和，记作a +b ，即a +b =AB +BC =AC.这种求向量和的方法，称为向量加法的三角形法则.对于零向量与任意向量a ，规定a +0 =0+a =a平行四边形法则以同一点O 为起点的两个已知向量a ，b 为邻边作▱OACB ，则以O 为起点的对角线OC就是a 与b 的和.把这种作两个向量和的方法叫做向量加法的平行四边形法则1.思考　|a +b |与|a |，|b |有什么关系？知识点二向量加法的运算律交换律a +b =b +a 结合律(a +b )+c =a +(b +c )2.0 +a =a +0=a .()3.AB +BC =AC .()4.AB +BA =0 .()5.AB +BC >AC .()6.|AB |+|BC|=|AC |.()一、向量加法法则【例1】.(1)如图①所示，求作向量a +b .(2)如图②所示，求作向量a +b +c .【跟踪训练1.1】.如图所示，O 为正六边形ABCDEF 的中心，化简下列向量.(1)OA +OC =；(2)BC +FE =；(3)OA +FE=.二、向量加法运算律的应用【例2】.化简：(1)BC +AB ；(2)DB +CD +BC ；(3)AB +DF +CD +BC +FA .【跟踪训练2.1】.已知正方形ABCD 的边长等于1，则|AB +AD +BC +DC |=.三、向量加法的实际应用【例3】.河水自西向东流动的速度为10km/h ，小船自南岸沿正北方向航行，小船在静水中的速度为103km/h ，求小船的实际航行速度.【跟踪训练3.1】.如图，用两根绳子把重10N 的物体W 吊在水平杆子AB 上，∠ACW =150°，∠BCW =120°，求A 和B 处所受力的大小.(绳子的重量忽略不计)1.化简CB +AD+BA 等于()A.DBB.CAC.CDD.DC2.下列等式不正确的是()①a +(b +c )=(a +c )+b ；②AB +BA=0；③AC =DC +AB +BD .A.②③B.②C.①D.③3.在四边形ABCD 中，AC =AB +AD，则()A.四边形ABCD 一定是矩形B.四边形ABCD 一定是菱形C.四边形ABCD 一定是正方形D.四边形ABCD 一定是平行四边形4.如图，四边形ABCD 是梯形，AD ∥BC ，对角线AC 与BD 相交于点O ，则OA +BC +AB +DO等于()A.CDB.DCC.DAD.DO5.已知向量a 表示“向东航行3km ”，b 表示“向南航行3km ”，则a +b 表示.1.化简AE +EB +BC等于()A.ABB.BAC.0D.AC2.如图，在正六边形ABCDEF 中，BA +CD +EF等于()A.0B.BEC.ADD.CF3.若正方形ABCD 的边长为1，则|AB +AD|等于()A.1B.2C.3D.224.已知四边形ABCD 为菱形，则下列等式中成立的是()A.AB +BC =CAB.AB +AC =BCC.AC +BA =ADD.AC +AD =DC5.(多选)下列说法错误的有()A.如果非零向量a 与b 的方向相同或相反，那么a +b 的方向必与a 或b 的方向相同B.在△ABC 中，必有AB +BC +CA =0C.若AB +BC +CA=0，则A ，B ，C 一定为一个三角形的三个顶点D.若a ，b 均为非零向量，则|a +b |=|a |+|b |6.已知AB =a ，BC =b ，CD =c ，DE =d ，AE =e ，则a +b +c +d =________.7.在菱形ABCD 中，∠BAD =60°，|AB |=1，则|BC +CD |=________.8.如图，在平行四边形ABCD 中，O 是AC 和BD 的交点.(1)AB +AD +CD =________；(2)AC +BA +DA =________.9.如图，已知在▱ABCD 中，O 是两条对角线的交点，E 是CD 的一个三等分点(靠近D 点)，求作：(1)AO +AC ；(2)DE +BA.10.在静水中船的速度为20m /min ，水流的速度为10m /min ，如果船从岸边出发沿垂直于水流的航线到达对岸，求船行进的方向.11.在矩形ABCD 中，|AB |=4，|BC |=2，则向量AB +AD +AC 的长度为()A.25B.45C.12D.612.若在△ABC 中，AB =AC =1，|AB +AC |=2，则△ABC 的形状是()A.正三角形B.锐角三角形C.斜三角形D.等腰直角三角形13.已知点G 是△ABC 的重心，则GA +GB +GC =.14.如图所示，已知电线AO 与天花板的夹角为60°，电线AO 所受拉力|F 1|=24N ，绳BO 与墙壁垂直，所受拉力|F 2|=12N .则F 1和F 2的合力为N .15.如图所示，P ，Q 是△ABC 的边BC 上两点，且BP =QC .求证：AB +AC =AP +AQ.16.如图，已知D ，E ，F 分别为△ABC 的三边BC ，AC ，AB 的中点，求证：AD +BE +CF =0 .6.2.2向量的减法运算知识点一　相反向量1.定义：与向量a 长度相等，方向相反的向量，叫做a 的相反向量，记作-a .2.性质(1)零向量的相反向量仍是零向量.(2)对于相反向量有：a +(-a )=(-a )+a =0 .(3)若a ，b 互为相反向量，则a =-b ，b =-a ，a +b =0 .知识点二　向量的减法1.定义：向量a 加上b 的相反向量，叫做a 与b 的差，即a -b =a +(-b )，因此减去一个向量，相当于加上这个向量的相反向量，求两个向量差的运算，叫做向量的减法.2.几何意义：在平面内任取一点O ，作OA =a ，OB=b ，则向量a -b =BA ，如图所示.3.文字叙述：如果把两个向量的起点放在一起，那么这两个向量的差是以减向量的终点为起点，被减向量的终点为终点的向量.1.思考　若a ，b 是不共线向量，|a +b |与|a -b |的几何意义分别是什么？2.相反向量就是方向相反的向量.()3.向量AB 与BA是相反向量.()4.a -b =b -a .()5.两个相等向量之差等于0.()一、向量的减法运算【例1】.如图，已知向量a ，b ，c 不共线，求作向量a +b -c .【跟踪训练1.1】.如图所示，O 为△ABC 内一点，OA =a ，OB =b ，OC =c .求作：b +c -a .二、向量减法法则的应用【例2】.(1)化简：(AD -BM)+(BC -MC )=________.(2)如图，P ，Q 是△ABC 的边BC 上的两点，且BP =QC，则化简AB +AC -AP -AQ 的结果为()A.0B.BPC.PQD.PC【跟踪训练2.1】.如图，已知O 为平行四边形ABCD 内一点，OA =a ，OB =b ，OC=c ，则OD =.1.在△ABC 中，若BA =a ，BC=b ，则CA 等于()A.aB.a +bC.b -aD.a -b2.化简OP -QP +PS +SP等于()A.QPB.OQC.SPD.SQ3.已知在四边形ABCD 中，DB -DA=AC -AD ，则四边形ABCD 一定是()A.平行四边形B.菱形C.矩形D.正方形4.下列等式成立的个数是()①a +b =b +a ；②a -b =b -a ；③0-a =-a ；④-(-a )=a ；⑤a +(-a )=0.A.5B.4C.3D.25.(多选)下列各向量运算的结果与AC相等的有()A.AO +OCB.AO -OCC.OA -OCD.OC -OA1.如图所示，在▱ABCD 中，AB =a ，AD =b ，则用a ，b 表示向量AC 和BD分别是()A.a +b 和a -bB.a +b 和b -aC.a -b 和b -aD.b -a 和b +a2.AB -CB -DC +DE等于()A.ABB.AEC.BED.CD3.下列各式中，恒成立的是()A.AB =BAB.a -a =0C.AB -AC =BCD.AB -CB +CA =04.(多选)下列四个式子中可以化简为AB的是()A.AC +CD -BDB.AC -CBC.OA +OBD.OB -OA5.如图，在四边形ABCD 中，设AB =a ，AD =b ，BC =c ，则DC 等于()A.a -b +cB.b -(a +c )C.a +b +cD.b -a +c6.OB -OA -OC -CO =.7.若菱形ABCD 的边长为2，则|AB -CB +CD|=.8.在边长为1的正三角形ABC 中，|AB -BC |的值为.9.如图，已知a ，b ，求作a -b .10.如图所示，已知正方形ABCD 的边长为1，AB =a ，BC =b ，AC =c ，试求：|a -b +c |.11.若|AB |=5，|AC |=8，则|BC|的取值范围是()A.[3,8]B.(3,8)C.[3,13]D.(3,13)12.平面上有三点A ，B ，C ，设m =AB +BC ，n =AB -BC ，若m ，n 的长度恰好相等，则()A.A ，B ，C 三点必在同一直线上B.△ABC 必为等腰三角形且∠ABC 为顶角C.△ABC 必为直角三角形且∠ABC =90°D.△ABC 必为等腰直角三角形13.已知OA =a ，OB =b ，若|OA |=12，|OB |=5，且∠AOB =90°，则|a -b |=.14.如图所示，O 是平行四边形ABCD 的对角线AC ，BD 的交点，设AB =a ，DA =b ，OC =c .证明：b +c -a =OA.15.设点M 是线段BC 的中点，点A 在直线BC 外，且|BC |=4，|AB +AC |=|AB -AC |，则|AM |=.16.如图，在五边形ABCDE 中，若四边形ACDE 是平行四边形，且AB =a ，AC =b ，AE =c ，试用a ，b ，c 表示向量BD ，BC ，BE ，CD及CE .6.2.3向量的数乘运算知识点一　向量数乘的定义实数λ与向量a 的积是一个向量，这种运算叫做向量的数乘，记作λa ，其长度与方向规定如下：(1)|λa |=|λ||a |.(2)λa (a ≠0)的方向当λ>0时，与a 的方向相同；当λ<0时，与a 的方向相反.特别地，当λ=0时，λa =0.当λ=-1时，(-1)a =-a .知识点二　向量数乘的运算律1.(1)λ(μa )=(λμ)a .(2)(λ+μ)a =λa +μa .(3)λ(a +b )=λa +λb .特别地，(-λ)a =-λa =λ(-a )，λ(a -b )=λa -λb .2.向量的线性运算向量的加、减、数乘运算统称为向量的线性运算，对于任意向量a ，b ，以及任意实数λ，μ1，μ2，恒有λ(μ1a ±μ2b )=λμ1a ±λμ2b .知识点三　向量共线定理向量a (a ≠0)与b 共线的充要条件是：存在唯一一个实数λ，使b =λa .1.思考　向量共线定理中为什么规定a ≠0?2.若向量b 与a 共线，则存在唯一的实数λ使b =λa .()3.若b =λa ，则a 与b 共线.()4.若λa =0 ，则a =0 .()5.|λa |=λ|a |.()一、向量的线性运算【例1】.若a =2b +c ，化简3(a +2b )-2(3b +c )-2(a +b )等于( )A.-aB.-bC.-cD.以上都不对【跟踪训练1.1】.若3(x +a )+2(x -2a )-4(x -a +b )=0，则x =.【跟踪训练1.2】.计算：(a +b )-3(a -b )-8a .二、用已知向量表示其他向量【例2】.如图，在▱ABCD 中，E 是BC 的中点，若AB =a ，AD =b ，则DE 等于()A.12a -b B.12a +b C.a +12b D.a -12b 【跟踪训练2.1】.在△ABC 中，若点D 满足BD=2DC ，则AD 等于()A.13AC +23AB B.53AB -23AC C.23AC -13ABD.23AC+13AB 三、向量共线的判定及应用【例3】.设a ，b 是不共线的两个向量.(1)若OA =2a -b ，OB =3a +b ，OC =a -3b ，求证：A ，B ，C 三点共线；(2)若8a +k b 与k a +2b 共线，求实数k 的值.【跟踪训练3.1】.已知向量e 1，e 2不共线，如果AB =e 1+2e 2，BC =-5e 1+6e 2，CD =7e 1-2e 2，则共线的三个点是.四、三点共线的常用结论【例4】.典例　如图所示，在△ABC 中，点O 是BC 的中点.过点O 的直线分别交直线AB ，AC 于不同的两点M ，N ，若AB =mAM ，AC =nAN，则m +n 的值为()A.1B.2C.3D.41.下列运算正确的个数是()①(-3)·2a =-6a ；②2(a +b )-(2b -a )=3a ；③(a +2b )-(2b +a )=0.A.0B.1C.2D.32.如图，已知AM 是△ABC 的边BC 上的中线，若AB =a ，AC =b ，则AM 等于()A.12(a -b ) B.-12(a -b ) C.12(a +b ) D.-12(a +b )3.设P 是△ABC 所在平面内一点，BC +BA =2BP，则()A.PA +PB =0B.PC +PA =0C.PB +PC =0D.PA +PB +PC =04.化简4(a -3b )-6(-2b -a )=.5.设e 1与e 2是两个不共线向量，AB =3e 1+2e 2，CB =k e 1+e 2，CD=3e 1-2k e 2，若A ，B ，D 三点共线，则k =.1.下列说法中正确的是()A.λa 与a 的方向不是相同就是相反B.若a ，b 共线，则b =λaC.若|b |=2|a |，则b =±2aD.若b =±2a ，则|b |=2|a |2.(多选)下列各式计算正确的有()A.(-7)6a =-42aB.7(a +b )-8b =7a +15bC.a -2b +a +2b =2aD.4(2a +b )=8a +4b3.设e 1，e 2是两个不共线的向量，若向量m =-e 1+k e 2(k ∈R )与向量n=e 2-2e 1共线，则()A.k =0B.k =1C.k =2D.k =124.下列各组向量中，一定能推出a ∥b 的是()①a =-3e ，b =2e ；②a =e 1-e 2，b =e 1+e 22-e 1；③a =e 1-e 2，b =e 1+e 2+e 1+e 22.A.①B.①②C.②③D.①②③5.已知m ，n 是实数，a ，b 是向量，则下列说法中正确的是()①m (a -b )=m a -m b ；②(m -n )a =m a -n a ；③若m a =m b ，则a =b ；④若m a =n a ，则m =n .A.②④B.①②C.①③D.③④6.已知向量a ，b 满足|a |=3，|b |=5，且a =λb ，则实数λ的值是.7.14(a +2b )-16(5a -2b )+14a =.8.设D ，E 分别是△ABC 的边AB ，BC 上的点，AD =12AB ，BE =23BC .若AB =a ，AC =b ，则DE =.(用a ，b 表示)9.计算：(1)6(3a -2b )+9(-2a +b )；(2)6(a -b +c )-4(a -2b +c )-2(-2a +c ).10.设a ，b 是两个不共线的非零向量，若向量2k a +b 与8a +k b 的方向相反，求k 的值.11.设D ，E ，F 分别为△ABC 的三边BC ，CA ，AB 的中点，则EB +FC 等于()A.BCB.12ADC.ADD.12BC 12.在△ABC 中，已知D 是AB 边上的一点，若CD =13CA +λCB，则λ等于()A.13B.23C.12D.3413.如果实数p 和非零向量a 与b 满足p a +(p +1)b =0，则向量a 和b .(填“共线”或“不共线”)14.已知在△ABC 中，点M 满足MA +MB +MC =0 ，若存在实数m 使得AB +AC =mAM成立，则m =.15.已知在四边形ABCD 中，AB =a +2b ，BC =-4a -b ，CD =-5a -3b ，求证：四边形ABCD 为梯形.16.设a ，b ，c 为非零向量，其中任意两向量不共线，已知a +b 与c 共线，且b +c 与a 共线，则b 与a +c 是否共线？请证明你的结论.6.2.4向量的数量积知识点一　两向量的夹角与垂直1.夹角：已知两个非零向量a 和b ，O 是平面上的任意一点，作OA =a ，OB=b ，则∠AOB =θ(0≤θ≤π)叫做向量a 与b 的夹角(如图所示).当θ=0时，a 与b 同向；当θ=π时，a 与b 反向.2.垂直：如果a 与b 的夹角是π2，则称a 与b 垂直，记作a ⊥b .知识点二　向量数量积的定义非零向量a ，b 的夹角为θ，数量|a ||b |c os θ叫做向量a 与b 的数量积(或内积)，记作a ·b ，即a ·b =|a ||b |c os θ，规定：零向量与任一向量的数量积等于0.1.思考　若a ≠0 ，且a ·b =0，是否能推出b =0 .知识点三　投影向量在平面内任取一点O ，作OM =a ，ON =b ，过点M 作直线ON 的垂线，垂足为M 1，则OM 1就是向量a 在向量b 上的投影向量.设与b 方向相同的单位向量为e ，a 与b 的夹角为θ，则OM 1与e ，a ，θ之间的关系为OM 1=|a |c os θe.知识点四　平面向量数量积的性质设向量a 与b 都是非零向量，它们的夹角为θ，e 是与b 方向相同的单位向量.则(1)a ·e =e·a =|a |·c os θ.(2)a ⊥b ⇔a ·b =0.(3)当a ∥b 时，a ·b =|a ||b |，a 与b 同向，-|a ||b |，a 与b 反向.特别地，a ·a =|a |2或|a |=a ·a .(4)|a ·b |≤|a ||b |.知识点五　平面向量数量积的运算律1.a ·b =b ·a (交换律).2.(λa )·b =λ(a ·b )=a ·(λb )(数乘结合律).3.(a +b )·c =a ·c +b ·c (分配律).2.思考　若a ·b =b ·c ，是否可以得出结论a =c ?3.向量a 在向量b 上的投影向量一定与b 共线.()4.若a ·b <0，则a 与b 的夹角为钝角.()5.向量的数量积运算满足(a ·b )·c =a ·(b ·c ).()6.已知a ≠0 ，且a ·c =a ·b ，则b =c .()一、求两向量的数量积【例1】.已知正三角形ABC 的边长为1，求：(1)AB ·AC ；(2)AB ·BC ；(3)BC ·AC .【跟踪训练1.1】.已知|a |=4，|b |=7，且向量a 与b 的夹角为120°，求(2a +3b )·(3a -2b ).二、向量的模和夹角的计算问题【例2】.已知向量a ，b 的夹角为60°，|a |=2，|b |=1，则|a +2b |=.【跟踪训练2.1】.已知非零向量a ，b 满足|a |=1，且(a -b )·(a +b )=34.①求|b |；②当a ·b =-14时，求向量a 与a +2b 的夹角θ的值.【跟踪训练2.2】.已知|a |=|b |=2，(a +2b )·(a -b )=-2，求a 与b 的夹角.三、与垂直有关的问题【例3】.已知非零向量m ，n 满足4|m |=3|n |，m 与n 夹角的余弦值为13，若n ⊥(tm +n )，则实数t 的值为()A.4B.-4C.94D.-94【跟踪训练3.1】.已知向量a ，b ，且|a |=1，|b |=2，(a +2b )⊥(3a -b )，求向量a 与b 夹角的大小.1.对于任意向量a ，b ，c ，下列命题中正确的是()A.|a ·b |=|a ||b |B.|a +b |=|a |+|b |C.(a ·b )c =a (b ·c )D.|a |=a 22.(多选)已知两个单位向量e 1，e 2的夹角为θ，则下列结论正确的是()A.e 1在e 2方向上的投影向量为c os θe 2B.e 21=e 22C.(e 1+e 2)⊥(e 1-e 2)D.e 1·e 2=13.设e 1和e 2是互相垂直的单位向量，且a =3e 1+2e 2，b =-3e 1+4e 2，则a ·b 等于()A.-2B.-1C.1D.24.已知向量a ，b 满足|a |=2，|b |=1，a ·b =1，则向量a 与a -b 的夹角为_.5.已知|a |=3，|b |=5，且a ·b =12，与b 同向的单位向量为e ，则向量a 在向量b 的方向上的投影向量为.1.已知|a |=1，|b |=2，a 与b 的夹角为π3，则a ·b 等于()A.1B.2C.3D.42.在等腰直角三角形ABC 中，若∠C =90°，AC =2，则BA ·BC的值等于( )A.-2B.2C.-22D.223.已知a ，b 方向相同，且|a |=2，|b |=4，则|2a +3b |等于()A.16B.256C.8D.644.已知|a |=8，与a 同向的单位向量为e ，|b |=4，a ，b 的夹角为120°，则向量b 在向量a 方向上的投影向量为()A.4eB.-4eC.2eD.-2e5.设向量a ，b 满足|a +b |=10，|a -b |=6，则a ·b 等于()A.1B.2C.3D.56.已知在△ABC 中，AB =AC =4，AB ·AC =8，则△ABC 的形状是.7.已知a ⊥b ，|a |=2，|b |=3，且3a +2b 与λa -b 垂直，则λ=.8.已知向量OA ⊥AB ，|OA |=3，则OA ·OB =.9.已知向量a ，b 的夹角为60°，且|a |=2，|b |=1，若c =2a -b ，d =a +2b ，求：(1)c ·d ；(2)|c +2d |.10.已知单位向量e 1与e 2的夹角为α，且c os α=13，向量a =3e 1-2e 2与b =3e 1-e 2的夹角为β，求β的余弦值.11.在△ABC 中，AB =6，O 为△ABC 的外心，则AO ·AB等于()A.6B.6C.12D.1812.已知菱形ABCD 的边长为a ，∠ABC =60°，则BD ·CD等于()A.-32a 2B.-34a 2 C.34a 2 D.32a 213.已知平面上三点A ，B ，C 满足|AB |=3，|BC |=4，|CA |=5，则AB ·BC +BC ·CA+CA ·AB的值等于()A.-7B.7C.25D.-2514.已知a 是平面内的单位向量，若向量b 满足b ·(a -b )=0，则|b |的最小值为，最大值为.15.已知a，b是单位向量，a·b=0，若向量c满足|c-b-a|=1，则|c|的取值范围为()A.[2-1，2+1]B.[2-1，2+2]C.[1，2+1]D.[1，2+2]16.已知平面上三个向量a，b，c的模均为1，它们相互之间的夹角均为120°.(1)求证：(a-b)⊥c；(2)若|k a+b+c|>1(k∈R)，求k的取值范围.6.3.1平面向量基本定理知识点　平面向量基本定理1.平面向量基本定理：如果e 1，e 2是同一平面内的两个不共线向量，那么对于这一平面内的任一向量a ，有且只有一对实数λ1，λ2，使a =λ1e 1+λ2e2.2.基底：若e 1，e 2不共线，我们把{e 1，e 2}叫做表示这一平面内所有向量的一个基底.1.平面内任意两个向量都可以作为平面内所有向量的一个基底.()2.{0 ，e}可以作为基底.()3.平面向量基本定理中基底的选取是唯一的.()4.若e 1，e 2是同一平面内两个不共线向量，则λ1e 1+λ2e 2(λ1，λ2为实数)可以表示该平面内所有向量.()一、平面向量基本定理的理解【例1】.(多选)设{e 1，e 2}是平面内所有向量的一个基底，则下列四组向量中，能作为基底的是()A.e 1+e 2和e 1-e 2B.3e 1-4e 2和6e 1-8e 2C.e 1+2e 2和2e 1+e 2D.e 1和e 1+e 2【跟踪训练1.1】.已知向量{a ，b }是一个基底，实数x ，y 满足(3x -4y )a +(2x -3y )b =6a +3b ，则x -y =.二、用基底表示向量【例2】.如图，已知在梯形ABCD 中，AB ∥CD ，AB =2CD ，E ，F 分别是DC ，AB 的中点，设AD =a ，AB =b ，试用{a ，b }为基底表示DC ，EF ，FC .延伸探究　1.本例中若取BC 的中点G ，则AG =.2.本例中若EF 的中点为H ，试表示出BH .【跟踪训练2.1】.如图，在正方形ABCD 中，设AB =a ，AD =b ，BD =c ，则以{a ，b }为基底时，AC 可表示为，以{a ，c }为基底时，AC 可表示为.1.设点O 是平行四边形ABCD 两对角线的交点，下列向量组：①AD 与AB ；②DA 与BC ；③CA 与DC ；④OD 与OB .其中可作为该平面其它向量基底的是()A.①②B.①③C.①④D.③④2.如果{e 1，e 2}是平面α内所有向量的一个基底，那么下列说法正确的是()A.若存在实数λ1，λ2使λ1e 1+λ2e 2=0，则λ1=λ2=0B.对空间任意向量a 都可以表示为a =λ1e 1+λ2e 2，其中λ1，λ2∈RC.λ1e 1+λ2e 2(λ1，λ2∈R )不一定在平面α内D.对于平面α内任意向量a ，使a =λ1e 1+λ2e 2的实数λ1，λ2有无数对3.给出下列三种说法：①一个平面内只有一组不共线的向量可作为表示该平面内所有向量的基底；②一个平面内有无数组不共线向量可作为表示该平面内所有向量的基底；③零向量不可作为基底中的向量.其中，说法正确的为()A.①②B.②③C.①③D.①②③4.在△ABC 中，若AD =12(AB +AC )，则下列关系式正确的是()A.BD =2CDB.BD =CDC.BD =3CDD.CD =2BD 5.如图，▱ABCD 的对角线AC 和BD 交于点M ，AB =a ，AD =b ，试用基底{a ，b }表示MC，MA ，MB .1.如图所示，用向量e 1，e 2表示向量a -b 为()A.-4e 1-2e 2B.-2e 1-4e 2C.e 1-3e 2D.3e 1-e 22.如图所示，在矩形ABCD 中，BC =5e 1，DC =3e 2，则OC 等于()A.12(5e 1+3e 2) B.12(5e 1-3e 2) C.12(3e 2-5e 1) D.12(5e 2-3e 1)3.如图，在△ABC 中，AD =13AC ，BP =23BD ，若AP =λAB +μAC，则λμ等于()A.32B.23C.3D.134.设{a ，b }为基底，已知向量AB =a -k b ，CB =2a +b ，CD=3a -b ，若A ，B ，D 三点共线，则实数k 的值等于()A.2B.-2C.10D.-105.(多选)若{e 1，e 2}是平面内的一个基底，则下列四组向量不能作为平面向量的基底的是()A.{e 1-e 2，e 2-e 1}B.2e 1-e 2，e 1-12e 2C.{2e 2-3e 1，6e 1-4e 2}D.{e 1+e 2，e 1+3e 2}6.已知e 1，e 2不共线，a =e 1+2e 2，b =2e 1+λe 2，要使{a ，b }能作为平面内的一个基底，则实数λ的取值范围为.7.已知λ1>0，λ2>0，{e 1，e 2}是一个基底，且a =λ1e 1+λ2e 2，则a 与e 1，a 与e 2.(填“共线”或“不共线”)8.已知向量a 在基底{e 1，e 2}下可以表示为a =2e 1+3e 2，若a 在基底{e 1+e 2，e 1-e 2}下可表示为a =λ(e 1+e 2)+μ(e 1-e 2)，则λ=，μ=.9.已知G 为△ABC 的重心，设AB =a ，AC =b .试用a ，b 表示向量AG.10.在△ABC 中，点D ，E ，F 依次是边AB 的四等分点，试以CB =e 1，CA =e 2表示CF .11.若OP 1=a ，OP 2=b ，P 1P =λPP 2(λ≠-1)，则OP 等于()A.a +λbB.λa +(1-λ)bC.λa +bD.11+λa +λ1+λb 12.已知A ，B ，C 是平面上不共线的三点，O 是△ABC 的重心，动点P 满足OP =1312OA +12OB +2OC，则点P 一定为()A.AB 边中线的中点B.AB 边中线的三等分点(非重心)C.△ABC 的重心D.AB 边的中点13.已知a =e 1+e 2，b =2e 1-e 2，c =-2e 1+4e 2(e 1，e 2是同一平面内的两个不共线向量)，则c =.(用a ，b 表示)14.如图，在△MAB 中，C 是边AB 上的一点，且AC =5CB ，设MA =a ，MB=b ，则MC =.(用a ，b 表示)15.已知单位圆O 上的两点A ，B 及单位圆所在平面上的一点P ，OA 与OB 不共线.(1)在△OAB 中，若点P 在AB 上，且AP =2PB，若AP =rOB +sOA ，求r +s 的值；(2)点P 满足OP=mOA +OB (m 为常数)，若四边形OABP 为平行四边形，求m 的值.16.如图，平面内有三个向量OA ，OB ，OC ，其中OA 与OB 的夹角为120°，OA 与OC 的夹角为30°，且|OA |=|OB |=1，|OC |=2 3.若OC =λOA +μOB(λ，μ∈R )，求λ+μ的值.6.3.2平面向量加、减运算的坐标表示知识点一　平面向量的正交分解把一个向量分解为两个互相垂直的向量，叫做把向量作正交分解.知识点二　平面向量的坐标表示1.在平面直角坐标系中，设与x 轴、y 轴方向相同的两个单位向量分别为i ，j ，取{i ，j }作为基底.对于平面内的任意一个向量a ，由平面向量基本定理可知，有且只有一对实数x ，y ，使得a =x i +y j .平面内的任一向量a 都可由x ，y 唯一确定，我们把有序数对(x ，y )叫做向量a 的坐标，记作a =(x ，y ).2.在直角坐标平面中，i =(1,0)，j =(0,1)，0=(0,0).1.思考　点的坐标与向量坐标有什么区别和联系？知识点三　平面向量加、减运算的坐标表示设a =(x 1，y 1)，b =(x 2，y 2)，数学公式文字语言表述向量加法a +b =(x 1+x 2，y 1+y 2)两个向量和的坐标分别等于这两个向量相应坐标的和向量减法a -b =(x 1-x 2，y 1-y 2)两个向量差的坐标分别等于这两个向量相应坐标的差已知点A (x 1，y 1)，B (x 2，y 2)，那么向量AB=(x 2-x 1，y 2-y 1)，即任意一个向量的坐标等于表示此向量的有向线段的终点的坐标减去起点的坐标.2.零向量的坐标是(0,0).()3.两个向量的终点不同，则这两个向量的坐标一定不同.()4.当向量的始点在坐标原点时，向量的坐标就是向量终点的坐标.()5.向量可以平移，平移前后它的坐标发生变化.()。

高中物理必修二全套精品课件讲义

第五章曲线运动一、曲线运动【要点导学】1、物体做曲线运动的速度方向是时刻发生变化的，质点经过某一点（或某一时刻）时的速度方向沿曲线上该点的。

2、物体做曲线运动时，至少物体速度的在不断发生变化，所以物体一定具有，所以曲线运动是运动。

3、物体做曲线运动的条件：物体所受合外力的方向与它的速度方向。

4、力可以改变物体运动状态，如将物体受到的合外力沿着物体的运动方向和垂直于物体的运动方向进行分解，则沿着速度方向的分力改变物体速度的；垂直于速度方向的分力改变物体速度的。

速度大小是增大还是减小取决于沿着速度方向的分力与速度方向相同还是相反。

做曲线运动的物体，其所受合外力方向总指向轨迹侧。

匀变速直线运动只有沿着速度方向的力，没有垂直速度方向的力，故速度的改变而不变；如果没有沿着速度方向的力，只有垂直速度方向的力，则物体运动的速度不变而不断改变，这就是今后要学习的匀速圆周运动。

【范例精析】例1、在砂轮上磨刀具时可以看到，刀具与砂轮接触处有火星沿砂轮的切线飞出，为什么由此推断出砂轮上跟刀具接触处的质点的速度方向沿砂轮的切线方向?解析火星是从刀具与砂轮接触处擦落的炽热微粒，由于惯性，它们以被擦落时具有的速度做直线运动，因此，火星飞出的方向就表示砂轮上跟刀具接触处的质点的速度方向。

火星沿砂轮切线飞出说明砂轮上跟刀具接触处的质点的速度方向沿砂轮的切线方向。

例2、质点在三个恒力F1、F2、F3的共同作用下保持平衡状态，若突然撤去F1，则质点（）A．一定做匀变速运动B．一定做直线运动C．一定做非匀变速运动D．一定做曲线运动解析：质点在恒力作用下产生恒定的加速度，加速度恒定的运动一定是匀变速运动。

由题意可知，当突然撤去F1时，质点受到的合力大小为F1，方向与F1相反，故A正确，C错误。

在撤去F1之前，质点保持平衡，有两种可能：一是质点处于静止状态，则撤去F1后，它一定做匀变速直线运动；其二是质点处于匀速直线运动状态，则撤去F1后，质点可能做直线运动（条件是：F1的方向和速度方向在一条直线上），也可能做曲线运动（条件是：F1的方向和速度方向不在一条直线上）。

物理必修二讲义

必修二讲义曲线运动特点、条件、运动的合成与分解一、曲线运动1、曲线运动的特点：质点做曲线运动时，在某一时刻的瞬时速度的方向就是通过这一点的切线方向，所以曲线运动一定是变速运动，但是变速运动不一定是曲线运动。

2、做曲线运动的条件：（1）从运动学的角度说：物体的加速度的方向跟它的速度方向不在同一直线上，物体就做曲线运动，（1）从动力学的角度说：如果物体所受的合力方向跟它的速度方向不在同一直线上，物体就做曲线运动。

（注意：上述说法中，只强调合力的方向与速度方向不在同一直线上，并没有说明合力的大小是否变化。

故当合力为恒力时，物体做匀变速曲线运动，合力为变力时，物体做非匀变速曲线运动）二、运动的合成与分解1、分运动与合运动：一个物体同时参与几个运动，参与的这几个运动都是分运动，物体的实际运动就是合运动。

2、运动的合成：已知分运动求合运动，叫做运动的合成。

（1）同一直线上的两个分运动的合成：同向相加，反向相减（2）不在同一直线上的两个分运动合成时，遵循平行四边形定则3、运动的分解：已知合运动求分运动，叫运动的分解（1）运动的分解是运动的合成的逆过程。

（2）分解方法：根据运动的实际效果分解或正交分解4、合运动与分运动的关系1、运动的独立性一个物体同时参与两个或多个运动时，其中的任何一个运动并不会受其它分运动的干扰，而保持不变2、运动的等时性各个分运动与合运动是同时开始，同时结束，经历时间相等。

3、运动的等效性各分运动叠加起来与合运动有相同的效果4、运动的同一性分运动与合运动，是指同一物体参与的分运动和实际发生的运动，不是几个不同物体发生的不同运动。

要点突破一、曲线运动的合力、轨迹、速度之间的关系1、做曲线运动的物体所受合力方向与轨迹的关系无力不拐弯，拐弯必有力。

曲线运动轨迹始终夹在合力方向与速度方向之间，而且向合力方向弯曲，或者说合力的方向总是指向曲线的凹侧2、由曲线运动物体的速度方向，合外力方向确定物体运动轨迹物体运动轨迹夹于上述速度方向与合外力方向之间二、曲线运动的物体的速率变化判断（1）当合外力方向与速度方向的夹角为锐角时，物体的速率增大。

高中化学必修2整套讲义全

化学必修二讲义普通高中课程标准实验教科书化学必修2第一章物质结构元素周期律第一节元素周期表第二节元素周期律第三节化学键归纳与整理第二章化学反应与能量第一节化学能与热能第二节化学能与电能第三节化学反应的速率和限度归纳与整理第三章有机化合物第一节最简单的有机化合物----甲烷第二节来自石油和煤的两种基本化工原料第三节生活中两种常见的有机物归纳与整理第四章化学与可持续发展第一节开发利用金属矿物和海水资源第二节化学与资源综合利用、环境保护归纳与整理结束语附录Ⅰ相对原子质量表附录Ⅱ部分酸、碱和盐的溶解性表（20℃）附录Ⅲ一些常见元素中英文名称对照表第一章物质结构元素周期律第一节元素周期表（一）核素1、原子结构：原子由原子核和核外电子构成，原子核在原子的中心，由带正电的质子与不带电的中子构成，带负电的电子绕核作高速运动。

也就是说，质子、中子和电子是构成原子的三种微粒。

在原子中，原子核带正电荷，其正电荷数由所含质子数决定。

（1）原子的电性关系：核电荷数 = 质子数 = 核外电子数（2）质量数：将原子核所有的质子和中子的相对质量取近似整数值加起来所得的数值，叫质量数。

质量数（A ）= 质子数（Z ）+ 中子数（N ）（3）离子指的是带电的原子或原子团。

带正电荷的粒子叫阳离子，带负电荷的粒子叫阴离子。

当质子数(核电荷数)＞核外电子数时，该粒子是阳离子，带正电荷；当质子数(核电核数＜核外电子数时，该粒子是阴离子，带负电荷。

（4）原子组成的表示方法2、核素和同位素（1）核素：具有一定数目的质子和一定数目的中子的原子叫核素。

如如氢元素有11H 、21H 、31H 三种不同核素。

（2）同位素：质子数相同而中子数不同的同一元素的不同原子互称为同位素。

①同位素中“同位”的含义：指在元素周期表中占据同一个位置的意思。

如氕、氘、氚，即同一元素的不同核素之间互称为同位素。

②同位素的性质：在天然存在的某种元素中，各种同位素原子个数百分含量一般是不变的；同一种元素的各种不同的同位素化学性质几乎完全相同，因为各同位素原子结构几乎相同（除中子数）。

高中物理必修二讲义

P蜡块得位置vv xv y涉及得公式:θv v 水 v 船θ ,d第五章平抛运动§5-1 曲线运动 & 运动得合成与分解一、曲线运动1、定义:物体运动轨迹就是曲线得运动。

2、条件:运动物体所受合力得方向跟它得速度方向不在同一直线上。

3、特点:①方向:某点瞬时速度方向就就是通过这一点得曲线得切线方向。

②运动类型:变速运动(速度方向不断变化)。

③F 合≠0,一定有加速度a 。

④F 合方向一定指向曲线凹侧。

⑤F 合可以分解成水平与竖直得两个力。

4.运动描述二、运动得合成与分解1.合运动与分运动得关系:等时性、独立性、等效性、矢量性。

2.互成角度得两个分运动得合运动得判断:①两个匀速直线运动得合运动仍然就是匀速直线运动。

②速度方向不在同一直线上得两个分运动,一个就是匀速直线运动,一个就是匀变速直线运动,其合运动就是匀变速曲线运动,a 合为分运动得加速度。

③两初速度为0得匀加速直线运动得合运动仍然就是匀加速直线运动。

④两个初速度不为0得匀加速直线运动得合运动可能就是直线运动也可能就是曲线运动。

当两个分运动得初速度得与速度方向与这两个分运动得与加速度在同一直线上时,合运动就是匀变速直线运动,否则即为曲线运动。

三、有关“曲线运动”得两大题型（一）小船过河问题模型一:过河时间t 最短: 模型二:直接位移x 最短: 模型三:间接位移x 最短: [触类旁通]1.(2011 年上海卷)如图 5－4 所示,人沿平直得河岸以速度v 行走,且通过不可伸长得绳拖船,船沿绳得方向行进.此过程中绳始终与水面平行,当绳与河岸得夹角为α时,船得速率为( C )。

解析:依题意,船沿着绳子得方向前进,即船得速度总就是沿着绳子得,根据绳子两端连接得物体在绳子方向上得投影速度相同,可知人得速度 v 在绳子方向上得分量等于船速,故v 船＝v cos α,C 正确.2.(2011 年江苏卷)如图 5－5 所示,甲、乙两同学从河中O 点出发,分别沿直线游到 A 点与 B 点后,立即沿原路线返回到 O 点,OA 、OB 分别与水流方向平行与垂直,且 OA ＝OB 、若水流速度不变,两人在静水中游速相等,则她们所用时间 t 甲、t 乙得大小关系为(C) A.t 甲<t 乙 B.t 甲＝t 乙 C.t 甲>t 乙 D.无法确定d vv 水v 船 θ 当v 水<v 船时,x min =d, ,A v 水 v 船 θ 当v 水>v 船时,, ,θ v 船 d解析:设游速为v ,水速为v 0,OA ＝OB ＝l ,则t 甲＝l v ＋v 0＋l v －v 0;乙沿OB 运动,乙得速度矢量图如图4所示,合速度必须沿OB 方向,则t 乙＝2·lv 2－v 2,联立解得t 甲>t 乙,C 正确. （二）绳杆问题(连带运动问题)1、实质:合运动得识别与合运动得分解。

人教版高一数学必修二辅导讲义：1.1空间几何体的结构

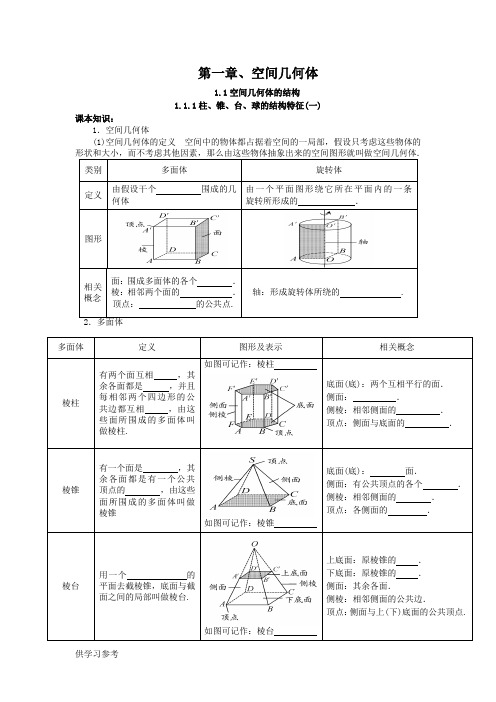
第一章、空间几何体1.1空间几何体的结构1.1.1柱、锥、台、球的结构特征(一)课本知识：1．空间几何体(1)空间几何体的定义空间中的物体都占据着空间的一局部，假设只考虑这些物体的形状和大小，而不考虑其他因素，那么由这些物体抽象出来的空间图形就叫做空间几何体．类别多面体旋转体定义由假设干个围成的几何体由一个平面图形绕它所在平面内的一条旋转所形成的．图形相关概念面：围成多面体的各个．棱：相邻两个面的．顶点：的公共点.轴：形成旋转体所绕的 .2．多面体多面体定义图形及表示相关概念棱柱有两个面互相，其余各面都是，并且每相邻两个四边形的公共边都互相，由这些面所围成的多面体叫做棱柱.如图可记作：棱柱底面(底)：两个互相平行的面．侧面：．侧棱：相邻侧面的．顶点：侧面与底面的．棱锥有一个面是，其余各面都是有一个公共顶点的，由这些面所围成的多面体叫做棱锥如图可记作：棱锥底面(底)：面．侧面：有公共顶点的各个．侧棱：相邻侧面的．顶点：各侧面的．棱台用一个的平面去截棱锥，底面与截面之间的局部叫做棱台.如图可记作：棱台上底面：原棱锥的．下底面：原棱锥的．侧面：其余各面．侧棱：相邻侧面的公共边．顶点：侧面与上(下)底面的公共顶点.知识梳理：要点一棱柱、棱锥、棱台的概念1.棱柱的结构特征侧棱都相等，侧面都是平行四边形，两个底面相互平行；2．棱锥的结构特征有一个面是多边形，其余各面是有一个公共顶点的三角形；3．棱台的结构特征上下底面相互平行，各侧棱的延长线交于同一点．典型例题1、有以下说法：①有两个面平行，其余各面都是平行四边形所围成的几何体一定是棱柱；②各个面都是三角形的几何体是三棱锥；③用一个平行于棱锥底面的平面去截棱锥，得到的几何体叫做棱台；④棱柱的各相邻侧面的公共边互相平行．以上说法中，正确说法的序号是________(写出所有正确说法的序号)．反应训练1、有以下说法：①一个棱锥至少有四个面；②如果四棱锥的底面是正方形，那么这个四棱锥的四条侧棱都相等；③五棱锥只有五条棱；④用与底面平行的平面去截三棱锥，得到的截面三角形和底面三角形相似．以上说法中，正确说法的序号是________(写出所有正确说法的序号)．典型例题2、长方体ABCD－A′B′C′D′，当用平面BCFE把这个长方体分成两局部后，各局部形成的多面体还是棱柱吗？如果不是，请说明理由；如果是，指出底面及侧棱．反应训练2、以下说法：①有两个面互相平行，其余的面都是平行四边形的几何体的侧棱一定不相交于一点，故一定不是棱台；②两个互相平行的面是平行四边形，其余各面是四边形的几何体不一定是棱台；③两个互相平行的面是正方形，其余各面是四边形的几何体一定是棱台．其中正确的个数为( ) A．3 B．2 C．1 D．0 要点三多面体的外表展开图1.绘制多面体的外表展开图要结合多面体的几何特征，发挥空间想象能力或者是亲手制作多面体模型，在解题过程中，常常给多面体的顶点标上字母，先把多面体的底面画出来，然后依次画出各侧面，便可得到其外表展开图．2．假设是给出多面体的外表展开图，来判断是由哪一个多面体展开的，那么可把上述过程逆推．典型例题3、请画出以下图所示的几何体的外表展开图．反应训练3、根据右图所给的几何体的外表展开图，画出立体图形1.1.1柱、锥、台、球的结构特征(二)1.1.2简单组合体的结构特征课本知识：1．旋转体旋转体结构特征图形表示圆柱以矩形的一边所在直线为旋转轴，其余三边旋转形成的所围成的旋转体叫做圆柱．旋转轴叫做圆柱的轴；于轴的边旋转而成的圆面叫做圆柱的底面；于轴的边旋转而成的曲面叫做圆柱的侧面；无论旋转到什么位置，于轴的边都叫做圆柱侧面的母线我们用表示圆柱轴的字母表示圆柱，左图可表示为圆锥以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转形成的所围成的旋转体叫做圆锥我们用表示圆锥轴的字母表示圆锥，左图可表示为圆台用平行于的平面去截圆锥，底面与截面之间的局部叫做圆台我们用表示圆台轴的字母表示圆台，左图可表示为球以半圆的直径所在直线为旋转轴，旋转一周所形成的旋转体叫做球体，简称球．半圆的圆心叫做球的，半圆的半径叫做球的半径，半圆的直径叫做球的直径球常用球心字母进行表示，左图可表示为(1)定义：由组合而成的几何体叫做简单组合体．(2)简单组合体的两种根本形式：由简单几何体而成；由简单几何体一局部而成．特别提醒：圆是一条封闭的曲线，圆面是一个圆围成的圆内平面．球是几何体，球面是指半圆沿直径旋转形成的曲面，球是旋转体．知识梳理：要点一、旋转体的结构特征圆柱、圆锥、圆台、球从生成过程来看，它们分别是由矩形、直角三角形、直角梯形、半圆绕着某一条直线旋转而成的几何体，因此它们统称为旋转体．但应注意的是：所谓旋转体就是一个平面图形绕着这个平面图形所在的平面内一条直线旋转一周所得到的几何体，因此它还含有除圆柱、圆锥、圆台、球之外的几何体．典型例题1、以下说法：①在圆柱的上、下两底面的圆周上各取一点，那么这两点的连线是圆柱的母线；②圆锥的顶点与底面圆周上任意一点的连线是圆锥的母线；③在圆台上、下两底面的圆周上各取一点，那么这两点的连线是圆台的母线；④圆柱的任意两条母线相互平行．其中正确的选项是( )A．①②B．②③C．①③D．②④反应训练1、以下说法中正确的选项是( )A．圆台是直角梯形绕其一边旋转而成的B．圆锥是直角三角形绕其一边旋转而成的C．圆柱不是旋转体D．圆台可以看作是平行于底面的平面截一个圆锥而得到的要点二圆柱、圆锥、圆台的侧面展开图把柱、锥、台体沿一条侧棱或母线展开成平面图，这样便把空间问题转化成了平面问题，对解决简单空间几何体的面积问题或侧面上(球除外)两点间的距离问题，是很有效的方法．典型例题2、如图，底面半径为1，高为2的圆柱，在A点有一只蚂蚁，现在这只蚂蚁要围绕圆柱由A点爬到B点，问蚂蚁爬行的最短距离是多少？反应训练2、假设本例中蚂蚁围绕圆柱转两圈，如下图，那么它爬行的最短距离是多少？要点三简单组合体的结构特征判断实物图是由哪些简单几何体所组成的图形问题，首先要熟练掌握简单几何体的结构特征，其次要善于将复杂的组合体“分割〞成几个简单的几何体．简单组合体有以下三种形式：1．多面体与多面体的组合体：即由两个或两个以上的多面体组合而成的几何体．2．多面体与旋转体的组合体：即由一个多面体与一个旋转体组合而成的几何体．3．旋转体与旋转体的组合体：即由两个或两个以上的旋转体组合而成的几何体．典型例题3、请描述如下图的组合体的结构特征．反应训练3、说出以下几何体的结构特征．一、选择题1．以下说法中正确的选项是( )A ．棱柱中两个互相平行的平面一定是棱柱的底面B ．棱柱的面中，至少有两个面互相平行C ．棱柱中一条侧棱的长叫棱柱的高D ．棱柱的侧面是平行四边形，但它的底面一定不是平行四边形2．如图，D ，E ，F 分别是等边△ABC 各边的中点，把该图按虚线折起，可以得到一个( )A ．棱柱 B ．棱锥 C ．棱台 D ．旋转体3．以下三个说法，其中正确的选项是( )①用一个平面去截棱锥，棱锥底面和截面之间的局部是棱台； ②两个底面平行且相似，其余各面都是梯形的多面体是棱台； ③有两个面互相平行，其余四个面都是等腰梯形的六面体是棱台． A ．0个 B ．1个 C ．2个 D ．3个4．在长方体ABCD －A 1B 1C 1D 1中，AB =3，AD =2，CC 1=1，一条绳子从点A 沿外表拉到点C 1，那么绳子的最短的长是( )A ．3 2 B ．2 5 C.26 D ．65．如图，以下几何体中，________是棱柱，________是棱锥，________是棱台．6．在正方体上任意选择4个顶点，它们可能是如下各种几何图形的4个顶点，这些几何体是________(写出所有正确结论的序号)．①矩形；②不是矩形的平行四边形；③有三个面为等腰直角三角形，有一个面为等边三角形的四面体；④每个面都是等边三角形的四面体；⑤每个面都是直角三角形的四面体．7．在如下图的三棱柱ABC －A 1B 1C 1中，请连接三条线，把它分成三局部，使每一局部都是一个三棱锥．8．如下图，在正三棱柱ABC －A 1B 1C 1中，AB =2，AA 1=2，由顶点B 沿棱柱侧面(经过棱AA 1)到达顶点C 1，与AA 1的交点记为M .求：(1)三棱柱侧面展开图的对角线长；(2)从B 经M 到C 1的最短路线长及此时A 1MAM的值．1．以下说法正确的选项是( )A．圆锥的母线长等于底面圆直径B．圆柱的母线与轴垂直C．圆台的母线与轴平行D．球的直径必过球心2．底面半径为2且底面水平放置的圆锥被过高的中点且平行于底面的平面所截，那么截得的截面圆的面积为( )A．πB．2π C．3πD．4π3．以下说法正确的有( )①球的半径是球面上任意一点与球心的连线段②球的直径是球面上任意两点间的连线段③用一个平面截一个球，得到的是一个圆④不过球心的截面截得的圆的半径小于球半径A．①② B．①④ C．①②④D．③④4．如下图的几何体，关于其结构特征，以下说法不正确的选项是( )A．该几何体是由两个同底的四棱锥组成的几何体B．该几何体有12条棱、6个顶点C．该几何体有8个面，并且各面均为三角形D．该几何体有9个面，其中一个面是四边形，其余均为三角形5．给出以下说法：(1)直角三角形绕一边旋转得到的旋转体是圆锥(2)夹在圆柱的两个平行截面间的几何体还是一个旋转体(3)圆锥截去一个小圆锥后剩余局部是圆台(4)通过圆台侧面上一点，有无数条母线其中正确的说法是________(写出所有正确说法的序号)．6．把一个圆锥截成圆台，圆台的上下底面半径之比是14，母线长为10，那么圆锥的母线长是________．7．如图(1)所示，正三棱柱的底面边长是4cm、过BC的一个平面交侧棱AA′于D，假设AD的长为2cm，求截面△BCD的面积．图(1) 图(2)8.从一个底面半径和高都是R的圆柱中，挖去一个以圆柱上底面为底，下底面中心为顶点的圆锥，得到如以下图所示的几何体．如果用一个与圆柱下底面距离等于l并且平行于底面的平面去截它，求所得截面的面积．。

高中数学必修第二册讲义

第1讲数列的概念一、数列的概念及分类数列：按照一定顺序排列的一列数称为数列，数列中的每一个数叫做这个数列的项，排在第一位的数称为这个数列的第1项，通常也叫做首项。

数列的分类：①按项的个数分类：有穷数列，无穷数列；②按项的变化趋势分类：递增数列，递减数列，常数列和摆动数列；③按项的绝对值分类：有界数列，无界数列。

二、数列的通项公式数列的通项公式：如果数列{}n a 的第n 项与序号n 之间的关系可以用一个式子来表示，那么这个公式叫做这个数列的通项公式。

1、根据下面各数列前几项的值，写出数列的一个通项公式：（1）1 、7、13 、19、 (2)23、415、635、863、1099、 (3)12、2、92、8、252、…… （4）5、55、555、5 555、……2、根据下面数列的前几项的值，写出数列的一个通项公式：（1）12、14、58 、1316、2932 、6164、…… （2）32、1、710、917、……3、写出数列的一个通项公式，使得它的前几项是下列各数：（1）1 、12、13 、14、……（2、3…… （3）0.9、0.99、0.999、0.9999、…… （4）3、5、3、5、……4、数列0、23、45、67、…的一个通项公式为（）。

A 、1(*)1n n a n N n B 、1(*)21n n a n N n C 、2(1)(*)21n n a n N nD 、2(*)21n na n N n5、已知数列{}n a 的通项公式为2328n a n n 。

（1）写出数列的第4项和第6项；（2）问49 是否是该数列的一项？如果是，应是哪一项？68是否是该数列的一项？6、数列{}n a 的通项公式是276n a n n 。

（1）这个数列的第4项是多少？（2）150是不是这个数列的项？若是这个数列的项，它是第几项？（3）该数列从第几项开始各项都是正数？三、求递推数列的通项公式如果已知数列{}n a 的第1项（或前几项），且从第2项（或某一项）开始任一项n a 与它前一项1n a （或前几项）间的关系可以用一个公式来表示，则这个公式就叫做这个数列的递推公式。

数学必修二讲义(完整资料)

1．经过两条直线2x －3y ＋10＝0和3x ＋4y －2＝0的交点，且垂直于直线3x －2y ＋4＝0的直线方程为______________．解法一：解方程组⎩⎪⎨⎪⎧2x －3y ＋10＝0，3x ＋4y －2＝0，求出交点坐标(－2，2)，设所求直线的斜率为k ，则k ·32＝－1，解得k ＝－23.∴所求直线的方程为y －2＝－23(x ＋2)，即2x ＋3y －2＝0. 解法二：设所求直线l 的方程为2x －3y ＋10＋λ(3x ＋4y －2)＝0，即(2＋3λ)x ＋(4λ－3)y＋(10－2λ)＝0，其中斜率为k ＝2＋3λ3－4λ，∵直线l 与3x －2y ＋4＝0垂直，∴2＋3λ3－4λ·32＝－1，解得λ＝－12.故所求直线方程为[2＋3×(－12)]x ＋[4×(－12)－3]y ＋[10－2×(－12)]＝0.即2x ＋3y －2＝0.故填2x ＋3y －2＝0.2.已知一个圆同时满足下列条件：①与x 轴相切；②圆心在直线3x －y ＝0上；③被直线l ：x －y ＝0截得的弦长为27.则此圆的方程为____________________．解：由①可设所求圆的方程为(x －a )2＋(y －b )2＝b 2，由②知b ＝3a ，而圆心(a ，b )到直线l 的距离为d ＝|a －b |2，又由③知b 2－d 2＝7，联立⎩⎪⎨⎪⎧b ＝3a ，d ＝||a －b 2，b 2－d 2＝7，解得a ＝1，b ＝3或a ＝－1，b ＝－3.故填(x －1)2＋(y －3)2＝9或(x ＋1)2＋(y ＋3)2＝9.3．已知函数f (x )＝x 2－4x ＋3，集合M ＝{(x ，y )|f (x )＋f (y )≤0}，集合N ＝{(x ，y )|f (x )－f (y )≥0}，则集合M ∩N 的面积是( )A ．π4B ．π2C ．πD ．2π 解：由已知可得M ＝{(x ，y )|f (x )＋f (y )≤0}＝{(x ，y )|(x －2)2＋(y －2)2≤2}，N ＝{(x ，y )|f (x )－f (y )≥0}＝{(x ，y )|(x －y )(x ＋y －4)≥0}，则M ∩N ＝{(x ，y )|⎩⎪⎨⎪⎧（x －2）2＋（y －2）2≤2，（x －y ）（x ＋y －4）≥0}，作出其交集部分如图所示(阴影部分)，其面积为圆面积的一半，即S ＝12π(2)2＝π.故选C.4.设m ，n ∈R ，若直线(m ＋1)x ＋(n ＋1)y －2＝0与圆(x －1)2＋(y －1)2＝1相切，则m ＋n 的取值范围是( )A ．[1－3，1＋3]B ．(－∞，1－3]∪[1＋3，＋∞)C ．[2－22，2＋22]D ．(－∞，2－22]∪[2＋22，＋∞)解：圆心(1，1)到直线的距离d ＝||（m ＋1）＋（n ＋1）－2（m ＋1）2＋（n ＋1）2＝1，有mn ＝m ＋n ＋1≤⎝ ⎛⎭⎪⎫m ＋n 22，设t ＝m ＋n ，则t 24≥t ＋1，解得t ∈(－∞，2－22]∪[2＋22，＋∞)．故选D.5.已知圆O ：x 2＋y 2＝5，直线l ：x cos θ＋y sin θ＝1⎝⎛⎭⎫0<θ<π2.设圆O 上到直线l 的距离等于1的点的个数为k ，则k ＝____________．解：∵圆心O (0，0)到直线l 的距离d ＝||0·cos θ＋0·sin θ－1cos 2θ＋sin 2θ＝1， ∴过圆心O 作直线l 1∥l 交圆于两点，则它们到直线l 的距离为1.又∵圆O的半径r＝5>2，∴l1关于直线l对称的直线l2也与圆O有两个交点，且它们到直线l的距离为1.综上知，k＝4.故填4.6.如图，正方体ABCD-A1B1C1D1中，O为底面ABCD的中心，M为棱BB1的中点，则下列结论中错误．．的是()A．D1O∥平面A1BC1B．D1O⊥平面MACC．异面直线BC1与AC所成的角等于60°D．二面角M-AC-B等于90°解：取A1C1中点O1，连接BO1，易知D1O∥BO1，故D1O∥平面A1BC1，A正确．取AB中点E，连接OE，A1E，易知A1E⊥AM，A1D1∥OE，而A1D1⊥AM，故AM⊥平面A1D1OE，AM⊥D1O，同理CM⊥D1O，AM∩MC＝M，所以D1O⊥平面MAC，B正确．易知△A1BC1为等边三角形，故C正确．连MO，BO，由AC⊥平面BDD1B1知∠MOB为二面角M-AC-B的平面角，显然不等于90°，故D错误．故选D.7.棱长为1的正方体ABCD-A1B1C1D1中，点P，Q，R分别是面A1B1C1D1，BCC1B1，ABB1A1的中心，给出下列结论：①PR与BQ是异面直线；②RQ⊥平面BCC1B1；③平面PQR∥平面D1AC；④过P，Q，R的平面截该正方体所得截面是边长为2的等边三角形．以上结论正确的是______．(写出所有正确结论的序号)解：由于PR是△A1BC1的中位线，所以PR∥BQ，故①不正确；由于RQ∥A1C1，而A1C1不垂直于面BCC1B1，所以②不正确；由于PR∥BC1∥D1A，PQ∥A1B∥D1C，所以③正确；由于△A1BC1是边长为2的正三角形，所以④正确．故填③④.8.（选做）如图，二面角α-l-β的大小是60°，线段AB⊂α，B∈l，AB与l所成的角为30°.则AB与平面β所成的角的正弦值是________．解：过点A作平面β的垂线，垂足为C，连接BC，在β内作CD⊥l，交l于点D，连接AD.∵l⊥CD，l⊥AC，AC∩CD＝C，∴l⊥面ACD.∴l⊥AD.故∠ADC为二面角α-l-β的平面角，即∠ADC＝60°，易知∠ABC 为直线AB 与平面β所成的角．设CD ＝a ，则AD ＝2a ，AC ＝3a .又∵∠ABD ＝30°，∴AB ＝4a . ∴sin ∠ABC ＝AC AB ＝3a 4a ＝34.故填34. 9．把等腰直角△ABC 沿斜边上的高AD 折成直二面角B -AD -C ，则BD 与平面ABC 所成角的正切值为( )A ． 2B ．22C ．1D ．33解：在面ADC 中，过D 作DE ⊥AC ，交AC 于点E .连接BE ，二面角B -AD -C 为直二面角，∴BD ⊥平面ADC ，BD ⊥AC .又∵DE ∩BD ＝D ，∴AC ⊥平面BDE .∴平面BDE ⊥平面ABC ，故∠DBE 是BD 与平面ABC 所成角，由翻折不变性可知DE ＝12AB ＝22BD ，在Rt △BDE 中，tan ∠DBE ＝DE BD ＝22(亦可由射影法cos ∠BED ＝S 射S 原＝S △ADC S △ABC ＝DE BE ＝33或坐标法求得)．故选B.。

高一必修二讲义教材

高一化学必修二出版人：乐发鹏时间：2014、10、30目录第一章、物质结构元素周期律、、、、、4第一节：元素周期表、、、、、、第二节：元素周期律、、、、、、第三节：化学键、、、、第一章单元检测、、、、、、第二章、化学反应与能量、、、、、第一节：化学能与热能、、、、、第二节：化学能与电能、、、、、第三节：化学反应的速率与限度、、、、、、第二章单元检测、、、、、、第三章、有机化合物、、、、、、第一节：最简单的有机化合物——甲烷、、、第二节：来自石油和煤的两种基本化工原料、、第三节：生活中两种常见的有机物、、、、第四节：基本营养物质、、、、第三章单元检测、、、、第四章、化学与自然资源的开发利用、、、、第一节：开发利用金属矿物和海水资源、、、第二章:资源综合利用环境保护、、、第四章单元检测、、、、、、期中测试（一）、、、、、期中测试（二）、、、、、、期末测试（一）、、、、、期末测试（二）、、、、、、、、第一章、物质结构元素周期律第一节：元素周期表一、原子结构质子（Z个）原子核注意：中子（N个）质量数(A)＝质子数(Z)＋中子数(N)1.）原子序数=核电荷数=质子数=原子的核外电子数核外电子（Z个）★熟背前20号元素，熟悉1～20号元素原子核外电子的排布：H He Li Be B C N O F Ne Na Mg Al Si P S Cl Ar K Ca例1、X、Y、Z和R分别代表四种元素，如果a X m＋、b Y n＋、c Z n－、d R m－四种离子的电子层结构相同(a、b、c、d为元素的核电荷数)，则下列关系正确的是( )A．b－d＝n＋m B．a－b＝n－mC．a－c＝m－n D．c－d＝m＋n例2、已知R2+离子核外有a个电子，b个中子．表示R原子符号正确的是（）A.abR B.22a ba+--R C.22a ba+++R D.2a ba+-R例3、10e-微粒和18e-微粒。

2.原子核外电子的排布规律：①电子总是尽先排布在能量最低的电子层里；②各电子层最多容纳的电子数是2n2；③最外层电子数不超过8个（K层为最外层不超过2个），次外层不超过18个，倒数第三层电子数不超过32个。

人教版生物必修二讲义：第2章第1节减数分裂和受精作用(Ⅰ)含答案

第1节减数分裂和受精作用(Ⅰ)1．阐明减数分裂的概念。

2.阐述同源染色体、四分体、联会等概念。

(重点) 3.阐明减数分裂产生染色体数量减半的精细胞。

4．描述精子形成过程中各时期染色体的行为变化。

(重、难点)知识点减数分裂的概念、精子的形成过程[学生用书P20]阅读教材P16～19 1．减数分裂的概念点拨真核生物的细胞分裂方式一般有三种，精子和卵细胞的形成依靠减数分裂，体细胞的增殖主要依靠有丝分裂，其次依靠无丝分裂。

2．精子的形成过程 (1)形成场所：睾丸。

(2)细胞名称的变化⎭⎪⎬⎪⎫ 精原细胞――→染色体复制减数第一次分裂前的间期⎭⎪⎬⎪⎫初级精母细胞 ――→分裂减数第一次分裂⎭⎪⎬⎪⎫次级精母细胞――→分裂减数第二次分裂⎭⎬⎫精细胞――→变形精子变形过程 (3)形成过程1．减数分裂中的相关概念(1)同源染色体与非同源染色体①同源染色体概念：形状和大小一般都相同，一条来自父方，一条来自母方。

上图甲中A 和B ，C 和D 为同源染色体。

②非同源染色体概念：形状和大小一般不相同，来源可能相同，也可能不同。

(2)姐妹染色单体与非姐妹染色单体姐妹染色单体：连在同一个着丝点上的染色单体。

上图乙中1和2、3和4、5和6、7和8为姐妹染色单体；而1和3、4、5、6、7、8为非姐妹染色单体。

(3)联会和四分体①联会：同源染色体两两配对的现象。

②四分体：联会后的每对同源染色体含有4条染色单体。

③相互关系：同源染色体――→复制、联会四分体④数量关系：1个四分体＝1对同源染色体＝2条染色体＝4条染色单体＝4个DNA 分子。

2．减数分裂过程中两个分裂阶段的比较项目减数第一次分裂减数第二次分裂间期DNA 复制与否复制不复制(无间期)同源染色体有，分离无着丝点变化不分裂分裂染色体主要行为①同源染色体联会；②四分体中非姐妹染色单体交叉互换；③同源染色体分离，非同源染色体自由组合着丝点分裂，姐妹染色单体分开染色体数目 2N →N (减半) N →2N →N (不减半)DNA 数目 2N →4N →2N 2N →N 染色单体数0→4N →2N2N →01．下列关于同源染色体的叙述，不正确的是()A．一条来自父方、一条来自母方的染色体是同源染色体B．同源染色体上的非姐妹染色单体间能互换对应部分C．在人的正常精子中没有同源染色体D．减数分裂中联会的染色体是同源染色体[解析]选A。

必修二知识点讲义

m 2r

m
4 2
T2
r
ma
a

GM r2

GM r3
v GM r
T 2 r3
GM
线速度、角速度、周期及加速度皆与环绕天体的质量无关，只与中心天体质量
和轨道半径有关。“越大越慢”
思路二：不考虑地球或天体自转影响时，物体在地球或天体表面受到的万有引力约等于物体的重力。即
我们做题时：先研究分运动，再确定合运动。
5速度关系：

vx vy

v0 gt
v v 大小： v
2
x
2 y
方向： tan vy gt
vx v0
6.位移关系：

x y
v0t 1 gt
2
大小：s x2 y2
方向：tan

y x

gt 2v0
6.平抛运动的轨迹是一条抛物线。 7.平抛物体在空中飞行时间仅仅取决于下落的高度h，与初速度无关。
v s t
3.线速度的方向：物体在某点的线速度的方向沿圆周上该点的切线方向，与圆弧相切。
4.匀速圆周运动：如果物体沿着圆周运动，并且线速度的大小处处相等，这种运动叫做匀速圆周运动。匀速圆周运动也是角速度不变的圆周运动。
5.角速度：连接物体与圆心的半径扫过的角度跟所用时间的比值，叫做角速度。
做向心力。
2.向心力不是一种特定性质的力。向心力是效果力，对物体受力分析时不需要考虑向心力。
3向心力的公式
Fn

m
v2 r
Fn m 2r
Fn mv
Fn

m（ 2

必修二讲义

高一数学授课讲义(必修二)

高中物理必修二讲义全

高中物理必修二讲义

高中数学必修二讲义 专题4.3 空间直角坐标系

高中数学必修第二册讲义

高中物理必修二全套精品课件讲义

物理必修二讲义

高中化学必修2整套讲义全

高中物理必修二讲义

人教版高一数学必修二辅导讲义：1.1空间几何体的结构

高中数学必修第二册讲义

数学必修二讲义(完整资料)

高一必修二讲义教材

人教版生物必修二讲义：第2章 第1节 减数分裂和受精作用(Ⅰ)含答案

必修二知识点讲义

高中数学必修二讲义专题4.3 空间直角坐标系

人教版生物必修二讲义：第2章第1节减数分裂和受精作用(Ⅰ)含答案