高等数学空间向量与空间解析几何63页PPT
合集下载
高等数学之空间解析几何与向量代数PPT课件

半径为 5 的球面.
说明: 如下形式的三元二次方程 ( A≠ 0 )
A(x2 y2 z2 ) Dx Ey Fz G 0
都可通过配方研究它的图形. 其图形可能是 一个球面 , 或点 , 或虚轨迹.机动 目录 上页 下页 Nhomakorabea回 结束
二、空间曲线的一般方程
空间曲线可视为两曲面的交线, 其一般方程为方程组
z 特别,当M0在原点时,球面方程为
x2 y2 z2 R2
z R2 x2 y2 表示上(下)球面 . o
x
M0
M
y
机动 目录 上页 下页 返回 结束
例2. 研究方程 x2 y2 z2 2x 4 y 0 表示怎样
的曲面.
解: 配方得 (x 1)2 ( y 2)2 z2 5 此方程表示: 球心为 M 0 (1, 2, 0 ),
M
解:在 xoy 面上, x2 y2 R2表示圆C,
C
o
M1
y
在圆C上任取一点M1(x, y,0), 过此点作 x
平行 z 轴的直线 l , 对任意 z , 点M (x, y, z)
l
的坐标也满足方程 x2 y2 R2
沿曲线C平行于 z 轴的一切直线所形成的曲面称为圆
柱面. 其上所有点的坐标都满足此方程, 故在空间中
化简得 2x 6y 2z 7 0
说明: 动点轨迹为线段 AB 的垂直平分面. 显然在此平面上的点的坐标都满足此方程, 不在此平面上的点的坐标不满足此方程.
机动 目录 上页 下页 返回 结束
定义1. 如果曲面 S 与方程 F( x, y, z ) = 0 有下述关系:
(1) 曲面 S 上的任意点的坐标都满足此方程;
机动 目录 上页 下页 返回 结束
说明: 如下形式的三元二次方程 ( A≠ 0 )
A(x2 y2 z2 ) Dx Ey Fz G 0
都可通过配方研究它的图形. 其图形可能是 一个球面 , 或点 , 或虚轨迹.机动 目录 上页 下页 Nhomakorabea回 结束
二、空间曲线的一般方程
空间曲线可视为两曲面的交线, 其一般方程为方程组
z 特别,当M0在原点时,球面方程为
x2 y2 z2 R2
z R2 x2 y2 表示上(下)球面 . o
x
M0
M
y
机动 目录 上页 下页 返回 结束
例2. 研究方程 x2 y2 z2 2x 4 y 0 表示怎样
的曲面.
解: 配方得 (x 1)2 ( y 2)2 z2 5 此方程表示: 球心为 M 0 (1, 2, 0 ),
M
解:在 xoy 面上, x2 y2 R2表示圆C,
C
o
M1
y
在圆C上任取一点M1(x, y,0), 过此点作 x
平行 z 轴的直线 l , 对任意 z , 点M (x, y, z)
l
的坐标也满足方程 x2 y2 R2
沿曲线C平行于 z 轴的一切直线所形成的曲面称为圆
柱面. 其上所有点的坐标都满足此方程, 故在空间中
化简得 2x 6y 2z 7 0
说明: 动点轨迹为线段 AB 的垂直平分面. 显然在此平面上的点的坐标都满足此方程, 不在此平面上的点的坐标不满足此方程.
机动 目录 上页 下页 返回 结束
定义1. 如果曲面 S 与方程 F( x, y, z ) = 0 有下述关系:
(1) 曲面 S 上的任意点的坐标都满足此方程;
机动 目录 上页 下页 返回 结束
高等数学 第八章 空间解析几何与向量代数ppt精选课件

对两点 A( x1 , y1 , z1) 与 B( x2 , y2 , z2 ), 因
AB OB OA ( x2 x1 , y2 y1 , z2 z1 ) 得两点间的距离公式:
B
A
AB AB ( x2 x1)2 ( y2 y1)2 (z2 z1)2
.
2. 方向角与方向余弦
ijk, ij jk k i 0 ,
|i| |j| |k | 1 ,
ii jj k k 1 .
a
b
a x bx
ayby
azbz
.
a b |a |b ||co scos|a a||bb|,
由此得两向量夹角余弦的坐标表示式
cos
axbx a yby azbz
ax2 a y2 az 2 bx2 by2 bz2
(2)a b 0 ab 证 () a b 0,|a|0, |b|0,
co s0, , a b .
() a a b b ,|a |b ||c 2 , 2o 0 c .o s s0,
.
2、数量积符合下列运算规律: (1) 交换律: a b b a (2) 分配律: ( a b ) c a c b c
|c |1 2 0 5 2 55 ,
c0
|
c c|
2
j
5
15k.
.
作业 P23习题8-2
1(1)、(3),3,4,9
.
第三节 平面及其方程
.
一、平面的点法式方程
对支点O
的力矩是一向量
M
,它的模
F
|M | |O|F |Q |
O
P
L
|O|F |P |s in
Q
M
的方向垂直于OP
高等数学向量代数与空间解析几何总结 ppt课件

( p与q同号 )
3、空间曲线
[1] 空间曲线的一般方程
F(x, y,z) 0 G(x, y,z) 0
[2] 空间曲线的参数方程
x x(t)
y
y(t)
z z ( t )
如图空间曲线 一般方程为
z 1 x2 y2
(x
1)2 2
y2
(1)2 2
x
1 cos 2
t 1 2
参数方程为
右 手 系 .
向量积的坐标表达式
ab(aybzazby)i (azbxaxbz)j
(axbyaybx)k
i j k ab ax ay az
bx by bz
a // b
ax ay az bx by bz
请归纳向量的数量积和向量积
在几何中的用途
(①求1)向数量量的积模(1 :)a a |a |2.
f (x, y2 z2 ) 0
(2) 曲线L绕 y 轴旋转所成的旋转曲 方面 程为
f ( x2 z2, y) 0
(1)球面 (2)圆锥面 (3)旋转双曲面
x2y2z21 x2y2z2
x2 y2 z2 a2 a2 c2 1
[2] 柱面
定义:平行于定直线并沿定曲线C移动的直线 L所形成的曲面称之.
a { a x ,a y ,a z} b { b x ,b y ,b z}
a b { a x b x , a y b y , a z b z }
( a x b x ) i ( a y b y ) j ( a z b z ) k a b { a x b x , a y b y , a z b z }
[4] 两直线的夹角
直线 L1 : 直线 L2 :
《高数空间解析几何》课件

《高数空间解析几何》 PPT课件
在本次课程中,我们将深入探讨高等数学中的空间解析几何知识,并通过精 美的PPT课件来呈现内容,帮助大家更好地学习与理解。
空间直角坐标系与向量
直角坐标系特点
定义直角坐标系、特点及应用 场景。
向量的概念与表示
介绍空间向量的概念、表示方 法以及向量的几何意义。
向量的加减与数量积
平面方程与性质
讨论空间平面的方程表达式和具体特性。
平面之间的位置关系
讲解空间中平面之间的相交、平行和垂直关系。
空间曲线与曲面
1
曲线的参数方程与极坐标方程
介绍空间曲线的参数方程和极坐标方程的表示方法。
2ห้องสมุดไป่ตู้
曲面的参数方程与二次曲面方程
讨论空间曲面的参数方程和二次曲面方程的特点和应用。
3
曲线与曲面的位置关系
结束语
通过本次课程的学习,相信大家已经对高数空间解析几何有了更深入的理解。 感谢大家的参与与支持!希望你们可以将所学知识应用到更广阔的领域中。
讲解向量的加减法和数量积的 性质与计算方法。
向量的线性相关与线性无关
介绍向量的线性相关与线性无关的概念以及相关的 定理。
向量的基底与坐标
讲解空间向量的基底与坐标系的概念及相关计算方 法。
空间直线与平面
直线方程与性质
解释空间直线的方程表达式和相关性质。
直线之间的位置关系
介绍空间中直线之间的相交、平行和垂直关系。
讲解空间曲线与曲面之间的相交、相切和位置关系。
三维几何应用
球面坐标与柱面坐标
探讨球面坐标系和柱面坐标系的定义和转换。
直线与平面的最小距离
介绍计算空间中直线与平面之间最小距离的公式和 应用。
在本次课程中,我们将深入探讨高等数学中的空间解析几何知识,并通过精 美的PPT课件来呈现内容,帮助大家更好地学习与理解。
空间直角坐标系与向量
直角坐标系特点
定义直角坐标系、特点及应用 场景。
向量的概念与表示
介绍空间向量的概念、表示方 法以及向量的几何意义。
向量的加减与数量积
平面方程与性质
讨论空间平面的方程表达式和具体特性。
平面之间的位置关系
讲解空间中平面之间的相交、平行和垂直关系。
空间曲线与曲面
1
曲线的参数方程与极坐标方程
介绍空间曲线的参数方程和极坐标方程的表示方法。
2ห้องสมุดไป่ตู้
曲面的参数方程与二次曲面方程
讨论空间曲面的参数方程和二次曲面方程的特点和应用。
3
曲线与曲面的位置关系
结束语
通过本次课程的学习,相信大家已经对高数空间解析几何有了更深入的理解。 感谢大家的参与与支持!希望你们可以将所学知识应用到更广阔的领域中。
讲解向量的加减法和数量积的 性质与计算方法。
向量的线性相关与线性无关
介绍向量的线性相关与线性无关的概念以及相关的 定理。
向量的基底与坐标
讲解空间向量的基底与坐标系的概念及相关计算方 法。
空间直线与平面
直线方程与性质
解释空间直线的方程表达式和相关性质。
直线之间的位置关系
介绍空间中直线之间的相交、平行和垂直关系。
讲解空间曲线与曲面之间的相交、相切和位置关系。
三维几何应用
球面坐标与柱面坐标
探讨球面坐标系和柱面坐标系的定义和转换。
直线与平面的最小距离
介绍计算空间中直线与平面之间最小距离的公式和 应用。
《高等数学(应用类)》课件 第八章 空间解析几何与向量代数

LOGO 第八章 空间解析几何与向量代数
第4 页
第 一 节
空空
间间
直直
角 坐 标
角 坐 标 系
系一
像讨论平面上曲线与方程的关系需要建立平面直角坐标系一样,讨 论空间几何图形与方程的关系也需要建立空间直角坐标系.
如左图所示,三条垂直相交且具有相同长 度单位的数轴,构成一个空间直角坐标系,交点 O称为坐标原点,这三条轴分别称为x轴〔横轴〕、 y轴〔纵轴〕和z轴〔竖轴〕.
看出,这个长方体对角线的长度就是点M1和M2之间的距离.
由于△M1NM2和 △M1PN都为直角三角形, M1M2和M1N为斜边,所以
| M1M 2 |2 | M1N |2 | NM 2 |2 ,| M1N |2 | M1P |2 | PN |2
于是有 | M1M 2 |2 | M1P |2 | PN |2 | NM 2 |2 由于 | M1P| | x2 x1 |,| PN | | y2 y1 | ,| NM 2 | | z2 z1 | 所以
坐标原点的坐标为(0,0,0).
LOGO 第八章 空间解析几何与向量代数
第8 页
第
一 节
空 间 两
空 间
点 之 间
直的
角距
坐离
标公 系式
二
设 M1(x1 ,y1 ,z1) 与 M 2 (x2 ,y2 ,z2 ) 是空间的两个点,过M1和M2各作三 个垂直于坐标轴的平面,这六个平面围成一个长方体,如下图所示.可以
{(ax bx ) ,(ay by ) ,(az bz )}
a b (axi ay j az k ) (bxi by j bz k ) (ax bx ) i (ay by ) j (az bz )k
《高等数学》课件第7章 空间解析几何与向量代数

右手定则,即以右手握住z 轴,当右手的四个手指从 x轴正向以 角度转向 y 轴正向时,大拇指的指向就是z
2 轴的正向.
Ⅲ
yOz面
Ⅳ
xOy面
x
Ⅶ Ⅷ
z zOx面
Ⅱ
Ⅰ
•O
y
Ⅵ Ⅴ
二、空间两点间的距离公式
空间两点间的距离:P1( x1, y1, z1 )、P2( x2 , y2 , z2 )
z
P2
P1
ki j,
j i k, k j i , i k j.
(a ybz azby )i (azbx axbz ) j (axby a ybx )k
设 a ax i ay j az k , b bx i by j bz k , 则 ( ax i ay j az k ) (bx i by j bz k ) i j jk ki 0
(2) 结合律 ( a ) b a ( b ) ( a b )
向量积的坐标表达式
设
a
axi
ay j
azk,
b bxi by j bzk
ab
(a
x
i
a
y
j
az k
)
(bxi
by
j
bzk )
i i j j k k 0,
i j k,
jk i,
第 七 章 向空 量间 代解 数析 几 何 与
目录
第一节 空间直角坐标系 第二节 向量及其线性运算 第三节 向量的坐标 第四节 向量的数量积与向量积 第五节 平面及其方程 第六节 空间直线及其方程 第七节 常见曲面的方程及图形
第一节 空间直角坐标系
一、空间直角坐标系简介
三条垂直相交且具有相同长度单位的数轴,构成一 个空间直角坐标系,交点O称为坐标原点,这三条轴分别 叫做z 轴(横轴)、y 轴(纵轴)和x轴(竖轴).
2 轴的正向.
Ⅲ
yOz面
Ⅳ
xOy面
x
Ⅶ Ⅷ
z zOx面
Ⅱ
Ⅰ
•O
y
Ⅵ Ⅴ
二、空间两点间的距离公式
空间两点间的距离:P1( x1, y1, z1 )、P2( x2 , y2 , z2 )
z
P2
P1
ki j,
j i k, k j i , i k j.
(a ybz azby )i (azbx axbz ) j (axby a ybx )k
设 a ax i ay j az k , b bx i by j bz k , 则 ( ax i ay j az k ) (bx i by j bz k ) i j jk ki 0
(2) 结合律 ( a ) b a ( b ) ( a b )
向量积的坐标表达式
设
a
axi
ay j
azk,
b bxi by j bzk
ab
(a
x
i
a
y
j
az k
)
(bxi
by
j
bzk )
i i j j k k 0,
i j k,
jk i,
第 七 章 向空 量间 代解 数析 几 何 与
目录
第一节 空间直角坐标系 第二节 向量及其线性运算 第三节 向量的坐标 第四节 向量的数量积与向量积 第五节 平面及其方程 第六节 空间直线及其方程 第七节 常见曲面的方程及图形
第一节 空间直角坐标系
一、空间直角坐标系简介
三条垂直相交且具有相同长度单位的数轴,构成一 个空间直角坐标系,交点O称为坐标原点,这三条轴分别 叫做z 轴(横轴)、y 轴(纵轴)和x轴(竖轴).
大学课件-《高等数学》-第九章向量代数与空间解析几何

b
3a
2
5
(1
3)a
1
5 2
1 5
5
b
2a
5
b.
2
例4 试用向量方法证明:对角线互相平分的 四边形必是平行四边形.
证 AM MC BM MD
D b
A
a
M
C B
AD AM MD MC BM BC
思考题二解答
D b
A
a
C
M
B
BC
AD
AM
MD
1
(a
b ).
2
DC
AB
AM
MB
1 2
(a
b ).
思考题三
设 m
i
j
,n
2 j
k
,求以向量
m , n为边的平行四边形的对角线的长度.
思考题三解答
n
对角线的长为 | m n |, | m n |,
(2)分配律:( )a a a
(a
b)
a
b
两个向量的平行关系
定理
设向量
a
0,那末向量
b
平行于
a
的充
分必要条件是:存在唯一的实数
,使
b
a.
证 充分性显然;
当
b
必要性
设 b‖
a
《高数空间解析几何》PPT课件
类似地, 方程 f( y , z)= 0在空间表示以 yoz 坐标面上的 曲线为准线,平行于 x 轴的直线为母线的柱面. 方程 f( x , z)= 0在空间表示以 xoz 坐标面上的曲线为准线, 平行于 y 轴的直线为母线的柱面.
8
椭圆柱面:
z
x2 a2
y2 b2
1
xoy 坐标面上的椭圆为准线、
3
P26例 5
xoz 坐标面上的双曲线
x2 a2
z2 c2
1分别绕 x、z 轴旋
转一周,求所得旋转曲面方程
x2 y2y2 z2
绕 x 轴转所得曲面称为旋转双叶双曲面,
z
曲面方程为
x2 y2 z2 a2 c2 c2 1
o
x
绕 z 轴转所得曲面称为旋转单叶双曲面,
z
曲面方程为
x2 y2 z2 a2 a2 c2 1
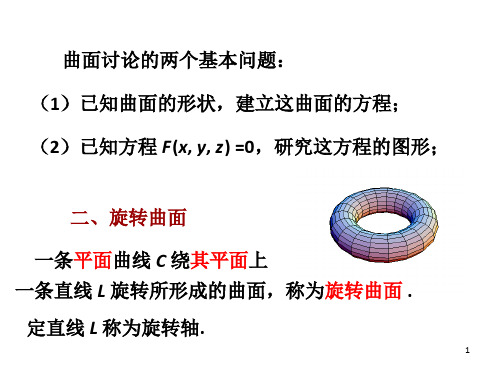
曲面讨论的两个基本问题: (1)已知曲面的形状,建立这曲面的方程; (2)已知方程 F(x, y, z) =0,研究这方程的图形;
二、旋转曲面 一条平面曲线 C 绕其平面上 一条直线 L 旋转所形成的曲面,称为旋转曲面 . 定直线 L 称为旋转轴.
1
建立 y oz 面上曲线 C : f ( y , z ) = 0绕 z 轴旋转所成
例
求曲线
:
x2
x
2
y2 y2
z2 8y
64
,
在 xoy, y0z 坐标面上的投影曲线的方程.
解 关于xo y 坐标面的投影
柱面方程 x 2 y 2 8 y
因而曲线 在 xo y 坐标
面上的投影曲线是圆.
1
y 0
y2 z2
b2
c2
8
椭圆柱面:
z
x2 a2
y2 b2
1
xoy 坐标面上的椭圆为准线、
3
P26例 5
xoz 坐标面上的双曲线
x2 a2
z2 c2
1分别绕 x、z 轴旋
转一周,求所得旋转曲面方程
x2 y2y2 z2
绕 x 轴转所得曲面称为旋转双叶双曲面,
z
曲面方程为
x2 y2 z2 a2 c2 c2 1
o
x
绕 z 轴转所得曲面称为旋转单叶双曲面,
z
曲面方程为
x2 y2 z2 a2 a2 c2 1
曲面讨论的两个基本问题: (1)已知曲面的形状,建立这曲面的方程; (2)已知方程 F(x, y, z) =0,研究这方程的图形;
二、旋转曲面 一条平面曲线 C 绕其平面上 一条直线 L 旋转所形成的曲面,称为旋转曲面 . 定直线 L 称为旋转轴.
1
建立 y oz 面上曲线 C : f ( y , z ) = 0绕 z 轴旋转所成
例
求曲线
:
x2
x
2
y2 y2
z2 8y
64
,
在 xoy, y0z 坐标面上的投影曲线的方程.
解 关于xo y 坐标面的投影
柱面方程 x 2 y 2 8 y
因而曲线 在 xo y 坐标
面上的投影曲线是圆.
1
y 0
y2 z2
b2
c2
高数A第八章 空间解析几何和向量PPT课件

3.向量的线性运算
加法:平行四边形法则 数乘:大小与方向
4. 空间两向量的夹角的概念:
向 量 aa 与 0向 , 量 bb 的 0,夹 角
b
a
(a ,b )(b,a)
(0)
二、向量坐标及坐标线性运算
设a是以 M1( x1 , y1 , z1 )为起点、 M2 ( x2 , y2 , z2 )
1.球心在点 M0 ( x0 , y0 , z0 )、半径为R的球面方程:
x x 0 2 y y 0 2 z z 0 2 R 2
2. 旋转曲面:
如图 设M(x,y,z),
(1) zz1
(2)点M 到z轴的距离
dx2y2 |y1| x
z
d M 1(0,y1,z1)
M f(y,z)0
(5)
a//
b
ax
ay
az
bx by bz
例2
求与a
3i
2
j
4k ,b
i
j
2k 都垂
直的单位向量.
解
i
jki
j
c ab ax ay az 3 2
bx by bz 1 1
|c |1 2 0 5 2 55 ,
c0 c
|c|
2
j
5
15k.
k
4 1j0 5k, 2
第八章 空间解析几何与向量代数
一、向量及其线性运算
1. 空间的点 1 1有序数组(x,y,z)
2. 空间两点间的距离
设 M1( x1 , y1 , z1 )、M2 ( x2 , y2 , z2 )为空间两点,则
M 1 M 2 x 2 x 1 2 y 2 y 1 2 z 2 z 1 2 .
向量代数与空间解析几何—空间解析几何(高等数学课件)

1 + 1 + 1 + 1 = 0 ,
2 + 2 + 2 + 2 = 0 .
方程组(1)我们称之为直线的一般式方程。
(1)
2.空间直线的点向式方程
1.二元极限定义
与直线平行(共线)的非零向量称为直线的方向向量.
设已知直线 L 过点 M 0 ( x0 , y0 , z0 ),其方向向
(1)过点 A(1, 2,3) , B(1,1, 1) 的直线方程;
x 1 y 1 z 2
(2)过点 M (0, 2,3) ,且与直线 L1 :
平行的直线方程;
3
2
1
(3)过点 P(2,1,3) ,且与平面 π : 3x 2 y z 1 0 垂直的直线方程.
例题
一点.因为向量 ⊥平面,0 ⊂平面,所以 ⊥ 0 .
由向量垂直的充要条件可知 ⋅ 0 = 0,
而0 = − 0 , − 0 , − 0 ,根据向量数量积的坐标表达式有:
− 0 + − 0 + − 0 = 0
此方程是由平面上一个点的坐标和平面的法向量确定的,因此,我们称之为平面的
出了平面平行或垂
直的判定方法。
空间上点到平面
的距离公式。
思考题
求满足下列条件的平面方程:
(1)过原点且法向量 = 1,2,3 ;
一元函数,但在自然科学和工程两
(2)在, , 轴上的截距分别是2, −3,4
空间直线及其方程
知识点讲解
1.空间直线的一般式方
程
2.空间直线的点向式方程
3.空间直线的参数方程
1.空间直线的一般方程式
2 + 2 + 2 + 2 = 0 .
方程组(1)我们称之为直线的一般式方程。
(1)
2.空间直线的点向式方程
1.二元极限定义
与直线平行(共线)的非零向量称为直线的方向向量.
设已知直线 L 过点 M 0 ( x0 , y0 , z0 ),其方向向
(1)过点 A(1, 2,3) , B(1,1, 1) 的直线方程;
x 1 y 1 z 2
(2)过点 M (0, 2,3) ,且与直线 L1 :
平行的直线方程;
3
2
1
(3)过点 P(2,1,3) ,且与平面 π : 3x 2 y z 1 0 垂直的直线方程.
例题
一点.因为向量 ⊥平面,0 ⊂平面,所以 ⊥ 0 .
由向量垂直的充要条件可知 ⋅ 0 = 0,
而0 = − 0 , − 0 , − 0 ,根据向量数量积的坐标表达式有:
− 0 + − 0 + − 0 = 0
此方程是由平面上一个点的坐标和平面的法向量确定的,因此,我们称之为平面的
出了平面平行或垂
直的判定方法。
空间上点到平面
的距离公式。
思考题
求满足下列条件的平面方程:
(1)过原点且法向量 = 1,2,3 ;
一元函数,但在自然科学和工程两
(2)在, , 轴上的截距分别是2, −3,4
空间直线及其方程
知识点讲解
1.空间直线的一般式方
程
2.空间直线的点向式方程
3.空间直线的参数方程
1.空间直线的一般方程式
第八章 空间解析几何与向量代数 ppt课件

【例4】P11例8 uuur
方法2 :设 OA ( x, y, z)
则由
cos
3
uuxur |OA|
x
6
1 2
3
z
A
O
4 y
x3
cos
4
uuyur y 6 |OA|
2 3 2
2
uuur | OA | x2 y2 z2 6 z 3
A(3, 3 2, 3)
ppt课件
18
目录 上页 下页 返回 结束
(3)
ar
r 0
则
若 0,则 ar 若ar 0,则
分配律.
r r0 ; 0.
见P4
.
(4)定理1.1:设
r a
r 0
,则
r a
/
r /b
1
r R, 使得b
ar
.
(5)与
r a
同向的单位向量为:er
ar o
ar r
.
|a|
ppt课件
6
目录 上页 下页 返回 结束
【例1】如果四边形对角线互相平分,则它是
ppt课件
2
目录 上页 下页 返回 结束
§1 向量及其线性运算
第一次课
一、向量的概念 二、向量的线性运算 三、空间直角坐标系 四、利用坐标作向量的线性运算 五、向量的模、方向角、投影
ppt课件
3
目录 上页 下页 返回 结束
一、向量的概念
1.向量: 既有大小, 又有方向的量称为向量 (又称矢量).
r rr
gi j k
r
ri 1 0 0
j0 1 0
r
k0 0 1
r
r
大学数学专业空间解析几何向量代数PPT课件

它 们 的 和 是 零 矢 量.
C
证 必 要 性 设 三 矢 量a,b,c可 以
构 成 三 角 形ABC, 即 有AB a, BC A
B
b,CA c, 那 么AB+BC+CA=AA 0,即a b c 0
充 分 性 设a b c 0, 作AB a, BC b, 那 么AC
a b, 所 以AC c 0, 从 而c是 AC的反矢 量,因此c=
叫 做 矢 量a1 , a2 ,, an的 线 性 组 合.
定理1.4.4 在n 2时,矢量a1, a2 ,, an线性相关的 充 要 条 件 是 其 中 有 一 个矢 量 是 其 余 矢 量 的 线 性组 合.
第34页/共137页
定理1.4.6 两矢量共线的充要条件是它们线性相关.
定 义1.4.2 对 于n(n 1)个 矢 量a1, a2 ,, an, 如 果 存
r xe1 ye2 ze3 ,
(1.4 3)
并 且 其 中 系 数x, y, z被e1 , e2 , e3 , r唯 一 确 定.
这时e1, e2 , e3叫做空间矢量的基底.
第38页/共137页
定 理1.4.3 如 果 矢 量e1 , e2 , e3不 共 面 , 那 么 空 间
任 意 矢 量r可 以 由 矢 量e1 , e2 , e3线 性 表 示 , 或 说 空 间 任 意 矢 量r可 以 分 解 成 矢 量e1 , e2 , e3的 线 性 组 合 , 即
A
Q M
B
P
CB
由条件可知: BC = 2BP, AC = 2AQ.
S
Q
T
P
C
设AS = AP, B2T = BQ,
2
3
《高等数学》第7章空间向量与空间解析几何

ay
j
az
k
标式.
向量线性运算规律
分解式
a
b
ax
bx
i
ay by
j
az
bz
k
a
(ax
)i
(a y
)
j
(az
)k
( 为常数)
坐标式
a
b
ax bx,ay by,az bz
a ax,ay,az
a
c
b
c
例题
设
a
2,b
3,(a,b)
,求(a
b)
(a
b)
与(a
b)
(a
b ).
3
解:
(a
b)
(a
b)
a
a
b
b
a 2
2 b
5
因为
a
b
a
b
c os(a,b )
b
a
b
3分配律
(a
b)
ca来自 c b
c
向量的混合积
设a
ax,ay,az ,b
bx,by,bz ,c
cx,cy,cz
,
则它们的混合积为:
[实用]向量代数与空间解析几何课件PPT文档
![[实用]向量代数与空间解析几何课件PPT文档](https://img.taocdn.com/s3/m/7a46667fdaef5ef7bb0d3ca4.png)
a M 1 P M 1 Q M 1 P a x i a y j a z k
z
R
k M 1•
向 向向
•M 2
量 量量 在 在在
Q x yz
x
P
o
j
i
N
轴
y上
axx2x1
的 投
轴 上 的 投
轴 上 的 投
ay y2y1
az z2z1 影 影
影
M 1 M 2 ( x 2 x 1 ) i ( y 2 y 1 ) j ( z 2 z 1 ) k
利用坐标作向量的线性运算
a { ax,ay,az},b{bx,by,bz},
a b { a x b x , a y b y ,a z b z }
( a x b x ) i ( a y b y ) j ( a z b z ) k a b { a x b x , a y b y ,a z b z }
按基本单位向量的坐标分解式:
M 1 M 2 ( x 2 x 1 ) i ( y 2 y 1 ) j ( z 2 z 1 ) k
在三个坐标轴上的分向量:a x i,a yj,a zk ,
向量的坐标: ax, ay, az,
向量的坐标表达式:
a { a x ,a y ,a z}
M 1 M 2 { x 2 x 1 ,y 2 y 1 ,z 2 z 1 } 特殊地: O M {x ,y ,z}
三、向量的坐标表示
1. 起点在原点的向量(向径)OM
z zC
设点 M(x,y,z)
以 i, j,k分别表示沿x, y, z
k
轴正向的单位向量, 称为基本单
位向量. rOM = OA + AN +NM
z
R
k M 1•
向 向向
•M 2
量 量量 在 在在
Q x yz
x
P
o
j
i
N
轴
y上
axx2x1
的 投
轴 上 的 投
轴 上 的 投
ay y2y1
az z2z1 影 影
影
M 1 M 2 ( x 2 x 1 ) i ( y 2 y 1 ) j ( z 2 z 1 ) k
利用坐标作向量的线性运算
a { ax,ay,az},b{bx,by,bz},
a b { a x b x , a y b y ,a z b z }
( a x b x ) i ( a y b y ) j ( a z b z ) k a b { a x b x , a y b y ,a z b z }
按基本单位向量的坐标分解式:
M 1 M 2 ( x 2 x 1 ) i ( y 2 y 1 ) j ( z 2 z 1 ) k
在三个坐标轴上的分向量:a x i,a yj,a zk ,
向量的坐标: ax, ay, az,
向量的坐标表达式:
a { a x ,a y ,a z}
M 1 M 2 { x 2 x 1 ,y 2 y 1 ,z 2 z 1 } 特殊地: O M {x ,y ,z}
三、向量的坐标表示
1. 起点在原点的向量(向径)OM
z zC
设点 M(x,y,z)
以 i, j,k分别表示沿x, y, z
k
轴正向的单位向量, 称为基本单
位向量. rOM = OA + AN +NM
向量代数与空间解析几何-PPT

解: 由 cos2+cos2+cos2 =1,且 = = ,有
3cos2=3cos2=3cos2 =1,从而
cos cos cos 1 或 cos cos cos 1
3
3
例4. 设有P1P2,已知|| P1P2||=2,且与x轴和y轴的夹角
分别为
3
和
解. 设 P1P2
的4 方,向若角P1为为(1, ,0,,3),,有求P2的坐, 标 .
则力F 所作的功为 W=||F||cos ·||r||
定义1 对于向量a, b,数量
|| a |||| b || cosa, b
F
r
称为向量a与b的数量积;记为a·b.
这里0〈a, b〉 . 数量积亦称点 积或内积.
W = F·r
=〈a, b〉= 〈b, a〉
限定 0〈a, b〉 向量在轴 u 上的投影
设 a M1M 2
O
Pr ju M1M 2 u2 u1
a
b M2
a
M1
u1
u2
u
(1) Pr ju M1M 2 || M1M 2 || cos = ||a|| cos〈a, u〉
(2) Pr ju (a1 a2 an ) Pr jua1 Pr jua2 Pr juan
但 M1P P1P2
z
R2
R
M1Q Q1Q2 M1R R1R2
R1 M1
P
M2 Q
N
y
M1M 2
P1 O
Q1
Q2
P2
P1P2 Q1Q2 R1R2 x
称 P1P2 , Q1Q2 , R1R2 为 M1M 2 在Ox,Oy,Oz轴上的分向量 .
