压强与浮力常见题型(一)
压强浮力专题(含答案)

压强浮力专题(含答案)一、单选题1.如图所示,将一挂在弹簧测力计下的圆柱体金属块缓慢浸入水中(水足够深),在圆柱体接触容器底之前,能正确反映弹簧测力计示数F和圆柱体下表面到水面距离h的关系图是()A.B.C.D.2.下列物理量的估测中,最接近实际的是()A.教室里课桌的高度约为80dmB.人的正常体温约为37℃C.一个鸡蛋悬浮在盐水中,所受浮力约为2ND.家用电脑的额定功率约为1000W3.如图所示是a、b两种物质的质量与体积关系图,用b物质制成实心长方体,并将其放入水中,则物体在水中最终()A.漂浮B.悬浮C.沉底D.无法判断4.如图甲所示,物体A是一个正立方体,重力为4.8N,硬杆B一端固定在容器底,另一端固定在A底部。
现缓慢向容器中倒入密度为 的某种液体至A刚好浸没,硬杆B受到物体A的作用力F的大小随水深h变化的图象如图乙所示,不计杆的质量和体积,g取10N/kg。
下列说法正确的是()A.液体密度 为0.8×103kg/m3B.硬杆B的长度为6cmC.液体深h为13cm时,仅将硬杆B撤去,物体A在原来的位置保持静止D.液体深h达到13cm后继续向容器内倒入液体,F可能增大为4.8N5.下列估计最接近实际的是()A.一张报纸平铺在水平地面上产生的压强约为1000PaB.一个普通中学生站立在水平地面上对地面的压力约为50NC.鲁能巴蜀中学教室的大气压可达到1000mmHgD.海洋里100m深处的鱼受到海水的压强约为106Pa6.如图所示,甲、乙两容器质量相等、底面积相同,内装两种不同液体,两容器底部受到的液体压强相等,液体质量分别为m甲和m乙,距离容器底部等高的位置有A、B两点,受到的液体压强分别为p A和p B,则()A.m甲>m乙,p A>p B B.m甲=m乙,p A>p BC.m甲=m乙,p A<p B D.m甲<m乙,p A=p B7.如图所示实验中得出的结论不正确的是()A.甲图:用力推另一只船,自己的船也动起来,说明力的作用是相互的B.乙图:物体在力的作用下做圆周运动,说明物体运动需要力来维持C.丙图:探头在水中越深,U形管两侧液面的高度差越大,说明液体内部压强越大D.丁图:沿纸条上方吹气,纸条会飘起来,说明流速大的地方压强小8.下列数据符合实际的是()A.手托起一个鸡蛋的力是2N B.一个苹果的质量大约是0.15kgC.珠穆朗玛峰顶的大气压约为1.5×105Pa D.正常成年人的鞋子的面积约为100cm2 9.在初中物理的学习中,我们常会用到一些科学研究方法,如在“探究动能大小与哪些因素有关”时,通过小车推出物体的远近,判断小车动能大小。
压强浮力例题及练习(含答案)

压强浮力例题讲解及练习例1 张强同学家的高压锅盖上标有“××铝制品厂18cm压力锅”的字样,他测得高压锅限压阀的质量为70g,排气孔的横截面积约为10mm2.问这个高压锅工作时,其内部水蒸气的最大压强为多大?若锅盖面积为260cm2,则它所能承受的压力至少多大才能保证安全?(设大气压P0=105Pa)解析①高压锅内部的压强乘以排气孔的横截面积就是内部的蒸汽压力,当蒸汽压力等于限压阀的重力与外部大气压力之和时,高压锅处于平衡状态,据此即可求出高压锅内部水蒸气的最大压强.②为了能保证安全,锅盖所需要承受的压力应该等于锅内的蒸汽压力减去外部大气压力.解答①排气孔的横截面积为:S1=10mm2=10-5m2,限压阀的质量为:m=70g=0.07kg,锅内最大气压为:P0S1+mg=PS1,则P=P0S1+mgS1=1.0×105Pa×10-5m2+0.07kg×10N/kg10-5m2=1.7×105Pa;②锅盖面积为:S2=260cm2=2.6×10-2m2,锅盖所承受的最小压力为:F=P?S2-P0S2=1.7×105Pa×2.6×10-2m2-1.0×105Pa×2.6×10-2m2=1.82×103N.答:其内部水蒸气的最大压强为1.7×105Pa;它所能承受的压力至少为1.82×103N时才能保证安全.例2.(04湖北黄冈)(综合题)如图所示,是小明为防止家中停水而设计的贮水箱。
当水箱中水深达到1.2m时,浮子A恰好堵住进水管向箱内放水,此时浮子A有体积露出水面(浮子A只能沿图示位置的竖直方向移动)。
若进水管口水的压强为1.2×105Pa,管口横截面积为2.5㎝2,贮水箱底面积为0.8m2,浮子A重10N。
求:(1)贮水箱能装多少水?(2)浮子A的体积应多大?解:⑴V=Sh=0.8m2×1.2m=0.96m3M=ρV=1.0×103㎏/m3×0.96m3=960㎏⑵当浮子恰好堵住出水管时,F浮=GA+F压F压=pS=1.2×105Pa×2.5×10-4m2=30Nρ水Vg= GA+F压=10N+30N V=6×10-6m2例3.(04福建漳州)有一艘质量为2.0×106kg的运输船,在一次海难中沉入海底,打捞船利用超声波测出沉船到海面的距离约100m;潜水员潜入海底,找到沉船的一个舱盖,面积约0.5m2,打开它进入船舱,察看情况,以便制定打捞方案,打捞沉船的方案之一是用许多浮力代绑在船身上,每个浮力袋的体积约10m3,利用这些浮力袋受到的浮力使船上浮(海水的密度是1.03*103kg/m3)求:(1)海水对舱盖的压强(2)根据题目提供的信息,请你再求出两个物理量。
浮力压强计算题(含答案)_(1)
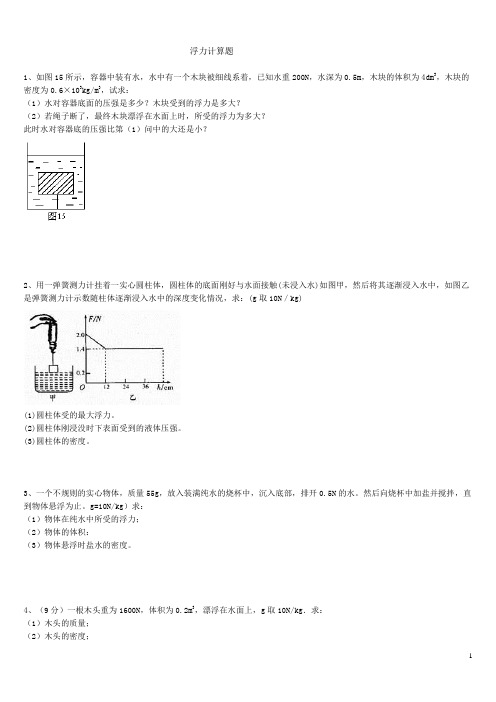
浮力计算题1、如图15所示,容器中装有水,水中有一个木块被细线系着,已知水重200N,水深为0.5m,木块的体积为4dm3,木块的密度为0.6×103kg/m3,试求:(1)水对容器底面的压强是多少?木块受到的浮力是多大?(2)若绳子断了,最终木块漂浮在水面上时,所受的浮力为多大?此时水对容器底的压强比第(1)问中的大还是小?2、用一弹簧测力计挂着一实心圆柱体,圆柱体的底面刚好与水面接触(未浸入水)如图甲,然后将其逐渐浸入水中,如图乙是弹簧测力计示数随柱体逐渐浸入水中的深度变化情况,求:(g取10N/kg)(1)圆柱体受的最大浮力。
(2)圆柱体刚浸没时下表面受到的液体压强。
(3)圆柱体的密度。
3、一个不规则的实心物体,质量55g,放入装满纯水的烧杯中,沉入底部,排开0.5N的水。
然后向烧杯中加盐并搅拌,直到物体悬浮为止。
g=10N/kg)求:(1)物体在纯水中所受的浮力;(2)物体的体积:(3)物体悬浮时盐水的密度。
4、(9分)一根木头重为1600N,体积为0.2m3,漂浮在水面上,g取10N/kg.求:(1)木头的质量;(2)木头的密度;(3)木头受到的浮力.5、一带阀门的圆柱形容器,底面积是300cm2,装有13cm深的水。
正方体A边长为12cm,重25N,用细绳悬挂放入水中,有1/6的体积露出水面,如图11所示。
试求:(1)A受到的浮力,此时水对容器底部的压强。
(2)若细绳所能承受的最大拉力是14.92N,通过阀门K缓慢放水,当绳子刚要被拉断的瞬间,容器中液面下降的高度。
(取g =10N/kg)6、如图所示的木块浸没在水中,细线对木块的拉力是2N.剪断细线,待木块静止后,将木块露出水面的部分切去,再在剩余的木块上加1N向下的压力时,木块有20cm3的体积露出水面.求木块的密度.(g取10N/kg)7、密度是0.6×103 kg/ m3的木块,体积是4 m3当它浮在水面上时,取g=10 N/kg,求:(1)木块重力;(2)木块受到的浮力;(3)木块排开水的体积;(4)木块露出水面的体积.8、如图所示,水面上漂有一块体积为2米3的浮冰,露出水面的体积为0.2米3,。
压强浮力中考典型题

压强浮力中考典型题
一、一个物体浸没在水中时,它受到的浮力与什么因素有关?
A. 物体的密度
B. 物体的体积
C. 物体在水中的深度
D. 液体的密度和物体排开液体的体积(答案)D
二、将一个木块放入水中,木块漂浮在水面上,此时木块受到的浮力与什么力平衡?
A. 木块的重力
B. 木块对水的压力
C. 水对木块的压力
D. 木块对地球的引力(答案)A
三、一个铁球和一个木球,体积相同,浸没在水中,哪个受到的浮力大?
A. 铁球
B. 木球
C. 一样大
D. 无法确定(答案)C
四、一个密闭的容器内装有水,将一个空心的铁球放入水中,铁球漂浮在水面上,当向容器内加盐使水变成盐水时,铁球的浮沉状态会如何变化?
A. 仍然漂浮
B. 沉入水底
C. 悬浮在水中
D. 无法确定(答案)A
五、一个潜水艇在水下匀速上升时,它所受的浮力与重力的大小关系如何?
A. 浮力大于重力
B. 浮力小于重力
C. 浮力等于重力
D. 无法确定(答案)C
六、将一个物体从水面缓慢浸入水中,当物体完全浸没在水中后,继续向下移动,物体所受浮力会如何变化?
A. 一直增大
B. 一直减小
C. 先增大后不变
D. 先增大后减小(答案)C
七、两个体积相同的球,一个是铁球,一个是木球,将它们同时放入水中,哪个球受到的浮力大?(假设两球均完全浸没)
A. 铁球
B. 木球
C. 一样大
D. 无法确定(答案)C
八、一个物体漂浮在液面上,如果将该液体换成密度更大的液体,物体在液面下的体积会如何变化?
A. 增大
B. 减小
C. 不变
D. 无法确定(答案)B。
压强浮力专题(及答案)

压强浮力专题(及答案)一、单选题1.关于生活中的一些物理现象,下列表述正确的是()A.骑自行车刹车时,用力捏紧刹车闸是为了增大接触面的粗糙程度从而增大摩擦B.石头沉入水底,是因为石头不受浮力的作用C.用重垂线来检查所砌的墙是否竖直是应用了重力与质量成正比的性质D.看到有人掉入湖里的冰窟,应匍匐前进救人,这是为了减小人对冰面的压强2.浸没在水中的石块,在石块下沉过程中所受压强和浮力的变化情况是()A.浮力和压强都减小B.浮力和压强都增大C.浮力减小,压强不变D.浮力不变,压强增大3.如图所示是a、b两种物质的质量与体积关系图,用b物质制成实心长方体,并将其放入水中,则物体在水中最终()A.漂浮B.悬浮C.沉底D.无法判断4.如图所示是航母舰载飞机训练时的图片。
下列说法中正确的是()A.飞机在航母甲板上加速过程,飞机受到平衡力B.飞机飞离航母时,惯性将消失C.飞机飞离航母后,航母所受浮力变小D.飞机获得向上的升力,是机翼上下空气流速差产生的5.如图所示,将甲、乙两个容器放在水平桌面上,甲、乙两容器的底面积分别为S甲和S ,容器内装有同种液体。
现将体积相等的A、B两个物体分别放入甲、乙两容器后,物体乙A悬浮,物体B漂浮且有一半体积露出液面,此时两容器中液面相平。
液体对甲容器底部的压强为p1、压力为F1,A物体的密度为ρA、受到的浮力为F A,液体对乙容器底部的压强为p2、压力为F2,B物体的密度为ρB、受到的浮力为F B。
已知S乙等于4S甲。
则下列判断正确的是()A.p1=p2,F1=4F2B.4p1=p2,4F1=F2C.F A=2F B,ρA=2ρB D.2F A=F B,2ρA=ρB6.电动自行车因方便、快捷深受人们的喜爱。
下列关于电动自行车结构及使用说法正确的是()A.刹车装置相当于省力杠杆B.电动自行车转弯时受到平衡力的作用C.车鞍做成宽且软是为了减小压力D.电动自行车在正常行驶过程中是将机械能转化为电能7.如图所示,完全相同的两个容器中分别装入甲、乙两种不同的液体,下列分析正确的是()A.若甲乙液体的质量相等,则A点的压强等于B点的压强B.若甲乙液体的质量相等,则C点的压强小于D点的压强C.若甲乙液体对容器底部的压强相等,则甲液体的质量等于乙液体的质量D.若甲乙液体对容器底部的压强相等,则甲液体的质量小于乙液体的质量8.乒乓球前进过程中由于不同的旋转方向会沿不同的径迹运动。
压强、浮力中考题型汇编

压强、浮⼒中考题型汇编第⼀节压强 1. 物体表⾯上的⼒,叫压⼒。
压⼒的作⽤效果与和有关。
物理学上,把物体上受到的压⼒叫压强。
公式是,单位是,符号是。
2. 如图13-1所⽰,A 、B 两个正⽅体,它们的边长之⽐为2:1,重⼒之⽐为4:3,先将B 放在⽔平桌⾯上,再将A 叠放在B 的正上⽅,则A 对B 的压强与B 对桌⾯的压强之⽐P A :P B 。
3.啄⽊鸟的嘴⽐较尖,这对它的觅⾷很有好处:当啄⽊鸟⽤嘴敲击树⽊时,听到有空洞的声⾳,说明害⾍住在⾥⾯。
它的嘴尖,相当于减⼩了与树⽊之间的,增⼤了对树⽊的,这样有利于将树⽊啄破,取出⾥⾯的害⾍。
5.下列⽣活中的实例,属于增⼤压强的是()A.滑雪时,在脚上穿滑雪板B.软包装饮料的吸管有⼀端被削尖C.铁轨铺在枕⽊上D.推⼟机上安装的两条履带8.冬天⼩华在“⽩鹭公园”结冰的湖⾯上玩耍时,不⼩⼼压破冰⾯掉进了冰窟窿,公园的⼯作⼈员需要接近冰窟窿去营救他,旁边⼀块有长、宽都差不多的⽊板,为了救⼈,应建议⼯作⼈员采取以下措施是(A.⽴即跑向冰窟窿B.将⽊板铺在冰⾯上,从上⾯爬过去救⼈C.从冰⾯上爬过去救⼈D.从冰⾯上直接翻滚过去9、⼀块砖平放在⽔平地⾯上,将它切去⼀半,剩下的⼀半对地⾯的压强( )A 、⼀定是原来的1/2 ;B 、⼀定和原来的⼀样;C 、⼀定是原来的2倍;D 、条件不⾜⽆法确定。
10、如右图所⽰,物体重10 N ,它与竖直墙⾯的接触⾯积是0.5 dm 2,现⽤24 N 的⽔平⼒把物体按在墙上,墙⾯受到物体的压⼒和压强分别为()A.10 N ,2×103 PaB.10 N ,4.8×103 PaC.24 N ,2×103 PaD.24 N ,4.8×103 Pa9.画出图13-4所⽰,两图中物体A 受到物体B 压⼒的⽰意图。
10. 军事上坦克要越过敌⽅的壕沟,有⼈提出了⼀种简易的⽅案:条履带着地⾯积为2.5m 2,⽓囊能承受的最⼤压强为2×105Pa 带与⽓囊接触⾯积⾄少为多⼤?(设坦克的前后重是均匀的)第⼆节 1. 如图13-5所⽰,瓶中⽔从⼩孔A 、B 些,说明液体的压强随的增加⽽增⼤。
(压强与浮力)常见题型精选,题型一:两物体连接问题

(压强与浮力)常见题型精选专题一:两物体连接问题2018年2月8日于例1、如图所示,金属块A 用细线悬挂在漂浮在水中的木块B 下面,静止后木块B 露出水面的体积为V 1,木块B 下表面受到水的压强为P 1,若将细线剪断再将金属块A 放在木块B 上面,静止后金属A 露出水面的体积为V 2,木块B 下表面受到水的压强为P 2,则下面关系式成立的是(D )A .V 1=V 2,P 1=P 2B .V 1>V 2,P 1<P 2C .V 1<V 2,P 1>P 2D .V 1=V 2,P 1<P 2解:把物体A 和B 看做一个整体,两种情况都是处于漂浮状态,浮力等于AB 的总重力,浮力相等.在同种液体中,浮力相等,则排开液体的体积一定相等. V 1=V A +V B -V 排,V 2=V A +V B -V 排,所以V 1=V 2.液体压强的大小与液体的密度和物体浸入液体的深度有关.根据P=ρgh ,第二种情况下木块B 下表面浸入液体深度大,受到的液体压强就大.P 1<P 2.类似题:如图所示,金属块甲用细绳吊于物体 M 下方,金属块乙放在 M 上方。
在甲、乙金属块的作用下,物体 M 都刚好浸没在水中静止。
则( AD )A. 甲的重力一定大于乙的重力B. 甲的重力可能小于乙的重力C. 甲的体积一定大于乙的体积D. 甲的体积可能等于乙的体积例2、如图所示,在三个相同的容器中装有质量相同的盐水、水、酒精,将木块A 、金属块B 按不同的方式放入液体中,待A 、B 静止时,比较三个容器中木块下表面所受液体的压强p1、p2、p3的大小关系应是______________。
解:由图可知木块A 和金属块B 在甲、乙两图中都是处于漂浮状态,所以受到的浮力都等于它们的总重力,甲、乙两种情况中A 、B 两物体受到的浮力相等,根据阿基米德原理可知它们排开水的体积相等,则甲图中木块A 排开水的体积等于乙图中金属块B 和木块A 排开M 甲乙 M水的体积和,所以甲图中木块A排开水的体积大于乙图中木块A排开水的体积,甲图中木块下表面所处的深度大于乙图中木块下表面所处的深度,所以甲图中木块下表面所受的压强大于乙图中木块下表面所受的压强;即P1>P2由图丙可知,图丙中木块A处于漂浮状态,木块A受到的浮力等于木块的重力,金属块B下沉,金属块B受到的浮力小于金属块的重力,则图丙中A、B两物体受到的浮力和小于它们的重力和,所以丙图中排开水的体积小于乙图中排开水的体积,在乙、丙两种情况下B排开水的体积相等,所以丙图中A排开水的体积小于乙图中A排开水的体积,所以乙图中木块下表面所处的深度大于丙图中木块下表面所处的深度,所以乙图中木块下表面所受的压强大于丙图中木块下表面所受的压强.即P2>P3类似题:如图所示,在三个相同的容器中装有质量相同的水,将木块A、金属块B按不同的方式放入水中,待A、B静止时,三个容器中木块下表面所受的压强相比较,正确的是(A)A.P 甲>P 乙>P 丙B.P 甲=P 乙>P 丙C.P 甲<P 乙=P 丙D.P 甲=P 乙=P 丙解:由图可知木块A和金属块B在甲、乙两图中都是处于漂浮状态,所以受到的浮力都等于它们的总重力,甲、乙两种情况中A、B两物体受到的浮力相等,根据阿基米德原理可知它们排开水的体积相等,则甲图中木块A排开水的体积等于乙图中金属块B和木块A排开水的体积和,所以甲图中木块A排开水的体积大于乙图中木块A排开水的体积,甲图中木块下表面所处的深度大于乙图中木块下表面所处的深度,所以甲图中木块下表面所受的压强大于乙图中木块下表面所受的压强;由图丙可知,图丙中木块A处于漂浮状态,木块A受到的浮力等于木块的重力,金属块B下沉,金属块B受到的浮力小于金属块的重力,则图丙中A、B两物体受到的浮力和小于它们的重力和,所以丙图中排开水的体积小于乙图中排开水的体积,在乙、丙两种情况下B 排开水的体积相等,所以丙图中A排开水的体积小于乙图中A排开水的体积,所以乙图中木块下表面所处的深度大于丙图中木块下表面所处的深度,所以乙图中木块下表面所受的压强大于丙图中木块下表面所受的压强.故选A.例3、如图,放有铁块的杯子漂浮在水面上,如果把铁块用细线悬挂在杯底,杯子和铁块受到的浮力将(不变),水对容器底部的压强将(不变).(填增大、减小或不变)解:①把铁块和杯子看做一个整体,根据漂浮状态下F浮=G物,由于铁块和杯子的重力和始终不变,所以杯子和铁块受到总浮力不变;②由阿基米德原理知,杯子和铁块受到的浮力为F浮=ρ液gV排,因为总浮力一直保持不变,且ρ液和g均不变,所以V排也不变,因此前后水面的高度h 是不变的,又因为P底=ρ液gh,ρ液gh始终不变,所以水对容器底的压强不变.例4、如图所示,挂有实心铁块的平底试管漂浮在水面,如果将铁块取下放入试管中,试管仍漂浮,则下列说确的是(D)A.水对容器底的压强减小B .水对容器底的压强增大C .试管下表面受到水的压强减小D .试管下表面受到水的压强增大分析:如图所示和将铁块取下放入试管中,两种情况均为漂浮,并且总重不变,根据物体的漂浮条件得出两种情况下受到的水的浮力不变,根据阿基米德原理知道排开水的体积不变,水深不变,根据液体压强公式得出水对容器底的压强不变;如图所示排开水的总体积等于试管排开水的体积加上铁块排开水的体积;将铁块取下放入试管中,二者排开水的总体积等于试管排开水的体积,因为前后排开水的总体积不变,所以试管排开水的体积变大,试管下表面所处深度变大,根据液体压强公式得出试管下表面受到水的压强的变化情况.例6、如图所示,一木块漂浮在水面上,露出水面的体积为在水下体积的1/3,若在木块上放一个重为5牛的物体,木块正好全部浸入水中,求:(1)木块的密度 (2)木块的重力解答:(1)当木块漂浮在水面上时,F 浮=G 木,即ρ水gV 排=ρ木V 木g,所以ρ木=V 排ρ水/V 木,再根据V 排和V 木的关系,可计算得出ρ木=0.75×103Kg/m 3,(2)当木块上放一物体时,把木块和物体当作一个整体,它们仍然漂浮在水上,设整体受到的浮力为F 浮1,则可列出关系式:F 浮1=G 木+G 物=ρ水gV 排=ρ水gV 木,即:G 木+5牛=ρ水gV 木,(1)因为ρ木:ρ水=3:4,所以(1)式可以变形为:G 木+5牛=(4/3)ρ木gV 木,进一步变形为:G 木+5牛=(4/3)G 木所以:G 木=15牛。
压强与浮力好题+解析

压强与浮力好题+解析一、压强和压力典型题目分析1.液体对容器底部的压力和压强:F容器底=G同一底面水柱;P容器底=ρ液gh=G柱/S2.容器对水平桌面的压力和压强:F桌面=G;P桌面=G/S甲F<G液乙 F=G液。
丙F>G液图3甲容器口大底小,对液体提供向上的支持力的,不仅仅是容器底部,周围侧壁对液体也提供向上的支持力,这就减轻了液体对容器底部的压力,使F<G。
乙容器的侧壁对液体也有作用力,但方向是水平的,不能减轻了液体对容器底部的压力,所以F=G。
丙容器的侧壁对液体的力的方向向下(依据:压力的方向总是与接触面垂直),使容器底部不仅承受液体的重力,还要承受侧壁对液体向下的压力,使F>G。
由于液体对容器底部的压力并不一定等于液体的重力,所以在计算液体对容器底部的压力时,应先根据公式p= ρgh求出液体的压强,再根据F=pS求出压力。
3.压力与压强的变化分析①如图所示,某同学用弹簧测力计拉着放在水平桌面上的木块匀速滑动,在木块前端离开桌面至一半移出桌面的过程中,弹簧测力计的示数,木块对桌面的压力块对桌面的压强(均选填“变大”、“变小”或“不变”)解:在滑动过程中,木块对桌面的压力始终等于木块的重力,(重心是物体各部分受力的等效作用点)所以F不变,摩擦力大小与接触面积无关,所以f不变,弹簧测力计示数不变;因为受力面积减小,所以压强变大.故答案为:不变;不变;变大.②(2011年上海市)如图所示,底面积不同的圆柱形容器A和B分别盛有甲、乙两种液体,两液面相平且甲的质量大于乙的质量.若在两容器中分别加入原有液体后,液面仍保持相P B和压力F A、F B的关系是(P A>P B,F A>F B)平.则此时液体对各自容器底部的压强PA、(液体压强不一定只能用ρ液gh分析,若为柱体,亦可用G柱/S)③(2011年北京市)甲、乙两个圆柱形容器盛有相同深度的液体,放置于水平桌面上,如图所示.甲、乙两容器的底面积分别为S1和S2,且2S1=3S2.甲容器中液体的密度为ρ1,液体对容器底产生的压强为p1.乙容器中液体的密度为ρ2,液体对容器底产生的压强为p2,且p2=2p1.将A球浸在甲容器的液体中,B球浸在乙容器的液体中,两容器中均无液体溢出.液体静止后,甲、乙两容器底受到液体的压力相等,A、B两球所受浮力分别为F1和F2.则下列判断正确的是()A.F1>F2,ρ1<ρ2B.F1=F2,ρ1<ρ2C.F1<F2,ρ1>ρ2D.F1<F2,ρ1<ρ2密度大小关系不难判断,根据液体压强公式和题目条件即可。
压强和浮力测试题及答案

压强和浮力测试题及答案1. 某容器内装有水,水的深度为10米。
求容器底部受到的压强。
2. 一个体积为0.01立方米的木块漂浮在水面上,求木块受到的浮力。
3. 一个体积为0.01立方米的铁块完全浸没在水中,求铁块受到的浮力。
4. 一个体积为0.01立方米的铁块漂浮在水面上,求铁块受到的浮力。
答案1. 根据压强的定义,压强p等于单位面积上受到的压力F除以面积S,即p = F/S。
在液体中,压强还与液体的密度ρ和重力加速度g有关,即p = ρgh。
在这个问题中,水的密度ρ约为1000千克/立方米,重力加速度g约为9.8牛顿/千克,水的深度h为10米。
因此,容器底部受到的压强为:p = 1000 kg/m³ × 9.8 N/kg × 10 m = 98000 Pa。
2. 根据阿基米德原理,物体在液体中受到的浮力等于它排开的液体的重量。
木块漂浮在水面上,所以木块受到的浮力等于木块的重力。
木块的重力G等于木块的质量m乘以重力加速度g,即G = mg。
木块的体积V为0.01立方米,假设木块的密度ρ木约为500千克/立方米,则木块的质量m = ρ木V = 500 kg/m³ × 0.01 m³ = 5 kg。
因此,木块受到的浮力为:F浮= G = mg = 5 kg × 9.8 N/kg = 49 N。
3. 铁块完全浸没在水中,所以铁块排开的水的体积等于铁块的体积。
铁块受到的浮力等于排开的水的重量。
水的密度ρ水约为1000千克/立方米,重力加速度g约为9.8牛顿/千克,铁块的体积V为0.01立方米。
因此,铁块受到的浮力为:F浮= ρ水gV = 1000 kg/m³ × 9.8 N/kg × 0.01 m³ = 98 N。
4. 铁块漂浮在水面上,所以铁块受到的浮力等于铁块的重力。
铁块的密度ρ铁约为7800千克/立方米,重力加速度g约为9.8牛顿/千克,铁块的体积V为0.01立方米。
浮力压强练习题

浮力压强练习题浮力是物体在液体中所受到的向上的力,它的大小等于排斥液体的体积乘以液体的密度和重力加速度。
根据阿基米德原理,浸在液体中的物体所受到的浮力等于所排斥液体的重量。
而浮力压强则是指浸在液体中的物体所受到的浮力在单位面积上的压力。
本文将通过一些练习题,帮助读者更好地理解和计算浮力压强。
练习题一:一个半径为5cm的浮标完全浸没在水中。
已知水的密度为1g/cm³,重力加速度为9.8m/s²。
请计算这个浮标受到的浮力压强。
解答:根据阿基米德原理可知,物体在液体中所受到的浮力等于所排斥液体的重量。
由于浮标完全浸没在水中,所以它排斥的水的体积等于浮标的体积。
浮标的体积可以通过球体积公式计算,即4/3πr³,其中r为半径。
代入数值可得体积为523.6cm³。
浮标排斥的水的质量等于体积乘以水的密度,即523.6g。
而浮标受到的浮力等于排斥水的质量乘以重力加速度,即523.6g * 9.8m/s²。
将浮力除以浮标所接触水的表面积,即圆面积πr²,即可得到浮力压强。
练习题二:一个长方体木块的底边长为10cm,高为20cm,在水中的深度为15cm。
已知水的密度为1g/cm³,重力加速度为9.8m/s²。
请计算这个木块受到的浮力压强。
解答:首先求出这个木块排斥的水的体积。
木块的体积可以通过底面积乘以高度计算,即10cm * 20cm * 15cm,得到体积为3000cm³。
木块排斥的水的质量等于体积乘以水的密度,即3000g。
浮力等于排斥水的质量乘以重力加速度,即3000g * 9.8m/s²。
再将浮力除以木块所接触水的底面积,即10cm * 20cm,即可得到浮力压强。
练习题三:一个圆柱体木块的底面半径为8cm,高为10cm,在水中的深度为6cm。
已知水的密度为1g/cm³,重力加速度为9.8m/s²。
压强与浮力专题训练 练习题(含答案)

压强与浮力专题训练 练习题(含答案)一、单选题1.疫情期间,人们利用5G无人配送车实现了非接触安心送,如图为一辆在水平路面上匀速行驶的无人配送车,速度为10 km/h,空载时质量为360 kg,轮胎与路面的总接触面积为240cm2。
下列说法正确的是( )A.该车所受的牵引力和阻力是一对相互作用力B.空载时该车对路面的压强为1.5×104 PaC.该车行驶2 km需要12 minD.该车若加速向左转弯时,车可能向左倾倒2.水平桌面上有一溢水杯,装满某种液体,将小球A放入溢水杯中静止时(如图所示)从杯中溢出了0.6N的液体。
下列说正确..的是( )A.小球A放入后溢水杯对桌面的压力不变B.小球A的重力小于0.6NC.小球A在杯中受到的浮力大于0.6ND.小球A放入后,液体对溢水杯底的压强增大3.浸没在水中的石块,在石块下沉过程中所受压强和浮力的变化情况是()A.浮力和压强都减小B.浮力和压强都增大C.浮力减小,压强不变D.浮力不变,压强增大4.日常生活中有很多现象都与我们学习过的物理知识有关。
下列说法正确的是( )A.自行车前后轮安装在滚动轴承上,可以增大摩擦B.投掷出去的铅球在空中飞行的过程中,运动员对铅球做了功C.高压锅是利用液体的沸点随液面上方气压增大而升高的原理工作的D.短跑运动员在到达终点后不会立即停下来,是因为受到惯性的作用5.电动自行车因方便、快捷深受人们的喜爱。
下列关于电动自行车结构及使用说法正确的是( )A.刹车装置相当于省力杠杆B.电动自行车转弯时受到平衡力的作用C.车鞍做成宽且软是为了减小压力D.电动自行车在正常行驶过程中是将机械能转化为电能6.如图所示,完全相同的两个容器中分别装入甲、乙两种不同的液体,下列分析正确的是( )A.若甲乙液体的质量相等,则A点的压强等于B点的压强B.若甲乙液体的质量相等,则C点的压强小于D点的压强C.若甲乙液体对容器底部的压强相等,则甲液体的质量等于乙液体的质量D.若甲乙液体对容器底部的压强相等,则甲液体的质量小于乙液体的质量7.如图所示,水平面上有质量和底面积都相同的甲乙容器,分别装有质量和深度均相等的A、B两种不同液体,下列说法正确的是( )A.甲容器对水平地面的压强大于乙容器对水平地面的压强B.A液体对甲容器底部的压强大于B液体对乙容器底部的压强C.甲容器对水平地面的压力大于乙容器对水平地面的压力D.A液体对甲容器底部的压力等于B液体对乙容器底部的压力8.下列数据符合实际的是( )A.手托起一个鸡蛋的力是2N B.一个苹果的质量大约是0.15kgC.珠穆朗玛峰顶的大气压约为1.5×105Pa D.正常成年人的鞋子的面积约为100cm2 9.如图所示是与压强知识相关的实验和实例,其中分析正确的是( )A.甲图实验,帕斯卡裂桶实验,证明液体压强随高度的增加而增加B.乙图实验,在两纸片中间向下吹气,两纸片均会向外运动C.丙图实验,若只将玻璃管换成较粗的管子,则实验结果会偏小D.丁图实验,塑料吸盘能粘在光滑墙壁上不掉下来说明了大气压强的存在10.如图所示,放在细沙面上的饮料瓶子,内部剩有部分饮料,如将瓶盖旋紧后倒过来放在细沙面上,下列分析正确的是( )A.倒放时液体对瓶塞的压强小于正放时液体对瓶底的压强B.倒放时液体对瓶塞的压力小于正放时液体对瓶底的压力C.倒放时瓶子对沙面的压强小于正放时瓶子对沙面的压强D.倒放时瓶子对沙面的压力大于正放时瓶子对沙面的压力11.如图所示,用阴影部分面积描述的物理量中,不正确的是( )A.用电器的电功率B.物体所受的压强C.物体的质量D.物体运动的路程12.水平桌面上有一溢水杯,装满某种液体,将小球A放入溢水杯中静止时(如图所示)从杯中溢出了0.6N的液体。
压强及浮力练习题精选

"压强与浮力"练习题一、填空题:1、著名的马德堡半球实验证实了,意大利科学家第一个用实验的方法测出大气压的值.1标准大气压等于Pa,假设桌面的面积是2 m2,在标准气压下,大气作用对桌面上的压力是N。
2、书包的背带做得很宽是为了;汽车轮胎上有花纹是为了。
3、潜水艇是靠改变它受到的来实现潜水和上浮的,浸没在水中的潜水艇当它从大海进入长江时所受的浮力,漂浮在海面上的一艘轮船从海里驶人河里,它受到的浮力,它排开水的体积(三空均选填"变大〞、"变小〞或"不变〞)4、如下图,物体A在水平推力F的作用下从甲图位置匀速运动到乙图位置。
此过程中,物体A受到的摩擦力________水平推力F〔选填"大于〞、"等于〞或"小于〞〕,物体A对桌面的压力〔选填"变大〞、"变小〞或"不变〞〕,物体A对桌面的压强将。
〔选填"变大〞、"变小〞或"不变〞〕5、一头质量为6×103kg的大象,每只脚掌的面积为600cm2,它的重力为N,它四脚着地时对地面的压强为Pa.假设大象抬起一条腿,它对地面的压力〔选填"变大〞、"变小〞或"不变〞〕。
(g取10N/kg)6、小明同学的质量为50kg,他的一只平底鞋放在方格纸上描绘出的形状如下图,每个方格都是边长为2cm的正方形,数一下鞋底覆盖的方格数〔不满一格的都计为半格〕,可算出这只鞋底的面积约为cm2,小明穿上这双鞋站立时对地面的压力等于N,以此可以估算出双脚对地面的压强为Pa。
7、如右图所示,金鱼吐出的气泡在水中上升的过程中,气泡受到水的压强将〔填"变大〞、"变小〞或"不变〞〕;气泡受到水的浮力将〔填"变大〞、"变小〞或"不变〞〕。
8、一只苹果的质量为140g、体积为1.8×10-4m3,用手将其浸没在水中时,苹果受到的浮力为N〔g取10N/kg〕,松手后苹果将〔选填"上浮〞、"下沉〞或"悬浮〞〕.9、把重10N,体积为1.2×103cm3的物体投入水中,当物体静止时,物体的状态是。
压强浮力例题及练习(含答案)

A.刹车装置相当于省力杠杆 B.电动自行车转弯时受到平衡力的作用 C.车鞍做成宽且软是为了减小压力 D.电动自行车在正常行驶过程中是将机械能转化为电能 7.关于图中现象及其解释正确的是( )
A.航空母舰所受的浮力大于它所受的重力
B.航空母舰排开的海水越多受到的浮力越大
C.战斗机升空后,航空母舰受到的浮力变大
D.战斗机升空后,航空母舰受到的浮力不变
19.有一小石蜡块,其质量为 10g,体积为 11cm3,先将它轻轻放入盛满水的溢水杯中,
当石蜡块静止时,溢出水的质量为 10g;把它取出擦干,再轻轻放入盛满煤油的溢水杯中
从图像可知该液体密度_______水的密度(选填“大于”、“小于”或“等于”),若用 ρ 、ρ
液
水
分别表示该液体和水的密度,那么液体密度可表示为 ρ =______。(用题目中的字母表 液
示)
41.同学们利用压强计等装置“探究液体内部压强的规律”,进行了如下的操作。
(1)如果所用的压强计 U 形管中可选择装染色的酒精、水以及水银中的一种液体,为了
B
A
B
A. , F F
A
B
A
B
B. , F F
A
B
A
B
C. , F F
A
B
A
B
D. , F F
A
B
A
B
17.如图所示,水平桌面上放置着一个装有水的圆柱形容器和质量相等的 A、B 两个小
(完整版)压强与浮力计算题复习专题(含答案)

.中考压强与浮力计算题专题31.体积是 50cm ,质量是 45g 的物体,将其慢慢放入装满水的烧杯中,物体静止后,溢出水的质量是多少 g.将其慢慢放入装满酒精的烧杯中,溢出酒精的质量是多少g.3 3(酒=×10 kg/m )2.一个金属块挂在弹簧测力计上,在空气中称读数为34 牛,把它侵没在水中称测力计读数为24 牛,此金属块碰到的浮力是多少? 体积为多大?密度为多大?(g=10N/ ㎏ )3..有一金属块挂在弹簧测力计下,在空气中称时弹簧测力计的示数为15N,将它吞没在水中称时弹簧测力计的示数为5N, g=10N/kg .求:①金属块碰到的浮力;②金属块的体积;③金属块的密度。
..4.以下列图,将边长是10cm 的实心立方体木块轻轻放入盛满水的大水槽中。
待木块静止时,从水槽中溢出了550g 水, g 取 10N/kg ,求:(1)木块静止时碰到的浮力大小;(2)木块的密度;(3)木块静止时下表面碰到的水的压富强小。
5.为增加学生的国防知识,某中学九(7)班同学到东海舰队参观某型号潜水艇。
潜水艇的艇壳是用高强度的特种钢板制造,最大下潜深度可达350m .潜水艇的整体积为×103 m3,艇内两侧有水舱,潜水艇截面以下列图。
经过向水舱中充水或从水舱中向外排水来改变潜水艇的.自重,从而使其下沉或上浮。
(海水密度为×103kg/m 3,g 取 10N/kg )(1)水舱未充海水时,潜水艇总重力为×106N,此时,飘扬在海面的潜水艇排开海水的体积是多少?(2)为使潜水艇完满潜入水中,最少应向水舱充入海水的重力是多少?(3)潜水艇的艇壳用高强度的特种钢板制造的原因是什么?6.以下列图,容器重为16N ,底面积 100cm2,容器中装有水,水中有一个木块被细线系着并完满吞没在水中,已知水重200N ,木块的体积为 4dm 3,木块的密度为×103kg/m 3,g 取10N/kg ,试求:( 1)容器对桌面的压强是多少?木块碰到的浮力是多大?( 2)若绳子断了,最后木块飘扬在水面上时,所受的浮力为多大?.7.以下列图,边长分别为0.2 米和 0.1 米的实心正方体A、B 放置在水平川面上,ρA=0.1 ×103kg/m 3、ρB×103kg/m 3。
压强与浮力综合计算题(一)

压强与浮力综合计算题〔一〕1、如下图,放在水平桌面上的薄壁圆柱形容器重6N,底面积100cm2,弹簧测力计的挂钩上挂着重为27N的金属块,现将金属块浸没水中,容器内水面由20cm 上升到30cm〔g=10N/kg〕.求:〔1〕金属块未放入水中时〔如下图〕,容器底部受到的水的压强:〔2〕金属块的密度;〔3〕金属块浸没水中静止后弹簧测力计的示数;〔4〕金属块浸没水中后〔未于底部接触〕,容器对桌面的压强.2、如图14所示,一个重为6牛、容积为V容的圆柱形容器放在水平地面上,容器的底面积S为2×10-2米2。
①求该容器对水平地面的压强p地面。
②假设在该容器中倒入体积为V水的水后,求水面下0.1米深处水的压强p水。
③假设将一个体积为V物的金属物块浸没在水中后,讨论水对容器底部压强增加量的变化范围。
〔要求:讨论中涉及的物理量均用字母表示〕3、如图18,密度为0.6×103kg/m3、体积为10-3m3的正方体木块,用一条质量可忽略不计的细绳系住,绳的两端分别系于木块底部中心和容器底部中心。
细绳对木块的最大拉力为3N。
容器内有一定量的水,木块处于漂浮状态,但细绳仍然松软,对木块没有拉力。
容器的底面积为0.03 m2。
求:〔1〕此时木块受到的浮力?〔2〕当向容器中注水,直到细绳对木块的拉力到达最大值,在细绳断裂前的一瞬间停止注水,则此时木块浸入水中的体积为多大?4、某教师用“试管爬升”实验验证大气压的存在,其做法如下:取两个直径相差很小的平底试管,将细试管底部插入装满水的粗试管内,再将两试管迅速倒置〔保持竖直〕,会看到细试管慢慢“爬进”粗试管里,如图23所示,细试管能否在粗试管内竖直向上“爬升”,取决于开始时插入粗试管的深度,如果插入过浅细试管就不能自动上升。
假设细试管的重为G,外直径为d,水的密度为ρ0,大气压强为p0,请你通过推导计算,答复以下问题:〔1〕细试管在“爬升”时,受到大气对它竖直向上的压力是多少?〔2〕细试管开始插入的深度h0满足什么条件时,它刚好可以向上“爬升”。
2021年中考物理专题复习之压强浮力专题(1)

九年级物理中考专题复习之专题六 压强浮力(1)知识点梳理一、压强1、固体压强:①压力与重力大小关系:A 、物体处于水平面时: ;B 、物体处于斜面时: ; ②压强公式:S GS FP ==(水平面)=gh ρ(均匀规则柱体);2、液体压强:①液体由于受到 的作用,故对容器的 和 产生压强作用。
②液体压强公式:P= =S G(柱体容器)。
③补充:A\只要求液体压强,一定用P= 公式来分析;B\只要求液体压力,一定先用P= 公式来求压强,再利用F= 来求值;3、浮力:①阿基米德原理:F 浮= ;②阿基米德原理推导:F 浮= ;(浮力的影响因素: 、 ) 浮力应用:①称重法浮力公式(受力分析,建立等式): ;②漂浮法(受力分析,二次分解): ;中考真题链接(压强专题)1、如图所示充满液体圆台状容器,将它倒置过来放在桌面上,与原来相比较,容器底部受到的()A 、压力不变,压强增大B 、压强不变,压力增大C 、压力不变,压强不变D 、压强不变,压力变小拓展:如图所示的圆台状容器内充满液体,将它倒置过来放在桌面上,跟原来相比较,水平桌面受到的( )A 、压力不变,压强增大B 、压强不变,压力增大C 、压力不变,压强不变D 、压强不变,压力变小2、如右图所示,盛有一定质量水的封闭容器放在水平面上,液体对容器底部的压力和压强分别为F 1和p 1,如果将容器倒过来放在水平面上,液体对容器底部的压力和压强分别为F 2和p 2,比较F 1,F 2和p 1,p 2,下列说法中正确的是( )A. 21F F >,21p p <B. 21F F <,21p p >C. 21F F >,21p p >D. 21F F <,21p p <拓展:如图所示,盛有一定质量水的封闭容器放在水平面上,液体对桌面的压力和压强分别为F 1和p 1,如果将容器倒过来放在水平面上,液体对桌面的压力和压强分别为F 2和p 2,比较F 1,F 2和p 1,p 2,则. F1 F2;P1 P2.3、如图所示,长木板重10 N,底面积为10cm 2,现将其底面积的32与水平桌面接触,木板静止时对桌面的压强为 Pa;在水平外力作用下推动木板缓慢向左运动,直至木板全部移到桌面,在这个过程中,木板对桌面的压强 ( 变大/不变/变小),木板所受摩擦力的大小 (变大/不变/变小).4、如图所示,质地均匀的实心圆柱体A、B叠放在水平地面上,已知他们的密度之比ρA:ρB=1:3,底面积之比S A:S B=4:3,A对B的压强和B对地面的压强之比P A:P B=1:2,则他们的高度之比h A:h B为()A: 9:4 B: 3:2 C: 3:1 D: 9:25、如图所示,甲、乙是放在水平地面上的两个质量均匀的长方体,它们的密度之比ρ甲:ρ乙=2:3,底面积之S甲: S乙=3: 4,对水平地面的压强之比P甲: P乙=8: 5,下列有关甲、乙的说法正确的是()A.甲、乙的重力之比是1: 2B.甲、乙的体积之比是16: 5C.甲、乙的高度之比是5: 12D.将他们沿水平方向切去相同的高度后,剩余部分对地面的压强甲大于乙6、如图所示,把用ρ=1.0×103kg/m3 的复合材料制成棱长分别为2m和3 m的甲、乙两实心均匀正方体放在水平地面上,甲、乙对地面的压强分别为P甲、P乙;把G1=2×104N的物体放在甲上,G2=3×104 N的物体放在乙上,此时甲、乙对地面的压强分别为P甲'、P乙’,则下列结果正确的是()A.P甲:P乙=2 :3,P甲':P乙’=3 :4B.P甲:P乙=2 :3,P甲':P乙’=4 :3C.P甲:P乙=3 :2,P甲':P乙’=3 :4D.P甲:P乙=3 :2,P甲':P乙’=4 :37、中国南极泰山站采用轻质材料装配而成,为避免被南极强横风吹得移位,其独特的支架悬空形状发挥了作用泰山站的悬空形状接近于下列图中的()8、小柯设计了一个“不用绳子扎口的气球”,如图所示,先将气球放入玻璃瓶中,再将球口紧套在玻璃瓶口,从抽气口抽气,观察到气球变大;停止抽气后,马上用橡皮套封住抽气口,此时气球不用绳子扎,也能保持膨胀状态。
压强、浮力 (简单题型)

压强1.如图所示三个规格相同的杯子里分别装有水、盐水和煤油。
它们对容器底部的压强相同,根据杯中液面的位置可以判定:()A.甲杯是水,乙杯是盐水B.甲杯是盐水,乙杯是煤油C.乙杯是盐水,丙杯是水D.乙杯是水,丙杯是煤油2.为了将压强减小到原来的1/4,以下做法中可达到目的的是( )A、受力面积不变,压力减小1/4 ;B、压力不变,受力面积减小到原来的3/4 ;C、压力和受力面积同时减小到原来的1/4 ;D、压力减小1/2 ,同时受力面积增大1倍。
3.制药厂在培养液中提取抗菌素时,要通过加热去掉培养液中的水分,但又不允许温度达到100℃,下列的办法中可采用的是( )A、减小火力;B、加大火力;C、减小液面上的气压;D、增大液面上的气压;4.一块砖平放在水平地面上,将它切去一半,剩下的一半对地面的压强( )A、一定是原来的1/2 ;B、一定和原来的一样;C、一定是原来的2倍;D、条件不足无法确定。
5.有铜、铁、铝三个金属块(ρ铜>ρ铁>ρ铝),高度相等,底面积不等,放在水平桌面上,它们对桌面的压强分别是P铀、P铁、P铝,则:( )A、P铀<P铁<P铝B、P铀=P铁=P铝C、P铀>P铁>P铝D、无法判定6.如图:密封的圆台形容器装有一定量的水,从甲到乙,则水对容器底的作用情况是:( )A、压强减小,压力不变B、压强不变,压力增大甲乙C、压强减小,压力减小D、压强不变,压力减小7.下列叙述中属于减小压强的是( )A、菜刀被磨得很薄B、书包带扁而宽C、啄木鸟有细长而尖硬的嘴D、铁路钢轨不直接铺到路基上而铺在枕木上8.很多动物为了适应自身生存的环境,进化出了符合一定物理规律的身体部位,对此,从物理学的角度给出的解释中不正确...的是()A、骆驼的脚很大,可以减小压力,从而使其在沙漠中自如行走B、啄木鸟的嘴很尖细,可以增大压强,从而凿开树干,捉到虫子C、壁虎的脚掌上有许多“吸盘”,从而利用大气压使其在天花板上也不会掉下来D、深水里的海鱼捕到岸上时会死掉,主要原因是水面上的压强比深水处小得多9.如图展示了日常生活或生产技术中的四种情境,其中哪种情境运用了增大压强的知识()滑雪 细线分割 肥 皂 螺丝连接工 件 拖拉机 螺母、垫片 A B C D10.如图是北京奥运会部分运动项目图标,在这些项目中运动员对地面压强最大的是( )11.下列选项中对应关系不正确的是A .潜水员潜入深水时要穿潜水服——液体压强B .用注射器推药液——大气压强C .汽车突然刹车,乘客向前倾倒——惯性现象D .火车进站时,人要站在安全线外——流体压强与流速的关系12.如图所示,质量相同的甲、乙两个均匀实心正方体放在水平地面上。
初中物理浮力与压强例题及详细解析(经典9题)

初中物理浮力与压强例题及详细解析(经典9题)例1 下列说法中正确的是()A、物体浸没在水中越深,受的浮力越大B、密度较大的物体在水中受的浮力大C、重的物体受的浮力小D、同体积的铁块和木块浸没在水中受的浮力一样大精析阿基米德原理的数学表达式为:F浮=液gV排,公式表明了物体受到的浮力大小只跟液体的密度和物体排开液体的体积有关、根据公式分析题目叙述的内容,问题就可以迎刃而解了、解A选项:物体浸没在水中,无论深度如何,V排不变,水的密度不变,F浮不变、A选项不正确、B选项:物体所受的浮力与物体密度的大小没有直接的关系,B选项不正确、C选项:重力的大小对物体所受的浮力无影响、例如:大铁块比小铁块要重一些,但将两者浸没于水中,大铁块受的浮力反而大些,因为大铁块的V排大、C选项不正确、D选项:同体积的铁块和木块,浸没于水中,V排相同,水相同,F浮铁=F浮木,铁块和木块受的浮力一样大、答案 D注意:物体所受的浮力跟物体自身的重力、自身的密度、自身的形状无关、例2 质量为79g的铁块,密度是7、9g/cm3,这个铁块的质量是多少?重多少?将这个铁块浸没于水中,排开水的质量是多少?所受浮力是多少?(g取10N/kg)精析这道题考查学生对计算物体重力和计算浮力的公式的区别、计算物体重力:G=物gV物计算物体在液体中受的浮力:F浮=液gV排、可以说:从计算的方法上没有本质的区别,但计算的结果却完全不同、已知:m=79g=0、079kg铁=7、9g/cm3求:m铁、G铁、m排、F浮解m铁=0、079kgG铁=m铁g=0、079kg10N/kg=0、79NV排=V铁===10 cm3m排=液gV排=1g/cm310 cm3=10g=0、01kgF浮=m浮gF=43N3m3浸没:V=V排=1103m3V空=V3m33m3=0、51103m3例4(广州市中考试题)将重为4、5N、体积为0、5dm3的铜球浸没在水后放手,铜球静止后所受的浮力是________N、精析此题考查学生是否注意了在解题前先要对物体作“状态的判定”,即铜球静止时是漂浮于水面,还是沉于水中、有的学生拿到题后,就认定V排=0、5 dm3,然后根据F浮=液gV 排,求出浮力F浮=4、9N、【分析】当题目未说明铜球静止时处于什么状态,可以用下面两种方法判定物体的状态、解法1 求出铜球的密度:球==(g取10N/kg)球==0、9kg/dm3=0、9kg/dm3103kg/m3这是一个空心铜球,且球<水,所以球静止后,将漂浮于水面,得F浮=G=4、5N、解法2 求出铜球浸没在水中时受的浮力F浮=液gV排=1103kg/m310N/kg0、510-3m3=5N、答案4、5N例5 体积是50cm3,质量是45g的物体,将其缓缓放入装满水的烧杯中,物体静止后,溢出水的质量是________g、将其缓缓放入装满酒精的烧杯中,溢出酒精的质量是________g、(酒=0、8103kg/m3)解判断此物体在水中和酒精中的状态求出物体密度:物===0、9g/cm3∵物<水,物体在水中漂浮、F水浮=Gm排水g=m物g∴m排水=m物=45g又∵物<酒精,物体在酒精中沉底、F酒精浮=酒精V排g,浸没:V排=V=50cm3m排精浮=酒精V排=0、8g/cm350cm3=40g答案溢出水的质量是45g,溢出酒精的质量是40g有的同学对物体在液体中的状态不加判断,而是两问都利用V排=50cm3进行求值、造成结果错误、V排=50 cm3进行求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(压强与浮力)常见题型精选 一、两物连接问题例1、如图所示,金属块A 用细线悬挂在漂浮在水中的木块B 下面,静止后木块B 露出水面的体积为V 1,木块B 下表面受到水的压强为P 1,若将细线剪断再将金属块A 放在木块B 上面,静止后金属A 露出水面的体积为V 2,木块B 下表面受到水的压强为P 2,则下面关系式成立的是(D )A .V 1=V 2,P 1=P 2B .V 1>V 2,P 1<P 2C .V 1<V 2,P 1>P 2D .V 1=V 2,P 1<P 2解:把物体A 和B 看做一个整体,两种情况都是处于漂浮状态,浮力等于AB 的总重力,浮力相等.在同种液体中,浮力相等,则排开液体的体积一定相等. V 1=V A +V B -V 排,V 2=V A +V B -V 排,所以V 1=V 2.液体压强的大小与液体的密度和物体浸入液体的深度有关.根据P=ρgh ,第二种情况下木块B 下表面浸入液体深度大,受到的液体压强就大.P 1<P 2. 类似题:如图所示,金属块甲用细绳吊于物体 M 下方,金属块乙放在 M 上方。
在甲、乙金属块的作用下,物体 M 都刚好浸没在水中静止。
则( AD )A. 甲的重力一定大于乙的重力B. 甲的重力可能小于乙的重力C. 甲的体积一定大于乙的体积D. 甲的体积可能等于乙的体积例2、如图所示,在三个相同的容器中装有质量相同的盐水、水、酒精,将木块A 、金属块B 按不同的方式放入液体中,待A 、B 静止时,比较三个容器中木块下表面所受液体的压强p1、p2、p3的大小关系应是______________。
解:由图可知木块A 和金属块B 在甲、乙两图中都是处于漂浮状态,所以受到的浮力都等于它们的总重力,甲、乙两种情况中A 、B 两物体受到的浮力相等,根据阿基米德原理可知它们排开水的体积相等,则甲图中木块A 排开水的体积等于乙图中金属块B 和木块A 排开水的体积和,所以甲图中木块A 排开水的体积大于乙图中木块A 排开水的体积,甲图中木块下表面所处的深度大于乙图中木块下表面所处的深度,所以甲图中木块下表面所受的压强大于乙图中木块下表面所受的压强;即P1>P2由图丙可知,图丙中木块A 处于漂浮状态,木块A 受到的浮力等于木块的重力,金属块B 下沉,金属块B 受到的浮力小于金属块的重力,则图丙中A 、B 两物体受到的浮力和小于它们的重力和,所以丙图中排开水的体积小于乙图中排开水的体积,在乙、丙两种情况下B 排开水的体积相等,所以丙图中A 排开水的体积小于乙图中A 排开水的体积,所以乙图中木块下表面所处的深度大于丙图中木块下表面所处的深度,所以乙图中木块下表面所受的压强大于丙图中木块下表面所受的压强.即P2>P3M 甲乙M类似题:如图所示,在三个相同的容器中装有质量相同的水,将木块A、金属块B按不同的方式放入水中,待A、B静止时,三个容器中木块下表面所受的压强相比较,正确的是(A)A.P 甲>P 乙>P 丙B.P 甲=P 乙>P 丙C.P 甲<P 乙=P 丙D.P 甲=P 乙=P 丙解:由图可知木块A和金属块B在甲、乙两图中都是处于漂浮状态,所以受到的浮力都等于它们的总重力,甲、乙两种情况中A、B两物体受到的浮力相等,根据阿基米德原理可知它们排开水的体积相等,则甲图中木块A排开水的体积等于乙图中金属块B和木块A排开水的体积和,所以甲图中木块A排开水的体积大于乙图中木块A排开水的体积,甲图中木块下表面所处的深度大于乙图中木块下表面所处的深度,所以甲图中木块下表面所受的压强大于乙图中木块下表面所受的压强;由图丙可知,图丙中木块A处于漂浮状态,木块A受到的浮力等于木块的重力,金属块B下沉,金属块B受到的浮力小于金属块的重力,则图丙中A、B两物体受到的浮力和小于它们的重力和,所以丙图中排开水的体积小于乙图中排开水的体积,在乙、丙两种情况下B排开水的体积相等,所以丙图中A排开水的体积小于乙图中A排开水的体积,所以乙图中木块下表面所处的深度大于丙图中木块下表面所处的深度,所以乙图中木块下表面所受的压强大于丙图中木块下表面所受的压强.故选A.例3、如图,放有铁块的杯子漂浮在水面上,如果把铁块用细线悬挂在杯底,杯子和铁块受到的浮力将(不变),水对容器底部的压强将(不变).(填增大、减小或不变)解:①把铁块和杯子看做一个整体,根据漂浮状态下F浮=G物,由于铁块和杯子的重力和始终不变,所以杯子和铁块受到总浮力不变;②由阿基米德原理知,杯子和铁块受到的浮力为F浮=ρ液gV排,因为总浮力一直保持不变,且ρ液和g均不变,所以V排也不变,因此前后水面的高度h 是不变的,又因为P底=ρ液gh,ρ液gh始终不变,所以水对容器底的压强不变.例4、如图所示,挂有实心铁块的平底试管漂浮在水面,如果将铁块取下放入试管中,试管仍漂浮,则下列说法正确的是(D)A.水对容器底的压强减小B.水对容器底的压强增大C.试管下表面受到水的压强减小D.试管下表面受到水的压强增大分析:如图所示和将铁块取下放入试管中,两种情况均为漂浮,并且总重不变,根据物体的漂浮条件得出两种情况下受到的水的浮力不变,根据阿基米德原理知道排开水的体积不变,水深不变,根据液体压强公式得出水对容器底的压强不变;如图所示排开水的总体积等于试管排开水的体积加上铁块排开水的体积;将铁块取下放入试管中,二者排开水的总体积等于试管排开水的体积,因为前后排开水的总体积不变,所以试管排开水的体积变大,试管下表面所处深度变大,根据液体压强公式得出试管下表面受到水的压强的变化情况.D .木块排开水的体积变小,水面高度不变例6、如图所示,一木块漂浮在水面上,露出水面的体积为在水下体积的1/3,若在木块上放一个重为5牛的物体,木块正好全部浸入水中,求:(1)木块的密度 (2)木块的重力解答:(1)当木块漂浮在水面上时,F 浮=G 木,即ρ水gV 排=ρ木V 木g,所以ρ木=V 排ρ水/V 木,再根据V 排和V 木的关系,可计算得出ρ木=0.75×103Kg/m 3,(2)当木块上放一物体时,把木块和物体当作一个整体,它们仍然漂浮在水上,设整体受到的浮力为F 浮1,则可列出关系式:F 浮1=G 木+G 物=ρ水gV 排=ρ水gV 木,即:G 木+5牛=ρ水gV 木,(1)因为ρ木:ρ水=3:4,所以(1)式可以变形为:G 木+5牛=(4/3)ρ木gV 木,进一步变形为:G 木+5牛=(4/3)G 木解:A 单独漂浮时所受浮力F 浮1=GA=mAg=ρ水gV 排;所以A 排开水的体积V 排=mA /ρ水=0.12kg /1000kg/m 3=1.2×10-4m 3; 所以A 的体积为V=2V 排=2×1.2×10-4m 3=2.4×10-4m 3=240cm 3;AB 完全浸没后,受到的浮力:F 浮=ρ水g×2V=1000kg/m 3×10N/kg×2×2.4×10-4m 3=4.8N ;所以F 浮=G A +G B =4.8N ;所以B 的重力为G B =F 浮-G A =4.8N -0.12kg×10N/kg=3.6N ;例7、如图所示,在一块浮在水面的长方体木块上放一质量为272克的铁块甲,木块的上表面恰好与水面相平,拿掉铁块甲,用细线把铁块乙系在木块下面,木块的上表面恰好也与水面相平,则铁块乙的质量为:312克(g 取10牛/千克,铁的密度为7.8×103Kg/m 3) 解答:设铁块乙的质量为A 千克,铁块乙的体积为V 铁,则根据题意和左右两图可得到代数式为:G 木+2.72牛=ρ水gV 木 (1)G 木+Ag =ρ水g (V 木+V 铁) (2)将(1)式代入(2)式,可得:Ag -2.72牛=ρ水gV 铁,即:10ρ铁V 铁-2.72牛=ρ水gV 铁可求得V 铁=4×10-5立方米,故A =312克类似题:有一长方体木块浮在水面上,在木块上面放一个重G的铁块后,木块刚好浸入水中,取出铁块,在木块的下面挂另一 个重为G1的铁块时,则木块也恰好没入水中,如图所示,求G 与G1的比值。
(铁的密度为7.8×103Kg/m 3)解:由图可知,当G 和G1都在水中时,整体所受的浮力要大些,这个增加的浮力正好等于G1-G ,即:F 浮=G1-G ,两边同除以一个G1,可变形为: G ∕G1=1-F 浮∕G1,因为F 浮=ρ水g V G1,G1=ρ铁g V G1故:G ∕G1=34∕39例8、一木块浮在水面上,露出水面的体积占总体积的2/5,在木块上部放一个重物A ,或在其下部吊一个重物B (不计细线的重力和体积),能使木块刚好全部浸没在水中,若 A 和B 的密度都为ρ,则A 与B 的体积之比是( )解:设A 、B 的体积分别为V A 、V B ,重力分别为G A 、G B ,木块重力为G 木,取整体为研究对象,由力的平衡得:G 木+G A =ρ水gV 木…①G 木+G B =ρ水g (V 木+V B )…②解法一:如图,A 和B 漂浮在水面上,F 浮=ρ水V 1g=G A +G B =G A +ρB V B g ,--------①将石块B 从木块A 上取下,放入水中,静止时,木块漂浮、石块下沉,二者受到的浮力:F 浮′=ρ水V 2g=G A +F 浮B =G A +ρ水V B g ,--------②①-②得:ρB V B g -ρ水V B g=ρ水V 1g -ρ水V 2g ,所以:V B =ρ水(V 1-V 2) /(ρB -ρ水)=(1g/cm 3×2dm 3)/(3g/cm 3-1g/cm 3) =1dm 3=0.001m 3B 在水中下沉,静止时,受到的重力等于浮力加上支持力,即F 浮B +F 支=G B , F 浮B =ρ水V B g=1×103kg/m 3×1000cm 3×10N/kg=10N ,G B =ρB V B g=3×103kg/m 3×1000cm 3×10N/kg=30N ,∴F 支=G B -F 浮B =30N -10N=20N .故选B .了题中给中的条件。
ABA ================================== 解法二:当B 放在A 上时,有F 浮=G A +G B 。
ρ水V1 g =ρA V A g +ρB V B g 所以V1 =(ρA V A +ρB V B )/ρ水当B 取下放入水中有 F 浮′=F A 浮+F B 浮因为B 浸没在水中 F B 浮=ρ水V B g A 仍漂浮有F A 浮=G A =ρA V A g 所以 F 浮′=ρA V A g +ρ水V B g 即ρ水V2 g =ρ水V B g +ρA V A g 因此V2=(ρ水V B +ρA V A )/ρ水因为 V1-V2=2dm³=0.002m³所以 (ρA V A +ρB V B )/ρ水-(ρ水V B +ρA V A )/ρ水=0.002m³解得 V B =0.001m³容器对石块B 的支持力 F B =G B -F B 浮=ρB V B g -ρ水V B g =(ρB -ρ水)V B g =20N 点评:这种方法也不容易,也需要有相当的基础。
