正四面体的外接球和内接球的半径求法

四面体外接球的球心、半径求法

四面体外接球的球心、在立体几何中，几何体外接球是一个常考的知识点，对于学生来说这是一个难点，一方面图形不会画，另一方面在画出图形的情况下无从下手，不知道球心在什么位置，半径是多少而无法解题。

本文章在给出图形的情况下解决球心位置、半径大小的问题。

、出现“墙角”结构利用补形知识，联系长方体。

【原理】：长方体中从一个顶点出发的三条棱长分别为a,b,c，则体对角线长为________ / 2 . b2 + ~2I = J a2+b2+C2，几何体的外接球直径2R为体对角线长I即R = ---------- --【例题】：在四面体ABCD中，共顶点的三条棱两两垂直, 其长度分别为1, V6,3，若该四面体的四个顶点在一个球面上，求这个球的表面积。

解:因为：长方体外接球的直径为长方体的体对角线长所以：四面体外接球的直径为AE的长即：4R2=AB2+AC2+AD2C 4R2 =12+32+ 府=16 所以R =2球的表面积为S=4；IR2=16；I二、出现两个垂直关系，利用直角三角形结论。

【原理】：直角三角形斜边中线等于斜边一半。

球心为直角三角形斜边中点。

【例题】：已知三棱锥的四个顶点都在球0的球面上，AB丄BC且PA =7，PB=5, PC =751，AC =10,求球0 的体积。

解：AB 丄BC 且PA =7，PB=5，P C=妬，AC =10,!_ 2因为=102所以知AC2=PA2+ PC2设球心坐标为O(x, y,z)贝U AO=BO=CO =DO ,由空间两点间距离公式知x 2 +y 2 +z 2 =(x -1)2 +(y -73)2 +z 2J 3解得 “1 y=- z =1所以PA 丄PC 所以可得图形为:在RtAABC 中斜边为AC 在RU PAC 中斜边为AC取斜边的中点0 , 在 RUABC 中 0A = 0B = 0C在 RtiPAC中 OP = OB =OC 所以在几何体中OP = OB =OC =OA ，即O 为该四面体的外接球的球心1R = — AC = 52 所以该外接球的体积为V 丄职―500工3 3 【总结】斜边一般为四面体中除了直角顶点以外的两个点连线。

多面体外接球半径内切球半径的常见几种求法

多面体外接球、内切球半径常见的5种求法如果一个多面体的各个顶点都在同一个球面上，那么称这个多面体是球的内接多面体，这个球称为多面体的外接球.有关多面体外接球的问题，是立体几何的一个重点，也是高考考查的一个热点.研究多面体的外接球问题，既要运用多面体的知识，又要运用球的知识，并且还要特别注意多面体的有关几何元素与球的半径之间的关系，而多面体外接球半径的求法在解题中往往会起到至关重要的作用.公式法例1 一个六棱柱的底面是正六边形，其侧棱垂直于底面，已知该六棱柱的顶点都在同一个球面上，且该六棱柱的体积为98，底面周长为３，则这个球的体积为 . 解设正六棱柱的底面边长为x ，高为h，则有263,1,296,8x x x h h =⎧⎧=⎪⎪∴⎨⎨=⎪⎪=⎩⎩ ∴正六棱柱的底面圆的半径12r =，球心到底面的距离d =.∴外接球的半径1R ==.43V π∴=球. 小结本题是运用公式222R r d =+求球的半径的，该公式是求球的半径的常用公式.多面体几何性质法例2 已知各顶点都在同一个球面上的正四棱柱的高为4，体积为16，则这个球的表面积是A.16πB.20πC.24πD.32π解设正四棱柱的底面边长为x ，外接球的半径为R ，则有2416x =，解得2x =.∴2R R ==∴= .∴这个球的表面积是2424R ππ=.选C. 小结本题是运用“正四棱柱的体对角线的长等于其外接球的直径”这一性质来求解的.补形法例3 若三棱锥的三个侧棱两两垂直，则其外接球的表面积是 . 解据题意可知，该三棱锥的三条侧棱两两垂直，∴把这个三棱锥可以补成一个棱长为.设其外接球的半径为R ，则有()222229R =++=.∴294R =. 故其外接球的表面积249S R ππ==.小结一般地，若一个三棱锥的三条侧棱两两垂直，且其长度分别为a b c 、、，则就可以将这个三棱锥补成一个长方体，于是长方体的体对角线的长就是该三棱锥的外接球的直径.设其外接球的半径为R，则有2R =寻求轴截面圆半径法例4 正四棱锥S ABCD -S A B C D 、、、、都在同一球面上，则此球的体积为 .解设正四棱锥的底面中心为1O ，外接球的球心为O ，如图3所示.∴由球的截面的性质，可得1OO ABCD ⊥平面.又1SO ABCD ⊥平面，∴球心O 必在1SO 所在的直线上.∴ASC ∆的外接圆就是外接球的一个轴截面圆，外接圆的半径就是外接球的半径.在ASC ∆中，由2SA SC AC ===，得222SA SC AC +=.∴ASC AC ∆∆是以为斜边的Rt . ∴12AC =是外接圆的半径，也是外接球的半径.故43V π=球. 小结根据题意，我们可以选择最佳角度找出含有正棱锥特征元素的外接球的一个轴截面圆，于是该圆的半径就是所求的外接球的半径.本题提供的这种思路是探求正棱锥外接球半径的通解通法，该方法的实质就是通过寻找外接球的一个轴截面圆，从而把立体几何问题转化为平面几何问题来研究.这种等价转化的数学思想方法值得我们学习.确定球心位置法例5 在矩形ABCD 中，4,3AB BC ==，沿AC 将矩形ABCD 折成一个直二面角B AC D --，则四面体ABCD 的外接球的体积为 A.12512π B.1259π C.1256π D.1253π 解设矩形对角线的交点为O ，则由矩形对角线互相平分，可知OA OB OC OD ===.∴点O 到四面体的四个顶点A B C D 、、、的距离相等，即点O 为四面体的外接球的球心，如图2所示.∴外接球的半径52R OA ==.故3412536V R ππ==球.选C. 出现多个垂直关系时建立空间直角坐标系，利用向量知识求解【例题】：已知在三棱锥BCD A -中，ABC AD 面⊥，︒=∠120BAC ，2===AC AD AB解：由已知建立空间直角坐标系)000(，，A )002(，，B )200(，，D 3，， CD A B S O 1图3A O D B 图4C y设球心坐标为),,(z y x O 则DO CO BO AO ===,由空间两点间距离公式知222222)2(z y x z y x ++-=++ 222222)2(-++=++z y x z y x 222222)3()1(z y x z y x +-+-=++解得 1331===z y x 所以半径为3211331222=++=）（R 【结论】：空间两点间距离公式：221221221)()()(z z y y x x PQ -+-+-=四面体是正四面体外接球与内切球的圆心为正四面体高上的一个点，根据勾股定理知，假设正四面体的边长为a 时，它的外接球半径为a 46。

四面体外接球的球心、半径求法

四面体外接球的球心、半径求法在立体几何中，几何体外接球是一个常考的知识点，对于学生来说这是一个难点，一方面图形不会画，另一方面在画出图形的情况下无从下手，不知道球心在什么位置，半径是多少而无法解题。

本文章在给出图形的情况下解决球心位置、半径大小的问题。

一、出现“墙角”结构利用补形知识，联系长方体。

【原理】：长方体中从一个顶点出发的三条棱长分别为c b a ,,，则体对角线长为222c b a l ++=，几何体的外接球直径R 2为体对角线长l 即2222c b a R ++=【例题】：在四面体ABCD 中，共顶点的三条棱两两垂直，其长度分别为3,61，，若该四面体的四个顶点在一个球面上，求这个球的表面积。

解：因为：长方体外接球的直径为长方体的体对角线长所以：四面体外接球的直径为AE 的长即：22224AD AC AB R ++=1663142222=++=R 所以2=R 球的表面积为ππ1642==R S二、出现两个垂直关系，利用直角三角形结论。

【原理】：直角三角形斜边中线等于斜边一半。

球心为直角三角形斜边中点。

【例题】：已知三棱锥的四个顶点都在球O 的球面上，BC AB ⊥且7=PA ，5=PB ，51=PC ，10=AC ,求球O 的体积。

解：BC AB ⊥且7=PA ，5=PB ，51=PC ，10=AC , 因为22210517=+ 所以知222PC PA AC +=所以 PC PA ⊥ 所以可得图形为：在ABC Rt ∆中斜边为AC 在PAC Rt ∆中斜边为AC 取斜边的中点O ，在ABC Rt ∆中OC OB OA ==在PAC Rt ∆中OC OB OP ==所以在几何体中OA OC OB OP ===，即O 为该四面体的外接球的球心521==AC R 所以该外接球的体积为3500343ππ==R V【总结】斜边一般为四面体中除了直角顶点以外的两个点连线。

三、出现多个垂直关系时建立空间直角坐标系，利用向量知识求解【例题】：已知在三棱锥BCD A -中，ABC AD 面⊥，︒=∠120BAC ，2===AC AD AB解：由已知建立空间直角坐标系)000(，，A )002(，，B )200(，，D (C设球心坐标为),,(z y x O 则DO CO BO AO ===,由空间两点间距离公式知222222)2(z y x z y x ++-=++ 222222)2(-++=++z y x z y x 222222)3()1(z y x z y x +-+-=++解得 1331===z y xACCy所以半径为3211331222=++=）（R 【结论】：空间两点间距离公式：221221221)()()(z z y y x x PQ -+-+-=四、四面体是正四面体处理球的“内切”“外接”问题与球有关的组合体问题，一种是内切，一种是外接。

探求正四面体外接球、内切球半径求法知识讲解

探求正四面体外接球、内切球半径求法探求正四面体外接球、内切球半径正四面体是特殊的正三棱锥，所有的棱长都相等，四个面是全等的等边三角形，有外接球、内切球，且球心重合.已知正四面体ABCD 棱长为a ，设外接球半径为R ，内切球半径为r ，球心为O ，则正四面体的高h a a 即34R h =；内切球a 即14r h =. 外接球半径是内切球半径的3倍. 下面从不同角度、用不同方法进行探求：方法一：（勾股定理）作平面于点,则点H 是的中心，AH BCD H BCD ⊥V高3h AH a ==，设O 为球心，则.O AH ∈ 连结,.BH BO 在Rt BOH V 中，222BO BH OH =+，即222()()33R a a R =+-，,.R a r h R a a a ∴==-=-= 方法二：（三角正切倍角公式）作平面于点,则点H 是的中心，AH BCD H BCD ⊥V高3h AH a ==，设O 为球心，则.O AH ∈ 连结,.BH BO = ,2.AO BO ABO BAO BOH θθ=∴∠=∠∠=Q在Rt ABHV中，tan,23aBHAHθ===在Rt OBHV中，3tan2,3aBHOH r rθ===23r⨯∴==,.r a R h r a a a∴==-=-=方法三：（分割等体积）作平面于点,则点H是的中心，AH BCD H BCD⊥V高3h AH a==，设O为球心，则.O AH∈连结,,,BO CO DO得到四个以O为顶点的小棱锥，它们的底面是正四面体的一个面，高是内切球的半径r，设正四面体每个面的面积为S，则4,O BCD A BCDV V--=即114,33S r S AH⨯=g g11,4412.3124r AH h aR h r a a a∴====-=-=方法四：（侧棱、高相似或三角）作平面于点,则点H是的中心，AH BCD H BCD⊥V22tantan2,1tanθθθ=-Q高3h AH a ==，设O 为球心，则.O AH ∈ 设M 是AB 的中点，连结,,,OM OB BHAO BO OM AB =∴⊥QAMO AHB Rt ∴∠=∠=∠，又MAO HAB ∠=∠，AMO AHB ∴V :V ， AM AO AH AB∴=，即,aR a =,.R a r h R a a a ∴==-=-= 或：设BAH MAO θ∠=∠=，则在Rt ABH V中，3cos a AH AB aθ==，在Rt AMO V 中，2cos .aAM AO Rθ==32a aa R∴= ，以下同上. 方法五：（斜高、高相似或三角）作平面于点,则点H 是的中心，AH BCD H BCD ⊥V高h AH a ==，设O 为球心，则.O AH ∈ 设E 为BC 中点，连结,AE EH ，作ON AE ⊥于N 点，则N 是ABC V 中心，N 是AE 的三等分点，平面，ON 是内切圆半径r,ON ABC ⊥且 ,Rt ANO Rt AEH V :VAN AO AH AE ∴=，32a R = ，,.43412R a r h R a a a ∴==-=-= 或：设EAH NAO θ∠=∠=，则在Rt AEH V中，cos 2a AH AEθ==，在Rt ANO V中，3cos .a AN AO Rθ==3aa R∴=，以下同上. 方法六：（斜高、侧棱相似或三角）作平面于点,则点H 是的中心，AH BCD H BCD ⊥V高h AH a ==，设O 为球心，则.O AH ∈ 设E 为BC 中点，连结,,AE DE DO ，延长DO 交AE 于N ，则N 是AE 的三等分点，.H DE ∈ 且DN ⊥平面.ABC则,Rt ODH Rt DNE V :V OH OD NE DE∴= 即 OH OD = NE DE 13=， 13r R ∴=， 3.R r ∴=又,R r AH h a +===13,.41244r h a R h a ∴==== 或：在Rt DNE V 中，1sin ,3NE NDE DE ∠== 在Rt DOH V 中，sin sin ,OH NDE ODH OD∠=∠= 13OH OD ∴=，即13r R =， 3.R r ∴=又,3R r AH h a +===13,.41244r h a R h a ∴==== 方法七：（构造正方体）正四面体的四个顶点是正方体的顶点，此时正四面体的外接球也是正方体的外接球，正四面体的棱长为a的棱长为.2a 正方体的体对角线等于外接球直径，有22a R ⨯=，,.43412R a r h R a a a ∴==-=-= 方法八：（相交弦定理）设外接球球心为O ，半径为R ，过A 点作球的直径，交底面BCD V 于H ，则H 为BCD V 的外心，求得,,33AH a BH a == 由相交弦定理得2(2)).333a R a a -=g解得.4R a =.r h R a a a ∴=-=-= 以上从不同角度针对正四面体的外接球半径、内切球半径作了讨论，从而从不同方面对思维作了训练，不仅对正四面体的外接球半径、内切球半径有了透彻的认识，同时对解题能力的提高是有帮助的.。

正四面体外接球半径公式

一.正四面体外接球半径公式是什么？
答：R=（√6）a/4。

a为正四面体的棱长。

设正四面体的棱长为a,求其外接球的半径.设正四面体V-ABC,D为BC的中点,E 为面ABC的中心,外接球半径为R,则AD=（√3）a/2,AE=2/3*AD=（√3）a/3.在Rt△VAE中,有VE^2=VA^2-AE^2=a^2-a^2/3=(2a^2)/3,VE=(√6)a/3。

在Rt△AEO中,有AO^2=AE^2+OE^2=R^2+(VE-R) ^2,即R^2=a^2/3+[(√6)a/3-R] ^2,可解得：R=（√6）a/4.另外,我们也可以先求出OE,因为OE恰好是四面体的内切球的半径r。

利用等积法可求得r.设四面体的底面积为S,则1/3*S*（R+r）=4*1/3*S*r,可得r=R/3.于是在Rt△AEO中,有R^2 = AE^2+r^2=a^2/3+R^2/9,从而得R=（√6）a/4。

扩展资料：
正四面体的性质：
1、正四面体的四个旁切球半径均相等，等于内切球半径的2倍，或等于四面体高线的一半。

2、正四面体的内切球与各侧而的切点是侧I面三角形的外心，或内心，或垂心，或重心，除外心外，其逆命题均成立。

3、正四面体的外接球球心到四面体四顶点的距离之和，小于空间中其他任一点到四顶点的距离之和。

4、正四面体内任意一点到各侧面的垂线长的和等于这四面体的高。

5、对于四个相异的平行平面，总存住一个正四面体，其顶点分别在这四个平面上。

简单几何体的外接球和内切球的半径的求法

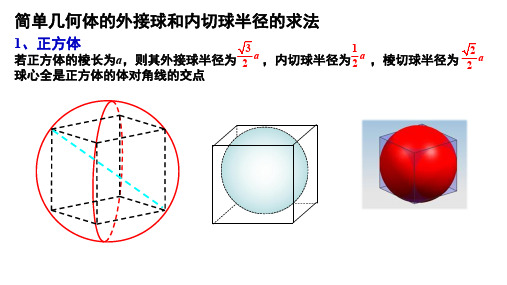
简单几何体的外接球和内切球半径的求法1、正方体若正方体的棱长为a ，则其外接球半径为，内切球半径为，棱切球半径为球心全是正方体的体对角线的交点32a 12a 22a例：一个正方体的顶点都在球面上，它的棱长是a cm ，求球的体积．解：该球是正方体的外接球，球心到正方体各顶点的距离相等，因此球心是正方体的体对角线的交点，球的直径是正方体的体对角线长设球的半径为R ，a R a R 2332==得则)(23)23(34343333cm a a R πππ==∴球的体积为若一个多面体的各顶点都在一个球的球面上，则称这个多面体是这个球的内接多面体，这个球是这个多面体的外接球。

外接球的球心到多面体各顶点的距离均相等。

例：将一个棱长为6cm 的正方体铁块磨制成一个球体零件，求可能制作的最大零件的体积。

解：这个最大的球体是正方体的内切球，球心到正方体各个面的距离相等，因此球心是正方体的体对角线的交点，球的直径是正方体的棱长设球的半径为R ，则2R =6，得R =3)(3633434333cm R πππ=⨯=∴最大零件的体积为若一个多面体的各面都与一个球的球面相切，则称这个多面体是这个球的外切多面体，这个球是这个多面体的内切球。

内切球的球心到多面体各面的距离均相等。

⑴正方体的内切球直径＝⑵正方体的外接球直径＝⑶与正方体所有棱相切的球直径＝探究若正方体的棱长为a ，则a3a2a右图，红色球是正方体的棱切球棱切球的球心到正方体各条棱的距离相等，因此球心是正方体的体对角线的交点，球的直径是正方体的面对角线的长2、长方体若长方体的长、宽、高分别为a、b、c，则其外接球半径为球心是长方体的体对角线的交点222 1+2a b c例：有一个球与长方体的面相切，这个球的最大直径是多少？长方体的长、宽、高中的最小者例：一个长方体的各顶点均在同一个球的球面上，且一个顶点上的三条棱的长分别为1,2,3，则此球的表面积为____________若一个多面体的各顶点都在一个球的球面上，则称这个多面体是这个球的内接多面体，这个球是这个多面体的外接球。

正四面体内切球半径推导过程

正四面体内切球半径推导过程
内切球。

内切球关键特征为内“切”。

因此，各“切”点到球心距离相等且等于半径，且与球心的连线垂直切面，解题时无论构造图形还是计算都要对此善加利用。

考情分析：
正四面体是棱长都相等的三棱锥，在高考中常常围绕它求外接球半径或内切球半径，或者三棱锥体积等等，高考考得比较频繁，所以我们要对它充分掌握，在这里我们来推导它的外接内切球半径。

我们画一个正四面体和外接球，设棱长为a，则每一面上的高为二分之根号3a。

然后在高AD上取点E，使AE=2DE，E为等边三角形ABC的中心，底面外接圆的圆心，连接PE，则pe垂直底面。

然后在PE上取一点O，则PO=AO=r,oE=三分之根号6a-r，利用勾股定理。

所以棱长a的为正四面体外接球半径为四分之根号6a。

四面体外接球的球心半径求法

四面体外接球得球心、半径求法在立体几何中,几何体外接球就是一个常考得知识点,对于学生来说这就是一个难点,一方面图形不会画,另一方面在画出图形得情况下无从下手,不知道球心在什么位置,半径就是多少而无法解题。

本文章在给出图形得情况下解决球心位置、半径大小得问题、一、出现“墙角”结构利用补形知识,联系长方体。

【原理】:长方体中从一个顶点出发得三条棱长分别为,则体对角线长为,几何体得外接球直径为体对角线长即【例题】:在四面体中,共顶点得三条棱两两垂直,其长度分别为,若该四面体得四个顶点在一个球面上,求这个球得表面积。

解:因为:长方体外接球得直径为长方体得体对角线长所以:四面体外接球得直径为得长即:所以球得表面积为二、出现两个垂直关系,利用直角三角形结论。

【原理】:直角三角形斜边中线等于斜边一半。

球心为直角三角形斜边中点。

【例题】:已知三棱锥得四个顶点都在球得球面上,且,,,,求球得体积。

解:且,,,,因为所以知所以所以可得图形为:在中斜边为在中斜边为取斜边得中点,在中在中所以在几何体中,即为该四面体得外接球得球心A C所以该外接球得体积为【总结】斜边一般为四面体中除了直角顶点以外得两个点连线、三、出现多个垂直关系时建立空间直角坐标系,利用向量知识求解ﻩ【例题】:已知在三棱锥中,,,,求该棱锥得外接球半径、解:由已知建立空间直角坐标系解得所以半径为【结论】:空间两点间距离公式:四、四面体就是正四面体处理球得“内切”“外接"问题与球有关得组合体问题,一种就是内切,一种就是外接。

作为这种特殊得位置关系在高考中也就是考查得重点,但同学们又因缺乏较强得空间想象能力而感到模糊。

解决这类题目时要认真分析图形,明确切点与接点得位置及球心得位置,画好截面图就是关键,可使这类问题迎刃而解。

一、棱锥得内切、外接球问题例1.正四面体得外接球与内切球得半径就是多少？分析:运用正四面体得二心合一性质,作出截面图,通过点、线、面关系解之。

探求正四面体外接球、内切球半径求法

在中，，
在中，
，以下同上. 方法五：（斜高、高相似或三角）作
高，设为球心，则
设为中点，连结，
作于点，则是中心，是的三等分点，且，即，或：设，则在中，，在中，
，以下同上. 方法六：（斜高、侧棱相似或三角）作
高，设为球心，则
设为中点，连结，延长交于，
则是的三等分点，且平面
则即 =，，又或：在中，
以上从不同角度针对正四面体的外接球半径、内切球半径作了讨论，从而从不同方面对思维作了训练，不仅对正四面体的外接球半径、内切球半径有了透彻的认识，同时对解题能力的提高是有帮助的
方法一：（勾股定理）作高，设为球心，则连结在中，，即，方法二：（三角正切倍角公式）作高，设为球心，则连结在中，在中，
方法三：（分割等体积）作高，设为球心，则连结得到四个以为顶点的小棱锥，它们的底面是正四面体的一个面，高是内切球的半径，设正四面体每个面的面积为，则即方法四：（侧棱、高相似或三角）作高，设为球心，则设是的中点，连结，又，，，即或：设，则
探求正四面体外接球、内切球半径
正四面体是特殊的正三棱锥，所有的棱长都相等，四个面是全等的等边三角形，有外接球、内切球，且球心重合.
已知正四面体棱长为，设外接球半径为，内切球半径为，球心为，则正四面体的高是，外接球半径是即；内切球半径是即. 外接球半径是内切球半径的3倍. 下面从不同角度、用不同方法进行探求：
在中，，即，又
方法七：（构造正方体）正四面体的四个顶点是正方体的顶点，此时正四面体的
外接球也是正方体的外接球，正四面体的棱长为，则正方体
的棱长为正方体的体对角线等于外接球直径，有

正四面体相关结论

正四面体相关结论正四面体是一种具有特殊性质的几何图形，它由四个相等的正三角形组成，每个角都是60度。

在正四面体中，有一些重要的结论和性质，这些结论和性质在解决相关的几何问题时非常有用。

1、中心与顶点之间的关系正四面体的中心到四个顶点的距离相等，也就是说，中心是四个顶点所组成的菱形的中心。

这个结论可以用于计算正四面体的半径和中心到顶点的距离。

2、边长与高之间的关系正四面体的边长和高之间有一个重要的关系，即高是边长的2/3。

这个结论可以用于计算正四面体的高，也可以用于解决与正四面体的边长和高有关的问题。

3、体积与半径之间的关系正四面体的体积与半径之间有一个重要的关系，即体积是半径的立方根。

这个结论可以用于计算正四面体的体积，也可以用于解决与正四面体的体积和半径有关的问题。

4、三个两两垂直的平面相交于一点在正四面体中，三个两两垂直的平面相交于一点，这个结论可以用于解决与正四面体的三个两两垂直的平面相交有关的问题。

5、相对的两条边互相垂直在正四面体中，相对的两条边互相垂直，这个结论可以用于解决与正四面体的相对的两条边互相垂直有关的问题。

正四面体的一些重要结论和性质在解决相关的几何问题时非常有用，这些结论和性质可以帮助我们更好地理解和解决正四面体的问题。

正四面体外接球和内切球的半径的求法在几何学中，正四面体是一种具有特殊性质的几何形态。

它由四个相等的正三角形构成，每个面都是一个等边三角形。

这种几何形态在许多领域都有广泛的应用，包括物理学、化学、工程学等。

在解决实际问题时，我们常常需要找出正四面体的外接球和内切球的半径。

下面将介绍两种求法。

第一种方法是通过几何计算直接求解。

首先，我们需要找到正四面体的中心点。

这个点可以通过连接正四面体的四个顶点并取其中间位置来找到。

一旦找到了中心点，我们就可以通过连接这个点和正四面体的各个顶点，找到外接球的球心。

外接球的半径就是从球心到正四面体顶点的距离。

内切球的半径则是从球心到正四面体四个面的中心的距离。

四面体外接球的球心、半径求法

For personal use only in study and research; not forcommercial use四面体外接球的球心、半径求法在立体几何中，几何体外接球是一个常考的知识点，对于学生来说这是一个难点，一方面图形不会画，另一方面在画出图形的情况下无从下手，不知道球心在什么位置，半径是多少而无法解题。

本文章在给出图形的情况下解决球心位置、半径大小的问题。

一、出现“墙角”结构利用补形知识，联系长方体。

【原理】：长方体中从一个顶点出发的三条棱长分别为c b a ,,，则体对角线长为222c b a l ++=，几何体的外接球直径R 2为体对角线长l 即2222c b a R ++= 【例题】：在四面体ABCD 中，共顶点的三条棱两两垂直，其长度分别为3,61，，若该四面体的四个顶点在一个球面上，求这个球的表面积。

解：因为：长方体外接球的直径为长方体的体对角线长所以：四面体外接球的直径为AE 的长即：22224AD AC AB R ++= 1663142222=++=R 所以2=R球的表面积为ππ1642==R S二、出现两个垂直关系，利用直角三角形结论。

【原理】：直角三角形斜边中线等于斜边一半。

球心为直角三角形斜边中点。

【例题】：已知三棱锥的四个顶点都在球O 的球面上，BC AB ⊥且7=PA ，5=PB ，51=PC ，10=AC ,求球O 的体积。

解：BC AB ⊥且7=PA ，5=PB ，51=PC ，10=AC , 因为22210517=+ 所以知222PC PA AC += A CD B E所以 PC PA ⊥ 所以可得图形为：在ABC Rt ∆中斜边为AC在PAC Rt ∆中斜边为AC取斜边的中点O ，在ABC Rt ∆中OC OB OA == 在PAC Rt ∆中OC OB OP == 所以在几何体中OA OC OB OP ===，即O 为该四面体的外接球的球心所以该外接球的体积为3500343ππ==R V 【总结】斜边一般为四面体中除了直角顶点以外的两个点连线。

四面体外接球的球心、半径求法

四面体外接球的球心、半径求法在立体几何中，几何体外接球是一个常考的知识点，对于学生来说这是一个难点，一方面图形不会画，另一方面在画出图形的情况下无从下手，不知道球心在什么位置，半径是多少而无法解题。

本文章在给出图形的情况下解决球心位置、半径大小的问题。

一、出现“墙角”结构利用补形知识，联系长方体。

【原理】：长方体中从一个顶点出发的三条棱长分别为c b a ,,，则体对角线长为222c b a l ++=，几何体的外接球直径R 2为体对角线长l 即2222c b a R ++=【例题】：在四面体ABCD 中，共顶点的三条棱两两垂直，其长度分别为3,61，，若该四面体的四个顶点在一个球面上，求这个球的表面积。

解：因为：长方体外接球的直径为长方体的体对角线长所以：四面体外接球的直径为AE 的长即：22224AD AC AB R ++=1663142222=++=R 所以2=R 球的表面积为ππ1642==R S二、出现两个垂直关系，利用直角三角形结论。

【原理】：直角三角形斜边中线等于斜边一半。

球心为直角三角形斜边中点。

【例题】：已知三棱锥的四个顶点都在球O 的球面上，BC AB ⊥且7=PA ，5=PB ，51=PC ，10=AC ,求球O 的体积。

解：BC AB ⊥且7=PA ，5=PB ，51=PC ，10=AC , 因为22210517=+ 所以知222PC PA AC +=A CDBE所以 PC PA ⊥ 所以可得图形为：在ABC Rt ∆中斜边为AC 在PAC Rt ∆中斜边为AC 取斜边的中点O ，在ABC Rt ∆中OC OB OA ==在PAC Rt ∆中OC OB OP ==所以在几何体中OA OC OB OP ===，即O 为该四面体的外接球的球心521==AC R 所以该外接球的体积为3500343ππ==R V【总结】斜边一般为四面体中除了直角顶点以外的两个点连线。

三、出现多个垂直关系时建立空间直角坐标系，利用向量知识求解【例题】：已知在三棱锥BCD A -中，ABC AD 面⊥，︒=∠120BAC ，2===AC AD AB ，求该棱锥的外接球半径。

四面体外接球的球心、半径求法

For personal use only in study and research; not forcommercial use四面体外接球的球心、半径求法在立体几何中，几何体外接球是一个常考的知识点，对于学生来说这是一个难点，一方面图形不会画，另一方面在画出图形的情况下无从下手，不知道球心在什么位置，半径是多少而无法解题。

本文章在给出图形的情况下解决球心位置、半径大小的问题。

一、出现“墙角”结构利用补形知识，联系长方体。

【原理】：长方体中从一个顶点出发的三条棱长分别为c b a ,,，则体对角线长为222c b a l ++=，几何体的外接球直径R 2为体对角线长l 即2222c b a R ++= 【例题】：在四面体ABCD 中，共顶点的三条棱两两垂直，其长度分别为3,61，，若该四面体的四个顶点在一个球面上，求这个球的表面积。

解：因为：长方体外接球的直径为长方体的体对角线长所以：四面体外接球的直径为AE 的长即：22224AD AC AB R ++= 1663142222=++=R 所以2=R球的表面积为ππ1642==R S二、出现两个垂直关系，利用直角三角形结论。

【原理】：直角三角形斜边中线等于斜边一半。

球心为直角三角形斜边中点。

【例题】：已知三棱锥的四个顶点都在球O 的球面上，BC AB ⊥且7=PA ，5=PB ，51=PC ，10=AC ,求球O 的体积。

解：BC AB ⊥且7=PA ，5=PB ，51=PC ，10=AC , 因为22210517=+ 所以知222PC PA AC += A CD B E所以 PC PA ⊥ 所以可得图形为：在ABC Rt ∆中斜边为AC在PAC Rt ∆中斜边为AC取斜边的中点O ，在ABC Rt ∆中OC OB OA == 在PAC Rt ∆中OC OB OP == 所以在几何体中OA OC OB OP ===，即O 为该四面体的外接球的球心所以该外接球的体积为3500343ππ==R V 【总结】斜边一般为四面体中除了直角顶点以外的两个点连线。

多面体外接球半径内切球半径的常见几种求法

多面体外接球、内切球半径常见的5种求法如果一个多面体的各个顶点都在同一个球面上，那么称这个多面体是球的内接多面体，这个球称为多面体的外接球.有关多面体外接球的问题，是立体几何的一个重点，也是高考考查的一个热点.研究多面体的外接球问题，既要运用多面体的知识，又要运用球的知识，并且还要特别注意多面体的有关几何元素与球的半径之间的关系，而多面体外接球半径的求法在解题中往往会起到至关重要的作用.公式法例1 一个六棱柱的底面是正六边形，其侧棱垂直于底面，已知该六棱柱的顶点都在同一个球面上，且该六棱柱的体积为98，底面周长为３，则这个球的体积为 . 解设正六棱柱的底面边长为x ，高为h，则有263,1,296,8x x x h h =⎧⎧=⎪⎪∴⎨⎨=⎪⎪=⎩⎩ ∴正六棱柱的底面圆的半径12r =，球心到底面的距离d =.∴外接球的半径1R ==.43V π∴=球. 小结本题是运用公式222R r d =+求球的半径的，该公式是求球的半径的常用公式.多面体几何性质法例2 已知各顶点都在同一个球面上的正四棱柱的高为4，体积为16，则这个球的表面积是A.16πB.20πC.24πD.32π解设正四棱柱的底面边长为x ，外接球的半径为R ，则有2416x =，解得2x =.∴2R R ==∴= .∴这个球的表面积是2424R ππ=.选C. 小结本题是运用“正四棱柱的体对角线的长等于其外接球的直径”这一性质来求解的.补形法例3 若三棱锥的三个侧棱两两垂直，则其外接球的表面积是 . 解据题意可知，该三棱锥的三条侧棱两两垂直，∴把这个三棱锥可以补成一个棱长为.设其外接球的半径为R ，则有()222229R =++=.∴294R =. 故其外接球的表面积249S R ππ==.小结一般地，若一个三棱锥的三条侧棱两两垂直，且其长度分别为a b c 、、，则就可以将这个三棱锥补成一个长方体，于是长方体的体对角线的长就是该三棱锥的外接球的直径.设其外接球的半径为R，则有2R =寻求轴截面圆半径法例4 正四棱锥S ABCD -S A B C D 、、、、都在同一球面上，则此球的体积为 .解设正四棱锥的底面中心为1O ，外接球的球心为O ，如图3所示.∴由球的截面的性质，可得1OO ABCD ⊥平面.又1SO ABCD ⊥平面，∴球心O 必在1SO 所在的直线上.∴ASC ∆的外接圆就是外接球的一个轴截面圆，外接圆的半径就是外接球的半径.在ASC ∆中，由2SA SC AC ===，得222SA SC AC +=.∴ASC AC ∆∆是以为斜边的Rt . ∴12AC =是外接圆的半径，也是外接球的半径.故43V π=球. 小结根据题意，我们可以选择最佳角度找出含有正棱锥特征元素的外接球的一个轴截面圆，于是该圆的半径就是所求的外接球的半径.本题提供的这种思路是探求正棱锥外接球半径的通解通法，该方法的实质就是通过寻找外接球的一个轴截面圆，从而把立体几何问题转化为平面几何问题来研究.这种等价转化的数学思想方法值得我们学习.确定球心位置法例5 在矩形ABCD 中，4,3AB BC ==，沿AC 将矩形ABCD 折成一个直二面角B AC D --，则四面体ABCD 的外接球的体积为 A.12512π B.1259π C.1256π D.1253π 解设矩形对角线的交点为O ，则由矩形对角线互相平分，可知OA OB OC OD ===.∴点O 到四面体的四个顶点A B C D 、、、的距离相等，即点O 为四面体的外接球的球心，如图2所示.∴外接球的半径52R OA ==.故3412536V R ππ==球.选C. 出现多个垂直关系时建立空间直角坐标系，利用向量知识求解【例题】：已知在三棱锥BCD A -中，ABC AD 面⊥，︒=∠120BAC ，2===AC AD AB解：由已知建立空间直角坐标系)000(，，A )002(，，B )200(，，D 3，， CD A B S O 1图3A O D B 图4C y设球心坐标为),,(z y x O 则DO CO BO AO ===,由空间两点间距离公式知222222)2(z y x z y x ++-=++ 222222)2(-++=++z y x z y x 222222)3()1(z y x z y x +-+-=++解得 1331===z y x 所以半径为3211331222=++=）（R 【结论】：空间两点间距离公式：221221221)()()(z z y y x x PQ -+-+-=四面体是正四面体外接球与内切球的圆心为正四面体高上的一个点，根据勾股定理知，假设正四面体的边长为a 时，它的外接球半径为a 46。

四面体外接球的球心、半径求法

一、出现“墙角”结构利用补形知识，联系长方体。

【原理】：长方体中从一个顶点出发的三条棱长分别为c b a ,,，则体对角线长为222c b a l ++=，几何体的外接球直径R 2为体对角线长l 即2222c b a R ++=【例题】：在四面体ABCD 中，共顶点的三条棱两两垂直，其长度分别为3,61，，若该四面体的四个顶点在一个球面上，求这个球的表面积。

解：因为：长方体外接球的直径为长方体的体对角线长所以：四面体外接球的直径为AE 的长即：22224AD AC AB R ++=1663142222=++=R 所以2=R 球的表面积为ππ1642==R S二、出现两个垂直关系，利用直角三角形结论。

【原理】：直角三角形斜边中线等于斜边一半。

球心为直角三角形斜边中点。

【例题】：已知三棱锥的四个顶点都在球O 的球面上，BC AB ⊥且7=PA ，5=PB ，51=PC ，10=AC ,求球O 的体积。

解：BC AB ⊥且7=PA ，5=PB ，51=PC ，10=AC , 因为22210517=+ 所以知222PC PA AC += 所以 PC PA ⊥ 所以可得图形为：在ABC Rt ∆中斜边为AC 在PAC Rt ∆中斜边为AC 取斜边的中点O ，在ABC Rt ∆中OC OB OA == 在PAC Rt ∆中OC OB OP ==所以在几何体中OA OC OB OP ===，即O 为该四面体的外接球的球心521==AC R所以该外接球的体积为3500343ππ==R V【总结】斜边一般为四面体中除了直角顶点以外的两个点连线。

三、出现多个垂直关系时建立空间直角坐标系，利用向量知识求解【例题】：已知在三棱锥BCD A -中，ABC AD 面⊥，︒=∠120BAC ，2===AC AD AB ，求该棱锥的外接球半径。

解：由已知建立空间直角坐标系)000(，，A )002(，，B )200(，，D )031(，，-C设球心坐标为),,(z y x O 则DO CO BO AO ===,由空间两点间距离公式知222222)2(z y x z y x ++-=++ 222222)2(-++=++z y x z y x 222222)3()1(z y x z y x +-+-=++解得 1331===z y x所以半径为3211331222=++=）（R 【结论】：空间两点间距离公式：221221221)()()(z z y y x x PQ -+-+-=四、四面体是正四面体处理球的“内切”“外接”问题与球有关的组合体问题，一种是内切，一种是外接。

内切球

内切球，外接球球内接长方体的对角线是球的直径。

正四面体（棱长为a ）的外接球半径R 与内切球半径r 之比为R ：r ＝3：1。

外接球半径：a R 46=。

内切球半径：a r 126= 结论：正四面体与球的接切问题，可通过线面关系证出，内切球和外接球的两个球心是重合的，为正四面体高的四等分点，即定有内切球的半径h r 41=(h 为正四面体的高)，且外接球的半径r R 3=．正四面体的外接球问题：已知正四面体A BCD -，H 为底面的中心，O 为外接球的球心，设棱长为a ，外接球半径为R ，内切球半径为r ，试求R.方法一：易知，由等积法得：（可求外接球半径和内切球半径）A BCD O ABC O BCD O CDA O DAB V V V V V -----=+++所以：11433BCD BCD AH S r S ∆∆⋅=⋅⋅ 故14r AH =,34R AH =所以 4R =.方法二：如图AHM BNM ∆≅∆所HM ON AM OA =，即13r R =,又由可得R =. 方法三：如图设延长AH 交球面上一点K,则AK=2R,在直角三角形ABK 中由射影定理得2AB AH AK =⋅ 即22a R =⋅ 故得R =.方法四：如图正四面体可补成一个边长为2a 的正方体，显然正方体的外接球即为正)22R =故可得4R a =. 四面体的内切球问题：关键是抓住球心到四面体的每个面的距离等于球的半径来找等量关系．【例6】求棱长为a 的正四面体内切球的体积．练习1.（球内接正四面体问题）（2003年江苏卷第12题）一个四面体的所有棱长都为2，四个顶点在同一球面上，则此球的表面积为（）ππππ6)33)4)3)D C B A方法一：将这个正四面体放入一个正方体中，再将这个正方体放入球中与球相外接。

因为正方体的对角线就是球的直径，而正四面体的棱就是正方体的侧面对角线。

所以，设正方体的棱长为a ，则有2a=2，a=1，.3,23,332π==∴==∴球S R a R 故选A 。

正四面体内切球半径推导过程

正四面体内切球半径推导过程正四面体是一个四个等边等角的三角形构成的多面体，内切球则是能够刚好与多面体的四个面接触的球体。

要推导出正四面体内切球的半径，我们可以使用几何和三角学的知识。

首先，我们设正四面体的边长为a。

假设内切球的半径为r。

我们可以使用勾股定理求出正四面体的高h：h=a√2/3```/\/\/\/\/\/\/______\/______\ra/2```根据勾股定理，我们可以得到三角形两边及斜边的关系：a^2=h^2+(a/2)^2代入我们之前计算得到的h，可以得到：a^2=(a^2/3)+(a^2/4)通过简化上式，我们可以解出a的平方的值：a^2=36r^2/45解这个方程可以得到a的平方的值为：a^2=10r^2/3然后，我们可以计算出正四面体的表面积S。

由于正四面体有四个等边三角形的表面，我们可以按照如下公式计算总的表面积：S=4*[√3*(a/2)^2]=√3*a^2代入我们之前计算得到的a的平方的值，可以得到表面积的计算式：S=4*(√3*10r^2/3)=4*√3*10/3*r^2最后，我们可以计算出正四面体体积V。

体积V等于正四面体所包围的空间的体积，可由下式计算：V=(1/3)*S*h=(1/3)*√3*a^2*(a√2/3)代入我们之前计算得到的a的平方和h的值，得到体积的计算式：V=(1/3)*√3*(10r^2/3)*(a√2/3)=(10/9)*√2*√3*r^2*a^3由于正四面体的体积V等于正四面体内切球的体积的四倍，我们可以得到：4/3*π*r^3=(10/9)*√2*√3*r^2*a^3然后我们可以解这个方程，计算出内切球的半径r：r=(√6*a)/12π因此，正四面体内切球的半径为(√6*a)/12π。

四面体外接球的球心、半径求法

四面体外接球的球心、半径求法之宇文皓月创作在立体几何中，几何体外接球是一个常考的知识点，对于学生来说这是一个难点，一方面图形不会画，另一方面在画出图形的情况下无从下手，不知道球心在什么位置，半径是多少而无法解题。

本文章在给出图形的情况下解决球心位置、半径大小的问题。

一、出现“墙角”结构利用补形知识，联系长方体。

【原理】：长方体中从一个顶点出发的三条棱长分别为c b a ,,，则体对角线长为222c b a l ++=，几何体的外接球直径R 2为体对角线长l 即2222c b a R ++=【例题】：在四面体ABCD 中，共顶点的三条棱两两垂直，其长度分别为3,61，，若该四面体的四个顶点在一个球面上，求这个球的概况积。

解：所以：四面体外接球的直径为AE 的长即：22224AD AC AB R ++=1663142222=++=R 所以2=R球的概况积为ππ1642==R S二、出现两个垂直关系，利用直角三角形结论。

【原理】：直角三角形斜边中线等于斜边一半。

球心为直角三角形斜边中点。

【例题】：已知三棱锥的四个顶点都在球O 的球面上，BC AB ⊥且7=PA ，5=PB ，51=PC ，10=AC ,求球O 的体积。

解：BC AB ⊥且7=PA ，5=PB ，51=PC ，10=AC ,因为22210517=+ 所以知222PC PA AC += 所以 PC PA ⊥ 所以可得图形为：在ABC Rt ∆中斜边为AC 在PAC Rt ∆中斜边为AC 取斜边的中点O ，在ABC Rt ∆中OC OB OA == 在PAC Rt ∆中OC OB OP ==所以在几何体中OA OC OB OP ===，即O 为该四面体的外接球的球心所以该外接球的体积为3500343ππ==R V 【总结】斜边一般为四面体中除了直角顶点以外的两个点连线。

三、出现多个垂直关系时建立空间直角坐标系，利用向量知识求解【例题】：已知在三棱锥BCD A -中，ABC AD 面⊥，︒=∠120BAC ，2===AC AD AB=ACCy式知222222)2(z y x z y x ++-=++222222)2(-++=++z y x z y x 解得 1331===z y x所以半径为3211331222=++=）（R 【结论】：空间两点间距离公式：221221221)()()(z z y y x x PQ -+-+-=四、四面体是正四面体处理球的“内切”“外接”问题与球有关的组合体问题，一种是内切，一种是外接。