七年级下学期数学题(周考7)

合集下载

七年级数学下学期第七周校际联考试题

广东省高州市2016-2017学年七年级数学下学期第七周校际联考试题说明：一、全卷共6页，考试时刻100分钟，总分值为120分.二、考生务必用黑色笔迹的签字笔或钢笔在答题卡上填写姓名、试室号、座位号等.3、选择题每题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦擦干净后，再选涂其他答案，答案不能答在试题上.4、非选择题必需用黑色笔迹钢笔或签字笔作答，答案必需写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原先的答案，然后再写上新的答案.五、考生务必维持答题卡的整洁，考试终止后，将试卷和答题卡一并交回.一、选择题（本大题10小题，每题3分，共30分）在每题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑.1．计算a 6、a 2的结果是（）A ．a 12B ．a 8C ．a 10D ．a 22．(x 3)2等于（）A ．x 5B ．x 6C ．x 9D ．2x 33．计算(－2a 3)2的结果是（）A ．2a 5B ．4a 5C ．－2a 6D ．4a 64．以下算式：①0.001°=1 ②10－3=0.001 ③10－5=－0.00001 ④(6－3×2)°=1，其中正确的有（）A ．1个B ．2个C ．3个D ．4个5．以下用科学记数法表示正确的选项是（）A ．0.00027=27×10－5B ．0.00027=0.027×10－2 C ．0.00027=0.27×10－3 D ．0.00027=2.7×10－4 6．计算(a ＋b)2－(a －b)2的结果是（）A ．4abB ．2abC ．2a 2D ．2b 2 7．已知a ＋a 1=4，那么a 2＋21a的值是（） A ．4 B ．16 C ．14 D ．158．如图，直线a ，b 相交于点O ，假设∠1=40°，则∠2等于（）A ．50°B ．60°C ．140°D ．160°9．如下图，已知直线c 与a ，b 别离交于点A 、B 且∠1=120°，当∠2=_____时，直线a ∥b （）A ．60°B ．120°C ．30°D ．150°10．如图，∠A=50°，∠1=∠2，那么∠ACD 等于（）A ．130°B ．60°C ．50°D ．40°二、填空题（本大题6小题，每题4分，共24分）请将以下各题的正确答案填写在答题卡相应的位置上。

新课标人教版七年级数学下册周末试卷

个三角形，BD是三角形
中
边上的中线，BE是三角形
中边上的中线；
图1 4
A 图25
E
1
B DE C A
C3
图6
D
23
BB
A D E
C
12.如图 7，在⊿ABC中，AD是中线，则⊿ABD的面积 ⊿ACD的面积（填“＞”“＜”“＝”）。
13.如图 8，⊿ABC中，∠A = 40°，∠B = 72°，CE平分∠ACB，CD⊥AB于 D，DF⊥CE，则∠
D.∠C 的对边是 DE
5.如图C 3 所示,在△ABC中,已知点 D,E,F分别为边 BC,AD,CE 的中点, 且 S △ABC=4cm2
影等于( )
A.2cm2
B.1cm2
C. 1cm2 2
D. 1 cm2 4
,则 S 阴
6.下列长度的三条线段中，能组成三角形的是（）
A、 3cm，5cm ，
A、5
B、6
C、7
D、8
二、填空题
9.如图 4，图中所有三角形的个数为，在△ABE中，AE所对的角是
，∠ABC所对的边
是，AD在△ADE中，是的对边，在△ADC中，是
的对边；
10.如图 5，已知∠1=0.5∠BAC，∠2 =∠3，则∠BAC的平分线为
，∠ABC的平分线
为
；
11.如图 6，D、E 是边 AC的三等分点，图中有
CDF =
度。
A
C
B
D
CA
F E
D
B
图7
图8
14.等腰三角形的高线、角平分线、中线的总条数为________.
图9
15.如图 9，木工师傅做完门框后，为了防止变形，常常像图中所示那样钉上两条斜拉的木条（图

七年级数学下学期第七周周练试题试题_1

宁化城东中学2021-2021学年七年级数学下学期第七周周练试题一、选择题〔每一小题3分，一共30分〕1．以下运算正确的选项是〔〕A ．1055a a a =+B ．2446a a a =⨯C ．a a a =÷-10D ．044a a a =-2．以下说法错误的选项是〔〕A ．两直线平行，内错角相等B ．两直线平行，同旁内角相等C ．同位角相等，两直线平行D ．平行于同一条直线的两直线平行3．以下关系式中，正确的选项是〔〕A. ()222b 2ab a b a +-=+B. ()222b a b a -=- C. D.4．一段导线，在O ℃时的电阻为2Ω〔电阻单位〕，温度每增加1℃，电阻增加0.008Ω，那么电阻R 〔Ω〕表示为温度t 〔℃〕的关系式是〔〕A. R=0.008tB. R=2+0.008tC. R=2.008tD.5．如图，AB ∥ED ，那么∠A ＋∠C ＋∠D ＝〔〕A ．180°B ．270°C ．360°D ．540°6．以下各式中不能用平方差公式计算的是〔〕 A ．))((y x y x +-- B ．))((y x y x --+-C ．))((y x y x ---D ．))((y x y x +-+7.汽车开场行驶时，油箱内有油40升，假如每小时耗油5升，那么油箱内余油量Q 〔升〕与行驶时间是t 〔时〕的关系用图象表示应为图中的A BC D E第5题()()22b a b a b a -=-+()222b a b a +=+8．假如一假如一盒圆珠笔有12支，售价18元，用y 〔元〕表示圆珠笔的售价，x 表示圆珠笔的支数，那么y 与x 之间的关系应该是〔〕A ．y=12xB ．y=18xC ．y=23xD ．32x 9．23,24m n ==，那么322m n -等于〔〕 A ．1 B ．98 C ．278 D ．271610．一根蜡烛长20 cm ，点燃后每小时燃烧5 cm,燃烧时剩下的高度y 〔cm 〕与燃烧时间是x〔小时〕的关系用以下图中________图象表示.二．填空题〔每一小题3分，一共27分〕11．变量s 与t 的关系式是2235t t s -=，那么当2=t 时，S=__________ . 12．一个角的补角是它的余角的4倍，那么这个角是_________度.13．假设x 2-mx ＋25是完全平方式，那么m=___________ .14． 9))((2-=+-x a x a x , 那么 a = .15．假设梯形的上底长是2，下底长是8，那么梯形的面积y 与高x 之间的关系式是_ _____ .16．：如图1，∠EAD=∠DCF ，要得到AB//CD ，那么需要的条件 .〔填一个你认为正确的条件即可〕17．假设，那么=__________. 18. 如图2，在△ABC 中，∠A=800，∠ABC 与∠ACB 的平分线义交于点O ，那么∠BOC=_______度.19．如今规定两种新的运算“﹡〞和“◎〞：a ﹡b=22b a +；a ◎b=2ab,如〔2﹡3〕〔2◎3〕=〔22+32〕〔2×2×3〕=156，那么[2﹡〔-1〕][2◎〔-1〕]= . 20．如图5，将一张长方形纸片的一角斜折过去，顶点A 落在A ′处，BC 为折痕，再将BE 翻折过去与BA ′重合BD 为折痕，那么两条折痕的夹角∠CBD ＝度三．解答题〔一共43分〕 21化简求值：)2)(2(2))(2()2(2y x y x y x y x y x +--+--+，其中21=x ，2-=y22．〔9分〕如图，点E 在直线DF 上，点B 在直线AC 上，假设∠AGB ＝∠EHF ，∠C ＝∠D ，那么∠A 与∠F 相等吗，为什么?图1E B F DA C 图223．〔10分〕小明在暑期社会理论活动中，以每千克0.8元的价格从批发场购进假设干千克西瓜到场上去销售，在销售了40千克西瓜之后，余下的每千克降价0.4元，全部售完．销售金额与售出西瓜的千克数之间的关系如下图．请你根据图象提供的信息完成以下问题：〔1〕求降价前销售金额y〔元〕与售出西瓜x〔千克〕之间的关系式．〔2〕小明从批发场一共购进多少千克西瓜？〔3〕小明这次卖瓜赚了多少钱励志赠言经典语录精选句；挥动**，放飞梦想。

甘肃省2021年七年级下学期周考数学试题

甘肃省202X-2021年七下数学第十七周周考试卷班级姓名学号一、选择题：（本大题共12小题，每小题2分，共24分，只有一项符合题目要求） 1．如图，直线a 与直线c 相交于点O ，∠1的度数是A. 60°B. 50°C. 40°D. 30° 2．下列计算正确的是A. 223a a a += B. 235a a a ⋅= C. 33a a ÷= D. 33()a a -= 3．下列事件为必然事件的是A ．小王参加本次数学考试，成绩是120分B ．某射击运动员射靶一次，正中靶心C ．打开电视机，CCTV 第一套节目正在播放新闻D ．口袋中装有2个红球和1个白球，从中摸出2个球，其中必有红球 4．下列图案中不是．．轴对称图形的是 A ． B ． C ． D ．5．芝麻作为食品和药物，均广泛使用．经测算，一粒芝麻约有0.00000201千克，用科学记数法表示为A.2.01×10-6千克B.0.201×10-5千克C.20.1×10-7千克D.2.01×10-7千克 6．以下列各组线段为边，能组成三角形的是A.1cm ，2cm ，4cmB.4cm ，6cm ，8cmC.5cm ，6cm ，12cmD.2cm ，3cm ，5cm7．如图，已知点A ，D ，C ，F 在同一条直线上，AB =DE ，BC =EF ，要使△ABC ≌△DEF ，还需要添加一个条件是A. ∠BCA =∠FB. ∠A =∠EDFC. ∠B =∠ED. BC ∥EF8．将一副三角尺按如图所示放置，则∠1的度数为 A. 100° B. 105° C. 110° D. 120°9．弹簧挂重物会后伸长，测得弹簧长度y （cm ）极限伸长量为20cm ，y （cm ）与所挂物体质量x （kg ）间有下面的关系.下列说法不正确的是A. x 与y 都是变量，x 是自变量，y 是因变量B. 所挂物体为6kg 时，弹簧长度为11cmC. 物体每增加1kg 时，弹簧长度就增加0.5cmD. 挂30kg 物体时一定比原来增加15cm 10．如图，△ABC 中，AB =AC ，∠A =40°，DE 垂直平分AB ，则∠DBC 为A. 30°B. 20°C. 15°D. 10°11、下列语句中正确的是A. 9-的平方根是3-B.9的平方根是3C. 9的算术平方根是3±D. 9的算术平方根是312．已知，如图，长方形ABCD 中，AB=3，AD=9，将此长方形折叠，使点B 与点D 重合，折痕为EF ，△ABE 的面积为（） A.6 B.8 C.10 D.12二、填空题（本大题共10个小题，每小题2分，共20分．把答案填在题中的横线上．） 13.已知直角三角形的三边长为6、8、x ，x 为斜边，则以x 为边的正方形的面积为 14.直角三角形两直角边长分别为5和12，则它斜边上的高为__________15.2)3(-=________，327- =_________， 0)5(-的立方根是；16．20130 －2=__________．233222(168)8x y z x y z x y +÷=______________________.17．某体育训练小组有2名女生和3名男生，现从中任选1人去参加学校组织的“我为奥运添光彩”志愿者活动，则选中女生的概率为___________.18．如图，小强利用全等三角形的知识测量池塘两端M 、N 的距离，如果△PQO ≌△NMO ，则只需测出其中线段_________的长度.19．在△ABC 中，当面积S 一定时，底边BC 的长度a 与底边BC 上的高h 之间的关系式为__________________.20．如图，在△ABC 中，DE ∥BC ，∠B =50°，现将△ADE 沿DE 折叠，点A 落在三角形所在平面内的点为A 1，则∠BDA 1的度数为_________. 21．如图，C 岛在A 岛的北偏东45°方向，在B 岛的北偏西25°方向，则从C 岛看A 、B 两岛的视角∠ACB＝__________度.22．如图，在△ABC 中，∠B 与∠C 的平分线交于点O . 过O 点作DE ∥BC ，分别交AB 、AC 于D 、E ．若AB =5，AC =4，则△ADE 的周长是 .三、解答题（本大题共7个小题，共56分．解答应写出文字说明、证明过程或演算步骤．） 23．（每小题3分，共18分）（1）（2）92731⋅+ （3） 2)52(-（4）154510-- （5）3（x ＋1）（x ＋2）－3（x 2＋2）题号 1 2 3 4 5 6 7 8 9 10 11 12 答案x /kg 0 1 2 3 4 ……y /cm 8 8.5 9 9.5 10第7题图 1 第8题图A C E DB 第10题图)31(33122-++（6）先化简，再求值：2b 2 ＋（a ＋b ）（a －b ）－（a －b ）2，其中a =－3，b =12．23．(本小题满分6分) 已知：如图，AD ∥BE ，∠1=∠2．请说明∠A =∠E ．24．(本小题满分6分) 在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共20只. 某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复. 下表是活动摸球的次数100 150 200 500 800 1000 摸到白球的次数m58 96 116 295 484 601 摸到白球的频率nm 0.58 0.64 0.58 0.59 0.605 0.601（1（2）假如你去摸一次，你摸到白球的概率是＿＿＿，摸到黑球的概率是＿＿＿；（3）试估计口袋中黑、白两种颜色的球各有多少只？25．一架方梯长25米，如图，斜靠在一面墙上，梯子底端离墙7米，（1）这个梯子的顶端距地面有多高？（2）如果梯子的顶端下滑了4米，那么梯子的底端在水平方向滑动了几米？（8分）26．(本小题满分9分) 乘法公式的探究及应用.（1）如下图，可以求出阴影部分的面积是_______________.（写成两数平方差的形式）；（2）如下图，若将阴影部分裁剪下来，重新拼成一个矩形，它的宽是，长是，面积是（写成多项式乘法的形式）. （3）比较左、右两图的阴影部分面积，可以得到乘法公式（用式子表达）（4）运用你所得到的公式，计算下列各题： ① 10.39.7②（2m – n+p ）(2m - n - p )26．(本小题满分9分) 甲、乙两人从少年宫出发，沿相同的路线分别以不同的速度匀速跑向体育馆，甲先跑一段路程后，乙开始出发，当乙超出甲150米时，乙停在原地等候甲，两人相遇后乙又继续以原来的速度跑向体育馆，如图是甲、乙两人在跑步的全过程中经过的路程y （米）与甲出发的时间x （秒）之间关系的图象.（1）在跑步的全过程中，甲共跑了________米，甲的速度为________米/秒；（2）图中标注的a 的值及乙跑步的速度分别是多少.？（3）乙在途中等候了多少时间？a a bb AB C D Ea 900 500 560 600x /秒O 150y /米。

七下数学周周测答案

七下数学周周测答案1、6、已知点A的坐标是，如果且，那么点A在（）[单选题] *x轴上y轴上x轴上，但不能包括原点(正确答案)y轴上，但不能包括原点2、15、如果m/n<0，那么点P（m,n）在（）[单选题] *A. 第二象限B. 第三象限C. 第四象限D. 第二或第四象限(正确答案)3、10．如图，点O在直线AE上，OC平分∠AOE，∠DOB是直角．若∠1＝25°，那么∠AOB的度数是（）[单选题] *A．65°B．25°(正确答案)C．90°D．115°4、多项式x2+ax+b=(x+1)(x-3)，则a、b的值分别是（）[单选题] *A. a=2，b=3B. a=-2，b=-3(正确答案)C. a=-2，b=3D. a=2，b=-35、35．若代数式x2﹣16x+k2是完全平方式，则k等于（）[单选题] * A．6B．64C．±64D．±8(正确答案)6、12．下列说法正确的是（）[单选题] *A．一个数前面加上“–”号这个数就是负数B．非负数就是正数C．0既不是正数，也不是负数(正确答案)D．正数和负数统称为有理数7、k·360°-30°（k是整数）所表示的角是第（）象限角。

[单选题] *A. 一B. 二C. 三D. 四(正确答案)8、4．﹣3的相反数是（）[单选题] *A.BC -3D 3(正确答案)9、46．若a+b＝7，ab＝10，则a2+b2的值为（）[单选题] *A．17B．29(正确答案)C．25D．4910、21．已知集合A={x|－2m}，B={x|m＋1≤x≤2m－1}≠?，若A∩B=B，则实数m的取值范围为___. [单选题] *A 2≤x≤3(正确答案)B 2<x≤3C 2≤x<3D 2<x<311、△ABC中的边BC上有一点D，AB=13，BD=7，DC=5，AC=7，则AD的长（）[单选题] *A、8(正确答案)B、9C、6D、312、8．如图，在数轴上表示的点可能是（）[单选题] *A．点PB．点Q(正确答案)C．点MD．点N13、260°是第（）象限角？[单选题] *第一象限第二象限第三象限(正确答案)第四象限14、33、点P(-5,-7)关于原点对称的点的坐标是（）[单选题] *A. (-5,-7)B. (5,7)(正确答案)C. (5,-7)D. (7,-5)15、若sinα＜0,则α角是在（）[单选题] *A、第一、二象限B、第三、四象限(正确答案)C、第一、三象限D、第二、四象限16、已知5m－2n－3＝0，则2??÷22?的值为( ) [单选题] *A. 2B. 0C. 4D. 8(正确答案)17、两数之和为负数，则这两个数可能是? [单选题] *A.都是负数B.0和负数(正确答案)C.一个正数与一个负数D.一正一负或同为负数或0和负数18、28.已知点A（2,3）、B（1,5），直线AB的斜率是（）[单选题] *A.2B.-2C.1/2D.-1/2(正确答案)19、45．下列运算正确的是（）[单选题] *A．（5﹣m）（5+m）＝m2﹣25B．（1﹣3m）（1+3m）＝1﹣3m2C．（﹣4﹣3n）（﹣4+3n）＝﹣9n2+16(正确答案)D．（2ab﹣n）（2ab+n）＝4ab2﹣n220、26.不等式|2x-7|≤3的解集是（）[单选题] *A。

七年级周测数学试卷

一、选择题（每题4分，共40分）1. 下列各数中，绝对值最小的是（）A. -3B. -2C. 0D. 22. 下列等式中，正确的是（）A. -5 + 3 = -2B. -5 + 3 = 2C. -5 - 3 = -2D. -5 - 3 = 23. 若a > b，则下列不等式中正确的是（）A. a - b > 0B. a + b > 0C. a - b < 0D. a + b < 04. 下列代数式中，同类项的是（）A. 3x^2B. 2xyC. 4x^2yD. 5x^2 + 2xy5. 已知a、b、c是等差数列，且a + b + c = 9，则a + c的值为（）A. 3B. 6C. 9D. 126. 下列函数中，是二次函数的是（）A. y = 2x + 3B. y = x^2 + 2x - 1C. y = 3x^2 - 2x + 1D. y = 4x - 37. 下列图形中，是圆的是（）A. 正方形B. 等边三角形C. 梯形D. 圆形8. 在直角三角形ABC中，∠C = 90°，AC = 3cm，BC = 4cm，则AB的长度为（）A. 5cmB. 6cmC. 7cmD. 8cm9. 下列方程中，有唯一解的是（）A. 2x + 3 = 5B. 3x - 2 = 7C. 2x^2 - 5x + 3 = 0D. 3x^2 - 2x + 1 = 010. 下列数中，是质数的是（）A. 15B. 16C. 17D. 18二、填空题（每题5分，共50分）11. 计算：-3 + (-2) = _______12. 等差数列{an}中，首项a1 = 2，公差d = 3，则第10项a10 = _______13. 已知二次函数y = -x^2 + 2x - 1，其顶点坐标为（_______，_______）。

14. 在直角坐标系中，点A（2，3）关于x轴的对称点坐标为（_______，_______）。

七年级下学期第七周周末练习数学试卷

七年级下学期第七周周末练习数学试卷班级：________ 姓名：___________ 成绩：_________一、选择题(每题3分，共21分）。

1．3338(2)a b ab -等于 ( )A ．0B ．6616a b -C ．6664a b -D ．4616a b -2.下列关系式中正确的是( )A.222()a b a b -=-B.22()()a b a b a b +-=-C.222()a b a b +=+D.222()2a b a ab b +=-+3.一个长方体的高为x cm ，长是高的3倍少4 cm ，宽是高的2倍，则这个长方体的体积是( )A ．321(34)2342x x x x x -=- B ．22(34)268x x x x x +=+ C ．32(34)268x x x x x -=- D ．22(34)68x x x x -=-4.2(1)(2)x mx x -+-的积中x 的二次项系数为零，则m 的值是 ( ) A ．1 B ．一1 C ．一2 D ．25.已知13x x -=，则221x x+的值( ) A.9 B.7 C.11 D.不能确定6.若2x y +=，2xy =-，则(1)(1)x y --的值是( )A.1-B.1C.5D.3-7.若(3)(5)M x x =--，(2)(6)N x x =--，则M 与N 的关系为( )A.M N =B.M N >C.M N <D. M 与N 的大小由x 的取值而定二、填空题（每空3分，共36分）8.计算：(1) 2325x x = ； (2) 2(1)x += ； (3) (2)(5)x x --= ．2013201220142 1.5(1)3⎛⎫⨯⨯- ⎪⎝⎭的结果是；9.已知长方体长为4×102mm ，宽为3×102mm ，高为2×102mm ，这个长方体的体积是3mm ．10.若229x mx -+是一个完全平方式，则m 的值为．11.已知2213x y +=，6xy =，则4()x y +的值是．12.将正方形的边长由a cm 增加6 cm ，则正方形的面积增加 2cm13.(1)若28,232m n ==，则 242m n +-= ；(2)若221a a +=，则2241a a +-= ．14．若22(3)16x m x +-+是完全平方式，则m 的值是．15．若2()()12x m x n x ax ++=++，则a 的取值有种．三、计算题16.计算：（每题分，共24分）(1) 23213(2)()34a b ab bc a b --+-； (2) ；2233(-5ab x)(-)10a bx y(3)2244()()()()x y x y x y x y ++-+ ； (4) (23)(23)a b a b -++-(5)22(2)(2)x y x y +-； (6)；3(2)(2)(1)(34)x x x x +---+17.（10分）已知11,5x y xy +==，求下面各式的值： (1) x2+y 2； (2) 22(1)(1)x y ++18.（9分）已知2222210x xy y x ++-+=，求xy 的值．。

七年级数学下学期第7周周练试题B试题(共3页)

七年级数学(sh ùxu é)试题〔B 〕一、选择题〔每一小题5分，一共25分〕1．是大于1的自然数,那么等于 ( ) A. B. C. D. 2．，，假如，那么的取值范围是〔〕 A 、 B 、 C 、 D 、3．数a 、b 、c 在数轴上对应的点如下图，那么以下式子中正确的选项是A ．a －c>b －cB ．a ＋c<b ＋cC ．ac>bcD ．4．设a 、b 、c 的平均数为M ，a 、b 的平均数为N ，N 、c 的平均数为P ，假设a>b c ，那么M 与P 的大小关系是 ( ) A. M < P B. M > P C. MP D. 不确定5．不等式组的解集在数轴上表示正确的选项是〔〕二、填空题〔每一小题5分，一共30分〕6．计算：498×502－5002＝．7．不等式有5个正整数解，那么的取值范围是．A B C D…………….……………..…………..密……...封……...线……...内……...请……...勿……...答……...8．不等式组有解，那么(nà me)n的取值范围是．9．关于x的方程x－(2x－a)＝2的解是负数，那么a的取值范围是．10．计算所得的结果是三、计算：〔7分+12分+9分+10分+12分=50分〕11、解不等式组，并把解集在数轴上表示出来,同时写出解集中的所有整数解．12、因式分解：〔1〕〔2〕13．假设关于x、的方程组的解都为正数，求a的取值范围．14．甲、乙两商场以同样价格出售同样的商品，并且又推出不同的优惠方案：在甲商场累计购物超过100元后，超出100元的局部按90%收费；在乙商场累计购物超过50元后，超出50元的局部按95%收费．(1)假设小明妈妈准备用120元去商场购物，你建议小明妈妈去商场花费少〔直接写“甲〞或者“乙〞〕；(2)根据两家商场的优惠活动方案，问顾客到哪家商场购物花费少？请说明理由．15、某电脑经销商方案同时购进一批电脑机箱和液晶显示器，假设(jiǎshè)购进电脑机箱10台和液晶显示器8台，一共需要资金7000元；假设购进电脑机箱2台和液晶显示器5台，一共需要资金4120元．(1)每台电脑机箱、液晶显示器的进价各是多少元?(2)该经销商方案购进这两种商品一共50台，而可用于购置这两种商品的资金不超过22240元．根据场行情，销售电脑机箱、液晶显示器一台分别可获利10元和160元．该经销商希望销售完这两种商品，所获利润不少于4100元．试问：该经销商有哪几种进货方案?哪种方案获利最大?最大利润是多少?内容总结（1）.（2）(2)根据两家商场的优惠活动方案，问顾客到哪家商场购物花费少（3）最大利润是多少。

七年级数学周测试卷答案

一、选择题（每题3分，共15分）1. 下列各数中，有理数是（）A. √9B. πC. √-1D. √0答案：D解析：有理数包括整数和分数，而√0=0是一个整数，因此选D。

2. 如果a=3，那么下列等式中不正确的是（）A. a²=9B. a³=27C. a⁴=81D. a⁵=243答案：C解析：将a=3代入各选项中，可得：A. 3²=9B. 3³=27C. 3⁴=81D. 3⁵=243显然，C选项中的81不正确，因此选C。

3. 下列各数中，无理数是（）A. √4B. √2C. √-1D. √9答案：B解析：无理数是不能表示为两个整数比的实数。

√2是无理数，因为它不能表示为两个整数的比，而其他选项都可以表示为整数，因此选B。

4. 已知a+b=5，a-b=3，则a的值为（）A. 4B. 2C. 3D. 1答案：A解析：将两个等式相加，得2a=8，因此a=4。

5. 下列图形中，中心对称图形是（）A. 等腰三角形B. 矩形C. 等边三角形D. 正方形答案：B解析：中心对称图形是指存在一个点，使得图形上的任意一点关于这个点对称。

矩形具有这个性质，因此选B。

二、填空题（每题4分，共16分）6. 5的平方根是_________。

答案：±√5解析：5的平方根是一个无理数，它可以表示为±√5。

7. 如果x²=4，那么x的值为_________。

答案：±2解析：x²=4可以写成x²-4=0，即(x+2)(x-2)=0，因此x=±2。

8. 下列等式中，正确的是_________。

答案：2(x+3)=2x+6解析：将等式两边都乘以2，得2x+6=2x+6，因此等式成立。

9. 一个长方形的长是8cm，宽是4cm，它的周长是_________cm。

答案：24解析：长方形的周长计算公式为2(长+宽)，代入长8cm和宽4cm，得周长为2(8+4)=24cm。

七年级下册数学第一周周考测试题

七年级下册数学第一周周测姓名：班级：得分：一．选择题（共12小题）1．下列各图中，∠1与∠2是对顶角的是（）A ．B ．C ．D ．2．如图，一副三角尺按不同的位置摆放，其中符合∠α＝∠β的图形共有（）A．4个B．3个C．2个D．1个3．下列说法中：①两点之间的所有连线中，线段最短；②相等的角是对顶角；③过一点有且只有一条直线与已知直线垂直；④若AB＝BC，则点B为线段AC的中点．其中说法正确的个数是（）A．1个B．2个C．3个D．4个4．如图，∠AOB＝68°，OC平分∠AOD且∠COD＝15°，则∠BOD的度数为（）A．28°B．38°C．48°D．53°5．如图，∠ACB＝90°，CD⊥AB，垂足为D，则点B到直线CD的距离是指（）A．线段BC的长度B．线段CD的长度C．线段BE的长度D．线段BD的长度6．如图，下列说法错误的是（）A．∠1与∠2是对顶角B．∠1与∠3是同位角C．∠1与∠4是内错角D．∠B与∠D是同旁内角7．如图，直线DE与BC相交于点O，∠COE与∠AOE互余，∠BOD＝35°，则∠AOE的度数是（）A．55°B．45°C．35°D．65°8．如图，下列说法错误的是（）A．∵∠1＝∠2，∴l3∥l4 B．∵∠2+∠5＝180°，∴l3∥l4C．∵∠1＝∠4，∴l1∥l2 D．∵∠1＝∠3，∴l1∥l29．如图，点P在直线l外，点A、B在直线l上，若P A＝4，PB＝7，则点P到直线l的距离可能是（）A．3 B．4 C．5 D．710．已知OA⊥OC，∠AOB：∠AOC＝2：3，则∠BOC的度数为（）A．30B．150C．30或150D．以上都不对11．平面内两两相交的7条直线，其交点个数最少是m个，最多是n个，则m+n的值为（）A．18B．20C．22D．2412．如图，直线AB，CD交于点O，OE平分∠AOC，OF⊥AB，OG平分∠EOF，若∠BOC ＝48°，则∠AOG等于（）A．10°B．12°C．14°D．16°二．填空题（共6小题）13．已知∠1的对顶角为123°，则∠1的邻补角度数为．14．如图，想在河堤两岸搭建一座桥，图中搭建方式中，最短的是PB ，理由．15．如图，在∠1，∠2，∠3，∠4四个角中，同位角有对，它们是；内错角有对，它们是；同旁内角有对，它们是．16．钟表上的时间是8：30时，时针与分针的夹角为度．17．如图，点A，B是直线l上的两点，点C，D在直线l上且点C在点D的左侧，点D在点B的右侧．AC：第1页共4页◎第2页共4页CB＝2：1，BD：AB＝3：2．若CD＝11，则AB ＝．18．如图1，两条直线相交，以交点为端点的射线有4条；如图2，三条直线相交，以交点为端点的射线最多有12条；如图3，四条直线相交，以交点为端点的射线最多有24条．那么六条直线相交，以交点为端点的射线最多有条．三．解答题（共6小题）19．计算：（1）﹣|﹣5|×2﹣5÷（﹣）+（﹣3）2；（2）﹣3x2﹣[7x﹣（4x﹣3）﹣2x2]．20．解方程：（1）2x﹣11＝3（2x﹣1）；（2）﹣＝1．21．已知：如图，点M，点P，点N在线段AB上，点P，点N分别是AB，BP的中点，PM＝AM，若MN＝12，试求线段AB的长．22．如图所示，已知∠AED＝62°，∠2＝31°，EF平分∠AED，可以判断BD∥EF吗？为什么？23．如图，直线AB与CD相交于点O，OC平分∠AOM，且∠AOM＝90°，射线ON在∠BOM内部．（1）求∠AOD的度数；（2）若∠BOC＝5∠NOB，求∠MON的度数．24．如图①，直线AB与直线CD相交于点O，∠COE＝90°，过点O作射线OF．（1）若射线OF平分∠AOC且∠BOF＝130°，求∠BOE的度数；（2）若将图①中的直线CD绕点O逆时针旋转至图②，∠COE＝90°，当射线OE平分∠BOF时，射线OC是否平分∠AOF，请说明理由；（3）若∠BOE＝20°，∠BOF＝130°，将图①中的直线CD绕点O按每秒5°的速度逆时针旋转α度（0°＜α＜180°），∠COE始终保持为90°，设旋转的时间为t秒，当∠AOC+∠EOF＝90°时，求t的值．第3页共4页◎第4页共4页。

七年级数学周考测试卷

七年级数学周考测试卷一、选择题：1.以下图形中,能够折叠成正方体的是( )A B C D2.假设a 是有理数,那么4a 与3a 的大小关系是( )A.4a>3aB.4a=3aC.4a<3aD.不能确定3.以下各对数中互为相反数的是( )A.32与-23B.-23与(-2)3;C.-32与(-3)2D.(-3×2)2与23×(-3)4.某班有40名学生,将他们的身高分成4组,在160～165cm 区间的有8名学生,那么这个小组的人数占全体的( )A.10%B.15%C.20%D.25%5.一个数的倒数的相反数是135,这个数是( ) A.165 B.516 C.-165 D.-5166.为了了解1万台某种电视机的使用寿命,从中抽出10台进行测试, 以下表达正确的选项是( )A.1万台某种电视机是总体;B.每台电视机是个体;C.10台电视机的使用寿命是样本;D.以上说法都不正确7.当a<0,化简a a a,得( ) A.-2 B.0 C.1 D.28.把27430按四舍五入取近似值,保存两个有数数字, 并用科学记数法表示应是( )A.2.8×104B.2.8×103C.2.7×104D.2.7×1039.某养鱼专业户年初在鱼塘中投放了500条草鱼苗,6个月后从中随机捞取17条草鱼,称重如下:估计这鱼塘中年初投放的500条草鱼此时的总质量大约为( )千克.A.845B.854C.846D.847 10．一条船在灯塔的北偏东030方向,那么灯塔在船的什么方向〔〕A ．南偏西030;B ．西偏南040;C ．南偏西060;D ．北偏东030O C ABD 11．假设2x+3=5,那么6x+10等于〔〕A ．15;B ．16;C ．17;D ． 3412.∠AOB=3∠BOC,假设∠BOC=30°,那么∠AOC 等于( )A.120°B.120°或60°C.30°D.30°或90°13．某商店有两个进价不同的计算器都卖了80元,其中一个赢利60％,另一个亏本20％,在这次买卖中,A ．不赔不赚;B ．赚了10元;C ．赔了10元;D ．赚了50元 14.城镇人口占总人口比例的大小表示城镇化水平的上下,由下面统计图可知, 我国城镇化水平提升最快的时期是( )A.1953年～1964年;B. 1964年～1982年;C. 1982年～1990年;D. 1990年～2022年;二、填空题：15.调查某城市的空气质量,应选择_______(填抽样或全面)调查.16.假设│x+2│+〔y-3〕2=0,那么xy=____. 17．∠α=72°36′,那么∠α的余角的补角是_____度.18．如图,∠AOC 和∠BOD 都是直角,如果∠DOC=︒36,那么∠AOB=_ __. 19．观察以下数字的排列规律,然后在括号内填入适当的数：3,-7,11,15-,19,-23,〔〕,( ).20.假设线段AB=10cm,在直线AB 上有一点C,且BC=4cm,M 是线段AC 的中点,那么AM=______cm.三、解做题:21. 计算：(1) 22350(5)1--÷--; (2) 2211210.53(2)3⎡⎤⎛⎫⎡⎤----⨯⨯-- ⎪⎢⎥⎣⎦⎝⎭⎣⎦.22.解方程：(1) 6)5(34=--x x ; (2)53210232213+--=-+x x x .39.1%1982年1964年807060504030果树数挂果树23．一条射线OA,如果从点O 再引两条射线OB 和OC,使∠AOB=60°, ∠BOC=20°, 求∠AOC 的度数.24．某果农承包了一片果林,为了了解整个果林的挂果情况, 果家随机抽查了局部果树挂果树进行分析.以下图是根据这组数据绘制的统计图,图中从左到右各长方形之比为5:6:8:4:2,又知挂果数大于60的果树共有48棵.(1)果农共抽查了多少棵果树?(2)在抽查的果树中,挂果树在40～60之间的树有多少棵,占百分之几?25. 某车间22名工人生产螺钉和螺母,每人每天平均生产螺钉1200个或螺母2000个,一个螺钉要配两个螺母.为了使每天的产品刚好配套,应该假设何分配工人？26．甲、乙、丙三人在长400米的环形跑道上,同时同地分别以每秒6米、4米、8米的速度跑步出发,并且甲、乙反向,甲、丙同向,当丙遇到乙时,即反向迎甲而跑,遇上甲时,又反向迎乙,如此练习下去,直到甲、乙、丙三人相遇为止,当这一过程结束时,求丙跑了多少米？27．“五一〞长假日,弟弟和妈妈从家里出发一同去外婆家,他们走了1小时后,哥哥发现带给外婆的礼品忘在家里,便马上带上礼品以每小时6千米的速度去追,如果弟弟和妈妈每小时行2千米,他们从家里到外婆家需要1小时45分钟,问哥哥能在弟弟和妈妈到外婆家之前追上他们吗？28. 某学校班主任暑假带着该班三好学生去旅游,甲旅行社说：“如果教师买全票一张,其余学生享受半价优惠.〞乙旅行社说：“教师在内全部按票价的6折优惠.〞假设全部票价是240元.〔1〕如果有10名学生,应参加哪个旅行社,并说出理由.〔2〕当学生人数是多少时,两家旅行社收费一样多？]29. 某地的一种绿色蔬菜,在市场上假设直接销售,每吨利润为1000元,经粗加工后销售,每吨利润4000元,经精加工后销售,每吨利润7000元.当地一家公司现有这种蔬菜140吨,该公司加工厂的生产水平是：如果对蔬菜进行粗加工,每天可加工16吨,如果对蔬菜进行精加工,每天可加工6吨,但每天两种方式不能同时进行.受季节等条件的限制,必须用15天时间将这批蔬菜全部销售或加工完毕.为此,公司研制了三种方案：方案一：将蔬菜全部进行粗加工；方案二：尽可能地对蔬菜进行精加工,没来得及加工的蔬菜,在市场上直接出售；方案三：将一局部蔬菜进行精加工,其余蔬菜进行粗加工,并刚好15天完成.如果你是公司经理,你会选择哪一种方案,说说理由.答案：一、选择题：C D C C D C A C C A B B B D二、填空题：15. 抽样调查;16.-617．162.618．144019．27,-31;20.3或7cm三、解做题:21.解:当OC 在∠AOB 的内部时,如答图(1),此时∠AOC=∠AOB-∠BOC=60°- 20°=40°. 当OC 在∠AOB 的外部时,如图(2),此时∠AOC=∠AOB+∠BOC=60°+20°=80°, ∴∠AOC 等于40°或80°.(1)OCA B (2)O C A B 22.略. 23.(1) -12,(2)416-; 24．(1) x=3, (2)167=x ; 25.(1)200棵,(2)56%;26．解：设哥哥追上弟弟需要x 小时,由题意得：x x 226+=解这个方程得： 21=x 所以,弟弟行走了211+小时小于1小时45分,未到外婆家,哥哥能够追上. 27．解：〔1〕甲 240×10×0.5+240=1440乙 240×〔10+1〕×0.6=1584〔2〕设当学生人数为 x 人时.240·x ·0.5+240=240(x+1) ·0.6x=428. 解：方案一：4000×140=560000〔元〕；方案二：15×6×7000+〔140-15×6〕×1000=680000〔元〕；方案三：设精加工x 吨,那么 14015616x x-+= 解得,x=60,7000×60+4000×〔140-60〕=740000〔元〕答：选择第三种.。

七年级数学第7周周末作业

证明：∵BD⊥AC，EF⊥AC( ∴∠2=∠3=90°
)
A
∴BD∥EF( ∴∠4=_____( ∵∠1=∠4(
)
)
D
G
)
F
31

∴∠1=_____( ∴DG∥BC( ∴∠ADG=∠C(
)
)C
)
2
4
5
E
B
五、探索题（4 分）
26.如图，AB∥CD,请分别探究三个图形中∠APC,∠PAB,∠PCD 三者之间的关系。
七年级数学第 7 周周末作业
班级
姓名
一、选择题：（每一题 2 分，共 20 分）
1、计算 (－2a2)2 的结果是
A 2a4 B －2a4 C 4a4 D －4a4
【】
2、下列运算正确的是
【】
A a 5 a 5 a10 B a 6 a 4 a 24 C a 0 a 1 a D a 4 a 4 a 0
密
----------------------------------------------------
24、(4 分) 如图，已知 AB∥DE,AE∥CD,问∠1 与∠2 有何关系？为什么？
.
A
D
1
2
B
C
E
封
25．根据下列证明过程填空：（9 分）
如图 20，BD⊥AC，EF⊥AC，D、F 分别为垂足，且∠1=∠4，求证：∠ADG=∠C
的大小为
A． 600
B． 100 0
C． 120 0
D． 130 0
10.△ABC 的角平分线、中线、高的画法错误的个数有（）
A:0
B:1
C:2
D:3

七年级下册第七周数学试题

七年级数学试题4、下列运算正确的是（）A.25102510a a a =÷B.1232+-+=÷n n n x x xC.()()b a a b b a -=-÷-2D.ac b a c b a 211053334-=÷-5、下列各式中，不能用平方差公式计算的是（）A 、))((y x y x +--B 、))((y x y x --+-C 、 ))((y x y x ---D 、))((y x y x +-+ 6、实验表明，人体内某种细胞的形状可近似地看作球，它的直径约为1560纳米，则这个数用科学记数法表示是（）A.50.15610-⨯米B.50.15610⨯米C.61.5610-⨯米D. 71.5610-⨯米 7、如图在△ABC 中，D.E.F 分别在AB,BC,AC 上，且EF//AB 要使DF//BC 只需再有下列条件中的（）即可．A. 21∠=∠B.DFE ∠=∠1C.AFD ∠=∠1D. AFD ∠=∠2图7 图8 图9 8、如图，OB ，OC 分别平分∠ABC 与∠ACB ，MN ∥BC ，若AB=24，AC=36，则△AMN 的周长是（）A ．60B ．66C 、72D ．789、如图己知︒=∠︒=∠⊥50,35,D A AB DF 则ACB ∠的度数为（）A.︒100B.︒105C.︒90D.︒8010、如图，小亮在操场上玩，一段时间内沿M A B M →→→的路径匀速散步，能近似刻画小亮到出发点M 的距离．．y 与时间x 之间关系的图象是（）11、葡萄熟了，从架子上落下来，可以大致反映葡萄下落过程中速度随时间变化情况的图象是（ )12、如图：向放在水槽底部的烧杯注水（流量一定）注满烧杯后，继续注水，直至注满水槽，水槽中水面上升高度与注水时间之间的关系大致是下列图象中的（）第10题图二、填空题13、计算： ()-=2324xy z ；2201319993-⎛⎫⨯-⨯ ⎪⎝⎭ = .14、一个角的补角是它的余角的3倍，则这个角的度数是________。

七年级下数学第七周

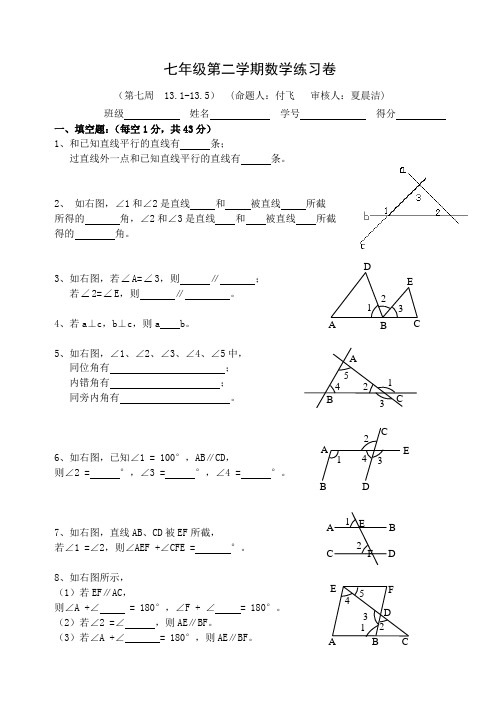
七年级第二学期数学练习卷（第七周 13.1-13.5） (命题人：付飞审核人：夏晨洁)班级姓名学号得分一、填空题：（每空1分，共43分）1、和已知直线平行的直线有条；过直线外一点和已知直线平行的直线有条。

2、如右图，∠1和∠2是直线和被直线所截所得的角，∠2和∠3是直线和被直线所截得的角。

3、如右图，若∠A=∠3，则∥；若∠2=∠E，则∥。

4、若a⊥c，b⊥c，则a b。

5、如右图，∠1、∠2、∠3、∠4、∠5中，同位角有；内错角有；同旁内角有。

6、如右图，已知∠1 = 100°，AB∥CD，则∠2 =°，∠3 =°，∠4 =°。

7、如右图，直线AB、CD被EF所截，若∠1 =∠2，则∠AEF +∠CFE =°。

8、如右图所示，（1）若EF∥AC，则∠A +∠= 180°，∠F + ∠= 180°。

（2）若∠2 =∠，则AE∥BF。

（3）若∠A +∠= 180°，则AE∥BF。

A B CED123ACB4 123524 31ABCDE12A BDCEF1 2345DFE9、填写下列各题的根据：（1）如右图，直线a 、b 交于O ，则∠1=∠3（）∠1+∠2=180°（）（2） ∵a ∥b,b ∥c ∴a ∥c( )（3）如右图， ∵ ∠1=∠2 a∴a ∥b( )∴∠1+∠4=180°（） b ∠2=∠3（）（4）如右图，∵∠1=∠ACD∴ ∥ （）∴∠B+∠ =180°（）∵AD ∥BC∴∠ =∠ （）10、如右图，AB∥CD，∠2 = 2∠1，则∠2 = 。

11、如右图，AB∥CD，EG⊥AB 于G ，∠1 = 50°，则∠E = 。

12、如右图，AB∥EF∥CD，EG∥BD，则图中与∠1相等的角（不包括∠1）共有个。

二、选择题：（每题3分，共12分）13、如右图，已知AB ∥CD ，则（）(A) ∠α+∠β+∠γ=360° (B) ∠α-∠β+∠γ=360° (C) ∠α+∠β-∠γ=180° (D) ∠α+∠β+∠γ=180°14、已知∠α和∠β是同旁内角，若∠α=50°，则∠β的度数为（） (A) 50 ° (B) 130° (C) 50°或130° (D) 不能确定15、如右图，∠1=65°，∠2=80°，∠3=35°，下列条件中能得到AB ∥CD 的是（） (A) ∠C=80° (B) ∠D=65° (C) ∠C=35° (D) ∠D=35°1 A BC DE FG H 1 2 A BC DE F 1A B F CD EG D 2 E C A B 1 316、下列说法正确的是（）(A) 邻补角的两条角平分线互相垂直。

七年级下学期数学第七章周考

七年级下学期第七章数学周测班级姓名成绩一、选择题1、如图，若m ∥n ，∠1=105 o ，则∠2= （） A 、55 o B 、60 o C 、65 o D 、75 o2、邻补角是（）A. 和为180°的两个角B. 有公共顶点且互补的两个角C. 有一条公共边且相等的两个角D. 有公共顶点且有一条公共边，另一边互为反向延长线的两个角 3、如图，直线AB 、CD 相交于点O ，OE ⊥AB 于O ，若∠COE=55°，则∠BOD 的度数为（） A. 40° B. 45° C. 30° D. 35°4、如图，已知ON ⊥l ，OM ⊥l ，所以OM 与ON 重合，其理由是（）A. 过两点只有一条直线B. 经过一点有且只有一条直线垂直于已知直线C. 垂线段最短D. 过一点只能作一条垂线5、如图所示，点E 在AC 的延长线上，下列条件中能判断．．．CD AB //（） A. 43∠=∠ B. 21∠=∠C. DCE D ∠=∠D. 180=∠+∠ACD D二、填空题 1、直线AB 、CD 相交于点O ，已知∠AOC+∠BOD=90°，则∠BOC= 。

2、在同一平面内，若a ⊥b ，c ⊥b ，则a c 。

3、如右图，CD AB //，且 25=∠A ， 45=∠C ，则E ∠的度数是_______4、如图，量得∠1=80°,∠2=80°，由此可以判定 ∥ ，它的根据是。

量得∠3=100°，∠4=100°，由此可以判定 ∥ ，它的根据是5、两直线平行，一组同位角的角平分线的位置关系是 . 三、将以下各推理过程的理由填入括号内。

1、如图EF ∥AD ，∠1=∠2，∠BAC=70 o ，求∠AGD 。

解：∵EF ∥AD ，∴∠2= （）又∵∠1=∠2， ∴∠1=∠3，∴AB ∥ （）∴∠BAC+ =180 o （）∵∠BAC=70 o ，∴∠AGD= 。

七年级数学下册第7周双休日作业试题

卜人入州八九几市潮王学校万盈二中七〔下〕数学双休日作业(第九周)班级家长签字一、选择题：(每一小题5分，一共40分) 1、以下方程是二元一次方程的是……………….〔〕A 、12-=+y xB 、12-=+yx C 、032=-y x D 、4=xy2、以下各对数值，不是二元一次方程62=+y x 的解的是……〔〕A 、⎩⎨⎧==60yx B 、⎪⎩⎪⎨⎧==521y x C 、⎩⎨⎧-=-=102y x D 、⎩⎨⎧==03y x3、以下方程组是二元一次方程组的是……………….〔〕A 、⎩⎨⎧=+=-12302y x y xB 、⎩⎨⎧=+-=-13332y z y xC 、⎩⎨⎧=-=-12422y x y xD 、⎪⎩⎪⎨⎧=+=-41102yxy x 4、二元一次方程组⎩⎨⎧=+=+3ny x y mx 的解是⎩⎨⎧-==21y x ，那么n m2+的值是〔〕A 、1B 、2C 、3D 、05、用代入法解方程组⎩⎨⎧=-=+)2........(52)1......(243y x y x 使得代入后化简比较容易的变形〔〕A 、由①得342y x -=B 、由①得432xy-=C 、由②得25+=y x D 、由②得52-=x y6、用加减法解方程组⎩⎨⎧=-=+)2...(..........823)1....(..........132y x y x 时，要使其中一个未知数的系数相等或者互为相反数，必须适当变形，以下四种变形中；①⎩⎨⎧=-=+869164y x y x ②⎩⎨⎧=-=+846196y x y x ③⎩⎨⎧-=+-=+1646396y x y x ④⎩⎨⎧=-=+2469264y x y x 正确的选项是………〔〕A 、①②B 、③④C 、①③D 、④7、假设方程组⎩⎨⎧=+=-py x py x 77482的解是方程3573=-y x 的解，那么P 的值是..〔〕A 、1B 、2C 、3D 、08、某同学买了x 枚1元的邮票与y 枚2元的邮票，一共12枚，花了20元钱，列出关于x 、y 的二元一次方程组为………〔〕A 、⎩⎨⎧=+=+20212y x y xB 、⎩⎨⎧=+=+20212y x y x C 、⎩⎨⎧=+=+12220y x y x D 、⎩⎨⎧=+=+12220y x y x二、填空题：(每一小题6分，一共42分)9、方程6312423=+-+nm y x是二元一次方程，那么m=.n=. 10、方程523=-y x ，用含有X 的代数式表示Y 是用含有Y 的代数式表示X 是11、假设⎩⎨⎧-==12y x 是二元一次方程53=+my x的解，那么m=.12、对于方程组⎩⎨⎧=-=+)2.....(2)1.....(4y x y x ，在⎩⎨⎧=-=51y x ，⎩⎨⎧==13y x ，⎩⎨⎧==46yx 这3对数值中，是方程①的解.是方程②的解.13、假设0)523(12=-++-+y x y x ，那么=+2005)(y x . 14、假设mn n m b a b a 4223542-+-与是同类项，那么m=.n=.15、请你任意写一个以⎩⎨⎧=-=31y x 为解的二元一次方程组是.三、解以下方程组：(每一小题7分，一共21分)16、用代入法解⎩⎨⎧=--=+)2....(932)1....(14y x y x 17、用加减法解⎩⎨⎧=--=+)2.........(32)1.....(143y x y x18、⎩⎨⎧=--=-)2(..........01283)1.......(..........872y x y x19、假设方程组４ｘ＋３ｙ＝１的解ｘ与ｙ相等，求ａ的值．ａｘ＋〔ａ－１〕ｙ＝３20、假设关于ｘ，ｙ的方程组３ｘ＋２ｙ＝ａ＋２的解满足ｘ＋ｙ＝４２ｘ＋３ｙ＝２ａ求ａ的值．四、解答题：〔此题总分值是10分〕21、假设方程组⎩⎨⎧=-=+)2...(..........023)1...(..........82y x y mx 的解是正整数，求正整数m 的值.五、用方程组解决问题：〔此题总分值是37分，20、21、22每一小题9分，23题10分〕22、一个长方形假设把它的长减少4㎝，宽增加2㎝，就可以得到一个正方形，且它的面积和长方形的面积相等.求这个长方形的长和宽。

初一数学第七周周考题及答案

学校班级姓名考号装订线七年级（下）数学第七周周考试卷（满分：50分出题人：赵帅审题人：初一数学组）一．选择题（本题共6小题，每题3分，共18分）1．在下图中，正确画出AC边上高的是（）．EBA C CABCABCABEEE（A）（B）（C）（D）2．下列说法中，正确的是（）A．一个钝角三角形一定不是等腰三角形，也不是等边三角形B．一个等腰三角形一定是锐角三角形，或直角三角形C．一个直角三角形一定不是等腰三角形，也不是等边三角形D．一个等边三角形一定不是钝角三角形，也不是直角三角形3．如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（）A．锐角三角形B．钝角三角形C．直角三角形D．无法确定4．若等腰三角形的一边是7，另一边是3，则此等腰三角形的周长是（）A．17 B．13 C．17或13 D．无法确定5．两根木棒分别为5cm和7cm，要选择第三根木棒，将它们钉成一个三角形，如果第三根木棒长为偶数，那么第三根木棒的取值情况有（）种A．3 B．4 C．5 D．66. 如图，在△ABC中，D、E分别为BC上两点，且BD＝DE＝EC，则图中面积相等的三角形有（）A．4对B．5对C．6对D．7对二、填空题（本题共5小题，每空2分，共18分）1.已知△ABC的高为BD，∠ABD=35°，则∠BAC的度数为______.2.如图所示，∠A+∠B+∠C+∠D+∠E =___________.ABCD E（2题图）（3题图）3.如图，△ABC中，∠A = 40°，∠B = 72°，CE平分∠ACB，CD⊥AB于D，DF⊥CE，则∠CDF = 度。

4.如图△ABC中，AD是BC上的中线，BE是△ABD中AD边上的中线，若 ABC的面积是24，则△ABE的面积是________。

5.如图，△ABC中，∠ABC、∠ACD的平分线相交于点E．（1）若∠ABC＝70°，∠ACB＝50°，则∠E＝________；（2）若∠ABC＋∠ACB＝120°，则∠E＝________；（3）若∠A＝60°，则∠E＝________；（4）若∠A＝100°，则∠E＝________；（5）若∠A＝n°，则∠E＝________．三、解答题（本题共小题，第1题6分，第2题8分，共14分）1. 某中学为筹备校庆活动，准备印制一批校庆纪念册。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

七年级数学（周考七）试题
出题人：高效时间：60分钟满分：100分
( )
A.30%
B.25%
C.10%
D.15%
2. 利用条形统计图中的数据,画成扇形统计图,则所有扇形的百分比的和为( )
A.60%
B.70%
C.90%
D.100%
3. 从右面的两个统计图中，可看出女生人数较多的是（）
A. 初一（1）班
B. 初一（2）班
两班一样多 D. 不能确定
C. 4. 将圆分成四个扇形，这四个扇形的面积之比为1：2：3：4，则最大那个扇形的圆心角为（） A ．36° B ．108° C ． 144°
D ．180°
5. 已知甲、乙、丙、丁共有课外书30本，又知甲、乙、丙、丁的课外书制作的条形统计图的高度之比为2︰4︰3︰1，则乙的课外书的本数为
（）
A ．12
B ．14
C ．16
D ．18
6. 为了了解某校初三年级400名学生的体重情况, 从中抽查了50名学生的体重进行统
计分析, 在这个问题中, 总体是指( )
A. 400名学生
B. 被抽取的50名学生
C. 400名学生的体重
D. 被抽取的50名学生的体重 7.下列调查中，适合用全面调查的方法的是（）. A 、电视厂要了解一批显象管的使用寿命 B 、要了解我市居民的环保意识
C 、要了解我市“阳山水蜜桃”的甜度和含水量
D 、要了解你校数学教师的年龄状况
8．一天的气温变化情况用（）统计图表示比较合适． A ．条形图 B ．扇形图 C ．折线图 D ．直方图
9.一个容量为80的样本最大值是141，最小值是50，取组距为10，则可以分成（）
A ．10组
B ．9组
C ．8组
D ．7组
10. 某农场今年粮食，棉花，油料三种作物种植面积的比是5：2：1，在扇形统计图上表示粮食面积的扇形圆心角是（）
A ．220°
B ．45°
C ．225°
D ．90°
二.填空题：（每空2分，共40分）
1. 要表示各班人数占全校总人数的百分比，你应选择__________统计图
2. 已知数据：25，21，23，27，29，24，22，26，27，26，25，25，26，28，30，28，29，26，24，25，在列频数分布表时，如果取组距为2，那么应分成组。

3. 为了掌握我校初中一年级女同学身高情况，从中抽测了60名女同学的身高，这个问
题中的总体是_______ ，样本是_______ ． 4. 为了对收集到的数据进行整理和分析，我们需要制作统计表或统计图．统计图
有、 . 和． 5. 一个扇形图中各个扇形的圆心角的度数是45°、60°、120°、135°，则各扇形占圆的百分比分别是_______、_______、_______、_______． 6. 某校八年级（1）班为了了解同学们一天零花钱的消费情况，对本班同学开展了调查，将同学一周的零花钱以2元为组距，绘制如图的频率分布直方图，已知从左到右各组的频数之比为2∶3∶4∶2∶1. （1
）若该班有48人，则零花钱用最多的是第组，有人；（2）零花钱在8元以上的共有人； 7.
某市为了了解七年级学生的身体素质情况，随机抽取了500名七年级学生进行检测，身体素质达标率为92％. 请你估计该市6万名七年级学生中，身体素质达标的大约有万人
8. 图1是初一（2）班英语成绩统计图根据图中的数据可以算出，优秀人数占总人数的__________；根据图中的数据画出的扇形统计图中，表示成绩中等的人数的扇形所对的圆心角是_______度.
9.对某班学生一次数学测试成绩进行统计,各分数段人数如图所示: 根据图示信息填空:
(1)该班有学生_________人;
(2)如果以大于或等于80分为优良,那么该班
的优良率为____________.
三、解答题：（每小题8分，共24分）分数
99.5
89.579.5
69.5
59.5
49.54
810
12
16人数
女生 50% 男生 50% 初一（1）班初一（2）班钱数(元)人数12108642（图1）
第2页共2页
1. 已知某圆恰好分成三个扇形,A 、B 、C,扇形A 、 B 占的百分数分别为25%,45%,又知整个圆代表学校的总人数,且C 中有150人,请求出该校共有多少人?
2. 根据图中提供信息.
(1)整个圆代表180人,另求甲、乙、丙、丁所代
表的人数. (2)画出条形统计图. 解：(1)图略
(2)甲人数=0
0120360×180=60(人)
乙人数=0
60360
×180=30(人) 丙人数=30%×180=54(人) 丁人数=20%×180=36(人)
3. 小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况. 他从中随机调查了40户居民家庭收入情况（收入取整数，单位：元），并绘制了如下的频数分布表和频数分布直方图.
根据以上提供的信息，解答下列问题：
（1）补全频数分布表.（2分）
（2）补全频数分布直方图.（2分）
（3）绘制相应的频数分布折线图.（2分）
（4）请你估计该居民小区家庭属于中等收入（大于或等于1000不足1600元）的大约
有多少户？（2分）
30%
20%60︒
120︒丁丙
甲
乙。