小学一年级的奥数学习的教案第六讲.doc
奥数 一年级 教案 第六讲 排队的学问讲课教案

排队问题是一个非常重要的知识点,在这节课中我们就将来初步学习什么是排队问题.首先进一步明确“第几”和“几个”基数和序数的区别.解答相应的计算队列总人数的应用题,在解答应用题的过程中学会画图的方法来解决问题.知识点:1、根据某个人(或物)的位置来计算总人数.2、已知某队的总人数,来判断某人(某物)的具体位置.3、计算两个人(或物)中间相隔的人(或物)的个数.1、教学点为各位老师准备了本节课的挂图.【教学思路】开课的时候跟学生一起做游戏,老师可以自己设计游戏形式,主要是通过一些口令让学生进一步明确“几”和“第几”的区别,巩固“前”“后”“左”“右”的方位顺序.为后面学习排队问题进行铺垫.趣味谜语一:鹰捉小鸡小伙伴,一起玩,鹰捉小鸡一长串.小明个高站前面,十位同学在后面.大勇对面跑得快,专抓龙尾玩得欢.想一想,算一算.共有几个小伙伴?()伸出你的左手,伸出你的右手.我们一起拍拍手:第一排左边第3个同学举起右手;第二排右边3个同学举起左手;第三排左边第4个同学,和你右边的同学握握手;第四排右边4个同学,和你前面的同学拍拍掌.……趣味谜语二:队列训练天蓝蓝,草青青,同学军训真高兴.队列训练最精彩,队伍排成一长串.正中站的是小新.前面同学有7名.后面同学也7名,前数后数都相等,仔细想,算分明,这队学生共几名?()趣味谜语三:座位几排影院门前人如海,进院对号坐下来,正数我坐第6排,倒着数来第5排,出个题目你猜猜,影院座位有几排? ()【教学思路】(1)第一个谜语是复习,除了10个小朋友扮演小鸡,还有1个同学扮演鸡妈妈,一个同学扮演老鹰,所以一共有10+1+1=12(个)同学.(2)小新前面7个同学,后面也7个同学,加上小新自己一共是:7+7+1=15(个)同学.(3)正数我第6排,倒数我第5排,说明我的前面有5排,我的后面有4排,一共是10排.对于(2)(3)是今天所学内容,在秋季的时候学生已经有了一些认知,如果孩子理解起来较难,可放在后面学完新课后解决.前面在学习几和第几时,我们提到了排队列的问题,今天我们就一起来学习队列中的数学问题.一些同学排成一行或一列,以其中某一人为标准来数人数,知道这个人从左右或从前后数的位置,就可以求得这一行或一列的人数,这类问题就是排队趣题.求队列人数时,一定要做到既不遗漏,也不能重复,尤其是作为标准的这个人是加上还是减去是解题的关键,排队的问题通过画图更容易解决.小动物们举行动物运动会,在长跑比赛中有4只动物跑在小松鼠的前面,有3只动物跑在小松鼠的后面,一共有几只动物参加长跑比赛?【教学思路】这道题要让学生明确问题的关键,我们可以把跑步的所有小动物看成一个队列,小松鼠前面有4只小动物,后面有3只小动物,在这个队列中,就是没有数松鼠自己,所以求这队的总人数还要把小松鼠加上.列式:4+3+1=8(只)答:一共有8只动物参加长跑比赛.同学们排成一队去植物园参观,从左边数小平排第3,从右边数小平排第6,一共有多少同学去参观?【教学思路】方法一:首先要让学生明确,从左边数小平排第3,也就是说小平左边有2个同学,从右边数小平排第6,这队同学的总人数就是2+6=8(人).或者这样想,从右边数小平排第6,也就是说小平右边有5个同学,从左数小平排第3,那么这队总人数就是3+5=8(人).列式:2+6=8(人)或者 3+5=8(人)方法二:也可以这样想:从左、从右一共有3+6=9(人)小平被数了两次,把重复数的一次去掉,9-1=8(人),这就是这队的总人数.列式:3+6-l=8(人)答:这队同学一共有8人.想想做做一群猴子排成一排,猴王排在正中间,从左边数它是第7个,从右边数它是第几个?这群猴子一共有多少只?【教学思路】猴王排在从左往右数的第7位,它又在正中间,说明猴王的左边有6只小猴,右边也有6只小猴,那么它应该排在从右边往左数的第7位.那么猴总共有:6+1+6=13(只),或7+(7-1)=13(只).共有13只猴子,猴王排在从右往左数的第7位.稀奇稀奇真稀奇,鸭子队里混只鸡,顺着数来它第5,倒着数来它第8,请你算一算,小鸭一共有几只?【教学思路】首先让学生明确什么是顺着数,什么是倒着数,然后再进行分析.在这个鸭子队里有一只鸡,这只鸡的位置就是这道题的标准.顺着数它是第5,倒着数它是第8,那么这个队的总数就是5+8-1=12(只),而这道题要我们求小鸭的只数,就要在12里面把1只鸡减掉才是小鸭的只数,所以应该是12-1=11(只)列式:5+8-1=12(只)12-1=11(只)答:小鸭一共有11只.16名同学排成一排,从左往右数,乐乐排在第7个,从右往左数,他排在第几个?【教学思路】排队的题目一般可以让学生画图来进行分析,这样对题意的理解更透彻更容易一些.从左往右数,乐乐排在第7个,也就是从左边第一个到乐乐共有7个人,这就说明乐乐的右面有16-7=9(人),那么从右边数乐乐就是第10个人,所以从右往左数,他排在第10个.列式:16-7+1=10(个)答:从右往左数他排在第10个.一年级同学外出春游,一(1)班20人排成一行,从左向右数,小雪是第8个,从右向左数,小芹是第9个,那么小雪和小芹中间有几个人?【教学思路】要想知道小雪和小芹中间有几个人,就要把小雪之前的人数(包括小雪)的和小芹之后的人数(包括小芹)减掉,才是小雪和小芹中间的人数,从图中看出,从左数小雪排在第8个,也就是从左边到小雪有8个人,从右数小芹排第9个,也就是从右到小芹有9个人,其余的人就排在小雪和小芹中间.列式:8+9=17(人) 20-17=3(人)或20-8-9=3(人)答:小雪和小芹中间有3人.想想做做在体育课上21名同学排成一排,从左往右数,小新是第8个;从右往左数,大毛是第9个,从小新数到大毛共有学生多少人?【教学思路】方法一:和上一题比较,这道题不仅要求出小新和大毛中间有几个同学,最后在数的时候还要加上小新和大毛.列式:21-8-9=4(人),4+2=6(人).方法二:从左往右数,小新是第8个,说明小新的左边有7个同学;从右往左数,大毛是第9个,说明大毛的右边有8个同学,这样从小新到大毛一共有21-7-8=6(人).动物园动物长跑比赛中,小猴暂列第4名,小兔暂列第10名,小兔应超过几只动物才能与小猴并列第4?【教学思路】首先让学生理解“小兔应超过几只动物才能与小猴并列第4”,其实也就是求“小猴和小兔之间有多少个小动物?”弄清了这个问题,这道题就简单了.小猴排第4名,小兔排第10名,那么小狗和小兔之间就5个小动物,也就是说小兔应超过5只动物才能与小猴并列第4.列式:10-1-4=5(个)答:小兔应超过5只动物才能与小猴并列第4.拓展与提高一群鸭子排队一溜走在小河边,鸭子中有两只是白鸭子,其余是黑鸭子,从前数第一只白鸭子排第6,从后数第二只白鸭子也排第6,两只白鸭中间还有6只黑鸭子,这群鸭子共有多少只?【教学思路】这道题通过画图分析可知,从前数第一只白鸭子排第6,也就是说它是第6只,它前面还有5只黑鸭子.从后数第二只白鸭子排第6,它后面还有5只黑鸭子.而两只白鸭中间还有6只黑鸭子,那么这群鸭子共有6+6+6=18(只)列式:6+6+6=18(只)答:这群鸭子共有18只.在排队趣题计算人数时,应注意:1.弄清排队顺序、计数方向,是从左往右,还是从前往后计数.2.计算总人数时,如果作为标准的人(或物)计数超过两次就要减去,如果没有计数就要加上.做到既不遗漏,也不重复.3.计算两个人(或物)中间个数时,可用总人数减去从前从后数的这两个附加题(老师可根据自己的课堂进度灵活处理讲义内容,附加题仅供老师参考使用.)在一次舞蹈表演中,18个同学排成一队,从右往左数丽丽是第8个,从左往右数她站在第几个?【教学思路】从右往左数,丽丽排在第8个,也就是从右边第一个到丽丽共有8个人,这就说明丽丽的左面有18-8=10(人),那么从左边数丽丽就是第11个人.列式:18-8+1=11(个)一个班的同学排成一队去参观历史博物馆.从排头数起李阳是第22个.从排尾数起,何平是第24个.已知李阳的前一个是何平.问这队共有同学多少人?【教学思路】方法一:列式:22+24-2=44(人)方法二:从排头数起李阳是第22个,而李阳的前一个是何平,说明从排头数何平在第21个,于是这道题我们可以把标准看成何平一个人,题目就变成了“一个班的同学排成一队去参观历史博物馆.从排头数何平在第21个,从排尾数起,何平在第24个,这队共有多少同学?”理解这道题就容易了.列式:24+21-1=44(人)1.在公园的售票处人们正在排队买票,小明前面有4个人,后面有7个人,问这队共有多少人?【答案】4+7+1=12(人),这队共有12人.2.同学们排成一排做游戏,从左数小冬排第11个,从右数小冬排第12个,一共有多少同学做游戏? 【答案】11+12-1=22(人)或(11-1)+12=22(人)、(12-1)+11=22(人),一共有22个同学做游戏.3.20名同学排成一队去做操,从前往后数,小星排第4个,从后往前数,小星排第几个?【答案】20-4+1=17(个),从后往前数,小星排第17个.4.有40幅儿童画在学校画廊展出,在这一行画中,小亮的画从左向右数是挂在第13位,小兰的画从右向左数挂在第20位,小亮和小兰的画中间还有多少幅?【答案】13+20=33(幅),40-33=7(幅);小亮和小兰的画中间还有7幅.5.同学们排成一队做游戏,其中有2名女同学.从前数,第一名女同学排在第5个,从后数,第二名女同学排在第7个,她们俩人中间有6名同学,算一算这队一共有多少名同学?【答案】5+7+6=18(名),这队一共有18名同学.【教学思路】小猴这一列有12个同学,小猴在第3个,那么它后面就有12-3=9(个)小动物.现在向 后转,就变成小猴前面有9个小动物,那么现在从前往后数,小猴就排在第十个.大盗贼狐狸作案后逃往花城,住进了百草园宾馆.百草园宾馆是一幢8层的方形大楼,客人全部住在大楼南侧.每层的房间都是一样的,各有8个房间,一共有64个房间.狐狸就住在其中的一个房间里. 猎狗探长得到消息,立刻带领猴侦探来到百草园宾馆,并问服务员:“狐狸住在哪个房间?”“对不起,先生,我只能用“是”或“不是”来回答您的问题.”服务员不冷不热地回答说. 猎狗探长说:“我只问你六个问题.” “它的房间在1—4楼吗?”“不是.”“那么在5—8楼的1—4号房间吗?”“是的.” “在7、8楼吗?”“是.”“在7、8楼的1、2号房间吗?”“不是.” “在8楼吗?”“是.”“在8楼的3号房间吗?”“不是.”猎狗探长说:“谢谢,我的提问结束了.”转身对身后的猴侦 探说:“走,到8楼4号房间去捉拿罪犯.”果然过了一会盗贼在8楼的4号房间被抓获.天天练 勇夺小冠军体育课上,小动物们排成队做广播体操.小猴这一列有12 个同学,从前往后数小猴在第3个.当老师喊“向后转”,你知 道现在小猴排在第几个?。
奥数-一年级-教案-第六讲-排队的学问

排队问题是一个非常重要的知识点,在这节课中我们就将来初步学习什么是排队问题.首先进一步明确“第几”和“几个”基数和序数的区别.解答相应的计算队列总人数的应用题,在解答应用题的过程中学会画图的方法来解决问题.知识点:1、根据某个人(或物)的位置来计算总人数.2、已知某队的总人数,来判断某人(某物)的具体位置.3、计算两个人(或物)中间相隔的人(或物)的个数.1、教学点为各位老师准备了本节课的挂图.【教学思路】开课的时候跟学生一起做游戏,老师可以自己设计游戏形式,主要是通过一些口令让学生进一步明确“几”和“第几”的区别,巩固“前”“后”“左”“右”的方位顺序.为后面学习排队问题进行铺垫.伸出你的左手,伸出你的右手. 我们一起拍拍手:第一排左边第3个同学举起右手; 第二排右边3个同学举起左手;第三排左边第4个同学,和你右边的同学握握手; 第四排右边4个同学,和你前面的同学拍拍掌. ……天蓝蓝,草青青,同学军训真高兴. 队列训练最精彩,队伍排成一长串. 正中站的是小新.前面同学有7名. 后面同学也7名,前数后数都相等,仔细想,算分明,这队学生共几名?( )趣味谜语三:座位几排影院门前人如海,进院对号坐下来,正数我坐第6排,倒着数来第5排,出个题目你猜猜,影院座位有几排? ( )【教学思路】(1)第一个谜语是复习,除了10个小朋友扮演小鸡,还有1个同学扮演鸡妈妈,一个同学扮演老鹰,所以一共有10+1+1=12(个)同学.(2)小新前面7个同学,后面也7个同学,加上小新自己一共是:7+7+1=15(个)同学. (3)正数我第6排,倒数我第5排,说明我的前面有5排,我的后面有4排,一共是10排.对于(2)(3)是今天所学内容,在秋季的时候学生已经有了一些认知,如果孩子理解起来较难,可放在后面学完新课后解决.前面在学习几和第几时,我们提到了排队列的问题,今天我们就一起来学习队列中的数学问题.一些同学排成一行或一列,以其中某一人为标准来数人数,知道这个人从左右或从前后小动物们举行动物运动会,在长跑比赛中有4只动物跑在小松鼠的前面,有3只动物跑在小松鼠的后面,一共有几只动物参加长跑比赛?【教学思路】这道题要让学生明确问题的关键,我们可以把跑步的所有小动物看成一个队列,小松鼠前面有4只小动物,后面有3只小动物,在这个队列中,就是没有数松鼠自己,所以求这队的总人数还要把小松鼠加上.列式:4+3+1=8(只)答:一共有8只动物参加长跑比赛.同学们排成一队去植物园参观,从左边数小平排第3,从右边数小平排第6,一共有多少同学去参观?【教学思路】方法一:首先要让学生明确,从左边数小平排第3,也就是说小平左边有2个同学,从右边数小平排第6,这队同学的总人数就是2+6=8(人).或者这样想,从右边数小平排第6,也就是说小平右边有5个同学,从左数小平排第3,那么这队总人数就是3+5=8(人).列式:2+6=8(人)或者 3+5=8(人)方法二:也可以这样想:从左、从右一共有3+6=9(人)小平被数了两次,把重复数的一次去掉,9-1=8(人),这就是这队的总人数.列式:3+6-l=8(人)答:这队同学一共有8人.想想做做一群猴子排成一排,猴王排在正中间,从左边数它是第7个,从右边数它是第几个?这群猴子一共有多少只?【教学思路】猴王排在从左往右数的第7位,它又在正中间,说明猴王的左边有6只小猴,右边也有6只小猴,那么它应该排在从右边往左数的第7位.那么猴总共有:6+1+6=13(只),或7+(7-1)=13(只).共有13只猴子,猴王排在从右往左数的第7位.稀奇稀奇真稀奇,鸭子队里混只鸡,顺着数来它第5,倒着数来它第8,请你算一算,小鸭一共有几只?【教学思路】首先让学生明确什么是顺着数,什么是倒着数,然后再进行分析.在这个鸭子队里有一只鸡,这只鸡的位置就是这道题的标准.顺着数它是第5,倒着数它是第8,那么这个队的总数就是5+8-1=12(只),而这道题要我们求小鸭的只数,就要在12里面把1只鸡减掉才是小鸭的只数,所以应该是12-1=11(只)列式:5+8-1=12(只)12-1=11(只)答:小鸭一共有11只.16名同学排成一排,从左往右数,乐乐排在第7个,从右往左数,他排在第几个?【教学思路】排队的题目一般可以让学生画图来进行分析,这样对题意的理解更透彻更容易一些.从左往右数,乐乐排在第7个,也就是从左边第一个到乐乐共有7个人,这就说明乐乐的右面有16-7=9(人),那么从右边数乐乐就是第10个人,所以从右往左数,他排在第10个.列式:16-7+1=10(个)答:从右往左数他排在第10个.一年级同学外出春游,一(1)班20人排成一行,从左向右数,小雪是第8个,从右向左数,小芹是第9个,那么小雪和小芹中间有几个人?【教学思路】要想知道小雪和小芹中间有几个人,就要把小雪之前的人数(包括小雪)的和小芹之后的人数(包括小芹)减掉,才是小雪和小芹中间的人数,从图中看出,从左数小雪排在第8个,也就是从左边到小雪有8个人,从右数小芹排第9个,也就是从右到小芹有9个人,其余的人就排在小雪和小芹中间.列式:8+9=17(人) 20-17=3(人)或20-8-9=3(人)答:小雪和小芹中间有3人.想想做做在体育课上21名同学排成一排,从左往右数,小新是第8个;从右往左数,大毛是第9个,从小新数到大毛共有学生多少人?【教学思路】方法一:和上一题比较,这道题不仅要求出小新和大毛中间有几个同学,最后在数的时候还要加上小新和大毛.列式:21-8-9=4(人),4+2=6(人).方法二:从左往右数,小新是第8个,说明小新的左边有7个同学;从右往左数,大毛是第9个,说明大毛的右边有8个同学,这样从小新到大毛一共有21-7-8=6(人).动物园动物长跑比赛中,小猴暂列第4名,小兔暂列第10名,小兔应超过几只动物才能与小猴并列第4?【教学思路】首先让学生理解“小兔应超过几只动物才能与小猴并列第4”,其实也就是求“小猴和小兔之间有多少个小动物?”弄清了这个问题,这道题就简单了.小猴排第4名,小兔排第10名,那么小狗和小兔之间就5个小动物,也就是说小兔应超过5只动物才能与小猴并列第4.列式:10-1-4=5(个)答:小兔应超过5只动物才能与小猴并列第4.【教学思路】这道题通过画图分析可知,从前数第一只白鸭子排第6,也就是说它是第6只,它前面还有5只黑鸭子.从后数第二只白鸭子排第6,它后面还有5只黑鸭子.而两只白鸭中间还有6只黑鸭子,那么这群鸭子共有6+6+6=18(只) 列式:6+6+6=18(只) 答:这群鸭子共有18只.(老师可根据自己的课堂进度灵活处理讲义内容,附加题仅供老师参考使用.)在一次舞蹈表演中,18个同学排成一队,从右往左数丽丽是第8个,从左往右数她站在第几个?【教学思路】从右往左数,丽丽排在第8个,也就是从右边第一个到丽丽共有8个人,这就说明丽丽的左面有18-8=10(人),那么从左边数丽丽就是第11个人.列式:18-8+1=11(个)拓展与提高一群鸭子排队一溜走在小河边,鸭子中有两只是白鸭子,其余是黑鸭子,从前数第一只白鸭子排第6,从后数第二只白鸭子也排第6,两只白鸭中间还有6只黑鸭子,这群鸭子共有多少只?一个班的同学排成一队去参观历史博物馆.从排头数起李阳是第22个.从排尾数起,何平是第24个.已知李阳的前一个是何平.问这队共有同学多少人?【教学思路】方法一:列式:22+24-2=44(人)方法二:从排头数起李阳是第22个,而李阳的前一个是何平,说明从排头数何平在第21个,于是这道题我们可以把标准看成何平一个人,题目就变成了“一个班的同学排成一队去参观历史博物馆.从排头数何平在第21个,从排尾数起,何平在第24个,这队共有多少同学?”理解这道题就容易了.列式:24+21-1=44(人)1.在公园的售票处人们正在排队买票,小明前面有4个人,后面有7个人,问这队共有多少人?【答案】4+7+1=12(人),这队共有12人.2.同学们排成一排做游戏,从左数小冬排第11个,从右数小冬排第12个,一共有多少同学做游戏?【答案】11+12-1=22(人)或(11-1)+12=22(人)、(12-1)+11=22(人),一共有22个同学做游戏.3.20名同学排成一队去做操,从前往后数,小星排第4个,从后往前数,小星排第几个?【答案】20-4+1=17(个),从后往前数,小星排第17个.4.有40幅儿童画在学校画廊展出,在这一行画中,小亮的画从左向右数是挂在第13位,小兰的画从右向左数挂在第20位,小亮和小兰的画中间还有多少幅?【答案】13+20=33(幅),40-33=7(幅);小亮和小兰的画中间还有7幅.5.同学们排成一队做游戏,其中有2名女同学.从前数,第一名女同学排在第5个,从后数,第二名女同学排在第7个,她们俩人中间有6名同学,算一算这队一共有多少名同学?【答案】5+7+6=18(名),这队一共有18名同学.【教学思路】小猴这一列有12个同学,小猴在第3个,那么它后面就有12-3=9(个)小动物.现在向 后转,就变成小猴前面有9个小动物,那么现在从前往后数,小猴就排在第十个.大盗贼狐狸作案后逃往花城,住进了百草园宾馆.百草园宾馆是一幢8层的方形大楼,客人全部住在大楼南侧.每层的房间都是一样的,各有8个房间,一共有64个房间.狐狸就住在其中的一个房间里.猎狗探长得到消息,立刻带领猴侦探来到百草园宾馆,并问服务员:“狐狸住在哪个房间?” “对不起,先生,我只能用“是”或“不是”来回答您的问题.”服务员不冷不热地回答说. 猎狗探长说:“我只问你六个问题.”天天练 勇夺小冠军体育课上,小动物们排成队做广播体操.小猴这一列有12 个同学,从前往后数小猴在第3个.当老师喊“向后转”,你知 道现在小猴排在第几个?“它的房间在1—4楼吗?”“不是.”“那么在5—8楼的1—4号房间吗?”“是的.”“在7、8楼吗?”“是.”“在7、8楼的1、2号房间吗?”“不是.”“在8楼吗?”“是.”“在8楼的3号房间吗?”“不是.”猎狗探长说:“谢谢,我的提问结束了.”转身对身后的猴侦探说:“走,到8楼4号房间去捉拿罪犯.”果然过了一会盗贼在8楼的4号房间被抓获.。
【1年级奥数详解(下)】一年级第6讲 七巧板

小学奥数创新体系一年级
(下册授课详解) 最
新
讲
义
小学奥数
第六讲七巧板
1.例题1
答案:答案不唯一
详解:先观察小图形中的特殊线条和特殊角,再从大图形中找出完整图形.
2.例题2
答案:答案不唯一
详解:基本平面图形有三角形、正方形、长方形、平行四边形、梯形、菱形等等,先认识一些图形,再用虚线分割.第一个图形可以分割成为三角形和梯形,第二个图形可以分割成为长方形和三角形,第三个图形可以分割成为2个平行四边形.注意是用一条直线进行分割,分割方法不唯一.
3.例题3
答案:
5
7
4
详解:2个小三角形可以拼成1个中三角形,2个小三角形可以拼成1个正方形,2个小三角可以拼成1个平行四边形.
4.例题4
答案:。
(完整)第六讲相遇问题教案

四年级奥数教案第六讲行程问题(一)——相遇问题从这一讲开始,我们讲涉及到“行程问题”, 行程问题是研究速度、路程、时间三个量的关系问题。
行程问题的基本关系式为:速度×时间=路程路程÷速度=时间路程÷时间=速度行程问题按照运动方向来分,可分为反向运动(相向相遇和反向相离),同向运动(追及问题).这一讲我们先学习行程问题中一典型问题——反向运动问题,即在同一道路上的两个运动物体作方向相反的运动问题。
它包括相遇问题和相背问题.所谓相遇问题,指的是上述两个物体以不同的点作为起点作反向运动的问题;所谓相背问题是指两个物体以同一点作为起点作背向运动的问题。
在解决反向运动问题时,要注意以下几点:(1)弄清题意,要抓住速度和,时间,路程三者的关系来分析;(2)对较复杂的反向运动问题,要借助直观图来帮助理解题意;(3)解题时要注意运用假设,设数的思考方法;(4)要善于从整体上把握题意,找准解题的突破口。
通过本讲学习,要求学生掌握相遇问题的解题方法,会借助线段图直观的解决各种复杂的相遇问题,为学好行程问题打下基础.解题技巧:要注意一些重点词语:相向、相背、同向、同时、相遇、相遇又相距、相距等,从重点语句中理解题意画出线段图,分析数量关系,最终找到解题方法。
第一课时教学时间:教学内容:掌握简单的相遇问题教学目标:理解和掌握简单的相遇问题教学重点:掌握相遇问题的基本公式教学难点:利用公式求简单的相遇问题教学过程:一、谈话导入。
今天我们来学习行程问题当中的相遇问题,它属于反向运动中的一种,下面我们就通过一个例子来给大家讲叙怎样解决相遇问题。
例子:小明和小强家相距2400米,两人同时从家中出发相向而行,小强每分钟走50米,小明每分钟走70米,问:他们经过多少时间相遇?师:这道题目就是典型的相遇问题.已知路程、两人的速度、求相遇时间,而且题目中还有相遇问题常见的关键字:相向而行。
即可判断是相遇问题。
小学奥数知识讲解-等差数列求和

第六讲等差数列求和(一)小朋友们,还记得我们第一讲的内容吗一一数中的规律。
那么对于一列有规律的数列我们怎么来求和呢?上一讲我们利用配对求和的方法能够很快解决一部分求和的问题,但是,当算式再复杂点又该怎样来解决呢?我们这一讲来介绍一种更快捷简单易懂的方法!我们先来认识什么是等差数列,如:1+2 + 3+……+ 49+ 50; 2 + 4 + 6+……+ 98+ 100。
这两列数都有共同的规律:每一列数从第二项开始,后一个数减去前一项的差都相等(相等差又叫公差)。
像这样的数列我们将它称之为等差数列。
我们再来掌握两个公式,对于等差数列,如果用字母S代表没一列数的和,字母a代表首项(即第1项),字母b代表末项,字母n 代表项数(加数的个数),那么S=(a+ b)x n —2。
如果n不容易直接看出,那么可用公式来计算出来:n =(b- a)宁d+ 1例【1】求1 + 2 + 3+……+ 1998+ 1999的和。
分析首项a= 1,末项b= 1999,项数n= 1999。
解S=( a+ b)x n —2=(1 + 1999)X 1999^ 2=2000X 1999^ 2=1000X 1999=1999000例【2】求111 + 112 + 113+……+ 288+ 289的和。
分析首项a= 111,末项b = 289,公差d= 1,项数n=(289—111)- 1 + 1 = 178+ 1 = 179。
解S=( a+ b)x n- 2=(111 + 289)X 179- 2=400X 179- 2=200X 179=35800例【3】求2+4 + 6+……+ 196+ 198的和。
分析首项a= 2,末项b= 198,公差d= 2,项数n= (198-2) -2+ 1 = 98+ 1 = 99。
解S=(a+ b)x n-2=(2+ 198)X 99-2=200X 99-2=100X 99=9900例【4】求297+ 294+ 291+……+ 9+6+ 3的和。
奥数 一年级 教案 第六讲 间隔之谜

第六讲 间隔之谜课前活动活动一:全班男同学站成一排,每两个男同学之间站一个女同学,数一数一共要站多少个女同学? 活动二:沿一条直线摆7个三角形,每两个三角形之间再摆一个正方形.数一数可以摆几个正方形? 活动三:拿6个圆片围成一个圈圈,在每两个圆片之间再放一个星星.数一数一共要放几个星星?【教学思路】这三个活动是课前的一个铺垫,让学生理解什么是间隔的含义,为后面的学习营造一个探究的空间,激发学生对间隔问题的兴趣.小朋友,如果家住在6楼,你爬楼梯回家,共爬了几层楼梯呢?对了,应该是五层,因为从一楼到二楼爬一层,二楼到三楼爬一层……共爬五层.如果把一根长绳剪成两段,应该剪几下呢?当然剪一下,正好有两段.以上这些例子都是关于间隔的谜题.通常像一段长绳剪成两段,如:发现规律比一比,想一想,段数和点数之间有什么关系?(1)( 3 )个点 ( 7 )个点 ( 2 )个点 ( 2 )段线 ( 6 )段线 ( 1 )段线你的发现段数与点数(2)( 2 )个点 ( 4 )个点 ( 4 )个点( 3 )段线 ( 5 )段线 ( 5 )段线你的发现段数与点数(3)( 3 )个点 ( 4 )个点 ( 8 )个点( 3 )段线 ( 4 )段线 ( 8 )段线你的发现段数与点数【教学思路】在开课时通过三组不同的情况让学生来发现规律,但是这种规律对于学生来说是很抽象不能理解的.所以我们不要着急把知识点强加给学生,我们只要让学生初步了解到这种规律就可以了,在后面的练习和以后的学习中我们会有更多的应用.实际应用操场边种了10棵杨数,如果在每两棵杨树之间再摆放一盆花,一共要摆放几盆花?【教学思路】植树问题对于一年级孩子来说是很抽象的内容,因此我们可以采取一些更直观的方法来引导孩子理解.比如画图,摆卡片等.操场边种了10棵杨数,10棵杨数之间就有9个间隔,一共有几个间隔就可以摆几盆花,每个间隔放一盆,10棵杨树之间一共能摆放9盆花.列式:10-1=9(盆)拓展练习操场边摆了10盆花,在这10盆花的两侧各栽一棵杨树,一共要栽几棵杨树?【答案】在10盆花两侧各栽一棵杨树,那么我们要栽的树的棵数要比间隔数多1,10盆花就是10个间隔,所以一共要栽11棵数.列式:10+1=11(棵)15名女同学(用“○”表示)围成三角形做游戏(如图),每两名女同学之间夹一名男同学(用“·”表示),共有多少名男同学?【教学思路】这15个女同学围成三角形做游戏,三角形是一个封闭的图形,那么有15个女同学,她们之间就有15个间隔,在每个间隔之间夹一个男同学,15个间隔就可以站15个男同学.通过这道题进一步巩固说明在封闭的线路中点数和间隔数是一样多的.把一根木头锯成3段,要锯几次?如果每锯一次用3分钟,一共要锯多少分钟?列式:3-1=2(次)3+3=6(分)答:要锯2次,一共需6分钟.拓展练习1.把一根木头锯成4段,要锯几次? 锯成6段呢?【答案】通过例题我们发现锯木头的时候,锯的次数总是比段数少1.因此把一根木头锯成 4段,要锯3次;锯成6段,就要锯5次.2.小亮家住在三楼,他每上一层楼要走14级台阶,小亮从一楼走到三楼要走多少级台阶?【答案】从第一层到第二层有14级台阶,从第二层到第三层又有14个台阶.也就是说从第一层到第二层要上两次台阶,所以一共要走14+14=28(个).在一条50米长的河岸边插彩旗,每10米插一面(两头都要插),一共需要插多少面彩旗?【教学思路】要在50米的河岸边插彩旗,每10米插1面, 50米可以分成5个10米,那么在插的这些彩旗中间一共就有5个间隔.我们先在最头上插一面,然后每10米插一面,这样我们插的彩旗就要比间隔多1,因此一共要插6面彩旗.同学们在一段马路的一边种树,从马路的一头到另一头共种了9棵,每两棵之间相距3米.问这段马路长多少米?列式:3+3+3+3+3+3+3+3=24(米) 答:这段马路长24米.拓展练习1.同学们在校门口走道的一旁插彩旗,从头至尾共插了10面,两面彩旗之间相距2米,问这条走道长多少米?【答案】在校门口走道的一旁一共插了10面彩旗,在这些彩旗之间一共就有9个间隔.每个间隔之间是2米,那么这条走道就有9个2米这么长.列式:2+2+2+2+2+2+2+2+2=18(米)或2×9=18(米)【注】一年级的孩子还没有理解乘法的意义,所以在这里不强求学生用乘法计算,可以介绍一下有这种方法,以后我们还会继续学习.在解题的过程中,主要是培养孩子通过画图来分析理解问题的能力.学校在圆形的花坛边放了10盆鲜花,每两盆之间相隔1米,这个花坛一圈长多少米?列式:1+1+1+1+1+1+1+1+1+1=10(米)或1×10=10(米)答:这个花坛一圈长10米.拓展练习小红家的时钟敲2下要2秒钟.敲8下要几秒钟?【答案】时钟敲打2下,中间只有一个间隔,1个间隔就是2秒钟;时钟敲8下,就是7个间隔,这样敲8下需要的时间即可求得.列式:2+2+2+2+2+2+2=14(秒钟)练 习 六1.把一根木头锯成5段,每锯一次要2分钟,一共要锯多少分钟?【答案】把一根木头锯成5段要锯4次,一次要2分钟,4次就要8分钟. 列式:2+2+2+2=8(分钟)2. 把一长方形铁丝(如图)共剪14下,剪断后有多少根小铁丝?【答案】正方形是一个封闭的图形,剪了14下,就有14根小铁丝.3. 公园的路边放了一些椅子,从起点到终点共计21把,每两把椅子之间有一头石狮子,问这条路边共有多少头石狮子?【答案】石狮子的个数应该比椅子的个数少1个,所以应该是20头狮子.4.在100米长的操场边,每10米修一个石凳,一共需要修多少个石凳? 【答案】列式:10+1=11(个)一共需要修11个石凳.5.在正方形的花圃周围共摆放了8盆鲜花,每两盆鲜花之间相隔1米,这个正方形花坛一周长多少米?【答案】这个正方形花坛一周长8米6.在一根绳子上晒被子,每两床被子之间要3个夹子,要晒10床被子,需要多少个夹子?【答案】需要的夹子应该比被子多1,因此需要11个夹子.7.有一个长方形池塘,在池塘四周种了20棵柳树,每两棵柳树之间又种了一棵桃树,桃树有多少棵?一共种树多少棵?【答案】池塘是长方形的,那么20棵柳树之间就有20个间隔,在每个间隔里种一棵桃树,桃树就有20棵,柳树和桃树一共有40棵.列式:20+20=40(棵)①小松鼠和小白兔上学迟到了.熊猫老师问:“你俩今天为什么迟到了?”②小松鼠说:“我在上学的路上遇到三个小弟弟,他们饿(e)得很,我就采了6个松果.分成数量不同的3份,送给他们每人一份.”③小白兔说:“我在上学的路上遇到四个小妹妹.她们饿得很,我就采了9个蘑菇.分成数量不同的4份,送给她们每人一份.”④熊猫老师说:“松鼠说的是实话.小白兔说的是谎话.”小朋友,熊猫老师怎么知道小白兔说的是谎话?。
(完整版)小学一年级奥数教案第六讲

第六讲火柴棒的游戏一.检查家庭作业针对学生所做情况,重点问题重点讲解,提高学生综合运用知识的能力,查缺补漏,等级评定。
二.梳理知识火柴棒可以摆出许多图形,如三角形、四边形等,也可以摆成一些生活中的物品,通过移动火柴棒,它们之间会出现一些有趣的转化。
下面,我们用火柴棒来做一些有趣的游戏。
例1 用火柴棒摆出一个三角形、一个正方形、一个长方形、一个五边形、一个六边形。
解例2用三根火柴棒可以摆出一个三角形,如图.(1)再加两根火柴棒,摆出两个三角形;(2)再加两根,摆出三个三角形来;(3)再加两根,摆出五个三角形来.解(2)(3)(1)例3把两根火柴棒添在那里,可以摆出5个正方形?例4 请给下面的每个数字只添上1根火柴棒,使它们变成一个新的数字。
例5请你在下面的算式中添上一根火柴,使其等式成立。
例6 拿走1根火柴棒,使等式成立。
例7 你能只移动下面算式中的一根火柴棒,使其等式成立吗?三.达标测试1、看图填数。
( )个三角形,( )根火柴2、请你添加上三根火柴,使下面的正方形变成3个。
你知道共用的火柴是哪几根吗?3、如图,9根火柴棒已摆成了5个三角形。
(1)拿掉哪三根,可以变成一个三角形?(2)拿掉哪两根,就可以变成两个三角形?(3)拿掉哪一根,就可以变成3个三角形?4、移动下面每个数字中的一根火柴棒,使它们变成一个新的数字。
5、请你在下面的算式中添上一根火柴,使其等式成立。
6、在下面的算式中拿掉一根火柴后,使等式成立。
四.家庭作业1、下图是用12根火柴摆成的“田”字,能不能拿走2根火柴棒,使它变成两个正方形?2、你能拿走2根火柴棒,使下面的等式成立吗?。
小学一年级奥数教案

小学一年级奥数教案小学一年级奥数教案一、教学目标1.培养学生观察问题、发现问题的能力;2.培养学生解决问题的能力;3.培养学生逻辑思维能力;4.增强学生的数学实践能力。
二、教学重点1.培养学生观察问题、发现问题的能力;2.培养学生解决问题的能力。
三、教学难点1.培养学生逻辑思维能力;2.增强学生的数学实践能力。
四、教学准备1.课程计划、教学材料;2.教学工具:计算器、尺子、图形模具。
五、教学过程1.导入教师可以用一道简单的数学题目导入,引起学生对奥数的兴趣。
2.讲解与启发教师根据教学材料,讲解奥数的基本概念和基本方法,并通过启发性提问,引导学生思考。
3.引出新知通过一道奥数题目引出新的数学概念或方法,激发学生的学习兴趣。
4.合作探究教师组织学生合作进行探究学习,通过小组合作解决一些实际问题,并记录下来。
5.展示成果学生通过小组展示自己的成果,互相分享和评价,从中了解到不同的解决方法和思路。
6.总结归纳教师引导学生总结归纳出学习到的新知识和解题方法,培养学生的逻辑思维和分析能力。
7.练习巩固教师出一些针对性的练习题,让学生巩固所学知识,并在解题过程中发现和解决问题。
8.作业布置教师布置适量的作业,巩固学生的知识,要求学生在作业中运用所学的方法解决问题。
六、板书设计奥数教案七、教学反思通过奥数教学,可以培养学生主动思考、观察问题的能力,并通过探究学习和合作解决实际问题的方式,培养学生的创造性思维和实践能力。
同时,奥数教学也可以让学生体验到数学的乐趣,激发学习兴趣,提高学习效果。
一年级奥数教案

第一讲数一数教学目标:1.初步经历从场景中抽象出数的过程,初步认识顺序数数的方法。
2.初步经历运用点子图表示物体个数的过程,初步建立数感和一一对应的思想。
3.初步学会用数学的眼光观察现实事物,渗透应用意识。
4.在他人的帮助下,初步体会学习数学的意义和乐趣。
教学过程:一、创设情境,激发兴趣谈话:小朋友喜欢玩吗你们喜欢到哪儿去玩呢悄悄地告诉你的同桌。
老师猜,小朋友一定非常喜欢到儿童乐园去玩吧。
(多媒体课件出示儿童乐园的情境图)二.自主探索,体验领悟1.初步感知。
(1)问:图上画了些什么?(2)小组交流后集体交流。
(3)描述:小朋友们自由自在地在儿童乐园里尽情游玩着,他们有的在骑木马,有的在荡秋千,有的在坐小飞机,有的在滑滑梯。
看!他们笑得多开心呀!学玩今天的新本领,咱们也到儿童乐园去玩,好吗? 2.看主题图数数(1)提问:图上画了滑梯、秋千、木马等东西,还画了人、鸟、花等,你能数出每一种有多少吗?(2)学生先自己数一数,再数给同桌听。
(3)集体交流,教师引导学生按顺序数,并指出在数较多的物体时,可以数一个轻轻地划掉一个,防止遗漏。
3.总结方法(1)开展讨论:怎样数数又对又快?小组讨论后再集体交流。
(2)小结:数数时,要一个一个按顺序数,可以从左往右或从右往左数,也可以从上往下数,这样就不会多数或少数了;如果数的是画在书上的图,可以用笔点着数,或者数一个用笔作一个记号,这样数就又对又快了!最后数到几,就说明一共有几个物体。
4.按顺序抢答。
(1)据图意找用不着、2、3、------10表示的东西有哪些?比一比谁说得好!(多媒体课件同步演示,从主题中逐个抽取出其不意0幅片段图)(2)自己看着陆0幅图说图意。
5.用点子图表示个数。
(1)讲述:我们可以用一些简单的符号表示物体个数,如点子,有一个滑梯就用一个点子表示。
(出示点子图)(2)讨论:怎样表示秋千的个数为什么(出示点子图)怎样表示木马、小飞机、蝴蝶、小鸟、气球的个数(出示点子图)(3)探索:图中什么物体的个数可以用法个点子来表示8个点子呢怎样表示气球的个数(自己在书上画好)10个点子表示什么三.巩固深化,再次体验1.门票游戏。
奥数-一年级-教案-第六讲-间隔之谜电子教案

奥数-一年级-教案-第六讲-间隔之谜第六讲间隔之谜课前活动活动一:全班男同学站成一排,每两个男同学之间站一个女同学,数一数一共要站多少个女同学?活动二:沿一条直线摆7个三角形,每两个三角形之间再摆一个正方形.数一数可以摆几个正方形?活动三:拿6个圆片围成一个圈圈,在每两个圆片之间再放一个星星.数一数一共要放几个星星?【教学思路】这三个活动是课前的一个铺垫,让学生理解什么是间隔的含义,为后面的学习营造一个探究的空间,激发学生对间隔问题的兴趣.小朋友,如果家住在6楼,你爬楼梯回家,共爬了几层楼梯呢?对了,应该是五层,因为从一楼到二楼爬一层,二楼到三楼爬一层……共爬五层.如果把一根长绳剪成两段,应该剪几下呢?当然剪一下,正好有两段.以上这些例子都是关于间隔的谜题.通常像一段长绳剪成两段,如:发现规律比一比,想一想,段数和点数之间有什么关系?(1)( 3 )个点 ( 7 )个点 ( 2 )个点( 2 )段线 ( 6 )段线 ( 1 )段线你的发现段数与点数(2)( 2 )个点 ( 4 )个点 ( 4 )个点( 3 )段线 ( 5 )段线 ( 5 )段线你的发现段数与点数(3)( 3 )个点 ( 4 )个点 ( 8 )个点( 3 )段线 ( 4 )段线 ( 8 )段线你的发现段数与点数间隔之间有什么奥秘呢?小朋友们下【教学思路】在开课时通过三组不同的情况让学生来发现规律,但是这种规律对于学生来说是很抽象不能理解的.所以我们不要着急把知识点强加给学生,我们只要让学生初步了解到这种规律就可以了,在后面的练习和以后的学习中我们会有更多的应用.实际应用操场边种了10棵杨数,如果在每两棵杨树之间再摆放一盆花,一共要摆放几盆花?【教学思路】植树问题对于一年级孩子来说是很抽象的内容,因此我们可以采取一些更直观的方法来引导孩子理解.比如画图,摆卡片等.操场边种了10棵杨数,10棵杨数之间就有9个间隔,一共有几个间隔就可以摆几盆花,每个间隔放一盆,10棵杨树之间一共能摆放9盆花.列式:10-1=9(盆)拓展练习操场边摆了10盆花,在这10盆花的两侧各栽一棵杨树,一共要栽几棵杨树?【答案】在10盆花两侧各栽一棵杨树,那么我们要栽的树的棵数要比间隔数多1,10盆花就是10个间隔,所以一共要栽11棵数.列式:10+1=11(棵)15名女同学(用“○”表示)围成三角形做游戏(如图),每两名女同学之间夹一名男同学(用“·”表示),共有多少名男同学?【教学思路】这15个女同学围成三角形做游戏,三角形是一个封闭的图形,那么有15个女同学,她们之间就有15个间隔,在每个间隔之间夹一个男同学,15个间隔就可以站15个男同学.通过这道题进一步巩固说明在封闭的线路中点数和间隔数是一样多的.把一根木头锯成3段,要锯几次?如果每锯一次用3分钟,一共要锯多少分钟?列式:3-1=2(次)3+3=6(分)答:要锯2次,一共需6分钟.拓展练习1.把一根木头锯成4段,要锯几次? 锯成6段呢?【答案】通过例题我们发现锯木头的时候,锯的次数总是比段数少1.因此把一根木头锯成4段,要锯3次;锯成6段,就要锯5次.2.小亮家住在三楼,他每上一层楼要走14级台阶,小亮从一楼走到三楼要走多少级台阶? 【答案】从第一层到第二层有14级台阶,从第二层到第三层又有14个台阶.也就是说从第一层到第二层要上两次台阶,所以一共要走14+14=28(个).在一条50米长的河岸边插彩旗,每10米插一面(两头都要插),一共需要插多少面彩旗?【教学思路】要在50米的河岸边插彩旗,每10米插1面, 50米可以分成5个10米,那么在插的这些彩旗中间一共就有5个间隔.我们先在最头上插一面,然后每10米插一面,这样我们插的彩旗就要比间隔多1,因此一共要插6面彩旗.同学们在一段马路的一边种树,从马路的一头到另一头共种了9棵,每两棵之间相距3米.问这段马路长多少米?列式:3+3+3+3+3+3+3+3=24(米)答:这段马路长24米.拓展练习1.同学们在校门口走道的一旁插彩旗,从头至尾共插了10面,两面彩旗之间相距2米,问这条走道长多少米?【答案】在校门口走道的一旁一共插了10面彩旗,在这些彩旗之间一共就有9个间隔.每个间隔之间是2米,那么这条走道就有9个2米这么长.列式:2+2+2+2+2+2+2+2+2=18(米)或2×9=18(米)【注】一年级的孩子还没有理解乘法的意义,所以在这里不强求学生用乘法计算,可以介绍一下有这种方法,以后我们还会继续学习.在解题的过程中,主要是培养孩子通过画图来分析理解问题的能力.学校在圆形的花坛边放了10盆鲜花,每两盆之间相隔1米,这个花坛一圈长多少米?列式:1+1+1+1+1+1+1+1+1+1=10(米)或1×10=10(米)答:这个花坛一圈长10米.拓展练习小红家的时钟敲2下要2秒钟.敲8下要几秒钟?【答案】时钟敲打2下,中间只有一个间隔,1个间隔就是2秒钟;时钟敲8下,就是7个间隔,这样敲8下需要的时间即可求得.列式:2+2+2+2+2+2+2=14(秒钟)解答间隔问题时,应注意分清3种类型:1.首尾相连接的封闭的图形,段数与点数同样多.2.两头无点的直线图形(如剪绳),点数(剪数)比段数少1,或者是段数比点数多1.3.两头有点的直线图形(如植树),点数(棵数)比段数(间隔)多1,或者是段数比点数少1.解题时,一定要分清间隔类型,才能正确解答.练习六1.把一根木头锯成5段,每锯一次要2分钟,一共要锯多少分钟?【答案】把一根木头锯成5段要锯4次,一次要2分钟,4次就要8分钟.列式:2+2+2+2=8(分钟)2. 把一长方形铁丝(如图)共剪14下,剪断后有多少根小铁丝?【答案】正方形是一个封闭的图形,剪了14下,就有14根小铁丝.3. 公园的路边放了一些椅子,从起点到终点共计21把,每两把椅子之间有一头石狮子,问这条路边共有多少头石狮子?【答案】石狮子的个数应该比椅子的个数少1个,所以应该是20头狮子.4.在100米长的操场边,每10米修一个石凳,一共需要修多少个石凳?【答案】列式:10+1=11(个)一共需要修11个石凳.5.在正方形的花圃周围共摆放了8盆鲜花,每两盆鲜花之间相隔1米,这个正方形花坛一周长多少米?【答案】这个正方形花坛一周长8米6.在一根绳子上晒被子,每两床被子之间要3个夹子,要晒10床被子,需要多少个夹子?【答案】需要的夹子应该比被子多1,因此需要11个夹子.7.有一个长方形池塘,在池塘四周种了20棵柳树,每两棵柳树之间又种了一棵桃树,桃树有多少棵?一共种树多少棵?【答案】池塘是长方形的,那么20棵柳树之间就有20个间隔,在每个间隔里种一棵桃树,桃树就有20棵,柳树和桃树一共有40棵.列式:20+20=40(棵)①小松鼠和小白兔上学迟到了.熊猫老师问:“你俩今天为什么迟到了?”②小松鼠说:“我在上学的路上遇到三个小弟弟,他们饿(e)得很,我就采了6个松果.分成数量不同的3份,送给他们每人一份.”③小白兔说:“我在上学的路上遇到四个小妹妹.她们饿得很,我就采了9个蘑菇.分成数量不同的4份,送给她们每人一份.”精品文档收集于网络,如有侵权请联系管理员删除④熊猫老师说:“松鼠说的是实话.小白兔说的是谎话.”⑤小白兔听后,惭愧地低下头,说:“老师,我错了,今后我一定做个诚实的孩子.”小朋友,熊猫老师怎么知道小白兔说的是谎话?。
【一升二】小学数学奥数第6讲:简单的年龄问题-教案

答:两年后妈妈比弟弟大26岁。
2. 妹妹今年7岁,5年后奶奶比妹妹大55岁,请问奶奶今年多少岁?
7+55=62(岁)
答:奶奶今年62岁。
3. 弟弟8岁时,哥哥12岁,那么弟弟12岁时,哥哥多少岁?
12-8=4(岁)12+4=16(岁)
答:哥哥16岁。
4. 卡尔比爸爸小30岁,比妈妈小26岁,请问妈妈比爸爸小多少岁?
三、教学难点:
随着时间的变化,每个人年龄的增加或减少是同样多。
四、教学准备:
PPT
五、教学过程:
第一课时(50分钟)
一、导入(5分)
师:同学们,大家好。今天上课前先给同学们讲一个笑话,这个笑话与今天的
学习内容可有联系,大家可要认真听啊。从前,有甲、乙两个地主,他们
是好朋友。甲地主头一年春天生了一个儿子,第二年春天,乙地主生了一
的年龄,喜羊羊说:“我今年17岁了,你呢?”灰太狼得意洋洋地说:“哈
哈!我比你大2岁呢!”喜洋洋很不服气地说:“有什么好得意,再过2
年我和你就同岁了。”同学们,你们说喜羊羊这样说正确吗?
生:不正确。
师:为什么呢?
生:……
师:真棒!看来同学们对上一节课的内容掌握得不错。那么接下来我们就来更
深入地学习年龄问题。
80岁了吗?如果你儿子活不到80岁,我女儿岂不要守寡吗?”甲地主听了,
笑着说:“你算错了,今年我儿子1岁,等到明年,你女儿也有1岁了,
不就和我儿子一样大了吗?”同学们,你们说,这两个地主哪一个说得对?
生:都错了。
师:对了,这两个地主为什么都错了?
生:(让学生讨论)
师:好,那就让我们带着问题来学习简单的年龄问题。
小学奥数平均数问题

第六讲平均数问题【1】【名师导航】把几个数,在总数不变的条件下,通过移多补少,使它们完全相等,求得的数就是平均数。
下面介绍求平均数的两种基本方法:1、直接求法:利用公式“总数量÷总份数=平均数”求出平均数,这是由“均分”思想产生的方法。
2、基数求法:利用公式“基数+各数与基数的差的总和÷总份数=平均数”求出平均数,这是由“补差”思想产生的方法。
【例题精讲】例1 工路队前4天平均每天筑路80米,增加工人后,第5天筑路100米,求工程队这5天平均每天筑路多少米?分析:(1)先求出5天筑路的总长度80×4+100=420(米),再求出工程队这5天平均每天筑路的平均数。
(2)从“补差”的角度考虑。
由于前4天筑路的平均数小于第5天的筑路米数,所以把前4天的平均数80米看做是基数,然后把第5天多筑的(100-80)米平均分成“5份”,用4份补进到前4天的平均数中去,留1份在第5天,从而求出这5天平均每天筑路的平均数。
解法一(米)解法二(米)答:工程队这5天平均每天筑路84米。
例2 笑笑上学期期末考试成绩:语文80分,音乐88分,体育84分,美术78分,数学成绩比五科平均成绩高6分,笑笑数学得了多少分?分析:本题关键是求出五科平均分,依题意,我们可以先求出语文、音乐、体育、美术这四科的平均分是(分),根据条件“数学成绩比五科平均成绩高6分”知,前四科的平均分低于五科平均分,要把前四科的平均分提高到五科的平均分,从“补差”的角度思考,需要把数学成绩比五科平均成绩高的6分补到前四科的每科平均分中去,平均每科补(分),所以,五科平均分是(分),那么数学成绩就是(分)。
解:(1)语文、音乐、体育、美术四科平均分:(2)五科平均分:(3)数学成绩:答:笑笑数学得了90分。
做一做1 淘气在期末考试中语文、外语和自然的平均分是81分,数学成绩公布后,四门成绩的平均分提高了2分。
淘气数学考多少分?例3 学校组织同学去旅行,同样价格的小点心小青买了8包,小红买了7包,小兰没有买。
奥数第六讲 行程问题

奥数第六讲行程问题行程问题是小学奥数中变化最多的一个专题,不论在奥数竞赛中还是在“小升初”的升学考试中,都拥有非常重要的地位。
行程问题中包括:火车过桥、流水行船、沿途数车、猎狗追兔、环形行程、多人行程,等等。
每一类问题都有自己的特点,解决方法也有所不同,但是,行程问题无论怎么变化,都离不开“三个量,三个关系”:这三个量是:路程(s)、速度(v)、时间(t)三个关系:1. 简单行程:路程 = 速度× 时间2. 相遇问题:路程和 = 速度和× 时间3. 追击问题:路程差 = 速度差× 时间牢牢把握住这三个量以及它们之间的三种关系,就会发现解决行程问题还是有很多方法可循的。
①追击及相遇问题一、例题与方法指导例1. 有甲、乙、丙三人同时同地出发,绕一个花圃行走,乙、丙二人同方向行走,甲与乙、丙相背而行。
甲每分钟走40米,乙每分钟走38米,丙每分钟走36米。
在途中,甲和乙相遇后3分钟和丙相遇。
问:这个花圃的周长是多少米?思路导航:这个三人行程的问题由两个相遇、一个追击组成,题目中所给的条件只有三个人的速度,以及一个“3分钟”的时间。
第一个相遇:在3分钟的时间里,甲、丙的路程和为(40+36)×3=228(米)第一个追击:这228米是由于在开始到甲、乙相遇的时间里,乙、丙两人的速度差造成的,是逆向的追击过程,可求出甲、乙相遇的时间为228÷ (38-36)=114(分钟)第二个相遇:在114分钟里,甲、乙二人一起走完了全程所以花圃周长为(40+38)×114=8892(米)我们把这样一个抽象的三人行程问题分解为三个简单的问题,使解题思路更加清晰。
例2. 东西两地间有一条公路长217.5千米,甲车以每小时25千米的速度从东到西地,1.5小时后,乙车从西地出发,再经过3小时两车还相距15千米。
乙车每小时行多少千米?思路导航:从图中可以看出,要求乙车每小时行多少千米,关键要知道乙车已经行了多少路程和行这段路程所用的时间。
(完整版)奥数一年级教案第六讲间隔之谜
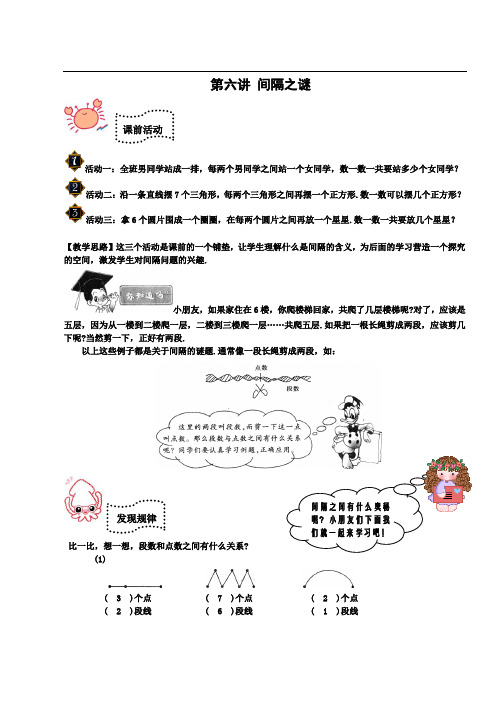
第六讲间隔之谜课前活动活动一:全班男同学站成一排,每两个男同学之间站一个女同学,数一数一共要站多少个女同学?活动二:沿一条直线摆7个三角形,每两个三角形之间再摆一个正方形.数一数可以摆几个正方形?活动三:拿6个圆片围成一个圈圈,在每两个圆片之间再放一个星星.数一数一共要放几个星星?【教学思路】这三个活动是课前的一个铺垫,让学生理解什么是间隔的含义,为后面的学习营造一个探究的空间,激发学生对间隔问题的兴趣.小朋友,如果家住在6楼,你爬楼梯回家,共爬了几层楼梯呢?对了,应该是五层,因为从一楼到二楼爬一层,二楼到三楼爬一层……共爬五层.如果把一根长绳剪成两段,应该剪几下呢?当然剪一下,正好有两段.以上这些例子都是关于间隔的谜题.通常像一段长绳剪成两段,如:发现规律比一比,想一想,段数和点数之间有什么关系?(1)( 3 )个点 ( 7 )个点 ( 2 )个点( 2 )段线 ( 6 )段线 ( 1 )段线间隔之间有什么奥秘呢?小朋友们下面我们就一起来学习吧!你的发现段数与点数(2)( 2 )个点 ( 4 )个点 ( 4 )个点( 3 )段线 ( 5 )段线 ( 5 )段线你的发现段数与点数(3)( 3 )个点 ( 4 )个点 ( 8 )个点( 3 )段线 ( 4 )段线 ( 8 )段线你的发现段数与点数【教学思路】在开课时通过三组不同的情况让学生来发现规律,但是这种规律对于学生来说是很抽象不能理解的.所以我们不要着急把知识点强加给学生,我们只要让学生初步了解到这种规律就可以了,在后面的练习和以后的学习中我们会有更多的应用.实际应用操场边种了10棵杨数,如果在每两棵杨树之间再摆放一盆花,一共要摆放几盆花?【教学思路】植树问题对于一年级孩子来说是很抽象的内容,因此我们可以采取一些更直观的方法来引导孩子理解.比如画图,摆卡片等.操场边种了10棵杨数,10棵杨数之间就有9个间隔,一共有几个间隔就可以摆几盆花,每个间隔放一盆,10棵杨树之间一共能摆放9盆花.列式:10-1=9(盆)拓展练习操场边摆了10盆花,在这10盆花的两侧各栽一棵杨树,一共要栽几棵杨树?【答案】在10盆花两侧各栽一棵杨树,那么我们要栽的树的棵数要比间隔数多1,10盆花就是10个间隔,所以一共要栽11棵数.列式:10+1=11(棵)15名女同学(用“○”表示)围成三角形做游戏(如图),每两名女同学之间夹一名男同学(用“·”表示),共有多少名男同学?【教学思路】这15个女同学围成三角形做游戏,三角形是一个封闭的图形,那么有15个女同学,她们之间就有15个间隔,在每个间隔之间夹一个男同学,15个间隔就可以站15个男同学.通过这道题进一步巩固说明在封闭的线路中点数和间隔数是一样多的.把一根木头锯成3段,要锯几次?如果每锯一次用3分钟,一共要锯多少分钟?列式:3-1=2(次)3+3=6(分)答:要锯2次,一共需6分钟.拓展练习1.把一根木头锯成4段,要锯几次? 锯成6段呢?【答案】通过例题我们发现锯木头的时候,锯的次数总是比段数少1.因此把一根木头锯成4段,要锯3次;锯成6段,就要锯5次.2.小亮家住在三楼,他每上一层楼要走14级台阶,小亮从一楼走到三楼要走多少级台阶?【答案】从第一层到第二层有14级台阶,从第二层到第三层又有14个台阶.也就是说从第一层到第二层要上两次台阶,所以一共要走14+14=28(个).在一条50米长的河岸边插彩旗,每10米插一面(两头都要插),一共需要插多少面彩旗?【教学思路】要在50米的河岸边插彩旗,每10米插1面, 50米可以分成5个10米,那么在插的这些彩旗中间一共就有5个间隔.我们先在最头上插一面,然后每10米插一面,这样我们插的彩旗就要比间隔多1,因此一共要插6面彩旗.同学们在一段马路的一边种树,从马路的一头到另一头共种了9棵,每两棵之间相距3米.问这段马路长多少米?列式:3+3+3+3+3+3+3+3=24(米)答:这段马路长24米.拓展练习1.同学们在校门口走道的一旁插彩旗,从头至尾共插了10面,两面彩旗之间相距2米,问这条走道长多少米?【答案】在校门口走道的一旁一共插了10面彩旗,在这些彩旗之间一共就有9个间隔.每个间隔之间是2米,那么这条走道就有9个2米这么长.列式:2+2+2+2+2+2+2+2+2=18(米)或2×9=18(米)【注】一年级的孩子还没有理解乘法的意义,所以在这里不强求学生用乘法计算,可以介绍一下有这种方法,以后我们还会继续学习.在解题的过程中,主要是培养孩子通过画图来分析理解问题的能力.学校在圆形的花坛边放了10盆鲜花,每两盆之间相隔1米,这个花坛一圈长多少米?列式:1+1+1+1+1+1+1+1+1+1=10(米)或1×10=10(米)答:这个花坛一圈长10米.拓展练习小红家的时钟敲2下要2秒钟.敲8下要几秒钟?【答案】时钟敲打2下,中间只有一个间隔,1个间隔就是2秒钟;时钟敲8下,就是7个间隔,这样敲8下需要的时间即可求得.列式:2+2+2+2+2+2+2=14(秒钟)练习六1.把一根木头锯成5段,每锯一次要2分钟,一共要锯多少分钟?【答案】把一根木头锯成5段要锯4次,一次要2分钟,4次就要8分钟.列式:2+2+2+2=8(分钟)2. 把一长方形铁丝(如图)共剪14下,剪断后有多少根小铁丝?【答案】正方形是一个封闭的图形,剪了14下,就有14根小铁丝.3. 公园的路边放了一些椅子,从起点到终点共计21把,每两把椅子之间有一头石狮子,问这条路边共有多少头石狮子?【答案】石狮子的个数应该比椅子的个数少1个,所以应该是20头狮子.4.在100米长的操场边,每10米修一个石凳,一共需要修多少个石凳?【答案】列式:10+1=11(个)一共需要修11个石凳.5.在正方形的花圃周围共摆放了8盆鲜花,每两盆鲜花之间相隔1米,这个正方形花坛一周长多少米?【答案】这个正方形花坛一周长8米6.在一根绳子上晒被子,每两床被子之间要3个夹子,要晒10床被子,需要多少个夹子?解答间隔问题时,应注意分清3种类型:1.首尾相连接的封闭的图形,段数与点数同样多.2.两头无点的直线图形(如剪绳),点数(剪数)比段数少1,或者是段数比点数多1.3.两头有点的直线图形(如植树),点数(棵数)比段数(间隔)多1,或者是段数比点数少1.解题时,一定要分清间隔类型,才能正确解答.【答案】需要的夹子应该比被子多1,因此需要11个夹子.7.有一个长方形池塘,在池塘四周种了20棵柳树,每两棵柳树之间又种了一棵桃树,桃树有多少棵?一共种树多少棵?【答案】池塘是长方形的,那么20棵柳树之间就有20个间隔,在每个间隔里种一棵桃树,桃树就有20棵,柳树和桃树一共有40棵.列式:20+20=40(棵)①小松鼠和小白兔上学迟到了.熊猫老师问:“你俩今天为什么迟到了?”②小松鼠说:“我在上学的路上遇到三个小弟弟,他们饿(e)得很,我就采了6个松果.分成数量不同的3份,送给他们每人一份.”③小白兔说:“我在上学的路上遇到四个小妹妹.她们饿得很,我就采了9个蘑菇.分成数量不同的4份,送给她们每人一份.”④熊猫老师说:“松鼠说的是实话.小白兔说的是谎话.”⑤小白兔听后,惭愧地低下头,说:“老师,我错了,今后我一定做个诚实的孩子.”小朋友,熊猫老师怎么知道小白兔说的是谎话?。
【奥数】一年级上册趣味数学教案-6.神奇的小棒 苏教版

【奥数】一年级上册趣味数学教案-6.神奇的小棒苏教版一、教学目标1. 让学生通过操作小棒,感知数学的趣味性,培养学生对数学的兴趣。
2. 使学生掌握小棒的基本使用方法,培养学生的动手操作能力。
3. 培养学生观察、分析、归纳和解决问题的能力。
二、教学内容1. 小棒的基本使用方法。
2. 利用小棒进行简单的数学运算。
3. 利用小棒解决实际问题。
三、教学重点与难点1. 教学重点:小棒的基本使用方法,利用小棒进行简单的数学运算。
2. 教学难点:利用小棒解决实际问题,培养学生的观察能力、分析能力和解决问题的能力。
四、教具与学具准备1. 教具:PPT课件,小棒,计算器。
2. 学具:小棒,计算器。
五、教学过程1. 导入:通过PPT展示一些有趣的数学问题,引发学生的兴趣,引导学生思考如何解决这些问题。
2. 新课导入:介绍小棒的基本使用方法,让学生动手操作,感知小棒的神奇之处。
3. 实践操作:让学生利用小棒进行简单的数学运算,如加法、减法、乘法等。
4. 小组讨论:分组让学生讨论如何利用小棒解决实际问题,培养学生的合作能力和团队精神。
5. 课堂小结:总结本节课的主要内容,强调小棒在数学学习中的作用。
六、板书设计1. 神奇的小棒2. 课题:一年级上册趣味数学教案-63. 主要内容:小棒的基本使用方法,利用小棒进行简单的数学运算,利用小棒解决实际问题。
七、作业设计1. 让学生利用小棒完成课后练习题。
2. 让学生回家后与家长一起用小棒进行数学游戏,增进亲子关系。
八、课后反思1. 教师要关注学生在课堂上的动手操作情况,及时给予指导和鼓励。
2. 教师要关注学生在小组讨论中的表现,培养学生的合作能力和团队精神。
3. 教师要关注学生在课后作业的完成情况,及时了解学生的学习效果。
总结:本节课通过让学生操作小棒,感知数学的趣味性,培养学生对数学的兴趣。
同时,通过小组讨论和课后作业,培养学生的合作能力和团队精神。
在教学过程中,教师要关注学生的动手操作情况,及时给予指导和鼓励,以提高学生的学习效果。
小升初奥数专题-第六讲图形面积

第六讲图形面积简单的面积计算是小学数学的一项重要内容.要会计算面积,首先要能识别一些特别的图形:正方形、三角形、平行四边形、梯形等等,然后会计算这些图形的面积.如果我们把这些图形画在方格纸上,不但容易识别,而且容易计算.上面左图是边长为 4的正方形,它的面积是 4×4= 16(格);右图是 3×5的长方形,它的面积是 3×5= 15(格).上面左图是一个锐角三角形,它的底是5,高是4,面积是 5×4÷2= 10(格);右图是一个钝角三角形,底是4,高也是4,它的面积是4×4÷2=8(格).这里特别说明,这两个三角形的高线一样长,钝角三角形的高线有可能在三角形的外面.上面左图是一个平行四边形,底是5,高是3,它的面积是 5× 3= 15(格);右图是一个梯形,上底是 4,下底是7,高是4,它的面积是(4+7)×4÷2=22(格).上面面积计算的单位用“格”,一格就是一个小正方形.如果小正方形边长是1厘米,1格就是1平方厘米;如果小正方形边长是1米,1格就是1平方米.也就是说我们设定一个方格的边长是1个长度单位,1格就是一个面积单位.在这一讲中,我们直接用数表示长度或面积,省略了相应的长度单位和面积单位.6.1 三角形的面积用直线组成的图形,都可以划分成若干个三角形来计算面积.三角形面积的计算公式是:三角形面积= 底×高÷2.这个公式是许多面积计算的基础.因此我们不仅要掌握这一公式,而且要会灵活运用.例1 右图中BD长是4,DC长是2,那么三角形ABD的面积是三角形ADC面积的多少倍呢?解:三角形ABD与三角形ADC的高相同.三角形ABD面积=4×高÷2.三角形 ADC面积=2×高÷2.因此三角形ABD的面积是三角形ADC面积的2倍.注意:三角形的任意一边都可以看作是底,这条边上的高就是三角形的高,所以每个三角形都可看成有三个底,和相应的三条高.例2 右图中,BD,DE,EC的长分别是2,4,2.F是线段AE的中点,三角形ABC的高为4.求三角形DFE的面积.解: BC= 2+ 4+ 2= 8.三角形 ABC面积= 8× 4÷2=16.我们把A和D连成线段,组成三角形ADE,它与三角形ABC的高相同,而DE长是4,也是BC的一半,因此三角形ADE面积是三角形ABC面积的一半.同样道理,EF是AE的一半,三角形DFE面积是三角形ADE面积的一半.三角形 DFE面积= 16÷4=4.例3 右图中长方形的长是20,宽是12,求它的内部阴影部分面积.解:ABEF也是一个长方形,它内部的三个三角形阴影部分高都与BE一样长.而三个三角形底边的长加起来,就是FE的长.因此这三个三角形的面积之和是FE×BE÷2,它恰好是长方形ABEF面积的一半.同样道理,FECD也是长方形,它内部三个三角形(阴影部分)面积之和是它的面积的一半.因此所有阴影的面积是长方形ABCD面积的一半,也就是20×12÷2=120.通过方格纸,我们还可以从另一个途径来求解.当我们画出中间两个三角形的高线,把每个三角形分成两个直角三角形后,图中每个直角三角形都是某个长方形的一半,而长方形ABCD是由这若干个长方形拼成.因此所有这些直角三角形(阴影部分)的面积之和是长方形ABCD面积的的一半.例4 右图中,有四条线段的长度已经知道,还有两个角是直角,那么四边形ABCD(阴影部分)的面积是多少?解:把A和C连成线段,四边形ABCD就分成了两个,三角形ABC和三角形ADC.对三角形ABC来说,AB是底边,高是10,因此面积=4×10÷2= 20.对三角形 ADC来说, DC是底边,高是 8,因此面积=7×8÷2=28.四边形 ABCD面积= 20+ 28= 48.这一例题再一次告诉我们,钝角三角形的高线有可能是在三角形的外面.例5 在边长为6的正方形内有一个三角形BEF,线段AE=3,DF=2,求三角形BEF的面积.解:要直接求出三角形BEF的面积是困难的,但容易求出下面列的三个直角三角形的面积三角形 ABE面积=3×6×2= 9.三角形 BCF面积= 6×(6-2)÷2= 12.三角形 DEF面积=2×(6-3)÷2= 3.我们只要用正方形面积减去这三个直角三角形的面积就能算出:三角形 BEF面积=6×6-9-12-3=12.例6 在右图中,ABCD是长方形,三条线段的长度如图所示,M是线段DE的中点,求四边形ABMD(阴影部分)的面积.解:四边形ABMD中,已知的太少,直接求它面积是不可能的,我们设法求出三角形DCE 与三角形MBE的面积,然后用长方形ABCD的面积减去它们,由此就可以求得四边形ABMD 的面积.把M与C用线段连起来,将三角形DCE分成两个三角形.三角形 DCE的面积是 7×2÷2=7.因为M是线段DE的中点,三角形DMC与三角形MCE面积相等,所以三角形MCE面积是 7÷2=3.5.因为 BE= 8是 CE= 2的 4倍,三角形 MBE与三角形MCE高一样,因此三角形MBE 面积是3.5×4=14.长方形 ABCD面积=7×(8+2)=70.四边形 ABMD面积=70-7- 14= 49.6.2 有关正方形的问题先从等腰直角三角形讲起.一个直角三角形,它的两条直角边一样长,这样的直角三角形,就叫做等腰直角三角形.它有一个直角(90度),还有两个角都是45度,通常在一副三角尺中.有一个就是等腰直角三角形.两个一样的等腰直角三角形,可以拼成一个正方形,如图(a).四个一样的等腰直角三角形,也可以拼成一个正方形,如图(b).一个等腰直角三角形,当知道它的直角边长,从图(a)知,它的面积是直角边长的平方÷2.当知道它的斜边长,从图(b)知,它的面积是斜边的平方÷4例7 右图由六个等腰直角三角形组成.第一个三角形两条直角边长是8.后一个三角形的直角边长,恰好是前一个斜边长的一半,求这个图形的面积.解:从前面的图形上可以知道,前一个等腰直角三角形的两个拼成的正方形,等于后一个等腰直角三角形四个拼成的正方形.因此后一个三角形面积是前一个三角形面积的一半,第一个等腰直角三角形的面积是8×8÷2=32.这一个图形的面积是32+16+ 8+ 4 + 2+1= 63.例8 如右图,两个长方形叠放在一起,小长形的宽是2,A点是大长方形一边的中点,并且三角形ABC是等腰直角三角形,那么图中阴影部分的总面积是多少?解:为了说明的方便,在图上标上英文字母 D,E,F,G.三角形ABC的面积=2×2÷2=2.三角形ABC,ADE,EFG都是等腰直角三角形.三角形ABC的斜边,与三角形ADE的直角边一样长,因此三角形 ADE面积=ABC面积×2=4.三角形EFG的斜边与三角形ABC的直角边一样长.因此三角形EFG面积=ABC面积÷2=1.阴影部分的总面积是 4+1=5.例9 如右图,已知一个四边形ABCD的两条边的长度AD=7,BC=3,三个角的度数:角B和D是直角,角A是45°.求这个四边形的面积.解:这个图形可以看作是一个等腰直角三角形ADE,切掉一个等腰直角三角形BCE.因为A是45°,角D是90°,角E是180°-45°-90°= 45°,所以ADE是等腰直角三角形,BCE也是等腰直角三角形.四边形ABCD的面积,是这两个等腰直角三角形面积之差,即7×7÷2-3×3÷2=20.这是1994小学数学奥林匹克决赛试题.原来试题图上并没有画出虚线三角形.参赛同学是不大容易想到把图形补全成为等腰直角三角形.因此做对这道题的人数不多.但是有一些同学,用直线AC把图形分成两个直角三角形,并认为这两个直角三角形是一样的,这就大错特错了.这样做,角 A是 45°,这一条件还用得上吗?图形上线段相等,两个三角形相等,是不能靠眼睛来测定的,必须从几何学上找出根据,小学同学尚未学过几何,千万不要随便对图形下结论.我们应该从题目中已有的条件作为思考的线索.有45°和直角,你应首先考虑等腰直角三角形.现在我们转向正方形的问题.例10 在右图 11×15的长方形内,有四对正方形(标号相同的两个正方形为一对),每一对是相同的正方形,那么中间这个小正方形(阴影部分)面积是多少?解:长方形的宽,是“一”与“二”两个正方形的边长之和,长方形的长,是“一”、“三”与“二”三个正方形的边长之和.长-宽 =15-11=4是“三”正方形的边长.宽又是两个“三”正方形与中间小正方形的边长之和,因此中间小正方形边长=11-4×2=3.中间小正方形面积=3×3= 9.如果把这一图形,画在方格纸上,就一目了然了.例11 从一块正方形土地中,划出一块宽为1米的长方形土地(见图),剩下的长方形土地面积是15.75平方米.求划出的长方形土地的面积.解:剩下的长方形土地,我们已知道长-宽=1(米).还知道它的面积是15.75平方米,那么能否从这一面积求出长与宽之和呢?如果能求出,那么与上面“差”的算式就形成和差问题了.我们把长和宽拼在一起,如右图.从这个图形还不能算出长与宽之和,但是再拼上同样的两个正方形,如下图就拼成一个大正方形,这个正方形的边长,恰好是长方形的长与宽之和.可是这个大正方形的中间还有一个空洞.它也是一个正方形,仔细观察一下,就会发现,它的边长,恰好是长方形的长与宽之差,等于1米.现在,我们就可以算出大正方形面积:15.75×4+1×1= 64(平方米).64是8×8,大正方形边长是 8米,也就是说长方形的长+宽=8(米).因此长=(8+1)÷2= 4.5(米).宽=8-4.5=3.5(米).那么划出的长方形面积是4.5×1=4. 5(平方米).例12 如右图.正方形ABCD与正方形EFGC并放在一起.已知小正方形EFGC的边长是6,求三角形AEG(阴影部分)的面积.解:四边形AECD是一个梯形.它的下底是AD,上底是EC,高是CD,因此四边形AECD面积=(小正方形边长+大正方形边长)×大正方形边长÷2三角形ADG是直角三角形,它的一条直角边长DG=(小正方形边长+大正方形边长),因此三角形ADG面积=(小正方形边长+大正方形边长)×大正方形边长÷2.四边形 AECD与三角形 ADG面积一样大.四边形AHCD是它们两者共有,因此,三角形AEH与三角形HCG面积相等,都加上三角形EHG面积后,就有阴影部分面积=三角形ECG面积=小正方形面积的一半= 6×6÷2=18.十分有趣的是,影阴部分面积,只与小正方形边长有关,而与大正方形边长却没有关系.6.3 其他的面积这一节将着重介绍求面积的常用思路和技巧.有些例题看起来不难,但可以给你启发的内容不少,请读者仔细体会.例13 画在方格纸上的一个用粗线围成的图形(如右图),求它的面积.解:直接计算粗线围成的面积是困难的,我们通过扣除周围正方形和直角三角形来计算.周围小正方形有3个,面积为1的三角形有5个,面积为1.5的三角形有1个,因此围成面积是4×4-3-5-1.5=6.5.例6与本题在解题思路上是完全类同的.例14 下图中 ABCD是 6×8的长方形,AF长是4,求阴影部分三角形AEF的面积.解:三角形AEF中,我们知道一边AF,但是不知道它的高多长,直接求它的面积是困难的.如果把它扩大到三角形AEB,底边AB,就是长方形的长,高是长方形的宽,即BC的长,面积就可以求出.三角形AEB的面积是长方形面积的一半,而扩大的三角形AFB是直角三角形,它的两条直角边的长是知道的,很容易算出它的面积.因此三角形AEF面积=(三角形 AEB面积)-(三角形 AFB面积)=8×6÷2-4×8÷2= 8.这一例题告诉我们,有时我们把难求的图形扩大成易求的图形,当然扩大的部分也要容易求出,从而间接地解决了问题.前面例9的解法,也是这种思路.例15 下左图是一块长方形草地,长方形的长是16,宽是10.中间有两条道路,一条是长方形,一条是平行四边形,那么有草部分的面积(阴影部分)有多大?解:我们首先要弄清楚,平行四边形面积有多大.平行四边形的面积是底×高.从图上可以看出,底是2,高恰好是长方形的宽度.因此这个平行四边形的面积与 10×2的长方形面积相等.可以设想,把这个平行四边形换成 10×2的长方形,再把横竖两条都移至边上(如前页右图),草地部分面积(阴影部分)还是与原来一样大小,因此草地面积=(16-2)×(10-2)= 112.例16 右图是两个相同的直角三角形叠在一起,求阴影部分的面积.解:实际上,阴影部分是一个梯形,可是它的上底、下底和高都不知道,不能直接来求它的面积.阴影部分与三角形BCE合在一起,就是原直角三角形.你是否看出, ABCD也是梯形,它和三角形BCE合在一起,也是原直角三角形.因此,梯形ABCD的面积与阴影部分面积一样大.梯形ABCD的上底BC,是直角边AD的长减去3,高就是DC的长.因此阴影部分面积等于梯形 ABCD面积=(8+8-3)×5÷2= 32.5.上面两个例子都启发我们,如何把不容易算的面积,换成容易算的面积,数学上这叫等积变形.要想有这种“换”的本领,首先要提高对图形的观察能力.例17 下图是两个直角三角形叠放在一起形成的图形.已知 AF,FE,EC都等于3, CB,BD都等于 4.求这个图形的面积.解:两个直角三角形的面积是很容易求出的.三角形ABC面积=(3+3+3)×4÷2=18.三角形CDE面积=(4+4)× 3÷2=12.这两个直角三角形有一个重叠部分--四边形BCEG,只要减去这个重叠部分,所求图形的面积立即可以得出.因为 AF= FE= EC=3,所以 AGF, FGE, EGC是三个面积相等的三角形.因为CB=BD=4,所以CGB,BGD是两个面积相等的三角形.2×三角形DEC面积= 2×2×(三角形 GBC面积)+2×(三角形 GCE面积).三角形ABC面积= (三角形 GBC面积)+3×(三角形GCE面积).四边形BCEG面积=(三角形GBC面积)+(三角形GCE面积)=(2×12+18)÷5=8.4.所求图形面积=12+ 18- 8.4=21.6.例18 如下页左图,ABCG是4×7长方形,DEFG是 2×10长方形.求三角形 BCM与三角形 DEM面积之差.解:三角形BCM与非阴影部分合起来是梯形ABEF.三角形DEM与非阴影部分合起来是两个长方形的和.(三角形BCM面积)-(三角形DEM面积)=(梯形ABEF 面积)-(两个长方形面积之和 =(7+10)×(4+2)÷2-(4×7 + 2×10) =3.例19 上右图中,在长方形内画了一些直线,已知边上有三块面积分别是13,35,49.那么图中阴影部分的面积是多少?解:所求的影阴部分,恰好是三角形ABC 与三角形CDE 的公共部分,而面积为13,49,35这三块是长方形中没有被三角形ABC 与三角形CDE 盖住的部分,因此 (三角形 ABC 面积)+(三角形CDE 面积)+(13+49+35) =(长方形面积)+(阴影部分面积).三角形ABC ,底是长方形的长,高是长方形的宽;三角形CDE ,底是长方形的宽,高是长方形的长.因此,三角形ABC 面积,与三角形CDE 面积,都是长方形面积的一半,就有 阴影部分面积=13 + 49+ 35= 97.6.4 几种常见模型一、等积模型①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如右图12::S S a b③夹在一组平行线之间的等积变形,如右图ACDBCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD . ④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形);⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.二、鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上), 则:():()ABC ADE S S AB AC AD AE =⨯⨯△△图⑴ 图⑵三、蝶形定理任意四边形中的比例关系(“蝶形定理”):①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++EDCBAEDCBADC BA S 4S 3S 2S 1O DCB A蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系. 梯形中比例关系(“梯形蝶形定理”): ①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +. 四、相似模型(一)金字塔模型 (二) 沙漏模型①AD AE DE AFAB AC BC AG===; ②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具.GF E ABCD AB CDEF G A BCDO ba S 3S 2S 1S 4在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.五、共边定理(燕尾模型和风筝模型)在三角形ABC 中,AD ,BE ,CF 相交于同一点O ,那么::ABO ACO S S BD DC ∆∆=. 上述定理给出了一个新的转化面积比与线段比的手段,因为ABO ∆和ACO ∆的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径.OFEDCBA。
小学奥数第六讲(沐风学堂)

第六讲:组合计数问题(一)1.(☆☆)15个位同学排成一圈。
从中取出3人,恰有两个相邻,有多少种取法? 2.(☆☆)用1个1,2个2,3个3能组成多少个不同的6位数? 3.(☆☆☆)有8个同学,把他们分成4组,每组恰好2位同学。
共有多少种分法? 4.(☆☆☆)1~3998中有多少个自然数的数字和能被4整除? 5.(☆☆☆)1~2004中含有数字1的自然数有多少个? 6.(☆☆☆)各位数字和等于50且能被4整除的6位数共有多少个? 7.(☆☆☆)在自然数1、2、3、…、1000中有多少个自然数n ,使得2n -n 2是7的倍数? 8. (☆☆☆)有编号为1、2、…、8的8个箱子如右图放置成3列,搬运工每次只能搬走某列中最上面的箱子;问搬走这8个箱子共有多少种不同的顺序?9. (☆☆☆☆)经理将要打印的信件交给秘书,每次给一封,且放在信封的最上面,秘书一有空就从最上面拿一封信来打。
有一天共有9封信要打完,经理按1号信,2号信,…,9号信的顺序交给秘书。
午饭时,秘书告诉同事,经理已经给了8封信,她已把8号信打印好了,但未透漏上午工作的其他情况。
根据以上信息,下午打印的信的顺序有多少种可能?10. (☆☆☆☆☆)包含0,1,2,……,9十个数字的十位数称为“十全数”,能被11整除的十全数共有多少个? 1. (☆☆)如图所示,从A 点出发到B 点,只能向右走、向上走、或向右上走;不同的走法共有多少种?2. (☆☆☆)(1)如图所示,图中每个小方格都是一样的小正方形,从A 点沿格线到B 点的最短路线共有多少条?(2)如果图中有两条街道禁止通行呢?3. (☆☆)有一段楼梯有8级台阶,规定每一步只能跨一级或两级台阶;问要从楼梯最下面登上第8级台阶有多少种不同走法?4. (☆☆☆)将2×10的卡片纸剪成10张2×1的小卡片,共有多少种不同的剪法?5. (☆☆☆)在如图6×5的网格图的点A 处有一只电子青蛙,它每一步可从一个格点跳到相邻的格点(上下左右斜);由于画上阴影的小正方形内出现了磁场干扰,电子青蛙不能跳往阴影小正方形的四个顶点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六讲火柴棒的游戏
一.检查家庭作业
针对学生所做情况,重点问题重点讲解,提高学生综合运用知识的能力,查缺补漏,等级评定。
二.梳理知识
火柴棒可以摆出许多图形,如三角形、四边形等,也可以摆成一些生活中的物品,通过移动火柴棒,它们之间会出现一些有趣的转化。
下面,我们用火柴棒来做一些有趣的游戏。
例 1 用火柴棒摆出一个三角形、一个正方形、一个长方形、一个五边形、一个六边形。
解
例 2 用三根火柴棒可以摆出一个三角
形,如图 .
(1)再加两根火柴棒,摆出两个三角形;
(2)再加两根,摆出三个三角形来;
(3)再加两根,摆出五个三角形来 .
解(1)(2) (3)
例 3 把两根火柴棒添在那里,可以摆出 5 个
正方形?
例 4 请给下面的每个数字只添上 1 根火柴棒,使它们变成一个新的数字。
例 5 请你在下面的算式中添上一根火柴,使其等式成立。
例 6 拿走 1 根火柴棒,使等式成立。
例 7你能只移动下面算式中的一根火柴棒,使其等式成立吗?
三. 达标测试
1、看图填数。
()个三角形, ()根火柴
2、请你添加上三根火柴,使下面的正方形变成 3 个。
你知道共用的火柴是哪几根吗?
3、如图, 9 根火柴棒已摆成了 5 个三角形。
(1)拿掉哪三根,可以变成一个三角形?
(2)拿掉哪两根,就可以变成两个三角形?
(3)拿掉哪一根,就可以变成 3 个三角形?
4、移动下面每个数字中的一根火柴棒,使它们变成一个新的数字。
5、请你在下面的算式中添上一根火柴,使其等式成立。
6、在下面的算式中拿掉一根火柴后,使等式成立。
四.家庭作业
1、下图是用 12 根火柴摆成的“田”字,能不能拿走 2 根火柴棒,使它变成两个正方形?
2、你能拿走 2 根火柴棒,使下面的等式成立吗?。
