材料力学习题册答案第3章扭转.doc
材料力学扭转答案

3-1 一传动轴作匀速转动,转速,轴上装有五个轮子,主动轮Ⅱ输入的功率为60kW,从动轮,Ⅰ,Ⅲ,Ⅳ,Ⅴ依次输出18kW,12kW,22kW和8kW。
试作轴的扭矩图。
解:kNkNkNkN返回3-2(3-3) 圆轴的直径,转速为。
假设该轴横截面上的最大切应力等于,试问所传递的功率为多大?解:故即又故返回3-3(3-5) 实心圆轴的直径mm,长m,其两端所受外力偶矩,材料的切变模量。
试求:〔1〕最大切应力及两端截面间的相对扭转角;〔2〕图示截面上A,B,C三点处切应力的数值及方向;〔3〕C点处的切应变。
解:=返回3-4(3-6) 图示一等直圆杆,,,,。
试求:〔1〕最大切应力;〔2〕截面A相对于截面C的扭转角。
解:〔1〕由得扭矩图〔a〕〔2〕返回3-5(3-12) 长度相等的两根受扭圆轴,一为空心圆轴,一为实心圆轴,两者材料一样,受力情况也一样。
实心轴直径为d;空心轴外径为D,径为,且。
试求当空心轴与实心轴的最大切应力均到达材料的许用切应力〕,扭矩T相等时的重量比和刚度比。
解:重量比=因为即故故刚度比==返回3-6(3-15) 图示等直圆杆,外力偶矩,,许用切应力,许可单位长度扭转角,切变模量。
试确定该轴的直径d。
解:扭矩图如图〔a〕〔1〕考虑强度,最大扭矩在BC段,且〔1〕(2〕考虑变形〔2〕比拟式〔1〕、〔2〕,取返回3-7(3-16) 阶梯形圆杆,AE段为空心,外径D=140mm,径d=100mm;BC段为实心,直径d=100mm。
外力偶矩,,。
:,,。
试校核该轴的强度和刚度。
解:扭矩图如图〔a〕〔1〕强度=,BC段强度根本满足=故强度满足。
〔2〕刚度BC段:BC段刚度根本满足。
AE段:AE段刚度满足,显然EB段刚度也满足。
返回3-8(3-17) 习题3-1中所示的轴,材料为钢,其许用切应力,切变模量,许可单位长度扭转角。
试按强度及刚度条件选择圆轴的直径。
解:由3-1题得:应选用。
返回3-9(3-18) 一直径为d的实心圆杆如图,在承受扭转力偶矩后,测得圆杆外表与纵向线成方向上的线应变为。
材料力学习题解答[第三章]
![材料力学习题解答[第三章]](https://img.taocdn.com/s3/m/ffe185e2551810a6f52486fd.png)
解:A-A截面上内力为:
截面的几何性:
欲使柱截面内不出现拉应力,则有:
=0(a)
分别代入(a)式得:
解之得:
此时: MPa
3-25传动轴上装有甲、乙两个皮带轮,它们的直径均为 ,重量均为 ,其受力情况如图示。若轴的直径为 。试分析该轴的危险截面和危险点,计算危险点的应力大小,并用图形标明该点所受应力的方向。
解:(1)约束反力:
(2)各杆轴力
题3-3图
(3)各杆的正应力
3-4钢杆 直径为20mm,用来拉住刚性梁 。已知F=10kN,求钢杆横截面上的正应力。
解:
题3-4图
3-5图示结构中,1、2两杆的横截面直径分别为10mm和20mm,试求两杆内的应力。设结构的横梁为刚体。
解:取BC段分析, 题3-5图
取AB段分析:
根据力矩平衡:
内力图如图所示。截面的几何特性计算:
危险点面在A面的D1和D2点,则合成弯矩为:
3-28圆截面短柱,承受一与轴线平行但不与轴线重合的压载荷F作用,圆截面半径为r,现要求整个截面只承受压应力,试确定F作用的范围。
解:压力引起的压应力:
而
解之得Zc=题3-21图所以:来自最大压应力在槽底上各点:
(3)如果在左侧也开槽,则为轴心受压:
3-22图示短柱受载荷 和 作用,试求固定端角点A、B、C及D的正应力,并确定其中性轴的位置。
题3-22图
解:在ABCD平面上的内力:
横截面的几何特性:
应力计算:
中性轴方程为:
3-23图3-64所示为一简易悬臂式吊车架。横梁AB由两根10号槽钢组成。电葫芦可在梁上来回移动。设电动葫芦连同起吊重物的重量共重 。材料的 。试求在下列两种情况下,横梁的最大正应力值:(1)、只考虑由重量W所引起的弯矩影响;(2)、考虑弯矩和轴力的共同影响。
材料力学 扭转答案

3—1 一传动轴作匀速转动,转速,轴上装有五个轮子,主动轮Ⅱ输入的功率为60kW,从动轮,Ⅰ,Ⅲ,Ⅳ,Ⅴ依次输出18kW,12kW,22kW和8kW。
试作轴的扭矩图。
解:kNkNkNkN返回3—2(3-3)圆轴的直径,转速为。
若该轴横截面上的最大切应力等于,试问所传递的功率为多大?解:故即又故返回3—3(3—5)实心圆轴的直径mm,长m,其两端所受外力偶矩,材料的切变模量。
试求:(1)最大切应力及两端截面间的相对扭转角;(2)图示截面上A,B,C三点处切应力的数值及方向;(3)C点处的切应变。
解:=返回3-4(3—6)图示一等直圆杆,已知,,,。
试求:(1)最大切应力;(2)截面A相对于截面C的扭转角。
解:(1)由已知得扭矩图(a)(2)返回3-5(3—12)长度相等的两根受扭圆轴,一为空心圆轴,一为实心圆轴,两者材料相同,受力情况也一样。
实心轴直径为d;空心轴外径为D,内径为,且。
试求当空心轴与实心轴的最大切应力均达到材料的许用切应力),扭矩T相等时的重量比和刚度比。
解:重量比=因为即故故刚度比==返回3—6(3-15)图示等直圆杆,已知外力偶矩,,许用切应力,许可单位长度扭转角,切变模量。
试确定该轴的直径d。
解:扭矩图如图(a)(1)考虑强度,最大扭矩在BC段,且(1)(2)考虑变形(2)比较式(1)、(2),取返回3-7(3—16) 阶梯形圆杆,AE段为空心,外径D=140mm,内径d=100mm;BC段为实心,直径d=100mm。
外力偶矩,,。
已知:,,。
试校核该轴的强度和刚度。
解:扭矩图如图(a)(1)强度=,BC段强度基本满足=故强度满足。
(2)刚度BC段:BC段刚度基本满足.AE段:AE段刚度满足,显然EB段刚度也满足.返回3—8(3-17)习题3—1中所示的轴,材料为钢,其许用切应力,切变模量,许可单位长度扭转角。
试按强度及刚度条件选择圆轴的直径。
解:由3—1题得:故选用.返回3-9(3-18)一直径为d的实心圆杆如图,在承受扭转力偶矩后,测得圆杆表面与纵向线成方向上的线应变为。
《材料力学》第章扭转习题解

《材料力学》第章-扭转-习题解————————————————————————————————作者:————————————————————————————————日期:第三章扭转习题解[习题3-1] 一传动轴作匀速转动,转速min/200rn=,轴上装有五个轮子,主动轮II输入的功率为60kW,从动轮,I,III,IV,V依次输出18kW,12kW,22kW和8kW。
试作轴的扭图。
解:(1)计算各轮的力偶矩(外力偶矩)nNT ke55.9=外力偶矩计算(kW换算成kN.m)题目编号轮子编号轮子作用功率(kW) 转速r/min Te(kN.m)习题3-1 I 从动轮18 200 0.859 II 主动轮60 200 2.865III 从动轮12 200 0.573IV 从动轮22 200 1.051V 从动轮8 200 0.382(2) 作扭矩图[习题3-2] 一钻探机的功率为10kW,转速min/180rn=。
钻杆钻入土层的深度ml40=。
如土壤对钻杆的阻力可看作是均匀分布的力偶,试求分布力偶的集度m,并作钻杆的扭矩图。
解:(1)求分布力偶的集度m)(5305.018010549.9549.9mkNnNM ke⋅=⨯==设钻杆轴为x轴,则:0=∑x MeMml=)/(0133.0405305.0mkNlMm e===T图(kN.m)(2)作钻杆的扭矩图 x x lM mx x T e0133.0)(-=-=-=。
]40,0[∈x 0)0(=T ; )(5305.0)40(m kN M T e ⋅-==扭矩图如图所示。
[习题3-3] 圆轴的直径mm d 50=,转速为120r/min 。
若该轴横截面上的最大切应力等于60MPa ,试问所传递的功率为多大? 解:(1)计算圆形截面的抗扭截面模量:)(245445014159.3161161333mm d W p =⨯⨯==π (2)计算扭矩2max /60mm N W Tp==τ )(473.1147264024544/6032m kN mm N mm mm N T ⋅=⋅=⨯=(3)计算所传递的功率 )(473.1549.9m kN nN M T ke ⋅=== )(5.18549.9/120473.1kW N k =⨯=[习题3-4] 空心钢轴的外径mm D 100=,内径mm d 50=。
材料力学答案03

T2 = M B + M C = 764 N ⋅ m Tmax = 764 N ⋅ m
其绝对值比第(1)种情况小,即对轴的受力有利。 3-3 试绘出图示截面上切应力的分布图,其中 T 为截面的扭矩。
(a1)
(b1)
(c1)
3-4 图示圆截面轴, AB 与 BC 段的直径分别为 d1 与 d 2 ,且 d1 = 4d 2 / 3 。求轴内的 最大扭转切应力。
ϕ = ∫ dϕ = ∫
l l
T (x ) dx GI p ( x )
上式适用于等截面圆轴和截面变化不大的圆锥截面轴。对等截面圆轴,若在长 l 的两横截面 间的扭矩 T 为常量,则
ϕ=
圆轴扭转的刚度条件为
Tl GI p
⎟ ≤ [θ ] θ max = ⎜ ⎜ GI ⎟ ⎝ p ⎠ max
⎛ T ⎞
对于等截面圆轴为 或
28
答 同一变速箱中的高速轴与低速轴指相对转速高低,其传递的功率相同(不计功率损 耗) ,啮合处线速度相同。要啮合处产生相同的线速度,则高速轴的啮合半径就较小;又因 为啮合处相互作用力相同,该作用力对啮合半径就较小的高速轴线产生的外力偶矩就较小, 从而在高速轴中产生的扭矩较小,故高速轴可做得较细。 3-12 图示轴 A 和套筒 B 牢固地结合在一起,两者切变模量分别为 G A 和 G B ,两端受扭 转力偶矩,为使轴和套筒承受的扭转相同而必须满足的条件是什么?
(
)
16 × 500 = 194 MPa ⎡ ⎛ 40 ⎞ 4 ⎤ 3 −9 π × 42 × 10 × ⎢1 − ⎜ ⎟ ⎥ ⎢ ⎝ 42 ⎠ ⎦ ⎥ ⎣
(2)若考虑薄壁 ,可求其平均扭转切应力
τ=
Me = 2 πR 2δ
《材料力学》第3章 扭转 习题解
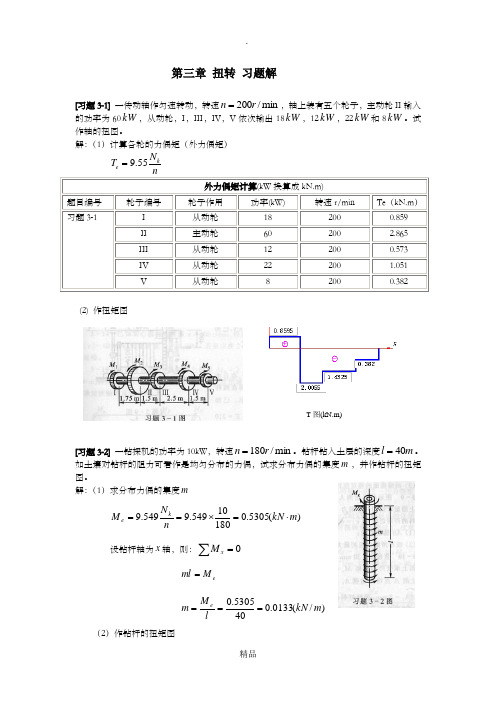
第三章扭转 习题解[习题3-1] 一传动轴作匀速转动,转速min /200r n =,轴上装有五个轮子,主动轮II 输入的功率为60kW ,从动轮,I ,III ,IV ,V 依次输出18kW ,12kW ,22kW 和8kW 。
试作轴的扭图。
解:(1)计算各轮的力偶矩(外力偶矩) nN T ke 55.9= 外力偶矩计算(kW 换算成kN.m)题目编号 轮子编号轮子作用 功率(kW) 转速r/minTe (kN.m ) 习题3-1I 从动轮 18 200 0.859 II 主动轮 60 200 2.865 III 从动轮 12 200 0.573 IV 从动轮 22 200 1.051 V从动轮82000.382(2) 作扭矩图[习题3-2] 一钻探机的功率为10kW ,转速min /180r n =。
钻杆钻入土层的深度m l 40=。
如土壤对钻杆的阻力可看作是均匀分布的力偶,试求分布力偶的集度m ,并作钻杆的扭矩图。
解:(1)求分布力偶的集度m)(5305.018010549.9549.9m kN n N M k e ⋅=⨯== 设钻杆轴为x 轴,则:0=∑xMe M ml =)/(0133.0405305.0m kN l M m e ===(2)作钻杆的扭矩图T 图(kN.m)x x lM mx x T e0133.0)(-=-=-=。
]40,0[∈x 0)0(=T ; )(5305.0)40(m kN M T e ⋅-==扭矩图如图所示。
[习题3-3] 圆轴的直径mm d 50=,转速为120r/min 。
若该轴横截面上的最大切应力等于60MPa ,试问所传递的功率为多大? 解:(1)计算圆形截面的抗扭截面模量:)(245445014159.3161161333mm d W p =⨯⨯==π (2)计算扭矩2max /60mm N W Tp==τ )(473.1147264024544/6032m kN mm N mm mm N T ⋅=⋅=⨯=(3)计算所传递的功率 )(473.1549.9m kN nN M T ke ⋅=== )(5.18549.9/120473.1kW N k =⨯=[习题3-4] 空心钢轴的外径mm D 100=,内径mm d 50=。
材料力学_陈振中_习题第三章扭转
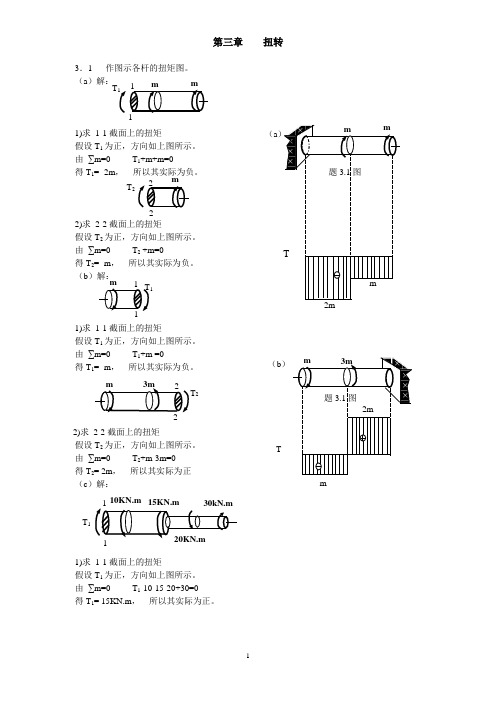
第三章 扭转3.1 作图示各杆的扭矩图。
(a )解:1)求 1-1截面上的扭矩假设T 1为正,方向如上图所示。
由 ∑m=0 T 1+m+m=0得T 1= -2m , 所以其实际为负。
2)求 2-2截面上的扭矩假设T 2为正,方向如上图所示。
由 ∑m=0 T 2 +m=0得T 2= -m , 所以其实际为负。
(b )解:1)求 1-1截面上的扭矩假设T 1为正,方向如上图所示。
由 ∑m=0 T 1+m =0得T 1= -m , 所以其实际为负。
2)求 2-2截面上的扭矩假设T 2为正,方向如上图所示。
由 ∑m=0 T 2+m-3m=0 得T 2= 2m , 所以其实际为正 (c )解:1)求 1-1截面上的扭矩假设T 1为正,方向如上图所示。
由 ∑m=0 T 1-10-15-20+30=0得T 1= 15KN.m , 所以其实际为正。
T 1T 2(a2(b )mTT 12)求 2-2截面上的扭矩假设T 2为正,方向如上图所示。
由 ∑m=0 T 2-15-20+30=0得T 2= 5KN.m , 所以其实际为正。
3)求 3-3截面上的扭矩 假设T 3为正,方向如上图所示。
由 ∑m=0 T 3-20+30=0得T 3= -10KN.m , 所以其实际为负。
4)求 4-4截面上的扭矩假设T 4为正,方向如上图所示。
由 ∑m=0 T 4 +30=0得T 4= -30KN.m , 所以其实际为负。
3.2 T 为圆杆横截面上的扭矩,试画出截面上与T 对应的剪应力分布图。
解:3.5 D=50mm 直径的圆轴,受到扭矩T=2.15KN .m 的作用。
试求在距离轴心10mm 处的剪应力,并求轴横截面上的最大剪应力。
T 230kN.m T 3T 4(题3.2图(a ) (b )解:求距离轴心10mm 处的剪应力, 由 I P =πD 4/32=π×0.054/32=6.13×10-7 m 4 W t = I P /R=6.13×10-7/0.025=2.454×10-5 m 3τρ=Tρ/ I P =2.15×103×10×10-3/(6.13 ×10-7 ) =35MPa求轴横截面上的最大剪应力τmax =T/ W t =2.15×103/(2.454 ×10-5 ) =87.6MPa3.8 阶梯形圆轴直径分别为d 1=40mm ,d 2=70mm ,轴上装有三个皮带轮,如图所示。
材料力学第3章 扭转 习题解

第三章 扭转 习题解[习题3-1] 一传动轴作匀速转动,转速min /200r n =,轴上装有五个轮子,主动轮II 输入的功率为60kW ,从动轮,I ,III ,IV ,V 依次输出18kW ,12kW ,22kW 和8kW 。
试作轴的扭图。
解:(1)计算各轮的力偶矩(外力偶矩)N T ke 55.9=(2) 作扭矩图[习题3-2] 一钻探机的功率为10kW ,转速min /180r n =。
钻杆钻入土层的深度m l 40=。
如土壤对钻杆的阻力可看作是均匀分布的力偶,试求分布力偶的集度m ,并作钻杆的扭矩图。
解:(1m )(5305.018010549.9549.9m kN n N M k e ⋅=⨯== 设钻杆轴为x 轴,则:0=∑xMe M ml =)/(0133.0405305.0m kN l M m e ===(2)作钻杆的扭矩图 x x lM mx x T e0133.0)(-=-=-=。
]40,0[∈x 0)0(=T ; )(5305.0)40(m kN M T e ⋅-==扭矩图如图所示。
[习题3-3] 圆轴的直径mm d 50=,转速为120r/min 。
若该轴横截面上的最大切应力等于60MPa ,试问所传递的功率为多大? 解:(1)计算圆形截面的抗扭截面模量:)(245445014159.3161161333mm d W p =⨯⨯==π (2)计算扭矩2max /60mm N W Tp==τ )(473.1147264024544/6032m kN mm N mm mm N T ⋅=⋅=⨯=(3)计算所传递的功率 )(473.1549.9m kN nN M T ke ⋅=== )(5.18549.9/120473.1kW N k =⨯=[习题3-4] 空心钢轴的外径mm D 100=,内径mm d 50=。
已知间距为m l 7.2=的两横截面的相对扭转角o8.1=ϕ,材料的切变模量GPa G 80=。
材料力学习题-第3章_扭转

第三章扭转一、是非判断题1.杆件受扭时,横截面上的最大切应力发生在距截面形心最远处。
2.薄壁圆管和空心圆管的扭转切应力公式完全一样。
3.非圆截面杆不能应用圆截面杆扭转切应力公式,是因为非圆截面杆扭转时“平截面假设”不能成立。
4.切应力互等定理仅适用于纯剪切情况。
5.受扭杆件的扭矩,仅与杆件受到的转矩(外力偶矩)有关,而与杆件的材料及其横截面的大小、形状无关。
6.受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。
7.受扭圆轴的最大切应力只出现在横截面上。
8.受扭圆轴内最大拉应力的值和最大切应力的值相等。
9.因木材沿纤维方向的抗剪能力差,故若受扭木质圆杆的轴线与木材纤维方向平行,当扭距达到某一极限值时,圆杆将沿轴线方向出现裂纹。
答案:×,×,√,×,√,√,×,√,×二、选择题1.内、外径之比为α的空心圆轴,扭转时轴内的最大切应力为τ,这时横截面上内边缘的切应力为()A τ;B ατ;C 零; D(1-4 )τ2.两根受扭圆轴的直径和长度均相同,但材料G不同,在扭矩相同的情况下,它们的最大切应力τ1、τ2和扭转角φ1、φ2之间的关系为( ) A 1τ=τ2, φ1=φ2 B 1τ=τ2, φ1≠φ2 C 1τ≠τ2, φ1=φ2 D 1τ≠τ2, φ1≠φ23.空心圆轴的外径为D ,内径为d, α=d /D,其抗扭截面系数为 ( ) A ()31 16p D W πα=- B ()321 16p DW πα=- C ()331 16p D W πα=- D ()341 16p D W πα=-4.对于受扭的圆轴,关于如下结论:①最大剪应力只出现在横截面上;②在横截面上和包含杆件的纵向截面上均无正应力;③圆轴内最大拉应力的值和最大剪应力的值相等。
现有四种答案,正确的是( )A ②③对B ①③对C ①②对D 全对5.单位长度扭转角θ与( )无关。
A 杆的长度;B 扭矩;C 材料性质;D 截面几何性质。
材料力学答案第三章

第三章 扭转第三章答案3.1 作图示各杆的扭矩图。
解:4kN·m6kN·m10kN·m 6kN·m4kN·m4kN·m3.2 T 为圆杆截面上的扭矩,试画出截面上与T 对应的剪应力分布图。
解:3.3 图示钢制圆轴,d 1 = 40mm, d 2 = 70mm, M eA = 1.4kN m ⋅, M eB = 0.6kN m ⋅, M eC = 0.8kN m ⋅,[]θ = 1o /m. []τ = 60MPa, G = 80GPa. 试校核轴的强度与刚度。
解:1)校核强度[]113311161660047.7MPa 4B t T m W d ττππ⨯====<⨯[]223322161680011.9MPa 7C t m T W d ττππ⨯====<⨯满足强度条件。
0.8kN·m2)校核刚度119412118032600180 1.71/m 80104010P T GI θπππ-⨯=⋅=⋅=︒⨯⨯⨯⨯222180328001800.24/m 80107010P T GI θπππ⨯=⋅=⋅=︒⨯⨯⨯⨯[]max 1 1.71/m θθθ==︒>此轴不满足刚度条件。
3.4 图示一传动轴,主动轮I 传递力偶矩m k N 1⋅, 从动轮II 传递力偶矩0.4m k N ⋅, 从动轮III 传递力偶矩0.6m k N ⋅。
已知轴的直径d = 40mm ,各轮间距各轮间距l = 500mm ,材料的剪切弹性模量G = 80GPa 。
(1)合理布置各轮的位置;(2)求出轴在合理位置时的最大剪应力和轮间的最大扭转角 。
0.6kN·m解:max 336161660047.7MPa 410t T m W d τππ-⨯====⨯⨯Ⅰ主动轮Ⅰ放在Ⅱ、Ⅲ轮之间,此时轴的最大扭矩最小。
max 494832326000.50.015rad8010410P Tl mlGI G d φππ-==⨯⨯==⨯⨯⨯⨯3.5 一空心圆轴和实心圆轴用法兰联结。
材料力学第三章扭转复习题

第三章 扭转1.等截面圆轴上装有四个皮带轮,如何安排合理,现有四种答案:(A ) 将C 轮与D 轮对调; (B ) 将B 轮与D 轮对调; (C ) 将B 轮与C 轮对调;(D ) 将B 轮与D 轮对调;然后将B 轮与C 轮对调;正确答案是 a 。
2.薄壁圆管受扭转时的剪应力公式为 ()t R T 22/πτ= ,(R 为圆管的平均半径,t 为壁厚)。
关于下列叙述,(1) 该剪应力公式可根据平衡关系导出;(2) 该剪应力公式可根据平衡、几何、物理三方面条件导出; (3) 该剪应力公式符合“平面假设”;(4) 该剪应力公式仅适用于R t <<的圆管。
现有四种答案: (A ) (1)、(3)对; (B ) (1)、(4)对; (C ) (2)、(3)对; (D ) 全对;正确答案是 b 。
3.建立圆轴的扭转应力公式 p p I T /ρτ=时,“平面假设”起到的作用于有 下列四种答案:(A ) “平面假设”给出了横截面上内力与应力的关系⎰=AdA T τρ;(B ) “平面假设”给出了圆轴扭转时的变形规律;(C ) “平面假设”使物理方程得到简化;(D ) “平面假设”是建立剪应力互等定理的基础。
正确答案是 。
4.满足平衡条件,但剪应力超过比例极限时,有下述四种结论:(A ) (B ) (C ) (D ) 剪应力互等定理: 成立 不成立 不成立 成立 剪切虎克定律 : 成立 不成立 成立 不成立 正确答案是 。
D5.一内、外直径分别为d 、D 的空心圆轴,其抗扭截面系数有四种答案:(A )()()16/16/33d D W t ππ-=;(B )()()32/32/33d DW t ππ-=;(C )()[]()4416/d D D W t-=π; (D )()()32/32/44d D W tππ-=;正确答案是 c 。
6.一内外径之比为D d /=α的空心圆轴, 当两端受扭转力偶矩时,横截面的最大剪应为τ,则内圆周处的剪应力有四种答案: (A )τ; (B )ατ;(C ) ()τα31-; (D )()τα41-正确答案是 b 。
材料力学第三章答案

材料力学第三章答案【篇一:材料力学习题册答案-第3章扭转】是非判断题二、选择题0 b 2t?d316?1?? ? b wp??d316?1?? ?2c wp??d316?1?? ? d w3p??d316?1?? ?46.对于受扭的圆轴,关于如下结论:①最大剪应力只出现在横截面上;②在横截面上和包含杆件的纵向截面上均无正应力;③圆轴内最大拉应力的值和最大剪应力的值相等。
现有四种答案,正确的是( a )a ②③对 b①③对 c①②对d 全对 7.扭转切应力公式?mnp?i?适用于( d)杆件。
pa 任意杆件;b 任意实心杆件;c 任意材料的圆截面;d 线弹性材料的圆截面。
9.若将受扭实心圆轴的直径增加一倍,则其刚度是原来的( d a 2倍; b 4倍; c 8倍; d 16倍。
三、计算题1.试用截面法求出图示圆轴各段内的扭矩t,并作扭矩图2.图示圆轴上作用有四个外力偶矩 me1 =1kn/m, me2 =0.6kn/m,)me3= me4 =0.2kn/m, ⑴试画出该轴的扭矩图;⑵若 me1与me2的作用位置互换,扭矩图有何变化?(1)(2)解: me1与me2的作用位置互换后,最大扭矩变小。
3.如图所示的空心圆轴,外径d=100㎜,内径d=80㎜,m=6kn/m,m=4kn/m.请绘出轴的扭矩图,并求出最大剪应力解:扭矩图如上,则轴面极惯性矩id4?d4)(1004?804)(10?3)4p=?(32??32?5.8?10?6m4㎜,l=500tr4?103?50?103ip5.8?104.图示圆形截面轴的抗扭刚度为g ip,每段长1m,试画出其扭矩图并计算出圆轴两端的相对扭转角。
ab+ad=cdab=t1l?90?gipgipad=bc=t2l100gipgipcd=t3l40gipgip?90?100?4050?gipgip【篇二:《材料力学》第3章扭转习题解】[习题3-1] 一传动轴作匀速转动,转速n?200r/min,轴上装有五个轮子,主动轮ii输入的功率为60kw,从动轮,i,iii,iv,v依次输出18kw,12kw,22kw和8kw。
材料力学习题册答案-第3章 扭转(完整资料).doc

此文档下载后即可编辑第三章扭转一、是非判断题1.圆杆受扭时,杆内各点处于纯剪切状态。
(×)2.杆件受扭时,横截面上的最大切应力发生在距截面形心最远处。
(×)3.薄壁圆管和空心圆管的扭转切应力公式完全一样。
(×)4.圆杆扭转变形实质上是剪切变形。
(×)5.非圆截面杆不能应用圆截面杆扭转切应力公式,是因为非圆截面杆扭转时“平截面假设”不能成立。
(√)6.材料相同的圆杆,他们的剪切强度条件和扭转强度条件中,许用应力的意义相同,数值相等。
(×)7.切应力互等定理仅适用于纯剪切情况。
(×)8.受扭杆件的扭矩,仅与杆件受到的转矩(外力偶矩)有关,而与杆件的材料及其横截面的大小、形状无关。
(√)9.受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。
(√)10.受扭圆轴的最大切应力只出现在横截面上。
(×)11.受扭圆轴内最大拉应力的值和最大切应力的值相等。
(√ )12.因木材沿纤维方向的抗剪能力差,故若受扭木质圆杆的轴线与木材纤维方向平行,当扭距达到某一极限值时,圆杆将沿轴线方向出现裂纹。
( × )二、选择题1.内、外径之比为α的空心圆轴,扭转时轴内的最大切应力为τ,这时横截面上内边缘的切应力为 ( B )A τ;B ατ;C 零;D (1- 4α)τ 2.实心圆轴扭转时,不发生屈服的极限扭矩为T ,若将其横截面面积增加一倍,则极限扭矩为( C )A0 B 20T 0 D 40T 3.两根受扭圆轴的直径和长度均相同,但材料C 不同,在扭矩相同的情况下,它们的最大切应力τ、τ和扭转角ψ、ψ之间的关系为( B )A 1τ=τ2, φ1=φ2B 1τ=τ2, φ1≠φ2C 1τ≠τ2, φ1=φ2D 1τ≠τ2, φ1≠φ2 4.阶梯圆轴的最大切应力发生在( D )A 扭矩最大的截面;B 直径最小的截面;C 单位长度扭转角最大的截面;D 不能确定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章扭转
一、是非判断题
1.圆杆受扭时,杆内各点处于纯剪切状态。
(×)
2.杆件受扭时,横截面上的最大切应力发生在距截面形心最远处。
(×)
3.薄壁圆管和空心圆管的扭转切应力公式完全一样。
(×)
4.圆杆扭转变形实质上是剪切变形。
(×)
5.非圆截面杆不能应用圆截面杆扭转切应力公式,是因为非圆截面杆扭转时“平截面假设”不能成立。
(√)
6.材料相同的圆杆,他们的剪切强度条件和扭转强度条件中,许用应力的意义相同,数值相等。
(×)
7.切应力互等定理仅适用于纯剪切情况。
(×)
8.受扭杆件的扭矩,仅与杆件受到的转矩(外力偶矩)有关,而与杆件的材料及其横截面的大小、形状无关。
(√)
9.受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。
(√)
10.受扭圆轴的最大切应力只出现在横截面上。
(×)
11.受扭圆轴内最大拉应力的值和最大切应力的值相等。
(√)
12.因木材沿纤维方向的抗剪能力差,故若受扭木质圆杆的轴线与木材纤维方向平行,当扭距达到某一极限值时,圆杆将沿轴线方向出现裂纹。
(×)
二、选择题
1.内、外径之比为α的空心圆轴,扭转时轴内的最大切应力为τ,这时横截面上内边缘的切应力为 ( B )
A τ;
B ατ;
C 零;
D (1- 4α)τ 2.实心圆轴扭转时,不发生屈服的极限扭矩为T ,若将其横截面面积增加一倍,则极限扭矩为( C )
0 B 20T 0 D 40T 3.两根受扭圆轴的直径和长度均相同,但材料C 不同,在扭矩相同的情况下,它们的最大切应力τ、τ和扭转角ψ、ψ之间的关系为( B )
A 1τ=τ2, φ1=φ2
B 1τ=τ2, φ1≠φ2
C 1τ≠τ2, φ1=φ2
D 1τ≠τ2, φ1≠φ2 4.阶梯圆轴的最大切应力发生在( D ) A 扭矩最大的截面; B 直径最小的截面; C 单位长度扭转角最大的截面; D 不能确定。
5.空心圆轴的外径为D ,内径为d, α=d /D,其抗扭截面系数为 ( D ) A ()3
1 16
p D W πα=
- B ()3
2
1 16
p D W πα=
-
C ()3
3
1 16
p D W πα=
- D ()3
4
1 16
p
D W
πα=
-
6.对于受扭的圆轴,关于如下结论: ①最大剪应力只出现在横截面上;
②在横截面上和包含杆件的纵向截面上均无正应力;
③圆轴内最大拉应力的值和最大剪应力的值相等。
现有四种答案,正确的是( A )
A ②③对
B ①③对
C ①②对
D 全对 7.扭转切应力公式n
P p
M I τρ=
适用于( D )杆件。
A 任意杆件; B 任意实心杆件; C 任意材料的圆截面; D 线弹性材料的圆截面。
8.单位长度扭转角θ与( A )无关。
A 杆的长度; B 扭矩; C 材料性质; D 截面几何性质。
9.若将受扭实心圆轴的直径增加一倍,则其刚度是原来的( D ) A 2倍; B 4倍; C 8倍; D 16倍。
三、计算题
1.试用截面法求出图示圆轴各段内的扭矩T ,并作扭矩图
2.图示圆轴上作用有四个外力偶矩1 e M =1KN/m, 2e M =0.6KN/m, 3e M
= 4e M =0.2KN/m, ⑴试画出该轴的扭矩图;⑵若1 e M 与2e M 的作用位置互换,扭矩图有何变化?
(1)(2)
解:1 e M 与2e M 的作用位置互换后,最大扭矩变小。
3.如图所示的空心圆轴,外径D=100㎜,内径d=80㎜,l=500㎜,M=6kN/m,M=4kN/m.
请绘出轴的扭矩图,并求出最大剪应力
解:扭矩图如上,则轴面极惯性矩
I P =
4
44443)
64()
(10080)(10 5.81032
32
D d m ππ----=
=⨯
则最大剪应力τmax =33
6
R 4105010P 34.45.810
P T a MPa I ⨯⨯⨯==⨯
4.图示圆形截面轴的抗扭刚度为G I P ,每段长1m,试画出其扭矩图并计算出圆轴两端的相对扭转角。
解:φAD= φAB+ φBC +φCD φAB=190
P P
T L GI GI -= φBC=2100P P T L GI GI = φCD=340P P T L GI GI = 所以φAD=901004050
P P
GI GI -++=
5.如图所示的阶梯形传动轴中,A 轮输入的转矩M=800N •m,B ﹑C 和D 轮输出的转矩分别为B M =C M =300N •m ,D M =200N •m 。
传动轴的许用切应力[τ]=400Mpa,许用扭转角[θ]=1°/m,材料的剪切弹性模量G=80Gpa.
⑴试根据轴的强度条件和刚度条件,确定传动轴各段的直径。
⑵若将传动轴改为等截面空心圆轴,并要求内外直径之比α=d/D=0.6,试确定轴的外径;并比较两种情况下轴的重量。
解: (1)max τ=
max 3
16max
T T T W d
π=≤[ τ] []max max max 4
32P T T GI G d θθπ=
=≤ 对于AB 段 11d d ≥≥138.5d mm ≥ 同理得AC 段的d 2 43.7mm ≥ CD 段d 3 34.8mm ≥
所以d 1应取值38.5mm ,d 2应取值43.7mm,d 3应取值34.8mm (2) []max max max max 3416(1)
t t T T T W W D ττπα===≤- []max max max 4432(1)
P T T GI G D θθπα=
=≤- 所以D=4.17m
6.图示的传动轴长l=510㎜,直径D=50㎜。
现将此轴的一段钻成内径d=25㎜的内腔,而余下一段钻成d=38㎜的内腔。
若材料的许用切应力[τ]=70Mpa,试求: ⑴此轴能承受的最大转矩max e M M
⑵若要求两段轴内的扭转角相等,则两段的长度应分别为多少?
M M e
e
M
解:⑴设半径为ρ P I M ρτ=
P I
M τρ
= P I 取441D -)32d π(,ρ=2
D
[]()[]()44441132
1609.86162D d D d M N M D
D
π
ττπ--=
=
=•
⑵P T GI θ=
1112()P P Tl T l l GI GI -∴= 即 1
14444
12()()3232
l l l D d D d ππ-=
-- 解得1l =298.1mm l 2=211.9mm
7.如图所示钢轴AD 的材料许用切应力[τ]=50Mpa ,切变模量G=80Gpa,许用扭转角[θ]=0.25°/m 。
作用在轴上的转矩M=800N •m ,1200N •m ,M=400N •m 。
试设计此轴的直径。
M/。
