人教版近似数_1

合集下载

人教版中考数学知识点分类知识点02 科学记数法,近似数(1)

一、选择题1. （2019广东深圳，3，3分）预计到2025年，中国5G 用户将超过460 000 000，将460 000 000用科学记数法表示为（）A ．4.6×109B ．46×107C ．4.6×108D ．0.46×109 【答案】C【解析】460 000 000整数位数有9位，所以将460 000 000用科学记数法表示为4.6×108．故选C ．【知识点】科学记数法2. （2019广西北部湾，4，3分）2019年6月6日，南宁市地铁3号线举行通车仪式，预计地铁3号线开通后，日均客流量为700000人次，其中数据700000用科学记数法表示为A.70×104B.7×105C.7×106D.0.7×106【答案】B.【解析】解：将数据700000用科学记数法表示为7×105；故选B ．【知识点】科学记数法．3. （ 2019贵州省毕节市，题号2，分值3分）举世瞩目的港珠澳大桥于2018年10月24日正式开通营运，它是迄今为止世界上最长的跨海大桥，全长约55000米．55000这个数用科学记数法可表示为（）A ．5.5×103B ．55×103C ．0.55×105D ．5.5×104 【答案】D ．【解析】解：55000这个数用科学记数法可表示为5.5×104，故选：D ．【知识点】科学记数法—表示较大的数．4. （2019贵州黔西南州，2，4分）举世瞩目的港珠澳大桥于2018年10月24日正式开通营运，它是迄今为止世界上最长的跨海大桥，全长约55000米．55000这个数用科学记数法可表示为（）A ．5.5×103B ．55×103C ．0.55×105D ．5.5×104【答案】D【解析】解：55000这个数用科学记数法可表示为5.5×104，故选：D ．【知识点】科学记数法—表示较大的数5. （2019贵州遵义，3，4分）今年5月26日-5月29日，2019中国国际大数据产业博览会在贵阳矩形，贵州省共签约项目125个，金额约1008亿，1008亿用科学记数法表示为(A)8101008⨯ (B)910008.1⨯ (C) 1010008.1⨯ (D) 1110008.1⨯【答案】D【解析】科学记数法表示为na 10⨯，其中1≤|a|＜10，n 为整数，表示时关键要正确确定a 的值以及n 的值。

人教版数学二年级下册《近似数》教案1

人教版数学二年级下册《近似数》教案1一. 教材分析《人教版数学二年级下册》中的《近似数》一课，主要让学生掌握近似数的含义，学会用四舍五入法求近似数。

教材通过生活中的实际例子，引导学生理解近似数的概念，培养学生的数感。

二. 学情分析二年级的学生已经掌握了整数的认识，对数的运算有一定的了解。

但近似数的概念对学生来说较为抽象，需要通过具体的例子和实践活动，让学生逐步理解和掌握。

三. 教学目标1.让学生理解近似数的含义，学会用四舍五入法求近似数。

2.培养学生的数感，提高学生解决实际问题的能力。

3.激发学生的学习兴趣，培养学生的合作意识。

四. 教学重难点1.近似数的概念。

2.四舍五入法的运用。

五. 教学方法采用情境教学法、游戏教学法和小组合作学习法，让学生在实际情境中感受近似数的概念，通过游戏和小组合作，提高学生的动手能力和团队协作能力。

六. 教学准备1.教学课件。

2.练习题。

3.小组合作学习材料。

七. 教学过程1.导入（5分钟）通过一个生活中的实际例子，如购物时找零钱，引入近似数的概念。

让学生思考：为什么有时候找零钱不是精确的整数呢？从而引出近似数的概念。

2.呈现（10分钟）呈现教材中的例题，让学生观察和思考：为什么4.56近似为5，而3.21近似为3呢？引导学生理解四舍五入法的原理。

3.操练（10分钟）让学生动手实践，用四舍五入法求近似数。

可以设计一些练习题，如把3.78近似为整数，把2.29近似为一位小数等。

让学生独立完成，然后交流答案，互相评价。

4.巩固（10分钟）通过一些实际问题，让学生运用近似数的概念。

如：一个水果摊卖苹果，每斤3.5元，顾客买了2.34斤，请问应付多少钱？让学生分组讨论，解决问题。

5.拓展（10分钟）引导学生思考：近似数在实际生活中有哪些应用？可以让学生举例说明，如身高、体重、温度等。

6.小结（5分钟）对本节课的内容进行总结，强调近似数的概念和四舍五入法的运用。

7.家庭作业（5分钟）设计一些练习题，让学生课后巩固所学知识。

人教版数学七年级上册1.5.3《近似数》教学设计1

人教版数学七年级上册1.5.3《近似数》教学设计1一. 教材分析《近似数》是人教版数学七年级上册1.5.3的内容，本节课主要介绍近似数的概念及其求法。

学生在学习本节课之前，已经掌握了有理数的概念和运算法则，因此，本节课是在已有知识基础上的拓展和应用。

通过本节课的学习，学生能够理解近似数的概念，掌握求近似数的方法，并能应用于实际问题中。

二. 学情分析七年级的学生已经具备了一定的数学基础，对有理数的概念和运算法则有一定的了解。

但是，对于近似数这一概念，学生可能比较陌生，因此需要通过实例和操作来帮助学生理解和掌握。

此外，学生可能对于求近似数的方法和应用有一定的困难，需要通过大量的练习和实际问题来培养学生的应用能力。

三. 教学目标1.了解近似数的概念，能正确地求一个数的近似值。

2.能够将近似数的概念和方法应用于实际问题中。

3.培养学生的数学思维能力和解决问题的能力。

四. 教学重难点1.近似数的概念及其求法。

2.近似数在实际问题中的应用。

五. 教学方法1.采用实例教学法，通过具体的例子来帮助学生理解和掌握近似数的概念和方法。

2.采用问题驱动法，通过提出实际问题来引导学生思考和应用近似数的概念和方法。

3.采用分组讨论法，让学生在小组内进行讨论和交流，培养学生的合作能力和解决问题的能力。

六. 教学准备1.准备相关的实例和练习题，用于引导学生进行思考和练习。

2.准备一些实际问题，用于让学生进行应用和拓展。

3.准备多媒体教学设备，用于展示和讲解实例和问题。

七. 教学过程1.导入（5分钟）通过提问方式引导学生回顾有理数的概念和运算法则，为新课的学习做好铺垫。

2.呈现（15分钟）通过实例引入近似数的概念，让学生直观地感受近似数的存在。

然后，讲解近似数的求法，引导学生理解并掌握。

3.操练（10分钟）让学生进行近似数的计算练习，巩固所学知识。

可以设置一些不同难度级别的练习题，让学生根据自己的实际情况选择练习。

4.巩固（10分钟）通过一些实际问题，让学生应用近似数的概念和方法进行解答。

初中数学人教版七年级上册《1.近似数》课件

精确数：8，2，4，6，56；近似数：3，20，3.5 和 4.5．
准确数：与实际完全符合的数,称为准确数.
近似数：许多实际情况中,较难取得准确数,把接近准确数但不等于准确数的数称为近似数.
近似数的来源 (1)用测量工具测量得到的数一般都是近似数；
(2)某些计算的结果也会产生近似数，例如，除不尽的数会对商取近似数,有圆周率 π 参与计算的结果也会取近似数； (3)不容易获得准确数或不可能得到准确数时，只能取近似数，如人口普查的结果就只能是一个近似数.
去尾法：去尾法是去掉数字的小数部分，取其整数部分的取近似数的方法.例如,把一根 20 cm 长的钢筋截成 6 cm 长的小段作零件，由20÷6=3.3…可知能截得的零件数为3.
进一法：进一法是去掉多余部分的数字后，在保留部分的最后一个数字上加 1 的取近似数的方法.例如，有112名学生外出旅游，计算租用 45 座的客车的辆数时，由于112÷45 =2. 48…，此时应取近似数 3，即租用 3 辆 45 座的客车才能确保 112 名学生旅游所需.
1.5.3
近似数
人教版七年级数学上
1.用科学记数法表示绝对值较大的数：把一个绝对值大于 10 的数表示成 a×10n（1≤|a|＜10，n 是正整数）的情势，其中 a 的整数位数为 1，数的正负符号不变，n 为原数的整数位数减 1.
2.将用科学记数法表示的数还原的方法：
把一个用科学记数法表示的数还原为原数时，只需将小数点向右移动 n 位（不足的数位用 0 补齐），并把 10n 去掉即可.
谢谢大家
(1) 0.0158（精确到0.001）；对8四舍五入 (2) 304.35（精确到个位）；对3四舍五入 (3) 1.804（精确到0.1）；对0四舍五入 (4) 1.804（精确到0.01）．对4四舍五入

人教版《近似数》_完美课件

2、两个近似数6.3万与6.3精确到的数位不同。
3、确定有效数字时应注意：①从左边第一个不是0的数字起。 ②从左边第一个不是0的数起，到精确到的数位（即最后一位四舍五入所得的数）止，所有的数字。
4、在写出近似数的每个有效数字时，用“，”号隔开。
如：38.006有五个有效数字，3，8，0，0，6，不能写成38006.
【获奖课件ppt】人教版《近似数》_ 完美课件1-课件分析下载
【获奖课件ppt】人教版《近似数》_ 完美课件1-课件分析下载
比一比：看谁反应快
思考，并回答问题：
近似数 00.1101...016.610610千0660 有几个有效数字，精确到哪一位？
有效数字两三两两个个个
【获奖课件ppt】人教版《近似数》_ 完美课件1-课件分析下载
【获奖课件ppt】人教版《近似数》_ 完美课件1-课件分析下载
【获奖课件ppt】人教版《近似数》_ 完美课件1-课件分析下载
按四舍五入法对圆周率π取近似值时,有
π≈3(精确到个位)
π≈3.1(精确到0.1,或叫做精确到十分位)
π≈3.14(精确到0.01,或叫做精确到百分位)
π≈3.142(精确到位)
,或叫做精确到分
π≈3.1416(精确到分位)
,或叫做精确到
·······
【获奖课件ppt】人教版《近似数》_ 完美课件1-课件分析下载
【获奖课件ppt】人教版《近似数》_ 完美课件1-课件分析下载
回答问题： 1、什么叫准确数？
准确数－－与实际完全符合的数
2、什么叫近似数？近似数－－与实际接近的数
【获奖课件ppt】人教版《近似数》_ 完美课件1-课件分析下载

秋人教版七年级数学上册课件：第一章近似数(共16张PPT)

13、He who seize the right moment, is the right man.谁把握机遇，谁就心想事成。2021/9/192021/9/192021/9/192021/9/199/19/2021 •14、谁要是自己还没有发展培养和教育好，他就不能发展培养和教育别人。2021年9月19日星期日2021/9/192021/9/192021/9/19 •15、一年之计，莫如树谷；十年之计，莫如树木；终身之计，莫如树人。2021年9月2021/9/192021/9/192021/9/199/19/2021 •16、教学的目的是培养学生自己学习，自己研究，用自己的头脑来想，用自己的眼睛看，用自己的手来做这种精神。2021/9/192021/9/19September 19, 2021 •17、儿童是中心，教育的措施便围绕他们而组织起来。2021/9/192021/9/192021/9/192021/9/19
略.
启后
任务三：学习教材第44～45页，完成题目 1. 在任务二的第2小题中，第___（__1_）__（__2_）___题中的数字是准确的，第_（__3_）__（__4_）__题中的数字是与实际接近的，这种只是接近实际数字，但与实际数字还有差别的数被称为___近__似__数____.
2. 按四舍五入对圆周率π取近似数时，有：π≈3 （精确到个位）， π≈3.1（精确到0.1，或叫精确到十分位）， π≈3.14（精确到__0_._0_1_，或叫精确到___百__分__位）， π≈3.142（精确到___0_._0_0_1___，或叫精确到__千__分_ 位）， π≈3.141 6（精确到___0_._0_0_0__1___，或叫精确到 __万__分___位）, ……
•9、要学生做的事，教职员躬亲共做；要学生学的知识，教职员躬亲共学；要学生守的规则，教职员躬亲共守。2021/9/192021/9/19Sunday, September 19, 2021 •10、阅读一切好书如同和过去最杰出的人谈话。2021/9/192021/9/192021/9/199/19/2021 6:31:27 AM •11、只有让学生不把全部时间都用在学习上，而留下许多自由支配的时间，他才能顺利地学习……（这）是教育过程的逻辑。2021/9/192021/9/192021/9/19Sep-2119-Sep-21 •12、要记住，你不仅是教课的教师，也是学生的教育者，生活的导师和道德的引路人。2021/9/192021/9/192021/9/19Sunday, September 19, 2021

人教版初中数学七年级上册第一章近似数

这里的1.8和1.80的精确度相同吗?表示近似
数时，能简单地把 1.80后面的0去掉吗？
(2) 1.8935 ≈1.89 (3) 1.804 ≈1.8 (4) 1.804 ≈1.80
1.8与1.80的精确度不同，表示近似数时，不能简单地把 1.80后面的0去掉
练习：下列由四舍五入得到的近似数，各精确到哪一位？
分层作业
必做题：
1、按括号内的要求，写出下列各数的近似值：（1）69.5（精确到个位）；（2）3.99501（精确到0.001）；（3）1.9988（精确到千分位）；（4）175.65（精确到十分位）.
2、下列由四舍五入得到的近似数，各精确到哪一位？（1）25.8；（2）0.090；（3）3.2万；（4）6.51×105.
(× ) (× )
(√ )
你说我说大家说：
课堂小结：
一、三个概念：
1、准确数
2、近似数
3、精确度
二、已知精确度 → 写出近似数
给出近似数 → 判断精确到哪一位
三、温馨提示： 1、近似数1.8与1.80表示的精确程度不一样。 2、①求一个近似数a的取值范围
②带万、亿等单位的数的精确度； ③用科学记数法表示的数的精确度。
数还是近似数？
一般地，一个近似数，四舍五入到哪一位，就说这个近似数精确到哪一位。
二.精确度近似数与准确数的接近程度，可以用精确度来表示
按四舍五入法对圆周率π取近似值，填一填下面的问题
π =3.1415926···
π≈ 3 （精确到个位） π≈ 3.1 （精确到十分位，或叫做精确到0.1） π≈ 3.14 （精确到百分位，或叫做精确到0.01） π≈3.142（精确到千分位，或叫做精确到0.001 ） π≈3.1416（精确到万分位，或叫做精确到 0.0001 ）

人教版数学二年级下册《近似数》说课稿1

人教版数学二年级下册《近似数》说课稿1一. 教材分析人教版数学二年级下册《近似数》这一节的内容，主要让学生初步了解近似数的概念，学会用四舍五入法求一个数的近似数。

通过这一节的学习，让学生能够更好地理解数的意义，提高他们解决实际问题的能力。

二. 学情分析二年级的学生已经掌握了整数的认识和加减法，他们对数的概念有一定的理解。

但是，对于近似数的概念和求法，他们可能还比较陌生。

因此，在教学过程中，我需要从学生的实际出发，用他们熟悉的事物来帮助他们理解近似数的概念。

三. 说教学目标1.知识与技能：让学生掌握近似数的概念，学会用四舍五入法求一个数的近似数。

2.过程与方法：通过观察、操作、交流等活动，让学生体验求近似数的过程，提高他们的动手能力和解决问题的能力。

3.情感态度与价值观：激发学生学习数学的兴趣，培养他们勇于探索、积极思考的精神。

四. 说教学重难点1.教学重点：让学生掌握近似数的概念，学会用四舍五入法求一个数的近似数。

2.教学难点：让学生理解为什么要用四舍五入法求近似数，以及如何判断是四舍还是五入。

五. 说教学方法与手段1.教学方法：采用情境教学法、启发式教学法和小组合作学习法。

2.教学手段：利用多媒体课件、实物模型、计数器等辅助教学。

六. 说教学过程1.导入：通过一个生活中的实例，如天气预报中的温度，引入近似数的概念。

2.讲解：讲解近似数的概念，并用实例解释为什么要用四舍五入法求近似数。

3.操作：让学生动手实践，用四舍五入法求近似数。

4.交流：让学生分享自己的操作过程和心得，讨论如何判断是四舍还是五入。

5.巩固：通过一些练习题，让学生巩固所学知识。

6.总结：对本节课的内容进行总结，强调近似数在实际生活中的应用。

七. 说板书设计板书设计如下：八. 说教学评价通过学生在课堂上的表现、练习题的完成情况和课后的反馈，评价学生对近似数的理解和掌握程度。

九. 说教学反思在教学过程中，我注意观察学生的反应，根据他们的实际情况调整教学节奏和难度。

人教版七年级上册数学 1.5.2 科学计数法与近似数-1教学过程设计

例题
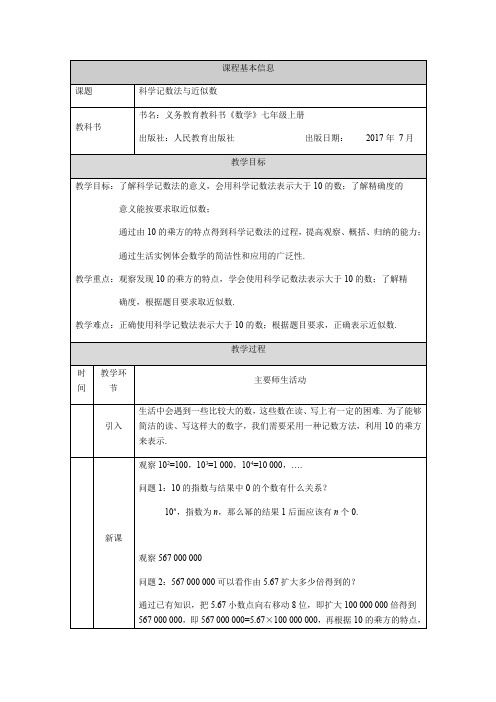
例3按括号内的要求，用四舍五入法对下列各数取近似数：
（1）0.0158（精确到0.001）；（2）304.35（精确到个位）
（3）1.804（精确到0.1）；（4）1.804（精确到0.01）
小结
1.精确度的两种形式，一种形式是说精确到个位，十分位，百分位等，另一种形式是精确到1，也就是精确到个位，精确到0.1，就是精确到十分位，精确到0.01，就是精确到百分位，等等.
课程基本信息
课题
科学记数法与近似数
教科书
书名：义务教育教科书《数学》七年级上册
出版社：人民教育出版社出版日期：2017年7月
教学目标
教学目标：了解科学记数法的意义，会用科学记数法表示大于10的数；了解精确度的
意义能按要求取近似数；
通过由10的乘方的特点得到科学记数法的过程，提高观察、概括、归纳的能力；
5.一天有8.64×104s，一年按365天计算，一年有多少秒（用科学记数法表示）？
例题
例1用科学记数法表示下列各数：
1 000 000，57 000 000，-123 000 000 000.
例2下列用科学记数法表示的数，原来分别是什么数？
1×105，2.03×107.
小结
问题5：如何快速准确的找出a×10n中的a和n呢？
可以从左边开始数，在第一个数后面点小数点，把左边数最后一个不是0的数后面的0去掉，即可得到a的值；n的值，它等于原数的整数部分的位数减1.
新课
观察102=100，103=1 000，104=10 000，….
问题1：10的指数与结果中0的个数有什么关系？
10n，指数为n，那么幂的结果1后面应该有n个0.
观察567000000

人教版七年级上册1.近似数课件(1)

(保留4个有效数字)
≈130.1
⑸460 215
(保留3个有效数字) ≈4.60×105
⑹2.746
（精确到十分位）
≈2.7
⑺3.40×105 (精确到万位） ≈ 3.4×105
实际问题
1.李明测得一根钢管的长度约为0.8米. （1）试举例说明该近似数可能是由哪些数四舍五入得来的？
（2）按照李明测得的结果，你能求出钢管的准确长度x应在什么范围吗？
练一练
用四舍五入法，按括号中的要求对下列各数
取近似数：
(1)0.37046(精确到千分位)；解：
(1)0.370；
(2)4.3049(精确到0.01)；
(2)4.30；
(3)34567(精确到千位)；
(3)3.5×104；
(4)6034001(精确到百万位)． (4)6×106.
能力提升
若用四舍五入法取得的近似数4.3的准确值为 k，求k的取值范围.
解:(1)四舍五入到百分位为1.03米;
近似数1.0后面的0能去掉吗？
(2)四舍五入到十分位为1.0米; 近似数1和
1.0精确度相同吗？
(3)四舍五入到个位为1米.
例2：下列由四舍五入法得到的近似数,各精确到哪一位？有几个有效数字？
(1)132.4精确到_十__分_位__,有 _4_个有效数字，分别为__1_, _3_, _2_,_4_. (2) 0.057 2精确到万__分__位__,有 _3_个有效数字，分别为__5_, _7_, _2__.
（2）0.03086精确到：十万分位或0.00001
（3）2.4万精确到：千位（4）2.40万精确到：百位（5）2.4×103精确到：百位

人教版四年级数学下册小数的近似数(1)

人教版四年级数学下册小数的近似数(1)百度文库――让每个人平等地提升自我5.小数近似数第1课时小数近似数（1）【教学内容】教材第52页例1“做一做”及第54页练习十三第1~2题。

【教学目标】1.能够根据题目建议用四舍五入法精确地求出来一个小数对数数。

2.通过小组讨论、实例分析，知道在表示小数近似数时，末尾0不能去掉，知道在求近似数时，保留小数位数越多结果越精确。

3.通过生活中事例，感受到谋小数对数数在生活中广泛应用。

【重点难点】根据建议用四舍五入法求一个小数对数数。

【教学准备工作】多媒体课件、主题图。

【情景引入】明明妈妈去超市买水果，电子秤上显示总价是22.398元，你认为，妈妈应付给超市多少钱？为什么？学生探讨交流。

小结：由于现在仪器越来越先进，我们日常生活中经常会出现精确到小数点后多位情况，但我们往往没有必要那么精确，只要求出它近似数就可以。

板书：四舍五入法求一个数对数数。

【新课讲授】知识点四舍五入法求一个数近似数出示教材第52页例1：1.一个叫做豆豆小朋友体重――0.984米。

这个数倒是并不大，但数位太多，不好说道不好记，我们可以怎么办？提问：这个三位小数近似数可能是一个什么样数呢？学生讨论交流。

小结：三位小数对数数可能将就是两位小数、一位小数、整数。

提问：求小数近似数通常用什么方法？小结：四舍五入法求小数近似数。

尝试用四舍五入法求小数近似数。

2.（1）试试看，运用四舍五入法把豆豆体重用一个最吻合两位小数则表示出。

说道说道见解。

小结：0.984≈0.98像这样将一个小数百分位后面数字去掉，就可以说成保留两位小数。

回答：说道说道对“留存两位小数”认知。

说道说道留存两位小数方法。

回答：留存两位小数和准确至百分位意思一样吗？小结：保留两位小数和精确到百分位意思一样。

（2）如果将一个小数十分位后面数字去掉，可以怎么说呢？“保留一位小数”是什么意思？请写出结果。

说说保留一位小数方法。

小结：0.984≈1.0提问：0.984保留一位小数时可以写作1吗？小结：强调表示近似数时，小数末尾0不能去掉。

新人教版七年级数学上册第一章《近似数》教案

新人教版七年级数学上册第一章《近似数》教案三维目标一、知识与技能（1）给了一个近似数，你能说出它精确到哪一位，有几个有效数字．（2）给了一个数，会按照精确到哪一位或保留几个有效数字的要求，•四舍五入取近似数．二、过程与方法从测量引入近似数，使学生体会近似数的意义和生活中的应用．三、情感态度与价值观培养学生认真细致的学习态度，合作交流的意识．教学重、难点与关键1．重点：近似数，精确度，有效数字概念．2．难点：由给出的近似数求其精确度及有效数字．3．关键：理解有效数字的概念和小数点末尾的零的意义．四、教学过程，课堂引入1．准确数和近似数．在日常生活和生产实际中，我们接触到很多这样的数．例如：对于参加同一个会议的人数，有两种报道，•一种报道说：“会议秘书处宣布，•参加今天会议的有513人”．这里数字513确切地反映了实际人数，它是一个准确数，另一种报道说： “约有500人参加了今天的会议”，500这个数只能接近实际人数，但与实际人数还有差别，它是一个近似数．例如，统计班上喜欢看球赛同学的人数是35，这个数是与实际完全符合的准确数，一个也不多，一个也不少，又如，初一（1）班有55个学生，某工厂有126台机床，•我有8本练习本，这些数都是与实际完全符合的准确数．如果量得语文课本的宽为13.5cm，由于所用尺的刻度有精确度限制，而且用眼观察时不可能非常细致，因此与实际宽度有一点偏差，这里的13.5cm只是一个与实际宽度非常接近的数，又如，宇宙现在的年龄约为200亿年，长江长约6300千米，•圆周率约为3.14，这些数都是近似数．五、新授在许多情况下，很难取得准确数，或者不必使用准确数，而可以使用近似数．你还能举出一些日常遇到的近似数吗？2．关于精确度问题近似数与准确数的接近程度，可以用精确度表示，例如，前面的500是精确到百位的近似数，它与准确数513的误差为13．我们都知道圆周率π=3.141592…计算时我们需按照要求取近似数．如果要求按四舍五入精确到个位，那么≈3；如果要求按四舍五入精确到0.1（或精确到十分位），那么π≈3.1；如果要求按四舍五入精确到0.01（或精确到百分位），那么π≈3.14；如果要求按四舍五入精确到0.001（或精确到千分位），那么π≈_______；反过来，若π≈3.1416，那么精确到________，或叫精确到_______．一般地，一个近似数，四舍五入到哪一位，就说这个近似数精确到哪一位．3．近似数的有效数字．一个近似数，从左边第一个不是零的数字起，到末位数字止，•所有数字都是这个数的有效数字，一共包含的有效数字的个数，叫这个近似数的有效数字的个数．例如近似数0.025有两个有效数字：2，5；1500有4个有效数字：1，5，0，0；0.103•有有3个有效数字：1，0，3．对于用科学记数法表示的数a×10n，规定它的有效数字就是a中的有效数字，例如近似数5.104×106有4个有效数字：5，1，0，4．规定有效数字的个数，也是对近似数精确程度的一种要求．一般说，对于同一个数取近似数时，有效数字个数越多，精确程度越高．如果四舍五入法对π取近似数时，若要求保留1个有效数字，则π≈3；若要求保留3个有效数字，•则π≈3.14．例6：按括号内的要求，用四舍五入法对下列数取近似数．（1）0.0158（保留2个有效数字）；（2）30435（保留2个有效数字）；（3）1.804（保留2个有效数字）；（4）1.804（保留3个有效数字）；（5）3.5046（精确到百分位）；（6）2.971×104（保留2个有效数字）．解：（1）0.0158≈0.016；（2）30435=3.0435≈104≈3.04≈104（或3.04万）；（3）1.804≈1.8；（4）1.804≈1.80；（5）3.5049≈3.50；（6）2.971×104≈3.0×104．思路点拨：（2）题，不能写成30435≈30400，如果这样写，•那就看不出哪些是保留的有效数字，而近似数30400是有5个有效数字，所以做这类题，•先将它用科学记数法表示，再按照规定保留有效数字，或者写成3.04万．（4）题中，1.80，这里的0不能去掉，由四舍五入得到的1.8与1.80的精确度是不同的，前者是精确到0.1，是保留2个有效数字，而后者是精确到0.01，保留3个有效数字，同理（6）题中3.0×104的0也不能丢了．（5）题，不能先约等于3.505，再约等于3.51，四舍五入精确到百分位，•是将千分位四舍五入，与千分位后面的数字无关．例7：下列是由四舍五入法得到的近似数，各精确到哪一位？保留几个有效数字？（1）132.4；（2）0.0572；（3）2.40万；（4）3000．解：（1）132.4是精确到0.1，保留4个有效数字．（2）0.0572是精确到0.0001，保留3个有效数字．（3）2.40万是精确到百位，保留3个有效数字．（4）3000是精确到个位，保留4个有效数字．六、巩固练习1．课本第46页练习．七、课堂小结正确理解和掌握近似数、准确数和有效数字的概念，给出一个近似数，能准确地确定它精确到哪一位，有哪几个有效数字，并能按要求求一个数的近似数．八、作业布置1．课本第47页至第48页习题1．5第6、7、11题．九、板书设计：1.5.3 近似数第四课时1．一个近似数，从左边第一个不是零的数字起，到末位数字止，•所有数字都是这个数的有效数字，一共包含的有效数字的个数，叫这个近似数的有效数字的个数．2、随堂练习。

人教版小学四年级数学下册求一个小数的近似数(例1)

1、求小数的近似数可以用什么方法？
2、怎样求一个小数保留两位小数的近似数？
3、怎样求一个小数保留一位小数的近似数？
(自学时间3分钟左右）
保留两位小数，试着写一写：
保留到百分位，省略后面的尾数
0.984 ≈0.98 ▲
保留两位小数，看小数部分第三位。小数部分的第三位是4应该舍去。
保留一位小数，试着写一写
想一想:
全课小结
你有哪些收获？在哪方面还需努力？
他们是怎样得出豆豆身高的近似数的？
学习目标：
能根据要求正确地运用“四舍五入法”保留一定的小数数位,求出一个小数的近似数．
豆豆的身高是0.984米：
实际应用小数时，没有必要说出它的准确数，只要求它的近似数就可以了。
100
90
0.984米
同位讨论：
0.984的近似数是多少呢？
自学思考题:
（ 15 ）< 15.83 < （ 16 ）
5、按四舍五入法写出表中各小数的近似数。
保留保留一保留两整数位小数位小数 9.956 10 10.0 9.96 0.905 1 0.9 0.91 51.463 51 51.5 51.46
ቤተ መጻሕፍቲ ባይዱ
一个两位小数精确到十分位后大约是3.2，那么这个两位数最大可能是几？最小可能是几？
在表示近似数时，小数末保尾留的到0不十能分去位掉。，省略后面的尾数。
0.984 ≈1.0
▲
保留一位小数，看小数部分的第二位。 8应该往前进一，而前一位是9， 9加上1得10，满十又要向前一位进一，也就是要向个位进一。
保留整数，试着写一写
保留到个位，省略小数部分。
0.984 ≈1

《近似数》ppt课件人教版1

⑴0.6328
(精确到0.001)
⑵7.9122
(精确到个位)
⑶47155
(精确到百位)
⑷130.06
(精确到0.1)
⑸460215
(精确到百位)
⑹2.746
（精确到十分位）
⑺3.40105 (精确到万位）
2 下列由四舍五入得到的近似数，各精确到哪一位？
（1） 600万；（2） 7.03万；
（3） 5.8亿
问题2：近似数与准确数有何区别？
(4)2.4 10 精确到______。千位例0020：1，用或四叫舍做五精入确法到，万按分括位号）中4，的要求对下列各数取近似数。
解：30542 ≈3.
5 km外去郊游，大约玩了 4.
金钥匙： 4 104精确到______。
⑷30542 (精确到百位)
近似数精确到哪一位，只需看这
（1） 600万；
例如，2016年全国高考报名
⑸460215 (精确到百位)
（有3时）实5际. 问题中的无需考得到生准确共数据940万人.
5 km外去郊游，大约玩了 4.
4精确到______。
9122 (精确到个位)
所以应该租用10辆客车。
2．小民与小李买了 2 瓶水，4 根黄瓜，6 袋香巴拉牛肉干，约 20 元，然后骑车去大约 3.
（1） 600万；
1·5·3 近似数
解：因为100 6=16.
5 km外去郊游，大约玩了 4. 精确度—— 近似数与准确数的接近程度可以用精确度表示. 有时实际问题中无需得到准确数据
与实际非常
⑸460215 (精确到百位) 用四舍五入法，按括号中的要求对下列各数取近似数。
接近的数

人教版七年级数学上册：1.5.3 《近似数》教学设计

人教版七年级数学上册：1.5.3 《近似数》教学设计一. 教材分析人教版七年级数学上册1.5.3《近似数》是学生在学习了有理数、实数等基础知识后，对数的进一步理解。

本节内容主要介绍近似数的概念、求法及其应用，通过学习，使学生掌握求近似数的方法，能够准确地运用近似数进行计算和估算，为后续的学习和实际应用打下基础。

二. 学情分析七年级的学生已经具备了一定的数学基础，对实数、有理数等概念有了初步的了解。

但学生在求近似数方面可能还存在一定的困难，因此，在教学过程中，需要注重引导学生理解近似数的概念，以及如何准确地求出近似数。

三. 教学目标1.理解近似数的概念，掌握求近似数的方法。

2.能够准确地运用近似数进行计算和估算。

3.培养学生的数感，提高学生的数学思维能力。

四. 教学重难点1.近似数的概念及其求法。

2.运用近似数进行计算和估算。

五. 教学方法采用情境教学法、启发式教学法和小组合作学习法。

通过生活实例引入近似数的概念，引导学生主动探究求近似数的方法，并在小组合作中互相交流、讨论，从而达到理解掌握的目的。

六. 教学准备1.教学课件：制作课件，展示近似数的定义、求法及应用。

2.教学素材：准备一些生活实例，用于引入近似数的概念。

3.练习题：准备一些练习题，用于巩固所学知识。

七. 教学过程1.导入（5分钟）利用生活实例，如购物时找零、测量身高等，引导学生思考：什么是近似数？为什么要用近似数？从而引出本节内容。

2.呈现（10分钟）介绍近似数的定义，通过课件展示，使学生对近似数有直观的认识。

接着讲解求近似数的方法，如四舍五入、进一法、去尾法等，并给出具体例子，让学生明白各种方法的适用场景。

3.操练（10分钟）学生在课堂上进行近似数的计算练习，教师巡回指导，解答学生疑问。

练习题可包括简单的生活实例和计算题，让学生在实际操作中掌握求近似数的方法。

4.巩固（10分钟）学生分组进行小组讨论，总结近似数的求法及其应用。

教师引导学生归纳总结，加深对知识点的理解。

人教版四年级下册4-5小数的近似数(一)(例1)

百分位是满十向前一位进1
9.0548≈ 9.1
小于5，舍去。
大于5，向前一位进1。等于5，向前一位进1。
姚明叔叔：2.260米
小曾同学：1.559米
李老师：1.603米
姚明叔叔、小曾同学和李老师都约2米高！
火眼金睛按要求写出表中三人身高值的近似数。
保留整数保留一位小数保留两位小数
2.260米（姚明叔叔）
谢谢观看！
四年级—人教版—数学—第四单元
答疑环节
答疑解惑
课本55页第6题：下面的说法都正确吗？正确的画“√”，错误的画“×”。
（1）3.56精确到十分位是4。
（）
（2）6.05和6.0599保留一位小数都是6.1。（）
（3）近似数是6.32的三位小数不止一个。（）
（4）5.29在自然数5和6之间，它约等于5。（）
类比求0.984的近似数。
保留整数的方法是什么？
（1）保留两位小数
0.984≈ 0.98
小于5，舍去。
（2）保留一位小数
0.984≈ 1.0
大于5，向前一位进1。
（3）保留整数
0.984≈ 1
大于5，向前一位进1。
保留整数，表示精确到个位，就要把十分位上和后面的数省略。要看十分位上的数，运用“四舍五入”法。
1.559米（小曾同学）
1.603米（李老师）
2
2.3
2.26
2
1.6
1.56
2
1.6
小曾同学和李老师约1.6米！
1.60
二年级下册：万以内数的近似数
课堂总结
四年级上册：求整数的近似数
在表示近似数时，小数末尾的0不能去掉。