最小二乘法公式
最小二乘法求a,b的公式

最小二乘法求a,b的公式
用最小二乘法求回归直线方程中的a,b有下面的公式:
最小二乘法:总离差不能用n个离差之和来表示,通常是用离差的平方和,即作为总离差,并使之达到最小,这样回归直线就是所有直线中Q取最小值的那一条,这种使“离差平方和最小”的方法,叫做最小二乘法:
由于绝对值使得计算不变,在实际应用中人们更喜欢用:Q=(y1-bx1-a)?(y2-bx-a 玻?。
+(yn-bxn-a)? 这样,问题就归结于:当a,b取什么值时Q最小,即到点直线y=bx+a的“整体距离”最小。
扩展资料:
回归分析的最初目的是估计模型的参数以便达到对数据的最佳拟合。
在决定一个最佳拟合的不同标准之中,最小二乘法是非常优越的。
这种估计可以表示为:
1)样本是在母体之中随机抽取出来的。
2)因变量Y在实直线上是连续的,
3)残差项是独立同分布的,也就是说,残差是独立随机的,且服从高斯分布。
这些假设意味着残差项不依赖自变量的值,所以和自变量X(预测变量)之间是相互独立的。
在这些假设下,建立一个显示线性回归作为条件预期模型的简单线性回归方程,可以表示为:
给一个随机样本,一个线性回归模型假设回归子和回归量之间的关系是除了X的影响以外,还有其他的变数存在。
我们加入一个误差项(也是一个随机变量)来捕获除了之外任何对的影响。
最小二乘法LSQ(least square)_计算公式

的一个二元函数, 把 M 看成自变量 a 和 b 的一个二元函数, 那么问题就可归结为求函数 M = M ( a , b ) 在那 些点处取得最小值. 些点处取得最小值
7 ∂M ∂a = −2∑ [ yi − (at i + b )]t i = 0, i =0 令 7 ∂M = −2∑ [ yi − (at i + b )] = 0; ∂b i =0
7 7 7
(1)
计算得
∑t
i =0 7 i =0
7
i
= 28, = 208.5,
∑t
i =0 7 i =0
7
2 i
= 140, = 717.0
∑y
i
∑yt
i i
代入方程组( ) 代入方程组(1)得
140a + 28b = 717, 28a + 8b = 208.5.
解此方程组, 解此方程组,得到 a = −0.3036, b = 27.125. 这样便得到所求经验公式(回归方程 为 这样便得到所求经验公式 回归方程 )为
在研究单分子化学反应速度时,得到下列数据: 例2 在研究单分子化学反应速度时,得到下列数据:
i
1 3
2 6
3 9
4 12
5 15
6 18
7 21 8.9
8 24 6.5
τi
yi
57.6 41.9 31.0 22.7 16.6 12.2
y 表示从实验开始算起的时间, 其中 τ 表示从实验开始算起的时间, 表示时刻τ 反应物的量. 反应物的量.试定出经验公式 y = f (τ ).
试根据上面的试验数据建立 y 和 t 之间的经验公 式 y = f (t ).
最小二乘法与最小二分法

最小二乘法公式最小二乘法公式∑(X--X平)(Y--Y平)=∑(XY--X平Y--XY平+X平Y平)=∑XY--X平∑Y--Y平∑X+nX平Y平=∑XY—nX平Y平--nX平Y平+nX平Y平=∑XY--nX 平Y平∑(X --X平)^2=∑(X^2--2XX平+X平^2)=∑X^2--2nX平^2+nX平^2=∑X^2--nX平^2编辑本段最小二乘法原理用各个离差的平方和M=Σ(i=1到n)[yi-(axi+b)]^2最小来保证每个离差的绝对值都很小。
解方程组?M/?a=0;?M/?b=0,整理得(Σxi^2)a+(Σxi)b=Σxiyi;(Σxi)a+nb=Σyi。
解出a,b。
在我们研究两个变量(x, y)之间的相互关系时,通常可以得到一系列成对的数据(x1, y1、x2, y2... xm , ym);将这些数据描绘在x -y直角坐标系中, 若发现这些点在一条直线附近,可以令这条直线方程如(式1-1)。
Y计= a0 + a1 X (式1-1)其中:a0、a1 是任意实数为建立这直线方程就要确定a0和a1,应用《最小二乘法原理》,将实测值Yi与利用(式1-1)计算值(Y计=a0+a1X)的离差(Yi-Y计)的平方和〔∑(Yi - Y计)2〕最小为“优化数据”。
令: φ = ∑(Yi - Y计)2 (式1-2)把(式1-1)代入(式1-2)中得:φ = ∑(Yi - a0 - a1 Xi)2 (式1-3)当∑(Yi-Y计)平方最小时,可用函数φ对a0、a1求偏导数,令这两个偏导数等于零。
(式1-4)(式1-5)亦即:m a0 + (∑Xi ) a1 = ∑Yi (式1-6)(∑Xi ) a0 + (∑Xi2 ) a1 = ∑(Xi, Yi) (式1-7)得到的两个关于a0、 a1为未知数的两个方程组,解这两个方程组得出:a0 = (∑Yi) / m - a1(∑Xi) / m (式1-8)a1 = [n∑Xi Yi - (∑Xi ∑Yi)] / [n∑Xi2 - (∑Xi)2 )] (式1-9) 这时把a0、a1代入(式1-1)中, 此时的(式1-1)就是我们回归的元线性方程即:数学模型。
最小二乘法原理

最小二乘法最小二乘法是一种在误差估计、不确定度、系统辨识及预测、预报等数据处理诸多学科领域得到广泛应用的数学工具。
最小二乘法还可用于曲线拟合,其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
最小二乘法公式:设拟合直线的公式为,其中:拟合直线的斜率为:;计算出斜率后,根据和已经确定的斜率k,利用待定系数法求出截距b。
在我们研究两个变量(x, y)之间的相互关系时,通常可以得到一系列成对的数据(x1, y1),(x2, y2).. (xm , ym);将这些数据描绘在x -y 直角坐标系中(如图1), 若发现这些点在一条直线附近,可以令这条直线方程如(式1-1)。
Y计= a0 + a1 X (式1-1)其中:a0、a1 是任意实数为建立这直线方程就要确定a0和a1,应用《最小二乘法原理》,将实测值Yi与利用(式1-1)计算值(Y计=a0+a1X)的离差(Yi-Y计)的平方和〔∑(Yi - Y计)²〕最小为“优化判据”。
令: φ= ∑(Yi - Y计)² (式1-2)把(式1-1)代入(式1-2)中得:φ= ∑(Yi - a0 - a1 Xi)2 (式1-3)当∑(Yi-Y计)²最小时,可用函数φ对a0、a1求偏导数,令这两个偏导数等于零。
(式1-4)(式1-5)亦即m a0 + (∑Xi ) a1 = ∑Yi (式1-6)(∑Xi ) a0 + (∑Xi2 ) a1 = ∑(Xi, Yi) (式1-7)得到的两个关于a0、a1为未知数的两个方程组,解这两个方程组得出:a0 = (∑Yi) / m - a1(∑Xi) / m (式1-8)a1 = [∑Xi Yi - (∑Xi ∑Yi)/ m] / [∑Xi2 - (∑Xi)2 / m)] (式1-9) 这时把a0、a1代入(式1-1)中, 此时的(式1-1)就是我们回归的元线性方程即:数学模型。
普通最小二乘法的原理

普通最小二乘法的原理
普通最小二乘法(Ordinary Least Squares,OLS)是用来估计参数最受欢迎
的线性回归方法。
它用来估计线性模型中的参数,也就是方程的未知数。
其假设是,观测值之间没有任何关系,这里就不考虑协变量间的相关性,而且所有观测值都是模型下的服从正态分布。
普通最小二乘法的计算公式如下:设现有数据集X和Y,X是样本变量矩阵,Y
为结果变量矩阵。
设B是需要推断的各参数的系数,则可以用最小二乘法表示为:
min((Y-XB)T (Y-XB))
将以上公式求导,得到最优解B(hat):
B(hat) =(XT*X)-1 * XT*Y
普通最小二乘法旨在找到能够最好地拟合观测值的参数系数,其假设是数据
集中每一对观测值互相独立,由于回归模型是线性的,所以每个变量与回归模型的关系也是线性的。
普通最小二乘法最重要的优点是可以更准确地估算参数。
在大数据量的情况下,它可以更好地拟合观测值,而且它既可以解决多变量回归模型,也可以解决只有一个变量的单变量回归。
然而,普通最小二乘法也有缺点,最明显的是它无法检测出某个变量与观测值
之间的关系,它只能计算出每个变量与观测值之间的差异。
如果存在异常值,它可能造成过拟合,影响模型的准确性。
总的来说,普通最小二乘法是统计学中最有用的估计参数的方法,具有较高的
准确度和较快的收敛速度,因此被广泛地使用和推广。
平面度最小二乘法公式和原理

平面度最小二乘法公式和原理一、引言在工程领域中,我们经常需要对平面度进行评估和测量。
平面度是指一个物体或表面与一个理想平面之间的偏差程度。
平面度评估的目的是为了确定物体或表面是否符合设计要求。
平面度最小二乘法是一种常用的评估方法,本文将介绍其公式和原理。
二、平面度最小二乘法公式平面度最小二乘法的公式可以用数学语言描述如下:假设我们有n个待测点,分别表示为(xi, yi),其中i从1到n。
我们需要找到一个平面方程z = f(x, y),使得所有的点(xi, yi, zi)到这个平面的距离之和最小。
平面方程f(x, y)可以表示为:f(x, y) = ax + by + c其中a、b和c是待求的系数。
我们的目标是最小化所有点到这个平面的距离之和,即最小化以下目标函数:E = Σ[(axi + byi + c - zi)^2]我们需要找到a、b和c的取值,使得目标函数E达到最小值。
三、平面度最小二乘法原理平面度最小二乘法的原理是基于最小化误差的思想。
通过调整平面方程的系数a、b和c,我们可以使得所有点到这个平面的距离之和最小。
具体来说,我们可以使用最小二乘法的优化算法,例如梯度下降法或牛顿法,来求解最小化目标函数的系数a、b和c。
这些优化算法会迭代地调整系数的取值,直到目标函数达到最小值。
在实际应用中,我们可以使用计算机编程语言来实现这些优化算法,以自动化地求解系数的取值。
通过输入待测点的坐标和高度,我们可以得到最佳的平面方程,从而评估平面度。
四、应用案例平面度最小二乘法广泛应用于工程领域。
以下是一些应用案例:1. 汽车制造:在汽车制造过程中,平面度评估是确保车身和零件质量的关键步骤。
通过使用平面度最小二乘法,制造商可以检查车身表面的平整度,以确保其符合设计要求。
2. 电子制造:在电子产品的制造过程中,平面度评估对于保证电路板和元器件的连接性和稳定性非常重要。
通过使用平面度最小二乘法,制造商可以检查电路板表面的平整度,以确保其能够正常工作。
最小二乘法

最小二乘法1. 最小二乘法原理:最小二乘法是常用的线性拟合方法,原理和计算公式简述如下:假定线性关系为y kx b =+,做N 次实验得到'i i y kx b =+,式中与假定关系比较误差为,'21()N i i i W yy ==-∑。
为了使W 值最小,应有0,0WWk b ∂∂==∂∂。
于是得到求解k 、b 的方程式为,211111NN N i i i i i i i N N i ii i k x b x x y k x bN y =====+=+=∑∑∑∑∑,计算求得斜率k 与截距b 的值。
2. 数据处理:电压值经过运放输出到AD 转换器,然后由AD 转换得到一个数值。
在这个过程中,从0.0000到10.0000间隔1.0000取一个值共11个输入值,对应这11个输入值有11个最终的输出值。
依据这11组不同的数据,我们可以依据最小二乘法来求得一个线性关系:y = k*x + b 。
3. 程序设计:(1) 从文本文件中读取输入输出值。
文本文件的格式为:两列数据,第一列为输入数据,第二列为输出数据。
(2) 对于数据利用最小二乘法进行计算求得直线的斜率和截距。
具体步骤为:1)计算输入x 数组的叠加和xtotal 和平方和xsqua ;计算输出y 数组的叠加和ytotal 和平方和ysqua ,以及xy 乘积的叠加和xymul ;2)计算sxx=xsqua-xtotal*xtotal/11,syy=ysqua-ytotal-ytotal,sxy=xmul-xtotal*ytotal/11;3)计算斜率k 和截距b 。
xaver=xtotal/11,yaver=ytotal/11,k=sxy/sxx,b=yaver-k*xaver 。
(3) 计算误差百分比。
具体步骤为:1)计算输入x 条件下的输出拟和值yy[I]=k*x[I]+b ;2)计算拟和值与测量值的差值diff[I]=yy[I]-y[I];3)计算误差百分比per[I]=diff[I]/y[I]。
最小二乘法系数计算公式

最小二乘法系数计算公式最小二乘法系数计算公式这玩意儿,在数学和统计学里那可是相当重要!咱先来说说啥是最小二乘法。
打个比方,你想研究身高和体重之间有没有啥关系。
你找了一堆人,量了他们的身高和体重。
这一堆数据放那,看起来乱哄哄的,你就想找个规律,让一条线能尽量好地穿过这些数据点。
这条线呢,就是通过最小二乘法算出来的。
那最小二乘法系数计算公式到底是啥呢?其实就是通过一些数学运算,找到能让实际数据点和预测线之间的误差平方和最小的系数。
比如说,有一组数据(x1,y1),(x2,y2),……,(xn,yn)。
我们设要拟合的直线方程是 y = a + bx 。
那误差平方和 S 就等于(y1 - (a + bx1))² + (y2 - (a + bx2))² + …… + (yn - (a + bxn))²。
为了找到让 S 最小的 a 和 b ,就得用一些数学方法来算啦。
这计算过程啊,可有点复杂,得用到求偏导数啥的。
我记得有一次,给学生们讲这个的时候,有个小家伙一脸懵地看着我,说:“老师,这咋这么难啊!”我就跟他说:“别着急,咱们一步步来。
”然后我带着他们从最简单的例子开始,一个数据一个数据地分析,慢慢他们就有点感觉了。
其实在实际生活中,最小二乘法的用处可大了。
比如说预测股票的走势,虽然不能百分百准确,但能给咱一个大概的参考。
或者分析某个产品的销量和广告投入之间的关系,帮助企业做决策。
还有啊,搞科研的时候也经常用到。
比如研究气候变化和某些因素的关系,通过最小二乘法找到规律,就能更好地预测未来的气候变化。
学习最小二乘法系数计算公式,一开始可能会觉得头疼,但只要多做几道题,多琢磨琢磨,慢慢就会发现其中的乐趣。
就像解谜一样,当你算出正确的系数,找到那条最合适的线,那种成就感可太棒啦!所以啊,同学们,别害怕这个小小的难题,加油去攻克它,你会发现数学的世界里有很多奇妙的东西等着你们去探索呢!。
线性回归之最小二乘法
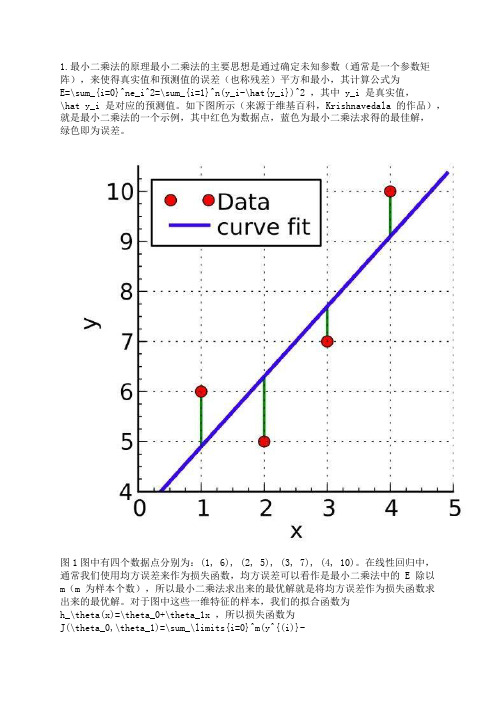
1.最小二乘法的原理最小二乘法的主要思想是通过确定未知参数(通常是一个参数矩阵),来使得真实值和预测值的误差(也称残差)平方和最小,其计算公式为E=\sum_{i=0}^ne_i^2=\sum_{i=1}^n(y_i-\hat{y_i})^2 ,其中 y_i 是真实值,\hat y_i 是对应的预测值。
如下图所示(来源于维基百科,Krishnavedala 的作品),就是最小二乘法的一个示例,其中红色为数据点,蓝色为最小二乘法求得的最佳解,绿色即为误差。
图1图中有四个数据点分别为:(1, 6), (2, 5), (3, 7), (4, 10)。
在线性回归中,通常我们使用均方误差来作为损失函数,均方误差可以看作是最小二乘法中的 E 除以m(m 为样本个数),所以最小二乘法求出来的最优解就是将均方误差作为损失函数求出来的最优解。
对于图中这些一维特征的样本,我们的拟合函数为h_\theta(x)=\theta_0+\theta_1x ,所以损失函数为J(\theta_0,\theta_1)=\sum_\limits{i=0}^m(y^{(i)}-h_\theta(x^{(i)}))^2=\sum_\limits{i=0}^m(y^{(i)}-\theta_0-\theta_1x^{(i)})^2 (这里损失函数使用最小二乘法,并非均方误差),其中上标(i)表示第 i 个样本。
2.最小二乘法求解要使损失函数最小,可以将损失函数当作多元函数来处理,采用多元函数求偏导的方法来计算函数的极小值。
例如对于一维特征的最小二乘法, J(\theta_0,\theta_1) 分别对 \theta_0 , \theta_1 求偏导,令偏导等于 0 ,得:\frac{\partial J(\theta_0,\theta_1)}{\partial\theta_0}=-2\sum_\limits{i=1}^{m}(y^{(i)}-\theta_0-\theta_1x^{(i)}) =0\tag{2.1}\frac{\partial J(\theta_0,\theta_1)}{\partial\theta_1}=-2\sum_\limits{i=1}^{m}(y^{(i)}-\theta_0-\theta_1x^{(i)})x^{(i)} = 0\tag{2.2}联立两式,求解可得:\theta_0=\frac{\sum_\limits{i=1}^m(x^{(i)})^2\sum_\limits{i=1}^my^{(i)}-\sum_\limits{i=1}^mx^{(i)}\sum_\limits{i=1}^mx^{(i)}y^{(i)}}{m\sum_\limits{i=1}^m(x^{(i)})^2-(\sum_\limits{i=1}^mx^{(i)})^2} \tag{2.3}\theta_1=\frac{m\sum_\limits{i=1}^mx^{(i)}y^{(i)}-\sum_\limits{i=1}^mx^{(i)}\sum_\limits{i=1}^my^{(i)}}{m\sum_\limits{i=1}^m(x^{(i)})^2-(\sum_\limits{i=1}^mx^{(i)})^2} \tag{2.4}对于图 1 中的例子,代入公式进行计算,得: \theta_0 = 3.5, \theta_1=1.4,J(\theta) = 4.2 。
最小二乘法

性质2:只要适当大,总成立:S( xk z) S( xk ).
性质3:当充分大时,方向z与方向 S( xk )充分接近。
6.采用进退方法调整:一次成功迭代后将缩小,迭代 遇到困难时将放大。
Ax * b 2 A 2 可见,当δ 0时取到最小值.
例
给定方程组
2 x1 x1
2x2 2x2
3 1
,
试用最小二乘法求此方程组
x1 4 x2 3
的近似解。
解:令 F ( x) ( 2x1 2x2 3 )2 ( x1 2x2 1)2 ( x1 4x2 3 )2 ,
(3)
性质:若f(x)满足一定条件且x0充分接近x *,
则: (1)由迭代得到的{ x k }是收敛的; (2) 在一定条件下,收敛阶是二阶的。
3.改进的Gauss-Newton法:
因为S( x)
m
2
fi ( x)fi ( x)
2 AT
(x)
f
(x),
i 1
记 Hk 2 AkT Ak , 则Hk 是 ( x) 在点 xk 的Hesse 矩阵。
f1
其中
A(
x
k
)
x1
fm
x1
... ...
f1
xn
fm
xn
(
fi ( x x j
k
)
)mn
。
x xk
记 Ak A( x k ) , 则有
S( x) f ( xk ) Ak ( x xk ) 2 Akd k f ( xk ) 2
[ Akd k f ( x k ) ]T [ Akd k f ( x k ) ], 其中:d k x xk。 记 ( x) [ Akd k f ( xk ) ]T [ Akd k f ( xk ) ],则可用min ( x) 的极小点近似原问题的极小点。
最小二乘法的公式

最小二乘法的公式最小二乘法是一种常用的回归分析方法,用来寻找一个线性模型来拟合给定的数据。
最小二乘法的目标是最小化实际数据与拟合模型之间的残差平方和,即找到使得残差平方和最小的系数。
在回归分析中,最小二乘法是一种经典的统计学方法,有着广泛的应用。
一般来说,给定一个数据集,我们需要找到一个线性模型,使得该模型能最好地拟合这些数据。
这个线性模型可以通过最小二乘法来求解,具体的公式如下:1. 线性模型公式假设我们的数据集包含了n个样本数据,每个数据由p个特征和一个目标变量组成。
我们可以将每个样本数据表示为一个向量,并将这些向量组合成一个矩阵X,其中X的维度是n x p,n为样本数量,p为特征数量。
我们的目标是找到一个系数向量β,使得线性模型的预测值与实际值之间的残差平方和最小。
我们用y表示实际值,用Xβ表示线性模型的预测值,残差向量为ε = y - Xβ。
2. 残差平方和的最小化为了最小化残差平方和,我们需要最小化ε的平方和。
我们可以用L2范数(欧氏距离)来度量残差向量的长度,即我们的目标是最小化||ε||^2。
所以,我们的最小二乘法的公式可以表述为:min ||ε||^2 = min (y - Xβ)^T(y - Xβ)为了求解这个最小化问题,我们需要计算残差平方和的导数,并令导数为0,从而找到导数为0时的系数β。
3. 求解最小二乘法的一般公式求解最小二乘法的公式可以通过求导的方式来推导,具体的推导过程比较繁琐,这里我们直接给出最后的结果。
设关于β的残差平方和为F(β),则我们需要求解的最优解β的一般公式为:∂F(β)/∂β = -2X^T(y - Xβ) = 0整理方程,我们可以得到最小二乘法的一般公式:X^T(y - Xβ) = 0我们可以进一步解这个等式,求得β的一般解:β = (X^TX)^(-1)X^Ty其中,(X^TX)^(-1)表示X^TX的逆矩阵。
通过这个公式,我们可以计算出最小二乘法的系数β,从而得到拟合数据的线性模型。
最小二乘法公式

最小二乘法公式
最小二乘法公式是一个数学的公式,在数学上称为曲线拟合,此处所讲最小二乘法,专指线性回归方程!最小二乘法公式为b=y(平均)-a*x(平均)。
拓展资料:
曲线拟合俗称拉曲线,是一种把现有数据透过数学方法来代入一条数式的表示方式。
科学和工程问题可以通过诸如采样、实验等方法获得若干离散的数据,根据这些数据,我们往往希望得到一个连续的函数(也就是曲线)或者更加密集的离散方程与已知数据相吻合,这过程就叫做拟合。
回归直线a与b最小二乘法

回归直线a与b最小二乘法
在回归分析中,最小二乘法是一种常用的方法,用于估计自变量与因变量之间的线性关系。
最小二乘法本质上是寻找一条直线,使得这条直线与所有数据点的距离的平方之和最小。
回归直线的系数 a 和 b 的计算公式如下:
b = (nΣxy - ΣxΣy) / (nΣx^2 - (Σx)^2)
a = (Σy - bΣx) / n
其中,n 表示样本数量,Σ表示求和。
x 和y 分别表示自变量和因变量的取值,而xy 表示x 和y 的积。
通过计算样本数据的x、y、xy、x^2 四个统计量的和,就可以求得回归直线的系数 a 和b。
一般来说,最小二乘法的计算可以借助统计软件或Excel 等电子表格软件完成。
在Excel 中,可以使用“线性回归”功能,自动计算出回归直线的系数 a 和b。
具体操作步骤为:在相邻的两列中输入自变量和因变量数据,然后使用“数据分析”工具中的“回归”命令,选择自变量和因变量数据的输入范围及其他参数,即可计算出回归直线的系数。
最小二乘法

最小二乘法一、简介最小二乘法(又称最小平方法)是一种数学优化技术。
它通过最小化误差的平方和寻找数据的最佳函数匹配。
利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
最小二乘法还可用于曲线拟合。
本文主要讲直线拟合。
二、最小二乘法原理在我们研究两个变量(x,y )之间的相互关系时,通常可以得到一系列成对的数据(x 1,y 1.x 2,y 2... x m ,y m );将这些数据描绘在x -y 直角坐标系中,若发现这些点在一条直线附近,可以令这条直线方程如下: x a y 10a +=计 (式1-1)其中:a 0、a 1 是任意实数为建立这直线方程就要确定a 0和a 1,将实测值y i 与利用(式1-1)计算值的离差计y y i -的平方和2)(∑-计y y i 最小为“优化判据”。
令:2)(∑-=计y y i ϕ (式1-2)把(式1-1)代入(式1-2)中得:210)(∑--=i i x a a y ϕ (式1-3)要求φ最小值,可用函数 φ 对a 0、a 1 求偏导数,令这两个偏导数等于零:)51(0)(x 2)41(0)(2101100-=---=∂∂-=---=∂∂∑∑式式i i i i i x a a y a x a a y a ϕϕ 亦即:)7-1()x ()x ()6-1()(12i 010式式∑∑∑∑∑=+=+i i i i i y x a a y a x ma得到的两个关于a0、 a1为未知数的两个方程组,解这两个方程组得出: )9-1()()8-1()(22110式式∑∑∑∑∑∑∑--=-=i i i i i i i i x x m y x y x m a m x a y a或 ∑∑∑∑∑∑--=2220)()()(i i i i i i i x x m y x x y x a把a 0、a 1 代入(式1-1)中即可。
在统计学中,这种最小二乘拟合通常成为线性回归。
最小二乘公式

最小二乘法公式最小二乘法公式∑(X--X平)(Y--Y平)=∑(XY--X平Y--XY平+X平Y平)=∑XY--X平∑Y--Y平∑X+nX平Y平=∑XY--nX平Y平--nX平Y平+nX平Y平=∑XY--nX平Y平∑(X --X平)^2=∑(X^2--2XX平+X平^2)=∑X^2--2nX平^2+nX平^2=∑X^2--nX平^2最小二乘公式(针对y=ax+b形式):a=(NΣxy-ΣxΣy)/(NΣx^2-(Σx)^2)b=y(平均)-ax(平均)最小二乘法在我们研究两个变量(x, y)之间的相互关系时,通常可以得到一系列成对的数据(x1, y1、x2, y2 (x)m , y m);将这些数据描绘在x -y直角坐标系中(如图1), 若发现这些点在一条直线附近,可以令这条直线方程如(式1-1)。
Y计= a0 + a1 X (式1-1)其中:a0、a1 是任意实数为建立这直线方程就要确定a0和a1,应用《最小二乘法原理》,将实测值Y i与利用(式1-1)计算值(Y计=a0+a1X)的离差(Y i-Y计)的平方和〔∑(Y i -Y计)2〕最小为“优化判据”。
令: φ = ∑(Y i -Y计)2 (式1-2)把(式1-1)代入(式1-2)中得:φ = ∑(Y i -a0 - a1 Xi)2 (式1-3)当∑(Y i-Y计)平方最小时,可用函数φ 对a0、a1求偏导数,令这两个偏导数等于零。
(式1-4)(式1-5)亦即:m a0 + (∑Xi )a1 = ∑Y i (式1-6)(∑Xi )a0 + (∑Xi2 )a1 = ∑(Xi, Yi) (式1-7)得到的两个关于a0、a1为未知数的两个方程组,解这两个方程组得出:a0 = (∑Y i)/ m -a1(∑Xi) / m (式1-8)a1 = [∑Xi Y i - (∑Xi ∑Y i)/ m] / [∑Xi2 - (∑Xi)2 / m)] (式1-9)这时把a0、a1代入(式1-1)中, 此时的(式1-1)就是我们回归的元线性方程即:数学模型。
最小二乘法拟合曲线公式

最小二乘法拟合曲线公式
最小二乘法是一种常用的数学方法,可以用来拟合一条曲线,使得曲线上的点与实际观测值的误差最小化。
最小二乘法拟合曲线的公式为:
y = a + bx
其中,y 是因变量,x 是自变量,a 和 b 是拟合曲线的系数。
最小二乘法通过最小化误差平方和来确定 a 和 b 的值,即:
b = (n∑xy - ∑x∑y) / (n∑x^2 - (∑x)^2)
a = (∑y - b∑x) / n
其中,n 是数据点的个数,∑表示求和符号,x 和 y 分别表示自变量和因变量的值。
拟合曲线的误差可以通过计算残差平方和来评估,即:
SSR = ∑(y - )^2
其中,y 是实际观测值,是拟合曲线的预测值。
最小二乘法拟合曲线的优点在于可以用简单的数学公式表示,易于理解和应用。
- 1 -。
带遗传因子的最小二乘法公式

带遗传因子的最小二乘法公式
最小二乘法是一种常用的数学方法,用于拟合数据并找到最佳拟合线。
然而,当考虑到遗传因子时,最小二乘法的公式会稍有不同。
遗传因子是影响个体性状的基因和环境因素的组合。
在最小二乘法中,我们可以将遗传因子视为一个额外的变量,代表着影响因素之一。
最小二乘法的公式为:
y = β0 + β1x1 + β2x2 + β3g + ε
其中,y是因变量,x1和x2是自变量,g是遗传因子,β0、β1、β2和β3是回归系数,ε是误差项。
当我们希望通过遗传因子来预测个体性状时,可以通过最小二乘法公式来计算出最佳的回归系数。
这些系数可以用来构建一个线性模型,通过输入自变量和遗传因子的值,预测因变量的值。
需要注意的是,遗传因子的值通常不是直接可观测的,而是需要通过基因分析等方法来确定。
另外,遗传因子与自变量之间可能存在交互作用,需要进一步探究。
总之,带遗传因子的最小二乘法公式是一种重要的统计工具,可用于探究遗传因子对个体性状的影响。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最小二乘法公式
∑(X--X平)(Y--Y平)
=∑(XY--X平Y--XY平+X平Y平)
=∑XY--X平∑Y--Y平∑X+nX平Y平
=∑XY--nX平Y平--nX平Y平+nX平Y平
=∑XY--nX平Y平
∑(X --X平)^2
=∑(X^2--2XX平+X平^2)
=∑X^2--2nX平^2+nX平^2
=∑X^2--nX平^2
最小二乘公式(针对y=ax+b形式)
a=(NΣxy-ΣxΣy)/(NΣx^2-(Σx)^2)
b=y(平均)-ax(平均)
最小二乘法
在我们研究两个变量(x, y)之间的相互关系时,通常可以得到一系列成对的数据(x1, y1),(x2, y2).. (xm , ym);将这些数据描绘在x -y直角坐标系中(如图1), 若发现这些点在一条直线附近,可以令这条直线方程如(式1-1)。
Y计= a0 + a1 X (式1-1)
其中:a0、a1 是任意实数
为建立这直线方程就要确定a0和a1,应用《最小二乘法原理》,将实测值Yi与利用(式1-1)计算值(Y计=a0+a1X)的离差(Yi-Y计)的平方和〔∑(Yi - Y计)²〕最小为“优化判据”。
令: φ = ∑(Yi - Y计)² (式1-2)
把(式1-1)代入(式1-2)中得:
φ = ∑(Yi - a0 - a1 Xi)2 (式1-3)
当∑(Yi-Y计)²最小时,可用函数φ 对a0、a1求偏导数,令这两个偏导数等于零。
(式1-4)
(式1-5)
亦即
m a0 + (∑Xi ) a1 = ∑Yi (式1-6)
(∑Xi ) a0 + (∑Xi2 ) a1 = ∑(Xi, Yi) (式1-7)
得到的两个关于a0、 a1为未知数的两个方程组,解这两个方程组得出:
a0 = (∑Yi) / m - a1(∑Xi) / m (式1-8)
a1 = [∑Xi Yi - (∑Xi ∑Yi)/ m] / [∑Xi2 - (∑Xi)2 / m)] (式
1-9)
这时把a0、a1代入(式1-1)中, 此时的(式1-1)就是我们回归的元线性方程即:数学模型。
在回归过程中,回归的关联式是不可能全部通过每个回归数据点(x1, y1、 x2, y2...xm,ym),为了判断关联式的好坏,可借助相关系数“R”,统计量“F”,剩余标准偏差“S”进行判断;“R”越趋近于 1 越好;“F”的绝对值越大越好;“S”越趋近于 0 越好。
R = [∑XiYi - m (∑Xi / m)(∑Yi / m)]/ SQR{[∑Xi2 - m (∑Xi / m)2][∑Yi2 - m (∑Yi / m)2]} (式1-10) *
在(式1-1)中,m为样本容量,即实验次数;Xi、Yi分别任意一组实验X、Y的数值。
微积分应用课题一最小二乘法
从前面的学习中, 我们知道最小二乘法可以用来处理一组数据, 可以从一组测定的数据中寻求变量之间的依赖关系, 这种函数关系称为经验公式. 本课题将介绍最小二乘法的精确定义及如何寻求与之间近似成线性关系时的经验公式. 假定实验测得变量之间的个数据, , …, , 则在平面上, 可以得到个点 , 这种图形称为“散点图”, 从图中可以粗略看出这些点大致散落在某直线近旁, 我们认为与之间近似为一线性函数, 下面介绍求解步骤.
考虑函数 , 其中和是待定常数. 如果在一直线上, 可以认为变量之间的关系为 . 但一般说来, 这些点不可能在同一直线上. 记 , 它反映了用直线来描述 , 时, 计算值与实际值产生的偏差. 当然要求偏差越小越好, 但由于可正可负, 因此不能认为总偏差时, 函数就很好地反
映了变量之间的关系, 因为此时每个偏差的绝对值可能很大. 为了改进这一缺陷, 就考虑用来代替 . 但是由于绝对值不易作解析运算, 因此, 进一步用来度量总偏差. 因偏差的平方和最小可以保证每个偏差都不会很大. 于是问题归结为确定中的常数和 , 使为最小. 用这种方法确定系数 , 的方法称为最小二乘法.
由极值原理得 , 即
解此联立方程得
(*)
问题 I 为研究某一化学反应过程中, 温度℃)对产品得率 (%)的影响, 测得数据如下:
温度℃)
100 110 120 130 140 150 160 170 180 190
得率 (%)
45 51 54 61 66 70 74 78 85 89
(1) 利用“ListPlot”函数, 绘出数据的散点图(采用格式: ListPlot[{ , , …, }, Prolog->AbsolutePointSize[3]] );
(2) 利用“Line”函数, 将散点连接起来, 注意观察有何特征 (采用格式: Show[Graphics[Line[{ , , …, }]] , Axes->True ]) ;
(3) 根据公式(*), 利用“Apply”函数及集合的有关运算编写一个小的程序, 求经验公式 ;
(程序编写思路为: 任意给定两个集合A (此处表示温度)、B(此处表示得率), 由公式(*)可定义两个二元函数(集合A和B为其变量)分别表示
和 . 集合A元素求和: Apply[Plus,A] 表示将加法施加到集合A上, 即各元素相加, 例如Apply[Plus,{1,2,3}]=6;Length[A]表示集合A 元素的个数, 即为n; 表示两集合元素相乘相加;A*B表示集合A与B元素对应相乘得到的新的集合.)
(4) 在同一张图中显示直线及散点图;
(5) 估计温度为200时产品得率.
然而, 不少实际问题的观测数据, , …, 的散点图明显地不能用线性关系来描叙, 但确实散落在某一曲线近旁, 这时可以根据散点图的轮廓和实际经验, 选一条曲线来近似表达与的相互关系.
问题 II 下表是美国旧轿车价格的调查资料, 今以表示轿车的使用年数, (美元)表示相应的平均价格, 求与之间的关系.
1 2 3 4 5 6 7 8 9 10
平均价格
2651 1943 1494 1087 765 538 484 290 226 204
(1) 利用“ListPlot”函数绘出数据的散点图, 注意观察有何特征
(2) 令 , 绘出数据的散点图, 注意观察有何特征
(3) 利用“Line”函数, 将散点连接起来, 说明有何特征
(4) 利用最小二乘法, 求与之间的关系;
(5) 求与之间的关系;
(6) 在同一张图中显示散点图及关于的图形.
思考与练习
1. 假设一组数据: , , …, 变量之间近似成线性关系, 试利用集合的有关运算, 编写一简单程序: 对于任意给定的数据集合 , 通过求解极值原理所包含的方程组, 不需要给出、计算的表达式, 立即得到、的值, 并就本课题 I /(3)进行实验.
注: 利用Transpose函数可以得到数据A的第一个分量的集合, 命令格式为:
先求A的转置, 然后取第一行元素, 即为数据A的第一个分量集合, 例如
(A即为矩阵 )
= (数据A的第一个分量集合)
= (数据A的第二个分量集合)
B-C表示集合B与C对应元素相减所得的集合, 如 = .
2. 最小二乘法在数学上称为曲线拟合, 请使用拟合函数“Fit”重新计算与的值, 并与先前的结果作一比较.。
