相似三角形---一线三等角型
数学人教版九年级下册三角形相似——一线三等角模型

教学设计
教学过程二、新课讲解
1、学生先观看一段关于一线三等角模型的视频
2、对所看视频有所总结提升
3、如图,已知A、D、E在一条直线上,∠BAC=90°,BD⊥DE于D,CE⊥DE于E,你能得出哪些结论?
三、例题讲解
例1、如图,四边形ABCD是正方形,且AB=4,E为BC上一点,F为CD上一点,且∠AEF=90°
(1)求证:ΔABE∽ΔECF (2)当BE=1,求CF的长度自主学习,认真思考
学生抢答
例题学生首先思考,然后由老师讲解并板书
练习巩固:1、如图,在等
边ΔABC中,边长为6,D是BC上的动点,∠ADE=60°(1)求证:ΔABD∽ΔDCE;(2)若BD=x,CE=y,求y与x之间的函数表达式;
联系中考:1、如图,正△ABC的边长为4 ,点P为BC 边上的任意一点(不与点B、C重合),且∠APD=60°,PD 交AB于点D.设BP=x,BD=y,则y关于x的函数图象大致是()学生思考并完成来练习巩固,并随机抽一名学生上黑板展示并对此题进行讲解,学生做完练习巩固后将中考原来抛给学生,让学生思考并完成
能力提升:例2、如图,在平面直角坐标系中,A (0,1),B(2,0),第一象限内的点C满足AC⊥AB,且AC=3,求点C的坐标. 学生作答,并统计学生的答题情况
课堂小结模型的简单归纳:
小结。
中考数学相似三角形重要模型一线三等角模型
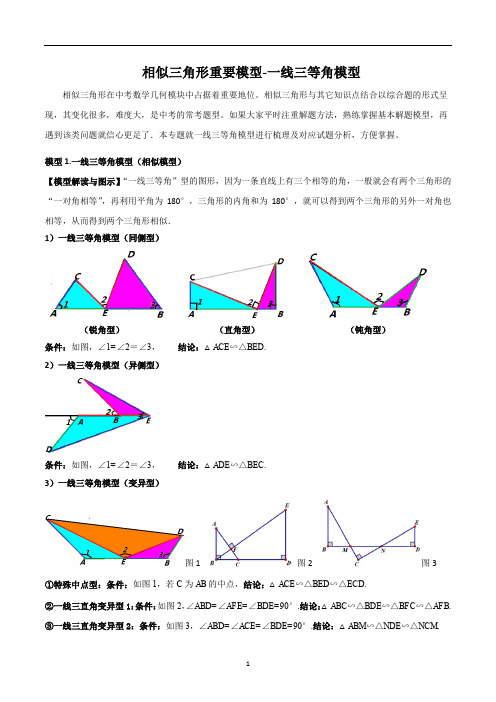
相似三角形重要模型-一线三等角模型相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了.本专题就一线三等角模型进行梳理及对应试题分析,方便掌握。
模型1.一线三等角模型(相似模型)【模型解读与图示】“一线三等角”型的图形,因为一条直线上有三个相等的角,一般就会有两个三角形的“一对角相等”,再利用平角为180°,三角形的内角和为180°,就可以得到两个三角形的另外一对角也相等,从而得到两个三角形相似.1)一线三等角模型(同侧型)(锐角型)(直角型)(钝角型)条件:如图,∠1=∠2=∠3,结论:△ACE∽△BED.2)一线三等角模型(异侧型)条件:如图,∠1=∠2=∠3,结论:△ADE∽△BEC.3)一线三等角模型(变异型)图1 图2 图3①特殊中点型:条件:如图1,若C为AB的中点,结论:△ACE∽△BED∽△ECD.②一线三直角变异型1:条件:如图2,∠ABD=∠AFE=∠BDE=90°.结论:△ABC∽△BDE∽△BFC∽△AFB.③一线三直角变异型2:条件:如图3,∠ABD=∠ACE=∠BDE=90°.结论:△ABM∽△NDE∽△NCM.例1.(2023·山东东营·统考中考真题)如图,A B C为等边三角形,点D,E分别在边B C,A B上,60A D E∠=︒,若4B D D C=, 2.4D E=,则A D的长为()A.1.8B.2.4C.3D.3.2例2.(2023·湖南·统考中考真题)如图,,C A ADE D A D⊥⊥,点B是线段A D上的一点,且C B B E⊥.已知8,6,4A B A C D E===.(1)证明:A B C D E B∽△△.(2)求线段B D的长.例3.(2022·河南新乡·九年级期中)某学习小组在探究三角形相似时,发现了下面这种典型的基本图形.(1)如图1,在ABC中,∠BAC=90°,A BA C=k,直线l经过点A,BD⊥直线I,CE上直线l,垂足分别为D、E.求证:B DA E=k.(2)组员小刘想,如果三个角都不是直角,那么结论是否仍然成立呢?如图2,将(1)中的条件做以下修改:在ABC中,A BA C=k,D、A、E三点都在直线l上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问(1)中的结论还成立吗?若成立,请你给出证明;若不成立,请说明理由.(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,在ABC中,沿ABC的边AB、AC向外作矩形ABDE和矩形ACFG,A BA E =A CA G=12,AH是BC边上的高,延长HA交EG于点I.①求证:I是EG的中点.②直接写出线段BC与AI之间的数量关系:.例4.(2022·四川·一模)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形:(1)如图1,已知:在△ABC 中,A B A C=,D 、A 、E 三点都在直线m 上,并且有B D AA E CB AC α∠=∠=∠=.试猜想DE 、BD 、CE 有怎样的数量关系,请证明你的结论;(2)老师鼓励学习小组继续探索相似的情形.于是,学习小组又研究以下问题:如图2,△ABC 中,(060)B C αα∠=∠=<<︒.将一把三角尺中30°角顶点P 放在BC 边上,当P 在BC 边上移动时,三角尺中30°角的一条边始终过点A ,另一条边交AC 边于点Q ,P 、Q 不与三角形顶点重合.设C P Qβ∠=.当β在许可范围内变化时,α取何值总有△ABP ∽△PCQ ?当α在许可范围内变化时,β取何值总有△ABP ∽△QCP ?(3)试探索有无可能使△ABP 、△QPC 、△ABC 两两相似?若可能,写出所有α、β的值(不写过程);若不可能,请说明理由.例5.(2022·山西晋中·一模)阅读材料:我们知道:一条直线经过等腰直角三角形的直角顶点,过另外两个顶点分别向该直线作垂线,即可得三垂直模型”如图①,在A B C中,90A C B ∠=︒,A C B C=,分别过A 、B 向经过点C 直线作垂线,垂足分别为D 、E ,我们很容易发现结论:A D C C E B△≌△.(1)探究问题:如果A CB C≠,其他条件不变,如图②,可得到结论;A D CC E B△∽△.请你说明理由.(2)学以致用:如图③,在平面直角坐标系中,直线12y x=与直线C D 交于点()2,1M ,且两直线夹角为α,且3ta n 2α=,请你求出直线C D 的解析式.(3)拓展应用:如图④,在矩形A B C D 中,3A B=,5B C=,点E为B C 边上—个动点,连接A E ,将线段A E 绕点E 顺时针旋转90︒,点A 落在点P 处,当点P 在矩形A B C D外部时,连接P C ,P D .若D P C △为直角三角形时,请你探究并直接写出B E 的长.Rt ABD中,上一动点,连接折叠得H E F,延长②B E M H E M≅;③当M2B,则正确的有(九年级校考阶段练习)已知A B C是等边三角形,E F和B D F∠,将B C E沿B则A F=P C D△;九年级校考阶段练习)如图,在A B C中,12.(2022·山东济宁·二模)情境观察:将含45°角的三角板的直角顶点R放在直线l上,分别过两锐角的顶点M,N作l的垂线,垂足分别为P,Q,(1)如图1.观察图1可知:与NQ相等的线段是______________,与N R Q∠相等的角是_____(2)问题探究直角A B C中,90B∠=︒,在AB边上任取一点D,连接CD,分别以AC,DC为边作正方形ACEF 和正方形CDGH,如图2,过E,H分别作BC所在直线的垂线,垂足分别为K,L.试探究EK与HL之间的数量关系,并证明你的结论.(3)拓展延伸:直角A B C中,90B∠=︒,在AB边上任取一点D,连接CD,分别以AC,DC为边作矩形ACEF和矩形CDGH,连接EH交BC所在的直线于点T,如图3.如果A C kC E=,试探究TE与TH=,C D kC H之间的数量关系,并证明你的结论.将.A B P沿着这样的点P,使得点问题解决(3)15.(2023春·四川广安·九年级校考阶段练习)如图1和图2,在平面直角坐标系中,点C的坐标为(0,4),A是x轴上的一个动点,M是线段AC的中点.把线段AM以A为旋转中心、按顺时针方向旋转90°得到AB.过B作x轴的垂线、过点C作y轴的垂线,两直线交于点D,直线DB交x轴于点E.设A点的横坐标为m.(1)求证:△AOC∽△BEA;(2)若m=3,则点B的坐标为;若m=﹣3,则点B的坐标为;(3)若m>0,△BCD的面积为S,则m为何值时,S=6?(4)是否存在m,使得以B、C、D为顶点的三角形与△AOC相似?若存在,求此时m的值;若不存在,请说明理由.16.(2020·四川雅安·中考真题)如图,已知边长为10的正方形A B C D E、不重,是B C边上一动点(与B C 合),连结A E G,是B C延长线上的点,过点E作A E的垂线交D C G∠的角平分线于点F,若F G B G⊥.(1)求证:A B E E G FE C=,求C E F△△;(2)若2∽△的△的面积;(3)请直接写出E C为何值时,C E F面积最大.的何位置时有B E H B A E∽?B C。
(挑战压轴)专项27.4 相似三角形-一线三等角综合应用(解析版)
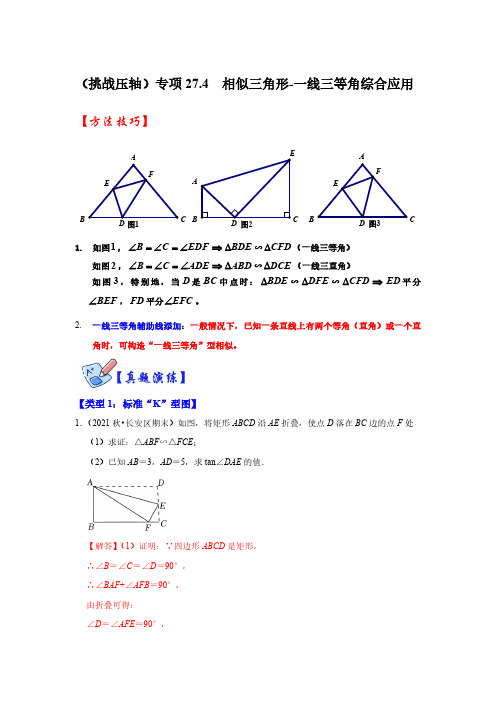
(挑战压轴)专项27.4 相似三角形-一线三等角综合应用【方法技巧】1.如图1,BDE EDF C B ∆⇒∠=∠=∠∽CFD ∆(一线三等角)如图2,ABD ADE C B ∆⇒∠=∠=∠∽DCE ∆(一线三直角)如图3,特别地,当D 是BC 中点时:BDE ∆∽DFE ∆∽CFD ∆⇒ED 平分BEF ∠,FD 平分EFC ∠。
2.一线三等角辅助线添加:一般情况下,已知一条直线上有两个等角(直角)或一个直角时,可构造“一线三等角”型相似。
【类型1:标准“K ”型图】1.(2021秋•长安区期末)如图,将矩形ABCD 沿AE 折叠,使点D 落在BC 边的点F 处(1)求证:△ABF ∽△FCE ;(2)已知AB =3,AD =5,求tan ∠DAE 的值.【解答】(1)证明:∵四边形ABCD 是矩形,∴∠B =∠C =∠D =90°,∴∠BAF +∠AFB =90°,由折叠可得:∠D =∠AFE =90°,CB BC A A∴∠AFB+∠EFC=180°﹣∠AFE=90°,∴∠BAF=∠EFC,∴△ABF∽△FCE;(2)解:∵四边形ABCD是矩形,∴AB=CD=3,AD=BC=5,由折叠可得:AD=AF=5,∴BF===4,∴CF=BC﹣BF=1,∵△ABF∽△FCE,∴=,∴=,∴CE=,∴DE=CD﹣CE=3﹣=,∴tan∠DAE===,∴tan∠DAE的值为.2.如图,在正方形ABCD中,M为BC上一点,ME⊥AM,ME交CD于F,交AD的延长线于点E.(1)求证:△ABM∽△MCF;(2)若AB=4,BM=2,求△DEF的面积.【解答】(1)证明:∵四边形ABCD是正方形,∴AB=BC=CD,∠B=∠C=90°,BC∥AD,∴∠BAM+∠AMB=90°,∵ME⊥AM,∴∠AME=90°,∴∠AMB+∠FMC=90°,∴∠BAM=∠FMC,∴△ABM∽△MCF;(2)解:∵AB=4,∴AB=BC=CD=4,∵BM=2,∴MC=BC﹣BM=4﹣2=2,由(1)得:△ABM∽△MCF,∴=,∴=,∴CF=1,∴DF=CD﹣CF=4﹣1=3,∵BC∥AD,∴∠EDF=∠MCF,∠E=∠EMC,∴△DEF∽△CMF,∴=,∴=,∴DE=6,∴△DEF的面积=DE•DF=×6×3=9,答:△DEF的面积为9.3.已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.如图,已知折痕与边BC交于点O,连接AP、OP、OA.(1)求证:=;(2)若OP与PA的比为1:2,求边AB的长.【解答】(1)证明:由折叠的性质可知,∠APO=∠B=90°,∴∠APD+∠OPC=90°,∵四边形ABCD为矩形,∴∠D=∠C=90°,∴∠POC+∠OPC=90°,∴∠APD=∠POC,∴△OCP∽△PDA,∴=;(2)解:∵△OCP∽△PDA,∴,∵OP与PA的比为1:2,AD=8,∴,∴PC=4,设AB=x,则DC=x,AP=x,DP=x﹣4,在Rt△APD中,AP2=AD2+PD2,∴x2=82+(x﹣4)2,解得:x=10,∴AB=10.4.(2020•香洲区校级一模)如图,四边形ABDC为矩形,AB=4,AC=3,点M为边AB上一点(点M不与点A、B重合),连接CM,过点M作MN⊥MC,MN与边BD交于点N.(1)当点M为边AB的中点时,求线段BN的长;(2)直接写出:当DN最小时△MNB的面积为 .【解答】解:(1)∵AB=4,∴当点M为边AB的中点时,AM=BM=2,∵四边形ABDC为矩形,∴∠A=∠B=90°,∵MN⊥MC,∴∠CMN=90°,∵∠ACM+∠AMC=90°,∠BMN+∠AMC=180°﹣∠CMN=90°,∴∠ACM=∠BMN,又∵∠A=∠B,∴△ACM∽△BMN,∴,∵AC=3,AM=BM=2,∴=,∴BN=;(2)设BM=x,DN=y,∵四边形ABDC为矩形,AB=4,AC=3,∴AM=AB﹣BM=4﹣x,BN=BD﹣DN=3﹣y,由(1)知,,∴=,∴(4﹣x)x=3(3﹣y),∴﹣x2+4x=9﹣3y,∴y=x2﹣x+3=(x﹣2)2+,∴当x=2时,y取得最小值,即DN最小,此时DN=y=,∴BM=2,BN=3﹣=,∴△MNB的面积为:×2×=.故答案为:.5.(2019•玉州区二模)已知:如图,正方形ABCD中,E是边AB上一点,AM⊥DE于点M,CN⊥DE于点N.(1)求证:MN=DM﹣AM;(2)连接AN,如果=,求证:MN=ME.【解答】证明:(1)∵四边形ABCD是正方形,∴AD=DC,∠ADC=90°,∴∠ADM+∠CDN=90°,∵AM⊥DE,CN⊥DE,∴∠AMD=∠CND=90°,∴∠CDN+∠DCN=90°,∴∠ADM=∠DCN,∴△ADM≌△DCN(AAS),∴DN=AM,∵MN=DM﹣DN,∴MN=DM﹣AM;(2)如图:∵四边形ABCD是正方形,∴AD=DC,∠DAE=90°,∵∠DAE=∠DNC=90°,∠ADM=∠DCN,∴△CDN∽△DEA,∴=,∴=,∵=,∴=,∴AE=AN,∵AM⊥DE,∴MN=ME.6.(2022•郴州)如图1,在矩形ABCD中,AB=4,BC=6.点E是线段AD上的动点(点E不与点A,D重合),连接CE,过点E作EF⊥CE,交AB于点F.(1)求证:△AEF∽△DCE;(2)如图2,连接CF,过点B作BG⊥CF,垂足为G,连接AG.点M是线段BC的中点,连接GM.①求AG+GM的最小值;②当AG+GM取最小值时,求线段DE的长.【解答】(1)证明:∵四边形ABCD是矩形,∴∠A=∠D=90°,∴∠CED+∠DCE=90°,∵EF⊥CE,∴∠CED+∠AEF=90°,∴∠DCE=∠AEF,∴△AEF∽△DCE;(2)解:①连接AM,如图2,∵BG⊥CF,∴△BGC是直角三角形,∵点M是BC的中点,∴MB=CM=GM=,∴点G在以点M为圆心,3为半径的圆上,当A,G,M三点不共线时,由三角形两边之和大于第三边得:AG+GM>AM,当A,G,M三点共线时,AG+GM=AM,此时,AG+GM取得最小值,在Rt△ABM中,AM===5,∴AG+GM的最小值为5.②方法一:如图3,过点M作MN∥AB交FC于点N,∴△CMN∽△CBF,∴,设AF=x,则BF=4﹣x,∴MN=BF=(4﹣x),∵MN∥AB,∴△AFG∽△MNG,∴,由(2)可知AG+GM的最小值为5,即AM=5,又∵GM=3,∴AG=2,∴,解得x=1,即AF=1,由(1)得,设DE=y,则AE=6﹣y,∴,解得:y=3+或y=3﹣,∵0<6,0<3﹣<6,∴DE=3+或DE=3﹣.方法二:如图4,过点G作GH∥AB交BC于点H,∴△MHG∽△MBA,∴,由(2)可知AG+MG的最小值为5,即AM=5,又∵GM=3,∴,∴GH=,MH=,由GH∥AB得△CHG∽△CBF,∴,即,解得FB=3,∴AF=AB﹣FB=1.由(1)得,设DE=y,则AE=6﹣y,∴,解得:y=3+或y=3﹣,∵0<6,0<3﹣<6,∴DE=3+或DE=3﹣.、【类型2:做辅助线构造“K”型图】7.(2022春•定海区校级月考)【基础巩固】(1)如图1,在△ABC中,∠ACB=90°,直线l过点C,分别过A、B两点作AE⊥l,BD⊥l,垂足分别为E、D.求证:△BDC∽△CEA.【尝试应用】(2)如图2,在△ABC中,∠ACB=90°,D是BC上一点,过D作AD的垂线交AB 于点E.若BE=DE,,AC=20,求BD的长.【拓展提高】(3)如图3,在平行四边形ABCD中,在BC上取点E,使得∠AED=90°,若AE=AB,,CD=,求平行四边形ABCD的面积.【解答】(1)证明:∵∠ACB=90°,∴∠BCD+∠ACE=90°,∵AE⊥CE,∴∠AEC=90°,∴ACE+∠CAE=90°.∴∠BCD=∠CAE.∵BD⊥DE,∴∠BDC=90°,∴∠BDC=∠AEC.∴△BDC∽△CEA.(2)解:过点E作EF⊥BC于点F.由(1)得△EDF∽△DAC.∴.∵AD⊥DE,,AC=20,∴,∴DF=16.∵BE=DE,∴BF=DF.∴BD=2DF=32.(3)解:过点A作AM⊥BC于点M,过点D作DN⊥BC的延长线于点N.∴∠AMB=∠DNC=90°.∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.∴∠B=∠DCN.∴△ABM≌△DCN(AAS).∴BM=CN,AM=DN.∵AB=AE,AM⊥BC,∴BM=ME,∵,设AM=b,BE=4a,EC=3a.∴BM=ME=CN=2a,EN=5a.∵∠AED=90°,由(1)得△AEM∽△EDN.∴,∴,∴,∵,∴(2a)2+b2=14,∴a=1,.∴平行四边形ABCD的面积=【类型2:特殊“K”型图】8.(2022秋•二道区月考)如图,在△ABC中,AB=AC=9,BC=12,D,E分别是BC,AB上的动点(点D与B,C不重合),且2∠ADE+∠BAC=180°,若BE=4,则CD的长为 .【解答】解:∵AB=AC,∴∠C=∠B,∴∠C+∠B+∠BAC=2∠C+∠BAC=180°,又∵2∠ADE+∠BAC=180°,∴∠C=∠ADE,又∵∠BDE+∠ADC=180°﹣∠ADE,∠CAD+∠ADC=180°﹣∠C,∴∠BDE=∠CAD,∴△BDE∽△CAD,∴=,即=,解得CD=6.故答案为:6.9.(2020秋•南京期末)如图,在等边△ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,2BP=3CD,BP=1.(1)求证△ABP∽△PCD;(2)求△ABC的边长.【解答】(1)证明:∵△ABC是等边三角形,∴AB=BC=AC,∠B=∠C=60°,∵∠BPA+∠APD+∠DPC=180°,且∠APD=60°,∴∠BPA+∠DPC=120°,∵∠DPC+∠C+∠PDC=180°,∴∠DPC+∠PDC=120°,∴∠BPA=∠PDC,∴△ABP∽△PCD;(2)解:∵2BP=3CD,且BP=1,∴CD=,∵△ABP∽△PCD,∴=,设AB=x,则PC=x﹣1,∴,∴x=3.即AB=3.∴△ABC的边长为3.10.如图,AB=9,AC=8,P为AB上一点,∠A=∠CPD=∠B,连接CD.(1)若AP=3,求BD的长;(2)若CP平分∠ACD,求证:PD2=CD•BD.【解答】(1)解:∵AB=9,AC=3,∴BP=AB﹣AP=9﹣3=6,∵∠A=∠CPD,∠ACP+∠APC=180°﹣∠A,∠APC+∠BPD=180°﹣∠CPD,∴∠ACP=∠BPD,∵∠A=∠B,∴△ACP∽△BPD,∴=,∴=,∴BD=,∴BD的长为;(2)证明:∵CP平分∠ACD,∴∠PCD=∠ACP,∵∠ACP=∠DPB,∴∠PCD=∠DPB,∵∠CPD=∠B,∴△CPD∽△PBD,∴=,∴PD2=CD•BD.。
初三相似三角形几何模型-一线三等角

相似三角形几何模型——一线三等角【模型讲解】模型一:一线三直角图一 图二90;B ACE D ABC CDE ∠=∠=∠=∆∆如图一、二,已知:结论:(1)∽(2)AB DE=BC CD模型二:一线三等角图三 图四 ;B ACE D ABC CDE ABC CDE ACEα∠=∠=∠=∆∆∆∆∆如图三、四,已知:结论:(1)∽(2)AB DE=BC CD(3)当C 为BD 中点时,∽∽【典型例题】1.△ABC 和△DEF 是两个全等的等腰直角三角形,∠BAC =∠EDF =90°,△EDF 的顶点E 与△ABC 的斜边BC 的中点重合,将△DEF 绕点E 旋转,旋转过程中,线段DE 与线段AB 相交于点P ,线段EF 与射线CA 相交于点Q .(1)如图①,当点Q 在线段AC 上,且AP=AQ 时,求证:△BPE≌△CQE;(2)如图②,当点Q 在线段CA 的延长线上时,求证:△BPE∽△CEQ;(3)在(2)的条件下,BP=2,CQ=9,则BC 的长为_______.2.如图,已知AB BD ⊥,CD BD ⊥.(1)若9AB =,4CD =,10BD =,请问在BD 上是否存在点P ,使以P ,A ,B 三点为顶点的三角形与以P ,C ,D 三点为顶点的三角形相似?若存在,求BP 的长;若不存在,请说明理由;(2)若9AB =,4CD =,12BD =,请问在BD 上存在几个点使以三点为顶点的三角形与以P ,C ,D 三点为顶点的三角形相似?并求BP 的长.3.如图,点P是正方形ABCD边AB上一点(点P不与点A,B重合),连接PD,将线段PD 绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE,DF.(1)求∠PBE的度数;(2)若△PFD∽△BFP,求APAB的值.4.感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,CE=4,则DE的长为______.5.如图,点B 在线段AC 上,点D 、E 在AC 同侧,90A C ∠=∠=︒,BD BE ⊥,AD BC =.若3AD =,5CE =,点P 为线段AB 上的动点,连结DP ,作PQ DP ⊥,交直线BE 于点Q .(1)当点P 与A ,B 两点不重合时,求DP PQ的值; (2)当点P 从A 点运动到AC 的中点时,求线段DQ 的中点所经过的路径(线段)长.(直接写出结果,不必写出解答过程)6.如图,在ABC △中,点D E 、分别在边BC AC 、上,连接AD DE 、,且B ADE C ∠=∠=∠.(1)证明:BDA CED △∽△;(2)若45,2B BC ∠=︒=,当点D 在BC 上运动时(点D 不与B C 、重合),且ADE △是等腰三角形,求此时BD 的长.。
培优专题25相似三角形的一线三等角模型-解析版

A.-9
B.-12
C.-15
D.-18
【答案】A
【分析】根据∠AOB=90°,∠ABO=30°,可求出 OA 与 OB 的比,设出点 B 的坐标,再根据相似三角形的
性质,求出点 A 的坐标,可得 ab 的值,进而求出 m 的值.
【详解】解:过 A、B 分别作 AM⊥x 轴,BN⊥x 轴,垂足为 M、N,
3a 3b ∴B(-a,b),A( 3 , 3 ),
3 ∵点 A 在反比例函数 y= x 上,
33 ab
则 3 × 3 =3, ∴ab=9,
m ∵点 B 在反比例函数 y= x 上, ∴-a×b=m=-9, 故选 A.
【点睛】本题考查反比例函数的图象和性质,直角三角形的性质、相似三角形的判定和性质等知识,求出 反比例函数图象上点的坐标是解答前提的关键. 3.(2021·浙江·九年级专题练习)如图,正方形 ABCD 边长为 4,边 B过点 A,则矩形 EDFG 的面积是( )
2. 当一个直角放在平面直角坐标系中时,亦常构造“K 型图”解题
3. 由“K 型图”得到的相似比,基本都可以转化成“特定角”的正切值来计算
4. “K 型图”常和“A 字图”或“8 字图”类的平行相似结合在一起求长度
“K 型图”常见构造方法:过直角订单分别作水平或竖直的直线,再过直角两边顶点分别作直线的垂 线。 如图:
∵四边形 EDFG 为矩形,
∴∠EDF=∠F=90°,
∵∠ADF+∠ADE=90°,∠ADE+∠EDC=90°,
∴∠ADF=∠EDC,
∴△ADF∽△CDE,
AD DF
4 DF
∴ DE DC ,即 DE 4 ,
16
∴DF= DE ,
相似三角形模型讲解_一线三等角问题

第一部分 相似三角形模型分析一、相似三角形判定的基本模型认识(一)A 字型、反A 字型(斜A 字型)ABCDE(平行)CBA DE(不平行)(二)8字型、反8字型J OADBCAB CD(蝴蝶型)(平行) (不平行)(三)母子型ABCDCAD(四)一线三等角型:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景(五)一线三直角型:(六)双垂型:CAD二、相似三角形判定的变化模型旋转型:由A 字型旋转得到。
8字型拓展CB EDA共享性GABCEF一线三等角的变形一线三直角的变形第二部分 相似三角形典型例题讲解母子型相似三角形例1:如图,梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于点O ,BE ∥CD 交CA 延长线于E . 求证:OE OA OC ⋅=2.例2:已知:如图,△ABC 中,点E 在中线AD 上, ABC DEB ∠=∠.求证:(1)DA DE DB ⋅=2; (2)DAC DCE ∠=∠.例3:已知:如图,等腰△ABC 中,AB =AC ,AD ⊥BC 于D ,CG ∥AB ,BG 分别交AD 、AC 于E 、F . 求证:EG EF BE ⋅=2.相关练习:1、如图,已知AD 为△ABC 的角平分线,EF 为AD 的垂直平分线.求证:FC FB FD ⋅=2.AC D E B2、已知:AD 是Rt △ABC 中∠A 的平分线,∠C=90°,EF 是AD 的垂直平分线交AD 于M ,EF 、BC 的延长线交于一点N 。
求证:(1)△AME ∽△NMD; (2)ND 2=NC ·NB3、已知:如图,在△ABC 中,∠ACB=90°,CD ⊥AB 于D ,E 是AC 上一点,CF ⊥BE 于F 。
求证:EB ·DF=AE ·DB4.在∆ABC 中,AB=AC ,高AD 与BE 交于H ,EF BC ⊥,垂足为F ,延长AD 到G ,使DG=EF ,M 是AH 的中点。
中考复习相似三角形---一线三等角型

相似三角形——“一线三等角型”教学目标:1、掌握相似三角形的判定和性质,并能熟练运用其解决重要类型“一线三等角”的类型题.2、经历运用相似三角形知识解决问题的过程,体验图形运动、分类讨论、方程与函数等数学思想.3、通过问题的解决,体验探究问题成功的乐趣,积极探索,提高学习几何的兴趣.重点:相似三角形的判定性质及其应用.难点:与相似、函数有关的综合性问题的解决技巧和方法.教学方法:启发式教学方法,尝试指导教学法.一、知识梳理:(图1)(图2)(1)如图1,已知三角形ABC中,AB=AC,∠ADE=∠B,那么一定存在的相似三角形有;(2)如图2,已知三角形ABC中,AB=AC,∠DEF=∠B,那么一定存在的相似三角形有.二、【例题解析】【例1】如图,等边△ABC中,边长为4,D是BC上动点,∠EDF=60°,(1)求证:△BDE∽△CFD;(2)当BD=1,FC=52时,求BE.【变式1】在边长为4的等边ABC∆中,D是BC的中点,点E、F分别在AB、AC上,且保持ABCEDF∠=∠,连接EF.(1) 已知BE=1,DF=2,求DE的值; (2) 求证:∠BED=∠DEF.【变式2】在边长为4的等边ABC ∆中,若BD =1时,当△DEF 与△AEF 相似,求BE 的值.【变式3】如图,已知边长为3的等边ABC ∆,点F 在边BC 上,CF =1,点E 是射线BA 上一动点,以线段EF 为边向右侧作等边EFG ∆,直线EG ,FG 交直线AC 于点M ,N ,(1)写出图中与BEF ∆相似的三角形;(2)证明其中一对三角形相似;(3)设BE =x ,MN =y ,,求y 与x 之间的函数关系式,并写出自变量x 的取值范围.【例2】在ABC ∆中,O BC AC C ,3,4,90===∠o 是AB 上的一点,且52=AB AO ,点P 是AC 上的一个动点,OP PQ ⊥交线段BC 于点Q (不与点B ,C 重合),已知AP =2,求CQ .【变式1】 如图,在△ABC 中,8==AC AB ,10=BC ,D 是BC 边上的一个动点,点E 在AC 边上,且C ADE ∠=∠.(1) 求证:△ABD ∽△DCE ;(2) 如果x BD =,y AE =,求y 与x 的函数解析式,并写出自变量x 的定义域;(3) 当点D 是BC 的中点时,试说明△ADE 是什么三角形,并说明理由.QC P【变式2】在直角三角形ABC 中,D BC AB C ,,90==∠o 是AB 边上的一点,E 是在AC 边上的一个动点(与A ,C 不重合),DF DE DF ,⊥与射线BC 相交于点F .(1) 如图1,当点D 是边AB 的中点时,求证:DF DE =;(2) 如图2,当m DB AD =,求DF DE 的值.图(2)图(1)F CF C A BB A D E D E【例3】已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且AD =5,AB =DC =2,P 为AD 上的一点,满足∠BPC =∠A . ① 求证;△ABP ∽△DPC ; ② 求AP 的长.【变式1】如果点P 在AD 边上移动(点P 与点A 、D 不重合),且满足∠BPE =∠A ,PE 交直线BC 于点E ,同时交直线DC 于点Q ,那么①当点Q 在线段DC 的延长线上时,设AP =x ,CQ =y ,求y 关于x 的函数解析式,并写出函数的定义域;②当CE =1时,写出AP 的长.C B AD C B A D【变式2】在梯形ABCD 中,AD ∥BC ,6AB CD BC ===,3AD =.点M 为边BC 的中点,以M 为顶点作EMF B ∠=∠,射线ME 交腰AB 于点E ,射线MF 交腰CD 于点F ,联结EF .(1)求证:△MEF ∽△BEM ;(2)若△BEM 是以BM 为腰的等腰三角形,求EF 的长;(3)若EF CD ⊥,求BE 的长.【作业】1、如图,在ABC ∆中,90C ∠=︒,6AC =,43=BC AC ,D 是BC 边的中点,E 为AB 边上的一个动点,作90DEF ∠=︒,EF 交射线BC 于点F .设BE x =,BED ∆的面积为y .(1)求y 关于x 的函数关系式,并写出自变量x 的取值范围;(2)如果以B 、E 、F 为顶点的三角形与BED ∆相似,求BED ∆的面积.2、如图,已知在△ABC 中, AB =AC =6,BC =5,D 是AB 上一点,BD =2,E 是BC 上一动点,连结DE ,并作DEF B ∠=∠,射线EF 交线段AC 于F .(1)求证:△DBE ∽△ECF ;(2)当F 是线段AC 中点时,求线段BE 的长;(3)联结DF ,如果△DEF 与△DBE 相似,求FC 的长.3、已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且BC =6,AB =DC =4,点E 是AB 的中点.(1)如图,P 为BC 上的一点,且BP =2.求证:△BEP ∽△CPD ;(2)如果点P 在BC 边上移动(点P 与点B 、C 不重合),且满足∠EPF =∠C ,PF 交直线CD 于点F ,同时交直线AD 于点M ,那么:①当点F 在线段CD 的延长线上时,设BP =x ,DF =y ,求y 关于x 的函数解析式,并写出函数的定义域;②当BEP DMF S S ∆∆=49时,求BP 的长.。
初三相似三角形之一线三等角专题

相似三角形——“一线三等角型”一、知识梳理:一线三等角:两个等角的一边在同一直线上,另一边在该直线的同侧。
若有第三个与之相等的角、其顶点在该直线上,角的两边(或两边所在直线)分别与两等角的非共线边(或该边所在直线)相交,此时通过证明,一般都可以得到一组相似三角形,该组相似三角形习惯上被称为“一线三等角型”相似三角形.(图1)(图2)(1)如图1,已知三角形ABC中,AB=AC,∠ADE=∠B,那么一定存在的相似三角形有;(2)如图2,已知三角形ABC中,AB=AC,∠DEF=∠B,那么一定存在的相似三角形有 .二、【例题解析】【例1】如图,等边△ABC中,边长为4,D是BC上动点,∠EDF=60°,(1)求证:△BDE∽△CFD;(2)当BD=1,FC=52时,求BE.【变式1】在边长为4的等边ABC∆中,D是BC的中点,点E、F分别在AB、AC上,且保持ABCEDF∠=∠,连接EF.(1) 已知BE=1,DF=2,求DE的值;(2) 求证:∠BED=∠DEF.【变式2】在边长为4的等边ABC ∆中,若BD =1时,当△DEF 与△AEF 相似,求BE 的值.【变式3】如图,已知边长为3的等边ABC ∆,点F 在边BC 上,CF =1,点E 是射线BA 上一动点,以线段EF 为边向右侧作等边EFG ∆,直线EG ,FG 交直线AC 于点M ,N ,(1)写出图中与BEF ∆相似的三角形;(2)证明其中一对三角形相似;(3)设BE =x ,MN =y ,,求y 与x 之间的函数关系式,并写出自变量x 的取值范围.【例2】在ABC ∆中,O BC AC C ,3,4,90===∠o 是AB 上的一点,且52=AB AO ,点P 是AC 上的一个动点,OP PQ ⊥交线段BC 于点Q (不与点B ,C 重合),已知AP =2,求CQ .【变式1】 如图,在△ABC 中,8==AC AB ,10=BC ,D 是BC 边上的一个动点,点E 在AC 边上,且C ADE ∠=∠.(1) 求证:△ABD ∽△DCE ;(2) 如果x BD =,y AE =,求y 与x 的函数解析式,并写出自变量x 的定义域;(3) 当点D 是BC 的中点时,试说明△ADE 是什么三角形,并说明理由.QC P【变式2】在直角三角形ABC 中,D BC AB C ,,90==∠o是AB 边上的一点,E 是在AC 边上的一个动点(与A ,C 不重合),DF DE DF ,⊥与射线BC 相交于点F .(1) 如图1,当点D 是边AB 的中点时,求证:DF DE =;(2) 如图2,当m DB AD =,求DF DE 的值.图(2)图(1)F CF C A BB A D E D E【例3】已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且AD =5,AB =DC =2,P 为AD 上的一点,满足∠BPC =∠A . ① 求证;△ABP ∽△DPC ; ② 求AP 的长.【变式1】如果点P 在AD 边上移动(点P 与点A 、D 不重合),且满足∠BPE =∠A ,PE 交直线BC 于点E ,同时交直线DC 于点Q ,那么①当点Q 在线段DC 的延长线上时,设AP =x ,CQ =y ,求y 关于x 的函数解析式,并写出函数的定义域;②当CE =1时,写出AP 的长.C B AD C B A D【变式2】在梯形ABCD 中,AD ∥BC ,6AB CD BC ===,3AD =.点M 为边BC 的中点,以M 为顶点作EMF B ∠=∠,射线ME 交腰AB 于点E ,射线MF 交腰CD 于点F ,联结EF .(1)求证:△MEF ∽△BEM ;(2)若△BEM 是以BM 为腰的等腰三角形,求EF 的长;(3)若EF CD ⊥,求BE 的长.【作业】1、如图,在ABC ∆中,90C ∠=︒,6AC =,43=BC AC ,D 是BC 边的中点,E 为AB 边上的一个动点,作90DEF ∠=︒,EF 交射线BC 于点F .设BE x =,BED ∆的面积为y .(1)求y 关于x 的函数关系式,并写出自变量x 的取值范围;(2)如果以B 、E 、F 为顶点的三角形与BED ∆相似,求BED ∆的面积.2、如图,已知在△ABC 中, AB =AC =6,BC =5,D 是AB 上一点,BD =2,E 是BC 上一动点,连结DE ,并作DEF B ∠=∠,射线EF 交线段AC 于F .(1)求证:△DBE ∽△ECF ;(2)当F 是线段AC 中点时,求线段BE 的长;(3)联结DF ,如果△DEF 与△DBE 相似,求FC 的长.3、已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且BC =6,AB =DC =4,点E 是AB 的中点.(1)如图,P 为BC 上的一点,且BP =2.求证:△BEP ∽△CPD ;(2)如果点P 在BC 边上移动(点P 与点B 、C 不重合),且满足∠EPF =∠C ,PF 交直线CD于点F ,同时交直线AD 于点M ,那么:①当点F 在线段CD 的延长线上时,设BP =x ,DF =y ,求y 关于x 的函数解析式,并写出函数的定义域;②当BEP DMF S S ∆∆=49时,求BP 的长.。
初中数学突破中考压轴题几何模型之相似三角形中的一线三等角模型
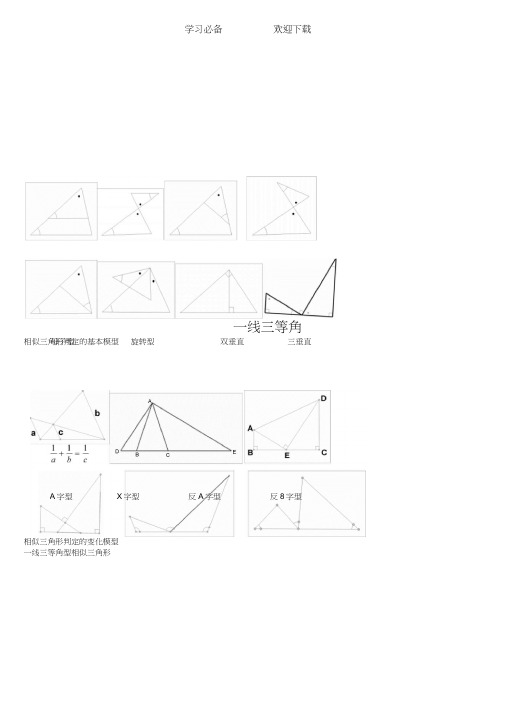
一线三等角母子型 旋转型 双垂直 三垂直相似三角形判定的变化模型 一线三等角型相似三角形相似三角形判定的基本模型 A 字型 X 字型 反A 字型 反8字型三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景,一个与等腰三角形的底角相等的顶点在底边所在的直线上,角的两边分别与等腰三角形的两边相交如图所示:等角的顶点在底边上的位置不同得到的相似三角形的结论也不同,当顶点移动到底边的延长线时,形成变式图形, 图形虽然变化但是求证的方法不变。
此规律需通过认真做题,细细体会。
典型例题【例1】如图,等边△ ABC 中,边长为6,D 是BC 上动点,/ EDF=60(1) 求证:△ BDE CFD(2) 当 BD=1 , FC=3 时,求 BE【例2】如图,等腰△ ABC 中,AB=AC , D 是BC 中点,/ EDF = / B ,求证:△ BDE DFE【例3】如图,在△ ABC 中,AB=AC=5cm , BC=8,点P 为BC 边上一动点(不与点 B 、C 重合),过点P 作射线PM交AC 于点M ,使/ APM= / B ;(1) 求证:△ ABPPCM ;(2) 设BP=x , CM=y .求y 与x 的函数解析式,并写出函数的定义域.(3)当厶APM 为等腰三角形时, 求PB 的长.合),且保持N APQ =NABC .① 若点P 在线段CB 上(如图),且BP =6,求线段CQ 的长;② 若BP =x , CQ =y ,求y 与x 之间的函数关系式,并写出函数的定义域; 【例4] ( 1)在ABC 中,AB 二 AC 二 5 , BC =8,点P 、Q 分别在射线 CB 、AC 上(点P 不与点C 、点B 重C(2)正方形ABCD的边长为5 (如图12),点P、Q分别在直.线CB、DC上(点P不与点C、点B重合),且保持.APQ =90 .当CQ =1时,写出线段BP的长(不需要计算过程,请直接写出结果) .图12点评:此题是典型的图形变式题,记住口诀:“图形改变,方法不变”。
初中数学突破中考压轴题几何模型之相似三角形中的一线三等角模型

一线三等角相似三角形判定的基本模型A字型X字型反A字型反8字型母子型旋转型双垂直三垂直相似三角形判定的变化模型AD B C E一线三等角型相似三角形三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景,一个与等腰三角形的底角相等的顶点在底边所在的直线上,角的两边分别与等腰三角形的两边相交如图所示:等角的顶点在底边上的位置不同得到的相似三角形的结论也不同,当顶点移动到底边的延长线时,形成变式图形,图形虽然变化但是求证的方法不变。
此规律需通过认真做题,细细体会。
典型例题【例△1】如图,等边ABC中,边长为6,D是BC上动点,∠EDF=60°A(△1)求证:BDE∽△CFD(2)当BD=1,FC=3时,求BEE FB D C【例△2】如图,等腰ABC中,AB=AC,D是BC中点,∠EDF=∠B,求证:△BDE∽△DFEAFEB D C【例△3】如图,在ABC中,AB=AC=5cm,BC=8,点P为BC边上一动点(不与点B、C重合),过点P作射线PM 交AC于点M,使∠APM=∠B;(△1)求证:ABP∽△PCM;A(2)设BP=x,CM=y.求y与x的函数解析式,并写出函数的定义域.(△3)当APM为等腰三角形时,求PB的长.MB P C【例4】(1)在∆ABC中,AB=AC=5,BC=8,点P、Q分别在射线C B、AC上(点P不与点C、点B重合),且保持∠APQ=∠ABC.A①若点P在线段CB上(如图),且BP=6,求线段CQ的长;②若BP=x,CQ=y,求y与x之间的函数关系式,并写出函数的定义域;BQP C(2)正方形ABCD的边长为5(如图12),点P、Q分别在直线C B、DC上..(点P不与点C、点B重合),且保持∠APQ=90︒.当CQ=1时,写出线段BP的长(不需要计算过程,请直接写出结果).AB C备用图A DB C图12点评:此题是典型的图形变式题,记住口诀:“图形改变,方法不变”。
一线三等角教案

相似三角形的判定---“一线三等角”
一、教学目标
1.学生会运用两组对应角分别相等的两个三角形为相似三角形的判定方法证明两个三角形相似。
2.学生经历观察、比较、归纳的学习过程,归纳出“一线三等角”图形的基本特征,并且能够在不同的背景中认识和把握基本图形。
3.学生在学习过程中感受几何直观图形对几何学习的重要性。
二、教学重点、难点
1、重点:运用判定方法解决“一线三等角”的相关计算与证明
2、难点:在不同背景中识别基本图形
三、教学方法:教师主导与学生合作探究相结合。
四、教学过程
四知识巩固:
1已知,如图,在矩形ABCE 中,
D 为EC 上一点,沿线段AD 翻折,使得点
E 落在BC 上,若BC=12,BE ∶EC=2∶1.求AB 的长
A
B
C
D
E
借助此题,让学生感到在矩形中因为矩形四个角为直角
的特点,容易和“一线三直
角”基本图形建立联系。
本题融入了轴对称的变换,
让题目更鲜活
教师引导学生观察图形,找基本图
形。
师生共同完成
2. 在平面直角坐标系中,A(0,1),B (2,0),AC ⊥AB,AC=
3.
求点C 的坐标。
B
A
C
在坐标系中感受基本图形的作用。
引导学生分析如果要求出点c 的坐标应求那条线段的长?鼓励学生添加辅助线,构造
基本图形。
学生到黑板
上完成。
完整版相似三角形模型讲一线三等角问题讲义解答

」、相似三角形判定的基本模型认识(一) A 字型、反 A 字型(斜A 字型)(二) 8字型、反8字型(四)一线三等角型:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景(六)双垂型: A(平行)(不平行)△B(平行) (三)母子型(蝴蝶型)相似三角形判定的变化模型一线三直角的2AB=AC ADL BC 于 D, CG// AB BG 分别交 AD AC 于 E 、F .求证:BE=EF? EG2 .如图,在△ ABC 中,AB=AC=10 BC=16点D 是边BC 上(不与 B, C 重合)一动点,/ ADE=Z B=a, DE 交 AC 于点E .下列结论:①AD 2=AE? A B ② 3.6 W AE V 10;③当 AD=2 i 时,△ ABD^A DCE ④厶DCE 为直角三角形时, BD 为8或12.5 . 其中正确的结论是 _____________ .(把你认为正确结论的序号都填上)3.已知:如图,△ ABC 中,点 E 在中线 AD 上,/ DEB=/ ABC 求证:(1) DB=DE? D A(2 )Z DCE=/ DACAD// BC,对角线 AG BD 交于点O, BE// CD 交CA 延长线于 E.求证:OC=OA?OE6.已知:如图,在 Rt △ ABC 中,/ C=90°, BC=2 AC=4 P 是斜边 AB 上的一个动点, PD 丄AB 交边 AC 于点 D (点D 与点A C 都不重合),E 是射线DC 上一点,且/ EPD=/ A.设A P 两点的距离为 x ,A BEP 的面积为 (1)求证:AE=2PE(2)求y 关于x 的函数解析式,并写出它的定义域;8.如图,已知△ ABC 是等边三角形,点 D B C E 在同一条直线上,且/ DAE=120 (1) 图中有哪几对三角形相似?请证明其中的一对三角形相似;9.(已知:如图,在 Rt △ ABC 中,AB=AC / DAE=45 .求证:BC=2DE10.如图,在等边厶 ABC 中,边长为 6, D 是BC 边上的动点,/ EDF=60 (1) 求证:△ BD 0A CFD②若BP=x CQ=y 求y 与x 之间的函数关系式,并写出函数的定义域;(2) 正方形ABCD 勺边长为5 (如图),点P 、Q 分别在直线CB DC 上 (点P 不与点C 点B 重合),且保持 / APQ=90度.当CQ=1时,写出线段BP 的长(不需要计算过程,请直接写出结果)13 .已知梯形 ABCD 中, AD// BC,且 AD< BC, AD=5, AB=DC=2 (1) 如图,P 为AD 上的一点,满足/ BPC=ZA ,求AP 的长;(2) 如果点P 在AD 边上移动(点 P 与点A D 不重合),且满足/ BPE=Z A, PE 交直线BC 于点E ,同时交直 线DC 于点Q.①当点Q 在线段DC 的延长线上时,设 AP=x CQ=y 求y 关于x 的函数关系式,并写出自变量 x的取值范围;求BE 的长.11. (1)在厶ABC 中,AB=AC=5 BC=8点P 、Q 分别在射线 CB AC 上(点P 不与点 C 点B 重合),且保持 / APQ 2 ABC14.如图,在梯形ABCD中, AD// BC, AB=CD=BC=,6 AD=3.点M为边BC的中点,以M为顶点作/ EMF M B, 射线ME交腰AB于点E,射线MF交腰CD于点F,连接EF.(1)求证:△ ME®A BEM(2)若厶BEM是以BM为腰的等腰三角形,求EF的长;(3 )若EF丄CD求BE的长.15 .已知在梯形ABCD中, AD// BC AD< BC 且BC=6 AB=DC=4 点E 是AB 的中点.(1) 如图,P为BC上的一点,且BP=2.求证:△ BEP^A CPD(2) 如果点P在BC边上移动(点P与点B C不重合),且满足/ EPF=Z C, PF交直线CD于点F,同时交直线AD于点M,那么①当点F在线段CD的延长线上时,设BP=x, DF=y,求y关于x的函数解析式,并写出函数的定义域;16.如图所示,已知边长为3的等边△ ABC点F在边BC上, CF=1,点E是射线BA上一动点,以线段EF为边向右侧作等边厶EFG直线EG FG交直线AC于点M, N,(1)写出图中与△ BEF相似的三角形;(2)证明其中一对三角形相似;(3)设BE=x , MN=y求y与x之间的函数关系式,并写出自变量x的取值范围;(4)若AE=1,试求△ GMN勺面积.丄CP 交直线AB 于点E ,设PD=x AE=y,(1)写出y 与x 的函数解析式,并指出自变量的取值范围; (2)如果△ PCD 的面积是△ AEP 面积的4倍,求CE 的长;(3) 是否存在点 卩,使厶APE 沿PE 翻折后,点A 落在BC 上?证明你的结论.18. 如图,在 Rt △ ABC 中,/ C=90°, AB=5,工匸-=,点D 是BC 的中点,点 E 是AB 边上的动点, 交射线AC 于点F .(1 )求AC 和BC 的长;(2) 当 EF// BC 时,求 BE 的长;(3) 连接EF ,当厶DEF 和△ ABC 相似时,求 BE 的长.(备用图)19. 如图,在 Rt △ ABC 中,/ C=90°, AC=BC D 是AB 边上一点,E 是在AC 边上的一个动点(与点 重合),DF 丄DE DF 与射线BC 相交于点F .(1) 如图2,如果点 D 是边AB 的中点,求证:DE=DF (2) 如果 AD: DB=m 求DE DF 的值;17.如图所示,已知矩形 ABCD 中, CD=2 AD=3,点P 是AD 上的一个动点(与 A 、D 不重合),过点 P 作PEDF 丄DEA 、C 不(3)如果AC=BC=6 AD DB=1: 2,设AE=x BF=y,①求y关于x的函数关系式,并写出定义域;(2)如果以线段BC 为直径的圆与以线段 AE 为直径的圆相切,求线段 BE 的长;421. 如图,在梯形 ABCD 中, AB// CD AB=2 AD=4, tanC=^,/ ADC M DAB=90 , P 是腰 BC 上一个动点(不J含点B C ),作PQLAP 交CD 于点Q.(图1) (1 )求BC 的长与梯形 ABCD 勺面积;(2)当PQ=DQ 寸,求BP 的长;(图2)20. 如图,在厶ABC 中,/ C=90° EF 交射线BC 于点F .设BE=x , (1 )求y 关于x 的函数关系式, ,AC=6 •斗_彳,D 是BC 边的中点, △ BED 的面积为y .并写出自变量 x 的取值范围; E 为AB 边上的一个动点, 作/ DEF=90 ,②以CE 为直径的圆与直线 AB 是否可相切?若可能,求出此时 x 的值;若不可能,请说明理由.BED 相似,求△ BED 的面积.(2)••• AD 是中线,• CD=BD • C D=AD? DE,又/ ADC N CDE DEC^A DCA :丄 DCE N DAC证明:连接CE 如右图所示,•/ AB=AC AD L BC, • AD 是/ BAC 的角平分线,• BE=CE •••/ EBC=z ECB 又•••/ ABC=Z ACBABC- / EBC 2 ACB-Z ECB1. 解 答:2. 解 答: 证明:••• AD// BC4,又 BE// CD •••丄』,二二丄,即 OC=OA? OEOC OBOB OE OC OE解:①••• AB=ACB=Z C ,又•••/ ADE=Z B.••/ ADE N C ,「.A ADE^A ACD •••4 仝,.•• AE J =AE ? AB,AE AD故①正确,②易证得厶 CDE^A BAD T BC=16 设 BD=y, CE=x •••魁=—,•1° 工,整理得: CD CE 16-y x2即(y - 8) =64 - 10x , • O v x < 6.4 ,•/ AE=AC- CE=10- x , • 3.6 < AE< 10.故②正确. 2y - 16y+64=64 - 10x ,3.解 答: ③作AGL BC 于G •/ AB=AC=10 / ADE 玄 B=a ,COS a_4•/ BC=1Q • AG=6 •/ AD=2 I ,• DG=2 • CD=8 • AB=CD •△ ABD-与^ DCE 全等;故③正确; ④当/ AED=90 时,由①可知:△ ADE^A ACD •/ ADC=Z AED •••/ AED=90 , ADC=90 , 即 AD L BC, •/ AB=AC • BD=CD ADE 玄 B=a 且 COS a = , AB=10, BD=8/ B=a 且 COS a J. AB=10, ••• cosB=二 •• BD 」.故④正确5 BD 5 2当/ CDE=90 时,易厶 CDE^A BAD •••/ CDE=90 , BAD=90 ,故答案为:①②④.B U G C证明:(1)在厶BDE 和A DAB 中•••/ DEB=/ ABC / BDE=/ ADB BDE^A ADBD£__BD • BE J =AD ? DE4.解 答:.CD 二 AD'DE _CD实用文档即/ ABEK ACE又••• CGI AB,:/ ABEh CGF :丄 CGF 2 FCE 又/ FEC=/ CEGCEF^A GEC 二 CE EF=EG CE 即 C^=EF? EG 又 CE=BE ••• BU=EF? EG又 EF 为 AD 的垂直平分线,• AF=FD / DAF=/ ADF, DAC / CAF=/ B+/ BAD•••/ CAF=/ B ,•// AFC 玄 AFC •△ ACF^A BAF,即丄仝,• AF "=CF? BF ,即 F[J=CF? BF.AF B?ripr r>ri i •// EPD=/ A, /PED=/ AER EPD^A EAR •定义域是 0< x v 一-—5得 「二_二= 21寸PEAP 2 (2)由厶 EPD^A EAR6.解 答:PD BC 1AP AC 2• PE=2DE • AE=2PE=4DE 作EHL AB,垂足为点H,•/ AP=x •- PD 二x , •/ PD// HE2又AB=2 ■ , y =—•-上J 亠- 'PD AD 3.(2 _ ";- x)? —x ,即 y=-3^ • HE :x .3X 2+二' 3x .另解:由厶EPD^A EAR 得DE PD 1 PE• PE=2DE • AE=2PE=4DE • AE --S AAB =—X y x ——X X 2=1 x , • ABx .定义域是 0< x < —'.厂丄• PE 二x? • HE AC ,当厶BEP-与^ ABC 相似时,只有两种情形:/(3)由厶 PEH ^A BAC 得x .32BEP=/ C=90° 或/ EBP=/ C=90°.• △ ADP ^A ABC • A=/ A ,X2 x,2SAABE 2 1…y= - — x2 37.解 答:8.解 答:证明:••• BD CE 分别是AC 与AB 边上的高,•/ BEC 2 BDC• B 、C D E 四点共圆,•/ AED=/ ACB 而/ A=Z A, • △ AED^A ACB •- -丄; BC AR•/ BD 丄AC,且/ A=60°,A Z ABD=30 , AD=迅,• BC=2DE•/△ ABC 是等边三角形•/ ABC=/ ACB 玄 BAC=60 . •/ D+Z DAB=60 , •••/ DAE=120,•/ DAB+Z EAC=60 . •/ D=Z CAE / E=Z DAB •••/ D=Z D,Z E=Z E ,「.A DAE^A DBA^A ACE(2)•••△ DBA^A ACE •- DB: AC=AB CE•/ AB=AC=BC DB=2 CE=6i BC ?=DB? CE=12 •/ BO0, • BC=2,/ £.Z E+Z CAE=60 .9.解证明:(1)在Rt △ ABC 中, 答: •/ AB=AC •/ B=Z C=45.•••/ BAE=/ BAD+Z DAE Z DAE=45,•/ BAE=/ BAD+45 . 而/ ADC Z BAD+Z B=Z BAD+45 , • Z BAE=/ CDA • △ ABE^A DCA(2)由厶 ABE^^ DCA 得翌• BE? CD=AB AC.AB CD2 2 2 2 2 2而 AB=AC BC=AB+AC ,「. BC=2AB . • BC=2BE? CD10.解(1)证明:•••△ ABC 为等边三角形,•/ B=Z C=60°, 答: vZ EDF=60,•/ BED+Z EDB 玄 EDB+Z FDC=120 ,• Z BED Z FDC •△ BD 0A CFD(2)解:由(1 )知厶 BDE^A CFDBE =BD CD =CF(i )当/ BEP=90时,旦县,•••罗》=丄.解得x 型迈.PB 起药厂V5 4• y=-二x X_X 5+''X …亠.31&3 4 16(ii )当/ EBP=90时,同理可得 x=邑匹,y=J .24•/ BC=6 BD=1,「. CD=B G BD=5, •••翌=丄,解得 BE 壬.5 3 3解解:(1)①•••/ APQ+Z CPQ 2 B+Z BAP, / APQ 2 ABC BAP=Z CQP又••• AB=AC •••/ B=Z C.• △ CPQ^A BAP若点P 在线段CB 的延长线上,如图.•••/ APQ M APB 亡 CPQ/ ABC 玄 APB+Z PAB /APQ M ABC •••/ CPQ MPAB又 T Z ABP=180 -Z ABC Z PCQ=180 -Z ACB Z ABC Z ACB • Z ABP=/ PCQ11. 答:BP AB•/ AB=AC=5 BC=8 BP=6 CP=8- 6=2 , • CQ CP•/ BP=x, BC=8,「. CP=BC- BP=8- x , ,即丁 _ 7 y5②若点P 在线段CB 上,由(1 )知又••• CQ=y AB=5 •工E _ 1X 5故所求的函数关系式为CQ 2» 12 6 3CQ 飞CQ PC ■/ BP=x CP=BC+BP=8+, AB=5, CQ=y实用文档QCP^ PBA 里/:.实用文档圉①(2)①当点P 在线段BC 上,•••/ APQ=90,•/ APB+Z QPC=90 , •••/ PAB 亡 APB=90,•/ PAB=/ QPC•••/ B=/ C=90°.・.A ABP^A PCQ • AB: PC=BP CQ-J : 或. | -②当点P 在线段BC 的延长线上,则点 Q 在线段 同理可得:△ ABN A PCQ • AB: PC=BP CQ即 5: ( 5 - BP ) =BP 1,解得:2DC 的延长线上,••• 5: (BP- 5) =BP: 1,解得: BP=— ③当点P 在线段CB 的延长线上,则点 Q 在线段 同理可得:△ ABN A PCQ • AB: PC=BP CQ • 5: (BP+5) =BP 1,解得:E _ . DC 的延长线上, A=Z D 13.解 解:(1)v ABCD 是梯形,AD// BC AB=DC 「./ •••/ ABP+/ APB+/ A=180°,Z APB-/ DPC / BPC=180 , / BPC 玄 A 解得:AP=1 或 AP=4.答: •••/ ABPK DPC ABN A DPC. AP 民即. AP 2 CD FD 2 ~5-AP 14. 答: (2)①由(1) •;」即:DQ~PD②当CE=1时,富二22fy~ 5-i•/△ PDQ^A ECQ • CE_CQPD~DQ ,:,解得:AP=2或(舍去).G怙 ■ 4. 『-t * -i;\Fi/i解证明:(1)在梯形ABCD 中,•/ AD// BC, AB=CD 「・/ B=/ C ,•••/ BMF / EMB / EMF / C+/ MFC又•••/ EMF=/ B, •/ EMB / MFC •△ EMB^A MFC •- _L "一EM ~MF ' •/ MC=M , • 一 UL關—和,又丄即匕B’iEi B EM(2)解:若△ BEM 是以BM 为腰的等腰三角形,则有两种情况:① BM=ME 那么根据厶 ME &A BEM .•.二1="- ,•. £=也,即 EF=MFHE 01 ME EF根据第(1)问中已证厶BM 0A MFC ■ ■, 即 MF=FC •••/ FMC 2 C,HE FC又•••/ B=Z C,.Z FMC M B ,. MF// AB延长BA 和CD 相交于点 G 又点M 是BC 的中点, • MF >^ GBC 的中位线,• MF=GB2!又••• AD// BC,GAD^A GBC • 塑=型=丄4 ,•.塑=1, 即 AG=AB=6GB BC 6 2 AG• GB=12 • MF=EF=6② BM=BE=3 .•点E 是AB 的中点,又厶 MEF^A BEM.•.型=世=1,即MF=ME • EF 是梯形 ABCD 勺中位线,• EF 丄(AD+BC — ( 3+6)戈;Bg ME 2 2 2(3 )T EF ± CD• / BEP=/ FPC •△ BEP^A CPF , • ^^^-4 (2< x v 4)•②当点F 在线段CD 的延长线上时,•••/ FDM Z C=Z B, / BEP=/ FPCK FMD •△ BEP^A DMF DF 3 y.T , • x - 3x+8=0 , △< 0.•此方程无实数根..•尸gF - 3K +4 .2 ____________、,15. 答:• / EFC=90 , △ MEF^A BEM / MFE / MFC / BME=45 ,解一:过点E 作EH! BC,则可得△ EHM 等腰直角三角形, EH=MH 」 故 EH=MH 设 BE=x 贝U BH 丄•-, 4解二:过点M 作MN L DC MC=3由厶 MEF^A MFCt • T ,即 P 旳TCI 5 4NIC 』.M43弓&亏"解 (1)证明:•••在梯形 ABCD 中 , AD// BC, AB=DC=FN FC= i i : - - 2BE —— 丨.• / B=Z C.BE=2, BP=2, CP=4 CD=4 •••里=!!?.•••△ BEP^A CPDCP CD(2)解:①•••/ B=Z C=Z EPF• 180 —/ B=180-Z EPF=/ BEP+Z BPE=Z BPE+Z CPFHE 閏.•crP 2 si 6-iSZ1DJIF^43ABEP, … DF BP"3 y 八. △ BEP^A CPF , • EB BPl • 1 2 xCP '"cr£ - 工 4 _ y.、/9•当 £ADMF ^^ABEP,得 2故当点F 在线段CD 的延长线上时,不存在点 P 使SADMF =-|SABEP ; 当点F 在线段 CD 上时,同理△ BEP^A DMF• x - 9x+8=0 ,解得X1=1 , X2=8.由于X2=8 不合题意舍去.• x=1 ,即BP=1. 时,BP的长为1.实用文档16.解解:(BE&A AM 0A CFW A GMN 答:证明:(2)在厶BEF 与厶AME 中,•••/ B=Z A=60°,「./ AEM 社 AME=120 ,•/△ BEF^A AME •- BE: AM=BF AE ,同理可证厶 BEF ^A CFN • BE: CF=BF CN即:x : 1=2: CN •- CN 丄,即: x : AM=2 (3- x ) , • AM=•••/ GEF=60 ,•••/ AEM # BEF=120BEF=Z AME :, △ BEF ^A AME备用图一备甲图二解:(3) (i )当点E 在线段AB 上,点M N 在线段AC 上时,如图,实用文档(ii )当点E 在线段AB 上,点6在厶ABC 内时,如备用图一,同上可得:AM= 丁 i ;, C N L ,2x•/ AC=AM+CN MN ••• 3= _ /+%+上—yy=— J %*民 一 4 ( o v x < 1 );2 x2x(iii )当点E 在线段BA 的延长线上时,如备用图二,AM= -------- 二,CN=,2 £ •/ AC=MN+C Z AM • 3=y+Z - ' _ 刃,• y=J 一 彳&张—° ( x > 3);± 2 2x综上所述:y= -£-娄细竺( o v x < 1),或y=^-3,十6豪 -4( x > 1); 2x 2x(4) (i )当AE=1时,△ GMN 是边长为1等边三角形,S MM =_X 1 X 二=丄;(1 分)::(ii )当 AE=1 时,△ GMN1 有一个角为 30° 的 Rt △, ••• x=4,. y= 「一,一丄,NG=FG FN=4X ;- 1 X ・;=;, 2X4 2 222• s =1X22 2 g17. 答: 解(1)解:T PEI CP,.可得:△ y 3 _ Xx" 2(2)解:当△ PCD 的面积是厶AEP 面积的4倍, 则:相似比为2: 1 , •又••• CD=2 AD=3 设 PD=x, AE=y,.・.AF PAEAP^^ PDC ••亠-PD CD• y = — 1 2 卫 ,…y = - r ,0v x v 3;................... .AE AP_1'PD"CD"2,_•/ CD=2 • AP=1, PD=2 • PE= - , PC=2 :■: , • EC= 111. (3 )不存在.作AF 丄PE,交PE 于O, BC 于 F ,连接EFT AF 丄 PE, CP 丄 PE/. AF=CP= , •, PE=::,-.',(3-7~2 •/△ CDP^A POA=£2 23x —6x+4=0,OA=PA PC (3- x)x =l 2△ =6 — 4 X 4 X 3= — 12 x 无解因此,不存在.实用文档y—, •••设 AC=3k, BC=4k, /• AB=5k=5,「. k=1,「. AC=3 BC=4 BC 4| (2)过点E 作EH! BC,垂足为 H.易得△ EHB^A ACB 设 EH=CF=3k BH=4k, BE=5k ; •/ EF// BC ••/ EFD=/ FDC•••/ FDE 玄 C=90°A ^ EFD^^ FDC ・ —F D=EF? CD,即 9k 2+4=2 (4 -4k )化简,得 9k 2+8k - 4=0(负值舍去),•••二_■丨 ';19.解(1)证明:如图2,连接DC答: •••/ ACB=90 , AC=BC A=Z B=45° ,•••点 D 是 AB 中点,BCD 2 ACD=45 , CD=BD ACD=/ B=45°•/ ED ! DF , CD!AB,•••/ EDC 丄 CDF=90 , / CDF+Z FDB=90 , EDC M FDB•••△ CED^A BFD (ASA ) , • DE=DF(2) 解:如图1,作DP ! AC, DQL BC,垂足分别为点 Q, P.•••/ B=Z A , / APD=/ BQD=90 , ADP^A BDQ• DP DQ=AD DB=m•••/ CPD / CQD=90 , / C=90°, •/ QDP=90 , •/ DF 丄 DE, •/ EDF=90 , •/ QDF / PDE•••/ DQF / DPE=90 , DQF^A DPE• DE DF=DP DQ • DE DF=DP DQ=AD DB=m(3) 解:①如备用图1,作EGL AB, FH! AB,垂足分别为点 G H. 在 Rt △ ABC 中,/ C=90° , AC=BC=6 •- AB= ■:,18. 答: E 作EH! BC,垂足为H.易得△ BE=5k(3)过点 设 EH=3k, •••/ HED 丄 HDE=90 / FDC+ZHDE=90EHB^A ACB•••/ EHD 2 C=90°•••△ EHD^A DCF•••/ HED=/FDC • I 方五,当厶DEF 和△ ABC 相似时,有两种情况:1°CD~4,即.解得••-丄,24 K 厲 DE BC 4 综合1°、2 ° , 2° 2,•呼5匸卫 • 即亠CD -3 2 "3 当厶DEF 和△ ABCt 目似时,BE 的长为上或丄 2 g 解得w ,—丄.FD _CD解 解:(1)在 Rt △ ABC 中,/C=90°实用文档20. 答:•/ AD DB=1: 2,:. AD三•:, DB= 「由/ AGE M BHF=90,/ A=Z B=45°可得AG=EG= 一.,BH=FH2 K 2易证△ DG0A FHD :• DG GE匸」「,GD= —_ .,<2 V2----- 資 ----- V2 2rW2②如备用图2,取CE的中点0,作OM L AB于M.可得CE=6- x, A0=-十二,HD=:'7,0M=]:「_±,.AB相切,贝U —2 _ 2 2若以CE为直径的圆与直线解得.•:当八时,以,•: y=8 -2x,CE为直径的圆与直线AB相切.备冒图1 备用图』解解: (1)T在厶ABC中,/ C=90°, AC=6 t述斗,•:BC=8 AB=10,定义域是•: CD=DB=4过点E作EH! CB于H.则可求得EH丄x.54 x '■ x= x (0 V x <5 5-'或5V x w 10).(2)取AE OGL BC于G 连接OD则x10+y32 '(10+x), GD=C- CG=4-I (10-x)4 2-- T •251 2 2两圆外切,则可得*BC1;AE=OD:.( BC+AE =4OD,2 Q 2+——x ]25•: 0D=2:•( 8+10- x) =4[ (10+x)100若两圆内切,得|-;BC--;AEFOD,解得4实用文档•••( BC — AE ) 2=4OD ,.・.(8 - 10+x )2=4[— ( 10+x )100解得x=-二J (舍去),所以两圆内切不存在•所以,线段7(3)由题意知/ BEF M 90°,故可以分两种情况. ①当/ BEF 为锐角时,由已知以 B E 、F 为顶点的三角形与△ BED 相似,又知/ EBF=Z DBE / BEF <Z BED 所以/ BEF=Z BDE过点D 作DM L BA 于M 过E 作EH L BC 于H. 根据等角的余角相等,可证得/ MDE N HDE • EM=EH21.解解:(1)作BHLCD ,垂足为H,则四边形 ABHD 为矩形;答: • BH=DA=4 DH=AB=2在 Rt △ BCH 中,上皿二寻• 6冷讣■=$,(1 分)BC 討E H '+CH~5; 又 CD=CH+DH=5 • S 梯形 ABCI ^ (血+CD) AD =14;2(2)连接AQ由 DQ=PQ 可知△ APQ AP=AD=4 作PE! AB 交AB 的延长线于点 E , (1分)在 Rt △ BPE 中,二工_;二上--口一-二,令 BE=3k PE=4k. 则在Rt △ APE 中, AF ^A W+P E ,2224A /21 - &即 4=(2+3k ) + (4k ),解得:2+—x 2]25BE 的长为二丄3又 EM=M — EB — - x ,5由(1)知:EH 士 x ,「亍冗兀②当/ BEF 为钝角时,同理可求得 x - ,• x=2.•16 =3x=8.「. y=§X 8=坐 5 512或 48 55x ,•所以,△ BED 的面积是实用文档•『'i :■ - ' | :厂-「- -(3)作PF丄CD交CD于点F,由/ AEF=/ EFD=/ APQ=90 , 可得:△ AEP^A PFQaQF _屮芹H• OF EPPF~AE,化简得:QF二一16 卫二"SO+ISX5 50+15X3010•….定义域为(0v x v 5).。
相似三角形几何模型一线三等角(知识讲解)学年九年级数学上册基础知识讲与练(北师大版)

专题4.37 相似三角形几何模型-一线三等角(知识讲解)模型一:一线三直角图一 图二90;B ACE D ABC CDE ∠=∠=∠=∆∆如图一、二,已知:结论:(1)(2)AB DE =BC CD模型二:一线三等角图三 图四;B ACE D ABC CDE ABC CDE ACE α∠=∠=∠=∆∆∆∆∆如图三、四,已知:结论:(1)(2)AB DE =BC CD(3)当C 为BD 中点时,特别说明:一线三等角相似三角形往往以等腰三角形或等边三角形为背景,如下图五。
图五特别说明:一线三直角相似三角形往往以矩形或正方形背景,如下图六。
图六【典型例题】类型一、一线三直角模型1.如图,在四边形ABCD 中,AB ∥CD ,90B =∠,7CD =,E 为BC 上一点,且AE ED ⊥,若12BC =,:1:2BE EC =,求AB 的长.【答案】327【分析】由题意易知AB 和CD 所在的两个三角形相似,再利用相似比即可求出所求线段的长度.解:∵AB 平行CD ,90B =∠,∵180B C ∠+∠=, ∵90B =∠,∵90B C ∠=∠=,90BEA BAE ∠+∠=, ∵AE ED ⊥,∵90AEB DEC ∠+∠=, ∵BAE DEC ∠=∠, ∵ABE ECD ∆∆∽, ∵AB BEEC DC=, ∵12BC =,12BE EC =, ∵48BE EC ==,, ∵7DC =, ∵432877BE AB EC DC =⋅=⨯=. 【点拨】此题主要考查学生对梯形的性质及相似三角形的性质的理解及运用.举一反三【变式1】如图,将矩形ABCD 沿CE 向上折叠,使点B 落在AD 边上的点F 处,AB=8,BC=10.(1)求证:∵AEF∵∵DFC ;(2)求线段EF的长度.EF=.【答案】(1)证明见分析;(2)5【分析】(1)由四边形ABCD是矩形,于是得到∵A=∵D=∵B=90°,根据折叠的性质得∵EFC=∵B=90°,推出∵AEF=∵DFC,即可得到结论;(2)根据折叠的性质得CF=BC=10,根据勾股定理得到6D F,求得AF=4,然后根据勾股定理列方程即可得到结论.解:(1)∵四边形ABCD是矩形,∵∵A=∵D=∵B=90°,CD=AB=8,根据折叠的性质得∵EFC=∵B=90°,∵∵AFE+∵AEF=∵AFE+∵DFC=90°,∵∵AEF=∵DFC,∵∵AEF∵∵DFC;(2)根据折叠的性质得:CF=BC=10,BE=EF,∵6D F=,∵AF=4,∵AE=AB-BE=8-EF,∵EF2=AE2+AF2,即EF2=(8-EF)2+42,EF=.解得:5【点拨】本题主要考查了相似三角形的判定,矩形的性质、翻折变换的性质及其应用问题.解题的关键是灵活运用矩形的性质、翻折变换的性质来分析、判断、解答.【变式2】如图1,在矩形ABCD中,E为DC边上一点,把ADE沿AE翻折,使点D 恰好落在BC边上的点F处.~;(1)求证:ABF FCEAD=,求EC的长;(2)若AB=6+(3)如图2,在第(2)问的条件下,若P,Q分别是AE,AD上的动点,求PD PQ 的最小值.【答案】(1)见分析;(2)EC =;(3)PD PQ +的最小值为 【分析】(1)选证得AFB CEF ∠=∠,即可证明结论;(2)利用折叠的性质,在Rt △ABF 中,求得BF 的长,设CE =x ,在Rt △CEF 中,利用勾股定理构建关于x 的方程,即可求解;(3)根据折叠的性质,点F 、D 关于直线AE 对称,过F 作FQ ∵AD 于Q ,交AE 于P ,此时PD +PQ 的最小值为FQ ,证明四边形QFCD 是矩形,即可求解.(1)证明:∵四边形ABCD 是矩形,∵90B C D ∠=∠=∠=︒, ∵90CEF EFC ∠+∠=︒, ∵AEF 由ADE 翻折得到, ∵90AFE D ∠=∠=︒, ∵90AFB EFC ∠+∠=︒,∵AFB CEF ∠=∠,90ABF FCE ∠=∠=︒, ∵ABF FCE ~;(2)∵四边形ABCD 是矩形,∵AB CD ==6AD BC ==.设CE x =,则DE x =,在Rt ABF 中,3BF ==, ∵633CF BC BF =-=-=,在Rt CEF 中,222EF CE CF =+,即222)3x x =+,解得x =EC =(3)如图,根据折叠的性质,点F 、D 关于直线AE 对称,过F 作FQ ∵AD 于Q ,交AE 于P ,此时PD +PQ 的最小值为FQ ,∵四边形ABCD 是矩形, ∵∵C =∵ADC =90︒,又FQ ∵AD , ∵四边形QFCD 是矩形,∵FQ =CD =AB∵PD PQ +的最小值为【点拨】本题考查了矩形的性质折叠变换,相似三角形的判定和性质,轴对称的性质等知识,解题的关键是正确寻找相似三角形解决问题,学会利用参数解决问题.类型二、一线三等角模型2.如图,在∵ABC 中,点D 、E 分别在边BC 、AC 上,连接AD 、DE .且∵B =∵ADE=∵C .(1)证明:∵BDA ∵∵CED ;(2)若∵B =45°,BC =6,当点D 在BC 上运动时(点D 不与B 、C 重合).且∵ADE 是等腰三角形,求此时BD 的长.【答案】()见分析;(2)6-或3. 【分析】(1)根据题目已知条件可知180ADE ADB EDC ∠+∠+∠=︒,180B ADB DAB ∠+∠+∠=︒,所以得到DAB EDC ∠=∠,即可得证.(2)由题意易得ABC 是等腰直角三角形,所以90BAC ∠=︒,当ADE 是等腰三角形时,根据分类讨论有三种情况:∵AD =AE ,∵AD =DE ,∵AE =DE ;因为点D 不与B C 、重合,所以第一种情况不符合,其他两种情况根据等腰三角形的性质“等边对等角”及45B ADE ∠=∠=︒,求出问题即可.解:(1)180ADE ADB EDC ∠+∠+∠=︒在ABD △中,180B ADB DAB ∠+∠+∠=︒B ADE ∠=∠∴EDC DAB ∠=∠又B C ∠=∠∴BDA CED △∽△;(2)B ADE C ∠=∠=∠,45B ∠=︒∴ABC 是等腰直角三角形 ∴90BAC ∠=︒BC =6,∴AB =AC ∵当AD =AE 时,则ADE AED ∠=∠45B ∠=︒,∴=45B ADE AED ∠=∠∠=︒ ∴90DAE ∠=︒ ∴90DAE BAC ∠=∠=︒点D 在BC 上运动时(点D 不与B C 、重合),点E 在AC 上 ∴此情况不符合题意.∵当AD =DE 时,如图,∴DAE DEA ∠=∠∴由(1)可知EDC DAB ∠=∠又B C ∠=∠ BDA CED ≌∴AB =DC =∴6BD =-∵当AE =DE 时,如图45B ∠=︒,∴==45B C DAE ADE ∠∠∠=∠=︒ ∴AD 平分BAC ∠,AD BC ⊥ ∴1=32BD BC =.综上所述:BD =6-3.【点拨】本题主要考查相似三角形的判定及等腰三角形的存在性问题,解题的关键是利用“K ”型相似模型及根据“等边对等角”、等腰直角三角形的性质得到线段的等量关系,进而求解问题.举一反三【变式1】如图,点M 是AB 上一点,AE 与BD 交于点C ,DME A B α∠=∠=∠=,且DM 交AC 于F ,ME 交BC 于G .(1)求证:∽AMF BGM ; (2)请你再写出两对相似三角形.【答案】(1)见分析;(2)AME MFE △∽△,DMG DBM ∽△△. 【分析】(1)根据三角形内角和证AFM BMG ∠=∠即可;(2)根据公共角相等,利用两个角对应相等,写出相似三角形即可. (1)证明:∵DME A ∠=∠,180AMF BMG DME ∠+∠+∠=︒,180A AMF AFM ∠+∠+∠=︒,∵AFM BMG ∠=∠, ∵A B ∠=∠,∵∽AMF BGM ;(2)∵DME A ∠=∠,∵E=∵E ,∵AME MFE △∽△,同理,DMG DBM ∽△△. 【点拨】本题考查了相似三角形的判定,熟记相似三角形判定定理并能灵活应用是解题关键.【变式2】∵ABC 中,AB =AC ,∵BAC =90°,P 为BC 上的动点,小慧拿含45°角的透明三角板,使45°角的顶点落在点P ,三角板可绕P 点旋转.(1)如图a ,当三角板的两边分别交AB 、AC 于点E 、F 时.求证:∵BPE ∵∵CFP ; (2)将三角板绕点P 旋转到图b 情形时,三角板的两边分别交BA 的延长线、边AC 于点E 、F .∵BPE 与∵CFP 还相似吗?(只需写出结论)(3)在(2)的条件下,连结EF ,∵BPE 与∵PFE 是否相似?若不相似,则动点P 运动到什么位置时,∵BPE 与∵PFE 相似?说明理由.【答案】(1)证明见分析;(2)∵BPE ∵∵CFP ;(3)动点P 运动到BC 中点位置时,∵BPE 与∵PFE 相似,理由见分析.【分析】(1)找出∵BPE 与∵CFP 的对应角,其中∵BPE+∵BEP=135°,∵BPE+∵CPF=135°,得出∵BEP=∵CPF ,从而解决问题;(2)利用(1)小题证明方法可证:∵BPE∵∵CFP ;(3)动点P 运动到BC 中点位置时,∵BPE 与∵PFE 相似,同(1),可证∵BPE∵∵CFP ,得 CP :BE=PF :PE ,而CP=BP ,因此 PB :BE=PF :PE ,进而求出,∵BPE 与∵PFE 相似.(1)证明:∵在∵ABC 中,∵BAC =90°,AB =AC ,∵∵B =∵C =45°.∵∵B +∵BPE +∵BEP =180°, ∵∵BPE +∵BEP =135°. ∵∵EPF =45°,又∵∵BPE +∵EPF +∵CPF =180°, ∵∵BPE +∵CPF =135°,∵∵BEP =∵CPF , 又∵∵B =∵C , ∵∵BPE ∵∵CFP .(2)∵BPE ∵∵CFP ;理由:∵在∵ABC 中,∵BAC =90°,AB =AC ,∵∵B =∵C =45°.∵∵B +∵BPE +∵BEP =180°, ∵∵BPE +∵BEP =135°. ∵∵EPF =45°,又∵∵BPE +∵EPF +∵CPF =180°, ∵∵BPE +∵CPF =135°, ∵∵BEP =∵CPF , 又∵∵B =∵C , ∵∵BPE ∵∵CFP .(3)动点P 运动到BC 中点位置时,∵BPE 与∵PFE 相似,证明:同(1),可证∵BPE ∵∵CFP , 得CP :BE =PF :PE , 而CP =BP ,因此PB :BE =PF :PE . 又因为∵EBP =∵EPF , 所以∵BPE ∵∵PFE【点拨】此题主要考查了相似三角形的判定.它以每位学生都有的三角板在图形上的运动为背景,既考查了学生图形旋转变换的思想,静中思动,动中求静的思维方法,又考查了学生动手实践、自主探究的能力.类型三、一线三等角综合3.数学模型学习与应用.【学习】如图1,90BAD ∠=︒,AB AD =,BC AC⊥于点C ,DE AC ⊥于点E .由12290D ∠+∠=∠+∠=︒,得∵1=∵D ;又90ACB AED ∠=∠=︒,可以通过推理得到ABC ∵DAE △.我们把这个数学模型称为“一线三等角”模型;(1)【应用】如图2,点B ,P ,D 都在直线l 上,并且ABP APC PDC α∠=∠=∠=.若BP x =,2AB =,5BD =,用含x 的式子表示CD 的长;(2)【拓展】在ABC 中,点D ,E 分别是边BC ,AC 上的点,连接AD ,DE ,B ADEC ∠=∠=∠,5AB =,6BC =.若CDE △为直角三角形,求CD 的长;(3)如图3,在平面直角坐标系xOy 中,点A 的坐标为()2,4,点B 为平面内任一点.AOB 是以OA 为斜边的等腰直角三角形,试直接写出点B 的坐标.【答案】(1)21522CD x x =-+(2)3(3)()3,1或()1,3-(1)解:∵ABP APC PDC α∠=∠=∠=,∵A APB APB CPD ∠+∠=∠+∠, ∵A CPD ∠=∠, 又∵ABP PDC ∠=∠, ∵ABP △∵PDC △, ∵AB BP PD CD =, 即25x CD x=-, ∵21522CD x x =-+.(2)解:如图4,当90CED ∠=︒时,∵ADE C ∠=∠,CAD DAE ∠=∠, ∵ACD △∵ADE , ∵90ADC AED ∠=∠=︒,∵B C ∠=∠,90ADC ∠=︒∵点D 为BC 的中点, ∵116322CD BC ==⨯=. 如图5,当90EDC ∠=︒时,∵B C ∠=∠,∵90BAD EDC ∠=∠=︒,过点A 作AF BC ⊥,交BC 于点F , ∵132BF BC ==,3cos 5BF AB B AB BD ===, 2563BD =>,不合题意,舍去, ∵3CD =.(3)解:分两种情况:∵如图6所示,过A 作AC ∵y 轴于D ,过B 作BE ∵x 轴于E ,DA 与EB 相交于C ,则∵C =90°,∵四边形OECD 是矩形∵点A 的坐标为(2,4),∵AD =2,OD =CE =4,∵∵OBA =90°,∵∵OBE +∵ABC =90°,∵∵ABC +∵BAC =90°,∵∵BAC =∵OBE ,在△ABC 与△BOE 中,90C BEO BAC OBE AB BO ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩∵∵ABC ∵∵BOE (AAS ),∵AC =BE ,BC =OE ,设OE =x ,则BC =OE =CD =x ,∵AC =BE =x -2,∵CE =BE +BC =x -2+x =OD =4,∵x =3,x -2=1,∵点B 的坐标是(3,1);∵如图7,同理可得,点B 的坐标(-1,3),综上所述,点B 的坐标为(3,1)或(-1,3).【点拨】本题是三角形综合题目,考查了全等三角形的判定和性质,等腰三角形的性质,等腰直角三角形的性质等知识;正确的作出辅助线,证明三角形全等是解题的关键.举一反三【变式1】感知:(1)数学课上,老师给出了一个模型:如图1,90BAD ACB AED ∠=∠=∠=︒,由12180BAD ∠+∠+∠=︒,2180D AED ∠+∠+∠=︒,可得1D ∠=∠ ;又因为90ACB AED =∠=︒,可得ABC DAE △△∽,进而得到BC AC=______.我们把这个模型称为“一线三等角”模型. 应用:(2)实战组受此模型的启发,将三等角变为非直角,如图2,在ABC 中,10AB AC ==,12BC =,点P 是BC 边上的一个动点(不与B 、C 重合),点D 是AC 边上的一个动点,且APD B ∠=∠.∵求证:ABP PCD △△∽;∵当点P 为BC 中点时,求CD 的长;拓展:(3)在(2)的条件下如图2,当APD △为等腰三角形时,请直接写出BP 的长.【答案】感知:(1)AEDE;应用:(2)∵见分析;∵3.6;拓展:(3)2或113【分析】(1)根据相似三角形的性质,即可求解;(2)∵根据等腰三角形的性质得到∵B=∵C,根据三角形的外角性质得到∵BAP=∵CPD,即可求证;∵根据相似三角形的性质计算,即可求解;(3)分P A=PD、AP=AD、DA=DP三种情况,根据等腰三角形的性质、相似三角形的性质,即可求解.解:感知:(1)∵∵ABC∵∵DAE,∵BC AC AE DE=,∵BC AE AC DE=,故答案为:AE DE;应用:(2)∵∵∵APC=∵B+∵BAP,∵APC=∵APD+∵CPD,∵APD=∵B,∵∵BAP=∵CPD,∵AB=AC,∵∵B=∵C,∵∵ABP∵∵PCD;∵BC=12,点P为BC中点,∵BP=PC=6,·∵∵ABP∵∵PCD,∵AB BPPC CD=,即1066CD=,解得:CD=3.6;拓展:(3)当P A=PD时,∵ABP∵∵PCD,∵PC=AB=10,∵BP=BC-PC=12-10=2;当AP =AD 时,∵ADP =∵APD ,∵∵APD =∵B =∵C ,∵∵ADP =∵C ,不合题意,∵AP ≠AD ;当DA =DP 时,∵DAP =∵APD =∵B ,∵∵C =∵C ,∵∵BCA ∵∵ACP , ∵BC AC AC CP =,即121010CP=, 解得:253CP =, ∵25111233BP BC CP =-=-=, 综上所述,当APD △为等腰三角形时, BP 的长为2或113 . 【点拨】本题考查的是三角形相似的判定定理和性质定理、全等三角形的判定定理和性质定理以及三角形的外角性质,掌握相似三角形的判定定理和性质定理是解题的关键.【变式2】【感知模型】“一线三等角”模型是平面几何图形中的重要模型之一,请根据以下问题,把你的感知填写出来:∵如图1,ABC 是等腰直角三角形,90C ∠=︒,AE =BD ,则AED ≌_______; ∵如图2,ABC 为正三角形,,60BD CF EDF =∠=︒,则BDE ≌________; ∵如图3,正方形ABCD 的顶点B 在直线l 上,分别过点A 、C 作AE l ⊥于E ,CF l ⊥于F .若1AE =,2CF =,则EF 的长为________.【模型应用】(2)如图4,将正方形OABC 放在平面直角坐标系中,点O 为原点,点A的坐标为(,则点C 的坐标为________.【模型变式】(3)如图5所示,在ABC 中,90ACB ∠=︒,AC BC =,BE CE ⊥于E ,AD ∵CE 于D ,4cm DE =,6cm AD =,求BE 的长.【答案】∵∵BDF ;∵∵CFD ;∵3;(2)((3)2cm 【分析】∵根据等腰直角三角形的性质及和角关系,可得∵AED ∵∵BDF ;∵根据等边三角形的性质及和角关系,可得∵BDE ∵∵CFD ;∵根据正方形的性质及和角关系,可得∵ABE ∵∵BCF ,由全等三角形的性质即可求得EF 的长;(2)分别过A 、C 作x 轴的垂线,垂足分别为点D 、E ,根据正方形的性质及和角关系,可得∵COE ∵∵OAD ,从而可求得OE 、CE 的长,进而得到点C 的坐标;(3)由三个垂直及等腰直角三角形可证明∵BCE ∵∵CAD ,由全等三角形的性质即可求得BE 的长.解:∵∵∵ABC 是等腰直角三角形,∵C =90゜∵∵A =∵B =45゜∵∵BDF +∵BFD =180゜−∵B =135゜∵∵EDF =45゜∵∵ADE +∵BDF =180゜−∵EDF =135゜∵∵ADE =∵BFD在∵AED 和∵BDF 中A B ADE BFD AE BD ∠=∠⎧⎪∠=∠⎨⎪=⎩∵∵AED ∵∵BDF (AAS )故答案为:∵BDF ;∵∵∵ABC 是等边三角形∵∵B =∵C =60゜∵∵BDE +∵BED =180゜−∵B =120゜∵∵EDF =60゜∵∵BDE +∵CDF =180゜−∵EDF =120゜∵∵BED =∵CDFB C BED CDF BD CF ∠=∠⎧⎪∠=∠⎨⎪=⎩∵∵BDE ∵∵CFD (AAS )故答案为:∵CFD ;∵∵四边形ABCD 是正方形∵∵ABC =90゜,AB =BC∵∵ABE +∵CBF =180゜−∵ABC =90゜∵AE ∵l ,CF ∵l∵∵AEB =∵CFB =90゜∵∵ABE +∵EAB =90゜∵∵EAB =∵CBF在∵ABE 和∵BCF 中AEB CFB EAB CBF AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩∵∵ABE ∵∵BCF (AAS )∵AE =BF =1,BE =CF =2∵EF =BE +BF =2+1=3故答案为:3;(2)分别过A 、C 作x 轴的垂线,垂足分别为点D 、E ,如图所示∵四边形OABC 是正方形∵∵AOC =90゜,AO =OC∵∵COE +∵AOD =180゜−∵ACO =90゜∵AD ∵x 轴,CE ∵x 轴∵∵CEO =∵ADO =90゜∵∵ECO +∵COE =90゜∵∵ECO =∵AODCEO ADO ECO AOD OC AO ∠=∠⎧⎪∠=∠⎨⎪=⎩∵∵COE ∵∵OAD (AAS )∵CE =OD ,OE =AD∵A∵OD =1,AD =∵CE =1,OE =∵点C 在第二象限∵点C的坐标为(故答案为:(; (3)∵∵ACB =90゜∵∵BCE +∵ACD =90゜∵BE ∵CE ,AD ∵CE∵∵CEB =∵ADC =90゜∵∵BCE +∵CBE =90゜∵∵CBE =∵ACD在∵BCE 和∵CAD 中CBE ACD CEB ADC BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∵∵BCE ∵∵CAD (AAS )∵BE =CD ,CE =AD =6cm∵BE =CD =CE -DE =6-4=2(cm)【点拨】本题是三角形全等的综合,考查了全等三角形的判定与性质,掌握全等三角形的判定方法是关键.。
【公开课教案】相似三角形专题复习—“一线三等角”型

相似三角形专题复习————“一线三等角”型【教学目标】1、会用“一线三等角”的基本图形解决相似中的相关问题2、通过抽象模型,图形变换,变式类比等方法提高综合解题能力【重点】运用“一线三等角”相似型的基本图形解题。
【难点】“一线三等角”的基本图形的提炼、变式和运用【教学方法】合作探究、分析讲授【教具准备】三角尺,多媒体.【教学过程】一.基本图形回顾:设计意图一、复习回顾,揭示目标情景,引入课题:三个基本图形呈现提供不同类型的相似三角形,让学生说出每一个图形中相似形的对应关系,使学生的“直观经验”由“量”变产生“质“变。
从模型引入本专题,使学生对产生模型有个感性的认识,为下一环节抽象模型打好铺垫引入课题:二、抽象模型,揭示实质:二、抽象模型,揭示实质抽象模型的目的是让学生的认识从“特殊“上升到“一般”,这是核心结论的生成阶段,时间上用多一点,要求学生写出证明过程,为后续的学习提供帮助,同时让学生对“一线三等角”基本图形的本质理解,在整节课的设计中起承上启下的作用,为下面的运用规律和知识有枢纽的效果。
三.运用新知,看图作三.运用新知,看图作答:四:从特殊到一般:答通过前面的学习,为了让学生学以致用,设置一个练习及变式训练注意:这里要求学生提炼“一线三等角的基本图形,说出两个相似三角形,要求对应的顶点写在对应的位置,并利用相似的性质求解四、从特殊到一般:从特殊的直角改变成一般的角,并让学生证明,明白从特殊到一般的原理,同时展示三种常见形态五、典例解析,综合运用:五、典例解析,综合运用六、深入探究:七、小结收获交流归纳(1)由“一线三等角”基本图形搭建桥梁可以得到识开始在具体题目中的实际运用,设计上承接了前面的图形,能结合动点问题,勾股定理等知识并运用“一线三等角”相似型解决问题。
学生重点分析解题方法和数学思想的渗透,提高学生综合应用能力。
六、深入探究:相似三角形,熟悉这类题经常是以等边三角形、等腰梯形、正方形、矩形为图形背景出现。
第七讲一线三等角型相似三角形

第七讲一线三等角型相似三角形在前几讲我们已经学习了相似三角形的概念和判定方法,本讲我们将继续学习一线三等角型相似三角形。
一线三等角型相似三角形是指两个三角形的对应角均相等,并且有一对对应边成比例。
下面我们将详细讨论这一概念。
一线三等角型相似三角形可以分为三种情况:一线三等角型全等三角形、一线三等角型相似背边相等三角形和一线三等角型相似底角相等三角形。
下面我们分别介绍这三种情况。
一、一线三等角型全等三角形当两个三角形的对应角全部相等,并且对应边成比例时,这两个三角形就是一线三等角型全等三角形。
例如,已知三角形ABC和三角形DEF,已知∠A=∠D,∠B=∠E,∠C=∠F,且AB/DE=BC/EF=AC/DF=k(k为常数),则可以判定三角形ABC全等于三角形DEF。
这是由于全等三角形的定义所决定的。
全等三角形的定义是:对于两个三角形ABC和DEF,如果它们的三个对应角全部相等,且对应边成比例,则可以判定三角形ABC全等于三角形DEF。
因此,根据已知条件,我们可以判定三角形ABC和三角形DEF是一线三等角型全等三角形。
二、一线三等角型相似背边相等三角形当两个三角形的对应角全部相等,并且其中一对对应边成比例时,这两个三角形就是一线三等角型相似背边相等三角形。
例如,已知三角形ABC和三角形DEF,已知∠A=∠D,∠B=∠E,∠C=∠F,且AB/DE=k(k为常数),则可以判定三角形ABC相似于三角形DEF,并且AB/DE=k。
这是由于相似三角形的定义所决定的。
相似三角形的定义是:对于两个三角形ABC和DEF,如果它们的三个对应角全部相等,并且其中一对对应边成比例,则可以判定三角形ABC相似于三角形DEF,并且对应边成比例。
因此,根据已知条件,我们可以判定三角形ABC和三角形DEF是一线三等角型相似背边相等三角形。
三、一线三等角型相似底角相等三角形当两个三角形的对应角全部相等,并且底边成比例时,这两个三角形就是一线三等角型相似底角相等三角形。
中考数学专题---相似三角形中的常考模型 课件

C
D
8字型
3.如图,已知抛物线 与 轴交于 , 两点,与 轴交于点 , 是线段 上一动点, 的延长线交抛物线于点 .(1)求这个函数关系解析式:(2)求 的最大值.
8字型
将 , , 代入 ,得 ,解得 ,∴抛物线的解析式为 .设直线 的解析式为 ,将 , 代入,得
A字型
1.如图, , 分别为 的边 , 上的点,若 , , 的面积等于2,则 的面积为( )
A. B. C. D.
2.如图,在 <m></m> 中, <m></m> ,点 <m></m> , <m></m> 分别在 <m></m> , <m></m> 边上, <m></m> ,且 <m></m> ,若 <m></m> ,则 <m></m> 的长为 _____.
C
一线三垂直型
13.如图,在四边形 中, , ,以 为直径的半圆 与边 相切于点 , ,求 的长.
解:如右图,连接 , ,
是 的切线, 是切点, .又 , , , . , .
一线三垂直型
设 ,则 . 为 的直径, , . , , , ,
一线三等角型
1.如图,已知 , , 分别为 的边 , , 上的点, , , , , , ,则 的长为( )
A. B. C. D.
2.如图,在四边形 中, , , ,若点 是 边上一点 ,且 ,则 ( )
,解得 ,∴直线 的解析式为 . 轴, ,∴易得 , .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似三角形(3)“一线三等角型”
教学目标:
1、掌握相似三角形的判定和性质,并能熟练运用其解决重要类型“一线三等角”的类型题.
2、经历运用相似三角形的基础知识解决问题的过程,再次体验图形运动、分类讨论、方程
与函数等数学思想.
3、通过问题的解决,体验探究问题成功的乐趣,积极探索,提高学习几何的兴趣.
重点:
相似三角形的判定性质及其应用.
难点:
与相似、函数有关的综合性问题的解决技巧和方法.
教学方法:
启发式教学方法,尝试指导教学法.
一、知识梳理:
(图1) (图2)
(1)如图1:已知三角形ABC 中,AB=AC,∠ADE=∠B,那么一定存在的相似三角形有___
(2)如图2:已知三角形ABC 中,AB=AC,∠DEF=∠B,那么一定存在的相似三角形有___
二、【例题解析】
【例1】如图,在边长为2的等边三角形ABC 中,D 是BC 边上任意一点,AB 边上有一点E ,
AC 边上有一点F ,使∠EDF=∠ABC. 已知BD=1,BE=3
1,求CF 的长
【练】1、已知△ABC 中AB=AC=6、BC=8,∠BAC=120度,D 是BC 边上任意一点,AB 边上有
一点E ,AC 边上有一点F ,使∠EDF=∠C. 已知BD=6、BE=4,求:CF 的长
2、如图,等边△ABC 中,边长为6,D 是BC 上动点,∠EDF =60°
(1)求证:△BDE ∽△CFD
(2)当BD =23,FC =1时,求BE
【例2】在ABC ∆中,O BC AC C ,3,4,90===∠o 是AB 上的一点,且5
2=AB AO ,点P 是AC 上的一个动点,OP PQ ⊥交线段BC 于点Q ,(不与点B,C 重合),已知AP=2,求CQ
【练】在直角三角形ABC 中,D BC AB C ,,90==∠o 是AB 边上的一点,E 是在AC 边
上的一个动点,(与A,C 不重合),DF DE DF ,⊥与射线BC 相交于点F.
(1)、当点D 是边AB 的中点时,求证:DF DE =
(2)、当m DB
AD =,求DF DE 的值
【例3】已知在等腰三角形ABC 中,AB=AC,D 是BC 的中点,∠EDF=∠B,
求证:△BDE ∽△DFE.
【练】在边长为4的等边ABC ∆中,D 是BC 的中点,点E 、F 分别在AB 、AC 上(点D 不与点C 、点B 重合),且保持ABC EDF ∠=∠,连接EF .
(1)已知BE=1,DF=2.求DE 的值
(2)求∠BED=∠DEF
【例4】 如图,已知边长为3的等边ABC ∆,点F 在边BC 上,1CF =,点E 是射线BA 上一动点,以线段EF 为边向右侧作等边EFG ∆,直线,EG FG 交直线AC 于点,M N ,
(1)写出图中与BEF ∆相似的三角形;
(2)证明其中一对三角形相似;
(3)设,BE x MN y ==,求y 与x 之间的函数关系式,并写出自变量x 的取值范围;
【练】 如图,在△ABC 中,8==AC AB ,10=BC ,D 是BC 边上的一个动点,点E 在
AC 边上,且C ADE ∠=∠.
(1) 求证:△ABD ∽△DCE ;
(2) 如果x BD =,y AE =,求y 与x 的函数解析式,并写出自变量x 的定义域;
(3) 当点D 是BC 的中点时,试说明△ADE 是什么三角形,并说明理由.
【例5】已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且AD =5,AB =DC =2.
(1)如图8,P 为AD 上的一点,满足过点D 作DG ⊥EF 于点G ,∠BPC =∠A . ①求证;△ABP ∽△DPC
②求AP 的长.
【练】如图,在梯形ABCD 中,AD ∥BC ,6AB CD BC ===,3AD =.点M 为边BC 的中点,以M 为顶点作EMF B ∠=∠,射线ME 交腰AB 于点E ,射线MF 交腰CD 于点F ,联结EF .
(1)求证:△MEF ∽△BEM ;
(2)若△BEM 是以BM 为腰的等腰三角形,求EF 的长;
(3)若EF CD ⊥,求BE 的长.
【家庭作业】 1、如图,在ABC ∆中,90C ∠=︒,6AC =,4
3=BC AC ,D 是BC 边的中点,E 为AB 边
上的一个动点,作90DEF ∠=︒,EF 交射线BC 于点F .设BE x =,BED ∆的面积为y .
(1)求y 关于x 的函数关系式,并写出自变量x 的取值范围;
(2)如果以B 、E 、F 为顶点的三角形与BED ∆相似,求BED ∆的面积.
2、如图,已知在△ABC 中, AB =AC =6,BC =5,D 是AB 上一点,BD =2,E 是BC 上一动
点,联结DE ,并作DEF B ∠=∠,射线EF 交线段AC 于F .
(1)求证:△DBE ∽△ECF ;
(2)当F 是线段AC 中点时,求线段BE 的长;
(3)联结DF ,如果△DEF 与△DBE 相似,求FC 的长.
3、已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且BC =6,AB =DC =4,点E 是AB 的中点.
(1)如图,P 为BC 上的一点,且BP =2.求证:△BEP ∽△CPD ;
(2)如果点P 在BC 边上移动(点P 与点B 、C 不重合),且满足∠EPF =∠C ,PF 交直
线CD 于点F ,同时交直线AD 于点M ,那么
①当点F 在线段CD 的延长线上时,设BP =x ,DF =y ,求y 关于x 的函数解析式,
并写出函数的定义域;
②当BEP DMF S S ∆∆=4
9时,求BP 的长。
