第五章时间序列.pptx
合集下载
时间序列简介讲解课件

MA(q)模型可以表示为 y(t) = ε(t) - θ1ε(t-1) - θ2ε(t-2) - ... θqε(t-q)
θ1, - θ2, ..., - θq 是移动平均 系数,ε(t) 是白噪声误差项。
ARMA模型
总结词
自回归移动平均模型
详细描述
公式
参数
ARMA模型是自回归模型( AR)和移动平均模型(MA )的组合,它基于时间序列 的过去值和过去误差来预测 未来值。通过同时建立自回 归和移动平均过程,ARMA 模型能够捕捉时间序列中的 长期依赖关系和短期波动。
时间序列简介讲解课件
contents
目录
• 时间序列基本概念 • 时间序列分析方法 • 时间序列预测模型 • 时间序列在金融中的应用 • 时间序列在气候中的应用 • 时间序列在市场调研中的应用
01
时间序列基本概念
时间序列定义
时间序列定义
时间序列是指按照时间的顺序排 列的一组数据,通常用于描述某 个变量在不同时间点的取值。
06
时间序列在市场调研中的 应用
销售预测
01
02
03
预测未来销售趋势
通过分析时间序列数据, 可以了解销售量的历史变 化趋势,从而对未来销售 趋势进行预测。
制定销售策略
基于销售预测结果,可以 制定相应的销售策略,如 库存管理、价格调整、促 销活动等。
优化销售计划
通过对销售预测结果的分 析,可以优化销售计划, 提高销售效率和利润。
感谢您的观看
THANKS
利用时间序列分析预测货币供应量
通过分析货币供应量的时间序列数据,利用统计方法和模型来预测未来的货币供应量走势 ,为货币政策制定提供参考。
考虑因素
时间序列分析课件.pptx
第5章 时间序列分析
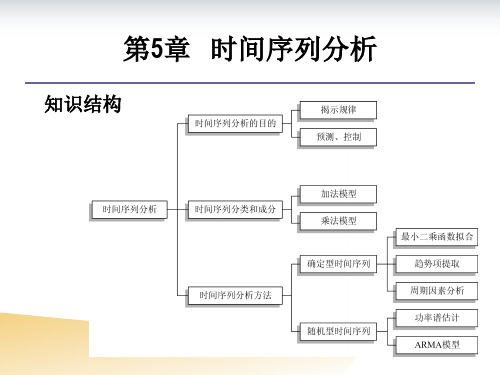
知识结构
第5章 时间序列分析
What is time series analysis?
Why to do ?
How to do?
日行迹
第5章 时间序列分析
时间序列
➢ 时间序列的概念 ➢ 时间序列的表示 ➢ 时间序列分析 ➢ 时间序列的分类 ➢ 时间序列的组合成分
时间序列分析方法
时间序列分析方法
时间序列分析的一般步骤: (1) 序列的预处理:如果原始序列为非等间隔序列,通常采用 曲线拟合及等距化重采样得到等距序列。 (2) 描述性时序分析:通过直观的数据比较或绘图观测,寻找 序列中蕴含的发展规律,往往可直观地判断序列是否具有趋势 项、周期变化等特性。 (3) 统计时序分析:计算时间序列的各种统计量,如均值,方 差,正态性检验等。利用统计特性剔除不符合统计规律的异常 样本。 (4) 判断时间序列的组合成分,对不同的成分采用不同的分析 方法。 (5) 利用不同成分的模型进行预测后叠加,得到最终的时间序 列预测值。
时间序列可能是应用最普遍的数据表现形式和数据存储格式。 在生物医学领域也存在着大量的时间序列,
人体从清晨到深夜的体温记录 人体餐后血糖浓度的变化 不同睡眠阶段的脑电波形等都是时间序列 。。。。。。
绝大多数情况下时间序列被看作为随机序列。
时间序列
时间序列的表示
X {x(T ), x(2T ),, x(kT )} {x[n]}
时间序列
时间序列分析
时间序列分析的实现是通过对观察值序列的性质进行推断,即 通过对历史观察值的分析预测而得出未来观察值的预测值。
cool! What will be next?
汽车发展的时间序列
时间序列
时间序列分析 时间序列分析的目的主要在于: (1) 描述事物在过去时间的状态。 (2) 分析事物发展变化的规律。 (3) 对事物的发展变化趋势进行预测或施加控制。
知识结构
第5章 时间序列分析
What is time series analysis?
Why to do ?
How to do?
日行迹
第5章 时间序列分析
时间序列
➢ 时间序列的概念 ➢ 时间序列的表示 ➢ 时间序列分析 ➢ 时间序列的分类 ➢ 时间序列的组合成分
时间序列分析方法
时间序列分析方法
时间序列分析的一般步骤: (1) 序列的预处理:如果原始序列为非等间隔序列,通常采用 曲线拟合及等距化重采样得到等距序列。 (2) 描述性时序分析:通过直观的数据比较或绘图观测,寻找 序列中蕴含的发展规律,往往可直观地判断序列是否具有趋势 项、周期变化等特性。 (3) 统计时序分析:计算时间序列的各种统计量,如均值,方 差,正态性检验等。利用统计特性剔除不符合统计规律的异常 样本。 (4) 判断时间序列的组合成分,对不同的成分采用不同的分析 方法。 (5) 利用不同成分的模型进行预测后叠加,得到最终的时间序 列预测值。
时间序列可能是应用最普遍的数据表现形式和数据存储格式。 在生物医学领域也存在着大量的时间序列,
人体从清晨到深夜的体温记录 人体餐后血糖浓度的变化 不同睡眠阶段的脑电波形等都是时间序列 。。。。。。
绝大多数情况下时间序列被看作为随机序列。
时间序列
时间序列的表示
X {x(T ), x(2T ),, x(kT )} {x[n]}
时间序列
时间序列分析
时间序列分析的实现是通过对观察值序列的性质进行推断,即 通过对历史观察值的分析预测而得出未来观察值的预测值。
cool! What will be next?
汽车发展的时间序列
时间序列
时间序列分析 时间序列分析的目的主要在于: (1) 描述事物在过去时间的状态。 (2) 分析事物发展变化的规律。 (3) 对事物的发展变化趋势进行预测或施加控制。
时间序列分析ppt课件

... 1k r0
k
rk r0
1k ,
1 1, 当 k增大时,即序列之间的 间隔增大时,
k 减小,且以指数速度减 小,这种现象称为拖尾 ,
越来越与 0接近,
按照 PACF 的递推公式有:
1 , 22
2 1 11 1 1 11
, 21
11 22 11
33
3 2 21 1 22 1 1 21 2 22
四、 随机序列的特征描述 (1)样本均值
1 n
z n t1 zt c
(2)样本自协方差函数
平稳时间序列自协方差仅与时间隔有关,当 间隔为 零时,自协方差应相等:
4、自协方差与自相关函数的性质 (1) rk=r-k ρk= ρ-k k、-k仅是时间先后 顺序上的差异,它们代表的间隔是相同的。
(2)
1,
rk r0
1rk
r0
三、偏自相关函数(PACF) 1、偏自相关函数用来考察扣除zt 和zt+k之间zt+1 ,
当t取遍所有可能整数时,就形成了离散时间的函数ut 称ut 为时间序列的均值函数。
3、自协方差函数和自相关函数
r ( t , s ) E [ z t ( u t ) z s ( u s ) ] ( z t u t ) z s ( u s ) d t , s ( z t F , z s )
例1、设动态数据16,12,15,10,9,17,11, 16,10,14,求样本均值、样本自相关函数 (SACF)和偏自相关函数(SPACF)(各 求前三项)
(1) z
1 10
时间序列分析课件

模型的诊断
残差诊断
检查模型是否符合残差的正态性和 平稳性,如是否存在自相关性等。
精度评估
使用MAPE、RMSE等指标对预测值 和实际值的误差进行评价。
过度拟合
注意模型过度拟合数据,需要在稳 定性和预测精度之间寻找平衡点。
时间序列模型的应用
股票价格的时间序列 分析
利用ARIMA模型对股票价格进行 预测和交易策略的优化。
真实案例:COVID-1 9疫情数据的时间序列分 析
数据收集
收集全球COVID-19疫情历史数据, 包括新增确诊、治愈、死亡等。
数据可视化
数据分析和预测
使用时间序列图表和热力图等方式, 使用ARIMA模型对未来疫情趋势进 展示疫情随时间和地域的变化趋势。 行预测和分析。
宏观经济指标的时间 序列分析
理解各项经济数据的趋势和关系, 对政策制定具有重要意义。
人口统计数据的时间 序列分析
预测社会变化,如人口流动、城 市化趋势等。
时间序列分析的未来展望
机器学习与数据挖掘
在更大的数据集上应用机器学习和 数据挖掘技术,进行复杂变量和非 线性关系的预测。
动态因果模型
建立具有时间约束和因果关系的复 杂模型,包括时间滞后、时间间隔 等。
差分技术
减少时间序列的非平稳性,包括一阶差分、季节性差分 等。
ARIMA模型
1
自回归模型
当前值受前阶数的过去值和噪声的影响。
2
差分
将非平稳时间序列转化为平稳时间序列。
3
移动平均模型
误差受前阶数的过去误差和噪声的影响。
Байду номын сангаас
ARMA模型
1 自回归模型
2 移动平均模型
《时间序列》PPT课件 (2)

根据微积分的极值原理,有
Q Q ba22([1al)gyi[l(gyliga(tligalgbt)i](lgbtbi))]00
精选ppt
36
一次指数曲线法
lg yi N•lg alg b• ti tilg yi lg a• ti lg b• ti2
解此联立方程,可以得到
精选ppt
37
▪ 时间序列预测法也叫历史延伸法或外推法。
▪ 时间序列预测法的基本特点是:
假定事物的过去趋势会延伸到未来;
预测所依据的数据具有不规则性;
撇开了市场发展之间的因果关系。
精选ppt
3
从回归分析法的角度看,时间序列分析法
实际上是一种特殊的回归分析法,因为此时
不再考虑事物之间的因果关系或其他相关关 系,而仅考虑研究对象与时间之间的相关关
ti=??,
ti=23, 可得预测值为
y073.5 7 509 .2 3 2 32101
精选ppt
23
一次曲线
为了衡量所得的回归方程与实际值的偏 离程度,引入不一致系数u。
u
ei2
Q
yi2
yi2
式Q 中
(yi yi)2
ei2剩余平方和
不一致系数u值越小,说明所得的拟合曲 线(回归方程)与实际值倾向线的偏差越
具有均匀时间间隔的各种社会、自然现象的 数量指标依时间次序排列起来的统计数据。
时间序列分析法是通过对历史数据变化的分
析,来评价事物的现状和估计事物的未来变 化。这种方法在科学决策、R&D和市场开拓 活动中的许多场合有广泛的应用,如市场行
情分析、产品销售预测等。
精选ppt
2
▪ 时间序列预测法是一种定量分析方法,它是在时 间序列变量分析的基础上,运用一定的数学方法 建立预测模型,使时间趋势向外延伸,从而预测 未来市场的发展变化趋势,确定变量预测值。
Q Q ba22([1al)gyi[l(gyliga(tligalgbt)i](lgbtbi))]00
精选ppt
36
一次指数曲线法
lg yi N•lg alg b• ti tilg yi lg a• ti lg b• ti2
解此联立方程,可以得到
精选ppt
37
▪ 时间序列预测法也叫历史延伸法或外推法。
▪ 时间序列预测法的基本特点是:
假定事物的过去趋势会延伸到未来;
预测所依据的数据具有不规则性;
撇开了市场发展之间的因果关系。
精选ppt
3
从回归分析法的角度看,时间序列分析法
实际上是一种特殊的回归分析法,因为此时
不再考虑事物之间的因果关系或其他相关关 系,而仅考虑研究对象与时间之间的相关关
ti=??,
ti=23, 可得预测值为
y073.5 7 509 .2 3 2 32101
精选ppt
23
一次曲线
为了衡量所得的回归方程与实际值的偏 离程度,引入不一致系数u。
u
ei2
Q
yi2
yi2
式Q 中
(yi yi)2
ei2剩余平方和
不一致系数u值越小,说明所得的拟合曲 线(回归方程)与实际值倾向线的偏差越
具有均匀时间间隔的各种社会、自然现象的 数量指标依时间次序排列起来的统计数据。
时间序列分析法是通过对历史数据变化的分
析,来评价事物的现状和估计事物的未来变 化。这种方法在科学决策、R&D和市场开拓 活动中的许多场合有广泛的应用,如市场行
情分析、产品销售预测等。
精选ppt
2
▪ 时间序列预测法是一种定量分析方法,它是在时 间序列变量分析的基础上,运用一定的数学方法 建立预测模型,使时间趋势向外延伸,从而预测 未来市场的发展变化趋势,确定变量预测值。
统计学原理时间序列分析PPT课件
(二)增减速度
❖ 1、定义:增长量与基期水平之比 ❖ 2、反映内容:现象的增长程度 ❖ 3、公式:增长速度
vi
增长量 基期 水平 1 0% 0
发展水平1
第26页/共77页
(三)平均发展速度
❖ 1、定义 ❖ 各个时间单位的环比发展速度的序时平均数 ❖ 2、反映内容: ❖ 较长时期内逐期平均发展变化的程度 ❖ 3、平均发展速度的计算
年 份 旅游人数
季平均旅游人数
1999
1614020来自0202512001
272
68
第40页/共77页
缺点 ❖ 扩大的时距大小要符合现象的自身特点。 ❖ 扩大的时距要一致。 ❖ 信息损失过多,无法预测。
第41页/共77页
移动平均法
❖(1)原理:是时距扩大法的改良,
按照事先规定的移动时间长度K,采取逐项 向后递移,计算出序时平均数序列,主要 修匀不规则变动和季节变动的影响,使序 列呈现出比较明显的趋势。
均增长速度。
第29页/共77页
例题
某企业第四季度总产值和劳动生产率资料如下:
要求:(1)计算该企业第四季度的月平均劳动生产率。 (2)计算该企业第四季度劳动生产率。
第30页/共77页
第三节 时间序列模型分析
一、时间序列的构成及模型 二、长期趋势的测定和分析 三、季节变动的分析原理与方法 四、循环变动分析 五、不规则变动分析
第42页/共77页
移动平均法
首先,确定移动平均数的移动周期长度。
①移动周期一般以季节周期、循环变动周期长度为准; ②如若不存在明显的季节周期和循环周期,一般而言,我们在确
i1
a a 累计增长量:
i
0
4、二者关系:各逐期增长量第之12页和/共等77于页 相应的累计增长量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(二)序时平均数与一般平均数的区别
1.计算依据不同:序时平均数依据动态数列,一般平均数 依据变量数列。 2.说明问题不同:序时平均数从动态上说明现象在不同 时间上某一数值的一般水平,一般平均数从静态上说明 总体某个数量标志的一般水平。
(三)平均发展水平的计算
1.绝对数时间序列的序时平均数
(1)时期数列的序时平均数(简单算术平均法)。
相关概念:
最初水平:动态数列中的第一项指标数值 最末水平:动态数列中最后一项指标数值 报告期水平:要研究的那一时期的指标值 基期水平:作为对比的基础时期的指标值
(二)意义:是计算其他水平指标和速度指标的基础。
二、平均发展水平
(一)概念
又称序时平均数或动态平均数,是将不同时期的发展 水平加以平均得到的平均值。
特点: (1)时点数列中各指标值不能相加。 (2)时点数列中各指标值大小与时间间隔无关。 (3)时点数列通过间断登记获取数据。
二、时间序列的种类
(二)相对数时间序列:由相对指标排列形成。
特点: 1.由两个绝对数数列相比形成。 2.不同时期的相对指标数值不可直接相加。
(三)平均数时间序列:由平均指标排列形成。
计算某企业第二季度月平均劳动生产率
月份 工业增加值/万元
职工月末人数
3 107 1340
4 106 1342
5 118 1344
6 109 1324
三、增长水平(增长量)
(一)概念:报告期水平与基期水平之差。 (二)分类
(1)逐期增长量=报告期水平-前一期水平
a1-a0 ,a2-a1 , … ,an-an-1
(2) 时点数列的序时平均数
①连续时点数列:逐日登记。
未分组资料:逐日登记,每日都有数据(简单算术平 均法)。
分组资料:逐日登记,非每日都有数据(加权算术平 均法)。
其中,权数 f 代表间隔日数。
(2) 时点数列的序时平均数
②间断时点数列:资料不是逐日记录逐日排列,而是有 一定间隔的期初或期末的资料。 时间间隔相等时:首末折半法。
原煤 产量
8.72 8.94 9.28 9.80 10.54 10.80 10.62
二、时间序列的种类
(一)绝对数时间序列:由绝对指标排列形成。
1.时期数列:由时期指标排列形成。 特点: (1)时期数列中各指标值可以相加。 (2)时期数列中各指标值大小与时间间隔正相关。 (3)时期数列通过连续登记获取数据。 2.时点数列:由时点指标排列形成。
第五章 时间序列分析
学习目的及重难点提示
本章学习目的
了解时间序列的概念、种类、因素构成和编制原则。 掌握水平指标和速度指标的计算方法、应用条件及指标 间的相互关系。 掌握长期趋势的分析测定方法。
本章重难点提示
重点:时间序列水平指标和速度指标的计算、最小二乘 法预测长期趋势。 难点:季节比率法分析季节变动、最二乘法预测长期趋 势。
月初工人数
124 126 124 122 126 128 124
(人)
月初固定资产 600 600 610 640 640 700 700
额(万元)
例5-3答案
[分析上半] 年属平于均时固间定间资隔产相额等为的:间断时点数列,采用首末折
半法计算。 上半年平均职工人数为:
序时平均数计算示例
[例5-4]根据表计5-5算2001年的平均职工人数。
表5-5 某企业2001年职工人数资料 单位:人
时间 职工人数
1月1日 500
4月1日 560
7 月 31 日 12 月 31 日
580
600
[分析] 属于时间间隔不b等的间断时点数列,采用加 权算术平均法计算。
作业: 1、根据下表资料计算某企业月平均职工人数。
时 间 1月1日 4月1日 5月1日 8月1日 12月1日 12月31日
职工人数 / 230
242 250
244
238
236
人
2、某管理局所属两个企业元月份产值及每日在册
工人数资料如下:
企业
总产值(万元)
每日在册工人数 1–15日 16–21日 22–31日
甲
31.5
230
212
245
乙
35.2
232
214
228
计算该管理局元月份的月平均劳动生产率。
2.相对数时间序列的序时平均数
相对数时间序列的序时平均数不能直接计算, 而应根据分子数列的序时平均数除以分母数列的 序时平均数计算,用公式表示为:
2.相对数时间序列的序时平均数
(1)时期数列/时期数列形成的相对数时间序列。 分子分母数列均简单平均:
2.相对数时间序列的序时平均数
(2)时点数列/时点数列形成的相对数时间序列。 在时间间隔相等时,分子分母均首末折半:
库存表量5-3 1某50企业4月1份30 钢材库存85 量 4单8 位:万吨24
[分析] 属于连续时点数列,但非每日都有数据,应采用加 权算术平均法计算。
序时平均数计算示例
[例5-3]根据表5-4资料计算企业上半年平均职工人数及
平均固定资产额。
月 份 表5-一4月 某二企月业2三0月05年四上月半年五统月 计资六月料 七月
第一节 时间序列概述
一、时间序列的概念及构成要素
(一)定义
现象在不同时间上的一系列指标值按时间先后排列形 成的数列,又称动态数列。
(二)构成要素
现象所属的时间 指标数值
(三)与分配数列的区别
时间序列示例
表5-1 1985~1991年我国原煤产量 单位:亿吨
年 份 1985 1986 1987 1988 1989 1990 1991
时间间隔不等时:加权平均法。
式中f1,f2,…,fn-1:相邻时点指标间隔的月(季)数。
序时平均数计算示例
[例5-1]根据表5-2计算4月下旬商店营业员平均人数
表5-2 某商店4月下旬营业员人数
单位:人
[分析] 属于连续时点数列且每日都有数据,采用简单算 术平均法计算。
序时平均数计算示例
[时例5-间2]根据1 日表5-3计3 日算4月份9 日钢材平1均7 日库存量27。日
特点:不同时期的平均指标数值不可直接相加。
三、时间序列的编制原则
基本原则——可比性原则 具体原则
1.时间长短应当一致。 2.总体范围保持一致。 3.指标的经济内容保持一致。 4.指标的计算方法和计量单位保持一致。源自第二节 时间序列的水平分析
一、发展水平
(一)概念:时间序列中各项具体的指标数值。
字母表示: a0,a1, a2 ,an-1, …,an
1.计算依据不同:序时平均数依据动态数列,一般平均数 依据变量数列。 2.说明问题不同:序时平均数从动态上说明现象在不同 时间上某一数值的一般水平,一般平均数从静态上说明 总体某个数量标志的一般水平。
(三)平均发展水平的计算
1.绝对数时间序列的序时平均数
(1)时期数列的序时平均数(简单算术平均法)。
相关概念:
最初水平:动态数列中的第一项指标数值 最末水平:动态数列中最后一项指标数值 报告期水平:要研究的那一时期的指标值 基期水平:作为对比的基础时期的指标值
(二)意义:是计算其他水平指标和速度指标的基础。
二、平均发展水平
(一)概念
又称序时平均数或动态平均数,是将不同时期的发展 水平加以平均得到的平均值。
特点: (1)时点数列中各指标值不能相加。 (2)时点数列中各指标值大小与时间间隔无关。 (3)时点数列通过间断登记获取数据。
二、时间序列的种类
(二)相对数时间序列:由相对指标排列形成。
特点: 1.由两个绝对数数列相比形成。 2.不同时期的相对指标数值不可直接相加。
(三)平均数时间序列:由平均指标排列形成。
计算某企业第二季度月平均劳动生产率
月份 工业增加值/万元
职工月末人数
3 107 1340
4 106 1342
5 118 1344
6 109 1324
三、增长水平(增长量)
(一)概念:报告期水平与基期水平之差。 (二)分类
(1)逐期增长量=报告期水平-前一期水平
a1-a0 ,a2-a1 , … ,an-an-1
(2) 时点数列的序时平均数
①连续时点数列:逐日登记。
未分组资料:逐日登记,每日都有数据(简单算术平 均法)。
分组资料:逐日登记,非每日都有数据(加权算术平 均法)。
其中,权数 f 代表间隔日数。
(2) 时点数列的序时平均数
②间断时点数列:资料不是逐日记录逐日排列,而是有 一定间隔的期初或期末的资料。 时间间隔相等时:首末折半法。
原煤 产量
8.72 8.94 9.28 9.80 10.54 10.80 10.62
二、时间序列的种类
(一)绝对数时间序列:由绝对指标排列形成。
1.时期数列:由时期指标排列形成。 特点: (1)时期数列中各指标值可以相加。 (2)时期数列中各指标值大小与时间间隔正相关。 (3)时期数列通过连续登记获取数据。 2.时点数列:由时点指标排列形成。
第五章 时间序列分析
学习目的及重难点提示
本章学习目的
了解时间序列的概念、种类、因素构成和编制原则。 掌握水平指标和速度指标的计算方法、应用条件及指标 间的相互关系。 掌握长期趋势的分析测定方法。
本章重难点提示
重点:时间序列水平指标和速度指标的计算、最小二乘 法预测长期趋势。 难点:季节比率法分析季节变动、最二乘法预测长期趋 势。
月初工人数
124 126 124 122 126 128 124
(人)
月初固定资产 600 600 610 640 640 700 700
额(万元)
例5-3答案
[分析上半] 年属平于均时固间定间资隔产相额等为的:间断时点数列,采用首末折
半法计算。 上半年平均职工人数为:
序时平均数计算示例
[例5-4]根据表计5-5算2001年的平均职工人数。
表5-5 某企业2001年职工人数资料 单位:人
时间 职工人数
1月1日 500
4月1日 560
7 月 31 日 12 月 31 日
580
600
[分析] 属于时间间隔不b等的间断时点数列,采用加 权算术平均法计算。
作业: 1、根据下表资料计算某企业月平均职工人数。
时 间 1月1日 4月1日 5月1日 8月1日 12月1日 12月31日
职工人数 / 230
242 250
244
238
236
人
2、某管理局所属两个企业元月份产值及每日在册
工人数资料如下:
企业
总产值(万元)
每日在册工人数 1–15日 16–21日 22–31日
甲
31.5
230
212
245
乙
35.2
232
214
228
计算该管理局元月份的月平均劳动生产率。
2.相对数时间序列的序时平均数
相对数时间序列的序时平均数不能直接计算, 而应根据分子数列的序时平均数除以分母数列的 序时平均数计算,用公式表示为:
2.相对数时间序列的序时平均数
(1)时期数列/时期数列形成的相对数时间序列。 分子分母数列均简单平均:
2.相对数时间序列的序时平均数
(2)时点数列/时点数列形成的相对数时间序列。 在时间间隔相等时,分子分母均首末折半:
库存表量5-3 1某50企业4月1份30 钢材库存85 量 4单8 位:万吨24
[分析] 属于连续时点数列,但非每日都有数据,应采用加 权算术平均法计算。
序时平均数计算示例
[例5-3]根据表5-4资料计算企业上半年平均职工人数及
平均固定资产额。
月 份 表5-一4月 某二企月业2三0月05年四上月半年五统月 计资六月料 七月
第一节 时间序列概述
一、时间序列的概念及构成要素
(一)定义
现象在不同时间上的一系列指标值按时间先后排列形 成的数列,又称动态数列。
(二)构成要素
现象所属的时间 指标数值
(三)与分配数列的区别
时间序列示例
表5-1 1985~1991年我国原煤产量 单位:亿吨
年 份 1985 1986 1987 1988 1989 1990 1991
时间间隔不等时:加权平均法。
式中f1,f2,…,fn-1:相邻时点指标间隔的月(季)数。
序时平均数计算示例
[例5-1]根据表5-2计算4月下旬商店营业员平均人数
表5-2 某商店4月下旬营业员人数
单位:人
[分析] 属于连续时点数列且每日都有数据,采用简单算 术平均法计算。
序时平均数计算示例
[时例5-间2]根据1 日表5-3计3 日算4月份9 日钢材平1均7 日库存量27。日
特点:不同时期的平均指标数值不可直接相加。
三、时间序列的编制原则
基本原则——可比性原则 具体原则
1.时间长短应当一致。 2.总体范围保持一致。 3.指标的经济内容保持一致。 4.指标的计算方法和计量单位保持一致。源自第二节 时间序列的水平分析
一、发展水平
(一)概念:时间序列中各项具体的指标数值。
字母表示: a0,a1, a2 ,an-1, …,an
