匈牙利算法matlab源程序及实例(适合各种矩阵)
匈牙利法的matlab实现

匈牙利法的Matlab实现引言匈牙利法(Hungarian algorithm)是一种经典的组合优化算法,用于解决二分图的最佳匹配问题。
该算法的基本思想是通过不断修改图中的顶标以及通过交换匹配边和非匹配边来寻找最佳匹配。
在本文中,我们将介绍匈牙利法的原理,并使用Matlab编写相应的实现代码。
通过具体的例子,我们将展示如何使用Matlab解决实际问题。
二级标题一:匈牙利法的原理匈牙利法是一种基于图论的算法,用于在二分图中找到最佳匹配。
二分图是一种图,其顶点可以划分为两个不相交的集合,并且所有边都连接两个不同集合中的顶点。
最佳匹配是指在图中找到一组边,使得每个顶点最多与一条边相连,并且使得匹配边的权重之和最小。
匈牙利法的基本思路如下: 1. 给定一个二分图和初始的匹配。
2. 对于每个未匹配的顶点,尝试通过增广路径来扩展当前匹配。
3. 如果找到增广路径,则修改当前匹配以增加一个匹配边。
4. 重复步骤2和3,直到无法找到增广路径。
匈牙利法的关键在于如何寻找增广路径。
其核心算法是通过深度优先搜索来查找增广路径,该算法使用了一种可行的贪心策略来优化搜索过程。
二级标题二:Matlab实现在Matlab中,我们可以使用图论工具包来实现匈牙利法。
首先,我们需要创建一个二分图并初始化初始匹配。
然后,我们使用深度优先搜索来寻找增广路径,并通过修改匹配来扩展当前匹配。
最后,我们重复这个过程,直到无法找到增广路径。
下面是匈牙利法在Matlab中的实现代码:function [matching, cost] = hungarian_algorithm(cost_matrix)n = size(cost_matrix, 1);m = size(cost_matrix, 2);% 初始化初始匹配为空matching = zeros(1, n);for u = 1:n% 初始化顶标slack = inf(1, m);% 初始化访问标记visited = false(1, m);% 尝试扩展当前匹配while true% 初始化增广路径为空predecessor = zeros(1, m);max_slack = inf;% 寻找增广路径for v = 1:mif ~visited(v)curr_slack = cost_matrix(u, v) - matching(u);if curr_slack < slack(v)slack(v) = curr_slack;predecessor(v) = u;endif slack(v) < max_slackmax_slack = slack(v);endendend% 更新顶标和访问标记for v = 1:mif visited(v)cost_matrix(u, v) = cost_matrix(u, v) - max_slack; matching(u) = matching(u) + max_slack;elseslack(v) = slack(v) - max_slack;endendfor v = 1:mif ~visited(v) && slack(v) == 0if matching(v) == 0% 找到增广路径while predecessor(v) ~= 0matching(v) = predecessor(v);u = predecessor(v);v = matching(u);endbreak;else% 继续寻找增广路径visited(v) = true;u = matching(v);endendendif v ~= mbreak;endendend% 计算匹配的总权重cost = sum(cost_matrix(sub2ind(size(cost_matrix), 1:n, matching)));end二级标题三:案例研究在这个案例研究中,我们将使用上述实现代码来解决一个具体的问题。
利用匈牙利算法求完美匹配例题

一、概述匈牙利算法是一种用于求解二分图最大匹配的经典算法,它的时间复杂度为O(n^3),在实际应用中具有广泛的用途。
本文将通过一个具体的例题,详细介绍利用匈牙利算法求解完美匹配的具体步骤和方法。
二、问题描述假设有一个二分图G=(V, E),其中V={U,V},U={u1,u2,u3},V={v1,v2,v3},E={(u1,v1),(u1,v2),(u2,v2),(u3,v3)},现在希望求解这个二分图的最大匹配。
三、匈牙利算法详解1. 初始化:需要初始化一个大小为|U|的数组match[],用来记录每一个U中的顶点匹配的V中的顶点,初始化为-1,表示初始时没有匹配的顶点。
2. 寻找增广路径:通过遍历U中的每一个顶点,逐个寻找增广路径。
对于每一个未匹配的顶点,都尝试进行增广路径的寻找。
3. 匹配顶点:如果找到了一条增广路径,将增广路径上的顶点逐个匹配,并更新match[]数组。
4. 寻找最大匹配:重复上述步骤,直至无法继续寻找增广路径为止,此时match[]数组中记录的就是二分图的最大匹配。
四、具体例题求解接下来通过一个具体的例题来详细介绍匈牙利算法的求解过程。
假设有一个二分图G=(V, E),其中V={U,V},U={u1,u2,u3},V={v1,v2,v3},E={(u1,v1),(u1,v2),(u2,v2),(u3,v3)}。
首先初始化match[]数组为{-1,-1,-1}。
(1)对u1进行增广路径的寻找由于u1未匹配,从u1开始寻找增广路径。
首先考虑与u1相连的v1和v2。
对v1进行匹配,得到match[0]为1。
对v2进行匹配,得到match[0]为1。
(2)对u2进行增广路径的寻找由于u2未匹配,从u2开始寻找增广路径。
考虑与u2相连的v2。
对v2进行匹配,得到match[1]为2。
(3)对u3进行增广路径的寻找由于u3未匹配,从u3开始寻找增广路径。
考虑与u3相连的v3。
对v3进行匹配,得到match[2]为3。
匈牙利法的matlab实现

[知乎文章标题:匈牙利法的MATLAB实现](摘要:匈牙利法是一个经典的图论算法,用于解决最大二分匹配问题。
本文将介绍匈牙利法的原理和基本步骤,并给出MATLAB实现代码,帮助读者更好地理解和应用该算法。
1. 引言匈牙利法(Hungarian algorithm)是由匈牙利数学家Kuhn和Harold W. Kuhn于二十世纪五十年代提出的,用于求解二分图的最大权匹配问题。
它是一种非常高效且广泛应用的算法,常用于任务分配、解决最大二分匹配问题等领域。
本文将详细介绍匈牙利法的原理,并给出MATLAB实现代码供读者参考。
2. 匈牙利法原理在介绍匈牙利法的实现之前,我们先来了解一下该算法的原理。
匈牙利法通过一系列的增广路径来不断改进当前的匹配结果,最终得到最大的二分匹配。
下面是匈牙利法的基本步骤:步骤一:初始化对于给定的二分图,我们先初始化一个空的匹配集合。
为每个顶点分配一个标记集合,初始值均为0。
步骤二:寻找增广路径从未匹配的左侧顶点开始,依次寻找每个顶点的增广路径。
具体操作如下: 1. 从一个未匹配的左侧顶点开始,将其标记为已访问。
2. 遍历与该顶点相连接的所有右侧顶点。
3. 如果当前右侧顶点未匹配,则说明找到了增广路径,更新匹配集合并结束。
4. 如果当前右侧顶点已匹配,且该顶点未被访问过,则将该顶点标记为已访问,并递归寻找与该顶点相连接的新的增广路径。
5. 如果当前右侧顶点已匹配,且该顶点已被访问过,则继续遍历下一个右侧顶点。
步骤三:改进匹配如果找到了增广路径,就将该路径上所有已匹配的边删除,并将路径上所有未匹配的边添加到匹配集合中。
返回步骤二,继续寻找新的增广路径。
步骤四:结束当无法找到新的增广路径时,匈牙利法结束,得到的匹配集合即为最大二分匹配。
3. MATLAB实现代码下面给出MATLAB实现的代码,用于解决最大二分匹配问题。
function [max_match, match] = hungarian_algorithm(adj_matrix)% 初始化n = size(adj_matrix, 1);match = zeros(n, 1);max_match = 0;for u = 1:n% 访问标记visited = false(n, 1);if find_path(u)max_match = max_match + 1;endend% 寻找增广路径function found = find_path(u)for v = 1:nif adj_matrix(u, v) && ~visited(v)visited(v) = true;if match(v) == 0 || find_path(match(v))match(v) = u;found = true;return;endendendfound = false;endend4. 总结本文介绍了匈牙利法的原理和基本步骤,并给出了MATLAB实现代码。
匈牙利算法示例

0 0 0 1 1 0 0 0
15
3 ◎ 2 2
3 ◎ Ø 5 1 ◎ 4 4 6 ◎ Ø 4
得到4个独 立零元素, 所以最优解 矩阵为:
练习:
费 工作 用 人员
A
7
B
5
C
9
D
8
E
11
甲
乙
丙 丁 戊
9
8 7 4
12
5 3 6
7
4 6 7
11
6 9 5
0 13 11 2 6 0 10 11 0 5 7 4 0 1 4 2
4 2
0 13 7 0 6 0 6 9 0 5 3 2 0 1 0 0
Ø 0 0 13 7 ◎ 6 0 6 9 ◎ ◎ 0 5 3 2 ◎ Ø 0 0 1 0 Ø
0 0 1 0
0 0 1 1 0 0 0 0 0 0 1 0
例二、 有一份中文说明书,需译成英、日、德、俄四种 文字,分别记作A、B、C、D。现有甲、乙、丙、丁四 人,他们将中文说明书译成不同语种的说明书所需时 间如下表所示,问如何分派任务,可使总时间最少?
任务
人员
例一:
任务
人员
A 2
10 9 7
B 15
4 14 8
C 13
14 16 11
D 4
15 13 9
甲
乙 丙 丁
2 10 9 7
15 13 4 4 14 15 14 16 13 8 11 9
2 4
9
7
0 13 11 2 6 0 10 11 0 5 7 4 0 1 4 2
2 2 4 4 ◎ 0
运筹学指派问题的匈牙利法

运筹学课程设计指派问题的匈牙利法专业:姓名:学号:1.算法思想:匈牙利算法的基本思想是修改效益矩阵的行或列,使得每一行或列中至少有一个为零的元素,经过修正后,直至在不同行、不同列中至少有一个零元素,从而得到与这些零元素相对应的一个完全分配方案。
当它用于效益矩阵时,这个完全分配方案就是一个最优分配,它使总的效益为最小。
这种方法总是在有限步內收敛于一个最优解。
该方法的理论基础是:在效益矩阵的任何行或列中,加上或减去一个常数后不会改变最优分配。
2.算法流程或步骤:1.将原始效益矩阵C的每行、每列各元素都依次减去该行、该列的最小元素,使每行、每列都至少出现一个0元素,以构成等价的效益矩阵C’。
2.圈0元素。
在C’中未被直线通过的含0元素最少的行(或列)中圈出一个0元素,通过这个0元素作一条竖(或横)线。
重复此步,若这样能圈出不同行不同列的n个0元素,转第四步,否则转第三步。
3.调整效益矩阵。
在C’中未被直线穿过的数集D中,找出最小的数d,D中所有数都减去d,C’中两条直线相交处的数都加的d。
去掉直线,组成新的等价效益矩阵仍叫C’,返回第二步。
X=0,这就是一种最优分配。
最低总4.令被圈0元素对应位置的X ij=1,其余ij耗费是C中使X=1的各位置上各元素的和。
ij算法流程图:3.算法源程序:#include<iostream.h>typedef struct matrix{float cost[101][101];int zeroelem[101][101];float costforout[101][101];int matrixsize;int personnumber;int jobnumber;}matrix;matrix sb;int result[501][2];void twozero(matrix &sb);void judge(matrix &sb,int result[501][2]);void refresh(matrix &sb);void circlezero(matrix &sb);matrix input();void output(int result[501][2],matrix sb);void zeroout(matrix &sb);matrix input(){matrix sb;int m;int pnumber,jnumber;int i,j;float k;char w;cout<<"指派问题的匈牙利解法:"<<endl;cout<<"求最大值,请输入1;求最小值,请输入0:"<<endl;cin>>m;while(m!=1&&m!=0){cout<<"请输入1或0:"<<endl;cin>>m;}cout<<"请输入人数(人数介于1和100之间):"<<endl;cin>>pnumber;while(pnumber<1||pnumber>100){cout<<"请输入合法数据:"<<endl;cin>>pnumber;}cout<<"请输入工作数(介于1和100之间):"<<endl;cin>>jnumber;while(jnumber<1||jnumber>100){cout<<"请输入合法数据:"<<endl;cin>>jnumber;}cout<<"请输入"<<pnumber<<"行"<<jnumber<<"列的矩阵,同一行内以空格间隔,不同行间以回车分隔,以$结束输入:\n";for(i=1;i<=pnumber;i++)for(j=1;j<=jnumber;j++){cin>>sb.cost[i][j];sb.costforout[i][j]=sb.cost[i][j];}cin>>w;if(jnumber>pnumber)for(i=pnumber+1;i<=jnumber;i++)for(j=1;j<=jnumber;j++){sb.cost[i][j]=0;sb.costforout[i][j]=0;}else{if(pnumber>jnumber)for(i=1;i<=pnumber;i++)for(j=jnumber+1;j<=pnumber;j++){sb.cost[i][j]=0;sb.costforout[i][j]=0;}}sb.matrixsize=pnumber;if(pnumber<jnumber)sb.matrixsize=jnumber;sb.personnumber=pnumber;sb.jobnumber=jnumber;if(m==1){k=0;for(i=1;i<=sb.matrixsize;i++)for(j=1;j<=sb.matrixsize;j++)if(sb.cost[i][j]>k)k=sb.cost[i][j];for(i=1;i<=sb.matrixsize;i++)for(j=1;j<=sb.matrixsize;j++)sb.cost[i][j]=k-sb.cost[i][j];}return sb;}void circlezero(matrix &sb){int i,j;float k;int p;for(i=0;i<=sb.matrixsize;i++)sb.cost[i][0]=0;for(j=1;j<=sb.matrixsize;j++)sb.cost[0][j]=0;for(i=1;i<=sb.matrixsize;i++)for(j=1;j<=sb.matrixsize;j++)if(sb.cost[i][j]==0){sb.cost[i][0]++;sb.cost[0][j]++;sb.cost[0][0]++;}for(i=0;i<=sb.matrixsize;i++)for(j=0;j<=sb.matrixsize;j++)sb.zeroelem[i][j]=0;k=sb.cost[0][0]+1;while(sb.cost[0][0]<k){k=sb.cost[0][0];for(i=1;i<=sb.matrixsize;i++){if(sb.cost[i][0]==1){for(j=1;j<=sb.matrixsize;j++)if(sb.cost[i][j]==0&&sb.zeroelem[i][j]==0)break;sb.zeroelem[i][j]=1;sb.cost[i][0]--;sb.cost[0][j]--;sb.cost[0][0]--;if(sb.cost[0][j]>0)for(p=1;p<=sb.matrixsize;p++)if(sb.cost[p][j]==0&&sb.zeroelem[p][j]==0){sb.zeroelem[p][j]=2;sb.cost[p][0]--;sb.cost[0][j]--;sb.cost[0][0]--;}}}for(j=1;j<=sb.matrixsize;j++){if(sb.cost[0][j]==1){for(i=1;i<=sb.matrixsize;i++)if(sb.cost[i][j]==0&&sb.zeroelem[i][j]==0)break;sb.zeroelem[i][j]=1;sb.cost[i][0]--;sb.cost[0][j]--;sb.cost[0][0]--;if(sb.cost[i][0]>0)for(p=1;p<=sb.matrixsize;p++)if(sb.cost[i][p]==0&&sb.zeroelem[i][p]==0){sb.zeroelem[i][p]=2;sb.cost[i][0]--;sb.cost[0][p]--;sb.cost[0][0]--;}}}}if(sb.cost[0][0]>0)twozero(sb);elsejudge(sb,result);}void twozero(matrix &sb){int i,j;int p,q;int m,n;float k;matrix st;for(i=1;i<=sb.matrixsize;i++)if(sb.cost[i][0]>0)break;if(i<=sb.matrixsize){for(j=1;j<=sb.matrixsize;j++){st=sb;if(sb.cost[i][j]==0&&sb.zeroelem[i][j]==0){sb.zeroelem[i][j]=1;sb.cost[i][0]--;sb.cost[0][j]--;sb.cost[0][0]--;for(q=1;q<=sb.matrixsize;q++)if(sb.cost[i][q]==0&&sb.zeroelem[i][q]==0){sb.zeroelem[i][q]=2;sb.cost[i][0]--;sb.cost[0][q]--;sb.cost[0][0]--;}for(p=1;p<=sb.matrixsize;p++)if(sb.cost[p][j]==0&&sb.zeroelem[p][j]==0){sb.zeroelem[p][j]=2;sb.cost[p][0]--;sb.cost[0][j]--;sb.cost[0][0]--;}k=sb.cost[0][0]+1;while(sb.cost[0][0]<k){k=sb.cost[0][0];for(p=i+1;p<=sb.matrixsize;p++){if(sb.cost[p][0]==1){for(q=1;q<=sb.matrixsize;q++)if(sb.cost[p][q]==0&&sb.zeroelem[p][q]==0)break;sb.zeroelem[p][q]=1;sb.cost[p][0]--;sb.cost[0][q]--;sb.cost[0][0]--;for(m=1;m<=sb.matrixsize;m++)if(sb.cost[m][q]=0&&sb.zeroelem[m][q]==0){sb.zeroelem[m][q]=2;sb.cost[m][0]--;sb.cost[0][q]--;sb.cost[0][0]--;}}}for(q=1;q<=sb.matrixsize;q++){if(sb.cost[0][q]==1){for(p=1;p<=sb.matrixsize;p++)if(sb.cost[p][q]==0&&sb.zeroelem[p][q]==0)break;sb.zeroelem[p][q]=1;sb.cost[p][q]--;sb.cost[0][q]--;sb.cost[0][0]--;for(n=1;n<=sb.matrixsize;n++)if(sb.cost[p][n]==0&&sb.zeroelem[p][n]==0){sb.zeroelem[p][n]=2;sb.cost[p][0]--;sb.cost[0][n]--;sb.cost[0][0]--;}}}}if(sb.cost[0][0]>0)twozero(sb);elsejudge(sb,result);}sb=st;}}}void judge(matrix &sb,int result[501][2]){int i,j;int m;int n;int k;m=0;for(i=1;i<=sb.matrixsize;i++)for(j=1;j<=sb.matrixsize;j++)if(sb.zeroelem[i][j]==1)m++;if(m==sb.matrixsize){k=1;for(n=1;n<=result[0][0];n++){for(i=1;i<=sb.matrixsize;i++){for(j=1;j<=sb.matrixsize;j++)if(sb.zeroelem[i][j]==1)break;if(i<=sb.personnumber&&j<=sb.jobnumber)if(j!=result[k][1])break;k++;}if(i==sb.matrixsize+1)break;elsek=n*sb.matrixsize+1;}if(n>result[0][0]){k=result[0][0]*sb.matrixsize+1;for(i=1;i<=sb.matrixsize;i++)for(j=1;j<=sb.matrixsize;j++)if(sb.zeroelem[i][j]==1){result[k][0]=i;result[k++][1]=j;}result[0][0]++;}}else{refresh(sb);}}void refresh(matrix &sb){int i,j;float k;int p;k=0;for(i=1;i<=sb.matrixsize;i++){for(j=1;j<=sb.matrixsize;j++)if(sb.zeroelem[i][j]==1){sb.zeroelem[i][0]=1;break;}}while(k==0){k=1;for(i=1;i<=sb.matrixsize;i++)if(sb.zeroelem[i][0]==0){sb.zeroelem[i][0]=2;for(j=1;j<=sb.matrixsize;j++)if(sb.zeroelem[i][j]==2){sb.zeroelem[0][j]=1;}}for(j=1;j<=sb.matrixsize;j++){if(sb.zeroelem[0][j]==1){sb.zeroelem[0][j]=2;for(i=1;i<=sb.matrixsize;i++)if(sb.zeroelem[i][j]==1){sb.zeroelem[i][0]=0;k=0;}}}}p=0;k=0;for(i=1;i<=sb.matrixsize;i++){if(sb.zeroelem[i][0]==2){for(j=1;j<=sb.matrixsize;j++){if(sb.zeroelem[0][j]!=2)if(p==0){k=sb.cost[i][j];p=1;}else{if(sb.cost[i][j]<k)k=sb.cost[i][j];}}}}for(i=1;i<=sb.matrixsize;i++){if(sb.zeroelem[i][0]==2)for(j=1;j<=sb.matrixsize;j++)sb.cost[i][j]=sb.cost[i][j]-k;}for(j=1;j<=sb.matrixsize;j++){if(sb.zeroelem[0][j]==2)for(i=1;i<=sb.matrixsize;i++)sb.cost[i][j]=sb.cost[i][j]+k;}for(i=0;i<=sb.matrixsize;i++)for(j=0;j<=sb.matrixsize;j++)sb.zeroelem[i][j]=0;circlezero(sb);}void zeroout(matrix &sb){int i,j;float k;for(i=1;i<=sb.matrixsize;i++){k=sb.cost[i][1];for(j=2;j<=sb.matrixsize;j++)if(sb.cost[i][j]<k)k=sb.cost[i][j];for(j=1;j<=sb.matrixsize;j++)sb.cost[i][j]=sb.cost[i][j]-k;}for(j=1;j<=sb.matrixsize;j++){k=sb.cost[1][j];for(i=2;i<=sb.matrixsize;i++)if(sb.cost[i][j]<k)k=sb.cost[i][j];for(i=1;i<=sb.matrixsize;i++)sb.cost[i][j]=sb.cost[i][j]-k;}}void output(int result[501][2],matrix sb) {int k;int i;int j;int p;char w;float v;v=0;for(i=1;i<=sb.matrixsize;i++){v=v+sb.costforout[i][result[i][1]];}cout<<"最优解的目标函数值为"<<v;k=result[0][0];if(k>5){cout<<"解的个数超过了限制."<<endl;k=5;}for(i=1;i<=k;i++){cout<<"输入任意字符后输出第"<<i<<"种解."<<endl;cin>>w;p=(i-1)*sb.matrixsize+1;for(j=p;j<p+sb.matrixsize;j++)if(result[j][0]<=sb.personnumber&&result[j][1]<=sb.jobnumber)cout<<"第"<<result[j][0]<<"个人做第"<<result[j][1]<<"件工作."<<endl;}}void main(){result[0][0]=0;sb=input();zeroout(sb);circlezero(sb);output(result,sb);}4. 算例和结果:自己运算结果为:->⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡3302102512010321->⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡330110241200032034526635546967562543----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡可以看出:第1人做第4件工作;第2人做第1件工作;第3人做第3件工作;第4人做第2件工作。
匈牙利算法示例范文

匈牙利算法示例范文匈牙利算法是一种解决二分图最大匹配问题的经典算法,也称为增广路径算法。
它的核心思想是通过不断寻找增广路径来不断增加匹配数,直到无法找到新的增广路径为止。
下面我将通过一个示例来详细介绍匈牙利算法的流程和原理。
假设有一个二分图G=(V,E),其中V={U,V}是图的两个顶点集合,E 是边集合。
我们的目标是找到一个最大的匹配M,即图中不存在更多的边可以加入到匹配中。
首先,我们需要为每个顶点u∈U找到一个能和它相连的顶点v∈V,这个过程称为初始化匹配。
我们可以将所有的顶点u初始化为null,表示还没有和它相连的顶点v。
然后,我们选择一个u∈U的顶点作为起始点,尝试寻找一条增广路径。
增广路径是指一条交替经过未匹配边和已匹配边的路径。
我们从起始点u开始,按照深度优先的方式扩展路径,不断寻找下一个可以加入路径的顶点v。
1. 如果u没有和任何顶点相连,那么说明找到了一条增广路径。
我们将路径上的未匹配边变为已匹配边,已匹配边变为未匹配边,然后返回true,表示找到了一条增广路径。
2. 如果u有和一些顶点v相连,但是v还没有和其他顶点相连,即v的匹配点为null,那么说明找到了一条增广路径。
我们将路径上的未匹配边变为已匹配边,已匹配边变为未匹配边,并将v设置为u的匹配点。
然后返回true,表示找到了一条增广路径。
3. 如果v已经和其他顶点相连,那么我们尝试寻找一条从v的匹配点u'出发的增广路径。
如果找到了一条增广路径,我们将路径上的未匹配边变为已匹配边,已匹配边变为未匹配边,并将v设置为u'的匹配点。
然后返回true,表示找到了一条增广路径。
4. 如果无法找到可行的增广路径,返回false。
通过不断重复上述过程,直到无法找到新的增广路径为止。
此时,我们得到的匹配M就是最大匹配。
下面我们通过一个具体的例子来演示匈牙利算法的运行过程。
假设我们有一个二分图,U={1,2,3},V={4,5,6},边集E={(1,4),(1,5),(2,4),(3,5),(3,6)}。
超详细!!!匈牙利算法流程以及Python程序实现!!!通俗易懂
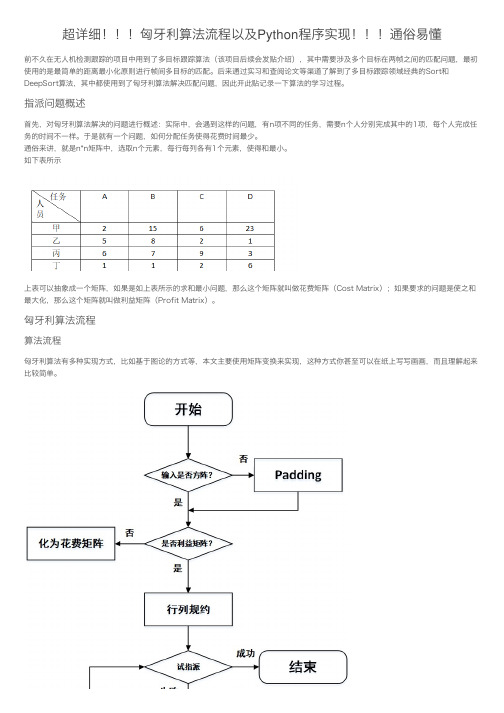
超详细匈⽛利算法流程以及Python程序实现通俗易懂前不久在⽆⼈机检测跟踪的项⽬中⽤到了多⽬标跟踪算法(该项⽬后续会发贴介绍),其中需要涉及多个⽬标在两帧之间的匹配问题,最初使⽤的是最简单的距离最⼩化原则进⾏帧间多⽬标的匹配。
后来通过实习和查阅论⽂等渠道了解到了多⽬标跟踪领域经典的Sort和DeepSort算法,其中都使⽤到了匈⽛利算法解决匹配问题,因此开此贴记录⼀下算法的学习过程。
指派问题概述⾸先,对匈⽛利算法解决的问题进⾏概述:实际中,会遇到这样的问题,有n项不同的任务,需要n个⼈分别完成其中的1项,每个⼈完成任务的时间不⼀样。
于是就有⼀个问题,如何分配任务使得花费时间最少。
通俗来讲,就是n*n矩阵中,选取n个元素,每⾏每列各有1个元素,使得和最⼩。
如下表所⽰上表可以抽象成⼀个矩阵,如果是如上表所⽰的求和最⼩问题,那么这个矩阵就叫做花费矩阵(Cost Matrix);如果要求的问题是使之和最⼤化,那么这个矩阵就叫做利益矩阵(Profit Matrix)。
匈⽛利算法流程算法流程匈⽛利算法有多种实现⽅式,⽐如基于图论的⽅式等,本⽂主要使⽤矩阵变换来实现,这种⽅式你甚⾄可以在纸上写写画画,⽽且理解起来⽐较简单。
本⽂算法流程如上图所⽰,⾸先进⾏列规约,即每⾏减去此⾏最⼩元素,每⼀列减去该列最⼩元素,规约后每⾏每列中必有0元素出现。
接下来进⾏试指派,也就是划最少的线覆盖矩阵中全部的0元素,如果试指派的独⽴0元素数等于⽅阵维度则算法结束,如果不等于则需要对矩阵进⾏调整,重复试指派和调整步骤直到满⾜算法结束条件。
以上是我简要描述的算法流程,值得⼀提的是,⽤矩阵变换求解的匈⽛利算法也有多种实现,主要不同就在于试指派和调整矩阵这块,但万变不离其宗都是为了⽤最少的线覆盖矩阵中全部的零元素。
咱们废话少说,来看⼀个例⼦。
程序实现完整代码(带测试⽤例)'''@Date: 2020/2/23@Author:ZhuJunHui@Brief: Hungarian Algorithm using Python and NumPy'''import numpy as npimport collectionsimport timeclass Hungarian():""""""def__init__(self, input_matrix=None, is_profit_matrix=False):"""输⼊为⼀个⼆维嵌套列表is_profit_matrix=False代表输⼊是消费矩阵(需要使消费最⼩化),反之则为利益矩阵(需要使利益最⼤化) """if input_matrix is not None:# 保存输⼊my_matrix = np.array(input_matrix)self._input_matrix = np.array(input_matrix)self._maxColumn = my_matrix.shape[1]self._maxRow = my_matrix.shape[0]# 本算法必须作⽤于⽅阵,如果不为⽅阵则填充0变为⽅阵matrix_size =max(self._maxColumn, self._maxRow)pad_columns = matrix_size - self._maxRowpad_rows = matrix_size - self._maxColumnmy_matrix = np.pad(my_matrix,((0,pad_columns),(0,pad_rows)),'constant', constant_values=(0)) # 如果需要,则转化为消费矩阵if is_profit_matrix:my_matrix = self.make_cost_matrix(my_matrix)self._cost_matrix = my_matrixself._size =len(my_matrix)self._shape = my_matrix.shape# 存放算法结果self._results =[]self._totalPotential =0else:self._cost_matrix =Nonedef make_cost_matrix(self,profit_matrix):'''利益矩阵转化为消费矩阵,输出为numpy矩阵'''# 消费矩阵 = 利益矩阵最⼤值组成的矩阵 - 利益矩阵matrix_shape = profit_matrix.shapeoffset_matrix = np.ones(matrix_shape, dtype=int)* profit_matrix.max()cost_matrix = offset_matrix - profit_matrixreturn cost_matrixdef get_results(self):"""获取算法结果"""return self._resultsdef calculate(self):"""实施匈⽛利算法的函数"""result_matrix = self._cost_matrix.copy()# 步骤 1: 矩阵每⼀⾏减去本⾏的最⼩值for index, row in enumerate(result_matrix):result_matrix[index]-= row.min()# 步骤 2: 矩阵每⼀列减去本⾏的最⼩值for index, column in enumerate(result_matrix.T):result_matrix[:, index]-= column.min()#print('步骤2结果 ',result_matrix)#print('步骤2结果 ',result_matrix)# 步骤 3:使⽤最少数量的划线覆盖矩阵中所有的0元素# 如果划线总数不等于矩阵的维度需要进⾏矩阵调整并重复循环此步骤total_covered =0while total_covered < self._size:time.sleep(1)#print("---------------------------------------")#print('total_covered: ',total_covered)#print('result_matrix:',result_matrix)# 使⽤最少数量的划线覆盖矩阵中所有的0元素同时记录划线数量cover_zeros = CoverZeros(result_matrix)single_zero_pos_list = cover_zeros.calculate()covered_rows = cover_zeros.get_covered_rows()covered_columns = cover_zeros.get_covered_columns()total_covered =len(covered_rows)+len(covered_columns)# 如果划线总数不等于矩阵的维度需要进⾏矩阵调整(需要使⽤未覆盖处的最⼩元素)if total_covered < self._size:result_matrix = self._adjust_matrix_by_min_uncovered_num(result_matrix, covered_rows, covered_columns) #元组形式结果对存放到列表self._results = single_zero_pos_list# 计算总期望结果value =0for row, column in single_zero_pos_list:value += self._input_matrix[row, column]self._totalPotential = valuedef get_total_potential(self):return self._totalPotentialdef_adjust_matrix_by_min_uncovered_num(self, result_matrix, covered_rows, covered_columns):"""计算未被覆盖元素中的最⼩值(m),未被覆盖元素减去最⼩值m,⾏列划线交叉处加上最⼩值m"""adjusted_matrix = result_matrix# 计算未被覆盖元素中的最⼩值(m)elements =[]for row_index, row in enumerate(result_matrix):if row_index not in covered_rows:for index, element in enumerate(row):if index not in covered_columns:elements.append(element)min_uncovered_num =min(elements)#print('min_uncovered_num:',min_uncovered_num)#未被覆盖元素减去最⼩值mfor row_index, row in enumerate(result_matrix):if row_index not in covered_rows:for index, element in enumerate(row):if index not in covered_columns:adjusted_matrix[row_index,index]-= min_uncovered_num#print('未被覆盖元素减去最⼩值m',adjusted_matrix)#⾏列划线交叉处加上最⼩值mfor row_ in covered_rows:for col_ in covered_columns:#print((row_,col_))adjusted_matrix[row_,col_]+= min_uncovered_num#print('⾏列划线交叉处加上最⼩值m',adjusted_matrix)return adjusted_matrixclass CoverZeros():"""使⽤最少数量的划线覆盖矩阵中的所有零输⼊为numpy⽅阵""""""def__init__(self, matrix):# 找到矩阵中零的位置(输出为同维度⼆值矩阵,0位置为true,⾮0位置为false)self._zero_locations =(matrix ==0)self._zero_locations_copy = self._zero_locations.copy()self._shape = matrix.shape# 存储划线盖住的⾏和列self._covered_rows =[]self._covered_columns =[]def get_covered_rows(self):"""返回覆盖⾏索引列表"""return self._covered_rowsdef get_covered_columns(self):"""返回覆盖列索引列表"""return self._covered_columnsdef row_scan(self,marked_zeros):'''扫描矩阵每⼀⾏,找到含0元素最少的⾏,对任意0元素标记(独⽴零元素),划去标记0元素(独⽴零元素)所在⾏和列存在的0元素''' min_row_zero_nums =[9999999,-1]for index, row in enumerate(self._zero_locations_copy):#index为⾏号row_zero_nums = collections.Counter(row)[True]if row_zero_nums < min_row_zero_nums[0]and row_zero_nums!=0:#找最少0元素的⾏min_row_zero_nums =[row_zero_nums,index]#最少0元素的⾏row_min = self._zero_locations_copy[min_row_zero_nums[1],:]#找到此⾏中任意⼀个0元素的索引位置即可row_indices,= np.where(row_min)#标记该0元素#print('row_min',row_min)marked_zeros.append((min_row_zero_nums[1],row_indices[0]))#划去该0元素所在⾏和列存在的0元素#因为被覆盖,所以把⼆值矩阵_zero_locations中相应的⾏列全部置为falseself._zero_locations_copy[:,row_indices[0]]= np.array([False for _ in range(self._shape[0])])self._zero_locations_copy[min_row_zero_nums[1],:]= np.array([False for _ in range(self._shape[0])])def calculate(self):'''进⾏计算'''#储存勾选的⾏和列ticked_row =[]ticked_col =[]marked_zeros =[]#1、试指派并标记独⽴零元素while True:#print('_zero_locations_copy',self._zero_locations_copy)#循环直到所有零元素被处理(_zero_locations中没有true)if True not in self._zero_locations_copy:breakself.row_scan(marked_zeros)#2、⽆被标记0(独⽴零元素)的⾏打勾independent_zero_row_list =[pos[0]for pos in marked_zeros]ticked_row =list(set(range(self._shape[0]))-set(independent_zero_row_list))#重复3,4直到不能再打勾TICK_FLAG =Truewhile TICK_FLAG:#print('ticked_row:',ticked_row,' ticked_col:',ticked_col)TICK_FLAG =False#3、对打勾的⾏中所含0元素的列打勾for row in ticked_row:#找到此⾏row_array = self._zero_locations[row,:]#找到此⾏中0元素的索引位置#找到此⾏中0元素的索引位置for i in range(len(row_array)):if row_array[i]==True and i not in ticked_col:ticked_col.append(i)TICK_FLAG =True#4、对打勾的列中所含独⽴0元素的⾏打勾for row,col in marked_zeros:if col in ticked_col and row not in ticked_row:ticked_row.append(row)FLAG =True#对打勾的列和没有打勾的⾏画画线self._covered_rows =list(set(range(self._shape[0]))-set(ticked_row)) self._covered_columns = ticked_colreturn marked_zerosif __name__ =='__main__':#以下为3个测试⽤例cost_matrix =[[4,2,8],[4,3,7],[3,1,6]]hungarian = Hungarian(cost_matrix)print('calculating...')hungarian.calculate()print("Expected value:\t\t12")print("Calculated value:\t", hungarian.get_total_potential())# = 12print("Expected results:\n\t[(0, 1), (1, 0), (2, 2)]")print("Results:\n\t", hungarian.get_results())print("-"*80)profit_matrix =[[62,75,80,93,95,97],[75,80,82,85,71,97],[80,75,81,98,90,97],[78,82,84,80,50,98],[90,85,85,80,85,99],[65,75,80,75,68,96]]hungarian = Hungarian(profit_matrix, is_profit_matrix=True)hungarian.calculate()print("Expected value:\t\t543")print("Calculated value:\t", hungarian.get_total_potential())# = 543print("Expected results:\n\t[(0, 4), (2, 3), (5, 5), (4, 0), (1, 1), (3, 2)]")print("Results:\n\t", hungarian.get_results())print("-"*80)profit_matrix =[[62,75,80,93,0,97],[75,0,82,85,71,97],[80,75,81,0,90,97],[78,82,0,80,50,98],[0,85,85,80,85,99],[65,75,80,75,68,0]]hungarian = Hungarian(profit_matrix, is_profit_matrix=True)hungarian.calculate()print("Expected value:\t\t523")print("Calculated value:\t", hungarian.get_total_potential())# = 523print("Expected results:\n\t[(0, 3), (2, 4), (3, 0), (5, 2), (1, 5), (4, 1)]")print("Results:\n\t", hungarian.get_results())print("-"*80)print("-"*80)总结如开篇所⾔,匈⽛利算法具有多种实现⽅式,可见该算法多么优秀,本⽂的实现⽅式不⼀定是最优的,但相对⽽⾔⽐较通俗易懂。
求kM算法和匈牙利算法的程序代码

求kM算法和匈牙利算法的程序代码kM算法和匈牙利算法的程序代码,最好是用matlab给出的,用c语言亦可。
不要用其他的编程语言。
//二分图最佳匹配,kuhn munkras算法,邻接阵形式,复杂度O(m*m*n)//返回最佳匹配值,传入二分图大小m,n和邻接阵mat,表示权值//match1,match2返回一个最佳匹配,未匹配顶点match值为-1//一定注意m<=n,否则循环无法终止//最小权匹配可将权值取相反数#include <string.h>#define MAXN 310#define inf 1000000000#define _clr(x) memset(x,0xff,sizeof(int)*n)int kuhn_munkras(int m,int n,int mat[][MAXN],int* match1,int* match2){ int s[MAXN],t[MAXN],l1[MAXN],l2[MAXN],p,q,ret=0,i,j,k;for (i=0;i<m;i++)for (l1[i]=-inf,j=0;j<n;j++)l1[i]=mat[i][j]>l1[i]?mat[i][j]:l1[i];for (i=0;i<n;l2[i++]=0);for (_clr(match1),_clr(match2),i=0;i<m;i++){for (_clr(t),s[p=q=0]=i;p<=q&&match1[i]<0;p++)for (k=s[p],j=0;j<n&&match1[i]<0;j++)if (l1[k]+l2[j]==mat[k][j]&&t[j]<0){s[++q]=match2[j],t[j]=k;if (s[q]<0)for (p=j;p>=0;j=p)match2[j]=k=t[j],p=match1[k],match1[k]=j;}if (match1[i]<0){for (i--,p=inf,k=0;k<=q;k++)for (j=0;j<n;j++)if (t[j]<0&&l1[s[k]]+l2[j]-mat[s[k]][j]<p)p=l1[s[k]]+l2[j]-mat[s[k]][j];for (j=0;j<n;l2[j]+=t[j]<0?0:p,j++);for (k=0;k<=q;l1[s[k++]]-=p);}}for (i=0;i<m;i++)ret+=mat[i][match1[i]];return ret;}昨天帮一个同学完成了他的毕业论文上的指派问题的匈牙利算法程序。
匈牙利算法代码解析

匈牙利算法代码解析匈牙利算法又称作增广路算法,主要用于解决二分图最大匹配问题。
它的基本思想是在二分图中查找增广路,然后将这条增广路上的边反转,这样可以将匹配数增加一个,由此不断寻找增广路并反转边直到无法找到为止,最后所找到的就是二分图的最大匹配。
匈牙利算法的流程如下:1. 从左边开始选择一个未匹配的节点,将其标记为当前节点;2. 再从当前节点出发,依次寻找与它相连的未匹配节点;3. 如果找到了一个未匹配节点,则记录该节点的位置,并将当前节点标记为该节点;4. 如果当前节点的所有连边都不能找到未匹配节点,则退回到上一个节点,再往其他的连接点继续搜索;5. 如果到达已经匹配节点,则将该节点标记为新的当前节点,返回步骤4;6. 如果找到了一条增广路,则将其上的边反转,并将匹配数+1;7. 重复以上步骤,直至无法找到增广路为止。
在匈牙利算法中,增广路的查找可以使用DFS或BFS,这里我们以DFS为例进行解释。
匈牙利算法的时间复杂度为O(nm),n和m分别表示左边和右边的节点数,因为每条边至多遍历两次,所以最多需要执行2n次DFS。
以下为匈牙利算法的Python代码:```Pythondef findPath(graph, u, match, visited):for v in range(len(graph)):if graph[u][v] and not visited[v]:visited[v] = Trueif match[v] == -1 or findPath(graph, match[v], match, visited):# 如果v没有匹配或者匹配的右匹配节点能找到新的匹配match[v] = u # 更新匹配return Truereturn Falsedef maxMatching(graph):n = len(graph)match = [-1] * n # 右部节点的匹配数组,初始化为-1表示没有匹配count = 0return match, count```其中,findPath函数是用来查找增广路的DFS函数,match数组是右边节点的匹配数组,初始化为-1表示没有匹配,count则表示匹配数。
匈牙利法的matlab实现

匈牙利法的matlab实现一、什么是匈牙利法匈牙利算法,也称为Kuhn-Munkres算法,是解决二分图最大权匹配问题的经典算法。
其基本思想是通过增广路径来不断扩大已有的匹配,直到无法再找到增广路径为止。
二、如何实现匈牙利算法1. 确定初始匹配首先需要确定一个初始的匹配方案。
一般可以将所有的边都标记为未匹配状态,然后从左侧顶点开始遍历,依次找到能够与其相连的未匹配右侧顶点进行匹配。
2. 寻找增广路径在寻找增广路径时,可以采用深度优先搜索或广度优先搜索等方法。
以深度优先搜索为例,在每次递归时会尝试扩展当前左侧顶点所连接的所有未访问过的右侧顶点。
如果找到了一条能够扩展当前匹配方案的路径,则将该路径上所有边进行反转操作,并返回true表示成功找到一条增广路径。
3. 更新匹配方案当无法再找到新的增广路径时,已经得到了最大权匹配方案。
此时需要对当前的匹配方案进行更新。
具体做法是将所有在交错树上的左侧顶点与右侧顶点进行交换,从而得到一个新的匹配方案。
4. 重复迭代更新匹配方案后,需要重新开始一轮迭代。
如果发现当前的匹配方案已经达到最大权匹配,则算法结束。
三、如何用Matlab实现匈牙利算法1. 确定初始匹配在Matlab中,可以使用矩阵来表示二分图,并将所有边都标记为未匹配状态。
例如,假设有一个5个左侧顶点和6个右侧顶点的二分图,则可以使用如下代码生成相应的矩阵:n = 5; % 左侧顶点数m = 6; % 右侧顶点数w = rand(n, m); % 权重矩阵match = zeros(1, m); % 初始匹配方案其中,w表示权重矩阵,match表示初始匹配方案。
由于初始时所有边都是未匹配状态,因此可以将match中所有元素设置为0。
2. 寻找增广路径在Matlab中,可以采用递归函数来寻找增广路径。
具体做法是从每个未匹配的左侧顶点开始进行深度优先搜索,并记录搜索过程中所经过的右侧顶点。
如果找到了一条增广路径,则将该路径上所有边进行反转操作,并返回true表示成功找到一条增广路径。
匈牙利算法示例

(1) 从(cij)的每行元素都减去该行的最小元素; (2) 再从所得新系数矩阵的每列元素中减去该列的最 小元素。
1
第二步:进行试指派,以寻求最优解。 在(bij)中找尽可能多的独立0元素,若能找出n个独
2
6
0
0
0 0 0 1
1
0
0
0
0 1 0 0
0
0
1
0
1152
练习:
费 工作
用
人员
A
B
C
D
E
甲
7
5
9
8
11
乙
9
12
7
11
9
丙
8
5
4
6
8
丁
7
3
6
9
6
戊
4
6
7
5
11
13
7 5 9 8 11 5
9 12
7 11
9
7
8 5 4 6 9 4
7
3
6
9
6
3
4 6 7 5 11 4
2 0 4 3 6
2
◎0 2
3
Ø0
0Ø 4 4 0◎ 6
22
Ø0 Ø0 3 ◎0 3
1
6
0Ø 2
◎0
3 2 0◎ 0Ø 3
2
◎0 2
3
Ø0
0◎ 4 4 0Ø 6
23
用匈牙利法求解下列指派问题,已知效率矩 阵分别如下:
7 9 10 12
1
3
匈牙利算法matlab源程序及实例(适合各种矩阵)

匈牙利算法matlab源程序及实例(适合各种矩阵)function [Matching,Cost] = Edmonds(a)Matching = zeros(size(a));num_y = sum(~isinf(a),1);num_x = sum(~isinf(a),2);x_con = find(num_x~=0);y_con = find(num_y~=0);P_size = max(length(x_con),length(y_con));P_cond = zeros(P_size);P_cond(1:length(x_con),1:length(y_con)) = a(x_con,y_con); if isempty(P_cond)Cost = 0;returnendEdge = P_cond;Edge(P_cond~=Inf) = 0;cnum = min_line_cover(Edge);Pmax = max(max(P_cond(P_cond~=Inf)));P_size = length(P_cond)+cnum;P_cond = ones(P_size)*Pmax;P_cond(1:length(x_con),1:length(y_con)) = a(x_con,y_con); exit_flag = 1;stepnum = 1;while exit_flagswitch stepnumcase 1[P_cond,stepnum] = step1(P_cond);case 2[r_cov,c_cov,M,stepnum] = step2(P_cond);case 3[c_cov,stepnum] = step3(M,P_size);case 4[M,r_cov,c_cov,Z_r,Z_c,stepnum] = step4(P_cond,r_cov,c_cov,M);case 5[M,r_cov,c_cov,stepnum] = step5(M,Z_r,Z_c,r_cov,c_cov);case 6[P_cond,stepnum] = step6(P_cond,r_cov,c_cov);case 7exit_flag = 0;endendMatching(x_con,y_con) = M(1:length(x_con),1:length(y_con));Cost = sum(sum(a(Matching==1)));function [P_cond,stepnum] = step1(P_cond)P_size = length(P_cond);for ii = 1:P_sizermin = min(P_cond(ii,:));P_cond(ii,:) = P_cond(ii,:)-rmin;endstepnum = 2;function [r_cov,c_cov,M,stepnum] = step2(P_cond)P_size = length(P_cond);r_cov = zeros(P_size,1);c_cov = zeros(P_size,1);M = zeros(P_size);for ii = 1:P_sizefor jj = 1:P_sizeif P_cond(ii,jj) == 0 && r_cov(ii) == 0 && c_cov(jj) == 0M(ii,jj) = 1;r_cov(ii) = 1;c_cov(jj) = 1;endendendr_cov = zeros(P_size,1); % A vector that shows if a row is coveredc_cov = zeros(P_size,1); % A vector that shows if a column is coveredstepnum = 3;function [c_cov,stepnum] = step3(M,P_size)c_cov = sum(M,1);if sum(c_cov) == P_sizestepnum = 7;elsestepnum = 4;endfunction [M,r_cov,c_cov,Z_r,Z_c,stepnum] = step4(P_cond,r_cov,c_cov,M)P_size = length(P_cond);zflag = 1;while zflagrow = 0; col = 0; exit_flag = 1;ii = 1; jj = 1;while exit_flagif P_cond(ii,jj) == 0 && r_cov(ii) == 0 && c_cov(jj) == 0row = ii;col = jj;exit_flag = 0;endjj = jj + 1;if jj > P_size; jj = 1; ii = ii+1; endif ii > P_size; exit_flag = 0; endendif row == 0stepnum = 6;zflag = 0;Z_r = 0;Z_c = 0;elseM(row,col) = 2;if sum(find(M(row,:)==1)) ~= 0r_cov(row) = 1;zcol = find(M(row,:)==1);c_cov(zcol) = 0;elsestepnum = 5;zflag = 0;Z_r = row;Z_c = col;endendendfunction [M,r_cov,c_cov,stepnum] = step5(M,Z_r,Z_c,r_cov,c_cov)zflag = 1;ii = 1;while zflagrindex = find(M(:,Z_c(ii))==1);if rindex > 0ii = ii+1;Z_r(ii,1) = rindex;Z_c(ii,1) = Z_c(ii-1);elsezflag = 0;endif zflag == 1;cindex = find(M(Z_r(ii),:)==2);ii = ii+1;Z_r(ii,1) = Z_r(ii-1);Z_c(ii,1) = cindex;endendfor ii = 1:length(Z_r)if M(Z_r(ii),Z_c(ii)) == 1M(Z_r(ii),Z_c(ii)) = 0;elseM(Z_r(ii),Z_c(ii)) = 1;endendr_cov = r_cov.*0;c_cov = c_cov.*0;M(M==2) = 0;stepnum = 3;function [P_cond,stepnum] = step6(P_cond,r_cov,c_cov)a = find(r_cov == 0);b = find(c_cov == 0);minval = min(min(P_cond(a,b)));P_cond(find(r_cov == 1),:) = P_cond(find(r_cov == 1),:) +minval;P_cond(:,find(c_cov == 0)) = P_cond(:,find(c_cov == 0)) - minval;stepnum = 4;function cnum = min_line_cover(Edge)[r_cov,c_cov,M,stepnum] = step2(Edge);[c_cov,stepnum] = step3(M,length(Edge));[M,r_cov,c_cov,Z_r,Z_c,stepnum] = step4(Edge,r_cov,c_cov,M);cnum = length(Edge)-sum(r_cov)-sum(c_cov);》a=[0.9400 0.9700 0.8600 0.9700 0.9680 0.9480 0.9680 0.98000.8600 0.9300 0.9200 0.9300 0.9680 0.9680 0.9880 0.96000.9000 0.9300 0.9400 0.9500 0.9080 0.9480 0.9680 0.96000.9400 0.9300 0.9400 0.9500 0.9680 0.9080 0.9880 0.92000.8600 0.8900 0.9200 0.9500 0.9880 0.9480 0.9680 0.92000.9200 0.9300 0.9200 0.9500 0.9080 0.9480 0.9880 0.92000.9400 0.9700 0.9000 0.9300 0.9680 0.9480 0.9680 1.00000.9200 0.9700 0.9200 0.9300 0.9880 0.9880 0.9480 0.96000.9400 0.9700 0.9000 0.9700 0.9680 0.9480 0.9480 0.96000.9200 0.9500 0.9200 0.9700 0.9480 0.9480 0.9480 0.9800];》[z,ans]=Edmonds(a)运行结果:z =0 0 1 0 0 0 0 01 0 0 0 0 0 0 00 0 0 0 1 0 0 00 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0ans =7.2240。
匈牙利算法代码范文

匈牙利算法代码范文匈牙利算法(Hungarian Algorithm)是用于解决最佳二分匹配问题(Bipartite Matching Problem)的一种经典算法。
它通过递归地寻找增广路径来不断优化匹配,直到找到最佳的匹配方案。
以下是一个实现匈牙利算法的Python代码:```pythondef hungarian_algorithm(graph):#初始化顶点的标记数组rows = len(graph)cols = len(graph[0])row_match = [-1] * rowscol_match = [-1] * cols#为每个未匹配的顶点寻找增广路径for row in range(rows):if row_match[row] == -1:path = [False] * colsfind_augmenting_path(graph, row, row_match, col_match, path) return row_matchdef find_augmenting_path(graph, row, row_match, col_match, path):cols = len(graph[0])for col in range(cols):if graph[row][col] and not path[col]:path[col] = Trueif col_match[col] == -1 or find_augmenting_path(graph,col_match[col], row_match, col_match, path):row_match[row] = colcol_match[col] = rowreturn Truereturn False```在这个代码中,`graph`是一个二维矩阵,表示二分图的邻接矩阵。
其中,`graph[i][j]`表示顶点i和顶点j是否存在一条边。
匈牙利算法及程序

匈牙利算法及程序匈牙利算法及程序匈牙利算法自然避不开Hall定理,即是:对于二部图G,存在一个匹配M,使得X的所有顶点关于M饱和的充要条件是:对于X的任意一个子集A,和A邻接的点集为T(A),恒有:│T(A)│ = │A│匈牙利算法是基于Hall定理中充分性证明的思想,其基本步骤为:1.任给初始匹配M;2.若X已饱和则结束,否则进行第3步;3.在X中找到一个非饱和顶点x0,作V1 ← {x0}, V2 ← Φ;4.若T(V1) = V2则因为无法匹配而停止,否则任选一点y ∈T(V1)\V2;5.若y已饱和则转6,否则做一条从x0 →y的可增广道路P,M←M?E(P),转2;6.由于y已饱和,所以M中有一条边(y,z),作V1 ← V1 ∪{z}, V2 ← V2 ∪ {y},转4;设数组up[1..n] --- 标记二分图的上半部分的点。
down[1..n] --- 标记二分图的下半部分的点。
map[1..n,1..n] --- 表示二分图的上,下部分的点的关系。
True-相连,false---不相连。
over1[1..n],over2[1..n] 标记上下部分的已盖点。
use[1..n,1..n] - 表示该条边是否被覆盖。
首先对读入数据进行处理,对于一条边(x,y) ,起点进集合up,终点进集合down。
标记map中对应元素为true。
1. 寻找up中一个未盖点。
2. 从该未盖点出发,搜索一条可行的路线,即由细边出发,由细边结束,且细粗交错的路线。
3. 若找到,则修改该路线上的点所对应的over1,over2,use的元素。
重复步骤1。
4. 统计use中已覆盖的边的条数total,总数n减去total即为问题的解。
匈牙利算法开放分类:算法、数据结构、离散数学、二分图匹配求最大匹配的一种显而易见的算法是:先找出全部匹配,然后保留匹配数最多的。
但是这个算法的时间复杂度为边数的指数级函数。
因此,需要寻求一种更加高效的算法。
分配问题匈牙利算法的Matlab实现

分配问题匈牙利算法的Matlab实现function [x,fVal]=Hungary(C)% 输出参数:% x--Decision Varables, n*n矩阵% fval--Objective function Value% 输入参数:% C--效益矩阵c=C; %将效益矩阵暂存入c,以下的操作将针对c进行[iMatrixRow,iMatrixCol]=size(c);%求约化矩阵:将效益矩阵的每行每列各减去其最小值c=c-repmat(min(c,[],2),1,iMatrixCol);c=c-repmat(min(c,[],1),iMatrixRow,1);%进行试分配,求出初始分配方案while 1%对所有零元素均已画⊙(inf)或画×(-inf)c=CircleOrCross(c);%划线,决定覆盖所有零元素的最少直线数iIndepentZeroNum=find(c==inf);if length(iIndepentZeroNum)==iMatrixRowbreak;else[Row,Col]=line(c);end%查找没有被直线段覆盖的元素中的最小元素,并存入fMininumVlaue中fMininumVlaue=inf;for i=1:iMatrixRowfor j=1:iMatrixColif Row(i)~=1 && Col(j)~=1 && c(i,j)<fmininumvlaue fMininumVlaue=c(i,j);endendend%修改约化矩阵中的相关数据for i=1:iMatrixRowfor j=1:iMatrixColif c(i,j)==inf||c(i,j)==-infc(i,j)=0;endif Row(i)~=1 && Col(j)~=1c(i,j)=c(i,j)-fMininumVlaue;endif Row(i)==1 && Col(j)==1c(i,j)=c(i,j)+fMininumVlaue;endendendend%返回分配方案及目标函数值fVal=0;for i=1:iMatrixRowfor j=1:iMatrixColif c(i,j)==infx(i,j)=1;fVal=fVal+C(i,j); elsex(i,j)=0;endendend</fmininumvlaue。
匈牙利算法的步骤:

匈牙利算法的步骤:
第一步变换效率矩阵,使各行各列都出现 0 元素。
1°效率矩阵每行元素都减去该行最小元素;
2°效率矩阵每列元素都减去该列最小元素。
第二步圈出不同行且不同列的 0 元素,进行试指派。
1°(行搜索)给只有一个0 元素的行中的0 画圈,记作“◎”,并划去与其同列的其余0元素;
2°(列搜索)给只有一个0 元素的列中的0 画圈,记作“◎”,并划去与其同行的其余0元素;
3°反复进行1°、2°,直至所有0元素都有标记为止。
4°若行(列)的0元素均多于一个,则在0元素最少的行(列)中选定一个0元素,标“◎”,并划去与其同行同列的其余0元素。
5°若不同行且不同列的“◎”已达n个,则令它们对应的xij =1,其余xij =0,已得最优解,计算停,否则转第三步。
第三步用最少直线覆盖效率矩阵中的0元素。
1°对没有“◎”的行打“√”;
2°对打“√”行中的0元素所在列打“√”;
3°对打“√”列中“◎”所在行打“√”;
4°反复进行2°、 3°,直至打不出新“√”为止。
5°对没打“√”的行画横线,对打“√”列画竖线,则效率矩阵中所有0元素被这些直线所覆盖。
第四步调整效率矩阵,使出现新的0元素。
1°找出未被划去元素中的最小元素,以其作为调整量θ;2°矩阵中打“√”行各元素都减去θ,打“√”列各元素都加θ(以保证原来的0元素不变),然后去掉所有标记,转第二步。
匈牙利算法的MATLAB 程序代码

匈牙利算法的MATLAB 程序代码如下(算例):m=5;n=5;A=[0 1 1 0 01 1 0 1 10 1 1 0 00 1 1 0 00 0 0 1 1];M(m,n)=0;for(i=1:m)for(j=1:n)if(A(i,j))M(i,j)=1;break;end;end %求初始匹配Mif(M(i,j))break;end;end %获得仅含一条边的初始匹配Mwhile(1)for(i=1:m)x(i)=0;end %将记录X中点的标号和标记*for(i=1:n)y(i)=0;end %将记录Y中点的标号和标记*for(i=1:m)pd=1;%寻找X中M的所有非饱和点for(j=1:n)if(M(i,j))pd=0;end;endif(pd)x(i)=-n—1;end;end %将X中M的所有非饱和点都给以标号0 和标记*, 程序中用n+1 表示0 标号, 标号为负数时表示标记*pd=0;while(1)xi=0;for(i=1:m)if(x(i)〈0)xi=i;break;end;end %假如X 中存在一个既有标号又有标记*的点, 则任取X中一个既有标号又有标记*的点xiif(xi==0)pd=1;break;end %假如X中所有有标号的点都已去掉了标记*,算法终止x(xi)=x(xi)*(—1); %去掉xi 的标记*k=1;for(j=1:n)if(A(xi,j)&y(j)==0)y(j)=xi;yy(k)=j;k=k+1;end;end %对与xi 邻接且尚未给标号的yj 都给以标号iif(k〉1)k=k-1;for(j=1:k)pdd=1;for(i=1:m)if(M(i,yy(j)))x(i)=—yy(j);pdd=0;break;end;end %将yj 在M中与之邻接的点xk (即xkyj∈M), 给以标号j 和标记*if(pdd)break;end;endif(pdd)k=1;j=yy(j);%yj 不是M的饱和点while(1)P(k,2)=j;P(k,1)=y(j);j=abs(x(y(j))); %任取M的一个非饱和点yj, 逆向返回if(j==n+1)break;end %找到X中标号为0 的点时结束,获得M—增广路Pk=k+1;endfor(i=1:k)if(M(P(i,1),P(i,2)))M(P(i,1),P(i,2))=0;%将匹配M 在增广路P 中出现的边去掉else M(P(i,1),P(i,2))=1;end;end %将增广路P 中没有在匹配M中出现的边加入到匹配M中break;end;end;endif(pd)break;end;end %假如X中所有有标号的点都已去掉了标记*, 算法终止M %显示最大匹配M,程序结束。
匈牙利算法的MATLAB代码

程序文件 fenpei.mfunction [z,ans]=fenpei(marix)%//////////////////////////////////////////////////%输入效率矩阵 marix 为方阵;%若效率矩阵中有 M,则用一充分大的数代替;%输出z为最优解,ans为最优分配矩阵;%//////////////////////////////////////////////////a=marix;b=a;%确定矩阵维数s=length(a);%确定矩阵行最小值,进行行减ml=min(a');for i=1:sa(i,:)=a(i,:)-ml(i);end%确定矩阵列最小值,进行列减mr=min(a);for j=1:sa(:,j)=a(:,j)-mr(j);end% start workingnum=0;while(num~=s) %终止条件是“(0)”的个数与矩阵的维数相同%index用以标记矩阵中的零元素,若a(i,j)=0,则index(i,j)=1,否则index(i,j)=0 index=ones(s);index=a&index;index=~index;%flag用以标记划线位,flag=0 表示未被划线,%flag=1 表示有划线过,flag=2 表示为两直线交点%ans用以记录 a 中“(0)”的位置%循环后重新初始化flag,ansflag = zeros(s);ans = zeros(s);%一次循环划线全过程,终止条件是所有的零元素均被直线覆盖,%即在flag>0位,index=0while(sum(sum(index)))%按行找出“(0)”所在位置,并对“(0)”所在列划线,%即设置flag,同时修改index,将结果填入ansfor i=1:st=0;l=0;for j=1:sif(flag(i,j)==0&&index(i,j)==1)l=l+1;t=j;endendif(l==1)flag(:,t)=flag(:,t)+1;index(:,t)=0;ans(i,t)=1;endend%按列找出“(0)”所在位置,并对“(0)”所在行划线, %即设置flag,同时修改index,将结果填入ansfor j=1:st=0;r=0;for i=1:sif(flag(i,j)==0&&index(i,j)==1)r=r+1;t=i;endendif(r==1)flag(t,:)=flag(t,:)+1;index(t,:)=0;ans(t,j)=1;endendend %对 while(sum(sum(index)))%处理过程%计数器:计算ans中1的个数,用num表示num=sum(sum(ans));% 判断是否可以终止,若可以则跳出循环if(s==num)break;end%否则,进行下一步处理%确定未被划线的最小元素,用m表示m=max(max(a));for i=1:sfor j=1:sif(flag(i,j)==0)if(a(i,j)<m)m=a(i,j);endendendend%未被划线,即flag=0处减去m;线交点,即flag=2处加上mfor i=1:sfor j=1:sif(flag(i,j)==0)a(i,j)=a(i,j)-m;endif(flag(i,j)==2)a(i,j)=a(i,j)+m;endendendend %对while(num~=s)%计算最优(min)值zm=ans.*b;z=0;z=sum(sum(zm));/////////////////////////////////////////////////////////////////////////////// /////////////////////////////////////////////////////////////////////////////// ///////////////////////运行实例:>> a=[37.7 32.9 38.8 37 35.443.4 33.1 42.2 34.7 41.833.3 28.5 38.9 30.4 33.629.2 26.4 29.6 28.5 31.10 0 0 0 0];>> [z,ans]=fenpei(a)z =127.8000ans =0 0 0 0 10 0 0 1 00 1 0 0 01 0 0 0 00 0 1 0 01 1 12 2 2 2 02 4 43 3 1 1 0 7 2 24 4 7 7 03 5 5 7 7 5 5 04 3 3 9 9 6 6 0 8 8 8 1 1 4 4 0 6 6 6 12 12 11 11 05 9 9 13 13 12 12 0欢迎您的下载,资料仅供参考!致力为企业和个人提供合同协议,策划案计划书,学习资料等等打造全网一站式需求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
case 3
[c_cov,stepnum] = step3(M,P_size);
case 4
[M,r_cov,c_cov,Z_r,Z_c,stepnum] = step4(P_cond,r_cov,c_cov,M);
case 5
for ii = 1:P_size
rmin = min(P_cond(ii,:));
P_cond(ii,:) = P_cond(ii,:)-rmin;
end
stepnum = 2;
function [r_cov,c_cov,M,stepnum] = step2(P_cond)
row = ii;
col = jj;
exit_flag = 0;
end
jj = jj + 1;
if jj > P_size; jj = 1; ii = ii+1; end
P_size = length(P_cond);
zflag = 1;
while zflag
row = 0; col = 0; exit_flag = 1;
ii = 1; jj = 1;
while exit_flag
if P_cond(ii,jj) == 0 && r_cov(ii) == 0 && c_cov(jj) == 0
P_size = length(P_cond)+cnum;
P_cond = ones(P_size)*Pmax;
P_cond(1:length(x_con),1:length(y_con)) = a(x_con,y_con);
exit_flag = 1;
if isempty(P_cond)
Cost = 0;
return
end
Edge = P_cond;
Edge(P_cond~=Inf) = 0;
cnum = min_line_cover(Edge);
Pmax = max(max(P_cond(P_cond~=Inf)));
P_cond(find(r_cov == 1),:) = P_cond(find(r_cov == 1),:) + minval;
P_cond(:,find(c_cov == 0)) = P_cond(:,find(c_cov == 0)) - minval;
stepnum = 4;
function cnum = min_line_cover(Edge)
if ii > P_size; exit_flag = 0; end
end
if row == 0
stepnum = 6;
zflag = 0;
Z_r = 0;
Z_c = 0;
0.8600 0.9300 0.9200 0.9300 0.9680 0.9680 0.9880 0.9600
0.9000 0.9300 0.9400 0.9500 0.9080 0.9480 0.9680 0.9600
0.9400 0.9300 0.9400 0.9500 0.9680 0.9080 0.9880 0.9200
0.8600 0.8900 0.9200 0.9500 0.9880 0.9480 0.9680 0.9200
else
M(row,col) = 2;
if sum(find(M(row,:)==1)) ~= 0
r_cov(row) = 1;
zcol = find(M(row,:)==1);
function [c_cov,stepnum] = step3(M,P_size) c_cov = Fra bibliotekum(M,1);
if sum(c_cov) == P_size
stepnum = 7;
else
stepnum = 4;
end
function [M,r_cov,c_cov,Z_r,Z_c,stepnum] = step4(P_cond,r_cov,c_cov,M)
P_size = length(P_cond);
r_cov = zeros(P_size,1);
c_cov = zeros(P_size,1);
M = zeros(P_size);
for ii = 1:P_size
for jj = 1:P_size
cnum = length(Edge)-sum(r_cov)-sum(c_cov);
》a=[0.9400 0.9700 0.8600 0.9700 0.9680 0.9480 0.9680 0.9800
end
r_cov = zeros(P_size,1); % A vector that shows if a row is covered
c_cov = zeros(P_size,1); % A vector that shows if a column is covered
stepnum = 3;
if P_cond(ii,jj) == 0 && r_cov(ii) == 0 && c_cov(jj) == 0
M(ii,jj) = 1;
r_cov(ii) = 1;
c_cov(jj) = 1;
end
end
y_con = find(num_y~=0);
P_size = max(length(x_con),length(y_con));
P_cond = zeros(P_size);
P_cond(1:length(x_con),1:length(y_con)) = a(x_con,y_con);
[M,r_cov,c_cov,stepnum] = step5(M,Z_r,Z_c,r_cov,c_cov);
case 6
[P_cond,stepnum] = step6(P_cond,r_cov,c_cov);
case 7
exit_flag = 0;
M(M==2) = 0;
stepnum = 3;
function [P_cond,stepnum] = step6(P_cond,r_cov,c_cov)
a = find(r_cov == 0);
b = find(c_cov == 0);
minval = min(min(P_cond(a,b)));
function [Matching,Cost] = Edmonds(a)
Matching = zeros(size(a));
num_y = sum(~isinf(a),1);
num_x = sum(~isinf(a),2);
x_con = find(num_x~=0);
c_cov(zcol) = 0;
else
stepnum = 5;
zflag = 0;
Z_r = row;
Z_c = col;
end
0.9200 0.9300 0.9200 0.9500 0.9080 0.9480 0.9880 0.9200
0.9400 0.9700 0.9000 0.9300 0.9680 0.9480 0.9680 1.0000
[r_cov,c_cov,M,stepnum] = step2(Edge);
[c_cov,stepnum] = step3(M,length(Edge));
[M,r_cov,c_cov,Z_r,Z_c,stepnum] = step4(Edge,r_cov,c_cov,M);
end
end
function [M,r_cov,c_cov,stepnum] = step5(M,Z_r,Z_c,r_cov,c_cov)
zflag = 1;
ii = 1;
while zflag
rindex = find(M(:,Z_c(ii))==1);
if rindex > 0
ii = ii+1;
Z_r(ii,1) = rindex;
Z_c(ii,1) = Z_c(ii-1);
else
zflag = 0;
end
if zflag == 1;
end
end
Matching(x_con,y_con) = M(1:length(x_con),1:length(y_con));
Cost = sum(sum(a(Matching==1)));
function [P_cond,stepnum] = step1(P_cond)
P_size = length(P_cond);
if M(Z_r(ii),Z_c(ii)) == 1
M(Z_r(ii),Z_c(ii)) = 0;
else
M(Z_r(ii),Z_c(ii)) = 1;
end
end
r_cov = r_cov.*0;
c_cov = c_cov.*0;
stepnum = 1;
while exit_flag
switch stepnum
case 1
[P_cond,stepnum] = step1(P_cond);
case 2
[r_cov,c_cov,M,stepnum] = step2(P_cond);
