第三讲 几何图形剪拼
四年级几何图形剪拼学生版

知识要点图形剪拼菱形面积公式将一个等边三角形分割成若干个等边三角形(不要求大小相等)将一个正方形分割成若干个正方形(不要求大小相等)n 边形内角和公式常用图形的剪拼梯形面积公式平行四边形面积公式三角形面积公式 几何(本讲)一、 三角形面积公式:三角形面积=底⨯高2÷,即S 三角形2a h =⨯÷。
二、 平行四边形面积公式:平行四边形面积=底⨯高,即S 平行四边形a h =⨯。
三、 梯形面积公式:梯形面积=(上底+下底)⨯高2÷,即S 梯形()2a b h =+⨯÷。
四、 菱形面积公式:菱形面积=两条对角线乘积的一半,即S 菱形2m n =⨯÷ 五、n 边形的内角和公式:n 边形的内角和(2)180n =-⨯o 。
图形面积【例 1】如图所示,已知三角形的一条边为a,这条边上的高为h。
请用图形剪拼的方法,求出这个三角形的面积S三角形。
hahaha【例 2】如图所示,已知平行四边形的一条边为a,这条边上的高位h。
请用图形剪拼的方法,求出这个平行四边形的面积S平行四边形。
ha【例 3】如图所示,已知梯形的两条平行的边分别为a、b,梯形的高为h。
请用图形剪拼的方法,求出这个梯形的面积S梯形。
hab【例 4】如图所示,已知菱形的两条对角线分别为m、n。
请用图形剪拼的方法,求出这个平行四边形的面积S菱形。
(提示:菱形的两条对角线相互垂直)mn图形分割【例 5】 (2005年12月第六届“中环杯”小学生思维能力训练活动四年级复赛第二(5)题)将一个长方形分成形状完全一样的四块,至少画出8种分法,请用图表示。
(形状一样,排列方向不一样,只能看作一种分法)【例 6】 如图所示为一个34⨯的长方形方格纸,请用5种不同的方法将它分割成完全相同的两部分(保持每个小方格的完整)。
【例 7】 如图所示,请将44⨯的正方形分成形状相同、大小相等的四个图形,并且使其中每个图形都含有“上海世博”这四个字。
小学四年级数学培优第三部分“几何问题”
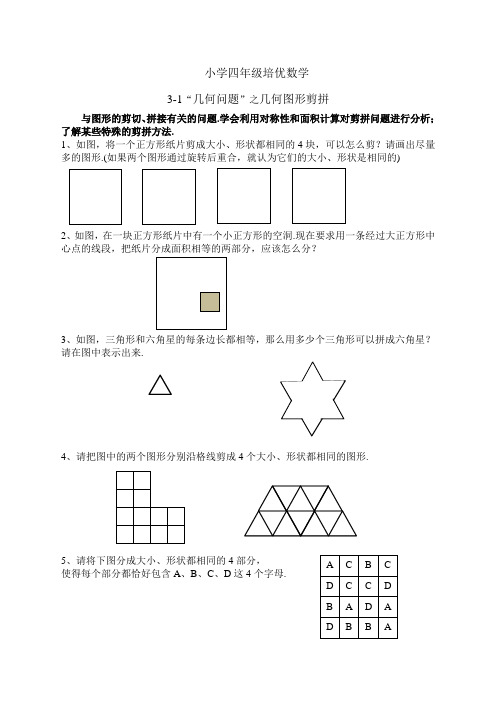
3-1“几何问题”之几何图形剪拼与图形的剪切、拼接有关的问题.学会利用对称性和面积计算对剪拼问题进行分析;了解某些特殊的剪拼方法.1、如图,将一个正方形纸片剪成大小、形状都相同的4块,可以怎么剪?请画出尽量多的图形.(如果两个图形通过旋转后重合,就认为它们的大小、形状是相同的)2、如图,在一块正方形纸片中有一个小正方形的空洞.现在要求用一条经过大正方形中心点的线段,把纸片分成面积相等的两部分,应该怎么分?3、如图,三角形和六角星的每条边长都相等,那么用多少个三角形可以拼成六角星?请在图中表示出来.4、请把图中的两个图形分别沿格线剪成4个大小、形状都相同的图形.5、请将下图分成大小、形状都相同的4部分, 使得每个部分都恰好包含A 、B 、C 、D 这4个字母.3-2“几何问题”之直线形计算一掌握正方形、长方形、平行四边形、三角形以及梯形的面积计算公式,并能够熟练应用;计算平行四边形和三角形的面积时,学会选择适当的底和高.1、如图,由16个同样大小的正方形组成一个“5”字.如果这个图形的周长是102厘米,那么它的面积是多少平方厘米?2、如图,用两块长方形纸片和一块小正方形纸片拼成了一个大正方形纸片,其中小正方形纸片的面积是49平方厘米,其中一个长方形纸片的面积是28平方厘米.那么最后拼成的大正方形纸片的面积是多少平方厘米?2、如图,小、中、大三个正方形从左到右依次紧挨着摆放,边长分别是3、7、9.那么图中两个阴影平行四边形的面积分别是多少?4、如图,大正方形的边长是8厘米,小正方形的边长是6厘米.请问:图中阴影部分的面积是多少平方厘米?28 495、如图,从梯形ABCD 中分出两个平行四边形ABEF 和CDFG ,其中ABEF 的面积是60平方米,且AF 的长度为10米,FD 的长度为4米.那么平行四边形CDFG 的面积等于多少平方米?小学四年级培优数学3-2“几何问题”之格点与割补明确格点多边形的概念,学会通过分割和添补的方法计算其面积;学会利用割补法计算不规则图形的面积;掌握格点多边形的面积计算公式.1、下图1中相邻两格点间的距离均为1厘米,三个多边形的面积分别是多少平方厘米?2、下图2中相邻两格点间的距离均为1厘米,三个阴影图形的面积分别是多少平方厘米?3、图中的每个小正方形的面积均为2平方厘米,阴影多边形的面积是多少平方厘米?4、上图2中是一个三角形点阵,其中能连出的最小的等边三角形的面积为1平方厘米,三个多边形的面积分别是多少平方厘米?5、图中的数字代表对应线段的长度,试求这个多边形的面积.(单位:厘米)6、如图,在正方形ABCD内部有一个长方形EFGH.正方形ABCD 的边长是6厘米,AE、AH都等于2厘米,求长方形EFGH的面积.7、如图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形A的面积是36平方厘米,那么正方形B的面积是多少平方厘米?52214 3A B。
四年级几何图形剪拼教师版

知识要点图形剪拼菱形面积公式将一个等边三角形分割成若干个等边三角形(不要求大小相等)将一个正方形分割成若干个正方形(不要求大小相等)n 边形内角和公式常用图形的剪拼梯形面积公式平行四边形面积公式三角形面积公式 几何(本讲)一、 三角形面积公式:三角形面积=底⨯高2÷,即S 三角形2a h =⨯÷。
二、 平行四边形面积公式:平行四边形面积=底⨯高,即S 平行四边形a h =⨯。
三、 梯形面积公式:梯形面积=(上底+下底)⨯高2÷,即S 梯形()2a b h =+⨯÷。
四、 菱形面积公式:菱形面积=两条对角线乘积的一半,即S 菱形2m n =⨯÷ 五、n 边形的内角和公式:n 边形的内角和(2)180n =-⨯o 。
图形面积【例 1】 如图所示,已知三角形的一条边为a ,这条边上的高为h 。
请用图形剪拼的方法,求出这个三角形的面积S 三角形。
hahaha【分析】当三角形的高在三角形的边上;用两个一摸一样的直角三角形拼在一起,斜边重合,拼成一个长方形。
长方形的长和宽分别是a 和h ,面积S 长方形=a h ⨯;所以直角三角形的面积是长方形的面积的一半,即S 三角形2a h =⨯÷。
当三角形的高在三角形的内部,用两个一摸一样的三角形拼在一起,其中一个沿高剪开,拼成一个长方形。
长方形的长和宽分别是a 和h ,面积S 长方形=a h ⨯;所以三角形的面积是长方形的面积的一半,即S 三角形2a h =⨯÷。
当三角形的高在三角形的外部,三角形的面积等于大直角三角形的面积减去小直角三角形的面积, 即S 三角形(')2'22a a h a h a h =+⨯÷-⨯÷=⨯÷。
所以三角形的面积三角形2a h =⨯÷。
ahaha'ha【例 2】 如图所示,已知平行四边形的一条边为a ,这条边上的高位h 。
四年级数学专题讲义第三讲 图形的剪拼

第四讲图形的剪拼把一个几何图形剪成几块形状相同的图形,或是把一个几何图形剪开后拼成另一种满足某种条件的图形,完成这样的图形剪拼,需要考虑图形剪开后各部分的形状、大小以及它们之间的位置关系.〖经典例题〗例1、如右图所示是由三个正方形组成的图形,请把它分成大小、形状都相同的四个图形?分析:如果我们不考虑分成的四个图形的形状,只考虑它的面积,就要求把原来三个正方形分成四个面积相等的部分.每部分面积应是正方形面积的34,再把三个14个正方形合成一个与34正方形形状形同的图形。
于是我们就有了如图(2)的分法.例2、把一个等边三角形分别分成8块和9块形状、大小都一样的三角形.分析:分成8块的方法是:先取各边的中点并把它们连接起来,得到4个大小、形状相同的三角形,然后再把每一个三角形分成一半,得到如下左图所示的图形.分成9块的方法是:先把每边三等分,然后再把分点彼此连接起来,得到加上右图所示的符合条件的图形.〖巩固练习〗练习1:右图是由五个同样大小的正方形组成的,请把它分成形状相同,面积相等的四块。
练习2:右图由三个同样大小的正三角形组成的,请把它分成形状相同,面积相等的四块。
练习3:在一块长方形的地里有一个圆形的水池(如图),试画一条直线把除水池外的这块地平均分成两部分。
经过圆心和长方形的中心点〖经典例题〗例3、把一个正方形分成8块,再把它们拼成一个正方形和一个长方形,使这个正方形和长方形的面积相等.分析:连接正方形的对角线,把正方形分成了4个相等的等腰直角三角形,再连接各腰中点,又把它们分成4个小等腰直角三角形和4个等腰梯形.(如下页图(1)所示)出于分成正方形、长方形面积相等的要求考虑:分别取出两个小等腰直角三角形和两个梯形,就能一一拼出所要求的正方形和长方形了(如图(2)、(3)所示). 除这种方法外,还有多种拼接方法.例4、在下左图中画5条线,把小圆圈分开,并使每块大小、形状都相等.分析:因为图中有8个小圆圈,画5条线把图形应分成8块,根据小圆圈的分布特点,分法如下图(右)所示.例5、把下图中两个图形中的某一个分成三块,最后都拼在一起,使它们成为一个正方形.分析:不管分其中的哪一块,最后拼得正方形的面积与图中两块面积和相等,甲面积=10×5=50平方厘米;乙面积=10×7-(7-2)×4=70-20=50平方厘米.所以甲面积+乙面积=50+50=100平方厘米,也就是最后拼得正方形的边长为10厘米.甲、乙两图形各有一边是10厘米,可视为正方形的一条边,然后把乙剪成三块(如下图所示)拼成的正方形,即可.当然,除这种拼凑的方法之外,还有其他多种方法,同学们可自行构思、设计.〖巩固练习〗练习1:长方形的长和宽各是9厘米和4厘米,要把它剪成大小、形状都相同的两块,并使它们拼成一个正方形.分析:已知长方形面积9×4=36(平方厘米),所以正方形的边长应为6厘米,因此可以把长方形上半部剪下6厘米,下半部剪下3厘米,分成相等的两块,合起来正好拼成一个边长为6厘米的正方形,如下右图.练习2:将右图剪成形状、大小都相同的四块,然后拼成一个大正方形。
图形剪拼教案

图形剪拼教案【篇一:图形的分割与拼接(教案案)】图形的分割与拼接【专题知识点概述】本讲中的知识点比较抽象,在这一讲中我们主要学习几种图形处理方法: 1、理解掌握图形的分割; 2、理解掌握图形的拼合; 3、理解图形的剪拼;4、利用剪拼图形计算、解决问题.图形的分割与拼接的概念把一个几何图形按某种要求分成几个图形,就叫做图形的分割.反过来,按一定的要求也可以把几个图形拼成一个完美的图形,就叫做图形的拼合.将一个或者多个图形先分割开,再拼成一种指定的图形,则叫做图形的剪拼.我们在图形的分割、拼合和剪拼的过程中,都要结合所提供的图形特点来思考.如果把一个图形分割成若干个大小、形状相等的部分,那么就要想办法找图形的对称点,把图形先分少,再分多.图形中,如果有数量方面的要求,可以先从数量入手,找出平分后每块上所含数量的多少,再结合数量来分割图形.如果是要把几个图形拼合成一个大图形,要特别注意每条边的长度,把相等的边长拼合在一起,先拼少的,再拼多的.如果是剪拼图形,要抓住“剪、拼前后图形的面积相等”这个关键,根据已知条件和图形的特点,通过分析推理和必要的计算,确定剪拼的方法.【重点难点解析】1.根据题目需要找合适的方法进行剪拼 2.如何根据相等的量来剪拼图形【竞赛考点挖掘】1.方格纸的分割与拼接2.简单平面基本图形(长方形、三角形等)的分割与拼接【习题精讲】【例1】(难度等级※)介绍一种分割技巧——染色法,先选中一个小格,找它关于中心点或中心线的对称位置,标上相应的符号,当找它关于中心线的对称位置时是一种情况,关于中心点的对称位置是另一种情况,具体如下图所示.【例2】(难度等级※※)【例3】(难度等级※※※)请把右面这个长方形沿方格线剪成形状、大小都相同的4块,使每一块内都含有“奥数读本”这四个字中的一个,该怎么剪? 【分析与解】如下图.【例4】(难度等级※※※)学习与思考对小学生的发展是很重要的,学习改变命运,思考成就未来,请你将右图分成形状和大小都相同的四个图形,并且使其中每个图形都含有“学习思考”这四个字.应怎样分? 【分析与解】【例5】(难度等级※※※)图中是由三个正三角形组成的梯形.你能把它分割成4个形状相同、面积相等的梯形吗? 【分析与解】这道题的要点在于通过计算解决问题,要求把原来三个正三角分成四个大小、形状都相同的四个梯形,先不考虑形状,大小相同也就是面积相等,即把整个梯形的面积分成四份,分割后的每一个梯形占一份,可以考虑把每一个三角形的面积分成四份,再把三个正三角形中的每一个小三角形合成要求的梯形,这种类型的题目可以从中点入手,找到每个正三角形的中点并连接,如下图.【例6】(难度等级※※※※)如何把图a中的三个图形分割成两个相同的部分(除了沿正方形的边进行分割外,还可沿正方形的对角形进行分割).【分析与解】要把图形分成两个相同的部分,首先要保证分得的两部分面积相同,其次要保证分得的两部分形状相同,从面积入手进行分割会使问题更容易解决.第一个图形一共有6个小正方形,2个三角形,要分割成两块完全相同的部分,每一部分都要有3个正方形、1个三角形,这样很容易就可以解决这个问题了;同样,对第二个图形,一共有7个正方形,2个三角形,因为正方形的个数是奇数,所以,肯定有一个正方形被分成相同的两块,对于这个图形,我们很容易看出有一个正方形的位置很特殊,在最中间,所以考虑将它分成两部分,由对称的原则,从对角线分开;第三个图形更复杂一些,一共有6个正方形,6个三角形,分成的两块每一块都要有3个正方形、3个三角形,因为最上面的两个三角形组合成了一个大的三角形,所以右下方的两个三角形不能分开,再根据对称的原则,就容易解决这个问题了,具体分法见下图.【例7】(难度等级※※※)下图是由18个小正方形组成的图形,请你把它分成6个完全相同的图形.【分析与解】与由6结合染色法,如下图.,通过观察,上面的图形具有对称性,不可能分成6个,是【例8】(难度等级※※※)把右图剪成形状、大小相等的8个小图形,怎么剪?作出分出的小图形.【分析与解】总格数为12,用总格数除以8,得到每个小图形应该是一个半小正方形,根据平均一个小图形的格数作图,如右图.【例9】(难度等级※※)用同样大小的四块等腰直角三角板,能否拼出一个三角形、一个正方形、一个长方形、一个梯形、一个平行四边形五种图形?若能,画出示意图.【分析与解】能用四块同样大小的等腰直角三角板拼出一个三角形、一个正方形、一个长方形、一个梯形、一个平行四边形五种图形.建议用等腰直角三角板,把不同的边进行重合,不要漏掉旋转重合,或者准备一些等腰直角三角形的纸片,由学生拼接后贴到黑板上,具体拼法如图所示.【例10】(难度等级※※※)下面哪些图形自身用4次就能拼成一个正方形?【分析与解】用4块图(4)和图(5)那样的图形显然能够拼成一个大正方形.其实用图(1)、图(2)、图(3)也能拼成一个大正方形,拼法见下图.【例11】(难度等级※※)将方格纸剪成面积是4的图形,形状只有七种,如下图所示.其中有哪几种可以拼成面积是16的正方形?【分析与解】面积是16的正方形,其边长等于4,用图形(5)和(7)显然能拼成边长是4的正方形(如左下图所示).用图形(1)、(2)和(6)也能拼成边长为4的正方形(如右下图所示).通过观察与试验,无法用所给图中的(3)和(4)拼成题目要求的正方形.因此,用所给图中的七种图形,共可以拼成5种面积是16的正方形.【例12】(难度等级※※)试用图a中的8个相等的直角三角形,拼成图b中的空心正八边形和图c中的空心正八角星.【分析与解】把一个直角三角形的斜边与另一个直角三角形的【篇二:一年级数学下册图形的拼组教学设计教案】人教版新课标实验教科书小学一年级下册数学第三单元《图形的拼组》教学设计灯盏小学余文田设计并执教第一课时教学设计教学内容:图形的拼组(一)教学目标:1、通过直观使学生知道长方形、正方形的形状和边的特点,并能用自己的语言描述长方形、正方形的特征。
小学数学 图形的剪拼 课件+作业(带答案)

先把每一个正方形分割成四个小 正方形。
20÷4=5(个) 5个小正方形组成的图形,可以选择
一种剪法如右图所示:
答案不唯一。
总结:对于不好直接剪切的图形,我们可以先画网格线,再进行剪切。
练习2:下图是由18个小正方形组成的图形,请将它沿格线分割成 6 个完全相同的图形。
春夏 夏 秋冬春 春冬秋夏 秋冬夏春冬秋
总结:要先求出分割出来的图形所占的方格数量,最后剪切时要注意限制条件。
练习6:请将下图沿格线分割成形状相同、大小相等的四个图形,并使每个图形中都有“学习思考”这
四个字。 16÷4=4(个)
4个小正方形可以拼成的形状有:
一种剪法如右图所示:
知识点三:复杂分割
8、下图是由五个相同的正方形组成的图形,要把它分成形状相同、大小相等的四个图形,应该怎样分?
先把每一个正方形分割成四个小 正方形。
20÷4=5(个) 5个小正方形组成的图形,可以选择
一种剪法如右图所示:
9、把下图沿哪条格线剪开后,可以拼成一个正方形? 如下图所示 拼成
10、请将下图沿格线分割成大小相等、形状相同的四块,并拼成一个正方形。
经过尝试,一种剪法 如右图所示:
知识点三:复杂分割
例题6:请将下面的图形沿格线分割成形状相同、大小相等的四块,并使每一块中都有“春夏秋冬”四
个字。
分析:
16÷4=4(个)
先计算出,分割成的四块, 每块中有几个小正方形。
4个小正方形可以拼成的形状有:
注意限制条件,每一块中都 有“春夏秋冬”四个字。
一种剪法如右图所示:
长方形纸条的面积:5×3=15(平方厘米) 大正方形的面积:11×11=121(平方厘米) 121÷15=8(个)……1(平方厘米) 理论上,最多能裁出8个长5厘米,宽3厘米的 长方形纸条。
图形的折叠剪拼与分割

图形的折叠、剪拼与分割一页普通的纸,童年时我们用稚气的双手把它折成有趣的动物,民间艺人可以把它剪成美丽的图案.折纸与剪纸是最富于自然情趣而又形象生动的实验,是丰富想象力与心灵手巧的结合.对图形进行折叠与剪拼,是学习几何不可或缺的重要一环,通过折叠与剪拼图形,我们可以发现一些几何结论并知晓这些结论是怎样被证明的.把图形或部分沿某直线翻折叫图形的折叠,对图形通过有限次的剪裁再重新拼接成新的图形叫图形的剪拼.解与图形折叠或剪拼相关的问题,利用不变量解题是关键,在折叠过程中,线段的长度、角的度数保持不变;在剪拼过程中,新图形与原图形的面积一般保持不变.例题求解【例1】如图,有一块直角三角形纸片,两直角边AC=6㎝,BC=8㎝,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于.(2002年南通市中考题)思路点拨设CD=x,由折叠的性质实现等量转换,将条件集中到Rt△BDE中,建立x的方程.注图形折叠与剪拼问题可考壹我们的动手操作能力和分析推理能力,解题时需要把计算、推理与合情想象结合起来.折叠问题可以对称观点认识:(1)折痕两边是全等的;(2)对应点连线被折痕垂直平分.解折叠问题常用到勾股定理、相似形、方程思想等知识与方法.【例2】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,则重叠部分△AFC的面积为( )A.12 D10 C.8 D.6 (2004年武汉市选拔赛试题)思路点拨只需求出AF长即可.【例3】取一张矩形的纸进行折叠,具体操作过程如下:第一步:先把矩形ABCD 对折,折痕为MN ,如图1;第二步:再把B 点叠在折痕线MN 上,折痕为AE ,点B 在MN 上的对应点为B ′,得Rt △AB'E ,如图2;第三步:沿EB'线折叠得折痕EF ,如图3.利用展开图4探究:(1)△AEF 是什么三角形?证明你的结论.(2)对于任一矩形,按照上述方法是否都能折出这种三角形?请说明理由.(2003年山西省中考题)思路点拨 本例没有现成的结论,需经历实验、观察、猜想、证明等数学活动,从而探究得到结论.【例4】如图,是从边长为40cm 、宽为30cm 的矩形钢板的左上角截取一块长为20cm 、宽为10cm 的矩形后,剩下的一块下脚料.工人师傅要将它作适当地切割,重新拼接后焊成一个面积与原下脚料的面积相等,接缝尽可能短的正方形工件.(1)请根据上述要求,设计出将这块下脚料适当分割成三块或三块以上的两种不同的拼接方案(在图2和图3中分别画出切割时所沿的虚线,以及拼接后所得到的正方形,保留拼接的痕迹);(2)比较(1)中的两种方案,哪种更好一些?说说你的看法和理由.(2002年山东省中考题)思路点拨 拼接后正方形的边长为221030 ㎝,它恰是以30cm 和10cm 为两直角边的直角三角形的斜边的长,为此可考虑设法在原钢板上构造两直角边长分别为30㎝和l0cm 的直角三角形,这是解本例的关键.注 有效的数学学习过程不能单纯地依赖模仿与记忆,应该通过观察、实验、操作、猜测、验证、推理等数学活动,形成自己对数学知识的理解和有效的学习策略,从而使知识得到内化,形成能力.近年中考中涌现的设计新颖、富有创意的折叠、剪拼与分割等问题,注重对动手实践操作、应用意识、学习潜能的考查.【例5】 用10个边长分别为3,5,6,11,17,19,22,23,24,25的正方形,可以拼接成一个矩形.(1)求这个矩形的长和宽;(2)请画出拼接图.思路点拨 利用拼接前后图形面积不变求矩形的长和宽;运用矩形对边相等这一性质画拼接图.【例6】 如图,已知△ABC 中,∠B=∠C=30°,请设计三种不同的分法,将△ABC 分割成四个三角形,使得其中两个是全等三角形,而另外两个是相似但不全等的直角三角形.请画出分割线段,标出能够说明分法的所得三角形的顶点和内角度数(或记号).(画图工具不限,不要求证明,不要求写出画法) (2003年温州市中考题)思路点拨 充分运用几何计算、推理和作图,综合运用动手操作、空间想象、解决问题.学历训练1. 将一张长方形的纸对折,如图所示可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折四次可以得到 条折痕,如果对折n 次,可以得到 条折痕.(2002年南宁市中考题)2.一张直角三角形的纸片,像图中那样折叠,使两个锐角顶点A 、B 重合,若∠B=30°,AC=3,则折痕DE 的长等于 . (2003年三明市中考题)3.如图,将一块长为12的正方形纸片ABCD 的顶点A 折至DC 边上的点E ,使DE =5,折痕为PQ ,则线段PM= .(第2题) (第3题) (第6题)4.在△ABC 中,已知AB=20,∠A=30°,CD 是AB 边的中线,若将△ABC 沿CD 对折起来,折叠后两个小三角形ACD 与三角形BCD 重叠部分的面积恰好等于折叠前△ABC 的面积的41,有如下结论:①AC 边的长可以等于a ;②折叠前的△ABC 的面积可以等于223a ;③折叠后,以A 、B 为端点的线段AB 与中线CD 平行且相等,其中,正确结论有个.(2003年天津市中考题)5.将四个相同的矩形(长是宽的3倍),用不同的方式拼成一个大矩形,设拼得大矩形的面积是四个小矩形的面积和,则大矩形周长的值只可能有( )A.1种B.2种C.3种D.4种(2003年南昌市中考题)6.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( ) A.∠A=∠1+∠2; B.2∠A=∠1+∠2;C.3∠A=2∠1+∠2; D.3∠A=2(∠l+∠2). (2003年北京市海淀区中考题)7.将一张矩形纸对折再对折(如图),然后沿着图中的虚线剪下,得到①、②两部分.将①展开后得到的平面图形是( )A.矩形B.三角形C.梯形D.菱形(2003年陕西省中考题)8.如图1,小强拿一张正方形的纸,沿虚线对折一次得图2,再对折一次得图3,然后用剪刀沿图3中的虚线剪去一个角,再打开后的形状是( ) (2003年济南市中考题)9.如图,东风汽车公司冲压厂冲压汽车零件的废料都是等腰三角形的小钢板,其中AB=AC,该冲压厂为了降低汽车零件成本,变废为宝,把这些废料再加工成红星农业机械厂粉碎机上的零件,销售给红星农业机械厂,这些零件的形状都是矩形.现在要把如图所示的等腰三角形钢板切割后再焊接成两种不同规格的矩形,每种矩形的面积正好等于该三角形的面积,每次切割的次数最多两次(切割的损失可忽略不计).(1)请你设计两种不同的切割焊接方案,并用简要的文字加以说明;(2)若要把该三角形废料切割后焊接成正方形零件(只切割一次),则该三角形需满足什么条件? (2003年十堰市中考题)10.如图,ABCD是矩形纸片,E是AB上一点,且BE:EA=5:3,EC=155,把△BCE 沿折痕EC向上翻折,若点B恰好落在AD边上,设这个点为F,求AB、BC的长.11.如图,在△ABC中,AB=3,AC=4,BC=5,现将它折叠,使点B与点C重合,则折痕的长是.(2003年四川省竞赛题)(第11题)(第12题)(第13题)12.如图,一张矩形纸片沿BC折叠,顶点A落在点A,处,第二次过A,再折叠,使折痕DE∥BC,若AB=2,AC=3,则梯形BDEC的面积为.(2002年“宇振杯”上海市竞赛题)13.如图,将矩形ABCD的四个角向内折起,恰好拼成既无缝隙又无重叠的四边形EFGH,若EH=3,EF=4,那么线段AD与AB的比等于.(第12届“希望杯”邀请赛试题)14.要剪切如图l(尺寸单位mm)所示的两种直角梯形零件,且使两种零件的数量相等.有两种面积相等的矩形铝板,第一种长500mm,宽300mm(如图2);第二种长600mm,宽250mm(如图3);可供选用.(1)填空:为了充分利用材料,应选用第种铝板,这时一块铝板最多能剪甲、乙两种零件共个,剪出这些零件后,剩余的边角料的面积是mm2.(2)画图,从图2或图3中选出你要用的铝板示意图,在上面画出剪切线,并把边角余料用阴影表示出来.15.如图,EF为正方形ABCD的对折线,将∠A沿DK折叠使它的顶点A落在EF上的G 点,则∠DKG为( )A.15°B.30°C.55°D.75°(第15题)(第16)16.某班在布置新年联欢会会场时,需要将直角三角形彩纸裁成长度不等的矩形彩条,如图,在Rt△ABC中,∠C=90°,AC=30㎝,AB=50cm,依次裁下宽为1㎝的矩形纸条a1,a2,a3,…,若使裁得的矩形纸条的长都不小于5cm,则每张直角三角形彩纸能裁成的矩形纸条的总数是( )A.24 B.25 C.26 D.27 (2001年山东省济南市中考题) 17.如图,若将左边正方形剪成四块,恰能拼成右边的矩形,设a=1,则这个正方形的面积为( )A.2537+B.253+C.251+D.2)21(+. (2003年山东省竞赛题)、。
三年级几何图形的剪拼学生版

知识要点找对称【例 1】 把一个33 的的网格分成形状、大小完全相同的四份。
【例 2】 哥哥和弟弟一起做手工,想把一张红色的平行四边形蜡光纸沿着一条直线,把它剪成大小、形状完全相同的两部分。
想一想,你可以有多少种剪法?【例 3】 要把一个正方形剪成形状相同、大小相等的4个图形,该怎样分?按照题目要求(形状和面积),根据图形与图形之间的内在联系,通过在纸上画图或者实际的剪拼,来掌握图形的变化,包括把一个几何图形分割成几个图形以及把几个几何图形拼成几个图形。
有兴趣的学生还可以自制“七巧板”或者“伤脑筋十二块”等中国传统益智拼板游戏,在闲暇时间尝试拼一下,说不定还能拼出自创的新颖有趣的图形。
图形的剪拼【例 4】你能把下面的图形分割成4个形状相同、大小相等的图形吗?【例 5】一个长6厘米,宽4厘米的长方形,从中间剪开,如图所示,得到2个大小、形状都相同的长方形,这两个新长方形的周长是多少?图形剪切【例 6】你能把一个正三角形分成形状相同,大小相等的2个、3个、4个、6个、9个三角形吗?分成【例 7】你能把一个正方形分成6个、7个、8个、9个小正方形吗?(不要求面积相等)【例 8】你能把下面的图形分割成4个形状相同、大小相等的图形吗?【例 9】把下图分成5个形状相同、大小相等的图形。
【例 10】下图是由18个小正方形组成的图形,请你把它分成6个完全相同的图形。
【例 11】你能把下面的图形分成7个大小相等的长方形吗?动手画一画。
【例 12】如右图所示是由三个正方形组成的图形,请把它分成大小、形状都相同的四个图形。
【例 13】阿凡提周游世界,有一天来到一个村庄。
一个地主对他说:“都传说你很聪明,我有一块地,你能把它分成大小相等、形状相同的2份,我就把地送给你。
”聪明的阿凡提不慌不忙,用木棍画了一道线,把这块地分成大小相等、形状相同的2份。
地主傻了眼,只好履行诺言。
后来,阿凡提把地分给了最穷的2户人家,你知道阿凡提是怎么分的吗?图形拼合【例 14】 用下面的四块图形能拼成右边的正方形吗?怎样拼?1212124321【例 15】 晚饭后,平平和妈妈玩拼木板游戏。
小学数学 图形的剪拼 课件+作业(带答案)

总结:要先求出分割出来的图形所占的方格数量,最后剪切时要注意限制条件。
课后作业:
1、下图是一个3×4 的方格纸,总面积是12平方厘米,请将它沿格线分割成 完全相同的 3 部分。每部分的面积是多少平方厘米?
12÷3=4(平方厘米) 答:每部分的面积是4平方厘米。
2、如图:一个大正方形被剪去了面积为总面1积 的小正方形。请将其分割成 12个完全相同的小正方形
练习1:请将下图沿格线分割成五个大小相等、形状相同的图形。填出。
15÷5=3(个) 3个小正方形可以拼成的形状有:
一种剪法如下图所示: 答案不唯一。
知识点一:简单分割
例题2:下图是由同样大小的五个正方形组成的,请将该图形分割成四个形状相同、大小相等的
图形。
分析:
5个正方形无法直接分割成 4个形状、大小都相同的部 分。
图形的剪拼
课前铺垫 图形分割、拼合和剪拼的概念
分割:将一个图形按要求分成几个图形,叫作图形的分割。 拼合:按一定要求将几个图形拼成一个完整的图形,叫作图形的拼合。 剪拼:将一个或多个图形先分割再拼成另一个图形,叫作图形的剪拼。
图形剪拼问题的特点
剪拼前后图形的面积相等。
知识点一:简单分割
例题1:请将下图沿格线剪成五个形状相同、大小相等的图形。
拼成的正方形如下图所示
答案不唯一。
练习3:下图是一张塔形的方格纸,沿着哪条格线剪开后,可 以拼成一个正方形?
原图中,小正方形的个数:9个
剪拼后,所得大正方形的每条边应 有3个小正方形。 一种剪切方式如下图:
拼成的正方形如下图所示
例题4:请将下图沿格线分成大小相等、形状相同的四块, 并拼成一个正方形。
总结:对于这种复杂的图形分割,要先计算出理论上的最大值,然后去尝试。
图形剪拼分割

教师: 王喜才 学生: 时间: 年 月 日 段 一、 授课目的与考点分析:图形剪拼分割二、授课内容:【例1】已知两个连体的正方形(有两条边在同一条直线上)在正方形网格上的位置如图所示,请你把它分割后,拼接成一个新...的.正方形....要求:在正方形网格图中用实线画出拼接成的新正方形且新正方形的顶点在网格的格点上,不写作法).分析:利用图形分割中面积不变性,先求出剪拼后的图形 所需关键线段的长度,再从剪拼前图形中找这些长度裁剪。
【例2】在ABC △中,BC a =,BC 边上的高2h a =,沿图中线段DE 、CF 将ABC △剪开,分成的三块图形恰能拼成正方形CFHG ,如图1所示.图1③②①HGF E DC BA图2C′B′A′图2C′B′A′请你解决如下问题:在A B C '''△中,B C a ''=,B C ''边上的高12h a =.请你设计两种不同的分割方法,将A B C '''△沿分割线剪开后,所得的三块图形恰能拼成一个正方形,请在图2、图3中,画出分割线及拼接后的图形.分析:正方形四个角都是直角,四边相等,剪拼时要充分利用线段的中点和垂直关系。
【例3】已知:如图,△ABC 中, AC <AB <BC .(1)在B C 边上确定点P 的位置,使∠A P C =∠C .请画 出图形,不写画法;(2)在图中画出一条直线l ,使得直线l 分别与AB 、BC 边 交于点M 、N ,并且沿直线l 将△A B C 剪开后可拼成 一个等腰梯形.请画出直线l 及拼接后的等腰梯形,并 简要说明你的剪拼方法.说明:本题只需保留作图痕迹,无需尺规作图.要剪拼成等腰梯形,首先要找到相等的角。
:大兴22. 如图8-1、9-1,现将二张形状、大小完全相同的平行四边形透明纸片,分别放在方格纸中,方格纸中的每个小正方形的边长均为1,并且平行四边形纸片的每个顶点与小正方形的顶点重合.分别在图8-1、图9-1中,经过平行四边形纸片的任意一个顶点画一条裁剪线,沿此裁剪线将平行四边形纸片裁成两部分,按所采裁图形的实际大小,在图8-2中拼成正方形,在图9-2中拼成一个角是︒135的三角形.要求:(1)裁成的两部分在拼成几何图形时要互不重叠且不留空隙; (2)所拼出的几何图形的各顶点必须与小正方形的顶点重合.石景山22.(1)如图1,把边长是3的等边三角形的各边三等分,分别以居中那条线段为一边向外作等边三角形,并去掉居中的那条线段,得到图2,再把图2中图形各边三等分,分别以居中那条线段为一边向外作等边三角形,并去掉居中的那条线段,得到一个新图形,则这个新图形的周长是 ;(2)如图3,在55⨯的网格中有一个正方形,把正方形的各边三等分,分别以居中那条线段为斜边向外作等腰直角三角形,去掉居中的那条线段,得到图4,请把图4中的图形剪拼成正方形,并在图4中画出剪裁线,在图5中画出剪拼后的正方形. 房山22.阅读下列材料:小明遇到一个问题:如图1,正方形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 和DA 边上靠近A 、B 、C 、D 的n 等分点,连结AF 、BG 、CH 、DE ,形成四边形MNPQ .求四边形MNPQ 与正方形ABCD 的面积比(用含n 的代数式表示).小明的做法是:先取n=2,如图2,将△ABN 绕点B 顺时针旋转90゜至△CBN ′,再将△ADM 绕点D 逆时针旋转90゜至△CDM ′,得到5个小正方形,所以四边形MNPQ 与正方形ABCD 的面积比是15; 然后取n=3,如图3,将△ABN 绕点B 顺时针旋转90゜至△CBN ′,再将△ADM 绕点D 逆时针旋转90゜至△CDM ′,得到10个小正方形,所以四边形MNPQ 与正方形ABCD 的面积比是410,即25;……请你参考小明的做法,解决下列问题:(1)在图4中探究n=4时四边形MNPQ 与正方形ABCD 的面积比(在图4上画图并直接写出结果);(2)图5是矩形纸片剪去一个小矩形后的示意图,请你将它剪成三块后再拼成正方形(在图5中画出并指图1 图2图3 图4 图5明拼接后的正方形).丰台22.在图1中,正方形ABCD 的边长为a,等腰直角三角形FAE 的斜边AE =2b ,且边AD 和AE 在同一直线上.操作示例当2b <a 时,如图1,在BA 上选取点G ,使BG=b ,连结FG 和CG ,裁掉△F AG 和△CGB并分别拼接到△FEH 和△CHD 的位置构成四边形FGCH .思考发现:小明在操作后发现:该剪拼方法就是先将△F AG 绕点F 逆时针旋转90°到△FEH 的位置,易知EH 与AD 在同一直线上.连结CH ,由剪拼方法可得DH =BG ,故△CHD ≌△CGB,从而又可将△CGB 绕点C 顺时针旋转90°到△CHD 的位置.这样,对于剪拼得到的四边形FGCH (如图1),过点F作FM ⊥AE 于点M (图略),利用SAS 公理可判断△HFM ≌△CHD ,易得FH =HC =GC =FG ,∠FHC =90°.进而根据正方形的判定方法,可以判断出四边形FGCH 是正方形.实践探究(1)正方形FGCH 的面积是 ;(用含a ,b 的式子表示)(2)类比图1的剪拼方法,请你就图2—图4的三种情形分别画出剪拼成一个新正方形的示意图.联想拓展小明通过探究后发现:当b ≤a 时,此类图形都能剪拼成正方形,且所选取的点G的位置在BA 方向上随着b 的增大不断上移.当b >a 时(如图5),能否剪拼成一个正方形?若能,请你在图5中画出剪拼成的正方形的示意图;若不能,简要说明理由.M’E B A Q P NG H F E D C B A M M’A B E H C P G D Q H M N F B E A图 图1 图3 图4图5 图3E图 4图22b =a a <2b <2ab =a 图12b <a①②③怀柔22.直角三角形通过剪切可以拼成一个与该直角三角形面积相等的矩形,方法如下: 请你用上面图示的方法,解答下列问题:(1)对任意三角形,设计一种方案,将它分成若干块,再拼成一个与原三角形面积相等的矩形; (2)对任意四边形,设计一种方案,将它分成若干块,再拼成一个与原四边形面积相等的矩形.朝阳:在下面所给的图形中,若连接BC ,则四边形ABCD 是矩形,四边形CBEF 是平行四边形. (1)请你在图1中画出两条线段,将整个图形分为两部分,使这两部分面积相等(不写画法);(2)请你在图2中画出一条线段,将整个图形分为两部分,使这两部分面积相等.简要说明你的画法.昌平22.阅读下列材料:将图1的平行四边形用一定方法可分割成面积相等的八个四边形...,如图2,再将图2中的八个四边形适当组合拼成两个面积相等且不全等的平行四边形.(要求:无缝隙且不重叠) 请你参考以上做法解决以下问题:(1)将图4的平行四边形分割成面积相等的八个三角形...; (2)将图5的平行四边形用不同于(1)的分割方案,分割成面积相等的八个三角形...,再将这八个三角形适当组合拼成两个面积相等且不全等的平行四边形,类比图2,图3,用数字1至8标明.图1图24图3653126877584321门头沟22.如图1,方格纸中有一透明等腰三角形纸片,按图中裁剪线将这个纸片裁剪成三部分.请你将这三部分小纸片重新分别拼接成(1)一个等腰梯形;(2)一个正方形.请在图2和图3中分别画出拼接后的这两个图形,要求每张三角形纸片的顶点与小方格顶点重合.图1 图2 图3 密云22.阅读下列材料:在学习小组,小明接到这样一个任务:把一个正方形分割成9个、10个和11个小正方形.为完成任务,小明先学习了两种简单的“基本分割法”.基本分割法1:如图①,把一个正方形分割成4个小正方形,即在原来1个正方形的基础上增加了3个正方形. 基本分割法2:如图②,把一个正方形分割成6个小正方形,即在原来1个正方形的基础上增加了5个正方形.学习了上述两种“基本分割法”后,小明很从容的就完成了分割的任务: (1)把一个正方形分割成9个小正方形.方法一:如图③,把图①中的任意1个小正方形按“基本分割法2”进行分割,就可增加5个小正方形,从而分割成459+=(个)小正方形.方法二:如图④,把图②中的任意1个小正方形按“基本分割法1”进行分割,就可增加3个小正方形,从而分割成639+=(个)小正方形.(2)把一个正方形分割成10个小正方形.如图⑤,把图①中的任意2个小正方形按“基本分割法1”进行分割,就可增加32⨯个小正方形,从而分割成43210+⨯=(个)小正方形.请你参照上述分割方法解决下列问题(只要求画图,不用说明分割方法):(1)请你替小明同学把图⑥给出的正方形分割成11个小正方形; (2)仿照基本分割法1:请把图a 中的正三角形分割成4个小正三角形; (3)仿照基本分割法2:请把图b 中的正三角形分割成6个小正三角形; (4)分别把图c 和图d 中的正三角形分割成9个和10个小正三角形.图① 图② 图③ 图④ 图⑤ 图⑥ABC DEOA B CDA B CDABCABC西城22. 如图,在△ABC 中,∠B =∠C =30°.请你设计两种不同的分法,将△ABC 分割成四个小三角形,使得其中两个是全等..三角形,而另外两个是相似..但不全等...的直角三角形.请画出分割线段,并在两个全等三角形中标出一对相等的内角的度数(画图工具不限,不要求证明,不要求写出画法).东城22.请阅读下面材料,完成下列问题:(1)如图1,在⊙O 中,AB 是直径,CD AB ⊥于点E ,AE a =,EB b =.计算CE 的长度(用a 、b 的代数式表示);(2)如图2,请你在边长分别为a 、b (a b >)的矩形ABCD 的边AD 上找一点M ,使得线段CM =,保留作图痕迹;(3)请你利用(2)的结论,在图3中对矩形ABCD 进行拆分并拼接为一个与其面积相等的正方形.要求:画出拼成的正方形,并用相同的数字表明拼接前与拼接后的同一图形.(第22题图1) (第22题图2) (第22题图3)丰台22.认真阅读下列问题,并加以解决:问题1:如图1,△ABC 是直角三角形,∠C =90º.现将△ABC 补成一个矩形.要求:使△ABC 的两个顶点成为矩形一边的两个端点,第三个顶点落在矩形这一边的对边上.请将符合条件的所有矩形在图1中画出来;图1 图2问题2:如图2,△ABC 是锐角三角形,且满足BC >AC >AB ,按问题1中的要求把它补成矩形.请问符合要求的矩形最多可以画出 个,并猜想它们面积之间的数量关系是 (填写“相等”或“不相等”);问题3:如果△ABC 是钝角三角形,且三边仍然满足BC >AC >AB ,现将它补成矩形.要求:△ABC 有两个顶点成为矩形的两个顶点,第三个顶点落在矩形的一边上,那么这几个矩形面积之间的数量关系是 (填写“相等”或“不相等”). 房山22.(本小题满分5分)小明想把一个三角形拼接成面积与它相等的矩形.他先进行了如下部分操作,如图1所示:ADE第22题图1A ADCB A①取△ABC 的边AB 、AC 的中点D 、E ,联结DE ; ②过点A 作AF ⊥DE 于点F ;(1)请你帮小明完成图1的操作,把△ABC 拼接成面积与它相等的矩形.(2)若把一个三角形通过类似的操作拼接成一个与原三角形面积相等的正方形,那么原三角形的一边与这边上的高之间的数量关系是________________.(3)在下面所给的网格中画出符合(2)中条件的三角形,并将其拼接成面积与它相等的正方形.平谷22.一种电讯信号转发装置的发射直径为31km .现要求:在一边长为30km 的正方形城区选择若干个安装点,每个点安装一个这种转发装置,使这些装置转发的信号能完全覆盖这个城市.问:(1)能否找到这样的4个安装点,使得这些点安装了这种转发装置后能达到预设的要求?在图1中画出安装点的示意图,并用大写字母M 、N 、P 、Q 表示安装点;(2)能否找到这样的3个安装点,使得在这些点安装了这种转发装置后能达到预设的要求?在图2中画出示意图说明,并用大写字母M 、N 、P 表示安装点,用计算、推理和文字来说明你的理由.(2.)中的结论....求△ABC 的面积.延庆22.阅读下列材料:根据所给的图形解答下列问题:(1)如图1,ABC ∆中,AC AB =,90=∠BAC ,D BC AD 于⊥,把ABD ∆绕点A 旋转,并拼 接成一个正方形,请你在图1中完成这个作图;(2)如图2,ABC ∆中,AC AB =,90=∠BAC ,请你设计一种与(1)不同方法,将这个三角形拆分并拼接成一个与其面积相等的正方形,画出利用这个三角形得到的正方形;(3)设计一种方法把图3中的矩形ABCD 拆分并拼接为一个与其面积相等的正方形,请你依据此矩形画出正方形.图1 C D 图2 C D朝阳22.阅读并操作:如图①,这是由十个边长为1的小正方形组成的一个图形,对这个图形进行适当分割(如图②),然后拼接成新的图形(如图③).拼接时不重叠、无空隙,并且拼接后新图形的顶点在所给正方形网格图中的格点上(网格图中每个小正方形边长都为1).图①图②图③请你参照上述操作过程,将由图①所得到的符合要求的新图形画在下边的正方形网格图中.(1)新图形为平行四边形;(2)新图形为等腰梯形.顺义22.如图,将正方形沿图中虚线(其x y)剪成①②③④四块图形,用这四块图形恰好能拼成一个矩形(非正方形).(1)画出拼成的矩形的简图;(2)求xy的值.东城22. 如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形.现将宽为15cm 的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.在图3中,将三棱柱沿过点A的侧棱剪开,得到如图4的侧面展开图.为了得到裁剪的角度,我们可以根据展开图拼接出符合条件的平行四边形进行研究.(1)请在图4中画出拼接后符合条件的平行四边形;(2)请在图2中,计算裁剪的角度(即∠ABM的度数).yyxyxy xx④③②①图4F ED C BA顺义22.请阅读下列材料:问题:现有5个边长为1的正方形,排列形式如图1,请把它们分割后拼接成一个新的正方形.要求:画出分割线并在正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.小东同学的做法是:设新正方形的边长为x (x >0). 依题意,割补前后图形面积相等, 有52=x , 解得5=x .由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长.于是,画出如图2所示的分割线,拼出如图3所示的新正方形.请你参考小东同学的做法,解决如下问题:(1) 如图4,是由边长为1的5个小正方形组成,请你通过分割,把它拼成一个正方形(在图4上画出分割线,在图4的右侧画出拼成的正方形简图);(2)如图5,是由边长分别为a 和b 的两个正方形组成,请你通过分割,把它拼成一个正方形(在图5上画出分割线,在图5的右侧画出拼成的正方形简图).西城22.如图1,若将△AOB 绕点O 逆时针旋转180°得到△COD ,则△AOB ≌△COD .此时,我们称△AOB与△COD 为“8字全等型”.借助“8字全等型”我们可以解决一些图形的分割与拼接问题.例如:图2中,图3图2图1图3图2图1-----您值 龙文 学校 ----- 您值 得信赖的 专业化个性辅 导学校 △ABC 是锐角三角形且 AC>AB,点 E 为 AC 中点,F 为 BC 上一点且 BF≠FC(F 不与 B,C 重合) ,沿 EF 将其剪开,得到的两块图形恰能拼成一个梯形.请分别按下列要求用直线将图 2 中的△ABC 重新进行分割,画出分割线及拼接后的图形. (1)在图 3 中将△ABC 沿分割线剪开,使得到的两块图形恰能拼成一个平行四边形; (2) 在图 4 中将△ABC 沿分割线剪开,使得到的三块图形恰能拼成一个矩形,且其中的两块为直角三角形; (3)在图 5 中将△ABC 沿分割线剪开,使得到的三块图形恰能拼成一个矩形,且其中 的一块为钝角三角 形.门头沟 22.如图 1,有一张菱形纸片 ABCD,AC=8,BD=6. (1)若沿着 AC 剪开,把它分成两部分,把剪开 的两部分拼成一个平行四边形,请在图 2 中 用实线画出你所拼成的平行四边形,并直接 写出这个平行四边形的面积; (2)若沿着 BD 剪开,把它分成两部分,把剪开 的两部分拼成一个平行四边形,请在图 3 中 用实线画出你所拼成的平行四边形,并直接 写出这个平行四边形的周长; (3)沿着一条直线剪开,把它分成两部分,把剪开的两部分拼成与上述两种都不全等的平行四边形,请在 图 4 中用实线画出你所拼成的平行四边形. (注:上述所画的平行四边形都不能与原菱形全等) 上述所画的平行四边形都不能与原菱形全等)D CDCA 图1BDCDCA 图2 面面周BA 图3 周周周BA 图4B(本小题满分 5 分) 门头沟 22.媒体村龙文学校 84955492-----您值 龙文 学校 ----- 您值 得信赖的 专业化个性辅 导学校 如图所示,有两种形状不同的直角三角形纸片各两块,其中一种纸片的两条直角边长都为 3,另一种纸片的 两条直角边长分别为 1 和 3.图 1、图 2、图 3 是三张形状、大小完全相同的方格纸,方格纸中的每个小正 方形的边长均为 1. (1)请用三种方法(拼出的两个图形只要不全等就认为是不同的拼法)将图中所给四块直角三角形纸片拼成 平行四边形(非矩形) ,每种方法要把图中所给的四块直角三角形纸片全部用上,互不重叠且不留空隙, 并把你所拼得的图形按实际大小画在图 1、图 2、图 3 的方格纸上(要求:所画图形各顶点必须与方格 纸中的小正方形顶点重合;画图时,要保留四块直角三角形纸片的拼接痕迹) ; (2)三种方法所拼得的平行四边形的面积是否是定值?若是定值,请直接写出这个定值;若不是定值,请直 接写出三种方法所拼得的平行四边形的面积各是多少; (3)三种方法所拼得的平行四边形的周长是否是定值?若是定值,请直接写出这个定值;若不是定值,请直 接写出三种方法所拼得的平行四边形的周长各是多少.3 33 31 31 3 图1图2图3顺义 22. 现有 12 个边长为 1 的正方形,排列形式如图① ,请把它们分割后拼成面积为 12 的一个特殊三角形形 和一个三边都不相等的三角形(顶点在格点上) 。
三年级几何图形的剪拼学生版

图形的剪拼知识要点按照题目要求(形状和面积),根据图形与图形之间的内在联系,通过在纸上画图或者实际的剪拼,来掌握图形的变化,包括把一个几何图形分割成几个图形以及把几个几何图形拼成几个图形。
有兴趣的学生还可以自制“七巧板”或者“伤脑筋十二块”等中国传统益智拼板游戏,在闲暇时间尝试拼一下,说不定还能拼出自创的新颖有趣的图形。
找对称例1】把一个 3 3 的的网格分成形状、大小完全相同的四份。
例2】哥哥和弟弟一起做手工,想把一张红色的平行四边形蜡光纸沿着一条直线,把它剪成大小、形状完全相同的两部分。
想一想,你可以有多少种剪法?例3】要把一个正方形剪成形状相同、大小相等的 4 个图形,该怎样分?例 4】 你能把下面的图形分割成 4 个形状相同、大小相等的图形吗?例 6】 你能把一个正三角形分成形状相同,大小相等的 2个、 3个、 4个、 6个、 9 个三角形吗?例 7】 你能把一个正方形分成 6 个、 7 个、 8 个、 9 个小正方形吗? ( 不要求面积相等 )例 8】 你能把下面的图形分割成 4个形状相同、大小相等的图形吗?例 5】 一个长 6 厘米,宽 4 厘米的长方形,从中间剪开,如图所示,得到 形,这两个新长方形的周长是多少?2个大小、形状都相同的长方分成例9】把下图分成 5 个形状相同、大小相等的图形。
例13】阿凡提周游世界,有一天来到一个村庄。
一个地主对他说:“都传说你很聪明,我有一块地,你能把它分成大小相等、形状相同的 2 份,我就把地送给你。
”聪明的阿凡提不慌不忙,用木棍画了一道线,把这块地分成大小相等、形状相同的 2 份。
地主傻了眼,只好履行诺言。
后来,阿凡提把地分给了最穷的 2 户人家,你知道阿凡提是怎么分的吗?33例 14】 用 下面的四块图形能拼成右边的正方形吗?怎样拼?1例 15】晚饭后,平平和妈妈玩拼木板游戏。
妈妈拿出 15块木板 (如下图 ),1要求平平把这 5 块1木板拼成一个正方形。
89-29 图形的剪拼

29 图形的剪拼阅读思考把一张纸经过数次折叠后, 用剪刀剪去其中一部分, 往往能得到美丽的图案·把一个图形通过分割后再重新拼接, 常常能得到一个新的图形.图形的剪拼, 是学习平面几何过程中重要一环, 通过对图形的剪拼, 我们可以发现一些几何结论并知晓这些结论是怎样被证明的.解图形的剪拼问题, 可借助现成材料, 动手操作, 观察思考, 得出结论. 但由于考场条件和环境的限制, 我们常需要运用对称、全等, 利用不变量等知识方法解决相关问题.问题解决例l现有一张长5cm、宽1cm的矩形纸, 请你将它分成5块, 再拼合成一个正方形画在横线上_________·试一试先求出拼合成的正方形的边长, 将计算与剪拼相结合.例2如图, 把一个正方形三次对折后沿虚线剪下, 则得到的图形是( ).试一试把原题中折剪的过程倒过来, 再利用对称知识, 可得到展开过程.例3正方形通过剪切可以拼成三角形, 方法如下:仿上用图示的方法, 解答下列问题:(1)如图(2), 对直角三角形, 设计一种方案, 将它分成若干块, 再拼成一个与原三角形等面积的矩形.(2)如图(3), 对任意三角形, 设计一种方案, 将它分成若干块, 再拼成一个与原三角形等面积的矩形.(安徽省中考题) 试一试题目要求拼成矩形, 而矩形四个角都是直角及对边相等, 故在设计剪拼方案时, 应充分利甩线段的中点及垂直关系, 图中已有的要充分利用, 图中没有的要先作出.例4 如图, 是从边长为40cm、宽为30cm的矩形钢板的左上角截取一块长为20cm、宽为10cm的矩形后, 剩下的一块下脚料. 工人师傅要将它作适当地切割, 重新拼接后焊成一个面积与原下脚料的面积相等, 接缝尽可能短的正方形工件.(1)请根据上述要求, 设计出将这块下脚料适当分割成三块或三块以上的两种不同的拼接方案(在图2和图3中分别画出切割时所沿的虚线,以及拼接后所得到的正方形, 保留拼接的痕迹);(2)比较(1)中的两种方案, 哪种更好一些?说说你的看法和理由.(山东省中考题)试一试 拼接后正方形的边长为221030 cm, 它恰是以30cm 和10cm 为直角边的直角三角形的斜边的长, 为此可考虑设法在原钢板上构造两直角边长分别为30cm 和10cm 的直角三角形, 这是解本例韵关键.例5 如图, 现有两个边长之比为1:2的正方形ABCD 与A ’B ’C ’D ’. 已知点B 、C 、B ’、C ’在同一直线上, 且点C 与点B ’重合, 请你利用这两个正方形, 通过截割、平移、旋转的方法, 拼出两个相似比为l:3的三角形.(山东省烟台市中考题)试一试设小正方形的边长为1, 则大正方形的边长为2, 两者的面积之和为12+22=5. 从面积入手, 利用图形分割中面积的不变性, 结合相似三角形性质确定小三角形面积, 这是解本例的关键.数学冲浪1. 将一个无盖正方体纸盒展开(如图①), 沿虚线剪开, 用得到的5张纸片(其中4张是全等的直角三角形纸片)拼成一个正方形(如图②). 则所剪得的直角三角形较短的与较长的直角边的比是___________.2. 要拼出和图①中的菱形相似的较长对角线为88cm 的大菱形(如图②所示), 需要图①中的菱形的个数为__________.3. 如图, 已知四边形纸片ABCD, 现需将该纸片剪拼成一个与它面积相等的平行四边形纸片. 如果限定裁剪线最多有两条, 能否做到:__________(用“能”或“不能”填空). 若填“能”, 请确定裁剪线的位置, 并说明拼接方法;若填“不能”, 请简要说明理由.(2006年天津市中考题)4. [尝试]如图①, 把一个等腰直角△ABC 沿斜边上的中线(裁剪线)剪一刀, 把分割成的两部分拼成一个四边形A ’BCD, 如图②(以下有画图要求的, 工具不限, 不必写画法和证明).(1)猜一猜:四边形A ’BCD 一定是___________;(2)试一试:按上述的裁剪方法, 请你拼一个与图①不同的四边形, 并在图②中画出示意图.[探究]在等腰Rt△ABC中, 请你沿一条中位线(裁剪线)剪一刀, 把分割成的两部分拼成一个特殊四边形.(1)想一想:你能拼得的特殊四边形分别是___________(写出两种);(2)画一画:请分别在图④、图⑤中画出你拼得的这两个特殊四边形的示意图.[拓广]在等腰Rt△ABC中, 请你沿一条与中线、中位线不同的裁剪线剪一刀, 把分割成的两部分拼成一个特殊四边形.(1)变一变:你确定的裁剪线是_______(写出一种), 拼得的特殊四边形是________;(2)拼一拼:请在图⑥中画出你拼得的这个特殊四边形的示意图.(2006年荆门市中考题) 5. 如图(1), 小强拿一张正方形的纸, 沿虚线对折一次得到图(2), 再对折一次得到图(3), 然后用剪刀沿图(3)中的虚线剪去一个角, 再打开后的形状为( ).6. 如图, 一张长方形纸沿AB对折, 以AB中点O为顶点将平角五等分, 并沿五等分的折线折叠, 再沿CD剪开, 使展开后为正五角星(正五边形对角线所构成的图形), 则∠OCD的值为( ).A. 108○B. 144○C. 126○D. 129○(浙江省绍兴市中考题) 7. 如图①是用硬纸板做成的两个全等的直角三角形, 两直角边的长分别为a和b, 斜边长为c. 图②是以c为直角边的等腰直角三角形. 请你开动脑筋, 将它们拼成一个能证明勾股定理的图形.(1)画出拼成的这个图形的示意图, 写出它是什么图形;(2)用这个图形证明勾股定理;(3)假设图①中的直角三角形有若干个, 你能运用图①中所给的直角三角形拼出另一种能证明勾股定理的图形吗?请画出拼后的示意图(无需证明).(济南市中考题) 8. 请阅读下列材料:问题:现有5个边长为1的正方形, 排列形式如图①, 请把它们分割后拼接成一个新的正方形. 要求:画出分割线并在正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.小东同学的做法是:设新正方形的边长为x(x>0). 依题意, 割补前后图形的面积相等,有x2=5, 解得x=5. 由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长. 于是, 画出如图②所示的分割线, 拼出如图③所示的新正方形.请你参考小东同学的做法, 解决如下问题:现有10个边长为1的正方形, 排列形式如图④, 请把它们分割后拼接成一个新的正方形. 要求:在图④中画出分割线, 并在图⑤的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形(说明:直接画出图形不要求分析过程. ).9. 操作示例:对于边长均为以的两个正方形ABCD和EFGH, 按图①所示的方式摆放, 再沿虚线BD, EG 剪开瑶, 可以按图中所示的移动方式拼接为图①中的四边形BNED.从拼接的过程容易得到结论:①四边形BNED是正方形;②S正方形ABCD+S正方形EFGH=S正方形BNED.实践与探究:(1)对于边长分别为a, b(a>b)的两个正方形ABCD和EFGH, 按图所示的方式摆放, 连结DE, 过点D作DM⊥DE, 交AB于点M, 过点M作MN⊥DM, 过点E作EN⊥DE, MN与EN相交于点N.①证明四边形MNED是正方形, 并用含a, b的代数式表示正方形MNED的面积;②在图②中, 将正方形ABCD和正方形EFGH沿虚线剪开后, 能够拼接为正方形MNED. 请简略说明你的拼接方法(类比图①, 用数字表示对应的图形).(2)对于n(n是大于2的自然数)个任意的正方形, 能否通过若干次拼接, 将其拼接为一个正方形?请简要说明你的理由.(2005年河北省中考题) 10. 如果有四个多边形A、B、C、D如图所示, 你能否使A拼上B后与C拼上D的轮廓相同;同时还能使A拼上C后与B拼上D后的轮廓也相同;甚至使A拼上D后与B拼上C 后的轮廓也相同吗?(俄罗斯萨温数学竞赛题)。
几何图形剪拼

1.如图,把下图沿格线剪成四个形状、大小都相同的图形,那么剪成的每个图形应该有几个格?
来源:2015·乐乐课堂·练习
难度:简单
类型:填空题
A. (红色)B. (绿色)C. (蓝色)
来源:2015·乐乐课堂·练习
难度:简单
类型:选择题
答案:C
30.如图,将下图分割成形状、大小都相同的四块,使得每一块中都有A、B、C、D各一个.图中已经给出了一条黑色的分割线,那么这条线绕中心旋转不可能得到下面的哪条线?
A. (红色)B. (绿色)C. (蓝色)
A. B. C.
来源:2015·乐乐课堂·练习
难度:简单
类型:选择题
答案:A
44.将下图沿格线剪成两块,再拼成一个正方形,下面哪种分法是正确的?(红线表示分割线)
A. B. C.
来源:2015·乐乐课堂·练习
难度:简单
类型:选择题
答案:C
45.将下图沿格线剪成两块,再拼成一个正方形,下面哪种分法是正确的?(红线表示分割线)
A. B. C.
来源:2015·乐乐课堂·练习
难度:中等
类型:选择题
答案:C
首页上一页12345下一页尾页
A. (红色)B. (紫色)C. (绿色)D. (蓝色)
来源:2015·乐乐课堂·练习
难度:简单
类型:选择题
答案:C
26.如图,将下图分割成形状、大小都相同的四块,使得每一块中都有A、B、C、D各一个.那么以下哪条分割线不是最终分割线的一部分?
初中数学精品教案: 图形拼剪问题
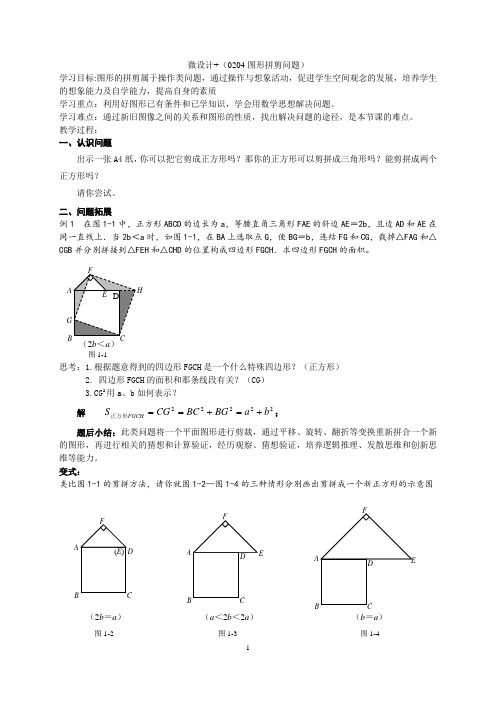
1图1-1 (2b <a )微设计+(0204图形拼剪问题)学习目标:图形的拼剪属于操作类问题,通过操作与想象活动,促进学生空间观念的发展,培养学生的想象能力及自学能力,提高自身的素质学习重点:利用好图形已有条件和已学知识,学会用数学思想解决问题。
学习难点:通过新旧图像之间的关系和图形的性质,找出解决问题的途径,是本节课的难点。
教学过程:一、认识问题出示一张A4纸,你可以把它剪成正方形吗?那你的正方形可以剪拼成三角形吗?能剪拼成两个正方形吗?请你尝试。
二、问题拓展例1 在图1-1中,正方形ABCD 的边长为a ,等腰直角三角形FAE 的斜边AE =2b ,且边AD 和AE 在同一直线上.当2b <a 时,如图1-1,在BA 上选取点G ,使BG =b ,连结FG 和CG ,裁掉△FAG 和△CGB 并分别拼接到△FEH 和△CHD 的位置构成四边形FGCH .求四边形FGCH 的面积。
思考:1.根据题意得到的四边形FGCH 是一个什么特殊四边形?(正方形)2. 四边形FGCH 的面积和那条线段有关?(CG )3.CG 2用a 、b 如何表示?解 22222b a BG BC CG S FGCH +=+==正方形;题后小结:此类问题将一个平面图形进行剪裁,通过平移、旋转、翻折等变换重新拼合一个新的图形,再进行相关的猜想和计算验证,经历观察、猜想验证,培养逻辑推理、发散思维和创新思维等能力。
变式:类比图1-1的剪拼方法,请你就图1-2—图1-4的三种情形分别画出剪拼成一个新正方形的示意图图1-3图1-4图1-2(2b =a ) (a <2b <2a ) (b =a )2思考:1.如何确定点G 的位置?2.如何确定点H 的位置?3. 如何确定新正方形的边长?解 如图所示题后小结:考查了学生利用类比的数学思想解决问题的能力,开始就提供了解题的关键——构造直角三角形,确定了新正方形的边长(CG ),只有发现了这一点,才能顺利解决。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
巩固练习 1、如图,请把图形沿格线分割成形状、大小都相同的四个 部分,并在图中标出分割线。(如果两个图形通过旋转或翻 转后重合,就认为它们的形状、大小是相同的)
2、如图,请把右图沿格线分成形状、大小都相同的五部分, 使得每部分都恰好含有一个“○”。
3、如图,从一张边长为 10 厘米的正方形纸片中,最多能裁 出多少个长 4 厘米、宽 2 厘米的长方形纸条?请画图说明剪 裁方法。
例题3:从一张边长为7厘米的正方形纸片中, 最多能裁出多 少个长4厘米、宽1厘米的长方形纸条?请画图说明剪裁方法。
练习3:从一张长10厘米、宽8厘米的长方形纸片中,最多能 裁出多少个长5厘米、宽3厘米的长方形纸条?请画图说明剪 裁方法。
例题4:将下图分割成大小、形状都相同的四部分, 使得每 一部分中都有A、 B、 C、 D各一个。
4、如图,将下面的图形分割成形状、大小都相同的四块, 使得每一块中都有一个黑色圆圈和一个白色圆圈。
5、如图,将左图分割成四部分, 拼成如右图的长方形。请 在左图中画出分割线, 在右图中画出拼接。
练习1:请在图中标出分割线,把图形沿格线分割成形状、 大小都相同的四个部分.(如果两个图形通过旋转或翻转后 重合,就认为它们的形状、大小是相同的)
例题2:下图是由五个相同大小的小正方形拼成的.请把图 形分别剪成四个形状、 大小都相同的图形.
练习2:下图是由一个正方形和一个等腰直角三角形拼成的 图形. 请把这个图形剪成四个形 状、大小都相同的图形.
第三讲 几何图形剪拼
知识精讲 几何图形剪拼主要包括图形的分割与拼接两方面。
无论是分割还是拼接,图形的面积都是保持不变的,既 不能凭空多出一块,也不能有任何一块无故消失。本讲 主要考察对于图形的直观感觉与判断,所以大家要勤于 动手,勇于实践,擅于总结规律,这才是解决图形剪拼 问题的法宝。
例题1:请在图中标出分割线,把图形沿格线分割成形状、 大小都相同的四个部分.(如果两个图形通过旋转或翻转后 重合,就认为它们的形状、大小是相同的.)
练习4:将下面的图形分割成形状、大小都相同的四部分, 使得每一块中都有A、B、C、 D各一个.
例题5:将左图分割成三部分,拼成右图的正方形.请在左 图中画出分割线,在右图中画出拼接线.
例题6:左图是一块25×49 (单位:厘米)的长方形纸片。 现在要沿虚线将它分割成三部分,再拼成右图所示的边长为 35厘米的正方形纸片.请在左图中画出分割线,在右图中画 出拼接线.在这里,虚线划分成的小长方形的大小均为5×7 (单位:厘米)
