(完整版)解二元一次方程组基础练习

合集下载

二元一次方程练习题及答案

二元一次方程练习题及答案一、二元一次方程的概念和解法二元一次方程是代数学中的基础内容，它由两个未知数和一个或多个含有这两个未知数的一次方程组成。

在解二元一次方程时，我们需要找到一个满足方程的有序数对，使得方程两边的值相等。

二、二元一次方程练习题1. 问题：解下列方程组：(1) 2x + y = 5x - y = 1(2) 3x - y = 72x + y = 12. 问题：求下列方程的解：(1) 3x + 2y = 102x - y = 4(2) 5x - 3y = 74x + 6y = 163. 问题：解方程组：(1) 2x + 3y = 13x - 2y = -5(2) 4x - 5y = 63x + 2y = 144. 问题：求下列方程的解：(1) 3x + 4y = 9x - 2y = -2(2) 2x - 5y = 1x + y = 3三、二元一次方程的解答1. 解答：(1) 解：将第二个方程中的x表示为y的函数：x = y + 1代入第一个方程中得：2(y+1) + y = 5，化简得：3y + 2 = 5解得：y = 1将y = 1代入x = y + 1得：x = 2所以方程组的解为：x = 2, y = 1(2) 解：将两个方程相加得：5x = 8，解得：x = 8/5将x代入第一个方程得：y = 3 - 2x = 3 - 2(8/5) = 3 - 16/5 = -1/5所以方程组的解为：x = 8/5， y = -1/52. 解答：(1) 解：将第二个方程中的x表示为y的函数：x = (4 + y)/2代入第一个方程中得：3((4 + y)/2) + 2y = 10，化简得：3y + 8 = 10解得：y = 2将y = 2代入x = (4 + y)/2得：x = (4 + 2)/2 = 3所以方程组的解为：x = 3, y = 2(2) 解：将第一个方程乘以2，得到2(5x - 3y) = 2(7)，化简得：10x - 6y = 14将第二个方程乘以3，得到3(4x + 6y) = 3(16)，化简得：12x + 18y = 48将两个方程相加得：22x = 62，解得：x = 62/22 = 31/11将x代入第一个方程得：5(31/11) - 3y = 7，化简得：155/11 - 3y = 7解得：y = (155 - 77)/33 = 78/33 = 26/11所以方程组的解为：x = 31/11， y = 26/11(1) 解：将第二个方程中的x表示为y的函数：x = (6 + 5y)/4代入第一个方程中得：2((6 + 5y)/4) + 3y = 13，化简得：3y + 3 = 13解得：y = 10/3将y = 10/3代入x = (6 + 5y)/4得：x = (6 + 5(10/3))/4 = (6 +50/3)/4 = 56/12 = 14/3所以方程组的解为：x = 14/3， y = 10/3(2) 解：将第一个方程乘以2，得到2(4x - 5y) = 2(6)，化简得：8x - 10y = 12将第二个方程乘以5，得到5(3x + 2y) = 5(14)，化简得：15x + 10y = 70将两个方程相加得：23x = 82，解得：x = 82/23将x代入第一个方程得：4(82/23) - 5y = 6，化简得：328/23 - 5y = 6解得：y = (328 - 138)/115 = 190/115 = 38/23所以方程组的解为：x = 82/23， y = 38/23(1) 解：将第二个方程中的x表示为y的函数：x = 5 - 2y代入第一个方程中得：3(5 - 2y) + 4y = 9，化简得：15 - 6y + 4y = 9解得：y = 6将y = 6代入x = 5 - 2y得：x = 5 - 2(6) = -7所以方程组的解为：x = -7, y = 6(2) 解：将第二个方程中的x表示为y的函数：x = 1 - y代入第一个方程中得：2(1 - y) - 5y = 1，化简得：2 - 2y - 5y = 1解得：y = -2将y = -2代入x = 1 - y得：x = 1 - (-2) = 3所以方程组的解为：x = 3, y = -2四、总结通过以上的习题练习，我们学习了解二元一次方程的方法。

二元一次方程组解法练习题精选(含答案)

二元一次方程组解法练习题精选（含答案）一．解答题（共16小题）1．求适合的x，y的值．2．解下列方程组（1）（2）（3）（4）．3．解方程组：4．解方程组：5．解方程组：6．已知关于x，y的二元一次方程y=kx+b的解有和．（1）求k，b的值．（2）当x=2时，y的值．（3）当x为何值时，y=3？7．解方程组：（1）；（2）．8．解方程组：9．解方程组：10．解下列方程组：（1）（2）11．解方程组：（1）（2）12．解二元一次方程组：（1）；（2）．13．在解方程组时，由于粗心，甲看错了方程组中的a，而得解为，乙看错了方程组中的b，而得解为．（1）甲把a看成了什么，乙把b看成了什么？（2）求出原方程组的正确解．14．15．解下列方程组：（1）；（2）．16．解下列方程组：（1）（2）第二十六章《二次函数》检测试题1，（2008年芜湖市）函数2y ax b y ax bx c =+=++和在同一直角坐标系内的图象大致是（）2，在一定条件下，若物体运动的路程s （米）与时间t （秒）的关系式为s ＝5t 2+2t ，则当t ＝4时，该物体所经过的路程为（）3，已知二次函数y ＝ax 2+bx +c (a ≠0)的图象如图2所示，给出以下结论：① a +b +c ＜0；② a －b +c ＜0；③ b +2a ＜0；④ abc ＞0 .其中所有正确结论的序号是（）A. ③④B. ②③C. ①④D. ①②③4，二次函数y ＝ax 2+bx +c 的图象如图3所示，若M ＝4a +2b +c ，N ＝a －b +c ，P ＝4a +2b ，则（）A.M ＞0，N ＞0，P ＞0B. M ＞0，N ＜0，P ＞0C. M ＜0，N ＞0，P ＞0D. M ＜0，N ＞0，P ＜05，如果反比例函数y ＝k x 的图象如图4所示，那么二次函数y ＝kx 2－k 2x －1的图象大致为（）6，用列表法画二次函数y ＝x 2+bx +c 的图象时先列一个表，当表中对自变量x 的值以相等间隔的值增加时，函数y 所对应的函数值依次为：20，56，110，182，274，380，506，650.其中有一个值不正确，这个不正确的值是( )A. 506B.380C.274D.18图3y x O 图4 y x O A ． y x O B ． y x O C ． y x O D ．图5 x -11yO 图2 图1A. y ＝x 2－2B. y ＝(x －2)2C. y ＝x 2+2D. y ＝(x +2)28如图6，小敏在今年的校运动会跳远比赛中跳出了满意一跳，函数h ＝3.5t －4.9t 2（t 的单位：s ，h 的单位：m ）可以描述他跳跃时重心高度的变化，则他起跳后到重心最高时所用的时间是（）A.0.71sB.0.70sC.0.63sD.0.36s9，如果将二次函数y ＝2x 2的图象沿y 轴向上平移1个单位，那么所得图象的函数解析式是 .10，平移抛物线y ＝x 2+2x －8，使它经过原点，写出平移后抛物线的一个解析式______ .11，若二次函数y ＝x 2－4x ＋c 的图象与x 轴没有交点，其中c 为整数，则c ＝12，二次函数y ＝ax 2+bx +c 的图像如图7所示，则点A (a ，b )在第＿＿＿象限.13，已知抛物线y ＝x 2－6x +5的部分图象如图8，则抛物线的对称轴为直线x ＝，满足y ＜0的x 的取值范围是 .14，已知一抛物线与x 轴的交点是)0,2( A 、B （1，0），且经过点C （2，8）。

（完整版）解二元一次方程组基础练习

（完整版）解二元一次方程组基础练习4x y 5 3x 2y 1知识点 (1) 解二元一次方程组基础练习肖老师一：代入消元法解方程组： y 2x 3 7x 5y 3 ((23x 2y 1 2x y 4(3)x y 2 3 3x 4y 18 x 5y 6 3x 6y 4 0知识点 (1) 二：用加减法解方程组:x y 3x y 14x 3y 0 12x 3y 8(3)4x 3y 5 4x 6y 145x 4y 6 2x 3y 1 3x 2y 7 2x 3y 17拓展训练: 解下列方程:(1)(先化简) 3(y 2) x 12(x 1) 5y 8(2)(化简后整体法)3x 4y 18(3)(整体法) 4x 15y 17 06x 25y 23 0(4)(先化简)13-23一2y-y 1 x 2(5)(化简后整体法)"7 丁2x 3y 1 (6)(整体法)21x 23y 24323x 21y 241综合训练：一.填空题 1. 在方程y __________________ 3x 2中若x 2,则y ____ 若y 2,则x；2. 若方程2x y 3写成用含x 的式子表示y 的形式: _______________________ 写成用含y 的式子表示x 的形式: _____________________________ ;x 23. 已知是方程2x+ay=5的解，贝U a= ______ .y 1x 14. 二元一次方程3x my 4和mx ny 3有一个公共解，则y 1(7)(先化简)2x 1 3y 2 243x 1 3y 2 门 054(8)(可化简或整体法)3x 2y 2x 3y i73x 2y 2x 3y 567(9)(你懂的)3K - 2y 5K 4-/(10)(先化简)気 _ y+1L0?2 "O T S(11)(先化简)f 廿产50018O%x+eoay= 500X 74^(12))整体法)宣■上号丄二4 (i-l)3x-2 (2y+l) ~im= 5.已知 |a b 2| (b 3)2 0,那么 ab 6.方程 3x+y=7 的正整数解为、选择题 1.对于方程组 xy3 x10,(2) x5 ,(4)y y r 是二元次方程组的为 A.（1）和（2） )B.(3)和(4)C.(1)和⑶D.(2)和⑷22是方程 5kx 2y 2的一个解，则k 等于（ A .85 B .53C.6D.3.方程组 3x 1 x 2 4y 1 y 31的解为（ 8x A. y x B.yC.丄2 3 8D.4.已知a,b 满足方程组 a 2a 2bb ，则ab 的值为（A.-1B.0 5.如果方程组C.1 xD.2 y 1by 有唯一的一组解，那么 a , b , C 的值应当满足（） A . a=1, C =1 B . a M b C . a=b=1 , C M 1D x m 4 6.已知 x , y 满足方程组，则无论m 取何值， x , y y 5 mA . x+y=1B . x+y= — 1C . x+y=9D . x+y=9ax .a=1, C M 1 恒有关系式是（） C、解答题x 3m 11、若，是方程组4x 3y 10的一组解，求m的值y 2m 22X_3Xy_的值.2.已知y=3xy+x，求代数式x 2xy y3、已知等式(2A —7B)x+(3A —8B)=8x+10,对一切实数x都成立，求A、B的值。

二元一次方程组解法练习题精选(含答案)

二元一次方程组解法练习题精选（含答案）之巴公井开创作一．解答题（共16小题）1．求适合的x，y的值．2．解下列方程组（1）（2）（3）（4）．3．解方程组：4．解方程组：5．解方程组：6．已知关于x，y的二元一次方程y=kx+b的解有和．（1）求k，b的值．（2）当x=2时，y的值．（3）当x为何值时，y=3？7．解方程组：（1）；（2）．8．解方程组：9．解方程组：10．解下列方程组：（1）（2）11．解方程组：（1）（2）12．解二元一次方程组：（1）；（2）．13．在解方程组时，由于粗心，甲看错了方程组中的a，而得解为，乙看错了方程组中的b，而得解为．（1）甲把a看成了什么，乙把b看成了什么？（2）求出原方程组的正确解．14．15．解下列方程组：（1）；（2）．16．解下列方程组：（1）（2）17.方程组2528x yx y+=⎧⎨-=⎩的解是否满足2x－y=8？满足2x－y=8的一对x，y的值是否是方程组2528x yx y+=⎧⎨-=⎩的解？二元一次方程组解法练习题精选（含答案）参考答案与试题解析一．解答题（共16小题）1．求适合的x，y的值．考点：解二元一次方程组．分析：先把两方程变形（去分母），得到一组新的方程，然后在用加减消元法消去未知数x，求出y的值，继而求出x的值．解答：解：由题意得：，由（1）×2得：3x﹣2y=2（3），由（2）×3得：6x+y=3（4），（3）×2得：6x﹣4y=4（5），（5）﹣（4）得：y=﹣，把y的值代入（3）得：x=，∴．点评：本题考查了二元一次方程组的解法，主要运用了加减消元法和代入法．2．解下列方程组（1）（2）（3）（4）．考点：解二元一次方程组．分析：（1）（2）用代入消元法或加减消元法均可；（3）（4）应先去分母、去括号化简方程组，再进一步采取适宜的方法求解．解答：解：（1）①﹣②得，﹣x=﹣2，解得x=2，把x=2代入①得，2+y=1，解得y=﹣1．故原方程组的解为．（2）①×3﹣②×2得，﹣13y=﹣39，解得，y=3，把y=3代入①得，2x﹣3×3=﹣5，解得x=2．故原方程组的解为．（3）原方程组可化为，①+②得，6x=36，x=6，①﹣②得，8y=﹣4，y=﹣．所以原方程组的解为．（4）原方程组可化为：，①×2+②得，x=，把x=代入②得，3×﹣4y=6，y=﹣．所以原方程组的解为．点利用消元法解方程组，要根据未知数的系数特点选择代入法还是加减法：评：①相同未知数的系数相同或互为相反数时，宜用加减法；②其中一个未知数的系数为1时，宜用代入法．3．解方程组：考点：解二元一次方程组．专题：计算题．分析：先化简方程组，再进一步根据方程组的特点选用相应的方法：用加减法．解答：解：原方程组可化为，①×4﹣②×3，得7x=42，解得x=6．把x=6代入①，得y=4．所以方程组的解为．点评：注意：二元一次方程组无论多复杂，解二元一次方程组的基本思想都是消元．消元的方法有代入法和加减法．4．解方程组：考点：解二元一次方程组．专题：计算题．分析：把原方程组化简后，观察形式，选用合适的解法，此题用加减法求解比较简单．解答：解：（1）原方程组化为，①+②得：6x=18，∴x=3．代入①得：y=．所以原方程组的解为．点评：要注意：两个二元一次方程中同一未知数的系数相反或相等时，把这两个方程的两边相加或相减，就能消去这个未知数，得到一个一元一次方程，这种方法叫做加减消元法．本题适合用此法．5．解方程组：考点：解二元一次方程组．专题：计算题；换元法．分析：本题用加减消元法即可或运用换元法求解．解答：解：，①﹣②，得s+t=4，①+②，得s﹣t=6，即，解得．所以方程组的解为．点评：此题较简单，要熟练解方程组的基本方法：代入消元法和加减消元法．6．已知关于x，y的二元一次方程y=kx+b的解有和．（1）求k，b的值．（2）当x=2时，y的值．（3）当x为何值时，y=3？考点：解二元一次方程组．专题：计算题．分析：（1）将两组x，y的值代入方程得出关于k、b的二元一次方程组，再运用加减消元法求出k、b的值．（2）将（1）中的k、b代入，再把x=2代入化简即可得出y的值．（3）将（1）中的k、b和y=3代入方程化简即可得出x的值．解答：解：（1）依题意得：①﹣②得：2=4k，所以k=，所以b=．（2）由y=x+，把x=2代入，得y=．（3）由y=x+把y=3代入，得x=1．点评：本题考查的是二元一次方程的代入消元法和加减消元法，通过已知条件的代入，可得出要求的数．7．解方程组：（1）；（2）．考点：解二元一次方程组．分析：根据各方程组的特点选用相应的方法：（1）先去分母再用加减法，（2）先去括号，再转化为整式方程解答．解答：解：（1）原方程组可化为，①×2﹣②得：y=﹣1，将y=﹣1代入①得：x=1．∴方程组的解为；（2）原方程可化为，即，①×2+②得：17x=51，x=3，将x=3代入x﹣4y=3中得：y=0．∴方程组的解为．点评：这类题目的解题关键是理解解方程组的基本思想是消元，掌握消元的方法有：加减消元法和代入消元法．根据未知数系数的特点，选择合适的方法．8．解方程组：考点：解二元一次方程组．专题：计算题．分析：本题应把方程组化简后，观察方程的形式，选用合适的方法求解．解答：解：原方程组可化为，①+②，得10x=30，x=3，代入①，得15+3y=15，y=0．则原方程组的解为．点评：解答此题应根据各方程组的特点，有括号的去括号，有分母的去分母，然后再用代入法或加减消元法解方程组．9．解方程组：考点：解二元一次方程组．专题：计算题．分析：本题为了计算方便，可先把（2）去分母，然后运用加减消元法解本题．解答：解：原方程变形为：，两个方程相加，得4x=12，x=3．把x=3代入第一个方程，得4y=11，y=．解之得．点评：本题考查的是二元一次方程组的解法，方程中含有分母的要先化去分母，再对方程进行化简、消元，即可解出此类题目．10．解下列方程组：（1）（2）考点：解二元一次方程组．专题：计算题．分析：此题根据观察可知：（1）运用代入法，把①代入②，可得出x，y的值；（2）先将方程组化为整系数方程组，再利用加减消元法求解．解答：解：（1），由①，得x=4+y③，代入②，得4（4+y）+2y=﹣1，所以y=﹣，把y=﹣代入③，得x=4﹣=．所以原方程组的解为．（2）原方程组整理为，③×2﹣④×3，得y=﹣24，把y=﹣24代入④，得x=60，所以原方程组的解为．点评：此题考查的是对二元一次方程组的解法的运用和理解，学生可以通过题目的训练达到对知识的强化和运用．11．解方程组：（1）（2）考点：解二元一次方程组．专题：计算题；换元法．分析：方程组（1）需要先化简，再根据方程组的特点选择解法；方程组（2）采取换元法较简单，设x+y=a，x﹣y=b，然后解新方程组即可求解．解答：解：（1）原方程组可化简为，解得．（2）设x+y=a，x﹣y=b，∴原方程组可化为，解得，∴∴原方程组的解为．点评：此题考查了学生的计算能力，解题时要细心．12．解二元一次方程组：（1）；（2）．考点：解二元一次方程组．专题：计算题．分析：（1）运用加减消元的方法，可求出x、y的值；（2）先将方程组化简，然后运用加减消元的方法可求出x、y的值．解答：解：（1）将①×2﹣②，得15x=30，x=2，把x=2代入第一个方程，得y=1．则方程组的解是；（2）此方程组通过化简可得：，①﹣②得：y=7，把y=7代入第一个方程，得x=5．则方程组的解是．点评：此题考查的是对二元一次方程组的解法的运用和理解，学生可以通过题目的训练达到对知识的强化和运用．13．在解方程组时，由于粗心，甲看错了方程组中的a，而得解为，乙看错了方程组中的b，而得解为．（1）甲把a看成了什么，乙把b看成了什么？（2）求出原方程组的正确解．考点：解二元一次方程组．专题：计算题．分析：（1）把甲乙求得方程组的解分别代入原方程组即可；（2）把甲乙所求的解分别代入方程②和①，求出正确的a、b，然后用适当的方法解方程组．解答：解：（1）把代入方程组，得，解得：．把代入方程组，得，解得：．∴甲把a看成﹣5；乙把b看成6；（2）∵正确的a是﹣2，b是8，∴方程组为，解得：x=15，y=8．则原方程组的解是．点评：此题难度较大，需同学们仔细阅读，弄清题意再解答．14．考点：解二元一次方程组．分析：先将原方程组中的两个方程分别去掉分母，然后用加减消元法求解即可．解答：解：由原方程组，得，由（1）+（2），并解得x=（3），把（3）代入（1），解得y=，∴原方程组的解为．点评：用加减法解二元一次方程组的一般步调：1．方程组的两个方程中，如果同一个未知数的系数既不互为相反数又不相等，就用适当的数去乘方程的两边，使一个未知数的系数互为相反数或相等；2．把两个方程的两边分别相加或相减，消去一个未知数，得到一个一元一次方程；3．解这个一元一次方程；4．将求出的未知数的值代入原方程组的任意一个方程中，求出另一个未知数，从而得到方程组的解．15．解下列方程组：（1）；（2）．考点：解二元一次方程组．分将两个方程先化简，再选择正确的方法进行消元．析：解答：解：（1）化简整理为，①×3，得3x+3y=1500③，②﹣③，得x=350．把x=350代入①，得350+y=500，∴y=150．故原方程组的解为．（2）化简整理为，①×5，得10x+15y=75③，②×2，得10x﹣14y=46④，③﹣④，得29y=29，∴y=1．把y=1代入①，得2x+3×1=15，∴x=6．故原方程组的解为．点评：方程组中的方程不是最简方程的，最好先化成最简方程，再选择合适的方法解方程．16．解下列方程组：（1）（2）考点：解二元一次方程组．分析：观察方程组中各方程的特点，用相应的方法求解．解答：解：（1）①×2﹣②得：x=1，将x=1代入①得：2+y=4，y=2．∴原方程组的解为；（2）原方程组可化为，①×2﹣②得：﹣y=﹣3，y=3．将y=3代入①得：x=﹣2．∴原方程组的解为．。

解二元一次方程50道练习题(带答案)

解二元一次方程50道练习题(带答案)
1. 解方程组：
{2x - y = 3
{3x + 2y = 8
解答：
首先，可以通过消元法来解决这个问题。

将第一个方程乘以2，并将第二个方程乘以3，得到：
{4x - 2y = 6
{9x + 6y = 24
接下来，将第一个方程的两倍加到第二个方程上，得到：
{4x - 2y = 6
{13x + 4y = 30
然后，将第一个方程的2倍加到第二个方程上，得到：
{4x - 2y = 6
{8x - 8y = 12
接下来，将第二个方程的两倍加到第一个方程上，得到：
{36x = 18
{8x - 8y = 12
最后，解方程得到：
{x = 0.5
{y = 2
2. 解方程组：
{3x + 2y = 7
{5x + 3y = 11
解答：
可以使用消元法来解决这个方程组。

将第一个方程乘以3，并将第二个方程乘以2，得到：
{9x + 6y = 21
{10x + 6y = 22
接下来，将第二个方程的两倍减去第一个方程，得到：
{9x + 6y = 21
{2x = 1
最后，解方程得到：
{x = 0.5
{y = 2
3. ...
...
50. ...
...
这是前面五道解二元一次方程的练习题，你可以根据相同的方法解答剩下的题目。

希望这些练习题对你有帮助！。

二元一次方程组解法练习题精选(含答案)

二元一次方程组解法练习题精选(含答案) 二元一次方程组解法练题精选（含答案）一．解答题（共16小题）1.求适合 $3x-2y=2$ 和 $6x+y=3$ 的 $x$，$y$ 的值。

解答：由 $(1)\times2$ 得：$3x-2y=2$（3），由$(2)\times3$ 得：$6x+y=3$（4），$(3)\times2$ 得：$6x-4y=4$（5），$(5)-(4)$ 得：$y=-\frac{1}{2}$，把 $y$ 的值代入 $(3)$ 得：$x=\frac{1}{2}$，故原方程组的解为$(x,y)=(\frac{1}{2},-\frac{1}{2})$。

2.解下列方程组：begin{cases} \frac{x}{2}+\frac{y}{3}=1 \\\frac{x}{3}+\frac{y}{2}=2 \end{cases}$$解答：由题意得：$\frac{x}{2}+\frac{y}{3}=1$（1），$\frac{x}{3}+\frac{y}{2}=2$（2），先把两方程变形（去分母），得到一组新的方程，然后在用加减消元法解二元一次方程组。

把 $(1)\times3$ 减去 $(2)\times2$，得到 $x=-1$，把$x=-1$ 代入 $(1)$，得到 $y=6$，故原方程组的解为 $(x,y)=(-1,6)$。

3.解方程组：begin{cases} 3x+2y=7 \\ 2x+3y=8 \end{cases}$$解答：把两方程相加得到 $5x+5y=15$，即 $x+y=3$，把$x+y=3$ 代入其中一个方程，如 $(1)$，得到 $x=-1$，再把$x=-1$ 代入 $(1)$ 或 $(2)$ 中的一个方程，如 $(1)$，得到$y=4$，故原方程组的解为 $(x,y)=(-1,4)$。

4.解方程组：begin{cases} x+y=5 \\ 2x-y=4 \end{cases}$$解答：把两方程相加得到 $3x=9$，即 $x=3$，把$x=3$ 代入其中一个方程，如 $(1)$，得到 $y=2$，再把 $x=3$，$y=2$ 代入原方程组检验，发现符合，故原方程组的解为$(x,y)=(3,2)$。

专题解二元一次方程组(计算题50题)(原卷版)

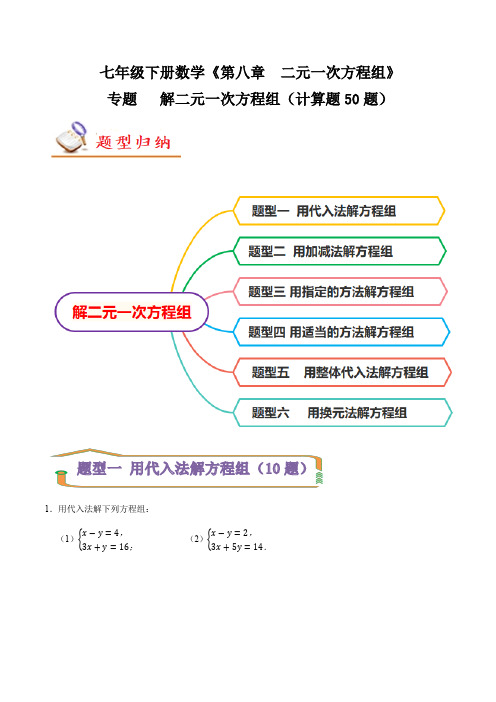
七年级下册数学《第八章二元一次方程组》专题解二元一次方程组（计算题50题）1．用代入法解下列方程组：（1）{x−y=4，3x+y=16；（2）{x−y=2，3x+5y=14．2．用代入法解下列方程组：（1）{2x −y =33x +2y =8；（2）{u +v =103u −2v =5．3．用代入法解下列方程组：（1）{3x −y =2，9x +8y =17；（2）{3x −4y =10x +3y =12.4．用代入法解下列方程组．（1）{x +2y =4y =2x −3；（2）{x −y =44x +2y =−2．5．用代入法解下列方程组：（1）{5x +4y =−1.52x −3y =4 （2）{4x −3y −10=03x −2y =06．用代入法解下列方程组：（1）{x −y =42x +y =5；（2）{3x −y =29x +8y =17；（3）{3x +2y =−86x −3y =−9．7．用代入法解下列方程组：（1）{3x +2y =11，①x =y +3，② （2）{4x −3y =36，①y +5x =7，② （3）{2x −3y =1，①3x +2y =8，②8．用代入法解下列方程组：（1）{5x +2y =15①8x +3y =−1②；（2）{3(y −2)=x −172(x −1)=5y −8．9．用代入法解下列方程组：（1）{x =6−5y 3x −6y =4 （2）{5x +2y =15x +y =6（3）{3x +4y =22x −y =5 （4）{2x +3y =73x −5y =110．用代入法解下列方程组：（1）{2x +y =3x +2y =−6；（2）{x +5y =43x −6y =5；（3）{2x −y =63x +2y =2；（4）{5x +2y =113y −x =−9；1．用加减法解下列方程组：（1）{4x −y =143x +y =7（2）{12x −2y =712x −3y =−82．用加减法解下列方程组：（1）{2m +7n =53m +n =−2（2）{2u −5v =124u +3v =−2（3）{x 3−y 7=12x 3+y 7=133．用加减法解下列方程组：（1）{x −y =52x +y =4；（2）{x −2y =33x +4y =−1．4．用加减法解下列方程组：（1）{4x −3y =11，2x +y =13；（2）{x −y =3，2y +3(x −y)=115．用加减法解下列方程组：（1）{3μ+2t =76μ−2t =11 （2）{2a +b =33a +b =4．6．（2023•市北区校级开学）用加减法解下列方程组：（1）{3y −4x =04x +y =8；（2）{2x +y =312x −32y =−1．7．（2022秋•陕西期末）用加减法解下列方程组：（1）{x −y =33x −8y =14；（2）{3x +2y =10x 2=1+y+13．8．用加减法解下列方程组：（1）{x +3=y ，2(x +1)−y =6；（2）{x +y =2800，96%x +64%y =2800×92%．9．用加减法解下列方程组：（1）{x −y =5，①2x +y =4；②（2）{x −2y =1，①x +3y =6；②（3）{2x −y =5，①x −1=12(2y −1)．②10．用加减法解下列方程组：（1）{x +3y =62x −3y =3 （2）{7x +8y =−57x −y =4（3）{y −1=3(x −2)y +4=2(x +1) （4）{x3+y4=1x 2−y 3=−1．1．（2022春•新田县期中）用指定的方法解下列方程组：（1）{2x −5y =14①y =−x②（代入法）；（2）{2x +3y =9①3x +5y =16②（加减法）．2．（2022春•安岳县校级月考）解下列方程组：（1）{3x −y =75x +2y =8（用代入法）；（2）{m4+n3=10m 3−n 4=5（用加减法）．3．（2022春•大连期中）用指定的方法解下列方程组：（1）{x −3y =42x +y =13（代入法）；（2）{5x +2y =4x +4y =−6（加减法）．4．（2022春•宁远县月考）请用指定的方法解下列方程组（1）{5a −b =113a +b =7（代入消元法）；（2）{2x −5y =245x +2y =31（加减消元法）．5．（2021秋•蒲城县期末）请用指定的方法解下列方程组：（1）{2x +3y =11①x =y +3②（代入消元法）；（2）{3x −2y =2①4x +y =10②（加减消元法）．6．（2022秋•历下区期中）请用指定的方法解下列方程组：（1）{m −n2=22m +3n =12（代入法）；（2）{6s −5t =36s +t =−15（加减法）．7．（2022春•泰安期中）用指定的方法解下列方程组（1）{3x +4y =19x −y =4（代入消元法）；（2）{2x +3y =−53x −2y =12（加减消元法）；（3）{5(x −9)=6(y −2)x 4−y+13=2．8．（2021秋•历下区期中）请用指定的方法解下列方程组：（1）{3x +2y =14x =y +3；（代入法）（2）{2x +3y =123x +4y =17．（加减法）9．（2021春•沙河口区期末）用指定的方法解下列方程组：（1）{y =2x −33x +2y =8（代入法）；（2）{3x +4y =165x −6y =33（加减法）．10．用指定的方法解下列方程组：（1）{3x +4y =19x −y =4（代入法）；（2）{2x +3y =−53x −2y =12（加减法）．1．（2022•苏州模拟）用适当的方法解下列方程组．（1）{x +2y =9y −3x =1；（2）{23x −34y =14(x −y)−(y −4x)=4．2．（2022秋•锦江区校级期末）用适当的方法解下列方程组．（1）{x =2y −14x +3y =7；（2）{3x +2y =22x +3y =28，．3．用适当的方法解下列方程组：（1）{x +2y =0，3x +4y =6；（2）{x+13=2y2(x +1)−y =11（3）{x +0.4y =40，0.5x +0.7y =35；（4）{m+n 3+n−m 4=−14，m+86−5(n+1)12=2．4．（2022•天津模拟）用适当的方法解下列方程组：（1）{x +y =52x −y =4；（2）{x+13=y+24x−34−y−33=112．5．（2021•越城区校级开学）用适当的方法解下列方程组：（1）{2x −3y =7x −3y =7．（2）{0.3p +0.4q =40.2p +2=0.9q ．6．（2022春•东城区校级月考）用适当的方法解下列方程组（1）{x +y =52x +y =8；（2）{2x +3y =73x −2y =4．7．（2021春•哈尔滨期末）用适当的方法解下列方程组（1）{x +2y =93x −2y =−1 （2）{2x −y =53x +4y =28．（2022春•椒江区校级期中）用适当的方法解下列方程组：（1）{2x +3y =16①x +4y =13②；（2）2s+t 3=3s−2t 8=3．9．（2022春•诸暨市期中）用适当的方法解下列方程组：（1）{y =2x −1x +2y =−7 （2）{x 4+y 3=7x 3+y 2=810．（2021春•南湖区校级期中）用适当的方法解下列方程组：（1）{3x +2y =9x −y =8；（2）{x−y3=x+y22x −5y =7．1．先阅读材料，然后解方程组：材料：解方程组{x +y =4①3(x +y)+y =14②在本题中，先将x +y 看作一个整体，将①整体代入②，得3×4+y ＝14，解得y ＝2．把y ＝2代入①得x ＝2，所以{x =2y =2这种解法称为“整体代入法”，你若留心观察，有很多方程组可采用此法解答，请用这种方法解方程组{x −y −1=0①4(x −y)−y =5②．2．（2021秋•乐平市期末）解方程组{3x −2y =8⋯⋯⋯①3(3x −2y)+4y =20⋯．②时，可把①代入②得：3×8+4y ＝20，求得y ＝﹣1，从而进一步求得{x =2y =−1这种解法为“整体代入法“，请用这样的方法解下列方程组{2x −3y =123(2x −3y)+5y =26．3．先阅读，然后解方程组．解方程组{x −y −1=0①4(x −y)−y =5②时，可由①得x ﹣y ＝1．③，然后再将③代入②得4×1﹣y ＝5，求得y ＝﹣1，从而进一步求得{x =0y =−1这种方法被称为“整体代入法”，请用这样的方法解下列方程组：{2x −3y +5=06y−4x+37=2y +1．4．（2022春•太和县期末）先阅读，然后解方程组．解方程组{x −y −1=0①4(x −y)−y =5②时，可由 ①得x ﹣y ＝1，③然后再将③代入②得4×1﹣y ＝5，求得y ＝﹣1，从而进一步求得{x =0①y =−1②这种方法被称为“整体代入法”，请用这样的方法解下列方程组{2x −3y −2=02x−3y+57+2y =9．5．先阅读，然后解方程组．解方程组{x −y −1=0①4(x −y)−y =5②时，可由①得x ﹣y ＝1③，然后再将③代入②得4×1﹣y ＝5，求得y ＝﹣1，从而进一步求得x 这种方法被称为“整体代入法”，请用这样的方法解下列方程组：{2x −3y −2=03(2x −3y)+y =7．1．用换元法解下列方程组{2x +2y =125x −1y =342．用换元法解下列方程组：（1）{3(x +y)+2(x −y)=36(x +y)−4(x −y)=−16 （2）{x−4y 2+x+5y 3=2x−4y 3−(x +5y)=5．3．（2022春•云阳县期中）阅读探索：解方程组{(a −1)+2(b +2)=62(a −1)+(b +2)=6解：设a ﹣1＝x ，b +2＝y 原方程组可以化为{x +2y =62x +y =6，解得{x =2y =2，即：{a −1=2b +2=2∴{a =3b =0，此种解方程组的方法叫换元法．（1）拓展提高运用上述方法解下列方程组{(a 4−1)+2(b 5+2)=102(a 4−1)+(b 5+2)=11；（2）能力运用已知关于x ，y 的方程组{a 1x +b 1y =c 1a 2x +b 2y =c 2的解为{x =6y =7，求关于m 、n 的方程组{a 1(m −2)+b 1(n +3)=c 1a 2(m −2)+b 2(n +3)=c 2的解．4．在学过了二元一次方程组的解法后，课堂上老师又写出了一个题目：{x+y 6+x−y 10=3①x+y 6−x−y 10=−1②，你会解这个方程组吗？小明、小刚、小芳争论了一会儿，他们分别写出了一种方法：小明：把原方程组整理得{8x +2y =90③2x +8y =−30④④×4﹣③得30y ＝﹣210，所以y ＝﹣7把y ＝﹣7代入③得8x ＝104，所以x ＝13，即{x =13y =−7小刚：设x+y 6=m ，x−y 10=n ，则{m +n =3③m −n =−1④③+④得m ＝1，③﹣④得m ＝2，即{x+y 6=1x−y 10=2，所以{x +y =6x −y =20，所以{x =13y =−7．小芳：①+②得2(x+y)6=2，即x +y ＝6．③ ①﹣②得2(x−y)10=4，即x ﹣y ＝20．④③④组成方程组得x ＝13③﹣④得y ＝﹣7，即{x =13y =−7．老师看过后，非常高兴，特别是小刚的方法独特，像小刚的这种方法叫做换元法，你能用换元法解下列方程组吗？{3x−2y 6+2x+3y 7=13x−2y 6−2x+3y 7=5．5．（2022春•卧龙区校级月考）阅读探索（1）知识积累解方程组{(a −1)+2(b +2)=62(a −1)+(b +2)=6．解：设a ﹣1＝x ，b +2＝y ．原方程组可变为{x +2y =62x +y =6，解这个方程组得{x =2y =2，即{a −1=2b +2=2，所以{a =3b =0，这种解方程组的方法叫换元法．（2）拓展提高运用上述方法解下列方程组：{(m 3−1)+2(n 5+2)=43(m 3−1)−(n 5+2)=5．（3）能力运用已知关于x ，y 的方程组{a 1x +b 1y =c 1a 2x +b 2y =c 2的解为{x =3y =4，请直接写出关于m 、n 的方程组{a 1(m +2)−b 1n =c 1a 2(m +2)−b 2n =c 2的解是．。

二元一次方程组练习题(含答案)

二元一次方程组练习题(含答案) 二元一次方程组练题一．解答题（共16小题）1.解下列方程组：1）x+2y-1=23x-2y=52）1-yx+2/3=1/22y+3=3x3）5x+2y=11a4x-4y=6a4）2x+3y=73x-2y=15）2x-3y=75x+4y=176）2x+3y=13x-2y=57）3x-4y=-12x+5y=138）x(y+1)+y(1-x)=2x(x+1)-y-x^2=09）3x+y=72x-3y=-810）x^2+xy=2y-x+2=02.求适合的x，y的值。

已知关于x，y的二元一次方程y=kx+b的解有和。

1）求k，b的值。

2）当x=2时，y的值。

3）当y=3时，x的值为多少？解答：1.1）将第二个方程变形得到y=(3x-5)/2，代入第一个方程中，得到x=3，y=-2.2）将第一个方程变形得到y=(1/2-1+xy)/x，代入第二个方程中，得到x=3，y=-1.3）将第二个方程变形得到y=x-3/2，代入第一个方程中，得到x=2，y=1.4）将第二个方程变形得到y=(3x-1)/2，代入第一个方程中，得到x=2，y=1.5）将第一个方程变形得到y=(2x-7)/3，代入第二个方程中，得到x=1，y=-1.6）将第二个方程变形得到y=(3x-5)/2，代入第一个方程中，得到x=1，y=-1.7）将第二个方程变形得到y=(3x+1)/4，代入第一个方程中，得到x=5，y=2.8）将第一个方程变形得到y=(2-x^2)/(1-x)，代入第二个方程中，得到x=1，y=1.9）将第二个方程变形得到y=(2x+8)/3，代入第一个方程中，得到x=1，y=1.10）将第一个方程变形得到y=2/x-x，代入第二个方程中，得到x=1，y=0.2.1）由于y=kx+b，所以当x=1时，y=k+b；当x=2时，y=2k+b。

又因为已知y=3时，x的值为多少，所以将y=kx+b代入得到kx+b=3，解得x=(3-b)/k。

二元一次方程组(例题、解方程组、练习及答案)

的x. y 的值.s+y=l 2x+y=3⑵2K -3y=-52y —12弩=4Cx-1)-2(2y+l)=43.解方程组：举-4y=24.解方程组： x+1.y~1 ~2'玄-11-L 2-2(x+2y)=3⑵L L1K +4(x+2y)=45解二元一次方程组练习及答案专题一：二元一次方程组解法精练一.解答题（共16小题）2.解下列方程组(s _t)-2(s+t)=10 5.解方程组上(日一t)+2Cs+t)=266.已知关于x,y 的二元一次方程y 二kx+b 的解有（1）求k,b 的值. ⑵当x=2时，y 的值. ⑶当x 为何值时，y=3?7.解方程组：2y=3“至_y_7⑴［电文-10；=13_X "12,乙看错了方程组中的b.蓋二- £时，由于粗心，甲看错了方程组中的a,而得解为（沪5而得解为尸°.（1）甲把a 看成了什么，乙把b 看成了什么？（2）求出原方程组的正确解.亠一空二5 14.I X0.315.解下列方程组：8.解方程组:卩（旳）(K -3y)=159.解方程组：10.解下列方程组: fs-y=4 ⑴4贵 11.解方程组： "T⑵［4(葢十7)-5(K-y)=212.解二元一次方程组： f 9s+2y=20（1）.办十4尸10；乜(K -1)-4(y-4)=0⑵占〔厂"二3匕+5)鮎曲+5尸1013.在解方程组(1) 匹站3y=15 “x+1_y+4 ⑵f2x+y=4 16.解下列方程组：（1）时戈产5 p+y=l(2)■20^1+30^25^X2专题二：方程组解法强化训练 ■>二1+尸j3^-2/=6 2(右十为*175x+y+z=145 15 3.x+y —2z-5 仝％+4®二1124.5. 17 r0.25x+3ty+3)=156.匚(工十1)—1.5(^十刀二35 r 3(x-y 十E 二0'mJ4耳+2了+£=3i4 l 税25t+5v+z=6O 盲8.9.—2 4 J2 3 XH -/=60 J y +z =40 x+i=50 10. H 十JJ-H-Z=11<3A +J 二25z=4^11.L》+z -了工二号 5-3^+4-7y=1121」心+5我彳z +z-3j=5 13.乐十》）-4&p ）二4土+二=118.21. fi-2j=7y x+1—二36y-1=3fx+|)16.y—1x二y-I2_y+2.2x=+13T" 33(x-0=4(卩一4)17.+500,[60%^+80%-7=500x72%.19.宝”一1)=3(兀+5)20.卜223A-3J-9=^±13r2(z+^+3(x-y)=1322.j-2z+3y=1123.尸（*）亠4决2刃=8724. 25. 弘+»=198jc-3y=6727. =-1=4IZ尹-1=128.30. SI兰工_气2十3-5巧P=〔23-_答案专题一1.x=6"X=1 「K=3、「K=3「⑵•卄8•解万程组：9•解方程组：1歼-1(y=0\y=0工二3114V——3⑷•y=-3•解方程组fl4•解方程组：鳥I尸4,尸亍6••(1)求k,b的值.k二言,b二号•7⑵当x=2时，y的值•把x=2代入，得y=p•(3)当x为何值时，y=3?把y=3代入，得x=1 7•解方程组：10•解下列方程组：17 \=60:'尸-2411•解方程组:⑴12⑵¥二广1712•解二元一次方程组：13.(1)甲把a看成了什么，乙把b看成了什么？fa=-2 [b=6(2)求出原方程组的正确解.P=152•解下列方程组专题二：=50rz=4rz=5K=5[75rz=-70rA=61.2.3.4.5.6.g1715•解下列方程组:⑴16•解下列方程组:⑴rx=-2cm =49.严=35L=2510.厂=30 12.J=_10 严=-17/4K=_19/413r=_5厂=17/15 厂1=714."11⑴15.J=-316.=1厂=20017.J=300 18. J -A =-1/4丫尹=3/819.29/6 -7/422. 23.CI ；rz =2324.f A =-11/2 25.f A =826.5=-127.rz=428.J -A =4.5 29.rz=6.530.。

二元一次方程组解法练习题精选(含答案)

二元一次方程组解法练习题精选（含答案）一．解答题（共16小题）1．求适合的x，y的值．2．解下列方程组（1）（2）（3）（4）．解方程组：4．解方程组：5．解方程组：3．6．已知关于x，y的二元一次方程y=kx+b 的解有和．（1）求k，b的值．（2）当x=2时，y的值．（3）当x为何值时，y=3？.7．解方程组：（1）；（2）．解方程组：9．解方程组：8．10．解下列方程组：（1）（2）11．解方程组：（1）（2）12．解二元一次方程组：（1）；（2）．13．在解方程组时，由于粗心，甲看错了方程组中的a，而得解为，乙看错了方程组中的b，而得解为．（1）甲把a看成了什么，乙把b看成了什么？（2）求出原方程组的正确解．14．15．解下列方程组：（1）；（2）．解下列方程组：（1）（2）16．.二元一次方程组解法练习题精选（含答案）参考答案与试题解析一．解答题（共16小题）1．求适合的x，y的值．，然后在用加减消元法消去未知数，，2．解下列方程组（1）（2）（3）（4）．故原方程组的解为故原方程组的解为）原方程组可化为．所以原方程组的解为，x=，代入×﹣．所以原方程组的解为3．解方程组：解：原方程组可化为所以方程组的解为4．解方程组：）原方程组化为，．所以原方程组的解为5．解方程组：，．所以方程组的解为6．已知关于x，y的二元一次方程y=kx+b的解有和．（1）求k，b的值．（2）当x=2时，y的值．（3）当x为何值时，y=3？的二元一次方程组）依题意得：，．y=x+y=y=x+7．解方程组：（1）；（2）．）原方程组可化为，；）原方程可化为．8．解方程组：解：原方程组可化为则原方程组的解为9．解方程组：解：原方程变形为：10．解下列方程组：（1）（2））﹣代入﹣=所以原方程组的解为）原方程组整理为所以原方程组的解为11．解方程组：（1）（2），∴原方程组可化为，∴原方程组的解为12．解二元一次方程组：（1）；（2）．；）此方程组通过化简可得：．13．在解方程组时，由于粗心，甲看错了方程组中的a，而得解为，乙看错了方程组中的b，而得解为．（1）甲把a看成了什么，乙把b看成了什么？（2）求出原方程组的正确解．）把代入方程组．代入方程组．∴方程组为则原方程组的解是14．∴原方程组的解为15．解下列方程组：（1）；（2）．）化简整理为故原方程组的解为）化简整理为故原方程组的解为16．解下列方程组：（1）（2）∴原方程组的解为）原方程组可化为∴原方程组的解为。

七年级数学下册专题解二元一次方程组(计算题50题)(解析版)

七年级下册数学《第八章二元一次方程组》专题解二元一次方程组（计算题50题）1．用代入法解下列方程组：（1）−=4，3+=16；（2）−=2，3+5=14．【分析】（1）−=4①3+=16②，由①得：x＝y+4，代入②得：3（y+4）+y＝16，即可求出y的值，则x的值也就迎刃而解了；（2）−=4①3+5=14②，由①得：y＝x﹣2，代入②得：3x+5（x﹣2）＝14，即可求出x的值，则y的值也就可以求出了．【解答】解：（1）−=4①3+=16②，由①得：x＝y+4，代入②得：3（y+4）+y＝16，解得y＝1．将y＝1代入x＝y+4中得x＝5，故方程组的解为：=5=1；（2）−=4①3+5=14②，由①得：y＝x﹣2，代入②得：3x+5（x﹣2）＝14，解得x＝3．将x＝3代入y＝x﹣2，得y＝1．故方程组的解为：=3=1．【点评】本题主要考查了二元一次方程组的解法，解题的关键是掌握代入法解方程．2．用代入法解下列方程组：（1）2−=33+2=8；（2）+=103−2=5．【分析】两方程组利用代入消元法求出解即可．【解答】解：（1）2−=3①3+2=8②，由①得：y＝2x﹣3③，把③代入②得：3x+2（2x﹣3）＝8，解得：x＝2，把x＝2代入③得：y＝4﹣3＝1，则方程组的解为=2=1；（2）+=10①3−2=5②，由①得：u＝10﹣v③，把③代入②得：3（10﹣v）﹣2v＝5，解得：v＝5，把v＝5代入①得：5+u＝10，解得：u＝5，则方程组的解为=5=5．【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．3．用代入法解下列方程组：（1）3−=2，9+8=17；（2）3−4=10+3=12.【分析】（1）由①得出y ＝3x ﹣2③，把③代入②得出9x +8（3x ﹣2）＝17，求出x ，再把x ＝1代入③求出y 即可；（2）由②得出x ＝12﹣3y ③，把③代入①得出3（12﹣3y ）﹣4y ＝10，求出y ，再把y ＝2代入③求出x 即可．【解答】解：（1）3−=2①9+8=17②，由①，得y ＝3x ﹣2③，把③代入②，得9x +8（3x ﹣2）＝17，解得：x ＝1，把x ＝1代入③，得y ＝3×1﹣2，即y ＝1，所以原方程组的解是=1=1；（2）3−4=10①+3=12②，由②，得x ＝12﹣3y ③，把③代入①，得3（12﹣3y ）﹣4y ＝10，解得：y ＝2，把y ＝2代入③，得x ＝12﹣3×2，即x ＝6，所以原方程组的解是=6=2．【点评】本题考查了解二元一次方程组，能把二元一次方程组转化成一元一次方程是解此题的关键．4．用代入法解下列方程组．（1）+2=4=2−3；（2）−=44+2=−2．【分析】（1）方程组利用代入消元法求出解即可；（2）方程组利用加减消元法求出解即可．【解答】解：（1）+2=4①=2−3②，把②代入①得：x +2（2x ﹣3）＝4，解得：x ＝2，把x ＝2代入②得：y ＝4﹣3＝1，则方程组的解为=2=1；（2）方程组整理得：−=4①2+=−1②，①+②得：3x ＝3，解得：x ＝1，把x ＝1代入①得：1﹣y ＝4，解得：y ＝﹣3，则方程组的解为=1=−3．【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．5．用代入法解下列方程组：（1）5+4=−1.52−3=4（2）4−3−10=03−2=0【分析】（1）方程组利用代入消元法求出解即可；（2）方程组利用代入消元法求出解即可．【解答】解：（1）5+4=−1.5①2−3=4②，由②得：x =3r42③，把③代入①得：15r202+4y ＝﹣1.5，去分母得：15y +20+8y ＝﹣3，移项合并得：23y ＝﹣23，解得：y ＝﹣1，把y ＝﹣1代入③得：x =12，则方程组的解为=12=−1；（2）方程组整理得：4−3−10=0①=23t ，把②代入①得：83y ﹣3y ﹣10＝0，去分母得：8y ﹣9y ﹣30＝0，解得：y＝﹣30，把y＝﹣30代入②得：x＝﹣20，则方程组的解为=−20=−30．【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．6．用代入法解下列方程组：（1）−=42+=5；（2）3−=29+8=17；（3）3+2=−86−3=−9．【分析】各方程组利用代入消元法求出解即可．【解答】解：（1）−=4①2+=5②，由①得：x＝y+4③，把③代入②得：2（y+4）+y＝5，解得：y＝﹣1，把y＝﹣1代入③得：x＝﹣1+4＝3，则方程组的解为=3=−1；（2）3−=2①9+8=17②，由①得：y＝3x﹣2③，把③代入②得：9x+8（3x﹣2）＝17，解得：33x＝33，解得：x＝1，把x＝1代入③得：y＝3﹣2＝1，则方程组的解为=1=1；（3）3+2=−8①2−=−3②，由②得：y＝2x+3③，把③代入①得：3x+2（2x+3）＝﹣8，解得：x＝﹣2，把x＝﹣2代入②得：﹣4﹣y＝﹣3，解得：y＝﹣1，则方程组的解为=−2=−1．【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．7．用代入法解下列方程组：（1）3+2=11，①=+3，②（2）4−3=36，①+5=7，②（3）2−3=1，①3+2=8，②【分析】（1）将方程②代入方程①进行求解；（2）将方程②变形为y＝﹣5x+7，再代入方程①进行求解；（3）将方程①变形为y=2K13，再代入方程②进行求解．【解答】解：（1）将方程②代入方程①得，3（y+3）+2y＝11，解得y=25，把y=25代入②得，x=175，∴该方程组的解为=175=25；（2）将方程②变形为y＝﹣5x+7③，把③代入①得，4x﹣3（﹣5x+7）＝36，解得x＝3，将x＝3代入③得，y＝﹣5×3+7，解得y＝﹣8，∴该方程组的解为=3=−8；（3）将方程①变形为y=2K13③，把③代入②得，3x+2×2K13=8，解得x＝2，将x ＝2代入③得，y =2×2−13，解得y ＝1，∴该方程组的解为=2=1．【点评】此题考查了利用代入法解二元一次方程组的能力，关键是能直接或将某方程变式后进行代入消元求解．8．用代入法解下列方程组：（1）5+2=15①8+3=−1②；（2）3(−2)=−172(−1)=5−8．【分析】（1）用代入消元法解二元一次方程组即可；（2）用代入消元法解二元一次方程组即可．【解答】解：（1）5+2=15①8+3=−1②，由①得，y =15−52③，将③代入②得，8x +15−52×3＝﹣1，解得，x ＝﹣47，将x ＝﹣47代入①得，y ＝125，∴方程组的解为=−47=125；（2）3(−2)=−172(−1)=5−8，整理得，3−=−11①2−5=−6②，由①得，x ＝3y +11③，将③代入②得，y ＝﹣28，将y ＝﹣28代入①得，x ＝﹣73，∴方程组的解为=−73=−28．【点评】本题考查二元一次方程组的解，熟练掌握代入消元法和加减消元法解二元一次方程组是解题的关键．9．用代入法解下列方程组：（1）=6−53−6=4（2）5+2=15+=6（3）3+4=22−=5（4）2+3=73−5=1【分析】（1）用代入消元法解方程组即可．（2）用代入消元法解方程组即可．（3）用代入消元法解方程组即可．（4）用代入消元法解方程组即可．【解答】解：（1）=6−5s3−6=4②，把①代入②得3（6﹣5y）﹣6y＝4，解得y=23，∴x＝6−5×23=83，所以方程组的解为=83=23；（2）5+2=15①+=6②，由②得x＝6﹣y③，把③代入①，得y＝5，∴x＝6﹣5＝1，所以原方程组的解为=1=5；（3）3+4=2①2−=5②，由②得y＝2x﹣5③，把③代入①得，解得x＝2，∴y＝2×2﹣5＝﹣1，所以原方程组的解为=2=−1；（4）2+3=7①3−5=1②，由①得x=7−32③，把③代入②得解得y＝1，∴x=7−3×12=2，所以原方程组的解为=2=1．【点评】本题考查二元一次方程组的解法，解题关键是熟知代入消元法解方程组的步骤．10．用代入法解下列方程组：（1）2+=3+2=−6；（2）+5=43−6=5；（3）2−=63+2=2；（4）5+2=113−=−9；【分析】（1）用代入消元法解方程组即可．（2）用代入消元法解方程组即可．（3）用代入消元法解方程组即可．（4）用代入消元法解方程组即可．【解答】解：（1）2+=3①+2=−6②，由①得y＝3﹣2x，把y＝3﹣2x代入②得x+2（3﹣2x）＝﹣6，解得x＝4，∴y＝3﹣2×4＝﹣5．∴方程组的解为=4=−5．（2）+5=4①3−6=5②，由①得x＝4﹣5y，把x＝4﹣5y代入②得3（4﹣5y）﹣6y＝5，解得y=13，∴x＝4﹣5×13=73．∴方程组的解为=73=13．（3）2−=6①3+2=2②，由①得y＝2x﹣6，把y＝2x﹣6代入②得3x+2（2x﹣6）＝2，解得x＝2，∴y＝2x﹣6＝2×2﹣6＝﹣2．方程组的解为=2=−2．（4）5+2=11①3−=−9②，由②得x＝3y+9，把x＝3y+9代入①得5（3y+9）+2y＝11，解得y＝﹣2，∴x＝3×（﹣2）+9＝3．∴方程组的解为=3=−2．【点评】本题考查二元一次方程组的解法，解题关键是熟知代入消元法解方程组的步骤．1．用加减法解下列方程组：（1）4−=143+=7（2−2=7−3=−8【分析】（1）方程组利用加减消元法求出解即可；（2）方程组利用加减消元法求出解即可．【解答】解：（1）4−=14①3+=7②，①+②得：7x＝21，解得：x＝3，把x＝3代入②得：y＝﹣2，则方程组的解为=3=−2；（2−2=7①−3=−8②，①﹣②得：y＝15，把y＝15代入①得：x＝74，则方程组的解为=74=15．【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．2．用加减法解下列方程组：（1）2+7=53+=−2（2）5=123=−2（37=127=13【分析】（1）由②得出n＝﹣2﹣3m③，把③代入①得出2m+7（﹣2﹣3m）＝5，求出m，把m＝﹣1代入③求出n即可；（2）②﹣①×2得出13v＝﹣26，求出v，把v＝﹣2代入①求出u即可；（3）整理后①+②得出28x＝35，求出x，②﹣①求出y即可．【解答】解：（1）2+7=5①3+=−2②由②得：n＝﹣2﹣3m③，把③代入①得：2m+7（﹣2﹣3m）＝5，解得：m＝﹣1，把m＝﹣1代入③得：n＝1，所以原方程组的解是：=−1=1；（2）2−5=12①4+3=−2②②﹣①×2得：13v＝﹣26，解得：v＝﹣2，把v＝﹣2代入①得：2u+10＝12，解得：u＝1，所以原方程组的解是：=1=−2；（3）整理得：14−6=21①14+6=14②，①+②得：28x＝35，解得：x=54，②﹣①得：12y＝﹣7，解得：y=−712，所以原方程组的解是：=54=−712．【点评】本题考查了解二元一次方程组，能把二元一次方程组转化成一元一次方程是解此题的关键．3．用加减法解下列方程组：（1）−=53+4=−1．2+=4；（2）−2=3【分析】（1）方程组利用加减消元法求出解即可；（2）方程组利用加减消元法求出解即可．【解答】解：（1）−=5①2+=4②，①+②得：3x ＝9，解得：x ＝3，把x ＝3代入①得：3﹣y ＝5，解得：y ＝﹣2，则方程组的解为=3=−2；（2）−2=3①3+4=−1②，①×2+②得：5x ＝5，解得：x ＝1，把x ＝1代入①得：1﹣2y ＝3，解得：y ＝﹣1，则方程组的解为=1=−1．【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．4．用加减法解下列方程组：（1）4−3=11，2+=13；（2）−=3，2+3(−p =11【分析】（1）方程组利用加减消元法求出解即可；（2）方程组整理后，利用加减消元法求出解即可．【解答】解：（1）4−3=11①2+=13②，①+②×3得：10x ＝50，解得：x ＝5，把x ＝5代入①得：20﹣3y ＝11，解得：y ＝3，所以方程组的解为=5=3；（2）方程组整理得：−=3①3−=11②，②﹣①得：2x ＝8，解得：x ＝4，把x＝4代入①得：4﹣y＝3，解得：y＝1，所以方程组的解为=4=1．【点评】此题考查了解二元一次方程组，解方程组利用了消元的思想，消元的方法有：代入消元法与加减消元法．5．用加减法解下列方程组：（1）3+2=76−2=11（2）2+=33+=4．【分析】各个方程组利用加减消元法求出解即可．【解答】解：（1）3+2=7①6−2=11②，①+②得：9μ＝18，即μ＝2，把μ＝2代入①得：6+2t＝7，解得：t=12，则方程组的解为=2=12；（2）2+=3①3+=4②，②﹣①得：a＝1，把a＝1代入①得：2+b＝3，解得：b＝1，则方程组的解为=1=1．【点评】此题考查了解二元一次方程组，熟练掌握运算法则是解本题的关键．6．（2023•市北区校级开学）用加减法解下列方程组：（1）3−4=04+=8；（2+=3−32=−1．【分析】（1）方程组利用加减消元法求出解即可；（2）方程组整理后，利用加减消元法求出解即可．【解答】解：（1）3−4=0①4+=8②，①+②得：4y＝8，解得：y＝2，把y＝2代入②得：4x+2＝8，解得：x=32，则方程组的解为=32=2；（2）方程组整理得：2+=3①−3=−2②，①×3+②得：7x＝7，解得：x＝1，把x＝1代入①得：2+y＝3，解得：y＝1，则方程组的解为=1=1．【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法是代入消元法与加减消元法．7．（2022秋•陕西期末）用加减法解下列方程组：（1）−=33−8=14；（2+2=10=1+r13．【分析】（1）根据加减消元法解二元一次方程组即可求解；（2）将第二个方程去分母化简，然后根据加减消元法解二元一次方程组即可求解．【解答】解：（1）−=3①3−8=14②，①×3﹣②得：﹣3y+8y＝9﹣14，解得：y＝﹣1，将y＝﹣1代入①得：x+1＝3，解得：x＝2，∴原方程组的解为：=2=−1；（2+2=10①=1+r13②，由②得3x＝6+2（y+1），即3x﹣2y③，①﹣③得：4y＝2，解得：=12，①+③得：6x＝18，解得：x＝3，∴原方程组的解为：=3=12．【点评】本题考查了加减消元法解二元一次方程组，掌握解二元一次方程组的方法是解题的关键．8．用加减法解下列方程组：（1）+3=，2(+1)−=6；（2）+=2800，96%+64%=2800×92%．【分析】（1）先用第二个方程减去第一个方程即可得到x 的值，然后将x 的值代入任意一个方程，解方程即可得到y 的值；（2）先对方程组进行化简可得+=2800①3+2=8050②，易得两个方程中y 的系数存在2倍关系，故只需用方程②减去方程①乘2的积即可得到关于x 的方程，解方程即可．【解答】解：（1）+3=，①2(+1)−=6．②②﹣①，得x ﹣1＝6，∴x ＝7，x ＝7代入①得y ＝10，所以原方程组的解为=7=10．（2）原方程化简得+=2800，①3+2=8050．②②﹣①×2，得﹣x ＝﹣2450，∴x ＝2450，将x ＝2450代入①得：y ＝350，∴原方程组的解为：=2450=350．【点评】本题考查二元一次方程组的解法，利用正确的方法求解是本题的关键．9．用加减法解下列方程组：（1）−=5，①2+=4；②（2）−2=1，①+3=6；②（3）2−=5，①−1=12(2−1)．②【分析】（1）利用加减消元法解答即可；（2）利用加减消元法解答即可；（3）利用加减消元法解答即可．【解答】解：（1）−=5①2+=4②，①+②得：3x＝9，解得：x＝3，把x＝3代入①得：3﹣y＝5，解得：y＝﹣2，所以方程组的解为：=3=−2；（2）−2=1①+3=6②，②﹣①得：5y＝5，解得：y＝1，把y＝1代入①得：x﹣2＝1，解得：x＝3，所以方程组的解为：=3=1；（3）2−=5①−1=12(2−1)②，由②得：2x﹣2y＝1③，①﹣③得：y＝4，把y＝4代入①得：2x﹣4＝5，解得：x=92，所以方程组的解为：=92=4．【点评】此题考查了解二元一次方程组，以及解一元一次方程，熟练掌握运算法则是解本题的关键．10．用加减法解下列方程组：（1）+3=62−3=3（2）7+8=−57−=4（3）−1=3(−2)+4=2(+1)（4+4=1−3=−1．【分析】各方程组整理后，利用加减消元法求出解即可．【解答】解：（1）+3=6①2−3=3②，①+②得：3x＝9，即x＝3，把x＝3代入①得：y＝1，则方程组的解为=3=1；（2）7+8=−5①7−=4②，①﹣②得：9y＝﹣9，即y＝﹣1，把y＝﹣1代入①得：x=37，则方程组的解为=37=−1；（3）方程组整理得：3−=5①2−=2②，①﹣②得：x＝3，把x＝3代入①得：y＝4，则方程组的解为=3=4；（4）方程组整理得：4+3=12①3−2=−6②，①×2+②×3得：17x＝6，即x=617，①×3﹣②×4得：17y＝60，即y=6017，则方程组的解为=617=6017．【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．1．（2022春•新田县期中）用指定的方法解下列方程组：（1）2−5=14①3+5=16②（加减法）．=−t（代入法）；（2）2+3=9①【分析】（1）方程组利用代入消元法求出解即可；（2）方程组利用加减消元法求出解即可．【解答】解：（1）把②代入①得：2x+5x＝14，解得：x＝2，把x＝2代入②，得：y＝﹣2，则原方程组的解是=2=−2；（2）①×3得：6x+9y＝27③，②×2得：6x+10y＝32④，④﹣③得：y＝5，把y＝5代入①得：2x+15＝9，解得：x＝﹣3，则原方程组的解是=−3=5．【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．2．（2022春•安岳县校级月考）解下列方程组：（1）3−=75+2=8（用代入法）；（23=104=5（用加减法）．【分析】（1）方程组利用代入消元法求出解即可；（2）方程组利用加减消元法求出解即可．【解答】解：（1）3−=7①5+2=8②，由①得：y＝3x﹣7③，把③代入②得：5x+2（3x﹣7）＝22，解得：x＝2，把x＝2代入①得：6﹣y＝7，解得：y＝﹣1，则方程组的解为=2=−1；（2）方程组整理得：3+4=120①4−3=60②，①×3+②×4得：25m＝600，解得：m＝24，把m＝24代入①得：72+4n＝120，解得：n＝12，则方程组的解为=24=12．【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．3．（2022春•大连期中）用指定的方法解下列方程组：（1）−3=42+=13（代入法）；（2）5+2=4+4=−6（加减法）．【分析】（1）利用代入法解方程组；（2）利用加减消元法解方程组．【解答】解：（1）−3=4①2+=13②，由①得x ＝3y +4③，把③代入②，得2（3y +4）+y ＝13，解得y =57，∴x ＝3×57+4＝617，∴方程组的解为=617=57；（2）5+2=4①+4=−6②，①×2﹣②，得9x ＝14，解得x =149，把x =149代入②，得149+4y ＝﹣6，解得y =−179．∴方程组的解为=149=−179．【点评】本题考查了解二元一次方程组，做题的关键是掌握加减消元法，和代入消元法解二元一次方程组．4．（2022春•宁远县月考）请用指定的方法解下列方程组（1）5−=113+=7（代入消元法）；（2）2−5=245+2=31（加减消元法）．【分析】（1）由方程①，得b ＝5a ﹣11，再代入方程②求出未知数a ，进而得出未知数b ；（2）用方程①×2﹣②×5，可消去未知数y ，求出未知数x ，进而得出y 的值．【解答】解：（1）5−=11①3+=7②，由①，得b ＝5a ﹣11③，把③代入②，得3a +5a ﹣11＝7，解得a =94，把a=94代入③，得b=14，故方程组的解为=94=14；（2）2−5=24①5+2=31②，①×2﹣②×5，得29x＝203，解得x＝7，把x＝7代入①，得y＝﹣2，故方程组的解为=7=−2．【点评】本题考查了解二元一次方程组，掌握加减消元法和代入消元法是解答本题的关键．5．（2021秋•蒲城县期末）请用指定的方法解下列方程组：（1）2+3=11①=+3②（代入消元法）；（2）3−2=2①4+=10②（加减消元法）．【分析】（1）利用代入消元法进行求解即可；（2）利用加减消元法进行求解即可．【解答】解：（1）2+3=11①=+3②，把②代入①得：2（y+3）+3y＝11，解得y＝1，把y＝1代入②得：x＝1+3＝4，故原方程组的解是：=4=1；（2）3−2=2①4+=10②，②×2得：8x+2y＝20③，①+③得：11x＝22，解得x＝2，把x＝2代入②得：8+y＝10，解得y＝2，故原方程组的解是：=2=2．【点评】本题主要考查解二元一次方程组，解答的关键是对解二元一次方程组的方法的掌握．6．（2022秋•历下区期中）请用指定的方法解下列方程组：（1）−2=22+3=12（代入法）；（2）6−5=36+=−15（加减法）．【分析】（1）整理后由①得出n ＝2m ﹣4③，把③代入②得出2m +3（2m ﹣4）＝12，求出m ，再把m ＝3代入③求出n 即可；（2）②﹣①得出6t ＝﹣18，求出t ，再把t ＝﹣3代入①求出s 即可．【解答】解：（1）整理得：2−=4①2+3=12②，由①，得n ＝2m ﹣4③，把③代入②，得2m +3（2m ﹣4）＝12，解得：m ＝3，把m ＝3代入③，得n ＝2×3﹣4＝6﹣4＝2，所以原方程组的解是=3=2；（2）6−5=3①6+=−15②，②﹣①，得6t ＝﹣18，解得：t ＝﹣3，把t ＝﹣3代入①，得6s +15＝3，解得：s ＝﹣2，所以原方程组的解是=−2=−3．【点评】本题考查了解二元一次方程组，能把二元一次方程组转化成一元一次方程是解此题的关键，解二元一次方程组的方法有代入消元法和加减消元法两种．7．（2022春•泰安期中）用指定的方法解下列方程组（1）3+4=19−=4（代入消元法）；（2）2+3=−53−2=12（加减消元法）；（3−9)=6(−2)r13=2．【分析】（1）方程组利用代入消元法求出解即可；（2）方程组利用加减消元法求出解即可；（3）方程组整理后，利用加减消元法求出解即可．【解答】解：（1）3+4=19①−=4②，由②得：x ＝y +4③，把③代入①得：3（y +4）+4y ＝19，解得：y＝1，把y＝1代入③得：x＝1+4＝5，则方程组的解为=5=1；（2）2+3=−5①3−2=12②，①×2+②×3得：13x＝26，解得：x＝2，把x＝2代入①得：4+3y＝﹣5，解得：y＝﹣3，则方程组的解为=2=−3；（3）方程组整理得：5−6=33①3−4=28②，①×2﹣②×3得：x＝﹣18，把x＝﹣18代入①得：﹣90﹣6y＝33，解得：y=−412，则方程组的解为=−18=−412．【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．8．（2021秋•历下区期中）请用指定的方法解下列方程组：（1）3+2=143+4=17．（加减法）=+3；（代入法）（2）2+3=12【分析】（1）用代入消元法解方程组即可；（2）用加减消元法解方程组即可．【解答】解：（1）3+2=14①=+3②，将②代入①，得3y+9+2y＝14，解得y＝1，将y＝1代入②得x＝4，∴方程组的解为=4=1；（2）2+3=12①3+4=17②，①×3得，6x+9y＝36③，②×2得，6x+8y＝34④，③﹣④，得y＝2，将y＝2代入①得，x＝3，∴方程组的解为=3=2．【点评】本题考查二元一次方程组的解，熟练掌握代入消元法和加减消元法解二元一次方程组的方法是解题的关键．9．（2021春•沙河口区期末）用指定的方法解下列方程组：（1）=2−33+2=8（代入法）；（2）3+4=165−6=33（加减法）．【分析】（1）把①代入②得出x的值，再把x的值代入①求出y的值，从而得出方程组的解；（2）①×3+②×2得出19x＝114，求出x，把x＝6代入①求出y即可．【解答】解：（1）=2−3①3+2=8②，把①代入②得：3x+2（2x﹣3）＝8，解得：x＝2，把x＝2代入①得：y＝1，则原方程组的解是：=2=1．（2）3+4=16①5−6=33②，①×3+②×2得：19x＝114，解得：x＝6，把x＝6代入①得：18+4y＝16，解得：y=−12，所以方程组的解=6=−12．【点评】本题考查了解二元一次方程组，能把二元一次方程组转化成一元一次方程是解此题的关键．10．用指定的方法解下列方程组：（1）3+4=19−=4（代入法）；（2）2+3=−53−2=12（加减法）．【分析】（1）由②得出x＝4+y③，把③代入①得出3（4+y）+4y＝19，求出y，把y ＝1代入③求出x即可；（2）①×2+②×3得出13x＝26，求出x，把x＝2代入①求出y即可．【解答】解：（1）3+4=19①−=4②，由②得：x＝4+y③，把③代入①得：3（4+y）+4y＝19，解得：y＝1，把y＝1代入③得：x＝4+1＝5，所以方程组的解是=5=1；（2）2+3=−5①3−2=12②，①×2+②×3得：13x＝26，解得：x＝2，把x＝2代入①得：4+3y＝﹣5，解得：y＝﹣3，所以方程组的解=2=−3．【点评】本题考查了解二元一次方程组，能把二元一次方程组转化成一元一次方程是解此题的关键．1．（2022•苏州模拟）用适当的方法解下列方程组．（1）+2=9−3=1；（2−34=1−p−(−4p=4．【分析】（1）利用加减消元法，方程组可化为：7y＝28，解得：y＝4，将y＝4代入①得：x＝1；（2）先将方程组化为：8−9=12①8−5=4②，利用加减消元法解得：y＝﹣2，将y＝﹣2代入①得：=−34．【解答】解：（1）+2=9①−3=1②①×3+②得：7y＝28，解得：y＝4，将y＝4代入①得：x＝1，即方程的解为：=1=4；（2）原方程组可化为：8−9=12①8−5=4②，①﹣②得：﹣4y＝8，解得：y＝﹣2，将y＝﹣2代入①得：=−34，即方程的解为：=−34=−2．【点评】本题主要考查的是二元一次方程组的解法，利用合适的方法解方程组即可．2．（2022秋•锦江区校级期末）用适当的方法解下列方程组．（1）=2−14+3=7；（2）3+2=22+3=28，．【分析】（1）方程组利用代入消元法求解即可；（2）用方程①×3﹣②×2，可消去未知数y，求出未知数x，进而得出y的值．【解答】解：（1）=2−1①4+3=7②，把①代入②，得4（2y﹣1）+3y＝7，解得y＝1，把y＝1代入①，得x＝1，故原方程组的解为=1=1；（2）3+2=2①2+3=28②，①×3﹣②×2，得5x＝﹣50，解得x＝﹣10，把x＝﹣10代入①，得y＝16，故原方程组的解为=−10=16．【点评】本题考查了解二元一次方程组，掌握加减消元法和代入消元法是解答本题的关键．3．用适当的方法解下列方程组：（1）+2=0，3+4=6；（2=21)−=11（3）+0.4=40，0.5+0.7=35；（4K4=−14，5(r1)12=2．【分析】（1）由x+2y＝0可用y表示x，利用代入消元法求第一个方程组的解．同理解（2）（3）利用加减消元法求方程组的解．（4）对于关于m、n的方程，将其化为整系数方程时，给第一个方程两边同时乘12，给第二个方程两边同时乘12．利用加减消元法求方程组的解．【解答】解：（1）+2=0，①3+4=6；②由①，得x＝﹣2y，③把③代入②，得﹣6y+4y＝6，解得y＝﹣3，把y＝﹣3代入①，得x＝6．∴原方程组的解为=6=−3；（2=2s1)−=11②由①，得x+1＝6y，③把③代入②，得12y﹣y＝11，解得y＝1．把y＝1代入③，得x+1＝6，解得x＝5．∴原方程组的解为=5=1；（3）+0.4=40，①0.5+0.7=35；②②×2，得x+1.4y＝70，③③﹣①，得y＝30．把y＝30代入①，得x+0.4×30＝40，解得x＝28．∴原方程组的解为=28=30；（4K4=−14，5(r1)12=2，原方程组化为：+7=−3，①2−5=13，②，①×2﹣②，得19n＝﹣19，解得n＝﹣1．把n＝﹣1代入①，得m﹣7＝﹣3，解得m＝4．∴原方程组的解为=4=−1．【点评】此题主要考查了解二元一次方程组的方法，灵活运用代入消元法和加减消元法是解题的关键．4．（2022•天津模拟）用适当的方法解下列方程组：（1）+=52−=4；（2=r24−K33=112．【分析】（1）应用代入消元法，求出方程组的解即可．（2）应用加减消元法，求出方程组的解即可．【解答】解：（1）+=5①2−=4②，由①，可得：x＝5﹣y③，③代入②，可得：2（5﹣y）﹣y＝4，解得y＝2，把y＝2代入③，可得：x＝5﹣2＝3，∴原方程组的解是=3=2．（2=r24①−K33=112②，由①，可得：4x﹣3y＝2③，由②，可得：3x﹣4y＝﹣2④，③×4﹣④×3，可得7x＝14，解得x＝2，把x＝2代入③，可得：4×2﹣3y＝2，解得y＝2，∴原方程组的解是=2=2．【点评】此题主要考查了解二元一次方程组的方法，注意代入消元法和加减消元法的应用．5．（2021•越城区校级开学）用适当的方法解下列方程组：（1）2−3=7−3=7．（2）0.3+0.4=40.2+2=0.9．【分析】（1）利用加减法消元法解二元一次方程组即可；（2）先整理方程，再利用加减消元法解二元一次方程组即可．【解答】解：（1）2−3=7①−3=7②，①﹣②得x ＝0，把x ＝0代入②得0﹣3y ＝7，解得y =−73，∴方程组的解为=0=−73；（2）整理原方程组得3+4=40①2−9=−20②，①×2﹣②×3得35q ＝140，q ＝4，把q ＝4代入②得2p ﹣36＝﹣20，解得p ＝8，∴方程组的解为=8=4．【点评】本题考查了解二元一次方程组，做题关键是掌握加减消元法和代入消元法解二元一次方程组．6．（2022春•东城区校级月考）用适当的方法解下列方程组（1）+=52+=8；（2）2+3=73−2=4．【分析】（1）应用代入消元法，求出方程组的解是多少即可．（2）应用加减消元法，求出方程组的解是多少即可．【解答】解：（1）+=5①2+=8②，由①，可得：x ＝5﹣y ③，③代入②，可得：2（5﹣y ）+y ＝8，解得y ＝2，把y ＝2代入③，解得x ＝3，∴原方程组的解是=3=2．（2）2+3=7①3−2=4②，①×2+②×3，可得13x＝26，解得x＝2，把x＝2代入①，解得y＝1，∴原方程组的解是=2=1．【点评】此题主要考查了解二元一次方程组的方法，注意代入消元法和加减消元法的应用．7．（2021春•哈尔滨期末）用适当的方法解下列方程组（1）+2=93−2=−1（2）2−=53+4=2【分析】（1）利用加减消元法进行求解即可；（2）利用加减消元法进行求解即可．【解答】解：（1）+2=9①3−2=−1②，①+②得：4x＝8，解得：x＝2，把x＝2代入①得：2+2y＝9，解得：y=72，故原方程组的解是：=2=72；（2）2−=5①3+4=2②，①×4得：8x﹣4y＝20③，②+③得：11x＝22，解得：x＝2，把x＝2代入①得：4﹣y＝5，解得：y＝﹣1，故原方程组的解是：=2=−1．【点评】本题主要考查解二元一次方程组，解答的关键是熟练掌握解二元一次方程组的方法．8．（2022春•椒江区校级期中）用适当的方法解下列方程组：（1）2+3=16①+4=13②；（2）2r3=3K28=3．【分析】（1）②×2﹣①得出5y＝10，求出y，再把y＝2代入②求出x即可；（2）整理后得出得2+=9①3−2=24②，①×2+②得出7s＝42，求出s，再把s＝6代入①求出t即可．【解答】解：（1）2+3=16①+4=13②，②×2﹣①，得5y＝10，解得：y＝2，把y＝2代入②，得x+8＝13，解得：x＝5，所以方程组的解为=5=2；（2）整理方程组，得2+=9①3−2=24②，①×2+②，得7s＝42，解得：s＝6，把s＝6代入①，得12+t＝9，解得：t＝﹣3，所以方程组的解为=6=−3．【点评】本题考查了解二元一次方程组，能把二元一次方程组转化成一元一次方程是解此题的关键．9．（2022春•诸暨市期中）用适当的方法解下列方程组：（1）=2−1+2=−7（2+3=7+2=8【分析】（1）用代入消元解二元一次方程组即可；（2）用加减消元解二元一次方程组即可；【解答】解：（1）=2−1①+2=−7②，把①代入②得，x+2（2x﹣1）＝﹣7，解得x＝﹣1，将x＝﹣1代入①得y＝﹣3，∴方程组的解为=−1=−3．（2）整理得3+4=84①2+3=48②，①×2﹣②×3得，﹣y＝24，解得y＝﹣24，将y＝﹣24代入②得x＝60，∴方程组的解为=60=−24．【点评】本题考查二元一次方程组的解，熟练掌握加减消元法和代入消元法解二元一次方程组是解题的关键．10．（2021春•南湖区校级期中）用适当的方法解下列方程组：（1）3+2=9−=8；（2=r25=7．【分析】（1）由②可得x＝8+y③，再把③代入①，可得y的值，然后把y的值代入③求出x的值即可；（2）方程组整理后可得+5=0①2−5=7②，利用①+②可得x的值，然后把x的值代入①求出y的值即可．【解答】解：（1）3+2=9①−=8②，由②得，x＝8+y③，将③代入①得，3（8+y）+2y＝9，解得，y＝﹣3，把y＝﹣3代入③得，x＝5，则方程组的解为=5=−3；（2）方程组整理得：+5=0①2−5=7②，①+②得：3x＝7，解得：x=73，把x=73代入①得：y=−715，则方程组的解为=73=−715．【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．1．先阅读材料，然后解方程组：材料：解方程组+=4①3(+p+=14②在本题中，先将x+y看作一个整体，将①整体代入②，得3×4+y＝14，解得y＝2．把y＝2代入①得x＝2，所以=2=2这种解法称为“整体代入法”，你若留心观察，有很多方程组可采用此法解答，请用这种方法解方程组−−1=0①4(−p−=5②．【分析】根据阅读材料中的方法求出方程组的解即可．【解答】解：由①得：x﹣y＝1③，把③代入②得：4﹣y＝5，即y＝﹣1，把y＝﹣1代入③得：x＝0，则方程组的解为=0=−1．【点评】此题考查了解二元一次方程组，熟练掌握运算法则是解本题的关键．2．（2021秋•乐平市期末）解方程组3−2=8⋯⋯⋯①3(3−2p+4=20⋯．②时，可把①代入②得：3×8+4y＝20，求得y＝﹣1，从而进一步求得=2=−1这种解法为“整体代入法“，请用这样的方法解下列方程组2−3=123(2−3p+5=26．【分析】利用整体代入法的求解方法进行解答即可．【解答】解：2−3=12①3(2−3p+5=26②，把①代入②得：3×12+5y＝26，解得y＝﹣2，把y＝﹣2代入①得：2x+6＝12，解得x ＝3，故原方程组的解是：=3=−2．【点评】本题主要考查解二元一次方程组，解答的关键是对解二元一次方程组的方法的掌握与运用．3．先阅读，然后解方程组．解方程组−−1=0①4(−p −=5②时，可由①得x ﹣y ＝1．③，然后再将③代入②得4×1﹣y ＝5，求得y ＝﹣1，从而进一步求得=0=−1这种方法被称为“整体代入法”，请用这5=0=2+1．【分析】利用整体代入法解方程组即可．5=0①=2+1②，由①得，2x ﹣3y ＝﹣5，③，把③代入②得，10+37=2y +1，解得，y =37，把y =37代入③得，x =−137，则方程组的解为：=−137=37．【点评】本题考查的是二元一次方程组的解法，掌握整体代入法解方程组的一般步骤是解题的关键．4．（2022春•太和县期末）先阅读，然后解方程组．解方程组−−1=0①4(−p −=5②时，可由①得x ﹣y ＝1，③然后再将③代入②得4×1﹣y ＝5，求得y ＝﹣1，从而进一步求得=0①=−1②这种方法被称为“整体代入法”，2=02=9．【分析】仿照所给的题例先把①变形，再代入②中求出y 的值，进一步求出方程组的解即可．2=0①+2=9②，由①得，2x﹣3y＝2③，代入②得2+57+2y＝9，解得y＝4，把y＝4代入③得，2x﹣3×4＝2，解得x＝7．故原方程组的解为=7=4．【点评】本题考查的是在解二元一次方程组时整体思想的应用，利用整体思想可简化计算．5．先阅读，然后解方程组．解方程组−−1=0①4(−p−=5②时，可由①得x﹣y＝1③，然后再将③代入②得4×1﹣y＝5，求得y＝﹣1，从而进一步求得x这种方法被称为“整体代入法”，请用这样的方法解下列方程组：2−3−2=03(2−3p+=7．【分析】把2x﹣3y看作一个整体，代入第二个方程求出y的值，进而求出x的值即可．【解答】解：2−3−2=0①3(2−3p+=7②，把①变形得：2x﹣3y＝2③，③代入②得：6+y＝7，即y＝1，把y＝1代入③得：x＝2.5，则方程组的解为=2.5=1．【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元方法与加减消元法．1．用换元法解下列方程组+2=12−1=34【分析】方程组利用换元法求出解即可．【解答】解：设1=a，1=b，方程组变形为2+2=12①5−=34②，①+②×2得：12a＝2，解得：a=16，把a=16代入②得：b=112，则方程组的解为=16=112，即=6=12．【点评】此题考查了解二元一次方程组，熟练掌握运算法则是解本题的关键．2．用换元法解下列方程组：（1）3(p+2(−p=36(−4(−p=−16（2+r53=2−(+5p=5．【分析】（1）令x+y＝m、x﹣y＝n得关于m、n的方程组，解得m、n的值，从而可得关于x、y的方程组，求解可得；（2）令x﹣4y＝a、x+5y＝b得关于a、b的方程组，解该方程组可得a、b的值，从而可得关于x、y的方程组，求解可得．【解答】解：（1）令x+y＝m，x﹣y＝n，则原方程组可化为：3+2=36−4=−16，解得：=8=6，即+=8−=6，解得：=7=1；（2）令x﹣4y＝a，x+5y＝b，+3=2−=5，解得：=6=−3，即：−4=6+5=−3，解得：=2=−1．【点评】本题主要考查换元法解方程组的能力，熟练而准确地解方程组是基础，正确找到共同的整体加以换元是关键．3．（2022春•云阳县期中）阅读探索：解方程组(−1)+2(+2)=62(−1)+(+2)=6解：设a﹣1＝x，b+2＝y原方程组可以化为+2=62+=6，解得=2=2，即：−1=2+2=2∴=3=0，此种解方程组的方法叫换元法．（1）拓展提高运用上述方法解下列方程组(4−1)+2(5+2)=102(4−1)+(5+2)=11；（2）能力运用已知关于x，y的方程组1+1=12+2=2的解为=6=7，求关于m、n的方程组1(−2)+1(+3)=12(−2)+2(+3)=2的解．【分析】（1）仿照“阅读探索“的思路，利用换元法进行计算即可解答；（2）仿照“阅读探索“的思路，利用换元法进行计算即可解答．【解答】解：（1）设4−1＝x，5+2＝y，∴原方程组可变为：+2=102+=11，解这个方程组得：=4=3，−1=45+2=3，所以：=20=5；（2）设−2=+3=，可得：−2=6+3=7，解得：=8=4．【点评】本题考查了解二元一次方程组，二元一次方程组的解，理解并掌握例题的换元法是解题的关键．4．在学过了二元一次方程组的解法后，+K10=3①−K10=−1②，你会解这个方程组吗？小明、小刚、小芳争论了一会儿，他们分别写出了一种方法：小明：把原方程组整理得8+2=90③2+8=−30④④×4﹣③得30y＝﹣210，所以y＝﹣7把y＝﹣7代入③得8x＝104，所以x＝13，即=13=−7小刚：设r6=m，K10=n，则+=3③−=−1④③+④得m＝1，③﹣④得m＝2，=1=2，所以+=6−=20，所以=13=−7．小芳：①+②得2(rp6=2，即x+y＝6．③①﹣②得2(Kp10=4，即x﹣y＝20．④③④组成方程组得x＝13③﹣④得y＝﹣7，即=13=−7．老师看过后，非常高兴，特别是小刚的方法独特，像小刚的这种方法叫做换元法，你能用换元法解下列方程组吗？+2r37=1−2r37=5．【分析】设3K26=m，2r37=n，方程组整理后求出m与n的值，即可确定出x与y 的值．【解答】解：设3K26=m，2r37=n，方程组整理得：+=1①−=5②，①+②得：2m＝6，即m＝3，①﹣②得：2n＝﹣4，即n＝﹣2，=32r3=−2，整理得：3−2=182+3=−14，解得：=2=−6．【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．5．（2022春•卧龙区校级月考）阅读探索（1）知识积累解方程组(−1)+2(+2)=62(−1)+(+2)=6．解：设a﹣1＝x，b+2＝y．原方程组可变为+2=62+=6，解这个方程组得=2=2，即−1=2+2=2，所以=3=0，这种解方程组的方法叫换元法．（2）拓展提高运用上述方法解下列方程组：(3−1)+2(5+2)=43(3−1)−(5+2)=5．（3）能力运用已知关于x，y的方程组1+1=12+2=2的解为=3=4，请直接写出关于m、n的方程组1(+2)−1=12(+2)−2=2的解是．【分析】（2）仿照（1）的思路，利用换元法进行计算即可解答；（3）仿照前两个题的思路，利用换元法进行计算即可解答．【解答】解：（2）设3−1＝x，5+2＝y，∴原方程组可变为：+2=43−=5，解这个方程组得：=2=1，−1=25+2=1，所以：=9=−5；（3）设+2=−=，可得：+2=3−=4，解得：=1=−4．。

二元一次方程20道题

二元一次方程20道题一、基础型题目（1 - 10题）1. 已知方程2x + 3y=12，当x = 3时，求y的值。

- 解析：将x = 3代入方程2x+3y = 12中，得到2×3+3y=12，即6 + 3y=12。

方程两边同时减去6，得到3y=12 - 6=6，解得y = 2。

2. 解方程组x + y=5 x - y = 1- 解析：将两个方程相加，(x + y)+(x - y)=5 + 1，即2x=6，解得x = 3。

把x = 3代入x + y=5中，得到3+y = 5，解得y=2。

3. 若3x - 2y=11，且y = 2x - 4，求x和y的值。

- 解析：把y = 2x-4代入3x - 2y=11中，得到3x-2(2x - 4)=11，展开括号得3x-4x + 8 = 11，移项得3x-4x=11 - 8，即-x = 3，解得x=-3。

把x = - 3代入y = 2x-4，得y=2×(-3)-4=-6 - 4=-10。

4. 解方程组2x+3y = 8 3x - 2y=-1- 解析：给第一个方程2x + 3y=8两边同时乘以2，得到4x + 6y = 16；给第二个方程3x-2y=-1两边同时乘以3，得到9x-6y=-3。

将这两个新方程相加，(4x +6y)+(9x-6y)=16+(-3)，即13x = 13，解得x = 1。

把x = 1代入2x + 3y=8中，2×1+3y = 8，3y=8 - 2 = 6，解得y = 2。

5. 已知x、y满足方程4x - 3y=1，且x = 2y - 2，求x和y的值。

- 解析：将x = 2y-2代入4x-3y = 1中，得到4(2y-2)-3y = 1，展开括号得8y-8 - 3y=1，移项得8y-3y=1 + 8，5y=9，解得y=(9)/(5)。

把y=(9)/(5)代入x = 2y-2，得x=2×(9)/(5)-2=(18)/(5)-(10)/(5)=(8)/(5)。

二元一次方程组练习题(含答案)

二元一次方程组练习题(含答案)1.解下列方程组：1) 5x + 2y = 11a，-4y = 6a；2) 4x + 3y - 1 = 0，2x + y - 2 = 0；3) x + 2y/3 - 1/3 = 2，x/3 + 1 - y/2 = 1/2；4) x - y/2 = 1，x + y/2 = 3.2.求解以下方程组：1) 2x + 3y = 7，x - y = 1；2) x + 2y = 5，2x + y = 7；3) 3x + 2y = 8，4x - 3y = -11.3.已知二元一次方程y = kx + b的解有（2，5）和（-1，0）。

1) 求k，b的值；2) 当x = 2时，y的值；3) 当y = 3/5时，x的值。

4.在解方程组2x + y = 5，x - y = 1时，甲看错了方程组中的a，而得到解x = 2，y = 1.乙看错了方程组中的b，而得到解x = 3，y = -1.1) 甲把a看成了什么，乙把b看成了什么？2) 求出原方程组的正确解。

参考答案与解析：1.解下列方程组：1) 5x + 2y = 11a，-4y = 6a。

将第二个方程式化简为y = -3/2a，代入第一个方程式中得到5x + 2(-3/2a) = 11a，化简得到x = (23/10)a，y = (-9/5)a。

2) 4x + 3y - 1 = 0，2x + y - 2 = 0.将第二个方程式中的y用第一个方程式中的x表示，得到y = 2 - 2x，代入第一个方程式中得到4x + 3(2 - 2x) - 1 = 0，化简得到x = 1/2，y = 1.3) x + 2y/3 - 1/3 = 2，x/3 + 1 - y/2 = 1/2.将第二个方程式中的x用第一个方程式中的y表示，得到x = 6 - 2y，代入第一个方程式中得到6 - 4y/3 = 2，化简得到y = 3/2，x = 0.4) x - y/2 = 1，x + y/2 = 3.将两个方程式相加得到2x = 4，化简得到x = 2，代入第一个方程式中得到y = 2.2.求解以下方程组：1) 2x + 3y = 7，x - y = 1.将第二个方程式中的x用第一个方程式中的y表示，得到x = y + 1，代入第一个方程式中得到2(y + 1) + 3y = 7，化简得到y = 1，x = 2.2) x + 2y = 5，2x + y = 7.将第一个方程式中的x用第二个方程式中的y表示，得到x = (7 - y)/2，代入第一个方程式中得到(7 - y)/2 + 2y = 5，化简得到y = 1，x = 2.3) 3x + 2y = 8，4x - 3y = -11.将第一个方程式中的x用第二个方程式中的y表示，得到x = (3y - 11)/4，代入第一个方程式中得到3(3y - 11)/4 + 2y = 8，化简得到y = 1，x = 1.3.已知二元一次方程y = kx + b的解有（2，5）和（-1，0）。

二元一次方程专项练习60题+解析答案

一元二次方程专练60题一．解答题（共60小题）1．解二元一次方程组．（1）；（2）．2．解下列方程组：（1）；（2）．3．解方程组：（1）；（2）．4．解方程组．（1）；（2）．5．解方程组：（1）；（2）．6．解下列方程组：（1）；（2）．7．解方程组：（1）；（2）．8．解二元一次方程组：（1）；（2）．9．按要求解下列方程组：（1）（用代入消元法）；（2）（用加减消元法）．10．解方程组：（1）；（2）．11．解下列方程组：（1）（代入消元法）；（2）（加减消元法）．12．解下列方程组：（1）；（2）．13．用指定的方法解下列方程组：（1）（代入法）；（2）（加减法）．14．解下列方程组．（1）；（2）．15．解方程组：（1）；（2）．16．解下列方程组：（1）；（2）．17．解二元一次方程组：（1）．（2）．18．解方程组：（1）；（2）．19．解方程组：（1）；（2）．20．用适当的方法解下列方程组：（1）（2）．21．解方程组：（1）；（2）．22．解二元一次方程组：（1）；（2）．23．解二元一次方程组：（1）；（2）．24．解方程组：（1）；（2）．25．解方程组：（1）；（2）．26．解方程组：（1）；（2）．27．解方程组：（1）；（2）．28．解方程组：（1）；（2）．29．解方程组：（1）；（2）．30．解方程组：（1）；（2）．31．解方程组：（1）；（2）．32．解方程组：（1）；（2）．33．用适当的方法解方程组：（1）；（2）．34．解下列方程组：（1）；（2）．35．解方程组：（1）；（2）．36．解方程组：（1）；（2）．37．解方程组：（1）；38．解方程组：（1）；（2）．39．解方程组：（1）；（2）．40．解下列方程组：（1）；41．解下列方程组：（1）；（2）．42．用加减消元法解方程：（1）；（2）．43．解二元一次方程组：（1）；44．解方程组：（1）；（2）．45．解方程：（1）；（2）．46．用适当的方法解下列方程组：（1）；47．解方程组：（1）；（2）．48．解方程组：（1）；（2）．49．解方程组：（1）；（2）．50．解方程组：（1）；（2）．51．阅读以下材料：解方程组：；小亮在解决这个问题时，发现了一种新的方法，他把这种方法叫做“整体代入法”，解题过程如下：解：由①得x﹣y＝1③，将③代入②得：（1）请你替小亮补全完整的解题过程；（2）请你用这种方法解方程组：．52．已知关于x、y的方程组的解满足x+y ＝﹣10，求代数式m2﹣2m+1的值．53．在解方程组时，由于粗心，甲看错了方程组中的a，得解为；乙看错了方程组中的b，得解为．（1）甲把a错看成了什么？乙把b错看成了什么？（2）求出原方程组的正确解．54．已知方程组和方程组的解相同求a、b的值．55．甲和乙两人同解方程组甲因抄错了a，解得，乙因抄错了b，解得，求5a﹣2b 的值．56．对于实数x、y，定义新运算：x*y＝ax+by；其中a、b是常数，等式右边是通常的加法和乘法运算，已知1*2＝1，（﹣3）*3＝6．（1）分别求出a、b的值；（2）根据上述定义新运算，试求2*（﹣4）的值．57．甲、乙两位同学在解方程组时，甲把字母a看错了得到方程组的解为；乙把字母b看错了得到方程组的解为．（1）求a，b的正确值；（2）求原方程组的解．58．定义一种新运算“※”：规定m※n＝am+bn﹣mn，其中a，b为常数，且6※15＝270，8※10＝360，求﹣2※1的值．59．若关于x，y的方程组与方程组的解相同．（1）求两个方程组的相同解；（2）求（3a﹣b）2023的值．60．已知方程组和有相同的解，求a﹣2b的值．一元二次方程专练60题参考答案与试题解析一．解答题（共60小题）1．解二元一次方程组．（1）；（2）．【解答】解：（1）①+②，得4x＝12，∴x＝3．把x＝3代入②，得3+2y＝3，解得y＝0所以原方程组的解为；（2），②化简得：2（x﹣2）﹣3（y﹣2）＝6，即2x﹣3y＝4③，①+③得：3x＝18，解得：x＝6，将x＝6代入①得：6+3y＝14，解得：y＝，∴原方程组的解为：．2．解下列方程组：（1）；（2）．【解答】解：（1），由①得，3x+2y＝12③，②×③﹣③×2，得5y＝60，解得y＝12，将y＝12代入③，得3x+24＝12，解得x＝﹣4，∴原方程组的解为；（2），由①得x+1＝5y+10，∴x＝5y+9③，由②得6x﹣15﹣12y﹣16＝5，整理，得6x﹣12y＝36，∴x﹣2y＝6④，将③代入④，得5y+9﹣2y＝6，解得y＝﹣1，将y＝﹣1代入③，得x＝﹣5+9＝4，∴原方程组的解为．3．解方程组：（1）；（2）．【解答】解：（1），把①代入②，得3x+4x＝7，解得x＝1，把x＝1代入①，得y＝2，故原方程组的解为；（2），①+②，得6x＝24，解得x＝4，把x＝4代入②，得y＝5，故原方程组的解为．4．解方程组．（1）；（2）．【解答】解：（1），①﹣②得：9y＝18，解得：y＝2，把y＝2代入①中得：3x+10＝5，解得：x＝﹣，∴原方程组的解为：；（2）将原方程组化简整理得：，①×3得：24u+27v＝36③，③﹣②得：2v＝22，解得：v＝11，把v＝11代入①中得：8u+99＝12，解得：u＝﹣，∴原方程组的解为：．5．解方程组：（1）；（2）．【解答】解：（1），①×2﹣②得：5x＝﹣5，解得：x＝﹣1，将x＝﹣1代入①得：﹣3﹣y＝﹣4，解得：y＝1，故原方程组的解为；（2），①×5+②×3得：19x＝19，解得：x＝1，将x＝1代入①得：2+3y＝8，解得：y＝2，故原方程组的解为．6．解下列方程组：（1）；（2）．【解答】解：（1），把②代入①得，6y﹣7﹣y＝13，解得y＝4；把y＝4代入②得，x＝6×4﹣7＝17，故方程组的解为；（2），①×3﹣②×2得，6x+15y﹣6x﹣4y＝24﹣10，解得y＝，把y＝代入②得，3x+2×＝5，解得x＝，故方程组的解为．7．解方程组：（1）；（2）．【解答】解：（1），①+②×2，得11x＝33，解得：x＝3，把x＝3代入①，得9+2y＝7，解得：y＝﹣1，所以方程组的解是；（2）整理得：，①×2+②，得5x＝15，解得：x＝3，把x＝3代入①，得3+2y＝7，解得：y＝2，所以方程组的解是．8．解二元一次方程组：（1）；（2）．【解答】解：（1），①﹣②×2，得7y＝﹣14，解得y＝﹣2，将y＝﹣2代入①，得2x﹣2＝2，解得x＝2，∴原方程组的解为；（2），由①得，3x+4y＝36③，由②得3x﹣2y＝9④，③﹣④，得6y＝27，解得y＝，将y＝代入④，得3x﹣9＝9，解得x＝6，∴原方程组的解为．9．按要求解下列方程组：（1）（用代入消元法）；（2）（用加减消元法）．【解答】解：（1），由②，得y＝5﹣3x③，把③代入①，得3x+2（5﹣3x）＝7，解得x＝1，把x＝1代入①，得y＝2，故原方程组的解为；（2），①+②×2，得7x＝21，解得x＝3，把x＝3代入②，得y＝5，故原方程组的解为．10．解方程组：（1）；（2）．【解答】解：（1），①×4得：8x﹣4y＝20③，②+③得：11x＝22，解得：x＝2，把x＝2代入①得：4﹣y＝5，解得：y＝﹣1，故原方程组的解是：；（2），整理得：，①+②得：8y＝24，解得：y＝3，把y＝3代入②得：x+15＝10，解得：x＝﹣5，故原方程组的解是：．11．解下列方程组：（1）（代入消元法）；（2）（加减消元法）．【解答】解：（1），由①得：x＝1+2y③，把③代入②，得4（1+2 y）+3y＝26，解得：y＝2，把y＝2代入③，得x＝1+2×2＝5，所以；（2），由①+②，得7x＝21，解得：x＝3，把x＝3代入①，得2×3+3y＝3，解得：y＝﹣1，所以．12．解下列方程组：（1）；（2）．【解答】解：（1）将原方程组化简整理得：，②×4得：8x+20y＝28③，③﹣①得：27y＝27，解得：y＝1，把y＝1代入②中得：2x+5＝7，解得：x＝1，∴原方程组的解为：；（2）将原方程组化简整理得：，①×3得：9x﹣12y＝﹣21③，②×4得：8x+12y＝4④，③+④得：17x＝﹣17，解得：x＝﹣1，把x＝﹣1代入②中得：﹣2+3y＝1，解得：y＝1，∴原方程组的解为：．13．用指定的方法解下列方程组：（1）（代入法）；（2）（加减法）．【解答】解：（1），把①代入②得：4x+3（2x﹣2）＝5，解得x＝，把x＝代入①得：y＝2×﹣2＝，∴方程组的解为；（2），①×3得：3x+9y＝﹣3③，③﹣②得：11y＝﹣11，解得：y＝﹣1，把y＝﹣1代入①得：x﹣3＝﹣1，解得：x＝2，∴方程组的解为．14．解下列方程组．（1）；（2）．【解答】解：（1），由①+②得，5x＝﹣5，解得x＝﹣1，将x＝﹣1代入①，得﹣2+5y＝8，解得y＝2，∴方程组的解为；（2），由①×3，②×2得：，由③+④得，13x＝26，解得：x＝2，把x＝2代入①，得y＝4，所以方程组的解为：．15．解方程组：（1）；（2）．【解答】解：（1），由①得，x＝1+2y③，把③代入②，得3（1+2y）﹣y＝3，解得y＝0，把y＝0代入③，得x＝1，所以原方程组的解为：；（2）原方程组可化为，①+②得，4x＝24，解得x＝6，①﹣②得，6y＝﹣6，解得y＝﹣1，所以原方程组的解为：．16．解下列方程组：（1）；（2）．【解答】解：（1），①+②，得2x＝12，解得x＝6，将x＝6代入①，得6﹣y＝5，解得y＝1，∴原方程组的解为；（2）原方程组化为，①﹣②，得25y＝10，解得y＝，将y＝代入①，得5x+6＝6，解得x＝0，∴原方程组的解为．17．解二元一次方程组：（1）．（2）．【解答】解：（1），②﹣①×2得：x＝6，把x＝6代入①得：6+2y＝0，解得y＝﹣3．∴方程组的解是．（2），①×2+②×3得：13x＝65，解得x＝5．把x＝5代入①得：10+3y＝16，解得y＝2．∴方程组的解是．18．解方程组：（1）；（2）．【解答】解：（1）对于方程组，①×2得：4x﹣10y＝24③，②﹣③得：﹣13y＝26，∴y＝﹣2，将y＝﹣2代入①得：x＝1，∴原方程组的解为：．（2）对于方程组，将①代入②得：2×2y+y＝5，∴y＝1，将y＝1代入①得：x＝2，∴原方程组的解为：．19．解方程组：（1）；（2）．【解答】解：（1），①+②得4x＝8，∴x＝2，把x＝2代入①得2+2y＝3，，∴原方程组的解是．（2），整理得：，由①得：s＝﹣2t③，把③代入②得：t＝﹣2；把t＝﹣2 代入③得：s＝4，∴原方程组的解是．20．用适当的方法解下列方程组：（1）（2）．【解答】解：（1），①+②得：6x＝18，解得：x＝3，把x＝3代入①得：y＝﹣4，则方程组的解为；（2），把①代入②得：4x﹣14＝2，解得：x＝4，把x＝4代入①得：y＝3，则方程组的解为．21．解方程组：（1）；（2）．【解答】解：（1），原方程可化为：，①+②×5得：46y＝46，∴y＝1，将y＝1代入①得：x＝7，∴原方程组得解为：；（2），原方程可化为：，①×4+②得：19x＝57，∴x＝3，将x＝3代入①得：y＝0，∴原方程组得解为：．22．解二元一次方程组：（1）；（2）．【解答】解：（1），②﹣①，得y＝1，把y＝1代入①，得x＝2，故原方程组的解为；（2）原方程组整理，得，②﹣①×2，得7y＝7，解得y＝1，把y＝1代入①，得x＝5．故原方程组的解为．23．解二元一次方程组：（1）；（2）．【解答】解：（1），由②得y＝13﹣2x③，把③代入①，得4x﹣3（13﹣2x）＝11，解得x＝5，把x＝5代入③，得y＝3，∴这个方程组的解是；（2），①×2﹣②×3，得﹣19y＝19，解得y＝﹣1．把y＝﹣1代入①，得3x+2＝5，解得x＝1，∴这个方程组的解为．24．解方程组：（1）；（2）．【解答】解：（1），把①代入②，得3x﹣8（x﹣3）＝14，解得x＝2，把x＝2代入①，得y＝﹣1，故原方程组的解为；（2），①×2﹣②，得7x＝35，解得x＝5，把x＝5代入①，得y＝0，故原方程组的解为．25．解方程组：（1）；（2）．【解答】解：（1），由①+②得：4x＝8，解得：x＝2，将x＝2代入①得：2﹣2y＝1，解得：y＝，∴方程组的解为：；（2），由①可得：x＝3﹣2y③，将③代入②得：3（3﹣2y）﹣4y＝4，解得：y＝，将y＝代入③得：x＝3﹣2×，解得：x＝2，∴原方程组的解为：．26．解方程组：（1）；（2）．【解答】解：（1），①×2得：4x﹣2y＝0③，②+③得：5x＝5，解得：x＝1，把x＝1代入①中得：y＝2，∴原方程组的解为：．（2），②×2，8x﹣2y＝6③，①+③得：11x＝11，解得：x＝1，把x＝1代入②，得4﹣y＝3，解得：y＝1，∴原方程组的解为：．27．解方程组：（1）；（2）．【解答】解：（1），①+②，得7x＝35，解得：x＝5，把x＝5代入①，得10﹣3y＝﹣2，解得：y＝4，所以方程组的解是；（2），①+②×2，得11x＝11，解得：x＝1，把x＝1代入②，得4﹣y＝3，解得：y＝1，所以方程组的解是．28．解方程组：（1）；（2）．【解答】解：（1），把②代入①得y﹣9+3y＝7，解得y＝4，把y＝4代入②得x＝4﹣9＝﹣5，所以方程组的解为；（2），①×2+②得10x+3x＝34+5，解得x＝3，把x＝3代入②得9+4y＝5，解得y＝﹣1，所以方程组的解为．29．解方程组：（1）；（2）．【解答】解：（1），①+②得：4x＝8，解得：x＝2，把x＝2代入①得：2+2y＝﹣1，解得：，∴方程组的解为；（2），由②得：y＝2x﹣2，把y＝2x﹣2代入①得：4x﹣3（2x﹣2）＝5，解得：，把代入y＝2x﹣2得：，∴方程组的解为．30．解方程组：（1）；（2）．【解答】解：（1），将①代入②，可得：3x+2x+3＝18，解得x＝3，把x＝3代入①，可得：y＝9，∴原方程组的解是．（2），①×2﹣②，可得7y＝35，解得y＝5，把y＝5代入①，可得：x＝0，∴原方程组的解是．31．解方程组：（1）；（2）．【解答】解：（1），把①代入②得：3x+2（2x﹣1）＝5，解得：x＝1，把x＝1代入①得：y＝2﹣1＝1，故原方程组的解是：；（2），①+②得：3m＝6，解得：m＝2，把m＝2代入①得：2+3n＝5，解得：n＝1，故原方程组的解是：．32．解方程组：（1）；（2）．【解答】解：（1）把②代入①中，得3x+2（2x﹣8）＝5．解得x＝3．把x＝3代入②中，得y＝2×3﹣8解得y＝﹣2．∴这个方程组的解为；（2）①﹣②，得﹣4y＝8．解得y＝﹣2．把y＝﹣2代入①中，得2x+2＝10．解得x＝4．∴这个方程组的解为．33．用适当的方法解方程组：（1）；（2）．【解答】解：（1），②﹣①×3得：x＝1，把x＝1代入①中，解得：y＝1，∴这个方程组的解为；（2）方程组整理为：，②×2+①得：5x＝30，解得：x＝6，把x＝6代入②中，解得：y＝9，∴这个方程组的解为．34．解下列方程组：（1）；（2）．【解答】解：（1），将①代入②，得：3x﹣2（2x+1）＝2，解得：x＝﹣4，把x＝﹣4代入①得：y＝﹣7，∴方程组的解为：；（2）①×2+②，得：5x＝10，解得：x＝2，把x＝2代入①，得：4+y＝1，解得：y＝﹣3，∴方程组的解为：．35．解方程组：（1）；（2）．【解答】解：（1），①+②得，7x＝14，解得x＝2，把x＝2代入①得，3×2+7y＝9，解得y＝，∴方程组的解是；（2），①×3得，15x+6y＝12③，②×2得，16x+6y＝14④，④﹣③得，x＝2，把x＝2代入①得，y＝﹣3，∴方程组的解是．36．解方程组：（1）；（2）．【解答】解：（1），②﹣①得：y＝2，把y＝2代入①得：，∴方程组的解为：；（2），由③得：y＝3﹣2x，把y＝3﹣2x代入④得：3x﹣5（3﹣2x）＝11，3x﹣15+10x＝11，13x＝26，x＝2，把x＝2代入y＝3﹣2x得：y＝﹣1，∴方程组的解为：．37．解方程组：（1）；（2）．【解答】解：（1），①×3得：3x﹣15y＝0③，②﹣③得：17y＝17，解得：y＝1，把y＝1代入①得：x﹣5＝0，解得：x＝5，∴原方程组的解为：；（2），把①代入②得：y﹣13﹣6y＝7，解得：y＝﹣4，把y＝﹣4代入①得：x＝﹣4﹣13＝﹣17，∴原方程组的解为：．38．解方程组：（1）；（2）．【解答】解：（1），①+②得：5x＝25，解得：x＝5，把x＝5代入①得：5﹣3y＝10，解得：y＝﹣，故原方程组的解是：；（2），由①得：3x﹣2y＝8③，②+③得：6x＝12，解得：x＝2，把x＝2代入②得：6+2y＝4，解得：y＝﹣1，故原方程组的解是：．39．解方程组：（1）；（2）．【解答】解：（1），①+②得：3x＝12，解得：x＝4，把x＝4代入①得：4﹣y＝2，解得：y＝2，则方程组的解为；（2）方程组整理得：，①×4﹣②×3得：﹣7x＝﹣14，解得：x＝2，把x＝2代入①得：4﹣3y＝1，解得：y＝1，则方程组的解为．40．解下列方程组：（1）；（2）．【解答】解：（1），由①，得x＝y+3③，把③代入②，得3y+9﹣8y＝14，解得y＝﹣1，把y＝﹣1代入①，得x＝2，故原方程组的解为；（2），①×2+②，得11x＝11，解得x＝1，把x＝1代入①，得x＝﹣2，故原方程组的解为．41．解下列方程组：（1）；（2）．【解答】解：（1），②代入①，可得x+2x﹣1＝2，解得，x＝1，将x＝1代入②，可得y＝1，故方程组的解为．（2），②﹣①，可得，解得，x＝3，将x＝3代入①，可得y＝2，故方程组的解为．42．用加减消元法解方程：（1）；（2）．【解答】解：（1），①﹣②得：12y＝﹣36，即y＝﹣3，把y＝﹣3代入①得：x＝，则方程组的解为；（2）方程组整理得：，①﹣②得：4y＝28，即y＝7，把y＝7代入①得：x＝5，则方程组的解为．43．解二元一次方程组：（1）；（2）．【解答】解：（1）方程整理得，由①+②得：5a+5b＝﹣5，即a+b＝﹣1③，由①﹣③×2得：b＝1，把b＝1代入③得：a+1＝﹣1，解得a＝﹣2，∴方程组的解是．（2），由②得：x＝3y﹣2③，把③代入①得：9（3y﹣2）﹣7y﹣12＝0，解得y＝，把y＝代入③得x＝﹣2＝，∴方程组的解是．44．解方程组：（1）；（2）．【解答】解：（1），解：①+②得3x＝33，解得x＝11，把x＝11代入①得y＝14，∴方程组的解是；（2），解：原方程组可化为，①﹣②得6x＝6，解得x＝1，把x＝1代入①得，∴方程组的解是．45．解方程：（1）；（2）．【解答】解：（1），①代入②得，2x+（3x+1）＝﹣9，解得：x＝﹣2，将x＝﹣2代入①得，y＝﹣5，∴方程组的解为：；（2），①×2+②得，6x+x＝14，解得：x＝2，将x＝2代入①得6﹣2y＝5，解得：，∴方程组的解为：．46．用适当的方法解下列方程组：（1）；（2）．【解答】解：（1），由①﹣②×2得：3y﹣（﹣2y）＝1﹣5×2，解得：，将代入②得：，解得：，∴原方程组的解为；（2），由①×2+②得：7x＝14，解得：x＝2，把x＝2代入①得：2×2+y＝2，解得：y＝﹣2，∴原方程组的解为．47．解方程组：（1）；（2）．【解答】解：（1），①×3+②得：7y＝28，解得：y＝4，将y＝4代入①得：x＝1，∴方程组的解为：；（2）整理得：，①+②×5得：23y＝23，解得y＝1，把y＝1代入①得：5x﹣2＝﹣12，解得x＝﹣2，∴方程组的解为．48．解方程组：（1）；（2）．【解答】解：（1），①+②得，2x＝6，解得：x＝3，把x＝3代入①得y＝﹣1，∴方程组的解为；（2），①×2，得10x+4y＝50③，③﹣②，得7x＝35，解得：x＝5，把x＝5代入①得，25+2y＝25，解得：y＝0，所以方程组的解为．49．解方程组：（1）；（2）．【解答】解：（1），整理得：，由①﹣②得：4y＝28，解得：y＝7，把y＝7代入①得：3x﹣7＝8，解得：x＝5，∴原方程组的解为：；（2），由②﹣①得：5x＝15，解得：x＝3，把x＝3代入①得：y﹣2×3＝0，解得：y＝6，∴原方程组的解为．50．解方程组：（1）；（2）．【解答】解：（1），②×3得：15x+3y＝21③，①+③得：19x＝38，解得：x＝2，把x＝2代入②得：10+y＝7，解得：y＝﹣3，故原方程组的解是：；（2），①×2得：2x﹣4y＝16③，②+③得：5x＝10，解得：x＝2，把x＝2代入①得：2﹣2y＝8，解得：y＝﹣3，故原方程组的解是：．51．阅读以下材料：解方程组：；小亮在解决这个问题时，发现了一种新的方法，他把这种方法叫做“整体代入法”，解题过程如下：解：由①得x﹣y＝1③，将③代入②得：（1）请你替小亮补全完整的解题过程；（2）请你用这种方法解方程组：．【解答】解：（1）由①得x﹣y＝1③，将③代入②得：4×1﹣y＝0，解得y＝4，把y＝4代入①得：x﹣4﹣1＝0，解得x＝5，故原方程组的解是：；（2），整理得：，把③代入④得：2×2+1+15y＝50，解得y＝3，把y＝3代入①得：3x﹣3﹣2＝0，解得x＝，故原方程组的解是：．52．已知关于x、y的方程组的解满足x+y ＝﹣10，求代数式m2﹣2m+1的值．【解答】解：，①×2﹣②×3得：y＝4﹣m，把y＝4﹣m代入②得：x＝2m﹣6，代入x+y＝﹣10得：4﹣m+2m﹣6＝﹣10，解得：m＝﹣8，则原式＝（m﹣1）2＝81．53．在解方程组时，由于粗心，甲看错了方程组中的a，得解为；乙看错了方程组中的b，得解为．（1）甲把a错看成了什么？乙把b错看成了什么？（2）求出原方程组的正确解．【解答】解：（1）将x＝，y＝﹣2代入方程组得：，解得：，将x＝3，y＝﹣7代入方程组得：，解得：，则甲把a错看成了1；乙把b错看成了1；（2）根据（1）得正确的a＝2，b＝3，则方程组为，解得：．54．已知方程组和方程组的解相同求a、b的值．【解答】解：方程组的解为，由于方程组和方程组的解相同，所以，解得．55．甲和乙两人同解方程组甲因抄错了a，解得，乙因抄错了b，解得，求5a﹣2b的值．【解答】解：由题意，是bx+y＝12的解得5b+2＝12，解得b＝2．又是x+ay＝5的解得3+2a＝5，解得a＝1，∴5a﹣2b＝5×1﹣2×2＝1．56．对于实数x、y，定义新运算：x*y＝ax+by；其中a、b是常数，等式右边是通常的加法和乘法运算，已知1*2＝1，（﹣3）*3＝6．（1）分别求出a、b的值；（2）根据上述定义新运算，试求2*（﹣4）的值．【解答】解：（1）根据题中的新定义化简得：，解得：；（2）根据题中的新定义得：原式＝2×（﹣1）+（﹣4）×1＝﹣2﹣4＝﹣6．57．甲、乙两位同学在解方程组时，甲把字母a看错了得到方程组的解为；乙把字母b看错了得到方程组的解为．（1）求a，b的正确值；（2）求原方程组的解．【解答】解：（1）由题意，将代入bx﹣4y＝4，得4b﹣4＝4，∴b＝2，将代入ax+3y＝9，得3a+6＝9，∴a＝1；（2），①×2﹣②，得y＝1.4，将y＝1.4代入①得，x＝4.8，∴方程组的解为．58．定义一种新运算“※”：规定m※n＝am+bn﹣mn，其中a，b为常数，且6※15＝270，8※10＝360，求﹣2※1的值．【解答】解：∵6※15＝270，8※10＝360，∴，解得：，∴﹣2※1＝﹣100+4﹣（﹣2）×1＝﹣94．59．若关于x，y的方程组与方程组的解相同．（1）求两个方程组的相同解；（2）求（3a﹣b）2023的值．【解答】解：（1）两方程组化简可得，，∵两方程组同解，∴①×2+②得：7x＝21，解得：x＝3，把x＝3代入①式得：y＝1，∴两个方程组的相同解为；（2）把代入方程组可得：①﹣②式得：2a＝﹣4，解得：a＝﹣2，把a＝﹣2代入②式得：b＝﹣5，∴（3a﹣b）2023＝（﹣6+5）2023＝﹣1．60．已知方程组和有相同的解，求a﹣2b的值．【解答】解：联立得：，①×2+②得：11x＝11，解得：x＝1，把x＝1代入②得：y＝﹣2，把代入，得，解得：，则a﹣2b＝14﹣4＝10．。

(完整版)解二元一次方程组基础练习

二元一次方程练习题及答案

二元一次方程组解法练习题精选(含答案)

（完整版）解二元一次方程组基础练习

二元一次方程组解法练习题精选(含答案)

解二元一次方程50道练习题(带答案)

二元一次方程组解法练习题精选(含答案)

专题解二元一次方程组(计算题50题)(原卷版)

二元一次方程组练习题(含答案)

二元一次方程组(例题、解方程组、练习及答案)

二元一次方程组解法练习题精选(含答案)

七年级数学下册 专题 解二元一次方程组(计算题50题)(解析版)

二元一次方程20道题

二元一次方程组练习题(含答案)

二元一次方程专项练习60题+解析答案

七年级数学下册专题解二元一次方程组(计算题50题)(解析版)