载流线圈在均匀磁场中受到的磁力矩
大学物理10.6 磁场对载流线圈的作用Xiao

10.6
M
M m B
南 京 理 工
大 学
矢量式 mB sin m B
应 用 物 理 系
IB sin dS IB sin dS IBS sin
dM
磁场对载流线圈的作用 磁力的功 M mB sin 讨论: M m B 1)n 方向与 B 相同 2)方向相反 3)方向垂直 稳定平衡 不稳定平衡 力矩最大 . . . . .
dF Idl B sin IBdl cos
y
B
J
把线圈分成左右两半: 右半边: 受力垂直于纸面向里
cos 0 , dF 0
I
Q
z
用 物 理
R
o P
Id l
B
K x
左半边: 受力垂直于纸面向外
cos 0 , dF 0
南 京 理 工 大 学 应
C C’
F BIl A Fl AA' BIll AA'
BIS
A I
南 京 理 工 大 学
磁力所做的功,等于电 流与穿过电流回路的磁 通量的增量的乘积。
应 用 物 理 系
10.6
磁场对载流线圈的作用
磁力的功
2 .载流线圈在磁场中转动时磁力矩的功 匀强磁场B, 线圈转动过程中, 电流保持不变. 磁力矩 M BIS sin d 0 功 dA Md BIS sin d Id ( BS cos )
10.6 磁场对载流线圈的作用 磁力的功
南
京
理
工
大
学
应
用
物
理
大学物理磁学部分复习资料..

41 磁 学基本内容一、稳恒磁场 磁感应强度1. 稳恒磁场电流、运动电荷、永久磁体在周围空间激发磁场。
稳恒磁场是指不随时间变化的磁场。
稳恒电流激发的磁场是一种稳恒磁场。
2. 物质磁性的电本质无论是永磁体还是导线中的电流,它们的磁效应的根源都是电荷的运动。
因此,磁场是运动电荷的场。
3. 磁感应强度磁感应强度B是描述磁场的基本物理量,它的作用与E 在描述电场时的作用相当。
磁场对处于其中的载流导线、运动电荷、载流线圈、永久磁体有力及力矩的作用。
可以根据这些作用确定一点处磁场的强弱和方向——磁感应强度B。
带电q 的正点电荷在磁场中以速度v运动,若在某点不受磁力,则该点磁感应强度B 的方向必与电荷通过该点的速度v平行。
当该电荷以垂直于磁感应强度B 通过该点时受磁力⊥F ,则该点磁感应强度大小qvF B ⊥=,且⊥F ,v ,B两两互相垂直并构成右手系。
二、毕奥—萨伐尔定律 运动电荷的磁场1. 磁场的叠加原理空间一点的磁感强度等于各电流单独存在时在该点产生磁感应强度的矢量和:∑=ii B B 可推广为 ⎰=B d B42B d是电流强度有限而长度无限小的电流元l d I 或电流强度无限小而空间大小不是无限小的元电流的磁场。
上式中矢量号一般不能略去,只有当各电流产生磁场方向相同时,才能去掉矢量号。
2. 毕奥—萨伐尔定律电流元l d I 在空间一点产生的磁场B d为: 304rr l d I B d πμ⨯= 大小: 02I sin(I ,r)dB 4r dl dl μπ∠=方向:B d 垂直于电流元l d I 与r 所形成的平面,且B d与l d I 、r构成右手螺旋。
3. 电流与运动电荷的关系导体中电荷定向运动形成电流,设导体截面积为S ,单位体积载流子数为n 。
每个载流子带电q ,定向运动速率为v ,则nqvS I =。
电量为q 的带电体作半径为R 、周期为T 的匀速圆周运动相当于半径为R 、电流强度T q I /=的圆电流,具有磁矩TqR I R p m 22ππ==。
闭合载流线圈在均匀磁场中受到的磁力矩

闭合载流线圈在均匀磁场中受到的磁力矩闭合载流线圈是一种重要的电磁元件,广泛应用于电机、发电机、电磁铁等各种电气装置中。
当闭合载流线圈置于均匀磁场中时,它会受到一个方向垂直于磁感线并且大小与线圈电流、线圈面积、磁场强度及线圈法向距离等因素有关的磁力矩。
1.磁力矩的定义磁力矩是一个物理量,它描述了由于磁场对于磁性物体的影响而使得物体发生转动的程度。
它是一个矢量量,它的方向是线圈所受合力的方向,大小是线圈上的每一个磁偶极子受到的力矩之和。
当闭合载流线圈放置于均匀磁场中时,由于磁场的存在,线圈内部会形成电动势,并且通过取样线圈可以检测到这个电动势的变化。
2.线圈受力的基本原理设线圈的面积为S,通电的电流为I,线圈中的磁感应强度为B。
此时,线圈所受的合力矩大小M可以表示为M=nBSIr sinθ 其中,n是线圈的匝数,r是线圈法向距离,θ是约定线圈法线和磁场方向的夹角。
有上式可知:当线圈和磁场方向成0度或180度时,磁力矩为零;当磁场方向与线圈法线垂直时,磁力矩最大。
3.线圈的应用线圈的应用范围广泛,众多的电磁元件就是利用了磁力矩原理来实现的。
例如,电机、发电机、电磁铁都是利用线圈在磁场中受到磁力矩产生转动或制动的原理。
在电磁悬浮列车的轴承系统中,也是利用了线圈受到磁力矩产生的转动来实现轴承的功能;在核磁共振成像中也有应用,我们需要将一个原子核置于包含强磁场的线圈中,当我们加热样品时,原子核将产生旋转,进而形成一个拥有一定的自旋磁矩,利用线圈接收这个磁场信号就可以得到影像。
总的来说,闭合载流线圈在均匀磁场中受到的磁力矩,它是众多电磁装置的基础,它的性质和应用决定了许多机械和电磁设备的性能和功能,对于电子信息行业的发展有着至关重要的作用。
第9章-10章磁介质电磁感应

D
在有磁介质时,一般根据自由电流的分布求 H 的分布, 再利用 B H ,求 B 。
[例] 无限长直螺线管,电流为 I,单位长度的匝数为 n, 管内充满磁导率为 r 的均匀介质,求管内的磁感应强 度
解: 无限长螺线管外磁场为零 B外 = 0,内部磁场与轴线平行,根 据 H 的环路定理,磁场强度沿如图所示矩形回路的积分为
无 L E dl 0
旋 L D dl 0
静电场
q 点电荷 E e ˆ 2 r 电场 4 π 0 r
E dE
ˆ 电流元 0 Idl er dB 磁场 4π r 2 B dB
无限长 直电流
稳恒磁场
λ 无限长 E 带电线 2π 0 r
[例] 一无限长同轴电缆,内导体的半径和外导体圆柱面半径分 别为 R1 和 R2,它们之间充满相对磁导率为 r 的均匀磁介 质,内外导体中均匀地载有大小相等方向相反的电流 I, 设导体的 0。求:(1) 磁介质内的磁感应强度分布; ( 2 ) 圆 柱 体 内 的 磁场;(3)同轴电缆外的磁场。 解:(1) 由对称性,轴线等距离的各点 H 应 I 相等,方向与径向垂直。作圆形安培 环路 L,利用 H 的环路定理,有:
6. 一面积为 S,载有电流 I 的平面闭合线圈置于磁感应强度为 B
的均匀磁场中,此线圈受到的最大磁力矩的大小为 ISB , 此时通过线圈的磁通量为 0 。当此线圈受到最小的磁力 SB 。 矩作用时,线圈的磁通量为
7. 有一半径为 a,通有稳恒电流 I 的四分 之一圆弧形载流导线 CB,处于均匀磁 场 B 中,则该载流导线所受安培力的 大小为 IaB ,方向为 垂直纸面向里 。
H dl 2 πrH = I L I H 2π r 0 r I B = 0 r H 2π r
大学物理八九章部分习题解答

第8章 磁场8-10一均匀密绕直螺线管的半径为 ,单位长度上有 匝线圈,每匝线圈中的电流为 ,用毕奥—萨伐尔定律求此螺线管轴线上的磁场。
分析:由于线圈密绕,因此可以近似地把螺线管看成一系列圆电流的紧密排列,且每一匝圆电流在轴线上任一点的磁场均沿轴向。
解: 取通过螺线管的轴线并与电流形成右旋的方向(即磁场的方向)为x 轴正向,如习题8-10图解(a )所示。
在螺线管上任取一段微元dx ,则通过它的电流为dI nIdx =,把它看成一个圆线圈,它在轴线上O 点产生的磁感应强度dB 为2022322()R nIdxdB R x μ=+ 由叠加原理可得,整个螺线管在O 点产生的磁感应强度B 的大小为212022322()x Lx R nIdxB dB R x μ==+⎰⎰0212212221221[]2()()nIx x R x R x μ=-++ 由图可知12122212221212cos os ()()x x R x R x ββ==++ c ,代入上式并整理可得 021(cos cos )2nIB μββ=-式中12ββ和分别为x 轴正向与从O 点引向螺线管两端的矢径r 之间的夹角。
讨论:(1)若螺线管的长度远远大于其直径,即螺线管可视为无限长时,20β=,1βπ=,则有nI B 0μ=上式说明,无限长密绕长直螺线管内部轴线上各点磁感应强度为常矢量。
理论和实验均证明:在整个无限长螺线管内部空间里,上述结论也适用。
即无限长螺线管内部空间里的磁场为均匀磁场,其磁感应强度B 的大小为0nI μ,方向与轴线平行;(2)若点O 位于半无限长载流螺线管一端,即12πβ=,20β=或12πβ=,2βπ=时,无论哪一种情况均有nI B 021μ=------(8-19) 可见半无限长螺线管端面中心轴线上磁感应强度的大小为管内的一半;综上所述,密绕长直螺线管轴线上各处磁感应强度分布见习题8-10图解(b )所示,从图中也可看出,长直螺线管内中部的磁场可以看成是均匀的。
大学物理复习题

图1-9 1-9(1-121、静电场的高斯定理描述了它是 场。
2、在点电荷+q 的电场中,若取图1-2中P 点处电势为零点,则M 点的电势为: 。
3、如图1-3电路中两个电容器1和2,串联以后接上电动势恒定的电源充电。
在电源保持联接的情况下,若把电介质充入电容器2中,则电容器1上的电势差 电容器1极板上的电量 ;电容器2上的电势差 电容器2极板上的电量 。
(填增大、减小、不变) 5、载有电流为I 的无限长导线,弯成如图1-5所示形状,其中有一部分为半径为R 的半圆弧,则其圆心O 点的磁感应强度的大小为 ,方向为 。
6、闭合导体回路电阻R =5 ,回路所包围面积为0.08m 2,均匀磁场垂直于线圈平面。
欲使电路中有一稳定的感应电流i = 0.08 A ,则磁感应强度的变化率为:d B /d t = T/s 。
7、产生动生电动势和感生电动势的非静电力分别为 、 。
8、磁场能量密度为: ,电场能量密度为: 。
一个电容器加了电压之后储存的电场的能量为: 。
一个自感回路,其中通有电流时,其周围空间磁场的能量为: 。
9、如图1-9,一个矩形线圈与通有相同大小电流的平行直导线在同一平面,而且处在两导线的中央,如图(1-9)所示。
(1)两电流同向且随时间均匀增大时,线圈中有无感应电流 。
(2)两电流反向且随时间均匀增大时,线圈中有无感应电流 。
10、真空中两只长直螺线管1和2,长度相等,单层密绕匝数相同,直径之比d 1/d 2 =1/2,当它们通以相同电流时,两螺线管贮存的磁能之比为W 1/W 2= 。
11、杨氏双缝干涉实验时,用红光和绿光分别做实验时,红光的干涉条纹间距比绿光图1-3图1-5 图1-2的 。
(填:宽 或 窄)。
12、获得相干光常用的方法有两种是: , 。
13、波长为 的单色光垂直照射到宽a 的单缝上,单缝后面放置一个凸透镜, 在凸透镜的焦平面上放置一个屏幕,用以观测衍射条纹,今测得屏幕上中央明条纹两侧第二级暗纹之间的距离为 d ,则透镜的焦距 f 为: 。
大学物理电磁学知识点总结

大学物理电磁学知识点总结篇一:大学物理电磁学知识点总结大学物理电磁学总结一、三大定律库仑定律:在真空中,两个静止的点电荷q1和q2之间的静电相互作用力与这两个点电荷所带电荷量的乘积成正比,与它们之间距离的平方成反比,作用力的方向沿着两个点电荷的连线,同号电荷相斥,异号电荷相吸。
uuurqqurF21=k122errurur高斯定理:a)静电场:Φe=EdS=∫s∑qiiε0(真空中)b)稳恒磁场:Φm=uurrBdS=0∫s环路定理:a)静电场的环路定理:b)安培环路定理:二、对比总结电与磁∫LurrLEdl=0∫urrBdl=0∑Ii(真空中)L电磁学静电场稳恒磁场稳恒磁场电场强度:E磁感应强度:B定义:B=ururF定义:E=(N/C)q0基本计算方法:1、点电荷电场强度:E=urrurdF(dF=Idl×B)(T)Idlsinθ方向:沿该点处静止小磁针的N极指向。
基本计算方法:urqurer4πε0r21ruruIdl×er0r1、毕奥-萨伐尔定律:dB=24πr2、连续分布的电流元的磁场强度:2、电场强度叠加原理:urnur1E=∑Ei=4πε0i=1rqiuueri∑r2i=1inrururur0Idl×erB=∫dB=∫4πr23、安培环路定理(后面介绍)4、通过磁通量解得(后面介绍) 3、连续分布电荷的电场强度:urρdVurE=∫ev4πεr2r0urdSururλdlurE=∫er,E=∫es4πεr2l4πεr2r004、高斯定理(后面介绍)5、通过电势解得(后面介绍)几种常见的带电体的电场强度公式:几种常见的磁感应强度公式:1、无限长直载流导线外:B=2、圆电流圆心处:电流轴线上:B=ur1、点电荷:E=qurer4πε0r210I2R0I2πr2、均匀带电圆环轴线上一点:urE=B=3、圆rqxi22324πε0(R+x)R2IN2(x2+R2)3210α23、均匀带电无限大平面:E=2ε0(N为线圈匝数)4、无限大均匀载流平面:B=4、均匀带电球壳:E=0(r<R)(α是流过单位宽度的电流)urE=qurer(r>R)4πε0r25、无限长密绕直螺线管内部:B=0nI(n是单位长度上的线圈匝数)6、一段载流圆弧线在圆心处:B=(是弧度角,以弧度为单位)7、圆盘圆心处:B=rurqr(rR)20I4πR0ωR2(是圆盘电荷面密度,ω圆盘转动的角速度)6、无限长直导线:E=λ2πε0xλ0(r>R)2πε0r7、无限长直圆柱体:E=E=λr(r<R)4πε0R2电场强度通量:N·m2·c-1)(磁通量:wb)(sΦe=∫dΦe=∫EcosθdS=∫ssururEdS通量uurrΦm=∫dΦm=∫BdS=∫BcosθdSsss若为闭合曲面:Φe=∫sururEdS若为闭合曲面:uurrΦm=BdS=BcosθdS∫∫ss均匀电场通过闭合曲面的通量为零。
第6章 稳恒磁场习题

1第6章 稳恒电流的磁场一 基本要求1. 掌握磁感应强度B的概念。
2. 掌握毕奥-萨伐尔定律,并能用该定律计算一些简单问题中的磁感应强度。
3. 掌握用安培环路定律计算磁感应强度的条件及方法,并能熟练应用。
4. 理解磁场高斯定理。
5. 了解运动电荷的磁场。
6. 理解安培定律,能用安培定律计算简单几何形状的载流导体所受到的磁场力。
7. 理解磁矩的概念,能计算平面载流线圈在均匀磁场中所受到的磁力矩,了解磁力矩所作的功。
8. 理解并能运用洛伦兹力公式分析点电荷在均匀磁场(包括纯电场、纯磁场)中的受力和运动的简单情况。
9. 了解霍耳效应。
10. 了解磁化现象及其微观解释。
11. 了解磁介质的高斯定理和安培环路定理,能用安培环路定理处理较简单的介质中的磁场问题。
12. 了解各向同性介质中H 与B的联系与区别。
13. 了解铁磁质的特性。
二 内容提要1. 毕奥-萨伐尔定律 电流元Id l 在真空中某一场点产生的磁感应强度d B 的大小与电流元的大小、电流元到该点的位矢r与电流元的夹角θ的正弦的乘积成正比,与位矢大小的平方成反比,即204r l I B θπμsin d d =dB 的方向与r l I⨯d 相同,其矢量式为304r rl I B⨯=d d πμ 2. 几种载流导体的磁场 利用毕奥-萨伐尔定律可以导出几种载流导体磁场的分布,这些结果均可作公式应用。
(1)有限长直载流导线的磁感应强度的大小)cos (cos π2104θθμ-=aIB方向与电流成右手螺旋关系。
式中,a 为场点到载流直导线的距离,21θθ、分别为直导线始末两端到场点的连线与电场方向的夹角。
2(2)长载流直导线(无限长载流直导线)的磁感应强度的大小rIB πμ20=方向与电流成右手螺旋关系。
(3) 直载流导线延长线上的的磁感应强度 0=B(4) 载流圆导线(圆电流)轴线上的磁感应强度的大小2322202)(x R IR B +μ=方向沿轴线,与电流成右手螺旋关系。
大物磁场答案
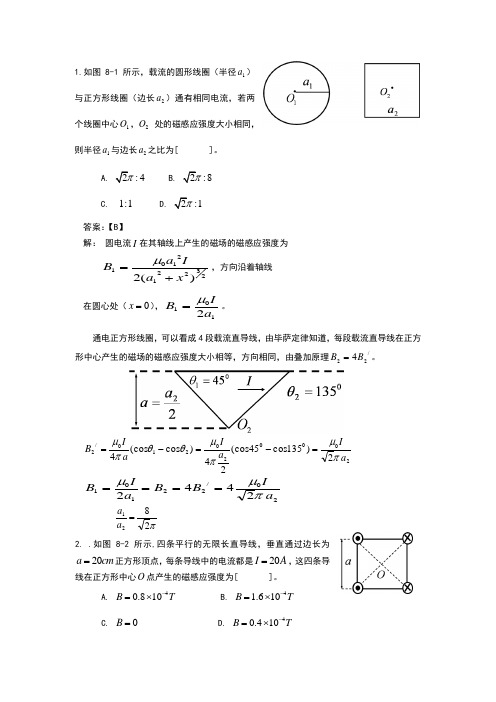
1.如图8-1所示,载流的圆形线圈(半径1a )与正方形线圈(边长2a )通有相同电流,若两个线圈中心1O ,2O 处的磁感应强度大小相同,则半径1a 与边长2a 之比为[ ]。
A. 2:4πB. 2:8πC. 1:1D. 2:1π答案:【B 】解: 圆电流I 在其轴线上产生的磁场的磁感应强度为232212101)(2x a Ia B +=μ,方向沿着轴线 在圆心处(0=x ),1012a IB μ=。
通电正方形线圈,可以看成4段载流直导线,由毕萨定律知道,每段载流直导线在正方形中心产生的磁场的磁感应强度大小相等,方向相同,由叠加原理/224B B =。
200020210/22)135cos 45(cos 24)cos (cos 4a I a I a I B πμπμθθπμ=-=-= 20/221012442a I B B a IB πμμ====π2821=a a 2. .如图8-2所示,四条平行的无限长直导线,垂直通过边长为20a cm =正方形顶点,每条导线中的电流都是20I A =,这四条导线在正方形中心O 点产生的磁感应强度为[ ]。
A. 40.810B T -=⨯B. 41.610B T -=⨯C. 0B =D. 40.410B T -=⨯答案:【A 】解:建立直角坐标系,则4根无限长载流直导线在正方形中心产生的磁感应强度为i a I B 45cos 201πμ=,j a I B 45cos 202πμ= i a IB 45cos 203πμ=,j a I B45cos 204πμ= )(45cos 2204321j i a I B B B B B+=+++=πμ T B 5108-⨯= 3.一根无限长直导线abcde 弯成图8-3所示的形状,中部bcd 是半径为R 、对圆心O 张角为0120的圆弧,当通以电流I 时,O 处磁感应强度的大小B = ,方向为 。
a 答案:)32(2600-=RI R IB πμμ+, 方向垂直纸面向里解:将整个载流导线分为三段:直线ab 、圆弧bcd 、直线de 。
磁力矩公式在非均匀磁场中的应用

Abstract : This article illust rate t he variety of met hods of calculating t he magnetic moment subjected to t he current2carrying coil in t he non - uniform magnetic field and t he flexibilit y of applying t he magnetic moment formula M = Pm ×B t hrough t hese two specific calculations of instance. Key words : magnetic moment ;moment of couple ;non2uniform magnetic field ;current2carrying coil
②用磁力矩公式计算 :
+
acco sθ
c2
+
1 a2 4+
acco sθ
k
·106 ·
陕西科技大学学报 第 21 卷
取微元面如图 2 所示 , d Pm = I2 bd x j ,根据磁场分布 ,d Pm 所受的磁力不是一对力偶 ,即 :
d M = d M 1 + d M2 M = M1 + M2
∫ M 1 y
=
μ0 I1 π
I2
R
π
2 2cos2αdα
0
=-
μ0 I1 I2 2
R
与用力矩定义 M = r ×F 计算结果完全一致 (可参阅有关题解〔1〕) 。
实例 2 。载流为 I1 的长直导线旁放一载流为 I2 ,长 、宽分别为 b 、a 的矩形线圈如图 2 。
大学物理课后习题及答案(2)

习 题 十 三13-1 求各图中点P 处磁感应强度的大小和方向。
[解] (a) 因为长直导线对空间任一点产生的磁感应强度为:()210cos cos 4θθπμ-=aIB 对于导线1:01=θ,22πθ=,因此aI B πμ401=对于导线2:πθθ==21,因此02=BaIB B B πμ4021p =+= 方向垂直纸面向外。
(b) 因为长直导线对空间任一点产生的磁感应强度为:()210cos cos 4θθπμ-=aIB 对于导线1:01=θ,22πθ=,因此r I a I B πμπμ44001==,方向垂直纸面向内。
对于导线2:21πθ=,πθ=2,因此rI a I B πμπμ44002==,方向垂直纸面向内。
半圆形导线在P 点产生的磁场方向也是垂直纸面向内,大小为半径相同、电流相同的圆形导线在圆心处产生的磁感应强度的一半,即rIr I B 4221003μμ==,方向垂直纸面向内。
所以,rIr I r I r I r I B B B B 4244400000321p μπμμπμπμ+=++=++=(c) P 点到三角形每条边的距离都是a d 63=o 301=θ,o 1502=θ每条边上的电流在P 点产生的磁感应强度的方向都是垂直纸面向内,大小都是()aI d IB πμπμ23150cos 30cos 400000=-=故P 点总的磁感应强度大小为aIB B πμ29300== 方向垂直纸面向内。
13-2 有一螺线管长L =20cm ,半径r =2.0cm ,导线中通有强度为I =5.0A 的电流,若在螺线管轴线中点处产生的磁感应强度B =310166-⨯.T 的磁场,问该螺线管每单位长度应多少匝?[解] 已知载流螺线管轴线上场强公式为()120cos cos 2θθμ-=nIB由图知: 10410cos 2=θ,10410cos 1-=θ,所以,⎪⎪⎭⎫ ⎝⎛⨯=10410220nI B μ, 所以,匝=1000101040IBn μ=13-3 若输电线在地面上空25m 处,通以电流31081⨯.A 。
26线圈磁矩磁力矩
考虑左右两线段受力情况,
ˆ 线圈磁矩 定义: m ISn
M m B
5
m
6
稳定平衡
M m B
非稳定平衡
已知: 均匀磁场 B ,方向如图 B 内放一矩形导线框,如图 它在外力作用下转动 d 角 求:转动过程中磁场力做的功 d m dA Md 力矩的功 M m B M mB sin 方向:⊙ dA mB sin d (负号源于 M是阻力矩)
方向:垂直板面向外 R2 总磁矩: N
R2 R1
m dm
R1
I R
2
R1
r dr
2
1 2 IN ( R2 R2 R1 R12 ) 3 方向:垂直板面向外
dr
I
r R2
R1
B
12
(2)线圈在该位置所受到的磁力矩 1 2 m IN ( R2 R2 R1 R12 ) 方向:垂直纸面向外 总磁矩: 3 磁力矩 M m B
1
8
结论: 1.均匀磁场中,载流线圈所受的合外力 F 0
2.均匀磁场中,载流线圈所受的合外力力矩 M m B 3.均匀磁场中,磁矩的势能为 W m B
9
例 一半径为R=0.1m的半圆形闭合线圈,载有电流 I=10A,放在均匀磁场中,磁场方向与线圈平行, 已知B=0.5T,求 线圈所受力矩的大小和方向 I R 1 2 B 解 : M m B m R I • 2 1 2 M R IB 方向:沿转轴向上 2
铅板
16
例、一磁场 B ai bj ck T ,则通过半径为R、 2 开口向z轴正方向的半球壳表面的磁通量为 cR 。
14章磁场 例题习题

第十四章 稳恒磁场例题1--30、在真空中,电流由长直导线1沿垂直于底边bc 方向经a 点流入一由电阻均匀的导线构成的正三角形金属线框,再由b 点从三角形框流出,经长直导线2沿cb 延长线方向返回电源(如图).已知长直导线上的电流强度为I ,三角框的每一边长为l ,求正三角形的中心点O 处的磁感强度B.解:令1B 、2B 、acb B 和ab B分别代表长直导线1、2和三角形框ac 、cb边和ab 边中的电流在O 点产生的磁感强度.则 ab acb B B B B B+++=211B :由于O 点在导线1的延长线上,所以1B= 0. 2B :由毕-萨定律)60sin 90(sin 402︒-︒π=dI B μ 式中 6/330tan 21l l Oe d =︒⋅==)231(34602-⋅π=lI B μ)332(40-π=lIμ 方向:垂直纸面向里.acb B 和ab B:由于ab 和acb 并联,有 a c b a c b ab ab R I R I ⋅=⋅又由于电阻在三角框上均匀分布,有21=+=cbac ab R R acbab ∴ acb ab I I 2=由毕奥-萨伐尔定律,有ab acb B B =且方向相反. ∴ )332(402-π==lIB B μ,B的方向垂直纸面向里.27、如图所示,一无限长载流平板宽度为a ,线电流密度(即沿x 方向单位长度上的电流)为δ ,求与平板共面并且距离平板一边为b 的任意点P 的磁感强度. 解:利用无限长载流直导线的公式求解.(1) 取离P 点为x 宽度为d x 的无限长载流细条,它的电流 x i d d δ=(2) 这载流长条在P 点产生的磁感应强度 xiB π=2d d 0μxxπ=2d 0δμ方向垂直纸面向里.(3) 所有载流长条在P 点产生的磁感强度的方向都相同,所以载流平板在P 点产生的磁感强度 ==⎰B B d ⎰+πba bxdx x20δμbb a x+π=ln20δμ 方向垂直纸面向里.例题34、如图所示,半径为R ,线电荷密度为λ (>0)的均匀带电的圆线圈,绕过圆心与圆平面垂直的轴以角速度ω 转动,求轴线上任一点的B的大小及其方向.解: λωR I = 2/32230)(2y R R B B y +==λωμB的方向与y 轴正向一致.例题35、平面闭合回路由半径为R 1及R 2 (R 1 > R 2 )的两个同心半圆弧和两个直导线段组成(如图).已知两个直导线段在两半圆弧中心O 处的磁感强度为零,且闭合载流回路在O 处产生的总的磁感强度B 与半径 为R 2的半圆弧在O 点产生的磁感强度B 2的关系为B = 2 B 2/3,求R 1与R 2的关系.解:由毕奥-萨伐尔定律可得,设半径为R 1的载流半圆弧在O 点产生的磁感强度为B 1,则 1014R I B μ= 同理, 2024R IB μ=∵ 21R R > ∴ 21B B < 故磁感强度 12B B B -= 204R I μ=104R I μ-206R I μ=∴ 213R R =13、在图(a)和(b)中各有一半径相同的圆形回路L 1、L 2,圆周内有电流I 1、I 2,其分布相同,且均在真空中,但在(b)图中L 2回路外有电流I 3,P 1、P 2为两圆形回路上的对应点,则: (A) =⎰⋅1d L l B⎰⋅2d L l B,21P P B B = (B) ≠⎰⋅1d L l B⎰⋅2d L l B,21P P B B =. (C) =⎰⋅1d L l B⎰⋅2d L l B,21P P B B ≠.(D)≠⎰⋅1d L l B⎰⋅2d L l B,21P P B B ≠. [ C ]31、在安培环路定理∑⎰⋅=i LI l B 0d μ 中,∑i I 是指 ;B是指 .环路L 所包围的所有稳恒电流的代数和 环路L 上的磁感强度例题32、如图,一条任意形状的载流导线位于均匀磁场中,试证明导线a 到b 之间的一段上所受的安培力等于载同一电流的直导线ab 所受的安培力.I abB1 2 I 3 (a)(b)⊙证明:由安培定律 B l I f⨯=d d ,ab 整曲线所受安培力为 ⎰⎰⨯==b aB l I f f d d因整条导线中I 是一定的量,磁场又是均匀的,可以把I 和B提到积分号之外,即 ⎰⨯=b aB l I f d B l I ba⨯=⎰)d (B ab I⨯=载流相同、起点与终点一样的曲导线和直导线,处在均匀磁场中,所受安培力一样.33、判断下列说法是否正确,并说明理由:(1) 若所取围绕长直载流导线的积分路径是闭合的,但不是圆,安培环路定理也成立.(2) 若围绕长直载流导线的积分路径是闭合的,但不在一个平面内,则安培环路定理不成立. 答:第一说法对,第二说法不对.∵ 围绕导线的积分路径只要是闭合的,不管在不在同一平面内,也不管是否是圆,安培环路定理都成立.3、如图所示,一半径为R 的均匀带电无限长直圆筒,面电荷密度为σ.该筒以角速度ω绕其轴线匀速旋转.试求圆筒内部的磁感强度.解:如图所示,圆筒旋转时相当于圆筒上具有同向的面电流密度i , σωσωR R i =ππ=)2/(2作矩形有向闭合环路如右图中所示.从电流分布的对称性分析可知,在ab 上各点B 的大小和方向均相同,而且B的方向平行于ab ,在bc 和fa 上各点B的方向与线元垂直,在de , cd fe ,上各点0=B .应用安培环路定理 ∑⎰⋅=I l B 0d μ可得 ab i ab B 0μ= σωμμR i B 00== 圆筒内部为均匀磁场,磁感强度的大小为σωμR B 0=,方向平行于轴线朝右.4、如右图,匀强磁场中有一矩形通电线圈,它的平面与磁场平行,在磁场作用下,线圈发生转动,其方向是(A) ab 边转入纸内,cd 边转出纸外. (B) ab 边转出纸外,cd 边转入纸内. (C) ad 边转入纸内,bc 边转出纸外. (D) ad 边转出纸外,bc 边转入纸内. [ A ]28、如图,长载流导线ab 和cd 相互垂直,它们相距l ,ab 固定不动,cd 能绕中点O 转动,并能靠近或离开ab .当电流方向如图所示时,导线cd 将(A) 顺时针转动同时离开ab . (B) 顺时针转动同时靠近ab .(C) 逆时针转动同时离开ab . (D) 逆时针转动同时靠近ab . [ D ]9、两个同心圆线圈,大圆半径为R ,通有电流I 1;小圆半径为r ,通有电流I 2,方向如图.若r << R (大线圈在小线圈处产生的磁场近似为均匀磁场),当它们处在同一平面内时小线圈所受磁力矩的大小为 (A) RrI I 22210πμ. (B)Rr I I 22210μ.(C)rRI I 22210πμ. (D) 0. [ D ]14、载流平面线圈在均匀磁场中所受的力矩大小与线圈所围面积 ;在面积一定时,与线圈的形状.(填: 有关、无关)有关 无关习题22、边长为l 的正方形线圈,分别用图示两种方式通以电流I (其中ab 、cd 与正方形共面),在这两种情况下,线圈在其中心产生的磁感强度的大小分别为(A) 01=B ,02=B . (B) 01=B ,lI B π=0222μ.(C) lI B π=0122μ,02=B . (D) lI B π=0122μ,lI B π=0222μ. [ C ]10、在真空中,电流I 由长直导线1沿垂直bc 边方向经a 点流入一由电阻均匀的导线构成的正三角形线框,再由b 点沿平行ac 边方向流出,经长直导线2返回电源(如图).三角形框每边长为l ,则在该正三角框中心O 点处磁感强度的大小为 ;磁感强度的方向为 。
西南交通大学 大物AI作业参考解答_No.10 安培环路定理 磁力 磁介质

《大学物理AI 》作业No.10安培环路定理磁力磁介质参考答案--------------------------------------------------------------------------------------------------------------------****************************本章教学要求****************************1、理解磁场的高斯定理、磁场安培环路定理的物理意义,能熟练应用安培环路定律求解具有一定对称性分布的磁场磁感应强度;2、掌握洛仑兹力公式,能熟练计算各种运动电荷在磁场中的受力;3、掌握电流元在磁场中的安培力公式,能计算任意载流导线在磁场中的受力;4、理解载流线圈磁矩的定义,并能计算它在磁场中所受的磁力矩;5、理解霍尔效应并能计算有关的物理量;6、理解顺磁质、抗磁质磁化的微观解释,了解铁磁质的特性;7、理解磁场强度H 的定义及H 的环路定理的物理意义,并能利用它求解有磁介质存在时具有一定对称性的磁场分布。
--------------------------------------------------------------------------------------------------------------------一、选择题1.在图(a)和(b)中各有一半径相同的圆形回路L 1、L 2,圆周内有电流I 1、I 2,其分布相同,且均在真空中,但在(b)图中L 2回路外有电流I 3,P 1、P 2为两圆形回路上的对应点,则:[B ](A)2121,d d P P L L B B l B l B (B)2121,d d P P L L B B l B l B(C)2121,d d P P L L B B l B l B(D)2121,d d P P L L B B l B l B解:根据安培环路定理 内I l B L0d,可以判定21d d L L l B l B;而根据磁场叠加原理(空间任一点的磁场等于所有电流在那点产生的磁场的矢量叠加),知21P P B B。
大学物理第13章磁力

我国于1994 年建成的第 一台强流质 子加速器 , 可产生数十 种中短寿命 放射性同位 素.
§13.2 Hall 效应
霍耳效应:磁场中的载流半导体出现横向电压的现
象
§13.2 Hall 效应
B
IB 霍耳电压 U H RH d F
m
+ + + + b vd +q - - - - qEH qvd B
B
dl
I nevd S
dF IdlB sin IdlB sin 安培力 dF Idl B
§13.3 载流导线在磁场中受的磁力
有限长载流导线所受的安培力
dF Idl B F l dF l Idl B
Id l
F1
M
P
O
I
N
F4
F2
B
en
O,P
线圈有N匝时 M NISen B
F2
M,N F1
B
en
e (1) n 与 B
讨 论
同向 (2)方向相反 (3)方向垂直 不稳定平衡
×
稳定平衡
× ×
力矩最大
×
×
×
I
×
×
. .
.
×
× × ×
×
× × ×
磁聚焦 在均匀磁场中点 A 发射一束 与 初速度相差不大的带电粒子,它们的 v0 B 之间的夹角 不同,但都较小,这些粒 子沿半径不同的螺旋线运动,因螺距近似 相等,相交于屏上同一点,此现象称为磁 聚焦 . 应用 电子光学,电 子显微镜等 .
三 带电粒子在电场和磁场中运动举例
大学物理第13章

' I
4. 如图,一根载流无限长直导线与一个载流 正三角形线圈在同一个平面内。若长直导线固定 A 不动,则载流三角形线圈将 [ ] A.向着长直导线平移 C.远离长直导线平移 B.转动 D.不动
I1
I2
5.一圆形电流 I1 与一根长直电流 I2 共面,并 与其一直径相重合,如图,两者间绝缘。设长直 电流不动,则圆形电流将[ ] A)绕 I2 旋转 C)向右运动 B)向左运动 D)不动
特例:均匀磁场中的任意 闭合电流所受合力为零。
注:本题是非均匀磁场。 [例3] 一根无限长直导线载有电流 I1 ,它与长为 L、载有电流 I2 的直 导线相互垂直,距离为 d,如图所示。求导线 L 所受磁力。 解:考虑 L 上的电流元 I 2 dr ,它距无限长直 导线为 r 。无限长直导线在该电流元处产生的磁 感强的方向垂直纸面向里,大小为
0 4 107 N/A 2
这是依照 SI 中确定电流强度单位“安培”的方法而得出的。 1948年第九届国际计量大会确定:“安培是一恒定电流,若 保持在处于真空中相距 1 米的两无限长而圆截面可以忽略的平行 直导线内,则这两导线之间产生的力在每米长度上等于 2 107 牛顿。”
dF 0 I 2 dl 2d
D
B
解: F IL B ILB sin IB 2a sin 135 IBa (方向垂直纸面向里)
2.如图,一根载流 I 的导线,被折成长度分别 为 a、b ,夹角为120度的两段,并置于均匀磁场 B 中,若导线的长度为 b 的一段与 B 平行,则 a、b 两段所受的合磁力的大小为[ 3IBa/ 2 ]
5.一圆形电流 I1 与一根长直电流 I2 共面,并 与其一直径相重合,如图,两者间绝缘。设长直 电流不动,则圆形电流将[ C ]
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M ISen B
4、载流线圈的磁矩 I
en
S 载流线圈
m
m ISen
磁矩
载流线圈在均匀磁场中的磁力矩
M ISen B
M m B
补充说明 考虑磁场的均匀性
一般情况下,小载流线圈等效于磁矩
5、磁矩在磁场中的势能
m
M m B
I
A
2 1 2 1
如将 1 / 2 的位置当成势能零点,则
Wm mB cos m B
电偶极矩 p 力矩 势能
M p E W p E
磁矩 m
M m B W m B
6、磁矩在磁场中的受力 磁矩在磁场中的势能
W m B
磁矩在磁场中的受力
F W (m B ) (m x Bx m y B y mz Bz ) m x Bx m y B y m z Bz
对 z 轴的力矩
dM rdF R sin IRd B sin R2 IB sin 2 d
对 z 轴的总力矩
2
M
dM
0
2
0
R2 IB sin 2 d R2 IB R2 IB sin
M SIen B
3、任意形状载流线圈
Topography (height)
40 μm
40 μm
B B// B
Idl1 受到的作用力
dF1 Idl1 B sin 1
dh
B
Idl2 受到的作用力
dF2 Idl2 B sin 2 dl2 in 2 dl1 sin 1 dh
dF1 dF2 IB dh
合力为零, 但有力矩
dM x1dF1 x2 dF2 IB dh( x1 x2 ) IB sin dS
en
垂直于线圈平面与电流的方向符合右手螺旋关系
F
I
俯视图
en
B I
ቤተ መጻሕፍቲ ባይዱ
z
a
I
F
b
a
IbB
每条长边受到的力 力矩大小
M a cos IbB IS cos B IS sin B
M ISen B
2、载流圆线圈
磁场的平行分量对合力矩的贡献为零
电流元 Idl
en
dF IdlB sin
7.4 载流线圈在均匀磁
场中受的磁力矩
闭合的载流线圈在均匀磁场中 合磁力为零 载流矩形线圈 载流圆形线圈 载流任意线圈 磁力矩可不为零
的磁力矩
1、载流矩形线圈
z
en
I F
B
F
F IbB
M aIbB ISB
b
M ISen B
a
定义 线圈平面的法线方向
B
M mB sin
当 从1 增大到 2 磁力做的负功为
2 Md mB sin d mB cos mB(cos1 cos 2 ) 1
磁力的功,与转动的路径没有关系 势能 Wm
Wm Wm 2 Wm1 mB(cos1 cos 2 )
如果磁场只有 x 方向分量 Bx
F m x B x m x ( Bx Bx Bx , , ) x y z
7、磁力显微镜原理
deflection sensor
amplifier
sample scanning tube
computer
driving electronics
Videotape
