二次回归正交试验
第七章 响应面回归设计

二次回归正交设计
应用二次回归正交设计法,所得的 回归系数的估计之间相互独立,因 此删除某些因子时不会影响其它的 回归系数的估计,从而很容易写出 所有系数为显著的回归方程。 二次回归正交设计的试验点由正交 点、主轴点和中心点组成。
二次回归正交设计
两个变量的试验点组合方案
试验号 1 2 3 4 5 6 7 8 9 M n x1 1 1 −1 −1 x2 1 −1 1 −1 0 0 3 2 用 L 4 ( 2 ), m c = 2 = 4 星号点 , 2 p = 4 中心点 m 0
Ey H0: : 假设: 假设: Ey H1: : = β 0 + β 1 x1 + L + β p x p
≠ β 0 + β 1 x1 + L + β p x p
统计量: 统计量:
FLf =
S Lf / f Lf Se / fe
当拒绝H 需要寻找原因, 当拒绝 0时,需要寻找原因,改变模型 否则认为线性回归模型合适,可以将S 否则认为线性回归模型合适,可以将 e 合并作为S 检验方程是否显著。 与SLf合并作为 E检验方程是否显著。
回归设计
回归设计概述 回归模型 因素水平编码 Box-Benhken设计 - 设计 二次回归正交设计
概述
回归设计也称为响应面设计。 是一种通过少量试验,获得数据, 估计参数,有效地建立试验指标和 连续变量之间的定量关系的方法。 它是由英国统计学家G.Box在20世 纪50年代初真对化工生产提出的, 后来这一方法得到了广泛的应用。
(
)
Y —响应变量;xj —第j个自变量; ε—正态随机误差;β0 —回归截距; βj βjj’βjj —回归系数;
第七章 回归正交试验设计

个因素之间的函数关系。
因素水平编码表
自然变量xj 规范变量zj 1 -1 0 △j x1 700 300 500 200 x2 2400 1800 2100 300 x3 10 8 9 1
7.1.2一次回归方程的建立
设总的试验次数为N,其中原正交表所规定的二水平试验次数为 mc,零水平试验次数为m0,即有: N 建立回归方程
m
mc m0
ˆ a b j x j bkj xk x j,k 1,2,, m 1( j k ) y
j 1 k j
其系数的计算公式如下:
将被剔除变量的偏回归平方和、自由度并入到剩余平方和与自由度中,
然后再进行相关的方差分析计算。具体例子见书P126~129例8-1。
7.1 一次回归正交试验设计及结果分析
14
用石墨炉原子吸收分光光度计法测定食品中的铅,为提高吸光度,
对x1(灰化温度/℃)、x2(原子化温度/℃)和x3(灯电流/mA)三个
F0.05(1,6)=5.99 F0.01(1,6)=13.74
可见因素z2对指标影响高度显著,所建的回归方程高度显著:
y 0.50475 0.03375z2
7.1 一次回归正交试验设计及结果分析
N 1 SST Lyy ( yi y ) 2 yi2 ( yi ) 2 N i 1 i 1 i 1 N N
7.1 一次回归正交试验设计及结果分析
10
②一次项zj偏回归平方和
SS j m b ,j= 1 , 2, ,m
二次回归正交旋转组合设计优化大肥蘑菇液体培养基

二次回归正交旋转组合设计优化大肥蘑菇液体培养基杨琴;张桂香;杨建杰;王英利【摘要】为优化大肥蘑菇液体培养基,通过单因子试验确定大肥蘑菇最佳碳源(葡萄糖)、最佳氮源(蛋白胨)及矿物质的适宜浓度(用量)范围,采用二次回归旋转组合设计研究3个参数对大肥蘑菇菌丝生物量的影响,建立数学模型,以获得适宜的配方组合.结果表明,葡萄糖浓度、蛋白胨浓度对大肥蘑菇菌丝体生物量的影响达极显著水平,矿物质添加剂用量达显著水平.最优培养基参数为葡萄糖浓度33.26 g/L、蛋白胨浓度4.24 g/L、矿物质添加剂1.82 mL/L,在该参数组合下,28℃振荡培养8 d,菌丝干重可达16.44 g/L,且经反复试验验证可行.【期刊名称】《甘肃农业科技》【年(卷),期】2017(000)011【总页数】6页(P12-17)【关键词】大肥蘑菇;培养基;二次回归旋转组合;优化【作者】杨琴;张桂香;杨建杰;王英利【作者单位】甘肃省农业科学院蔬菜研究所, 甘肃兰州 730070;甘肃省农业科学院蔬菜研究所, 甘肃兰州 730070;甘肃省农业科学院蔬菜研究所, 甘肃兰州 730070;甘肃省农业科学院蔬菜研究所, 甘肃兰州 730070【正文语种】中文【中图分类】S646.9博斯腾湖位于巴音郭楞蒙古自治州焉耆盆地的博湖县境内,总面积1 228 km2,蓄水量8.0×109m3,是开都河的归宿,孔雀河的源头,更是一座天然的大型调节水库,也是新疆最大的内陆淡水湖。
大肥蘑菇(经ITS序列分析确定[1])是在新疆博斯腾湖特殊环境条件下形成的极为珍贵的野生食用菌,在分类上隶属于担子菌纲(Basidiomycetes)伞菌目(Agaricales)蘑菇科(Agaricaceae)蘑菇属(Agaricua),其子实体硕大、菌肉肥厚细嫩,通过营养成分、氨基酸组成、矿物质、脂肪酸营养成分的测定[2-3],发现大肥蘑菇具有极高的风味物质、营养价值和保健作用。
二次回归正交旋转组合设计优化21~42日龄肉仔鸡胆碱和蛋氨酸需要量

汤建平
( 中国农 业科学院饲 料研究所 , 家禽 营养与饲料 研究室, 北京 10008 1)
要: 本试验以低胆碱 � 低蛋氨酸饲粮为基础饲粮, 通过两因子二次回归正交旋转组合设计, 对 21 42 日龄肉仔鸡胆碱和蛋氨酸需要量进行研究� 试验选用 21 日龄爱拔益加( A A ) 肉仔鸡 摘 48 0 只 , 9 12 组为 中心组 , 随机分为 12 个组 , 其中 1 8 组为试验组 , 每组 4 个重复 , 每个重复 10 只鸡, 公母各占 1/ 2� 分别以胆碱和蛋 氨酸为自变量, 以反映 肉仔鸡生长性能 和屠宰性能的 各项指标为因变量 拟合回 归方 程, 估计 21 42 日 龄肉 仔鸡 胆碱和 蛋氨 酸的 需要 量� 试验期 21 d� 结果表明 : 胆碱和蛋氨酸水平对 21 42 日龄肉仔鸡的平均日采食量 � 料重比 � 腹脂率和肝 kg 时 , 脂率有显著影响( P < 0.05) � 当胆碱水平在 8 60 1 120 m g / 肉仔鸡平均日采食量随着蛋 氨酸水平的增加而升高, 蛋氨酸水平增至 0.40% 后, 继续增 加对平均日采食量的改善作用不明 0.42% , kg 时 , 显 ; 蛋氨酸水平在 0.35% 胆碱水平在 8 6 0 1 120 m g / 肉仔鸡的料重比达到最 0.47 % 时 , 低值 ; 蛋氨酸水平在 0.30% 随着胆碱水平的增加肉仔鸡腹脂率呈下降趋势 ; 当蛋氨 酸水平在0.30% 0.40% , 胆碱水平在 1 000 1 400 m g / kg 时, 肉仔鸡肝脂率随着胆碱水平的 增加和蛋氨酸水平的降低呈下降趋势 � � 在本试验条件下, 当 胆碱水平为 99 0 1 030 m g / kg , 蛋 0.40% � 0. 43% , ; 1 7 8 0 氨酸 水 平 为 时 肉 仔 鸡 可 达到 最 佳 生 长性 能 当胆 碱 水 平 为 1 8 8 0 mg / kg , 蛋氨酸水平为 0.37 % 中图分类号 : S8 31 0.38 % 时 , 肉仔鸡可达到最佳屠宰性能 � 关键词: 胆碱 ; 蛋氨酸 ; 肉仔鸡; 二次回归正交旋转组合设计 ; 响应面 文献标识码 : A 文章编号 : 1006 267 X ( 2012) 06 1019 11 数都是围绕胆碱与其他营养物质的 相互关系进行 的
回归正交试验设计

回归正交试验设计一、概述(1)回归分析与正交试验设计的主要优缺点回归分析的主要优点是可以由试验数据求出经验公式,用于描述自变量与因变量之间的函数关系。
它的主要缺点是毫不关心试验数据如何取得,这样,不仅盲目地增加了试验次数,而且试验数据还往往不能提供充分的信息。
因此,有些工作者将经典的回归分析方法描述成:“这是撒大网,捉小鱼,有时还捉不到鱼”。
所以说,回归分析只是被动地处理试验数据,并且回归系数之间存在相关关系,若从回归方程中剔除某个不显著因素时,需重新计算回归系数,耗费大量的时间。
正交试验设计的主要优点是科学地安排试验过程,用最少的试验次数获得最全面的试验信息,并对试验结果进行科学分析(如方差分析),从而得到最佳试验条件,但是它的主要缺点是试验结果无法用一个经验公式来表达,从而不便于考察试验条件改变后,试验指标将作如何变化。
(2)回归正交试验设计回归正交试验设计,实际上就是将线性回归分析与正交试验设计两者有机地结合起来而发展出的一种试验设计方法,它利用正交试验设计法的“正交性”特点,有计划、有目的、科学合理地在正交表上安排试验,并将试验结果用一个明确的函数表达式即回归方程来表示,从而达到既减少试验次数、又能迅速地建立经验公式的目的。
根据回归模型的次数,回归正交试验设计又分为一次回归试验设计和二次回归试验设计。
二、一次回归正交试验设计(一)一次回归正交试验设计的概念一次回归设计研究的是一个因素z (或多个因素z 1,z 2,……)与试验指标y 之间的线性关系。
当只研究一个因素时,其线性回归模型:y =β0+β1z +e (1)其回归方程为:z y ∧∧∧+=10ββ (2)式中∧0β、∧1β称为回归系数,e 是随机误差,是一组相互独立、且服从正态分布N(0,σ2)的随机变量。
可以证明,∧0β、∧1β和∧y 是β0、β1和y 的无偏估计,即E(∧0β)=β0,E(∧1β)=β1,E(∧y )=y一次回归正交试验设计是通过编码公式x =f(z) −− 即变量变换,将式(2)变为:x b b y 10+=∧(3)且使试验方案具有正交性,即使得编码因素X的各水平之和为零:∑==mi ix1(4)式中m 是因素x 的水平数。
第8章回归正交试验设计

②二次项的中心化 对二次项的每个编码进行中心化处理 :
(二次项编码)-(二次项编码算术平均值)
z ji
'
z
j
2 i
1 n
n i 1
z
j
2 i
二元二次回归正交组合设计编码表
试验号
z1
1
1
z2
z1 z2
z12
1
1
1
2
1
-1
-1
1
3
-1
1
-1
1
4
-1
-1
1
1
5
1
0
0
1
6
-1
0
0
1
7
0
1
0
0
8
0
-1
0
1.414
1.483
3 1.147 1.353
1.471
1.547
4 1.210 1.414
1.525
1.607
5 1.267 1.471
1.575
1.664
6 1.320 1.525
1.623
1.719
7 1.369 1.575
1.668
1.771
8 1.414 1.623
1.711
1.820
9 1.457 1.668
bkj
i 1 n
(zk z j )i2
i 1
二次项偏回归系数bjj :
n
(
z
' ji
)
yi
b jj
i 1 n
(
z
' ji
)
2
i 1
⑤回归方程显著性检验
二次回归正交试验设计优化桐油超声辅助提取工艺

145 - 148. [6]蔡华珍,张 丽. 蛋白酶法提取乌骨鸡黑色素的研究[J]. 肉类
工业,2005( 12) : 24 - 26. [7]豁银强,邓卫东,毛华明. 乌骨绵羊与黑色素的研究进展[J]. 畜
牧与兽医,2006,38( 7) : 57 - 59. [8]毋智深,李正英,高爱武. 蝌蚪黑色素体外抗氧化作用研究[J].
— 296 —
江苏农业科学 2012 年第 40 卷第 12 期
杨海涛 . 二次回归正交试验设计优化桐油超声辅助提取工艺[J]. 江苏农业科学,2012,40( 12) : 296 - 298.
二次回归正交试验设计优化桐油超声辅助提取工艺
杨海涛
( 陕西理工学院化学与环境科学学院,陕西汉中 723000)
食品科学,1998,19( 8) : 5 - 7. [9]张莲姬. 泥鳅鱼黑色素抗氧化作用[J]. 食品研究与开发,2010,
31( 8) : 11 - 14.
色素资源提供了参考依据。
[10]徐 磊,王 长 海. 短梗霉黑色素的提取及其 理 化 性 质 的 研 究
参考文献:
[J]. 食品科学,2006,27( 8) : 122 - 125. [11]张莲姬,崔泰花. 泥鳅鱼皮黑色素提取工艺的研究[J]. 江苏农
收稿日期: 2012 - 05 - 25
பைடு நூலகம்
DGG - 9140B 型电热恒温鼓风干燥箱( 上海森信实验仪
作者简介: 杨海涛( 1960—) ,男,陕西蓝田人,教授,主要从事天然产 器公司) ; JBT / C - YCL400T /3P( D) 超声药品处理机( 济宁金
物提取与开发方面的研究。E - mail: yanghaitaohz@ 163. com。
【国家自然科学基金】_二次回归正交设计_基金支持热词逐年推荐_【万方软件创新助手】_20140803

科研热词 推荐指数 番茄 5 灌水量 5 钾 3 磷 3 氮 3 硝酸盐 2 温度 2 正交试验 2 雾滴沉积量 1 雾化 1 银杏叶 1 邓恩桉 1 遗传算法 1 轻量化 1 超微粉碎 1 自燃煤矸石 1 红花 1 硝态氮 1 破壁 1 番茄红素 1 电导率 1 生态化学计量特征 1 甘肃 1 猕猴桃籽 1 熔盐电解法 1 灵敏度分析 1 激发剂 1 滴灌 1 湿度控制 1 浸出 1 水酶法 1 水肥耦合 1 水肥处理 1 氮、磷及钾肥用量 1 氟碳铈矿 1 正交设计 1 模拟氮-硫沉降 1 桁架式 1 根际微生物 1 杉木 1 有限元分析 1 有机酸 1 施肥量 1 抗退磁能力 1 微咸水 1 小麦 1 定西 1 复合材料转子导条 1 堵转转矩 1 堵转电流 1 地质聚合物 1 四元二次正交旋转组合设计 1
53 54 55
2011年 科研热词 推荐指数 回归分析 2 黄芪多糖 1 高光谱 1 风洞 1 非线性规划求解 1 补充营养 1 血小板聚集率 1 蒸腾速率 1 苜蓿草颗粒 1 结晶温度 1 紫椴 1 稳健设计 1 秸秆 1 磷 1 番茄红素 1 番茄 1 电渣 1 玉米芯 1 灌水量 1 温度 1 淡足侧沟茧蜂 1 液化 1 注塑工艺参数 1 氮 1 正交试验 1 木糖 1 有机肥 1 施肥 1 成虫寿命 1 带鱼蛋白 1 工艺控制 1 多目标优化 1 复合酶解 1 均匀光照系统 1 固沙 1 回归正交 1 参数 1 制粒过程模拟 1 净光合速率 1 光周期 1 信息采集 1 信噪比 1 优化 1 亚铁螯合多肽 1 五元二次正交旋转组合设计 1 二次正交旋转回归组合设计 1
科研热词 黏结剂 黏度 预测模型 试验设计 表面粗糙度 耐热纤维素酶 综合相关系数 穴距准确性 穴粒数合格率 种绳 玉米淀粉 潜在去除率 活化 氟化钙渣系 正交旋转回归 正交回归分析 抗撞性 抗拉强度 微细铣削 失重率 大豆根腐病 外源dom 响应面法 响应面 响应曲面法 吸能 发酵 出苗率 优化设计 优化 二次回归正交设计 cu(ⅱ)
回归正交试验设计

z
2
20 10
,x3
z3 0.2 0.1
通过上述变换后,编码空间为中心在原点的立方体,其边
长为2。 在后面我们将会看到,在编码时,有时立方体的边长可以
大于2。
2020/7/18
试验设计与数据处理
20
今后称x (x1, x2 ,, xp ) 的可能取值的空间为编码空间。我们可以 先在编码空间中寻找一个点x0使E(y)满足质量要求,然后通过 编码式寻找到z0。
y b0
bjzj
b
jj
z
2 j
bij zi z j
j
j
i j
为y关于 z1, z2 ,, z p 的多项式回归方程。
2020/7/18
试验设计与数据处理
5
在实际中常用的是如下的一次与二次回归方程(也称一阶 与二阶模型):
yˆ b0 bj z j
j
yˆ b0
bjzj
b jj
著性之前,先对y 的期望是否是 x1, x2 ,, x p的线性函数进行检
验,这种检验称为失拟检验,它要检验如下假设:
H0: Ey 0 1x1 p x p
H1: Ey 0 1x1 p xp 当在 (xi1, xi2 ,, xip )上有重复试验或观察时,将数据记为
(xi1 ,
xi2 ,,
2020/7/18
试验设计与数据处理
21
§7.2 一次回归正交设计 7.2.1 一次回归正交设计
建立一次回归方程的回归设计方法有多种,这里介绍一种常
用的方法,它是利用二水平正交表来安排试验的设计方法。 其主要步骤如下: 1.确定因子水平的变化范围
设影响指标y的因子有p个 z1, z2 ,, z p ,希望通过试验建立y
基于二次正交回归试验的烤烟高产施肥优化方案

施 P O。单 施 K O 水平 下均 存 在 最 大值 , 。 、 烤烟 产 量在 达到 最大 值 后 又 随着 施 肥 量 的增 加 而 降 低 。
的产 量 与氮 磷钾 肥 的施用 量之 间关 系 可得 出 回归
(06 2 0 BAD1 BO )。 5 6
同 淑 娥等 : 于 二 次 正 交 回 归试 验 的烤 烟 高产 施 肥 优 化 方 案 基
・3 ・ 9
1 3 测定项 目及 方 法 .
1 3 1 土壤 分 析 项 目 . .
HC , 1震荡 5ri, 滤 , 容 至 10ml分别 在 2 6 n过 a 定 0 , 3
n 2 9n 2 2n 波长处测 吸光值 。 m,5 m,8 m
土壤 全氮 含量 的测定 : S u O K。 O 一C S 消煮 , 凯 氏定 氮 法 ; 土 壤碱解 氮 含量 的测定 : 扩散 法 ; 土 壤速 效磷 含量 的测定 : 钼锑 抗 比色法 ; 土 壤速 效钾 含 量 的测 定 : NH4 OAC浸 提 , 火 焰 光度 计 比色法 ; 土 壤有 机质 含量 的测定 : 重铬 酸钾容 量法 ;
陕
西
农
业
科
学
2l () O l 4
基 于 二 次 正 交 ቤተ መጻሕፍቲ ባይዱ归试 验 的烤 烟 高 产施 肥 优 化 方 案
同淑 娥 王 胜男。 李 海 民。 耿军 红。 , , , ( . 南市烟 草公 司, 西 渭南 7 4 0 ;. 1渭 陕 1 0 0 2 西北 农林科 技 大 学, 西 杨 凌 7 2 0 ; 陕 1 1 0
验, 能得 出各 种 肥 料 在 各 地不 同土 壤 上 的 增 产效
果 和肥 料利 用 率 , 清土 壤养 分校 正 系数 、 摸 土壤供
第5章 回归正交试验设计

第一节 一次回归正交试验设计
(4)失拟性检验
本例中,零水平试验次数m0=3,进行失拟行检验。
FLf
SSLf / dfLf SSe1 / dfe1
0.0963/ 5 0.00667/ 2
5.775
F0.1(5,2)
9.29
表明失拟不显著,回归模型与实际情况拟合得很好。
第一节 一次回归正交试验设计
4 回归方程及偏回归系数的方差分析 4.1 无零水平试验 4.1.2 计算自由度
第一节 一次回归正交试验设计
4 回归方程及偏回归系数的方差分析 4.1 无零水平试验 4.1.3 计算均方
MSj
SS j df j
MSkj
SSkj dfkj
j k,k 1,2,...,(m 1)
n i 1
yi
y
n
z ji yi
bj
i 1
mc
n
(zk z j )i yi
bkj i1 mc
j k,k 1,2,...,(m 1)
第一节 一次回归正交试验设计
3 一次回归方程的建立 通过计算得到回归系数之后,可以直接根据它们绝对值的大
小来判断各因素和交互作用的相对重要性,而不用转换成标准 回归系数。
n
z ji 0
i 1
n
z ji zki 0 ( j k )
i 1
这些特点说明了转换之后的正交表同样具有正交性。
第一节 一次回归正交试验设计
2.4 试验方案的确定
确定试验方案时,将规范变量zj安排在一次回归正交编码表 相应的列中,即进行表头设计。
第四节 二次回归正交设计

第四节二次回归正交设计在应用一次回归正交设计时,如果经过假设检验,发现一次回归方程不合适,就需要用二次或更高次回归方程描述。
通常情况下,使用二次回归一般即可满足要求。
一、二次回归正交试验的组合设计方法二次回归设计就是采用二次多项式作为回归方程。
当变量数为P 时,二次回归模型的一般形式为(3-3-18) 在二次回归模型中,共有q个待估计参数因此,要建立有p个变量的二次回归方程,试验次数应大于q。
而且为了估计未知参数,每个变量所取得的水平不应小于3。
在三水平上做p个变量的全因素试验,试验次数为3p。
当p=4时,三水平的全因素试验次数数量是81次,比p=4时的二次回归系数要多4倍以上,以致剩余度过大。
为了有效地减少不必要的试验次数,提出一种组合设计法。
这种方法是在因素空间中选择几类具有不同特点的点,把它们适当组合成为一个试验计划,此计划应尽量减少试验次数,并且有正交性。
以p=2为例,在有两个变量x1,x2场合下,组合设计由以下9个试验点组成(见表3-3-13):表3-3-13这9个试验点在平面图上的位置如图3-3-2所示。
图3-3-2当p=3,即有三个变量时,组合设计由15个试验点组成,见表2-14。
这15个试验点在空间的位置,如图3-3-3所示。
表3-3-14一般地,p个变量的组合设计由下列三类试验点组成:第一类点为二水平(-1和1)全因素试验的试验点,这类试验点共有2p个,如果采用1/2或1/4 实施法,则为2p-1或2p-2个试验点。
第二类点为分布在p个坐标轴上的星号点,这类试验点共有2p个,它们与中心点的距离为,称为星号臂。
是待定系数,可根据不同的要求确定值。
第三类试验点为中心点,即各变量都取零水平的试验点。
在中心点上的试验可以只做一次,也可以重复做若干次。
若以N0表示第一类试验点个数,以m0表示第三类试验点个数,则p个变量的组合设计试验点数N为:N=N0+2p+m0用组合设计安排的试验计划有一系列优点:首先,它的试验点比三水平的全因素试验少得多,但仍保持足够的剩余度。
一次回归正交设计、二次回归正交设计、二次回归旋转设计说明
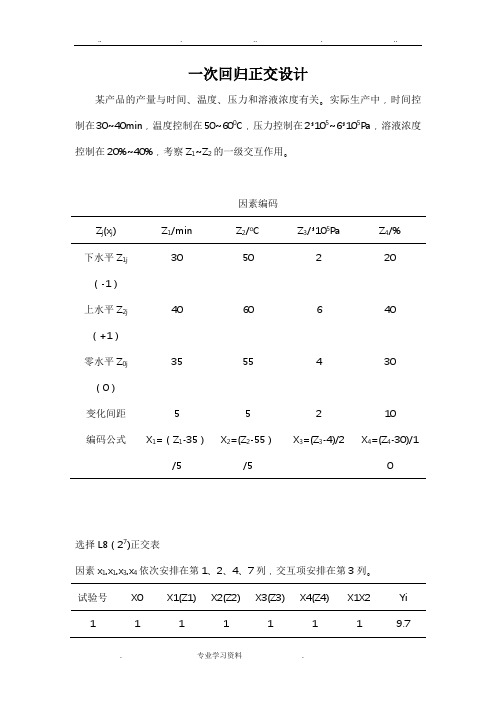
一次回归正交设计某产品的产量与时间、温度、压力和溶液浓度有关。
实际生产中,时间控制在30~40min,温度控制在50~600C,压力控制在2*105~6*105Pa,溶液浓度控制在20%~40%,考察Z1~Z2的一级交互作用。
因素编码Z j(x j) Z1/min Z2/o C Z3/*105Pa Z4/%下水平Z1j(-1)30 50 2 20上水平Z2j(+1)40 60 6 40零水平Z0j(0)35 55 4 30变化间距 5 5 2 10编码公式X1=(Z1-35)/5 X2=(Z2-55)/5X3=(Z3-4)/2 X4=(Z4-30)/1选择L8(27)正交表因素x1,x1,x3,x4依次安排在第1、2、4、7列,交互项安排在第3列。
试验号X0 X1(Z1) X2(Z2) X3(Z3) X4(Z4) X1X2 Yi1 1 1 1 1 1 1 9.72 1 1 1 -1 -1 1 4.63 1 1 -1 1 -1 -1 10.04 1 1 -1 -1 1 -1 11.05 1 -1 1 1 -1 -1 9.06 1 -1 1 -1 1 -1 10.07 1 -1 -1 1 1 1 7.38 1 -1 -1 -1 -1 1 2.49 1 0 0 0 0 0 7.910 1 0 0 0 0 0 8.111 1 0 0 0 0 0 7.4 Bj=∑xjy 87.4 6.6 2.6 8.0 12.0 -16.0aj=∑xj2 11 8 8 8 8 8bj = Bj7.945 0.825 0.325 1.000 1.500 -2.00/aj393 5.445 0.845 8.000 18.000 32.000Qj =Bj2 /aj可建立如下的回归方程。
Y=7.945+0.825x1+0.325x2+x3+1.5x4-2x1x2显著性检验:1、回归系数检验回归关系的方差分析表变异来源SS平方和Df自由度MS均方F显著水平x1 5.4451 5.44576.250.01 x20.84510.84511.830.05 x38.00018.000112.040.01 x4 18.000118.000252.100.01 x1x2 32.000132.000448.180.01 回归64.29 5 12.858180.080.01 剩余0.357 5 0.0714失拟0.097 3 0.0323 0.25 <1 误差e 0.2620.13总和64.64710经F检验不显著的因素或交互作用直接从回归方程中剔掉,不必再重新进行回归分析。
回归正交试验设计

规范变量z 规范变量 j 上星号臂γ 上星号臂 上水平1 上水平 零水平0 零水平 下水平-1 下水平- 下星号臂- 下星号臂-γ 变化间距 变化间距 j
②确定合适的二次回归正交组合设计 参考表8-22 参考表
正交表的选用 因素数m 因素数 2 3 4(1/2实施) ( 实施 实施) 4 5(1/2实施) ( 实施 实施) 5 选用正交表 L4(23) L8(27) L8(27) L16(215) L16(215) L32(231) 表头设计 1,2列 , 列 1,2,4列 , , 列 1,2,4,7列 , , , 列 1,2,4,8列 , , , 列 1,2,4,8,15列 , , , , 列 1,2,4,8,16列 , , , , 列 mc 22= 4 23= 8
(3)回归方程的建立 ) m0=0,n=mc=8 , = 计算表 计算各回归系数 写出y与规范变量 写出 与规范变量zj的回归方程 与规范变量 根据偏回归系数绝对值大小, 根据偏回归系数绝对值大小,确定因素和交互作用主次 根据偏回归系数正负, 根据偏回归系数正负,得到各因素对试验指标的影响方向 (4)方差分析 ) 与自然变量x (5)回归方程的回代:得到试验指标 与自然变量 j的回归 )回归方程的回代:得到试验指标y与自然变量 方程
1 m0 SSe1 = ∑ ( y0i y 0 ) 2 = ∑ y0i2 (∑ y0i ) 2 m0 i =1 i =1 i =1
m0
m0
重复试验误差的自由度: 重复试验误差的自由度: ②回归方程失拟部分: 回归方程失拟部分: 失拟平方和 :
df e1 = m0 1
SS Lf = SST SS R SS e1 = SS e SS e1
回归平方和 : SS R = ∑ SS 一次项 + ∑ SS 交互项 残差平方和 :
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次回归正交试验
为了检测某种原料的吸水倍率,重点考察氮肥含量和催化剂对试验指标的影响,已知氮肥含量(x1)的变化范围为0.7~0.9,催化剂(x2)的变化范围为1~3 mL,用二次正交组合设计分析出这两个因素与试验指标(y)之间的关系。
(1)因素水平编码
计算依据
m=2,取m0=2,根据星号臂γ计算公式或查表得γ=1.078
X(1γ)=0.9 ,x(-1γ)=0.7, x(10)=0.8
Δ1=(0.9-0.8)/1.078=0.093
X(2γ)=3 ,x(-1γ)=1, x(10)=2
Δ2=(3-2)/1.078=0.93
(2)试验方案
(3)回归方程的建立借助excel分析如下:
①回归方程显著性检验:F=186.5564,,,12.4)74(95.0=F
因此回归方程非常显著。
'74.41'37.2375.656.2609.952.468y 212121z z z z z z ----+= ②偏回归系数的显著性检验
9
.496.113305.113806.113308.47058.14583.1822.44615.5528.4705701.274.41)(8.1458701.224.23)(3.182475.6)(2
.4461324.656.265.552324.609.95.113801046852206303)(122111221221222222221
121111221
21212
1222
1222222
1121122121
=-=-==++++=++++==⨯===⨯===⨯===⨯===⨯===-=-=∑∑∑∑∑∑∑=======R T e R n
i i
n i i n
i n
i i n i i
n i i n i i
T SS SS SS SS SS SS SS SS SS z b SS z
b SS z z b SS z b SS z b SS y n y SS 方差分析:
dfT=n-1=10-1=9 df1=df2=df12=df1’=df2’=1
dfR=df1+df2+df12+df1’+df2’=1+1+1+1+1=5
dfe=dfT-dfR=9-5=4
MS1=522.5/1=522.5 MS2=SS2/df2=4461.2/1=4461.2 MS12=SS12/df12=182.3
MS1’=SS1’/df1’=1458.8
MS2’=SS2’/df1’=4705.8
MSR=SSR/dfR=11330.6/5=2266.1
MSe=SSe/dfe=49.9/4=12.5
F1=MS1/MSe=522.5/12.5=41.8
F2=MS2/MSe=4461.2/12.5=356.9
F12=MS12/MSe=182.3/12.5=14.6
F1’=MS1’/MSe=1458.8/12.5=116.7
F2’=MS2’/MSe=4705.8/12.5=376.5
FR=MSR/MSe=2266.1/12.5=181.3
F0.01(1,4)=21.20 F0.05(1,4)=7.71 F0.01(5,4)=15.52 F0.05(5,4)=6.26
失拟性检验
本例零水平试验次数m0=2,可进行失拟性检验
5.45.521220521225)509512(2
1)259081262144()(12201020101=-=+-+=-=∑∑==m i i m i i
e y m y SS
SSLf=SSe-SSe1=49.9-4.5=45.4 dfe1=m0-1=2-1=1 dfLf=dfe-dfe1=4-1=3
59
.53)1,3(37.31/5.43/5.45/1/1,01====F df SSe df SS FLf e Lf
Lf
检验结果表明,失拟不显著,回归模型与实际情况拟合很好。
最终的回归方程
y=-1544.0+4539.8x1+227.0x2-78.0x1x2-2678.7x12-48.3x22。
