二次函数全章导学案(史上最全!)

合集下载

苏科版初三九年级数学《二次函数》全章导学案教案(共11课时)

官墩九年制学校九年级班数学学案
官墩九年制学校九年级班数学学案
官墩九年制学校九年级班数学学案
官墩九年制学校九年级班数学学案
与
官墩九年制学校九年级班数学学案
画出函数
、你能否在这个直角坐标系中，再画出函数
上课时间：年月日
官墩九年制学校九年级班数学学案
官墩九年制学校九年级班数学学案
轴有两个公共点（x1,0）、(x2,0),
个不相等的实数根：。

2-6x+9与y= x2-2x+3的图象与x轴的公共点的个数；
）判断一元二次方程x2-6x+9=0和x2-2x+3=0的根的情况；
上课时间：年月日
官墩九年制学校九年级班数学学案
两点，求C，A，B的坐标；
上课时间：年月日
官墩九年制学校九年级班数学学案
上课时间：年月日
官墩九年制学校九年级班数学学案
结果球离球洞的水平距离还有2m．
上课时间：年月日
官墩九年制学校九年级班数学学案
１．河北省赵县的赵州桥的桥拱是抛物线型，建立如图所示的坐标系，其函数的
位置时，水面宽 AB = 30米，这时水面离。

人教版本初中九年级的数学下册的二次函数全章精品导学案

人教版九年级数学下册二次函数全章精选导教案【师生共用】第 1 课时 26.1二次函数一、阅读教科书第4— 6 页上方二、学习目标：1．知道二次函数的一般表达式；2．会利用二次函数的看法剖析解题；3．列二次函数表达式解实质问题．三、知识点：一般地，形如 ____________________________ 的函数，叫做二次函数。

此中x 是________， a 是 __________， b 是 ___________， c 是 _____________．四、基本知识练习2 3 2 ＋ 30x ；③ y＝ 200x 2 ＋ 400x＋ 200 ．这三个式子中，虽1．察看：① y＝ 6x ；② y＝－x2然函数有一项的，两项的或三项的，但自变量的最高次项的次数都是______次．一般地，假如 y＝ ax2＋ bx ＋ c（ a、b、c 是常数， a≠ 0），那么 y 叫做 x 的 _____________．2．函数 y＝ (m－ 2)x 2＋ mx － 3（ m 为常数）．（1）当 m__________ 时，该函数为二次函数；（2）当 m__________ 时，该函数为一次函数．3．以下函数表达式中，哪些是二次函数？哪些不是？假如二次函数，请指出各项对应项的系数．（ 1）y＝ 1－ 3x2（2）y＝3x2＋2x（3）y＝x (x－5)＋ 2（ 4）y＝ 3x 3＋ 2x2 （ 5） y＝ x＋1x五、讲堂训练1． y＝(m ＋ 1)x m2 m－ 3x＋ 1 是二次函数，则 m 的值为 _________________ ．2．以下函数中是二次函数的是（）1B ． y＝ 3 (x － 1) 2 C． y＝ (x＋ 1) 2 2 1A． y＝ x＋－ x D． y＝2－x2 x3．在必定条件下，若物体运动的路段s（米）与时间t（秒）之间的关系为s＝ 5t2＋ 2t，则当 t＝ 4 秒时，该物体所经过的行程为（）A．28 米B．48 米C．68 米D．88 米4．n 支球队参加竞赛，每两队之间进行一场竞赛．写出竞赛的场次数 m 与球队数 n 之间的关系式 _______________________ ．25．已知 y 与 x 成正比率，而且当x＝－ 1 时， y＝－ 3．（2）当 x＝ 4 时， y 的值；（3）当 y＝－1时， x 的值．36．为了改良小区环境，某小区决定要在一块一边靠墙（墙长形绿化带 ABCD ，绿化带一边靠墙，另三边用总长为25m ）的空地上修筑一个矩40m 的栅栏围住（如图）．若设绿化带的 BC 边长为 x m ，绿化带的面积为y m 2．求出自变量x 的取值范围．y 与 x 之间的函数关系式，并写六、目标检测1．若函数 y ＝ (a － 1)x 2＋ 2x ＋ a 2－ 1 是二次函数，则（）A ． a ＝ 1B ． a ＝± 1C ． a ≠ 1D ． a ≠－ 12．以下函数中，是二次函数的是（）2－1B ． y ＝x － 1C ． y ＝ 8 8A ． y ＝x x D ．y ＝ 2x 3．一个长方形的长是宽的 2 倍，写出这个长方形的面积与宽之间的函数关系式．4．已知二次函数 y ＝－ x 2＋ bx ＋ 3．当 x ＝ 2 时， y ＝ 3，求这个二次函数分析式．第 2 课时二次函数 y ＝ax 2 的图象与性质一、阅读课本：P6 — 8 二、学习目标：1．知道二次函数的图象是一条抛物线； 2．会画二次函数y ＝ ax 2的图象；3．掌握二次函数y ＝ ax 2的性质，并会灵巧应用．三、研究新知：2【提示：绘图象的一般步骤：①列表（取几组x 、y 的对应值；②描点（表中x 、 y 的数值在座标平面中描点（ x ， y ）；③连线（用光滑曲线）．】列表：x ⋯－3－2－1 0 1 2 3 ⋯y＝x2 ⋯⋯描点，并由象可得二次函数 y＝ x2的性：1．二次函数 y＝ x 2 是一条曲，把条曲叫做______________．2．二次函数 y＝ x2中，二次函数a＝ _______，抛物 y＝ x2的象张口 __________ ．3．自量 x 的取范是 ____________ ．4．察象，当两点的横坐互相反数，函数 y 相等，所描出的各点对于________称，进而象对于 ___________称．5．抛物 y＝x2与它的称的交点（，）叫做抛物y＝x2的 _________．所以，抛物与称的交点叫做抛物的_____________．6．抛物 y＝x 2有 ____________点（填“最高”或“最低”）．四、例剖析例 1 在同向来角坐系中，画出函数1 2 2 2的象．y＝ x ， y＝ x ， y＝2x2解：列表并填：x ⋯－4－3 －2 －1 01 2 34⋯1 2⋯⋯y＝2xy＝ x2的象画，再把它画出来．xy＝ 2x2 ⋯－ 2 ⋯－ 1.5 － 1 － 0.5 0 0.5 1 1.52 ⋯⋯1 2 2，y ＝2x 2 的二次系数a_______0；点都是 __________ ；：抛物 y ＝ x ，y ＝x2称是 _________ ；点是抛物的最_________点（填“高”或“低” ）．例 2在例 1 的直角坐系中画出函数y ＝－ x 2， y ＝－1x 2， y ＝－ 2x 2 的象．2列表：x ⋯－3－2－112 3⋯ y ＝ x 2⋯⋯x ⋯－4－3－2－10 1234⋯12⋯⋯y=－ 2xx y ＝－ 2x 2⋯ －4 ⋯－ 3 － 2 － 10 1 2 3 4⋯ ⋯：抛物 y ＝－ x 2，y ＝－12x 2， y ＝－ 2x 2的二次系数a______0，点都是 ________，称是 ___________，点是抛物的最________点（填“高”或“低” ）．五、理一理 1．抛物 y ＝ ax 2 的性象（草）张口称有最高或点最方向最低点当 x ＝ ____ a ＞ 0， y 有最_______ ，是______．当 x ＝ ____ a ＜ 0， y 有最_______ ，是______．2．抛物线 y＝ x2与 y＝－ x2 对于 ________对称，所以，抛物线y＝ax2与 y＝－ ax2对于_______对称，张口大小 _______________．3．当 a＞ 0 时， a 越大，抛物线的张口越___________；当 a＜ 0 时，｜ a｜越大，抛物线的张口越 _________；所以，｜ a｜越大，抛物线的张口越________，反之，｜ a｜越小，抛物线的张口越________．六、讲堂训练1．填表：张口方向极点有最高或最值对称轴最低点2 2 当 x＝ ____ 时， y 有最y＝3x _______值，是 ______．y＝－8x 22．若二次函数y＝ ax2的图象过点（ 1，－ 2），则 a 的值是 ___________ ．3．二次函数y＝(m－ 1)x 2的图象张口向下，则m____________．24．如图，①y＝ax② y＝ bx2③ y＝ cx2④ y＝ dx2比较 a、 b、c、 d 的大小，用“＞”连结．___________________________________七、目标检测1．函数 y＝37x2的图象张口向 _______，极点是 __________，对称轴是 ________，当 x＝ ___________时，有最 _________值是 _________．22．二次函数y＝mx m2 有最低点，则m＝ ___________．23．二次函数y＝(k ＋ 1)x 的图象以下图，则k 的取值4．写出一个过点（1， 2）的函数表达式_________________．第 3 课时二次函数y＝ax2＋k的图象与性质一、本：P9— 10二、学目：1．会画二次函数y＝ ax2＋ k 的象；2．掌握二次函数y＝ ax2＋ k 的性，并会用；3．知道二次函数y＝ ax2与 y＝的 ax2＋ k 的系．三、研究新知：在同向来角坐系中，画出二次函数y＝ x2＋ 1，y＝ x2－ 1 的象．解：先列表x ⋯－3－2 － 10 1 2 3 ⋯y＝ x2＋ 1 ⋯⋯y＝ x2－ 1 ⋯⋯描点并画察象得：1．张口方向点称有最高（低）点最y＝ x2y＝ x2－1y＝ x 2＋12．能够发现，把抛物线 y＝ x2向 ______平移 ______个单位，就获得抛物线y＝ x2＋ 1；把抛物线 y＝ x2向 _______平移 ______ 个单位，就获得抛物线y＝ x2－ 1．3．抛物线 y＝x2， y＝ x2－ 1 与 y＝ x2＋ 1 的形状 _____________ ．四、理一理知识点1．y＝ ax2 y＝ ax2＋ k张口方向极点对称轴有最高（低）点a＞0 时，当 x＝ ______时， y 有最 ____ 值为 ________；最值a＜0 时，当 x＝ ______时， y 有最 ____ 值为 ________．增减性2．抛物线 y＝ 2x2向上平移 3 个单位，就获得抛物线__________________ ；抛物线 y＝ 2x 2向下平移 4 个单位，就获得抛物线__________________ ．所以，把抛物线 y＝ ax2向上平移 k（k＞ 0）个单位，就获得抛物线 _______________；把抛物线 y＝ ax 2向下平移 m（ m＞ 0）个单位，就获得抛物线 _______________．3．抛物线 y＝－ 3x2与 y＝－ 3x2＋ 1 是经过平移获得的，进而它们的形状__________，由此可得二次函数y＝ ax2与 y＝ ax2＋ k 的形状 __________________ ．五、讲堂稳固训练1．填表函数草图张口对称轴对称轴右边的增减极点最值性方向y＝ 3x2y＝－ 3x2＋12y＝－ 4x －2 ．将二次函数 y ＝ 5x2－ 3向上平移7个单位后所得到的抛物线解析式为_________________．3．写出一个极点坐标为（ 0，－ 3），张口方向与抛物线y＝－ x2的方向相反，形状同样的抛物线分析式 ____________________________ ．4．抛物线 y＝ 4x2＋ 1 对于 x 轴对称的抛物线分析式为______________________ ．六、目标检测1．填表函数张口对称轴最值对称轴左边的增减性极点方向y＝－ 5x 2＋ 3 y＝ 7x2－ 11 2－2 1 22．抛物线 y＝－x 可由抛物线 y＝－ x ＋ 3 向 ___________平移 _________个单位3 3获得的．3．抛物线 y＝－ x2＋h 的极点坐标为（ 0， 2），则 h＝ _______________ ．4．抛物线 y＝ 4x 2－ 1 与 y 轴的交点坐标为_____________ ，与 x 轴的交点坐标为_________．第 4 课时二次函数y＝a(x-h)2的图象与性质一、阅读课本：P10— 11二、学目：1．会画二次函数y ＝ a （ x- h ）2的象；2．掌握二次函数y ＝ a （ x- h ）2的性，并要会灵巧用；三、研究新知：画出二次函数y ＝－1 21 2的象，并考它的张口方向、称、(x ＋1)， y － (x － 1)22点以及最、增减性．先列表：x⋯－4－3－2－101234⋯12⋯⋯ y ＝－ 2(x ＋ 1)1 2⋯y ＝－ 2(x － 1)⋯描点并画． 1．察象，填表：函数张口点称最增减性方向12 y ＝－ 2(x ＋ 1)1 2 y ＝－ 2(x － 1)1 2也画上去（草）．2．在上把抛物 y ＝－ x2①抛物 y ＝－1(x ＋1) 2， y ＝－ 1x 2， y ＝－ 1(x － 1)2的形状大小 ____________ ．2 2 2②把抛物线 y＝－1 2向左平移 _______个单位，就获得抛物线y＝－1 2；x2(x＋ 1)2把抛物线 y＝－1 2向右平移 _______个单位，就获得抛物线y＝－1 2 x (x ＋1) ．2 2四、整理知识点1．y＝ ax2 y＝ ax2＋ k y＝ a (x- h)2 张口方向极点对称轴最值增减性（对称轴左边）2．对于二次函数的图象，只需｜a｜相等，则它们的形状_________，不过 _________不一样．五、讲堂训练1．填表张口对称对称轴极点右边的增减图象（草图）最值方向轴性1 2y＝2xy＝－ 5 (x ＋ 3)2y＝ 3 (x－ 3)22．抛物线 y＝ 4 (x － 2)2与 y 轴的交点坐标是___________，与 x 轴的交点坐标为________．3 ．把抛物线y ＝ 3x 2向右平移4个单位后，得到的抛物线的表达式为____________________ ．把抛物线y ＝ 3x2向左平移6个单位后，得到的抛物线的表达式为____________________ ．4．将抛物线 y＝－1(x－ 1)x 2向右平移 2 个单位后，获得的抛物线分析式为____________ ．35．写出一个极点是（ 5，0），形状、张口方向与抛物线y＝－ 2x2都同样的二次函数解析式___________________________ ．六、目标检测1．抛物线 y＝ 2 (x ＋ 3)2的张口 ______________；极点坐标为 __________________；对称轴是 _________；当 x＞－ 3 时， y______________ ；当 x＝－ 3 时， y 有 _______ 值是 _________．2．抛物线 y＝ m (x ＋ n) 2 向左平移 2 个单位后，获得的函数关系式是 y＝－ 4 (x － 4)2，则m＝ __________ ，n＝ ___________．3 ．若将抛物线 y ＝ 2x2＋ 1向下平移2个单位后，得到的抛物线解析式为_______________ ．4．若抛物线y＝ m (x ＋1) 2过点（ 1，－ 4），则 m＝ _______________．第 5 课时二次函数y＝a(x－h)2＋k的图象与性质一、阅读课本：第12页～第13页上方．二、学习目标：1．会画二次函数的极点式y＝ a (x－ h)2＋ k 的图象；2．掌握二次函数y＝ a (x－ h)2＋ k 的性；3．会用二次函数y＝ a (x－ h)2＋ k 的性解．三、研究新知：画出函数 y＝－12(x ＋1)2－1 的象，指出它的张口方向、称及点、最、增减性．列表：x ⋯－4－3－2－10 12⋯y＝－1 2－ 1 ⋯⋯(x＋ 1)2由象：1．函数张口称最增减性点方向1 2－ 1 y＝－ (x＋1)22．把抛物 y＝－1x2向 _______平移 ______个位，再向 _______平移 _______ 个位，2就获得抛物 y＝－1(x ＋1) 2－1．2四、理一理知点y＝ ax2 y＝ ax2＋ k y＝ a (x- h) 2 y＝ a (x－ h)2＋ k张口方向极点对称轴最值增减性（对称轴右侧）2．抛物线y＝ a (x－ h)2＋ k 与 y＝ax2形状 ___________，地点 ________________ ．五、讲堂练习1．y＝ 3x2 y＝－ x2＋ 1 y＝1(x＋ 2)2 y＝－ 4 (x－ 5)2－3 2张口方向极点对称轴最值增减性（对称轴左侧）2． y＝ 6x2＋ 3 与 y＝ 6 (x － 1)2＋ 10_____________ 同样，而 ____________ 不一样．3．极点坐标为（－ 2， 3），张口方向和大小与抛物线y＝1 x2同样的分析式为（）21 2 1 2－ 3A ． y＝(x －2) ＋ 3B ． y＝ (x＋ 2)2 21 2 1 2＋ 3C． y＝ (x ＋2) ＋ 3 D ．y＝－ (x ＋2)2 24．二次函数 y＝ (x－ 1)2＋ 2 的最小值为 __________________ ．5．将抛物线 y＝ 5(x－ 1)2＋ 3 先向左平移 2 个单位，再向下平移 4 个单位后，获得抛物线的分析式为 _______________________ ．6．若抛物线 y＝ ax2＋ k 的极点在直线y＝－ 2 上，且 x＝ 1 时， y＝－ 3，求 a、 k 的值．7．若抛物线y＝ a (x－ 1)2＋ k 上有一点 A （3， 5），则点 A 对于对称轴对称点A’的坐标为__________________．六、目标检测1．张口方向极点对称轴y＝ x2＋ 1y＝ 2 (x－3) 2y＝－(x＋ 5)2－ 42．抛物线y＝－ 3 (x ＋ 4)2＋ 1 中，当 x＝ _______时， y 有最 ________值是 ________．3．足球守门员大脚开出去的球的高度随时间的变化而变化，这一过程可近似地用以下哪幅图表示（）ABCD4．将抛物线y＝ 2 (x ＋ 1)2－ 3 向右平移 1 个单位，再向上平移 3 个单位，则所得抛物线的表达式为 ________________________ ．5．一条抛物线的对称轴是x＝ 1，且与 x 轴有独一的公共点，而且张口方向向下，则这条抛物线的分析式为____________________________ ．（任写一个）第 6 课时二次函数y＝ax2＋bx＋c的图象与性质一、本：第 14 ～第 15 上方．二、学目：21．配方法求二次函数一般式y ＝ax ＋ bx ＋ c 的点坐、称； 22．熟二次函数y ＝ ax ＋ bx ＋c 的点坐公式；23．会画二次函数一般式y ＝ ax ＋ bx ＋ c 的象．三、研究新知：1．求二次函数y ＝12x 2－ 6x ＋21 的点坐与称．1 2解：将函数等号右配方：y ＝ x －6x ＋ 21 2．画二次函数 y ＝1x 2－ 6x ＋21 的象．2解： y ＝1x 2－ 6x ＋ 21 配成点式 _______________________ ．2 列表：x⋯345678 9⋯y ＝ 1x 2－ 6x ＋ 21 ⋯ ⋯ 23．用配方法求抛物 y ＝ ax 2＋ bx ＋ c （ a ≠ 0）的点与称．四、理一理知点：y ＝ ax 2y ＝ ax 2＋ k y ＝a( x － h)2 y ＝ a( x － h)2＋k y ＝ ax 2＋ bx＋ c张口方向点对称轴最值增减性（对称轴左边）五、讲堂练习1．用配方法求二次函数y＝－ 2x2－ 4x＋ 1 的极点坐标．2．用两种方法求二次函数y＝ 3x2＋ 2x 的极点坐标．3．二次函数 y＝ 2x2＋ bx ＋c 的极点坐标是（ 1，－ 2），则 b＝ ________，c＝ _________ ．4．已知二次函数 y＝－ 2x 2－ 8x－6，当 ___________时， y 随 x 的增大而增大；当x＝________时， y 有 _________值是 ___________．六、目标检测1 2的极点坐标．1．用极点坐标公式和配方法求二次函数y＝ x － 2－ 122．二次函数y＝－ x2＋ mx 中，当 x＝ 3 时，函数值最大，求其最大值．第 7 课时二次函数y＝ax2＋bx＋c的性质一、复习知识点：第 6 课中“理一理知识点”的内容．二、学习目标：21．懂得求二次函数y＝ ax ＋ bx＋ c 与 x 轴、 y 轴的交点的方法；22．知道二次函数中a， b，c 以及△＝ b － 4ac 对图象的影响．三、基本知识练习1．求二次函数y＝ x2＋ 3x－ 4 与 y 轴的交点坐标为_______________ ，与 x 轴的交点坐标____________ ．2．二次函数y＝ x2＋ 3x－ 4 的极点坐标为 ______________，对称轴为 ______________．3．一元二次方程x2＋ 3x－ 4＝ 0 的根的鉴别式△＝______________．4．二次函数y＝ x2＋ bx 过点（ 1， 4），则 b＝ ________________ ．5．一元二次方程y＝ax2＋bx＋ c（ a≠ 0），△＞ 0 时，一元二次方程有_______________，△＝ 0 时，一元二次方程有___________，△＜ 0 时，一元二次方程_______________．四、知识点应用1．求二次函数y＝ ax2＋ bx＋ c 与 x 轴交点（含 y＝ 0 时，则在函数值y＝ 0 时， x 的值是抛物线与 x 轴交点的横坐标）．例 1求y＝x2－2x－3与x轴交点坐标．2．求二次函数 y＝ ax2＋ bx＋ c 与 y 轴交点（含 x＝ 0 时，则 y 的值是抛物线与 y 轴交点的纵坐标）．2例 2求抛物线y＝ x － 2x－ 3 与 y 轴交点坐标．23． a、 b、 c 以及△＝ b － 4ac 对图象的影响．（ 1） a 决定：张口方向、形状（ 2） c 决定与 y 轴的交点为（0，c）b（ 3） b 与－共同决定b 的正负性0与 x轴有两个交点（4）△＝ b2－ 4ac0与 x轴有一个交点0与 x轴没有交点例 3 如图，由图可得：a_______0b_______0c_______0△______0例 4已知二次函数y＝ x2＋ kx ＋ 9．①当 k 为何值时，对称轴为y 轴；②当 k 为何值时，抛物线与x 轴有两个交点；③当 k 为何值时，抛物线与x 轴只有一个交点．五、课后练习1．求抛物线 y＝ 2x2－7x－ 15 与 x 轴交点坐标 __________ ，与 y 轴的交点坐标为_______．2．抛物线 y＝ 4x2－ 2x＋ m 的极点在 x 轴上，则 m＝ __________ ．3．如图：由图可得：a_______0b_______0c_______0△＝ b2－ 4ac______0六、目标检测1．求抛物线y＝ x2－ 2x＋ 1 与 y 轴的交点坐标为 _______________．2．若抛物线y＝ mx2－ x＋ 1 与 x 轴有两个交点，求 m 的范围．3．如图：由图可得： a _________0b_________0c_________0△＝ b2－ 4ac_________0第 8 课时二次函数y＝ax2＋bx＋c分析式求法一、学习目标：1．会用待定系数法求二次函数的分析式；2．实质问题中求二次函数分析式．二、课前基本练习1．已知二次函数y＝ x2＋ x＋m 的图象过点（1， 2），则 m 的值为 ________________ ．2．已知点 A （ 2，5）， B（ 4， 5）是抛物线y＝4x2＋bx＋ c 上的两点，则这条抛物线的对称轴为 _____________________ ．3．将抛物线y＝－ (x－ 1)2＋ 3 先向右平移 1 个单位，再向下平移3 个单位，则所得抛物线的分析式为 ____________________．4．抛物线的形状、张口方向都与抛物线y＝－12x2同样，极点在（1，－ 2），则抛物线的解析式为 ________________________________ ．三、例题剖析例 1 已知抛物线经过点 A （－ 1， 0）， B（ 4，5）， C（0，－ 3），求抛物线的分析式．例 2 已知抛物线极点为（ 1，－ 4），且又过点（ 2，－ 3）．求抛物线的分析式．例 3 已知抛物线与 x 轴的两交点为（－ 1， 0）和（ 3， 0），且过点（ 2，－ 3）．求抛物线的分析式．四、概括用待定系数法求二次函数的分析式用三种方法：1．已知抛物线过三点，设一般式为y＝ ax2＋ bx＋ c．2．已知抛物线极点坐标及一点，设极点式y＝ a(x－ h)2＋ k．3．已知抛物线与x 轴有两个交点（或已知抛物线与x 轴交点的横坐标），设两根式： y＝ a(x－ x1)(x －x2 )．（此中 x1、 x2是抛物线与x 轴交点的横坐标）五、实质问题中求二次函数分析式例 4要修筑一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为1m 处达到最高，高度为3m，水柱落地处离池中心3m，水管应多长？六、讲堂训练1．已知二次函数的图象过（0， 1）、（ 2， 4）、（ 3， 10）三点，求这个二次函数的关系式．2．已知二次函数的图象的极点坐标为（－2，－ 3），且图像过点（－3，－ 2），求这个二次函数的分析式．3．已知二次函数y＝ ax2＋ bx＋c 的图像与x 轴交于 A （1， 0）， B（ 3， 0）两点，与y轴交于点 C（ 0， 3），求二次函数的极点坐标．4．如图，在△ ABC 中，∠ B ＝ 90°， AB ＝ 12mm， BC ＝ 24mm，动点 P 从点 A 开始沿边 AB 向 B 以 2mm/s 的速度挪动，动点Q 从点 B 开始沿边BC 向 C 以 4mm/s 的速度挪动，假如P、Q 分别从 A 、 B 同时出发，那么△PBQ 的面积 S 随出发时间t 如何变化？写出函数关系式及t 的取值范围．APBQC七、目标检测1．已知二次函数的图像过点A（－ 1，0），B（ 3，0），C（ 0，3）三点，求这个二次函数分析式．第 9 课时二次函数y＝ax2＋bx＋c的性质一、阅读教科书：P15 的研究二、学习目标：几何问题中应用二次函数的最值．三、课前基本练习1．抛物线y＝－ (x ＋1)2＋2 中，当 x＝ ___________时， y 有 _______值是 __________．1 2－x＋ 1 中，当 x＝ ___________时， y 有 _______ 值是 __________ ．2．抛物线 y＝ x23．抛物线 y＝ ax2＋ bx＋（ca≠ 0）中，当 x＝ ___________时，y 有 _______ 值是 __________ ．四、例题剖析：（ P15 的研究）用总长为 60m 的篱笆围成矩形场所，矩形面积S 随矩形一边长l的变化而变化，当l 是多少时，场所的面积S 最大？五、课后练习1．已知直角三角形两条直角边的和等于8，两条直角边各为多少时，这个直角三角形的面积最大，最大值是多少？2．从地面竖直向上抛出一小球，小球的高度h（单位： m）与小球运动时间t（单位：2高度是多少？3．如图，四边形的两条对角线AC 、BD 相互垂直， AC ＋ BD ＝ 10，当 AC 、BD 的长是D多少时，四边形ABCD 的面积最大？CAB 4．一块三角形废料以下图，∠ A ＝ 30°，∠ C＝ 90°， AB ＝12．用这块废料剪出一个长方形 CDEF ，此中，点 D、 E、 F 分别在 AC 、 AB 、 BC 上．要使剪出的长方形CDEF 面积最大，点E 应造在哪处？AEDC F B六、目标检测如图，点 E、F、G、H 分别位于正方形ABCD 的四条边上，四边形 EFGH 也是正方形．当点 E 位于哪处时，正方形EFGH 的面积最小？D G CHFAEB第 10 课时用函数看法看一元二次方程一、阅读课本：第 20～ 22 页二、学习目标：1．知道二次函数与一元二次方程的关系．2．会用一元二次方程 ax2＋ bx＋c＝ 0 根的鉴别式△＝ b2－ 4ac 判断二次函数y＝ ax2＋ bx ＋c 与 x 轴的公共点的个数．三、研究新知1．问题：如图，以40m/s 的速度将小球沿与地面成30°角的方向击出时，球的飞翔路线将是一条抛物线．假如不考虑空气阻力，球的飞翔高度h（单位： m）与飞翔时间t（单位：s）之间具相关系h＝ 20t－ 5t2．考虑以下问题：（1）球的飞翔高度可否达到 15m？如能，需要多少飞翔时间？（2）球的飞翔高度可否达到 20m？如能，需要多少飞翔时间？（3）球的飞翔高度可否达到 20.5m？为何？（4）球从飞出到落地要用多少时间？2．察看图象：2＋ x－ 2 的图象与 x 轴有 ____个交点，则一元二次方程x2＋ x－ 2 （ 1）二次函数y＝ x＝0 的根的鉴别式△＝ _______0；（ 2）二次函数 y＝ x2－ 6x＋ 9 的图像与x 轴有 ___________ 个交点，则一元二次方程x2－ 6x＋ 9＝ 0 的根的鉴别式△＝_______0；（ 3）二次函数 y＝ x 2－ x＋1 的图象与x 轴 ________公共点，则一元二次方程x2－ x＋1＝ 0 的根的鉴别式△ _______0．四、理一理知识1．已知二次函数y＝－ x2＋ 4x 的函数值为3，求自变量x 的值，能够看作解一元二次方程__________________ ．反之，解一元二次方程－x2＋ 4x＝3 又能够看作已知二次函数__________________ 的函数值为3 的自变量 x 的值．一般地：已知二次函数 y＝ax2＋bx ＋ c 的函数值为 m，求自变量 x 的值，能够看作解一元二次方程 ax2＋ bx ＋ c＝ m．反之，解一元二次方程 ax2＋ bx＋ c＝ m 又能够看作已知二次函数 y＝ ax2＋ bx＋ c 的值为 m 的自变量 x 的值．2．二次函数y＝ ax2＋ bx＋ c 与 x 轴的地点关系：一元二次方程ax2＋ bx＋ c＝0 的根的鉴别式△＝b2－ 4ac．2（ 1）当△＝ b－4ac＞时（ 2）当△＝ b 2－4ac ＝ 0 时（ 3）当△＝ b 2－4ac ＜ 0 时五、基本知识练习 2 1．二次函数y ＝ x － 3x ＋ 2，当 22．二次函数y ＝ x － 4x ＋ 6，当 3．如图， 4．如图抛物线 y ＝ ax 2＋ bx ＋ c 与 x 轴有两个交点；抛物线 y ＝ ax 2＋ bx ＋ c 与 x 轴只有一个交点；抛物线 y ＝ ax 2＋ bx ＋ c 与 x 轴没有公共点．x ＝ 1 时， y ＝ ________；当 y ＝ 0 时， x ＝ _______．x ＝ ________时， y ＝ 3．2一元二次方程ax ＋ bx ＋ c ＝ 0 一元二次方程ax 2＋ bx ＋ c ＝ 3 的解为 _________________5．如图填空：（1） a________0 （2） b________0 （3） c________0（4） b 2－ 4ac________0六、讲堂训练1．特别代数式求值： ①如图看图填空：（1） a ＋ b ＋c_______0 （2） a － b ＋c_______0 （3） 2a － b_______0②如图2a ＋b_______04a ＋ 2b ＋c_______02．利用抛物线图象求解一元二次方程及二次不等式（1）方程 ax2＋bx＋ c＝ 0 的根为 ___________；（2）方程 ax2＋bx＋ c＝－ 3 的根为 __________；（3）方程 ax2＋bx＋ c＝－ 4 的根为 __________；（4）不等式 ax2＋ bx＋ c＞0 的解集为 ________；（5）不等式 ax2＋ bx＋ c＜0 的解集为 ________；6）不等式－ 4＜ ax2＋ bx＋ c＜ 0 的解集为 ________．七、目标检测依据图象填空：（1） a_____0；（ 2） b_____0；（ 3） c______0；（4）△＝ b2－ 4ac_____0；（ 5） a＋ b＋ c_____0；（6） a－ b＋ c_____0；（ 7） 2a＋ b_____0；（8）方程 ax2＋ bx＋ c＝ 0 的根为 __________ ；（9）当 y＞ 0 时， x 的范围为 ___________；（10）当 y＜ 0 时， x 的范围为 ___________ ；八、课后训练1．已知抛物线 y＝ x2－ 2kx ＋ 9 的极点在 x 轴上，则 k＝ ____________．2．已知抛物线 y＝ kx 2＋ 2x－ 1 与坐标轴有三个交点，则k 的取值范围 ___________ ．3．已知函数 y＝ ax2＋ bx＋ c（ a，b，c 为常数，且 a≠ 0）的图象以下图，则对于x 的方程ax 2＋ bx＋c－ 4＝ 0 的根的状况是（）A ．有两个不相等的正实数根B．有两个异号实数根C．有两个相等实数根D．无实数根4．如图为二次函数y＝ ax2＋ bx＋ c 的图象，在以下说法中：①a c＜ 0；②方程 ax2＋ bx ＋c＝ 0 的根是 x1＝－ 1， x2＝ 3；③ a＋b＋ c＞0；④当 x＞ 1 时， y 随 x 的增大而增大．正确的说法有 __________________ （把正确的序号都填在横线上）．第 11 课时实质问题与二次函数商品价风格整问题一、阅读课本：第25～26页上方（研究1）二、学习目标：1．懂得商品经济等问题中的相等关系的找寻方法；2．会应用二次函数的性质解决问题．三、研究新知某商品此刻的售价为每件60 元，每礼拜可卖出300 件，市场检查反应：如调整价钱，每涨价 1 元，每礼拜要少卖出10 件；每降价 1 元，每礼拜可多卖出20 件．已知商品的进价为每件40 元，如何订价才能使利润最大？剖析：调整价钱包含涨价和降价两种状况，用如何的等量关系呢？解：（ 1）设每件涨价 x 元，则每礼拜少卖_________件，实质卖出 _________件，设商品的利润为y 元．（ 2）设每件降价x 元，则每礼拜多卖_________件，实质卖出 __________件．四、讲堂训练1．某种商品每件的进价为30 元，在某段时间内若以每件x 元销售，可卖出（100－ x）件，应如何订价才能使利润最大？2．蔬菜基地栽种某种蔬菜，由市场行情剖析知，1 月份至 6 月份这类蔬菜的上市时间x（月份）与市场售价P（元 /千克）的关系以下表：上市时间x/（月份）123456市场售价P（元 /千克）3这类蔬菜每千克的栽种成本y（元 / 千克）与上市时间x（月份）知足一个函数关系，这个函数的图象是抛物线的一段（如图）．（ 1）写出上表中表示的市场售价P（元 /千克）对于上市时间x（月份）的函数关系式；（ 2）若图中抛物线过 A 、 B、 C 三点，写出抛物线对应的函数关系式；（ 3）由以上信息剖析，哪个月上市销售这类蔬菜每千克的利润最大？最大值为多少？（利润＝市场售价－栽种成本）五、目标检测元，某旅馆客房部有60 个房间供游旅居住，当每个房间的订价为每日住满．当每个房间每日的订价每增添10 元时，就会有一个房间空间．对有旅客入住的房间，旅馆需对每个房间每日支出20 元的各样花费．求：（1）房间每日入住量 y（间）对于 x（元）的函数关系式；（2）该旅馆每日的房间收费 z（元）对于 x（元）的函数关系式；（3）该旅馆客房部每日的利润 w（元）对于 x（元）的函数关系式，当每个房间的订价为多少元时， w 有最大值？最大值是多少？第 12 课时实质问题与二次函数一、阅读课本：第27页研究 3二、学习目标：1．会成立直角坐标系解决实质问题；2．会解决桥洞水面宽度问题．三、基本知识练习1．以抛物线的极点为原点，以抛物线的对称轴为y 轴成立直角坐标系时，可设这条抛物线的关系式为 ___________________________________ ．1 2AB 地点时，水面2．拱桥呈抛物线形，其函数关系式为y＝－ x ，当拱桥下水位线在4宽为12m，这时水面离桥拱顶端的高度h 是（）A ． 3mB． 2 6m C． 4D． 9m3m3．有一抛物线拱桥，已知水位线在AB 地点时，水面的宽为 4 6米，水位上升4 米，就达到戒备线CD，这时水面宽为 4 3米．若洪水到来时，水位以每小时0.5 米的速度上升，则水过戒备线后几小时吞没到拱桥顶端M 处？四、讲堂练习1．一座拱桥的轮廓是抛物线（如图①所示），拱高6m，跨度20m，相邻两支柱间的距离均为 5m．（ 1）将抛物线放在所给的直角坐标系中（如图②所示），其关系式 y＝ ax 2＋ c 的形式，请依据所给的数据求出a、c 的值；（ 2）求支柱 MN 的长度；（ 3）拱桥下地平面是双向行车道（正中间是一条宽2m 的隔绝带），此中的一条行车道可否并排行驶宽 2m，高 3m 的三辆汽车（汽车间的间隔忽视不计）？请谈谈你的原因．2．如图，有一座抛物线形拱桥，在正常水位时水面AB的宽为20m，假如水位上升的宽是 10m．（ 1）建图①立以下图的直角坐标系，求此抛物线的分析式．（ 2）现有一辆载有营救物质的货车从甲地出发需经过此桥开往乙地，已知甲地距此桥 280km （桥长忽视不计）．货车正以每小时 40km 的速度开往乙地，当行驶1h 时，突然接到紧迫通知：前面连降暴雨，造成水位以每小0.25m 的速度持续上升（货车接到通知时水位在CD 处，当水位达到桥拱最高点O 时，严禁车辆通行）．试问：假如货车按本来速度行驶，可否安全经过此桥？若能，请说明原因．若不可以，要使货车安全经过此桥，速度应超出每小时多少千米？第 13 课时二次函数综合应用一、复习二次函数的基天性质二、学习目标：灵巧运用二次函数的性质解决综合性的问题．三、课前训练1．二次函数y＝ kx 2＋ 2x＋ 1（ k＜ 0）的图象可能是（）2．如图：（ 1）当 x 为何范围时， y1＞ y2?（ 2）当 x 为何范围时， y1＝ y2?（ 3）当 x 为何范围时， y1＜ y2?3．如图，是二次函数y＝ ax2－ x＋ a2－ 1 的图象，则a＝ ____________．13 5 24．若 A（－4，y1），B（－ 1，y2）， C（3，y3）为二次函数y＝－ x － 4x＋ 5 图象上的三点，则 y1、 y2、 y3的大小关系是（）A ．y1＜ y2＜ y3B ． y3＜ y2＜ y1 C． y3＜ y1＜ y2 D． y2＜ y1＜ y35．抛物线 y＝(x －2) (x ＋ 5)与坐标轴的交点分别为 A 、B、C，则△ ABC 的面积为 __________ ．6．如图，已知在平面直角坐标系中，矩形ABCD的边AD在x轴上，点A在原点，AB＝3，AD ＝ 5．若矩形以每秒 2 个单位长度沿x 轴正方向做匀速运动，同时点P 从 A 点出发以每秒 1 个单位长度沿A→ B→C→ D 的路线做匀速运动．当点P 运动到点D 时停止运动，矩形 ABCD 也随之停止运动．（1）求点 P 从点 A 运动到点 D 所需的时间．（2）设点 P 运动时间为 t （秒）①当 t＝ 5 时，求出点P 的坐标．②若△ OAP 的面积为S，试求出S 与t之间的函数关系式（并写出相应的自变量 t 的取值范围）．五、目标检测如图，二次函数y＝ ax2＋ bx＋ c 的图像经过 A （－ 1， 0），B （ 3，0）两交点，且交y 轴于点 C．（1）求 b、 c 的值；（2）过点 C 作 CD ∥x 轴交抛物线于点 D ，点 M 为此抛物线的极点，试确立△ MCD 的形状．。

二次函数导学案(全章)

第1课时二次函数的概念【进修目的】1．阅历摸索,剖析和树立两个变量之间的二次函数关系的进程,进一步体验若何用数学的办法描写变量之间的数目关系;2．摸索并归纳二次函数的界说;3．可以或许暗示简略变量之间的二次函数关系. 【进修重点】控制二次函数的概念并能应用概念解答相干的题型. 【课时类型】概念课【进修进程】一.进修预备1．函数的界说：在某个变更进程中,有两个变量x 和y,假如给定一个x 值,响应地就肯定了一个y 值,那么我们称是的函数,个中是自变量,是因变量.2．一次函数的关系式为y=(个中k.b 是常数,且k≠0);正比例函数的关系式为y ＝(个中k 是的常数);反比例函数的关系式为y=(k 是的常数).二.解读教材——数学常识源于生涯3．某果园有100棵橙子树,每一棵树平均结600个橙子.现预备多种一些橙子树以进步产量,但是假如多种树,那么树之间的距离和每一棵树所接收的阳光就会削减.依据经验估量,每多种一棵树,平均每棵树就会少结5个橙子.假设果园增种x 棵橙子树,那么果园共有棵橙子树,这时平均每棵树结个橙子,假如果园橙子的总产量为y 个,那么y=.4．假如你到银行存款100元,设人平易近币一年按期储蓄的年利率是x,一年到期后,银行将本金和利钱主动按一年按期储蓄转存.那么你能写出两年后的本息和y(元)的表达式(不斟酌利钱税)吗？. 5．可否依据适才推导出的式子y=5x2+100x+60000和y=100x2+200x+100猜测出二次函数的界说及一般情势吗？一般地,形如y ＝ax2+bx+c(a,b,c 是常数,a ≠0)的函数叫做x 的二次函数.它就是二次函数的一般情势,例1 下列函数中,哪些是二次函数？(1)2321x y +-=(2)112+=x y(3)x y 222+= (4)251t t s ++=(5)22)3(x x y -+= (6)210r s π=即时演习：下列函数中,哪些是二次函数？(1)2x y =(2)252132+-=x x y (3))1(+=x x y (4)1132--=）（x y (5)cax y -=2(6)12+=x s 三.发掘教材6．对二次函数界说的深入懂得及应用例2 若函数1232++=+-kx x y k k 是二次函数,求k 的值.剖析：x 的最高次数等于2,即k23k+2=2,求出k 的值即可.解：即时演习：若函数1)3(232++-=+-kx x k y k k 是二次函数,则k 的值为.四.反思小结1．我们经由过程不雅察.思虑.合作,交换,归纳出二次函数的概念,并从中领会函数的建模思惟.2．界说：一般地,形如y=ax²+bx+c(a,b,c 是常数,a≠0)的函数叫做x 的二次函数.3．二次函数y=ax²+bx+c(a,b,c 是常数,a≠0)的几种不合暗示情势：(1) y=ax² (a≠0); (2) y=ax²+c (a≠0且c≠0); (3) y=ax²+bx (a≠0且b≠0).4．二次函数界说的焦点是症结字“二”,即必须知足自变量最高次项的指数为_____,且______项系数不为_____的整式. 【达标测评】1．下列函数不属于二次函数的是（） A ．y=(x －1)(x+2)B ．y=21(x+1)2 C ．y=2(x+3)2－2x2 D ．y=1－3x22．在边长为6 cm 的正方形中央剪去一个边长为x cm(x<6)的小正方形,剩下的四方框形的面积为y,则y 与x 之间的函数关系是.3．用总长为60m 的篱笆围成矩形场地,场地面积S(m²)与矩形一边长a(m)之间的关系式是,它是函数.4．正方形的边长是5,若边长增长x,面积增长y,则y 与x 之间的函数表达式为.5．当m=时,22)2(--=m x m y 是二次函数;若函数m m x m y --=2)2(是二次函数,则m= .6．已知函数y=ax2＋bx ＋c （个中a,b,c 都是常数）：当a 时,它是二次函数;当a,b 时,它是一次函数;当a,b,c 时,它是正比例函数. 7．若函数y=(k2－4)x2+(k+2)x+3是二次函数,则k.,【进修难点】可以或许应用描点法作出函数的图象,并能依据图象熟悉和懂得二次函数y ＝ax2的性质. 【进修进程】一.进修预备1．正比例函数y=kx(k≠0)是图像是. 2．一次函数y=kx+b(k≠0)的图像是. 3．反比列函数y=k x(k≠0)的图像是.4．当我们还不懂得一种函数图像的外形时,只能用描点法研讨,描点法的一般步调是：,,. 二.解读教材5．试作出二次函数y ＝x2的图象.（1）画出图象：①列表：（留意选择恰当的y值）②描点：（在右图坐标系中描点）③连线：（应留意用滑腻的曲线衔接各点）（2）依据图像,进行小结：①y＝x2的图像是,且启齿偏向是 .②它是对称图像,对称轴是轴.在对称轴的左侧（x>0）,y 随x 的增大而;在对称轴的右侧（x<0）,y 随x 的增大而.③图像与对称轴有交点,称为抛物线的极点,的最低点,此时,坐标为（,）.④因为图像有最低点,所以函数有最值,当x=0.小结：①y＝x2的图像是,且启齿向 .②对称轴是,在对称轴阁下的增减性分离是：在对称轴左侧,y 随x 的增大 ,在对称轴的右侧,y 随x 的增大.③极点坐标是：（,）,且从图像看出它有最点,所以函数有最值.当x=0时,.7．变式练习2作出y ＝2x2,y ＝0.5x2的图像.三.发掘教材8．依据上面的图象,从图象的启齿偏向.对称轴.增减性.极点坐标.最同时,a 决议图象在统一向角坐标系中的启齿偏向,|a|越小图象启齿. 9．例已知：抛物线102-+=m m mx y ,当x>0时,y 随x 的增大而增大,求m 的值.10．已知抛物线y=ax2经由点A （2,8）,（1）求此抛物线的函数解析式;（2）断定点B （1, 4）是否在此抛物线上;（3）求出此抛物线上纵坐标为6的点的坐标. 四.反思小结二次函数的y ＝ax2（a≠0）的图象与性质：五个方面懂得：,,,,. 【达标测评】1．抛物线y=2x2的极点坐标是,对称轴是,在侧,y 跟着x 的增大而增大;在侧,y 跟着x 的增大而减小.当x=时,函数y 的值最小,最小值是.抛物线y=2x2的图象在方（除极点外）.2．函数y ＝x2的极点坐标为,若点（a,4）在其图象上,则a 的值是. 3．函数y ＝x2与 y ＝x2的图象关于对称,也可以以为y ＝x2 是函数y＝x2的图象绕扭转得到的.4．求出函数y=x+2与函数y ＝x2的图象的交点坐标.5．若a>1,点（a1,y1）,（a,y2）,（a+1,y3）都在函数y ＝x2的图象上,断定y1,y2,y3的大小关系是.; 【进修难点】懂得二次函数y ＝ax2与y ＝ax2+k 的关系. .小结：①y＝2x2+1的图像是,且启齿向.②对称轴是,在对称轴阁下的增减性分离是：在对称轴左侧,y随x的增大而;在对称轴的右侧,y随x的增大而.③极点是：(,),且从图像看它有最点,则函数y有最值,即当x=时y有最值是.3．在统一向角坐标系中,作出二次函数y＝②对称轴是,当a>0时,在对称轴左侧,y随x侧,y随x的增大而. 且函数y当x=0时ymin=.当a<时,在对称轴左侧,y随x的增大而,在对称轴的右侧,y随x 的增大而.且函数y当x=0时ymax=.③极点坐标是（,）.④y＝x2的极点坐标是（ , ）,y＝x2+2的极点坐标是（ , ）所以y＝x2向平移个单位即可以得到y＝x2+2.y＝x22的极点坐标是（ , ）所以y＝x2+2向平移个单位即可以得到y＝x22.4．变式练习1二次函数y=54x2+3的图像是线,启齿向,极点坐标是,对称轴是;当x>0时,y随x的增大而.当x=时,y有最值为.三.发掘教材抛物线y＝ax2+k可以由抛物线y＝ax2经由向上（k>0）或向下(k<0)平移|k|个单位得到.5．函数y＝2x2的图像向下平移3个单位,就得到函数;函数y=4+32x2的图像可以看作函数y=3x2的图像向平移个单位而得到.2的图像有一个6．已知：二次函数y＝ax2+1的图像与反比列函数y=kx公共点是（1,1）.（1）求二次函数及反比例函数解析式;（2）在统一坐标系中画出它们的图形,解释x取何值时,二次函数与反比例函数都随x的增大而减小.四.反思小结：1．填表回想2.抛物线y=ax2+k 可以由抛物线y=ax2经由向（k>0）或向 (k<0)平移个单位得到.【达标测评】1．抛物线y=x25可以看作是抛物线经由向平移个单位得到.2．抛物线y=x2+4 的启齿向,对称轴是,在对称轴左侧,y随x的增大而,在对称轴的右侧,y随x的增大而;极点坐标是,当x=时,y有最值为. 3．抛物线y=3x2上有两点A（x,27）,B（2,y）,则x=,y=.4．抛物线y=3x2与直线y=kx+3的交点为（2,b）,则k=,b=.第4课时二次函数y=a(xh)2和y＝a(xh)2+k的图象与性质【进修目的】1．可以或许作出函数y=a(xh)2和y＝a(xh)2+k的图象,并能懂得它与y＝ax2的图象的关系,懂得a,h,k对二次函数图象的影响;2．可以或许准确说出二次函数的极点式y＝a(xh)2+k图象的启齿偏向.对称轴和极点坐标.【进修重点】可以或许作出函数y=a(xh)2和y说出y ＝a(xh)2+k 【进修进程】一.进修预备1．说出下列函数图象的启齿偏向,对称轴, （1）y=2x² （2）y=2x²+12．请说出二次函数y=ax²+c 与y=ax²的关系.3．我们已知y=ax²,y=ax²+c 的图像及性质,如今同窗们可能想探讨y=ax²+bx 的图像,那我们就着手绘图像.列表.描点.连线. 二.解读教材4．由进修预备可知,我们假如知道一条抛物线的极点坐标,那么绘图像就比较简略,所以我们可以先配成完整平方法构造.如今我们画二次函数y=3(x1)2+2不雅察后得到：二次函数y ＝3x2,y=3(x1)2,y=3(x1)2+2的图象都是抛物线．并且外形雷同,启齿偏向雷同,只是地位不合,极点不合,对称轴不合,将函数y ＝3x2的图象向右平移1个单位,就得到函数y=3(x1)2的图象;再向上平移2个单位,就得到函数y=3(x1)2+2的图象．三.发掘教材5．抛物线的极点式y＝a(xh)2+k在前面的进修中你发明二次函数y＝a(xh)2+k中的a,h,k 决议了图形什么？用本身的说话整顿得：即时演习：直接说出抛物线x+1）²,y=0.5（x+1）²1 的启齿偏向.对称轴.极点坐标.6．例已知：抛物线y=a(xh)2+kx=2时,函数有最大值3,求a,h,k的值.即时演习已知抛物线的极点坐标是（3,5）且经由点A（2,5）,请你求出此抛物线的解析式.7.例二次函数()2221y x=-+的极点坐标是,把它的图像向右平移2个单位再向下平移2个单位此时得到的抛物线极点坐标为,它的解析式为.四.反思小结1．一般地,平移二次函数y=ax2的图象即可得到二次函数为y=ax2+c,y ＝,右正左负）2y＝的图象是轴对称图形,对称轴为x=h,极点坐标为, a＞0时,启齿向上,有最小值k; a＜0时,启齿向下,有最大值k.【达标测评】y = axh )2= a( x–h )2 + ky1．指出下面函数的启齿偏向,对称轴,极点坐标,最值.(4) y=2(x2)2+5 (5) y=0.5(x+4)2+2 (6) y=0.75(x3)22．函数y= x2的图象向平移个单位得到y=x2+3的图象;再向平移个单位得到y ＝(x1)2+3的图象.,;【进修重点】会用公式求二次函数c bx ax y ++=2的极点坐标,对称轴. 【进修难点】懂得用配办法推导公式的进程. 【课时类型】公式轨则进修一.进修预备2．二次函数25(3)2y x =--的极点坐标是,对称轴是. 二.解读教材3．公式推导——二次函数c bx ax y ++=2图象的极点坐标,对称轴公式.由上一节课,我们看到一个二次函数经由过程配方化成极点式k h x a y +-=2)(来研讨了二次函数中的a.h.k 对二次函数图象的影响.但我以为,如许的恒等变形运算量较大,并且轻易出错.那么这节课,我们就研讨一般情势的二次函数图象的作法和性质.例1 求二次函数c bx ax y ++=2图象的极点坐标,对称轴. 解：c bx ax y ++=2=2()b c a x x a a++ =222[2()()]222b b b c a x x a a a a++-+ =224()24b ac b a x a a-++二次函数c bx ax y ++=2的极点坐标是（24,24b ac b a a--）,对称轴是直线2bx a=-. 4．公式应用——用公式求函数c bx ax y ++=2的极点坐标,对称轴.(1)分离用配办法,公式法肯定下列二次函数的极点坐标,对称轴并比较其解值.①221213y x x =-++ ②2252y x x =-+ 5．现实操纵——画二次函数c bx ax y ++=2的图象（2）已知：二次函数2463y x x =-+①指出函数图象的极点坐标,对称轴.②画出所给函数的草图,并研讨它的性质.三.发掘教材——二次函数c bx ax y ++=2的性质6．抛物线c bx ax y ++=2（0a ≠）经由过程配方可变形为y=224()24b ac b a x a a-++(1)启齿偏向：当0a >时,启齿向;当0a <时,启齿向. (2)对称轴是直线;极点坐标是.(3)最大（小）值：当0a >,2bx a=-时,ymin=244ac b a -;当0a <,2bx a =-时,ymax=. (4)增减性：当0a >时,对称轴左侧（2b x a<-）,y 随x 增大而;对称轴右侧（2bx a>-）,y 随x 增大而;当0a <时,对称轴左侧（2b x a<-）,y 随x 增大而;对称轴右侧（2bx a>-）,y 随x 增大而;【达标测评】依据公式法指出下列抛物线的启齿偏向.极点坐标,对称轴.最值和增减性.①422+-=x x y ②1422++-=x x y ③221y x x =-++④2516y x x =-+题.【进修进程】一.进修预备1．已学二次函数的哪两种表达式？ 2．分化因式：x22x3;3．解方程：x2 2x3=0 二.解读教材4．一元二次方程的两根x1,x2在哪里？在坐标系中画出二次函数y= x2 2x3的图象,,你发明了什么？再找一个一元二次方程和二次函数试一试吧! 5．二次函数的两根式（交点式）二次函数)0(2≠++=a c bx ax y 的另一种表达式：叫做二次函数的两根式又称交点式. 演习：将下列二次函数化为两根式：（1）y=x2+2x15; （2）y= x2+x2;（3）y=2x2+2x12;（4）y=3(x1)23 （5）y=4x2+8x+4; （6）y=2(x3)2+8x 三.发掘教材6．抛物线)0(2≠++=a c bx ax y 与x 轴是否有交点？例你能应用 a.b.c 之间的某种关系断定二次函数)0(2≠++=a c bx ax y 的图象与x 轴何时有两个交点,何时一个交点,何时没有交点吗？即时练习：（1）已知二次函数y=mx22x+1的图象与x 轴有两个交点,则k 的取值规模为.（2）抛物线y=x2(m4)xm 与x 轴的两个交点y 轴对称,则其极点坐标为. （3）抛物线y=x2(a+2)x+9与x 轴相切,则a=.7．弦长公式：抛物线与xAB ）.例求抛物线y= x2 2x3与x 轴两个交点间的距离. 总结：已知抛物线)0(2≠++=a c bx ax y 与x B （x2,0）,那么抛物线的对称轴x=,AB=21x x -=221)(x x -=.即时练习：抛物线y=2(x2)(x ＋5)的对称轴为,与x 轴两个交点的距离为.四.反思小结——二次函数与一元二次方程的关系常识点1．二次函数y=ax2＋bx ＋c 的图象与x 轴的交点有三种情形,,,交点横坐标就是一元二次方程ax2＋bx ＋c=0的.常识点2．二次函数y=ax2＋bx ＋c 的图象与x 轴的弦长公式：. 【达标测评】1．抛物线y=9(x4)(x ＋6)与x 轴的交点坐标为.2．抛物线y=2x2＋8x ＋m 与x 轴只有一个交点,则m=.3．二次函数y=kx2＋3x －4的图象与x 轴有两个交点,则k 的取值规模. 4．抛物线y=3x2＋5x 与两坐标轴交点的个数为（）A ．3个B ．2个C ．1个D ．0个5．与x 轴不订交的抛物线是（）A ．y=3x24 B ．y=2x26 C ．y=x26 D ．y=31(x+2)216．已知二次函数y=x2＋mx ＋m －2．求证：无论m 取何实数,抛物线总与x 轴有两个交点.7．抛物线y=mx2＋(3－2m)x ＋m －2（m≠0）与x 轴有两个不合的交点. （1）求m 的取值规模; （2）断定点P(1,1)是否在此抛物线上？ 8．二次函数y=x2－(m －3)x －m 的图象如图所示.（1）试求m 为何值时,抛物线与x 轴的两个交点间的距离是3？（2）当m 为何值时,方程x2－(m －3)x －m=0的两个根均为负数？（3）设抛物线的极点为M,与x 轴的交点P.Q,求当PQ 最短时△MPQ 的面积.第7课时刷图练习【进修目的】据二次函数系数a.b.c 画出抛物线的须要前提：启齿偏向.对称轴.极点坐标与坐标轴的交点坐标.【进修重点】二次函数一般式与极点式.交点式的互化;找特别点的坐标.【候课朗读】【进修进程】一.进修预备1．二次函数的一般式为：y=（个中0a ≠,a.b.c 为常数）;极点式为：y=,它的极点坐标是,对称轴是;交点式为：（个中1x ,2x 是0y =时得到的一元二次方程20ax bx c ++=的根）.2．函数2y ax bx c =++(0a ≠)中,a 肯定抛物线的启齿偏向：当a ＞0时,当a ＜0时;a 和b 肯定抛物线的对称轴的地位：当a .b 同号时对称轴在y轴的侧;当a .b 异号时对称轴在x 轴的侧;（可记为“左同右异” ）c 肯定抛物线与的交点地位：当c ＞0时交于y 轴的半轴;当c ＜0时交于y 轴的负半轴. 二.浏览懂得3．界说：抛物线的草图：能大致表现抛物线的启齿偏向.对称轴.极点坐标.与y 轴的交点.x 轴上的两根为整根的抛物线叫抛物线的草图. 4．在抛物线的三种解析式的图象信息：教授教养跋文x一般式能直接表现启齿偏向.与y 轴的交点;极点式能直接表现启齿偏向.对称轴.极点坐标;两根式能直接表现启齿偏向.与x 轴的两个交点.是以,它们各有好坏,个中以极点式为最佳. 5①1,a b ==偶,例1 作出函数242y x x =-+解：242y x x =-+②1,a b ==奇,例2 作出函数253y x x =-+解：∴552212b a --=-=⨯③1a ≠（公式法）例3 作出函数2241y x x =-+的大致图象.解：∵4124b a -=-=, 24816148ac b a --==-,∴则大致图象是：（在空白处绘图）即时演习：在右边空白处作出函数222y x x =-+-④两根式（先转化为一般式,再转换成极点式）例4 作出函数()()212y x x =-+的大致图象. 解：()()212y x x =-+219222x ⎛⎫=-- ⎪⎝⎭ 则大致图象是：6．含有参数的抛物线中的图象信息例5作出函数22y x x m =-+-的大致图象.即时演习：在右边空白处画出函数y=－x2+n 的大致图象. 变式练习：画出函数y=－x2+mx+3的大致图象.x三.巩固练习：作出下列函数的大致图象 ①232y x x =-+- ②244y x x =-- ③221y x =+ ④()()1122y x x =-+：轴是__________,极点坐标是. 二.典例示范例 1 已知函数2y ax bx c =++的图象如图所示,1x =为该图象的对称轴,依据图象信息,你能得到关于系数a b c 、、解：由图可得：⑴a ＞0; ⑵1-＜c ＜0; ⑶123b a -=,即又2ba-＜1而a ＞0则得b -＜2a ,∴2a+b>0;⑷由⑴⑵⑶得abc ＞0;⑸斟酌1x =时y ＜0,所以有a b c ++＜0; ⑹斟酌1x =-时y ＞0,所以有a b c -+＞0;⑺斟酌2x =时y ＞0,所以有42a b c ++＞0,同理2x =-时,42a b c -+＞0; ⑻图象与x 轴有两个交点,所以24b ac -＞0.例2 如图是二次函数2y ax bx c =++图像的一部分,图像过点A ()3,0-,对称轴1x =-,给出四个结论： ①2b ＞4ac ,②20a b +=,③0a b c -+=,④5a ＜b ,个中（）A.②④B.①④C.②③D.①③剖析：由图象可以知道a ＜0;抛物线与x 轴有两个交点,∴24b ac -＞0,即2b ＞4ac ;又对称轴1x =-,即12ba-=-,∴2a b =,b ＜0; ∴20a b -=,a 、b 均为负数,5a ＜b ;当1x =-时,∴a b c -+＞0;综上,准确的是①④,故选B.例3 如图所示的抛物线是二次函数223y ax x a =-+_____.剖析：由图象可知：a ＜0;当0x =时1y =,即21a =,∴1a =±,但是a ＜0,故1a =-.三.巩固练习1．抛物线2y ax bx c =++如图所示,则（）A.a ＞0,b ＞0,c ＞0B.a ＞0,b ＜0,c ＜0C.a ＞0,b ＞0,c ＜0D.a ＞0,b ＜0,c ＞02．已知二次函数2y ax bx c =++的图像如图所示,下列结论中准确的个数是（）①a b c ++＜0,②a b c -+＞0,③abc ＞0,④2b a =A.4个B.3个C.2个D.1个3x c +的部分图像如图所示,则c0,当x_____时,y 随x 4ax b +则关于抛物线23y ax bx =-+(1x =;③当a ＜0时,其极点的纵坐标的最小值为3, ） A.0 B.1 C.2 D.35．已知二次函数()20y ax bx c a =++≠的图象如图所示,当y ＜0时,x 的取值规模是（）A.－1＜x ＜3B.x ＞3C.x ＜1D.x ＞3或x ＜16．抛物线c bx ax y ++=2的图象与x 轴的一个交点是()2,0-,极点是()1,3,下列说法中不准确的是（）A.抛物线的对称轴是1x =B.抛物线启齿向下C.抛物线与x 轴的另一个交点是()2,0D.当1x =时,y 有最大值是3 7．已知二次函数的图象如图所示,则这个二次函数的表达式为（） A.223y x x =-+ B.223y x x =--223y x x =+-2第第第3题8．在直角坐标系中画一个二次函数y=ax2+bx+c的图象,且知足b<0,c<0..9．已知y=x2+ax+a1的图象如图所示,则a的取值规模是.10．据图抛物线y=ax2+bx+c肯定式子符号：①a0,②b0,③c0,④b24ac0,⑤a+b+c0,⑥ab+c0.11．若函数y=ax2+bx+c的对称轴x=1如图所示,则下列关系成立的是：（）A.abc>0B.a+b+c<0C.a2>abacD.4acb2>0;2．控制已知极点及一点或对称轴或函数的最值,用极点式求函数的表达式.3．控制已知两根及一点,用两根式求函数解析式.【进修重点】用一般式.极点式求函数的表达式.【进修难点】用极点式和两根式求函数的表达式.【进修进程】一.进修预备：1．已知一次函数经由点（1,2）,（1,0）,则一次函数的解析式为 . 2．二次函数的一般式为,二次函数的极点式,二次函数的两根式（或交点式）为.二.办法探讨（一）——已知三点,用一般式求函数的表达式.3．例1 二次函数的图象经由（0,2）,（1,1）,（3,5）三点,求二次函数的解析式.4．即时演习已知抛物线经由A（1,0）,B（1,0）,C（0,1）三点,求二次函数的解析式.三.办法探讨（二）——已知极点及一点或对称轴或函数的最值,用极第5题第6题第7题第点式求出函数的解析式.5．例2 已知抛物线的极点坐标为（2,3）,且经由点（1,7）,求函数的解析式.解：设抛物线的解析式为2()y a x h k =-+.把极点（－2,3）,即h=2 , k=3 代入表达式为再把（－1,7）代入上式为解得4a =所以函数解析式为24(2)3y x =++ 即241619y x x =++6．即时演习（1）抛物线经由点（0,－8）,当1x =-时,函数有最小值为－9,求抛物线的解析式.（2）已知二次函数2()y a x h k =-+,当2x =时,函数有最大值2,其过点(0,2),求这个二次函数的解析式.四.办法探讨（三）——已知两根及一点或对称轴或函数的最值,用两根式求出函数的解析式.7．例3 已知抛物线经由（－1,0）,（3,0）,且过（2,6）三点,求二次函数的表达式.解：设抛物线的解析式为12()()y a x x x x =--把抛物线经由的（－1,0）,（3,0）两点代入上式为：再把（2,6）带入上式为6(21)(3)a x =+- 解得2a =-所以函数的解析式为2(1)(3)y x x =-+- 即2246y x x =-++8．即时演习已知抛物线经由A （2,0）,B （4,0）,C(0,3),求二次函数的解析式.五.反思小结——求二次函数解析式的办法 1．已知三点,求二次函数解析式的步调是什么？2．用极点式求二次函数的解题思绪是：已知极点及一点或对称轴或函数的最值,用极点式求解析式比较简略.3．用两根式求二次函数的解题思绪是：已知两根及一点或对称轴或函数的最值,用两根式求解析式比较简略. 【达标测评】求下列二次函数的解析式：1．图象过点（1,0）.（0,2）和（2,3）. 2．当x=2时,y 最大值=3,且过点（1,3）.3．图象与x 轴交点的横坐标分离为2和4,且过点(1,10)第10课时求二次函数的解析式（二）【进修目的】1．懂得二次函数的三种暗示方法;2．会灵巧地应用恰当的办法求二次函数的解析式.【进修重点】灵巧地应用恰当的办法求二次函数的解析式. 【进修进程】一.进修预备1．函数的暗示方法有三种：法,法,法. 2．二次函数的表达式有：.,.二.典范例题——用恰当的办法求出二次函数的表达式3．例1 已知抛物线2(0)y ax bx c a =++≠与x 轴的两个交点的横坐标是－1,3,极点坐标是（1,－2）,求函数的解析式（用三种办法） 4．即时演习：用恰当的办法求出二次函数的解析式.一条抛物线的外形与2y x =雷同,且对称轴是直线12x =-,与y 轴交于点（0,1）,求抛物线的解析式.5．例 2 已知如图,抛物线b ax ax y ++-=22与x 轴的一个交点为A(1,0),与y 轴的正半轴交于点C.⑴直接写出抛物线的对称轴,及抛物线与x 轴的另一个交点B 的坐标; ⑵当点CO=3时,求抛物线的解析式.6．即时演习：已知直线y=2x4与抛物线y=ax2+bx+c 的图象订交于A （2,m ）,B(n,2)两点,且抛物线以直线x=3为对称轴,求抛物线的解析式.三.反思小结——求二次函数解析式的办法1．已知三点或三对x.y 的对应值,通经常应用2(0)y ax bx c a =++≠. 2．已知图象的极点或对称轴,通经常应用2()(0)y a x h k a =-+≠. 3．已知图象与x 轴的交点坐标,通经常应用12()()(0)y a x x x x a =--≠. 四.巩固练习1．已知二次函数图象的极点坐标为C(1,0),该二次函数的图象与x 轴教授教养跋文交于A.B 两点,个中A 点的坐标为(4,0). （1）求B 点的坐标（2）求这个二次函数的关系式;2．如图,在平面直角坐标系中,直线y =-x交于点C ,抛物线2(0)y ax x c a =+≠经由A B C ，，（1）求过A B C ，，三点抛物线的解析式并求出极点F （2）在抛物线上是否消失点P ,使ABP △出P 点坐标;若不消失,请解释来由.【进修重点】用“数形联合”的思惟懂得公式,并能应用公式解决现实问题.【进修难点】剖析和暗示现实问题中变量之间的二次函数关系. 【进修进程】一.进修预备1．二次函数y=ax2+bx+c 的图像是一条____________,它的对称轴是直线x=－ab2,极点是______________. 2．二次函数y=2x2+3x1的图象启齿______,所以函数有最_______值,即当x=时,ymax =_________. 二.解读教材3．例1某商经营T 恤衫,已知成批购置时的单价是5元.依据市场查询拜访,发卖量与发卖单价知足如下关系：在一段时光内,单价是15元时,发卖量是500件,而单价每下降1元,就可以多售200件.问发卖价是若干时,可以获利最多？剖析：若设发卖单价为x(x≤15)元,所获利润为y元,则：(1)发卖量可以暗示为______________________________;(2)发卖额可以暗示为____________________________;(3)发卖成本可以暗示为____________________________;(4)所获利润可暗示为y=_________________________.解：设＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿依据题意得关系式：y=____________________,即y=.∵a=<0,∴y有最值.即当x=_______________=______________时,ymax=_________________=__________________.答：办法小结：解决此类问题的一般步调是：(1)设——设出问题中的两个变量（即设未知数）;(2)列——用含变量的代数式暗示出等量关系,列出函数解析式;(3)自——找出自变量的取值规模;(4)图——作出函数图像（留意自变量的取值规模）;(5)最——在自变量的取值规模内,取函数的最值;(6)答——依据请求作答.4．即时演习某市肆购置一批单价为20元的日用品,假如以单价30元发卖,那么半月内可以售出400件.据发卖经验,进步发卖单价会导致发卖量的削减,即发卖单价每进步一元,发卖量响应削减20件.若何进步发卖价,才干在半月内获得最大利润？三.发掘教材5．例2某商经营T恤衫,已知成批购置时的单价是5元.依据市场查询拜访,发卖量与发卖单价知足如下关系：在一段时光内,单价是15元时,发卖量是500件,而单价每下降1元,就可以多售于10元,问发卖价是若干时,可以获利最多？6．即时演习求二次函数y= x22x3在2≤x≤0时的最大.最小值.四.反思小结1．二次函数是解决现实问题中“最值”问题类较好的数学模子;2．留意解决此类问题的一般步调——“设”,“列”,“自”,“图”,“最”,“答”. 【达标测评】1．某市肆购置一批单价为8元的商品,假如以单价10元发卖,那么天天可以售出100件.据发卖经验,发卖单价每进步1元,发卖量响应削减10件.将发卖价定为若干,才干使天天获得最大利润？最大利润是若干？2．某观光社组团旅游,30人起组团,每人单价800元,每团乘坐一辆准载50人的大客车.观光社对超出30人的团赐与优惠,即每增长一人,每人的单价下降10元.你能帮忙盘算一下,当一个观光团的人数是若干时,观光社可以获得最大营业额？=ab ac 442-解决现实问题中的最大（小）值问题.【进修重点】应用二次函数的有关常识解决现实问题. 【进修进程】一.进修预备1．函数y=ax2+bx+c(a≠0)中,若a>0,则当x=ab2时,y( )=;若a<0,则当x=时,y( )=.2．在二次函数y=2x28x+9中当x=时,函数y 有最值等于.3．如图,在边BC 长为20cm,高AM 为16cm 的△ABC 它的一边FG 在△ABC 的边BC 上,E.F 分离在AB.AC 请用x 的代数式暗示EH.解：∵矩形EFGH, ∴EH∥BC∴ △AEH∽___________.x D E CBA 又∵BC 上的高AM 交EH 于T. ∴AMAT =_______,即1616x=________. ∴EH=.二.解读教材4．在上题图中,若要使矩形EFGH 获得最大面积,那么它的长和宽各是若干？最大面积是若干？解：设矩形面积为y,而EF=x,EH=,则y==.∵a=45<0 则y 有最_______值.∴当x=______时,则y 最大值=______________.此时EH=.答：.5．想一想：活动4经由过程设EH 为xcm 能解决问题吗？（试一试吧！）6．即时演习：（1）在Rt△的内部作内接矩形ABCD,个中AB 和AD 分离在两条直角边上,点C 在斜边上.①设矩形ABCD 的边AB ＝x m,那么AD 边的长度若何暗示？②设矩形的面积为y m2,当x 取何值时,y 的值最大？最大值是若干？解：（2）将（1）题变式：其它前提和图形都不变,设AD 边的长为x m,则问题又如何解决呢？三.发掘教材：7．在Rt△QMN 的内部作内接矩形ABCD,点A 和D 分离在两直角边上,BC 在斜边MN 上.①设矩形的边BC=xm,则AB 边的长度若何暗示？②设矩形的面积为ym2,当x 取何值时,y 的最大值是若干?8．即时演习如图,某村修一条沟渠,横断面是等腰梯形,底角∠C=120°,两腰与下底AD 的和为4m.当沟渠深（x ）为何值时,横断面积（S ）最大？最大值为若干？解：四.反思小结：经由过程进修上节和本节解决问题的进程,你能总结一下解决此类问题的根本思绪吗？应用类似三角形性质和矩形面积公式列出二次函数,应用其性质解决.40m30m D N OABCM。

九年级数学《二次函数》单元复习(导学案)

九年级数学《二次函数》单元复习（导学案）复习目标:1.体会二次函数的意义,理解二次函数的有关概念.2.会运用配方法确定二次函数的图象的顶点、开口方向和对称轴,并会确定最值.3.会运用待定系数法求二次函数的解析式.4.能根据图象判断二次函数a、b、c的符号及一些特殊方程或不等式是否成立.5.会将实际问题转化为函数问题,并利用函数的性质进行决策.一、基础知识归类和整理1.二次函数的概念及图象特征:(1)二次函数:如果 ,那么y叫做x的二次函数,图象是线(2)二次函数顶点式:通过配方y=ax²+bx+c可写成 ,它的图象是以直线为对称轴，以为顶点的一条抛物线。

a值函数的图象及性质a>0 （1）开口向上，并向上无限伸展；（2）当时，函数有最小值当时，y随x的增大而减小；当时，y随x的增大而增大.a<0 （1）开口向下，并向下无限伸展；（2）当时，函数有最大值当时，y随x的增大而增大；当时，y随x的增大而减小.3.二次函数图象的平移规律:y=ax²⟺y=ax²+k ⟺y=a(x+h)²+k,抛物线y=ax²+bx+c(a≠0)可由抛物线y=ax²(a≠0)平移得到.由于平移时,抛物线上所有的点的移动规律都相同,所以只需研究其顶点移动的情况,因此有关抛物线的平移问题,需要利用二次函数的顶点式来讨论。

4.二次函数解析式的确定:用待定系数法可求出二次函数的解析式,确定二次函数一般需要三个独立的条件,根据不同的条件选择不同的设法:(1)设一般形式: ；(2)设顶点形式: ；(3)设交点式: 。

a 的作用决定开口方向a>0开口；a<0开口决定开口的大小︳a| 越大，抛物线的开口b 的作用b 与a 同号ab2-＜0，顶点在y 轴的侧 b 与a 异号ab2-＞0，顶点在y 轴的侧顶点在y 轴上c 的作用 c>0抛物线与y 轴的交点在y 轴的 c<0 抛物线与y 轴的交点在y 轴的c=0 抛物线过点 b ²-4ac b ²-4ac>0抛物线与x 轴有交点 b ²-4ac<0 抛物线与x 轴有交点 b ²-4ac=0抛物线与x 轴有交点解决实际应用问题的关键是选准变量,建立好二次函数模型,同时还要注意符合实际情景。

【人教版】九上数学：《二次函数》全章导学案

第二十二章二次函数22． 1二次函数的图象和性质22． 1.1二次函数结合具体情境体会二次函数的意义，理解二次函数的有关概念；能够表示简单变量之间的二次函数关系．重点：能够表示简单变量之间的二次函数关系．难点：理解二次函数的有关概念．一、自学指导．(10 分钟 )自学：自学课本P28～ 29，自学“思考” ，理解二次函数的概念及意义，完成填空．2，其中二次项系数、一次项系数和常数项分别为a，b，c．现在我们已学过的函数有一次函数、二次函数，其表达式分别是 y＝ ax＋b(a， b 为常数，且 a≠ 0) 、y＝ ax2＋ bx＋c(a，b， c 为常数，且 a≠ 0)．二、自学检测：学生自主完成，小组内展示，点评，教师巡视．(5分钟)1．下列函数中，是二次函数的有__A， B， C__．2A． y＝ (x－ 3) － 1B． y＝ 1－2x21C．y＝3(x＋ 2)(x － 2)22D． y＝ (x－ 1) － x2．二次函数 y＝－ x2＋ 2x 中，二次项系数是 __－ 1__，一次项系数是 __2__，常数项是__0__．3．半径为 R 的圆，半径增加 x，圆的面积增加 y，则 y 与 x 之间的函数关系式为 y＝π x2＋2π Rx(x ≥ 0) ．点拨精讲：判断二次函数关系要紧扣定义．一、小组合作：小组讨论交流解题思路，小组活动后，小组代表展示活动成果．(10 分钟)探究 1若y＝(b－2)x2＋4是二次函数，则__b≠ 2__．探究 2某超市购进一种单价为40 元的篮球，如果以单价50 元出售，那么每月可售出500 个，根据销售经验，售价每提高 1 元，销售量相应减少10 个，如果超市将篮球售价定为 x 元 (x>50) ，每月销售这种篮球获利y 元．(1)求 y 与 x 之间的函数关系式；(2)超市计划下月销售这种篮球获利8000 元，又要吸引更多的顾客，那么这种篮球的售价为多少元？解： (1)y ＝－ 10x 2＋ 1400x－ 40000(50<x<100) ．(2)由题意得：－10x 2＋ 1400x－ 40000＝ 8000，2化简得 x － 140x ＋ 4800＝ 0，∴ x1＝ 60， x2＝ 80.二、跟踪练习：学生独立确定解题思路，小组内交流，上台展示并讲解思路．(8 分钟 )22．设 y＝ y1－ y2，若 y1与 x2成正比例，y2与1成反比例，则 y 与 x 的函数关系是 ( A ) xA．二次函数B．一次函数C．正比例函数D．反比例函数3．已知，函数 y＝ (m－ 4)xm 2－ m＋2x 2－ 3x－ 1 是关于 x 的函数．(1)m 为何值时，它是 y 关于 x 的一次函数？(2)m 为何值时，它是 y 关于 x 的二次函数？点拨精讲：第 3 题的第 (2)问，要分情况讨论．4．如图，在矩形 ABCD 中，AB ＝ 2 cm， BC＝ 4 cm，P 是 BC 上的一动点，动点 Q 仅在BC PC 或其延长线上，且BP＝PQ，以PQ为一边作正方形方向运动，设 BP＝ x cm，正方形 PQRS 与矩形 ABCDPQRS，点 P 从 B 点开始沿射线2重叠部分面积为y cm ，试分别写出 0≤ x≤ 2 和 2≤ x≤ 4 时， y 与 x 之间的函数关系式．点拨精讲： 1.二次函数不要忽视二次项系数a≠ 0.2．有时候要根据自变量的取值范围写函数关系式．学生总结本堂课的收获与困惑．(2 分钟)学习至此，请使用本课时的对应训练部分．(10 分钟 )22． 1.2 二次函数2y＝ ax 的图象和性质1．能够用描点法作出函数的图象，并能根据图象认识和理解其性质．2．初步建立二次函数表达式与图象之间的联系，体会数形的结合与转化，体会数学内在的美感．重点：描点法作出函数的图象．难点：根据图象认识和理解其性质．一、自学指导．(7 分钟 )自学：自学课本 P30～ 31“例 1”“思考”“探究”，掌握用描点法作出函数的图象，理解其性质，完成填空．(1)画函数图象的一般步骤：取值－描点－连线；(2)在同一坐标系中画出函数y＝ x2， y＝12x2和 y＝ 2x2的图象；点拨精讲：根据y≥0，可得出y 有最小值，此时 x＝ 0，所以以 (0 ，0)为对称点，对称取点．(3)观察上述图象的特征：形状是抛物线，开口向上，图象关于 y 轴对称，其顶点坐标是(0 ， 0)，其顶点是最低点 (最高点或最低点 )；(4)找出上述三条抛物线的异同： __________ ．212和 y＝－ 2x 2(5)在同一坐标系中画出函数y＝－ x， y＝－2x的图象，找出图象的异同．点拨精讲：可从顶点、对称轴、开口方向、开口大小去比较寻找规律．总结归纳：一般地，抛物线的对称轴是y 轴，顶点是 (0，0)，当 a>0 时，抛物线的开口向上，顶点是抛物线的最低点． a 越大，抛物线的开口越小；当 a<0 时，抛物线的开口向下，顶点是抛物线的最高点， a 越大，抛物线的开口越大．二、自学检测：学生自主完成，小组内展示，点评，教师巡视．(5分钟)1．教材 P41 习题 22.1 第 3， 4 题．一、小组合作：小组讨论交流解题思路，小组活动后，小组代表展示活动成果．(13 分钟)探究 1填空：(1)函数y＝(－2x) 2的图象形状是______，顶点坐标是 ______，对称轴是______ ，开口方向是 ______．212和 y＝－ 2x 2(2)函数 y＝x，y＝2x的图象如图所示，请指出三条抛物线的解析式．解： (1)抛物线， (0， 0)， y 轴，向上；(2)根据抛物线 y＝ ax2中， a 的值来判断，在 x 轴上方开口小的抛物线为y＝ x2，开口大的为 y＝12x2，在 x 轴下方的为y＝－ 2x 2.点拨精讲：解析式需化为一般式，再根据图象特征解答，避免发生错误．抛物线 y＝ax2中，a>0 时，开口向上； a<0 时，开口向下； |a|越大，开口越小．探究 2已知函数y＝ (m＋ 2)xm 2＋ m－ 4 是关于 x 的二次函数．(1)求满足条件的m 的值；(2)m 为何值时，抛物线有最低点？求这个最低点；当 x 为何值时，y 随 x 的增大而增大？(3)m 为何值时，函数有最大值？最大值为多少？当x 为何值时，y 随 x 的增大而减小？解： (1)由题意得m2＋ m－ 4＝ 2，m＋2≠ 0.m＝ 2或 m＝－ 3，解得∴当 m＝ 2 或 m＝－ 3 时，原函数为二次函数．m≠－ 2.(2)若抛物线有最低点，则抛物线开口向上，∴m＋2>0 ，即m> －2，∴只能取 m＝2.∵这个最低点为抛物线的顶点，其坐标为 (0， 0)，∴当 x>0 时， y 随 x 的增大而增大．(3)若函数有最大值，则抛物线开口向下，∴ m＋2<0，即m<－2，∴只能取 m ＝－ 3.∵函数的最大值为抛物线顶点的纵坐标，其顶点坐标为 (0， 0)，∴ m ＝－ 3 时，函数有最大值为 0.∴ x>0 时， y 随 x 的增大而减小．二、跟踪练习：学生独立确定解题思路，小组内交流，上台展示并讲解思路．(5分钟)1．二次函数 y ＝ ax 2 与 y ＝－ ax 2 的图象之间有何关系？2．已知函数 y ＝ ax 2 经过点 (－ 1， 3)． (1)求 a 的值；(2)当 x<0 时， y 的值随 x 值的增大而变化的情况．的关系是 __y 1＜ y 23．二次函数 y ＝－2x 2，当 x 1 2>0 ，则 y 1 与 y 2 __．2 >x4．二次函数 y ＝ ax 与一次函数 y ＝－ ax(a ≠ 0)在同一坐标系中的图象大致是 (B )点拨精讲： 1.二次函数 y ＝ax 2 的图象的画法是列表、描点、连线，列表时一般取 5～ 7 个点，描点时可描出一侧的几个点，再根据对称性找出另一侧的几个点，连线将几个点用平滑的曲线顺次连接起来，抛物线的两端要无限延伸，要“出头”；2．抛物线 y ＝ax 2 的开口大小与 |a|有关，|a|越大，开口越小， |a|相等，则其形状相同．学生总结本堂课的收获与困惑．(2 分钟)学习至此，请使用本课时对应训练部分．(10 分钟 )22． 1.3 二次函数 y ＝ a (x － h )2＋ k 的图象和性质 (1)1．会作函数 y ＝ ax 2 和 y ＝ ax 2＋ k 的图象，能比较它们的异同；理解 a ，k 对二次函数图象的影响，能正确说出两函数图象的开口方向、对称轴和顶点坐标．2．了解抛物线 y ＝ ax 2 上下平移规律．重点：会作函数的图象．难点：能正确说出两函数图象的开口方向、对称轴和顶点坐标．一、自学指导． (10 分钟 )自学：自学课本 P32～ 33“例 2”及两个思考，理解 y ＝ ax 2＋ k 中 a ，k 对二次函数图象的影响，完成填空．总结归纳：二次函数 y ＝ax 2 的图象是一条抛物线，其对称轴是 y 轴，顶点是 (0，0)，开口方向由 a 的符号决定：当 a>0 时，开口向上；当 a<0 时，开口向 __下 __．当 a>0 时，在对称轴的左侧， y 随 x 的增大而减小；在对称轴的右侧， y 随 x 的增大而增大．抛物线有最 __低__点，函数 y 有最 __小__值．当 a<0 时，在对称轴的左侧， y 随 x 的增大而增大；在对称轴的右侧， y 随 x 的增大而减小．抛物线有最 __高__点，函数 y 有最 __大 __值．抛物线 y ＝ ax 2＋ k 可由抛物线 y ＝ax 2 沿 __y__轴方向平移 __|k|__单位得到，当 k>0 时，向__上 __平移；当 k<0 时，向__下 __平移．二、自学检测：学生自主完成，小组内展示，点评，教师巡视． (7 分钟 ) 1．在抛物线 y ＝ x 2－ 2 上的一个点是 ( C)A ． (4， 4)B ． (1，－ 4)C ．(2， 2)D ． (0， 4)2．抛物线 y ＝x 2 － 16 与 x 轴交于 B ， C 两点，顶点为 A ，则△ ABC 的面积为 __64__．点拨精讲：与 x 轴的交点的横坐标即当y 等于 0 时 x 的值，即可求出两个交点的坐标．3．画出二次函数 y ＝ x 2－ 1，y ＝ x 2， y ＝ x 2 ＋1 的图象，观察图象有哪些异同？点拨精讲：可从开口方向、对称轴、形状大小、顶点、位置去找．一、小组合作：小组讨论交流解题思路，小组活动后，小组代表展示活动成果．(5 分钟)探究 1 抛物线 y ＝ ax 2 与 y ＝ ax 2± c 有什么关系？解： (1)抛物线 y ＝ ax 2± c 的形状与 y ＝ ax 2 的形状完全相同，只是位置不同； (2)抛物线 y ＝ ax 2 向上平移 c 个单位得到抛物线 y ＝ ax 2＋ c ；抛物线 y ＝ ax 2 向下平移 c 个单位得到抛物线y ＝ ax 2－ c.探究 2 已知抛物线 y ＝ ax 2＋ c 向下平移 2 个单位后，所得抛物线为 y ＝－ 2x 2＋4，试求 a ， c 的值．a ＝－ 2， a ＝－ 2，解：根据题意，得解得c － 2＝ 4，c ＝ 6.二、跟踪练习：学生独立确定解题思路，小组内交流，上台展示并讲解思路． (13 分钟 )1．函数 y ＝ ax 2－ a 与 y ＝ ax － a(a ≠ 0)在同一坐标系中的图象可能是 ( D )2．二次函数的图象如图所示，则它的解析式为 ( B )2A ． y ＝ x － 43 2B ． y ＝－ 4x ＋ 332C ．y ＝ 2(2－ x)D ． y ＝3(x 2－ 2)23．二次函数 y ＝－ x 2＋ 4 图象的对称轴是y 轴，顶点坐标是 (0， 4)，当 x<0 ， y 随 x 的增大而增大．224．抛物线 y＝ ax ＋ c 与 y＝－ 3x 的形状大小，开口方向都相同，且其顶点坐标是(0，225)，则其表达式为y＝－ 3x ＋ 5，它是由抛物线y＝－ 3x 向__上 __平移 __5__个单位得到的．5．将抛物线y＝－ 3x2＋ 4 绕顶点旋转180°，所得抛物线的解析式为y＝ 3x2＋ 4．6．已知函数 y＝ ax2＋ c 的图象与函数 y＝5x2＋ 1 的图象关于 x 轴对称，则 a＝ __－ 5__，c ＝__－ 1__．点拨精讲： 1.函数的图象与性质以及抛物线上下平移规律．(可结合图象理解)2．抛物线平移多少个单位，主要看两顶点坐标，确定两顶点相隔的距离，从而确定平移的方向与单位长，有时也可以比较两抛物线上横坐标相同的两点相隔的距离，从而确定平移的方向与单位长．学生总结本堂课的收获与困惑．(2 分钟)学习至此，请使用本课时对应训练部分．(10分钟 )22． 1.3二次函数y＝ a(x－ h)2＋ k 的图象和性质(2)1．进一步熟悉作函数图象的主要步骤，会作函数y＝a(x －h)2的图象．2．能正确说出y＝ a(x－ h)2的图象的开口方向、对称轴和顶点坐标．3．掌握抛物线y＝ a(x－ h)2的平移规律．重点：熟悉作函数图象的主要步骤，会作函数 y＝ a(x－ h)2的图象．难点：能正确说出图象的开口方向、对称轴和顶点坐标，掌握抛物线 y＝ a(x－ h)2的平移规律．一、自学指导．(10 分钟 )自学：自学课本P33～ 34“探究”与“思考”，掌握 y＝ a(x－ h)2与 y＝ ax2之间的关系，理解并掌握 y＝ a(x－ h)2的相关性质，完成填空．1212和 y＝－1(x－ 1)2的图象，观察后两个函数图象与抛物画函数 y＝－ x、y＝－ (x＋ 1)22212有何关系？它们的对称轴、顶点坐标分别是什么？线 y＝－ x2点拨精讲：观察图象移动过程，要特别注意特殊点(如顶点 )的移动情况．总结归纳：二次函数 y＝a(x－ h)2的顶点坐标为 (h，0)，对称轴为直线 x＝ h．当 a>0 时，在对称轴的左侧 y 随 x 的增大而减小，在对称轴的右侧y 随 x 的增大而增大，抛物线有最低点，函数 y 有最小值；当 a<0 时，在对称轴的左侧y 随 x 的增大而增大，在对称轴的右侧 y 随 x 的增大而减小，抛物线有最高点，函数 y 有最大值．抛物线 y＝ ax2向左平移h 个单位，即为抛物线 y＝ a(x ＋ h)2(h>0) ；抛物线 y＝ ax2向右平移 h 个单位，即为抛物线y＝ a(x －h)2(h>0) ．二、自学检测：学生自主完成，小组内展示，点评，教师巡视． (7 分钟 )1．教材 P35 练习题；12的开口向下，顶点坐标是 (1，0)，对称轴是 x＝ 1，通过向左平2．抛物线 y＝－ (x － 1)2移 1 个单位后，得到抛物线y＝－12x2.一、小组合作：小组讨论交流解题思路，小组活动后，小组代表展示活动成果．(8 分钟)探究 1 在直角坐标系中画出函数12的图象．y＝ (x＋ 3)2(1)指出函数图象的对称轴和顶点坐标；(2)根据图象回答，当 x 取何值时，y 随 x 的增大而减小？当 x 取何值时，y 随 x 的增大而增大？当 x 取何值时， y 取最大值或最小值？12的图象得到函数12的图象？(3)怎样平移函数 y＝ x y＝ (x＋ 3)22解： (1)对称轴是直线x＝－ 3，顶点坐标 (－ 3，0)； (2)当 x<－ 3 时， y 随 x 的增大而减小；当 x> － 3 时， y 随 x 的的增大而增大；当x＝－ 3 时， y 有最小值；1 2的(3)将函数 y＝ x212的图象．图象沿 x 轴向左平移 3 个单位得到函数 y＝ (x＋ 3)2点拨精讲：二次函数的增减性以对称轴为分界，画图象取点时以顶点为分界对称取点．探究 2 已知直线 y＝ x＋ 1 与 x 轴交于点 A，抛物线 y＝－ 2x2平移后的顶点与点 A 重合．(1)求平移后的抛物线 l 的解析式； (2)若点B(x1，y12，y212，1)，C(x) 在抛物线l 上，且－2<x <x试比较 y1， y2的大小．解： (1) ∵ y＝ x＋ 1，∴令 y＝ 0，则 x＝－ 1，∴ A( － 1，0)，即抛物线 l 的顶点坐标为 (－1，0)，又抛物线 l 是由抛物线 y＝－ 2x2平移得到的，∴抛物线 l 的解析式为 y＝－ 2(x＋ 1)2.(2)由 (1) 可知，抛物线 l 的对称轴为x＝－ 1，∵ a＝－ 2<0，∴当 x> － 1 时， y 随 x 的增1大而减小，又－2<x 1<x 2，∴y1>y 2.二、跟踪练习：学生独立确定解题思路，小组内交流，上台展示并讲解思路．(10 分钟 )1．不画图象，回答下列问题：(1)函数 y＝3(x － 1) 2的图象可以看成是由函数y＝ 3x2的图象作怎样的平移得到的？(2)说出函数y＝ 3(x－ 1)2的图象的开口方向、对称轴和顶点坐标．(3)函数有哪些性质？2(4)若将函数y＝ 3(x－ 1) 的图象向左平移 3 个单位得到哪个函数图象？2．与抛物线 y＝－ 2(x＋ 5)2顶点相同，形状也相同，而开口方向相反的抛物线所对应的函数关系式是 y＝ 2(x ＋ 5)2．3．对于函数 y＝－ 3(x ＋ 1)2，当 x> － 1 时，函数 y 随 x 的增大而减小，当 x＝－ 1 时，函数取得最大值，最大值 y＝ 0．4．二次函数 y＝ ax2＋ bx＋ c 的图象向左平移 2 个单位长度得到 y＝x2－2x＋ 1 的图象，则b＝－ 6， c＝ 9．点拨精讲：比较函数值的大小，往往可根据函数的性质，结合函数图象，能使解题过程简洁明了．学生总结本堂课的收获与困惑．(2 分钟)学习至此，请使用本课时对应训练部分．(10 分钟 )22． 1.3 二次函数 y＝ a(x－ h)2＋ k的图象和性质 (3)1．进一步熟悉作函数图象的主要步骤，会作函数y＝a(x －h) 2＋k 的图象．2．能正确说出y＝ a(x－ h)2＋ k 的图象的开口方向、对称轴和顶点坐标．3．掌握抛物线y＝ a(x－ h)2＋ k 的平移规律．重点：熟悉作函数图象的主要步骤，会作函数 y＝ a(x－ h)2＋ k 的图象．难点：能正确说出 y＝ a(x－ h)2＋ k 的图象的开口方向、对称轴和顶点坐标，掌握抛物线y＝ a(x－ h)2＋ k 的平移规律．一、自学指导．(10 分钟 )自学：自学课本P35～ 36“例 3、例 4”，掌握 y＝ a(x－ h)2＋ k 与 y＝ ax2之间的关系，理解并掌握y＝ a(x－ h)2＋ k 的相关性质，完成填空．总结归纳：一般地，抛物线y＝ a(x－ h)2＋ k 与 y＝ ax2的形状相同，位置不同，把抛物线 y＝ ax2向上 (下 )向左 (右 )平移，可以得到抛物线y＝a(x －h) 2＋ k，平移的方向、距离要根据 h， k 的值来决定：当h>0 时，表明将抛物线向右平移h 个单位；当k<0 时，表明将抛物线向下平移 |k|个单位．抛物线 y＝ a(x－ h)2＋ k 的特点是：当a>0 时，开口向上；当a<0 时，开口向下；对称轴是直线 x＝h；顶点坐标是(h， k)．二、自学检测：学生自主完成，小组内展示，点评，教师巡视．(7分钟1．教材 P37 练习题2．函数 y＝ 2(x ＋ 3)2－5 的图象是由函数y＝ 2x2的图象先向左平移 3 个单位，再向下平移 5 个单位得到的；3．抛物线 y＝－ 2(x － 3)2－1 的开口方向是向下，其顶点坐标是 (3，－ 1)，对称轴是直线 x ＝ 3，当 x>3 时，函数值 y 随自变量 x 的值的增大而减小．一、小组讨论：小组讨论交流解题思路，小组活动后，小组代表展示活动成果．(13 分钟)探究 1填写下表：解析式开口方向y＝－ 2x2向下y＝1x2＋ 1向上2y＝－ 5(x ＋ 2)2向下y＝3(x＋ 1)2－ 4向上点拨精讲：解这类型题要将不同形式的解析式统一为对称轴顶点坐标y 轴(0， 0)y 轴(0， 1)x＝－ 2(－ 2， 0)x＝－ 1(－1，－4)y＝ a(x－ h)2＋ k 的形式，便于解答．探究 2已知 y＝ a(x－ h)2＋k 是由抛物线 y＝－1x2向上平移 2 个单位长度，再向右平移21 个单位长度得到的抛物线．(1)求出 a， h，k 的值； (2)在同一坐标系中，画出 y＝ a(x－ h)2＋k 与 y＝－12的图象； (3)2x观察 y＝ a(x－ h) ＋ k 的图象，当 x 取何值时，y 随 x 的增大而增2大；当 x 取何值时，y 随 x 的增大而减小，并求出函数的最值； (4)观察 y ＝a(x －h) 2＋ k 的图象，你能说出对于一切 x 的值，函数 y 的取值范围吗？解： (1)∵抛物线 y ＝－ 1x 2 向上平移 2 个单位长度，再向右平移 1 个单位长度得到的抛2 1 21 物线是 y ＝－ 2(x － 1) ＋ 2， ∴a ＝－ 2， h ＝ 1， k ＝ 2；(2)函数 y ＝－ 1 (x － 1) 21 2 的图象如图；2 ＋ 2 与 y ＝－ x2(3)观察 y ＝－ 1 (x － 1)2＋ 2 的图象可知，当 x<1 时， y 随 x 的增大而增大； x>1 时，y 随2x 的增大而减小；(4)由 y ＝－12(x － 1) 2＋ 2 的图象可知，对于一切x 的值， y ≤2.二、跟踪练习：学生独立确定解题思路，小组内交流，上台展示并讲解思路．(5 分钟 )2是 y ＝－ 2(x －3) 2＋ 2．点拨精讲：抛物线的移动，主要看顶点位置的移动．2．若直线 y ＝2x ＋ m 经过第一、三、四象限，则抛物线 y ＝ (x － m)2 ＋1 的顶点必在第二象限．点拨精讲：此题为二次函数简单的综合题，要注意它们的图象与性质的区别．3．把 y ＝ 2x 2－1 的图象向右平移 1 个单位，再向下平移2 个单位，得到的新抛物线的解析式是 y ＝ 2(x － 1)2－ 3．4．已知 A(1 ， y 1 )， B( － 2， y 2)， C(－ 2， y 3 )在函数 y ＝ a(x ＋ 1)2＋ k(a>0) 的图象上，则y 1， y 2， y 3 的大小关系是 y 2 <y 3<y 1．点拨精讲：本节所学的知识是：二次函数 y ＝ a(x － h)2＋k 的图象画法及其性质的总结；平移的规律．所用的思想方法：从特殊到一般．学生总结本堂课的收获与困惑． (2 分钟)学习至此，请使用本课时对应训练部分．(10 分钟 )22．1.4二次函数 y ＝ax 2＋ bx ＋ c 的图象和性质 (1)1．会画二次函数 y ＝ ax 2＋ bx ＋c 的图象，能将一般式化为顶点式，掌握顶点坐标公式，对称轴的求法．2．能将一般式化为交点式，掌握抛物线与坐标轴交点坐标的求法． 3．会求二次函数的最值，并能利用它解决简单的实际问题．重点：会画二次函数 y ＝ ax 2＋bx ＋ c 的图象，能将一般式化为顶点式，掌握顶点坐标公式，对称轴的求法．难点：能将一般式化为交点式，掌握抛物线与坐标轴交点坐标的求法．一、自学指导． (10 分钟 )自学：自学课本 P37～39“思考、探究” ，掌握将一般式化成顶点式的方法，完成填空．总结归纳：二次函数 y ＝ a(x － h) 2＋k 的顶点坐标是 (h ， k)，对称轴是 x ＝ h ，当 a>0 时，开口向上，此时二次函数有最小值，当 x>h 时， y 随 x 的增大而增大，当 x<h 时， y 随 x 的增大而减小；当 a<0 时，开口向下，此时二次函数有最大值，当 x<h 时，y 随 x 的增大而增大，当 x>h 时， y 随 x 的增大而减小；22b4ac －b 2用配方法将 y ＝ ax ＋ bx ＋c化成 y ＝ a(x － h) ＋ k 的形式，则 h ＝－ 2a ， k ＝ 4a；则二次函数的图象的顶点坐标是4ac － b 2b ；当 x ＝－ b 时，二次函 (－ b ，2a4a )，对称轴是x ＝－ 2a 2a 数 y ＝ ax 2＋ bx ＋ c 有最大 (最小 )值，当 a<0 时，函数 y 有最大值，当 a>0 时，函数 y 有最小值．二、自学检测：学生自主完成，小组内展示，点评，教师巡视． (5 分钟 )1．求二次函数 y ＝ x 2＋ 2x － 1 顶点的坐标、对称轴、最值，画出其函数图象．点拨精讲：先将此函数解析式化成顶点式，再解其他问题，在画函数图象时，要在顶点的两边对称取点，画出的抛物线才能准确反映这个抛物线的特征．一、小组合作：小组讨论交流解题思路，小组活动后，小组代表展示活动成果．(13 分钟)探究 1 将下列二次函数写成顶点式 y ＝ a(x － h)2＋ k 的形式，并写出其开口方向、顶点坐标、对称轴．1 2＋21； (2)y ＝－ 3x 2－18x － 22.(1)y ＝ x － 3x41 2－3x ＋ 21解： (1)y ＝ x4＝ 1(x 2－ 12x) ＋ 2141 2＝ 4(x － 12x ＋36－ 36)＋ 2112＝ 4(x － 6) ＋ 12∴此抛物线的开口向上，顶点坐标为 (6， 12)，对称轴是 x ＝ 6.2(2)y ＝－ 3x － 18x － 222＝－ 3(x ＋ 6x) －222＝－ 3(x ＋ 6x ＋ 9－ 9)－ 222＝－ 3(x ＋ 3) ＋5 ∴此抛物线的开口向下，顶点坐标为 (－ 3， 5)，对称轴是 x ＝－ 3.点拨精讲：第 (2)小题注意 h 值的符号，配方法是数学的一个重要方法，需多加练习，熟练掌握；抛物线的顶点坐标也可以根据公式直接求解．探究 2 用总长为 60 m 的篱笆围成的矩形场地，矩形面积 S 随矩形一边长 l 的变化而变化， l 是多少时，场地的面积 S 最大？(1)S 与 l 有何函数关系？(2)举一例说明 S 随 l 的变化而变化？ (3)怎样求 S 的最大值呢？解： S ＝ l(30 －l)＝－ l 2＋ 30l(0 ＜ l ＜ 30)＝－ (l 2－ 30l) ＝－ (l － 15)2＋ 225画出此函数的图象，如图．∴ l ＝ 15 时，场地的面积 S 最大 (S 的最大值为 225)．点拨精讲：二次函数在几何方面的应用特别广泛，要注意自变量的取值范围的确定，同时所画的函数图象只能是抛物线的一部分．二、跟踪练习：学生独立确定解题思路，小组内交流，上台展示并讲解思路．(5 分钟 )1． y ＝－ 2x 2＋ 8x －7 的开口方向是向下，对称轴是 x ＝ 2，顶点坐标是 (2， 1)；当 x ＝ 2 时，函数 y 有最大值，其值为 y ＝ 1．2．已知二次函数 y ＝ax 2 ＋2x ＋ c(a ≠ 0)有最大值，且 ac ＝ 4，则二次函数的顶点在第四象限．3．抛物线 y ＝ax 2＋ bx ＋ c ，与 y 轴交点的坐标是 (0，c)，当 b 2－ 4ac ＝ 0 时，抛物线与 x轴只有一个交点 (即抛物线的顶点)，交点坐标是 (－ 2a b，0)；当 b 2－ 4ac ＞0 时，抛物线与x－ b ± b 2－ 4ac2轴有两个交点，交点坐标是 (， 0) ；当 b － 4ac<0 时，抛物线与 x 轴没有交点，2a若抛物线与 x 轴的两个交点坐标为(x 1， 0)， (x 2， 0)，则 y ＝ ax 2＋ bx ＋ c ＝ a(x － x 1)(x － x 2)．点拨精讲：与 y 轴的交点坐标即当 x ＝ 0 时求 y 的值；与 x 轴交点即当y ＝ 0 时得到一个一元二次方程，而此一元二次方程有无解，两个相等的解和两个不相等的解三种情况，所以二次函数与 x 轴的交点情况也分三种．注意利用抛物线的对称性，已知抛物线与 x 轴的两个交点坐标时，可先用交点式： y ＝a(x － x 1 )(x － x 2)， x 1， x 2 为两交点的横坐标．学生总结本堂课的收获与困惑．(2 分钟)学习至此，请使用本课时对应训练部分． (10 分钟 )22．1.4二次函数y＝ax2＋ bx＋ c 的图象和性质(2)能熟练根据已知点坐标的情况，用适当的方法求二次函数的解析式．重难点：能熟练根据已知点坐标的情况，用适当的方法求二次函数的解析式．一、自学指导．(10 分钟 )自学：自学课本P39～40，自学“探究、归纳” ，掌握用待定系数法求二次函数的解析式的方法，完成填空．总结归纳：若知道函数图象上的任意三点，则可设函数关系式为y＝ ax2＋ bx ＋ c，利用待定系数法求出解析式；若知道函数图象上的顶点，则可设函数的关系式为y＝ a(x－ h)2＋ k，把另一点坐标代入式中，可求出解析式；若知道抛物线与x 轴的两个交点 (x1， 0)， (x2， 0)，可设函数的关系式为y＝ a(x－ x1)(x － x2)，把另一点坐标代入式中，可求出解析式．二、自学检测：学生自主完成，小组内展示，点评，教师巡视． (7 分钟 )1．二次函数 y＝ 4x2－ mx＋2，当 x< － 2 时，y 随 x 的增大而减小；当x> － 2 时， y 随 x 的增大而增大，则当 x＝ 1 时， y 的值为 22．点拨精讲：可根据顶点公式用含m 的代数式表示对称轴，从而求出 m 的值．2．抛物线 y＝－ x2＋6x＋ 2 的顶点坐标是 (3， 11)．3．二次函数y＝ ax2＋ bx＋ c 的图象大致如图所示，下列判断错误的是( D )A． a<0B． b>0C． c>0D． ac>0第3题图第 4题图第 5题图4．如图，抛物线 y＝ ax2＋ bx＋ c(a>0)的对称轴是直线 x＝ 1，且经过点 P(3，0)，则 a－b＋ c 的值为 ( A )A．0 B．－ 1 C．1 D．2点拨精讲：根据二次函数图象的对称性得知图象与x 轴的另一交点坐标为 (－ 1， 0)，将此点代入解析式，即可求出 a－b＋ c 的值．5．如图是二次函数y＝ ax2＋ 3x＋ a2－ 1 的图象， a 的值是－ 1．点拨精讲：可根据图象经过原点求出 a 的值，再考虑开口方向．一、小组合作：小组讨论交流解题思路，小组活动后，小组代表展示活动成果． (13 分钟)探究 1 已知二次函数的图象经过点A(3 ， 0)， B(2 ，－ 3)， C(0，－ 3)，求函数的关系式和对称轴．解：设函数解析式为y＝ ax2＋ bx ＋ c，因为二次函数的图象经过点A(3 ，0)，B(2，－ 3)，9a＋ 3b＋ c＝ 0，C(0，－ 3)，则有4a＋ 2b＋c＝－ 3，c＝－ 3.a＝ 1，解得b＝－ 2，c＝－ 3.∴函数的解析式为y＝ x2－ 2x－ 3，其对称轴为x＝ 1.探究 2已知一抛物线与x 轴的交点是A(3 ， 0)， B( － 1，0)，且经过点C(2， 9)．试求该抛物线的解析式及顶点坐标．解：设解析式为y＝ a(x－ 3)(x ＋ 1)，则有a(2－ 3)(2＋ 1)＝ 9，∴ a＝－ 3，2点拨精讲：因为已知点为抛物线与x 轴的交点，解析式可设为交点式，再把第三点代入即可得一元一次方程，较之一般式得出的三元一次方程组简单．而顶点可根据顶点公式求出．二、跟踪练习：学生独立确定解题思路，小组内交流，上台展示并讲解思路．(5 分钟 )1．已知一个二次函数的图象的顶点是(－ 2，4)，且过点 (0，－ 4)，求这个二次函数的解析式及与x 轴交点的坐标．2．若二次函数y＝ ax2＋ bx＋ c 的图象过点 (1， 0)，且关于直线x＝1对称，那么它的图2象还必定经过原点．3．如图，已知二次函数12， 0)， B(0，－ 6)两点．y＝－ x ＋ bx＋ c 的图象经过 A(22(1)求这个二次函数的解析式；(2)设该二次函数的对称轴与x 轴交于点 C，连接 BA ， BC，求△ ABC 的面积．点拨精讲：二次函数解析式的三种形式： 1.一般式 y＝ ax2＋ bx＋c；2.顶点式 y＝a(x－h) 2＋k； 3.交点式 y＝ a(x－ x1)(x － x2 )．利用待定系数法求二次函数的解析式，需要根据已知点的情况设适当形式的解析式，可使解题过程变得更简单．学生总结本堂课的收获与困惑．(2 分钟)学习至此，请使用本课时的对应训练部分．(10 分钟 )22． 2二次函数与一元二次方程(1)1．理解二次函数与一元二次方程的关系．2．会判断抛物线与x 轴的交点个数．3．掌握方程与函数间的转化．重点：理解二次函数与一元二次方程的关系；会判断抛物线与难点：掌握方程与函数间的转化．x 轴的交点个数．一、自学指导．自学：自学课本关系，会判断抛物线与解，完成填空．(10 分钟 )P43～ 45.自学“思考”与“例题”，理解二次函数与一元二次方程的x 轴的交点情况，会利用二次函数的图象求对应一元二次方程的近似总结归纳：抛物线 y＝ ax2＋ bx＋ c 与 x 轴有公共点，公共点的横坐标是 x0，那么当 x＝ x0时，函数的值是 0，因此 x＝x0就是方程 ax2＋ bx ＋c＝0 的一个根．二次函数的图象与x 轴的位置关系有三种：当b2－4ac>0时，抛物线与x轴有两个交点；当 b2－ 4ac＝ 0 时，抛物线与 x 轴有一个交点；当 b2－ 4ac<0 时，抛物线与 x 轴有 0 个交点．这对应着一元二次方程 ax2＋ bx＋ c＝ 0 根的三种情况：有两个不等的实数根，有两个相等实数根，没有实数根．二、自学检测：学生自主完成，小组内展示，点评，教师巡视． (5 分钟 )1．观察图中的抛物线与x 轴的交点情况，你能得出相应方程的根吗？2方程 x ＋x－ 2＝ 0 的根是： x1＝－ 2， x2＝ 1；方程 x2－6x＋ 9＝ 0 的根是： x1＝x2＝ 3；方程 x2－x＋ 1＝ 0 的根是：无实根．2．如图所示，你能直观看出哪些方程的根？，即函数 y＝－ x2＋ 2x ＋点拨精讲：此题充分利用二次函数与一元二次方程之间的关系3 中，y 为某一确定值m(如 4，3，0)时，相应 x 值是方程－ x2＋2x ＋ 3＝ m(m ＝ 4，3，0)的根．错误 !错误 !,第3题图)根是3．已知抛物线x1＝ x2＝ 1．y＝ ax2＋ bx＋ c 的图象如图所示，则关于x 的方程ax2＋ bx＋c－ 3＝ 0 的一、小组合作：小组讨论交流解题思路，小组活动后，小组代表展示活动成果．(6分钟)探究已知二次函数y＝ 2x2－ (4k＋ 1)x ＋ 2k2－ 1 的图象与x 轴交于两点．求 k 的取值范围．解：根据题意知b2－4ac>0，即 [－ (4k ＋ 1)]2－ 4× 2×(2k 2－ 1)>0 ，9解得 k>－8.点拨精讲：根据交点的个数来确定判别式的范围是解题关键，要熟悉它们之间的对应关系．。

二次函数导学案(全章)之欧阳文创编

第1课时二次函数的概念【学习目标】1．经历探索，分析和建立两个变量之间的二次函数关系的过程，进一步体验如何用数学的方法描述变量之间的数量关系；2．探索并归纳二次函数的定义；3．能够表示简单变量之间的二次函数关系。

【学习重点】掌握二次函数的概念并能利用概念解答相关的题型。

【课时类型】概念课【学习过程】一、学习准备1．函数的定义：在某个变化过程中，有两个变量x和y，如果给定一个x值，相应地就确定了一个y值，那么我们称是的函数，其中是自变量，是因变量。

2．一次函数的关系式为y=(其中k、b是常数，且k≠0)；正比例函数的关系式为y＝(其中k是的常数)；反比例函数的关系式为y=(k是的常数)。

二、解读教材——数学知识源于生活3．某果园有100棵橙子树，每一棵树平均结600个橙子。

现准备多种一些橙子树以提高产量，但是如果多种树，那么树之间的距离和每一棵树所接受的阳光就会减少。

根据经验估计，每多种一棵树，平均每棵树就会少结5个橙子。

假设果园增种x棵橙子树，那么果园共有棵橙子树，这时平均每棵树结个橙子，如果果园橙子的总产量为y个，那么y=。

4．如果你到银行存款100元，设人民币一年定期储蓄的年利率是x，一年到期后,银行将本金和利息自动按一年定期储蓄转存。

那么你能写出两年后的本息和y(元)的表达式(不考虑利息税)吗？。

5．能否根据刚才推导出的式子y=5x2+100x+60000和y=100x2+200x+100猜想出二次函数的定义及一般形式吗？一般地，形如y ＝ax2+bx+c(a ，b ，c 是常数，a ≠0)的函数叫做x 的二次函数。

它就是二次函数的一般形式，理解并熟记几遍。

例1(1)2321xy +-=(2)112+=x y(3)x y 222+= (4)251t t s ++=(5)22)3(x x y -+= (6)210r s π=(1)2x y =(2)252132+-=x x y (3)=y (4)1132--=）（x y (5)cax y -=2(6)s 三、挖掘教材6．对二次函数定义的深刻理解及运用例2 若函数1232++=+-kx x y k k 是二次函数，求k 的值。

二次函数导学案全章(完整资料).doc

【最新整理，下载后即可编辑】二次函数导学案26.1 二次函数及其图像 26.1.1 二次函数【学习目标】1. 了解二次函数的有关概念．2. 会确定二次函数关系式中各项的系数。

3. 确定实际问题中二次函数的关系式。

【学法指导】类比一次函数，反比例函数来学习二次函数，注意知识结构的建立。

【学习过程】一、知识链接：1.若在一个变化过程中有两个变量x 和y ，如果对于x 的每一个值， y 都有唯一的值与它对应，那么就说y 是x 的，x 叫做。

2. 形如___________y =0)k ≠（的函数是一次函数，当______0=时，它是函数；二、自主学习：1．用16m 长的篱笆围成长方形圈养小兔，圈的面积y(㎡)与长方形的长x(m)之间的函数关系式为。

分析：在这个问题中，可设长方形生物园的长为x 米，则宽为米，如果将面积记为y 平方米，那么y 与x 之间的函数关系式为y = ，整理为y = .2.n 支球队参加比赛，每两队之间进行一场比赛．写出比赛的场次数m 与球队数n 之间的关系式_______________________．3.用一根长为40cm 的铁丝围成一个半径为r 的扇形，求扇形的面积S 与它的半径r 之间的函数关系式是。

4.观察上述函数函数关系有哪些共同之处？。

5.归纳：一般地，形如，（,,a b c a 是常数，且）的函数为二次函数。

其中x 是自变量，a 是__________，b 是___________，c 是_____________．三、合作交流：（1）二次项系数a 为什么不等于0？答：。

（2）一次项系数b 和常数项c 可以为0吗？答： . 四、跟踪练习1．观察：①26y x =；②235y x =-+；③y ＝200x 2＋400x ＋200；④32y x x =-；⑤213y x x =-+；⑥()221y x x =+-．这六个式子中二次函数有。

初中数学二次函数全章导学案(史上最全)

二次函数导学案26.1.1二次函数（第一课时）一．预习检测案一般地，形如____________________________的函数，叫做二次函数。

其中x是________，a是__________，b是___________，c是_____________．二．合作探究案：问题1: 正方体的六个面是全等的正方形,如果正方形的棱长为x,表面积为y,写出y与x的关系。

问题2: n边形的对角线数d与边数n之间有怎样的关系?提示：多边形有n条边，则有几个顶点？从一个顶点出发，可以连几条对角线？问题3: 某工厂一种产品现在的年产量是20件,计划今后两年增加产量.如果每年都比上一年的产量增加x倍,那么两年后这种产品的数量y将随计划所定的x的值而定,y与x之间的关系怎样表示?问题4：观察以上三个问题所写出来的三个函数关系式有什么特点?小组交流、讨论得出结论：经化简后都具有的形式。

问题5：什么是二次函数？形如。

问题6：函数y＝ax²＋bx＋c，当a、b、c满足什么条件时，(1)它是二次函数?(2)它是一次函数？(3)它是正比例函数？例1: 关于x的函数mmxmy-+=2)1(是二次函数, 求m的值.注意:二次函数的二次项系数必须是的数。

三．达标测评案：1．下列函数中,哪些是二次函数?(1)y＝3x－1; (2)y＝3x2＋2; (3)y＝3x3＋2x2; (4)y＝2x2－2x＋1; (5)y＝x2－x(1＋x); (6)y ＝x－2＋x.2.若函数y＝(a－1)x2＋2x＋a2－1是二次函数,则( )A.a＝1B.a＝±1C.a≠1D.a≠－13.一定条件下,若物体运动的路段s(米)与时间t(秒)之间的关系为s＝5t2＋2t,则当t＝4秒时,该物体所经过的路程为A.28米B.48米C.68米D.88米4.一个长方形的长是宽的2倍,写出这个长方形的面积与宽之间的函数关系式.5．一个圆柱的高等于底面半径，写出它的表面积Ｓ与半径Ｒ之间的关系式。

(导学案)1.1二次函数

第一章二次函数1.1二次函数【教学目标】知识与技能1．探索并归纳二次函数的概念，熟练掌握二次函数的一般形式及自变量的取值范围。

2．能够表示简单变量之间的二次函数关系。

过程与方法：通过用二次函数表示变量之间关系的体验过程，增强对函数的感性认识，培养学生分析问题，解决问题的能力。

情感态度价值观：通过学生之间的交流合作的过程，培养学生的合作意识，体验与他人交流合作的重要性。

【教学重难点】重点：建立二次函数数学模型和理解二次函数概念。

难点：建立二次函数数学模型。

【导学过程】【情景导入】我们已知道，可以建立数学模型一次函数ｙ＝ｋｘ＋ｂ（ｋ≠０）来刻画直线，反比例函数ｙ＝ｋ/ｘ（ｋ≠０）来刻画双曲线，那么像前面所看到的曲线，我们又该建立一个什么样的数学模型来刻画它们呢？要刻画它，我们今天还需要学习一种新的函数关系———二次函数．【新知探究】探究一、植物园的面积随着砌法的不同怎样变化？学校准备在校园里利用围墙的一段和篱笆墙围成一个矩形植物园。

如下图所示，已知篱笆墙的总长度为100m。

大家来讨论对应于不同的砌法，植物园的面积会发生什么样的变化. 解:设与围墙相邻的每一面墙的长度都为xm，则与围墙相对的一面墙的长度为（100－2x）m，于是矩形植物园的面积S为１）学生阅读审题，独立思考，自主探索．设与围墙相邻的每一面墙的长都为ｘｍ，则与围墙相对的一面墙的长为（１００－２ｘ）ｍ，于是矩形植物园的面积Ｓ＝ｘ(１００－２ｘ），即Ｓ＝－２ｘ２＋１００ｘ．（２）学生合作讨论ｘ的取值范围．由ｘ＞０，１００－２ｘ＞０，得０＜ｘ＜５０．（３）概括．由上述（1）、（2）可得关系式Ｓ=-２ｘ２+100ｘ，０＜ｘ＜５０，有了这个关系式，我们对植物园的面积Ｓ随着砌法的不同而变化的情况就了如指掌了．S=-2x2+100x,0<x<50 ①①式表示植物园的面积S与围墙相邻的一面篱笆墙长度x之间的关系，而且对于X的每一个取值，S都有唯一确定的值与它对应，即S是X的函数。

最全二次函数概念的图像与性质导学案完整版.doc

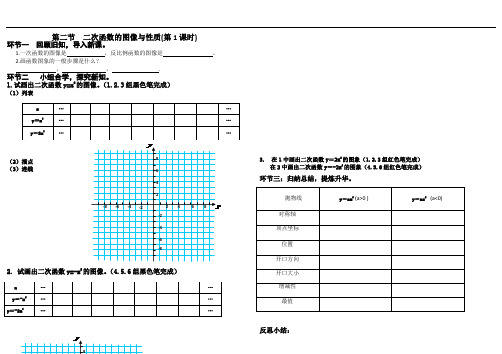
第二节二次函数的图像与性质(第1课时)环节一回顾旧知，导入新课。

1.一次函数的图像是，反比例函数的图像是。

2.画函数图象的一般步骤是什么？，， .环节二小组合学，探究新知。

1.试画出二次函数y=x 2的图像。

（1.2.3组黑色笔完成）（1）列表（2）描点（3）连线2. 试画出二次函数y=-x 2的图像。

（4.5.6组黑色笔完成）3. 在1中画出二次函数y ＝2x 2的图象（1.2.3组红色笔完成）在2中画出二次函数y ＝-2x 2的图象（4.5.6组红色笔完成）环节三：归纳总结，提炼升华。

反思小结：1.当a>0时，a 越大，a ，抛物线开口。

当a<0时，a 越小，a ，抛物线开口。

综上：对于任意a ≠0，a越大，抛物线开口。

环节四:达标检测，反馈提高 A 组1．二次函数2x y =的函数图像为_________,开口______,顶点坐标为______对称轴为________ 二次函数2-x y =的函数图像为_________,开口______,顶点坐标为______对称轴为________2.判断正误（1）函数y = x2与y = －x2的图像都是抛物线（）；（2）函数y = x2与y = －x2的图像对称轴都是x 轴（）；（3）函数y = x2与y = －x2的图像形状相同，开口方向相反（）（4）抛物线y = 3x2在x 轴的下方(除顶点外)（）（5）在抛物线y = -5x2左侧， y 随着x 的增大而增大（） 3.已知72)2(--=ax a y 是二次函数，且当0>x 时，y 随x 的增大而增大，则=a 。

4.设边长为x 的正方形的面积为y ，y 是x 的二次函数，该函数的图象是下列各图形中（）B 组：1．在函数y = x 2上有两点，（－1，y 1），（－3，y 2），那么y 1，y 2，0的大小关系是（）A .y 1 ＜ y 2 ＜0 B. y 2 ＜ y 1 ＜0 C. y 1 ＞ y 2 ＞0 D. y 2 ＞ y 1 ＞02、直线1+-=x y 与抛物线2x y =有（）A ．1个交点B . 2个交点C ．3个交点D ．没有交点3、如图边长为2的正方形ABCD 的中心在直角坐标系的原点O ，AD ∥x 轴，抛物线y = x 2和 y = －x 2别经过A ，B ，C ，D 点，将正方形成几部分，则图中阴影部分的面积为．探索乐趣：课下猜想并验证抛物线y = 3x2与y = 3x2+4之间有什么关系？它们是轴对称图形吗？开方方向，对称轴、定点坐标分别是什么？温馨提示：只有不断的思考,才会有新的发现;只有量的变化,才会有质的进步.赠送以下资料《二次函数的应用》中考题集锦10题已知抛物线222(0)y x mx m m =+-≠．（1）求证：该抛物线与x 轴有两个不同的交点；（2）过点(0)P n ，作y 轴的垂线交该抛物线于点A 和点B （点A 在点P 的左边），是否存在实数m n ，，使得2AP PB =？若存在，则求出m n ，满足的条件；若不存在，请说明理由．答案：解：（1）证法1：22229224m y x mx m x m ⎛⎫=+-=+- ⎪⎝⎭，当0m ≠时，抛物线顶点的纵坐标为2904m -<， ∴顶点总在x 轴的下方．而该抛物线的开口向上，∴该抛物线与x 轴有两个不同的交点．（或者，当0m ≠时，抛物线与y 轴的交点2(02)m -，在x 轴下方，而该抛物线的开口向上，∴该抛物线与x 轴有两个不同的交点．）证法2 ：22241(2)9m m m ∆=-⨯⨯-=，当0m ≠时，290m >，∴该抛物线与x 轴有两个不同的交点．（2）存在实数m n ，，使得2AP PB =．设点B 的坐标为()t n ，，由2AP PB =知，①当点B 在点P 的右边时，0t >，点A 的坐标为(2)t n -，，且2t t -，是关于x的方程222x mx m n +-=的两个实数根．2224(2)940m m n m n ∴∆=---=+>，即294n m >-．且(2)t t m +-=-（I ），2(2)t t m n -=--（II ）由（I ）得，t m =，即0m >．将t m=代入（II ）得，0n =．∴当0m >且0n =时，有2AP PB =．②当点B 在点P 的左边时，0t <，点A 的坐标为(2)t n ，，且2t t ，是关于x 的方程222x mx m n +-=的两个实数根． 2224(2)940m m n m n ∴∆=---=+>，即 294n m >-．且2t t m +=-（I ），222t t m n =--（II ）由（I ）得，3mt =-，即0m >．将3m t =-代入（II ）得，2209n m =-且满足294n m >-． ∴当0m >且2209n m =-时，有2AP PB =第11题一人乘雪橇沿如图所示的斜坡笔直滑下，滑下的距离S （米）与时间t （秒）间的关系式为210S t t =+，若滑到坡底的时间为2秒，则此人下滑的高度为（）Ａ．24米Ｂ．12米Ｃ．米Ｄ．6米答案：Ｂ第12题我市英山县某茶厂种植“春蕊牌”绿茶，由历年来市场销售行情知道，从每年的3月25日起的180天内，绿茶市场销售单价y （元）与上市时间t （天）的关系可以近似地用如图（1）中的一条折线表示．绿茶的种植除了与气候、种植技术有关外，其种植的成本单价z （元）与上市时间t （天）的关系可以近似地用如图（2）的抛物线表示．（2）求出图（2）中表示的种植成本单价z （元）与上市时间t （天）（0t >）的函数关系式；（3）认定市场销售单价减去种植成本单价为纯收益单价，问何时上市的绿茶纯收益单价最大？（说明：市场销售单价和种植成本单价的单位：元／500克．）答案：解：（1）依题意，可建立的函数关系式为：2160(0120)380(120150)220(150180)5t t y t t t ⎧-+<<⎪⎪=<⎨⎪⎪+⎩，，． ≤ ≤≤ （2）由题目已知条件可设2(110)20z a t =-+．图象过点85(60)3，，2851(60110)203300a a ∴=-+∴=．． 21(110)20300z t ∴=-+ (0)t >．（3）设纯收益单价为W 元，则W =销售单价-成本单价． )图(1)图(2)(天)故22221160(110)20(0120)3300180(110)20(120150)3002120(110)20(150180)5300t t t W t t t t t ⎧-+---<<⎪⎪⎪=---<⎨⎪⎪+---⎪⎩，，． ≤ ≤≤ 化简得2221(10)100(0120)3001(110)60(120150)3001(170)56(150180)300t t W t t t t ⎧--+<<⎪⎪⎪=-+<⎨⎪⎪--+⎪⎩，，． ≤ ≤≤①当21(10)100(0120)300W t t =--+<<时，有10t =时，W 最大，最大值为100； ②当21(110)60(120150)300W t t =--+<≤时，由图象知，有120t =时，W 最大，最大值为2593；③当21(170)56(150180)300W t t =--+≤≤时，有170t =时，W 最大，最大值为56．综上所述，在10t =时，纯收益单价有最大值，最大值为100元．第13题如图，足球场上守门员在O 处开出一高球，球从离地面1米的A 处飞出（A 在y 轴上），运动员乙在距O 点6米的B 处发现球在自己头的正上方达到最高点M ，距地面约4米高，球落地后又一次弹起．据实验，足球在草坪上弹起后的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半．（1）求足球开始飞出到第一次落地时，该抛物线的表达式．（2）足球第一次落地点C距守门员多少米？（取7=）（3）运动员乙要抢到第二个落点D，他应再向前跑多少米？（取5=）答案：解：（1）（3分）如图，设第一次落地时，抛物线的表达式为2(6)4y a x =-+．由已知：当0x =时1y =．即1136412a a =+∴=-，． ∴表达式为21(6)412y x =--+．（或21112y x x =-++）（2）（3分）令210(6)4012y x =--+=，．212(6)4861360x x x ∴-===-<．≈，（舍去）． ∴足球第一次落地距守门员约13米．（3）（4分）解法一：如图，第二次足球弹出后的距离为CD根据题意：CD EF =（即相当于将抛物线AEMFC 向下平移了2个单位）212(6)412x ∴=--+解得1266x x =-=+1210CD x x ∴=-=． 1361017BD ∴=-+=（米）．解法二：令21(6)4012x --+=．解得16x =-，2613x =+．∴点C 坐标为（13，0）．设抛物线CND 为21()212y x k =--+．将C 点坐标代入得：21(13)2012k --+=．解得：11313k =-（舍去），2667518k =+++=．21(18)212y x =--+ 令210(18)212y x ==--+，0．118x =-，21823x =+． 23617BD ∴=-=（米）．解法三：由解法二知，18k =，所以2(1813)10CD =-=，所以(136)1017BD =-+=．答：他应再向前跑17米．第14题荆州市“建设社会主义新农村”工作组到某县大棚蔬菜生产基地指导菜农修建大棚种植蔬菜．通过调查得知：平均修建每公顷大棚要用支架、农膜等材料费2.7万元；购置滴灌设备，这项费用（万元）与大棚面积（公顷）的平方成正比，比例系数为0.9；另外每公顷种植蔬菜需种子、化肥、农药等开支0.3万元．每公顷蔬菜年均可卖7.5万元．（1）基地的菜农共修建大棚x （公顷），当年收益（扣除修建和种植成本后）为y （万元），写出y 关于x的函数关系式．（2）若某菜农期望通过种植大棚蔬菜当年获得5万元收益，工作组应建议他修建多少公项大棚．（用分数表示即可）（3）除种子、化肥、农药投资只能当年受益外，其它设施3年内不需增加投资仍可继续使用．如果按3年计算，是否修建大棚面积越大收益越大？修建面积为多少时可以得到最大收益？请帮工作组为基地修建大棚提一项合理化建议．答案：（1）()227.5 2.70.90.30.9 4.5y x x x x x x =-++=-+．（2）当20.9 4.55x x -+=时，即2945500x x -+=，153x =，2103x =从投入、占地与当年收益三方面权衡，应建议修建53公顷大棚．（3）设3年内每年的平均收益为Z （万元）()()2227.50.90.30.30.3 6.30.310.533.075Z x x x x x x x =-++=-+=--+（10分）不是面积越大收益越大．当大棚面积为10.5公顷时可以得到最大收益．建议：①在大棚面积不超过10.5公顷时，可以扩大修建面积，这样会增加收益． ②大棚面积超过10.5公顷时，扩大面积会使收益下降．修建面积不宜盲目扩大．③当20.3 6.30x x -+=时，10x =，221x =．大棚面积超过21公顷时，不但不能收益，反而会亏本．（说其中一条即可）第15题一家用电器开发公司研制出一种新型电子产品，每件的生产成本为18元，按定价40元出售，每月可销售20万件．为了增加销量，公司决定采取降价的办法，经市场调研，每降价1元，月销售量可增加2万件．（1）求出月销售量y （万件）与销售单价x （元）之间的函数关系式（不必写x 的取值范围）；（2）求出月销售利润z （万元）（利润＝售价－成本价）与销售单价x （元）之间的函数关系式（不必写x 的取值范围）；（3）请你通过（2）中的函数关系式及其大致图象帮助公司确定产品的销售单价范围，使月销售利润不低于480万元．答案：略．第16题一座隧道的截面由抛物线和长方形构成，长方形的长为8m ，宽为2m ，隧道最高点P 位于AB 的中央且距地面6m ，建立如图所示的坐标系（1）求抛物线的解析式；（2）一辆货车高4m ，宽2m ，能否从该隧道内通过，为什么？（3）如果隧道内设双行道，那么这辆货车是否可以顺利通过，为什么？答案：（1）由题意可知抛物线经过点()()()024682A P B ，，，，，设抛物线的方程为2y ax bx c =++ 将A P D ，，三点的坐标代入抛物线方程．解得抛物线方程为21224y x x =-++ （2）令4y =，则有212244x x -++=解得1244x x =+=-212x x -=>∴货车可以通过．（3）由（2）可知21122x x -=>∴货车可以通过．第17题如图，在矩形ABCD 中，2AB AD =，线段10EF =．在EF 上取一点M ，分别以EM MF ，为一边作矩形EMNH 、矩形MFGN ，使矩形MFGN ∽矩形ABCD ．令M N x=，当x 为何值时，矩形EMNH 的面积S 有最大值？最大值是多少？答案：解：矩形MFGN ∽矩形ABCD ，MN MFAD AB∴=． 2AB AD MN x ==，，2MF x ∴=．102EM EF MF x ∴=-=-． (102)S x x ∴=-2210x x =-+ 2525222x ⎛⎫=--+ ⎪⎝⎭．∴当52x =时，S 有最大值为252．第18题某企业信息部进行市场调研发现：信息一：如果单独投资A 种产品，则所获利润A y （万元）与投资金额x （万元）之间存在正比例函数关系：A y kx =，并且当投资5万元时，可获利润2万元．信息二：如果单独投资B 种产品，则所获利润B y （万元）与投资金额x （万元）之间存在二次函数关系：2B y ax bx =+，并且当投资2万元时，可获利润2.4万元；当投资4万元时，可获利润3.2万元．（1）请分别求出上述的正比例函数表达式与二次函数表达式；（2）如果企业同时对AB ，两种产品共投资10万元，请你设计一个能获得最大利润的投资方案，并求出按此方案能获得的最大利润是多少？答案：解：（1）当5x =时，12250.4y k k ===，，， 0.4A y x ∴=，当2x =时， 2.4B y =；当4x =时， 3.2B y =．2.4423.2164a ba b =+⎧∴⎨=+⎩解得0.21.6a b =-⎧⎨=⎩∴20.2 1.6B y x x =-+．（2）设投资B 种商品x 万元，则投资A 种商品(10)x -万元，获得利润W 万元，根据题意可得220.2 1.60.4(10)0.2 1.24W x x x x x =-++-=-++ 20.2(3) 5.8W x ∴=--+当投资B 种商品3万元时，可以获得最大利润5.8万元，所以投资A 种商品7万元，B 种商品3万元，这样投资可以获得最大利润5.8万元．第19题如图所示，图（1）是一座抛物线型拱桥在建造过程中装模时的设计示意图，拱高为30m ，支柱3350m A B =，5根支柱1122334455A B A B A B A B A B ，，，，之间的距离均为15m ，1515B B A A ∥，将抛物线放在图（2）所示的直角坐标系中．（1）直接写出图（2）中点135B B B ，，的坐标；（2）求图（2）中抛物线的函数表达式；（3）求图（1）中支柱2244A B A B ，的长度．答案：（1）1(30)B -，0，3(030)B ，，5(300)B ，；（2）设抛物线的表达式为(30)(30)y a x x =-+，把3(030)B ，代入得(030)(030)30y a =-+=．B A D MFB 图(1)图(2)l130a =-∴． ∵所求抛物线的表达式为：1(30)(30)30y x x =--+．（3）4B ∵点的横坐标为15， 4B ∴的纵坐标4145(1530)(1530)302y =--+=． 3350A B =∵，拱高为30，∴立柱44458520(m)22A B =+=．由对称性知：224485(m)2A B A B ==。

二次函数导学案(全章)之欧阳理创编

【学习重点】掌握二次函数的概念并能利用概念解答相关的题型。

2．一次函数的关系式为y=(其中k、b是常数，且k≠0)；正比例函数的关系式为y＝(其中k是的常数)；反比例函数的关系式为y=(k是的常数)。

二、解读教材——数学知识源于生活3．某果园有100棵橙子树，每一棵树平均结600个橙子。

现准备多种一些橙子树以提高产量，但是如果多种树，那么树之间的距离和每一棵树所接受的阳光就会减少。

根据经验估计，每多种一棵树，平均每棵树就会少结5个橙子。

假设果园增种x棵橙子树，那么果园共有棵橙子树，这时平均每棵树结个橙子，如果果园橙子的总产量为y个，那么y=。

4．如果你到银行存款100元，设人民币一年定期储蓄的年利率是x，一年到期后,银行将本金和利息自动按一年定期储蓄转存。

那么你能写出两年后的本息和y(元)的表达式(不考虑利息税)吗？。

5．能否根据刚才推导出的式子y=-5x 2+100x+60000和y=100x 2+200x+100猜想出二次函数的定义及一般形式吗？一般地，形如y ＝ax 2+bx+c(a ，b ，c 是常数，a≠0)的函数叫做x 的二次函数。

它就是二次函数的一般形式，理解并熟记几遍。

例1 下列函数中，哪些是二次函数？(1)2321xy +-=(2)112+=x y(3)xy 222+= (4)251t t s ++= (5)22)3(xx y -+= (6)210rs π=即时练习(1)2x y =(2)252132+-=x x y (3))1(+=x x y (4)1132--=）（x y (5)cax y -=2(6)12+=x s 三、挖掘教材6．对二次函数定义的深刻理解及运用例2 若函数1232++=+-kx x y k k 是二次函数，求k 的值。

二次函数全章导学案

第二十六章二次函数教材分析本章是学生学习了正比例函数、一次函数和反比例函数以后，进一步学习函数知识，是函数知识螺旋发展的一个重要环节。

二次函数是描述现实世界变量之间关系的重要的数学模型。

本章的主要内容有二次函数的概念、二次函数的图象、二次函数的性质和二次函数的应用。

函数是数学的核心概念，也是初中数学的基本概念，函数不仅仅可以看成变量之间的依赖关系，同时，函数的思想方法将贯穿整个数学学习过程。

学生在学习了正比例函数、一次函数和反比例函数之后学习二次函数，这是对函数及其应用知识学习的深化和提高，是学生学习函数知识的过程中的一个重要环节，起到承上启下的作用，为学生进入高中后进一步学习函数知识奠定基础。

本章的内容在日常生活和生产实际中有着广泛的应用，是培养学生数学建模和数学思想的重要素材。

二次函数的图象是它性质的直观体现，对了解和掌握二次函数的性质具有形象直观的优势，二次函数作为初中阶段学习的重要函数模型，对理解函数的性质，掌握研究函数的方法，体会函数的思想是十分重要的。

本章的重点是二次函数的图象与性质的理解与掌握，应教会学生画二次函数图象，学会观察函数图象，借助函数图象来研究函数性质并解决相关的问题。

本章的难点是体会二次函数学习过程中所蕴含的数学思想方法，函数图象的特征和变换有及二次函数性质的灵活应用。

教学目标1.正确理解二次函数的概念，了解函数产生的背景，在原有的函数知识的基础上学习和掌握二次函数的概念和性质，能利用二次函数刻画事物的变化规律。

2.理解二次函数的意义，掌握二次函数的概念、图象和性质，知道二次函数是描述客观世界变化规律的重要数学模型。

3.了解二次函数与二次方程之间的关系，会利用函数图象求一些简单二次方程的近似解，了解二次函数模型及其意义，能准确、清晰、有条理地表述问题，会用二次函数知识分析问题，解决问题，使学生了解函数与方程是研究事物变化的重要工具。

4.培养学生的理性思维能力，辩证思维能力，分析问题和解决问题的能力，创新意识与探究能力，数学建模能力以及数学交流能力。

二次函数全章导学案(史上最全!)

导学案【2 】26.1.1二次函数（第一课时）一．预习检测案一般地,形如____________________________的函数,叫做二次函数.个中x是________,a是__________,b是___________,c是_____________．二．合作探讨案：问题1: 正方体的六个面是全等的正方形,假如正方形的棱长为x,表面积为y,写出y与x的关系. 问题2: n边形的对角线数d与边数n之间有如何的关系?提醒：多边形有n条边,则有几个极点？从一个极点动身,可以连几条对角线？问题3: 某工场一种产品如今的年产量是20件,筹划往后两年增长产量.假如每年都比上一年的产量增长x倍,那么两年后这种产品的数目y将随筹划所定的x的值而定,y与x之间的关系如何表示?问题4：不雅察以上三个问题所写出来的三个函数关系式有什么特色?小组交换.评论辩论得出结论：经化简后都具有的情势.问题5：什么是二次函数？形如.问题6：函数y=ax²+bx+c,当a.b.c知足什么前提时,(1)它是二次函数? (2)它是一次函数？(3)它是正比例函数？例1: 关于x的函数mmxmy-+=2)1(是二次函数, 求m的值.留意:二次函数的二次项系数必须是的数.三．达标测评案：1．下列函数中,哪些是二次函数?(1)y=3x-1 ; (2)y=3x2+2;(3)y=3x3+2x2;(4)y=2x2-2x+1; (5)y=x2-x(1+x);(6)y=x-2+x.2.若函数y＝(a－1)x2＋2x＋a2－1是二次函数,则( )A.a＝1B.a＝±1C.a≠1D.a≠－13.必定前提下,若物体活动的路段s(米)与时光t(秒)之间的关系为s＝5t2＋2t,则当t＝4秒时,该物体所经由的旅程为A.28米B.48米C.68米D.88米4.一个长方形的长是宽的2倍,写出这个长方形的面积与宽之间的函数关系式.5．一个圆柱的高级于底面半径,写出它的表面积Ｓ与半径Ｒ之间的关系式.6.n支球队参加竞赛,每两支之间进行一场竞赛.写出竞赛的场数m与球队数n之间的关系式.7.已知二次函数y=x²+px+q,当x=1时,函数值为4,当x=2时,函数值为- 5, 求这个二次函数的解析式.26.1.2 二次函数y ＝ax 2的图象与性质（第二课时）一．预习检测案：画二次函数y ＝x 2的图象．【提醒：绘图象的一般步骤：①列表;②描点;③连线（用腻滑曲线）．】由图象可得二次函数y ＝x 2的性质： 1．二次函数y ＝x 2是一条曲线,把这条曲线叫做______________．2．二次函数y ＝x 2中,二次函数a ＝_______,抛物线y ＝x 2的图象启齿__________． 3．自变量x 的取值规模是____________．4．不雅察图象,当两点的横坐标互为相反数时,函数y 值相等,所描出的各对应点关于________对称,从而图象关于___________对称．5．抛物线y ＝x 2与它的对称轴的交点（ , ）叫做抛物线y ＝x 2的_________．是以,抛物线与对称轴的交点叫做抛物线的_____________． 6．抛物线y ＝x 2有____________点（填“最高”或“最低”）．二．合作探讨案：例1 在统一向角坐标系中,画出函数y ＝12x 2,y ＝x 2,y ＝2x 2的图象．y ＝x 2的图象刚画过,再把它画出来．归纳：抛物线y ＝12x 2,y ＝x 2,y ＝2x 2的二次项系数a_______0;极点都是__________;对称轴是_________;极点是抛物线的最_________点（填“高”或“低”）．x … －3 －2 －1 0 1 2 3 … y ＝x 2……x … －4 －3 －2 －1 0 1 2 3 4 … y ＝12x 2 ……x … －2 －1.5 －1 －0.5 0 0.5 1 1.5 2 … y ＝2x 2……例2 请在统一向角坐标系中画出函数y ＝－x 2,y ＝－12x 2, y ＝－2x 2的图象．归纳：抛物线y ＝－x 2,y ＝－12x 2, y ＝－2x 2的二次项系数a______0,极点都是________, 对称轴是___________,极点是抛物线的最________点（填“高”或“低”）．总结：抛物线y ＝ax 2的性质1．抛物线y ＝x 2与y ＝－x 2关于________对称,是以,抛物线y ＝ax 2与y ＝－ax 2关于_______ 对称,启齿大小_______________．2．当a ＞0时,a 越大,抛物线的启齿越___________; 当a ＜0时,｜a ｜越大,抛物线的启齿越_________;是以,｜a ｜越大,抛物线的启齿越________,反之,｜a ｜越小,抛物线的启齿越________．三．达标测评案：1．填表：2．若二次函数y ＝ax 2的图象过点（1,－2）,则a 的值是___________． 3．二次函数y ＝(m －1)x 2的图象启齿向下,则m____________． 4．如图,① y ＝ax 2② y ＝bx 2 ③ y ＝cx 2 ④ y ＝dx 2比较a.b.c.d 的大小,用“＞”衔接． ___________________________________x … -4 -3 -2 -1 0 1 2 3 4 … y ＝-x 2… … y=－12x 2… … y ＝－2x 2 ……图象(草图) 启齿偏向极点对称轴有最高或最低点最值a ＞0当x ＝____时,y 有最___值,是______. a ＜0当x ＝____时,y 有最____值,是______.启齿偏向极点对称轴有最高或低点最值y ＝23x 2当x ＝____时,y 有最_____值,是______. y ＝－8x 25．函数y ＝37x 2的图象启齿向_______,极点是__________,对称轴是________,当x ＝___________时,有最_________值是_________． 6．二次函数y ＝mx22 m 有最低点,则m ＝___________．7．二次函数y ＝(k ＋1)x 2的图象如图所示,则k 的取值规模为___________．8．写出一个过点（1,2）的函数表达式_________________．26.1.3二次函数y ＝ax 2＋k 的图象与性质(第三课时)一．预习检测案：在统一向角坐标系中,画出二次函数y ＝x 2＋1,y ＝x 2－1的图象. 解:先列表描点并绘图1.不雅察图像得：2.可以发明,把抛物线y ＝x 2向______平移______个单位,就得到抛物线y ＝x 2＋1;把抛物线y ＝x 2向_______平移______个单位,就得到抛物线y ＝x 2－1. 3.抛物线y ＝x 2,y ＝x 2－1与y ＝x 2＋1的外形_____________.二．合作探讨案：1. y ＝ax 2y ＝ax 2＋k启齿偏向极点对称轴有最高(低)点最值a ＞0时,当x ＝______时,y 有最____值为________; a ＜0时,当x ＝______时,y 有最____值为________.增减性2.抛物线y ＝2x 2向上平移x … －3 －2 －1 0 1 2 3 … y ＝x 2＋1 … … y ＝x 2－1……启齿偏向极点对称轴有最高(低)点最值3个单位,就得到抛物线__________________;抛物线y ＝2x 2向下平移4个单位,就得到抛物线__________________.是以,把抛物线y ＝ax 2向上平移k(k ＞0)个单位,就得到抛物线_______________; 把抛物线y ＝ax 2向下平移m(m ＞0)个单位,就得到抛物线_______________. 3.抛物线y ＝－3x 2与y ＝－3x 2＋1是经由过程平移得到的,从而它们的外形__________, 由此可得二次函数y ＝ax 2与y ＝ax 2＋k 的外形__________________. 三．达标测评案：1.填表函数草图启齿偏向极点对称轴最值对称轴右侧的增减性y ＝3x 2y ＝－3x 2＋1 y ＝－4x 2－52.将二次函数y ＝5x 2－3向上平移7个单位后所得到的抛物线解析式为_________________. 3.写出一个极点坐标为(0,－3),启齿偏向与抛物线y ＝－x 2偏向相反,外形雷同的抛物线解析式____. 4.抛物线y ＝－13x 2－2可由抛物线y ＝－13x 2＋3向___________平移_________个单位得到的.5.抛物线y ＝4x 2－1与y 轴的交点坐标为_____________,与x 轴的交点坐标为_________.26.1.3二次函数y ＝a(x-h)2的图象与性质（第四课时）教授教养目的:会画二次函数y ＝a(x-h)2的图象,控制二次函数y ＝a(x-h)2的性质,并要会灵巧运用.一．预习检测案：画出二次函数y ＝－12(x ＋1)2,y －12(x －1)2的图象,并斟酌它们的启齿偏向.对称轴.极点以及最值.增减性.x … －4 －3 －2 －1 0 1 2 3 4 … y ＝－12(x ＋1)2… … y ＝－12(x －1)2……先列表:描点并绘图. 请在图上把抛物线y ＝－12x 2也画上去(草图).①抛物线y ＝－12(x ＋1)2 ,y ＝－12x 2,y ＝－12(x －1)2的外形大小____________.②把抛物线y ＝－12x 2向左平移_______个单位,就得到抛物线y ＝－12(x ＋1)2 ;把抛物线y ＝－12x 2向右平移_______个单位,就得到抛物线y ＝－12(x ＋1)2 .总结常识点：函数启齿偏向极点对称轴最值增减性y ＝－12(x ＋1)2y ＝－12(x －1)21. y＝ax2y＝ax2＋k y＝a (x-h)2启齿偏向极点对称轴最值增减性(对称轴左侧)3.对于二次函数的图象,只要｜a｜相等,则它们的外形_________,只是_________不同.三．达标测评案：1.抛物线y＝4 (x－2)2与y轴的交点坐标是___________,与x轴的交点坐标为________.2.把抛物线y＝3x2向右平移4个单位后,得到的抛物线的表达式为____________________.3.将抛物线y＝－13(x－1)2向右平移2个单位后,得到的抛物线解析式为____________.4.抛物线y＝2 (x＋3)2的启齿___________;极点坐标为____________;对称轴是_________; 当x＞－3时,y______________;当x＝－3时,y有_______值是_________.26.1.3二次函数y＝a(x－h)2＋k的图象与性质（第五课时）一．预习检测案：画出函数y＝－12(x＋1)2－1的图象,指出它的启齿偏向.对称轴及极点.最值.增减性.列表二．合作探讨案2.把抛物线y＝－12x2向____平移_____个单位,再向____平移_______个单位,就得到抛物线y＝－12(x＋1)2－1.总结常识点： 1.填表（a>0)函数关系式图象(草图) 启齿偏向极点对称轴最值对称轴右侧的增减性y＝1 2 x2y＝－5 (x＋3)2 y＝3 (x－3)2x …－4 －3 －2 －1 0 1 2 …y＝－12(x＋1)2－1 ……函数启齿偏向极点对称轴最值增减性y＝－12(x＋1)2－12.用配办法求抛物线y＝ax2＋bx＋c(a≠0)的极点与对称轴.二．教室探讨案：(a>0)y＝ax2y＝ax2＋k y＝a(x－h)2y＝a(x－h)2＋k y＝ax2＋bx＋c 启齿偏向极点对称轴最值增减性(对称轴左侧)三.常识点运用例1 求y＝x2－2x－3与x轴交点坐标.例2 求抛物线y＝x2－2x－3与y轴交点坐标.3.a.b.c以及△＝b2－4ac对图象的影响.(1)a决议:启齿偏向.外形 (2)c决议与y轴的交点为(0,c) (3)a与－b2a配合决议b的正负性 (4)△＝b2－4ac⎪⎩⎪⎨⎧<=>轴没有交点与轴有一个交点与轴有两个交点与xxx例3 如图,由图可得:a_______0,b_______0,c_______0,△______0例4 已知二次函数y＝x2＋kx＋9.①当k为何值时,对称轴为y轴;②当k为何值时,抛物线与x轴有两个交点;③当k为何值时,抛物线与x轴只有一个交点.四．达标测评案：1. 用极点坐标公式和配办法求二次函数y＝12x2－2－1的极点坐标.2.二次函数y＝2x2＋bx＋c的极点坐标是(1,－2),则b＝________,c＝_________.3.已知二次函数y＝－2x2－8x－6,当________时,y随x的增大而增大;当x＝________时,y 有______值是_____.4.二次函数y＝－x2＋mx中,当x＝3时,函数值最大,求其最大值.5.求抛物线y＝2x2－7x－15与x轴交点坐标__________,与y轴的交点坐标为_______.6.抛物线y＝4x2－2x＋m的极点在x轴上,则m＝__________.26.1.5 用待定系数法求二次函数的解析式（第七课时）3.已知抛物线与x轴有两个交点(或已知抛物线与x轴交点的横坐标),设两根式:y＝a(x－x1)(x－x2) .(个中x1.x2是抛物线与x轴交点的横坐标)现实问题中求二次函数解析式：例4 要建筑一个圆形喷水池,在池中间竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中间的程度距离为1m处达到最高,高度为3m,水柱落地处离池中间3m,水管应多长？三．达标检测案：1.已知二次函数的图象过(0,1).(2,4).(3,10)三点,求这个二次函数的关系式.2.已知二次函数的图象的极点坐标为(－2,－3),且图像过点(－3,－2),求这个二次函数的解析式.3.已知二次函数y＝ax2＋bx＋c的图像与x轴交于A(1,0),B(3,0)两点,与y轴交于点C(0,3),求二次函数的极点坐标.4.如图,在△ABC中,∠B＝90°,AB＝12mm,BC＝24mm,动点P从点A开端沿边AB向B以2mm/s 的速度移动,动点Q从点B开端沿边BC向C以4mm/s的速度移动,假如P.Q分离从A.B同时动身,那么△PBQ的面积S随动身时光t若何变化？写出函数关系式及t的取值规模.26.2 用函数的不雅点看一元二次方程（第八课时）教授教养目的:1.知道二次函数与一元二次方程的关系.2.会用一元二次方程ax 2＋bx ＋c ＝0根的判别式△＝b 2－4ac 断定二次函数y ＝ax 2＋bx ＋c 与x 轴的公共点的个数. 一．预习检测案：1.问题:如图,以40m/s 的速度将小球沿与地面成30°角的偏向击出时,球的飞翔路线将是一条抛物线.假如不斟酌空气阻力,球的飞翔高度h(单位:m)与飞翔时光t(单位:s)之间具有关系h ＝20t －5t 2.斟酌以下问题:(1)球的飞翔高度可否达到15m ？如能,须要若干飞翔时光？ (2)球的飞翔高度可否达到20m ？如能,须要若干飞翔时光？ (3)球的飞翔高度可否达到20.5m ？为什么？ (4)球从飞出到落地要用若干时光？2.不雅察图象:(1)二次函数y ＝x 2＋x －2的图象与x 轴有____个交点,则一元二次方程x 2＋x －2＝0的根的判别式△＝_______0;(2)二次函数y ＝x 2－6x ＋9的图像与x 轴有_ __个交点,则一元二次方程x 2－6x ＋9＝0的根的判别式△＝_____0;(3)二次函数y ＝x 2－x ＋1的图象与x 轴________公共点,则一元二次方程x 2－x ＋1＝0的根的判别式△_______0.二．合作探讨案：1.已知二次函数y ＝－x 2＋4x 的函数值为3,求自变量x 的值,可以看作解一元二次方程__________________.反之,解一元二次方程－x 2＋4x ＝3又可以看作已知二次函数__________________的函数值为3的自变量x 的值.一般地:已知二次函数y ＝ax 2＋bx ＋c 的函数值为m,求自变量x 的值,可以看作解一元二次方程 ax 2＋bx ＋c ＝m.反之,解一元二次方程ax 2＋bx ＋c ＝m 又可以看作已知二次函数y ＝ax 2＋bx ＋c 的值为m 的自变量x 的值.2.二次函数y ＝ax 2＋bx ＋c 与x 轴的地位关系:一元二次方程ax 2＋bx ＋c ＝0的根的判别式△＝b 2－4ac.(1)当△＝b 2－4ac ＞0时抛物线y ＝ax 2＋bx ＋c 与x 轴有两个交点; (2)当△＝b 2－4ac ＝0时抛物线y ＝ax 2＋bx ＋c 与x 轴只有一个交点; (3)当△＝b 2－4ac ＜0时抛物线y ＝ax 2＋bx ＋c 与x 轴没有公共点.QPCBA用总长为60m 的篱笆围成矩形场地,矩形面积S 随矩形一边长l 的变化而变化,当l 是若干4．一块三角形废料如图所示,∠A ＝30°,∠C ＝90°,AB ＝12．用这块废料剪出一个长方形何订价才能使利润最大？剖析：调剂价钱包括涨价和降价两种情形,用如何的等量关系呢？解：（1）设每件涨价x元,则每礼拜少卖_________件,现实卖出_________件,设商品的利润为y元．（2）设每件降价x元,则每礼拜多卖_________件,现实卖出__________件．四.达标测评案：1．某种商品每件的进价为30元,在某段时光内若以每件x元出售,可卖出（100－x）件,应若何订价才能使利润最大？2．蔬菜基地栽种某种蔬菜,由市场行情剖析知,1月份至6月份这种蔬菜的上市时光x（月份）与市场售价P（元/千克）的关系如下表：上市时光x/（月份）1 2 3 4 5 6市场售价P（元/千克）10.5 9 7.5 6 4.5 3这种蔬菜每千克的栽种成本y（元/千克）与上市时光x（月份）知足一个函数关系,这个函数的图象是抛物线的一段（如图）．（1）写出上表中表示的市场售价P（元/千克）关于上市时光x（月份）的一次函数关系式;（2）若图中抛物线过A.B.C三点,写出抛物线对应的函数关系式;（3）由以上信息剖析,哪个月上市出售这种蔬菜每千克的收益最大？最大值为若干？（收益＝市场售价－栽种成本）3. 某宾馆客房部有60个房间供旅客栖身,当每个房间的订价为天天200元时,房间可以住满．当每个房间天天的订价每增长10元时,就会有一个房间空间．对有旅客入住的房间,宾馆需对每个房间天天支出20元的各类费用．设每个房间天天的订价增长x元,求：（1）房间天天入住量y（间）关于x（元）的函数关系式;（2）该宾馆天天的房间收费z（元）关于x（元）的函数关系式;（3）该宾馆客房部天天的利润w（元）关于x（元）的函数关系式,当每个房间的订价为若干元时,w有最大值？最大值是若干？。

二次函数导学案(全章)之欧阳治创编

【学习重点】掌握二次函数的概念并能利用概念解答相关的题型。

【课时类型】概念课【学习过程】一、学习准备1．函数的定义：在某个变化过程中，有两个变量x 和y，如果给定一个x值，相应地就确定了一个y 值，那么我们称是的函数，其中是自变量，是因变量。

2．一次函数的关系式为y=(其中k、b是常数，且k≠0)；正比例函数的关系式为y＝(其中k是的常数)；反比例函数的关系式为y=(k是的常数)。

二、解读教材——数学知识源于生活3．某果园有100棵橙子树，每一棵树平均结600个橙子。

现准备多种一些橙子树以提高产量，但是如果多种树，那么树之间的距离和每一棵树所接受的阳光就会减少。

根据经验估计，每多种一棵树，平均每棵树就会少结5个橙子。

假设果园增种x棵橙子树，那么果园共有棵橙子树，这时平均每棵树结个橙子，如果果园橙子的总产量为y个，那么y=。

4．如果你到银行存款100元，设人民币一年定期储蓄的年利率是x ，一年到期后,银行将本金和利息自动按一年定期储蓄转存。

那么你能写出两年后的本息和y(元)的表达式(不考虑利息税)吗？。

它就是二次函数的一般形式，理解并熟记几遍。

例1 下列函数中，哪些是二次函数？ (1)2321x y +-=(2)112+=x y (3)x y 222+= (4)251t t s ++= (5)22)3(x x y -+= (6)210r s π=即时练习(1)2x y =(2)252132+-=x x y (3))1(+=x x y (4)1132--=）（x y (5)cax y -=2(6)12+=x s 三、挖掘教材6．对二次函数定义的深刻理解及运用例2 若函数1232++=+-kx x y k k 是二次函数，求k 的值。

二次函数导学案全章

二次函数导学案全章新人教版九年级数学第二十二章导学案22.1.1 二次函数主备人：刘春友审核人：梅耀发审批人：李春山执教人：刘春友使用时间：2021.09 班级：九年一班课题：22.1.1 二次函数课时：第一课时课型：新授课学习目标：1. 了解二次函数的有关概念．2. 会确定二次函数关系式中各项的系数。

3. 通过对实际问题的分析，体会二次函数的意义，确定函数的关系式。

学习重点：理解二次函数的定义。

学习难点：确定实际问题中二次函数的关系式。

学法指导：利用小组合作、交流、探究，类比一次函数来学习二次函数，注意知识结构的建立。

导学过程：一、课前测评1.函数2.正比例函数的一般形式一次函数的一般形式3.一元二次方程的一般形式二、自主学习：看引言中正方体的表面积的问题正方形的六个面是全等的正方形，设正方体的棱长为x，表面积为y，显然对于x的每一个值，y都有一个对应值，即y是x的函数，他们的具体关系可以表示为 .问题1.n个球队参加比赛，每两队之间进行一场比赛．比赛的场次数m与球队数n有什么关系？1问题2.某种产品现在的年产量是20t,计划今后两年增加产量。

如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定，y 与x之间的关系应怎样表示？观察上述函数关系有哪些共同之处？。

归纳：一般地，形如，（a,b,c是常数，且a ）的函数叫做二次函数。

其中x是自变量，a是__________，b是___________，c是_____________．巩固二次函数的定义例某小区要修建一块矩形绿地，设矩形的长为x m，宽为 y m，面积为 S m 2（x＞y）．（1）如果用 18 m 的建筑材料来修建绿地的边缘（即周长），求 S 与 x 的函数关系，并求出 x 的取值范围．（2）根据小区的规划要求，所修建的绿地面积必须是 18 m 2，在满足（1）的条件下，矩形的长和宽各为多少 m ？2三、课堂练习：2232y?6xy??3x?5y?x?2x；1．观察：①；②；③y＝200x＋400x＋200；④⑤y?x2?12?3y?x?1?x2??x；⑥．这六个式子中二次函数有。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

导学案之宇文皓月创作26.1.1二次函数（第一课时）一．预习检测案一般地，形如____________________________的函数，叫做二次函数。

其中x是________，a是__________，b是___________，c是_____________．二．合作探究案：问题1: 正方体的六个面是全等的正方形,如果正方形的棱长为x,概况积为y,写出y与x的关系。

问题2: n边形的对角线数d与边数n之间有怎样的关系?提示：多边形有n条边，则有几个顶点？从一个顶点出发，可以连几条对角线？问题3: 某工厂一种产品现在的年产量是20件,计划今后两年增加产量.如果每年都比上一年的产量增加x倍,那么两年后这种产品的数量y将随计划所定的x的值而定,y与x之间的关系怎样暗示?问题4：观察以上三个问题所写出来的三个函数关系式有什么特点?小组交流、讨论得出结论：经化简后都具有的形式。

问题5：什么是二次函数？形如。

问题6：函数y=ax²+bx+c，当a、b、c满足什么条件时，(1)它是二次函数?(2)它是一次函数？(3)它是正比例函数？例1: 关于x的函数mmxmy-+=2)1(是二次函数, 求m的值.注意:二次函数的二次项系数必须是的数。

三．达标测评案：1．下列函数中,哪些是二次函数?(1)y=3x-1 ; (2)y=3x2+2;(3)y=3x3+2x2;(4)y=2x2-2x+1; (5)y=x2-x(1+x);(6)y=x-2+x.2.若函数y＝(a－1)x2＋2x＋a2－1是二次函数,则( )A.a＝1B.a＝±1C.a≠1D.a≠－13.一定条件下,若物体运动的路段s(米)与时间t(秒)之间的关系为s＝5t2＋2t,则当t＝4秒时,该物体所经过的路程为A.28米B.48米C.68米D.88米4.一个长方形的长是宽的2倍,写出这个长方形的面积与宽之间的函数关系式.5．一个圆柱的高等于底面半径，写出它的概况积Ｓ与半径Ｒ之间的关系式。

6、n支球队介入角逐，每两支之间进行一场角逐。

写出角逐的场数m与球队数n之间的关系式。

7、已知二次函数y=x²+px+q,当x=1时,函数值为4,当x=2时,函数值为-5,求这个二次函数的解析式.26.1.2 二次函数y ＝ax 2的图象与性质（第二课时）一．预习检测案：画二次函数y ＝x 2的图象．【提示：画图象的一般步调：①列表；②描点；③连线（用平滑曲线）．】由图象可得二次函数y ＝x 2的性质：1．二次函数y ＝x 2是一条曲线，把这条曲线叫做______________． 2．二次函数y ＝x 2中，二次函数a ＝_______，抛物线y ＝x 2的图象开口__________．3．自变量x 的取值范围是____________．4．观察图象，当两点的横坐标互为相反数时，函数y 值相等，所描出的各对应点关于________对称，从而图象关于___________对称．5．抛物线y ＝x 2与它的对称轴的交点（，）叫做抛物线y ＝x 2的_________．因此，抛物线与对称轴的交点叫做抛物线的_____________． 6．抛物线y ＝x 2有____________点（填“最高”或“最低”）．二．合作探究案：例1 在同一直角坐标系中，画出函数y ＝12x 2，y ＝x 2，y ＝2x 2的图象．y ＝x 2的图象刚画过，再把它画出来．归纳：抛物线y ＝12x 2，y ＝x 2，y ＝2x 2的二次项系数a_______0；顶点都是__________；对称轴是_________；顶点是抛物线的最_________点（填“高”或“低”）．例2 请在同一直角坐标系中画出函数y ＝－x 2，y ＝－12x 2， y ＝－2x 2的图象．归纳：抛物线y ＝－x 2，y ＝－12x 2， y ＝－2x 2的二次项系数a______0，顶点都是________，对称轴是___________，顶点是抛物线的最________点（填“高”或“低”）．总结：抛物线y ＝ax 2的性质1．抛物线y ＝x 2与y ＝－x 2关于________对称，因此，抛物线y ＝ax 2与y ＝－ax 2关于_______x … －3 －2 －1 0 1 2 3 … y ＝x 2……x…－4－3 －2 －1 0 1 2 3 4 … y ＝12x 2... (x)… －2 －1.5 －1 －0.50 0.5 1 1.5 2… y ＝2x 2……x … -4 -3 -2 -1 0 1 2 3 4 … y ＝-x 2… …y=－12x 2… … y ＝－2x 2……对称，开口大小_______________．2．当a ＞0时，a 越大，抛物线的开口越___________；当a ＜0时，｜a ｜越大，抛物线的开口越_________；因此，｜a ｜越大，抛物线的开口越________，反之，｜a ｜越小，抛物线的开口越________．三．达标测评案： 1．填表：2．若二次函数y ＝ax 2的图象过点（1，－2），则a 的值是___________． 3．二次函数y ＝(m －1)x 2的图象开口向下，则m____________． 4．如图，① y ＝ax 2② y ＝bx 2③ y ＝cx 2 ④ y ＝dx 2比较a 、b 、c 、d 的大小，用“＞”连接．___________________________________5．函数y ＝37x 2的图象开口向_______，顶点是__________，对称轴是________，当x ＝___________时，有最_________值是_________． 6．二次函数y ＝mx22 m 有最低点，则m ＝___________．7．二次函数y ＝(k ＋1)x 2的图象如图所示，则k 的取值范围为___________．8．写出一个过点（1，2）的函数表达式_________________．26.1.3二次函数y ＝ax 2＋k 的图象与性质(第三课时)一．预习检测案：在同一直角坐标系中,画出二次函数y ＝x 2＋1,y ＝x 2－1的图象. 解:先列表描点并画图1.观察图像得：2.可以发现,把抛物线y ＝x 2向______平移______个单位,就得到抛物线y ＝x 2＋1;把抛物线y ＝x 2向_______平移______个单位,就得到抛物线y ＝x 2－图象(草图) 开口方向顶点对称轴有最高或最低点最值a ＞0当x ＝____时,y 有最___值,是______.a ＜0当x ＝____时,y 有最____值,是______.开口方向顶点对称轴有最高或低点最值y ＝23x 2当x ＝____时,y 有最_____值,是______. y ＝－8x 2x … －3 －2 －1 0 1 2 3 … y ＝x 2＋1 … … y ＝x 2－1……开口方向顶点对称轴有最高(低)点最值y ＝x 2y ＝x 2－1 y ＝x 2＋12.将二次函数y＝5x2－3向上平移7个单位后所得到的抛物线解析式为y＝－12(x－1)2……先列表:描点并画图. 请在图上把抛物线y＝－12x2也画上去(草图).①抛物线y＝－12(x＋1)2,y＝－12x2,y＝－12(x－1)2的形状大小____________.②把抛物线y＝－12x2向左平移_______个单位,就得到抛物线y＝－12(x＋1)2 ;把抛物线y＝－12x2向右平移_______个单位,就得到抛物线y＝－12(x＋1)2 .总结知识点：1. y＝ax2y＝ax2＋k y＝a (x-h)2开口方向顶点对称轴最值增减性(对称轴左侧)3.对于二次函数的图象,只要｜a｜相等,则它们的形状_________,只是_________分歧.三．达标测评案：1.抛物线y＝ 4(x－2)2与y轴的交点坐标是___________,与x轴的交点坐标为________.2.把抛物线y＝3x2向右平移4个单位后,得到的抛物线的表达式为____________________.3.将抛物线y＝－13(x－1)2向右平移2个单位后,得到的抛物线解析式为____________.4.抛物线y＝2 (x＋3)2的开口___________;顶点坐标为____________;对称轴是_________;当x＞－3时,y______________;当x＝－3时,y有_______值是_________.26.1.3二次函数y＝a(x－h)2＋k的图象与性质（第五课时）一．预习检测案：画出函数y＝－12(x＋1)2－1的图象,指出它的开口方向.对称轴及顶点.最值.函数开口方向顶点对称轴最值增减性y＝－12(x＋1)2y＝－12(x－1)2函数关系式图象(草图) 开口方向顶点对称轴最值对称轴右侧的增减性y＝1 2 x2y＝－5 (x＋3)2 y＝3 (x－3)2增减性.列表1.画二次函数y＝12x2－6x＋21的图象.(解:y＝12x2－6x＋21配成顶点式为_______________________.)2.用配方法求抛物线y＝ax2＋bx＋c(a≠0)的顶点与对称轴.二．课堂探究案：(a>0)y＝ax2y＝ax2＋k y＝a(x－h)2y＝a(x－h)2＋k y＝ax2＋bx＋c 开口方向顶点对称轴最值增减性(对称轴左侧)三.知识点应用例1 求y＝x2－2x－3与x轴交点坐标.例2 求抛物线y＝x2－2x－3与y轴交点坐标.3.a.b.c以及△＝b2－4ac对图象的影响.(1)a决定:开口方向.形状 (2)c决定与y轴的交点为(0,c)(3)a与－b2a 共同决定b的正负性 (4)△＝b2－4ac⎪⎩⎪⎨⎧<=>轴没有交点与轴有一个交点与轴有两个交点与xxx例3 如图,由图可得:a_______0,b_______0,c_______0,△______0例4 已知二次函数y＝x2＋kx＋9.①当k为何值时,对称轴为y轴；②当k为何值时,抛物线与x轴有两个交点；③当k为何值时,抛物线与x轴只有一个交点.四．达标测评案：1. 用顶点坐标公式和配方法求二次函数y＝12x2－2－1的顶点坐标.2.二次函数y＝2x2＋bx＋c的顶点坐标是(1,－2),则b＝________,c＝_________.3.已知二次函数y＝－2x2－8x－6,当________时,y随x的增大而增大;当x＝________时,y有______值是_____.4.二次函数y＝－x2＋mx中,当x＝3时,函数值最大,求其最大值.5.求抛物线y＝2x2－7x－15与x轴交点坐标__________,与y轴的交点坐标为_______.6.抛物线y＝4x2－2x＋m的顶点在x轴上,则m＝__________.26.1.5 用待定系数法求二次函数的解析式（第七课时）教学目标:1.会用待定系数法求二次函数的解析式;2.实际问题中求二次函数解析式.一．预习检测案：1.已知二次函数y＝x2＋x＋m的图象过点(1,2),则m的值为________________.x … 3 4 5 6 7 8 9 …y＝12x2－6x＋21 ……三．达标检测案：1.已知二次函数的图象过(0,1).(2,4).(3,10)三点,求这个二次函数的关系式.2.已知二次函数的图象的顶点坐标为(－2,－3),且图像过点(－3,－2),求这个二次函数的解析式.3.已知二次函数y＝ax2＋bx＋c的图像与x轴交于A(1,0),B(3,0)两点,与y轴交于点C(0,3),求二次函数的顶点坐标.4.如图,在△ABC中,∠B＝90°,AB＝12mm,BC＝24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动,动点Q从点B开始沿边BC向C以4mm/s的速度移动,如果P.Q分别从A.B同时出发,那么△PBQ的面积S随出发时间t如何变更？写出函数关系式及t的取值范围.26.2 用函数的观点看一元二次方程（第八课时）教学目标:1.知道二次函数与一元二次方程的关系.2.会用一元二次方程ax2＋bx＋c＝0根的判别式△＝b2－4ac判断二次函数y＝ax2＋bx＋c与x轴的公共点的个数.一．预习检测案：1.问题:如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线.如果不考虑空气阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系h＝20t－5t2.考虑以下问题:(1)球的飞行高度能否达到15m ？如能,需要多少飞行时间？(2)球的飞行高度能否达到20m？如能,需要多少飞行时间？(3)球的飞行高度能否达到20.5m？为什么？(4)球从飞出到落地要用多少时间？2.观察图象:(1)二次函数y＝x2＋x－2的图象与x轴有____个交点,则一元二次方程x2＋x－2＝0的根的判别式△＝_______0;(2)二次函数y＝x2－6x＋9的图像与x轴有_ __个交点,则一元二次方程x2－6x＋9＝0的根的判别式△＝_____0;(3)二次函数y＝x2－x＋1的图象与x轴________公共点,则一元二次方程x2－x＋1＝0的根的判别式△_______0.二．合作探究案：1.已知二次函数y＝－x2＋4x的函数值为3,求自变量x的值,可以看作解一元二次方程__________________.反之,解一元二次方程－x2＋4x＝3又可以看作已知二次函数__________________的函数值为3的自变量x的值.一般地:已知二次函数y＝ax2＋bx＋c的函数值为m,求自变量x的值,可以看作解一元二次方程 ax2＋bx＋c＝m.反之,解一元二次方程ax2＋bx＋c＝m又可以看作已知二次函数y＝ax2＋bx＋c的值为m的自变量x的值.2.二次函数y＝ax2＋bx＋c与x轴的位置关系:一元二次方程ax2＋bx＋c＝0的根的判别式△＝b2－4ac.(1)当△＝b2－4ac＞0时抛物线y＝ax2＋bx＋c与x轴有两个交点;(2)当△＝b2－4ac＝0时抛物线y＝ax2＋bx＋c与x轴只有一个交点;(3)当△＝b2－4ac＜0时抛物线y＝ax2＋bx＋c与x轴没有公共点.八.课后训练1.已知抛物线y＝x2－2kx＋9的顶点在x轴上,则k＝____________.2.已知抛物线y＝kx2＋2x－1与x轴有两个交点,则k的取值范围___________.26.3. 实际问题与二次函数-1（第九课时）教学目标：几何问题中应用二次函数的最值．一．预习检测案：1．抛物线y＝－(x＋1)2＋2中，当x＝___________时，y有_______值是__________．2．抛物线y＝12x2－x＋1中，当x＝___________时，y有_______值是__________．3．抛物线y＝ax2＋bx＋c（a≠0）中，当x＝___________时，y有_______值是__________．二．合作探究案：（P22的探究）而变更，当l是多少时，场地的面积S最大？这种蔬菜每千克的种植成本y（元/千克）与上市时间x（月份）满足一个函数关系，这个函数的图象是抛物线的一段（如图）．（1）写出上表中暗示的市场售价P（元/千克）关于上市时间x （月份）的一次函数关系式；（2）若图中抛物线过A、B、C三点，写出抛物线对应的函数关系式；（3）由以上信息分析，哪个月上市出售这种蔬菜每千克的收益最大？最大值为多少？（收益＝市场售价－种植成本）3. 某宾馆客房部有60个房间供游客居住，当每个房间的定价为每天200元时，房间可以住满．当每个房间每天的定价每增加10元时，就会有一个房间空间．对有游客入住的房间，宾馆需对每个房间每天支出20元的各种费用．设每个房间每天的定价增加x元，求：（1）房间每天入住量y（间）关于x（元）的函数关系式；（2）该宾馆每天的房间收费z（元）关于x（元）的函数关系式；（3）该宾馆客房部每天的利润w（元）关于x（元）的函数关系式，当每个房间的定价为多少元时，w有最大值？最大值是多少？。