2018年成都市锦江区八年级下期期末试题及答案

合集下载

2018-2019学年四川省成都市锦江区八年级(下)期末物理试卷

2018-2019学年四川省成都市锦江区八年级（下）期末物理试卷一、单项选择题（共30分，每小题2分）1．（2分）下列有关力的说法中，正确的是（）A．人用手推墙壁，人先推墙，墙再对人施力B．用力挤压玻璃瓶，玻璃瓶不会发生形变C．只要物体是运动的，就一定有力对它作用D．物体运动状态改变了，一定是受到了力的作用2．（2分）下列情景中，力使物体发生形变的是（）A ．被钢尺击打的棋子飞出B ．射箭运动员用力将弓拉弯C．小钢球的曲线运动D ．苹果在重力作用下下落3．（2分）关于惯性，以下说法正确的是（）A．歼击机战斗前抛掉副油箱是为了减小惯性、提高灵活性B．物体在失重时，惯性消失C．汽车驾驶员和乘客系安全带，是为了减小汽年行驶中人的惯性D．高速公路严禁超速，是因为速度越大惯性越大4．（2分）下列现象或事例中，能说明大气压存在的是（）A ．客机升空B ．帕斯卡裂桶实验C ．橡皮膜外凸D ．用吸盘挂钩挂物品5．（2分）如图所示，在探究液体压强特点的过程中，将微小压强计的金属盒放在水中，下列做法能够使压强计U 形管两边液面的高度差减小的是（）A．将压强计的金属盒放在同样深度的食盐水中B．将压强计的金属盒向下移动一段距离C．将压强计的金属盒在原位置转动180°D．将压强计的金属盒向上移动一段距离6．（2分）关于弹力，下列说法中错误的是（）A．在桌面上的物体对桌面产生的压力就是物体的重力B．平常所说的压力、支持力等都属于弹力C．跳水比赛时，是跳板的弹力把运动员弹起的D．两个物体直接接触且发生弹性形变时才会产生弹力7．（2分）下列叙述正确的是（）A．铅球运动员将铅球推出去，运动员对铅球没有做功B．货车司机沿着斜面将汽油桶推上车厢，司机对汽油桶做了功C．汽车在水平公路上匀速行驶，汽车所受重力对汽车做了功D．运动员将杠铃举着静止不动，运动员对杠铃做了功8．（2分）以下事例中属于有害摩擦的是（）A．自行车刹车时，刹车闸与车轮间的摩擦B．写字时笔与纸之间的摩擦C．载人飞船升空时，飞船与空气的摩擦D．黑板擦与黑板之间的摩擦9．（2分）关于功率，下列说法正确的是（）A．单位时间内做的功越多，其功率越大B．物体做功时间越长，功率越大C．使用功率大的机械做功时一定省力D．作用力越大，功率也越大10．（2分）根据如图对应情景，下列说法中，正确的是（）A ．F与f合力方向与重力G方向垂直B ．风力发电将风能转化为风车叶片的电能C ．螺旋钻头上的螺旋相当于斜面，费距离D ．将A管稍向右倾，稳定后比B管中的水面低11．（2分）下列估值中，最接近实际的是（）A．一名初二学生从教室一楼爬到三楼功率大约为1000WB．成年人双脚站在水平地面上对地面的压强大约为200PaC．一个标准大气压大约能够支持760mm高的水柱D．用手把2个鸡蛋举高1m，手对鸡蛋做的功大约为1J12．（2分）关于简单机械，下列说法正确的是（）A．功的原理只适用于杠杆和滑轮B．给滑轮的轮和轴之间滴加润滑油能提高滑轮组的机械效率C．汽车方向盘是一个轮轴，其本质是个等臂杠杆D．不论是定滑轮还是动滑轮，其轮心都相当于杠杆的支点13．（2分）如图，在伽利略理想实验中，小球每次均从斜面a点自由滚下，分别经过图中b，c，d各位置，关于小球的动能、重力势能、机械能描述正确的是（）A．小球的重力势能一直在减小B．在d点的重力势能小于在c点的重力势能C．从b点运动到c点的过程中，动能转化为重力势能D．从a到b小球速度越来越大，机械能越来越大14．（2分）如图，将小球竖直向上抛出，小球在A 、B 、C 三点的速度分别为v A ＝6m/s 、v B ＝4m/s 、v C ＝0（不考虑空气阻力）。

2017 2018四川省成都市锦江区八年级下期末物理试卷

2017-2018学年四川省成都市锦江区八年级（下）期末物理试卷一、单项选择题（每题2分，共30分）1．（2分）如图所示的四个实例中，目的是为了减小摩擦的是（）．运动员在手上涂抹镁粉 A．浴室地砖表面有凹凸花纹B．陆地冰球鞋上安装滚轮。

C．汽车轮胎上安装防滑链D2．（2分）关于力，下列说法正确的是（）A．自行车刹车时要用力捏闸，这是通过增加压力的方法来增大摩擦力的B．吃饭时，筷子与食物之间的摩擦是有害的C．对物体施加的力大小相同，力的作用效果一定相同D．固体对物体的压力一定等于它的重力3．（2分）下列器材或装置中，利用连通器原理工作的是（）． B注射A自制气压计．.器．乳牛自动喂水器 DC ．吸尘器4．（2分）关于力对物体做功，下列说法正确的是（）A．作用在物体上的力越大，做功越多B．用力扛着一袋米，沿水平方向前进，人对米袋做了功C．在光滑冰面上匀速滑行的冰块，是因为有力对它做功才一直运动的D．推出后的铅球在空中飞行过程中，运动员对铅球没有做功5．（2分）如图所示，能够运用流体压强与流速关系的知识来解释的是（）．马德堡半球实验A．乘客要在站台上的安全线外等候B．火箭升空 C.．壁虎靠脚上的“吸盘”在墙上爬行 D6．（2分）如图所示，人在水平路面上骑车，以下关于物体受力的描述正确的是（）A．自行车受到路面的支持力B．路面受到人的压力C．人受到路面的支持力D．人和自行车都受到路面的摩擦力7．（2分）下列估测正确的是（）A．一个鸡蛋的重大约为50NB．中学生双脚站立对水平地面压强大约为1.5×104PaC．大气压对你的一只大拇指指甲表面的压力大约为1000N D．一本八下的物理课本从课桌上掉落到地面，课本重力做的功约为150J8．（2分）关于大气压强，下列说法正确的是（）A．大气由于重力作用只向下产生大气压强B．同一地点的位置和海拔高度不变，所以该处的大气压是不变的.C．在其它条件相同时，海拔高度越高，大气压的值越小D．利用公式P＝ρgh，测出地面大气密度和压强，就可以算出大气层的高度h9．（2分）通过初中物理八年级下册学习，我们知晓了许多伟大的科学家，领略了他们卓越的成就。

2017-2018年四川省成都市锦江区英语八年级下期期未学业质量测试【无听力部分含答案-含解析】

八年级下学期期末英语测试A 卷（共 100 分）第二部分基础知识运用（共30 小题，计 40 分）六、单项选择。

A. 请从下面各题 A 、 B、 C 三个选须中选择正确答案。

（共10小题，每题 1 分；计 10 分）3l. John is _________ honest boy. He is telling the truth.A. aB. anC. the32. Many people think the government should provide food and water _________ the homeless.A. forB. withC. to33. We shouldn’ t only think about _________ since we are in a team.A. usB. oursC. ourselves34. --We need to make a notice to ask people to protect the environment.--That sounds good. I can help you to _________ them _________ on the bulletin board.A. hand...outB. fix...upC. put...up35. --Mum, could I buy this iPad?--Sorry, it’ s too expensive. But we can buy _________ one, and I think it is as good as this one.A. a cheapB. a cheaperC. the cheapest36.--Did you see a young man with glasses pass by?--Sorry, I _________ with my friend.A. talkedB. am talkingC. was talking37.Of all the classics here. I _________ like Cinderella, I’ ve read it a couple of times.A. mostlyB. simplyC. especially38.The pandas were eating bamboo _________ their keepers came into the cage.A. whileB. whenC. after39.I _________ the two reports carefully and found them almost the same.A. comparedB. collectedC. competed40.--I've been to the nature museum in Beijing a few times.--_____It is a great place.A. So do I.B. So have I.C. Neither have I.B. 补全对话。

{3套试卷汇总}2018年成都市八年级下学期期末考前模拟物理试题

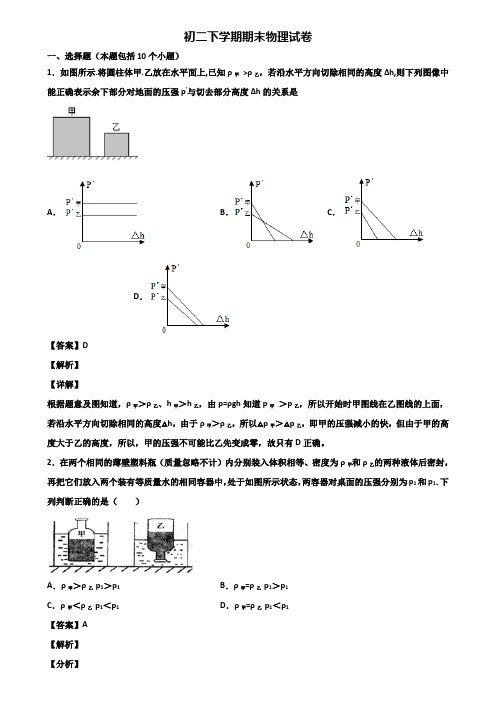
初二下学期期末物理试卷一、选择题（本题包括10个小题）1．如图所示.将圆柱体甲.乙放在水平面上,已知ρ甲>ρ乙，若沿水平方向切除相同的高度Δh,则下列图像中能正确表示余下部分对地面的压强p′与切去部分高度Δh的关系是A．B．C．D．【答案】D【解析】【详解】根据题意及图知道，ρ甲＞ρ乙、h甲＞h乙，由p=ρgh知道p甲＞p乙，所以开始时甲图线在乙图线的上面，若沿水平方向切除相同的高度△h，由于ρ甲＞ρ乙，所以△p甲＞△p乙，即甲的压强减小的快，但由于甲的高度大于乙的高度，所以，甲的压强不可能比乙先变成零，故只有D正确。

2．在两个相同的薄壁塑料瓶（质量忽略不计）内分别装入体积相等、密度为ρ甲和ρ乙的两种液体后密封，再把它们放入两个装有等质量水的相同容器中，处于如图所示状态，两容器对桌面的压强分别为p1和p1．下列判断正确的是（）A．ρ甲＞ρ乙p1＞p1B．ρ甲=ρ乙p1＞p1C．ρ甲＜ρ乙p1＜p1D．ρ甲=ρ乙p1＜p1【答案】A【详解】因图中V排甲＞V排乙，所以，由F浮=ρgV排可知，F浮甲＞F浮乙，因甲、乙在水中均漂浮，受到的浮力和它们自身的重力相等，且薄壁塑料瓶的质量忽略不计，所以，G甲＞G乙，又因甲乙两液体的体积相等，由ρ=m G V gV可知，ρ甲＞ρ乙，故BCD错误；因水平面上物体的压力和自身的重力相等，且容器和水的质量相等，所以，由F=G液+m容g+m水g可知，两容器对桌面的压力相等，因相同容器的底面积相等，即受力面积相等，所以，由p=FS可知，两容器对桌面的压强关系为p1＞p1，故A正确．3．下列关于一般中学生的估算中，最接近实际的是A．重约为100NB．正常步行速度为10km/hC．双站立于水平地面时，对地面的压强是5000PaD．游泳漂浮在水面时，受到的浮力是500N【答案】D【解析】【详解】Ａ．中学生的质量约为50kg，重力约为500N，故A不符合实际；B．中学生正常步行的速度约为1.1m/s，；故B不符合实际；C．中学生的体重在G=500N左右，双脚站立时与水平地面的接触面积在0.05m2左右，双脚对水平地面的压强在：左右。

2018-2019学年四川省成都市锦江区八年级(下)期末物理试卷

(已整理)2018-2019学年成都市锦江区八年级(下)数学期末试卷(含解析)

2018-2019 学年成都市锦江区八年级（下）期末数学试卷（考试时间：120 分钟满分：150 分）A 卷（共 100 分）一、选择题（本大题共 10 个小题，每小题 3 分，共 30 分，每小题均有四个选项，其中只有一项符合题目要求，答案涂在答题卡上）1．下列四个图形分别是四届国际数学家大会的会标，其中属于中心对称图形的有（）A.1个 B．2 个 C．3 个 D．4 个 2．若 a＞b，则下列式子正确的是（）A．a+2＜b+2B．﹣2a＞﹣2b C．a﹣2＞b﹣2D．＜3．多项式m2﹣4与多项式m2﹣4m+4的公因式是（）A．m﹣2 B．m+2 C．m+4 D．m﹣44.已知分式的值等于零，则x 的值为（）A．﹣2 B．﹣3 C．3 D．±35.将一次函数 y＝﹣2x 的图象向下平移 6 个单位，得到新的图象的函数解析式为（）A．y＝﹣8x B．y＝4x C．y＝﹣2x﹣6 D．y＝﹣2x+66.用正三角形和正方形镶嵌一个平面，在同一个顶点处，正三角形和正方形的个数之比为（）A．1：1 B．1：2 C．2：3 D．3：27.如图，将等边△ABC 沿直线 BC 平移到△DEF，使点 E 与点C 重合，连接 BD，若 AB＝2，则 BD 的长为（）A.2B． C．3 D．211 8.如图，在△ABC中，AB＝AC，直线l1∥l2，且分别与△ABC的两条边相交，若∠1＝40°，∠2＝23°，则∠C的度数为（）A．40° B．50° C．63°D．67°9.如图，在△ABC中，点 E，F 分别是边 BC 上两点，ED 垂直平分 AB，FG 垂直平分 AC，连接 AE，AF，若∠ BAC＝115°，则∠EAF的大小为（）A．45° B．50° C．60°D．65°10.如图，直线y1＝kx和直线y2＝ax+b相交于点（1，2）．则不等式组ax+b＞kx＞0的解集为（）A．x＜0 B．0＜x＜1 C．x＜1 D．x＜0 或x＞1二、填空题（本大题共 4 个小题，每小题 4 分，共 16 分，答案写在答题卡上）11．因式分解：x2﹣9y2＝．12.若关于x 的分式方程＝产生增根，则m＝．13.如图，两张等宽的纸条交叉叠放在一起，在重叠部分构成的四边形 ABCD 中，若 AB＝10，AC＝12，则BD 的长为．2214.如图，在▱ABCD 中，按以下步骤作图：①以C 为圆心，以适当长为半径画弧，分别交BC，CD 于M，N 两点；②分别以M，N 为圆心，以大于MN 的长为半径画弧，两弧在∠BCD的内部交于点P；⑨连接CP 并延长交AD 于E．若AE＝2，CE＝6，∠B＝60°，则ABCD 的周长等于．三、解答题（本大题共6个小题，共54分，解答过程写在答题卡上）15．（12分）（1）分解因式：a2b﹣4ab2+4b3．（2）解方程﹣2＝．16．（6分）解不等式组，并在数轴上表示出它的解集．33 17．（8分）化简求值：（﹣1）÷，其中a＝2﹣．18．（8分）如图，方格纸中每个小正方形的边长都是1个单位长度，Rt△ABC的三个顶点分别为A（0，4）， B （﹣4，2），C（0，2）．（1）画△A1B1C1，使它与△ABC关于点C成中心对称；（2）平移△AB C，使点A的对应点A2坐标为（﹣2，4），画出平移后对应的△A2B2C2；（3）若将△A1B1C1绕点P旋转可得到△A2B2C2，请直接写出旋转中心P的坐标．44 19．（10分）如图：在△ABC中，点E，F分别是BA，BC边的中点，过点A作AD∥BC交FE的延长线于点D，连接DB，DC．（1）求证：四边形 ADFC 是平行四边形；（2）若∠BDC＝90°，求证：CD 平分∠ACB；（3）在（2）的条件下，若 BD＝DC＝6，求 AB 的长．55 20．（10分）如图1，E为正方形ABCD的边BC上一点，F为边BA延长线上一点，且CE＝AF．（1）求证：DE⊥DF；（2）如图 2，若点 G 为边AB 上一点，且∠BGE＝2∠BFE，△BGE的周长为 16，求四边形 DEBF 的面积；（3）如图 3，在（2）的条件下，DG 与EF 交于点 H，连接 CH 且CH＝5 ，求 AG 的长．66B 卷（50 分）一、填空题（本大题共5 个小题，每小题4 分，共20 分，答案写在答题卡上）21．已知a+b＝0 且a≠0，则＝．22.如图，在Rt△ABC中，∠ACB＝90°，点D，E 分别是边AB，AC 的中点，延长BC 至F，使CF＝BC，若EF＝13，则线段AB 的长为．23.若次函数y＝（a﹣1）x+a﹣8 的图象经过第一，三，四象限，且关于y 的分式方程有整数解，则满足条件的整数a 的值之和为．24.如图，在△ABC 中，AC＝BC＝9，∠C＝120°，D 为AC 边上一点，且 AD＝6，E 是AB 边上一动点，连接DE，将线段 DE 绕点D 逆时针旋转 30°得到 DF，若 F 恰好在 BC 边上，则 AE 的长为．25.如图，将菱形OABC 放置于平面直角坐标系中，边OA 与x 轴正半轴重合，D 为边OC 的中点，点E，F，G 分别在边OA，AB 与BC 上，若∠COA＝60°，OA＝4，则当四边形DEFG 为菱形时，点G 的坐标为．77 二、解答题（本大题共 3 个小题，共 30 分，解答过程写在答题卡上）26．（8分）某市计划修建一条长60千米的地铁，根据甲，乙两个地铁修建公司标书数据发现：甲，乙两公司每天修建地铁长度之比为3：5；甲公司单独完成此项工程比乙公司单独完成此项工程要多用240天．（1）求甲，乙两个公司每天分别修建地铁多少千米？（2）该市规定：“该工程由甲，乙两个公司轮流施工完成，工期不超过450天，且甲公司工作天数不少于乙公司工作天数的”．设甲公司工作a天，乙公司工作b天．①请求出 b 与 a 的函数关系式及 a 的取值范围；②设完成此项工程的工期为 W 天，请求出 W 的最小值．88 27．（10分）如图，在矩形ABCD中，AB＝8，AD＝6，将矩形ABCD绕点A逆时针旋转得到矩形AEFG．（1）如图 1，若在旋转过程中，点 E 落在对角线 AC 上，AF，EF 分别交 DC 于点M，N．①求证：MA＝MC；②求 MN 的长；（2）如图 2，在旋转过程中，若直线 AE 经过线段 BG 的中点 P，连接 BE，GE，求△BEG的面积99 28．（12分）如图，在平面直角坐标系中，直线y＝2x+4与x轴交于点A，与y轴交于点B，过点B的直线交x轴于C，且△ABC面积为10．（1）求点 C 的坐标及直线 BC 的解析式；（2）如图 1，设点 F 为线段 AB 中点，点 G 为y 轴上一动点，连接 FG，以 FG 为边向 FG 右侧作正方形 FGQP，在 G 点的运动过程中，当顶点 Q 落在直线 BC 上时，求点 G 的坐标；（3）如图2，若M为线段BC上一点，且满足S△AMB＝S△AOB，点E为直线AM上一动点，在x轴上是否存在点D，使以点D，E，B，C为顶点的四边形为平行四边形？若存在，请直接写出点D的坐标；若不存在，请说明理由．1010 参考答案与试题解析一、选择题（本大题共 10 个小题，每小题 3 分，共 30 分，每小题均有四个选项，其中只有一项符合题目要求，答案涂在答题卡上）1.【解答】解：第一个图形是中心对称图形，第二个图形不是中心对称图形，第三个图形是中心对称图形，第四个图形不是中心对称图形，所以，中心对称图有 2 个．故选：B．2.【解答】解：若 a＞b，则 a+2＞b+2，故 A 选项错误；若 a＞b，则﹣2a＜﹣2b，故 B 选项错误；若 a＞b，则 a﹣2＞b﹣2，故 C 选项正确；若a＞b，则a＞b，故D 选项错误；故选：C．3．【解答】解：m2﹣4＝（m+2）（m﹣2），m2﹣4m+4＝（m﹣2）2，m2﹣4与多项式m2﹣4m+4的公因式是m﹣2，故选：A．4．【解答】解：∵x2﹣9＝0且x+2≠0∴x＝±3 且x≠﹣2．故选：D．5.【解答】解：将一次函数 y＝﹣2x 的图象向下平移 6 个单位，那么平移后所得图象的函数解析式为：y＝﹣2x﹣6，故选：C．6.【解答】解：正三角形的每个内角是 60°，正方形的每个内角是90°，∵3×60°+2×90°＝360°，∴用正三角形和正方形镶嵌平面，每一个顶点处有 3 个正三角形和 2 个正方形．∴正三角形和正方形的个数之比为 3：2，故选：D．7.【解答】解：由平移得：△ABC≌△DEF，1111 ∵△ABC 是等边三角形，且 AB＝2，∴BC＝EF＝DF＝2，∠DEF＝60°，∴∠CBD＝∠CDB＝30°，∵∠CDF＝60°，∴∠BDF＝90°，Rt△BDF 中，∠DBF＝30°，∴BD＝2 ，故选：A．8.【解答】解：过B作BD∥l1，∵l1∥l2，∴BD∥l1∥l2，∴∠ABD＝∠1＝40°，∠CBD＝∠2＝23°，∴∠ABC＝∠ABD+∠CBD＝63°，∵AB＝AC，∴∠C＝∠ABC＝63°，故选：C．9．【解答】解：∵∠BAC＝115°，∴∠B+∠C＝180°﹣115°＝65°，∵ED 垂直平分 AB，FG 垂直平分 AC，∴EA＝EB，FA＝FC，∴∠EAB＝∠B，∠FAC＝∠C，∴∠EAB+∠FAC＝∠B+∠C＝65°，∴∠EAF＝∠BAC﹣（∠EAB+∠FAC）＝50°，故选：B．121210．【解答】解：在x轴的上方，直线y1＝kx和直线y2＝ax+b的图象上方部分对应的自变量的取值范围即为不等式ax+b＞kx＞0的解集，观察图象可知：不等式的解集为：0＜x＜1，故选：B．二、填空题（本大题共4个小题，每小题4分，共16分，答案写在答题卡上）11．【解答】解：x2﹣9y2＝（x+3y）（x﹣3y）．12.【解答】解：方程去分母得：3x＝2x﹣m，解得：x＝﹣m，由方程有增根 x＝﹣2，得到﹣m＝﹣2，则 m 的值为 2．故答案为：2．13.【解答】解：过点 A 作AE⊥BC于E，AF⊥CD于F，设 AC、BD 交点为 O．∵两条纸条宽度相同，∴AE＝AF．∵AB∥CD，AD∥BC，∴四边形 ABCD 是平行四边形．∵S▱ABCD＝BC•AE＝CD•AF．又∵AE＝AF．∴BC＝CD，∴四边形 ABCD 是菱形；∴OB＝OD，OA＝OC＝6，AC⊥BD．∴OB＝＝＝8．∴BD＝2OB＝16．故答案为：16．14.【解答】解：由作图可知∠ECD＝∠ECB，1313 ∵四边形 ABCD 是平行四边形，∴AD∥BC，∠B＝∠D＝60°，∴∠DEC＝∠ECB＝∠ECD，∴DE＝DC，∴△DEC 是等边三角形，∴DE＝DC＝EC＝6，∴AD＝BC＝8，AB＝CD＝6，∴四边形 ABCD 的周长为28，故答案为 28．三、解答题（本大题共6个小题，共54分，解答过程写在答题卡上）15．【解答】解：（1）a2b﹣4ab2+4b3＝b（a2﹣4ab+4b2）＝b（a﹣2b）2；（2）去分母，得 4x﹣2（x﹣3）＝﹣x，解得x＝﹣2，经检验：x＝﹣2 是原方程的解．16．【解答】解：解不等式①，得：x≥﹣1，解不等式②，得：x＜3，则不等式组的解集为﹣1≤x＜3，将解集表示在数轴上如下：17．【解答】解：（﹣1）÷＝1414＝＝﹣＝，当a＝2﹣时，原式＝﹣＝． 18．【解答】解：（1）△A1B1C1即为所求．（2）△A2B2C2即为所求．（3）P（﹣1，2）．19．【解答】（1）证明：∵点E，F分别是BA，BC边的中点，∴EF是△ABC 的中位线，∴EF∥AC，∴DF∥AC，又∵AD∥BC，∴四边形 ADFC 是平行四边形；（2）解：∵∠BDC＝90°，F 是 BC 边的中点，∴DF＝BC＝CF，∴平行四边形 ADFC 为菱形，∴CD 平分∠ACB；（3）解：∵BD＝CD＝6，∠BDC＝90°，1515 ∴△BDC 为等腰直角三角形，∴BC＝BD＝6 ，∵F是BC 边的中点，∴DF⊥BC，FC＝BC＝3 ，∵四边形 ADFC 是菱形，∴四边形 ADFC 为正方形，∴∠ACB＝90°，AC＝FC＝3 ，∴AB＝＝＝3． 20．【解答】（1）证明：∵四边形ABCD是正方形，∴AD＝CD，∠DAF＝∠DCE＝90°，在△ADF 和△CDE 中，，∴△ADF≌△CDE（SAS）∴∠ADF＝∠CDE，∵∠ADE+∠CDE＝90°，∴∠ADF+∠ADE＝90°，即∠FDE＝90°，∴DE⊥DF；（2）解：∵∠BGE＝2∠BFE，∠BGE＝∠BFE+∠GEF，∴∠GEF＝∠GFE，∴GE＝GF，∵△BGE 的周长为 16∴BE+GB+GE＝16∴BE+GB+GF＝16∴BE+BA+AF＝16∵CE＝AF，∴BA+CB＝16，∴BC＝BA ＝8，∴S 四边形DEBF ＝S 四边形DEBA1616＝S 四边形DEBA +S △DC E＝S 正方形ABCD ＝AB 2＝64；（3）过点 H 作 HP⊥HC 交 CB 的延长线于点 P ，∵GF＝GE ，DF ＝DE ，∴DG 垂直平分 EF ，∵∠FDE＝90°，∴DH＝EH ，∠DHE＝∠PHC＝90°，∴∠DHE﹣∠EHC＝∠PHC﹣∠EHC，即∠DHC＝∠EHP，∵在四边形 DHEC 中，∠HDC+∠HEC＝180°，∠HEC+∠HEP＝180°，∴∠HEP＝∠HDC，在△HDC 和△HEP 中，，∴△HDC≌△HEP（ASA ）∴DC＝PE ＝8，CH ＝HP ＝5，∴在 Rt△PHC 中，PC ＝10，∴EC＝PC ﹣PE ＝2，∴AF＝2，BE ＝6，在 Rt △BGE 中，设 EG ＝x ，则 BG ＝10﹣x ，由勾股定理得，（10﹣x ）2+62＝x 2解得：x ＝，∴AG＝GF ﹣AF ＝．17一、填空题（本大题共5个小题，每小题4分，共20分，答案写在答题卡上）21．【解答】解：∵a+b＝0.\，∴a＝﹣b，＝＝＝＝＝﹣1故答案为﹣12.【解答】解：∵点 D，E 分别是边 AB，AC 的中点，∴DE＝BC，DE∥BC，∵CF＝BC，∴DE＝CF，又DE∥CF，∴四边形 DEFC 为平行四边形，∴CD＝EF＝13，∵∠ACB＝90°，点 D 是边 AB 的中点，∴AB＝2CD＝26，故答案为：26．23.【解答】解：∵函数 y＝（a﹣1）x+a﹣8 的图象经过第一，三，四象限，∴18 解得：1＜a＜8，方程两边同时乘以（y﹣1）得：﹣（y﹣5）+3（y﹣1）＝a，去括号得：﹣y+5+3y﹣3＝a，移项得：﹣y+3y＝a﹣5+3，合并同类项得：2y＝a﹣2，系数化为1 得：y＝，∵该方程有整数解，且y≠1， a﹣2 是 2 的整数倍，且 a﹣2≠2，即 a﹣2 是 2 的整数倍，且a≠4，∵1＜a＜8，∴整数 a 为：2，6，∴2+6＝8，故答案为8．24.【解答】解：如图，延长 DC 到G，使 DG＝AE，连接 FG，∵AC＝BC，∠C＝120°，∴∠A＝30°，∠FCG＝60°，∵∠A+∠1＝∠EDF+∠2，又∵∠EDF＝30°，∴∠1＝∠2，在△EDA 和△DFG 中，，∴△EDA≌△DFG（SAS）∴AD＝GF＝6，∠A＝∠G＝30°，∵∠G+∠FCG＝90°，∴∠CFG＝90°，设CF＝x，则CG＝2x，由CF2+FG2＝CG2得：x2+62＝（2x）2，解得x1＝，x2＝﹣（不合题意舍去），1919 ∴CG＝4 ，∴AE＝DG＝3+4 ，故答案为：3+4 ．25.【解答】解：过 D 作MN⊥OA于N，交 BC 的延长线于 M，连接 DF、EG，交于点 H，∵四边形 ABCO 是菱形，∴BM∥OA，∴∠M＝∠OND＝90°，∵OD＝DC，∠ODN＝∠MDC，∴△ODN≌△CDM（AAS），∴DN＝DM，∵OA＝OC＝4 ，∴OD＝2 ，Rt△DON 中，∠DON＝60°，∴∠ODN＝30°，∴O N＝，DN＝，∴MN＝2DN＝2 ，∵四边形 DEFG 是菱形，∴DF⊥EG，DH＝，DG＝DE，∴Rt△DMG≌Rt△DNE（HL），∴MG＝EN，2020 ∵MG∥EN，∠M＝90°，∴四边形 MNEG 为矩形，∴EG⊥BM，EG＝MN＝2 ，∵BC∥OA，DF⊥EG，EG⊥BC，∴DF∥OA∥BC，∵OD∥AF，∴四边形 DOAF 是平行四边形，∴DF＝OA＝4 ，∴DH＝EN＝DF＝2 ，∴OE＝ON+EN＝3 ，∴G（3，2），故答案为：（3，2）．二、解答题（本大题共 3 个小题，共 30 分，解答过程写在答题卡上）26.【解答】解：（1）设甲公司每天修3x千米，乙公司每天修5x千米，根据题意得，，解得，经检验，为原方程的根，∴，，答：甲公司每天修建地铁千米，乙公司每天修建地铁千米；（2）①由题意得，，∴，又∵ ，∴200≤a≤225；②由题意得 W＝a+b，∴W＝a+（﹣a+360），即W＝+360，2121 ∵k＝，∴W 随 a 的增大而增大，又∵200≤a≤225，∴a＝200 时，W 最小值为 440 天．27.【解答】（1）①证明：∵四边形 ABCD 是矩形，∴AB∥CD，∴∠DCA＝∠BAC，由旋转的性质得：∠FAE＝∠BAC，∴∠DCA＝∠FAE，∴MA＝MC；②解：设MA＝MC＝x，则DM＝8﹣x，在Rt△ADM中，62+（8﹣x）2＝x2，解得：x＝，在Rt△AEF中，AF＝＝＝10，∴MF＝AF﹣AM＝，∵∠AEF＝∠CE N＝90°，∴∠MCA+∠CNE＝∠MAC+∠AEF＝90°，又∵∠MCA＝∠MAC，∴∠AFE＝∠CNE＝∠MNF，∴MN＝MF＝；（2）解：分情况讨论：①如图 2 所示：过点 B 作BH⊥AE 于 H，则∠GAP＝∠BHP＝90°，在△HBP 和△AGP 中，，∴△HBP≌△AGP（AAS），∴AP＝HP，BH＝AG＝6，在Rt△ABH 中，AH＝＝＝2 ，2222 ∴AP＝AH＝，∴PE＝AE﹣AP＝8﹣，∴△BEG 的面积＝2△GPE的面积＝2××6×（8﹣）＝48﹣6 ；②如图3 所示：同①得：AH＝2，AP＝，∴PE＝8+ ，∴△BEG的面积＝2△GPE的面积＝2××6×（8+ ）＝48+6 ；综上所述，△BEG的面积为48﹣6 或48+6．28.【解答】解：（1）∵直线y＝2x+4与x轴交于点A，与y轴交于点B，∴A（﹣2，0），B（0，4），∴OA＝2，OB＝4，∵S＝•AC•OB＝10，△AB C∴AC＝5，2323 ∴OC＝3，∴C（3，0），设直线 B 的解析式为 y＝kx+b，则有，∴ ．∴直线BC 的解析式为y＝﹣x+4．（2）∵FA＝FB，A（﹣2，0），B（0，4），∴F（﹣1，2），设G（0，n），①当 n＞2 时，如图 2﹣1 中，点 Q 落在 BC 上时，过 G 作直线平行于 x 轴，过点 F，Q 作该直线的垂线，垂足分别为 M，N．∵四边形 FGQP 是正方形，易证△FMG≌△GNQ，∴MG＝NQ＝1，FM＝GN＝n﹣2，∴Q（n﹣2，n﹣1），∵点Q 在直线y＝﹣x+4 上，∴n﹣1＝﹣（n﹣2）+4，∴n＝，∴G（0，）．②当n＜2时，如图2﹣2中，同法可得Q（2﹣n，n+1），2424∵点Q 在直线y＝﹣x+4 上，∴n+1＝﹣（2﹣n）+4，∴n＝﹣1，∴G（0，﹣1）．综上所述，满足条件的点G坐标为（0，）或（0，﹣1）．（3）如图 3 中，设 M （m ，﹣m+4），∵S △AM B ＝S △AOB ，∴S △AB C ﹣S △AMC ＝S △AOB ，∴ ×5×4﹣ ×5×（﹣ m+4）＝ ×2×4，∴m＝，∴M （，），25 25∴直线 AM 的解析式为 y ＝ x+ ，作 BE ∥OC 交直线 AM 于 E ，此时 E （，4），当 CD ＝BE 时，可得四边形 BCDE ，四边形 BECD 1 是平行四边形，可得 D （，0），D 1（﹣，0），当点 E 在第三象限，根据 BC ＝DE ，可得 D 2（﹣，0）也符合条件，综上所述，满足条件的点 D 的坐标为（，0）或（﹣ ，0）或（﹣ ，0）26 26。

2017-2018学年四川省成都市锦江区八年级(下)期末数学试卷和答案

2017-2018学年四川省成都市锦江区八年级（下）期末数学试卷一、选择题（共10小题，每小题3分，满分30分）1．（3分）利用“分形”与“迭代”可以制作出很多精美的图形，以下是制作出的几个简单图形，其中是轴对称但不是中心对称的图形是（）A．B．C．D．2．（3分）下列等式从左到右的图形，属于因式分解的是（）A．m（a﹣b）＝ma﹣mb B．2a2+a＝a（2a+1）C．（x+y）2＝x2+2xy+y2D．m2+4m+4＝m（m+4）+43．（3分）若分式有意义，则实数x的取值范围是（）A．x＝0B．x＝3C．x≠0D．x≠34．（3分）如图，直线m∥n，点A在直线m上，点B、C在直线n上，AB＝CB，∠1＝70°，则∠BAC等于（）A．40°B．55°C．70°D．110°5．（3分）一个多边形的边数由原来的3增加到n时（n＞3，且n为正整数），它的外角和（）A．增加（n﹣2）×180°B．减小（n﹣2）×180°C．增加（n﹣1）×180°D．没有改变6．（3分）关于x的分式方程＝有增根，则a的值为（）A．﹣3B．﹣5C．0D．27．（3分）已知y是x的正比例函数，且函数图象经过点（4，﹣6），则在此正比例函数图象上的点是（）A．（2，3）B．（﹣4，6）C．（3，﹣2）D．（﹣6，4）8．（3分）如图，将矩形ABCD绕点A顺时针旋转得到矩形AB′C′D′的位置，旋转角为α（0＜α＜90°），若∠1＝110°，则∠α＝（）A．10°B．20°C．25°D．30°9．（3分）一次函数y＝x﹣1的图象交x轴于点A．交y轴于点B，在y＝x﹣1的图象上有两点（x1，y1）、（x2，y2），若x1＜0＜x2，则下列式子中正确的是（）A．y1＜0＜y2B．y1＜0＜y2C．y1＜﹣1＜y2D．y2＜0＜y1 10．（3分）如图，已知△ABC的面积为12，点D在线段AC上，点F在线段BC的延长线上，且BC＝4CF，四边形DCFE是平行四边形，则图中阴影部分的面积为（）A．2B．3C．4D．6二、填空题（本题共4个小题，每小题4分，共16分答案在答题卡上）11．（4分）分解因式：x3﹣16x＝．12．（4分）如图，平面直角坐标系中，A、B两点的坐标分别为（2，0）、（0，1），若将线段AB平移至A1B1，点A1的坐标为（3，1），则点B1的坐标为．13．（4分）如图，在▱ABCD中，AB＝4，BC＝6，∠ABC的平分线交AD于点E，则ED＝．14．（4分）如图，在△ABC中，∠A＝100°，∠B＝30°，分别以点B，C为圆心，以大于BC长为半径作弧，两弧相交于点P、点Q，作直线PQ交AB于点D，连接CD．则∠ACD＝．三、解答题（本题共6个小题，共54分，解答过程写在答题卡上）15．（12分）（1）因式分解：3x2﹣6xy+3y2．（2）解分式方程：．16．（6分）解不等式组：并在数轴上表示出它的解集．17．（8分）化简求值：，其中a＝．18．（8分）如图，在平面直角标系中，△ABC的三个顶点坐标为A（﹣3，4）、B（﹣4，2）、C（﹣2，1），△ABC绕原点顺时针旋转180°，得到△A1B1C1，再将△A1B1C1向左平移5个单位得到△A2B2C2（1）画出△A1B1C1，并写出点A的对应点A1的坐标；（2）画出△A2B2C2，并写出点A的对应点A2的坐标；（3）P（a，b）是△ABC的边AC上一点，△ABC经旋转，平移后点P的对应点分别为P1、P2，请直接写出点P2的坐标．19．（10分）如图，在Rt△BC中，∠ACB＝90°，点D，E分别是边AB，AC的中点，连接DE，DC，过点A作AF∥DC交DE的延长线于点F，连接CF．（1）求证：DE＝FE；（2）求证：四边形BCFD是平行四边形；（3）若AB＝6，∠BAC＝30°，求四边形ADCF的面积．20．（10分）如图，菱形ABCD的对角线AC，BD相交于点O，延长AC到E，使CE＝CO，连接EB，ED．（1）求证：EB＝ED；（2）过点A作AF⊥AD，交BC于点G，交BE于点F，若∠AEB＝45°，①试判断△ABF的形状，并加以证明；②设CE＝m，求EF的长（用含m的式子表示）．一、填空题（每小题4分，共20分，答案写在答题卡上）21．（4分）若＝3，则分式＝．22．（4分）已知不等式的解集为﹣1＜x＜1，求（a+1）（b﹣1）的值为．23．（4分）如图，AC，BD是四边形ABCD的对角线，AD⊥BD，点E为AB的中点，连接DE交AC于点F，AF＝CF，DF＝DE．若BC＝12，则AB长为．24．（4分）如图，矩形ABCO的边OC在x轴上，边OA在y轴上，且点C的坐标为（8，0），点A的坐标为（0，6），点E、F分别足OC、BC的中点，点M，N分别是线段OA、AB上的动点（不与端点重合），则当四边形EFNM的周长最小时，点N的坐标为．25．（4分）如图，正方形ABCD的边长AB＝3，点E、F分别是CB，DC延长线上的点，连AF交CB于点G，若BE＝1，连接AE，且∠EAF＝45°，则AG长为．二、解答题（本大题3个小题，共30分，解答过程写在答题卡上）26．（8分）在成都“白环改建工程中，某F罕轿建设将由甲，乙两个工程队共同施工完成，据调查得知：甲，乙两队单独完成这项上程所需天数之比为4：5，若先由甲，乙两队合作40天，剩下的工程再乙队做10天完成，（1）求甲．乙两队单独完成这取工程各需多少天？（2）若此项工程由甲队做m天，乙队n天完成，①请用含m的式子表示n；②已知甲队每天的施工费为15万元，乙队每天的施工费用为10万元，若工程预算的总费用不超过1150万元，甲队工作的天数与乙队工作的天数之和不超过90天．请问甲、乙两队各工作多少天，完成此项工程总费用最少？最少费用是多少？27．（10分）如图，△ABC与△ADE都为等腰直角三角形，∠ABC＝∠ADE＝90°，连接BD，EC，且F为EC的中点．（1）如图1，若D、A、C三点在同一直线上时，请判DF与BF的关系，并说明理由；（2）如图2，将图1中的△ADE绕点A逆时针旋转m°（0＜m＜90），请判断（1）中的结论是否仍然成立？并证明你的判断；（3）在（2）下，若△DEF与△BCF的面积之和于△DBF的而积，请直接写出m的值．28．（12分）已知菱形ABCD的边长为5，其顶点都在坐标轴上，且点A坐标为（0，﹣3）．（1）求点B的坐标及菱形ABCD的面积；（2）点P是菱形边上一动点，沿A→B→C→D运动（到达D点时停止）①如图1，当点P关于x轴对称的点Q恰好落在直线y＝x﹣3上时，求点P的坐标．②探究：如图2，当P运动到BC，CD边时，作△ABP关于直线AP的对称图形为△AB′P，是否存在这样的P点，使点B′正好在直线y＝x﹣3上？若存在，求出满足条件的点P 坐标；若不存在，请说明理由．2017-2018学年四川省成都市锦江区八年级（下）期末数学试卷参考答案与试题解析一、选择题（共10小题，每小题3分，满分30分）1．【解答】解：A、图形不是中心对称轴图形，是轴对称图形，此选项正确；B、图形是中心对称轴图形，也是轴对称图形，此选项错误；C、图形是中心对称轴图形，不是轴对称图形，此选项错误；D、图形是中心对称轴图形，也是轴对称图形，此选项错误；故选：A．2．【解答】解：A、m（a﹣b）＝ma﹣mb，是单项式乘以多项式，故此选项错误；B、2a2+a＝a（2a+1），是分解因式，符合题意；C、（x+y）2＝x2+2xy+y2，是整式乘法运算，故此选项错误；D、m2+4m+4＝m（m+4）+4，不符合因式分解的定义，故此选项错误．故选：B．3．【解答】解：由题意，得x﹣3≠0，解得x≠3．故选：D．4．【解答】解：∵m∥n，∴∠ACB＝∠1＝70°，∵AB＝BC，∴∠BAC＝∠ACB＝70°，故选：C．5．【解答】解：∵多边形的外角和等于360°，与边数无关，∴凸多边形的边数由3增加到n时，其外角度数的和还是360°，保持不变．故选：D．6．【解答】解：分式方程去分母得：x﹣2＝a，由分式方程有增根，得到x+3＝0，即x＝﹣3，把x＝﹣3代入整式方程得：a＝﹣5，故选：B．7．【解答】解：设正比例函数解析式为y＝kx（k≠0）．∵正比例函数图象经过点（4，﹣6），∴﹣6＝4k，∴k＝﹣．∵当x＝﹣4时，y＝﹣x＝6，∴点（﹣4，6）在此正比例函数图象上．故选：B．8．【解答】解：如图所示：∵∠B＝∠D′＝90°，∴∠2+∠D′AB＝180°．∴∠D′AB＝180°﹣∠2＝180°﹣110°＝70°．∵∠α＝∠DAD′，∴∠α＝90°﹣∠D′AB＝90°﹣70°＝20°．故选：B．9．【解答】解：∵y＝x﹣1，∴x＝0时，y＝﹣1，且y随x的增大而增大，∴若x1＜0＜x2，则y1＜﹣1＜y2．故选：C．10．【解答】解：连接AF、EC．∵BC＝4CF，S△ABC＝12，∴S△ACF＝×12＝3，∵四边形CDEF是平行四边形，∴DE∥CF，EF∥AC，∴S△DEB＝S△DEC，∴S阴＝S△ADE+S△DEC＝S△AEC，∵EF∥AC，∴S△AEC＝S△ACF＝3，∴S阴＝3．故选：B．二、填空题（本题共4个小题，每小题4分，共16分答案在答题卡上）11．【解答】解：原式＝x（x2﹣16）＝x（x+4）（x﹣4），故答案为：x（x+4）（x﹣4）12．【解答】解：∵A、B两点的坐标分别为（2，0）、（0，1），平移后A1（3，1），∴线段AB向右平移1个单位，向上平移1个单位，∴a＝0+1＝1，b＝1+1＝2，点B1的坐标为（1，2），故答案为：（1，2），13．【解答】解：∵四边形ABCD为平行四边形，∴AD∥BC，AD＝BC＝7，∴∠AEB＝∠EBC，∵BE平分∠ABC，∴∠ABE＝∠EBC，∴∠AEB＝∠ABE，∴AB＝AE＝4，∴ED＝AD﹣AE＝BC﹣AE＝6﹣4＝2．故答案为2．14．【解答】解：∵在△ABC中，∠A＝100°，∠B＝30°，∴∠ACB＝50°．由作图过程可知：QP为BC的垂直平分线，∴DB＝DC，∴∠B＝∠DCB＝30°．∴∠ACD＝∠ACB﹣∠DCB＝50°﹣30°＝20°．故答案为：20°．三、解答题（本题共6个小题，共54分，解答过程写在答题卡上）15．【解答】解：（1）原式＝3（x2﹣2xy+y2）＝3（x﹣y）2；（2）去分母得：x2﹣4x+4﹣x2+4＝16，解得：x＝﹣2，经检验x＝﹣2是增根，分式方程无解．16．【解答】解：解不等式①，得：x＜2，解不等式②，得：x≥﹣1，则不等式组的解集为﹣1≤x＜2，将不等式组的解集表示在数轴上如下：17．【解答】解：＝＝1﹣＝＝，当a＝时，原式＝＝．18．【解答】解：（1）如图所示，点A的对应点A1的坐标是（3，﹣4）；（2）如图所示，点A的对应点A2的坐标（﹣2，﹣4）；（3）根据规律可知：点P2的坐标为（﹣a﹣5，﹣b）．19．【解答】（1）证明：∵AF∥CD，∴∠AFE＝∠CDE，∵AE＝EC，∠AEF＝∠DEC，∴△AEF≌△CED，∴DE＝EF．（2）∵AD＝DB，AE＝EC，∴DE∥BC，DE＝BC，∵DE＝EF，∴BC＝DF，∴四边形BCFD是平行四边形．（3）在Rt△ABC中，AB＝6，∠BAC＝30°，∴BC＝AB＝3，AC＝3，∴DE＝EF＝，∵DE∥BC，∴∠AED＝∠ACB＝90°，∴AC⊥DF，∴S四边形ADCF＝•AC•DF＝××3＝．20．【解答】（1）证明：∵四边形ABCD是菱形，∴EA⊥BD，OB＝OD，∴EB＝ED（2）解：①结论：△ABF是等腰三角形（AB＝AF）；理由：∵∠AEB＝45°，EO⊥OB，∴△BOE是等腰直角三角形，∴∠OBE＝∠OEB＝45°，∵AG⊥BC，∴∠AGB＝∠BOC＝90°，∴∠GAC+∠ACB＝90°，∠ACB+∠OBC＝90°，∴∠CAG＝∠CBO＝∠ABO，∵∠ABF＝∠ABO+∠OBE＝∠ABO+45°，∠AFB＝∠CAG+∠AEB＝∠CAG+45°，∴∠AFB＝∠ABF，∴AB＝AF，∴△ABF是等腰三角形．②作EH⊥AF交AF的延长线于H．由题意CE＝OC＝OA＝m，OB＝AC═OD＝2m，AE＝3m，AB＝AF＝m，tan∠CBO＝tan∠CAG＝＝，∴EH＝m，AH＝m，∴FH＝AH﹣AF＝m，在Rt△EFH中，EF＝＝＝m．一、填空题（每小题4分，共20分，答案写在答题卡上）21．【解答】解：∵＝3，∴y﹣x＝3xy，∴原式＝＝＝8故答案为：822．【解答】解：由得．∵﹣1＜x＜1，∴＝1，3+2b＝﹣1，解得a＝1，b＝﹣2，∴（a+1）（b﹣1）＝（1+1）（﹣2﹣1）＝﹣6，故答案为﹣6．23．【解答】解：∵AD⊥BD，∴∠ADB＝90°，∵AE＝EB，∴AB＝2DE，∵AF＝FC，AE＝EB，∴EF＝BC＝6，∵DF＝DE，∴DF＝EF＝3，∴DE＝9，∴AB＝2DE＝18，故答案为18．24．【解答】解：如图所示：作点F关于AB的对称点F′，作点E关于y轴的对称点E′，连接E′F′交AB与点N．∵C的坐标为（8，0），点A的坐标为（0，6），点E、F分别足OC、BC的中点，∴OE＝OE′＝4，FB＝CF＝3，∴E′C＝12，CF′＝9．∵AB∥CE′，∴△F′NB∽△F′E′C．∴＝＝，即＝，解得BN＝4，∴AN＝4．∴N（4，6）．故答案为：（4，6）．25．【解答】解：把△ABE绕点A逆时针旋转90°至△ADH，可使AB与AD重合，则H在DC上．由旋转得：BE＝DH，∠DAH＝∠BAE，AE＝AH，∵∠BAD＝90°，∴∠BAE+∠BAH＝90°，∵∠EAF＝45°，∴∠F AH＝90°﹣45°＝45°，∴∠EAF＝∠F AG＝45°，在△EAF和△HAF中，AE＝AH，∠EAF＝∠HAF，AF＝AF，∴△EAF≌△HAF（SAS），∴EF＝FH，设EF＝FH＝x，则DF＝x+1，FC＝x﹣2．在Rt△EFC中，依据勾股定理可知：x2＝42+（x﹣2）2，解得：x＝5，∴FD＝6，FC＝3．∵BC∥AD，∴＝，即＝，解得：CG＝1.5．∴BG＝1.5．∴AG＝＝＝．故答案为：．二、解答题（本大题3个小题，共30分，解答过程写在答题卡上）26．【解答】解：（1）设甲．乙两队单独完成这取工程各需4x，5x天，由题意得：（+）×40+＝1，解得：x＝20，经检验：x＝20是原方程的根，∴4x＝80，5x＝100，答：甲．乙两队单独完成这取工程各需80，100天；（2）①由题意得：n＝（1﹣）÷＝100﹣，②令施工总费用为w万元，则w＝15m+10×（100﹣）＝m+1000．∵两队施工的天数之和不超过90天，工程预算的总费用不超过1150万元，∴m+1000≤1150，m+（100﹣）≤90，∴40≤m≤60，∴当m＝40时，完成此项工程总费用最少，∴n＝100﹣＝50，w＝1100元，答：甲、乙两队各工作40，50天，完成此项工程总费用最少，最少费用是1100元．27．【解答】解：（1）如图1中，结论：DF＝BF，DF⊥BF．理由：在Rt△BEC中，∵∠EBC＝90°，EF＝FC，∴BF＝EC，在Rt△DCE中，∵∠EDC＝90°，EF＝FC，∴DF＝EC，∴DF＝BF，∵∠FCB＝∠FBC，∠FED＝∠FDE，∴∠BFC+∠DFE＝（180°﹣2∠FCB）+（180°﹣2∠FDE）＝360°﹣2（∠FCB+∠FED）＝360°﹣2（45°+∠BEC+∠FCB）＝360°﹣270°＝90°，∴∠DFB＝90°，即DF⊥BF．（2）结论成立．理由：如图2中，如图作CM∥DE交DF的延长线于M，延长DA交MC的延长线于N，DN交BC于O．∵DE∥CM，∴∠FED＝∠FCM，∵∠DFE＝∠MFC，EF＝CF，∴△DFE≌△MFC，∴DF＝FM，DE＝CM＝AD，∵∠EDN+∠N＝180°，∠EDN＝90°，∴∠N＝∠ABO＝90°，∵∠AOB＝∠CON，∴∠DAB＝∠ACM，∵BA＝BC，AD＝CM，∴△BAD≌△BCM，∴BD＝BM，∠DBA＝∠CBM，∴∠DBM＝∠ABC＝90°，∴△DBM是等腰直角三角形，∵DF＝FM，∴BF⊥DF，BF＝DF＝FM．（3）如图2中，由（2）可知：△DFE≌△MFC，△BDM是等腰直角三角形，DF＝FM，∴S△DEF+S△BFC＝S△FCM＝S四边形BFMC，S△BDF＝S△BFM，∴当B、C、M共线时，△DEF与△BCF的面积之和于△DBF的面积，此时旋转角为45°，∴m＝45°．28．【解答】解：（1）如图1中，∵四边形ABCD菱形，∴AB＝BC＝CD＝AD＝5，OA＝OC，OB＝OD，∵A（0，﹣3），∴OA＝3，在Rt△AOD中，OD＝＝4，∴BD＝8，AC＝6，∴S菱形ABCD＝×BD×AC＝24．（2）①如图2中，由题意B（4，0），C（0，3），∴直线BC的解析式为y＝﹣x+3，由解得，∴Q（，），∴当点P坐标为（，﹣）时，点P关于x轴对称的点Q恰好落在直线y＝x﹣3上，当点P′与C重合时，点P′关于x轴对称的点Q′恰好落在直线y＝x﹣3上，此时P′（0，3），综上所述，满足条件的点P坐标为（，﹣）或（0，3）；②如图3中，当AP平分∠BAQ时，满足条件，由题意A（0，﹣3），B（4，0），Q（，），∴AQ＝，BQ＝，∵＝（角平分线性质定理，可以用面积法证明），∴＝，∴PB＝×＝，∴可得P（，）．当AP′⊥AP时，B″在直线AQ上，此时直线AP′的解析式为y＝﹣x﹣3，直线CD的解析式为y＝x+3，由，解得，∴P′（﹣，），综上所述，满足条件的点P坐标为（，）或（﹣，）．。

{3套试卷汇总}2018年成都市八年级下学期物理期末复习能力测试试题

初二下学期期末物理试卷一、选择题（本题包括10个小题）1．沙漠之舟骆驼，能在松散的沙漠中顺利行走而不会陷下去，这是因为A．骆驼的重量轻B．骆驼跑得快C．骆驼的耐力大D．骆驼脚掌面积大压强小【答案】D【解析】【分析】本试题考查的是如何减小压强．压力一定时，受力面积越大，压强越小．【详解】骆驼的脚掌大约是马蹄的3倍，由于受力面积的明显增大，对沙地的压强减小许多，所以骆驼在沙漠里行走自如．2．一颗质量是20克的子弹从枪膛中水平射出，子弹在枪膛中受火药爆炸后产生的气体的平均作用力是600N，枪膛长60cm，子弹从枪膛射出后飞行1200米，气体对子弹做的功为A．0.18焦B．120焦C．360焦D．7.2×105焦【答案】C【解析】【分析】＝计算出气体对子弹做的功。

已知子弹在枪膛中受平均作用力和枪膛长，利用公式W Fs【详解】子弹在枪膛中受火药爆炸气体的作用力而运动的距离为枪膛长度，即s＝60cm＝0.6m，子弹离开枪膛后就不再受火药爆炸产生的气体推力，子弹飞行1200米过程中，气体推力不再做功；所以气体对子弹做功：＝＝＝.600N0.6m360JW Fs故选C.3．下图表示四冲程内燃机工作时各冲程的示意图，它们正确的排列顺序为( )A．甲、乙、丙、丁B．甲、丙、乙、丁C．丁、丙、乙、甲D．丁、丙、甲、乙【答案】B【解析】【详解】图甲中的进气门打开，活塞向下运行，气缸容积增大，是吸气冲程；图乙中的气门都关闭，活塞向下运行，气缸容积增大，是做功冲程；图丙中的气门都关闭，活塞向上运行，气缸容积减小，是压缩冲程；图丁中的排气门打开，活塞向上运动，气缸容积减小，是排气冲程；故正确的顺序是甲、丙、乙、丁；故B符合题意，ACD不符合题意。

4．在国际单位制中，力的单位是A．N B．kg/m3C．kg D．Pa【答案】A【解析】【详解】在国际单位中，力的单位是牛顿，符号是N；密度的单位是千克/米3，符号是kg/m3；质量的单位是千克，符号是kg；压强的单位是帕斯卡，符号是Pa，故只有A符合题意。

四川省成都市八年级(下)期末数学试卷(含答案)

2017-2018学年四川省成都市金牛区八年级（下）期末数学试卷副标题一、选择题（本大题共8小题.共24.0分）1.若等腰三角形一个内角为100°.则此等腰三角形的顶角为（）A. 100B. 0C. 100或 0D. 02.已知a＜b.下列不等式中正确的是（）A. B. 11 C. D.3.已知关于x的分式方程1无解.则k的值为（）1A. 0B. 0或1C. 0D. 0或14.分式有意义的条件是（）A. B. C. D. 05.如图.菱形ABCD的对角线AC与BD交于点O.过点C作AB垂线交AB延长线于点E.连结OE.若AB=2.BD=4.则OE的长为（）A. 6B. 5C.D. 46.下列图形中.既是轴对称图形又是中心对称图形的是（）A. B. C. D.7.已知四边形ABCD.对角线AC与BD交于点O.从下列条件中：①AB∥CD；②AD=BC；③∠ABC=∠ADC；④OA=OC.任取其中两个.以下组合能够判定四边形ABCD是平行四边形的是（）A. ①②B. ②③C. ②④D. ①④8.已知关于x的不等式组1的解集是x≥1.则a的取值范围是（）A. 1B. 1C. 1D. 1二、填空题（本大题共8小题.共32.0分）9.已知关于x、y方程组的解满足x＞1.y≥ .则k的取值范围是______．10.已知关于x的分式方程1=a有解.则a的取值范围是______．111.多项式x2-kx+6因式分解后有一个因式为x-2.则k的值为______．12.如图.在矩形ABCD中.BC=AB.∠ADC的平分线交边BC于点E.AH⊥DE于点H.连接CH并延长交边AB于点F.连接AE交CF于点O.则的值是______．13.如图.在平行四边形ABCD中.∠A= °.AB=4.AD=2.M是AD边的中点.N是AB边上一动点.将线段M绕点M逆时针旋转90至MN′.连接N′B.N′C.则N′B+N′C的最小值是______．14.已知ab≠0.a2+2ab-3b2=0.那么分式的值等于______．15.如图.在△ABC中.BF平分∠ABC.AG⊥BF.垂足为点D.交BC于点G.E为AC的中点.连结DE.DE=2.5cm.AB=4cm.则BC的长为______cm．16.如图.一次函数y1=-2x+m与y2=ax+6的图象相交于点P（-2.3）.则关于x的不等式m-2x＜ax+6的解集是______三、计算题（本大题共3小题.共28.0分）17.（1）分解因式：2mx2-4mxy+2my2．（2）解方程：11．18.先化简.再求值：.其中x=-3．19.某新能源汽车销售公司销售A品牌电动汽车.今年5月份电动汽车的售价比去年同期降价了1万元.如果销售的数量相同.去年5月份的销售额为110万元.今年5月份的销售额就只有105万元．（1）求今年5月份A品牌电动汽车的售价；（2）该公司同时销售B品牌混合动力汽车.已知A、B品牌汽车的进价分别为20万元/辆、12万元/辆.若公司预计用不超过236万元且不少于204万元的资金购进两款汽车共15辆.求公司的进货方案有多少种？（3）在（2）的条件下.今年5月份B品牌汽车的售价为13.8万元/辆.且每售出一辆A品牌电动汽车.政府将给予公司a万元奖励（0＜α＜2）.已知该公司销售两款汽车的最大利润为28.4万元.求a的值．四、解答题（本大题共6小题.共56.0分）20.在平面直角坐标系中.△ABC的位置如图所示：（每个小方格都是边长为1个单位长度的正方形）（1）将△ABC沿y轴方向向下平移4个单位长度得到△A1B1C1.则点C1坐标为______；（2）将△ABC绕着点O逆时针旋转 0°.画出旋转后得到的△△A2B2C2；（3）直接写出点B2.C2的坐标．21.（1）如图1.正方形ABCD中.∠PCG= °.且PD=BG.求证：FP=FC；（2）如图2.正方形ABCD中.∠PCG= °.延长FG交CB的延长线于点F.（1）中的结论还成立吗？请说明理由；（3）在（2）的条件下.作FE⊥PC.垂足为点E.交CG于点N.连结DN.求∠NDC的度数．22.在某学校的八年级课外活动中.体育组想把篮球分给班级活动用.如果每个班分4个篮球.则剩余20个篮球；如果每个班分8个篮球.则最后一个班分到的篮球个数不到8个（也不为0个）.问：（1）这个学校八年级共有几个班？（2）如果每个班分8个篮球.最后一个班分到的篮球个数到底是多少个？23.在直角三角形ABC中.∠BAC= 0°.（AC＞AB）.在边AC上取点D.使得BD=CD.点E、F分别是线段BC、BD的中点.连接AF和EF.作∠FEM=∠FDC.交AC于点M.如图1所示.（1）请判断四边形EFDM是什么特殊的四边形.并证明你的结论；（2）将∠FEM绕点E顺时针旋转到∠GEN.交线段AF于点G.交AC于点N.如图2所示.请证明：EG=EN；（3）在第（2）条件下.若点G是AF中点.且∠C= 0°.AB=2.如图3.求GE的长度．24.如图.在平面直角坐标系中.直线AB分别交x、y轴于点A、B.直线BC分别交x、y轴于点C、B.点A的坐标为（2.0）.∠ABO=30.且AB⊥BC．（1）求直线BC和AB的解析式；（2）将点B沿某条直线折叠到点0.折痕分别交BC、BA于点E、D.在x轴上是否存在点F.使得点D、E、F为顶点的三角形是以DE为斜边的直角三角形？若存在.请求出F点坐标；若不存在.请说明理由；（3）在平面直角坐标系内是否存在两个点.使得这两个点与B、C两点构成的四边形是正方形？若存在.请直接写出这两点的坐标；若不存在.请说明理由．25.如图.在▱ABCD中.BE平分∠ABC交CD延长线于点E.作CF⊥BE于F．（1）求证：BF=EF；（2）若AB=6.DE=3.求▱ABCD的周长．答案和解析1.【答案】A【解析】解：①当这个角是顶角时.底角=（1 0°-100°）÷ = 0°；②当这个角是底角时.另一个底角为100°.因为100°+100°= 00°.不符合三角形内角和定理.所以舍去．故选：A．题中没有指明已知的角是顶角还是底角.故应该分情况进行分析.从而求解．此题主要考查等腰三角形的性质及三角形内角和定理的综合运用.关键是分情况进行分析．2.【答案】B【解析】解：A、两边都除以2.不等号的方向不变.故A错误；B、两边都减1.不等号的方向不变.故B正确；C、两边都乘-1.不等号的方向改变.故C错误；D、两边都加3.不等号的方向不变.故D错误；故选：B．根据不等式的性质.可得答案．本题考查了不等式的性质.利用不等式的性质是解题关键．3.【答案】D【解析】解：分式方程去分母得：x=3kx+3k.即（3k-1）x=-3k.当3k-1=0.即k=时.方程无解；当k≠时.x==0或-1.方程无解.此时k=0.综上.k的值为0或.故选：D．分式方程去分母转化为整式方程.由分式方程无解确定出j的值即可．此题考查了分式方程的解.始终注意分母不为0这个条件．4.【答案】C【解析】解：由题意可知：x- ≠0.∴x≠故选：C．根据分式有意义的条件即可求出答案．本题考查分式有意义的条件.解题的关键是熟练运用分式有意义的条件.本题属于基础题型．5.【答案】D【解析】解：∵四边形ABCD是菱形.∴OA=OC.BD⊥AC.∵CE⊥AB.∴OE=OA=OC.∵BD=4.∴OB=BD=2.在Rt△AOB中.AB=2.OB=2.∴OA==4.∴OE=OA=4．故选：D．先判断出OE=OA=OC.再求出OB=1.利用勾股定理求出OA.即可得出结论．此题主要考查了菱形的判定和性质.平行四边形的判定和性质.角平分线的定义.勾股定理.判断出CD=AD=AB是解本题的关键．6.【答案】D【解析】解：A、不是轴对称图形.是中心对称图形.故此选项错误；B、不是轴对称图形.也不是中心对称图形.故此选项错误；C、不是轴对称图形.是中心对称图形.故此选项错误；D、是轴对称图形.也是中心对称图形.故此选项正确．故选：D．根据轴对称图形与中心对称图形的概念求解．本题考查了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴.图形两部分沿对称轴折叠后可重合；中心对称图形是要寻找对称中心.旋转180度后与原图重合．7.【答案】D【解析】解：以①④作为条件.能够判定四边形ABCD是平行四边形．理由：∵AB∥CD.∴∠OAB=∠OCD.在△AOB和△COD中..∴△AOB≌△COD（ASA）.∴OB=OD.∴四边形ABCD是平行四边形．故选：D．以①④作为条件能够判定四边形ABCD是平行四边形.根据平行得出全等三角形.即可求出OB=OD.根据平行四边形的判定推出即可；本题考查了平行四边形的判定.相似三角形的性质和判定.等腰梯形的判定等知识点的应用.主要考查学生的推理能力和辨析能力.题目比较好.但是一道比较容易出错的题目．8.【答案】C【解析】解：∵关于x的不等式组的解集是x≥1.∴a＜1.故选：C．利用不等式取解集的方法判断即可确定出a的范围．此题考查了不等式的解集.熟练掌握不等式取解集的方法是解本题的关键．9.【答案】-1≤k＜1【解析】解：.解得：.∵x＞1.y≥ .∴解得：-1≤k＜1.故答案为：-1≤k＜1．解方程组得到含有k的x和与.根据x＞1.y≥ .得到关于k的一元一次不等式组.解之即可．本题考查解一元一次不等式组和解二元一次方程组.根据不等量关系列出不等式组是解题的关键．10.【答案】a≠【解析】解：分式方程去分母得：2a+1=ax+a.整理得：（a-2）x=1-a.当a- ≠0.即a≠ 时.x=.由分式方程有解.得到≠-1.解得：a≠ .则a的范围是a≠ ．分式方程去分母转化为整式方程.表示出分式方程的解.确定出a的范围即可．此题考查了分式方程的解.始终注意分母不为0这个条件．11.【答案】5【解析】解：∵多项式x2-kx+6因式分解后有一个因式为x-2.∴另一个因式是（x-3）.即x2-kx+6=（x-2）（x-3）=x2-5x+6.则k的值为5.故答案为：5利用十字相乘法法判断即可．此题考查了因式分解的意义.熟练掌握因式分解的方法是解本题的关键．12.【答案】1【解析】解：在矩形ABCD中.AD=BC=AB=CD.∵DE平分∠ADC.∴∠ADE=∠CDE= °.∵AH⊥DE.∴△ADH是等腰直角三角形.∴AD=AB.∴AH=AB=CD.∵△DEC是等腰直角三角形.∴DE=CD.∴AD=DE.∴∠AEH= 7. °.∴∠EAH= . °.∵DH=CD.∠EDC= °.∴∠DHC= 7. °.∴∠OHA= . °.∴∠OAH=∠OHA.∴OA=OH.∴∠AEH=∠OHE= 7. °.∴OH=OE.∴OH=AE.即=．故答案为：．根据矩形的性质得到AD=BC=AB=CD.由DE平分∠ADC.得到△ADH是等腰直角三角形.△DEC是等腰直角三角形.得到DE=CD.得到等腰三角形求出∠AED= 7. °.∠AEB=1 0°- °- 7. °= 7. °.进而求出△AOH和△OEH是等腰三角形.即可得出结论．本题考查了矩形的性质.角平分线的定义.等腰三角形的判定与性质.熟记各性质并仔细分析题目条件.根据相等的度数求出相等的角.从而判断出等腰三角形是解题的关键.也是本题的难点．13.【答案】210【解析】解：如图.作ME⊥AD交AB于E.连接EN′、AC、作CF⊥AB于F．∵∠MAE= °.∴△MAE是等腰直角三角形.∴MA=ME.∵∠AME=∠NMN′= 0°.∴∠AMN=∠EMN′.∵MN=MN′.∴△AMN≌△EMN′.∴∠MAN=∠MEN′= °.∴∠AEN′= 0°.∴EN′⊥AB.∵AM=DM=.AB=4.∴AE=2.EB=2.∴AE=EB.∴N′B=N′A.∴N′B+N′C=N′A+N′C.∴当A、N′、C共线时.N′B+N′C的值最小.最小值=AC.在Rt△BCF中.∵BC=AD=2.∠CBF=∠DAB= °.∴CF=BF=2.在Rt△ACF中.AC==2.故答案为2．如图.作ME⊥AD交AB于E.连接EN′、AC、作CF⊥AB于F．首先证明AN′=BN′.因为N′B+N′C=N′A+N′C.即可推出当A、N′、C共线时.N′B+N′C的值最小.最小值=AC；本题考查平行四边形的性质、旋转变换、两点之间线段最短、全等三角形的判定和性质、勾股定理等知识.解题的关键是学会添加常用辅助线.构造全等三角形解决问题.学会用转化的思想思考问题.属于中考填空题中的压轴题．14.【答案】3或17【解析】解：∵a2+2ab-3b2=0.∴（a2-b2）+（2ab-2b2）=0.∴（a+b）（a-b）+2b（a-b）=0.∴（a-b）（a+3b）=0.∴a-b=0或a+3b=0.∴a=b或a=-3b．当a=b时.原式=（ab≠0）=3；当a=-3b时.原式=（ab≠0）=．故答案为：3或．先将条件变形为a2+2ab-2b2-b2=0.得（a2-b2）+（2ab-2b2）=0.得（a+b）（a-b）+2b（a-b）=0.（a-b）（a+3b）=0.再将a用含b的式子表示出来代入代数式就可以求出结论．本题考查了利用因式分解把一个字母用另一个字母表示出来代入代数式求出其值的运用．在解答时注意不要漏解．15.【答案】6.5【解析】解：∵BF平分∠ABC.AG⊥BF.∴△ABG是等腰三角形.∴AB=GB=4cm.∵BF平分∠ABC.∴AD=DG.∵E为AC的中点.∴DE是△AGB的中位线.∴DE=CG.. .∴CG=2DE=5cm.∴BC=BG+CG=4+2.5=6.5cm.故答案为：6.5由条件“BF平分∠ABC.AG⊥BF”可判定三角形ABG是等腰三角形（AB=GB）.再由条件“E为AC的中点”.可判定DE是三角形AGB的中位线.由此可得GC=2DE.进而可求出BC的长．本题考查了等腰三角形的判断和性质、三角形中位线定理的运用.熟记判断等腰三角形的各种方法是解题的关键．16.【答案】x＞-2【解析】解：观察函数图象可知：当x＞-2时.一次函数y1=-2x+m的图象在y2=ax+6的图象的下方.∴关于x的不等式m-2x＜ax+6的解集是x＞-2．故答案为x＞-2．观察函数图象.根据两函数图象的上下位置关系即可找出关于x的不等式m-2x＜ax+6的解集．本题考查了一次函数与一元一次不等式.根据两函数图象的上下位置关系找出不等式的解集是解题的关键．17.【答案】解：（1）原式=2m（x2-2xy+y2）=2m（x-y）2；（2）两边都乘以x-2.得：1-x=x-2+3.解得：x=0.检验：x=0时.x-2=- ≠0.所以原分式方程的解为x=0．【解析】（1）先提取公因式2m.再利用完全平方公式分解可得；（2）分式方程去分母转化为整式方程.求出整式方程的解得到x的值.经检验即可得到分式方程的解．此题考查了提公因式与解分式方程.解分式方程的基本思想是“转化思想”.把分式方程转化为整式方程求解．解分式方程一定注意要验根．18.【答案】解：==.当x=-3时.原式==== 1 =．【解析】根据完全平方公式和提公因式法可以化简题目中的式子.然后将x的值代入化简后的式子即可解答本题．本题考查分式的化简求值.解答本题的关键是明确分式化简求值的方法．19.【答案】解：（1）设今年5月份A款汽车每辆售价m万元．则：10 1101.第12页，共19页解得：m=21．经检验.m=21是原方程的根且符合题意．答：今年5月份A款汽车每辆售价21万元；（2）设购进A款汽车x辆．则：0 ≤ 0x+12（15-x）≤ ．解得： ≤x≤7．∵x的正整数解为3.4.5.6.7.∴共有5种进货方案；（3）设总获利为W万元.购进A款汽车x辆.则：W=（21-20）x+（13.8-12-a）（15-x）=28.4．解得：a=1时.该公司销售两款汽车的最大利润为28.4万元．【解析】（1）求单价.总价明显.应根据数量来列等量关系．等量关系为：今年的销售数量=去年的销售数量．（2）关系式为： 0 ≤A款汽车总价+B款汽车总价≤ ．（3）设总获利为W万元.购进A款汽车x辆.根据题意列出方程解答即可．本题考查分式方程和一元一次不等式组的综合应用.找到合适的等量关系及不等关系是解决问题的关键．20.【答案】（3.0）【解析】解：（1）如图.△A1B1C1为所作.点C1坐标为（3.0）；故答案为（3.0）；（2）如图.△A2B2C2为所作；（3）点B2.C2的坐标分别为（-2.5）.（-4.3）；（1）利用点平移的坐标特征写出A1、B1、C1的坐标.然后描点即可得到△A1B1C1；（2）利用网格特点和旋转的性质画出点A、B、C的对应点A2、B2、C2.从而得到△A2B2C2；（3）利用（2）中所画图形写出点B2.C2的坐标．. .本题考查了作图-旋转变换：根据旋转的性质可知.对应角都相等都等于旋转角.对应线段也相等.由此可以通过作相等的角.在角的边上截取相等的线段的方法.找到对应点.顺次连接得出旋转后的图形．也考查了平移变换．21.【答案】解：（1）∵四边形ABCD是正方形.∴BC=CD.∠BCD=∠CBG=∠D= 0°.∵BG=DP.∴△BCG≌△DCP（SAS）.∴CP=CG.∠BCG=∠DCP.∵∠PCG= °.∴∠BCG+∠DCP= °.∴∠DCP=∠BCG= . °.∴∠PCF=∠PCG+∠BCG= 7. °.在△PCG中.CP=CG.∠PCG= °.∴∠CPG=1（1 0°- °）= 7. °=∠PCF.∴PF=CF；（2）如图2.∵四边形ABCD是正方形. ∴∠CBG=∠BCD= 0°.过点C作CH⊥CG交AD的延长线于H.∴∠CDH= 0°=∠HCG．∴∠BCG=∠DCH.∴△BCG≌△DCH（ASA）.∴CG=CH.∵∠HCG= 0°.∠PCG= °.∴∠PCH= °=∠PCG.∵CP=CP.∴△PCH≌△PCG（SAS）.∴∠CPG=∠CPH.∵∠CPD+∠DCP= 0°.∴∠CPF+∠DCP= 0°.∵∠PCF+∠DCP= 0°.∴∠CPF=∠PCF.∴PF=CF；（3）如图3.连接PN.由（2）知.PF=CF. ∵EF⊥CP.∴PE=CE.∴EF是线段CP的垂直平分线.∴PN=CN.∴∠CPN=∠PCN.∵∠PCN= °.∴∠CPN= °.∴∠CNP= 0°.∵PE=CE.∴EN=1CP.在Rt△CDP中.CE=PE.第14页，共19页∴DE=CE=1CP.∴EN=DE.∴∠DNE=∠NDE.设∠DCP=α.∴∠CED=∠DCP=α.∴∠DEP= α.∵∠PEF= 0°.∴∠DEN= 0°+ α.∴∠NDE=1（1 0°-∠DEN）= °-α.∴∠NDC=∠NDE+∠CDE= °-α+α= °．【解析】（1）先判断出△BCG≌△DCP（SAS）.得出CP=CG.∠BCG=∠DCP.进而求出∠PCF=∠PCG+∠BCG= 7. °.再求出∠CPG= 7. °=∠PCF.即可得出结论；（2）先判断出△BCG≌△DCH（ASA）.得出CG=CH.进而判断出△PCH≌△PCG （SAS）.得出∠CPG=∠CPH.再用等角的余角相等判断出∠CPF=∠PCF.即可得出结论；（3）先判断出∠CNP= 0°.再判断出EN=DE.得出∠DNE=∠NDE.设∠DCP=α.表示出∠CED=∠DCP=α.∠DEP= α.即可得出结论．此题是四边形综合题.主要考查了正方形的性质.全等三角形的判定和性质.直角三角形的判定和性质.三角形的外角的性质.判断出EN=DE是解本题的关键．22.【答案】解：（1）设学校八年级共有x个班.则有（4x+20）个篮球.依题意得：0＜（4x+20）-8（x-1）＜8.解得5＜x＜7.∵x是整数.∴x=6.答：学校八年级共有6个班．（2）由（1）可知.篮球的个数是： × + 0= （个）所以44- × = （个）答：如果每个班分8个篮球.最后一个班分到的篮球个数是4个．【解析】（1）首先设学校共有x个班.则篮球有（4x+9）个.再根据关键语句“如果每个班分6个.则最后一个班能分到球但不超过2个”可得不等式组.再解不等式组即可．（2）根据（1）中的数据进行计算．此题主要考查了一元一次不等式组的应用.关键是弄清题意.设出未知数.根据不等关系列出不等式组．23.【答案】解：（1）∵E.F是BC.BD的中点.∴EF∥CD.∴∠BFE=∠BDC.∵∠FEM=∠FDC.∴∠BFE=∠FEM.∴DF∥EM.. .∵EF∥CD.∴四边形EFDM是平行四边形.∵EM∥BD.点E是BC的中点.∴点M是CD的中点.∴DM=1CD.∵点F是BD中点.∴DF=1BD.∵BD=CD.∴DF=DM.∵四边形DFEM是平行四边形.∴▱DFEM是菱形；（2）由旋转知.∠FEM=∠GEN.∴∠FEG=∠MEN.在Rt△ABD中.点F是BD中点.∴AF=DF.∴∠DAF=∠ADF.∵EF∥CD.∴∠ADF=∠DFE.∴∠DAF=∠DFE.∴∠AFE=∠AFD+∠EFD=∠AFD+∠ADF=∠CDF.∵EM∥BD.∴∠CDF=∠EMN.∴∠AFE=∠CME.由（1）知.四边形DFEM是菱形.∴EF=EM.∴△EFG≌△EMN（AAS）.∴EG=EN；（3）在Rt△ABC中.∠C= 0°.AB=2.∴BC=4.∠ABC= 0°.∵点E是BC的中点.∴CE=2.∵BD=CD.∴∠CBD=∠C= 0°.∴∠ABD= 0°.∴BD=.∴CD=.AF=1BD=.∵G是AF的中点.∴FG=1AF=.∵△EFG≌△EMN（AAS）.∴EG=EN.MN=FG=.第16页，共19页∵E.F是BC.BD的中点.∴EF=1CD=.∴DM=EF=.∴CN=CD-DM-MN=--=过点N作NH⊥BC于H∴EH=1CN=.CH=EH=1.∴EH=CE-CH=.在Rt△ENH中.EN== 1.∴EG= 1．【解析】（1）先判断出DF∥EM.进而判断出EF∥CD.得出四边形DFEM是平行四边形.再判断出DF=DM.即可得出结论；（2）先判断出∠FEG=∠MEN.进而判断出∠DAF=∠ADF.即可得出∠AFE=∠CDF.进而得出∠AFE=∠CME.进而判断出△EFG≌△EMN（AAS）.即可得出结论；（3）先求出BC=4.进而求出CE=2.BD=.CD=.进而求出FG=AF=.即可求出MN=FG=.再求出EF=CD=.进而得出CN=.即可求出EH=CN=.CH=EH=.进而得出EH=CE-CH=.最后用勾股定理即可得出结论．此题是四边形综合题.主要考查了直角三角形的性质.全等三角形的判定和性质.三角形中位线的性质.平行四边形的判定.菱形的判定和性质.判断出EG=EN是解本题的关键．24.【答案】解：（1）在Rt△AOB中.∵OA=2.∠ABO= 0°.∴OB=2.在Rt△OBC中.∵∠BCO= 0°.OB=2.∴OC=6.∴B（0.2）.C（6.0）.设直线AB的解析式为y=kx+b.则有.解得.∴直线AB的解析式为y=-x+2.设直线BC的解析式为y=k′x+b′则有′′′0.. .解得′.∴直线BC的解析式为y=x+2．（2）如图1中.根据对称性可知.当点F与O重合时.∠EF′D=∠EBD= 0°.此时F′（0.0）.设DE交OB于K.作FH⊥DE于H．当△EFD≌△DF′E时.∠EFD=∠DF′E= 0°.易证DK=EH=1.DE=1AC=4.∴KH=OF=4-2=2.∴F（-2.0）.综上所述.满足条件的点F坐标为（-2.0）或（0.0）．（3）如图2中.∵B（0.2）.C（（-6.0）.∴BC=4.当BC为正方形BCMN的边时.M（-6-2.6）.N（-2.2+6）或M′（2-6.-6）.N′（2.2-6）．当BC为正方形的对角线时.M″（-3-.3+）.N″（-3.-3）．【解析】（1）解直角三角形求出B、C两点坐标.利用待定系数法即可解决问题；（2）如图1中.根据对称性可知.当点F与O重合时.∠EF′D=∠EBD= 0°.第18页，共19页此时F′（0.0）；设DE交OB于K.作FH⊥DE于H．当△EFD≌△DF′E时.∠EFD=∠DF′E= 0°.想办法求出OF的长即可解决问题；（3）画出图形.分两种情形分别求解即可解决问题；本题考查一次函数综合题、解直角三角形、全等三角形的判定和性质、正方形的性质、待定系数法等知识.解题的关键是熟练掌握待定系数法.学会用分类讨论的思想思考问题.属于中考压轴题．25.【答案】（1）证明：∵四边形ABCD是平行四边形.∴AB∥CE.∵BE平分∠ABC.∴∠ABE=∠CBE.∴∠E=∠CBE.∴CB=CE.∵CF⊥BE.∴BF=EF．（2）∵四边形ABCD是平行四边形.∴AB=CD=6.∵DE=3.∴BC=CE=9.∴平行四边形ABCD的周长为30．【解析】（1）只要证明CB=CE.利用等腰三角形的三线合一的性质即可解决问题；（2）根据CE=CB.求出BC的长即可解决问题；本题考查平行四边形的性质、角平分线的定义、等腰三角形的判定和性质等知识.解题的关键是熟练掌握基本知识.属于中考常考题型．. .。

┃精选3套试卷┃2018届成都某名校初中八年级下学期期末统考物理试题

初二下学期期末物理试卷一、选择题（本题包括10个小题）1．小萱用天平测出6 个不同物体的质量m，再用弹簧测力计测出它们所受的重力G。

她根据所测数据绘制的图像如图所示。

根据图像提供的信息，下列判断正确的是（）A．该图像表明物体的质量跟其所受重力成正比B．该图像表明物体所受的重力跟其质量成正比C．该图像表明物体所受的重力跟其质量的比值为10D．根据数据点E 可知：质量为0.21kg 的物体受到的重力为2.1N【答案】B【解析】【分析】【详解】AB．根据图象可知这是一个正比例函数图象，两个物理量之间满足正比例函数关系，因此可得出的结论是：物体所受重力大小跟它的质量成正比，但因为质量是物质的属性，所以不能说物体的质量跟其所受重力成正比，故A错误，B正确；C．该图像表明物体所受的重力跟其质量的比值为10N/kg，故C错误；D．由图可知，数据点E 表示：质量为0.22kg 的物体受到的重力为2.2N，故D错误。

故选B。

2．如图甲所示,木块放在水平面上,用弹簧测力计沿水平方向拉木块使其做直线运动,两次拉动木块得到的s-t关系图象如图乙所示．两次对应的弹簧测力计示数分别为F1、F2,两次拉力的功率分别为P1、P2,下列判断正确的是( )A．F1>F2，P1>P2B．F1=F2，P1>P2C．F1>F2，P1=P2D．F1<F2，P1<P2【答案】B【解析】【分析】【详解】由图乙可知两次情况下，木块作匀速直线运动，所以拉力和摩擦力是一对平衡力，即F= f．因运动过程中所受摩擦力是滑动摩擦力，滑动摩擦力与压力和接触面粗糙程度有关，木块运动过程中压力和接触面粗糙程度不变，所以两次情况下摩擦力不变，即拉力F1＝F2，由图乙可知v1>v2，因为拉力功率P=Fv，F1＝F2，所以P1＞P2，故B符合题意．3．某实验小组分别用天平和量筒测出了两种物质的质量和体积，并描绘出V―m图像如图所示，则下列判断正确的是（）A．ρ甲＞ρ乙B．ρ甲＝ρ乙C．若V甲＝V乙，则m甲＜m乙D．若m甲＝m乙，则V甲＜V乙【答案】C【解析】【分析】【详解】AB．由图象可知，两物质体积V相同时，m甲＜m乙，由密度公式ρ=mV可知：ρ甲＜ρ乙，故AB错误；C．由图象可知，V甲=V乙时，m甲＜m乙，故C正确；D．由图象可知，m甲=m乙时，V甲＞V乙，故D错误；4．以下现象中没有利用大气压强的是（）A．吸盘紧贴在墙壁上B．用吸管吸瓶中的饮料C．把药液注射进肌肉里D．登山到达海拔较高地区时好多人有高原反应【答案】C【解析】【分析】【详解】A．吸盘要固定在墙壁上，需要先用力挤压塑料吸盘，把盘内的空气挤出，然后吸盘就被外界的大气压紧压在了墙壁上，故A项不符合题意；B．吸管吸饮料是利用大气压强，吸饮料时，是先把吸管内的空气吸走，在外界大气压的作用下，饮料就被压进吸管里，故B项不符合题意；C．把药液注入肌肉，是靠活塞推进产生的压强，不是利用大气压强，故C项符合题意；D．高度越高，气压越小，登山到达海拔较高地区时，由于外界的气压小，会使得呼吸困难，容易产生高原反应，故D项不符合题意。

2018年成都市锦江区八年级物理下期期末试题

成都市锦江区2018年八年级物理下期期末试题A卷(满分100分)第1卷(选择题共30分)一、单项选择题（每题2分，共30分）1.如图所示的四个实验中，目的是为了减小摩擦的是（）A．运动员在手上涂抹镁粉 B．浴室地砖表面有凹凸花纹C．陆地冰球鞋上安装滚轮 D．汽车轮胎上安装防滑链2.关于力，下列说法正确的是（）A.自行车刹车时要用力捏闸，这是通过增加压力的方法来增大摩擦力的B.吃饭时，筷子与食物之间的摩擦是有害的C.对物体施加的力大小相同，力的作用效果一定相同D.固体对物体的压力一定等于它的重力3.下列器材或装置中，利用连通器原理工作的是（）A．自制气压计 B．注射器 C．乳牛自动喂水器 D．吸尘器4.关于力对物体做功，下列说法正确的是（）A．作用在物体上的力越大，做功越多B．用力扛着一袋米，沿水平方向前进，人对米袋做了功C．在光滑冰面上匀速滑行的冰块，是因为有力对它做功才一直运动的D.推出后的铅球在空中飞行过程中，运动员对铅球没有做功5.如图所示，能够运用流体压强与流速关系的知识来解释的是（）A.马德堡半球实验B.乘客要在站台上的安全线外等候C.火箭升空 D．壁虎靠脚上的“吸盘”在墙上爬行6.如图所示，人在水平路面上骑车，以下关于物体受力的描述正确的是（）A．自行车受到路面的支持力 B．路面受到人的压力C．人受到路面的支持力 D．人和自行车都受到路面的摩擦力7.下列估测正确的是（）A．一个鸡蛋的重大约为5ONB．中学生双脚站立对水平地面压强大约为1.5×104PaC.大气压对你的一只大拇指指甲表面的压力大约为1000ND．一本八下的物理课本从课桌上掉落到地面，课本重力做的功约为150J8.关于大气压强，下列说法正确的是（）A．大气由于重力作用只向下产生大气压强B．同一地点的位置和海拔高度不变，所以该处的大气压是不变的C.在其它条件相同时，海拔高度越高，大气压的值越小D．利用公式P=ρgh，测出地面大气密度和压强，就可以算出大气层的高度h9.通过初中物理八年级下册学习，我们知晓了许多伟大的科学家，领略了他们卓越的成就。

2017-2018学年成都市锦江区八年级(下)数学期末考试真卷

成都市锦江区2017-2018学年八年级下数学期末真卷精编（考试时间：120分满分：150分）A 卷（共100分）一、选择题（每小题3分，共30分）1、利用“分形”与“迭代”可以制作出很多精美的图形，以下是制作出的几个简单图形，其中是轴对称但不是中心对称的图形是（）A ．B ．C ．D ．2、下列等式从左到右的图形，属于因式分解的是（）A ．m （a ﹣b ）＝ma ﹣mbB ．2a 2+a ＝a （2a+1）C ．（x+y ）2＝x 2+2xy+y 2D ．m 2+4m+4＝m （m+4）+4 3、若分式35-x 有意义，则实数x 的取值范围是（） A ．x ＝0 B ．x ＝3 C ．x ≠0 D ．x ≠34、如图，直线m ∥n ，点A 在直线m 上，点B 、C 在直线n 上，AB ＝CB ，∠1＝70°，则∠BAC 等于（）A ．40°B ．55°C ．70°D ．110°5、一个多边形的边数由原来的3增加到n 时（n ＞3，且n 为正整数），它的外角和（）A ．增加（n ﹣2）×180°B ．减小（n ﹣2）×180°C ．增加（n ﹣1）×180°D ．没有改变 6、关于x 的分式方程332+=+-x a x x 有增根，则a 的值为（） A ．﹣3 B ．﹣5 C ．0 D ．27、已知y 是x 的正比例函数，且函数图象经过点（4，﹣6），则在此正比例函数图象上的点是（）A ．（2，3）B ．（﹣4，6）C ．（3，﹣2）D ．（﹣6，4）8、如图，将矩形ABCD 绕点A 顺时针旋转得到矩形AB ′C ′D ′的位置，旋转角为α（0＜α＜90°），若∠1＝110°，则∠α＝（）A ．10°B ．20°C ．25°D ．30°9、一次函数y ＝x ﹣1的图象交x 轴于点A ．交y 轴于点B ，在y ＝x ﹣1的图象上有两点（x 1，y 1）、（x 2，y 2），若x 1＜0＜x 2，则下列式子中正确的是（）A ．y 1＜0＜y 2B ．y 1＜0＜y 2C ．y 1＜﹣1＜y 2D ．y 2＜0＜y 110、如图，已知△ABC 的面积为12，点D 在线段AC 上，点F 在线段BC 的延长线上，且BC ＝4CF ，四边形DCFE 是平行四边形，则图中阴影部分的面积为（）A ．2B ．3C ．4D ．6二、填空题（本题共4个小题，每小题4分，共16分答案在答题卡上）11、分解因式：x 3﹣16x ＝．12、如图，平面直角坐标系中，A 、B 两点的坐标分别为（2，0）、（0，1），若将线段AB 平移至A 1B 1，点A 1的坐标为（3，1），则点B 1的坐标为．13、如图，在▱ABCD 中，AB ＝4，BC ＝6，∠ABC 的平分线交AD 于点E ，则ED ＝．14、如图，在△ABC 中，∠A ＝100°，∠B ＝30°，分别以点B ，C 为圆心，以大于21BC 长为半径作弧，两弧相交于点P 、点Q ，作直线PQ 交AB 于点D ，连接CD ．则∠ACD ＝．三、解答题（共54分）15、（每小题6分，共12分）（1）因式分解：3x 2﹣6xy+3y 2．（2）解分式方程：4161222-=-+-x x x ．16、（6分）解不等式组：()⎪⎩⎪⎨⎧+≤--+<-21513121315x x x x 并在数轴上表示出它的解集．17．（8分）化简求值：11112122---+÷+--a a a a a a a ，其中a ＝12-．18、（8分）如图，在平面直角标系中，△ABC的三个顶点坐标为A（﹣3，4）、B（﹣4，2）、C（﹣2，1），△ABC绕原点顺时针旋转180°，得到△A1B1C1，再将△A1B1C1向左平移5个单位得到△A2B2C2（1）画出△A1B1C1，并写出点A的对应点A1的坐标；（2）画出△A2B2C2，并写出点A的对应点A2的坐标；（3）P（a，b）是△ABC的边AC上一点，△ABC经旋转，平移后点P的对应点分别为P1、P2，请直接写出点P2的坐标．19、（10分）如图，在Rt△ABC中，∠ACB＝90°，点D，E分别是边AB，AC的中点，连接DE，DC，过点A作AF∥DC交DE的延长线于点F，连接CF．（1）求证：DE＝FE；（2）求证：四边形BCFD是平行四边形；（3）若AB＝6，∠BAC＝30°，求四边形ADCF的面积．20、（10分）如图，菱形ABCD的对角线AC，BD相交于点O，延长AC到E，使CE＝CO，连接EB，ED．（1）求证：EB＝ED；（2）过点A作AF⊥AD，交BC于点G，交BE于点F，若∠AEB＝45°，①试判断△ABF的形状，并加以证明；②设CE＝m，求EF的长（用含m的式子表示）．B 卷(共50分）一、填空题（每小题4分，共20分）21、若311=-y x ，则分式yxy x y xy x 25233-+-+＝． 22、已知不等式⎩⎨⎧>-<-3212b x a x 的解集为﹣1＜x ＜1，求（a+1）（b ﹣1）的值为．23、如图，AC ，BD 是四边形ABCD 的对角线，AD ⊥BD ，点E 为AB 的中点，连接DE 交AC 于点F ，AF ＝CF ，DF ＝31DE ．若BC ＝12，则AB 长为．24、如图，矩形ABCO 的边OC 在x 轴上，边OA 在y 轴上，且点C 的坐标为（8，0），点A 的坐标为（0，6），点E 、F 分别足OC 、BC 的中点，点M ，N 分别是线段OA 、AB 上的动点（不与端点重合），则当四边形EFNM 的周长最小时，点N 的坐标为．25、如图，正方形ABCD 的边长AB ＝3，点E 、F 分别是CB ，DC 延长线上的点，连AF 交CB 于点G ，若BE ＝1，连接AE ，且∠EAF ＝45°，则AG 长为．二、解答题（共30分）26、（8分）在成都“白环改建工程中，某F罕轿建设将由甲，乙两个工程队共同施工完成，据调查得知：甲，乙两队单独完成这项上程所需天数之比为4：5，若先由甲，乙两队合作40天，剩下的工程再乙队做10天完成，（1）求甲．乙两队单独完成这取工程各需多少天？（2）若此项工程由甲队做m天，乙队n天完成，①请用含m的式子表示n；②已知甲队每天的施工费为15万元，乙队每天的施工费用为10万元，若工程预算的总费用不超过1150万元，甲队工作的天数与乙队工作的天数之和不超过90天．请问甲、乙两队各工作多少天，完成此项工程总费用最少？最少费用是多少？27、（10分）如图，△ABC与△ADE都为等腰直角三角形，∠ABC＝∠ADE＝90°，连接BD，EC，且F为EC 的中点．（1）如图1，若D、A、C三点在同一直线上时，请判DF与BF的关系，并说明理由；（2）如图2，将图1中的△ADE绕点A逆时针旋转m°（0＜m＜90），请判断（1）中的结论是否仍然成立？并证明你的判断；（3）在（2）下，若△DEF与△BCF的面积之和于△DBF的面积，请直接写出m的值．28、（12分）已知菱形ABCD 的边长为5，其顶点都在坐标轴上，且点A 坐标为（0，﹣3）．（1）求点B 的坐标及菱形ABCD 的面积；（2）点P 是菱形边上一动点，沿A →B →C →D 运动（到达D 点时停止）①如图1，当点P 关于x 轴对称的点Q 恰好落在直线334-=x y 上时，求点P 的坐标． ②探究：如图2，当P 运动到BC ，CD 边时，作△ABP 关于直线AP 的对称图形为△AB ′P ，是否存在这样的P 点，使点B ′正好在直线334-=x y 上？若存在，求出满足条件的点P 坐标；若不存在，请说明理由．。

成都市锦江区八年级下学期语文期末考试试卷

成都市锦江区八年级下学期语文期末考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共7题；共14分)1. （2分）请选出下列划线字字音全对的一项（）A . 绯红（fēi）咫尺（zhǐ）迁徙（xí）期期艾艾（ài）B . 管束（sù）哂笑（shěn）文绉绉（zhōu）相形见绌（zhuō）C . 黝黑（yǒu）愚钝（yú）禁锢（gù）藏污纳垢（gòu）D . 吞噬（shì）媲美（bì）缄默（jiān）广袤无垠（mò）2. （2分）下列句子中划线的词语使用不恰当的一项是（）A . 当四野蛙声和其他虫鸣暂时沉寂时，我所听到的一点歌声则是非常柔和的，与夜色苍茫中的静谧气氛是再合适不过了。

B . 如果一只主教雀对着暖流歌唱起春天来，却发现自己搞错了，它还可以纠正自己的错误，继续保持它在冬季的缄默。

C . “水光潋滟晴方好”，从游船上纵目四望，西子湖春风送暖，碧波荡漾，长堤缀绿，群山围翠，真是赏心悦目。

D . 电影《狼图腾》，以场面的气势恢宏、情节的抑扬顿挫和风格的奇异独特，赢得了广大观众的一致好评。

3. （2分）马致远属于哪一个朝代？（）A . 宋B . 元C . 明D . 清4. （2分）下列句子中，没有语病的一项是（）A . 时至今日，距2013年中考还有大概不到一年左右的时间。

B . 他们需要得到鼓励，呵护和照顾。

C . 第十三届青歌赛，有我市两名歌手加盟的“兄妹组合”夺得了原生态唱法金奖。

D . 我渐渐为病损的枝叶可怜，虽则我恼怒它的固执，无亲热，我依旧不放走它。

5. （2分）提取下面句子的主干，正确的一项是（）。

英国一名专家援引最新证据提出中国明朝率领船队远航的郑和是历史上比哥伦布等西方航海家更早发现新大陆的第一个环绕地球航行的探险者的惊人学说。

A . 郑和比西方航海家更早发现新大陆。

四川省成都市八级下期末数学试卷含

2017-2018 学年四川省成都市金牛区八年级（下）期末数学试卷副标题题号一二三四总分得分一、选择题（本大题共8 小题，共 24.0 分）1.若等腰三角形一个内角为100°，则此等腰三角形的顶角为（）A. B. C.或 D.2.已知 a＜b，以下不等式中正确的选项是（）A. B. C. D.3.已知关于 x 的分式方程无解，则 k 的值为（）A. 0或 C. 0或4.分式有意义的条件是（）A. B. C. D.5.如图，菱形 ABCD 的对角线 AC 与 BD 交于点 O，过点 C 作 AB 垂线交 AB 延长线于点 E，连接 OE，若 AB=2 ，BD=4，则 OE 的长为（）A.6B.5C.D. 46.以下列图形中，既是轴对称图形又是中心对称图形的是（）A. B. C. D.7.已知四边形 ABCD，对角线 AC 与 BD 交于点 O，从以下条件中：①AB∥CD；② AD=BC；③∠ABC=∠ADC；④OA=OC，任取其中两个，以下组合可以判断四边形ABCD 是平行四边形的是（）A. ①②B. ②③C. ②④D. ①④8. 已知关于 x 的不等式组的解集是x≥1，则a的取值范围是（）A. B. C. D.二、填空题（本大题共8 小题，共32.0 分）9. 已知关于 x、y 方程组的解满足x＞1，y≥2，则k的取值范围是______．10.已知关于 x 的分式方程=a 有解，则 a 的取值范围是 ______．11.多项式 x2-kx+6 因式分解后有一个因式为 x-2，则 k 的值为 ______．12.如图，在矩形 ABCD 中， BC= AB，∠ADC 的均分线交边 BC 于点 E，AH ⊥DE 于点 H，连接 CH 并延长交边 AB 于点 F，连接 AE 交 CF 于点 O，则的值是 ______．13.如图，在平行四边形 ABCD 中，∠A=45°，AB=4，AD=2 ，M 是 AD 边的中点， N 是 AB边上一动点，将线段 M 绕点 M 逆时针旋转 90 至 MN′，连接 N′B，N′C，则 N′B+N′C 的最小值是 ______．14.已知 ab≠0，a2+2ab-3b2 =0，那么分式的值等于 ______．15.如图，在△ABC 中，BF 均分∠ABC， AG⊥BF，垂足为点 D，交 BC于点 G，E 为 AC 的中点，连接 DE，，AB=4cm，则 BC的长为 ______cm．16.17.18.如图，一次函数 y1=-2x+m 与 y2=ax+6 的图象订交于点 P（-2，3），则关于 x 的不等式 m-2x＜ ax+6 的解集是 ______19.20.21.22.23.24.三、计算题（本大题共 3 小题，共28.0 分）25. （1）分解因式： 2mx2-4mxy+2my2．26. （2）解方程：．27.28.29.30.31.32.33.34. 先化简，再求值：，其中x=-3．35.36.37.38.39.40.41.42.某新能源汽车销售公司销售 A 品牌电动汽车，今年 5 月份电动汽车的售价比昨年同期降价了 1 万元，若是销售的数量相同，昨年 5 月份的销售额为 110 万元，今年 5 月份的销售额就只有 105 万元．43.（1）求今年 5 月份 A 品牌电动汽车的售价；44.（2）该公司同时销售 B 品牌混杂动力汽车，已知 A、B 品牌汽车的进价分别为 20 万元 / 辆、12 万元 /辆，若公司预计用不高出 236 万元且很多于 204 万元的资本购进两款汽车共 15 辆，求公司的进货方案有多少种？45.（3）在（2）的条件下，今年 5 月份 B 品牌汽车的售价为 13.8 万元 /辆，且每售出一辆 A品牌电动汽车，政府将恩赐公司 a 万元奖励（ 0＜α＜ 2），已知该公司销售两款汽车的最大利润为 28.4 万元，求 a 的值．46.47.48.49.50.51.52.四、解答题（本大题共 6 小题，共56.0 分）53.在平面直角坐标系中，△ABC 的地址以下列图：（每个小方格都是边长为 1 个单位长度的正方形）54.（1）将△ABC 沿 y 轴方向向下平移 4 个单位长度获取△A1B1C1，则点 C1坐标为 ______；55.（2）将△ABC 绕着点 O 逆时针旋转 90°，画出旋转后获取的△△A2B2C2；56.（3）直接写出点 B2，C2的坐标．57.（1）如图 1，正方形 ABCD 中，∠PCG=45°，且 PD=BG，求证： FP=FC；58.（2）如图 2，正方形 ABCD 中，∠PCG=45°，延长 FG 交 CB 的延长线于点 F，（ 1）中的结论还成立吗？请说明原由；59.（3）在（ 2）的条件下，作 FE⊥PC，垂足为点 E，交 CG 于点 N，连接 DN，求∠NDC的度数．60.61.在某学校的八年级课外活动中，体育组想把篮球分给班级活动用，若是每个班分 4 个篮球，则节余 20 个篮球；若是每个班分 8 个篮球，则最后一个班分到的篮球个数不到 8 个（也不为 0 个），问：62.（1）这个学校八年级共有几个班？63.（2）若是每个班分 8 个篮球，最后一个班分到的篮球个数终究是多少个？64.65.66.67.68.69.70.71.在直角三角形 ABC 中，∠BAC=90°，（ AC＞ AB），在边 AC 上取点 D，使得 BD=CD，点 E、F 分别是线段 BC、BD 的中点，连接 AF 和 EF，作∠FEM=∠FDC，交 AC 于点 M，如图 1 所示，72.（1）请判断四边形 EFDM 是什么特其他四边形，并证明你的结论；73.（2）将∠FEM 绕点 E 顺时针旋转到∠GEN，交线段 AF 于点 G，交 AC 于点 N，如图 2所示，请证明： EG=EN；74.（3）在第（ 2）条件下，若点 G 是 AF 中点，且∠C=30°，AB=2，如图 3，求 GE 的长度．75.76.如图，在平面直角坐标系中，直线 AB 分别交 x、y 轴于点 A、B，直线 BC 分别交 x、y轴于点 C、B，点 A 的坐标为（ 2， 0），∠ABO=30，且 AB⊥BC．77.（1）求直线 BC 和 AB 的解析式；78.（2）将点 B 沿某条直线折叠到点 0，折痕分别交 BC、BA 于点 E、D，在 x 轴上可否存在点 F，使得点 D、E、 F 为极点的三角形是以 DE 为斜边的直角三角形？若存在，央求出 F 点坐标；若不存在，请说明原由；79.（3）在平面直角坐标系内可否存在两个点，使得这两个点与 B、C 两点构成的四边形是正方形？若存在，请直接写出这两点的坐标；若不存在，请说明原由．80.如图，在 ?ABCD 中， BE 均分∠ABC 交 CD 延长线于点 E，作 CF⊥BE 于 F．81.（1）求证： BF=EF；82.（2）若 AB=6，DE=3，求 ?ABCD 的周长．答案和解析1.【答案】 A【解析】解：① 当这个角是顶角时，底角=（180°-100 °）÷2=40°；②当这个角是底角时，另一个底角为 100 °，因为 100 °+100 °=200 °，不吻合三角形内角和定理，所以舍去．应选：A．题中没有指明已知的角是顶角还是底角，故应该分状况进行解析，进而求解．此题主要观察等腰三角形的性质及三角形内角和定理的综合运用，要点是分状况进行解析．2.【答案】 B【解析】解：A 、两边都除以 2，不等号的方向不变，故A 错误；B、两边都减 1，不等号的方向不变，故B 正确；C、两边都乘 -1，不等号的方向改变，故 C 错误；D、两边都加 3，不等号的方向不变，故D 错误；应选：B．依照不等式的性质，可得答案．此题观察了不等式的性质，利用不等式的性质是解题要点．3.【答案】 D【解析】解：分式方程去分母得：x=3kx+3k ，即（3k-1）x=-3k ，当 3k-1=0，即k=时，方程无解；当 k≠时，x=时k=0，=0 或-1，方程无解，此综上，k 的值为 0 或，应选：D．分式方程去分母转变成整式方程，由分式方程无解确定出j 的值即可．此题观察了分式方程的解，始终注意分母不为 0 这个条件．4.【答案】 C【解析】解：由题意可知：x- 2≠0，∴x ≠ 2应选：C．依照分式有意义的条件即可求出答案．此题观察分式有意义的条件，解题的要点是熟练运用分式有意义的条件，此题属于基础题型．5.【答案】 D【解析】解：∵四边形 ABCD 是菱形，∴OA=OC ，BD ⊥AC ，∵CE⊥AB ，∴OE=OA=OC ，∵BD=4，∴OB= BD=2，在 Rt△AOB 中，AB=2，OB=2，∴OA==4，∴OE=OA=4 ．应选：D．先判断出 OE=OA=OC ，再求出 OB=1，利用勾股定理求出 OA ，即可得出结论．此题主要观察了菱形的判断和性质，平行四边形的判断和性质，角均分线的定义，勾股定理，判断出 CD=AD=AB 是解此题的要点．6.【答案】 D【解析】解：A 、不是轴对称图形，是中心对称图形，故此选项错误；B、不是轴对称图形，也不是中心对称图形，故此选项错误；C、不是轴对称图形，是中心对称图形，故此选项错误；D、是轴对称图形，也是中心对称图形，故此选项正确．应选：D．依照轴对称图形与中心对称图形的看法求解．此题观察了中心对称图形与轴对称图形的看法：轴对称图形的要点是搜寻对称轴，图形两部分沿对称轴折叠后可重合；中心对称图形是要搜寻对称中心，旋转 180 度后与原图重合．7.【答案】 D【解析】解：以①④ 作为条件，可以判断四边形 ABCD 是平行四边形．原由：∵AB ∥CD，∴∠OAB= ∠OCD，在△AOB 和△COD 中，，∴△AOB ≌△COD（ASA ），∴OB=OD ，∴四边形 ABCD 是平行四边形．应选：D．以①④ 作为条件可以判断四边形 ABCD 是平行四边形，依照平行得出全等三角形，即可求出 OB=OD ，依照平行四边形的判断推出即可；此题观察了平行四边形的判断，相似三角形的性质和判断，等腰梯形的判断等知识点的应用，主要观察学生的推理能力和辨析能力，题目比较好，但是一道比较简单出错的题目．8.【答案】 C【解析】解：∵关于 x 的不等式组的解集是x≥1，∴a＜1，应选：C．利用不等式取解集的方法判断即可确定出 a 的范围．此题观察了不等式的解集，熟练掌握不等式取解集的方法是解本题的要点．9.【答案】 -1≤k＜1【解析】解：，解得：，∵x ＞1，y ≥2，∴解得：-1≤k＜1，故答案为：-1≤k＜1．解方程组获取含有 k 的 x 和与，依照 x＞ 1，y≥2，获取关于 k 的一元一次不等式组，解之即可．此题观察解一元一次不等式组和解二元一次方程组，依照不等量关系列出不等式组是解题的要点．10.【答案】 a≠2【解析】解：分式方程去分母得：2a+1=ax+a，整理得：（a-2）x=1-a，时当 a-2≠0，即a≠2，x=，由分式方程有解，获取≠-1，解得：a≠2，则 a 的范围是 a≠2．分式方程去分母转变成整式方程，表示出分式方程的解，确定出 a 的范围即可．此题观察了分式方程的解，始终注意分母不为 0 这个条件．11.【答案】 5 【解析】解：∵多项式 x 2-kx+6 因式分解后有一个因式为 x-2，∴另一个因式是（x-3），即x 2-kx+6= （x-2）（x-3）=x 2-5x+6，则 k 的值为 5，故答案为：5利用十字相乘法法判断即可．此题观察了因式分解的意义，熟练掌握因式分解的方法是解本题的要点．12.【答案】【解析】解：在矩形 ABCD 中，AD=BC= AB= CD ，∵DE 均分 ∠ADC ，∴∠ADE= ∠CDE=45°， ∵AH ⊥DE ，∴△ADH 是等腰直角三角形， ∴AD= AB ， ∴AH=AB=CD ，∵△DEC 是等腰直角三角形，∴DE= CD ， ∴AD=DE ，∴∠AEH=67.5 °， ∴∠EAH=22.5 °，∵DH=CD ，∠EDC=45°， ∴∠DHC=67.5 °， ∴∠OHA=22.5 °， ∴∠OAH= ∠OHA ， ∴OA=OH ，∴∠AEH= ∠OHE=67.5 °， ∴OH=OE ，∴OH= AE ，即= ．故答案为：．依照矩形的性质获取 AD=BC=AB=CD ，由DE 均分 ∠ADC ，获取△ADH 是等腰直角三角形，△DEC 是等腰直角三角形，获取 DE= CD ，获取等腰三角形求出 ∠°，∠AEB=180°-45 °-67.5 =67°.5 ，°进而求出 △AOH 和△OEH 是等腰三角形，即可得出结论．此题观察了矩形的性质，角均分线的定义，等腰三角形的判断与性质，熟记各性质并仔细分析题目条件，依照相等的度数求出相等的角，进而判断出等腰三角形是解题的要点，也是本题的难点．13.【答案】 2【解析】解：如图，作ME ⊥AD 交 AB 于 E，连接 EN′、AC 、作 CF⊥AB 于 F．∵∠MAE=45°，∴△MAE 是等腰直角三角形，∴MA=ME ，∵∠AME= ∠NMN′ =90 °，∴∠AMN= ∠EMN′，∵MN=MN′，∴△AMN ≌△EMN′，∴∠MAN= ∠MEN′ =45，°∴∠AEN′ =90，°∴EN′⊥AB ，∵AM=DM=，AB=4，∴AE=2，EB=2，∴AE=EB ，∴N′ B=N′A，∴N′ B+N′ C=N′ A+N，′C∴当 A 、N′、C 共线时，N′ B+N′C的值最小，最小值 =AC，在 Rt△BCF 中，∵BC=AD=2，∠CBF=∠DAB=45°，∴CF=BF=2，在 Rt△ACF 中，AC==2，故答案为 2．如图，作ME⊥AD连证为交AB于E，接 EN′、AC 、作CF⊥AB 于 F．第一明 AN′=BN′，因N′ B+N′ C=N′ A+N，′C即可推出当 A 、N′、C 共线时，N′ B+N′C的值最小，最小值=AC；此题观察平行四边形的性质、旋转变换、两点之间线段最短、全等三角形的判断和性质、勾股定理等知识，解题的要点是学会增加常用辅助线，构造全等三角形解决问题，学会用转变的思想思虑问题，属于中考填空题中的压轴题．14.【答案】 3 或【解析】解：∵a 2+2ab-3b 2=0，∴（a 2-b 2）+（2ab-2b 2）=0，∴（a+b ）（a-b ）+2b （a-b ）=0， ∴（a-b ）（a+3b ）=0， ∴a-b=0 或 a+3b=0， ∴a=b 或 a=-3b ．当 a=b 时，原式 =（ab ≠0）=3；当 a=-3b 时，原式 =ab ≠0=（）．故答案为：3 或．先将条件变形为 a 2+2ab-2b 2-b 2=0，得（a 2-b 2）+（2ab-2b 2）=0，得（a+b ）（a-b ）+2b （a-b ）=0，（a-b ）（a+3b ）=0，再将 a 用含 b 的式子表示出来代入代数式就可以求出结论．此题观察了利用因式分解把一个字母用另一个字母表示出来代入代数式求出其值的运用．在解答时注意不要漏解．15.【答案】【解析】解：∵BF 均分 ∠ABC ，AG ⊥BF ， ∴△ABG 是等腰三角形， ∴AB=GB=4cm ， ∵BF 均分 ∠ABC ， ∴AD=DG ，∵E 为 AC 的中点，∴DE 是△AGB 的中位线，∴DE=CG，∴CG=2DE=5cm，∴，故答案为：由条件“BF均分∠ABC ，AG ⊥BF”可判断三角形 ABG 是等腰三角形（AB=GB ），再由条件“E为AC 的中点”，可判断 DE 是三角形 AGB 的中位线，由此可得 GC=2DE，进而可求出 BC 的长．此题观察了等腰三角形的判断和性质、三角形中位线定理的运用，熟记判断等腰三角形的各种方法是解题的要点．16.【答案】 x＞-2【解析】解：观察函数图象可知：当 x＞-2 时，一次函数 y1=-2x+m 的图象在 y2=ax+6 的图象的下方，∴关于 x 的不等式 m-2x＜ ax+6 的解集是 x ＞-2．故答案为 x＞-2．观察函数图象，依照两函数图象的上下地址关系即可找出关于x 的不等式m-2x＜ax+6 的解集．此题观察了一次函数与一元一次不等式，依照两函数图象的上下地址关系找出不等式的解集是解题的要点．17.【答案】解：（ 1）原式 =2m（x2-2xy+y2） =2m（x-y）2；（2）两边都乘以 x-2，得： 1-x=x-2+3，解得： x=0，检验： x=0 时， x-2=-2≠0，所以原分式方程的解为x=0．【解析】（1）先提取公因式 2m，再利用完好平方公式分解可得；（2）分式方程去分母转变成整式方程，求出整式方程的解获取 x 的值，经检验即可获取分式方程的解．此题观察了提公因式与解分式方程，解分式方程的基本思想是“转变思想”，把分式方程转变为整式方程求解．解分式方程必然注意要验根．18.【答案】解：==，当 x= -3 时，原式 =====．【解析】依照完好平方公式和提公因式法可以化简题目中的式子，尔后将 x 的值代入化简后的式子即可解答本题．此题观察分式的化简求值，解答此题的要点是明确分式化简求值的方法．19.【答案】解：（ 1）设今年 5 月份 A 款汽车每辆售价m 万元．则：，解得： m=21．经检验， m=21 是原方程的根且吻合题意．答：今年 5 月份 A 款汽车每辆售价21 万元；（2）设购进 A 款汽车 x 辆．则：204≤ 20x+12（ 15-x）≤ 236．解得： 3≤x≤7．∵x 的正整数解为 3，4，5，6，7，∴共有 5 种进货方案；（3）设总盈利为 W 万元，购进 A 款汽车 x 辆，则：W=（21-20）x+（）（ 15-x）．解得： a=1 时，该公司销售两款汽车的最大利润为28.4 万元．【解析】（1）求单价，总价明显，应依照数量来列等量关系．等量关系为：今年的销售数量 =昨年的销售数量．（2）关系式为：204≤A款汽车总价+B 款汽车总价≤236．（3）设总盈利为 W 万元，购进 A 款汽车 x 辆，依照题意列出方程解答即可．此题观察分式方程和一元一次不等式组的综合应用，找到合适的等量关系及不等关系是解决问题的要点．20.【答案】（3， 0）【解析】解：（1）如图，△A 1B1C1为所作，点 C1坐标为（3，0）；故答案为（3，0）；（2）如图，△A 2B2C2为所作；（3）点B2，C2的坐标分别为（-2，5），-（4，3）；（1）利用点平移的坐标特点写出 A 1、B1、C1的坐标，尔后描点即可获取△A 1B1C1；（2）利用网格特点和旋转的性质画出点 A 、B、C 的对应点 A2、B2、C2，进而获取△A2B2C2；（3）利用（2）中所画图形写出点 B2，C2的坐标．此题观察了作图-旋转变换：依照旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以经过作相等的角，在角的边上截取相等的线段的方法，找到对应点，按次连接得出旋转后的图形．也观察了平移变换．21.【答案】解：（ 1）∵四边形 ABCD 是正方形，∴BC=CD，∠BCD=∠CBG=∠D=90 °，∵BG=DP，∴△BCG≌△DCP（SAS），∴CP=CG，∠BCG=∠DCP，∵∠PCG=45 °，∴∠BCG+∠DCP=45 °，∴∠DCP=∠BCG=22.5 ，°∴∠PCF=∠PCG+∠BCG=67.5 ，°在△PCG 中， CP=CG，∠PCG=45°，∴∠CPG= （180°-45 °）=67.5 °=∠PCF，∴PF=CF；（2）如图 2，∵四边形 ABCD 是正方形，∴∠CBG=∠BCD=90 °，过点 C 作 CH⊥CG 交 AD 的延长线于 H，∴∠CDH=90 °=∠HCG．∴∠BCG=∠DCH，∴△BCG≌△DCH （ASA），∴CG=CH，∵∠HCG=90 °，∠PCG=45 °，∴∠PCH=45 °=∠PCG，∵CP=CP，∴△PCH≌△PCG（ SAS），∴∠CPG=∠CPH，∵∠CPD+∠DCP=90 °，∴∠CPF+∠DCP=90 °，∵∠PCF+∠DCP=90 °，∴∠CPF=∠PCF，∴PF=CF；（3）如图 3，连接 PN，由（ 2）知， PF=CF，∵EF⊥CP，∴PE=CE，∴EF 是线段 CP 的垂直均分线，∴PN=CN，∴∠CPN=∠PCN，∵∠PCN=45 °，∴∠CPN=45 °，∴∠CNP=90 °，∵PE=CE，∴EN= CP，在Rt△CDP 中，CE=PE，∴DE=CE= CP，∴EN=DE，∴∠DNE=∠NDE，设∠DCP=α，∴∠CED=∠DCP=α，∴∠DEP=2α，∵∠PEF=90 °，∴∠DEN=90 ° +2，α∴∠NDE= （180°-∠DEN）=45°-α，∴∠NDC=∠NDE+∠CDE=45 °-α +α =45．°【解析】（1）先判断出△BCG≌△DCP（SAS），得出CP=CG，∠BCG=∠DCP，进而求出∠PCF=∠PCG+∠BCG=67.5 °，再求出∠CPG=67.5 °=∠PCF，即可得出结论；（2）先判断出△BCG≌△DCH （ASA ），得出CG=CH，进而判断出△PCH≌△PCG（SAS），得出∠CPG=∠CPH，再用等角的余角相等判断出∠CPF=∠PCF，即可得出结论；（3）先判断出∠CNP=90°，再判断出 EN=DE，得出∠DNE=∠NDE ，设∠DCP=α，表示出∠CED=∠DCP=α，∠DEP=2α，即可得出结论．此题是四边形综合题，主要观察了正方形的性质，全等三角形的判断和性质，直角三角形的判断和性质，三角形的外角的性质，判断出 EN=DE 是解此题的要点．22.【答案】解：（ 1）设学校八年级共有 x 个班，则有（ 4x+20）个篮球，依题意得： 0＜（ 4x+20） -8（x-1）＜ 8，解得 5＜x＜7，∵x 是整数，∴x=6，答：学校八年级共有 6 个班．（2）由（1）可知，篮球的个数是：4×6+20=44（个）所以 44-5 ×8=4（个）答：若是每个班分 8 个篮球，最后一个班分到的篮球个数是 4个．【解析】（1）第一设学校共有 x 个班，则篮球有（4x+9）个，再依照要点语句“若是每个班分 6 个，则最后一个班能分到球但不超过 2 个”可得不等式组，再解不等式组即可．（2）依照（1）中的数据进行计算．此题主要观察了一元一次不等式组的应用，要点是弄清题意，设出未知数，依照不等关系列出不等式组．23.【答案】解：（ 1）∵E，F 是 BC， BD 的中点，∴EF∥CD，∴∠BFE=∠BDC，∵∠FEM=∠FDC ，∴∠BFE=∠FEM ，∴DF ∥EM，∵EF∥CD，∴四边形 EFDM 是平行四边形，∵EM∥BD，点 E 是 BC 的中点，∴点 M 是 CD 的中点，∴DM= CD，∵点F是BD中点，∴DF= BD，∵BD=CD，∴DF=DM，∵四边形 DFEM 是平行四边形，∴?DFEM 是菱形；（2）由旋转知，∠FEM=∠GEN，∴∠FEG=∠MEN，在 Rt△ABD 中，点 F 是 BD 中点，∴AF=DF，∴∠DAF=∠ADF，∵EF∥CD，∴∠ADF=∠DFE，∴∠DAF=∠DFE，∴∠AFE=∠AFD+∠EFD =∠AFD+∠ADF=∠CDF，∵EM∥BD，∴∠CDF=∠EMN，∴∠AFE=∠CME，由（ 1）知，四边形 DFEM 是菱形，∴EF=EM，∴△EFG≌△EMN（AAS），∴EG=EN；（3）在 Rt△ABC 中，∠C=30°， AB=2，∴BC=4，∠ABC=60 °，∵点 E 是 BC 的中点，∴CE=2，∵BD=CD，∴∠CBD=∠C=30 °，∴∠ABD=30 °，∴BD=，∴CD=，AF= BD=，∵G 是 AF 的中点，∴FG= AF=，∵△EFG≌△EMN（AAS），∴EG=EN，MN=FG=，∵E，F 是 BC， BD 的中点，∴EF= CD=，∴DM=EF=，∴CN=CD-DM-MN= - - =过点 N作 NH⊥BC于 H∴EH= CN=，CH=EH= ，∴EH=CE-CH= ，在 Rt△ENH 中， EN==，∴EG=．【解析】（1）先判断出 DF∥EM ，进而判断出 EF∥CD，得出四边形 DFEM 是平行四边形，再判断出DF=DM ，即可得出结论；进进（2）先判断出∠FEG=∠MEN ，而判断出∠DAF= ∠ADF ，即可得出∠AFE= ∠CDF，而得出∠AFE=∠CME ，进而判断出△EFG≌△EMN （AAS ），即可得出结论；（3）先求出BC=4，进而求出 CE=2，BD=，CD=，进而求出 FG= AF=，即可求出MN=FG=，再求出 EF=CD=进，即可求出 EH= CN=，CH=进，而得出 CN=EH=，而得出 EH=CE-CH=，最后用勾股定理即可得出结论．此题是四边形综合题查质，全等三角形的判断和性质，三角形中，主要考了直角三角形的性位线的性质，平行四边形的判断，菱形的判断和性质，判断出 EG=EN 是解此题的要点．24.【答案】解：（ 1）在 Rt△AOB 中，∵OA=2，∠ABO=30°，∴OB=2，在 Rt△OBC 中，∵∠BCO=30°， OB=2 ，∴OC=6，∴B（0，2），C（6，0），设直线 AB 的解析式为 y=kx+b，则有，解得，∴直线 AB 的解析式为 y=-x+2，设直线 BC 的解析式为 y=k′x+b′则有，解得，∴直线 BC 的解析式为 y=x+2．（2）如图 1 中，依照对称性可知，当点 F 与 O 重合时，∠EF′D=∠EBD=90°，此时 F（′0，0），设 DE 交 OB 于 K，作 FH ⊥DE 于 H．当△EFD ≌△DF ′E 时，∠EFD=∠DF ′E=90°，易证 DK=EH=1， DE= AC=4，∴KH=OF=4-2=2，∴F（ -2，0），综上所述，满足条件的点 F 坐标为（ -2，0）或（ 0， 0）．（3）如图 2 中，∵B（0，2），C（（-6，0），∴BC=4，当 BC 为正方形 BCMN 的边时， M（-6-2，6），N（-2）或M′（2 -6，-6），，2 +6N′（2，2-6）．当 BC 为正方形的对角线时， M″（-3-，3+），N″（-3，-3）．【解析】（1）解直角三角形求出 B、C 两点坐标，利用待定系数法即可解决问题；（2）如图 1 中，依照对称性可知，当点 F 与 O 重合时，∠EF′D=∠EBD=90°，此时 F′（0，0）；设 DE交 OB 于 K ，作FH⊥DE 于 H．当△EFD≌△DF′E时，∠EFD=∠DF′E=90°，想方法求出OF 的长即可解决问题；（3）画出图形，分两种状况分别求解即可解决问题；此题观察一次函数综合题、解直角三角形、全等三角形的判断和性质、正方形的性质、待定系数法等知识，解题的要点是熟练掌握待定系数法，学会用分类谈论的思想思虑问题，属于中考压轴题．25.【答案】（1）证明：∵四边形 ABCD 是平行四边形，∴AB∥CE，∴∠E=∠ABE，∵BE 均分∠ABC，∴∠ABE=∠CBE，∴∠E=∠CBE，∴CB=CE，∵CF⊥BE，∴BF=EF．（2）∵四边形 ABCD 是平行四边形，∴AB=CD=6，∵DE=3，∴BC=CE=9，∴平行四边形 ABCD 的周长为 30．【解析】（1）只要证明 CB=CE，利用等腰三角形的三线合一的性质即可解决问题；（2）依照CE=CB，求出 BC 的长即可解决问题；此题观察平行四边形的性质、角均分线的定义、等腰三角形的判断和性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．。

〖汇总3套试卷〗成都市2018年八年级下学期物理期末统考试题

初二下学期期末物理试卷一、选择题（本题包括10个小题）1．关于惯性的理解和现象，以下说法正确的是（）A．高速行驶的火车不容易停下来，说明速度越大惯性越大B．物体只有保持匀速直线运动或静止时才有惯性C．行驶中的公交车紧急刹车时，乘客会向前倾，是由于惯性力的作用D．将衣服上的灰尘抖下去，利用了惯性【答案】D【解析】【分析】【详解】A．火车的质量大，其惯性也大，不易停下来，但惯性的大小与物体的速度无关，故A错误；B．惯性是物体的固有属性，一切物体在任何情况下都具有惯性，故B错误；C．行驶中的公交车紧急刹车时，乘客会向前倾，是由于乘客具有惯性，惯性不是力，不能说惯性力，故C错误；D．抖动衣服后，灰尘由于惯性仍将保持原来的运动状态，从衣服上面跑出来，这是利用了惯性，故D正确．2．对于热现象的描述，说法正确的是（）A．冰棍从冰箱拿出来时，包装袋外的“白粉”是凝固形成的B．冰棍包装袋周围出现的“白气”是汽化现象C．冰棍在口中觉得很冰凉，有熔化过程吸热的原因D．冰棍吸收热量的过程中，温度一定会不断升高【答案】C【解析】【分析】【详解】A．冰棍从冰箱拿出来时，包装袋外的“白粉”是水蒸气凝华形成；故A错误；B．冰棒包装袋周围出现的“白气”是水蒸气遇冷液化形成；故B错误；C．冰棒在口中觉得冰凉，是因为熔化过程吸热的原因；故C正确；D．晶体熔化过程中的特点是：吸热，温度不变。

故冰棍吸收热量的过程中，在熔化之前，温度升高，在熔化过程中，温度保持不变；故D错误；故选C。

3．汽车由平直的路段开到斜坡路段时，关于它受到的力的方向，下列描述正确的是（）A．重力的方向不变B．摩擦力的方向不变C．支持力的方向不变D．牵引力的方向不变【答案】A【解析】【分析】【详解】A．重力的方向总是竖直向下，汽车由平直的路段开到斜坡路段时，重力的方向不变，故A正确；B．摩擦力的方向与汽车运动方向相反，车由平直的路段开到斜坡路段时，摩擦力的方向发生改变，故B 不正确；C．支持力的方向与接触面垂直，车由平直的路段开到斜坡路段时，支持力的方向发生改变，故C不正确；D．牵引力的方向与运动方向相同，车由平直的路段开到斜坡路段时，牵引力的方向发生改变，故D不正确。

∥3套精选试卷∥2018年成都市八年级下学期期末考前验收物理试题

初二下学期期末物理试卷一、选择题（本题包括10个小题）1．下列物品中，重约为1N的是A．一枚壹圆硬币B．二只鸡蛋C．三枚回形针D．四张实验桌【答案】B【解析】【分析】【详解】A．一枚硬币的质量约为0.01kg，重力约为0.1N，A不符合题意；B．二只鸡蛋的质量约为0.1kg，重力约为1N，B符合题意；C．三枚回形针的质量约为0.001kg，重力约为0.01N，C不符合题意；D．四只实验桌的质量约为40kg，重力约为400N，D不符合题意．2．一位同学正在进行投掷实心球的训练，以下情境中，他对球做功的是（）A．手拿球静止B．手托球水平匀速直线运动C．将球举起D．抛出后的球在空中继续运动【答案】C【解析】【详解】A．手拿球静止，有力，但球没有在力的方向上移动距离，故没有做功，故A错误；B．手托球水平匀速直线运动，有力，但球没有在力的方向上移动距离，故没有做功，故B错误；C．将球举起，有力作用在球上，球在力的方向上通过了一定的距离，故有力做功，故C正确；D．球飞出去，球由于惯性向前运动，有距离，但没有对球施加力，没有对球做功，故D错误，3．潜水艇潜在水下航行,当它下潜的深度增加时,比较它所受到的水的压力和浮力关系是( )A．压力越大,浮力越大B．压力越大,浮力不变C．压力不变,浮力越大D．压力不变,浮力不变【答案】B【解析】【详解】∵F浮＝ρ水v排g，潜水艇的体积不变，下潜时，排开水的体积不变，∴潜水艇受到水的浮力不变；当潜水艇逐渐下潜时，深度h变大，∵p＝ρgh，∴潜水艇受到水的压强变大；∵F＝ps，潜水艇的表面积s不变，∴潜水艇受到水的压力变大．4．用相同的滑轮组成图所示的甲、乙两个滑轮组，把质量相同的物体匀速提升相同高度，不计绳重和摩擦，下列分析正确的是（）A．拉力F甲=F乙B．总功W甲=W乙C．有用功W甲＞W乙D．机械效率η甲＜η乙【答案】B【解析】【分析】【详解】A．不计绳重及摩擦,拉力F=1n(G物+G轮)，由图知,n甲=3,n乙=2，所以绳端的拉力分别为：F甲=13(G物+G轮),F乙=12(G物+G轮)，所以F甲＜F乙；故A错误；BC ．因为不计绳重及摩擦,动滑轮重相同,提升的物体重和高度相同,由W额=G轮h、W有用=G物h可知，利用滑轮组做的有用功相同、额外功相同，拉力做的总功相同，故B正确；C错误；D．因为η=WW有总，所以两滑轮组的机械效率相同．故D错误．5．如图所示,某同学将一漂浮在水面不开口的空饮料罐缓慢按入水中,同时开始计时，继续向下压一段距离，共用时t0，此过程中饮料罐所受的浮力随时间变化的图象可能是下列图中的A．B．C．D．【答案】A【解析】【分析】【详解】根据公式F浮＝ρgV排可知，排开水的体积一定时，受到的浮力将不再变化；A．在A中，表示一开始就受到浮力作用，然后浮力逐渐增加，最后保持不变，符合题意；B．在B中，表示物体逐渐浸没，所受浮力逐渐变大，最后不变，不合题意；C．在C中，表示物体完全浸没后，不管怎样移动，排开水的体积不再变化，受到的浮力保持不变；不合题意；D．在D中，表示物体受到的浮力逐渐增加，不合题意；故选A。

(汇总3份试卷)2018年成都市八年级下学期物理期末综合测试试题

初二下学期期末物理试卷一、选择题（本题包括10个小题）1．小周同学参加中考实心球投掷的过程如图所示，实心球在b 点离手，c 点是实心球运动的最高点，落到地面d 点．若不计空气阻力，下列说法正确的是A ．b 到d ，人对实心球做了功B ．b 到c ，动能逐渐增大C ．c 到d ，实心球的重力势能变大D ．b 到d ，实心球的机械能保持不变【答案】D【解析】【分析】【详解】A ．在b 到d 的过程中，实心球离开手，由于惯性继续运动，运动员对实心球没有作用力，所以人对实心球不做功，故A 错误；B ．从b 到c 的过程中，实心球质量不变，速度减小，动能减小，故B 错误；C ．在c 到d 的过程中，实心球的质量不变，高度减小，故重力势能减小，重力势能转化为动能，故C 错误；D ．在b 到d 的过程中，由于不计空气阻力，只有重力做功，实心球的机械能保持不变，故D 正确． 2．把体积相同的铜块和铝块分别浸没在水中，则它们所受浮力（）A ．铜块的大B ．铝块的大C ．一样大D ．无法判断【答案】C【解析】【分析】【详解】根据阿基米德浮力公式液排F gV ρ=可知，由于铜块和铝块分别浸没在水中的体积相同，故它们所受浮力相同。

3．小雨学习了简单机械后，用100牛的力提起了330牛的重物，那么他可能使用了（）A．一根杠杆B．一个动滑轮C．一个定滑轮和一个动滑轮组成的滑轮组D．一个定滑轮【答案】A【解析】【分析】【详解】A．使用杠杆时，若动力臂大于阻力臂，可以省力，且动力臂越长，所需动力越小，当动力臂与阻力臂之比适当时，则可以实现用100牛的力提起330牛的重物，故A符合题意；B．因为使用动滑轮省一半力，故使用动滑轮时，在不计绳重及摩擦，也不考虑动滑轮重的情况下，提起330牛的重物至少需用力F=330N2=165N>100N则使用动滑轮用100牛的力不可能提起330牛的重物，故B不符合题意；C．一个定滑轮和一个动滑轮组成的滑轮组最省力的绕法是从动滑轮开始绕绳，此时有三段绳子承担物重，在不计绳重及摩擦，也不考虑动滑轮重的情况下，提起330N的重物所用的力F=330N3=110N>100N则使用该用滑轮组用100牛的力不可能提起330牛的重物，故C不符合题意；D．使用定滑轮不能省力，故使用定滑轮时，用100牛的力无法提起330牛的重物，故D不符合题意。

(汇总3份试卷)2018年成都某名校初中八年级下学期期末统考物理试题

初二下学期期末物理试卷一、选择题（本题包括10个小题）1．下列所示过程中，对物体做功的是（）A．搬石头而未搬起B．提着滑板在水平路上前行C．将木箱推到斜面顶端D．举着杠铃在空中不动【答案】C【解析】【分析】【详解】A．搬石头而未搬起，有力无距离，故人没有做功，不符合题意；B．提着滑板在水平路上前行，人对滑板有向上的力，滑板没有在力的方向上通过距离，没有做功，不符合题意；C．将木箱推到斜面顶端，对木箱有力的作用，同时木箱在力的方向上移动了距离，故人对木箱做功，符合题意；D．运动员对杠铃有力的作用，但是在力的方向上没有距离，故人不做功，不符合题意。

故选C。

2．如图所示，一装有水的小桶放在水平面上，桶与水的总重为50N，用测力计吊着一个体积为300cm3的实心金属球，将金属球缓慢浸没在水中，使其在水中静止，且不与桶壁、桶底接触，此时测力计的示数为12N。

则下列说法正确的是A．金属球所受浮力为5N B．金属球的重力为12NC．金属球的密度为3×l03kg/m3D．桶对水平面的压力为53N【答案】D【解析】【详解】A．金属球受到的浮力：F 浮＝=1.0=3N，故A错误；B．金属球的重力：G=F浮+F示=3N+12N=15N，故B错误；C．金属球的密度===5kg/，故C错误；D．桶对水平面的压力为F=50N+15N-12N=53N．故D正确。

3．如图所示的实例中，为了增大压强的是A．载重汽车安装了很多车轮B．铁轨铺在枕木上C．吸管的一端剪成斜口D．图钉帽的面积做得较大【答案】C【解析】载重汽车安装许多车轮是通过增大受力面积的方法来减小压强的，故A错；铁轨铺在枕木上是通过增大受力面积的方法来减小压强的，故B错；吸管的一端剪成斜口是通过减小受力面积的方法来增大压强的，故C正确；图钉帽的面积做得较大是通过增大受力面积的方法来减小压强的，故D错；应选C．4．为安全起见，在下坡路上，小华握紧自行车刹把缓慢行驶。