回转体的相贯线(二)
回旋体表面相贯线的画法.

例 2:圆柱与圆锥相贯,求其相贯线的投影。
●
●
●
P
●
假想用水平面P截切立体,P面与圆柱 体的截交线为两条直线,与圆锥面的交线 为圆,圆与两直线的交点即为交线上的点。
例 2:圆柱与圆锥相贯,求其相贯线的投影。
● ●
● ●
●
●
●
●
●
●
●
●
●
解题步骤:
★ 求特殊点 ★ 用辅助平面法求
中间点 ★ 光滑连接各点
例4:求俯视图
●
●
●
●
●
●
● ●●
●
●●
●● ●
●
●●
例4:求俯视图
●
1
●
例3:补全主视图
三面共点
●
●
●
作图时要抓住 一个关键点,相贯 线汇交于这一点。
五、不完全形体相交
小结
一、本章的基本内容
⒈ 立体表面相贯线的概念
相贯线的性质:表面性 共有性 封闭性
⒉ 求相贯线的基本方法
利用积聚性面上找点法,辅助平面法,辅助球面法
二、解题过程
⒈ 交线分析
⑴ 空间分析: 分析相交两立体的表面形状, 形体大小及相
2.相贯线的主要性质
★ 表面性
相贯线位于两立体的表面上。
★ 封闭性
相贯线一般是封闭的空间折线(通 常由直线和曲线组成)或空间曲线。
★ 共有性
相贯线是两立体表面的共有线。
其作图实质是找出相贯的两立 体表面的若干共有点的投影。
7.2 平面体与回转体相贯
1.相贯线的性质
相贯线是由若干段平面曲 线(或直线)所组成的空间折 线,每一段是平面体的棱面与 回转体表面的交线。
两回转体表面相交
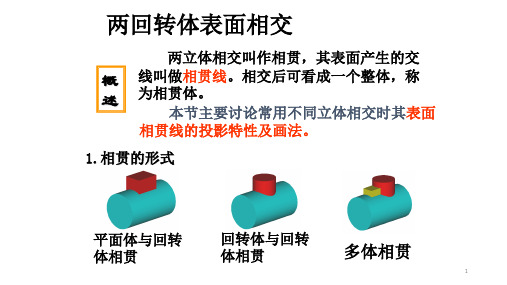
两回转体表面相交平面体与回转体相贯回转体与回转体相贯多体相贯 1.相贯的形式两立体相交叫作相贯,其表面产生的交线叫做相贯线。
相交后可看成一个整体,称为相贯体。
本节主要讨论常用不同立体相交时其表面相贯线的投影特性及画法。
概述立体表面相交有三种形式,一种是立体的外表面相交;一种是外表面与内表面相交;一种是内表面与内表面相交.实实相贯实虚相贯虚虚相贯相贯线1 相贯线的性质★表面性相贯线位于两立体的表面上。
★封闭性相贯线一般是封闭的空间折线(通常由直线和曲线组成)或空间曲线。
★共有性相贯线是两立体表面的共有线。
其作图实质是找出相贯的两立体表面的若干共有点的投影。
2 求相贯线的方法一、平面体与回转体相贯1.相贯线的性质相贯线是由若干段平面曲线(或直线)所组成的空间折线,每一段是平面体的棱面与回转体表面的交线。
2.作图方法求交线的实质是求各棱面与回转面的截交线。
∙分析各棱面与回转体表面的相对位置,从而确定交线的形状。
∙求出各棱面与回转体表面的截交线。
∙连接各段交线,并判断可见性。
例1:补全主视图空间分析:四棱柱的四个棱面分别与圆柱面相交,前后两棱面与圆柱轴线平行,截交线为两段直线;左右两棱面与圆柱轴线垂直,截交线为两段圆弧。
投影分析:由于相贯线是两立体表面的共有线,所以相贯线的侧面投影积聚在一段圆弧上,水平投影积聚在矩形上。
例2:求作主视图二、回转体与回转体相贯1. 相贯线的性质相贯线一般为光滑封闭的空间曲线,它是两回转体表面的共有线。
2.作图方法∙表面取点法利用投影的积聚性直接找点。
∙用辅助平面法。
一般是根据立体或给出的投影,分析两回转面的形状、大小极其轴线的相对位置,判断相贯线的形状特点和各投影的特点,从而选择适当的方法作图。
∙先找特殊点。
⒊作图过程∙补充中间点。
确定交线的弯曲趋势确定交线的范围如果两回转体相交,其中有一个是轴线垂直于投影面的圆柱,则相贯线在该投影面上的投影积聚在圆柱面上。
利用回转体表面取点的方法可以作出相贯线的其余投影。
相贯体及尺寸标注

第二节 平面立体与回转体相贯 (续)
例6-1 已知三 棱柱与圆锥体相 贯 (续)
分析:由已知两投影 分析可知,三棱柱中有两 个平面与圆锥面相交,产 生两段截交线。相贯线即 为这两段截交线组成。其 三棱柱中水平面与圆锥面 的交线为圆弧;正垂面与 圆锥面的交线为椭圆弧; 两弧的交点即是棱与圆锥 面的结合点。
第二节 平面立体与回转体相贯 (续)
例6-2 已 知三棱柱与半圆 球相贯,求其相 贯线的投影。
第二节 平面立体与回转体相贯 (续)
分析:由水平投影分析出,三棱柱的三个面中有两个面与圆球相交,一 个面平行于正投影面,与圆球的交线正面投影为圆弧,侧面投影为直线段; 另一个面为铅垂面,与圆球面的交线正面投影和侧面投影均为椭圆弧。
(4)整理轮廓线:对于两相贯体的轮廓线,存在的部分可见描 成粗实线;不可见描成虚线。对于不存在的轮廓线不必画出或用双 点画线画出。
第二节 平面立体与回转体相贯
由于平面立体的各表面均 为平面,因此平面立体中某一 表面与回转体表面的交线为截 交线,两部分截交线的交点称 为结合点,它是平面立体的棱 对回转面的贯穿点。因此,求 平面立体与回转体的相贯线, 可归结为求截交线和结合点的 问题。
第三节 两回转体相贯 (续)
三、相 贯线投影的 特殊情况:
一般情况 下,两回转 体相贯的交 线为空间曲 线,但在特 殊情况下其 相贯线可能 是平面曲线 或直线。
1、同轴回转体的相贯线——平面曲线
第三节 两回转体相贯 (续)
2、两相贯回转体公切于球——平面曲线
第三节 两回转体相贯 (续)
3、两相贯的圆 柱轴线平行相交—— 平面曲线和直线
2、外表面与内表面相贯(柱与孔); 3、内表面与内表面相贯(孔与孔)。
回转体表面相贯线
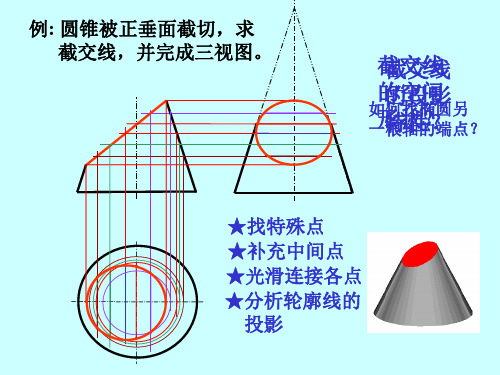
小 结
一、本章的基本内容 ⒈ 立体表面相贯线的概念
相贯线的性质: 相贯线的性质:表面性 共有性 封闭性
⒉ 求相贯线的基本方法
面上找点法 辅助平面法
二、解题过程 ⒈ 交线分析
空间分析: ⑴ 空间分析: 分析相交两立体的表面形状, 分析相交两立体的表面形状, 形体大小及相 对位置,预见交线的形状。 对位置,预见交线的形状。 投影分析: ⑵ 投影分析: 是否有积聚性投影?找出相贯线的已知投影, 相贯线的已知投影 是否有积聚性投影?找出相贯线的已知投影, 预见未知投影,从而选择解题方法 选择解题方法。 预见未知投影,从而选择解题方法。
●
回转体表面相贯线画法
概
述
两立体相交叫作相贯, 两立体相交叫作相贯,其表面产生的交 线叫做相贯线 相贯线。 线叫做相贯线。 本章主要讨论常用不同立体相交时其表 本章主要讨论常用不同立体相交时其表 面相贯线的投影特性及画法。 面相贯线的投影特性及画法。 1.相贯的形式 1.相贯的形式
平面体与回 转体相贯
五、多体相贯
每个局部都是两体相贯, 每个局部都是两体相贯,首先分析 它是由哪些基本体组成的,然后两两进 它是由哪些基本体组成的,然后两两进 行相贯线的分析与作图。 行相贯线的分析与作图。
叠加体的三视图
一、叠加体的基本形式及投影特点
重点分析以下几个问题: 重点分析以下几个问题: 叠加体的组成——由哪些基本体组成 • 叠加体的组成 由哪些基本体组成 • 这些基本体的形状和位置 • 基本体之间的叠加形式
面投影在该圆上。 面投影在该圆上。
圆柱与圆柱相贯,求其相贯线。 例 1 :圆柱与圆柱相贯,求其相贯线。
当圆柱直径变化时,相贯线的变化趋势。 当圆柱直径变化时,相贯线的变化趋势。
两共轴回转体表面相贯线的形状为

两共轴回转体表面相贯线的形状为相贯线是指两共轴回转体表面相互相交时形成的线段或曲线。
两共轴回转体表面相贯线的形状不仅与共轴回转体的几何形状有关,还与它们的位置、朝向以及相对运动方式等因素密切相关。
下面将从几何形状、位置与朝向、相对运动方式三个方面来探讨两共轴回转体表面相贯线的形状。
首先,两共轴回转体的几何形状对相贯线的形状有很大影响。
最简单的情况是两个圆柱体或圆锥体相贯。
当两个圆柱体或圆锥体的轴线相交于一点时,相贯线为一条射线。
当两个圆柱体或圆锥体的轴线平行时,相贯线为一条直线。
如果两个圆柱体或圆锥体的轴线相交于非垂直的点,相贯线为一条螺旋线。
此外,当一个圆柱体与一个球体相贯时,相贯线的形状为一条环线。
当两个球体相贯时,相贯线为一个球面。
其次,两共轴回转体的位置与朝向也对相贯线的形状产生影响。
当两个共轴回转体平行且轴线有一定的偏移时,相贯线为两个直线段,且与共轴回转体的轴线平行。
当两个共轴回转体有一定的夹角时,相贯线为一条曲线,其形状取决于夹角的大小和角的种类(如锥角、锐角或直角等)。
最后,两共轴回转体的相对运动方式也会影响相贯线的形状。
当两个共轴回转体以相同的转速和方向旋转时,相贯线为一条直线。
当两个共轴回转体以相同的转速但以相反的方向旋转时,相贯线为一条曲线,其形状取决于旋转速度的大小和方向。
如果两个共轴回转体以不同的转速旋转,相贯线的形状将会更加复杂,可能会出现多条线段或曲线。
综上所述,两共轴回转体表面相贯线的形状与共轴回转体的几何形状、位置与朝向以及相对运动方式密切相关。
通过对这些因素的分析,我们可以推测出相贯线的大致形状。
但是由于相贯线的形状高度复杂,没有明确的统一公式或规律可以描述,因此对于具体形状的相贯线的确定需要借助数学和计算机模拟等工具的支持。
网络教育工程制图作业《工程制图Ⅲ》作业答案

1.图纸幅面的代号有哪几种?2.图纸格式分为哪两种?按标题栏的方位又可将图纸格式分为哪两种?3.一个完整的尺寸,一般应包括哪四个组成部分,它们分别有哪些规定?4.标注平面图形的尺寸应达到哪三个要求?这三个要求主要体现哪些内容?5.什么是平面图形的尺寸基准、定形尺寸和定位尺寸?通常按哪几个步骤标注平面图形的尺寸?6.圆弧连接指什么?在图样上的圆弧连接处,为何必须比较准确作出连接圆弧的圆心和切点?在平面图形圆弧连接处的线段可分为哪三类?它们是根据什么区分的?在作图时应按什么顺序画这三类线段?7.机械图样中的线宽分为哪两种?设粗实线的线宽为d,虚线、点画线、细实线、波浪线的线宽是多少?参考答案: 1.A0/A1/A2/A3/A42.图纸格式分为需要装订和不需要装订两种。
按标题栏的长边置于水平方向并与图纸的长边平行时,构成X型图纸;若标题栏的长边与图纸的长边垂直时,则构成Y型图纸。
3.包括尺寸线、尺寸界线、尺寸数字和尺寸终端(箭头)。
尺寸数字注写在尺寸线上方;尺寸线用细实线绘制;尺寸界线用细实线绘制,一般应与尺寸线垂直,并超出尺寸线2mm;尺寸终端采用实心箭头。
4.正确、完整、清晰。
正确是指尺寸数字不能写错;完整是指尺寸要注写完全,不遗漏各组成部分的定形尺寸和定位尺寸。
清晰是指尺寸的位置要安排在图形的明显处,标注清楚,布局整齐。
5、尺寸基准是指尺寸的起点。
定形尺寸指确定各部分形状大小的尺寸;定位尺寸指确定各部分之间相对位置大小的尺寸。
先分析形状,确定尺寸基准;注出各部分定形尺寸;注出各部分所需的定位尺寸。
6.圆弧连接指直线与圆弧相切,圆弧与圆弧相切。
为了得到光滑相切的图形,必须准确作出连接圆弧的圆心和切点。
圆弧连接处的线段可分为已知线段、中间线段和连接线段。
有足够的定形尺寸和定位尺寸,称为已知线段;缺少一个定位尺寸,必须依靠一端与另一线段相切而画出的线段,称为中间线段;缺少两个定位尺寸,因而要依靠两端与另两线段相切,才能画出的线段,称为连接线段。
12,第十二讲回转体.回转体的截交线(二)相贯线(一)

2
3
4
判别相贯线可见性的原则 见的。
只有位于两形体都可见的面上的交线是可
例题7
平面立体与曲面立体相贯,完成相贯后的投影
解题步骤 1 分析 相贯线的侧面 投影已知,可利用表 面取点法求共有点; 2 求 出 相 贯 线上 的 特 殊点Ⅰ、Ⅱ 、 Ⅳ; 3 求出一般点Ⅲ ; 4 光 滑 且 顺 次地 连 接 各点,作出相贯线, 并且判别可见性; 5 整理轮廓线。
b
3
圆柱体截交线 直线与圆柱相交
姓名
学号
审核
成绩
33
复习题(例题6)
1' 4'
求圆柱截交线
10"(40“) (4“) 1" (5" 3" 2"
解题步骤
1 分析 截交线的正 投影和水平投影为已 知; 2 求出截交线上的特 殊点Ⅰ、 Ⅱ 、 Ⅲ 、Ⅳ; 3 求一般点Ⅴ; 4 顺次地连接各点, 作出截交线,并且判 别可见性; 5 整理轮廓线。
例题7
想象出物体及其侧面投影的形状
作业 评讲
复习题:求园柱被切割后的H、W投影。
45°
第十讲 曲面立体的投影(二)
基本要求
§7-3 曲面立体的截交线(锥和球) §7-4 曲面立体的贯穿点(自学) §7-5 曲面立体与平面立体相交 ☆
基本要求:
本讲是画法几何学中较难的部分,需要认真 练习。 熟练掌握基本曲面体的三面投影。 熟练掌握曲面立体表面取点的方法,这是本 章也是本讲的一个基本方法。 充分理解截交的几何意义及截交线的性质, 熟练掌握求截交线的方法。 掌握直线与曲面立体相交贯穿点的性质及求 解方法。 充分理解相贯的几何意义及相贯线的性质, 熟练掌握求相贯线的方法。
相贯线2

其他同学在练习本上画
绥芬职教中心汽修专业部 王海蛟
还剩 180 秒 101 102 104 105 107 108 109 110 113 115 117 118 120 122 123 125 126 128 129 132 134 136 139 143 144 146 147 148 149 150 151 152 153 154 155 156 158 159 162 164 166 167 168 169 170 171 172 173 175 176 179 10 11 12 13 16 17 18 19 20 22 24 25 27 28 32 34 38 40 43 44 46 49 50 51 52 53 59 60 64 68 69 73 75 78 83 85 86 87 88 89 92 98 0 3 4 6 7 8 9 100 103 106 111 112 114 116 119 121 124 127 130 131 133 135 137 138 140 141 142 145 157 160 161 163 165 174 177 178 14 15 21 23 26 29 30 31 33 35 36 37 39 41 42 45 47 48 54 55 56 57 58 61 62 63 65 66 67 70 71 72 74 76 77 79 80 81 82 84 90 91 93 94 95 96 97 99 1 2 5
第五章
绥芬河职教中心汽修专业部 王海蛟
学 习 目 标
1. 熟记相贯线的性质。 2. 掌握用辅助平面法求相贯线 。 3. 培养认真观察分析的能力和习惯。
重点:利用辅助平面法求相贯线。 难点:回转体相贯线的特殊情况。
2-3相贯线
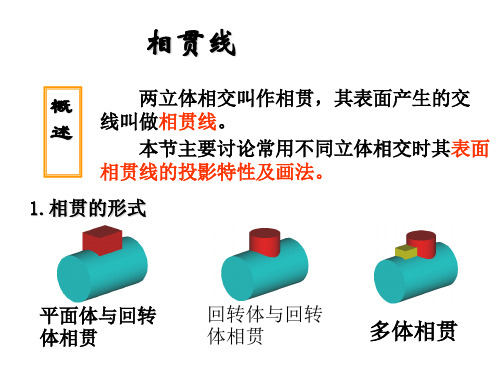
相贯线平面体与回转体相贯回转体与回转体相贯多体相贯 1.相贯的形式两立体相交叫作相贯,其表面产生的交线叫做相贯线。
本节主要讨论常用不同立体相交时其表面相贯线的投影特性及画法。
概述立体表面相交有三种形式,一种是立体的外表面相交;一种是外表面与内表面相交;一种是内表面与内表面相交.相贯线实实相贯实虚相贯虚虚相贯2.相贯线的主要性质★表面性相贯线位于两立体的表面上。
★封闭性相贯线一般是封闭的空间折线(通常由直线和曲线组成)或空间曲线。
★共有性相贯线是两立体表面的共有线。
其作图实质是找出相贯的两立体表面的若干共有点的投影。
二、平面体与回转体相贯1.相贯线的性质相贯线是由若干段平面曲线(或直线)所组成的空间折线,每一段是平面体的棱面与回转体表面的交线。
2.作图方法求交线的实质是求各棱面与回转面的截交线。
•分析各棱面与回转体表面的相对位置,从而确定交线的形状。
•求出各棱面与回转体表面的截交线。
•连接各段交线,并判断可见性。
例1:补全主视图空间分析:四棱柱的四个棱面分别与圆柱面相交,前后两棱面与圆柱轴线平行,截交线为两段直线;左右两棱面与圆柱轴线垂直,截交线为两段圆弧。
投影分析:由于相贯线是两立体表面的共有线,所以相贯线的侧面投影积聚在一段圆弧上,水平投影积聚在矩形上。
例2:求作主视图三、回转体与回转体相贯1. 相贯线的性质相贯线一般为光滑封闭的空间曲线,它是两回转体表面的共有线。
2.作图方法•表面取点法利用投影的积聚性直接找点。
•辅助平面法一般是根据立体或给出的投影,分析两回转面的形状、大小及其轴线的相对位置,判断相贯线的形状特点和各投影的特点,从而选择适当的方法作图。
•先找特殊点。
⒊作图过程•补充中间点。
确定交线的弯曲趋势确定交线的范围如果两回转体相交,其中有一个是轴线垂直于投影面的圆柱,则相贯线在该投影面上的投影积聚在圆柱面上。
利用回转体表面取点的方法可以作出相贯线的其余投影。
按已知曲面立体表面上点的投影求其它投影的方法,称为表面取点法。
第四章相贯线jiao8

两圆柱直径相等且轴线相交, 在平行于两轴线的投影面上, 相贯线的投影为直线。
圆柱和圆台组成,圆柱与圆台有 一个公切的球,主视图中相贯线 的投影为直线。
两圆柱轴线 平行相交, 交线为直线和 曲线
回转体同轴相交,交 线的空间形状为圆形。
回转体同轴相交,交 线的空间形状为圆形。
回转体同轴相交,交 线的空间形状为圆形。
1、相贯线的性质
(1).表面性 相贯线位于两立体的表面上。 (2).封闭性 由于形体具有一定的空间范围,所以相贯线一般都是封闭的。 在特殊情况下还可能是不封闭的。 (3).共有性 相贯线是两相交立体表面的共有线,也是两立体表面的分界线, 相贯线上的点一定是两相交立体表面的共有点。 (二)求相贯线的方法、步骤 求画两回转体的相贯线,就是要求出相贯线上一系列的共有点。 求共有点的方法有:面上取点法、辅助平面法和辅助同心球面 法。具体作图步骤为: (1)找出一系列的特殊点(特殊点包括:极限位置点、转向 点、可见性分界点); (2)求出一般点;(3)判别可见性; (4)顺次连接各点的同面投影;(5)整理轮廓线。
3.用辅助平面法求共有点的作图步骤 (1)作辅助平面; (2)分别作出辅助平面与两回转面的截交线; (3)两回转面截交线的交点,即为所求的共有点。 (三)一些典型几何形状的相贯线 [例5-12] 求轴线正交的圆柱与圆锥台的相贯线(图5-20) 如图5-20所示。圆柱和圆锥台的轴线垂直相交,相贯线 为一封闭的空间曲线。由于圆柱轴线是侧垂线,则圆柱 的侧面投影是有积聚性的圆,所以相贯线的侧面投影与 此圆重合,需要求的是相贯线的正面投影的水平投影。 由于圆锥台轴线垂直水平面,所以采用水平面作为辅助 平面。
条件:两圆柱正交(轴线垂
直相交)而且直径差别比较 大。 作图方法:利用两圆柱中大 圆柱的半径作为半径,在小 圆柱的轴线上找一点作为圆 心,过两圆柱矩形轮廓的交 点绘制一段圆弧,用这段圆 弧近似替代相贯线的投影。
两回转体表面相交

两回转体表面相交(一)、相贯线的概述1.相贯线的概念两立体表面的交线称为相贯线。
相贯线不仅出现在两立体外表面,有时还见到两立体内表面,以及立体被穿孔的情况。
2.影响相贯线形状的因素相交的两立体的形状。
相交的两立体的相对尺寸大小。
相交的两立体的相对位置。
3.相贯线的特性① 一般为空间曲线,特殊情况下为平面曲线。
② 为两回转体表面的共有线。
③ 为两回转体表面的分界线。
4.求相贯线的方法:① 表面取点法② 辅助平面法5.求相贯线的步骤:① 求特殊位置的点:转向线上的点、最高点、最低点、最左点、最右点、最前点、最后点。
② 求一般位置点。
③ 判断可见性:只有当相贯线同时属于两立体表面的可见部分时,才可见。
(二)、表面取点法1.什么是表面取点法当相交的两回转体中有一个是圆柱且轴线垂直于投影面时,圆柱面在该投影面上的投影积聚为圆,因此,相贯线在该投影面上的投影就积聚在圆柱面有积聚性的投影(圆)上。
这时,可以将相贯线看成是另一回转面上的曲线,利用回转面上取点的方法作出相贯线的其它投影。
表面取点法只适用于相交两回转体中至少有一个是圆柱,并且其轴线与投影面垂直的情况下。
2.作图举例已知两圆柱轴线垂直相交,求它们的相贯线投影。
分析:由图可以看出,大圆柱的轴线垂直于侧面,小圆柱的轴线垂直于水平面,两圆柱轴线垂直相交。
因为相贯线是两圆柱体表面上的共有线,所以相贯线的侧面投影与大圆柱的侧面投影重合,水平投影与小圆柱的水平投影重合。
需要求相贯线的正面投影。
因相贯线前后对称,相贯线前、后两部分的正面投影重合。
作图:1)作特殊点最左、最右、最前、最后、最高、最低点,转向轮廓线上点。
2)作一般点3)判别可见性并连线作图结果如图 d 所示。
(a)已知条件(b)作特殊点投影(c)作一般点投影(d)作图结果求正交圆柱体相贯线(三)辅助平面法1.什么是辅助平面法假想的用一个平面截切相贯的两回转体,分别求出该平面与两回转体的截交线,则两组截交线的交点,即为相贯线上的点。
回转体的相贯线(二)

辅助平面法
4 光滑且顺次地连 接各点,作出相贯 线,并且判别可见 性;
5 整理轮廓线。
精用选水可编平辑面pp作t 为辅助平面求共有点
31
用水平面作为辅助平面求共有点
精选可编辑ppt
32
例题4 求圆球与圆锥的相贯线
PV1
3' 4' 1' 5'
2'
PV2 PV3
辅助平面法
用水平面作为辅助平面求共有点
精选可编辑ppt
34
例题5分析并想象出物体相贯线投影的形状
精选可编辑ppt
35
§ 7-6 螺旋线和圆柱正螺旋面
一、 圆柱螺旋线
1 圆柱螺旋线的形成
当一个动点沿着一直线等 速移动,而该直线同时绕与它 平行的一轴线等速旋转时,动 点的轨迹就是一根圆柱螺旋线。
2 圆柱螺旋线的画法
精选可编辑ppt
36
螺旋线的画法
2 圆柱正螺旋面的画法
(1)圆柱正螺旋面(锥状) (2)圆柱正螺旋面(柱状)
3 圆柱正螺旋面的应用
精选可编辑ppt
38
圆柱正螺旋面(锥状)的画法
精选可编辑ppt
39
圆柱正螺旋面(柱状)的画法
•作出该曲面上各素线的投 影; •画出两条曲导线(圆柱螺 旋线); •作出直母线的两面投影;
精选可编辑ppt
上讲要点:
▪ 熟练掌握基本曲面体的三面投影及曲面 立体表面取点的方法。这是本章的一个 基础方法。
▪ 充分理解截交和相贯线的几何意义,以及 截交线和相贯线的性质,
▪ 熟练掌握求曲面立体截交线的方法。 ▪ 熟练掌握求(平曲相交)相贯线的方法 ▪ 掌握直线与曲面立体相交贯穿点的性质
2-4 两回转体表面相交 机械制图课件

四、小结: 求相贯线的一般步骤
(1) 根据二相贯立体的形状及位置分析相贯线的形状; (2) 求相贯线上特殊位置各点及一般位置点的投影; (3) 判别可见性后依次连接各点,擦去被相贯掉的轮
请点击鼠标左键显示后视图形
请点击鼠标左键显示侧视图形
请点击鼠标左键显示俯视图形
请点击左键显示侧视图形
请点击鼠标左键显示俯视图形
请点击鼠标左键显示侧视图形
请点击鼠标左键显示俯视图形
请点击鼠标左键显示侧视图形
请点击鼠标左键显示俯视图形
请点击鼠标左键显示仰视图形
请点击鼠标左键显示后视图形
第四节 两回转体表面相交
一、利用积聚性求相贯线 二、辅助平面法求相贯线 三、正交二圆柱相贯线分析 四、小结
一、利用积聚性求相贯线
相贯线的定义:二个回转体相互贯穿时, 表面的交线称为相贯线。
1. 相贯线的特性
相贯线是二立体表面上共有点的连线;
相贯线一般为一条封闭的空间曲线。
请点击鼠标左键显示后面内容
廓线,加深其余图线。
请点击鼠标左键显示后面内容
请点击鼠标左键显示侧视图形
请点击鼠标左键显示俯视图形
请点击鼠标左键显示后视图形
请点击鼠标左键显示侧视图形
请点击鼠标左键显示俯视图形
请点击鼠标左键显示后视图形
请点击鼠标左键显示另一图形
请点击鼠标左键显示对比图形
请点击鼠标左键显示主视图形
一、利用积聚性求相贯线
2.相贯线的求法
利用圆柱的有积聚性的圆投影求相 贯线上各点的投影。
圆柱与圆柱(孔)的相贯线;
圆柱与圆锥的相贯线; 用积聚性法可求:
回转体新表面相贯线画法介绍(ppt 31页)

平面体与回转体相贯回转体与回转体相贯多体相贯5.1 概述1.相贯的形式两立体相交叫作相贯,其表面产生的交线叫做相贯线。
本章主要讨论常用不同立体相交时其表面相贯线的投影特性及画法。
2.相贯线的主要性质★表面性相贯线位于两立体的表面上。
★封闭性相贯线一般是封闭的空间折线(通常由直线和曲线组成)或空间曲线。
★共有性相贯线是两立体表面的共有线。
其作图实质是找出相贯的两立体表面的若干共有点的投影。
5.2 平面体与回转体相贯1.相贯线的性质相贯线是由若干段平面曲线(或直线)所组成的空间折线,每一段是平面体的棱面与回转体表面的交线。
2.作图方法求交线的实质是求各棱面与回转面的截交线。
•分析各棱面与回转体表面的相对位置,从而确定交线的形状。
•求出各棱面与回转体表面的截交线。
•连接各段交线,并判断可见性。
空间分析:四棱柱的四个棱面分别与圆柱面相交,前后两棱面与圆柱轴线平行,截交线为两段直线;左右两棱面与圆柱轴线垂直,截交线为两段圆弧。
投影分析:由于相贯线是两立体表面的共有线,所以相贯线的侧面投影积聚在一段圆弧上,水平投影积聚在矩形上。
例2:求作主视图例2:求作主视图1. 相贯线的性质相贯线一般为光滑封闭的空间曲线,它是两回转体表面的共有线。
5.3 回转体与回转体相贯2.作图方法•利用投影的积聚性直接找点。
•用辅助平面法。
•先找特殊点。
⒊作图过程•补充中间点。
确定交线的弯曲趋势确定交线的范围例1 :圆柱与圆柱相贯,求其相贯线。
●●●●●●●●●空间及投影分析:小圆柱轴线垂直于H面,水平投影积聚为圆,根据相贯线的共有性,相贯线的水平投影即为该圆。
大圆柱轴线垂直于W面,侧面投影积聚为圆,相贯线的侧面投影在该圆上。
求相贯线的投影:利用积聚性,采用表面取点法。
☆找特殊点☆补充中间点☆光滑连接当圆柱直径变化时,相贯线的变化趋势。
交线向大圆柱一侧弯交线为两条平面曲线(椭圆)●●●●●●●●●●●●●●●●●●●★外形交线◆两外表面相贯◆一内表面和一外表面相贯★内形交线◆两内表面相贯无轮是两外表面相贯,还是一内表面和一外表面相贯,或者两内表面相贯,求相贯线的方法和思路是一样的。
回转体的截交线和相贯线

● ● ● ●
★找特殊点 ★补充中间点 ★光滑连接各点 ★分析轮廓素线的投影
截交线的侧面投 影是什么形状? 中国矿业大学 世行贷款实验教学改革项目 影是什么形状?
●
●
例4:求左视图
★找特殊点 ★找中间点 ★光滑连接各点 ★分析轮廓素线的投影
中国矿业大学 世行贷款实验教学改革项目
中国矿业大学 世行贷款实验教学改革项目
同一立体被多个平面截切,要逐个截平面进行截交线的分析和作图。 同一立体被多个平面截切,要逐个截平面进行截交线的分析和作图。
例1:求左视图
解题步骤: 解题步骤:
★空间及投影分析 截平面与体的相对位置 截平面与投影面的相对位置 ★求截交线 ★分析圆柱体轮廓素线的投影
中国矿业大学 世行贷款实验教学改革项目
例1:补全主视图 :
空间分析: 空间分析: 投影分析: 投影分析: 四棱柱的四个棱面分别与
由于相贯线是两立体表 圆柱面相交, 圆柱面相交,前后两棱面与圆 面的共有线, 截交线为两段直 面的共有线,所以相贯线的 柱轴线平行, 柱轴线平行, 侧面投影积聚在一段圆弧上, 侧面投影积聚在一段圆弧上, 线;左右两棱面与圆柱轴线垂 水平投影积聚在矩形上。 水平投影积聚在矩形上。 截交线为两段圆弧。 直,截交线为两段圆弧。
截平面与圆柱面的截交线的形状取决于 截平面与圆柱轴线的相对位置
PV PV PV
P
P
P
垂直 圆
倾斜 椭圆
中国矿业大学 世行贷款实验教学改革项目
平行 两平行直线
例1:求左视图
●
解题步骤: 解题步骤:
●
●
●
★空间及投影分析 截平面与体的相对位置 截平面与投影面的相对位置 ★求截交线 ★分析圆柱体轮廓素线的投影
机械制图-两回转体相交

三、相贯线的特殊情况
1、两回转体具有公共轴线时(过球心),其相贯线为垂直轴线 的圆。
相贯线 相贯线
相贯线
圆球与圆锥台相贯
2、两曲面立体相交,一般情况下相贯线为空间曲线,但 特殊情况下可能是平面曲线或直线。
A. 当两回转体相交并公切于一球时,相贯线为平面曲线 (椭圆)。
B.当两圆锥共锥顶或者两圆柱轴线平行时,相贯线为直线。
3.5 两回转体表面相交
一、相贯线概述
二、利用积聚性法求相贯线 三、相贯线的特殊情况
一、相贯线的概述
相贯线 ——立体相交后表面产生的交线。
性质:(表面性、共有性、封 闭性) 1)是相交两回转体表面的 共有线。相贯线上的点是两 回转体表面的共有点。
相贯线 圆台
2)一般来说交线是一封闭的 空间曲线,特殊情况下是平面 曲线或直线。
分析:当圆柱直径变化时,相贯线的变化趋势。
垂直直径<水平直径 上下两条空间曲线
直径相等 两条平面曲线(椭圆)
垂直直径>水平直径 左右两条空间曲线
相贯线投影关于小圆柱轴线对称,弯向大圆柱的轴线
例:补全主视图
1. 两外表面相贯(直径相等) 2. 一内表面和一外表面相贯(直径不等)
1’(2’)
● ●
2’’ 4’
●
1’’
3’
3’’( 4’’)
(2)
(3)
(4) (1)●
●
二)圆柱与圆锥、圆球相贯
相贯线
共有性
柱面上的曲线
积聚性
已知相贯线的 一个投影
锥(球)面上的曲线
也即已知锥(球)面上 曲线的一个投影
求相贯线即转化为锥(球) 面上求点、线。
例:已知圆柱与圆锥相交,完成H面投影。
回旋体表面相贯线画法(2)

3 2
●
● ●
●
● ●
这是一个多体 相贯的例子,首先 分析它是由哪些基 本体组成的,这些 基本体是如何相贯 的,然后分别进行 相线的分析与作 图。
●
1
●
例5:补全主视图 三面共点
● ●
●
作图时要抓住 一个关键点,相贯 线汇交于这一点。
例6:求俯视图
●
● ● ●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
例6:求俯视图
第 四 章 回转体表面相贯线画法
相贯线的特殊情况
1.当二等直径圆柱相交 时,相贯线为椭圆。
2. 当球与其它回转 体相交时,如果 球心位于其它回 转体的轴线上, 相贯线为圆。
例3:求主视图
● ●
●
●
●
×
相切处无线 外表面与外表
●
面相贯,内表面与 内表面相贯。分别 求其相贯线。
例3:求主视图
例5:补全主视图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
熟练掌握基本曲面体的三面投影及曲面 立体表面取点的方法。这是本章的一个 基础方法。 充分理解截交和相贯线的几何意义,以 及截交线和相贯线的性质, 熟练掌握求曲面立体截交线的方法。 熟练掌握求(平曲相交)相贯线的方法 掌握直线与曲面立体相交贯穿点的性质 及求解方法
复 椭圆 习 题双曲线 3: 求 圆线 圆 锥 被 切 割 后 的 投 影
螺旋楼梯的画法(右旋)
δ
1. 如同画正螺旋柱状面那样,画出螺 旋楼梯的H投影和内外螺旋线上的各 点(不画出螺旋线)。 2. 从内螺旋先3/4的各点下落梯板竖向 厚度δ;从外螺旋后3/4的各点下落 梯板竖向厚度δ。并将这些点分别 连接,画出内外螺旋线。 3. 按投影关系画出可见踢面(先1/2内 螺旋点及先1/4外螺旋点上升踢面高, 后1/2外螺旋点及后1/4内螺旋点上 升踢面高) 、踏面及梯轮廓线。 4. 判别可见性,加深图线。 轴线右侧踢面可见,轴线左侧 底面可见;先1/2梯内侧面可见,后 1/2梯外侧面可见;轴线右侧踏面积 聚线均可见,轴线左侧先1/4内侧和 后1/4外侧踏面边线可见。
y
C0
y
3 求出若干个一般点
D、E;
4 光滑且顺次地连接 各点,作出相贯线, 并且判别可见性; 5 整理轮廓线。
a c
b y d e
y
表面取点法
例题2 完成带圆柱孔的圆柱的投影。
a' d' c' e' b' a" b" d" e" c" 解题步骤 1 分析 相贯线的水 平投影和侧面投影已 知,可利用表面取点 法求共有点; y y 2 求出相贯线上的特 殊点A、B、 C; 3 求出若干个一般点 y a c b y
五.相贯线的特殊情况
(1)两个回转体具有公共轴线时,其表面的相贯线为圆,并 且该圆垂直于公共轴线。 当公共轴线处于投影面垂直位置时,相贯线有一个投影 反映圆的实形,其余投影积聚为直线段;
(2)外切于同一球面的圆锥、圆柱相交时,其相贯线为两条 平面曲线—椭圆。
当两立体的相交两轴线同时平行于某一投影面时,则此 两椭圆曲线在该投影面上的投影,为相交两直线段,例图。
h
螺旋楼梯的画法(右旋)
δ S
1. 如同画正螺旋柱状面那样,画出螺 旋楼梯的H投影和内外螺旋线上的各 点(不画出螺旋线)。 2. 从内螺旋先3/4的各点下落梯板竖向 厚度δ;从外螺旋后3/4的各点下落 梯板竖向厚度δ。并将这些点分别 连接,画出内外螺旋线。 3. 按投影关系画出可见踢面(先1/2内 螺旋点及先1/4外螺旋点上升踢面高, 后1/2外螺旋点及后1/4内螺旋点上 升踢面高) 、踏面及梯轮廓线。 4. 判别可见性,加深图线。 轴线右侧踢面可见,轴线左侧 底面可见;先1/2梯内侧面可见,后 1/2梯外侧面可见;轴线右侧踏面积 聚线均可见,轴线左侧先1/4内侧和 后1/4外侧踏面边线可见。
7-28.完成四棱锥和圆锥相贯后的投影。
F1
F2
F3
复习题:求半园柱与三棱椎相贯后的投影.
复习题:求半园柱与三棱椎相贯后的投影.
两段椭圆线
两段直线
第十三讲 曲面立体的投影(三) 基本要求
§7-4
两曲面立体的相贯线
§7-5
螺旋楼梯的画法
基本要求
• 本讲也是画法几何学中较难的部分,需要认 真练习。 • 充分理解曲面立体相贯线的性质。 • 掌握用表面取点的方法求相贯线,这是本章 也是本讲的一个基础方法。 • 熟练掌握用辅助平面法求相贯线,这是本章 也是本讲的重点和难点。 • 掌握特殊情况下相贯线的状态。
4
5
根据需要求出若干个一般点。
光滑且顺次地连接各点,作出相贯线,并且判别可见性。
6 最后,补全可见与不可见部分的轮廓线或转向轮廓素线,并 擦除被切割掉的轮廓线或转向轮廓素线。
特殊点
特殊点有极限位置点、轮廓转向点、曲线 特征点和结合点四种。 这里转向轮廓线上的转向点并不都是区别 相贯线可见与不可见部分的分界点,只有距离 观察者近的一个曲面立体转向线上的点才是区 别可见性的分界点。
圆线 双曲线 1′ 4′ 3′
抛物线
2′
5′ 6′
1〞 2〞 4〞 (5〞) (6〞) 3〞
1 4 3 5
2 6
求圆锥被切割后的投影
复习题:平面立体与曲面立体相贯,完成相贯后的投影
表面取点法
圆线
解题步骤
1 分析 通常是由立体的积聚 性分析出相贯线的已知投影分 别是什么;再利用表面取点法 或辅助平面法求出相贯线的共 有点; 2 求出相贯线上的若干个特殊 点(通常是在平面立体的棱线 上或曲面立体的轮廓线上); 3 求出相贯线上的若干个一般 点(取决于是什么相贯线);
四段直线
2 求出相贯线上的若干个特殊 点(通常是在平面立体的棱线 上或曲面立体的轮廓线上);
3 求出相贯线上的若干个一般 点(取决于是什么相贯线); 4 光滑且顺次地连接各点,作 出相贯线,并且判别可见性;
5 整理轮廓线。
四段椭圆线
7-25.完成圆锥和四棱柱相贯后的投影。
7-26.完成四棱锥和圆柱相贯后的投影。
可见性参考
螺旋扶手(右旋)投影图画法
1. 如同画正螺旋柱状面那样,画出螺旋 楼梯扶手的H投影和扶手顶面内外螺 旋线上的各点(暂不连螺旋线)。 2. 从内螺旋先3/4的各点下落扶手竖向 厚度h;从外螺旋后3/4的各点下落扶 手竖向高度h。并将这些点分别连接 画内、外螺旋线。 3. 画扶手顶面可见螺旋线。扶手顶面先 1/2内螺旋点及后1/4内螺旋点连两段 内螺旋线,后1/2外螺旋点及先1/4外 螺旋点连两段外螺旋线。 4. 判别可见性,加深图线,画扶手轮廓 线,完成全图。 轴线左侧底面可见,轴线右侧顶 面可见;先1/2扶手内侧面可见,后 1/2扶手外侧面可见。(建议加深顺 序:底内螺旋线、底外螺旋线、顶内 螺旋线、顶外螺旋线、直轮廓线)
§15-5
曲面立体相贯
一.相贯线的性质
1 相贯线是两曲面立体表面的共有线,相贯线上的点是两 曲面立体表面的共有点。 2 不同的立体以及不同的相贯位置、相贯线的形状不同。 两回转体相贯,相贯线一般是封闭的空间曲线, 特殊情况下 为平面曲线或直线。
曲面立体相贯线的性质图例
二.曲面立体相贯的三种基本形式
2 圆柱正螺旋面的画法
(1)圆柱正螺旋面(锥状) (2)圆柱正螺旋面(柱状)
3 圆柱正螺旋面的应用
圆柱正螺旋面(锥状)的画法
圆柱正螺旋面(柱状)的画法 •作出该曲面上各素线的投 影;
•画出两条曲导线(圆柱螺 旋线); •作出直母线的两面投影;
3 圆柱正螺旋柱状面应用举例
螺旋扶手
螺旋楼梯
圆柱正螺旋柱状面应用实例
1 2 两外表面相交; 外表面与内表面相交;
3
两内表面相交。
三.求曲面立体相贯线的方法
求作相贯线时,先求出适当数量的共有点,然后依次光滑 连接而成。求共有点的方法是: (1)若相贯线有一个投影已知,可采用辅助面法或表面取点法作出 ; (2)若相贯线有二个投影已知,可采用表面取点法或由二求三的方 法作出; (3)若相贯线的三个投影均为未知,可采用辅助面法作出; (4)若求轮廓素线上的点,有时须包括轮廓素线作辅助面。 1 2 表面取点法 辅助平面法
(2) (5) 3
1 4
y
辅助平面法
4 光滑且顺次地连 接各点,作出相贯 线,并且判别可见 性; 5 整理轮廓线。
y
用水平面作为辅助平面求共有点
用水平面作为辅助平面求共有点
例题4 求圆球与圆锥的相贯线
PV1
3' 5' 2' 4' 1' 1"
辅助平面法
用水平面作为辅助平面求共有点
PV2 PV3
4" P W2 3" PW3 5"
S
δ
S分理解曲面立体相贯线的性质(共有 性和分界性) 特殊情况下相贯线的状态。 用表面取点的方法求相贯线。 用辅助平面法求相贯线。 了解螺旋楼梯的画法
同学们 圣诞快乐!
§7-4
曲面立体的贯穿点
1、圆柱的贯穿点 2、圆锥的贯穿点 3、圆球的贯穿点
例题1:求直线与圆柱的贯穿点
辅助平面法
1、用辅助平面法求相贯线的作图原理
辅助平面的选择
Q
常用的辅助平面为投影面的平行面或垂直面,要使辅助平面 与两立体表面交线的投影为直线或圆。
四·求相贯线的一般步骤
1 分析 首先分析两曲面立体的几何形状、相对大小和相对 位置,进一步分析相贯线是空间曲线,还是处于特殊情况(平 面曲线或直线)。分析两曲面立体对投影面的相对位置,两曲 面立体的投影是否有积聚性,哪个投影有积聚性。分析相贯线 哪个投影是已知的,哪个投影是要求作的。 3 求出相贯线上的特殊点。
§ 7-6
螺旋线和圆柱正螺旋面
一、 圆柱螺旋线 1 圆柱螺旋线的形成
当一个动点沿着一直线等 速移动,而该直线同时绕与它 平行的一轴线等速旋转时,动 点的轨迹就是一根圆柱螺旋线。
2 圆柱螺旋线的画法
螺旋线的画法
13′
9′
3′
1′
二、圆柱正螺旋面
1 圆柱正螺旋面的形成
当一直母线沿一条圆柱螺旋线及该圆柱螺旋 线的轴线滑动,并始终平行于与轴线垂直的导平 面而形成的曲面。是锥状面的特例。圆柱正螺旋 面与一个同轴的小圆柱相交,交线依然是一相同 导程的圆柱螺旋线。大小圆柱之间的圆柱正螺旋 面是柱状面的特例,又称正螺旋柱状面,其形成 也可描述为两条曲导线皆为圆柱螺旋线,连续运 动的直母线始终垂直于圆柱轴线。
双曲线
直线
4 光滑且顺次地连接各点,作 出相贯线,并且判别可见性;
5 整理轮廓线(棱线及轮廓线 至贯穿点止)。
例题10:平面立体与曲面立 体相贯,完成相贯后的投影
