运筹学第十章图与网络优化
运筹学第十章 图与网络分析

下面介绍当赋权有向图中,存在具负权 的弧时,求最短路的方法. 令 d(1)(vs,vj)=wsj 对t=2,3,…, d(t)(vs,vj)=min{d(t-1)(vs,vi)+wij} (j=1,2, …, p)
i
若进行到某一步,例如第k步,对所有j=1, 2, …,p,有 d(k)(vs,vj)=d(k-1)(vs,vj)
(vi,vj)∈T
如果支撑树T*的权w(T*)是G的所有支撑树 的权中最小者,则称T*是G的最小支撑树(简 称最小树) w(T*)=min w(T)
T
求最小树的方法: 方法一(避圈法) 开始选一条最小权的 边,以后每一步中,总从未被选取的边中选 一条权最小的边,并使之与已选取的边不构 成圈.
方法二(破圈法) 任取一个圈,从圈中 去掉一条权最大的边.在余下的图中,重复 这个步骤,一直到一个不含圈的图为止,这 时的图便是最小树. 例 用破圈法求下图的最小树
中所对应的点边序列是一条链,则称这个点 弧交错序列是D的一条链. 如果(vi1,ai1,vi2,ai2,…,vik-1,aik-1,vik)是D中的 一条链,并且对t=1,2,…,k-1,均有 ait=(vit,vit+1),称之为从vi1到vik的一条路.若 路的第一个点和最后一点相同,则称之为回 路.
32 63
(44) v4 27 37
21 (0பைடு நூலகம்v1
45 (78) v6
47 v3 (31) 34
32 v5 (62)
§4 最大流问题 如下是一运输网络,弧上的数字表示每 条弧上的容量,问:该网络的最大流量是多 少?
v1 4 vs 3 v2 2 2 v4 1 2 4 3 v3 3 vt
4.1 基本概念和基本定理 (1) 网络与流 定义1 给定一个有向图D=(V,A),在V中 有一个发点vs和一收点vt,其余的点为中间点. 对于每一条弧(vi,vj),对应有一个c(vi,vj)≥0,(cij) 称为弧的容量.这样的有向图称为网络.记 为D=(V,A,C). 网络的流:定义在弧集合A上的一个函数 f={f(vi,vj)},称f(vi,vj)为弧(vi,vj)上的流量.(fij)
运筹学 图与网络分析PPT学习教案

ij
min{ V1到Vj中间最多经过t-2个点 P1j(t-1)=
P1j(t-2)
+wij}
终止原则:
1)当P1j(k)= P1j(k+1)可停止,最短路P1j*= P1j(k) 2)当P1j(t-1)= P1j(t-2)时,第1再9页多/共迭59页代一次P1j(t) ,若P1j(t) =
P1j(t-1) ,则原问题无解,存在负回路。
图与网络模型Graph Theory
最短路问题
v1,u1 =(M,W,G,H); v2,u2 =(M,W,G);
v3,u3 =(M,W,H);
v4,u4 =(M,G,H);
v5,u5 =(M,G)。
此游戏转化为在下面的二部图中求从 v1 到 u1 的最短路问题。
v1
v2
v3
v4
v5
u5
u4
例: 求下图所示有向图中从v1到各点 的最短路。
2 v1
v2
4
5 -2 v3 6
-3 4
v4
7
v6 -3 2
v5
3
4
v8
-1
v7
第20页/共59页
wij
d(t)(v1,vj)
v1 v2 v3 v4 v5 v6 v7 v8 t=1 t=2 t=3 t=4 t=5 t=6
v1 0 2 5 -3
0 0 0 00 0
参加的游客众多,游客甚至不惜多花机票钱暂转取道它地也愿参加
此游。旅行社只好紧急电传他在全国各地的办事处要求协助解决此
问题。很快,各办事处将其已订购机票的情况传到了总社。根据此
资料,总社要作出计划,最多能将多少游客从成都送往北京以及如
何取道转机。下面是各办事处已订购机票的详细情况表:
图论与网络优化-刘彬农庆琴

图与网 2 络基本
概念
连通性?
图的连通度、边连通度、块的概念 络进行建模的实
2 与基本性质
际问题 (包括工
图的搜索与连通性判定算法
件排序问题)
最短路 (SP)?
2
最短路问题、Dijkstra 算法和 Floyd 用数学软件求解
算法
最短路问题
3
树
什么是树 (Tree)?
最小支撑树 (MCST)?
2 树的定义与基本性质、割边、割点 1.MCST 其他算 法;
2. 主要参考书: [1] 图论与网络流理论,高随祥,高等教育出版社,2009.01. [2] Introduction to Graph Theory (Second Edition), Douglas B. West, Prentice Hall,
2001.(中译本:图论导引,李建中、骆吉周译,机械工业出版社,2006)
图论与网络优化以图和网络为研究对象,通过对事物间的联系、相互影响进行网 络建模,对网络结构以及建立在网络结构上行为决策进行研究。本课程主要介绍图论 与网络优化的基本概念、重要理论和算法以及理论的应用,主要包括以下三部分内容:
1)图的概念与结构:树、连通度、Euler 环游与 Hamilton 圈、匹配、独立集与团、 平面图染色等;
-2-
四、教材与主要参考书
1. 教材: [1] Graph theory with applications, J.A. Bondy and U.S.R. Murty, The Macmillan Press
Ltd, New York, 1976.(中译本:图论及其应用,科学出版社,1984) [2] 运筹学(第 4 版),运筹学教材编写组,清华大学出版社,2012.09。
《图与网络优化》PPT课件

• “充分性”:设图 G 中任两个点之间恰有一条链, 那么易见 G 是连通的。如果 G 中含有圈,那么这个 圈上的两个顶点之间有两条链,这与假设相矛盾, 故 G 不含圈,于是 G 是树。
• 由这个定理,很容易推出如下结论:
• (1)从一个树中去掉任意一条边,则余下的图是不 连通的。由此可知,在点集合相同的所有图中,树 是含边数最少的连通图。
么 G 本身就是一个树,从而 G 是它自身的一个支撑
树。现假设 G 含圈,任取一个圈,从圈中任意地去
掉一条边,得到图 G 的一个支撑子图 G1 。如果 G1 不含圈,那么 G1 就是 G 的一个支撑树(因为 G1 的 顶点数与 G 相同,且连通);如果 G1 仍然含圈,那 么从 G1 中任取一个圈,从圈中再任意去掉一条边, 得到图 G 的一个支撑子图 G2 ,如此重复,最终可以 得到 G 的一个支撑子图 Gk ,它不含圈,于是 Gk 是 G 的一个支撑树。
• 以点 v 为端点的边的个数称为 v 的次。记为 dG(v) 或 d(v) 。称次为1的点为悬挂点,悬挂点的关联边称为
悬挂边,次为零的点称为孤立点。
• 定理1:图 G=(V , E) 中,所有点的次之和是边数的
两倍,即有: dv2q vV
• 次为奇数的点称为奇点,否则称为偶点。
• 定理2:任一个图中,奇点的个数为偶数。
精选ppt
4
• 如果一个图 G 是由点及边所构成的,则称之为无向 图,简记为 G=(V , E),其中, V , E 分别是图 G 的点 集合和边集合。一条连接点 vi ,vj V 的边记为[vi ,vj ] (或 [vj , vi])。
• 如果一个图 D 是由点及弧所构成的,则称之为有向 图,简记为D =(V , A),其中, V , A 分别是图 G 的点 集合和弧集合。一条方向是从 vi 指向 vj 的弧记为 (vi ,vj)。
运筹学图与网络优化

证明
记 V0 {v V (G), d (v) 0(mod 2)};
V1 {v V (G), d(v) 1(mod 2)};
d (v) d (v) d (v) 0(mod2);
vV (G )
vV1
vV0
d (v) 0(mod2);
vV0
d (v) 0(mod2); vV1
定理3 设T是连通图G的一棵支撑树,e是T的任意一条边,则:
(1)T 不包含G的割集
(2)T e 包含G的唯一的割集。
定理4 设T1 和T2 是G的两个支撑树,令
k E(T1 ) \ E(T2 )
则T1 经过k次迭代后可得到T2。
最小树
设G是一个赋权图,T为G的一个支撑树。定义T的权为:
如F={ e },则记 G e G {e}。
子图图例
v1 e1
v2
e2
v3
e3
v5
v4
G
v1
v
v3
2
v5
v4
G的支撑子图
G-{ e1 , e 2 , e 3}
子图图例2 v2 e2
v3
G-{v 1,v 5 } v4
v1 e1
v2
e2
v3
e3
v5
v4
G
v1
v
2
G[v 1,v 2 ,v 5 ]
1 1 0 0 1 0 1 d (v1) 4
M (G) 1 1 1 0 0 0 0 0 0 1 1 0 0 1
d (v2 ) 3
d (v3 ) 3
0 0 0 1 1 2 0 d (v4 ) 4
2 22 2 222
图与网络优化决策的图论方法

图与网络优化决策的图论方法
图论方法在网络优化决策中起着非常重要的作用。
具体来说,图论方法可以用来表示和分析网络中的各种关系和结构,从而帮助优化决策。
以下列举了一些常见的图论方法在网络优化决策中的应用:
1. 最短路径算法:最短路径算法可以找到网络中两个节点之间的最短路径,从而帮助决策者选择最佳的路径来达到特定的目标。
2. 最小生成树算法:最小生成树算法可以找到一个网络中连接所有节点的最小成本的子图,从而帮助决策者选择最佳的连接方式来降低总体成本。
3. 最大流最小割算法:最大流最小割算法可以找到网络中的最大流量和最小割集,从而帮助决策者优化网络中的流量分配和资源利用。
4. 贪心算法:贪心算法是一种启发式算法,可以通过每次选择最优的局部决策来逐步优化整体决策。
在网络优化决策中,贪心算法可以用来选择最优的节点或边的顺序以达到最佳目标。
5. 随机图算法:随机图算法可以通过随机生成图形来模拟和分析网络中的不确定性和风险因素。
这可以帮助决策者对各种可能情况做出更合理的决策。
总之,图论方法在网络优化决策中可以提供对网络结构和关系的深入理解,帮助决策者做出最佳的选择和决策。
不同的图论方法可以根据具体问题的需求和约束选择和组合使用。
运筹学第10章图与网络分析清华大学出版社

由于2m为偶数, 而 d (v )是若干个偶数之和, 也是偶数.
vV2
所以 d (v )必为偶数,即 | V1 | 是偶数.
有向图中,以vi为始点的边数称为点vi的出次, 用d (vi )表示, 以vi为终点的边数称为点vi的入次, 用d (vi )表示, vi点的出次与入次之和就是该点的次.
六、第10章 图与网络分析
图与网络的基本知识 树及最小树问题 最短路问题 最大流问题 最小费用最大流问题
(Graph Theory and Network Analysis)
A
C
D
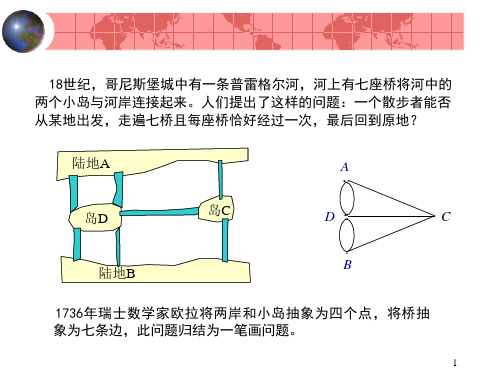
问题:一个游者怎样才 能一次连续走过这七座 桥且每座桥只走一次, 回到原出发点。
A
B
哥尼斯堡“七桥”难 题 欧拉用A,B,C,D四点表示河的 两岸和小岛,用两点间的联 线表示桥。七桥问题变为: 从A,B,C,D任一点出发,能否 通过每条边一次且仅一次, 再回到该点?
无路可通.那么加上一边( u, v )也不会形成圈, 与已知矛盾. 再证每舍去一边便不连通.若T中有一边( u, v ), 舍去( u, v )后
图T ( u, v )仍然连通, 那么T T ( u, v )由于无圈是一棵树
但T 加一边( u, v )后就是T 仍无圈, 与( 4)中树每加一新边必
从T中去掉(v , u)边及u点不会影响T的连通性, 得图T , T 为树 只有k 1个顶点, 所以有k 2条边, 再把(v , u),u加上去,可知
当T 有k个顶点时有k 1条边.
( 2) (3)
只需证明T 是连通图.
l
反证法.设T 不连通, 可以分为l个连通分图( l 2), 设第i个
e4
网络优化图及网络(运筹学)

最短路径问题有多种算法,如Dijkstra算法和Bellman-Ford算法。这些算法通 过不断优化路径长度,最终找到最短路径。在现实生活中,最短路径问题广泛 应用于交通网络、通信网络和电力网络等领域。
最小生成树问题
总结词
最小生成树问题是图论中的另一个经典问题,旨在在给定连 通图中找到一棵包含所有节点且总权重最小的树。
网络优化图及网络(运筹学)
目 录
• 网络优化图概述 • 网络(运筹学)基础 • 网络优化模型 • 网络优化算法 • 网络优化实例分析 • 网络(运筹学)的未来发展与挑战
01
网络优化图概述
定义与特点
定义
网络优化图是一种数学模型,用于描 述现实世界中各种网络系统的结构和 行为。
特点
网络优化图具有节点和边的概念,能 够表示各种对象之间的关系和交互作 用,同时可以引入各种参数和约束条 件,以实现特定的优化目标。
详细描述
大数据的爆炸式增长使得传统的数据 处理和分析方法难以应对,需要采用 新的数据处理和分析技术,如分布式 计算、流处理等,以提高数据处理效 率。
人工智能与网络优化
总结词
人工智能技术的发展为网络优化提供了 新的思路和方法,可以更好地解决复杂 的问题。
VS
详细描述
人工智能技术如机器学习、深度学习等可 以用于网络优化,例如通过学习历史数据 来预测未来的流量和需求,从而更好地进 行资源调度和路径选择。
遗传算法通过模拟生物进化 过程中的自然选择和遗传机 制,不断迭代和优化种群中 的个体,最终找到最优解。
遗传算法适用于多目标优化、 约束满足问题等复杂问题,具 有较好的鲁棒性和全局搜索能
力。
05
网络优化实例分析
最短路径问题
运筹学图与网络优化133页PPT

26、要使整个人生都过得舒适、愉快,这是不可能的,因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情,化为上进的力量,才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者,好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人,倚靠在明眼的跛子肩上。——叔本华
16、云无心以出岫,鸟倦飞而知还。 17、童孺纵行歌,斑白欢游诣。 18、福不虚至,祸不易来。 19、久在樊笼里,复得返自然。 20、羁鸟恋旧林,池鱼思故渊。
运
运筹学第十章图与收集优化山东大学期末考试知识点复习

第十章图与网络优化1.图的基本概念(1)两点之间的不带箭头的连线称为边,带箭头的连线称为弧。
(2)如果一个图G是由点及边所构成的,则称之为无向图(也简称为图),记为G=(V,E),式中V,E分别是G的点集合和边集合,一条连结点v i,v j∈V的边记为[v i,v j](或[v j,v i])。
(3)如果一个图D是由点及弧构成的,则称为有向图,记为D=(V,A),式中V,A分别表示D的点集合和弧集合,一条方向是从v i指向v j的弧记为(v i,v j)。
(4)在无向图G=(V,E)中,若边e=[u,v]∈E,则u,v是e的端点,也称u,v是相邻的,称e是点u(及点v)的关连边。
若图G中,某个边e的两个端点相同,则称e是环,若两点之间有多于一条的边,称这些为多重边。
一个多环,无多重边的图形称为简单图,一个无环,但允许有多重边的图称为多重图。
以点v为端点的边的个数称为v的次,记为如dG(v)或d(v)。
在图10一1中,d(v1)=4,d(v2)=3,d(v3)=3,d(v)=4(环e7在计算d(v4)时算作两次)。
称次为1的点为悬挂点,悬挂点的关连边称为悬挂边,次为零的点称为弧立点。
(5)定理1 图G=(V,E)中,所有点的次之和是边数的两倍,即。
次为奇数的点称为奇点,否则称为偶点。
(6)定理2 任一个图中,奇点的个数为偶数。
(7)图G中,若任何两个点之间至少有一条链,则称G是连通图,否则称为不连通图。
若G是不连通图,它的每个连通的部分称为G的一个连通分图(也简称分图)。
如图10—2是一个不连通图,它有两个连通分图。
给了一个图G=(V,E),如果图G'=(V',E')。
做V=V',及E'∈E,则称G'是G的一支撑子图。
设v∈V(G)用Gv0表示从图G中去掉点v及v的关联边后得到的一个图。
例如若G如图10—3(a),所示,则Gv3如图10—3(b)所示,图10—3(c)是图G的一个支撑子图。
运筹学第十章图与网络优化

16
称矩阵A为网络G的邻接矩阵。
v1
4
v2
7 3 2 v3 5
图的矩阵表示
3
v6 3 4
6
2 v5 v4
权矩阵为:
v1 0 v 2 4 v 3 0 A v 4 6 v 5 4 v 6 3 v1 4 0 6 4 3 0 2 7 0 0 2 0 5 0 3 7 5 0 2 0 0 0 2 0 3 0 3 0 3 0 v 2 v 3 v4 v5 v6
17
三、基本定理
• 定理1 图G=(V,E)中,所有点的次之和 是边数的两倍,即
d (v ) 2q
vV
• 定理2 任一图中奇点的个数为偶数。
18
第二节
一、定义
树
树的定义:一个无圈的连通图。 例1 在五个城市之间架设电话线,要求任两个城市之间都可 以相互通话(允许通过其他城市),并且电话线的根数最少。 用v1,v2,v3,v4,v5代表五个城市,如 果在某两个城市之间架设电话 线,则在相应的两点之间联一条 边,这样一个电话线网就可以用 一个图来表示。显然,这个图必 须是连通的,而且是不含圈的连 通图。如右图所示。 v1 v5
10
v1
e4
e3 e2 v3
v4
e5
v5
•链
•中间点 •初等链
e1
v2
e6
e7 e8
e9
•圈 •初等圈
v6
v7
•简单圈
在上图中,(v1,v2,v3,v4,v5,v3,v6,v7)是一条链, 但不是初等链
在该链中,v2,v3,v4,v5,v3,v6是中间点
网络优化图及网络运筹学
(13,v3)
(18,v5)
(22,v6)
(0,s) (10,v1)
(14,v3)
(16,v5)
实际中我们还可以从各点的标号找到v1到各点的距离, 以及从v1到各点最短路径.例如,从v4的标号(18,v5) 可知v1到v4的距离为18,并可找到v1到v4的最短路径为
25
例11:求节点1-6之间的最短路。
32
应用举例
例12 设备更新问题。某企业使用一台设备,在每年年初都要 决定是购置新设备还是继续使用旧的。购置新设备要支付一定 的购置费,使用旧设备则要支付维修费。制定一个五年内的设 备更新计划,使得总支付费用最少。
已知该设备在各年年初的价格为:
第一年 11
第二年 11
第三年 12
第四年 12
第五年 13
原问题图画为:
43
基本思路:
(1)找出一条从发点到收点的路,在这条路上的每一条弧的可用容 量都大于零。如果不存在这样的路,则已求得最大流。 (2)找出这条路上各条弧的最小的可用容量Pf,通过这条路增加网络 的流量Pf 。 (3)在这条路上,减少每一条弧的可用容量Pf ,同时增加这些弧的 流量Pf ,返回步骤(1)。 当然由于在步骤(1)中所选择的路不一样,计算过程也不一样,但 最终所求得的最大流量应该是一样的,为了使算法更快捷有效。 我们一般在步骤(1)中尽量选择包含弧数最少的路。
边,这样一个电话线网就可以用
一个图来表示。显然,这个图必
v4
须是连通的,而且是不含圈的连 通图。如左图所示。
3
例3 某工厂的组织机构如下图所示
行
生产计划科
政 办
技术科
设计组 工艺组
公
供销科
运筹学图论与网络优化

例:Hamilton图
游戏:用正十二面体上20个顶点表示20个城市, 要求参加游戏者沿着各边行走,走遍每一个城市且 仅走一次,最后回到出发城市。
公元1859年,哈密尔顿 (Hamilton)在给朋友格拉 伍斯(Grares)的信中提 出了这个游戏。
问题:如何判断一个图是 否具有这样的性质。如果 有,这样的行走路线如何 确定。
第十章 图论与网络优化
1 图的基本概念 2 最小树问题 3 最短路问题 4 网络最大流问题 5 最小费用最大流问题
一些问题
A
例:七桥问题
C
D
B
图问论题中:著 一名 个问 散题 步者. 能17否36走年过,七图座论桥的,创且始每人座Eu桥le只r巧走 妙地将过此一问次题,化最为后图回的到不出重发复点一。笔画问题,并证明
点:研究对象(陆地、路口、国家、球队); 点间连线:对象之间的特定关系(陆地间有桥、路
口之间道路、两国边界、两球队比赛及 结果)。 对称关系:桥、道路、边界;
用不带箭头的连线表示,称为边。
非对称关系:甲队胜乙队,用带箭头的连线表示, 称为弧。
图:点及边(或弧)组成。
对所要研究的问题确定具体对象及这些对象间的 性质关系,并用图的形式表示出来,这就是对所 研究原问题建立的模型。图是反映对象之间关系 的一种工具。
例:中国邮路问题
一个邮递员送信,要走完他所负责的全部街道 分送信件,最后返回邮局。邮递员都会本能地以尽 可能少的行程完成送信任务。如何走路线最短。
点:路口; 边:两路口之间道路,第i条道路长ei。
1962年,由我国数学家管梅谷提出,国际上称为中 国邮递员问题。
问题:求一个圈,过每边至少一次,并使圈的长度 最 短。
运筹学:动态规划、图与网络优化习题与答案

一、判断题1.动态规划分为线性动态规划和非线性动态规划。
()正确答案:×2.对于一个动态规划问题,应用顺推法和逆推法可能会得到不同的最优解。
()正确答案:×3.在用动态规划解题时,定义状态时应保证各个阶段中所做的决策的相互独立性。
()正确答案:√4.动态规划计算中的“维数障碍”主要是由问题中阶段数的急剧增加而引起的。
()正确答案:×二、选择题1.关于图论中图的概念,以下叙述()正确。
A.图中的有向边表示研究对象,结点表示衔接关系。
B.图中的点表示研究对象,边表示点与点之间的关系。
C.图中任意两点之间必有边。
D.图的边数必定等于点数减1。
正确答案:B2. 关于树的概念,以下叙述()正确。
A.树中的点数等于边数减1B.连通无圈的图必定是树C.含n个点的树是唯一的D.任一树中,去掉一条边仍为树。
正确答案:B3. 一个连通图中的最小树()。
A.是唯一确定的B.可能不唯一C.可能不存在D.一定有多个。
正确答案:B4.关于最大流量问题,以下叙述()正确。
A.一个容量网络的最大流是唯一确定的B.达到最大流的方案是唯一的C.当用标号法求最大流时,可能得到不同的最大流方案D.当最大流方案不唯一时,得到的最大流量应相同。
正确答案:D5. 图论中的图,以下叙述()不正确。
A.图论中点表示研究对象,边或有向边表示研究对象之间的特定关系。
B.图论中的图,用点与点的相互位置,边的长短曲直来表示研究对象的相互关系。
C.图论中的边表示研究对象,点表示研究对象之间的特定关系。
D.图论中的图,可以改变点与点的相互位置。
只要不改变点与点的连接关系。
正确答案:C6. 关于最小树,以下叙述()正确。
A.最小树是一个网络中连通所有点而边数最少的图B.最小树是一个网络中连通所有的点,而权数最少的图C.一个网络中的最大权边必不包含在其最小树内D.一个网络的最小树一般是不唯一的。
正确答案:B7.关于可行流,以下叙述()不正确。
运筹学图与网络分析.pptx

{a26,a46 } φ
min{ li Wij | Vj J } lh Whk
iI
min{l1+W12, l1+W13, l1+W14}= min{0+3,0+2,0+5}=2= l1+W13 min{l1+W12, l1+W13, l3+W34}= min{0+3,0+5,2+1}=3= l1+W12, l3+W34 min{l2+W26, l4+W46}= min{3+7,3+5}=8= l4+W46
{ a57,a68 }
min{ li Wij | Vj J } lh Whk
iI
min{l1+W12, l1+W13, l1+W14}= min{0+2,0+6,0+3}=2= l1+W12 min{l1+W13, l1+W14, l2+W23, l2+W26}= min{0+6,0+3,2+3, 2+7}=3= l1+W14 min{l1+W13,l2+W23, l2+W26, l4+W45}= min{0+6,2+3,2+7,3+6}=5= l2+W23 min{l2+W26, l3+W35, l3+W36, l4+W45}= min{2+7,5+3,5+7,3+6}=8= l3+W35 min{l2+W26, l3+W36, l5+W56, l5+W57}= min{2+7,5+7,8+1,8+6}=9= l2+W26, l5+W56 min{ l5+W57, l6+W68}= min{8+6,9+4}=13= l6+W68
运筹学( 图与网络优化)

七桥问题
七桥问题图形
原理及方法
七桥问题是图论中的著名问题。1736年,Euler巧妙 地将此问题化为图的不重复一笔画问题,并证明了 该问题不存在肯定回答。原因在于该图形有顶点连 接奇数条边。
§10.1
图的基本概念
一个图(Graph) 定义为三元有序组
(V (G ), E (G ), G )
几何实现图例
在一个图的几何实现中,两条边的交点可能不是图的顶 点。例如下图 中,它共有4个顶点,6条边;而e 3 与e 4 的交点不是这个图的顶点。
v1
e1
v2 e4
e2
v3
e3
e5
v4
e6
e3
v1
v4
e1 e4
v2
e2
v3 e6
e5
v4
平面图
一个图称为平面图,如它有一个平面图形,使得边与边仅在
u 1
f5 u3 f6
f2 f4
u2
u4
同构
给定两个图
G (V (G), E(G), G )
H (V ( H ), E( H ), H )
称G和H是同构的,记为 G H , 如果存在两个一一对应 ( , )
: V (G) V ( H )
: E (G) E ( H )
e7
v2
e3 v3
e6
v4
e4
关联矩阵性质
图G的关联矩阵M=(mij)为m×n矩阵;则每行元
素之和等于相应顶点的度;每列元素之和等于 2。
因此,图G的关联矩阵M所有元素之和既等于所
有顶点的度之和,又等于边数的2倍。 定理 设G是一个图,则
vV ( G )
d (v) 2
管理运筹学--第_10_章图与网络优化2

(7, v5 ) [ ]
1
v6
2 4
1 1
vt
[ ] (9, v8 )
3
v2
(1,,vss) [ v]
v5
[ ] (4, v2 )
v8
[8, v5 ] ( )
第七章 图论
(3, v2 ) [ ]
(4, vs )
4
v1
1 2 2
3 ( ) [4, v3 ] 1
(6, v1 )
v4
6
5 2
v7 [9, v ] ( )
ij ij
如果计算结果希望给出具体的最短路的路径, 则 构造路径矩阵S=(sij) nn , sij表示vi到vj的最短路的第 ( n) s 一条弧的终点。如ij t ,则从vi到vj的最短路的 第一条弧为( vi,vt), 第二条弧为从vt到vj的最短路的 第一条弧。
Floyd算法步骤:
第1步:U
uij min uij , ui 1 u1 j
再在D1中加入v2及D中与vi,vj,v1, v2相关联的 (2) 弧,得D2,D2中vi到vj的最短路长记为 uij ,则有
u
(2) ij
min u , u u
(1) ij (1) i2
(1) 2j
递推,D中n个点逐个加入子网络,终得D中vi到 (n) vj的最短路路长 u u
4
[9, v6 ] ( ) [ ] (9, v8 ) 3
1 1
vs
[0, vss ] ( )
1
v3
2
( ) 4 [7, v3 ] [3 2 ]( ) (3, v2 )[7, v5 ]
1 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
17
三、基本定理
• 定理1 图G=(V,E)中,所有点的次之和 是边数的两倍,即
d (v ) 2q
vV
• 定理2 任一图中奇点的个数为偶数。
18
第二节
一、定义
树
树的定义:一个无圈的连通图。 例1 在五个城市之间架设电话线,要求任两个城市之间都可 以相互通话(允许通过其他城市),并且电话线的根数最少。 用v1,v2,v3,v4,v5代表五个城市,如 果在某两个城市之间架设电话 线,则在相应的两点之间联一条 边,这样一个电话线网就可以用 一个图来表示。显然,这个图必 须是连通的,而且是不含圈的连 通图。如右图所示。 v1 v5
d (v ) p(G ), 这与q(G ) p(G ) 1矛盾。
i
设v1 是G的一个悬挂点,则图 G v1也是连通的。 由于q(G v1 ) q(G ) 1 p(G ) 2 p(G v1 ) 1, 因此由归纳假设知 G v1不含圈,于是 G也不含圈。
a8
a6 a5
v5
a10 a9 v4 v6 a11
v7
•路 • 初等路 • 回路
a1
v2
a7
(v1 , a2 , v 3 , a4 , v4 , a7 , v6 )是从v1到v6的路。也是一条初等路 。
在上图中 , (v3 , a3 , v2 , a5 , v4 , a6 , v5 , a8 , v3 )是一个回路。
15
•图的矩阵表示
对于网络(赋权图)G=(V,E),其中边 (vi , v j ) 有权 wi j ,构造矩阵 A (ai j )nn ,其中:
wi j ai j 0 (v i , v j ) E (v i , v j ) E
称矩阵A为网络G的权矩阵。
设图G=(V,E)中顶点的个数为n,构造一个矩阵 A (ai j )nn ,其中:
第十章 图与网络优化
(Graph Theory and Network Analysis)
1 2 3 4 5 6 图的基本概念 树及最小支撑树 最短路问题 网络最大流问题 最小费用最大流问题 中国邮递员问题
1
图论的起源和发展
• 1736年,Euler
哥尼斯堡七桥问题 (Kö nigsberg Bridge Problem) A
再证充分性。只要证 G中不含圈。用数学归纳 法。 当p(G ) 1,2时,结论显然成立。 设p(G ) n(n 2 )时,结论也成立。 则当p(G ) n 1时,G必有悬挂点。 否则,对每个点 v i , 有d (v i ) 2, 从而有 1 q(G ) 2
p(G ) i 1
可知需要4个库房, 其中一个答案是:
v3 v4 { v1 } { v2, v4, v7 } { v3, v5 } { v6, v8 } 还有其他的答案。
v8 v7
v6
v5
6
二、基本概念
v4
• 有向图 由点及弧所构成的图,记为 D=(V,A), V,A分别是D的点集 合和弧集合。 a5 v3 a6 a4
• 多重图 一个无环、但允许有多重边的图。
9
e7 v4
e5 v3 e6
e3
e2 e4
v1
e8
e1
v5
v2 如 d(v4)=5 d(v2)=4
• 点v的次 以点vi为端点边的个数,记为dG(vi)或d(vi)。 • 悬挂点 • 悬挂边 • 孤立点 • 偶点 • 奇点 次为1的点,如 v5 悬挂点的关联边,如 e8 次为0的点 次为偶数的点,如 v2 次为奇数的点, 如 v5
1 ai j 0 (v i , v j ) E (v i , v j ) E
16
称矩阵A为网络G的邻接矩阵。
v1
4
v2
7 3 2 v3 5
图的矩阵表示
3
v6 3 4
6
2 v5 v4
权矩阵为:
v1 0 v 2 4 v 3 0 A v 4 6 v 5 4 v6 3 v1 4 0 6 4 3 0 2 7 0 0 2 0 5 0 3 7 5 0 2 0 0 0 2 0 3 0 3 0 3 0 v 2 v 3 v4 v5 v6
10
v1
e4
e3 e2 v3
v4
e5
v5
•链
•中间点 •初等链
e1
v2
e6
e7 e8
e9
•圈 •初等圈
v6
v7
•简单圈
在上图中,(v1,v2,v3,v4,v5,v3,v6,v7)是一条链, 但不是初等链
在该链中,v2,v3,v4,v5,v3,v6是中间点
(v1,v2,v3,v6,v7)是一条初等链 ( v4,v1,v2,v3,v5,v7,v6,v3,v4)是一个简单圈 (v1,v2,v3,v4,v1)是一个初等圈
v1
v3
v2
v1 a1 v2
v3 v4 e5 v3 e6
v2 e3 e2 e4 G(D) v2
13
• 基础图 v4 a3 给定一个有向图 D=(V,A) ,从D a2 a5 a6 中去掉所有弧上 的箭头,所得到 的无向图称为基 v3 a4 础图。记之为 D=(V,A) G(D)。
v1 e1
v3
a2 v1 a3 a4
C4
叶
21
二、性质
定理1 设图G=(V,E) 是一个树,p(G)≥2, 则G中至少有两个悬挂点。 证明 反证法
设(v1 , v 2 , , v k )为G中边数最多的一条链。 当k 2时, 即p(G ) 2时, 命题成立。 当p(G ) 2时, 设v1不是悬挂点 , 即 d ( v 1 ) 2, 则存在v s , 使得(v s , v1 )为G中的一条边。 若v s 在上述链中 , 则G含圈, 与条件矛盾 ; 若v s不在上述链中 , 则存在链(v s , v1 , v 2 , , v k ), 与假设矛盾 . 所以v1为悬挂点。同理, v k 也是悬挂点。
25
三、图的支撑树
定义:设图T=(V,E’) 是图G的支撑子图,如果图 T=(V, E’) 是一个树,则称T是G的一个支撑树。 定理:图G有支撑树的充分必要条件是图G是连通的。
证明 必要性显然。 再证充分性。 设图G是连通图,若G不含圈,则G本身 是一个树,从而G是它自身的一个支撑树。
如果G含圈,任取一个圈,从圈中任意地去掉一条边,得 到图G的一个支撑子图G1。如果G1不含圈,那么G1是G的一 个支撑树;如果G1仍含圈,那么从G1中任取一个圈,从圈中 再任意去掉一条边,得到图G的一个支撑子图G2,如此重复, 最终可以得到G的一个支撑子图Gk,它不含圈,于是Gk是G的 一个支撑树。
如:v1,v4为e3的端 点,v1,v4是相邻的, e3 是v1(v4 )的关 联边。
8
e7 v4
e5 v3 e6
e3
e2 e4
v1
e1 v2
• 环 若在图G中,某个边的两个端点相同,则称e是环。如 e7 • 多重边 若两个点之间有多于一条的边,称这些边为多重边。如 e1,e2 • 简单图 一个无环,无多重边的图。
22
定理2 图G=(V,E) 是一个树的充分必要条件 是G中不含圈,且恰有p-1条边。 证明 先证必要性。即要证明 q(G ) p 1.
用数学归纳法。当 p 2时, 显然成立。 设p n时,命题成立,即含有 n 1条边。 当p n 1时,G中含有悬挂点 , 记为v1 . 因为G v1 是n个点的树,由题设 q(G v1 ) n 1 且p(G v1 ) n,q(G v1 ) q(G ) 1, 所以,q(G ) n p 1, 命题也成立。 再证充分性。即要证明 G是连通的。 用反证法。假设 G不连通,则G1 , G2 , , G S 为G的连通分图 .
3
第一节
图的基本概念
北京 天津
一、几个例子
例1 是北京、上海等 十个城市间的铁路交 通图。与此类似的还 有电话线分布图、煤 气管道图、航空路线 图等。 济南 徐州 青岛
郑州
连云港
武汉
南京
上海
4
例2 分别用点v1,v2,v3,v4,v5分别代表甲、乙、 丙、丁、戊五支球队。若有两支球队之间 比赛过,就在相应的点之间联一条线,且 这条线不过其他点。如下图所示:
邻接矩阵为:
v 1 0 v 2 1 v 3 0 B v 4 1 v 5 1 v6 1 v1 1 0 1 1 1 0 1 1 0 0 1 0 1 0 1 1 1 0 1 0 0 0 1 0 1 0 1 0 1 0 v 2 v 3 v4 v5 v6
• 简单有向图
• 多重有向图
14
• 权与网络
在实际应用中,给定一个图G=(V,E)或有向图D=(V, A),在V中指定两个点,一个称为始点(或发点),记作 v1 ,一个称为终点(或收点),记作vn ,其余的点称为中间 点。对每一条弧 (vi , v j ) A ,对应一个数 w i j ,称为弧上的 “权”。通常把这种赋权的图称为网络。
A
D C C
D
B
B
一笔画问题
2
• 1847年,kirchhoff,电网络,“树”; • 1852年,《四色猜想》; • 1857年,Cogley,同分异构,“树”; • 1956年,杜邦公司,CPM,关键路线法; • 1958年,美国海军部,PERT,计划评审技术; • 1962年,管梅谷,《中国邮路问题》; • 1964年,华罗庚,《统筹方法平话》。
24
定理4 图G是树的充分必要条件是 任意两个顶点之间恰有一条链。
证明 由树的定义,必要性显然。 因为任两个顶点间恰有一条链,显然G是连通的。 如果G中含有圈的话,则其中至少有两个顶点间 有两条链,这与题设矛盾。充分性得证。 推论: • 从一个树中去掉一条边,则余下的图是不连通的。 • 在树中不相邻的两个点间添上一条边,则恰好得到一个圈。
