运筹学图与网络(I)
合集下载
运筹学8图与网络分析
e3 。在剩下的图中，再取一个圈
定理8.7充分性的证明，提供了一个 寻找连通图支撑树的方法叫做“破圈法”。 就是从图中任取一个圈，去掉一条边。再 对剩下的图重复以上步骤，直到不含圈时 为止，这样就得到一个支撑树。
例8.4 用破圈法求出图8-11的一个支
撑树。
v2
e1
e7 e4
v1
e3 v4
e8
v5
e2
e5
v3
e6
图8-11
取一个圈(v1,v2,v3,v1)，在一个圈中去掉边
3
4
初等链：链中所含的 点均不相同, 也称通 路；
5
6
为闭链或回路或圈；
简单圈：如果在一个圈中所含的边均不相同 初等圈：除起点和终点外链中所含的点 均
不相同的圈；
连通图：图中任意两点之间均
至少有一条通路，否则 v1
v4 v5 v8
称为不连通图。
v2
初等链: (v1 , v2 , v3 , v6 ,
图的连通性：
简单链：链中所含的 边均不相同；
圈：若 v0 ≠ vn 则称该链为开链，否 则称
1
2
链：由两两相邻的点及其相 关联的边构成的点边序列。 如:v0 ,e1 ,v1 ,e2 ,v2，e3 ,v3 ,…,vn1 , en ， vn ; v0 ，vn 分别为链的起点和终点 。记 作（ v0 ,v1 , v2， ,v3 , …, vn-1 , vn ）
v5
v7
(v5
,v1v6),(v6
(v4 ,v6),(v5 ,v7)}
,v3),(v5
v6
,v4),
v2
v4
图8.5
下面介绍一些常用的名词：
运筹学(第6章 图与网络分析)
a1 (v1) 赵
(v2)钱
a2 a3 a4 a14 a15
a8 a9
a7 (v4) 李
(v3)孙
a5 (v5) 周 a6 a10 (v6)吴
图6-3
a12 a11 a13
(v7)陈
定义: 图中的点用v表示，边用e表示。对每条边可用它
所连接的点表示，记作：e1=[v1,v1]; e2=[v1,v2];
树是图论中结构最简单但又十分重要的图。在自然和社会领 域应用极为广泛。 例6.2 乒乓求单打比赛抽签后，可用图来表示相遇情况，如 下图所示。
运动员 A
B C
D
E
F G
H
例6.3 某企业的组织机构图也可用树图表示。
厂长
人事科
财务科
总工 程师
生产副 厂长
经营副 厂长
开发科
技术科
生产科
设备科
供应科
动力科
e2
(v1) 赵
e1
e3
e4 孙(v3) 李(v4)
周(v5)
图6-2
e5 吴(v6) 陈(v7)
(v2)钱
如果我们把上面例子中的“相互认识”关系改为“认识” 的关系，那么只用两点之间的联线就很难刻画他们之间的关 系了，这是我们引入一个带箭头的联线，称为弧。图6-3就是 一个反映这七人“认识”关系的图。相互认识用两条反向的 弧表示。
端点,关联边,相邻 若有边e可表示为e=[vi,vj]，称vi和
e2 v2 e6 e1 e4 v1 e3 v3 e8
vj是边e的端点，反之称边e为点vi
或vj的关联边。若点vi、vj与同一条 边关联，称点vi和vj相邻；若边ei和
e5
e7
(v2)钱
a2 a3 a4 a14 a15
a8 a9
a7 (v4) 李
(v3)孙
a5 (v5) 周 a6 a10 (v6)吴
图6-3
a12 a11 a13
(v7)陈
定义: 图中的点用v表示，边用e表示。对每条边可用它
所连接的点表示，记作：e1=[v1,v1]; e2=[v1,v2];
树是图论中结构最简单但又十分重要的图。在自然和社会领 域应用极为广泛。 例6.2 乒乓求单打比赛抽签后，可用图来表示相遇情况，如 下图所示。
运动员 A
B C
D
E
F G
H
例6.3 某企业的组织机构图也可用树图表示。
厂长
人事科
财务科
总工 程师
生产副 厂长
经营副 厂长
开发科
技术科
生产科
设备科
供应科
动力科
e2
(v1) 赵
e1
e3
e4 孙(v3) 李(v4)
周(v5)
图6-2
e5 吴(v6) 陈(v7)
(v2)钱
如果我们把上面例子中的“相互认识”关系改为“认识” 的关系，那么只用两点之间的联线就很难刻画他们之间的关 系了，这是我们引入一个带箭头的联线，称为弧。图6-3就是 一个反映这七人“认识”关系的图。相互认识用两条反向的 弧表示。
端点,关联边,相邻 若有边e可表示为e=[vi,vj]，称vi和
e2 v2 e6 e1 e4 v1 e3 v3 e8
vj是边e的端点，反之称边e为点vi
或vj的关联边。若点vi、vj与同一条 边关联，称点vi和vj相邻；若边ei和
e5
e7
第六章-运筹学图与网络优化
9
6 3
3
4
7
2
53
4 31
5
1
7
4
4
第3节 最短路问题
一、最短路的含义
赋权有向图D (V，A)，图中各弧(vi，v j )有权wij， vs，vt为图D中任意两点，求一条路P， 使它是从vs到vt的所有路中总权最小的路，
即w(
P
)
min
wij 。
(vi，vj )P
定义：路P的权是P中所有弧的权之和，记为w(P)
习题6-3：用Dijkstra方法求解下图从v1到v9的 最短‘路’。
v2
11
v7
3 6
2
5
5
v5
8
v1
v3
v9
2 4
4
3
7
v4
4
v6
6
v8
第3节 最短路问题
三、最短路问题的应用 ✓ 设备更新问题
第3节 最短路问题
例10：某工厂使用一台设备，每年年初工厂都要作出决定， 如果继续使用旧的，要付维修费；若购买一台新设备， 要付购买费。试制定一个5年的更新计划，使总支出最 少。已知设备在各年的购买费，及不同机器役龄时的 维修费如下表所示：
5
2
5 v6
v4
v7 8
习题6-2
2、
v2
2
v5
5
1
5
1
8
v1
7
5 v4 9
v6
6
v7
2
1
12
v3
第3节 最短路问题
（二）赋权无向图的最短‘路’问题的求解方 法
赋权无向图G=(V，E)，边[vi，vj]表示既可以 从vi到达vj，也可以从vj到达vi，所以边[vi， vj]可以看作是两条弧(vi，vj)和(vj，vi)，且 它们具有相同的权ωij。
运筹学第八章--图与网络分析-胡运权
运筹学
赵明霞山西大学经济与管理学院
2
第八章 图与网络分析
图与网络的基本概念 树 最短路问题 最大流问题 最小费用最大流问题
3
柯尼斯堡七桥问题
欧拉回路：经过每边且仅一次 厄尼斯堡七桥问题、邮路问题哈密尔顿回路：经过每点且仅一次 货郎担问题、快递送货问题
例8-9
28
基本步骤标号T(j)→P(j)
29
2017/10/26
30
最长路问题例8-10（7-9）设某台新设备的年效益及年均维修费、更新净费用如表。试确定今后5年内的更新策略，使总收益最大。
役龄项目
0
1
2
3
4
5
效益vk(t)
5
4.5
4
3.75
3
2.5
14
15
柯尼斯堡七桥问题
欧拉回路：经过每边且仅一次 厄尼斯堡七桥问题、邮路问题 充要条件：无向图中无奇点，有向图每个顶点出次等于入次
16
第二节 树
树是图论中的重要概念，所谓树就是一个无圈的连通图。
图8-4中，(a)就是一个树，而(b)因为图中有圈所以就不是树， (c)因为不连通所以也不是树。
7
G=(V,E)关联边(m)：ei端（顶）点(n)：vi, vj点相邻(同一条边)： v1, v3边相邻(同一个端点)：e2, e3环：e1多重边： e4, e5
8
简单图：无环无多重边
多重图：多重边
9
完全图：每一对顶点间都有边（弧）相连的简单图
10
次（d）：结点的关联边数目d(v3)=4，偶点d(v2)=3，奇点d(v1)=4d(v4)=1，悬挂点e6, 悬挂边d(v5)=0，孤立点
（一）线性(整数)规划法
赵明霞山西大学经济与管理学院
2
第八章 图与网络分析
图与网络的基本概念 树 最短路问题 最大流问题 最小费用最大流问题
3
柯尼斯堡七桥问题
欧拉回路：经过每边且仅一次 厄尼斯堡七桥问题、邮路问题哈密尔顿回路：经过每点且仅一次 货郎担问题、快递送货问题
例8-9
28
基本步骤标号T(j)→P(j)
29
2017/10/26
30
最长路问题例8-10（7-9）设某台新设备的年效益及年均维修费、更新净费用如表。试确定今后5年内的更新策略，使总收益最大。
役龄项目
0
1
2
3
4
5
效益vk(t)
5
4.5
4
3.75
3
2.5
14
15
柯尼斯堡七桥问题
欧拉回路：经过每边且仅一次 厄尼斯堡七桥问题、邮路问题 充要条件：无向图中无奇点，有向图每个顶点出次等于入次
16
第二节 树
树是图论中的重要概念，所谓树就是一个无圈的连通图。
图8-4中，(a)就是一个树，而(b)因为图中有圈所以就不是树， (c)因为不连通所以也不是树。
7
G=(V,E)关联边(m)：ei端（顶）点(n)：vi, vj点相邻(同一条边)： v1, v3边相邻(同一个端点)：e2, e3环：e1多重边： e4, e5
8
简单图：无环无多重边
多重图：多重边
9
完全图：每一对顶点间都有边（弧）相连的简单图
10
次（d）：结点的关联边数目d(v3)=4，偶点d(v2)=3，奇点d(v1)=4d(v4)=1，悬挂点e6, 悬挂边d(v5)=0，孤立点
（一）线性(整数)规划法
运筹学图与网络分析-最短路
(P0
)
min P
(P)
路P0的权称为从vs到vt的距离，记为d(vs,vt)。
求网络上的一点到其它点 的最短路
Dinkstra标号法
这是解决网络中某一点到其它点的最 短路问题时目前认为的最好方法。
适用于有向图权值非负的情况
有向图权值非负---- Dijkstra算法
Dijkstra算法的基本步骤（权值非负） 1、给顶点v1标号（0），v1称为已标号点，记标号点集为
(1,2)
2
2
0
1
2
5
7
(2,4)
3 5 55
7
3
1 (4,4) 3 1
4
6
7
(1,3)
5
④重复上述步骤，直至全部的
点都标完。
(1,2)
2
2
0
1
2
5
7
(2,4)
3 5 55
7
1
3
3
1
4
6
7
(1,3)
5
7
(1,2)
2
2
0
2
7
1
5
(2,4)
35
55
7
1
3
3
1
4
6
7
(1,3)
5
(3,7)
(1,2)
2
2
0
2
7
1
5 3 5 55 7
3
1
3 1
34 5 6
7
④重复上述步骤，直至全部的
(1,2)
点都标完。
2
2
0
2
7
1
5 3 5 55 7
图与网络分析 胡运权 第四版 运筹学PPT课件
4
3.关联与相邻
❖关联（边与点的关系）：若e是v1、v2两点间
的边，记e=[v1，v2 ]，称v1、v2 与e关联。
v1
e
v2
❖相邻（有公共边，称点v1与v2相邻；
边e1与e2 有公共点，称边e1与e2相邻。
e1
V2
V1
e2
V3
5
4. 链、圈与连通图
■链:由图G中的某些点与边相间构成的序列 {V1,e1,V2,e2, ……,Vk,ek},若满足 ei=[Vi, Vi ],则称此
（4）A={v1,v2,v4}
[0,v1]
[2,v1]
2
6
v1
v2
v3
1 [1,v1]10
5
9
3
v4
7
v5
6
5
2
3
4
v6
v7
4
[3,v1]
v8 8
考虑边（v1,v6),(v2,v3),(v2,v5),(v4,v7)
计算min { 0+3, 2+6, 2+5, 1+2}=min {3,8,7,3}=3
70
费用、容量等），则称这样 1
4
的图为网络图。
20
45
3
4.2 最小支撑树问题
C1 根
C2
C3
C4
叶
❖树：无圈的连通图，记为T。
8
❖树的性质
■ 树中任意两个节点间有 且只有一条链。
2
3
1
5
4
■ 在树中任意去掉一条边， 1
则不连通。
2
3
5
4
■如果树T有m个结点，则 边的个数为m-1。
3.关联与相邻
❖关联（边与点的关系）：若e是v1、v2两点间
的边，记e=[v1，v2 ]，称v1、v2 与e关联。
v1
e
v2
❖相邻（有公共边，称点v1与v2相邻；
边e1与e2 有公共点，称边e1与e2相邻。
e1
V2
V1
e2
V3
5
4. 链、圈与连通图
■链:由图G中的某些点与边相间构成的序列 {V1,e1,V2,e2, ……,Vk,ek},若满足 ei=[Vi, Vi ],则称此
（4）A={v1,v2,v4}
[0,v1]
[2,v1]
2
6
v1
v2
v3
1 [1,v1]10
5
9
3
v4
7
v5
6
5
2
3
4
v6
v7
4
[3,v1]
v8 8
考虑边（v1,v6),(v2,v3),(v2,v5),(v4,v7)
计算min { 0+3, 2+6, 2+5, 1+2}=min {3,8,7,3}=3
70
费用、容量等），则称这样 1
4
的图为网络图。
20
45
3
4.2 最小支撑树问题
C1 根
C2
C3
C4
叶
❖树：无圈的连通图，记为T。
8
❖树的性质
■ 树中任意两个节点间有 且只有一条链。
2
3
1
5
4
■ 在树中任意去掉一条边， 1
则不连通。
2
3
5
4
■如果树T有m个结点，则 边的个数为m-1。
运筹学第六章图与网络分析
S
2
4
7
2 A
0 5
S
5 45 B
98
14
5
13
D
T
C
E
4
4
4
7
最短路线：S AB E D T
最短距离：Lmin=13
2．求任意两点间最短距离的矩阵算法
⑴ 构造任意两点间直接到达的最短距离矩阵D（0）= dij（0）
S A B D（0）= C D E T
SABCDET 0 25 4 2 02 7 5 20 1 5 3 4 1 0 4 75 0 15 3 41 0 7 5 7 0
e1 v1
e5
v0 e2
e3
v2
e4
e6 e7
v3
v4
（4）简单图：无环、无多重边的图称为简单图。
（5）链：点和边的交替序列，其中点可重复，但边不能 重复。
（6）路：点和边的交替序列，但点和边均不能重复。
（7）圈：始点和终点重合的链。
（8）回路：始点和终点重合的路。
（9）连通图：若一个图中，任意两点之间至少存在一条 链，称这样的图为连通图。 （10）子图，部分图：设图G1=｛V1,E1｝, G2={V2,E2}, 如果有V1V2，E1E2，则称G1是G2的一个子图；若 V1=V2，E1E2，则称G1是G2的一个部分图。 （11）次：某点的关联边的个数称为该点的次，以d(vi)表示。
步骤：
1. 两两连接所有的奇点，使之均成为偶点；
2. 检查重复走的路线长度，是否不超过其所在 回路总长的一半，若超过，则调整连线，改 走另一半。
v1
4
v4
4
1
4
v2
v5
5
运筹学第6章 图与网络
也就是说| V1 |必为偶数。
定理6.2有学者也称作定理6.1的推论。根据定理6.2，握手定理也可以 表述为，在任何集体聚会中，握过奇次手的人数一定是偶数个。
12 该课件的所有权属于熊义杰
另外，现实中不存在面数为奇数且每个面的边数也是奇数的多面 体，如表面为正三角形的多面体有4个面，表面为正五边形的多面体有 12个面等等，也可以用这一定理予以证明。因为在任意的一个多面体 中， 当且仅当两个面有公共边时，相应的两顶点间才会有一条边，即 任意多面体中的一个边总关联着两个面。所以，以多面体的面数为顶
v j V2
(m为G中的边数）
因式中 2m 是偶数， d (v j ) 是偶数，所以 d (vi ) 也必为偶数
v j V2
vi V1
( 两个同奇同偶数的和差必为偶数 ), 同时,由于 d (vi ) 中的每个加数 d (vi )
均为奇数,因而 d (vi ) 为偶数就表明, d (vi ) 必然是偶数个加数的和 ,
图论、算法图论、极值图论、网络图论、代数图论、随机图论、 模糊图论、超图论等等。由于现代科技尤其是大型计算机的迅 猛发展，使图论的用武之地大大拓展，无论是数学、物理、化 学、天文、地理、生物等基础科学，还是信息、交通、战争、 经济乃至社会科学的众多问题．都可以应用图论方法子以解决。
1976年，世界上发生了不少大事，其中一件是美国数学家 Appel和Haken在Koch的协作之下，用计算机证明了图论难题— —四色猜想(4CC)：任何地图，用四种颜色，可以把每国领土染 上一种颜色，并使相邻国家异色。4CC的提法和内容十分简朴， 以至于可以随便向一个人(哪怕他目不识丁)在几分钟之内讲清 楚。1852年英国的一个大学生格思里(Guthrie)向他的老师德·摩 根(De Morgan)请教这个问题，德·摩根是当时十分有名的数学家， 他不能判断这个猜想是否成立，于是这个问题很快有数学界流 传开来。1879年伦敦数学会会员Kemple声称，证明了4CC成立， 且发表了论文。10年后，Heawood指出了Kemple的证明中
运筹学第六章图与网络分析a管理精品资料
min T (v j) T （ v j） ,L （ v i） d ij j
3. 在与固定标号点相邻的临时标号点中选取 具有最小标号的点vi给予固定标号，即:
L(vi)=min｛ T(vj) ｝ 返回第2步。 4. 当vn得到固定标号时，计算结束。 注： 固定标号L(vi)表示v1到vi的最短距离， 临时标号T(vj)表示v1到vi距离的上界。
能一笔画的图一定是欧拉圈或含有欧拉链。 定理：连通的多重图G是欧拉图的充要条件是G 中无奇点。 推论：连通的多重图G有欧拉链的充要条件是G 中恰有两个奇点。
第二节 树图和图的最小部分树
树图：无圈的连通图称为树图，记为T(V,E)。 2-1 树的性质 性质1：任何树中必存在至少两个次为1的点（悬 挂点）。
若一个简单图中任意两点之间均有边相连，
则称该图为完全图。
对含有n个顶点的完全图，其边数有
Cn2
1n(n1) 2
条。
如果图的顶点能分成两个互不相交的非空
集合V1和V2 ，使在同一集合中任意两个顶点 都不相邻，则称该图为偶图（或二分图）。
若偶图的顶点集合V1、V2之间的每一对不 同顶点之间都有一条边相连，则称该图为完全 偶图。在完全偶图中， V1若有m个顶点， V2 有n个顶点，则其边数共有m×n条。
临时标号
v2（5） v3（2） v4（∞） v5（∞） v6（∞） v7（∞） v2（5） v4（9） v5（∞） v6（6） v7（∞） v4（7） v5（12） v6（6） v7（∞） v4（7） v5（7） v7（12）
v5（7） v7（12）
v7（10）
❖ Dijkstra 算 法 仅 适 合 于 所 有 的 权
Hale Waihona Puke 3-2 求任意两点间最短距离的矩阵算法(Floyd) 设邻接矩阵为D,计算D1=D+D, D2= D1 +D ,
3. 在与固定标号点相邻的临时标号点中选取 具有最小标号的点vi给予固定标号，即:
L(vi)=min｛ T(vj) ｝ 返回第2步。 4. 当vn得到固定标号时，计算结束。 注： 固定标号L(vi)表示v1到vi的最短距离， 临时标号T(vj)表示v1到vi距离的上界。
能一笔画的图一定是欧拉圈或含有欧拉链。 定理：连通的多重图G是欧拉图的充要条件是G 中无奇点。 推论：连通的多重图G有欧拉链的充要条件是G 中恰有两个奇点。
第二节 树图和图的最小部分树
树图：无圈的连通图称为树图，记为T(V,E)。 2-1 树的性质 性质1：任何树中必存在至少两个次为1的点（悬 挂点）。
若一个简单图中任意两点之间均有边相连，
则称该图为完全图。
对含有n个顶点的完全图，其边数有
Cn2
1n(n1) 2
条。
如果图的顶点能分成两个互不相交的非空
集合V1和V2 ，使在同一集合中任意两个顶点 都不相邻，则称该图为偶图（或二分图）。
若偶图的顶点集合V1、V2之间的每一对不 同顶点之间都有一条边相连，则称该图为完全 偶图。在完全偶图中， V1若有m个顶点， V2 有n个顶点，则其边数共有m×n条。
临时标号
v2（5） v3（2） v4（∞） v5（∞） v6（∞） v7（∞） v2（5） v4（9） v5（∞） v6（6） v7（∞） v4（7） v5（12） v6（6） v7（∞） v4（7） v5（7） v7（12）
v5（7） v7（12）
v7（10）
❖ Dijkstra 算 法 仅 适 合 于 所 有 的 权
Hale Waihona Puke 3-2 求任意两点间最短距离的矩阵算法(Floyd) 设邻接矩阵为D,计算D1=D+D, D2= D1 +D ,
第六章物流运筹学——图与网络分析.
L( )
( vi ,v j )
l
ij
最小的 。
Dijkstra算法
算法的基本步骤： （1）给 v s 以 P 标号， P(vs ) 0 ，其余各点均给 T 标号， T (vi ) 。 （2）若 vi 点为刚得到 P 标号的点，考虑这样的点 v j： (vi , v j ) E ，且 v j 为 T 标号，对 v j 的 T 标号进行如下的更改：
v2
(4,3)
v4
(3,3)
(5,3) (1,1) (1,1) (3,0)
vs
(5,1)
vt
(2,1)
v1
(2,2)
v3
图 6-14
运输线路图
第四节 最小费用最大流问题
在容量网络 G (V , E, C ) ，每一条边 (vi , v j ) E 上，除了已 给容量 cij 外，还给了一个单位流量的费用 bij 0 ，记此时的容 量网络为 G (V , E, C , B) 。 所谓最小费用最大流问题就是要求一个最大流 f ，使流的 总运输费用 b( f )
定理 6-1 任何图中顶点次数的总和等于边数的 2 倍。 推论 6-1 任何图中，次为奇数的顶点必有偶数个。 图 G (V , E ) 和图 H (V , E ) ，若 V V且E E ，则 称 H 是 G 的子图，记作： H G ；特别的，当 V V 时， 称 H 为 G 的生成子图。
容量网络g若?为网络中从sv到tv的一条链给?定向为从sv到tv?上的边凡与?同向称为前向边凡与?反向称为后向边其集合分别用??和??表示??ijff?是一个可行流如果满足??????0ijijijijiijjffcvv??????????c???0ijijijfvv????则称?为从sv到tv的关于f的可增广链
( vi ,v j )
l
ij
最小的 。
Dijkstra算法
算法的基本步骤： （1）给 v s 以 P 标号， P(vs ) 0 ，其余各点均给 T 标号， T (vi ) 。 （2）若 vi 点为刚得到 P 标号的点，考虑这样的点 v j： (vi , v j ) E ，且 v j 为 T 标号，对 v j 的 T 标号进行如下的更改：
v2
(4,3)
v4
(3,3)
(5,3) (1,1) (1,1) (3,0)
vs
(5,1)
vt
(2,1)
v1
(2,2)
v3
图 6-14
运输线路图
第四节 最小费用最大流问题
在容量网络 G (V , E, C ) ，每一条边 (vi , v j ) E 上，除了已 给容量 cij 外，还给了一个单位流量的费用 bij 0 ，记此时的容 量网络为 G (V , E, C , B) 。 所谓最小费用最大流问题就是要求一个最大流 f ，使流的 总运输费用 b( f )
定理 6-1 任何图中顶点次数的总和等于边数的 2 倍。 推论 6-1 任何图中，次为奇数的顶点必有偶数个。 图 G (V , E ) 和图 H (V , E ) ，若 V V且E E ，则 称 H 是 G 的子图，记作： H G ；特别的，当 V V 时， 称 H 为 G 的生成子图。
容量网络g若?为网络中从sv到tv的一条链给?定向为从sv到tv?上的边凡与?同向称为前向边凡与?反向称为后向边其集合分别用??和??表示??ijff?是一个可行流如果满足??????0ijijijijiijjffcvv??????????c???0ijijijfvv????则称?为从sv到tv的关于f的可增广链
运筹学第六章图与网络分析(ppt文档)
§6.1 图的基本概念和模型
一、概念
（1）图：点V和边E的集合，用以表示对某种现实事物
的抽象。记作 G=｛V,E｝, V=｛v1,v2,···,vn｝, 点：表示所研究的事物对象； E=｛e1,e2,···,em｝
边：表示事物之间的联系。
e0
（2）若边e的两个端点重 合，则称e为环。
（3）多重边：若某两端点之 间多于一条边，则称为多重边。
D 8 64 5 0 15
E 7 53 4 1 0 6
T 14 11 9 10 5 6 0
i
dir（1）
r
drj（1）
j
⑷ 构造任意两点间最多可经过7个中间点到达的最短距 离矩阵 D（3）= dij（3）
其中
dij（3）=
min
r
{
dir（2）+
drj（2）
}
SABCDET
S 0 2 4 4 8 7 13
dir（0）
r i
drj（0）
j
⑶ 构造任意两点间最多可经过3个中间点到达的最短距 离矩阵 D（2）= dij（2）
其中
dij（2）=
min
r
{
dir（1）+
drj（1）}
SABCDET
S 0 2 4 4 8 7 14
A 2 0 2 3 6 5 11
B 4 20 1 43 9 D（2）= C 4 3 1 0 5 4 10
2. 破圈法：
⑴ 任取一圈，去掉其中一条最长的边， ⑵ 重复，至图中不存在任何的圈为止。
2. 破圈法
A
S
5 × B 5× D 5 T
C
4× E
最小部分树长Lmin=14
运筹学( 图与网络优化)
七桥问题
七桥问题图形
原理及方法
七桥问题是图论中的著名问题。1736年，Euler巧妙 地将此问题化为图的不重复一笔画问题，并证明了 该问题不存在肯定回答。原因在于该图形有顶点连 接奇数条边。
§10.1
图的基本概念
一个图(Graph) 定义为三元有序组
(V (G ), E (G ), G )
几何实现图例
在一个图的几何实现中，两条边的交点可能不是图的顶 点。例如下图 中，它共有4个顶点，6条边；而e 3 与e 4 的交点不是这个图的顶点。
v1
e1
v2 e4
e2
v3
e3
e5
v4
e6
e3
v1
v4
e1 e4
v2
e2
v3 e6
e5
v4
平面图
一个图称为平面图，如它有一个平面图形，使得边与边仅在
u 1
f5 u3 f6
f2 f4
u2
u4
同构
给定两个图
G (V (G), E(G), G )
H (V ( H ), E( H ), H )
称G和H是同构的，记为 G H ， 如果存在两个一一对应 ( , )
: V (G) V ( H )
: E (G) E ( H )
e7
v2
e3 v3
e6
v4
e4
关联矩阵性质
图G的关联矩阵M=(mij)为m×n矩阵；则每行元
素之和等于相应顶点的度；每列元素之和等于 2。
因此，图G的关联矩阵M所有元素之和既等于所
有顶点的度之和，又等于边数的2倍。 定理 设G是一个图，则
vV ( G )
d (v) 2
运筹学第7章图与网络优化
*
1
链，圈，初等链，初等圈，简单链（圈）
2
相邻节点的序列 {v1 ,v2 ,…, vn} 构成一条链(link)p178；
3
在无向图中，节点不重复出现的链称为初等链；
4
首尾相连的链称为圈(loop) ；首尾相连的初等链称为初等圈；
5
边不重复出现的链（圈）称为简单链（圈）
01
02
子图，部分图；连通图，成分
(1).与v3相连的临时标号有v5
第五步：
T(v5)=min{T(v5),P(v3)+d35}=min{9,7+3}=9
(2).P(v5)=9
最短路线：
vs→v1→v4→ v5 vs→v2→v4→ v5
vS
v2
v3
v4
v5
1
2
2
2
3
3
3
4
4
0
4
5
3
7
9
*
也可以用表格的形式求解。p190
斯坦纳树问题
假设我们在北京、上海、西安三城市之间架设电话线，一种办法是分别联通北京--上海和北京--西安。另一种办法是选第四个点，假设郑州。由此分别向三城市架线，可能你不会想到第二种办法所用的电话线只是第一种办法的86.6%，即可取得比第一种办法节约13%的显著经济效益。这就是离散数学界30年代提出的著名的斯坦纳树问题，但一直未能得到证明。
平面图(planar graph)，若在平面上可以画出该图而没有任何边相交
*
7基础图，路，回路，欧拉回路
在有向图D(V,A)中去掉箭头，称为D的基础图，G（D）
01
在有向图中，链 路
02
圈 回路
03
1
链，圈，初等链，初等圈，简单链（圈）
2
相邻节点的序列 {v1 ,v2 ,…, vn} 构成一条链(link)p178；
3
在无向图中，节点不重复出现的链称为初等链；
4
首尾相连的链称为圈(loop) ；首尾相连的初等链称为初等圈；
5
边不重复出现的链（圈）称为简单链（圈）
01
02
子图，部分图；连通图，成分
(1).与v3相连的临时标号有v5
第五步：
T(v5)=min{T(v5),P(v3)+d35}=min{9,7+3}=9
(2).P(v5)=9
最短路线：
vs→v1→v4→ v5 vs→v2→v4→ v5
vS
v2
v3
v4
v5
1
2
2
2
3
3
3
4
4
0
4
5
3
7
9
*
也可以用表格的形式求解。p190
斯坦纳树问题
假设我们在北京、上海、西安三城市之间架设电话线，一种办法是分别联通北京--上海和北京--西安。另一种办法是选第四个点，假设郑州。由此分别向三城市架线，可能你不会想到第二种办法所用的电话线只是第一种办法的86.6%，即可取得比第一种办法节约13%的显著经济效益。这就是离散数学界30年代提出的著名的斯坦纳树问题，但一直未能得到证明。
平面图(planar graph)，若在平面上可以画出该图而没有任何边相交
*
7基础图，路，回路，欧拉回路
在有向图D(V,A)中去掉箭头，称为D的基础图，G（D）
01
在有向图中，链 路
02
圈 回路
03
运筹学( 图与网络优化)
G是一棵树。 无圈且m=n-1。 G连通且m=n-1。 G连通并且每条边都是割边。 G中任意两点都有唯一的路相连。 G无圈，但在任意一对不相邻的顶点之间加连一条 边，则构成唯一的一个圈。
支撑树
图G的支撑树是G的支撑子图，并且是一棵树。
每个连通图都有支撑树
支撑树也称为连通图的极小连通支撑子图。 很显然，一个连通图只要本身不是一棵树，它的支撑 树就不止一个。
则T1 经过k次迭代后可得到T2。
最小树
设G是一个赋权图，T为G的一个支撑树。定义T的权为：
w(T )
eE ( T )
w(e ).
G中权最小的支撑树称为G的最小树。 定理5 设T是G的一个支撑树，则T是G的最小树的充分
d (v) 0(mod 2);
v V1 V1 0(mod 2)
d (v) 1(mod 2),
简单图
一个图称为简单图，如果它既没有环也没有多重边。 下图是简单图。
本书只限于讨论有限简单图，
即顶点集与边集都是有限集的图。 只有一个顶点的图称为平凡图； 边集是空集的图称为空图。 f3 f1
每个顶点用点表示，
每条边用连接端点的线表示。 图的几何实现有助与我们直观的了解图的许多 性质。
说明
一个图的几何实现并不是唯一的；表示顶点的点和表示边 的线的相对位置并不重要，重要的是图形描绘出 边与顶点之间保持的相互关系。 我们常常把一个图的图形当作这个抽象图自身. 并称图形的点为顶点，图形的线为边。 图论中大多数概念是根据图的表示形式提出的，例如：顶 点、边、多重边、环、路、圈、树等。
几何实现图例
在一个图的几何实现中，两条边的交点可能不是图的顶 点。例如下图 中，它共有4个顶点，6条边；而e 3 与e 4 的交点不是这个图的顶点。
北交大交通运输学院《管理运筹学》知识点总结与例题讲解第8章 图与网络分析
（a）
（b）
（c）
图 8-9 图、子图、支撑子图
（4）图的同构 设 G1 与 G2 是两个同阶图，若顶点集合 V1 和 V2 以及边集 E1 和 E2 之间在保持关联性
质条件下的一一对应，则称图 G1 和图 G2 同构。 例如：图 8-10（a）和图 8-10（b）就为同构。
（a）
(b)
图 8-10 同构图
（10）定理 8.1 对于图 G=(V ,E) ，其中 V = n , E = m ,则有：
∑d (v) = 2m
（8-2）
v∈V
证明：每条边都有两个端点，在计算顶点的次时，每个端点都要计算对应边次，故共有
2m 次。
通俗地讲，就是线有两头，共有 2m 个线头的意思。
（11）定理 8.2 奇次顶的总数是偶数。
第八章 图与网络分析
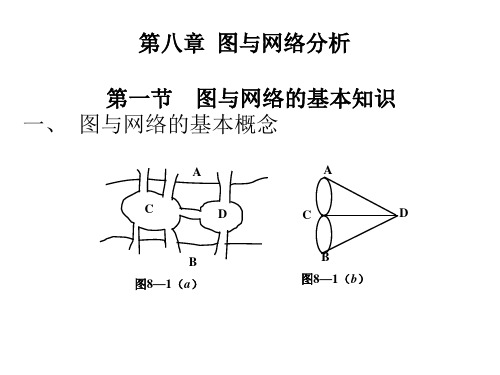
8.1 图与网络的基本知识
8.1.1 图与网络的基本概念 8.1.1.1 图的定义 自然界和人类社会中，大量的事物以及事物之间的关系，常可以用图形来描述。例如： 图 8-4 所示的我国北京、上海等十个城市间的交通图反映了这十个城市间铁路
分布情况。这里用点代表城市，用点和点之间的连线代表这两个城市之间有直通铁路。
图 8-7 一个无向图
G = (V, E) V= {v1, v2 ,v3 , v4} E={e1, e2 ,e3 , e4 ,e5 , e6 , e7}
其中
e1 = [v1 ,v2 ] , e2 = [v1 ,v2 ] , e3 = [v2 ,v3 ] , e4 = [v3 ,v4 ] ,
图 8-8 是一个有向图。该图可以表示为：
图 8-4 十个城市间铁路分布图
又如某单位储存五种化学药品，其中，某些药品是不能放在同一库房里的，为了反映这 种情况，可以用点 v1 、 v2 、 v3 、 v4 、 v5 分别代表这五种药品，若药品 vi 和药品 v j 是不能存 放在同一库房的，则在 vi 和 v j 之间连一条线，如图 8-5 所示。如果问题归结为寻求存放这种 化学药品的最少库房个数，则该问题就是染色问题。事实上，至少需要三个库房来存放这些 药品，即 v1 和 v5 、 v2 和 v4 、 v3 各存放在一个库房里。
运筹学图与网络分析
v6
07
含有奇点的连通图中不含欧拉圈，此时，最优的邮递路线是什么呢？
08
求解中国邮路问题的奇偶点图上作业法
奇偶点表上作业法
奇偶点表上作业法 (1)找出奇点(一定为偶数个)，在每两个奇点之间找一条链，在这些链经过的所有边上增加一条边，这样所有的奇点变为偶点，一定存在欧拉圈，但是不一定是路线最短的，所以需要检验和调整。 (2)检验增加的边的权值是否是最小的。 定理3 假设M是使得图G中不含奇点的所有增加边，则M是权值总和为最小的增加边的充分必要条件是： 1)图G中每条边上最多增加一条边； 2)在图G的每个圈上，增加的边的总权值不超过该圈总权值的一半。 如果上述两个条件都满足则已经找到权值最小的欧拉圈 否则转入3) 3)调整增加边。如果1)不满足，则从该条边的增加边中去掉偶数条； 如果2)不满足，则将这个圈上的增加边去掉，将该圈的其余边上添加增 加边，转入(2)
v1
v2
v3
v4
v5
v1
v2
v3
v4
v5
图2
图3
如果在比赛中： A胜E， B胜C， A胜D， C胜A， E胜D， A胜B，
v1
v2
v3
v4
v5
注：本章所研究的图与平面几何中的图不 同，这里我们只关心图有几个点，点与点 之间有无连线，两条线有无公共顶点，点 与线是否有关联，至于连线的方式是直线 还是曲线，点与点的相对位置如何都是无 关紧要的。
求从v1到v8的最短路
(0)
(1,1)
(1,3)
(3,5)
(2,6)
(5,10)
(5,9)
(5,12)
注：在给顶点编号时，如果在多个为标号点均取得最小值Llk则对这多个点同时标号，这些点的第二个标号相同，但是第一个标号不一定相同。
07
含有奇点的连通图中不含欧拉圈，此时，最优的邮递路线是什么呢？
08
求解中国邮路问题的奇偶点图上作业法
奇偶点表上作业法
奇偶点表上作业法 (1)找出奇点(一定为偶数个)，在每两个奇点之间找一条链，在这些链经过的所有边上增加一条边，这样所有的奇点变为偶点，一定存在欧拉圈，但是不一定是路线最短的，所以需要检验和调整。 (2)检验增加的边的权值是否是最小的。 定理3 假设M是使得图G中不含奇点的所有增加边，则M是权值总和为最小的增加边的充分必要条件是： 1)图G中每条边上最多增加一条边； 2)在图G的每个圈上，增加的边的总权值不超过该圈总权值的一半。 如果上述两个条件都满足则已经找到权值最小的欧拉圈 否则转入3) 3)调整增加边。如果1)不满足，则从该条边的增加边中去掉偶数条； 如果2)不满足，则将这个圈上的增加边去掉，将该圈的其余边上添加增 加边，转入(2)
v1
v2
v3
v4
v5
v1
v2
v3
v4
v5
图2
图3
如果在比赛中： A胜E， B胜C， A胜D， C胜A， E胜D， A胜B，
v1
v2
v3
v4
v5
注：本章所研究的图与平面几何中的图不 同，这里我们只关心图有几个点，点与点 之间有无连线，两条线有无公共顶点，点 与线是否有关联，至于连线的方式是直线 还是曲线，点与点的相对位置如何都是无 关紧要的。
求从v1到v8的最短路
(0)
(1,1)
(1,3)
(3,5)
(2,6)
(5,10)
(5,9)
(5,12)
注：在给顶点编号时，如果在多个为标号点均取得最小值Llk则对这多个点同时标号，这些点的第二个标号相同，但是第一个标号不一定相同。
运筹学基础及应用(第五版),(第六章图与网络分析)
树枝总长最小的部分树，称为该图的最小部分树(也称最小支
撑树)。
定理1. 图中任一个点 i ，若 j 是与 i 相邻点中距离最近的， 则边 [ i , j ] 一定包含在该图的最小部分树中。
给图中的点和边赋以具体的含义和权值，我们称这样的
图为网络图（赋权图）
2020/3/27
6
图中的点用 v 表示，边用 e 表示，对每条边可用它所
联结的点表示，如图，则有：
e1 = [v1 , v1]，
e2 = [v1 , v2]或e2= [v2 , v1]
2020/3/27
用点和点之间的线所构成的图，反映实际生产和生 活中的某些特定对象之间的特定关系。通常用点表 示研究对象,用点与点之间的线表示研究对象之间 的特定关系。一般情况下，图中点的相对位置如何 ，点与点之间线的长短曲直，对于反映研究对象之 间的关系，显的并不重要，因此，图论中的图与几 何图，工程图等本质上是不同的。
§2．树图和最小部分树
树图（简称树，记作 T(V, E)）是无圈的连通图。（无圈， 无多重边）
一. 树的性质
性质1. 任何树中必存在次为1 的点。
次为1的点称为悬挂点，与之关联的边称为悬挂边。 性质2. 具有 n 个顶点的树恰有（n-1）条边。
性质3. 任何具有n 个点、(n - 1)条边连通图是树。
A D
C B
2020/3/27
3
为了寻找答案 ，1736年欧拉 把陆地缩为一点，把桥作为连接点 的边，将这个问题抽象成图形的一 笔画问题。即能否从某一点开始不 重复地一笔画出这个图形，最终回 到原点。欧拉在他的论文中证明了 这是不可能的，因为这个图形中每 一个顶点都与奇数条边相连接，不 可能将它一笔画出，这就是古典图 论中的第一个著名问题。
撑树)。
定理1. 图中任一个点 i ，若 j 是与 i 相邻点中距离最近的， 则边 [ i , j ] 一定包含在该图的最小部分树中。
给图中的点和边赋以具体的含义和权值，我们称这样的
图为网络图（赋权图）
2020/3/27
6
图中的点用 v 表示，边用 e 表示，对每条边可用它所
联结的点表示，如图，则有：
e1 = [v1 , v1]，
e2 = [v1 , v2]或e2= [v2 , v1]
2020/3/27
用点和点之间的线所构成的图，反映实际生产和生 活中的某些特定对象之间的特定关系。通常用点表 示研究对象,用点与点之间的线表示研究对象之间 的特定关系。一般情况下，图中点的相对位置如何 ，点与点之间线的长短曲直，对于反映研究对象之 间的关系，显的并不重要，因此，图论中的图与几 何图，工程图等本质上是不同的。
§2．树图和最小部分树
树图（简称树，记作 T(V, E)）是无圈的连通图。（无圈， 无多重边）
一. 树的性质
性质1. 任何树中必存在次为1 的点。
次为1的点称为悬挂点，与之关联的边称为悬挂边。 性质2. 具有 n 个顶点的树恰有（n-1）条边。
性质3. 任何具有n 个点、(n - 1)条边连通图是树。
A D
C B
2020/3/27
3
为了寻找答案 ，1736年欧拉 把陆地缩为一点，把桥作为连接点 的边，将这个问题抽象成图形的一 笔画问题。即能否从某一点开始不 重复地一笔画出这个图形，最终回 到原点。欧拉在他的论文中证明了 这是不可能的，因为这个图形中每 一个顶点都与奇数条边相连接，不 可能将它一笔画出，这就是古典图 论中的第一个著名问题。
运筹学—第八章 图与网络分析
v5 1 v6 7 1 v7 －5 －3
e1 {v1 , v2 }
e3 {v2 , v3 }
e2 {v1 , v2 }
e4 {v3 , v4 } e6 {v3 , v5 } e8 {v5 , v6 } e10 {v1 , v6 }
e5 {v1 , v3 }
e7 {v3 , v5 } e9 {v6 , v6 }
v1
第二节 树 一、 树的概念和性质 例8.3 已知有六个城市，它们之间 要架设电话线，要求 任意两个城市均可以互相通话，并且电话线的总长度最短。
v1 v6 v5 v2
v3
v4
定义9 一个连通的无圈的无向图叫做树。
作为树T的定义，下列定义是等价的： （1）T是一个树。（设其顶点数为n ，边数为 m ） （2）T无圈，且m=n-1。 （3）T连通，且m=n-1 。 （4）T无圈，但在树中不相邻的两个点之间加上一条边， 那么恰好得到一个圈。 （5）T中任意两个顶点之间有且仅有一条链。 （6）T连通，但去掉T的任一条边，T就不连通。
( vi , v j )
一、 狄克斯屈拉(Dijkstra)算法 适用于wij≥0，给出了从vs到任意一个点vj的最短路。
算法步骤： 1.给始点vs以P标号 P(vs ) 0 ，这表示从vs到 vs的最短距离 T 为0，其余节点均给T标号， (vi ) (i 2 , 3,, n) 。 2.设节点 vi 为刚得到P标号的点，考虑点vj，其中 (vi , v j ) E ，且vj为T标号。对vj的T标号进行如下修改：
e1 v1
e2 e5
e8 v5
v2
d(v1)= 4，d(v6)= 4
e10 v6 e9
e3 e v4 4 e6 e7 v3
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二节欧拉图和哈密尔顿回路
一、欧拉图
欧拉（Euler）在1736年发表的关于图论方面的第一篇论文，解决了一个著名问题，称为哥尼斯堡七桥问题，从而使他成为图论的创始人。
问题是这样的：十八世纪的德国有座哥尼斯堡城，在流贯全城的普格尔河两岩和河中两个岛之间架设了七座桥，如图6.10（a）所示。
当时那里的居民热衷于这样一个游戏，即一个散步者能否从任一陆地出发，走过每座桥一次且仅走过一次，最后回到原地。
问题乍看起来很简单，但当时谁也不明白为什么没有人能够成功。
为了弄清这个问题，欧拉将每一块陆地用一顶点表示，每一座桥用连接相应的两个顶点的连线（即边）来代替，从而得到一个“图”（图 6.10（b））。
这个“图”使问题变得简洁明了。
直观上不难发现，为了能回到原来的陆地，要求与每个顶点（陆地）相关联的边数是偶数，这样才能保证从一条边出去，从另一条边回来。
由于在图6.10（b）中，与四个顶点相连的边数都是奇数，因而不可能
自任一顶点出发过每条边一次且仅一次而回到原地。
（a）图6.10（b）欧拉并不限于处理这个特殊事例，他推广了这个问题，提出并证明了下述定理。
定义1 在连通无向图G中，若存在经过每条边恰好一次的一个圈或一条链，就称此圈或链为欧拉圈或欧拉链。
或图G含一条欧拉圈，则称它为欧拉图。
显然，欧拉圈或欧拉链都可“一笔画出”；反之，若一个图能一笔画出，则它必然是欧拉圈或欧拉链。
定理1连通无向图G为欧拉图的充要条件是它的全部顶点都是偶次顶点。
事实上，若G是欧拉图，C是其欧拉圈，则由定义，C包含G的所有边，由于图连通，故亦包含所有顶点。
C是任一中间顶点每出现一次，必与两条不同的边相关联，另因C的起点也是终点，故所有顶点都是偶次顶点。
定理2 连通无向图G为欧拉链的充要条件是它恰含两个奇次顶点。
上述定理提供了判断一笔画问题的准则：若连通无向图G无奇次顶点，则可由任一点起一笔画成并回到起点；若有两个奇次顶点，则由一奇次顶点起到另一奇次顶点终可一笔画成。
为能将一个图一笔画下去，当去掉已画出部分时，乘下的部分不应成为不连通图。
二、哈密尔顿回路
1859年英国数学家哈密尔顿（Hamilton）提出了一种名为周游世界的游戏。
他用一个正十二面体的二十个顶点（参见图6.11），代表二十个大城市，要求沿着棱，从一个城市出发，经过每个城市恰好一次，然后回到出发点。
为了解答这个问题，现绘制一个如图6.12所示的平面图，它与图6.11所示的十二面体图同构。
由图6.12中粗线边组成的圈，符合哈密尔顿提出的要求，所以它是这个问题的一个解，需指出的是这个问题的解还不止一个。
如果不要求最后回到出发点，那么，解就更多了。
在一个图中，如果有一条链（圈）经过每个顶点恰好一次，那么这条链（圈）就称为哈密尔顿链（圈）。
表面上，哈密尔顿问题与欧拉问题很相似，但实际上，两者迥不同。
前者指的是过每个顶点恰好一次的回路，而后者说的是过每边恰好一次的圈。
用定理1很容易判断一个图是否为欧拉图，而求解哈密尔顿回路，迄今还没有比较简单的通用方法。
图6.11 图6.12
哈密尔顿回路是图论的重要课题之一，它具有重要的实际意义。
著名的旅行推销员问题（或称货郎担问题），就是要求出总路程最短的哈密尔顿回路。
三、中国邮路问题
某邮递员从邮局出发，走过每条街道至少一次去投递邮件，最后回到邮局，他应走什么样的路线才能使所走的总路程最短？这个问题是我国管梅谷教授于1962年首先研究的，国际上通称为中国邮路问题。
在邮递员服务范围的街道图上标明各条街的路长，就构成了一连通赋权图G。
若G无奇次顶点，根据定理1，G就是欧拉图，因每边仅过一次，故总权是最小的。
若G有奇次顶点，则它就不是欧拉图，然而题设条件是要求过每边至少一次，并未限制只许一次，故总可以在这些奇次顶点上添加一些与原图的边相重复的边，使这些奇次顶点成为偶次顶点，从而得到一个将重复边看成是另一条新边的欧拉图。
现在的问题是这些重复边如何添加，才能得到一个总权（总路长）最小的欧拉图。
定理3使图G成为总权最小的欧拉图的充要条件是：
（1）在有奇次顶点的图G中，通过加重复边的方法使图不再包含奇次顶点，但原图的每条边最多只能加一条重复边。
（2）在图G 的每个回路上，重复边之总权不超过该回路非重复边之总权。
根据以前的分析，本定理是显然的。
例1 试为图6.13（a ）构成总权最小的欧拉图，图中线旁的数字为相应边的权。
（a ） （b ）
图6.13
解 因顶点①和③为奇次，要使成欧拉图，需用加重复边的方法使这两个顶点变为偶次。
最易想到的作法是在边)3,1(e （即在顶点①与③之间）上加重复边，将其变为欧拉图。
但由于在回路（1，3，4）中)3,1(e 的权大于该回路总权（等于
7）的一半，故这样得到的欧拉图不是总权最小的欧拉图。
如在边)4,1(e 和)4,3(e 上加重复边（图6.13（b ）），则可满足定理3的要求，从而得总权最小的欧拉图（总权等于15）。
通过难于一次找到总权最小的欧拉图，这时可通过对欧拉图的逐步调整达到总权极小化，即对每一回路进行检查，不满足定理3时就调整重复边，但在该过程中始终保持各顶点的次数为偶数。
例2 试为图6.14（a ）所示的街道规划最优投递路线。
解 可按以上所述步骤进行，最终结果示于图6.14（b ），总权等于52，重复边的长度等于10。
（a ） （b ）
图6.14
四、旅行售货员问题
一个旅行售货员想去某些城镇售货，然后再回到他的出发地。
各城镇之间的路程是已知的，问应如何安排他的旅行路线，才能使他经过每个城镇恰好一次，且总路程最短。
用图论的术语来说，就是在一个加权图中，找出一条总权最小的哈密尔顿回路。
到目前为止，旅行售货员问题还没有有效的通用算法。
假如采用枚举法，售货员从城市i v 出发，去1v ，2v ，…，n v 城市售货，则有)!1(-n 种可能方案。
随着n 的增加，)!1(-n 的值迅速增加，例如当n =20时，)!1(-n =1.216×1710。
对这么多个方案逐个计算并比较，显然是不可能的。
下面介绍一种近似解法。
首先任取一条哈密尔顿回路，不失一般性，它经过的顶点序列为1v ，2v ，…，i v ，1+i v …，j v ，1+j v ，…，n v ，若对某一对顶点i v 和j v ，相应边权有如下关系：
),(),(11+++j i j i v v w v v w ＜),(),(11+++j j i i v v w v v w 则用边),(j i v v 和边),(11++j i v v
替换边),(1+i i v v 和边),(1+j j v v （参见图6.15），可
得另一哈密尔顿回路，其权更小。
用这种方法对
哈密尔顿回路进行若干次改进，即可获得比较好
的回路。
例3 用上述近似法对图6.16（a ）中的回 图6.15
路（1v ，2v ，3v ，4v ，5v ，6v ，1v ）进行改进。
图6.16
解 其各次改进方案示于图6.16（b ）、6.16（c ）和图6.16（d ）中。
图中各边旁的数字为该边的权，双线表示相应方案的哈密尔顿回路，图右下角括号内的数字为该回路的总权。