法向量求二面角-空间向量
求二面角的六种方法

求二面角的六种方法求解二面角是空间几何学中常见的问题,它在多个领域如物理学、化学和工程学中都有广泛的应用。
本文将介绍六种求解二面角的方法,包括向量法、坐标法、三角法、平面几何法、球面几何法和投影法。
一、向量法向量法是一种简便的求解二面角的方法。
它利用向量的夹角来表示二面角。
首先,我们需要确定两个平面的法向量,然后计算它们之间的夹角。
通过向量的点积和模长运算,可以得到二面角的大小。
二、坐标法坐标法是一种常用的求解二面角的方法。
它利用坐标系中的点来表示二面角。
我们可以通过给定的坐标点,计算两个平面的法向量,然后利用向量夹角的公式求解二面角。
三、三角法三角法是一种基于三角函数的求解二面角的方法。
它利用三角函数的性质来计算二面角的大小。
通过已知的边长和角度,可以利用正弦定理、余弦定理等公式求解二面角。
四、平面几何法平面几何法是一种利用平面几何关系求解二面角的方法。
它通过已知的平面形状和角度关系,利用平面几何的知识来求解二面角的大小。
例如,可以利用平行线的性质、垂直线的性质等来计算二面角。
五、球面几何法球面几何法是一种利用球面几何关系求解二面角的方法。
它通过已知的球面形状和角度关系,利用球面几何的知识来求解二面角的大小。
例如,可以利用球面上的弧长、球面上的角度等来计算二面角。
六、投影法投影法是一种利用投影关系求解二面角的方法。
它通过已知的投影长度和角度关系,利用投影几何的知识来求解二面角的大小。
例如,可以利用平面上的投影线段、平面上的角度等来计算二面角。
通过以上六种方法,我们可以灵活地求解二面角的大小。
不同的问题和场景可能适用不同的方法,我们可以根据具体情况选择合适的方法来解决问题。
这些方法在实际应用中具有重要的意义,能够帮助我们更好地理解和解决相关问题。
总结起来,求解二面角的六种方法分别是向量法、坐标法、三角法、平面几何法、球面几何法和投影法。
每种方法都有其特点和适用场景,我们可以根据具体问题选择合适的方法来求解二面角。
二面角法向量求法

二面角的表示方法
二面角是由两个半平面所组成 的图形,其大小由两个半平面
的夹角决定。
二面角可以用角度制或弧度制 来表示,与平面角和空间角类
似。
二面角的大小与两个半平面的 方向有关,与半平面的大小无 关。
在求解二面角的大小时,通常 需要先找到两个半平面的法向 量,然后计算两个法向量之间 的夹角即可得到二面角的大小 。
二面角法向量求法
汇报人:XX 2024-01-23
• 引言 • 二面角的表示方法 • 法向量的求解方法 • 二面角法向量的性质 • 二面角法向量的应用 • 总结与展望
01
引言
二面角的定义
二面角是由两个半平面所组成的 图形,其大小由这两个半平面的
夹角决定。
二面角的大小范围在0°到180°之 间,当两个半平面重合时,二面 角为0°;当两个半平面形成一条
面积射影定理
根据面积射影定理,二面角的余弦值等于两个半 平面在棱上的投影面积之比。因此,可以通过求 出两个半平面在棱上的投影面积,然后利用面积 射影定理求出二面角的大小。
三垂线定理及其逆定理法
利用三垂线定理或其逆定理,可以构造出与二面 角的棱垂直的线段,进而通过解三角形求出二面 角的大小。
空间向量夹角公式
03
法向量的求解方法
平面法向量的求解方法
直接法
如果平面上的一个向量 已知,则该向量即为平 面的法向量。
待定系数法
设平面的法向量为 n=(x,y,z),根据平面的 方程可以列出关于x,y,z 的方程组,通过求解方 程组得到法向量。
向量积法
如果平面上有两个不共 线的向量a和b,则平面 的法向量n可以通过计 算向量a和b的向量积得 到,即n=a×b。
法向量法求二面角课件-2025届高三数学一轮复习

平面,、 ⊂ 平面,则, .
∴ 以为原点,为x轴,以过点与平行的直线为轴,为轴 . 建立
空间直角坐标系.
1、建立坐标系
所以 0,0,0 , 0,0,1 , 1,1,0 , 1,0,0 ,
| ∙ |
1
1
3、利用数量积
所以: = | , | =
=
=
2∙ 2 2
所以二面角 − −
的大小为
3
4、判断角大小
变式训练,构建模型
2、如图,四棱柱ABCD-A1B1C1D1的所有棱长都相等,AC∩BD=O,
A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形,O1O⊥底
n1,
n2
n1,
n2
l
cos
n1,
n2
n1,
n2
l
cos n1, n2 cos
cos n , n
1
2
总结:解题时我们只需观察图形是二面角是锐角还是钝角,
再根据所求法向量夹角的余弦值下结论即可!
法向量法求二面角的步骤:
1、建立坐标系,两两互垂直
面ABCD. 求二面角B-A1C-D的余弦值.
解
因为四棱柱的所有棱长都相等,所以四边形ABCD为菱形,AC⊥BD,又
O1O⊥底面ABCD,所以OB,OC,OO1两两垂直.
如图,以O为原点,OB,OC,OO1所在直线分别为x,y,z轴,建立空间直角
坐标系.
设棱长为2,因为∠CBA=60°,
所以 OB= 3,OC=1,
利用法向量求二面角

2
课前热身
在正方体ABCD A1B1C1D1中,求锐二面角A1 DB A的余弦值。
解:作DB的中点O, 连结AO 1 , AO 在正方体中A1D AB, AD AB AO BD, AO BD 1
AOA 为二面角A1 DB A的平面角 1 A1 不妨设AA 2,则AO 2,
7
课后练习
在三棱锥P-ABC中,AB=AC,D为BC的中点,PO ⊥面ABC,垂足O落在线段AD上,已知BC=8, PO=4,AO=3,OD=2. 在线段AP上是否存在点M,使得二面角A-MC-B为直二 面角?若存在,求出AM的长;若不存在,请说明理 由。
P
A O Bห้องสมุดไป่ตู้D
C
课堂总 结
思想方法
1.利用空间向量求空间角,避免了寻找平面角和垂线段等诸多麻烦,使空间点、线、 面的位置关系的判定和计算程序化、简单化.主要是建系、设点、计算向量的坐标、 利用数量积的夹角公式计算. 2.合理建立空间直角坐标系 (1)使用空间向量解决立体几何问题的关键环节之一就是建立空间直角坐标系, 建系 方法的不同可能导致解题的简繁程度不同. (2)一般来说,如果已知的空间几何体中含有两两垂直且交于一点的三条直线时,就 以这三条直线为坐标轴建立空间直角坐标系;如果不存在这样的三条直线,则应尽 可能找两条垂直相交的直线,以其为两条坐标轴建立空间直角坐标系,即坐标系建 立时以其中的垂直相交直线为基本出发点. (3)建系的基本思想是寻找其中的线线垂直关系, 在没有现成的垂直关系时要通过其 他已知条件得到垂直关系,在此基础上选择一个合理的位置建立空间直角坐标系.
课题:利用法向量求二面角
——小越中学 章惠芳
1
复习回顾
向量法求空间距离和角

—的平而角“a®牆用向量方法求空间角和距离在高考的立体几何试题中,求角与距离是常考查的问题,其传统的“三步曲”解 法:“作图、证明、解三角形”,作辅助线多、技巧性强,是教学和学习的难点.向 量进入高中教材,为立体几何增添了活力,新思想、新方法与时俱进,木专题将运用 向量方法简捷地解决这些问题.1求空间角问题空间的角主要有:异面直线所成的角;直线和平面所成的角;二面角.(1)求异而直线所成的角.=arcsinli I/II H I法一、在Q 内N 丄/,在0内b 丄/,其方向如图,则二面角设方、乙分别为异而直线a 、b 的方向向量, a 则两异而直线所成的角 a — arccos 1 而Q 所成的角方向向量,;;是平而&的法 (3)求二而法二、设入云是二而角a-/-0的两个半平而的法向量,其方向一个指向内侧,另一个指向外侧,则二面角a-1-p的平而角a =arccos彳"22求空间距离问题构成空间的点、线、面之间有七种距离,这里着重介绍点面距离的求法,象异而直线间的距离、线而距离;而而距离都可化为点而距离来求.(1)求点而距离法一、设;;是平面Q的法向量,在a内取一点B,则A■ ■■I“・•到&的距离d =1 AB II cos 0\=空叫\n\法二、设AO丄a于O,利用AO丄a和点0在&内的向量表示,可确定点O的位置,从而求出I走1・(2)求异而直线的距离二 ___ ?—法一、找平而0使比0且砂0,则异而直线a、b的距离就转化为直线a到平面0的距离,又转化为点A到平面0的距离.法二、在a上取一点A,在b上取一点B,设方、b分别为异面直线a、b的方向向量,求;;(万丄方,齐丄乙),则・・D于点而距异而直线a、b的距离心而llcos弘空叫(此方法移植丨川(I )求异而直线DE 与FG 所成的角;rh 向量法求空间距离和角例1.如图,在棱长为2的正方体ABCD-gCQ 中,分别是棱4久心的中点•(II )求g 和ffiEFBD 所成的角;(III)求Q 到面EFBD 的距离解:(I )记异而直线DE 与g 所成的角为—则&等于向量码运的夹角或其补角,■ D E.FC 、|cos a =1—:_ I \DE\.\FC {\(II)缈初万冷万石)•(两霸頁艸坐标系D-小, —I 一 ・• II DE bl FC [丨呢= (1,0,2),面= (220)设面E 単翌進|=二・・・a 回風X^s£=("l ) A /5V5 5— _v 、 DE ・H = 0<DB • /z = 0得 7 = (-221)又 BC ; = (-2,0,2)记g 和而EFBD 所成的角为&则 sin 0 =1 cos 〈BC], n) 1=1 ."9 ? 1=I BC { II7? I 2 ・•・Bq 和面EFBD 所成的角为冬.4(III)点目到ffiEFBD 的距离d 等于向量丽;在而EFBD 的法向量上的投影的绝对值,BiTl 33.完成这3道小题后, 总结:例2・己知A BCD 是边长为1的正方形,四边形DA ・ q=0DC ・ q = 0向量法求空间距离和角设计说明:1・作为本专题的例1,首先选择以一个容易建立空间直角坐标系 的多而体 正方体为载体,来说明空间角和距离的向量求法易于学生理解.2.解决(1)后,可让学生进一步求这两条异而直线的距离,并让学生体会一下:如果用传统方法恐怕很难(不必多讲,高考对公垂线的作法不作要求).角、距离还是证明平行、垂直(是前者的特殊情况),都可用向量方法来解决, 向量方法可以人人学会,它程序化,不需技巧.AA'B'B 是矩形,平丄平面A3CD 。
向量法-求二面角大小

空间向量法---求二面角的大小
运用“空间向量法”---求“二面角的大小”的解题步骤:
① 建立空间直角坐标系; ② 求出所需各点的坐标; ③ 求出两个平面的法向量; ④ 求出两个法向量的夹角; ⑤ 写出所求二面角的大小。
空间向量法---求二面角的大小
运用“空间向量法”---求“二面角的大小”的解题步骤:
(1) 证明: AN⊥平面PAD .
(2) 求二面角C-AM-N的大小 .
P
M
A
D
B
NC
【练习3】 如图, 在四棱锥P-ABCD中, 底面是边长为2的菱形, ∠ABC=60O , PA⊥底面ABCD,PA=2, M,N分别为PC,BC的中点.
(1) 证明: AN⊥平面PAD .
(2) 求二面角C-AM-N的大小 .
∴ cosq =
6
3
得 tanq =
2
2
∴
所求面SCD与面SBA所成二面角的正切值是22
【练习2】 已知点E、F分别是正方体ABCD-A1B1C1D1的棱BB1、 CC1上的点, 且 BE1=2EB, CF=2FC1 .
(1) 求面AEF与面ABC所成二面角的正切值 .
【练习3】 如图, 在四棱锥P-ABCD中, 底面是边长为2的菱形, ∠ABC=60O , PA⊥底面ABCD,PA=2, M,N分别为PC,BC的中点.
=
3 3
由条件知,二面角A-CD-E为锐角,∴
所求二面角的余弦值为
3 3
【练习1】 如下图, 在底面是直角梯形的四棱锥S-ABCD中,
∠ABC=90O
,
SA⊥面ABCD,SA=AB=BC=1,
AD=
1 2
.
向量法求空间的距离和角

所以异面直线BD与D1A间的距离为
3 。 3
(2) A1 B1 = (0,1, 0), 设n = ( x, y, z )是平面A1DB的一 个法向量,因为DA1 = (1, 0,1), DB = (1,1, 0), ì ì x +z = 0 nDA1 = 0 镲 由眄 即 取x = - 1, 镲 î x+y =0 î nDB = 0 | nA1 B1 | 1 2 于是n = (-1,1,1, ),且 = = 。 2 |n| 2 2 所以点B1到平面A1 BD的距离为 。 2
例1:如图1所示: 三棱柱ABC - A1 B1C1中,CA=CB, AB = AA1, ? BAA1 60o, ( 1)求证:AB^ A1C (2)若平面ABC ^ 平面AA1 B1 B, AB =CB,求直线A1C与平面BB1C1C 所成角的正弦值。
C C1
B A A1
B1
图1
C
C1
O
B A1
Z
解:由(1)知OC ^ AB,OA1 ^ AB, 又平面ABC ^ 平面AA1 B1 B,交线 为AB,所以OC ^ 平面AA1 B1 B, 故OA、OA1、OC两两相互垂直。 建立如图所示的空间直角坐标系 A
O
C
C1
B A1
B1 图1-2
X o - xyz 设AB = 2,由题设知A(1, 0, 0)、B(- 1, 0, 0)、C (0, 0, 3)、A1 (0, 3, 0), 则BC = (1, 0, 3)、 BB1 = AA1 = (- 1, 3, 0)、 A1C = (0, - 3, 3). 设n = ( x, y, z )是平面BBCC的法向量,则 ì x + 3z = 0 ì nBC = 0 镲 即 可取n = ( 3,1, -1), 眄 镲 î nBB1 = 0 î - x + 3y = 0 nA1C 10 故 cos < n, A1C >= =. 5 | n | ×| A1C |
空间向量与立体几何向量法求二面角(二

D
AB CD
面面角:
②法向量法n1,n2源自 n1,n2n2
n1,n2
n2
n1,n2
n1
n1
l
l
cos cos n1, n2 cos cos n1, n2
注意法向量的方向:一进一出,二面角等于法向量夹角; 同进同出,二面角等于法向量夹角的补角
(2)求证:PB⊥平面EFD
(2)证明:依题意得B(1,1,0),PB (1,1,1)
又DE (0, 1 , 1),故PB DE 0 1 1 0
22
所以PB DE
2 2Z
由已知EF PB,
P
且EF DE E,
所以PB 平面EFD
E F
D
C Y
A B
X
BC SO,BC AO,SO AO O BC 平面SOA, BC SA
(2)求直线SD与平面SAB所成角的正弦值。 z
解:由(1)知SO,OA,BC两两垂直。
S
故以OA、OB、OS为正交基底建立
空间直角坐标系如图。则 S(0,0,1),D( 2,- 2 2,0),
C O By
四边形,侧面SBC 底面ABCD。已知 ABC 450
AB=2,BC= 2 2 ,SA=SB= 3 .
(1)求证 SA BC.
(2)求直线SD与平面SAB所成角的正弦值。
S
C
OB
D
A
证明:(1)取BC中点O,连接OA、OS。 S
则由BC 2 2得OB 2,
又AB 2,ABC 450, 得OA 2
依题意得A(1, 0, 0), P(0, 0,1), P
二面角的求法讲课周二

找点坐标
求法向量坐标
定值
求两法向量夹角
考点跟踪 1 :数量关系隐藏于几何图形中需要用平面几何中的有关知识去解决;连续四年均 以菱形为底面或侧面水平放置的几何体,特别是斜三棱柱为重点;要注意解题规范性训练, 有利于提高运算准确率;
考点跟踪2:①、求线线角、线面角、二面角仍然是热点. ②、注意给角求值也不容忽视.
D C E B F A
解析 (1)由已知可得 AF DF , AF FE ,所以 AF 平面 EFDC . 又 AF 平面 ABEF ,故平面 ABEF 平面 EFDC .
(2)过 D 作 DG EF ,垂足为 G ,由(1)知 DG 平面 ABEF .
F
D
C E B A
由已知, AB
又平面 ABCD
EF ,所以 AB
z D G C E A y
平面 EFDC .
CD , CD EF .
x F
B
平面 EFDC CD ,故 AB
由 BE
AF ,可得 BE 平面 EFDC ,所以 CEF 为二面角 C BE F 的平面角,
故
CEF 60 , 从 而 可 得 C (2,, 0 3) . 所 以 EC ( 1 ,, 0 3, ) EB (0,, 4 0) ,
G x F
B
跟踪训练( 2017 全国 1 卷理科 18 )如图所示,在四棱锥 P ABCD 中, AB //CD ,且
BAP CDP 90 .
(1)求证:平面 PAB 平面 PAD ; (2)若 PA PD AB DC , APD 90 ,求二面角 A PB C 的余弦值.
2 2
空间向量法求二面角
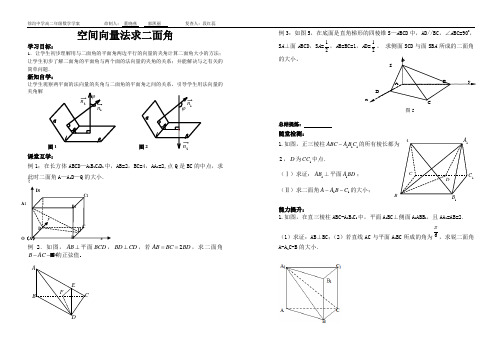
徐沟中学高二年级数学学案 命制人: 董晓燕 郭凯丽 复查人:段红蕊空间向量法求二面角学习目标:1.让学生初步理解用与二面角的平面角两边平行的向量的夹角计算二面角大小的方法;让学生初步了解二面角的平面角与两个面的法向量的夹角的关系;并能解决与之有关的简单问题.新知自学:让学生观察两平面的法向量的夹角与二面角的平面角之间的关系,引导学生用法向量的夹角解图1 图2课堂互学:例1;在长方体ABCD —A 1B 1C 1D 1中,AB=2,BC=4,AA 1=2,点Q 是BC 的中点,求此时二面角A —A 1D —Q 的大小.例2.如图,AB ⊥平面BCD ,BD CD ⊥,若2AB BC BD ==,求二面角B ACD --的正弦值例3:如图5,在底面是直角梯形的四棱锥S —A BCD 中,AD//BC ,∠A BC=900,S A ⊥面A BCD ,S A =21,A B=BC=1,A D=21。
求侧面SCD 与面SB A 所成的二面角的大小。
总结提炼:随堂检测:1.如图,正三棱柱111ABC A B C -的所有棱长都为2,D 为1CC 中点.(Ⅰ)求证:1AB ⊥平面1A BD ; (Ⅱ)求二面角11C B A A --的大小;能力提升:1.如图,在直三棱柱ABC-A 1B 1C 1中,平面A 1BC ⊥侧面A 1ABB 1,且AA 1=AB=2.(1)求证:AB ⊥BC ;(2)若直线AC 与平面A 1BC 所成的角为6π,求锐二面角A-A 1C-B 的大小.A BC DEF ϕω θ βlα2n 1nθ β lαϕ1n2n O (A ) B A 1 C 1 B 1D 1 D CQ zy x 图4AzyDCBS 图5ABCD1A1C1B。
二面角的求法和利用空间向量解决立体几何问题
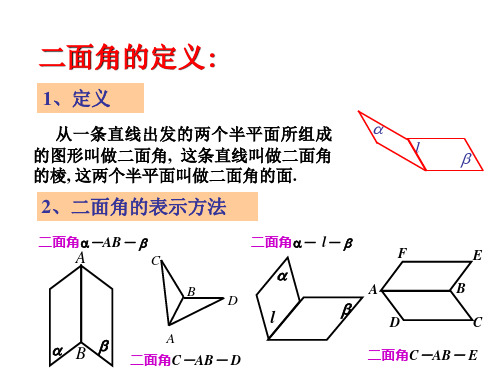
二面角的定义:
1、定义
从一条直线出发的两个半平面所组成
的图形叫做二面角, 这条直线叫做二面角
l
的棱, 这两个半平面叫做二面角的面.
2、二面角的表示方法
二面角-AB-
A
C
B
二面角- l-
D
l
B
A
二面角C-AB- D
F
E
A
B
D
C
二面角C-AB- E
二面角的平面角:
以二面角的棱上任意一点为端
点, 在两个面内分别作垂直于棱的 两条射线, 这两条射线所成的角叫 做二面角的平面角。
面面平行
∥ n1 ∥ n2 n1 kn2
二、垂直关系:
设直线 l, m 的方向向量分别为 AB,CD ,
平面 , 的法向量分别为 n1 , n2 , 线线垂直:
l ⊥ m AB ⊥ CD AB • CD 0 ;
Bl
A
平面 内的两个相交向量垂直
(4)解方程组,令其中一个量的值求另外两个, 即得法向量。
一、平行关系:
设直线 l, m 的方向向量分别为 AB,CD ,
lm
BD
平面 , 的法向量分别为
线线平行:
n1
, n2
,
l ∥ m AB ∥ CD AB kCD
;
x1 y1
=
A
x2 y2
=
C
x3 y3
线面平行
AB
l ∥ AB n1 AB n1 0 ;
分别作垂直于a 的两条射线OA,OB,则∠AOB就 是此二面角的平面角。
2、垂线法: 在一个平面 内选一点A向另一平面 作 垂线AB,
垂足为B,再过点B向棱a作垂线BO,垂足 为O, 连结AO,则∠AOB就是二面角的平面角。
向量法求二面角

用向量法求二面角
思考:能否用法向量求二面角的大小?
A n
B O
n2
n1
n1, n2
用向量法求二面角
n2 n1
同
进
同
出
n2 n1
取 补 角
n2来自n2n1 一
进
一
出
取
n1
等 角
法2:图形的特征来判定相等、互补
用向量法求二面角
例1 如所示,ABCD是一直角梯形,ABC=900 ,
SA 平面ABCD, SA AB BC 1, AD 1 , 2
求面SCD与面SBA所成二面角 z
的余弦值. 方法一:几何法
S n1
n2
方法二:向量法
B
C
易知面SBA的法向量n1
AD
1 (0, , 0)
A
x
2
面SCD的法向量可取n2 (1, 2,1)
Dy
用向量法求二面角
变式练习 如图所示,ABCD是一直角梯形,ABC=900 ,
二面角及其度量
用向量法求二面角
一、教材分析
二面角及其度量是高中数学选修2--1第3章空间向量在立体几 何中的应用中的部分内容。空间向量的引入为代数方法处理立 体几何问题提供了一种重要的工具和方法。本节课是在学生掌 握了用空间向量求线面角的基础上进行的延伸和拓展。求空间 角是立体几何的一类重要的问题,也是高考的热点之一。
二、教学目标
知识目标 :
掌握空间向量求二面角的方法;.
能力目标:
培养学生观察分析、类比转化的能力; 培养空间想象能力
利用法向量求二面角

利用法向量求二面角1. 什么是二面角在几何学中,二面角指的是两个平面的夹角,通常用来描述空间中的角度关系。
具体地说,二面角是由两个面的法向量所定义的角度,通过测量一个面对相邻面的法向量之间的夹角来计算。
2. 法向量的概念在三维空间中,平面可以通过一个法向量来定义。
法向量垂直于平面,并且指向平面的外部。
根据向量的定义,法向量具有方向和大小。
法向量的大小表示平面的倾斜程度,而法向量的方向则指示平面的朝向。
3. 利用法向量求二面角的方法要计算两个平面之间的二面角,可以利用它们的法向量。
具体的方法如下:步骤1:首先,确定两个平面的法向量。
可以通过计算平面上的三个非共线点的向量叉积来获得一个平面的法向量。
同样地,另一个平面的法向量也可以通过相同的方法来计算。
步骤2:然后,计算两个法向量之间的夹角。
夹角可以通过计算两个向量的内积的反余弦值来获得。
步骤3:最后,得到的夹角就是两个平面之间的二面角。
根据需要,可以将夹角的单位转换为度数或弧度。
4. 示例为了更好地理解利用法向量求二面角的方法,我们来看一个示例。
假设有两个平面,A和B,它们的法向量分别为n_n=(n,n,n)和n_n=(n,n,n)。
首先,计算法向量的夹角。
夹角n可以表示为n=nn+nn+nn。
然后,得到的角度n就是平面A和平面B之间的二面角。
5. 总结利用法向量可以方便地计算两个平面之间的二面角。
通过计算两个平面的法向量的夹角,可以得到二面角的值。
这个方法在计算几何学和计算机图形学中都有广泛的应用,用于描述三维空间中的角度关系。
以上就是利用法向量求二面角的说明文档,希望对你有所帮助。
如果你有任何问题或需要进一步的解释,请随时向我提问。
求二面角的方法

解题宝典空间角主要包括异面直线所成的角、直线与平面所成的角、二面角.二面角是指从一条直线出发的两个半平面所组成的图形.求二面角的大小是一类常见的问题.本文重点介绍求二面角大小的四种方法:定义法、向量法、面积投影法、三垂线定理法.一、定义法过二面角棱上的任一点,在两个半平面内分别作与棱垂直的射线,则两射线所成的角叫做二面角的平面角.一般地,要求得二面角的大小只需要求出二面角的平面角的大小即可.在求二面角的大小时,我们可以根据二面角的平面角的定义来求解.首先在二面角的棱上选取一点,在两个面内作棱的垂线,则两条垂线的夹角,即为二面角的平面角,求得平面角的大小即可得到二面角的大小.例题:如图1,在长方体ABCD-A1B1C1D1中,底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.(1)证明:BE⊥EB1C1;(2)若AE=A1E,求二面角B-EC-C1正弦值.图1图2解:(1)略;(2)由(1)知∠BEB1=90°.由题设知Rt△ABE≌Rt△A1B1E,所以∠AEB=45°,故AE=AB,AA1=2AB.如图2所示,在平面BCE内过B点作BM⊥CE于点M,取棱CC1的中点N,连结MN,EN.因为EC1=EC,所以EN⊥CC1,所以ΔCEN为直角三角形.因为BC⊥BE,所以ΔCEB为直角三角形.令AB=1,则BC=NC=1,BE=EN=2,CE=3,所以RtΔBEC≌RtΔNEC,所以MN⊥EC,则∠BMN即为二面角B-EC-C1的平面角.在RtΔBEC中,sin∠BCE=BE CE=BM BC,所以BM=,MN.在ΔBMN中,cos∠BMN=BM2+MN2-BN22BM∙MN=-12,则sin∠BMN=,故二面角B-EC-C1正弦值.利用定义法求二面角的大小的关键是作出二面角的平面角.在作图的过程中要充分利用题目条件中隐含的垂直关系,如等腰三角形三线合一的性质、菱形或正方形的对角线相互垂直、直角三角形中勾股定理及其逆定理等.另外在构造二面角的平面角时,常用的方法还有垂面法,即经过两个面的垂线的平面与两个平面的交线所夹的角即为二面角的平面角.二、三垂线法三垂线法是指利用三垂线定理求作二面角的平面角,求得二面角大小的方法.在求作二面角的平面角时,需过其中一个面内的一点作另一个面的垂线,再经过垂足作棱的垂线,连接该点与棱上的垂足,进而构造出与二面角的平面角相关的角,再结合图形中的垂直关系求得二面角的大小.以上述例题为例.解:如图3,连接BD,AC,交点为O,过点O作CE的垂线,垂足为P,连接BP.由三垂线定理可知BP垂直于CE,所以∠BPO即为所求二面角平面角的补角.设AB=1,由(1)可知AE=1,所以BE=2,CE=3.因为BC⊥BE,所以ΔBCE为直角三角形,所以RtΔBCP∽RtΔBCE.陈秀林图342解题宝典所以BP.在Rt△BOP 中,sin ∠BPO =BC BP=,即所求二面角正弦值为.此法与定义法的不同之处是将所求二面角的相关角置于直角三角形中,从而使解题的过程更加简洁.三、向量法向量法是通过空间向量的坐标运算,将所求的二面角转化为两个平面的法向量的夹角的方法.解题的思路是通过建立空间直角坐标系,求出两个平面的法向量,根据向量的数量积公式求出夹角,再利用法向量的夹角与二面角的关系来确定二面角的大小.值得说明的是,二面角的平面角与法向量的夹角的关系是相等或互补.以上述例题为例.解:(2)由(1)知∠BEB 1=90°.由题设知Rt△ABE ≌Rt△A 1B 1E ,所以∠AEB =45°,故AE =AB ,AA 1=2AB .以D 为坐标原点,建立如图4所示的空间直角坐标系D -xyz ,则C (0,1,0),B (1,1,0),C 1(0,1,2),E (1,0,1),所以 CB =(1,0,0),CE =(1,-1,1),CC 1=(0,0,2).设平面BCE 的法向量为n =(x ,y ,z ),则ìíî CB ∙n =0,CE ∙n =0,即{x =0,x -y +z =0,令y =-1,得n =(0,-1,-1).设平面ECC 1的法向量为m =(x ,y ,z ),则ìíî CC 1∙m =0,CE ∙m =0,即{2z =0,x -y +z =0,令x =1得m=(1,1,0).于是cos m,n =m ∙n |m |∙|n |=-12.所以二面角B -EC-C 1平面角正弦值为.向量的引入降低了立体几何问题的难度,但对同学们的运算能力提出了更高的要求.求法向量的原则是先找后求,即如果存在一条已知的直线与二面角的某一个平面垂直,则该直线的方向向量即可视为此平面的法向量.四、投影法投影法,即为构造出二面角的两个平面中的一个平面在另外一个平面内的投影,从而利用此平面与其投影的夹角θ来判断所求二面角的大小的方法.若该平面与其投影的面积分别为S 1,S 2,则cos θ=S 1S 2.θ与所求二面角的关系有两种,即相等或互补.以上述例题为例.解:如图5,连接BD 交AC 于点O ,连接EO .因为四边形ABCD 为正方形,所以BD ⊥AC ,所以点B 在面C 1CE 内的投影,三角形EOC 为ECB 的投影.设棱AB =1,由(1)可知AE =1,则AC =BE =2,EC =3,所以三角形OCE 的面积为S 1=12∙OC ∙AE =12,三角形BCE 的面积为S 2=12BC ∙BE =12×1×2.所以S 2S 1=42=12.所以面BCE 与面ECC 1所成锐二面角的余弦值为12,故二面角的正弦值为.在本题中,三角形ECB 与其在面ECC 1上的投影EOC 的夹角即为所求二面角的补角,而两角互补,则其正弦值相等,所以可直接利用投影法来求解.一般地,求二面角的问题主要有两类,即求有棱二面角的大小和无棱二面角的大小,虽然图形有所不同,但解题的方法基本上一致.同学们在解题的过程中要注意仔细审题,择优而用.(作者单位:江苏省大丰高级中学)图5图443。
空间向量求二面角

2014-2015学年上学期高二数学
立体几何中的向量方法——利用空间向量求二面角
基础知识:.
(1)二面角的取值范围是____________.
(2)二面角的向量求法:
①若AB 、CD 分别是二面角α—l —β的两个面内与棱l 垂直的异面直线,则二面角的大小
就是向量AB →与CD →的夹角(如图①).
②设n 1,n 2分别是二面角α—l —β的两个面α,β的法向量,则向量n 1与n 2的夹角(或其补
角)的大小就是二面角的平面角的大小(如图②③).
例1 如图,ABCD 是直角梯形,∠BAD =90°,SA ⊥平面ABCD ,SA =BC =BA =1,AD =12
,求面SCD 与面SBA 所成角的余弦值大小.
训练1如图,在三棱锥S —ABC 中,侧面SAB 与侧面SAC 均为等边三角形,∠BAC =90°,O 为BC 中点.
(1)证明:SO ⊥平面ABC ;
(2)求二面角A —SC —B 的余弦值.
课后作业
1.在如图所示的几何体中,四边形ABCD为平行四边形,∠ACB=90°,EA⊥平面ABCD,EF ∥AB,FG∥BC,EG∥AC,AB=2EF.
(1)若M是线段AD的中点,求证:GM∥平面ABFE;
(2)若AC=BC=2AE,求二面角A-BF-C的大小.
2.如图,在四棱锥P-ABCD中,底面ABCD是矩形,P A⊥平面ABCD,AP=AB=2,BC=22,E,F分别是AD,PC的中点.
(1)证明:PC⊥平面BEF;
(2)求平面BEF与平面BAP夹角的大小.。
向量法求空间角、距离和二面角

高考对空间向量的考查是以立体几何为载体,利用空间向量求有向线段的长度,求两条有向线段的夹角(或其余弦、正弦、正切),二面角、点到平面的距离、异面直线的距离、证明线线、线面、面面垂直等.下面是今年广东高考数学及广州一模,体现了高考对空间向量的考查要求.
证明:设 为公垂线段,取 (如图1所示),则
设直线 所成的角为 ,显然
1.4.直线 与平面 所成的角
在 上取定 ,求平面 的法向量 (如图2所示),再求 ,则 为所求的角.
1.5.二面角
方法一:构造二面角 的两个半平面 的法向量 (都取向上的方向,如图3所示),则
1若二面角 是“钝角型”的如图3甲所示,那么其大小等于两法向量 的夹角的补角,即 (例如2004年高考数学广东卷第18题第(1)问).
[例2](2004年全国普通高等学校招生全国统一考试数学广东卷第18题)
如右图8,在长方体ABCD—A1B1C1D1中,已知AB=4, AD=3,AA1= 2. E、F分别是A来自、BC上的点,且EB=FB=1.
(1)求二面角C—DE—C1的正切值;
(2)求直线EC1与FD1所成的角的余弦值.
解题分析:本题主要考查了二面角、异面直线所成的角等知识和空间想象能力、思维能力、运算能力.高考试卷给出的参考答案分别用了传统方法及向量法.在传统解法中,运用三垂线定理作出二面角的平面角并正明,通过延长和平移线段作出异面直线所成的角,进而通过解直角三角形和斜三角形解决问题.在用向量法的解答上,选择 为空间直角坐标系的原点, 分别为 轴, 轴, 轴的正向,这不是右手直角坐标系,虽然与右手直角坐标系没有本质上的区别,但教科书中所建立及提倡的是右手直角坐标系,所以考生习惯用右手直角坐标系. 用向量法解决第(1)问时只是用了本文所提到的“1.5.二面角”之“方法一”.
利用法向量求二面角5则

利用法向量求二面角5则以下是网友分享的关于利用法向量求二面角的资料5篇,希望对您有所帮助,就爱阅读感谢您的支持。
关于利用法向量求二面角的问题(一)关于利用法向量求二面角的问题我们知道法向量是解决立体几何问题的有力工具,但是在利用法向量在求二面角的时候,求出的两个法向量的夹角是与所求二面角相等还是互补,却没有认真思考过,这个还得从两个向量的外积说起.两个向量外积的定义:两个向量a与b的外积(也称向量积)是一个向量,即为a b,它的长度(模)为| |=||||,它的方向与和都垂直,并且按,, 的顺序构成右手标架(如下图所示)若是 ,则所得向量长度与 相等,但是方向却刚好相反,所以向量外积不满足交换律.我们可以根据这个定义来确定平面法向量的方向.设平面内有三个点A(x1y1,z1),B(x2,y2,z2),C(x3,y3,z3),则(x2 x1,y2 y1,z2 z1), (x3 x1,y3 y1,z3 z1),所以y2 y1y3 y1z2 z1z3 z1z2 z1z3 z1x2 x1x3 x1x2 x1x3 x1y2 y1y3 y1(,,),很明显,向量 可以为平面 的法向量.此时 的方向应该是垂直平面 并且向上.我们利用这个结论来求二面的大小. 说明:行列式abcdad b c,上面有关内容请参考高等代数的相关内容.如图所示,设平面 与平面 所成的二面角为 ,法向量分别为,,显然与所成的角为 ,且 ,即此时与所成的角 就是平面 与平面 所成的二面角为 ,从这里我们可以看出,只要平面 与平面 的法向量,方向一个朝向二面角的里面,一个朝向二面角的外面,求出的法向量的夹角即为所求二面角.那怎样做到这一点呢?那就要用到我们前面所讲到的右手标架.如图,我们来求平面与平面 所成的二面角 ,设 (x1,y1,z1),AC (x2,y2,z2),x1y1z1x1y1z1,且设z若x1y1x2y2,yz1x1z2x2,xy1z1y2z2x2y2z2x2y2z2则平面 的一个法向量 (x,y,z),根据右手标架应该是竖直向上,即朝向这个二面角的外面,此时我们求平面 的法向量方向应该是朝向二面角的里面.设 (x3,y3,z3), (x4,y4,z4),要使平面 的法向量方向朝向二面角的里面,根据右手标架,我们计算应该是 ,若x4y4z4x4y4z4x3y3z3x3y3z3,并且设cx4y4x3y3b ,x4y4x3y3,ay4z4y3z3,则平面 的一个法向量 (a,b,c)根据右手标架,此时n的方向就是朝向二面角的外面.那么m与n的夹角即为所求二面角.cosxa y b z cx y z a b c22222当然,这里需要注意的是,我们这里建立的空间直角坐标系一定要是右手直角坐标系.利用向量求二面角大小的又一方法(二)利用向量求二面角大小的又一方法福建南安国光中学黄耿跃文[1]给出一种判定“二面角的平面角与其面的法向量夹角的关系”,读完这篇文章后,获益匪浅.笔者通过研究给出另一种利用向量求二面角大小的可行性方法,此法可以避免产生二面角的平面角与其面的法向量夹角的关系误判,而且思路更直观、清晰.定理1如下左图已知二面角αLβ的平面角为θ,A∈α且AL,B∈β且BL,AM⊥L于MJJJ,BNGJJJ⊥L于N,则cosθ=|JJJJGMANBMA||JJJJNBG|.由二面角的平面角的定义易证定理1.定理2如上右图,空间任意一条直线L,A,B是直线L上的两个点,M是空间任意一点,MN⊥L于N,则JJJJNMG=JJJJAMGJJJJAGJJJG|JJJJMABJJJGABG|2AB.证明∵向量JJJGAN为JJJJAMG在JJJABG影向量,设GJJJ方向上的投e=JJJJJABGJJJGJJJJG|ABG|为AB方向的单位向量,JJJJ∴JJJGAN=AMJJJABGGAMGJJJABGJJJ|JJJJABG|e=ABG,|JJJJJABG2∴JJJJNMG=JJJJAMGJJJGJJJJ|GJJJGAN=JJJJAMGAMABJJJG|JJJJJAB.ABG|2例1(2004湖南理19)如图,在底面是菱形的四棱锥PABCD 中,∠ABC=60°,PA=AC=a,PB=PD=2a,点E在PD上,且PE:ED=2:1.(I)证明:PA⊥平面ABCD;(II)求以AC为棱,EAC与DAC为面的二面角θ的大小;(III)在棱PC上是否存在一点F,使BF//平面AEC?证明你的结论.解(I)略;(II)以A为坐标原点,直线AD、AP分别为y轴、z轴,过点A垂直平面PAD的直线为x轴,建立空间直角坐标系如右图.则A(0,0,0),c(32a,12a,0),JDJG=(0,a,0),E(0,2JJJ3a,13a),于是AEG=(0,23a,13a),JJJGAC=(31JJJG2a,2a,0),AD=(0,a,0).作EM⊥AC于M,DN⊥AC于N,则由定理1JJJJ得MEG:与JJJGND所成的角的大小为EAC与DAC为面的二面角θ的大小.由定理2可得JJJJMEG=JJJAEGJJJJAMG=JJJAEGJJJAEGJJJG|JJJACGACJJJG|2AC121a2=(0,a,a)3333a2(12a,2a,0)=(36a,12a,13a).JJJGND=JJJGADJJJGAN=JJJGJJJADADGJJJG |JJJACGACJJJG|2AC12=(0,a,0)2aa2(32a,12a,0)=(34a,34a,0),JJJJG∴cosθ=MEJJJNDG|JJJMEJG||JJJGND|293a2+3a2=248342=2.6a34a∴以AC为棱,EAC与DAC为面的二面角θ的大小为30°.例2(2004浙江)如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=2,AF=1,M是线段EF的中点.(I)求证AM⊥平面BDF;(II)求二面角ADFB的大小.解(I)略.(II)如图建立空间直角坐标Cxyz,∵A(2,2,0),B(0,2,0),D(2,0,0),F(2,∴JJJG2,1).DF=JJJDBGJJJDA=G(0,2,1),(0,2,0),JJJG=(2,2,0),DF=(0,2,1).作AM⊥DF于M,BN⊥DF的延长线于N,JJJG则由定理1得:MA与JJJNBG所成的解θ的大小为二面角ADFB的大小.由定理2可得:JJJGMA=JJJDAGJJJJDMG=JJJDAGJJJDAGJJJG DFJJJG|JJJGDF|2DF=(0,2,0)23(0,2,1)=(0,2,2),JJJNBG=JJJGDBJJJJDNGJJJG 3JJJG3=JJJDBGDBDFJJJG|JJJGDF|2DF=(2,2,0)2(0,2,1)/3=(2,JJJG2JJJ/3,2/3),cosθ=MANBG|JJJGMA||JJJNBG|6=91(6/3)(24/3)=2.∴二面角ADFB的大小为60°.例3(2005福建)如图,直二面角30DABE中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.(I)求证:AE⊥平面BCE;(II)求二面角BACE的大小;(III)求点D到平面ACE的距离.解(I)略;(Ⅱ)如图所示,以线段AB的中点原点O,OE所在的直线为x 轴,AB所在的直线为y轴,过O作平行于AD的直线为z轴,建立空间直角坐标系Oxyz,则A(0,1,0),E(1,0,0),C(0,1,2)B(0,1,0)JJJG=JJJ(0,2,2),JJJAEG,AC=(1,1,0),ABG=(0,2,0).作BM⊥AC于M,EN⊥AC理1得,JJJ于NEGN,则由定与JJJGMB所成的角θ的大小为二面角BACE的大小由定理JJJ2得NEG=JJJAEGJJJG=JJJAEGJJJANAEGJJJG|JJJACGACJJJ|2ACG=(1,1,0)2(0,2,2)=11JJJG2),MB=JJJ8(0,2,ABGJJJJGJJJAGMJJJG=JJJABGAB|JJJACJJJGACG|2AC=(0,2,0)4(0,2,2)=(0,1,1)JJJGJJJG8,cosθ=NEMB13|JJJNEG||JJJGMB|=3=3,22∴二面角BACE的大小为arccos33.参考文献[1]郑剑晖,郑毓青.二面角的平面角与其面的法向量夹角的关系判定.2005.1.利用空间向量求二面角的判定方法(三)利用空间向量求二面角的判定方法法一:若点A、B分别为二面角α−l−β的两个半平面α与β上的任两点,且A∉l,B∉l,n1、n2分别为平面α、β的法向量,则(1)当(ABn1)(ABn2)>0 时,二面角α−l−β的大小与两个法向量夹角相等;(2)当(ABn1)(ABn2)互补;l法二:若点P为二面角α−l−β的棱l上的任一点,Q 为两个二面角α−l−β内的任一点, n1、n2分别为平面α、β的法向量,则(1)当(PQn1)(PQn2)相等;(1)当(PQn1)(PQn2)>0 时,二面角α−l−β的大小与两个法向量夹角互补;l利用法向量求二面角的正负(四)利用法向量求二面角的平面角授课教师:陈诚班级:高二(14)班时间:2010-01-14 【教学目标】1、让学生初步理解二面角的平面角与半平面法向量的关系,并能解决与之有关的简单问题。
高考数学专题:向量求二面角(含答案)

高考数学专题:向量求二面角向量法求二面角大小的两种方法(1)分别求出二面角的两个面所在平面的法向量,然后通过两个平面的法向量的夹角得到二面角的大小,但要注意结合实际图形判断所求角的大小.(2)分别在二面角的两个半平面内找到与棱垂直且以垂足为起点的两个向量,则这两个向量的夹角的大小就是二面角的大小.1、如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=π3,M为BC上一点,且BM=12,MP⊥AP.(1)求PO的长;(2)求二面角A-PM-C的正弦值.2、如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F 分别为AC,DC的中点.(1)求证:EF⊥BC;(2)求二面角E-BF-C的正弦值.3、如图所示,在多面体ABCD-A1B1C1D1中,上、下两个底面A1B1C1D1和ABCD互相平行,且都是正方形,DD1⊥底面ABCD,AB=2A1B1=2DD1=2a.(1)求异面直线AB1与DD1所成角的余弦值;(2)已知F是AD的中点,求证:FB1⊥平面BCC1B1;(3)在(2)的条件下,求二面角F-CC1-B的余弦值.4、如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.(1)证明:平面ABEF⊥平面EFDC;(2)求二面角E-BC-A的余弦值.5、如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.(1)求证:EG∥平面ADF;(2)求二面角O-EF-C的正弦值;(3)设H为线段AF上的点,且AH=23HF,求直线BH和平面CEF所成角的正弦值6、如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=π2,PA=AD=2,AB=BC=1.(1)求平面PAB与平面PCD所成二面角的余弦值;(2)点Q是线段BP上的动点,当直线CQ与DP所成的角最小时,求线段BQ的长.7、如图所示,在多面体A1B1D1-DCBA中,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于F.(1)证明:EF∥B1C;(2)求二面角E-A1D-B1的余弦值.8、如图,三棱锥P-ABC中,PC⊥平面ABC,PC=3,∠ACB=π2,D,E分别为线段AB,BC上的点,且CD=DE=2,CE=2EB=2.(1)证明:DE⊥平面PCD;(2)求二面角A-PD-C的余弦值.答案:1、解:(1)如图,连接AC,BD,因为ABCD为菱形,则AC∩BD=O,且AC⊥BD.以O为坐标原点,OA →,OB →,OP →的方向分别为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系O -xyz .因为∠BAD =π3,所以OA =AB ·cos π6=3,OB =AB ·sin π6=1,所以O (0,0,0),A (3,0,0),B (0,1,0),C (-3,0,0),OB →=(0,1,0),BC →=(-3,-1,0).由BM =12,BC =2知, BM→=14BC →=⎝ ⎛⎭⎪⎫-34,-14,0, 从而OM→=OB →+BM →=⎝ ⎛⎭⎪⎫-34,34,0, 即M ⎝ ⎛⎭⎪⎫-34,34,0.设P (0,0,a ),a >0,则AP→=(-3,0,a ),MP →=⎝ ⎛⎭⎪⎫34,-34,a . 因为MP ⊥AP ,故MP →·AP→=0,即-34+a 2=0,所以a =32或a =-32(舍去), 即PO =32.(2)由(1)知,AP →=⎝ ⎛⎭⎪⎫-3,0,32,MP →=⎝ ⎛⎭⎪⎫34,-34,32,CP →=⎝ ⎛⎭⎪⎫3,0,32. 设平面APM 的法向量为n 1=(x 1,y 1,z 1),平面PMC 的法向量为n 2=(x 2,y 2,z 2),由n 1·AP →=0,n 1·MP →=0, 得⎩⎪⎨⎪⎧-3x 1+32z 1=0,34x 1-34y 1+32z 1=0,故可取n 1=⎝ ⎛⎭⎪⎫1,533,2. 由n 2·MP →=0,n 2·CP →=0, 得⎩⎪⎨⎪⎧34x 2-34y 2+32z 2=0,3x 2+32z 2=0,故可取n 2=(1,-3,-2). 从而法向量n 1,n 2的夹角的余弦值为 cos 〈n 1,n 2〉=n 1·n 2|n 1|·|n 2|=-155, sin 〈n 1,n 2〉=1-⎝⎛⎭⎪⎫-1552=105, 故所求二面角A -PM -C 的正弦值为105.2、(1)证明:由题意,以B 为坐标原点,在平面DBC 内过B 作垂直BC 的直线为x 轴,BC 所在直线为y 轴,在平面ABC 内过B 作垂直BC 的直线为z 轴,建立如图所示空间直角坐标系.易得B (0,0,0),A (0,-1,3),D (3,-1,0),C (0,2,0),因而E ⎝ ⎛⎭⎪⎫0,12,32,F ⎝ ⎛⎭⎪⎫32,12,0,所以EF →=⎝ ⎛⎭⎪⎫32,0,-32,BC →=(0,2,0),因此EF →·BC→=0. 从而EF →⊥BC →,所以EF ⊥BC .(2)平面BFC 的一个法向量为n 1=(0,0,1). 设平面BEF 的法向量为n 2=(x ,y ,z ). 又BF →=⎝ ⎛⎭⎪⎫32,12,0,BE →=⎝ ⎛⎭⎪⎫0,12,32,由⎩⎪⎨⎪⎧n 2·BF →=0,n 2·BE →=0得其中一个n 2=(1,-3,1).设二面角E -BF -C 大小为θ,且由题意知θ为锐角, 则cos θ=|cos 〈n 1,n 2〉| =⎪⎪⎪⎪⎪⎪n 1·n 2|n 1||n 2|=15. 因此sin θ=25=255,即所求二面角的正弦值为255.3、.解:以D 为坐标原点,以DA ,DC ,DD 1所在直线分别为x 轴、y 轴、z 轴建立如图所示的空间直角坐标系,则A (2a ,0,0),B (2a ,2a ,0),C (0,2a ,0),D 1(0,0,a ),F (a ,0,0),B 1(a ,a ,a ),C 1(0,a ,a ).(1)因为AB 1→=(-a ,a ,a ),DD 1→=(0,0,a ), 所以|cos 〈AB 1→,DD 1→〉|=⎪⎪⎪⎪⎪⎪⎪⎪AB 1→·DD 1→|AB 1→||DD 1→|=33,所以异面直线AB 1与DD 1所成角的余弦值为33. (2)证明:因为BB 1→=(-a ,-a ,a ),BC →=(-2a ,0,0),FB 1→=(0,a ,a ), 所以⎩⎪⎨⎪⎧FB 1→·BB 1→=0,FB 1→·BC →=0,所以FB 1⊥BB 1,FB 1⊥BC . 因为BB 1∩BC =B , 所以FB 1⊥平面BCC 1B 1.(3)由(2)知,FB 1→为平面BCC 1B 1的一个法向量. 设n =(x 1,y 1,z 1)为平面FCC 1的法向量, 因为CC 1→=(0,-a ,a ),FC →=(-a ,2a ,0), 所以⎩⎪⎨⎪⎧n ·CC 1→=0,n ·FC →=0,即⎩⎨⎧-ay 1+az 1=0,-ax 1+2ay 1=0.令y 1=1,则n =(2,1,1),所以||cos 〈FB 1→,n 〉=⎪⎪⎪⎪⎪⎪⎪⎪FB 1→·n |FB 1→||n |=33,因为二面角F -CC 1-B 为锐角, 所以二面角F -CC 1-B 的余弦值为33.4、解:(1)证明:由已知可得AF ⊥DF ,AF ⊥FE ,所以AF ⊥平面EFDC .又AF ⊂平面ABEF ,故平面ABEF ⊥平面EFDC . (2)如图,过D 作DG ⊥EF ,垂足为G , 由(1)知DG ⊥平面ABEF .以G 为坐标原点,GF →的方向为x 轴正方向,|GF →|为单位长,建立如图所示的空间直角坐标系G -xyz . 由(1)知∠DFE 为二面角D -AF -E 的平面角,故∠DFE =60°, 则|DF |=2,|DG |=3,可得A (1,4,0),B (-3,4,0),E (-3,0,0),D (0,0,3). 由已知,AB ∥EF , 所以AB ∥平面EFDC .又平面ABCD ∩平面EFDC =CD , 故AB ∥CD ,CD ∥EF .由BE ∥AF ,可得BE ⊥平面EFDC ,所以∠CEF 为二面角C -BE -F 的平面角,∠CEF =60°,从而可得C (-2,0,3).所以EC→=(1,0,3),EB →=(0,4,0),AC →=(-3,-4,3),AB →=(-4,0,0).设n =(x ,y ,z )是平面BCE 的法向量,则 ⎩⎪⎨⎪⎧n ·EC →=0,n ·EB →=0,即⎩⎨⎧x +3z =0,4y =0. 所以可取n =(3,0,-3). 设m 是平面ABCD 的法向量, 则⎩⎪⎨⎪⎧m ·AC →=0,m ·AB →=0.同理可取m =(0,3,4), 则cos 〈n ,m 〉=n·m |n ||m |=-21919.故二面角E -BC -A 的余弦值为-21919.5、解:依题意,OF ⊥平面ABCD ,如图,以O 为原点,分别以AD →,BA →,OF →的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系,依题意可得O (0,0,0),A (-1,1,0),B (-1,-1,0),C (1,-1,0),D (1,1,0),E (-1,-1,2),F (0,0,2),G (-1,0,0).(1)证明:依题意,AD→=(2,0,0),AF →=(1,-1,2). 设n 1=(x ,y ,z )为平面ADF 的法向量,则⎩⎪⎨⎪⎧n 1·AD →=0,n 1·AF →=0,即⎩⎨⎧2x =0,x -y +2z =0.不妨设z =1,可得n 1=(0,2,1).又EG →=(0,1,-2),所以EG →·n 1=0, 又因为直线EG ⊄平面ADF , 所以EG ∥平面ADF .(2)易证,OA→=(-1,1,0)为平面OEF 的一个法向量. 依题意,EF→=(1,1,0),CF →=(-1,1,2).设n 2=(x ,y ,z )为平面CEF 的法向量,则⎩⎪⎨⎪⎧n 2·EF →=0,n 2·CF →=0,即⎩⎨⎧x +y =0,-x +y +2z =0.不妨设x =1,可得n 2=(1,-1,1).因此cos 〈OA →,n 2〉=OA →·n 2|OA →||n 2|=-63,于是sin 〈OA →,n 2〉=33.所以,二面角O -EF -C 的正弦值为33.(3)由AH =23HF ,得AH =25AF .因为AF→=(1,-1,2),所以AH →=25AF →=⎝ ⎛⎭⎪⎫25,-25,45,进而有H ⎝ ⎛⎭⎪⎫-35,35,45,从而BH →=⎝ ⎛⎭⎪⎫25,85,45,因此cos 〈BH →,n 2〉=BH →·n 2|BH →||n 2|=-721.所以,直线BH 和平面CEF 所成角的正弦值为721.6、解:以{AB →,AD →,AP →}为正交基底建立如图所示的空间直角坐标系A -xyz ,则各点的坐标为B (1,0,0),C (1,1,0),D (0,2,0),P (0,0,2). (1)因为AD ⊥平面PAB ,所以AD→是平面PAB 的一个法向量,AD →=(0,2,0).因为PC→=(1,1,-2),PD →=(0,2,-2). 设平面PCD 的法向量为m =(x ,y ,z ), 则m ·PC →=0,m ·PD →=0, 即⎩⎨⎧x +y -2z =0,2y -2z =0. 令y =1,解得z =1,x =1.所以m =(1,1,1)是平面PCD 的一个法向量. 从而cos 〈AD →,m 〉=AD →·m |AD →||m |=33, 所以平面PAB 与平面PCD 所成二面角的余弦值为33. (2)因为BP→=(-1,0,2),设BQ →=λBP →=(-λ,0,2λ)(0≤λ≤1),又CB→=(0,-1,0),则CQ →=CB →+BQ →= (-λ,-1,2λ),又DP→=(0,-2,2),从而cos 〈CQ →,DP →〉=CQ →·DP →|CQ →||DP →|=1+2λ10λ2+2.设1+2λ=t ,t ∈[1,3],则cos 2〈CQ →,DP →〉=2t 25t 2-10t +9=29⎝ ⎛⎭⎪⎫1t -592+209≤910.当且仅当t =95,即λ=25时, |cos 〈CQ→,DP →〉|的最大值为31010. 因为y =cos x 在⎝ ⎛⎭⎪⎫0,π2上是减函数,所以此时直线CQ 与DP 所成角取得最小值. 又因为BP =12+22=5, 所以BQ =25BP =255.7、解:(1)证明:由正方形的性质可知A 1B 1∥AB ∥DC ,且A 1B 1=AB =DC ,所以四边形A 1B 1CD 为平行四边形,从而B 1C ∥A 1D .又A 1D ⊂平面A 1DE ,B 1C ⊄平面A 1DE ,于是B 1C ∥平面A 1DE . 又B 1C ⊂平面B 1CD 1,平面A 1DE ∩平面B 1CD 1=EF ,所以EF ∥B 1C .(2)因为四边形AA 1B 1B ,ADD 1A 1,ABCD 均为正方形,所以AA 1⊥AB ,AA 1⊥AD ,AB ⊥AD 且AA 1=AB =AD ,以A 为原点,分别以AB →,AD →,AA 1→为x 轴,y 轴和z 轴单位正向量建立如图所示的空间直角坐标系,可得点的坐标A (0,0,0),B (1,0,0),D (0,1,0),A 1(0,0,1),B 1(1,0,1),D 1(0,1,1),而E 点为B 1D 1的中点,所以E 点的坐标为(0.5,0.5,1).设面A 1DE 的法向量为n 1=(r 1,s 1,t 1),而该面上向量A 1E →=(0.5,0.5,0),A 1D →=(0,1,-1),由n 1⊥A 1E →,n 1⊥A 1D →得r 1,s 1,t 1应满足方程组⎩⎨⎧0.5r 1+0.5s 1=0,s 1-t 1=0,因为(-1,1,1)为其一组解,所以可取n 1=(-1,1,1).设面A 1B 1CD 的法向量为n 2=(r 2,s 2,t 2),而该面上向量A 1B 1→=(1,0,0),A 1D →=(0,1,-1),由此同理可得n 2=(0,1,1),所以结合图形知二面角E -A 1D -B 1的余弦值为|n 1·n 2||n 1|·|n 2|=23×2=63. 8、解:(1)证明:由PC ⊥平面ABC ,DE ⊂平面ABC ,得PC ⊥DE .由CE =2,CD =DE =2得△CDE 为等腰直角三角形,故CD ⊥DE .又PC ∩CD =C ,所以DE ⊥平面PCD .(2)由(1)知,△CDE 为等腰直角三角形,∠DCE =π4.如图,过D 作DF 垂直CE 于F ,易知DF =FC =FE =1.又EB =1,故FB =2.由∠ACB =π2得DF ∥AC ,DF AC =FB BC =23,故AC =32DF =32.如图,以C 为坐标原点,分别以CA→,CB →,CP →的方向为x 轴,y 轴,z 轴的正方向建立空间直角坐标系,则C (0,0,0),P (0,0,3),A ⎝ ⎛⎭⎪⎫32,0,0,E (0,2,0),D (1,1,0),ED →=(1,-1,0),DP →=(-1,-1,3),DA →=⎝ ⎛⎭⎪⎫12,-1,0. 设平面PAD 的法向量为n 1=(x 1,y 1,z 1),由n 1·DP →=0,n 1·DA →=0,得⎩⎪⎨⎪⎧-x 1-y 1+3z 1=0,12x 1-y 1=0, 故可取n 1=(2,1,1).由(1)可知,DE ⊥平面PCD ,故平面PCD 的法向量n 2可取为ED→, 即n 2=(1,-1,0).从而法向量n 1,n 2的夹角的余弦值为cos 〈n 1,n 2〉=n 1·n 2|n 1|·|n 2|=36, 故二面角A -PD -C 的余弦值为36.。
空间向量与立体几何用坐标法求二面角

B1(2,2,2),O(1,1,0)。 所以MA (2,0,1),MC (0,2,1),
D O
A
B1O (1,1, 2)
x
B1O MA 2 0 2 0,B1O MC 0 2 2 0
所以B1O MA , B1O MC 即B1O MA , B1O MC。又MA
6。 6
例练习四: 如所示,A B C D 是一直角梯形,A B C = 900,
SA
平面ABCD,
SA
AB
BC
1,
AD
1 2
, 求面zSCD与面SBA
所成二面角的余弦值.
解:建立空直角坐系A - xyz如所示,
S
A (0,0,0), C (- 1,1,0), D (0,1 ,0),
2
(1)求证:PA//平面EDB
(2)求证:PB⊥平面EFD
P
(3)求二面角C-PB-D的大小。
E F
D
C
A
G
B
解:如图所示建立空间直角坐标系,点D为坐标原点, 设DC=1
(1)证明:连结AC,AC交BD于点G,连结EG
依题意得A(1, 0, 0), P(0, 0,1),
Z
11
E(0, , ) 22
P
E F
D
C Y
A
G
B
X
(2)证明:依题意得B(1,1,0),PB (1,1,1)
又DE (0, 1 , 1),故PB DE 0 1 1 0
22
22
所以PB DE
Z
由已知EF PB,
且EF DE E,
二面角的求法

知: CP PE 。 又 DP PE ,即 CPD 即为所求的二面角。 在 RtCDP 中, CD 1, PD 2 , PC 3 。那么 cos CPD 6 。 3 即: CPD arccos 6 3 所以平面 PAD 与平面 PBC 所成二面角的大小是 arccos 6 。 3 在有些问题中,所给的图形不是能够很好观测到二面角的平面角,可以通过补形的
2 面角的大小。
图6
解:延长直线 DA 与 BC ,它们相交于点 E ,连接 PE 。 由题意可知, BA 平行于 CD , AB 的长度是 CD 的一半,且 BA AD , BA PA ,
6
那么 BA 平面PED , CD 平面PED , AE 1, PE 2 。 在三角形 PED 中, PD PE 2 , ED AE AD 2 。那么根据勾股定理可知
4.2.3 切平面法
切面法的基本思想是做一个垂面,它垂直于两个平面的交线,在所得的图形中就可 以很容易观察与计算二面角。如图 4 所示,可以作平面 CAB 垂直于两个平面的交线 DE ,平面 CAB 与平面 的交线是 AC ,平面 CAB 与平面 的交线是 AB ,根据二面 角的定义知 CAB 即为所求二面角的补角,根据补角法,可以求出二面角 F DE C 的大小。
直 接 求 解 二 面 角 F DE C 的 大 小 是 有 些 困 难 的 , 那 么 可 以 先 求 解 二 面 角 C DE B 。因为二面角 F DE C 与二面角 C DE B 是互补的关系,现在先求出 二面角 C DE B 后,二面角 F DE C 的大小就很容易计算了。 4.2.2 三垂线法
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
