考点三 用空间向量求二面角
空间向量求立体几何二面角中准确快速写出坐标的技巧

空间向量求立体几何二面角中准确快速写出坐标的技巧技巧:
一、用“叉乘”结合三角函数求解立体几何二面角:
1、先求空间向量的叉乘,叉乘结果的方向量D是二个空间向量的法向量。
2、计算该法向量D的坐标与另一空间向量的点积,就可以得到立体几何二面角的三角函数形式。
3、由计算的三角函数,使用反三角函数,计算出来的角度值就是二面角的度数,这就是求出坐标的技巧。
二、使用质心坐标系求解立体几何二面角:
1、先求两个空间向量的质心坐标系,即二质心坐标的差值。
2、把这个差值换成极坐标形式,这样就可以求出二面角的三角函数形式。
3、由计算的三角函数,使用反三角函数,计算出来的角度值就是二面角的度数,这就是求出坐标的技巧。
- 1 -。
高中立体几何中二面角经典求法

高中立体几何中二面角求法摘要:在立体几何中,求二面角的大小是历届高考的热点,几乎每年必考,而对于求二面角方面的问题,同学们往往很难正确地找到作平面角的方法,本文对求二面角的方法作了一个总结,希望对学生有帮助。
(一)、二面角定义的回顾:从一条直线出发的两个半平面所组成的图形就叫做二面角。
二面角的大小是用二面角的平面角来衡量的。
而二面角的平面角是指在二面角的棱上任取一点O,分别在两个半平面内作射线,则为二面角的平面角。
(二)1、由定义作出二面角的平面角;2、利用三垂线定理(逆定理)作出二面角的平面角;3、作二面角棱的垂面,则垂面与二面角两个面的交线所成的角就是二面角的平面角。
4、空间坐标法求二面角的大小5、平移或延长(展)线(面)法6、射影公式S射影=S斜面cosθ7、化归为分别垂直于二面角的两个面的两条直线所成的角1、利用定义作出二面角的平面角,并设法求出其大小。
例1、如图,已知二面角α-а-β等于120°,PA⊥α,A∈α,PB⊥β,B∈β. 求∠APB的大小.解: 设平面∩PABα=OA,平面PAB∩β=OB。
同理PB⊥а ∴а⊥平面PAB又∵OA⊂平面PAB ∴а⊥OA同理а⊥OB.∴∠AOB是二面角α-а-β的平面角.在四边形PAOB中, ∠AOB=120°,.∠PAO=∠POB=90°, 所以∠APB=60°2、三垂线定理(逆定理)法由二面角的一个面上的斜线(或它的射影)与二面角的棱垂直,推得它位于二面角的另一的面上的射影(或斜线)也与二面角的棱垂直,从而确定二面角的平面角。
例2:如图,ABCD-A 1B 1C 1D 1是长方体,侧棱AA 1长为1,底面为正方体且边长为2,E是棱BC的中点,求面C 1DE与面CDE所成二面角的正切值.解:在长方体ABCD—A 1B 1C 1D 1中由三垂线定理可得:CD =2 CE=1, DE=3、找(作)公垂面法由二面角的平面角的定义可知两个面的公垂面与棱垂直,因此公垂面与两个面的交线所成的角,就是二面角的平面角。
空间向量应用-二面角

04
二面角的应用
在几何学中的应用
向量投影
在求解向量的投影时,可以利用二面 角的概念,通过计算向量在某一平面 上的投影长度,来得到该向量与该平 面的夹角。
向量夹角
二面角的概念可以用于计算两个向量 的夹角,通过比较两个向量的夹角与 二面角的夹角,可以判断两个向量的 方向关系。
在物理学中的应用
力的合成与分解
建筑设计
在建筑设计中,利用二面角的概念可以确定建筑物的位置、方向和高度等信息, 以保证建筑物的安全和稳定性。
05
空间向量与二面角的关系
向量与二面角的关联
向量是既有大小又有方向的量,其大 小和方向可以用来表示二面角的大小 和方向。
二面角的大小和方向可以通过两个向 量的夹角来描述,这个夹角就是二面 角的平面角。
二面角的向量定义
总结词
二面角的向量定义是通过向量的投影 和叉积来定义的,它是一个标量值, 其大小等于两个向量的叉积的绝对值 再除以两向量的模的乘积。
详细描述
二面角的向量定义是通过向量的投影和叉积来 描述的。设两非零向量a和b分别属于两个半平 面,那么二面角θ的大小可以用公式 ∣a×b∣/∣a∣∣b∣表示,其中a×b表示向量a和b 的叉积,∣a∣和∣b∣分别表示向量a和b的模。这 个标量值的大小就等于二面角θ的大小。
二面角的性质
总结词
二面角具有一些重要的性质,如二面角的取值范围是[0,π],二面角的大小与观察方向有关,以及二面角的补角等 于其平面角的补角等。
详细描述
首先,二面角的取值范围是[0,π],这是由其几何定义直接得出的。其次,二面角的大小与观察方向有关,即观察 方向的不同可能导致二面角的大小发生变化。最后,二面角的补角等于其平面角的补角,这是由向量的性质得出 的。
一轮复习课件872利用空间向量求二面角与空间距离3

【解析】选B.设α∩β=a,若直线l∥a,且l⊄α,l⊄β,则l∥α,l∥β,因此α不一 定平行于β,故A错误;由于l∥α,故在α内存在直线l′∥l.又因为l⊥β.所以 l′⊥β,故α⊥β,所以B正确;若α⊥β,在β内作交线的垂线l,则l⊥α,此时l 在平面β内,因此C错误;已知α⊥β,若α∩β=a,l∥a,且l不在平面α,β内, 则l∥α且l∥β,因此D错误.
【迁移应用】 平面α外有两条直线m和n,如果m和n在平面α内的射影分别是直线m1和直线n1, 给出下列四个命题:①m1⊥n1⇒m⊥n;②m⊥n⇒m1⊥n1;③m1与n1相交⇒m与n相交 或重合;④m1与n1平行⇒m与n平行或重合. 其中不正确的命题个数是( ) A.1 B.2 C.3 D.4
【解析】选D.如图,在正方体ABCD-A1B1C1D1中,AD1,AB1,B1C在底面上的射影分别 是A1D1,A1B1,B1C1.
第二课时 利用空间向量求 二面角与空间距离
内容索引
核心考点·精准研析 核心素养·微ቤተ መጻሕፍቲ ባይዱ题 核心素养测评
【思想方法】 构造法判断空间线面的位置关系 设l是直线,α,β是两个不同的平面,则下列命题正确的是世纪金榜导 学号( ) A.若l∥α,l∥β,则α∥β B.若l∥α,l⊥β,则α⊥β C.若α⊥β,l⊥α,则l⊥β D.若α⊥β,l∥α,则l⊥β
[构造法解题] 借助于长方体模型解决本题: 对于A,如图①,α与β可相交; 对于B,如图②,不论β在何位置,都有α⊥β; 对于C,如图③,l可与β平行或l⊂β内; 对于D,如图④,l⊥β或l⊂β或l∥β.
【思想方法指导】 (1)构造法实质上是结合题意构造适合题意的直观模型,然后将问题利用模型 直观地作出判断,这样减少了抽象性,避免了因考虑不全面而导致解题错误. (2)对于线面、面面平行、垂直的位置关系的判定,可构造长方体或正方体化 抽象为直观去判断.
向量法-求二面角大小

空间向量法---求二面角的大小
运用“空间向量法”---求“二面角的大小”的解题步骤:
① 建立空间直角坐标系; ② 求出所需各点的坐标; ③ 求出两个平面的法向量; ④ 求出两个法向量的夹角; ⑤ 写出所求二面角的大小。
空间向量法---求二面角的大小
运用“空间向量法”---求“二面角的大小”的解题步骤:
(1) 证明: AN⊥平面PAD .
(2) 求二面角C-AM-N的大小 .
P
M
A
D
B
NC
【练习3】 如图, 在四棱锥P-ABCD中, 底面是边长为2的菱形, ∠ABC=60O , PA⊥底面ABCD,PA=2, M,N分别为PC,BC的中点.
(1) 证明: AN⊥平面PAD .
(2) 求二面角C-AM-N的大小 .
∴ cosq =
6
3
得 tanq =
2
2
∴
所求面SCD与面SBA所成二面角的正切值是22
【练习2】 已知点E、F分别是正方体ABCD-A1B1C1D1的棱BB1、 CC1上的点, 且 BE1=2EB, CF=2FC1 .
(1) 求面AEF与面ABC所成二面角的正切值 .
【练习3】 如图, 在四棱锥P-ABCD中, 底面是边长为2的菱形, ∠ABC=60O , PA⊥底面ABCD,PA=2, M,N分别为PC,BC的中点.
=
3 3
由条件知,二面角A-CD-E为锐角,∴
所求二面角的余弦值为
3 3
【练习1】 如下图, 在底面是直角梯形的四棱锥S-ABCD中,
∠ABC=90O
,
SA⊥面ABCD,SA=AB=BC=1,
AD=
1 2
.
空间向量法求二面角
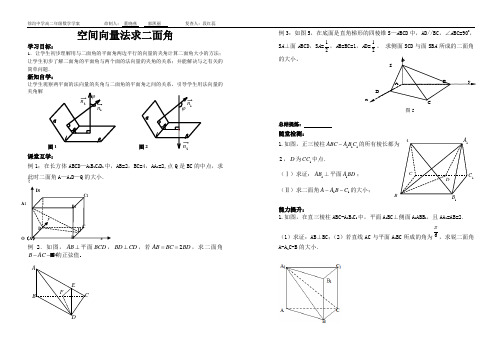
徐沟中学高二年级数学学案 命制人: 董晓燕 郭凯丽 复查人:段红蕊空间向量法求二面角学习目标:1.让学生初步理解用与二面角的平面角两边平行的向量的夹角计算二面角大小的方法;让学生初步了解二面角的平面角与两个面的法向量的夹角的关系;并能解决与之有关的简单问题.新知自学:让学生观察两平面的法向量的夹角与二面角的平面角之间的关系,引导学生用法向量的夹角解图1 图2课堂互学:例1;在长方体ABCD —A 1B 1C 1D 1中,AB=2,BC=4,AA 1=2,点Q 是BC 的中点,求此时二面角A —A 1D —Q 的大小.例2.如图,AB ⊥平面BCD ,BD CD ⊥,若2AB BC BD ==,求二面角B ACD --的正弦值例3:如图5,在底面是直角梯形的四棱锥S —A BCD 中,AD//BC ,∠A BC=900,S A ⊥面A BCD ,S A =21,A B=BC=1,A D=21。
求侧面SCD 与面SB A 所成的二面角的大小。
总结提炼:随堂检测:1.如图,正三棱柱111ABC A B C -的所有棱长都为2,D 为1CC 中点.(Ⅰ)求证:1AB ⊥平面1A BD ; (Ⅱ)求二面角11C B A A --的大小;能力提升:1.如图,在直三棱柱ABC-A 1B 1C 1中,平面A 1BC ⊥侧面A 1ABB 1,且AA 1=AB=2.(1)求证:AB ⊥BC ;(2)若直线AC 与平面A 1BC 所成的角为6π,求锐二面角A-A 1C-B 的大小.A BC DEF ϕω θ βlα2n 1nθ β lαϕ1n2n O (A ) B A 1 C 1 B 1D 1 D CQ zy x 图4AzyDCBS 图5ABCD1A1C1B。
二面角的求法和利用空间向量解决立体几何问题
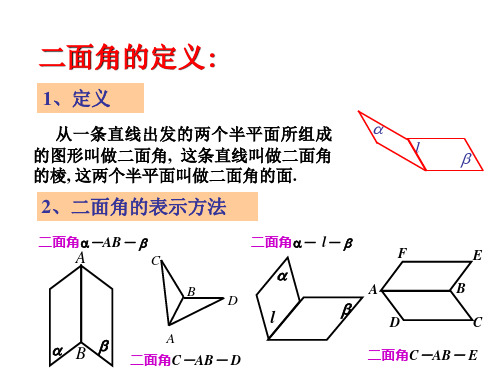
二面角的定义:
1、定义
从一条直线出发的两个半平面所组成
的图形叫做二面角, 这条直线叫做二面角
l
的棱, 这两个半平面叫做二面角的面.
2、二面角的表示方法
二面角-AB-
A
C
B
二面角- l-
D
l
B
A
二面角C-AB- D
F
E
A
B
D
C
二面角C-AB- E
二面角的平面角:
以二面角的棱上任意一点为端
点, 在两个面内分别作垂直于棱的 两条射线, 这两条射线所成的角叫 做二面角的平面角。
面面平行
∥ n1 ∥ n2 n1 kn2
二、垂直关系:
设直线 l, m 的方向向量分别为 AB,CD ,
平面 , 的法向量分别为 n1 , n2 , 线线垂直:
l ⊥ m AB ⊥ CD AB • CD 0 ;
Bl
A
平面 内的两个相交向量垂直
(4)解方程组,令其中一个量的值求另外两个, 即得法向量。
一、平行关系:
设直线 l, m 的方向向量分别为 AB,CD ,
lm
BD
平面 , 的法向量分别为
线线平行:
n1
, n2
,
l ∥ m AB ∥ CD AB kCD
;
x1 y1
=
A
x2 y2
=
C
x3 y3
线面平行
AB
l ∥ AB n1 AB n1 0 ;
分别作垂直于a 的两条射线OA,OB,则∠AOB就 是此二面角的平面角。
2、垂线法: 在一个平面 内选一点A向另一平面 作 垂线AB,
垂足为B,再过点B向棱a作垂线BO,垂足 为O, 连结AO,则∠AOB就是二面角的平面角。
2024年高考数学复习培优讲义专题15---几何法求二面角,线面角(含解析)

专题3-1几何法求二面角,线面角立体几何空间向量求解过程,丧失了立体几何求解的乐趣,无形中也降低了学生的空间想象能力。
这是空间向量求解的巨大优点,也是缺点,就这么共存着。
其实不建系而直接计算真的很比较锻炼空间想象的能力,方法上也更灵活一些,对于备考的中档学生来说,2种方法都要熟练掌握。
方法介绍一、定义法:交线上取点 等腰三角形共底边时作二面角步骤第一步:在交线l上取一点O第二步:在α平面内过O点作l的垂线OA第三步:在β平面内过O点作l的垂线OB∠AOB即为二面角,余弦定理求角αβl OAB二、三垂线法(先作面的垂直)—后续计算小使用情况:已知其中某个平面的垂线段第二步:过垂直B作l的垂线OB∠AOB即为二面角且△AOB为直角三角形,邻比斜三、作2次交线的垂线作二面角步骤第一步:作AO⊥l第二步:作OB⊥l连接AB,∠AOB即为二面角,余弦定理求角四、转换成线面角作二面角步骤第一步:作AO⊥l第二步:作AB⊥β(找不到垂足B的位置用等体积求AB长)连接AB,∠AOB即为二面角△AOB为直角三角形,邻比斜五、转换成线线角—计算小,也是法向量的原理提问:什么时候用?若α平面存在垂线AB,且β平面存在垂线AC则α平面与β平面的夹角等于直线AC与AB的夹角αβlOABαβlOABβαOABCαβlOAB六、投影面积法——面积比(三垂线法进阶)将cos θ=边之比∣面积之比,从一维到二维,可多角度求出两面积,最后求解如图△ABC 在平面α上的投影为△A 1BC , 则平面α与平面ABC 的夹角余弦值1cos A BCABCθ=△△即cos θ=投影原S S补充:即使交线没有画出来也可以直接用例题:一题多解2023汕头二模T20如图在正方体ABCD -A 1B 1C 1D 1中,PQ 是所在棱上的中点.1C 1CD ABA B 1αBCAA 1D(1)求平面APQ 与平面ABCD 夹角的余弦值 (2)补全截面APQ2023全国乙卷数学(理)T9——由二面角求线面角P C 1CDABA B 1P C 1DABA B 1P C 1CDABA B 1P C 1DABA B 1P C 1CDABA B 1PC 1DABA B 11.已知ABC 为等腰直角三角形,AB 为斜边,ABD △为等边三角形,若二面角C AB D −−为150︒,则直线CD 与平面ABC 所成角的正切值为( )A .15B .25C .35D .252021·新高考1卷·T20——由二面角求线段长2.如图,在三棱锥A BCD −中,平面ABD ⊥平面BCD ,AB AD =,O 为BD 的中点.(1)证明:OA CD ⊥;(2)若OCD 是边长为1的等边三角形,点E 在棱AD 上,2DE EA =,且二面角E BC D −−的大小为45︒,求三棱锥A BCD −的体积.题型一 定义法1.如图,在三棱锥S—ABC 中,SC ⊥平面ABC ,点P 、M 分别是SC 和SB 的中点,设PM=AC =1,∠ACB =90°,直线AM 与直线SC 所成的角为60°.(1)求证:平面MAP ⊥平面SAC . (2)求二面角M—AC—B 的平面角的正切值;2.(湛江期末)如图,在三棱锥P -ABC 中,PA ⊥平面ABC ,点M ,N 分别是PB ,AC 的中点,且MN ⊥A C . (1)证明:BC ⊥平面PA C .(2)若PA =4,AC =BC =22,求平面PBC 与平面AMC 夹角的余弦值.(几何法比较简单)3.如图1,在平行四边形ABCD 中,60,2,4A AD AB ∠=︒==,将ABD △沿BD 折起,使得点A 到达点P ,如图2.重点题型·归类精讲(1)证明:平面BCD⊥平面P AD;(2)当二面角D PA B−−的平面角的正切值为6时,求直线BD与平面PBC夹角的正弦值.题型二三垂线法4.(佛山期末)如图,四棱锥P-ABCD中,AB∥CD,∠BAD=90°,12PA AD AB CD===,侧面PAD⊥底面ABCD,E为PC的中点.(1)求证:BE⊥平面PCD;(2)若PA=PD,求二面角P-BC-D的余弦值.5.如图,在四棱锥P -ABCD 中,△P AD 是以AD 为斜边的等腰直角三角形,,,224,23BC AD CD AD AD CD BC PB ⊥====∥ (2023广州一模T19)(1) 求证:AD PB ⊥;(2)求平面P AB 与平面ABCD 交角的正弦值.6.如图,在三棱锥A BCD −中,平面ABD ⊥平面BCD ,AB AD =,O 为BD 的中点.(1)证明:OA CD ⊥;(2)若OCD 是边长为2的等边三角形,点E 在棱AD 上,2DE EA =且二面角E BC D −−的大小为60,求三棱锥A BCD −的体积.7.(2023·浙江·统考二模)如图,在三棱柱111ABCA B C 中,底面ABC ⊥平面11AA B B ,ABC 是正三角形,D 是棱BC 上一点,且3CD DB =,11A A A B =.(1)求证:111B C A D ⊥;(2)若2AB =且二面角11A BC B −−的余弦值为35,求点A 到侧面11BB C C 的距离.8.如图,在多面体ABCDE 中,平面ACD ⊥平面ABC ,BE ⊥平面ABC ,ABC 和ACD 均为正三角形,4AC =,3BE =.(1)在线段AC 上是否存在点F ,使得BF ∥平面ADE ?说明理由; (2)求平面CDE 与平面ABC 所成的锐二面角的正切值.题型三 作2次交线的垂线9.在三棱锥S ABC −中,底面△ABC 为等腰直角三角形,90SAB SCB ABC ∠=∠=∠=︒. (杭州二模) (1)求证:AC ⊥SB ;(2)若AB =2,22SC =,求平面SAC 与平面SBC 夹角的余弦值.题型四 找交线10.如图,在四棱锥P -ABCD 中,底面ABCI )是平行四边形,∠ABC =120°,AB =1,BC =2,PD ⊥C D . (1)证明:AB ⊥PB ;(2)若平面PAB ⊥平面PCD ,且102PA =,求直线AC 与平面PBC 所成角的正弦值. (广东省二模T19)题型五 转换成线线角湖北省武汉市江汉区2023届高三上学期7月新起点考试11.在直三棱柱111ABC A B C −中,已知侧面11ABB A 为正方形,2BA BC ==,D ,,E F 分别为AC ,BC ,CC 1的中点,BF ⊥B 1D .(1)证明:平面B 1DE ⊥平面BCC 1B 1;(2)求平面BC 1D 与平面1B DE 夹角的余弦值六、 题型六 投影面积法12.(2022·惠州第一次调研)如图,在四棱锥P -ABCD 中,已知//AB CD ,AD ⊥CD ,BC BP =,CD =2AB=4,△ADP 是等边三角形,E 为DP 的中点.(1)证明:AE ⊥平面PCD ;(2)若2,PA =求平面PBC 与平面PAD 夹角的余弦值13.(2022深圳高二期末)如图(1),在直角梯形ABCD 中,AB //CD ,AB ⊥BC ,且12,2BC CD AB ===取AB 的中点O ,连结OD ,并将△AOD 沿着OD 翻折,翻折后23AC =M ,N 分别是线段AD ,AB 的中点,如图(2).(1)求证:AC⊥OM.(2)求平面OMN与平面OBCD夹角的余弦值.专题3-1几何法求二面角,线面角立体几何空间向量求解过程,丧失了立体几何求解的乐趣,无形中也降低了学生的空间想象能力。
二面角的求法

二面角的几种求法1. 引言在高中空间几何的问题中,如何去求解两个平面的二面角的问题对很多同学来说十分棘手。
许多同学一遇到这种问题就比较头疼,特别是针对那些所给已知条件比较少的问题。
例如:在求二面角的问题中,许多都是没有给出直观的二面角的平面角,这就要求同学们会作辅助线,同时,一些问题中还需要很高的计算能力。
在历年的高考题中,很多都出现了求二面角的题目,如2010年的安徽卷(第18题)、2010年的浙江卷(第20题)、2010年的陕西卷(第18题)、2009年的山东卷(第18题)、2009 年的安徽卷(第18题)等等。
这就说明,二面角问题在高考中是一个热门的考点。
因此,研究求解二面角问题的方法,有很大的研究价值。
2. 二面角及二面角的平面角的概念先来叙述一下中学教材中二面角的概念以及二面角的平面角的概念。
([弓I])2.1二面角的概念从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,这两个半平面叫做二面角的面。
2.2二面角的平面角的概念如图1所示,在二面角I 的棱l上任意取一点O,以点O为垂足,在半平面和内分别作垂直于棱I的射线OA和OB,则射线OA和OB构成的AOB叫做二面角的平面角。
图13. 求解二面角问题的几个难点在求解空间几何问题的时候,经常会遇到求二面角的问题,求此类问题的难点具体体现在以下三个方面:3.1需要添加辅助线从二面角的定义来看,二面角的条件要求比较高,要求两条射线分别在两个半平面内且都垂直于这两个半平面的交线,在一般的空间图形中很难直接发现满足这样条件的角。
在这样的情况下只有借助添加辅助线等方法来解决问题,而添加辅助线是一个很难掌握的技巧。
同时新添加的辅助线的长度以及它们与其余各条直线、各个平面所成的角度,还需要经过进一步计算才能够得到。
这无形中给二面角的求解过程带来了很多困难。
3.2线面关系隐藏的深在有些问题中,没有直接给出直线所成的角度,只给出了空间图形中的部分线段长度。
立体几何中的向量方法及二面角的平面角求法总结

讲义:立体几何中的向量方法及二面角的平面角求法总结一、几种角的范围1、 _________________________________ 二面角平面角的范围:2、 _________________________________ 线面角的范围:3、 _________________________________ 直线倾斜角范围:4、异面直线夹角范围:_______________5、向量夹角范围:_________________二、立体几何中的向量方法1.三个重要向量(1)直线的方向向量:直线的方向向量是指和这条直线平行(或重合)的向量,一条直线的方向向量有 ______ .(2)平面的法向量:直线I丄平面a取直线I的方向向量,则这个向量叫做平面a的法向量.显然一个平面的法向量有 ____ ,它们是共线向量.(3)直线的正法向量:直线L:Ax+By+C=O的正法向量为n=(A,B).2.直线的方向向量与平面的法向量在确定直线和平面位置关系中的应用(1)直线l i的方向向量为u 1= (a i, b i, c i),直线l2的方向向量为比=(a2, b2, C2).女口果丨1 //丨2,那么U1 // U2? 5=右2? _____________________________ ;女口果丨1丄l2, 那么U1丄U2? U1 U2= 0? ________________⑵直线I的方向向量为u= (a1, b1, C1),平面a的法向量为n= (a2, b2, C2).若I // a 贝U u 丄n? u n = 0? _________________若I 丄a 贝U u // n? u = k n? _____________________(3)平面a的法向量为U1 = (a1, b1, C1),平面B的法向量为u2= (a2, b2, C2).若all B U1 / U2? U1 = k u2? (a1, b1, G)=_________ ;若a丄B 贝y U1 丄U2? U1 U2= 0? ____________________3.利用空间向量求空间角(1)求两条异面直线所成的角:设a, b分别是两异面直线I1, I2的方向向量,则(2) 求直线与平面所成的角:设直线I 的方向向量为a ,平面a 的法向量为n ,直线I 与平面a 所成的角为 0,则 si nA |cos 〈 a , n > |=(3) 求二面角的大小:(I )若 AB , CD 分别是二面角a — I — B 的两个半平面内与棱I 垂直的异面直线,则二面角的大 小就是向量AB , CD 的夹角(如图①所示).(H )设n i , n 2分别是二面角a — I — B 的两个半平面a, B 的法向量,贝U 向量n i 与n 2的夹角(或其补角)的大小就是二面角的大小(如图②③).4. 求点面距:平面a 外一点P 到平面a 的距离为:其中n 为平面a 的法向量,PQ 为平面a 的斜线,Q 为斜足 5. 平面法向量的求法设出平面的一个法向量n = (x , y , z),利用其与该平面内的两个不共线向量垂直,即数量积为 0, 列出方程组,两个方程,三个未知数,此时给其中一个变量恰当赋值,求出该方程组的一个非零 解,即得到这个法向量的坐标.注意,赋值不同得到法向量的坐标也不同, 法向量的坐标不唯一. 6. 射影面积公式:二面角的平面角为 a ,则cos a=7. 利用空间向量求角要注意的问题(1)异面直线所成的角、直线和平面所成的角、二面角都可以转化成空间向量的夹角来求.⑵空间向量的夹角与所求角的范围不一定相同,如两向量的夹角范围是[0, n,两异面直线所成的角的范围是o , n . (3)用平面的法向量求二面角时,二面角的大小与两平面法向量的夹角有相等和互补两种情况 .三、二面角的平面角的求法1、定义法: 从一条直线出发的两个半平面所组成的图形叫做二面角 ,这条直线叫做二面角的棱,这两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线d=② ③所成的角的大小就是二面角的平面角。
高考数学复习点拨 利用空间向量求二面角的两种策略

利用空间向量求二面角的两种策略策略一:先作出二面角的的平面角,再利用向量的内积公式求解:设∠AOB 是一二面角α-l -β的一个平面角,则向量OA →与OB →所成的角就是所求的二面角的大小.例1 在正方体ABCD-A 1B 1C 1D 1中,求平面A 1BD 与平面C 1BD 所成二面角.解法一:如图1,设AC 与BD 交于O ,连结A 1O ,C 1O ,因为A 1D=A 1B ,所以A 1O ⊥BD ,同理C 1D ⊥BD.∴∠A 1OC 1就是平面A 1BD 与平面C 1BD 所成二面角的平面角.设正方体棱长为1,则|AO →|=22,A 1O →=A 1A →+AO →,∴|A 1O →|2=(A 1A →+AO →)·(A 1A →+AO →)=|A 1A →|2+2A 1A →·AO →+|AO →|2=1+12+2×22×cos90︒=32,∴|A 1O →|=62,同理|C 1O →|=62,又OA 1→·OC 1→=(OA →+AA 1→)·(OC →+CC 1→)=OA →·OC →+OA →·CC 1→+AA 1→·OC →+AA 1→·CC 1→=﹣12+0+0+1=12,∴cos<OA 1→,OC 1→>=OA 1→·OC1→|A 1O →|·|C 1O →|=1262×62=13.故平面A 1BD 与平面C 1BD 所成二面角大小为arccos 13.解法二:设AC 与BD 交于E ,连结A 1E ,C 1E ,因为A 1D=A 1B ,所以A 1E ⊥BD , 同理C 1E ⊥BD.∴∠A 1EC 1就是平面A 1BD 与平面C 1BD 所成二面角的平面角. 建立如图2所示的空间直角坐标系D-xyz ,设正方体的棱长为2,则A 1(2,0,2),C 1(0,2,2),E(1,1,0),∴EA 1→=(1,-1,2),EC 1→=(-1,1,2), ∴EA 1→·EC 1→=1×(-1)+(-1)×1+2×2=2,|EA 1→|=|EC 1→|=6,∴cos<EA 1→,EC 1→>=EA 1→·EC 1→|EA 1→|·|EC 1→|=26×6=13.故平面A 1BD 与平面C 1BD 所成二面角大小为arccos 13.策略二:利用平面的法向量求解:设n 1→是平面α的法向量,n 2→是平面β的法向量.①若两个平面的二面角如图3所示的示意图,则n 1→与n 2→之间的夹角就是欲求的二面角;②若两个平面的二面角如图4所示的示意图,设n 1→与n 2→之间的夹角为θ.则两个平面的二面角为π﹣θ.图3图4图1图2例2如图5,四边形ABCD 是直角梯形,∠ABC=90︒,SA ⊥平面ABCD ,SA=AB=BC=1,AD=12,求平面SCD 与平面SAB 所成二面角的大小.解法一:平面SAB 的法向量是→A D ,平面SCD 的法向量可设为n →=λ→AD +μ→AB +→AS . ∵SA ⊥平面ABCD ,∴→AS ·→AB =0,→AS ·→DA =0,→AS ·→B C=0, 又AB ⊥AD ,AB ⊥BC ,∴→AB ·→AD =0,→AB ·→B C=0 由n →·→DC =(λ→AD +μ→AB +→AS )·(→DA +→AB +→B C)=λ→AD ·→DA +λ→AD ·→B C+μ→AB ·→AB =﹣14λ+12λ+μ=14λ+μ=0,又n →·→DS =(λ→AD +μ→AB +→AS )·(→AS ﹣→AD )=→AS ·→AS ﹣λ→AD ·→AD =1﹣14λ=0,∴λ=4,μ=﹣1,∴n →=4→AD ﹣→AB +→AS ,∴→AD ·n →=→AD ·(4→AD -→AB +→AS )=4|→AD |2=1 ∴|n →|2=(4→AD ﹣→AB +→AS )2=16|→AD |2+|→AB |2+|→AS |2=6,∴|n →|= 6.设θ表示平面SCD 与平面SAB 所成二面角,则cos θ=→AD ·n→|→AD |·|n →|=112·6=63.∴θ=arccos63. 故平面SCD 与平面SAB 所成二面角的大小为arccos63. 解法二:建立如图6所示的空间直角坐标系A ﹣xyz ,则A(0,0,0),D(12,0,0),C(1,1,0),S(0,0,1),由条件易知,AD →是面SAB 的法向量,且AD →=(12,0,0),设面SCD 的法向量为n →=(x ,y ,z),∵SD →=(12,0,﹣1),DC →=(12,1,0),又n →·SD →=0,n →·DC →=0,∴12x ﹣z=0。
向量法求空间角、距离和二面角

高考对空间向量的考查是以立体几何为载体,利用空间向量求有向线段的长度,求两条有向线段的夹角(或其余弦、正弦、正切),二面角、点到平面的距离、异面直线的距离、证明线线、线面、面面垂直等.下面是今年广东高考数学及广州一模,体现了高考对空间向量的考查要求.
证明:设 为公垂线段,取 (如图1所示),则
设直线 所成的角为 ,显然
1.4.直线 与平面 所成的角
在 上取定 ,求平面 的法向量 (如图2所示),再求 ,则 为所求的角.
1.5.二面角
方法一:构造二面角 的两个半平面 的法向量 (都取向上的方向,如图3所示),则
1若二面角 是“钝角型”的如图3甲所示,那么其大小等于两法向量 的夹角的补角,即 (例如2004年高考数学广东卷第18题第(1)问).
[例2](2004年全国普通高等学校招生全国统一考试数学广东卷第18题)
如右图8,在长方体ABCD—A1B1C1D1中,已知AB=4, AD=3,AA1= 2. E、F分别是A来自、BC上的点,且EB=FB=1.
(1)求二面角C—DE—C1的正切值;
(2)求直线EC1与FD1所成的角的余弦值.
解题分析:本题主要考查了二面角、异面直线所成的角等知识和空间想象能力、思维能力、运算能力.高考试卷给出的参考答案分别用了传统方法及向量法.在传统解法中,运用三垂线定理作出二面角的平面角并正明,通过延长和平移线段作出异面直线所成的角,进而通过解直角三角形和斜三角形解决问题.在用向量法的解答上,选择 为空间直角坐标系的原点, 分别为 轴, 轴, 轴的正向,这不是右手直角坐标系,虽然与右手直角坐标系没有本质上的区别,但教科书中所建立及提倡的是右手直角坐标系,所以考生习惯用右手直角坐标系. 用向量法解决第(1)问时只是用了本文所提到的“1.5.二面角”之“方法一”.
高考数学专题:向量求二面角(含答案)

高考数学专题:向量求二面角向量法求二面角大小的两种方法(1)分别求出二面角的两个面所在平面的法向量,然后通过两个平面的法向量的夹角得到二面角的大小,但要注意结合实际图形判断所求角的大小.(2)分别在二面角的两个半平面内找到与棱垂直且以垂足为起点的两个向量,则这两个向量的夹角的大小就是二面角的大小.1、如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=π3,M为BC上一点,且BM=12,MP⊥AP.(1)求PO的长;(2)求二面角A-PM-C的正弦值.2、如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F 分别为AC,DC的中点.(1)求证:EF⊥BC;(2)求二面角E-BF-C的正弦值.3、如图所示,在多面体ABCD-A1B1C1D1中,上、下两个底面A1B1C1D1和ABCD互相平行,且都是正方形,DD1⊥底面ABCD,AB=2A1B1=2DD1=2a.(1)求异面直线AB1与DD1所成角的余弦值;(2)已知F是AD的中点,求证:FB1⊥平面BCC1B1;(3)在(2)的条件下,求二面角F-CC1-B的余弦值.4、如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.(1)证明:平面ABEF⊥平面EFDC;(2)求二面角E-BC-A的余弦值.5、如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.(1)求证:EG∥平面ADF;(2)求二面角O-EF-C的正弦值;(3)设H为线段AF上的点,且AH=23HF,求直线BH和平面CEF所成角的正弦值6、如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=π2,PA=AD=2,AB=BC=1.(1)求平面PAB与平面PCD所成二面角的余弦值;(2)点Q是线段BP上的动点,当直线CQ与DP所成的角最小时,求线段BQ的长.7、如图所示,在多面体A1B1D1-DCBA中,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于F.(1)证明:EF∥B1C;(2)求二面角E-A1D-B1的余弦值.8、如图,三棱锥P-ABC中,PC⊥平面ABC,PC=3,∠ACB=π2,D,E分别为线段AB,BC上的点,且CD=DE=2,CE=2EB=2.(1)证明:DE⊥平面PCD;(2)求二面角A-PD-C的余弦值.答案:1、解:(1)如图,连接AC,BD,因为ABCD为菱形,则AC∩BD=O,且AC⊥BD.以O为坐标原点,OA →,OB →,OP →的方向分别为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系O -xyz .因为∠BAD =π3,所以OA =AB ·cos π6=3,OB =AB ·sin π6=1,所以O (0,0,0),A (3,0,0),B (0,1,0),C (-3,0,0),OB →=(0,1,0),BC →=(-3,-1,0).由BM =12,BC =2知, BM→=14BC →=⎝ ⎛⎭⎪⎫-34,-14,0, 从而OM→=OB →+BM →=⎝ ⎛⎭⎪⎫-34,34,0, 即M ⎝ ⎛⎭⎪⎫-34,34,0.设P (0,0,a ),a >0,则AP→=(-3,0,a ),MP →=⎝ ⎛⎭⎪⎫34,-34,a . 因为MP ⊥AP ,故MP →·AP→=0,即-34+a 2=0,所以a =32或a =-32(舍去), 即PO =32.(2)由(1)知,AP →=⎝ ⎛⎭⎪⎫-3,0,32,MP →=⎝ ⎛⎭⎪⎫34,-34,32,CP →=⎝ ⎛⎭⎪⎫3,0,32. 设平面APM 的法向量为n 1=(x 1,y 1,z 1),平面PMC 的法向量为n 2=(x 2,y 2,z 2),由n 1·AP →=0,n 1·MP →=0, 得⎩⎪⎨⎪⎧-3x 1+32z 1=0,34x 1-34y 1+32z 1=0,故可取n 1=⎝ ⎛⎭⎪⎫1,533,2. 由n 2·MP →=0,n 2·CP →=0, 得⎩⎪⎨⎪⎧34x 2-34y 2+32z 2=0,3x 2+32z 2=0,故可取n 2=(1,-3,-2). 从而法向量n 1,n 2的夹角的余弦值为 cos 〈n 1,n 2〉=n 1·n 2|n 1|·|n 2|=-155, sin 〈n 1,n 2〉=1-⎝⎛⎭⎪⎫-1552=105, 故所求二面角A -PM -C 的正弦值为105.2、(1)证明:由题意,以B 为坐标原点,在平面DBC 内过B 作垂直BC 的直线为x 轴,BC 所在直线为y 轴,在平面ABC 内过B 作垂直BC 的直线为z 轴,建立如图所示空间直角坐标系.易得B (0,0,0),A (0,-1,3),D (3,-1,0),C (0,2,0),因而E ⎝ ⎛⎭⎪⎫0,12,32,F ⎝ ⎛⎭⎪⎫32,12,0,所以EF →=⎝ ⎛⎭⎪⎫32,0,-32,BC →=(0,2,0),因此EF →·BC→=0. 从而EF →⊥BC →,所以EF ⊥BC .(2)平面BFC 的一个法向量为n 1=(0,0,1). 设平面BEF 的法向量为n 2=(x ,y ,z ). 又BF →=⎝ ⎛⎭⎪⎫32,12,0,BE →=⎝ ⎛⎭⎪⎫0,12,32,由⎩⎪⎨⎪⎧n 2·BF →=0,n 2·BE →=0得其中一个n 2=(1,-3,1).设二面角E -BF -C 大小为θ,且由题意知θ为锐角, 则cos θ=|cos 〈n 1,n 2〉| =⎪⎪⎪⎪⎪⎪n 1·n 2|n 1||n 2|=15. 因此sin θ=25=255,即所求二面角的正弦值为255.3、.解:以D 为坐标原点,以DA ,DC ,DD 1所在直线分别为x 轴、y 轴、z 轴建立如图所示的空间直角坐标系,则A (2a ,0,0),B (2a ,2a ,0),C (0,2a ,0),D 1(0,0,a ),F (a ,0,0),B 1(a ,a ,a ),C 1(0,a ,a ).(1)因为AB 1→=(-a ,a ,a ),DD 1→=(0,0,a ), 所以|cos 〈AB 1→,DD 1→〉|=⎪⎪⎪⎪⎪⎪⎪⎪AB 1→·DD 1→|AB 1→||DD 1→|=33,所以异面直线AB 1与DD 1所成角的余弦值为33. (2)证明:因为BB 1→=(-a ,-a ,a ),BC →=(-2a ,0,0),FB 1→=(0,a ,a ), 所以⎩⎪⎨⎪⎧FB 1→·BB 1→=0,FB 1→·BC →=0,所以FB 1⊥BB 1,FB 1⊥BC . 因为BB 1∩BC =B , 所以FB 1⊥平面BCC 1B 1.(3)由(2)知,FB 1→为平面BCC 1B 1的一个法向量. 设n =(x 1,y 1,z 1)为平面FCC 1的法向量, 因为CC 1→=(0,-a ,a ),FC →=(-a ,2a ,0), 所以⎩⎪⎨⎪⎧n ·CC 1→=0,n ·FC →=0,即⎩⎨⎧-ay 1+az 1=0,-ax 1+2ay 1=0.令y 1=1,则n =(2,1,1),所以||cos 〈FB 1→,n 〉=⎪⎪⎪⎪⎪⎪⎪⎪FB 1→·n |FB 1→||n |=33,因为二面角F -CC 1-B 为锐角, 所以二面角F -CC 1-B 的余弦值为33.4、解:(1)证明:由已知可得AF ⊥DF ,AF ⊥FE ,所以AF ⊥平面EFDC .又AF ⊂平面ABEF ,故平面ABEF ⊥平面EFDC . (2)如图,过D 作DG ⊥EF ,垂足为G , 由(1)知DG ⊥平面ABEF .以G 为坐标原点,GF →的方向为x 轴正方向,|GF →|为单位长,建立如图所示的空间直角坐标系G -xyz . 由(1)知∠DFE 为二面角D -AF -E 的平面角,故∠DFE =60°, 则|DF |=2,|DG |=3,可得A (1,4,0),B (-3,4,0),E (-3,0,0),D (0,0,3). 由已知,AB ∥EF , 所以AB ∥平面EFDC .又平面ABCD ∩平面EFDC =CD , 故AB ∥CD ,CD ∥EF .由BE ∥AF ,可得BE ⊥平面EFDC ,所以∠CEF 为二面角C -BE -F 的平面角,∠CEF =60°,从而可得C (-2,0,3).所以EC→=(1,0,3),EB →=(0,4,0),AC →=(-3,-4,3),AB →=(-4,0,0).设n =(x ,y ,z )是平面BCE 的法向量,则 ⎩⎪⎨⎪⎧n ·EC →=0,n ·EB →=0,即⎩⎨⎧x +3z =0,4y =0. 所以可取n =(3,0,-3). 设m 是平面ABCD 的法向量, 则⎩⎪⎨⎪⎧m ·AC →=0,m ·AB →=0.同理可取m =(0,3,4), 则cos 〈n ,m 〉=n·m |n ||m |=-21919.故二面角E -BC -A 的余弦值为-21919.5、解:依题意,OF ⊥平面ABCD ,如图,以O 为原点,分别以AD →,BA →,OF →的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系,依题意可得O (0,0,0),A (-1,1,0),B (-1,-1,0),C (1,-1,0),D (1,1,0),E (-1,-1,2),F (0,0,2),G (-1,0,0).(1)证明:依题意,AD→=(2,0,0),AF →=(1,-1,2). 设n 1=(x ,y ,z )为平面ADF 的法向量,则⎩⎪⎨⎪⎧n 1·AD →=0,n 1·AF →=0,即⎩⎨⎧2x =0,x -y +2z =0.不妨设z =1,可得n 1=(0,2,1).又EG →=(0,1,-2),所以EG →·n 1=0, 又因为直线EG ⊄平面ADF , 所以EG ∥平面ADF .(2)易证,OA→=(-1,1,0)为平面OEF 的一个法向量. 依题意,EF→=(1,1,0),CF →=(-1,1,2).设n 2=(x ,y ,z )为平面CEF 的法向量,则⎩⎪⎨⎪⎧n 2·EF →=0,n 2·CF →=0,即⎩⎨⎧x +y =0,-x +y +2z =0.不妨设x =1,可得n 2=(1,-1,1).因此cos 〈OA →,n 2〉=OA →·n 2|OA →||n 2|=-63,于是sin 〈OA →,n 2〉=33.所以,二面角O -EF -C 的正弦值为33.(3)由AH =23HF ,得AH =25AF .因为AF→=(1,-1,2),所以AH →=25AF →=⎝ ⎛⎭⎪⎫25,-25,45,进而有H ⎝ ⎛⎭⎪⎫-35,35,45,从而BH →=⎝ ⎛⎭⎪⎫25,85,45,因此cos 〈BH →,n 2〉=BH →·n 2|BH →||n 2|=-721.所以,直线BH 和平面CEF 所成角的正弦值为721.6、解:以{AB →,AD →,AP →}为正交基底建立如图所示的空间直角坐标系A -xyz ,则各点的坐标为B (1,0,0),C (1,1,0),D (0,2,0),P (0,0,2). (1)因为AD ⊥平面PAB ,所以AD→是平面PAB 的一个法向量,AD →=(0,2,0).因为PC→=(1,1,-2),PD →=(0,2,-2). 设平面PCD 的法向量为m =(x ,y ,z ), 则m ·PC →=0,m ·PD →=0, 即⎩⎨⎧x +y -2z =0,2y -2z =0. 令y =1,解得z =1,x =1.所以m =(1,1,1)是平面PCD 的一个法向量. 从而cos 〈AD →,m 〉=AD →·m |AD →||m |=33, 所以平面PAB 与平面PCD 所成二面角的余弦值为33. (2)因为BP→=(-1,0,2),设BQ →=λBP →=(-λ,0,2λ)(0≤λ≤1),又CB→=(0,-1,0),则CQ →=CB →+BQ →= (-λ,-1,2λ),又DP→=(0,-2,2),从而cos 〈CQ →,DP →〉=CQ →·DP →|CQ →||DP →|=1+2λ10λ2+2.设1+2λ=t ,t ∈[1,3],则cos 2〈CQ →,DP →〉=2t 25t 2-10t +9=29⎝ ⎛⎭⎪⎫1t -592+209≤910.当且仅当t =95,即λ=25时, |cos 〈CQ→,DP →〉|的最大值为31010. 因为y =cos x 在⎝ ⎛⎭⎪⎫0,π2上是减函数,所以此时直线CQ 与DP 所成角取得最小值. 又因为BP =12+22=5, 所以BQ =25BP =255.7、解:(1)证明:由正方形的性质可知A 1B 1∥AB ∥DC ,且A 1B 1=AB =DC ,所以四边形A 1B 1CD 为平行四边形,从而B 1C ∥A 1D .又A 1D ⊂平面A 1DE ,B 1C ⊄平面A 1DE ,于是B 1C ∥平面A 1DE . 又B 1C ⊂平面B 1CD 1,平面A 1DE ∩平面B 1CD 1=EF ,所以EF ∥B 1C .(2)因为四边形AA 1B 1B ,ADD 1A 1,ABCD 均为正方形,所以AA 1⊥AB ,AA 1⊥AD ,AB ⊥AD 且AA 1=AB =AD ,以A 为原点,分别以AB →,AD →,AA 1→为x 轴,y 轴和z 轴单位正向量建立如图所示的空间直角坐标系,可得点的坐标A (0,0,0),B (1,0,0),D (0,1,0),A 1(0,0,1),B 1(1,0,1),D 1(0,1,1),而E 点为B 1D 1的中点,所以E 点的坐标为(0.5,0.5,1).设面A 1DE 的法向量为n 1=(r 1,s 1,t 1),而该面上向量A 1E →=(0.5,0.5,0),A 1D →=(0,1,-1),由n 1⊥A 1E →,n 1⊥A 1D →得r 1,s 1,t 1应满足方程组⎩⎨⎧0.5r 1+0.5s 1=0,s 1-t 1=0,因为(-1,1,1)为其一组解,所以可取n 1=(-1,1,1).设面A 1B 1CD 的法向量为n 2=(r 2,s 2,t 2),而该面上向量A 1B 1→=(1,0,0),A 1D →=(0,1,-1),由此同理可得n 2=(0,1,1),所以结合图形知二面角E -A 1D -B 1的余弦值为|n 1·n 2||n 1|·|n 2|=23×2=63. 8、解:(1)证明:由PC ⊥平面ABC ,DE ⊂平面ABC ,得PC ⊥DE .由CE =2,CD =DE =2得△CDE 为等腰直角三角形,故CD ⊥DE .又PC ∩CD =C ,所以DE ⊥平面PCD .(2)由(1)知,△CDE 为等腰直角三角形,∠DCE =π4.如图,过D 作DF 垂直CE 于F ,易知DF =FC =FE =1.又EB =1,故FB =2.由∠ACB =π2得DF ∥AC ,DF AC =FB BC =23,故AC =32DF =32.如图,以C 为坐标原点,分别以CA→,CB →,CP →的方向为x 轴,y 轴,z 轴的正方向建立空间直角坐标系,则C (0,0,0),P (0,0,3),A ⎝ ⎛⎭⎪⎫32,0,0,E (0,2,0),D (1,1,0),ED →=(1,-1,0),DP →=(-1,-1,3),DA →=⎝ ⎛⎭⎪⎫12,-1,0. 设平面PAD 的法向量为n 1=(x 1,y 1,z 1),由n 1·DP →=0,n 1·DA →=0,得⎩⎪⎨⎪⎧-x 1-y 1+3z 1=0,12x 1-y 1=0, 故可取n 1=(2,1,1).由(1)可知,DE ⊥平面PCD ,故平面PCD 的法向量n 2可取为ED→, 即n 2=(1,-1,0).从而法向量n 1,n 2的夹角的余弦值为cos 〈n 1,n 2〉=n 1·n 2|n 1|·|n 2|=36, 故二面角A -PD -C 的余弦值为36.。
人教版A版高中数学选修2-1《利用空间向量法求二面角》

平面的法向量与二面角的关系
(Ⅱ)若PD=AD,求二面角A-PB-C的余弦值。
解:如图,以D为坐标原点,建立空间直角坐标系D-xyz, 建系
设AD=1,则
z
…1分
找量:
点的P坐标
设平nn 面APBBPA==B00的即法向x31y量1 为3z1y1 n00可(x取1, yn1
0,即
Байду номын сангаас
3x2 y2 =0,
m B1C1 0, 3x2 z2 0.
取m (1, 3, 3).
|cos n , m ||n m| 1 . nm 7
计算: 法向量、夹角
…2分
二面角A A1B1 C1的平面角为锐角,
二面角A
A1B1
C1的余弦值为
2、数学思想:化归与转化的思想 数形结合思想 方程的思想
七、课堂作业
OB1 OB+BB1 OB+AA1
x
z y
(Ⅱ)设二面角 D -A E-C 为 60°,A P=1,A D = 3 ,求三棱锥 E -A C D 的体积.
解(I)连接BD交AC于点O,连结EO。
ABCD为矩形,O为BD的中点。
又E为PD的中点, EO∥PB。
且EO 面AEC,PB 面AEC,
PB//面AEC,
O …4分
(Ⅱ)设二面角 D -A E-C 为 60°,A P=1,A D = 3 ,求三棱锥 E -A C D 的体积. 解: PA 面ABCD,且ABCD为矩形
1 7
.
④作答: 观察图形、定值
…1分
变式练习2
如图所示,四棱锥P-ABCD中,底面ABCD为正方 形,PD⊥平面ABCD,PD=AB=2,E,F,G分别 为PC,PD,BC的中点. (1)求证:PA⊥EF. (2)求二面角D-FG-E的余弦值.
用空间向量求二面角时角大小的确定

概 念 的 本 质 去 解 决 以“ 式 ” 现 的 具 体 问题 。 如 “ 算 ( 5 变 出 例 计 一— 2 )一 a5 ” 由于 学 生 只看 到平 方 差 公 式 为 一 字 母 或 一 具 体 a (2 + ) , 数 字 而 不 能 从 本 质 上 去 理 解 公 式 , 缩 小 了公 式 的外 延 , 能 故 不 解出此题。 概 念 的 僵 化 反 映 了思 维 的刻 板 . 即所 谓 “ 识 学 得 太 死 ” 知 。 为 克 服 概 念 的 僵 化 。有 必 要 从 初 一 到 高 三 的 教 学 中有 意 识 地 引 导启 发 学 生 注 意 表 示 概 念 的式 或 图 .又要 引 导 他 们 从 概 念 的 本 质 属 性 去认 识 . 察 各 种 “ 观 变式 ” 的情 形 。 别 注 意 到字 母 特 既 可 表 示 数 又 可 表 示 式 。 选 择 一 些 灵 活 应 用 概 念 的 练 习题 , 要 使学生 能正确 、 面地理解和应用概念 。 全
用 空 间 向 量 求 二 面 角 时 角 大 小 的 确 定
李 玉玲
( 苏省 新 海 高 级 中学 , 苏 连 云 港 江 江 在 立 体 几 何 中 。 们 经 常 利 用 空 间 向量 的 方 法 来 求 两 个 我 平 面所成的二面角的大小 。 即在 二 面 角 0 l1 。 平 面仅的法 【一 中 设 一 3 向 量 , 面 1 法 向量 n( ) 0 则 二 面 角 仪 l B 平 3 的 .m, = , 一 一— 的平 面 角
ny 密 1, …. - D ,
令X l则 l I l , n (,11 l , y -,=  ̄q 1 , = = Z 1O = - )
立体几何-利用空间向量求二面角的平面角

利用空间向量求二面角的平面角2 解:过D 作DF BC 于F ,过D 作DEFED 为二面角B AC D 的平面角, 又AB 平面BCD , AC 于E ,连结EF ,则AC 垂直于平面DEF ,• AB DF , AB CD , • DF 平面ABC ,• DF EF又••• AB CD , BD CD , • CD 平面 ABD , • CD AD ,设BD a ,贝U AB BC 2a , 在Rt BCD 中,S BCD 1-BC DF 21-BD CD , • DF 2.3 a1. 二面角的概念:二面角的定义•从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,每个半平面叫做 二面角的面.若棱为I ,两个面分别为 ,的二面角记为 丨2. 二面角的平面角:(1) 过二面角的棱上的一点 0分别在两个半平面内作棱的两条垂线 OA,OB ,则 AOB 叫做二面角 I 的平面角+(2)一个平面垂直于二面角 I 的棱I ,且与两半平面交线分别为 OA,OB, 0为垂足,则 AOB也是 I 的平面角+说明:(1) 二面角的平面角范围是 [0°,180°];(2) 二面角的平面角为直角时,则称为直二面角,组成直二面角的两个平面互相垂直 引导:请学生归纳已学过的求二面角的大小的方法,教师作必要的补充与引导•明确本节课的课题. 二. 求二面角的平面角:【回顾复习定义法求二面角的平面角】例 1:在棱长为1的正方体AC !中,求平面C^D 与底面ABCD 所成二面可以求得: sin COC 16,所以,平面GBD 与底面ABCD 所成3二面角C 1 BDC 的平面角的正弦值大小为63【回顾复习用三垂线法求二面角的平面角】例 2.如图,AB 平面BCD , BD CD ,若AB BC 2BD ,求.面角B AC D 的正弦值•分析:要求二面角的正弦值,首先要找到二面角的平面角角C 1 BD C 的平面角正弦值大小. 解:过C 1作C 1O BD 于点O ,•••正方体 AC 1 ,••• CC 1 平面 ABCD , 二 COC 1为平面GBD 与平面ABCD 所成二面角C 1G BD C 的平面角,C所以,二面角B AC D 的正弦值为一10 .5通过观察探究利用法向量解决: 例1 :解:建立空间直角坐标系得:DC i (0,1,1),DB (1,1,0),DC (0,1,0)设平面 GBD 的法向量 n-i(x 1, y 1, Z |),平面 CBD 的法向量 n 2 (x 2,y 2,z 2),可得 n (1, 1,1), n 2 (0,0,1),口 (0,0,1) , n 2所以,二面角B AC D 的正弦值为一105三. 归纳小结:本节课回忆巩固了求解二面角的一些方法,并且通过类比用空间向量知识求解二面角,我们感受到空 间向量的巧妙之处,但要让同学们认识到法向量之间的夹角与二面角的平面角的异同之处。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考点三用空间向量求二面角
【例3】(2019·北京海淀区模拟)如图1,在高为6的等腰梯形ABCD中,AB∥CD,且CD=6,AB=12,将它沿对称轴OO1折起,使平面ADO1O⊥平面BCO1O,如图2,点P为BC的中点,点E在线段AB上(不同于A,B两点),连接OE并延长至点Q,使AQ∥OB.
(1)(一题多解)证明:OD⊥平面P AQ;
(2)若BE=2AE,求二面角C-BQ-A的余弦值.
(1)证明法一取OO1的中点F,连接AF,PF,如图所示.
∵P为BC的中点,∴PF∥OB,
∵AQ∥OB,∴PF∥AQ,
∴P,F,A,Q四点共面.
由题图1可知OB⊥OO1,
∵平面ADO1O⊥平面BCO1O,且平面ADO1O∩平面BCO1O=OO1,OB⊂平面BCO1O,
∴OB⊥平面ADO1O,
∴PF⊥平面ADO1O,
又OD⊂平面ADO1O,∴PF⊥OD.
由题意知,AO=OO1,OF=O1D,∠AOF=∠OO1D,
∴△AOF≌△OO1D,
∴∠F AO =∠DOO 1,
∴∠F AO +∠AOD =∠DOO 1+∠AOD =90°,∴AF ⊥OD .
∵AF ∩PF =F ,且AF ⊂平面P AQ ,PF ⊂平面P AQ ,
∴OD ⊥平面P AQ .
法二 由题设知OA ,OB ,OO 1两两垂直,∴以O 为坐标原点,OA ,OB ,OO 1所在直线分别为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系,
设AQ 的长为m ,则O (0,0,0),A (6,0,0),B (0,6,0),C (0,3,6),D (3,0,6),Q (6,m ,0).
∵点P 为BC 的中点,∴P ⎝ ⎛⎭
⎪⎫0,92,3, ∴OD →=(3,0,6),AQ →=(0,m ,0),PQ →=⎝ ⎛⎭
⎪⎫6,m -92,-3. ∵OD
→·AQ →=0,OD →·PQ →=0, ∴OD
→⊥AQ →,OD →⊥PQ →,又AQ →与PQ →不共线, ∴OD ⊥平面P AQ .
(2)解 ∵BE =2AE ,AQ ∥OB ,∴AQ =12OB =3,
则Q (6,3,0),∴QB
→=(-6,3,0),BC →=(0,-3,6). 设平面CBQ 的法向量为n 1=(x ,y ,z ),
由⎩⎪⎨⎪⎧n 1·QB →=0,n 1·BC →=0,得⎩
⎨⎧-6x +3y =0,-3y +6z =0, 令z =1,则y =2,x =1,n 1=(1,2,1).
易得平面ABQ 的一个法向量为n 2=(0,0,1).
设二面角C -BQ -A 的大小为θ,由图可知,θ为锐角,
则cos θ=⎪⎪⎪⎪⎪⎪n 1·n 2|n 1|·|n 2|=66,。
