利用空间向量知识求空间中的二面角ppt课件
合集下载
高中数学选修2-1精品课件：§3.2 第3课时 用空间向量解决空间角
所成的角
＝
|a·b| |a||b|
范围 0，π2
直线与平面 所成的角
设直线l与平面α所成的角为θ，l的方向向量为a， 平面α的法向量为n，则sin θ＝_|_co_s_〈__a_，__n_〉__|_
＝
|a·n| |a||n|
0，π2
二ห้องสมุดไป่ตู้角
设二面角α－l－β为θ，平面α，β的法向量分别 为n1，n2，则|cos θ|＝ |cos〈n1，n2〉| ＝ |n1·n2|
|n1||n2|
[0，π]
思考辨析 判断正误
SIKAOBIANXIPANDUANZHENGWU
1.两条异面直线所成的角与两直线的方向向量所成的角相等.( × ) 2.直线与平面所成的角等于直线与该平面法向量夹角的余角.( × ) 3.二面角的大小就是该二面角两个面的法向量的夹角.( × ) 4.若二面角两个面的法向量的夹角为120°，则该二面角的大小等于60°或 120°.( √ )
(3)求平面的法向量n； →
(4)设线面角为 θ，则 sin θ＝|P→A·n|. |PA||n|
跟 踪 训 练 2 如 图 所 示 ， 三 棱 柱 ABC － A1B1C1 中 ， CA ＝ CB ， AB ＝ AA1 ， ∠BAA1＝60°. (1)证明：AB⊥A1C；
证明 取AB的中点O，连接OC，OA1，A1B. 因为CA＝CB，所以OC⊥AB. 由于AB＝AA1，∠BAA1＝60°， 故△AA1B为等边三角形，所以OA1⊥AB. 因为OC∩OA1＝O，所以AB⊥平面OA1C. 又A1C⊂平面OA1C，故AB⊥A1C.
(2)若平面ABC⊥平面AA1B1B，AB＝CB，求直线A1C与平面BB1C1C所成角的正 弦值.
二面角法向量求法
空间角的大小与两条直线的方向有关，与直线 的长度无关。
二面角的表示方法
二面角是由两个半平面所组成 的图形，其大小由两个半平面
的夹角决定。
二面角可以用角度制或弧度制 来表示，与平面角和空间角类
似。
二面角的大小与两个半平面的 方向有关，与半平面的大小无 关。
在求解二面角的大小时，通常 需要先找到两个半平面的法向 量，然后计算两个法向量之间 的夹角即可得到二面角的大小 。
二面角法向量求法
汇报人：XX 2024-01-23
• 引言 • 二面角的表示方法 • 法向量的求解方法 • 二面角法向量的性质 • 二面角法向量的应用 • 总结与展望
01
引言
二面角的定义
二面角是由两个半平面所组成的 图形，其大小由这两个半平面的
夹角决定。
二面角的大小范围在0°到180°之 间，当两个半平面重合时，二面 角为0°；当两个半平面形成一条
面积射影定理
根据面积射影定理，二面角的余弦值等于两个半 平面在棱上的投影面积之比。因此，可以通过求 出两个半平面在棱上的投影面积，然后利用面积 射影定理求出二面角的大小。
三垂线定理及其逆定理法
利用三垂线定理或其逆定理，可以构造出与二面 角的棱垂直的线段，进而通过解三角形求出二面 角的大小。
空间向量夹角公式
03
法向量的求解方法
平面法向量的求解方法
直接法
如果平面上的一个向量 已知，则该向量即为平 面的法向量。
待定系数法
设平面的法向量为 n=(x,y,z)，根据平面的 方程可以列出关于x,y,z 的方程组，通过求解方 程组得到法向量。
向量积法
如果平面上有两个不共 线的向量a和b，则平面 的法向量n可以通过计 算向量a和b的向量积得 到，即n=a×b。
二面角的表示方法
二面角是由两个半平面所组成 的图形，其大小由两个半平面
的夹角决定。
二面角可以用角度制或弧度制 来表示，与平面角和空间角类
似。
二面角的大小与两个半平面的 方向有关，与半平面的大小无 关。
在求解二面角的大小时，通常 需要先找到两个半平面的法向 量，然后计算两个法向量之间 的夹角即可得到二面角的大小 。
二面角法向量求法
汇报人：XX 2024-01-23
• 引言 • 二面角的表示方法 • 法向量的求解方法 • 二面角法向量的性质 • 二面角法向量的应用 • 总结与展望
01
引言
二面角的定义
二面角是由两个半平面所组成的 图形，其大小由这两个半平面的
夹角决定。
二面角的大小范围在0°到180°之 间，当两个半平面重合时，二面 角为0°；当两个半平面形成一条
面积射影定理
根据面积射影定理，二面角的余弦值等于两个半 平面在棱上的投影面积之比。因此，可以通过求 出两个半平面在棱上的投影面积，然后利用面积 射影定理求出二面角的大小。
三垂线定理及其逆定理法
利用三垂线定理或其逆定理，可以构造出与二面 角的棱垂直的线段，进而通过解三角形求出二面 角的大小。
空间向量夹角公式
03
法向量的求解方法
平面法向量的求解方法
直接法
如果平面上的一个向量 已知，则该向量即为平 面的法向量。
待定系数法
设平面的法向量为 n=(x,y,z)，根据平面的 方程可以列出关于x,y,z 的方程组，通过求解方 程组得到法向量。
向量积法
如果平面上有两个不共 线的向量a和b，则平面 的法向量n可以通过计 算向量a和b的向量积得 到，即n=a×b。
空间向量应用-二面角
04
二面角的应用
在几何学中的应用
向量投影
在求解向量的投影时，可以利用二面 角的概念，通过计算向量在某一平面 上的投影长度，来得到该向量与该平 面的夹角。
向量夹角
二面角的概念可以用于计算两个向量 的夹角，通过比较两个向量的夹角与 二面角的夹角，可以判断两个向量的 方向关系。
在物理学中的应用
力的合成与分解
建筑设计
在建筑设计中，利用二面角的概念可以确定建筑物的位置、方向和高度等信息， 以保证建筑物的安全和稳定性。
05
空间向量与二面角的关系
向量与二面角的关联
向量是既有大小又有方向的量，其大 小和方向可以用来表示二面角的大小 和方向。
二面角的大小和方向可以通过两个向 量的夹角来描述，这个夹角就是二面 角的平面角。
二面角的向量定义
总结词
二面角的向量定义是通过向量的投影 和叉积来定义的，它是一个标量值， 其大小等于两个向量的叉积的绝对值 再除以两向量的模的乘积。
详细描述
二面角的向量定义是通过向量的投影和叉积来 描述的。设两非零向量a和b分别属于两个半平 面，那么二面角θ的大小可以用公式 ∣a×b∣/∣a∣∣b∣表示，其中a×b表示向量a和b 的叉积，∣a∣和∣b∣分别表示向量a和b的模。这 个标量值的大小就等于二面角θ的大小。
二面角的性质
总结词
二面角具有一些重要的性质，如二面角的取值范围是[0,π]，二面角的大小与观察方向有关，以及二面角的补角等 于其平面角的补角等。
详细描述
首先，二面角的取值范围是[0,π]，这是由其几何定义直接得出的。其次，二面角的大小与观察方向有关，即观察 方向的不同可能导致二面角的大小发生变化。最后，二面角的补角等于其平面角的补角，这是由向量的性质得出 的。
用空间向量求空间角课件(共22张PPT)
向量的加法与数乘
向量的加法满足平行四边形法则或三 角形法则，即$vec{a} + vec{b} = vec{b} + vec{a}$。
数乘是指实数与向量的乘积，满足分 配律，即$k(vec{a} + vec{b}) = kvec{a} + kvec{b}$。
向量的数量积
向量的数量积定义为$vec{a} cdot vec{b} = left| vec{a} right| times left| vec{b} right| times cos theta$，其中$theta$为两 向量的夹角。
数量积满足交换律和分配律，即$vec{a} cdot vec{b} = vec{b} cdot vec{a}$和$(lambdavec{a}) cdot vec{b} = lambda(vec{a} cdot vec{b})$。
03 向量的向量积与混合积
向量的向量积
定义
两个向量a和b的向量积是一个向量，记作a×b，其模长为 |a×b|=|a||b|sinθ，其中θ为a与b之间的夹角。
适用范围
适用于直线与平面不垂直的情况。
利用向量的混合积求二面角
1 2 3
定义
二面角是指两个平面之间的夹角。
计算公式
cosθ=∣∣a×b×c∣∣∣∣a∣∣∣∣b∣∣∣∣c∣∣，其中a、 b和c分别是三个平面的法向量，θ是两个平面之 间的夹角。
适用范围
适用于两个平面不平行的情况。
06 案例分析
案例一：利用空间向量求线线角
定义
线线角是指两条直线之间的夹角。
计算公式
cosθ=∣∣a⋅b∣∣∣∣a∣∣∣∣b∣∣∣， 其中a和b是两条直线的方向向量，
立体几何中的向量方法求空间角 ppt课件
a， b
rr
结论：cos |cosa,b|
•
(2011·陕西卷)如图，在△ABC中，∠ABC
＝60°，∠BAC＝90°，AD是BC上的高，沿AD 把△ABD折起，使∠BDC＝90°.
• 设E为BC的中点，求AE与DB夹角的余弦值．
z
y
x
易得D(0，0，0)，B(1，0，0)，C(0，3，0)，
r uuur n， BA
2
r uuur n， BA
B
2
B
r
ruuu r n
结论：sin |cosn,AB|
• 1．若直线l的方向向量与平面α的法向量的夹 角等于120°，则直线l与平面α所成的角等于(
)
•
A．120°
B．60°
•
C．30°
D．60°或30°
• 解析： 由题意得直线l与平面α的法向量所在 直线的夹角为60°，∴直线l与平面α所成的角
b Br
An
sin | cosn,AB|
3.二面角：
B
O
①方向向量法：
r n
B
A
C
l
D
②法向量法：
【注意】法向量的方向：一
coscosu A uB ur,C uuD ur uu A uuu B rurC uuuu D uu rr
进一出，二面角等于法向量 夹角；同进同出，二面角等
ABCD 于法向量夹角的补角。
• (2)分别在二面角的两个平面内找到与棱垂直 且以垂足出发的两个向量，则这两个向量的夹 角的大小就是二面角的大小．
• 以上两种方法各有利弊，要善于结合题目的特 点选择适当的方法解题．
rC
rD
1.异面直线所成r r角： a
高中新课标数学-二面角课件
设平面的一个法向量为 = (1 , 1 , 1 ),
则ቐ
∙ = 1 = 0
∙ = 1 + 1 = 0
,
取1 =1，可得1 = −1, 1 = 0,此时 = (−1,0,1),
平面角的正切值.
分析由PC⊥平面ABC,知平面ABC⊥平面PAC,从而B在平面PAC上的射
影在AC上,由此可用三垂线定理作出二面角的平面角.
解:∵PC⊥平面ABC,
∴平面PAC⊥平面ABC,交线为AC.作BD⊥AC于D点,据面面垂直性
质定理,BD⊥平面PAC,作DE⊥PA于E点,连接BE,据三垂线定理,则
2
2√3
√2
=
√2
a,
4
= √6.
故二面角 B-PA-C 的平面角的正切值为√6.
归纳总结
1.本题解法使用了三垂线定理来作出二面角的平面角后,再用解三
角形的方法来求解.
2.二面角的定义求法主要有:
(1)由定义作出二面角的平面角;
(2)利用三垂线定理(逆定理)作出二面角的平面角;
(3)作二面角棱的垂面,则垂面与二面角两个面的交线所成的角就是
解:以题意，, , 1 两两相互垂直。
以C为原点, ，， 1 的方向分别为轴, 轴, 轴正方向，
建立如图所示直角坐标系，则： C 0,0,0 , 0,1,0 , D(1,0,1) 1 (1,1,1)
所以=(0,1,0), =(1,0,1) , 1 =(-1,0,1) , 1 =(0,-1,2) ,
人教2019B版 选择性必修 第一册
第一章
空间向量与立体几何
1.2.4 二 面 角（1）
学习目标
1.掌握二面角的概念
2.理解二面角的平面角的含义
则ቐ
∙ = 1 = 0
∙ = 1 + 1 = 0
,
取1 =1，可得1 = −1, 1 = 0,此时 = (−1,0,1),
平面角的正切值.
分析由PC⊥平面ABC,知平面ABC⊥平面PAC,从而B在平面PAC上的射
影在AC上,由此可用三垂线定理作出二面角的平面角.
解:∵PC⊥平面ABC,
∴平面PAC⊥平面ABC,交线为AC.作BD⊥AC于D点,据面面垂直性
质定理,BD⊥平面PAC,作DE⊥PA于E点,连接BE,据三垂线定理,则
2
2√3
√2
=
√2
a,
4
= √6.
故二面角 B-PA-C 的平面角的正切值为√6.
归纳总结
1.本题解法使用了三垂线定理来作出二面角的平面角后,再用解三
角形的方法来求解.
2.二面角的定义求法主要有:
(1)由定义作出二面角的平面角;
(2)利用三垂线定理(逆定理)作出二面角的平面角;
(3)作二面角棱的垂面,则垂面与二面角两个面的交线所成的角就是
解:以题意，, , 1 两两相互垂直。
以C为原点, ，， 1 的方向分别为轴, 轴, 轴正方向，
建立如图所示直角坐标系，则： C 0,0,0 , 0,1,0 , D(1,0,1) 1 (1,1,1)
所以=(0,1,0), =(1,0,1) , 1 =(-1,0,1) , 1 =(0,-1,2) ,
人教2019B版 选择性必修 第一册
第一章
空间向量与立体几何
1.2.4 二 面 角（1）
学习目标
1.掌握二面角的概念
2.理解二面角的平面角的含义
人教B版高中数学选择性必修第一册精品课件 第1章 空间向量与立体几何 1.2.4 二面角
θ=<n1,n2>或π-<n1,n2>,特别地,sin θ=sin<n1,n2>.
3.设a=(0,1,1),b=(1,0,1)分别是平面α,β的两个法向量,则锐二面角α-l-β的大
小是(
)
A.45° B.90°
C.60°D.120°
解析:设锐二面角α-l-β的大小是θ,
|·|
1
1
则 cos θ=|||| =
= .
答案:B
2
)
2.在正四面体ABCD中,二面角A-BC-D的余弦值为(
1
A.2
1
B.3
3
C. 3
)
3
D. 2
解析:如图,设BC的中点为E,底面正三角形BCD的中心为O,则∠AEO就是二
面角A-BC-D的平面角.
3
3
1
在 Rt△AOE 中,AE= 2 AB,EO= 6 AB,则 cos∠AEO= = 3.
二面角B-AP-C的大小.
解:如图,过点B作BM⊥AC交AC于点M,过点M作MN⊥AP交AP于点N,连接
BN,由三垂线定理知BN⊥PA.
∴∠MNB为所求二面角的平面角.
设AB=BC=AC=PC=1,
3
2
∴BM= ,MN= ,
2
4
3
∴tan∠MNB= 2 = √6.故∠MNB=arctan√6,
2
4
APC的一个法向量.
·
∵cos<a,n>=||||=0,∴<a,n>=90°,
∴二面角A-PC-B为90°.
用法向量法求二面角的大小的优点是不需要确定二面角的平面角,缺点是
计算量大.若二面角两个半平面的法向量分别是n1,n2,设二面角的大小为θ,
3.设a=(0,1,1),b=(1,0,1)分别是平面α,β的两个法向量,则锐二面角α-l-β的大
小是(
)
A.45° B.90°
C.60°D.120°
解析:设锐二面角α-l-β的大小是θ,
|·|
1
1
则 cos θ=|||| =
= .
答案:B
2
)
2.在正四面体ABCD中,二面角A-BC-D的余弦值为(
1
A.2
1
B.3
3
C. 3
)
3
D. 2
解析:如图,设BC的中点为E,底面正三角形BCD的中心为O,则∠AEO就是二
面角A-BC-D的平面角.
3
3
1
在 Rt△AOE 中,AE= 2 AB,EO= 6 AB,则 cos∠AEO= = 3.
二面角B-AP-C的大小.
解:如图,过点B作BM⊥AC交AC于点M,过点M作MN⊥AP交AP于点N,连接
BN,由三垂线定理知BN⊥PA.
∴∠MNB为所求二面角的平面角.
设AB=BC=AC=PC=1,
3
2
∴BM= ,MN= ,
2
4
3
∴tan∠MNB= 2 = √6.故∠MNB=arctan√6,
2
4
APC的一个法向量.
·
∵cos<a,n>=||||=0,∴<a,n>=90°,
∴二面角A-PC-B为90°.
用法向量法求二面角的大小的优点是不需要确定二面角的平面角,缺点是
计算量大.若二面角两个半平面的法向量分别是n1,n2,设二面角的大小为θ,
向量法-求二面角大小
空间向量法---求二面角的大小
运用“空间向量法”---求“二面角的大小”的解题步骤：
① 建立空间直角坐标系； ② 求出所需各点的坐标； ③ 求出两个平面的法向量； ④ 求出两个法向量的夹角； ⑤ 写出所求二面角的大小。
空间向量法---求二面角的大小
运用“空间向量法”---求“二面角的大小”的解题步骤：
(1) 证明: AN⊥平面PAD .
(2) 求二面角C-AM-N的大小 .
P
M
A
D
B
NC
【练习3】 如图, 在四棱锥P-ABCD中, 底面是边长为2的菱形, ∠ABC=60O , PA⊥底面ABCD,PA=2, M,N分别为PC,BC的中点.
(1) 证明: AN⊥平面PAD .
(2) 求二面角C-AM-N的大小 .
∴ cosq =
6
3
得 tanq =
2
2
∴
所求面SCD与面SBA所成二面角的正切值是22
【练习2】 已知点E、F分别是正方体ABCD-A1B1C1D1的棱BB1、 CC1上的点, 且 BE1=2EB, CF=2FC1 .
(1) 求面AEF与面ABC所成二面角的正切值 .
【练习3】 如图, 在四棱锥P-ABCD中, 底面是边长为2的菱形, ∠ABC=60O , PA⊥底面ABCD,PA=2, M,N分别为PC,BC的中点.
=
3 3
由条件知,二面角A-CD-E为锐角，∴
所求二面角的余弦值为
3 3
【练习1】 如下图, 在底面是直角梯形的四棱锥S-ABCD中,
∠ABC=90O
,
SA⊥面ABCD，SA=AB=BC=1,
AD=
1 2
.
高二数学选修课件：3-2-4二面角及其度量
人 教 B 版 数 学
第三章
空间向量与立体几何
[说明]
利用法向量求二面角
设 m1⊥α，m2⊥β，则〈m1，m2〉与该二面角相等或互 补．此方法的解题步骤如下： 依据几何条件建立适当的空间直角坐标系，在建立的坐 标系下求两个面的法向量 m1，m2，求 m1 与 m2 所成锐角 θ， |m1· 2| m cosθ＝|m ||m |，若二面角为锐角，则为 θ；若二面角为钝角， 1 2 则为 π－θ.
第三章
空间向量与立体几何
[分析] 由于不易建立空间直角坐标系，故可借助于 向量所成的角，求二面角大小． [解析] 如图，过A1作A1E⊥BA交BA的延长线于点E， ∵ABCD为正方形，
人 教 B 版 数 学
第三章
空间向量与立体几何
→ → ∴AD⊥AB， 则向量A1E与DA所成的角的大小即为二 面角 A1—AB—D 的大小． → → → ∵A1E＝A1A＋AE， → DA → ∴A1E· ＝(A1→＋AE)DA A → → → ＝|A1A||DA→cos → ，→ 〉 → ||DA|cos → ，→ 〉 | 〈A1A DA ＋|AE → 〈AE DA 1 ＝nmcos120° ＋0＝－ mn. 2
人 教 B 版 数 学
第三章
空间向量与立体几何
如图所示，甲站在水库底面上的点A，乙站在水坝斜 面上的点B.从A、B到直线l(库底与水坝CD的交线)的距离 AC和BD分别是a和b，CD长度为c，甲乙之间拉紧的绳长为 d.求库底水坝所成二面角的余弦值．
人 教 B 版 数 学
第三章
空间向量与立体几何
[解析] 量问题)．
第三章
空间向量与立体几何
1．二面角平面角的作法
(1)定义法 由二面角平面角的定义可知平面角的顶点可根据具体 题目选择棱上一个特殊点．求解用到的解三角形知识． (2)垂面法
第三章
空间向量与立体几何
[说明]
利用法向量求二面角
设 m1⊥α，m2⊥β，则〈m1，m2〉与该二面角相等或互 补．此方法的解题步骤如下： 依据几何条件建立适当的空间直角坐标系，在建立的坐 标系下求两个面的法向量 m1，m2，求 m1 与 m2 所成锐角 θ， |m1· 2| m cosθ＝|m ||m |，若二面角为锐角，则为 θ；若二面角为钝角， 1 2 则为 π－θ.
第三章
空间向量与立体几何
[分析] 由于不易建立空间直角坐标系，故可借助于 向量所成的角，求二面角大小． [解析] 如图，过A1作A1E⊥BA交BA的延长线于点E， ∵ABCD为正方形，
人 教 B 版 数 学
第三章
空间向量与立体几何
→ → ∴AD⊥AB， 则向量A1E与DA所成的角的大小即为二 面角 A1—AB—D 的大小． → → → ∵A1E＝A1A＋AE， → DA → ∴A1E· ＝(A1→＋AE)DA A → → → ＝|A1A||DA→cos → ，→ 〉 → ||DA|cos → ，→ 〉 | 〈A1A DA ＋|AE → 〈AE DA 1 ＝nmcos120° ＋0＝－ mn. 2
人 教 B 版 数 学
第三章
空间向量与立体几何
如图所示，甲站在水库底面上的点A，乙站在水坝斜 面上的点B.从A、B到直线l(库底与水坝CD的交线)的距离 AC和BD分别是a和b，CD长度为c，甲乙之间拉紧的绳长为 d.求库底水坝所成二面角的余弦值．
人 教 B 版 数 学
第三章
空间向量与立体几何
[解析] 量问题)．
第三章
空间向量与立体几何
1．二面角平面角的作法
(1)定义法 由二面角平面角的定义可知平面角的顶点可根据具体 题目选择棱上一个特殊点．求解用到的解三角形知识． (2)垂面法
第7讲 利用空间向量求空间角、空间距离
[注意] 直线与平面所成角的范围为[0，π2]，而向量之间的夹角的范围为 [0，π]，所以公式中要加绝对值．
6
利用空间向量求空间角、空间距离
《高考特训营》 ·数学 返 回
3．二面角
(1)若 AB，CD 分别是二面角αl-β 的两个平面内与棱 l 垂直的异面直线，
则二面角(或其补角)的大小就是向量A→B与C→D的夹角，如图①.
逻辑推理
的距离问题和简单夹角问题.
2.平面与平面的夹 数学运算
2.了解向量方法在研究立体几何问题中 角(二面角)
直观想象
的作用
3.距离问题
2
利用空间向量求空间角、空间距离
《高考特训营》 ·数学 返 回
01 02
知识特训 能力特训
3
利用空间向量求空间角、空间距离
《高考特训营》 ·数学 返 回
01
知识特训
范围为(0，π)，所以公式中要加绝对值．
5
利用空间向量求空间角、空间距离
《高考特训营》 ·数学 返 回
2．直线与平面所成角 如图所示，设 l 为平面α的斜线，l∩α＝A，a 为 l 的方向向量，n 为平面α 的法向量，θ为 l 与α所成的角，则 sin θ＝|cos 〈a，n〉|＝||aa|·|nn||.
(3)点到平面的距离
《高考特训营》 ·数学 返 回
如 B 到图平所面示，α 已的知距离AB为为|B→平O|面＝_α_|A的→_B_|n一_·_| 条_n_| 斜__线__段．，n 为平面 α 的法向量，则点
11
利用空间向量求空间角、空间距离
《高考特训营》 ·数学 返 回
[记结论·提速能] 【记结论】
9
利用空间向量求空间角、空间距离
高中数学空间向量与立体几何1.2.4二面角课件
则 sin θ＝
1－cos2θ
＝
55 10
.
即二面角 A-C1M-B1 的正弦值为
55 10
.
利用向量法求二面角的两种方法 方法一：分别在二面角 αlβ 的面 α，β 内，沿 α，β 延伸的方向作向量 n1⊥l，n2⊥l， 则可用〈n1，n2〉度量这个二面角的大小． 方法二：通过法向量求解 设 m1⊥α，m2⊥β， 则〈m1，m2〉与该二面角相等或互补．
2．对射影面积公式的理解： (1)来源：三垂线定理． (2)适用范围：当二面角的一个半平面上的封闭图形的面积及它在另一个半平面上 的射影的面积已知或者已求出． (3)优势：不需要作出二面角的平面角．
如图，在直三棱柱 ABC-A1B1C1 中，AB＝1，AC＝AA1＝ 3 ，∠ABC＝60°.
(1)证明：AB⊥A1C； (2)求二面角 A-A1C-B 的正切值．
面角 A A1C B 的平面角．在 Rt△AA1C 中，AD＝AAA1·1CAC ＝
3× 6
36 ＝2 .
在 Rt△BAD 中，tan
∠ADB＝AABD
＝
6 3
，
6 所以二面角 A A1C B 的正切值为 3 .
类型三 利用向量法求二面角(逻辑推理、数学运算)
角度1
利用棱的垂线的方向向量求二面角
【思考】 二面角的大小、二面角的平面角的大小、两个相交平面所成角的大小的范围是相 同的吗？
提示：不相同．二面角的大小和二面角的平面角的大小的范围是[0°，180°] ，两 个相交平面所成角的大小的范围是[0°，90°] .
2．射影面积公式 已知平面 β 内一个多边形的面积为 S，它在平面 α 内的射影图形的面积为 S′，平 面 α 和平面 β 所成的二面角的大小为 θ，则 cos θ＝SS′ .
二面角的求法和利用空间向量解决立体几何问题
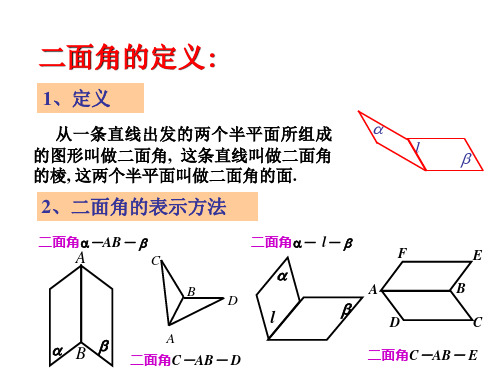
二面角的定义:
1、定义
从一条直线出发的两个半平面所组成
的图形叫做二面角, 这条直线叫做二面角
l
的棱, 这两个半平面叫做二面角的面.
2、二面角的表示方法
二面角－AB－
A
C
B
二面角－ l－
D
l
B
A
二面角C－AB－ D
F
E
A
B
D
C
二面角C－AB－ E
二面角的平面角:
以二面角的棱上任意一点为端
点, 在两个面内分别作垂直于棱的 两条射线, 这两条射线所成的角叫 做二面角的平面角。
面面平行
∥ n1 ∥ n2 n1 kn2
二、垂直关系：
设直线 l, m 的方向向量分别为 AB,CD ，
平面 , 的法向量分别为 n1 , n2 ， 线线垂直:
l ⊥ m AB ⊥ CD AB • CD 0 ；
Bl
A
平面 内的两个相交向量垂直
(4)解方程组，令其中一个量的值求另外两个， 即得法向量。
一、平行关系：
设直线 l, m 的方向向量分别为 AB,CD ，
lm
BD
平面 , 的法向量分别为
线线平行:
n1
, n2
，
l ∥ m AB ∥ CD AB kCD
；
x1 y1
=
A
x2 y2
=
C
x3 y3
线面平行
AB
l ∥ AB n1 AB n1 0 ；
分别作垂直于a 的两条射线OA,OB，则∠AOB就 是此二面角的平面角。
2、垂线法: 在一个平面 内选一点A向另一平面 作 垂线AB，
垂足为B，再过点B向棱a作垂线BO，垂足 为O， 连结AO，则∠AOB就是二面角的平面角。
3.2利用空间向量求二面角
AD (1,
SD. 得n (2, 1,1)
0, 0)是平面SAB的法向量，
cos AD, n AD n 6 | AD || n | 3
4.求两法向量夹角
所求二面角的余弦值为： 6 3
5.定值
巩固练习1： 正方体ABCD—A1B1C1D1的棱长为2，点Q 是BC的中点，求二面角A—DQ—A1的余弦 值．
3.2利用空间向量求二面角
温故知新
已学习：二面角及二面角的平面角的概念
会：建立空间直角坐标系 进行向量坐标运算 求平面的法向量
已掌握：用向量求解线线角、线面角的方法
温故知新 1.二面角的定义
从一条直线出发的两个半平面所组成的图形叫做二面角。
2.二面角的范围： [0, ]
O
探究方法
问题1：
求直线和平面所成的角可转化成直线的方向向量与 平面的法向量的夹角，那么二面角的大小与两个半 平面的法向量有着怎样的关系呢？
高考链接
(2019.18)如图，直四棱柱ABCD–A1B1C1D1的底面是菱形，AA1=4， AB=2，∠BAD=60°，E，M，N 分别是BC，BB1，A1D 的中点．
（1）证明：MN∥平面C1DE； （2）求二面角A-MA1-N的正弦值．
z
【点睛】
本题考查线面平行关系的证明、空
间向量法求解二面角的问题.求解二
面角的关键是能够利用垂直关系建
立空间直角坐标系，从而通过求解
O
法向量夹角的弦值来得到二面角
的正弦值，属于常规题型.
x
y
n
a
n1 n2
l
探究方法
问题2：二面角的大小与两个平面法向量夹角的关系？
n1，n2
n1，n2
SD. 得n (2, 1,1)
0, 0)是平面SAB的法向量，
cos AD, n AD n 6 | AD || n | 3
4.求两法向量夹角
所求二面角的余弦值为： 6 3
5.定值
巩固练习1： 正方体ABCD—A1B1C1D1的棱长为2，点Q 是BC的中点，求二面角A—DQ—A1的余弦 值．
3.2利用空间向量求二面角
温故知新
已学习：二面角及二面角的平面角的概念
会：建立空间直角坐标系 进行向量坐标运算 求平面的法向量
已掌握：用向量求解线线角、线面角的方法
温故知新 1.二面角的定义
从一条直线出发的两个半平面所组成的图形叫做二面角。
2.二面角的范围： [0, ]
O
探究方法
问题1：
求直线和平面所成的角可转化成直线的方向向量与 平面的法向量的夹角，那么二面角的大小与两个半 平面的法向量有着怎样的关系呢？
高考链接
(2019.18)如图，直四棱柱ABCD–A1B1C1D1的底面是菱形，AA1=4， AB=2，∠BAD=60°，E，M，N 分别是BC，BB1，A1D 的中点．
（1）证明：MN∥平面C1DE； （2）求二面角A-MA1-N的正弦值．
z
【点睛】
本题考查线面平行关系的证明、空
间向量法求解二面角的问题.求解二
面角的关键是能够利用垂直关系建
立空间直角坐标系，从而通过求解
O
法向量夹角的弦值来得到二面角
的正弦值，属于常规题型.
x
y
n
a
n1 n2
l
探究方法
问题2：二面角的大小与两个平面法向量夹角的关系？
n1，n2
n1，n2
用空间向量求空间角课件(共22张PPT)
1
M
2 x 0 z 0 即 取z =2得x=1，y = - 2 2 x 2 y z 0 A
D O B
C
y
所以平面B1MA的一个法向量为 n (1， 2， 2) 1 2 4 6 cos B1O， n 6 6 9
x
由图可知二面角为锐角
6 所以二面角B1 MA C的余弦值为 。 6
即为两直线的夹角；当向量夹角为钝角时，两直线的夹角为向
量夹角的补角．
直线和直线在平面内的射影所成的角， 二、线面角： 叫做这条直线和这个平面所成的角.
[0, ] 直线与平面所成角的范围：
A
2
n
思考：如何用空间向量的夹角 表示线面角呢？
B
O
结论： sin
| cos n, AB |
立体几何中的向量方法 ——空间“角”问题
空间的角常见的有：线线角、线面角、面面角
复习回顾
• 直线的方向向量:两点 • 平面的法向量：三点两线一方程 • 设a＝(a1，a2，a3)，b＝(b1，b2，b3) 则(1)a·b＝ a1b1＋a2b2＋a3b3 .
复习回顾
• 设直线l1、l2的方向向量分别为a、b，平面α、β的 法向量分别为n1、n2.
10 5
所以直线SA与OB所成角余弦值为
课堂小结：
1.异面直线所成角：
C
D
cos sin
|cos CD, AB | | cos n, AB |
A
B
D1
A
O
2.直线与平面所成角： 3.二面角：
n
B
n2
高中数学课件-第8讲 向量法求空间角
第8讲 向量法求空间角1.掌握空间向量的应用.2.会用空间向量求空间角.考试要求01聚焦必备知识知识梳理1.异面直线所成的角设异面直线l1，l2所成的角为θ，其方向向量分别是u，v，则cos θ＝___________________＝_________.2.直线与平面所成的角如图，直线AB与平面α相交于点B，设直线AB与平面α所成的角为θ，直线AB的方向向量为u，平面α的法向量为n，则sin θ＝________________＝_________.3.平面与平面的夹角如图，平面α与平面β相交，形成四个二面角，我们把四个二面角中不大于90°的二面角称为平面α与平面β的夹角.若平面α，β的法向量分别是n1和n2，则平面α与平面β的夹角即为向量n1和n2的夹角或其补角.设平面α与平面β的夹角为θ，则cos θ＝|cos 〈n1，n2〉|＝__________.提醒常用结论1.思考辨析(在括号内打“ √”或“×”)(1)两直线的方向向量所成的角就是两条直线所成的角.( )(2)直线的方向向量和平面的法向量所成的角就是直线与平面所成的角.( )(3)两个平面的法向量所成的角是这两个平面的夹角.( )夯基诊断×××√A(2)设M，N分别是正方体ABCD -A′B′C′D′的棱BB′和B′C′的中点，则直线MN与平面A′BCD′所成角的正弦值为________.(3)两个平面的法向量分别为n1＝(0，－1，1)，n2＝(1，0，－1)，则两个平面夹角的余弦值为________.02突破核心命题考 点 一异面直线所成的角D用向量法求异面直线所成的角的一般步骤(1)建立空间直角坐标系.(2)用坐标表示两异面直线的方向向量.(3)利用向量的夹角公式求出向量夹角的余弦值.反思感悟A考 点 二直线与平面所成的角例2 (2023·全国甲卷)如图，在三棱柱ABC -A1B1C1中，A1C⊥平面ABC，∠ACB＝90°，AA1＝2，A1到平面BCC1B1的距离为1.(1)证明：A1C＝AC；(2)已知AA1与BB1的距离为2，求AB1与平面BCC 1B 1所成角的正弦值.解：(1)证明：∵A1C⊥平面ABC，BC，AC⊂平面ABC，∴A1C⊥BC，A1C⊥AC.又∠ACB＝90°，∴AC⊥BC.∵A1C∩AC＝C，A1C，AC⊂平面ACC1A1，∴BC⊥平面ACC1A1.∵BC⊂平面BCC1B1，∴平面ACC1A1⊥平面BCC1B1.如图，过点A1作A1D⊥CC1于点D，∵平面ACC1A1⊥平面BCC1B1，向量法求直线与平面所成角的主要方法(1)分别求出斜线和它在平面内的射影直线的方向向量，将题目转化为求两个方向向量的夹角(或其补角).(2)通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角或钝角的补角，取其余角就是斜线和平面所成的角.反思感悟因为PD⊥平面ABCD，BD⊂平面ABCD，所以PD⊥BD，又PD∩AD＝D，PD，AD⊂平面PAD，所以BD⊥平面PAD.又PA⊂平面PAD，所以BD⊥PA.(2)由(1)知，DA，DB，DP两两垂直，如图，以点D为原点建立空间直角坐标系，考 点 三 平面与平面的夹角例3 (2023·新课标Ⅰ卷)如图，在正四棱柱ABCD -A1B1C1D1中，AB＝2，AA1＝4.点A2，B2，C2，D2分别在棱AA1，BB1，CC1，DD1上，AA2＝1，BB2＝DD2＝2，CC2＝3.(1)证明：B2C2∥A2D2；(2)点P在棱BB1上，当二面角P A2C2D2为150°时，求B 2P.别为x，y，z轴，建立空间直角坐标系.因为AB＝2，AA1＝4，AA2＝1，BB2＝DD2＝2，CC2＝3，所以A2(2，2，1)，B2(0，2，2)，C2(0，0，3)，D2(2，0，2)，反思感悟利用空间向量求平面与平面夹角的解题步骤(1)证明：EF∥平面ADO；(2)证明：平面ADO⊥平面BEF；(3)求二面角D -AO -C的正弦值.所以AO⊥平面BEF.又AO⊂平面ADO，所以平面ADO⊥平面BEF.(3)以B为原点，BA所在直线为x轴，03限时规范训练(五十四)(1)求异面直线A1B与AC1夹角的余弦值；(2)求平面A1BD与平面A1AD夹角的正弦值.。
二面角的求法(精华版)PPT课件
二面角－AB－
A
C
B
二面角－ l－
D
l
B
A
二面角C－AB－ D .
F
E
A
Bபைடு நூலகம்
D
C
二面角C－AB－2E
二面角的平面角:
以二面角的棱上任意一点为端
点, 在两个面内分别作垂直于棱的 两条射线, 这两条射线所成的角叫 做二面角的平面角。
l
P
B
A
P1
B1
A1
二面角的大小用它的平面角的大小来度量 ∠APB= ∠A1P1B1
D1 E
C1
A1
B1
A FEB
G
A1
C
D
A
F
C
B
cos SAFCG
S A1FCE
F
练习3：三棱锥P-ABC中，PA ⊥平面 ABC，PA=3，AC=4，PB=PC=BC （1）求二面角P-BC-A的大小； （2）求二面角A-PC-B的大小。
P D
cos SABC
SPBC
AE
C
B
二、向量法：
1、方向向量法:
注意: 二面角的平面角必须满足：
1）角的顶点在棱上 (与顶点位置无关) 2）角的两边分别在两个面内 3）角的两边都要垂直于二面角的棱
二面角的平面角的范围: 0180
.
3
一、几何法：
1、定义法: 以二面角的棱a上任意一点O为端点，在两个面内
分别作垂直于a 的两条射线OA,OB，则∠AOB就 是此二面角的平面角。
将二面角转化为二面角的两个面 的方向向量（在二面角的面内垂 直于二面角的棱且指向该面方向 的向量）所成的角。
D
空间向量处理二面角
二面角二面角的求解方法（范围： ）一、定义法：直接在二面角的棱上取一点（特殊点），分别在两个半平面内作棱的垂线，得出平面角，用定义法时，要认真观察图形的特性；例、在四棱锥P -ABCD 中，ABCD 是正方形，PA⊥平面ABCD ，PA=AB=a ，求二面角B -PC -D 的大小。
变式：如图,已知二面角α-а-β等于120°,PA ⊥α,A ∈α,PB ⊥β,B ∈β. 求∠APB 的大小.二、三垂线定理法：已知二面角其中一个面内一点到一个面的垂线，用三垂线定理或逆定理作出二面角的平面角； 例、在四棱锥P -ABCD 中，ABCD 是平行四边形，PA⊥平面ABCD ，PA=AB=a ，⊥ABC=30°，求二面角P -BC -A 的大小。
p ABCDL HjA BC DPH ABCD A 1 B 1C 1D 1EOPOBA变式1、如图,ABCD-A 1B 1C 1D 1是长方体,侧棱AA 1长为1,底面为正方体且边长为2,E 是棱BC 的中点,求面C 1DE 与面CDE 所成二面角的正切值.变式2、ΔABC 中，∠A=90°，AB=4，AC=3，平面ABC 外一点P 在平面ABC 内的射影是AB 中点M ，二面角P —AC —B 的大小为45°。
求（1）二面角P —BC —A 的大小；（2）二面角C —PB —A 的大小变式3、如图，平面α⊥平面β，α∩β=l ，A ∈α，B ∈β，点A 在直线l 上的射影为A 1，点B 在l 的射影为B 1，已知AB=2，AA 1=1，BB 1=2，求：二面角A 1－AB －B 1的大小.三、垂面法：已知二面角内一点到两个面的垂线时，过两垂线作平面与两个半平面的交线所成的角即为平面角，由此可知，二面角的平面角所在的平面与棱垂直；例、空间的点P 到二面角βα--l 的面α、β及棱l 的距离分别为4、3、3392，求二面角βα--l 的大小.PlCBAB 1AA 1BLE FCDPMBA四、射影法（无棱二面角）利用面积射影公式S 射＝S 原cos θ,其中θ为平面角的大小，此方法不必在图形中画出平面角；例、在四棱锥P-ABCD 中，ABCD 为正方形，PA⊥平面ABCD ，PA ＝AB ＝a ，求平面PBA 与平面PDC 所成二面角的大小。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
利用向量法求二面角的两种方法
(1) 若AB,CD分别是两个平面α,β内与棱 l垂直的异面直线, 则两个平面的夹角的大小就是向量 AB 与 CD 的夹角, 如图①. (2) 设n1, n2分别是平面α,β的法向量 , 则向量n1与n2的夹角 ( 或其补角) 就是两个平面夹角的大小, 如图②
第七章 空间中的向量方法
第八章 第七讲 立体几何中的向量方法
第3课时 利用向量知识求空间二面角
第七章 空间中的向量方法
掌握利用向量方法解决面面的夹角的求法． 重点：二面角与向量夹角的关系． 难点：如何用直线的方向向量和平面的法向量来表 达线面角和二面角．
第七章 空间中的向量方法
知识点：二面角 温故知新 1．回顾复习二面角及其平面角的定义，求法． 思维导航 2．怎样用空间向量来求二面角的大小？
? 1 ＝－ 1 . 3? 3 3
故所求两平面所成角的余弦值为 1.
3
第七章 空间中的向量方法
练习：如图所示，四棱锥 P-ABCD中，底面ABCD为 正方形，PD⊥平面 ABCD，PD＝AB＝2，E，F，G 分别为PC，PD，BC的中点． (1)求证：PA⊥EF. (2)求二面角 D-FG-E 的余弦值．
则 PA EF ＝1×0＋0×2＋( －2) ×0＝0， 所以PA⊥EF.
第七章 空间中的向量方法
(2) 易知 DF ＝(0 ，0，1) ， EF＝(1 ，0，0) ， FG＝ ( －2，1，－1) ， 设平面DFG的法向量 m＝(x 1，y1，z 1) ，
则
??m DF ? 0，
? ?m
FG
?
0，
第七章 空间中的向量方法
3．用向量方法求二面角 平面α与β相交于直线l，平面α的法向量为n1，平面β的法向
量大为小为n2，φ，<n则1，|cons2φ>|＝＝_θ_，|c_o_则s_θ_二|__面__角＝α_－_||n_ln－1_1|··_n|nβ_22为|_| _θ_或_．π－θ．设二面角
第七章 空间中的向量方法
例题讲解：正方体 ABEF-DCE′F′中 , M,N分别为 AC,BF 的中点 (如图 ),求平面 MNA 与平面 MNB 所成 角的余弦值 .
第七章 空间中的向量方法
【解析】 方法一：设正方体棱长为 1. 以B为坐标原点， BA，BE，BC所在直线分别为 x轴，y轴，z 轴建立空间 直角坐标系 B-xyz ，则A(1 ，0，0) ，B(0 ，0， 0) ．取MN的中点 G，连接 BG，AG，则 G( 1，1，1)． 因为△AMN，△BMN为等腰三角形， 2 4 4 所以AG⊥MN，BG⊥MN.所以∠AGB为 二面角的平面角或其补角．
因为 GA＝( 1，－ 1，－ 1 )，
244
GB＝(－ 1，－ 1，－ 1 )， 244
所以
cos〈GA，GB〉＝
GA GA
GB GB
＝?
1
8 ＝－1 .
3? 3
3
88
第七章 空间中的向量方法
故所求两平面所成角的余弦值为 1 .
3
方法二：设平面AMN的法向量n1＝(x ，y，z) ．
AM＝(－ 1，0，1 )，AN＝(－ 1，1，0．)
22
22
??AM n1 ? 0，
? ? AN
n1
?
0，
? ??
?
1 2
x
?
1 2
z
?
0，
?
? ?
பைடு நூலகம்
?
1 2
x
?
1 2
y
?
0.
令x＝1，解得y＝1，z ＝1，
所以n1＝(1 ，1，1) ．同理可求得平面BMN的一个法向量
n2＝(1 ，－1，－1) ．
所以
cos 〈n1，n2〉=
n1 n2 ＝ n1 n2
解得
?z1 ? 0，
? ?
?
2x1
?
y1
?
z1
?
0.
令x1＝1，得m＝(1 ，2，0) 是平面DFG的一个法向 量．
第七章 空间中的向量方法
设平面EFG的法向量n＝(x 2，y2，z 2) ，
同理可得n＝(0 ，1，1) 是平面EFG的一个法向量．
因为cos
〈m，n〉＝
|
m m|
n |n
＝ |
2 5
＝ 2
2＝ 10
10 ， 5
设二面角D-FG-E 的平面角为θ，由图可知θ＝π－〈 m，
n〉，
所以cos θ＝ － 10，
5
所以二面角D-FG-E 的余弦值为－
.150 ，
第七章 空间中的向量方法
课后训练： (1)在一个二面角的两个面内都和二面角的棱垂直的两个向 量分别为 (0,-1,3), (2,2,4), 则这个二面角的余弦值为( )
第七章 空间中的向量方法
A. 15 6
B．－ 15 6
C. 15 3
D．以上都不对
(2)PA ⊥平面ABC，AC⊥BC，PA ＝AC＝1，BC＝2. 求二面角A-PB-C的余弦值．
第七章 空间中的向量方法
课堂小结：利用空间向量求二面角的方法 (1) 若AB,CD分别是两个平面α,β内与棱 l垂直的异面直线, 则两个平面的夹角的大小就是向量 AB与 CD 的夹角。。。。 (2) 设n1, n2分别是平面α,β的法向量 , 则向量n1与n2的夹角 ( 或其补角) 就是两个平面夹角的大小。
第七章 空间中的向量方法
【解析】以D为坐标原点, 建立如图所示的空间直角坐标系 D-xyz,D(0,0,0),A(0,2,0),C(-2,0,0),P(0,0,2),E(-1,0,1), F(0,0,1),G(-2,1,0).
(1) 证明：由于 PA ＝(0 ，2，－2) ， EF ＝(1 ，0，0) ，