空间向量解决空间角的问题
空间向量的应用求空间角与距离

空间向量的应用----求空间角与距离一、考点梳理1.自新教材实施以来,近几年高考的立体几何大题,在考察常规解题方法的同时,更多地关注向量法〔基向量法、坐标法〕在解题中的应用。
坐标法〔法向量的应用〕,以其问题〔数量关系:空间角、空间距离〕处理的简单化,而成为高考热点问题。
可以预测到,今后的高考中,还会继续表达法向量的应用价值。
2.利用法向量求空间角和空间距离,其常用技巧与方法总结如下:1)求直线和直线所成的角假设直线AB 、CD 所成的角是α,cos α=|,cos |><CD AB ||||||CD AB CD AB •=2).利用法向量求线面角设θ为直线l 与平面α所成的角,ϕ为直线l 的方向向量v 与平面α的法向量n 之间的夹角,那么有2πϕθ=-或2πϕθ=+。
特别地0ϕ=时, 2πθ=,l α⊥;2πϕ=时,0θ=,l α⊂或l α。
计算公式为:||sin cos ||||v n v n θϕ==或||sin sin()cos (0)2||||||||v n v n v n v n v n πθϕϕ=-=-=-=<3).利用法向量求二面角设1n 、2n 分别为平面α、β的法向量,二面角l αβ--的大小为θ,向量1n 、2n 的夹角为ϕ,那么有θϕπ+=或θϕ=。
计算公式为:1212cos cos ||||n n n n θϕ=-=1212cos cos ||||n n n n θϕ==4).利用法向量求点面距离如图点P 为平面外一点,点A 为平面内的任一点,平面的法向量为n ,过点P 作平面α的垂线PO ,记∠OPA=θ,那么点P 到平面的距离θcos ||||PA PO d ==||||||||||||n PA PA n PA n PA n •=⊗•=5).法向量在距离方面除应用于点到平面的距离外,还能处理异面直线间的距离,线面间的距离,以及平行平面间的距离等。
其一,这三类距离都可以转化为点面间的距离;其二,异面直线间的距离可用如下方法操作:在异面直线上各取一点A 、B ,AB 在n 上的射影长即为所求。
利用空间向量求空间角考点与题型归纳

利用空间向量求空间角考点与题型归纳一、基础知识1.异面直线所成角设异面直线a ,b 所成的角为θ,则cos θ=|a ·b ||a ||b |❶, 其中a ,b 分别是直线a ,b 的方向向量.2.直线与平面所成角如图所示,设l 为平面α的斜线,l ∩α=A ,a 为l 的方向向量,n 为平面α的法向量,φ为l 与α所成的角,则sin φ=|cos 〈a ,n 〉|=|a ·n ||a ||n |❷.3.二面角(1)若AB ,CD 分别是二面角αl β的两个平面内与棱l 垂直的异面直线,则二面角(或其补角)的大小就是向量AB ―→与CD ―→的夹角,如图(1).(2)平面α与β相交于直线l ,平面α的法向量为n 1,平面β的法向量为n 2,〈n 1,n 2〉=θ,则二面角α l β为θ或π-θ.设二面角大小为φ,则|cos φ|=|cos θ|=|n 1·n 2||n 1||n 2|❸,如图(2)(3).两异面直线所成的角为锐角或直角,而不共线的向量的夹角为(0,π),所以公式中要加绝对值.直线与平面所成角的范围为⎣⎡⎦⎤0,π2,而向量之间的夹角的范围为[0,π],所以公式中要加绝对值.利用公式与二面角的平面角时,要注意〈n 1,n 2〉与二面角大小的关系,是相等还是互补,需要结合图形进行判断.二、常用结论解空间角最值问题时往往会用到最小角定理 cos θ=cos θ1cos θ2.如图,若OA 为平面α的一条斜线,O 为斜足,OB 为OA 在平面α内的射影,OC 为平面α内的一条直线,其中θ为OA 与OC 所成的角,θ1为OA 与OB 所成的角,即线面角,θ2为OB 与OC 所成的角,那么cos θ=cos θ1cos θ2. 考点一 异面直线所成的角[典例精析]如图,在三棱锥P ABC 中,P A ⊥底面ABC ,∠BAC =90°.点D ,E ,N 分别为棱P A ,PC ,BC 的中点,M 是线段AD 的中点,P A =AC =4,AB =2.(1)求证:MN ∥平面BDE ;(2)已知点H 在棱P A 上,且直线NH 与直线BE 所成角的余弦值为721,求线段AH 的长. [解] 由题意知,AB ,AC ,AP 两两垂直,故以A 为原点,分别以AB ―→,AC ―→,AP ―→方向为x 轴、y 轴、z 轴正方向建立如图所示的空间直角坐标系.依题意可得A (0,0,0),B (2,0,0),C (0,4,0),P (0,0,4),D (0,0,2),E (0,2,2),M (0,0,1),N (1,2,0).(1)证明:DE ―→=(0,2,0),DB ―→=(2,0,-2). 设n =(x ,y ,z )为平面BDE 的法向量, 则⎩⎪⎨⎪⎧n ·DE ―→=0,n ·DB ―→=0,即⎩⎪⎨⎪⎧2y =0,2x -2z =0.不妨取z =1,可得n =(1,0,1).又MN ―→=(1,2,-1),可得MN ―→·n =0. 因为MN ⊄平面BDE ,所以MN ∥平面BDE . (2)依题意,设AH =h (0≤h ≤4),则H (0,0,h ), 进而可得NH ―→=(-1,-2,h ), BE ―→=(-2,2,2). 由已知,得|cos 〈NH ―→,BE ―→〉|=|NH ―→·BE ―→||NH ―→||BE ―→|=|2h -2|h 2+5×23=721, 整理得10h 2-21h +8=0,解得h =85或h =12.所以线段AH 的长为85或12.[解题技法]用向量法求异面直线所成角的一般步骤(1)选择三条两两垂直的直线建立空间直角坐标系;(2)确定异面直线上两个点的坐标,从而确定异面直线的方向向量; (3)利用向量的夹角公式求出向量夹角的余弦值;(4)两异面直线所成角的余弦等于两向量夹角余弦值的绝对值.[提醒] 注意向量的夹角与异面直线所成的角的区别:当异面直线的方向向量的夹角为锐角或直角时,此夹角就是异面直线所成的角;当异面直线的方向向量的夹角为钝角时,其补角才是异面直线所成的角.[题组训练]1.如图所示,在三棱柱ABC A 1B 1C 1中,AA 1⊥底面ABC ,AB =BC =AA 1,∠ABC =90°,点E ,F 分别是棱AB ,BB 1的中点,则直线EF 和BC 1所成的角是( )A .30°B .45°C .60°D .90°解析:选C 以B 为坐标原点,以BC 为x 轴,BA 为y 轴,BB 1为z 轴,建立空间直角坐标系如图所示.设AB =BC =AA 1=2,则C 1(2,0,2),E (0,1,0),F (0,0,1),∴EF ―→=(0,-1,1),BC 1―→=(2,0,2),∴EF ―→·BC 1―→=2,∴cos 〈EF ―→,BC 1―→〉=22×22=12,则EF 和BC 1所成的角是60°,故选C.2.如图,在四棱锥P ABCD 中,P A ⊥平面ABCD ,底面ABCD 是菱形,AB =2,∠BAD =60°.(1)求证:BD ⊥平面P AC ;(2)若P A =AB ,求PB 与AC 所成角的余弦值. 解:(1)证明:因为四边形ABCD 是菱形, 所以AC ⊥BD .因为P A ⊥平面ABCD ,BD ⊂平面ABCD , 所以P A ⊥BD .又因为AC ∩P A =A ,所以BD ⊥平面P AC . (2)设AC ∩BD =O .因为∠BAD =60°,P A =AB =2, 所以BO =1,AO =CO = 3.如图,以O 为坐标原点,射线OB ,OC 分别为x 轴,y 轴的正半轴建立空间直角坐标系O xyz ,则P (0,-3,2),A (0,-3,0),B (1,0,0),C (0,3,0), 所以PB ―→=(1,3,-2),AC ―→=(0,23,0). 设PB 与AC 所成角为θ,则cos θ=|PB ―→·AC ―→||PB ―→||AC ―→|=622×23=64.即PB 与AC 所成角的余弦值为64. 考点二 直线与平面所成的角[典例精析](2019·合肥一检)如图,在多面体ABCDEF 中,四边形ABCD 是正方形,BF ⊥平面ABCD ,DE ⊥平面ABCD ,BF =DE ,M 为棱AE 的中点.(1)求证:平面BDM ∥平面EFC ;(2)若DE =2AB ,求直线AE 与平面BDM 所成角的正弦值. [解] (1)证明:连接AC 交BD 于点N ,连接MN , 则N 为AC 的中点,又M 为AE 的中点,∴MN ∥EC . ∵MN ⊄平面EFC ,EC ⊂平面EFC , ∴MN ∥平面EFC .∵BF ,DE 都与平面ABCD 垂直,∴BF ∥DE . ∵BF =DE ,∴四边形BDEF 为平行四边形,∴BD ∥EF . ∵BD ⊄平面EFC ,EF ⊂平面EFC , ∴BD ∥平面EFC .又MN ∩BD =N ,∴平面BDM ∥平面EFC . (2)∵DE ⊥平面ABCD ,四边形ABCD 是正方形,∴DA ,DC ,DE 两两垂直,如图,建立空间直角坐标系D xyz . 设AB =2,则DE =4,从而D (0,0,0),B (2,2,0),M (1,0,2),A (2,0,0),E (0,0,4),∴DB ―→=(2,2,0),DM ―→=(1,0,2), 设平面BDM 的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧n ·DB ―→=0,n ·DM ―→=0,得⎩⎪⎨⎪⎧2x +2y =0,x +2z =0.令x =2,则y =-2,z =-1,从而n =(2,-2,-1)为平面BDM 的一个法向量.∵AE ―→=(-2,0,4),设直线AE 与平面BDM 所成的角为θ, 则sin θ=|cosn ,AE ―→|=|n ·AE ―→||n |·|AE ―→|=4515,∴直线AE 与平面BDM 所成角的正弦值为4515.[解题技法]利用向量求线面角的2种方法(1)分别求出斜线和它所在平面内的射影直线的方向向量,转化为求两个方向向量的夹角(或其补角).(2)通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角,取其余角就是斜线与平面所成的角.[题组训练]1.在长方体ABCD A 1B 1C 1D 1中,AB =2,BC =AA 1=1,则D 1C 1与平面A 1BC 1所成角的正弦值为________.解析:建立如图所示的空间直角坐标系D xyz ,由于AB =2,BC =AA 1=1,所以A 1(1,0,1),B (1,2,0),C 1(0,2,1),D 1(0,0,1),所以A 1C 1―→=(-1,2,0),BC 1―→=(-1,0,1),D 1C 1―→=(0,2,0).设平面A 1BC 1的法向量为n =(x ,y ,z ),则有⎩⎪⎨⎪⎧A 1C 1―→·n =0, BC 1―→·n =0,即⎩⎪⎨⎪⎧-x +2y =0,-x +z =0,令x =2,得y =1,z =2,则n =(2,1,2).设D 1C 1与平面A 1BC 1所成角为θ,则sin θ=|cos 〈D 1C 1―→,n 〉|=|D 1C 1―→·n ||D 1C 1―→||n |=22×3=13,即D 1C 1与平面A 1BC 1所成角的正弦值为13.答案:132.如图,在直三棱柱ABC A 1B 1C 1中,BA =BC =5,AC =8,D 为线段AC 的中点.(1)求证:BD ⊥A 1D ;(2)若直线A 1D 与平面BC 1D 所成角的正弦值为45,求AA 1的长.解:(1)证明:∵三棱柱ABC A 1B 1C 1是直三棱柱,∴AA 1⊥平面ABC ,又BD ⊂平面ABC ,∴BD ⊥AA 1, ∵BA =BC ,D 为AC 的中点,∴BD ⊥AC ,又AC ∩AA 1=A ,AC ⊂平面ACC 1A 1,AA 1⊂平面ACC 1A 1, ∴BD ⊥平面ACC 1A 1,又A 1D ⊂平面ACC 1A 1,∴BD ⊥A 1D . (2)由(1)知BD ⊥AC ,AA 1⊥平面ABC ,以D 为坐标原点,DB ,DC 所在直线分别为x 轴,y 轴,过点D 且平行于AA 1的直线为z 轴建立如图所示的空间直角坐标系D xyz .设AA 1=λ(λ>0),则A 1(0,-4,λ),B (3,0,0),C 1(0,4,λ),D (0,0,0), ∴DA 1―→=(0,-4,λ),DC 1―→=(0,4,λ),DB ―→=(3,0,0), 设平面BC 1D 的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧n ·DC 1―→=0,n ·DB ―→=0,即⎩⎪⎨⎪⎧4y +λz =0,3x =0,则x =0,令z =4,可得y =-λ,故n =(0,-λ,4)为平面BC 1D 的一个法向量. 设直线A 1D 与平面BC 1D 所成角为θ,则sin θ=|cosn ,DA 1―→|=|n ·DA 1―→||n |·|DA 1―→|=|4λ+4λ|λ2+16·λ2+16=45,解得λ=2或λ=8, 即AA 1=2或AA 1=8.考点三 二面角[典例精析]如图,菱形ABCD 的对角线AC 与BD 交于点O ,AB =5,AC =6,点E ,F 分别在AD ,CD 上,AE =CF =54,EF 交BD 于点H .将△DEF 沿EF 折到△D ′EF 位置,OD ′=10.(1)证明:D ′H ⊥平面ABCD ; (2)求二面角B D ′A C 的余弦值.[解] (1)证明:由四边形ABCD 为菱形,得AC ⊥BD . 由AE =CF =54,得AE AD =CFCD ,所以EF ∥AC .因此EF ⊥DH ,从而EF ⊥D ′H . 由AB =5,AC =6,得DO =BO =AB 2-AO 2=4.由EF ∥AC 得OH DO =AE AD =14,所以OH =1,D ′H =DH =3,则OD ′2=OH 2+D ′H 2,所以D ′H ⊥OH . 又OH ∩EF =H ,所以D ′H ⊥平面ABCD .(2)以H 为坐标原点,HB ,HF ,HD ′分别为x 轴,y 轴,z 轴建立空间直角坐标系H xyz ,如图所示.则B (5,0,0),C (1,3,0),D ′(0,0,3),A (1,-3,0), (由口诀“起点同”,我们先求出起点相同的3个向量.) 所以AB ―→=(4,3,0), AD ′―→=(-1,3,3),AC ―→=(0,6,0). (由口诀“棱排前”,我们用行列式求出两个平面的法向量.) 由⎩⎪⎨⎪⎧ AD ′―→=(-1,3,3), AB ―→=(4,3,0),可得平面ABD ′的法向量n 1=(-3,4,-5),由⎩⎪⎨⎪⎧AD ′―→=(-1,3,3), AC ―→=(0,6,0),可得平面AD ′C 的法向量n 2=(-3,0,-1). 于是cos 〈n 1,n 2〉=n 1·n 2|n 1|·|n 2|=7525.所以二面角B D ′A C 的余弦值为7525.[解题技法](1)利用法向量求二面角的大小时,由于法向量的方向不同,两个法向量的夹角与二面角的大小可能相等,也可能互补.所以,两个法向量的夹角的余弦值与二面角的余弦值可能存在正负号的差异.(2)有时用观察法难以判定二面角是钝角还是锐角,为了保证解题结果准确无误,我们给出一种万无一失的方法:就是在两个半平面和二面角的棱上各取1个向量,要求这三个向量必须起点相同,在利用行列式计算法向量时,棱对应的向量必须排前面,即口诀“起点同,棱排前”,这样求出的两个法向量的夹角一定与二面角的大小相等.[题组训练]如图所示,四棱锥P ABCD 中,P A ⊥平面ABCD ,△DAB ≌△DCB ,E 为线段BD 上的一点,且EB =ED =EC =BC ,连接CE 并延长交AD 于F .(1)若G 为PD 的中点,求证:平面P AD ⊥平面CGF ; (2)若BC =2,P A =3,求二面角B CP D 的余弦值. 解:(1)证明:在△BCD 中,EB =ED =EC =BC , 故∠BCD =90°,∠CBE =∠BEC =60°.∵△DAB ≌△DCB ,∴∠BAD =∠BCD =90°,∠ABE =∠CBE =60°,∴∠FED =∠BEC =∠ABE =60°.∴AB ∥EF ,∴∠EFD =∠BAD =90°, ∴EF ⊥AD ,AF =FD . 又PG =GD ,∴GF ∥P A .又P A ⊥平面ABCD ,∴GF ⊥平面ABCD , ∵AD ⊂平面ABCD ,∴GF ⊥AD . 又GF ∩EF =F ,∴AD ⊥平面CGF .又AD ⊂平面P AD ,∴平面P AD ⊥平面CGF .(2)以A 为坐标原点,射线AB ,AD ,AP 分别为x 轴,y 轴,z 轴的正半轴建立如图所示的空间直角坐标系,则A (0,0,0),B (2,0,0),C (3,3,0),D (0,23,0),P (0,0,3),故CB ―→=(-1,-3,0), CP ―→=(-3,-3,3),CD ―→=(-3,3,0). 设平面BCP 的一个法向量为n 1=(1,y 1,z 1),则⎩⎪⎨⎪⎧ n 1·CB ―→=0,n 1·CP ―→=0,即⎩⎪⎨⎪⎧ -1-3y 1=0,-3-3y 1+3z 1=0,解得⎩⎨⎧y 1=-33,z 1=23,即n 1=⎝⎛⎭⎫1,-33,23. 设平面DCP 的一个法向量为n 2=(1,y 2,z 2),则⎩⎪⎨⎪⎧n 2·CD ―→=0,n 2·CP ―→=0,即⎩⎪⎨⎪⎧-3+3y 2=0,-3-3y 2+3z 2=0,解得⎩⎪⎨⎪⎧y 2=3,z 2=2,即n 2=(1,3,2). 所以cos 〈n 1,n 2〉=n 1·n 2|n 1||n 2|=43169×8=24, 由图知二面角B CP D 为钝角, 所以二面角B CP D 的余弦值为-24. [课时跟踪检测]A 级1.如图所示,在正方体ABCD A 1B 1C 1D 1中,已知M ,N 分别是BD 和AD 的中点,则B 1M 与D 1N 所成角的余弦值为( )A.3030 B.3015 C.3010D.1515解析:选C 建立如图所示的空间直角坐标系.设正方体的棱长为2,则B 1(2,2,2),M (1,1,0),D 1(0,0,2),N (1,0,0),∴B 1M ―→=(-1,-1,-2), D 1N ―→=(1,0,-2),∴B 1M 与D 1N 所成角的余弦值为|B 1M ―→·D 1N ―→||B 1M ―→|·|D 1N ―→|=|-1+4|1+1+4×1+4=3010. 2.如图,已知长方体ABCD A 1B 1C 1D 1中,AD =AA 1=1,AB =3,E 为线段AB 上一点,且AE =13AB ,则DC 1与平面D 1EC 所成角的正弦值为( )A.33535B.277C.33D.24解析:选A 如图,以D 为坐标原点,DA ,DC ,DD 1所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系,则C 1(0,3,1),D 1(0,0,1),E (1,1,0),C (0,3,0),∴DC 1―→=(0,3,1), D 1E ―→=(1,1,-1), D 1C ―→=(0,3,-1). 设平面D 1EC 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧n ·D 1E ―→=0,n ·D 1C ―→=0,即⎩⎪⎨⎪⎧x +y -z =0,3y -z =0,取y =1,得n =(2,1,3).∴cosDC 1―→,n=DC 1―→·n |DC 1―→|·|n|=33535, ∴DC 1与平面D 1EC 所成的角的正弦值为33535.3.在直三棱柱ABC A 1B 1C 1中,AA 1=2,二面角B AA 1C 1的大小为60°,点B 到平面ACC 1A 1的距离为3,点C 到平面ABB 1A 1的距离为23,则直线BC 1与直线AB 1所成角的正切值为( )A.7B.6C.5D .2解析:选A 由题意可知,∠BAC =60°,点B 到平面ACC 1A 1的距离为3,点C 到平面ABB 1A 1的距离为23,所以在三角形ABC 中,AB =2,AC =4,BC =23,∠ABC =90°,则AB 1―→·BC 1―→=(BB 1―→-BA ―→)·(BB 1―→+BC ―→)=4, |AB 1―→|=22,|BC 1―→|=4, cosAB 1―→,BC 1―→=AB 1―→·BC ―→|AB 1―→|·|BC ―→|=24,故tanAB 1―→,BC 1―→=7.4.如图,正三棱柱ABC A 1B 1C 1的所有棱长都相等,E ,F ,G 分别为AB ,AA 1,A 1C 1的中点,则B 1F 与平面GEF 所成角的正弦值为( )A.35 B.56 C.3310D.3610解析:选A 设正三棱柱的棱长为2,取AC 的中点D ,连接DG ,DB ,分别以DA ,DB ,DG 所在的直线为x 轴,y 轴,z 轴建立空间直角坐标系,如图所示,则B 1()0,3,2,F (1,0,1), E ⎝⎛⎭⎫12,32,0,G (0,0,2), B 1F ―→=()1,-3,-1,EF ―→=⎝⎛⎭⎫12,-32,1, GF ―→=(1,0,-1).设平面GEF 的法向量n =(x ,y ,z ), 则⎩⎪⎨⎪⎧ EF ―→·n =0,GF ―→·n =0,即⎩⎪⎨⎪⎧12x -32y +z =0,x -z =0,取x =1,则z =1,y =3,故n =()1,3,1为平面GEF 的一个法向量, 所以cos 〈n ,B 1F ―→〉=1-3-15×5=-35,所以B 1F 与平面GEF 所成角的正弦值为35.5.在正方体ABCD A 1B 1C 1D 1中,点E 为BB 1的中点,则平面A 1ED 与平面ABCD 所成的锐二面角的余弦值为( )A.12B.23C.33D.22解析:选B 以A 为坐标原点建立如图所示的空间直角坐标系A xyz ,设棱长为1,则A 1(0,0,1),E ⎝⎛⎭⎫1,0,12,D (0,1,0), ∴A 1D ―→=(0,1,-1), A 1E ―→=⎝⎛⎭⎫1,0,-12, 设平面A 1ED 的一个法向量为n 1=(1,y ,z ), 则⎩⎪⎨⎪⎧ n 1·A 1D ―→=0,n 1·A 1E ―→=0,即⎩⎪⎨⎪⎧y -z =0,1-12z =0,∴⎩⎪⎨⎪⎧y =2,z =2,∴n 1=(1,2,2). 又平面ABCD 的一个法向量为n 2=(0,0,1), ∴cos 〈n 1,n 2〉=23×1=23.即平面A 1ED 与平面ABCD 所成的锐二面角的余弦值为23.6.如图,菱形ABCD 中,∠ABC =60°,AC 与BD 相交于点O ,AE ⊥平面ABCD ,CF ∥AE ,AB =2,CF =3.若直线OF 与平面BED 所成的角为45°,则AE =________.解析:如图,以O 为坐标原点,以OA ,OB 所在直线分别为x 轴,y 轴,以过点O 且平行于CF 的直线为z 轴建立空间直角坐标系.设AE =a ,则B (0,3,0),D (0,-3,0),F (-1,0,3),E (1,0,a ),∴OF ―→=(-1,0,3),DB ―→=(0,23,0), EB ―→=(-1,3,-a ).设平面BED 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧n ·DB ―→=0,n ·EB ―→=0,即⎩⎪⎨⎪⎧23y =0,-x +3y -az =0,则y =0,令z =1,得x =-a , ∴n =(-a,0,1),∴cos 〈n ,OF ―→〉=n ·OF ―→|n ||OF ―→|=a +3a 2+1×10.∵直线OF 与平面BED 所成角的大小为45°, ∴|a +3|a 2+1×10=22, 解得a =2或a =-12(舍去),∴AE =2.答案:27.如图,已知四棱锥P ABCD 的底面ABCD 是等腰梯形,AB ∥CD ,且AC ⊥BD ,AC 与BD 交于O ,PO ⊥底面ABCD ,PO =2,AB =22,E ,F 分别是AB ,AP 的中点,则二面角F OE A 的余弦值为________.解析:以O 为坐标原点,OB ,OC ,OP 所在直线分别为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系O xyz , 由题知,OA =OB =2,则A (0,-2,0),B (2,0,0),P (0,0,2),E (1,-1,0),F (0,-1,1), OE ―→=(1,-1,0),OF ―→=(0,-1,1),设平面OEF 的法向量为m =(x ,y ,z ), 则⎩⎪⎨⎪⎧m ·OE ―→=0,m ·OF ―→=0,即⎩⎪⎨⎪⎧x -y =0-y +z =0.令x =1,可得m =(1,1,1).易知平面OAE 的一个法向量为n =(0,0,1),则cos 〈m ,n 〉=m ·n|m ||n |=33.由图知二面角F OE A 为锐角, 所以二面角F OE A 的余弦值为33. 答案:338.(2018·全国卷Ⅲ)如图,边长为2的正方形ABCD 所在的平面与半圆弧C D 所在平面垂直,M 是C D 上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;(2)当三棱锥M ABC 体积最大时,求平面MAB 与平面MCD 所成二面角的正弦值. 解:(1)证明:由题设知,平面CMD ⊥平面ABCD ,交线为CD .因为BC ⊥CD ,BC ⊂平面ABCD ,所以BC ⊥平面CMD ,又DM ⊂平面CMD ,所以BC ⊥DM .因为M 为CD 上异于C ,D 的点,且DC 为直径, 所以DM ⊥CM . 又BC ∩CM =C , 所以DM ⊥平面BMC . 因为DM ⊂平面AMD , 所以平面AMD ⊥平面BMC .(2)以D 为坐标原点, DA ―→的方向为x 轴正方向,建立如图所示的空间直角坐标系D xyz .当三棱锥M ABC 的体积最大时,M 为CD 的中点.由题设得D (0,0,0),A (2,0,0),B (2,2,0),C (0,2,0),M (0,1,1),AM ―→=(-2,1,1),AB ―→=(0,2,0),DA ―→=(2,0,0).设n =(x ,y ,z )是平面MAB 的法向量,又DA ―→是平面MCD 的一个法向量,所以cos 〈n ,DA ―→〉=n ·DA ―→|n ||DA ―→|=55,sin 〈n ,DA ―→〉=255.所以平面MAB 与平面MCD 所成二面角的正弦值是255.9.(2018·全国卷Ⅱ)如图,在三棱锥P ABC 中,AB =BC =22,P A =PB =PC =AC =4,O 为AC 的中点.(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且二面角M P A C 为30°,求PC 与平面P AM 所成角的正弦值.解:(1)证明:因为P A =PC =AC =4,O 为AC 的中点, 所以PO ⊥AC ,且PO =2 3.连接OB ,因为AB =BC =22AC , 所以△ABC 为等腰直角三角形,且OB ⊥AC ,OB =12AC =2.所以PO 2+OB 2=PB 2,所以PO ⊥OB . 又因为OB ∩AC =O , 所以PO ⊥平面ABC .(2)以O 为坐标原点,OB ―→的方向为x 轴正方向,建立如图所示的空间直角坐标系O xyz .由已知得O (0,0,0),B (2,0,0),A (0,-2,0),C (0,2,0),P (0,0,23),AP ―→=(0,2,23).取平面P AC 的一个法向量OB ―→=(2,0,0). 设M (a,2-a,0)(0<a ≤2),则AM ―→=(a,4-a,0). 设平面P AM 的法向量为n =(x ,y ,z ),令y =3a ,得z =-a ,x =3(a -4),所以平面P AM 的一个法向量为n =(3(a -4),3a ,-a ),所以cos 〈OB ―→,n 〉=23(a -4)23(a -4)2+3a 2+a 2.由已知可得|cos 〈OB ―→,n 〉|=cos 30°=32,所以23|a -4|23(a -4)2+3a 2+a 2=32, 解得a =43或a =-4(舍去).所以n =⎝⎛⎭⎫-833,433,-43.又PC ―→=(0,2,-23),所以cos 〈PC ―→,n 〉=833+8334+12·643+163+169=34.所以PC 与平面P AM 所成角的正弦值为34. B 级1.如图,四棱柱ABCD A 1B 1C 1D 1的底面ABCD 是菱形,AC ∩BD =O ,A 1O ⊥底面ABCD ,AB =2,AA 1=3.(1)证明:平面A 1CO ⊥平面BB 1D 1D ;(2)若∠BAD =60°,求二面角B OB 1C 的余弦值. 解:(1)证明:∵A 1O ⊥平面ABCD ,BD ⊂平面ABCD , ∴A 1O ⊥BD .∵四边形ABCD 是菱形,∴CO ⊥BD . ∵A 1O ∩CO =O ,∴BD ⊥平面A 1CO . ∵BD ⊂平面BB 1D 1D ,∴平面A 1CO ⊥平面BB 1D 1D .(2)∵A 1O ⊥平面ABCD ,CO ⊥BD ,∴OB ,OC ,OA 1两两垂直,以O 为坐标原点,OB ―→,OC ―→, OA 1―→的方向分别为x 轴,y 轴,z 轴的正方向建立如图所示的空间直角坐标系.∵AB =2,AA 1=3,∠BAD =60°, ∴OB =OD =1,OA =OC =3, OA 1=AA 21-OA 2= 6.则O (0,0,0),B (1,0,0),C (0,3,0),A (0,-3,0),A 1(0,0,6),∴OB ―→=(1,0,0),BB 1―→=AA 1―→=(0,3,6), OB 1―→=OB ―→+BB 1―→=(1,3,6). 设平面OBB 1的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧OB ―→·n =0,OB 1―→·n =0,即⎩⎪⎨⎪⎧x =0,x +3y +6z =0.令y =2,得z =-1,∴n =(0,2,-1)是平面OBB 1的一个法向量. 同理可求得平面OCB 1的一个法向量m =(6,0,-1), ∴cosn ,m=n ·m|n |·|m |=13×7=2121,由图可知二面角B OB 1C 是锐二面角, ∴二面角B OB 1C 的余弦值为2121. 2.如图,在四棱锥P ABCD 中,底面ABCD 是直角梯形,∠ADC =90°,AB ∥CD ,AB =2CD .平面P AD ⊥平面ABCD ,P A =PD ,点E 在PC 上,DE ⊥平面P AC .(1)求证:P A ⊥平面PCD ;(2)设AD =2,若平面PBC 与平面P AD 所成的二面角为45°,求DE 的长.解:(1)证明:由DE ⊥平面P AC ,得DE ⊥P A ,又平面P AD ⊥平面ABCD ,平面P AD ∩平面ABCD =AD ,CD ⊥AD ,所以CD ⊥平面P AD ,所以CD ⊥P A , 又CD ∩DE =D ,所以P A ⊥平面PCD . (2)取AD 的中点O ,连接PO , 因为P A =PD ,所以PO ⊥AD ,又平面P AD ⊥平面ABCD ,平面P AD ∩平面ABCD =AD , 所以PO ⊥平面ABCD ,以O 为坐标原点建立如图所示的空间直角坐标系O xyz ,由(1)得P A ⊥PD ,由AD =2得P A =PD =2,PO =1,设CD =a ,则P (0,0,1),D (0,1,0),C (a,1,0),B (2a ,-1,0), 则BC ―→=(-a,2,0),PC ―→=(a,1,-1). 设m =(x ,y ,z )为平面PBC 的法向量,由⎩⎪⎨⎪⎧m ·BC ―→=0,m ·PC ―→=0,得⎩⎪⎨⎪⎧-ax +2y =0,ax +y -z =0,令x =2,则y =a ,z =3a ,故m =(2,a,3a )为平面PBC 的一个法向量,由(1)知n =DC ―→=(a,0,0)为平面P AD 的一个法向量. 由|cosm ,n|=|m ·n ||m ||n |=|2a |a 10a 2+4=22,解得a =105,即CD =105,所以在Rt △PCD 中,PC =2155,由等面积法可得DE =CD ·PD PC =33.3.如图,在三棱锥P ABC 中,平面P AB ⊥平面ABC ,AB =6, BC =23,AC =26,D ,E 分别为线段AB ,BC 上的点,且AD =2DB ,CE =2EB ,PD ⊥AC .(1)求证:PD ⊥平面ABC ;(2)若直线P A 与平面ABC 所成的角为45°,求平面P AC 与平面PDE 所成的锐二面角大小.解:(1)证明:∵AC =26,BC =23,AB =6,∴AC 2+BC 2=AB 2,∴∠ACB =90°, ∴cos ∠ABC =236=33.又易知BD =2,∴CD 2=22+(23)2-2×2×23cos ∠ABC =8, ∴CD =22,又AD =4, ∴CD 2+AD 2=AC 2,∴CD ⊥AB .∵平面P AB ⊥平面ABC ,平面P AB ∩平面ABC =AB ,CD ⊂平面ABC , ∴CD ⊥平面P AB ,又PD ⊂平面P AB ,∴CD ⊥PD , ∵PD ⊥AC ,AC ∩CD =C , ∴PD ⊥平面ABC .(2)由(1)知PD ,CD ,AB 两两互相垂直,∴可建立如图所示的空间直角坐标系D xyz ,∵直线P A 与平面ABC 所成的角为45°,即∠P AD =45°,∴PD =AD =4,则A (0,-4,0),C (22,0,0),B (0,2,0),P (0,0,4),∴CB ―→=(-22,2,0),AC ―→=(22,4,0),P A ―→=(0,-4,-4). ∵AD =2DB ,CE =2EB ,∴DE ∥AC , 由(1)知AC ⊥BC ,∴DE ⊥BC ,又PD ⊥平面ABC ,BC ⊂平面ABC ,∴PD ⊥BC , ∵PD ∩DE =D ,∴CB ⊥平面PDE ,∴CB ―→=(-22,2,0)为平面PDE 的一个法向量. 设平面P AC 的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧n ·AC ―→=0,n ·P A ―→=0,即⎩⎪⎨⎪⎧22x +4y =0,-4y -4z =0,令z =1,得x =2,y =-1, ∴n =(2,-1,1)为平面P AC 的一个法向量. ∴cos n ,CB ―→=-4-24×12=-32, ∴平面P AC 与平面PDE 所成的锐二面角的余弦值为32, 故平面P AC 与平面PDE 所成的锐二面角为30°.。
用空间向量法求解立体几何问题典例及解析

用空间向量法求解立体几何问题典例及解析以多面体为载体,以空间向量为工具,来论证和求解空间角、距离、线线关系以及线面关系相关问题,是近年来高考数学的重点和热点,用空间向量解立体几何问题,极大地降低了求解立几的难度,很大程度上呈现出程序化思想。
更易于学生们所接受,故而执教者应高度重视空间向量的工具性。
首先,梳理一下利用空间向量解决立体几何的知识和基本求解方法 一:利用空间向量求空间角 (1)两条异面直线所成的夹角范围:两条异面直线所成的夹角的取值范围是 。
向量求法:设直线,a b 的方向向量为a,b ,其夹角为θ,则有cos ___________.θ= (2)直线与平面所成的角定义:直线与平面所成的角是指直线与它在这个平面内的射影所成的角。
范围:直线和平面所夹角的取值范围是 。
向量求法:设直线l 的方向向量为a ,平面的法向量为n ,直线与法向量所成角的余弦值为|cos |___________.θ=直线与平面所成的角为ϕ,则有sin ___________.ϕ=或在平面内任取一个向量m ,则|cos |___________.θ=.(3)二面角二面角的取值范围是 . 二面角的向量求法:方法一:在两个半平面内任取两个与棱垂直的向量,则这两个向量所成的 即为所求的二面角的大小;方法二:设1n ,2n 分别是两个面的 ,则向量1n 与2n 的夹角(或其补角)即为所求二面角的平面角的大小。
二:利用空间向量求空间距离 (1)点面距离的向量公式平面α的法向量为n ,点P 是平面α外一点,点M 为平面α内任意一点,则点P 到平面α的距离d 就是 ,即d =||||MP ⋅n n . (2)线面、面面距离的向量公式平面α∥直线l ,平面α的法向量为n ,点M ∈α、P ∈l ,平面α与直线l 间的距离d 就是MP 在向量n 方向射影的绝对值,即d = .平面α∥β,平面α的法向量为n ,点M ∈α、P ∈β,平面α与平面β的距离d 就是MP 在向量n 方向射影的绝对值,即d =||||MP ⋅n n . (3)异面直线的距离的向量公式设向量n 与两异面直线a 、b 都垂直,M ∈a 、P ∈b ,则两异面直线a 、b 间的距离d 就是MP 在向量n 方向射影的绝对值,即d =||||MP ⋅n n .三:利用空间向量解证平行、垂直关系1:①所谓直线的方向向量,就是指 的向量,一条直线的方向向量有 个。
用空间向量解决空间角与距离问题
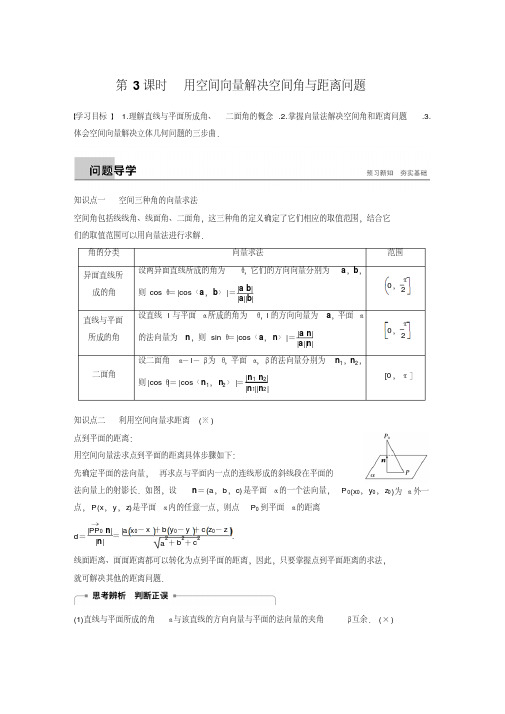
第3课时用空间向量解决空间角与距离问题学习目标 1.理解直线与平面所成角、二面角的概念.2.掌握向量法解决空间角和距离问题.3.体会空间向量解决立体几何问题的三步曲.知识点一空间三种角的向量求法空间角包括线线角、线面角、二面角,这三种角的定义确定了它们相应的取值范围,结合它们的取值范围可以用向量法进行求解.角的分类向量求法范围异面直线所成的角设两异面直线所成的角为θ,它们的方向向量分别为a,b,则cos θ=|cos〈a,b〉|=|a·b||a||b|0,π2直线与平面所成的角设直线l与平面α所成的角为θ,l的方向向量为a,平面α的法向量为n,则sin θ=|cos〈a,n〉|=|a·n||a||n|0,π2二面角设二面角α-l-β为θ,平面α,β的法向量分别为n1,n2,则|cos θ|=|cos〈n1,n2〉|=|n1·n2||n1||n2|[0,π]知识点二利用空间向量求距离(※)点到平面的距离:用空间向量法求点到平面的距离具体步骤如下:先确定平面的法向量,再求点与平面内一点的连线形成的斜线段在平面的法向量上的射影长.如图,设n=(a,b,c)是平面α的一个法向量,P0(x0,y0,z0)为α外一点,P(x,y,z)是平面α内的任意一点,则点P0到平面α的距离d=|PP0→·n||n|=|a x0-x+b y0-y+c z0-z|a2+b2+c2.线面距离、面面距离都可以转化为点到平面的距离,因此,只要掌握点到平面距离的求法,就可解决其他的距离问题.(1)直线与平面所成的角α与该直线的方向向量与平面的法向量的夹角β互余.(×)(2)二面角的大小范围是0,π2.(×)(3)二面角的大小等于其两个半平面的法向量的夹角的大小.(×)(4)直线与平面所成角的范围是0,π2.(√)类型一求线线角、线面角例1(1)在直三棱柱ABC -A 1B 1C 1中,∠BCA =90°,M ,N 分别是A 1B 1,A 1C 1的中点,BC=CA =CC 1,则BM 与AN 所成的角的余弦值为________.考点向量法求直线与直线所成的角题点向量法求线线角答案3010解析如图所示,以C 为坐标原点,直线CA 为x 轴,直线CB 为y 轴,直线CC 1为z 轴建立空间直角坐标系Cxyz.设CA =CB =CC 1=1,则B(0,1,0),M 12,12,1,A(1,0,0),N 12,0,1,故BM →=12,-12,1,AN →=-12,0,1,所以cos 〈BM →,AN →〉=BM →·AN →|BM →||AN →|=3462×52=3010. (2)如图,在四棱锥P -ABCD 中,底面为直角梯形,AD ∥BC ,∠BAD =90°,PA ⊥底面ABCD ,且P A =AD =AB =2BC ,M ,N 分别为PC ,PB 的中点.①求证:PB ⊥DM ;②求BD 与平面ADMN 所成的角.考点向量法求直线与直线所成的角题点向量法求线线角①证明如图,以A 为坐标原点,AB ,AD ,AP 所在直线分别为x 轴,y轴,z 轴,建立空间直角坐标系Axyz ,设BC =1,则A(0,0,0),P(0,0,2),B(2,0,0),D(0,2,0),C(2,1,0),M 1,12,1.∵PB →·DM →=(2,0,-2)·1,-32,1=0,∴PB ⊥DM. ②解∵PB →·AD →=(2,0,-2)·(0,2,0)=0,∴PB ⊥AD.又∵PB ⊥DM ,AD ∩DM =D ,∴PB ⊥平面ADMN .即PB →为平面ADMN 的一个法向量.因此〈PB →,DB →〉的余角即是BD 与平面ADMN 所成的角.∵cos 〈PB →,DB →〉=PB →·DB →|PB →||DB →|=422×22=12,且〈PB →,DB →〉∈[0,π],∴〈PB →,DB →〉=π3,∴BD 与平面ADMN 所成的角为π6.反思与感悟用向量法解决线线角、线面角问题时,首先需建立适当的坐标系,然后求解相应的向量表达式,再借助于空间向量的运算进行求解.跟踪训练1(1)已知在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E 是DC 的中点,建立如图所示的空间直角坐标系,则AB 1与D 1E 所成角的余弦值为()A.1010B.105C .-1010D .-105考点向量法求线线角题点向量法求线线角答案 A解析∵A(2,2,0),B 1(2,0,2),E(0,1,0),D 1(0,2,2),∴AB 1→=(0,-2,2),ED 1→=(0,1,2),∴|AB 1→|=22,|ED 1→|=5,AB 1→·ED 1→=0-2+4=2,∴cos 〈AB 1→,ED 1→〉=AB 1→·ED 1→|AB 1→||ED 1→|=222×5=1010,又异面直线所成角的范围是0,π2,∴AB 1与ED 1所成角的余弦值为1010. (2)如图所示,三棱柱ABC -A 1B 1C 1中,CA =CB ,AB =AA 1,∠BAA 1=60°.①证明:AB ⊥A 1C ;②若平面ABC ⊥平面AA 1B 1B ,AB =CB ,求直线A 1C 与平面BB 1C 1C 所成角的正弦值.考点向量法求线面角题点向量法求线面角①证明取AB 的中点O ,连接OC ,OA 1,A 1B.∵CA =CB ,∴OC ⊥AB. 由于AB =AA 1,∠BAA 1=60°,故△AA 1B 为等边三角形,∴OA 1⊥AB. ∵OC ∩OA 1=O ,∴AB ⊥平面OA 1C.又A 1C?平面OA 1C ,故AB ⊥A 1C. ②解由①知OC ⊥AB ,OA 1⊥AB.又平面ABC ⊥平面AA 1B 1B ,交线为AB ,OC?平面ABC ,所以OC ⊥平面AA 1B 1B ,故OA ,OA 1,OC 两两垂直.以O 为坐标原点,OA ,OA 1,OC 所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系Oxyz.设AB =2,则A(1,0,0),A 1(0,3,0),C(0,0,3),B(-1,0,0),则BC →=(1,0,3),BB 1→=AA 1→=(-1,3,0),A 1C -→=(0,-3,3).设n =(x ,y ,z)是平面BB 1C 1C 的法向量,则n ·BC →=0,n ·BB 1→=0,即x +3z =0,-x +3y =0,可取n =(3,1,-1).故cos 〈n ,A 1C -→〉=n ·A 1C -→|n ||A 1C -→|=-105,∴A 1C 与平面BB 1C 1C 所成角的正弦值为105. 类型二求二面角问题例2如图所示,正三棱柱ABC -A 1B 1C 1的所有棱长都为2,D 为CC 1的中点,求二面角A -A 1D -B 的余弦值.考点向量法求二面角题点向量法求二面角解取BC 的中点O ,连接AO ,因为△ABC 是正三角形,所以AO ⊥BC ,因为在正三棱柱ABC -A 1B 1C 1中,平面ABC ⊥平面BCC 1B 1,平面ABC ∩平面BCC 1B 1=BC ,AO?平面ABC ,所以AO ⊥平面BCC 1B 1. 取B 1C 1的中点O 1,以O 为坐标原点,分别以OB ,OO 1,OA 所在直线为x 轴,y 轴,z 轴,建立空间直角坐标系Oxyz ,则B(1,0,0),D(-1,1,0),A 1(0,2,3),A(0,0,3),B 1(1,2,0).设平面A 1AD 的法向量为n =(x ,y ,z),AD →=(-1,1,-3),AA 1→=(0,2,0).因为n ⊥AD →,n ⊥AA 1→,所以n ·AD →=0,n ·AA 1→=0,得-x +y -3z =0,2y =0,所以y =0,x =-3z.令z =1,得n =(-3,0,1)为平面A 1AD 的一个法向量.又因为AB 1→=(1,2,-3),BD →=(-2,1,0),BA 1→=(-1,2,3),所以AB 1→·BD →=-2+2+0=0,AB 1→·BA 1→=-1+4-3=0,所以AB 1→⊥BD →,AB 1→⊥BA 1→,即AB 1⊥BD ,AB 1⊥BA 1,且BD ∩BA 1=B ,所以AB 1⊥平面A 1BD ,所以AB 1→是平面A 1BD 的一个法向量,所以cos 〈n ,AB 1→〉=n ·AB 1→|n ||AB 1→|=-3-32×22=-64,又二面角A -A 1D -B 为锐二面角,所以二面角A -A 1D -B 的余弦值为64. 反思与感悟求角二面角时,可以用方向向量法,也可以采用法向量法求解.跟踪训练2如图,P A ⊥平面ABC ,AC ⊥BC ,BC =2,PA =AC =1,求二面角A -PB -C的余弦值.考点向量法求二面角题点向量法求二面角解以C 为坐标原点,CA ,CB 所在直线分别为x 轴,y 轴,建立如图所示的空间直角坐标系Cxyz ,取PB 的中点D ,连接DC ,可知DC ⊥PB ,作AE ⊥PB 于点E ,则向量DC →与EA →的夹角的大小为二面角A -PB -C 的大小.∵A(1,0,0),B(0,2,0),C(0,0,0),P(1,0,1),D 为PB 的中点,∴D12,22,12. 在Rt △P AB 中,由△P AB ∽△AEB ∽△PEA ,得PE EB =AP 2AB 2=13,∴E34,24,34. ∴EA →=14,-24,-34,DC →=-12,-22,-12,∴EA →·DC →=12.又|EA →|=32,|DC →|=1,∴cos 〈EA →,DC →〉=EA →·DC →|EA →||DC →|=1232×1=33,∴二面角A -PB -C 的余弦值为33. 类型三解决距离问题(※)例3已知正方体ABCD -A 1B 1C 1D 1的棱长为2,E ,F ,G 分别是C 1C ,D 1A 1,AB 的中点,求点A 到平面EFG 的距离.考点向量法求空间距离题点向量法求点与平面间的距离解以D 为坐标原点,DA ,DC ,DD 1所在直线分别为x 轴,y 轴,z轴,建立如图所示的空间直角坐标系Dxyz ,则A(2,0,0),E(0,2,1),F (1,0,2),G(2,1,0).所以AG →=(0,1,0),GE →=(-2,1,1),GF →=(-1,-1,2).设n =(x ,y ,z)是平面EFG 的法向量,点A 到平面EFG 的距离为d ,则n ·GE →=0,n ·GF →=0,所以-2x +y +z =0,-x -y +2z =0,所以x =z ,y =z.令z =1,此时n =(1,1,1),所以d =|AG →·n ||n |=13=33,即点A 到平面EFG 的距离为33.反思与感悟用向量法计算距离问题时,借助于空间向量的运算,并结合化归思想进行求解.跟踪训练3如图所示,在棱长为1的正方体ABCD -A 1B 1C 1D 1中,E ,F分别为BB 1,CC 1的中点,DG =13DD 1,过E ,F ,G 的平面交AA 1于点H ,求D 1A 1到平面EFGH 的距离.考点向量法求空间距离题点向量法求点与平面间的距离解因为点E ,F 分别为BB 1,CC 1的中点,所以EF ∥B 1C 1∥A 1D 1.又因为A 1D 1?平面EFGH ,EF ?平面EFGH ,所以A 1D 1∥平面EFGH ,所以D 1A 1到平面EFGH 的距离即为点D 1到平面EFGH 的距离.以D 为坐标原点,分别以DA ,DC ,DD 1所在直线为x 轴,y 轴,z 轴,建立空间直角坐标系Dxyz ,则E 1,1,12,F 0,1,12,G 0,0,13,D 1(0,0,1),所以EF →=(-1,0,0),FG →=0,-1,-16.设平面EFGH 的法向量为n =(x ,y ,z),则n ·EF →=0,n ·FG →=0,即-x =0,-y -16z =0,令z =6,可得n =(0,-1,6).设D 1A 1到平面EFGH 的距离为d ,连接D 1F ,又D 1F -→=0,1,-12,所以d =|D 1F -→·n ||n |=43737,即D 1A 1到平面EFGH 的距离为43737.1.已知向量m ,n 分别是直线l 的方向向量和平面α的法向量,若cos 〈m ,n 〉=-12,则l与α所成的角为()A .30°B .60°C .120°D .150°考点向量法求线面角题点向量法求线面角答案 A解析设l 与α所成的角为θ,则sin θ=|cos 〈m ,n 〉|=12.∴θ=30°.2.已知二面角α-l -β的两个半平面α与β的法向量分别为a ,b ,若〈a ,b 〉=π3,则二面角α-l -β的大小为()A.π3B.2π3C.π3或2π3 D.π6或π3考点向量法求二面角题点向量法求二面角答案C解析由于二面角的范围是[0,π],而二面角的两个半平面α与β的法向量都有两个方向,因此二面角α-l -β的大小为π3或2π3,故选 C.3.在正三棱柱ABC -A 1B 1C 1中,已知AB =1,D 在棱BB 1上,且BD =1,则AD 与平面AA 1C 1C 所成角的正弦值为()A.64B .-64C.104D .-104考点向量法求解直线与平面所成的角题点向量法解决直线与平面所成的角答案 A解析取AC 的中点E ,连接BE ,则BE ⊥AC ,以B 为坐标原点,BE ,BB 1所在直线分别为x 轴,z 轴,建立如图所示的空间直角坐标系Bxyz ,则A32,12,0,D (0,0,1),B(0,0,0),E 32,0,0,则AD →=-32,-12,1,BE →=32,0,0. ∵平面ABC ⊥平面AA 1C 1C ,平面ABC ∩平面AA 1C 1C =AC ,BE ⊥AC ,BE?平面ABC ,∴BE ⊥平面AA 1C 1C ,∴BE →=32,0,0为平面AA 1C 1C 的一个法向量.设AD 与平面AA 1C 1C 所成角为α,∵cos 〈AD →,BE →〉=-64,∴sin α=|cos 〈AD →,BE →〉|=64.4.设a ,b 是直线,α,β是平面,a ⊥α,b ⊥β,向量a 在a 上,向量b 在b 上,a =(1,1,1),b =(-3,4,0),则α,β所成二面角中较小的一个角的余弦值为________.考点向量法求二面角题点向量法求二面角答案315解析设α,β所成二面角中较小的一个角为θ,由题意得,cos θ=|cos 〈a ,b 〉|=|a ·b ||a ||b |=1,1,1·-3,4,03·5=315.5.已知等边三角形ABC 与正方形ABDE 有一公共边AB ,二面角C -AB -D 的余弦值为33,M ,N 分别是AC ,BC 的中点,则EM ,AN 所成角的余弦值为________.考点向量法求线线角题点向量法求线线角答案16解析过C 点作CO ⊥平面ABDE ,垂足为点O ,取AB 的中点F ,连接CF ,OF ,则∠CFO 为二面角C -AB -D 的平面角.设AB =1,则CF =32,∴OF =CF ·cos ∠CFO =32×33=12,∴OC =22,且O 为正方形ABDE 的中心.以O 为坐标原点,OA ,OB ,OC 所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系Oxyz ,则E 0,-22,0,M24,0,24,A 22,0,0,N 0,24,24,∴EM →=24,22,24,AN →=-22,24,24,∴cos 〈EM →,AN →〉=EM →·AN →|EM →||AN →|=16,又异面直线所成角的范围是0,π2,∴EM ,AN 所成角的余弦值为16. 1.向量法求角(1)两条异面直线所成的角θ可以借助这两条直线的方向向量的夹角φ求得,即cos θ=|cos φ|.(2)直线与平面所成的角θ可以通过直线的方向向量与平面的法向量的夹角φ求得,即sin θ=|cos φ|或cos θ=sin φ.(3)二面角的大小可以通过该二面角的两个面的法向量的夹角求得,它等于两个法向量的夹角或其补角.2.向量法求距离(※)(1)求P ,Q 两点间的距离,可转化为求PQ →的模.(2)点到平面距离的求法:设n 是平面α的法向量,B 是平面α外一点,A 是平面α内一点,AB 是平面α的一条斜线,则点B 到平面α的距离为d =|AB →·n ||n |.(3)线面距离、面面距离均可转化为点面距离,利用(2)中的方法求解.一、选择题1.在一个二面角的两个半平面内,与二面角的棱垂直的两个向量分别为(0,-1,3),(2,2,4),则这个二面角的余弦值为()A.156 B.-153C.153 D.156或-156考点向量法求二面角题点向量法求二面角答案 D 解析由0,-1,3·2,2,41+9×4+4+16=-2+1210×24=156,知这个二面角的余弦值为156或-156,故选D.2.已知两平面的法向量分别为m =(0,1,0),n =(0,1,1),则两平面所成的二面角为()A .45°B .135°C .45°或135°D .90°考点向量法求面面角题点向量法求面面角答案 C解析cos 〈m ,n 〉=m ·n |m ||n |=11·2=22,即〈m ,n 〉=45°.所以两平面所成二面角为45°或180°-45°=135°.3.设直线l 与平面α相交,且l 的方向向量为a ,α的法向量为n ,若〈a ,n 〉=2π3,则l 与α所成的角为()A.2π3B.π3C.π6D.5π6考点向量法求线面角题点向量法求线面角答案 C解析线面角的范围是0,π2.∵〈a ,n 〉=2π3,∴l 与法向量所在直线所成角为π3,∴l 与α所成的角为π6. 4.若平面α的一个法向量为n =(4,1,1),直线l 的一个方向向量a =(-2,-3,3),则l 与α所成角的余弦值为()A .-1111 B.1111C .-11011 D.91333考点向量法求线面角题点向量法求线面角答案 D解析设α与l 所成的角为θ,则sin θ=|cos 〈a ,n 〉|=|-2,-3,3·4,1,1|4+9+9×16+1+1=-4311=41133,故直线l 与α所成角的余弦值为1-411332=91333.5.在正方体ABCD -A 1B 1C 1D 1中,直线BC 1与平面A 1BD 所成的角的正弦值为()A.24 B.23C.63D.32考点向量法求线面角题点向量法求线面角答案 C解析以D 为坐标原点,DA →,DC →,DD 1→所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系Dxyz.设正方体的棱长为1,则D(0,0,0),A 1(1,0,1),B(1,1,0),C 1(0,1,1),A(1,0,0),∴BC 1→=(-1,0,1),AC 1→=(-1,1,1),A 1B -→=(0,1,-1),A 1D -→=(-1,0,-1).∴AC 1→·A 1B -→=1-1=0,AC 1→·A 1D -→=1-1=0. ∴AC 1⊥A 1B ,AC 1⊥A 1D.又A 1B ∩A 1D =A 1,且A 1B ,A 1D?平面A 1BD ,∴AC 1⊥平面A 1BD. ∴AC 1→是平面A 1BD 的一个法向量.∴cos 〈BC 1→,AC 1→〉=BC 1→·AC 1→|BC 1→||AC 1→|=1+12×3=63.∴直线BC 1与平面A 1BD 所成的角的正弦值为63. 6.如图所示,在正方体ABCD -A 1B 1C 1D 1中,M ,N ,P 分别是棱CC 1,BC ,A 1B 1上的点,若∠B 1MN =90°,则∠PMN 的大小()A .等于90°B .小于90°C .大于90°D .不确定考点向量法求线线角题点向量法求线线角答案 A解析A 1B 1⊥平面BCC 1B 1,故A 1B 1⊥MN ,MP →·MN →=(MB 1→+B 1P -→)·MN→=MB 1→·MN →+B 1P →·MN →=0,∴MP ⊥MN ,即∠PMN =90°.7.如图,S 是正三角形ABC 所在平面外一点,M ,N 分别是AB 和SC 的中点,SA =SB =SC ,且∠ASB =∠BSC =∠CSA =90°,则异面直线SM 与BN 所成角的余弦值为()A .-105 B.105C .-1010 D.1010考点向量法求线线角题点向量法求线线角答案 B解析不妨设SA =SB =SC =1,以S 为坐标原点,SA →,SB →,SC →所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系Sxyz ,则相关各点坐标为A(1,0,0),B(0,1,0),C(0,0,1),S(0,0,0),M 12,12,0,N 0,0,12. 因为SM →=12,12,0,BN →=0,-1,12,所以|SM →|=12,|BN →|=54,SM →·BN →=-12,cos 〈SM →,BN →〉=SM →·BN →|SM →||BN →|=-105,因为异面直线所成的角为锐角或直角,所以异面直线SM 与BN 所成角的余弦值为105. 二、填空题8.若两个平面α,β的法向量分别是n =(1,0,1),v =(-1,1,0),则这两个平面所成的锐二面角为________.考点向量法求面面角题点向量法求面面角答案60°解析cos 〈n ,v 〉=-12·2=-12,且〈n ,v 〉∈[0°,180°],∴〈n ,ν〉=120°.故两平面所成的锐二面角为60°.9.在正方体ABCD -A 1B 1C 1D 1中,点E 为BB 1的中点,则平面A 1ED 与平面ABCD 所成的锐二面角的余弦值为________.考点向量法求二面角题点向量法求二面角答案23解析如图所示,以A 为坐标原点,AB →,AD →,AA 1→所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系Axyz ,设正方体的棱长为1,则A 1(0,0,1),E 1,0,12,D (0,1,0),所以A 1D -→=(0,1,-1),A 1E -→=1,0,-12.设平面A 1ED 的法向量为n 1=(1,y ,z),则n 1·A 1D -→=0,n 1·A 1E -→=0,即y -z =0,1-12z =0,所以y =2,z =2.所以n 1=(1,2,2).平面ABCD 的一个法向量为n 2=(0,0,1),所以cos 〈n 1,n 2〉=n 1·n 2|n 1||n 2|=23×1=23,即所求的锐二面角的余弦值为23. 10.如图,平面P AD ⊥平面ABCD ,ABCD 为正方形,∠P AD =90°,且PA=AD =2,E ,F 分别是线段P A ,CD 的中点,则异面直线EF 与BD 所成角的余弦值为________.考点向量法求线线角题点向量法求线线角答案36解析以A 为坐标原点,AB ,AD ,AP 所在直线分别为x 轴,y 轴,z轴,建立如图所示空间直角坐标系Axyz ,则E(0,0,1),F (1,2,0),B(2,0,0),D(0,2,0).EF →=(1,2,-1),BD →=(-2,2,0),故cos 〈EF →,BD →〉=243=36.11.如图,已知矩形ABCD 与ABEF 全等,D-AB-E 为直二面角,M 为AB 的中点,FM 与BD 所成的角为θ,且cos θ=39.则AB 与BC 的边长之比为________.答案2∶2解析设AB =a ,BC =b ,以A 为坐标原点,AF →,AB →,AD →所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系Axyz ,则相关各点坐标为F (b,0,0),M 0,a2,0,B(0,a,0),D (0,0,b).FM →=-b ,a 2,0,BD →=(0,-a ,b),所以|FM →|=b 2+a 24,|BD →|=a 2+b 2,FM →·BD →=-a 22,|cos 〈FM →,BD →〉|=-a 22b 2+a 24·a 2+b 2=39,整理得,4b 4a 4+5b2a2-26=0,解得b 2a 2=2或b 2a 2=-134(舍).所以AB BC =ab =22. 三、解答题12.如图,在五面体ABCDEF 中,FA ⊥平面ABCD ,AD ∥BC ∥FE ,AB ⊥AD ,M 为EC 的中点,AF =AB =BC =FE =12AD.(1)求异面直线BF 与DE 所成的角的大小;(2)证明:平面AMD ⊥平面CDE ;(3)求二面角A -CD -E 的余弦值.考点向量法解决二面角问题题点求二面角(1)解如图所示,以A 为坐标原点,AB →,AD →,AF →所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系Axyz.设AB =1,依题意得B(1,0,0),C(1,1,0),D(0,2,0),E(0,1,1),F(0,0,1),M 12,1,12,A(0,0,0).则BF →=(-1,0,1),DE →=(0,-1,1),于是cos 〈BF →,DE →〉=BF →·DE →|BF →||DE →|=0+0+12×2=12.所以异面直线BF 与DE 所成的角的大小为60°.(2)证明由AM →=12,1,12,CE →=(-1,0,1),AD →=(0,2,0),可得CE →·AM →=0,CE →·AD →=0. 因此,CE ⊥AM ,CE ⊥AD.又AM ∩AD =A ,AM?平面AMD ,AD?平面AMD ,故CE ⊥平面AMD.又CE?平面CDE ,所以平面AMD ⊥平面CDE.(3)解设平面CDE 的法向量为u =(x ,y ,z),则u ·CE →=0,u ·DE →=0,即-x +z =0,-y +z =0,令x =1,可得u =(1,1,1).又由题设知,平面ACD 的一个法向量为v =(0,0,1).所以,cos 〈u ,v 〉=u ·v |u||v|=0+0+13×1=33.因为二面角A -CD -E 为锐角,所以其余弦值为33. 13.如图所示,在棱长为a 的正方体ABCD -A 1B 1C 1D 1中,E ,F 分别是BC ,A 1D 1的中点.(1)求直线A 1C 与DE 所成角的余弦值;(2)求直线AD 与平面B 1EDF 所成角的余弦值;(3)求平面B 1EDF 与平面ABCD 所成锐二面角的余弦值.考点向量法求面面角题点向量法求面面角解以A 为坐标原点,分别以AB ,AD ,AA 1所在直线为x 轴,y 轴,z轴,建立空间直角坐标系Axyz.(1)则A 1(0,0,a),C(a ,a,0),D(0,a,0),E a ,a2,0,∴A 1C -→=(a ,a ,-a),DE →=a ,-a 2,0,∴cos 〈A 1C -→,DE →〉=A 1C -→·DE →|A 1C -→||DE →|=1515,故A 1C 与DE 所成角的余弦值为1515. (2)连接DB 1,∵∠ADE =∠ADF ,∴AD 在平面B 1EDF 内的射影在∠EDF 的平分线上.又B 1EDF 为菱形,∴DB 1为∠EDF 的平分线,故直线AD 与平面B 1EDF 所成的角为∠ADB 1. 由A(0,0,0),B 1(a,0,a),D(0,a,0),得DA →=(0,-a,0),DB 1→=(a ,-a ,a),∴cos 〈DA →,DB 1→〉=DA →·DB 1→|DA →||DB 1→|=33,又直线与平面所成角的范围是0,π2,故直线AD 与平面B 1EDF 所成角的余弦值为33. (3)由已知得A(0,0,0),A 1(0,0,a),B 1(a,0,a),D (0,a,0),E a ,a 2,0,则ED →=-a ,a 2,0,EB 1→=0,-a2,a ,平面ABCD 的一个法向量为m =AA 1→=(0,0,a).设平面B 1EDF 的一个法向量为n =(1,y ,z),由n ·ED →=0,n ·EB 1→=0,得y =2,z =1,∴n =(1,2,1),∴cos 〈n ,m 〉=m ·n |m ||n |=66,∴平面B 1EDF 与平面ABCD 所成锐二面角的余弦值为66. 四、探究与拓展14.在棱长为1的正方体ABCD -A 1B 1C 1D 1中,M ,N 分别为A 1B 1和BB 1的中点,那么异面直线AM 与CN 所成角的余弦值为()A.32 B.1010C.35D.25考点向量法求线线角题点向量法求线线角答案 D解析如图所示,以D 为坐标原点,DA ,DC ,DD 1所在直线分别为x轴,y 轴,z 轴,建立空间直角坐标系Dxyz ,则A(1,0,0),M 1,12,1,C(0,1,0),N 1,1,12,∴AM →=0,12,1,CN →=1,0,12,∴AM →·CN →=12,|AM →|=|CN →|=52,∴cos 〈AM →,CN →〉=1252×52=25,又异面直线所成角的范围是0,π2,∴异面直线AM 与CN 所成角的余弦值为25. 15.如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,平面ABEF 为正方形,AF =2FD ,∠AFD =90°,且二面角D -AF -E 与二面角C -BE -F 都是60°.(1)证明:平面ABEF ⊥平面EFDC ;(2)求二面角E -BC -A 的余弦值.考点向量法求二面角题点向量法求二面角(1)证明由已知可得AF ⊥DF ,AF ⊥FE ,DF ∩FE =F ,DF ?平面EFDC ,FE ?平面EFDC ,所以AF ⊥平面EFDC.又AF ?平面ABEF ,故平面ABEF ⊥平面EFDC.(2)解过D 作DG ⊥EF ,垂足为G ,由(1)知DG ⊥平面ABEF.以G 为坐标原点,GF →的方向为x 轴正方向,|GF →|为单位长,建立如图所示的空间直角坐标系Gxyz.由(1)知∠DFE 为二面角D -AF -E 的平面角,故∠DFE =60°,则DF =2,DG =3,可得A(1,4,0),B(-3,4,0),E(-3,0,0),D(0,0,3).由已知得,AB ∥EF ,EF?平面EFDC ,AB?平面EFDC ,所以AB ∥平面EFDC .又平面ABCD ∩平面EFDC =CD ,故AB ∥CD ,CD ∥EF.由BE ∥AF ,可得BE ⊥平面EFDC ,所以∠CEF 为二面角C -BE -F 的平面角,即∠CEF =60°,从而可得C(-2,0,3).连接AC ,则EC →=(1,0,3),EB →=(0,4,0),AC →=(-3,-4,3),AB →=(-4,0,0).设n =(x ,y ,z)是平面BCE 的法向量,则n ·EC →=0,n ·EB →=0,即x +3z =0,4y =0,所以可取n =(3,0,-3).设m 是平面ABCD 的法向量,则m ·AC →=0,m ·AB →=0,同理可取m =(0,3,4).则cos 〈n ,m 〉=n ·m |n ||m |=-21919.故二面角E -BC -A 的余弦值为-21919.。
用空间向量求空间角课件(共22张PPT)

向量的加法与数乘
向量的加法满足平行四边形法则或三 角形法则,即$vec{a} + vec{b} = vec{b} + vec{a}$。
数乘是指实数与向量的乘积,满足分 配律,即$k(vec{a} + vec{b}) = kvec{a} + kvec{b}$。
向量的数量积
向量的数量积定义为$vec{a} cdot vec{b} = left| vec{a} right| times left| vec{b} right| times cos theta$,其中$theta$为两 向量的夹角。
数量积满足交换律和分配律,即$vec{a} cdot vec{b} = vec{b} cdot vec{a}$和$(lambdavec{a}) cdot vec{b} = lambda(vec{a} cdot vec{b})$。
03 向量的向量积与混合积
向量的向量积
定义
两个向量a和b的向量积是一个向量,记作a×b,其模长为 |a×b|=|a||b|sinθ,其中θ为a与b之间的夹角。
适用范围
适用于直线与平面不垂直的情况。
利用向量的混合积求二面角
1 2 3
定义
二面角是指两个平面之间的夹角。
计算公式
cosθ=∣∣a×b×c∣∣∣∣a∣∣∣∣b∣∣∣∣c∣∣,其中a、 b和c分别是三个平面的法向量,θ是两个平面之 间的夹角。
适用范围
适用于两个平面不平行的情况。
06 案例分析
案例一:利用空间向量求线线角
定义
线线角是指两条直线之间的夹角。
计算公式
cosθ=∣∣a⋅b∣∣∣∣a∣∣∣∣b∣∣∣, 其中a和b是两条直线的方向向量,
高考必考题—运用空间向量解决空间角(含解析)

运用空间向量解决空间角一、题型选讲题型一 、异面直线所成的角以及研究异面直线所成的角首先要注意交的范围,然后转化为有直线的方向向量的夹角。
例1、【2018年高考江苏卷】如图,在正三棱柱ABC −A 1B 1C 1中,AB =AA 1=2,点P ,Q 分别为A 1B 1,BC 的中点.(1)求异面直线BP 与AC 1所成角的余弦值; (2)求直线CC 1与平面AQC 1所成角的正弦值.例2、(2019南京学情调研) 如图,在正四棱柱ABCDA 1B 1C 1D 1中,已知底面ABCD 的边长AB =3,侧棱AA 1=2,E 是棱CC 1的中点,点F 满足AF →=2FB →.(1) 求异面直线FE 和DB 1所成角的余弦值; (2) 记二面角EB 1FA 的大小为θ,求|cos θ|.题型二、直线与平面所成的角直线与平面所成的角是通过研究直线的方向向量和平面的法向量的所成的角,因此,要特别注意所求的角与已求的角之间的关系。
例3、【2020年高考浙江】如图,在三棱台ABC—DEF中,平面ACFD⊥平面ABC,∠ACB=∠ACD=45°,DC =2BC.(Ⅰ)证明:EF⊥DB;(Ⅱ)求直线DF与平面DBC所成角的正弦值.例4、【2020年高考全国Ⅱ卷理数】如图,已知三棱柱ABC-A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点,过B1C1和P的平面交AB于E,交AC于F.(1)证明:AA1∥MN,且平面A1AMN⊥平面EB1C1F;(2)设O为△A1B1C1的中心,若AO∥平面EB1C1F,且AO=AB,求直线B1E与平面A1AMN所成角的正弦值.题型三、平面与平面所成的角利用平面的法向量求二面角的大小时,当求出两半平面α,β的法向量n1,n2时,要根据观察判断向量在图形中的方向,从而确定二面角与向量n1,n2的夹角是相等还是互补,这是利用向量求二面角的难点、易错点例5、【2019年高考全国Ⅱ卷理数】如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.(1)证明:BE⊥平面EB1C1;(2)若AE=A1E,求二面角B–EC–C1的正弦值.例6、【2019年高考全国Ⅲ卷理数】图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连结DG,如图2.(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)求图2中的二面角B−CG−A的大小.例7、(2020届山东省潍坊市高三上期中)如图,在棱长均为2的三棱柱111ABC A B C -中,平面1ACB ⊥平面11A ABB ,11AB A B =,O 为1AB 与1A B 的交点.(1)求证:1AB CO ⊥;(2)求平面11ACC A 与平面ABC 所成锐二面角的余弦值.二、达标训练1、【2019年高考天津卷理数】如图,AE ⊥平面ABCD ,,CF AE AD BC ∥∥,,AD AB ⊥1,2AB AD AE BC ====.(1)求证:BF ∥平面ADE ;(2)求直线CE 与平面BDE 所成角的正弦值; (3)若二面角E BD F --的余弦值为13,求线段CF 的长.2、【2019年高考浙江卷】如图,已知三棱柱111ABC A B C -,平面11A ACC ⊥平面ABC ,90ABC ∠=︒,1130,,,BAC A A AC AC E F ∠=︒==分别是AC ,A 1B 1的中点. (1)证明:EF BC ⊥;(2)求直线EF 与平面A 1BC 所成角的余弦值.3、【2018年高考全国Ⅰ卷理数】如图,四边形ABCD 为正方形,,E F 分别为,AD BC 的中点,以DF 为折痕把DFC △折起,使点C 到达点P 的位置,且PF BF ⊥. (1)证明:平面PEF ⊥平面ABFD ; (2)求DP 与平面ABFD 所成角的正弦值.4、(2020届山东省九校高三上学期联考)已知四棱柱1111ABCD A B C D -的底面为菱形,12AB AA ==,3BAD π∠=,ACBD O =,AO ⊥平面1A BD ,11A B A D =.(1)证明:1//B C 平面1A BD ; (2)求钝二面角1B AA D --的余弦值.5、(2020届山东省潍坊市高三上期末)在底面为正方形的四棱锥P ABCD -中,平面PAD ⊥平面,,,ABCD PA PD E F =分别为棱PC 和AB 的中点.(1)求证://EF 平面PAD ;(2)若直线PC 与AB ,求平面PAD 与平面PBC 所成锐二面角的大小.6、(2019南京、盐城一模)如图,四棱锥PABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=1,PA =AB=2,点E是棱PB的中点.(1) 求异面直线EC与PD所成角的余弦值;(2) 求二面角BECD的余弦值.一、题型选讲题型一 、异面直线所成的角以及研究异面直线所成的角首先要注意交的范围,然后转化为有直线的方向向量的夹角。
利用向量法求空间角》教案

利用向量法求空间角一、教学目标1. 让学生掌握空间向量的基本概念和性质。
2. 让学生学会使用向量法求解空间角。
3. 培养学生解决实际问题的能力。
二、教学内容1. 空间向量的基本概念和性质。
2. 向量法求解空间角的基本步骤。
3. 实际问题中的应用案例。
三、教学方法1. 采用讲授法,讲解空间向量的基本概念和性质。
2. 采用演示法,展示向量法求解空间角的步骤。
3. 采用案例教学法,分析实际问题中的应用。
四、教学步骤1. 引入空间向量的概念,讲解其基本性质。
2. 讲解向量法求解空间角的基本步骤。
3. 分析实际问题中的应用案例,引导学生运用向量法解决问题。
五、课后作业1. 复习本节课所学内容,整理笔记。
2. 完成课后练习题,巩固所学知识。
3. 选择一个实际问题,尝试运用向量法解决。
六、教学评价1. 课堂讲解:观察学生对空间向量概念和性质的理解程度。
2. 课后作业:检查学生对向量法求解空间角的掌握情况。
3. 实际问题解决:评估学生在实际问题中的应用能力。
七、教学资源1. 教案、PPT、教材等相关教学资料。
2. 计算机、投影仪等教学设备。
3. 实际问题案例库。
八、教学时间1课时(45分钟)九、教学重点与难点1. 空间向量的基本概念和性质。
2. 向量法求解空间角的基本步骤。
3. 实际问题中的应用案例。
十、教学PPT内容1. 空间向量的基本概念和性质。
2. 向量法求解空间角的基本步骤。
3. 实际问题中的应用案例。
十一、教学案例案例一:求解空间直角坐标系中两向量的夹角。
案例二:求解空间四边形的对角线夹角。
案例三:求解空间旋转体的主轴与旋转轴的夹角。
十二、教学反思本节课结束后,教师应认真反思教学效果,针对学生的掌握情况,调整教学策略,以提高学生对空间向量法的理解和应用能力。
十三、教学拓展1. 研究空间向量在几何中的应用。
2. 探索向量法在物理学、工程学等领域的应用。
十四、教学建议1. 注重学生空间想象能力的培养。
2. 鼓励学生积极参与课堂讨论,提高课堂氛围。
空间向量与立体几何(角度问题)教学设计

空间向量与立体几何(角度问题)教学设计空间向量与立体几何(角度问题)教学设计一、学习目标:1.能借助空间几何体内的位置关系求空间的夹角;2.能用向量方法解决线线、线面、面面的夹角的计算问题,体会向量方法在研究几何问题中的作用。
3、探究题型,掌握解法。
二、重难点:向量法在立体几何中求空间的夹角应用。
探究题型,掌握解法。
三、学情分析:本节内容是高考热点问题,需要学生做到非常熟练。
在平时的学习中,学生已经对该几类问题有所认识,本堂课重点在于让学生体会空间角度与向量角度之间的差异,培养学生养成良好的答题习惯。
四、教学过程本节课为高三复习课,所以从开始直奔主题,从回顾旧知开始直接进入例题讲解、课堂练习、方法提炼、课堂小结,重点在于提炼解决类型题的方法并配合相应例题进行巩固,提高课堂效率。
设计意图我们都已经学过空间向量,在空间中如何将点线面的位置量化?回顾旧知,让学生理解空间坐标系的作用在于量化点线面位置①点→空间直角坐标系下点的坐标②线→直线的方向向量③面→平面上一的一点、平面的法向量直线的方向向量→直线上任意两点坐标之差平面的法向量→①设;②找;③列;④求。
所谓平面的法向量,就是指所在的直线与的向量,显然一个平面的法向量有多个,它们是向量.明确点、线、面如何用空间直角坐标系里的坐标进行标示明确方向向量与平面法向量的求法,回顾旧知识。
因为在后续问题中,求已知平面的法向量会多次出现,在此再次回顾法向量为何能确定一个平面,让学生加深对平面法向量的认识。
在空间中,给定一个点A和一个向量a,那么以向量a为法向量且经过点A的平面是.二:几个空间角的范围(1)异面直线所成的角θ:0<θ≤π2;(2)直线与平面所成的角θ:0≤θ≤π2;(3)二面角θ:0≤θ≤π.回顾空间角的范围,先从范围的角度与向量与向量的夹角范围进行比较,强调两者的不同三、利用向量求空间角1.两条异面直线所成角的求法设两条异面直线a,b的方向向量为a,b,其夹角为θ,则cosφ=|cosθ|=(其中φ为异面直线a,b所成的角).2.直线和平面所成的角的求法如图所示,设直线l的方向向量为e,平面α的法向量为n,直线l与平面α所成的角为φ,两向量e与n的夹角为θ,则有sinφ=|cosθ|= .3.求二面角的大小(1)如图①,AB、CD是二面角α-l-β的两个面内与棱l垂直的直线,则二面角的大小θ=.结合图像,让学生更直观地了解到线面所成的角与直线方向向量同平面法向量之间所成的角存在的区别与联系,从而找到适当的方法进行调整结合图像,让学生更直观地了解到二面角与直线方向向量同平面法向量之(2)如图②③,n1,n2分别是二面角α-l -β的两个半平面α,β的法向量,则二面角的小大θ=.求空间角:设直线l1,l2的方向向量分别为a,b,平面α、β的法向量分别为n,m.①异面直线l1与l2所成的角为θ,则cosθ=|a·b||a||b|.②直线l1与平面α所成的角为θ,则sinθ=|a·n||a||n|.③平面α与平面β所成的二面角为θ,则|cosθ|=|n·m||n||m|.、间所成的角存在的区别与联系,从而找到适当的方法进行调整通过之前的对比,分析清楚空间角与向量角之间存在的差异后,找寻适当的方法去解决差异,从而统一解题方法。
3.2 向量法解决角度问题

解 由(1)知OC⊥AB,OA1⊥AB. 又平面ABC⊥平面AA1B1B,交线为AB, 所以OC⊥平面AA1B1B, 故OA,OA1,OC两两垂直,以O为坐标原点, 建立如图所示的空间直角坐标系Oxyz.
设 AB=2,则 A(1,0,0),A1(0, 3,0),C(0,0, 3),B(-1,0,0), 则B→C=(1,0, 3),B→B1=A→A1=(-1, 3,0), A→1C=(0,- 3, 3).
证明 取AB的中点O,连接OC,OA1,A1B. 因为CA=CB,所以OC⊥AB. 由于AB=AA1,∠BAA1=60°, 故△AA1B为等边三角形,所以OA1⊥AB. 因为OC∩OA1=O,所以AB⊥平面OA1C. 又A1C⊂平面OA1C,故AB⊥A1C.
(2)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C与平面BB1C1C所成角的正 弦值.
3,1,-
3· 7×
3,-1,- 7
3|=17.
∴异面直线 A1B 与 AO1 所成角的余弦值为17.
反思感悟 求异面直线夹角的方法 (1)传统法:作出与异面直线所成角相等的平面角,进而构造三角形求解. (2)向量法:在两异面直线 a 与 b 上分别取点 A,B 和 C,D,则A→B与C→D可分
30 C. 30
15 D. 15
解析 建立如图所示的空间直角坐标系,设正方体的棱长为2,
则B1(2,2,2),M(1,1,0),D1(0,0,2),N(1,0,0), ∴B→1M=(-1,-1,-2),
D→1N=(1,0,-2),
∴cos〈B→1M,D→1N〉=
-1+4 1+1+4×
= 1+4
30 10 .
所以 O(0,0,0),B1( 3,0,2),C1(0,1,2),
向量法求空间角(含解析)
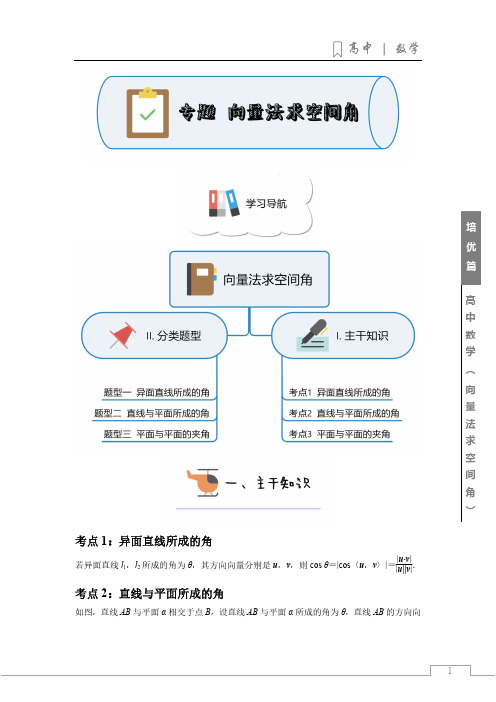
高中数学 ︵ 向量法求空间角︶培优篇考点1:异面直线所成的角若异面直线l 1,l 2所成的角为θ,其方向向量分别是u ,v ,则cos θ=|cos 〈u ,v 〉|=|u·v||u||v|.考点2:直线与平面所成的角如图,直线AB 与平面α相交于点B ,设直线AB 与平面α所成的角为θ,直线AB 的方向向高中数学 ︵ 向量法求空间角︶培优篇量为u ,平面α的法向量为n ,则sin θ=|cos 〈u ,n 〉|= u ·n |u ||n |=|u·n||u||n|.考点3:平面与平面的夹角如图,平面α与平面β相交,形成四个二面角,我们把这四个二面角中不大于90°的二面角称为平面α与平面β的夹角.若平面α,β的法向量分别是n 1和n 2,则平面α与平面β的夹角即为向量n 1和n 2的夹角或其补角.设平面α与平面β的夹角为θ,则cos θ=|cos 〈n 1,n 2〉|=|n 1·n 2||n 1||n 2|.【常用结论总结】1.线面角θ的正弦值等于直线的方向向量a 与平面的法向量n 所成角的余弦值的绝对值,即sin θ=|cos 〈a ,n 〉|,不要误记为cos θ=|cos 〈a ,n 〉|. 2.二面角的范围是[0,π],两个平面夹角的范围是0,2.【例1】 直三棱柱ABC -A 1B 1C 1如图所示,AB =4,BC=3,AC =5,D 为棱AB 的中点,三棱柱的各顶点在同一球面上,且球的表面积为61π,则异面直线A 1D 和B 1C 所成的角的余弦值为( )高中数学 ︵ 向量法求空间角︶培优篇A .5B .25C .5D .25【例2】 如图,四棱锥P −ABCD 中,底面ABCD 为正方形,△PAD 是正三角形,AB =2,平面PAD ⊥平面ABCD ,则PC 与BD 所成角的余弦值为( )A .14B .4C .13D 【例3】 如图四棱锥P -ABCD 中,底面ABCD 为正方形,各棱长均相等,E 是PB 的中点,则异面直线AE 与PC 所成角的余弦值为()A 6B C .13D .12学霸笔记用向量法求异面直线所成的角的一般步骤(1)建立空间直角坐标系;(2)用坐标表示两异面直线的方向向量; (3)利用向量的夹角公式求出向量夹角的余弦值;(4)注意两异面直线所成角的范围是(0,],即两异面直线所成角的余弦值等于两向量夹角的余弦值的绝对值.高中数学 ︵ 向量法求空间角︶培优篇【对点训练1】 如图,在三棱柱ABC -A 1B 1C 1中,底面边长和侧棱长均相等,∠BAA 1=∠CAA 1=60°,则异面直线AB 1与BC 1所成角的余弦值为()AB .13C .4D 【对点训练2】 “曲池”是《九章算术》记载的一种几何体,该几何体是上、下底面均为扇环形的柱体(扇环是指圆环被扇形截得的部分).现有一个如图所示的曲池,AA ⊥面ABCD ,AA 1=4,底面扇环所对的圆心角为π2,AD 的长度是BC 长度的2倍,CD =1,则异面直线A 1D 1与BC 1所成角的正弦值为()A .3B .13C .3D .4【对点训练3】 如图,在直三棱柱ABC -A 1B 1C 1中,AA 1=AC=AB=2,BC =2√2,Q 为A 1B 1的中点,E 为AQ 的中点,F 为BC 1的中点,则异面直线BE 与AF所成角的余弦值为( )A. BC .D高中数学 ︵ 向量法求空间角︶培优篇【例4】 在正方体ABCD −A B C D 中,如图E 、F 分别是BB 1、CD 的中点. (1)求证:平面AD F ⊥平面ADE ; (2)求直线EF 与AD F 所成角的正弦值.【例5】 如图,在四棱锥P -ABCD 中,底面ABCD 是平行四边形,P A ⊥平面ABCD ,P A=AD=2AB=8,点M 在棱PD 上,且PA =PM ⋅PD ,AM ⊥MC.(1)求证:CD ⊥平面P AD ;(2)求BM 与平面ACM 所成角的余弦值.高中数学 ︵ 向量法求空间角︶培优篇 学霸笔记利用空间向量求线面角的解题步骤【对点训练4】 如图,正方体ABCD -A 1B 1C 1D 1中,E 、F 分别为棱BC 、CD 的中点. (1)求证:D 1 F ∥平面A 1EC1;(2)求直线AC 1与平面A 1EC 1所成角的正弦值.高中数学 ︵ 向量法求空间角︶培优篇 【对点训练5】 如图所示,在直四棱柱ABCD -A 1B 1C 1D 1中,底面ABCD 为菱形,∠ABC =60°,AB =2,AA 1=2√3,E 为线段DD 1上一点.(1)求证:AC ⊥B 1D ;(2)若平面AB 1E 与平面ABCD 的夹角的余弦值为25,求直线BE与平面AB 1E 所成角的正弦值.高中数学 ︵ 向量法求空间角︶培优篇【例6】 在如图所示的空间几何体中,△ACD 与△ACB 均是等边三角形,直线ED ⊥平面ACD ,直线EB ⊥平面ABC ,DE ⊥BE . (1)求证:平面ABC ⊥平面ADC ;(2)求平面ACE 与平面BCE 夹角的余弦值.【例7】 如图,三棱锥A −BCD 中,DA =DB =DC ,BD ⊥CD ,∠ADB =∠ADC =60∘,E 为BC 的中点. (1)证明:BC ⊥DA ;(2)点F满足EF⃗=DA ⃗,求二面角D −AB −F 的正弦值.高中数学 ︵ 向量法求空间角︶培优篇学霸笔记利用空间向量求平面与平面夹角的解题步骤【对点训练6】 直三棱柱ABC −A B C 中,AA =AB =AC =2,AA ⊥AB,AC ⊥AB ,D 为A B 的中点,E 为AA 的中点,F 为CD 的中点. (1)求证:EF ∥平面ABC ;(2)求直线BE 与平面CCD所成角的正弦值; (3)求平面A CD 与平面CC D 夹角的余弦值.高中数学 ︵ 向量法求空间角︶培优篇 【对点训练7】 如图,在棱长为2的正方体ABCD −A B C D 中,E 为棱BC 的中点,F 为棱CD 的中点.(1)求证:D 1F ∥平面A EC ;(2)求直线AC 与平面A EC 所成角的正弦值. (3)求二面角A −A C −E 的正弦值.【对点训练8】 如图,PO 是三棱锥P −ABC 的高,PA =PB ,AB ⊥AC ,E 是PB 的中点. (1)证明:OE ∥平面PAC ;(2)若∠ABO=∠CBO =30°,PO =3,PA =5,求二面角C −AE −B 的正弦值.。
向量法求解空间距离与空间角

向量法求解空间距离与空间角要求能掌握用向量法解决空间距离与空间角问题。
一、 空间向量与空间距离由向量的数量积||||cos AB b AB b θ⋅=⋅可知,向量AB 在向量b (直线l 的方向向量)方向上的射影(投影)是||cos ||AB b AB b θ⋅=,也就是说向量AB 在向量b (直线l 的方向向量)方向上的射影(投影)是线段AB 在直线l 上射影线段的长。
1、 点面距离公式:平面α的法向量为n ,P 是平面α外一点,点M 为平面α内任一点,则P 到平面α的距离d 就是MP在向量n 方向上射影的绝对值,即||||n MP d n ⋅=。
2、 线面距离公式: 平面α∥直线l ,平面α的法向量为n ,P ∈直线l ,点M 为平面α内一点,则直线l 与平面α的距离d 就是MP 在向量n 方向上射影的绝对值,即||||n MP d n ⋅=。
3、 面面距离公式:平面α∥平面β,平面α的法向量为n,点M 为平面α内一点,点P 为β平面β内一点,则平面α与平面β的距离d就是MP 在向量n 方向上射影的绝对值,即||||n MP d n ⋅=。
4、向量法求解距离问题的步骤: ① 建立适当的空间直角坐标系;② 将相应线段及平面的法线等用向量或坐标表示出来; ③ 利用向量的相应距离公式求解。
5、典例评析: 例1、(03广东)已知四棱柱ABCD -A 1B 1C 1D 1中,AB=1,AA 1=2,点E 是CC 1的中点,F 是BD 1中点。
(1)证明:EF 是BD 1与CC 1的公垂线; (2)求点D 1到面BDE 的距离。
二、 空间向量与空间的角 1、 异面直线所成的角:异面直线a 、b 的方向向量分别为m 、n,其向量的夹角为θ,直线a 、b 的所成的角为α,(0,]2πα∈,则||cos |cos |||||m n m n αθ⋅== ,即||cos ||||m n arc m n α⋅=。
高中数学空间向量与立体几何立体几何中的向量方法利用空间向量求空间角空间距离问题数学.doc

3.2.3 利用空间向量求空间角、空间距离问题1.空间角及向量求法(1)两异面直线所成的角与两直线的方向向量所成的角相等.( )(2)直线l∥平面α,则直线l到平面α的距离就是直线l上的点到平面α的距离.( )(3)若平面α∥β,则两平面α,β的距离可转化为平面α内某条直线到平面β的距离,也可转化为平面α内某点到平面β的距离.( )答案 (1)× (2)√ (3)√2.做一做(请把正确的答案写在横线上)(1)已知两平面的法向量分别为m =(0,1,0),n =(0,1,1),则两平面所成的二面角的大小为________.(2)(教材改编P 111A 组T 11)如图,在正方体ABCD -A 1B 1C 1D 1中,M 是C 1C 的中点,O 是底面ABCD 的中点,P 是A 1B 1上的任意点,则直线BM 与OP 所成的角为________.(3)已知平面α的一个法向量为n =(-2,-2,1),点A (-1,3,0)在平面α内,则点P (-2,1,4)到平面α的距离为________.答案 (1)45°或135° (2)π2 (3)103解析 (2)建立如图所示的空间直角坐标系,设正方体棱长为2 ,则O (1,1,0),P (2,x,2),B (2,2,0),M (0,2,1),则OP→=(1,x -1,2),BM →=(-2,0,1).所以OP →·BM →=0,所以直线BM 与OP 所成角为π2. 探究1 利用空间向量求线线角例1 如图1,已知两个正四棱锥P -ABCD 与Q -ABCD 的高分别为1和2,AB =4.求异面直线AQ 与PB 所成角的余弦值.[解] 由题设知,ABCD 是正方形,连接AC ,BD ,交于点O ,则AC ⊥BD .连接PQ ,则PQ 过点O .由正四棱锥的性质知PQ ⊥平面ABCD ,故以O 为坐标原点,以直线CA,DB,QP分别为x轴、y轴、z轴建立空间直角坐标系(如图2),则P(0,0,1),A(22,0,0),Q(0,0,-2),B(0,22,0),∴AQ→=(-22,0,-2),PB→=(0,22,-1).于是cos〈AQ→,PB→〉=AQ→·PB→|AQ→||PB→|=39,∴异面直线AQ与PB所成角的余弦值为3 9 .拓展提升两异面直线所成角的求法(1)平移法:即通过平移其中一条(也可两条同时平移),使它们转化为两条相交直线,然后通过解三角形获解.(2)取定基底法:在一些不适合建立坐标系的题型中,我们经常采用取定基底的方法,这是小技巧.在由公式cos〈a,b〉=a·b|a||b|求向量a、b的夹角时,关键是求出a·b及|a|与|b|,一般是把a、b用一组基底表示出来,再求有关的量.(3)用坐标法求异面直线的夹角的方法①建立恰当的空间直角坐标系;②找到两条异面直线的方向向量的坐标形式;③利用向量的夹角公式计算两直线的方向向量的夹角;④结合异面直线所成角的范围得到异面直线所成的角.【跟踪训练1】如图,在三棱锥V-ABC中,顶点C在空间直角坐标系的原点处,顶点A,B,V分别在x,y,z轴上,D是线段AB 的中点,且AC =BC =2,∠VDC =θ.当θ=π3时,求异面直线AC 与VD 所成角的余弦值.解 由于AC =BC =2,D 是AB 的中点,所以C (0,0,0),A (2,0,0),B (0,2,0),D (1,1,0).当θ=π3时,在Rt △VCD 中,CD =2,故有V (0,0,6).所以AC →=(-2,0,0),VD →=(1,1,-6).所以cos 〈AC →,VD →〉=AC →·VD→|AC →||VD →|=-22×22=-24.所以异面直线AC 与VD 所成角的余弦值为24.探究2 利用空间向量求线面角例2 正三棱柱ABC -A 1B 1C 1的底面边长为a ,侧棱长为2a ,求AC 1与侧面ABB 1A 1所成的角.[解] 建立如下图所示的空间直角坐标系,则A (0,0,0),B (0,a,0),A 1(0,0, 2a ),C 1⎝⎛⎭⎪⎪⎫-32a ,a2, 2a , 取A 1B 1的中点M ,则M ⎝⎛⎭⎪⎫0,a2,2a ,连接AM ,MC 1,有MC 1→=⎝ ⎛⎭⎪⎪⎫-32a ,0,0, AB →=(0,a,0),AA1→=(0,0,2a ).∴MC 1→·AB →=0,MC 1→·AA 1→=0, ∴MC 1→⊥AB →,MC1→⊥AA 1→, 即MC 1⊥AB ,MC 1⊥AA 1,又AB ∩AA 1=A , ∴MC 1⊥平面ABB 1A 1 .∴∠C 1AM 是AC 1与侧面A 1ABB 1所成的角.由于AC 1→=⎝ ⎛⎭⎪⎪⎫-32a ,a 2,2a ,AM →=⎝ ⎛⎭⎪⎫0,a 2,2a ,∴AC 1→·AM →=0+a 24+2a 2=9a 24,|AC 1→|=3a 24+a 24+2a 2=3a , |AM →|=a 24+2a 2=32a , ∴cos 〈AC1→,AM →〉=9a 243a ×3a 2=32. ∴〈AC 1→,AM →〉=30°,即AC 1与侧面ABB 1A 1所成的角为30°. [解法探究] 此题有没有其他解法?解 与原解建立相同的空间直角坐标系,则AB →=(0,a,0),AA1→=(0,0,2a ),AC 1→=⎝ ⎛⎭⎪⎪⎫-32a ,a 2,2a . 设侧面ABB 1A 1的法向量n =(λ,x ,y ),∴n ·AB →=0且n ·AA1→=0.∴ax =0且2ay =0.∴x =y =0.故n =(λ,0,0).∵AC 1→=⎝ ⎛⎭⎪⎪⎫-32a ,a 2,2a , ∴cos 〈AC 1→,n 〉=n ·AC1→|n ||AC 1→|=-λ2|λ|.∴|cos 〈AC 1→,n 〉|=12. ∴AC 1与侧面ABB 1A 1所成的角为30°.[条件探究] 此题中增加条件“E ,F ,G 为AB ,AA 1,A 1C 1的中点”,求B 1F 与平面GEF 所成角的正弦值.解 建立如图所示的空间直角坐标系,则B 1(0,a ,2a ),E ⎝ ⎛⎭⎪⎫0,a 2,0,F ⎝ ⎛⎭⎪⎪⎫0,0,22a ,G ⎝⎛⎭⎪⎪⎫-34a ,a 4,2a , 于是B 1F →=⎝ ⎛⎭⎪⎪⎫0,-a ,-22a ,EF →=⎝ ⎛⎭⎪⎪⎫0,-a 2,22a , EG →=⎝ ⎛⎭⎪⎪⎫-34a ,-a 4,2a . 设平面GEF 的法向量n =(x ,y ,z ),则⎩⎨⎧n ·EF →=0,n ·EG →=0,即⎩⎪⎨⎪⎧-a 2y +22az =0,-34ax -a 4y +2az =0,所以⎩⎪⎨⎪⎧y =2z ,x =6z ,令z =1,得x =6,y =2,所以平面GEF 的一个法向量为n =(6,2,1), 所以|cos 〈B 1F →,n 〉|=|n ·B 1F →||n ||B 1F →|=⎪⎪⎪⎪⎪⎪⎪⎪-2a -22a 9×a 2+a 22=33. 所以B 1F 与平面GEF 所成角的正弦值为33.拓展提升求直线与平面的夹角的方法与步骤思路一:找直线在平面内的射影,充分利用面与面垂直的性质及解三角形知识可求得夹角(或夹角的某一三角函数值).思路二:用向量法求直线与平面的夹角可利用向量夹角公式或法向量.利用法向量求直线与平面的夹角的基本步骤:(1)建立空间直角坐标系; (2)求直线的方向向量AB →; (3)求平面的法向量n ;(4)计算:设线面角为θ,则sin θ=|n ·AB→||n ||AB→|.【跟踪训练2】 如图,四棱锥P -ABCD 中,PA ⊥底面ABCD ,AD ∥BC ,AB =AD =AC =3,PA =BC =4,M 为线段AD 上一点,AM =2MD ,N 为PC 的中点.(1)证明:MN ∥平面PAB ;(2)求直线AN 与平面PMN 所成角的正弦值.解 (1)证明:由已知得AM =23AD =2.取BP 的中点T ,连接AT ,TN .由N 为PC 的中点知TN ∥BC ,TN =12BC =2.又AD ∥BC ,故TN 綊AM ,四边形AMNT 为平行四边形,于是MN ∥AT .因为AT ⊂平面PAB ,MN ⊄平面PAB ,所以MN ∥平面PAB .(2)取BC 的中点E ,连接AE .由AB =AC 得AE ⊥BC ,从而AE ⊥AD ,且AE =AB 2-BE 2=AB2-⎝ ⎛⎭⎪⎫BC 22= 5.以A 为坐标原点,AE →的方向为x 轴正方向,建立如图所示的空间直角坐标系Axyz .由题意知,P (0,0,4),M (0,2,0),C (5,2,0),N ⎝⎛⎭⎪⎪⎫52,1,2, PM →=(0,2,-4),PN →=⎝ ⎛⎭⎪⎪⎫52,1,-2,AN →=⎝ ⎛⎭⎪⎪⎫52,1,2. 设n =(x ,y ,z )为平面PMN 的法向量,则⎩⎨⎧n ·PM →=0,n ·PN →=0,即⎩⎪⎨⎪⎧2y -4z =0,52x +y -2z =0,可取n =(0,2,1).于是|cos 〈n ,AN →〉|=|n ·AN →||n ||AN →|=8525,则直线AN 与平面PMN所成角的正弦值为8525.探究3 利用空间向量求二面角例3 如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,面ABEF 为正方形,AF =2FD ,∠AFD =90°,且二面角D -AF -E 与二面角C -BE -F 都是60°.(1)证明:平面ABEF⊥平面EFDC;(2)求二面角E-BC-A的余弦值.[解] (1)证明:由已知可得AF⊥DF,AF⊥FE,所以AF⊥平面EFDC.又AF⊂平面ABEF,故平面ABEF⊥平面EFDC.(2)过D作DG⊥EF,垂足为G,由(1)知DG⊥平面ABEF.以G为坐标原点,GF→的方向为x轴正方向,|GF→|为单位长,建立如图所示的空间直角坐标系Gxyz.由(1)知∠DFE为二面角D-AF-E的平面角,故∠DFE=60°,则DF=2,DG=3,可得A(1,4,0),B(-3,4,0),E(-3,0,0),D(0,0,3).由已知,AB∥EF,AB⊄平面EFDC,EF⊂平面EFDC,所以AB∥平面EFDC.又平面ABCD∩平面EFDC=CD,故AB∥CD,CD∥EF.由BE∥AF,可得BE⊥平面EFDC,所以∠CEF为二面角C-BE -F的平面角,∠CEF=60°.从而可得C(-2,0,3).连接AC,则EC→=(1,0,3),EB→=(0,4,0),AC→=(-3,-4,3),AB→=(-4,0,0).设n=(x,y,z)是平面BCE的法向量,则⎩⎨⎧n ·EC →=0,n ·EB →=0,即⎩⎪⎨⎪⎧x +3z =0,4y =0,所以可取n =(3,0,-3).设m 是平面ABCD 的法向量,则⎩⎨⎧m ·AC →=0,m ·AB →=0,同理可取m =(0,3,4).则cos 〈n ,m 〉=n ·m |n ||m |=-21919.故二面角E -BC -A 的余弦值为-21919.拓展提升二面角的向量求法(1)若AB ,CD 分别是二面角α-l -β的两个半平面内与棱l 垂直的异面直线,则二面角的大小就是向量AB →与CD →的夹角(如图①).(2)利用坐标法求二面角的步骤设n 1,n 2分别是平面α,β的法向量,则向量n 1与n 2的夹角(或其补角)就是两个平面夹角的大小,如图②.用坐标法的解题步骤如下:①建系:依据几何条件建立适当的空间直角坐标系. ②求法向量:在建立的坐标系下求两个面的法向量n 1,n 2.③计算:求n1与n2所成锐角θ,cosθ=|n1·n2| |n1||n2|.④定值:若二面角为锐角,则为θ;若二面角为钝角,则为π-θ.【跟踪训练3】若PA⊥平面ABC,AC⊥BC,PA=AC=1,BC =2,求二面角A-PB-C的余弦值.解 解法一:如下图所示,取PB 的中点D ,连接CD .∵PC =BC =2,∴CD ⊥PB .∴作AE ⊥PB 于E ,那么二面角A -PB -C 的大小就等于异面直线DC 与EA 所成的角θ的大小.∵PD =1,PE =PA 2PB =12,∴DE =PD -PE =12,又∵AE =AP ·AB PB =32,CD =1,AC =1,AC →=AE →+ED →+DC →,且AE →⊥ED →,ED →⊥DC→,∴|AC →|2=|AE →|2+|ED →|2+|DC →|2+2|AE →|·|DC →|·cos(π-θ), 即1=34+14+1-2×32×1×cos θ,解得cos θ=33.故二面角A -PB -C 的余弦值为33.解法二:由解法一可知,向量DC →与EA →的夹角的大小就是二面角A -PB -C 的大小,如图,建立空间直角坐标系Cxyz ,则A (1,0,0),B (0,2,0),C (0,0,0),P (1,0,1),D 为PB的中点,D ⎝⎛⎭⎪⎪⎫12,22,12. ∵PE EB =AP 2AB 2=13,即E 分PB →的比为13,∴E ⎝⎛⎭⎪⎪⎫34,24,34,EA →=⎝ ⎛⎭⎪⎪⎫14,-24,-34, DC →=⎝ ⎛⎭⎪⎪⎫-12,-22,-12,|EA →|=32,|DC →|=1,EA →·DC →=14×⎝ ⎛⎭⎪⎫-12+⎝ ⎛⎭⎪⎪⎫-24×⎝ ⎛⎭⎪⎪⎫-22+⎝ ⎛⎭⎪⎫-34×⎝ ⎛⎭⎪⎫-12=12.∴cos 〈EA →,DC →〉=EA →·DC →|EA →||DC →|=33. 故二面角A -PB -C 的余弦值为33.解法三:如右图所示,建立空间直角坐标系,则A (0,0,0),B (2,1,0),C (0,1,0),P (0,0,1),AP →=(0,0,1),AB →=(2,1,0),CB →=(2,0,0),CP →=(0,-1,1),设平面PAB 的法向量为m =(x ,y ,z ),则⎩⎨⎧m ·AP →=0,m ·AB →=0⇒⎩⎪⎨⎪⎧x ,y ,z ·0,0,1=0,x ,y ,z ·2,1,0=0⇒⎩⎪⎨⎪⎧y =-2x ,z =0,令x =1,则m =(1,-2,0),设平面PBC 的法向量为n =(x ′,y ′,z ′),则⎩⎨⎧n ·CB →=0,n ·CP →=0⇒⎩⎪⎨⎪⎧x ′,y ′,z ′·2,0,0=0,x ′,y ′,z ′·0,-1,1=0⇒⎩⎪⎨⎪⎧x ′=0,y ′=z ′.令y ′=-1,则n =(0,-1,-1),∴cos 〈m ,n 〉=m ·n |m ||n |=33.∴二面角A -PB -C 的余弦值为33.探究4 利用空间向量求距离例4 已知正方形ABCD 的边长为1,PD ⊥平面ABCD ,且PD =1,E ,F 分别为AB ,BC 的中点.(1)求点D 到平面PEF 的距离; (2)求直线AC 到平面PEF 的距离.[解] 解法一:(1)建立如图所示的空间直角坐标系,则D (0,0,0),P (0,0,1),A (1,0,0),C (0,1,0),E ⎝ ⎛⎭⎪⎫1,12,0,F ⎝ ⎛⎭⎪⎫12,1,0.设DH ⊥平面PEF ,垂足为H ,则DH →=xDE →+yDF →+zDP →=⎝ ⎛⎭⎪⎫x +12y ,12x +y ,z ·(x +y +z =1),PE →=⎝ ⎛⎭⎪⎫1,12,-1,PF →=⎝ ⎛⎭⎪⎫12,1,-1.∴DH →·PE →=x +12y +12⎝ ⎛⎭⎪⎫12x +y -z =54x +y -z =0.同理,DH →·PF →=x +54y -z =0,又x +y +z =1,∴可解得x =y =417,z =917.∴DH →=317(2,2,3).∴|DH →|=31717.因此,点D 到平面PEF 的距离为31717.(2)设AH ′⊥平面PEF ,垂足为H ′,则AH ′→∥DH →,设AH ′→=λ(2,2,3)=(2λ,2λ,3λ)(λ≠0),则EH ′→=EA →+AH ′→=⎝ ⎛⎭⎪⎫0,-12,0+(2λ,2λ,3λ)=⎝ ⎛⎭⎪⎫2λ,2λ-12,3λ.∴AH ′→·EH ′→=4λ2+4λ2-λ+9λ2=0,即λ=117.∴AH ′→=117(2,2,3),|AH ′→|=1717, 又AC ∥平面PEF ,∴AC 到平面PEF 的距离为1717.解法二:(1)由解法一建立的空间直角坐标系知EF →=⎝ ⎛⎭⎪⎫-12,12,0,PE →=⎝ ⎛⎭⎪⎫1,12,-1,DE →=⎝ ⎛⎭⎪⎫1,12,0,设平面PEF 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧-12x +12y =0,x +12y -z =0,解得⎩⎪⎨⎪⎧y =x ,z =32x ,令x =2,则n =(2,2,3), ∴点D 到平面PEF 的距离d =|DE →·n ||n |=|2+1|4+4+9=31717.(2)∵AC ∥EF ,∴直线AC 到平面PEF 的距离也即是点A 到平面PEF 的距离.又AE →=⎝ ⎛⎭⎪⎫0,12,0,∴点A 到平面PEF 的距离为 d =|AE →·n ||n |=117=1717.拓展提升1.向量法求点到直线的距离的两种思路(1)将求点到直线的距离问题转化为求向量模的问题,即利用待定系数法求出垂足的坐标,然后求出向量的模,这是求各种距离的通法.(2)直接套用点线距公式求解,其步骤为直线的方向向量a →所求点到直线上一点的向量PP ′→及其在直线的方向向量a 上的投影→代入公式.注意平行直线间的距离与点到直线的距离之间的转化. 2.点面距、线面距、面面距的求解方法线面距、面面距实质上都是求点面距,求直线到平面、平面到平面的距离的前提是线面、面面平行.点面距的求解步骤:(1)求出该平面的一个法向量;(2)找出从该点出发的平面的任一条斜线段对应的向量; (3)求出法向量与斜线段对应向量的数量积的绝对值,再除以法向量的模,即可求出点到平面的距离.【跟踪训练4】 正方体ABCD -A 1B 1C 1D 1的棱长为2,E ,F ,G 分别是C 1C ,D 1A 1,AB 的中点,求点A 到平面EFG 的距离.解 如图,建立空间直角坐标系,则A (2,0,0),E (0,2,1),F (1,0,2),G (2,1,0),∴EF →=(1,-2,1),EG →=(2,-1,-1),GA →=(0,-1,0). 设n =(x ,y ,z )是平面EFG 的法向量,则⎩⎨⎧n ·EF →=0,n ·EG →=0,∴⎩⎪⎨⎪⎧x -2y +z =0,2x -y -z =0,∴x =y =z ,可取n =(1,1,1), ∴d =|GA →·n ||n |=13=33,即点A 到平面EFG 的距离为33.探究5 与空间有关的探索性问题例5 如图,矩形ABCD 和梯形BEFC 所成的平面互相垂直,BE ∥CF ,∠BCF =∠CEF =90°,AD =3,EF =2.(1)求证:AE ∥平面DCF ;(2)当AB 的长为何值时,二面角A -EF -C 的大小为60°?[解] 如图,以点C 为坐标原点,以CB ,CF 和CD 所在直线分别作为x 轴、y 轴和z 轴,建立空间直角坐标系Cxyz .设AB =a ,BE =b ,CF =c ,则C (0,0,0),A (3,0,a ),B (3,0,0),E (3,b,0),F (0,c,0).(1)证明:AE →=(0,b ,-a ),CB →=(3,0,0),BE →=(0,b,0),∴CB →·AE →=0,CB →·BE →=0, 从而CB ⊥AE ,CB ⊥BE . 又AE ∩BE =E , ∴CB ⊥平面ABE . ∵CB ⊥平面DCF ,∴平面ABE ∥平面DCF .又AE ⊂平面ABE , 故AE ∥平面DCF .(2)∵EF →=(-3,c -b,0),CE →=(3,b,0), 且EF →·CE →=0,|EF→|=2, ∴⎩⎪⎨⎪⎧-3+b c -b =0,3+c -b2=2,解得b =3,c =4.∴E (3,3,0),F (0,4,0).设n =(1,y ,z )与平面AEF 垂直, 则n ·AE →=0,n ·EF →=0,即⎩⎪⎨⎪⎧1,y ,z ·0,3,-a =0,1,y ,z ·-3,1,0=0,解得n =⎝⎛⎭⎪⎪⎫1,3,33a.又∵BA ⊥平面BEFC ,BA →=(0,0,a ),∴|cos 〈n ,BA →〉|=|n ·BA →||n ||BA →|=334a 2+27=12, 解得a =92或a =-92(舍去).∴当AB =92时,二面角A -EF -C 的大小为60°.拓展提升利用向量解决存在性问题的方法策略求解存在性问题的基本策略是:首先,假定题中的数学对象存在;其次,构建空间直角坐标系;再次,利用空间向量法把存在性问题转化为求参数是否有解问题;最后,解方程,下结论.利用上述思维策略,可使此类存在性难题变为常规问题.【跟踪训练5】 在长方体ABCD -A 1B 1C 1D 1中,AD =AA 1=12AB ,点E 是棱AB 上一点,且AEEB=λ. (1)证明:D 1E ⊥A 1D ;(2)是否存在λ,使得二面角D 1-EC -D 的平面角为π4?并说明理由.解 (1)证明:以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴建立空间直角坐标系,如图所示.不妨设AD =AA 1=1,AB =2,则D (0,0,0),A (1,0,0),B (1,2,0),C (0,2,0),A 1(1,0,1),B 1(1,2,1),C 1(0,2,1),D 1(0,0,1).因为AEEB =λ,所以E ⎝⎛⎭⎪⎫1,2λ1+λ,0, 于是D 1E →=⎝ ⎛⎭⎪⎫1,2λ1+λ,-1,A 1D →=(-1,0,-1),所以D 1E →·A 1D →=⎝ ⎛⎭⎪⎫1,2λ1+λ,-1·(-1,0,-1)=-1+0+1=0,故D 1E ⊥A 1D .(2)因为DD 1⊥平面ABCD ,所以平面DEC 的一个法向量为n =(0,0,1),设平面D 1EC 的法向量为n 1=(x ,y ,z ),又CE →=⎝ ⎛⎭⎪⎫1,2λ1+λ-2,0,CD 1→=(0,-2,1), 则⎩⎨⎧n 1·CE →=0,n 1·CD 1→=0,即⎩⎪⎨⎪⎧n 1·⎝ ⎛⎭⎪⎫1,2λ1+λ-2,0=0,n 1·0,-2,1=0,整理得⎩⎪⎨⎪⎧x -y ·21+λ=0,-2y +z =0,取y =1,则n 1=⎝ ⎛⎭⎪⎫21+λ,1,2. 因为二面角D 1-EC -D 的平面角为π4,所以22=|n ·n 1||n ||n 1|,即22=21+4+⎝⎛⎭⎪⎫21+λ2,解得λ=233-1. 故存在λ=233-1,使得二面角D 1-EC -D 的平面角为π4.1.用空间向量解决立体几何问题的“三步曲”(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线,把立体几何问题转化为向量问题.(2)通过向量运算,研究点、直线、平面之间的位置关系以及相应的距离和夹角等问题.(3)把向量的运算结果“翻译”成相应的几何意义. 2.利用法向量求直线AB 与平面α所成的角θ的步骤 (1)求平面α的法向量n .(2)利用公式sin θ=|cos 〈AB →,n 〉|=|AB →·n ||AB →||n |,注意直线和平面所成角的取值范围为⎣⎢⎡⎦⎥⎤0,π2.3.利用法向量求二面角的余弦值的步骤 (1)求两平面的法向量.(2)求两法向量的夹角的余弦值.(3)由图判断所求的二面角是锐角、直角,还是钝角,从而下结论.在用法向量求二面角的大小时应注意:平面的法向量有两个相反的方向,取的方向不同求出来的角度当然就不同,所以最后还应该根据这个二面角的实际形态确定其大小.4.点面距的求解步骤(1)求出该平面的一个法向量.(2)找出从该点出发的平面的任一条斜线段对应的向量. (3)求出法向量与斜线段对应向量的数量积的绝对值,再除以法向量的模,即可求出点到平面的距离.1.若两异面直线l 1与l 2的方向向量分别为a =(0,4,-3),b =(1,2,0),则直线l 1与l 2的夹角的余弦值为( )A.32B.8525C.4315D.33答案 B解析 设l 1,l 2的夹角为θ,则cos θ=|cos 〈a ,b 〉|=0×1+4×2+-3×05×5=8525.2.直角△ABC 的两条直角边BC =3,AC =4,PC ⊥平面ABC ,PC =95,则点P 到斜边AB 的距离是( )A .5B .3C .3 2 D.125答案 B解析 以C 为坐标原点,CA ,CB ,CP 所在直线为x 轴、y 轴、z 轴,建立如图所示的空间直角坐标系.则A (4,0,0),B (0,3,0),P ⎝ ⎛⎭⎪⎫0,0,95,所以AB →=(-4,3,0),AP →=⎝⎛⎭⎪⎫-4,0,95, 所以AP →在AB →上的投影长为|AP →·AB →||AB →|=165,所以点P 到AB 的距离为d =|AP →|2-⎝ ⎛⎭⎪⎫1652=16+8125-25625=3.故选B.3.把正方形ABCD 沿对角线AC 折起成直二面角,点E ,F 分别是AD ,BC 的中点,O 是正方形中心,则折起后,∠EOF 的大小为( )A .(0°,90°)B .90°C .120°D .(60°,120°)答案 C解析 OE →=12(OA →+OD →),OF →=12(OB →+OC →),∴OE →·OF →=14(OA →·OB →+OA →·OC →+OD →·OB →+OD →·OC →)=-14|OA →|2.又|OE →|=|OF →|=22|OA →|,∴cos 〈OE →,OF →〉=-14|OA →|212|OA →|2=-12.∴∠EOF =120°.故选C. 4.平面α的法向量n 1=(1,0,-1),平面β的法向量n 2=(0,-1,1),则平面α与β所成二面角的大小为________.答案π3或2π3解析 设二面角的大小为θ,则cos 〈n 1,n 2〉=1×0+0×-1+-1×12·2=-12,所以cos θ=12或-12,∴θ=π3或2π3.5.如图,在长方体AC 1中,AB =BC =2,AA 1=2,点E ,F 分别是平面A 1B 1C 1D 1、平面BCC 1B 1的中心.以D 为坐标原点,DA ,DC ,DD 1所在直线分别为x ,y ,z 轴建立空间直角坐标系.试用向量方法解决下列问题:(1)求异面直线AF 和BE 所成的角;(2)求直线AF 和平面BEC 所成角的正弦值.解 (1)由题意得A (2,0,0),F ⎝ ⎛⎭⎪⎪⎫1,2,22,B (2,2,0),E (1,1,2),C (0,2,0).∴AF →=⎝⎛⎭⎪⎪⎫-1,2,22,BE →=(-1,-1,2), ∴AF →·BE →=1-2+1=0.∴直线AF 和BE 所成的角为90°.(2)设平面BEC 的法向量为n =(x ,y ,z ),又BC→=(-2,0,0),BE →=(-1,-1,2),则n ·BC →=-2x =0,n ·BE →=-x -y +2z =0,∴x =0,取z =1,则y =2,∴平面BEC 的一个法向量为n =(0,2,1).∴cos 〈AF →,n 〉=AF →·n|AF →||n |=522222×3=53333.设直线AF 和平面BEC 所成的角为θ,则sin θ=53333,即直线AF 和平面BEC 所成角的正弦值为53333.。
考点3.2 空间向量与空间角的计算问题(解析版)
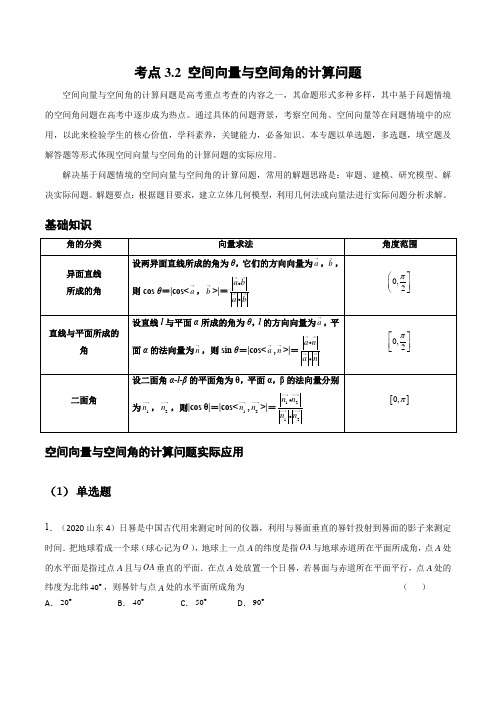
考点3.2 空间向量与空间角的计算问题空间向量与空间角的计算问题是高考重点考查的内容之一,其命题形式多种多样,其中基于问题情境的空间角问题在高考中逐步成为热点。
通过具体的问题背景,考察空间角、空间向量等在问题情境中的应用,以此来检验学生的核心价值,学科素养,关键能力,必备知识。
本专题以单选题,多选题,填空题及解答题等形式体现空间向量与空间角的计算问题的实际应用。
解决基于问题情境的空间向量与空间角的计算问题,常用的解题思路是:审题、建模、研究模型、解决实际问题。
解题要点:根据题目要求,建立立体几何模型,利用几何法或向量法进行实际问题分析求解。
基础知识a ,b ,a ,b >|=a b a b与平面α所成的角为θ,l 的方向向量为a ,平的法向量为n ,则sin θ=|cos<a ,n >|=a n a n的平面角为θ,平面α,β的法向量分别1n ,2n ,则|cos θ|=|cos<1n ,2n >|=1212n n n n空间向量与空间角的计算问题实际应用 (1) 单选题1.(2020山东4)日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O ),地球上一点A 的纬度是指OA 与地球赤道所在平面所成角,点A 处的水平面是指过点A 且与OA 垂直的平面.在点A 处放置一个日晷,若晷面与赤道所在平面平行,点A 处的纬度为北纬40︒,则晷针与点A 处的水平面所成角为 ( )A .20︒B .40︒C .50︒D .90︒【答案】B【思路导引】画出截面图,根据点A 处的纬度,计算出晷针与点A 处的水平面所成角.【解析】画出截面图如下图所示,其中CD 是赤道所在平面的截线;l 是点A 处的水平面的截线,依题意可知OA l ⊥;AB 是晷针所在直线.m 是晷面的截线,依题意可知//m CD 、AB m ⊥. 由于40,//AOC m CD ∠=︒,所以40OAG AOC ∠=∠=︒, 由于90OAG GAE BAE GAE ∠+∠=∠+∠=︒,所以40BAE OAG ∠=∠=︒,也即晷针与点A 处的水平面所成角为40BAE ∠=︒,故选:B .2.(2014浙江)如图,某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练,已知点A 到墙面的距离为AB ,某目标点P 沿墙面的射击线CM 移动,此人为了准确瞄准目标点P ,需计算由点A 观察点P 的仰角θ的大小(仰角θ为直线AP 与平面ABC 所成角).若15AB m =,25AC m =,30BCM ∠=︒则tan θ的最大值ABCD【答案】D【解析】作PH BC ⊥,垂足为H ,设PH x =,则CH =,由余弦定理AH =1tan tan(0)PHPAHAH xθ=∠==>,故当1x=tanθ,故选D.3.(2020·山东临沂市·高二期中)如图为某种礼物降落伞的示意图,其中有8根绳子和伞面连接,每根绳子和水平面的法向量的夹角均为60.已知礼物的质量为1kg,每根绳子的拉力大小相同.若重力加速度g取29.8m/s,则降落伞在匀速下落的过程中每根绳子拉力的大小为()A.2.25N B.2.45N C.2.5N D.2.75N【答案】B【分析】根据8根绳子的合力大小与礼物的重力大小相等可构造方程求得结果.【详解】由题意知:8根绳子的合力大小与礼物的重力大小相等,设每根绳子的拉力为T,则8cos6019.8T=⨯,解得: 2.45T=(N).故选:B.4.(2020·济南市·山东省实验中学高二期中)空间直角坐标系O xyz-中,经过点()000,,P x y z,且法向量为(),,m A B C=的平面方程为()()()000A x xB y yC z z-+-+-=,经过点()000,,P x y z且一个方向向量为()(),,0nμυωμυω=≠的直线l的方程为000x x y y z zμυω---==,阅读上面的材料并解决下面问题:现给出平面α的方程为3570x y z-+-=,经过()0,0,0的直线l的方程为321x y z==-,则直线l与平面a 所成角的正弦值为()AB.35CD.7【答案】B【分析】根据题设给出的材料可得平面的法向量和直线的方向向量,利用公式可求直线l 与平面a 所成角的正弦值. 【详解】因为平面α的方程为3570x y z -+-=,故其法向量为()3,5,1n =-, 因为直线l 的方程为321x y z ==-,故其方向向量为()3,2,1m =-, 故直线l 与平面a35==,故选:B. 【点睛】关键点点睛:此题为材料题,需从给定的材料中提炼出平面的法向量和直线的方向向量的求法,这是解决此题的关键.5.(2020·全国高二课时练习)在空间直角坐标系中,定义:平面α的一般方程为0Ax By Cz D +++=(,,,A B C D R ∈,且A ,B ,C 不同时为零),点()000,,P x y z 到平面α的距离d =,则在底面边长与高都为2的正四棱锥P ABCD -中,底面中心O 到侧面PAB 的距离d 等于( ) ABC .2D .5【答案】B 【分析】欲求底面中心O 到侧面的距离,先利用建立空间直角坐标系求出点A ,B ,P 的坐标,及侧面的方程,最后利用所给公式计算即可. 【详解】以底面中心O 为原点,建立空间直角坐标系Oxyz ,如图所示:则(0,0,0),(1,1,0),(1,1,0),(0,0,2)O A B P -,设平面PAB 的方程为0Ax By Cz D +++=,将点A ,B ,P 的坐标代入计算得0A =,B D =-,12C D =-,所以方程可化为102Dy Dz D --+=,即220y z +-=,所以d ==. 故选:B.【点睛】本小题主要考查点、线、面间的距离计算、空间直角坐标系的应用、空间直角坐标系中点到平面的距离等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.(2) 多选题6.(2020·长沙市·湖南师大附中)如图,大摆锤是一种大型游乐设备,常见于各大游乐园.设备启动后,座舱旋转的同时,悬挂座舱的主轴在电机的驱动下做单摆运动.今年国庆,小明去某游乐园玩“大摆锤”,他坐在点A 处,“大摆锤”启动后,主轴OB 在平面α内绕点O 左右摆动,平面α与水平地面垂直,OB 摆动的过程中,点A 在平面β内绕点B 作圆周运动,并且始终保持OB β⊥,B β∈.已知6OB AB =,在“大摆锤”启动后,以下结论正确的有( )A .点A 在某个定球面上运动;B .线段AB 在水平地面上的正投影的长度为定值;C .直线OA 与平面α所成角的正弦值的最大值为37D .β与水平地面所成角记为θ,直线OB 与水平地面所成角记为δ,当02πθ<<时,θδ+为定值【答案】ACD 【分析】计算出OA 判断A ,考虑AB 分别与水平面平行和垂直时在水平面上的投影可判断B ,由OA 最大时,得线面角最大,从而得其正弦值判断C ,结合直观图可判断D . 【详解】A.∵OB β⊥,∴OB AB ⊥,∴OA ,∴点A 在以O 的球面运动,A 正确;B .由题意知A 在平面β内绕点B 作圆周运动,当AB 垂直于水平面时,投影长度为0,当AB 平行于水平面时,投影长度为AB ,∴线段AB 在水平地面上的正投影长度范围为[0,]AB ,B 错误;C .当AB α⊥时,直线OA 与平面α的所成的角的正弦值为最大值,此时线面角为AOB ∠,sinAB AOB OA ∠===,C 正确. D .画出该模型的直观图,∵β与水平面所成的角为θ,且02πθ<<,∴DCE θ∠=,∵直线OB 与水平面所成的角为δ,且//FC OB ,∴FCG δ∠=, ∵OB CD ⊥,∴FC CD ⊥,∴2FCG DCE π∠+∠=,即θδ+为定值,定值为2π,D 正确. 故选:ACD . 【点睛】本题考查考查以实际问题为背景的立体几何题,明确线面关系,线面角的求解是解题关键,考查空间想象能力.运算与推理能力.7.(2020·全国高二课时练习)(多选)已知单位向量i ,j ,k 两两的夹角均为0,2πθθπθ⎛⎫<<≠⎪⎝⎭,若空间向量a 满足(,,)a xi y j zk x y z R =++∈,则有序实数组(,,)x y z 称为向量a 在“仿射”坐标系Oxyz (O为坐标原点)下的“仿射”坐标,记作(,,)a x y z θ=,则下列命题是真命题的有( ). A .已知(1,3,2)a θ=-,(4,0,2)b θ=,则0a b ⋅= B .已知(,,0)3a x y π=,(0,0,)3b z π=,其中,,0x y z >,则当且仅当x y =时,向量a ,b 的夹角取得最小值C .已知()111,,a x y z θ=,()222,,b x y z θ=,则()121212,,a b x x y y z z θ+=+++D .已知(1,0,0)3OA π=,(0,1,0)3OB π=,(0,0,1)3OC π=,则三棱锥O ABC -的表面积S =【答案】BC 【分析】根据“仿射”坐标的定义逐项判断即可. 【详解】(1,3,2)(4,0,2)(32)(42)421268412cos a b i j k i k i k i j j k k i θθθ⋅=-⋅=+-⋅+=+⋅+⋅+⋅-⋅-=因为0θπ<<,且2πθ≠,所以0a b ⋅≠,故A 错误;如图所示,设OB b =,OA a =,则点A 在平面xOy 上,点B 在z 轴上,由图易知当x y =时,AOB ∠取得最小值,即向量a 与b 的夹角取得最小值,故B 正确; 根据“仿射”坐标的定义可得,()()()()()()()()111222111222121212121212,,,,,,a b x y z x y z x i y j z k x i y j z k x x i y y j z z k x x y y z z θθθ+=+=+++++=+++++=+++,故C 正确;由已知可得三棱锥O ABC -为正四面体,棱长为1,其表面积214122S =⨯⨯⨯=D 错误. 故选:BC. 【点睛】新定义概念题,考查对新概念的理解能力以及运算求解能力,基础题.8.(2020·江苏南通市·海安高级中学高一月考)平面中两条直线l 和n 相交于O ,对于平面上任意一点M ,若p ,q 分别是M 到直线l 和n 的距离,则称有序非负实数对(p ,q )是点M 的“距离坐标”.则下列说法正确的( )A .若p =q =0,则“距离坐标”为(0,0)的点有且仅有一个B .若pq =0,且p +q ≠0,则“距离坐标”为(p ,q )的点有且仅有2个C .若pq ≠0,则“距离坐标”为(p ,q )的点有且仅有4个D .若p =q ,则点M 的轨迹是一条过O 点的直线 【答案】ABC 【分析】根据“距离坐标”的定义对选项逐一分析,由此确定正确选项. 【详解】首先点到直线的距离是唯一确定的.对于A 选项,由于0p q ==,所以()0,0表示O 点,有且仅有一个,故A 选项正确. 对于B 选项,由于0pq =,且0p q +≠,当00p q =⎧⎨≠⎩或0p q ≠⎧⎨=⎩时,分别表示点()0,q 或(),0p ,有且仅有两个,故B 选项正确.对于C 选项,由于l 和n 相交与O ,所以直线l 和直线n 确定一个平面α,根据对称性可知,在平面α的上方和下方,各有两个“距离坐标”为(),p q 的点.故“距离坐标”为(),p q 的点有且仅有4个,所以C 选项正确. 对于D 选项,设l 和n 相交与O ,直线l 和直线n 相交所形成的两组对角的角平分线上的点,都满足p q =,所以点M 的轨迹不只是一条过O 点的直线,所以D 选项错误. 由于p q =,故选:ABC 【点睛】本小题主要考查空间点与直线的位置关系,考查分析、思考与解决问题的能力,属于基础题.(3) 填空题9.(2016·上海金山区·高三一模)某种游戏中,黑、黄两个“电子狗”从棱长为1的正方体ABCD -A 1B 1C 1D 1的顶点A 出发沿棱向前爬行,每爬完一条棱称为“爬完一段”.黑“电子狗”爬行的路线是AA 1→A 1D 1→ ,黄“电子狗”爬行的路线是AB→BB 1→ ,它们都遵循如下规则:所爬行的第i+2段与第i 段所在直线必须是异面直线(其中i 是正整数).设黑“电子狗”爬完2015段、黄“电子狗”爬完2014段后各自停止在正方体的某个顶点处,这时黑、黄“电子狗”间的距离是________________. 【答案】【解析】试题分析:黑电子狗爬行的路径为111111AA A D DC C C CB BA →→→→→,黄电子狗爬行的路径为111111AB BB B C C D D D DA →→→→→,周期均为6,因此黑“电子狗”爬完2015段即爬完第5段,此时位于B 点,黄“电子狗”爬完2014段即爬完第4段,此时位于1D ,1BD 考点:1.数列周期;2.异面直线;3.空间两点间距离10.(2019·全国高三其他模拟(文))半正多面体亦称“阿基米德多面体”,是由边数不全相同的正多边形为面组成的多面体.如将正四面体所有棱各三等分,沿三等分点从原几何体割去四个小正四面体(如图所示),余下的多面体就成为一个半正多面体,若这个半正多面体的棱长为4,则这个半正多面体的外接球的半径为__________.【分析】先求出BC ,BG ,BF 的长度,在BFA ,求出正四面体的高AF ,在Rt BFO 中,求BO ;Rt BFA 中,求cos BAF ;EAO 中,由余弦定理求EO 即可. 【详解】 解:正四面体的棱长12BC =,且正四面体与半正多面体的外接球的球心相同,设为O ,F 为底面BCD 的中心,G 是边CD 中点,E 是半正多面体的一个顶点23BG BC BF BG ====AF ∴===设OA OB R ==,OF AF R R =-=在Rt OBF 中,222OB BF OF =+,2248)R R =+,R =Rt ABF中,cos 123AF BAF AB ∠===EAO中,cos cos 3EAO BAF ∠=∠= 由余弦定理,(222222cos 82822OE AE AO AE AO EAO =+-⨯⨯⨯∠=+-⨯⨯=OE =【点睛】考查半正多面体的外接球的半径的求法,中档题.11.(2021·江苏宿迁市·高二期末)自然界中,构成晶体的最基本的几何单元称为晶胞,其形状一般是平行六面体,具体形状大小由它的三组棱长a 、b 、c 及棱间交角α、β、γ(合称为“晶胞参数”)来表征.如图是某种晶体的晶胞,其中2a =,1b c ==,60α=︒,90β=︒,120γ=︒,则该晶胞的对角线1AC 的长为__________.【分析】数形结合以及使用向量的方法,可得11AC AB AD AA =++,然后先平方再开方可得结果.【详解】如图所示:所以1111=+AC AC CC AB AD CC AB AD AA =++=++ 依题可知:1=21AB AA AD ==,, 11=60,90,18060A AB A AD BAD αβγ∠=∠=∠=-== 所以22221111=+2+22AC AB AD AA AB AD AB AA AD AA ++⋅⋅+⋅所以21=411+221cos 60+221cos 60211cos90AC ++⨯⨯⨯⨯⨯⨯+⨯⨯则21=10AC ,故1=10AC12.(2020·全国高三专题练习(理))我们把平面内与直线垂直的非零向量称为直线的法向量,在平面直角坐标系中,利用求动点轨迹方程的方法,可以求出过点(3,4)A -,且法向量为(1,2)=-n 的直线方程为1(3)(2)(4)0x y ⨯++-⨯-=,即2110x y -+=.类比以上方法,在空间直角坐标系中,经过点(1,2,3)A ,且法向量为(1,2,1)=--m 的平面的方程为___________.【答案】220x y z +--=【解析】试题分析:根据法向量的定义,若n 为平面α的法向量,则n ⊥α,任取平面α内一点P (x ,y ,z ),则PA ⊥n ,∵PA =(1-x ,2-y ,3-z ),n =(-1,-2,1),∴(x -1)+2(y -2)+(3-z )=0,即x+2y -z -2=0,故答案为x+2y -z -2=0.考点:本题主要考查类比推理的概念和方法,向量的坐标运算.点评:类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).由于平面向量与空间向量的坐标运算类似,因此可以利用求平面曲线方程的办法,通过构造向量,利用向量的运算确定空间平面方程.13.(2020·福建省泉州市泉港区第一中学高二期中)如图所示的正方体是一个三阶魔方(由27个全等的棱长为1的小正方体构成),正方形ABCD 是上底面正中间一个正方形,正方形1111D C B A 是下底面最大的正方形,已知点P 是线段AC 上的动点,点Q 是线段1B D 上的动点,则线段PQ 长度的最小值为_______.【分析】建立空间直角坐标系,写出点的坐标,求出目标PQ 的表达式,从而可得最小值.【详解】以1B 为坐标原点,1111,B C B A 所在直线分别为x 轴,y 轴建立空间直角坐标系,则()()()()10,0,0,1,2,3,2,1,3,2,2,3B A C D ,设11BQ B D λ=,AP AC μ=,[],0,1λμ∈. ()12,2,3B Q λλλ=,()1111,2,3B P B A AP B A AC μμμ=+=+=+-.()1112,22,33QP B P B Q μλμλλ=-=+----,()()()2222122233QP μλμλλ=+-+--+-222215191730221417217234λλμμλμ⎛⎫⎛⎫=-+-+=-+-+ ⎪ ⎪⎝⎭⎝⎭当1517λ=且12μ=时,2QP 取到最小值934,所以线段PQ . 【点睛】本题主要考查空间向量的应用,利用空间向量求解距离的最值问题时,一般是把目标式表示出来,结合目标式的特征,选择合适的方法求解最值.(4) 解答题14.(2018·上海市南洋模范中学高三期末)已知111(,,)a x y z =,222(,,)b x y z =,333(,,)c x y z =,定义一种运算:123231312132213321()a b c x y z x y z x y z x y z x y z x y z ⨯⋅=++---,已知四棱锥P ABCD -中,底面ABCD 是一个平行四边形,(2,1,4)AB =-,(4,2,0)AD =,(1,2,1)AP =-(1)试计算()AB AD AP ⨯⋅的绝对值的值,并求证PA ⊥面ABCD ;(2)求四棱锥P ABCD -的体积,说明()AB AD AP ⨯⋅的绝对值的值与四棱锥P ABCD -体积的关系,并由此猜想向量这一运算()AB AD AP ⨯⋅的绝对值的几何意义.【答案】(1)48,证明见解析;(2)体积为16,()3P ABCD AB AD AP V -⨯⋅=,()AB AD AP ⨯⋅的绝对值表示以,,AB AD AP 为邻边的平行六面体的体积.【分析】(1)根据新定义直接计算,由向量法证明线线垂直,得线面垂直;(2)计算出棱锥体积后,根据数据确定关系.【详解】(1)由题意()AB AD AP ⨯⋅221424(1)(1)0=⨯⨯+⨯⨯+-⨯-⨯202-⨯⨯4(1)1-⨯-⨯(1)24--⨯⨯=48.122(1)140AP AB ⋅=-⨯+⨯-+⨯=,1422100AP AD ⋅=-⨯+⨯+⨯=,∴,AP AB AP AD ⊥⊥,即,AP AB AP AD ⊥⊥.,AB AD 是平面ABCD 内两相交直线,∴AP ⊥平面ABCD .(2)由题意2221,20AB AD ==,24(1)2406AB AD ⋅=⨯+-⨯+⨯=, 222sin ()ABCD S AB AD BAD AB AD AB AD =∠=-⋅== 6AP =∴111633P ABCD ABCD V S PA -==⨯. ∴()3P ABCD AB AD AP V -⨯⋅=,猜想:()AB AD AP ⨯⋅的绝对值表示以,,AB AD AP 为邻边的平行六面体的体积.【点睛】本题考查向量的新定义运算,解题时根据新定义的规则运算即可.考查学生的创新意识,同时考查学生的归纳推理能力.。
利用空间向量求空间角

利用空间向量求空间角1.能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题.2.了解向量方法在研究立体几何问题中的应用.知识点一 利用空间向量求异面直线所成角设两条异面直线a ,b 的方向向量为a ,b ,其夹角为θ,则cos φ=|cos θ|=|a ·b ||a||b |(其中φ为异面直线a ,b 所成的角).[典例] 如图,在四棱锥P -ABCD 中,PA ⊥平面ABCD ,底面ABCD 是菱形,AB =2,∠BAD =60°.(1)求证:BD ⊥平面PAC ;(2)若PA =AB ,求PB 与AC 所成角的余弦值.[解] (1)证明:因为四边形ABCD 是菱形,所以AC ⊥BD .因为PA ⊥平面ABCD ,所以PA ⊥BD .又因为AC ∩PA =A ,所以BD ⊥平面PAC . (2)设AC ∩BD =O .因为∠BAD =60°,PA =AB =2, 所以BO =1,AO =CO = 3.如图,以O 为坐标原点,建立空间直角坐标系O -xyz ,则P (0,-3,2),A (0,-3,0),B (1,0,0),C (0,3,0).所以PB ―→=(1,3,-2),AC ―→=(0,23,0).设PB 与AC 所成角为θ,则cos θ=⎪⎪⎪⎪⎪⎪⎪⎪PB ―→·AC ―→|PB―→||AC ―→|=622×23=64.即PB 与AC 所成角的余弦值为64. [方法技巧]向量法求两异面直线所成角的步骤(1)选好基底或建立空间直角坐标系; (2)求出两直线的方向向量v 1,v 2; (3)代入公式|cos 〈v 1,v 2〉|=|v 1·v 2||v 1||v 2|求解. [提醒] 两异面直线所成角θ的范围是⎝⎛⎦⎤0,π2,两向量的夹角α的范围是[0,π],当两异面直线的方向向量的夹角为锐角或直角时,就是这两条异面直线所成的角;当两异面直线的方向向量的夹角为钝角时,其补角才是两异面直线所成的角. [针对训练]1.如图,在空间直角坐标系中有直三棱柱ABC -A 1B 1C 1,CA =CC 1=2CB ,则直线BC 1与直线AB 1夹角的余弦值为( ) A.55B.53C.255D.35解析:选A 设CA =2,则C (0,0,0),A (2,0,0),B (0,0,1),C 1(0,2,0),B 1(0,2,1), 可得向量AB 1―→=(-2,2,1),BC 1―→=(0,2,-1),由向量的夹角公式得cos 〈AB 1―→,BC 1―→〉=-2×0+2×2+1×(-1)0+4+1·4+4+1=15=55.2.已知在长方体ABCD -A 1B 1C 1D 1中,B 1C 和C 1D 与底面所成角分别为60°和45°,求异面直线B 1C 和C 1D 所成角的余弦值.解:建立如图所示的空间直角坐标系,可知∠CB 1C 1=60°,∠DC 1D 1=45°,设B 1C 1=1,CC 1=3=DD 1.∴C 1D 1=3,则有B 1(3,0,0),C (3,1,3),C 1(3,1,0),D (0,1,3). ∴B 1C ―→=(0,1,3),C 1D ―→=(-3,0,3). ∴cos 〈B 1C ―→,C 1D ―→〉=B 1C ―→·C 1D ―→|B 1C ―→||C 1D ―→|=326=64.知识点二 直线与平面所成角如图所示,设直线l 的方向向量为e ,平面α的法向量为n ,直线l 与平面α所成的角为φ,向量e 与n 的夹角为θ,则有sin φ=|cos θ|=|n ·e ||n ||e |.[典例] (2018·全国卷Ⅱ)如图,在三棱锥P -ABC 中,AB =BC =22,PA =PB =PC =AC=4,O 为AC 的中点. (1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且二面角M -PA -C 为30°,求PC 与平面PAM 所成角的正弦值. AC ,且PO =2 3.连[解] (1)证明:因为PA =PC =AC =4,O 为AC 的中点,所以PO ⊥接OB ,因为AB =BC =22AC ,所以△ABC 为等腰直角三角形,且OB ⊥AC ,OB =12AC =2.所以PO 2+OB 2=PB 2,所以PO ⊥OB .又因为OB ∩AC =O ,所以PO ⊥平面ABC . (2)以O 为坐标原点,OB ―→的方向为x 轴正方向,建立如图所示的空间直角坐标系O -xyz .由已知得O (0,0,0),B (2,0,0),A (0,-2,0),C (0,2,0),P (0,0,23), AP ―→=(0,2,23).取平面PAC 的一个法向量OB ―→=(2,0,0). 设M (a,2-a,0)(0<a ≤2),则AM ―→=(a,4-a,0). 设平面PAM 的法向量为n =(x ,y ,z ). 由⎩⎪⎨⎪⎧AP ―→·n =0,AM ―→·n =0,得⎩⎨⎧2y +23z =0,ax +(4-a )y =0,令y =3a ,得z =-a ,x =3(a -4),所以平面PAM 的一个法向量为n =(3(a -4), 3a ,-a ), 所以cos 〈OB ―→,n 〉=23(a -4)23(a -4)2+3a 2+a 2. 由已知可得|cos 〈OB ―→,n 〉|=cos 30°=32,所以23|a -4|23(a -4)2+3a 2+a2=32, 解得a =43或a =-4(舍去).所以n =⎝⎛⎭⎫-833,433,-43.又PC ―→=(0,2,-23),所以cos 〈PC ―→,n 〉=833+8334+12·643+163+169=34.所以PC 与平面PAM 所成角的正弦值为34. [方法技巧]利用向量法求直线与平面所成角的注意点(1)求出直线的方向向量与平面的法向量所夹的锐角后(求出是钝角时取其补角),取其余角即为直线与平面所成的角.(2)若求线面角的余弦值,要注意利用平方关系sin 2θ+cos 2θ=1求出其值.不要误认为直线的方向向量与平面的法向量所成夹角的余弦值即为所求. [针对训练]1.如图,正三棱柱ABC -A 1B 1C 1中,AB =AA 1,则AC 1与平面BB 1C 1C 夹角的正弦值为________.解析:取B 1C 1中点O ,建立如图所示的空间直角坐标系.A 1O ―→=(3,0,0),设AB =AA 1=2,则A 1(-3,0,0),C 1(0,1,0),A (-3,0,2),O (0,0,0),A 1O ―→为平面BB 1C 1C 的法向量,AC 1―→=(3,1,-2),∴sin θ=|cos 〈A 1O ―→,AC 1―→〉|=⎪⎪⎪⎪⎪⎪⎪⎪A 1O ―→·AC 1―→|A 1O ―→||AC 1―→|=33·3+1+4=64. 答案:642.在如图所示的多面体中,四边形ABCD 是平行四边形,四边形BDEF 是矩形,ED⊥平面ABCD ,∠ABD =π6,AB =2AD .(1)求证:平面BDEF ⊥平面ADE ;(2)若ED =BD ,求直线AF 与平面AEC 所成角的正弦值. 解:(1)证明:在△ABD 中,∠ABD =π6,AB =2AD ,由余弦定理,得BD =3AD , 从而BD 2+AD 2=AB 2,故BD ⊥AD ,因为DE ⊥平面ABCD ,BD ⊂平面ABCD ,所以DE ⊥BD . 又AD ∩DE =D ,所以BD ⊥平面ADE .因为BD ⊂平面BDEF ,所以平面BDEF ⊥平面ADE . (2)由(1)可得,在Rt △ABD 中,∠BAD =π3,BD =3AD ,又由ED =BD ,设AD =1,则BD =ED = 3. 因为DE ⊥平面ABCD ,BD ⊥AD ,所以以点D 为坐标原点,DA ,DB ,DE 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系D -xyz ,如图所示.则A (1,0,0),C (-1,3,0),E (0,0,3),F (0,3,3), 所以AE ―→=(-1,0,3),AC ―→=(-2,3,0). 设平面AEC 的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧n ·AE ―→=0,n ·AC ―→=0,即⎩⎨⎧-x +3z =0,-2x +3y =0,令z =1,得n =(3,2,1)为平面AEC 的一个法向量.因为AF ―→=(-1,3,3),所以cos 〈n ,AF ―→〉=n ·AF ―→|n |·|AF ―→|=4214, 所以直线AF 与平面AEC 所成角的正弦值为4214. 知识点三 二面角(1)如图①,AB ,CD 是二面角α-l -β的两个面内与棱l 垂直的直线,则二面角的大小θ=〈AB ―→,CD ―→〉.(2)如图②和图③,n 1,n 2分别是二面角α-l -β的两个半平面α,β的法向量,则二面角的大小θ=〈n 1,n 2〉或π-〈n 1,n 2〉.[典例] (2019·惠州模拟)如图,在四棱锥P -ABCD 中,底面ABCD 是边长为2的菱形,∠ABC =60°,PA ⊥PB ,PC =2. (1)求证:平面PAB ⊥平面ABCD ;(2)若PA =PB ,求二面角A -PC -D 的余弦值. [解] (1)证明:取AB 的中点为O ,连接CO ,PO , ∵四边形ABCD 是边长为2的菱形,∴AB =BC =2. ∵∠ABC =60°,∴△ABC 是等边三角形, ∴CO ⊥AB ,OC = 3. ∵PA ⊥PB ,∴PO =12AB =1.∵PC =2,∴OP 2+OC 2=PC 2,∴CO ⊥PO . ∵AB ∩PO =O ,∴CO ⊥平面PAB .∵CO ⊂平面ABCD ,∴平面PAB ⊥平面ABCD . (2)∵OP 2+OA 2=12+12=(2)2=PA 2,∴PO ⊥AO . 由(1)知,平面PAB ⊥平面ABCD , ∴PO ⊥平面ABCD ,∴直线OC ,OB ,OP 两两垂直.以O 为坐标原点建立如图所示的空间直角坐标系O -xyz ,则O (0,0,0),A (0,-1,0),B (0,1,0),C (3,0,0),D (3,-2,0),P (0,0,1), ∴AP ―→=(0,1,1),PC ―→=(3,0,-1),DC ―→=(0,2,0). 设平面APC 的法向量为m =(x 1,y 1,z 1),由⎩⎪⎨⎪⎧ m ·AP ―→=0,m ·PC ―→=0,得⎩⎨⎧ y 1+z 1=0,3x 1-z 1=0,取x 1=1,得m =(1,-3,3), 设平面PCD 的法向量为n =(x 2,y 2,z 2), 由⎩⎪⎨⎪⎧n ·PC ―→=0,n ·DC ―→=0,得⎩⎨⎧3x 2-z 2=0,2y 2=0,取x 2=1,得n =(1,0,3), ∴cos 〈m ,n 〉=m ·n |m |·|n |=277,由图易知二面角A -PC -D 为锐二面角, ∴二面角A -PC -D 的余弦值为277.[方法技巧]利用法向量求二面角时的2个注意点(1)对于某些平面的法向量要注意题中条件隐含着,不用单独求.(2)注意判断二面角的平面角是锐角还是钝角,可结合图形进行,以防结论失误.[针对训练]1.如图,PA ⊥平面ABC ,AC ⊥BC ,PA =AC =1,BC =2,则平面PAB 与平面PBC 的夹角的余弦值为________.P (0,0,1),AP ―→=解析:建立如图所示的空间直角坐标系,则A (0,0,0),B (2,1,0),C (0,1,0),(0,0,1),AB ―→=(2,1,0),CB ―→=(2,0,0),CP ―→=(0,-1,1).设平面PAB 的法向量为m =(x ,y ,z ), 则⎩⎪⎨⎪⎧ m ⊥AP ―→,m ⊥AB ―→,即⎩⎪⎨⎪⎧m ·AP ―→=0,m ·AB ―→=0,∴⎩⎨⎧y =-2x ,z =0.令x =1,得m =(1,-2,0),设平面PBC 的法向量为n =(x ′,y ′,z ′),则⎩⎪⎨⎪⎧ n ⊥CB ―→,n ⊥CP ―→,即⎩⎪⎨⎪⎧n ·CB ―→=0,n ·CP ―→=0,∴⎩⎪⎨⎪⎧x ′=0,y ′=z ′.令y ′=1,∴n =(0,1,1). ∴cos 〈m ,n 〉=m ·n |m ||n |=-33.由图知所求二面角为锐角,∴平面PAB 与平面PBC 夹角的余弦值为33. 答案:332.(2019·江西五市联考)如图,在四棱锥P -ABCD 中,AD ∥BC ,AB ⊥AD ,AB =AD =AP =2BC =2,M 是棱PD 上的一点,PMPD =λ(0<λ<1).(1)若λ=13,求证:PB ∥平面MAC ;(2)若平面PAB ⊥平面ABCD ,平面PAD ⊥平面ABCD ,二面角D -AC -M 的余弦值为42121,求λ的值.解:(1)证明:连接BD 交AC 于点O ,连接MO . ∵AD ∥BC ,∴△BCO ∽△DAO , ∵AD =2BC ,∴DO =2BO .∵λ=13,∴DM =2MP ,∴PB ∥MO ,∵PB ⊄平面MAC ,MO ⊂平面MAC ,∴PB ∥平面MAC .(2)∵平面PAB ⊥平面ABCD ,平面PAB ∩平面ABCD =AB ,AD ⊂平面ABCD ,且AD ⊥AB , ∴AD ⊥平面PAB ,∴AD ⊥PA ,同理可得AB ⊥PA ,可知AB ,AD ,AP 两两垂直,建2-2λ),∴AC ―→=立如图所示的空间直角坐标系A -xyz ,则A (0,0,0),C (2,1,0),M (0,2λ,(2,1,0),AM ―→=(0,2λ,2-2λ).易知平面ACD 的一个法向量为m =(0,0,1). 设平面MAC 的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧n ·AC ―→=0,n ·AM ―→=0,得⎩⎪⎨⎪⎧2x +y =0,2λy +(2-2λ)z =0,令x =1,则y =-2,z =2λ1-λ,即n =⎝⎛⎭⎫1,-2,2λ1-λ为平面MAC 的一个法向量.由题意可知|m ·n ||m ||n |=42121,即⎪⎪⎪⎪2λ1-λ5+⎝⎛⎭⎫2λ1-λ2=42121,解得λ=23.[课时跟踪检测][A 级 基础题]1.已知两平面的法向量分别为m =(0,1,0),n =(0,1,1),则两平面所成的二面角为( ) A .45° B .135° C .45°或135°D .90°解析:选C cos 〈m ,n 〉=m ·n |m ||n |=11·2=22,即〈m ,n 〉=45°.∴两平面所成二面角为45°或180°-45°=135°.2.如图所示,在正方体ABCD -A 1B 1C 1D 1中,已知M ,N 分别是BD 和AD 的中点,则B 1M 与D 1N 所成角的余弦值为( ) A .3030 B.3015 C .3010D.1515解析:选C 建立如图所示的空间直角坐标系.设正方体的棱长为2,则B 1(2,2,2),M (1,1,0),D 1(0,0,2),N (1,0,0),∴B 1M ―→=(-1,-1,-2),D 1N ―→=(1,0,-2), ∴B 1M 与D 1N 所成角的余弦值为⎪⎪⎪⎪⎪⎪⎪⎪B 1M ―→·D 1N ―→|B 1M ―→|·|D 1N ―→| =⎪⎪⎪⎪⎪⎪-1+41+1+4×1+4=3010.故选C.3.如图,已知长方体ABCD -A 1B 1C 1D 1中,AD =AA 1=1,AB =3,E 为线段AB 上一点,且AE =13AB ,则DC 1与平面D 1EC 所成的角的正弦值为( )A.33535B.277C.33D.24解析:选A 如图,以D 为坐标原点,DA ,DC ,DD 1所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系,则C 1(0,3,1),D 1(0,0,1),E (1,1,0),C (0,3,0), ∴DC 1―→=(0,3,1),D 1E ―→=(1,1,-1),D 1C ―→=(0,3,-1). 设平面D 1EC 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧n ·D 1E ―→=0,n ·D 1C ―→=0,即⎩⎪⎨⎪⎧x +y -z =0,3y -z =0,取y =1,得n =(2,1,3).∵DC 1―→,n=DC 1―→·n |DC 1―→|·|n |=(0,3,1)·(2,1,3)10×14=33535,∴DC 1与平面D 1EC 所成的角的正弦值为33535.4.在直三棱柱ABC -A 1B 1C 1中,AA 1=2,二面角B -AA 1-C 1的大小为60°,点B 到平面ACC 1A 1的距离为3,点C 到平面ABB 1A 1的距离为23,则直线BC 1与直线AB 1所成角的正切值为( ) A.7 B . 6 C. 5D .2解析:选A 由题意可知,∠BAC =60°,点B 到平面ACC 1A 1的距离为3,点C 到平面ABB 1A 1的距离为23,所以在三角形ABC 中,AB =2,AC =4,BC =23,∠ABC =90°,则AB 1―→·BC 1―→=(BB 1―→-BA ―→)·(BB 1―→+BC ―→)=4,|AB 1―→|=22,|BC 1―→|=4,cos 〈AB 1―→,BC 1―→〉=AB 1―→·BC 1―→|AB 1―→|·|BC 1―→|=24,故tan 〈AB 1―→,BC 1―→〉=7. 5.如图,正三棱柱ABC -A 1B 1C 1的所有棱长都相等,E ,F ,G 分别为AB ,AA 1,A 1C 1的中点,则B 1F 与平面GEF 所成角的正弦值为( ) A.35 B.56 C.3310D.3610解析:选A 设正三棱柱的棱长为2,取AC 的中点D ,连接DG ,DB ,分别以DA ,DB ,DG 所在的直线为x 轴,y 轴,z 轴建立空间直角坐标系,如图所示,则B 1()0,3,2,F (1,0,1), E ⎝⎛⎭⎫12,32,0,G (0,0,2), B 1F ―→=()1,-3,-1,EF ―→=⎝⎛⎭⎫12,-32,1,GF ―→=(1,0,-1).设平面GEF 的法向量n =(x ,y ,z ), 则⎩⎪⎨⎪⎧ EF ―→·n =0,GF ―→·n =0,即⎩⎪⎨⎪⎧12x -32y +z =0,x -z =0,取x =1,则z =1,y =3,故n =()1,3,1为平面GEF 的一个法向量, 所以cos 〈n ,B 1F ―→〉=1-3-15×5=-35,所以B 1F 与平面GEF 所成角的正弦值为35.故选A.6.在正方体ABCD -A 1B 1C 1D 1中,点E 为BB 1的中点,则平面A 1ED 与平面ABCD 所成的锐二面角的余弦值为( ) A.12 B.23 C.33D.22解析:选B 以A 为坐标原点建立如图所示的空间直角坐标系A -xyz ,设棱长为1,则A 1(0,0,1),E ⎝⎛⎭⎫1,0,12,D (0,1,0), ∴A 1D ―→=(0,1,-1),A 1E ―→=⎝⎛⎭⎫1,0,-12, 设平面A 1ED 的一个法向量为n 1=(1,y ,z ),则⎩⎪⎨⎪⎧ n 1·A 1D ―→=0,n 1·A 1E ―→=0,即⎩⎪⎨⎪⎧y -z =0,1-12z =0,∴⎩⎪⎨⎪⎧y =2,z =2.∴n 1=(1,2,2).又平面ABCD 的一个法向量为n 2=(0,0,1), ∴cos 〈n 1,n 2〉=23×1=23.即平面A 1ED 与平面ABCD 所成的锐二面角的余弦值为23.7.如图所示,在三棱锥P -ABC 中,PA ⊥平面ABC ,D 是棱PB 的中点,已知PA =BC =2,AB =4,CB ⊥AB ,则异面直线PC ,AD 所成角的余弦值为__________. 解析:因为PA ⊥平面ABC ,所以PA ⊥AB ,PA ⊥BC .过点A 作AE ∥CB ,又CB ⊥AB , 则AP ,AB ,AE 两两垂直.如图,以A 为坐标原点,分别以AB ,AE ,AP 所在直线为x 轴,y 轴,z 轴建立空间直角坐标系A -xyz , 则A (0,0,0),P (0,0,2),B (4,0,0),C (4,-2,0). 因为D 为PB 的中点,所以D (2,0,1). 故CP ―→=(-4,2,2),AD ―→=(2,0,1). 所以AD ―→,CP ―→=AD ―→·CP ―→|AD ―→|·|CP ―→|=-65×26=-3010.设异面直线PC ,AD 所成的角为θ, 则cos θ=|cos 〈AD ―→,CP ―→〉|=3010.答案:30108.如图,菱形ABCD 中,∠ABC =60°,AC 与BD 相交于点O ,AE ⊥平面ABCD ,CF ∥AE ,AB =2,CF =3.若直线FO 与平面BED 所成的角为45°,则AE =________.解析:如图,以O 为原点,以OA ,OB 所在直线分别为x 轴,y 轴,以过点O 且平行于CF 的直线为z 轴建立空间直角坐标系.∴OF ―→=(-1,0,3),设AE =a ,则B (0,3,0),D (0,-3,0),F (-1,0,3),E (1,0,a ),DB ―→=(0,23,0),EB ―→=(-1,3,-a ).设平面BED 的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧n ·DB ―→=0,n ·EB ―→=0,即⎩⎨⎧23y =0,-x +3y -az =0,则y =0,令z =1,得x =-a , ∴n =(-a,0,1),∴cos 〈n ,OF ―→〉=n ·OF ―→|n ||OF ―→|=a +3a 2+1×10. ∵直线FO 与平面BED 所成角的大小为45°, ∴|a +3|a 2+1×10=22, 解得a =2或a =-12(舍去),∴AE =2.答案:2[B 级 提升练]=∠CDP =90°.1.(2017·全国卷Ⅰ)如图,在四棱锥P -ABCD 中,AB ∥CD ,且∠BAP(1)证明:平面PAB ⊥平面PAD ;(2)若PA =PD =AB =DC ,∠APD =90°,求二面角A -PB -C 的余弦值. 解:(1)证明:由已知∠BAP =∠CDP =90°, 得AB ⊥AP ,CD ⊥PD . 因为AB ∥CD ,所以AB ⊥PD . 又AP ∩PD =P ,所以AB ⊥平面PAD . 又AB ⊂平面PAB ,所以平面PAB ⊥平面PAD . (2)在平面PAD 内作PF ⊥AD ,垂足为F .由(1)可知,AB ⊥平面PAD ,故AB ⊥PF ,可得PF ⊥平面ABCD . 以F 为坐标原点,FA ―→的方向为x 轴正方向,|AB ―→|为单位长度,建立如图所示的空间直角坐标系F -xyz .由(1)及已知可得A ⎝⎛⎭⎫22,0,0,P ⎝⎛⎭⎫0,0,22,B ⎝⎛⎭⎫22,1,0,C ⎝⎛⎭⎫-22,1,0. 所以PC ―→=⎝⎛⎭⎫-22,1,-22,CB ―→=(2,0,0),PA ―→=⎝⎛⎭⎫22,0,-22,AB ―→=(0,1,0). 设n =(x 1,y 1,z 1)是平面PCB 的法向量, 则⎩⎪⎨⎪⎧ n ·PC ―→=0,n ·CB ―→=0,即⎩⎪⎨⎪⎧-22x 1+y 1-22z 1=0,2x 1=0.所以可取n =(0,-1,-2).设m =(x 2,y 2,z 2)是平面PAB 的法向量, 则⎩⎪⎨⎪⎧m ·PA ―→=0,m ·AB ―→=0,即⎩⎪⎨⎪⎧22x 2-22z 2=0,y 2=0.所以可取m =(1,0,1). 则cos 〈n ,m 〉=n ·m |n ||m |=-23×2=-33.由图知二面角A -PB -C 为钝角, 所以二面角A -PB -C 的余弦值为-33.2.(2019·合肥一检)如图,在多面体ABCDEF 中,四边形ABCD 是正方形,BF ⊥平面ABCD ,DE ⊥平面ABCD ,BF =DE ,M 为棱AE 的中点. (1)求证:平面BDM ∥平面EFC ;(2)若DE =2AB ,求直线AE 与平面BDM 所成角的正弦值. 解:(1)证明:连接AC 交BD 于点N ,连接MN , 则N 为AC 的中点,又M 为AE 的中点,∴MN ∥EC . ∵MN ⊄平面EFC ,EC ⊂平面EFC , ∴MN ∥平面EFC .∵BF ,DE 都与平面ABCD 垂直,∴BF ∥DE . ∵BF =DE ,∴四边形BDEF 为平行四边形,∴BD ∥EF . ∵BD ⊄平面EFC ,EF ⊂平面EFC , ∴BD ∥平面EFC .又MN ∩BD =N ,∴平面BDM ∥平面EFC .(2)∵DE ⊥平面ABCD ,四边形ABCD 是正方形,∴DA ,DC ,DE 两两垂直,如图,建立空间直角坐标系D -xyz .设AB =2,则DE =4,从而D (0,0,0),B (2,2,0),M (1,0,2),A (2,0,0),E (0,0,4),∴DB ―→=(2,2,0),DM ―→=(1,0,2), 设平面BDM 的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧n ·DB ―→=0,n ·DM ―→=0,得⎩⎪⎨⎪⎧2x +2y =0,x +2z =0.令x =2,则y =-2,z =-1,从而n =(2,-2,-1)为平面BDM 的一个法向量. ∵AE ―→=(-2,0,4),设直线AE 与平面BDM 所成的角为θ, 则sin θ=|cos 〈n ,AE ―→〉|=|n ·AE ―→||n |·|AE ―→|=4515,∴直线AE 与平面BDM 所成角的正弦值为4515.3.如图,EA ⊥平面ABC ,DB ⊥平面ABC ,△ABC 是等边三角形,AC =2AE ,M 是AB的中点.(1)求证:CM ⊥EM;(2)若直线DM 与平面ABC 所成角的正切值为2,求二面角B -CD -E 的余弦值. 解:(1)证明:因为△ABC 是等边三角形,M 是AB 的中点, 所以CM ⊥AM .因为EA ⊥平面ABC ,CM ⊂平面ABC ,所以CM ⊥EA . 因为AM ∩EA =A ,所以CM ⊥平面EAM . 因为EM ⊂平面EAM ,所以CM ⊥EM .(2)以点M 为坐标原点,MC 所在直线为x 轴,MB 所在直线为y 轴,过M 且与直线BD平行的直线为z 轴,建立空间直角坐标系M -xyz ,如图所示. 因为DB ⊥平面ABC ,所以∠DMB 为直线DM 与平面ABC 所成的角,所以tan ∠DMB =BDMB=2,即BD =2MB ,所以BD =AC . 不妨设AC =2,又AC =2AE ,则CM =3,AE =1. 故B (0,1,0),C (3,0,0),D (0,1,2),E (0,-1,1).所以BC ―→=(3,-1,0),BD ―→=(0,0,2),CE ―→=(-3,-1,1),CD ―→=(-3,1,2). 设平面BCD 与平面CDE 的一个法向量分别为m =(x 1,y 1,z 1),n =(x 2,y 2,z 2),由⎩⎪⎨⎪⎧ m ·BC ―→=0,m ·BD ―→=0,得⎩⎨⎧3x 1-y 1=0,2z 1=0,令x 1=1,得y 1=3,所以m =(1,3,0).由⎩⎪⎨⎪⎧n ·CE ―→=0,n ·CD ―→=0,得⎩⎨⎧-3x 2-y 2+z 2=0,-3x 2+y 2+2z 2=0.令x 2=1,得y 2=-33,z 2=233. 所以n =⎝⎛⎭⎫1,-33,233. 所以cos 〈m ,n 〉=m ·n|m ||n |=0.所以二面角B -CD -E 的余弦值为0.。
用空间向量方法求角和距离

用向量方法求空间角和距离在高考的立体几何试题中,求角与距离是常考查的问题,其传统的“三步曲”解法:“作图、证明、解三角形”,作辅助线多、技巧性强,是教学和学习的难点.向量进入高中教材,为立体几何增添了活力,新思想、新方法与时俱进,本专题将运用向量方法简捷地解决这些问题.1求空间角问题分别在直线n m ,b a ,所成的角或0a b a b ⊥⇔= , (2)求线面角特殊情形:当a = 一般情形:在直线图所示),再求cos 则sin cos βθ=(3)求二面角方法1:转化为分别是在二面角的两个半平面内且与棱都垂直的两条直线上的两个向量的夹角(注意:要特别关注两个向量的方向).方法2:先求出二面角一个面内一点到另一个面的距离及到棱的距离,然后通过解直角三角形求角.方法3:(法向量法)构造二面角βα--l 的两个半平面βα、的法向量21n n 、(都取向上的方向,如图所示)2)若二面角βα--l 是“锐角型”如图乙所示,那么其大小φ等于两法向量21n n 、的夹角即 1212cos cos .||||n n n n φθ⋅==⋅2.求空间距离问题(1)求点面距离 其中n 是平面α在法一、找平面β使面β法二:如图,d 是异面直线a 与 b 的距离,n是直线a 与b 的一个法向量 A 、 B 分别是 直线a , b 上的点,显然:||cos ,d AB θ=又||cos ,AB n θ= ||AB n d ∴= 图甲例1.如图,在棱长为2的正方体1111ABCD A B C D -中,E 、F 分别是棱1111,A D A B 的中点.(Ⅰ)求异面直线1DE FC 与所成角的余弦值; (II )求1BC 和面EFBD 所成的角; (III )求1B 到面EFBD 的距离例2.如图,三棱柱中,已知A BCD 是边长为1的正方形,四边形B B A A '' 是矩形,。
平面平面ABCD B B A A ⊥''(Ⅰ)若A A '=1,求直线AB 到面'DAC 的距离.(II ) 试问:当A A '的长度为多少时,二面角 A C A D -'-的大小为? 60(Ⅰ)求证:直线1B P 不可能与平面11ACC A 垂直;(II )当11BC B P ⊥时,求二面角11C B P C --的大小的余弦值.例4.如图,1BE AB ⊥;(Ⅱ)求二面角B (Ⅲ)求异面直线例5.(山东卷)如图,已知平面A 1B 1C 1平行于三棱锥V-ABC 的底面ABC ,等边∆ AB 1C 所在的平面与底面ABC 垂直,且∠ACB =90°,设AC =2a ,BC=a .(1)求证直线B 1C 1是异面直线AB 1与A 1C 1的公垂线; (2)求点A 到平面VBC 的距离; (3)求二面角A-VB-C 的大小例6.如图,在底面是菱形的四棱锥P —ABCD 中,60,ABC ∠=︒,PA AC a ==,PB PD ==点E 在PD上,且PE:ED= 2: 1. (Ⅰ)证明 PA⊥平面ABCD;(Ⅱ)求以AC 为棱,EAC 与DAC 为面的二面角θ的大小:(Ⅲ)在棱PC 上是否存在一点F, 使BF∥平面AEC?证明你的结论.练习:1.在正四面体S ABC -中,棱长为a ,E,F分别为SA 和BC 的中点,求异面直线BE 和SF 所成角的余弦值.2.在边长为1的菱形ABCD 中,60ABC ︒∠=,将菱形沿对角线AC 折起,使折起后BD =1,求二面角B ACD --的余弦值.3.在四棱锥P ABCD -中,底面ABCD 为矩形,PD ⊥底面,且PD AD a ==,问平面PBA 与平面PBC 能否垂直?试说明理由.(不垂直)4.在直三棱柱12AC AA ==. (1) 求1O(2) 求BCPA=2,(Ⅰ)求直线PA 与平面DEF 所成角的大小; (Ⅱ)求点P 到平面DEF 的距离。
用空间向量问题解决立几几何问题
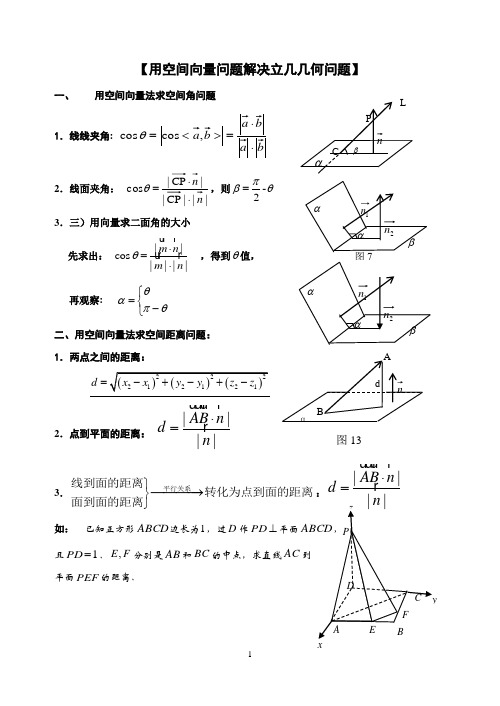
【用空间向量问题解决立几几何问题】
一、
用空间向量法求空间角问题
1.线线夹角
: =
><=,cos cos θ
2.线面夹角: cos =
θ,则-2
π
βθ=
3.三)用向量求二面角的大小
先求出: ||
cos ||||
m n m n θ⋅=⋅ ,得到θ值,
再观察:
θ
απθ
⎧=⎨-⎩
二、用空间向量法求空间距离问题: 1.两点之间的距离:
d =
2.点到平面的距离: ||
||
AB n d n ⋅=
3.⎫−−−−→⎬⎭
平行关系线到面的距离转化为点到面的距离面到面的距离:||
AB n d ⋅=
如: 已知正方形ABCD 边长为1,过D 作⊥PD 平面且1=PD .F E ,分别是AB 和BC 的中点,求直线AC 到 平面PEF 的距离.
图13
例1.(2010重庆理数)如图,四棱锥P-ABCD中,底面ABCD为矩形,PA 底面ABCD,
E是棱PB的中点。
(1)求直线AD与平面PBC的距离;
(2)若A-EC-D的平面角的余弦值。
例2.(2010湖南理数)
例3.(2011北京理) 如图,在四棱锥P ABCD -中,
PA ⊥平面ABCD ,底面ABCD 是菱形,
2,60AB BAD =∠=.
(Ⅰ)求证:BD ⊥平面;PAC
(Ⅱ)若,PA AB =求PB 与AC 所成角的余弦值; (Ⅲ)当平面PBC 与平面PDC 垂直时,求PA 的长.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
所以 BD 与
1
所成角的余弦值为 AF
1
30 10
题型一:线线角 练习: 在长方体 ABCD A1B1C1D1 中, AB= 5,AD 8,
AA1 4, M 为B1C1上的一点,且B1M 2,点N 在线段A1D上,
A1D AN . (1)求证:A1D AM .
A1 (2)求AD与平面ANM 所成的角. B1 M A(0,0,0), A1 (0,0, 4),D(0,8, 0), M (5, 2, 4) A
•小结
题型一:线线角
例一:Rt ABC中,BCA 900 , 现将 ABC沿着
平面ABC的法向量平移到A1B1C1位置,已知
求BD1与AF1所成的角的余弦值. C1
F1
取A1B1、AC BC CA CC1, 1 1的中点D 1、F 1,
B1
D1
A1
C
A
B
题型一:线线角 解:以点C为坐标原点建立空间直角坐标系 C xyz 如图 z 所示,设 则: CC1 1 C
n2
A
n2 n1
B
n1
cos | cos n1 , n2 |
关键:观察二面角的范围
cos | cos n1 , n2 |
例3 如所示, ABCD是一直角梯形,ABC=900 , 1 SA 平面ABCD, SA AB BC 1, AD , 求面SCD与面SBA 2 所成二面角的余弦值.
A(1,0,0), B(0,1,0),
1 1 1 F1 ( , 0, a), D1 ( , ,1) 2 2 2 1 所以: AF1 ( , 0,1), 2
1 1 BD1 ( , ,1) 2 2
F1
1
B1
A1
C
D1
A x
By
1 1 AF1 BD1 30 4 cos AF1 , BD1 10 5 3 | AF1 || BD1 | 4 2
2 5 cos AD, A1D 5 AD与平面ANM 所成角的正弦值是
B1 M A
D
C
y
x
B
2 5 5
题型二:线面角
练习1: 正方体 ABCD A1B1C1D1 的棱长为1.
求B1C1与面AB1C 所成的角.
A1 B1 C1 D1ຫໍສະໝຸດ A BCD
题型三:二面角
二面角的范围:
O
[0, ]
y x 0 2 yz0 2
S
练习2:
如图,PA⊥平面 ABC, AC⊥BC,PA=AC=1,BC= 2 , 求二面角 A-PB-C 的余弦值.
z
y
x
练习2: 如图,PA⊥平面 ABC,AC⊥BC,PA=AC=1,
BC= 2 ,求二面角 A-PB-C 的余弦值.
分析: 若用几何法本题不太好处 理,注意到适当建立空间直角坐 标系后各点坐标容易处理,可考 虑尝试用向量法处理 ,从而把问 x 题转化为向量运算问题.
空间向量的引入为代数方法处理立体几 何问题提供了一种重要的工具和方法,解题 时,可用定量的计算代替定性的分析,从而 避免了一些繁琐的推理论证。求空间角与距 离是立体几何的一类重要的问题,也是高考 的热点之一。本节课主要是讨论怎么样用向 量的办法解决空间角问题。
1.若a (a1 , a2 , a3 ), b (b1 , b2 , b3 ), 则:
AA1 4, M 为BC1上的一点,且B1M 2,点N 在线段A1D上,
A1D AN . (1)求证:A1D AM . A1 (2)求AD与平面ANM 所成的角正弦.
A(0,0,0), A1 (0,0, 4), D(0,8, 0),
z
N
C1
D1
AD (0,8,0), A1D (0,8, 4),
AB ( x2 x1 , y2 y1 , z2 z1 )
题型一:线线角
异面直线所成角的范围: 0, 2 思考: C D
结论:
A
B
D1
CD, AB 与的关系? DC , AB 与的关系?
cos
| cos CD, AB |
数量积: a b
a1b1 a2b2 a3b3
| a ||b |
| a | | b | cos a, b
a1b1 a2b2 a3b3 a12 a2 2 a32 b12 b2 2 b32
a b 夹角公式: cos a b
2.若A( x1 , y1 , z1 ), B( x2 , y2 , z2 ),则:
z
y x 2 任取n2 (1, 2,1) z y 2 n1 n2 6 6 cos n1 , n2 即所求二面角得余弦值是 | n1 || n2 | 3 3
解: 建立空直角坐系A - xyz如所示, 1 B - 1, 1, 0) , D (0, , 0), S (0, 0,1) A( 0, 0, 0) , C( C 2 1 易知面SBA的法向量n1 AD (0, , 0) 2 A y 1 1 D x CD (1, , 0), SD (0, , 1) 2 2 设平面SCD的法向量n2 ( x, y, z ), 由n2 CD, n2 SD, 得:
z
N
C1
D1
AM (5, 2, 4), A1D (0,8, 4),
D
C
y
AM A1D=0 A1D AM .
x
B
题型二:线面角
直线与平面所成角的范围: [0, ] 2
A
n
O
思考:
n, BA 与的关系?
B
结论:
sin
|
cos n, AB
|
题型二:线面角 例2: 在长方体 ABCD A1B1C1D1 中, AB= 5,AD 8,
z
y
例 4.如图,PA⊥平面 ABC,AC⊥BC,PA=AC z =1, BC= 2 ,求二面角 A-PB-C 的余弦值.
解:建立坐标系如图,
则 A(0,0,0),B( 2 ,1,0),C(0,1,0),P(0,0,1), x
y
AP =(0,0,1), AB ( 2,1,0), CB ( 2,0,0), CP (0, 1,1) , m AP 0 设平面 PAB 的法向量为 m =(x,y,z),则 m AB 0 ( x , y , z ) (0, 0,1) 0 y 2x ∴ ∴ ,令 x=1,则 m =(1, 2,0) ,
