重复测量两个因素的三因素实验设计 多因素 心理实验案例 原创
重复测量两个因素的三因素实验设计

.
μ:总体平均数 αj:A因素水平j理效应 πi(j):嵌套在水平aj内的被试误差 βk:B因素水平k的处理效应 (αβ) jk:水平aj和βk的两次交互作用
(βπ)ki(j):水平βk和嵌套在aj内的被试πi的交互作用的残差
np-1 P-1=1 p(n-1)=6 np(qr-1)=24 q-1=1 (p-1)(q-1)=1 p(n-1)(q-1)=6 r-1=1
153.125 4.708
12.500 24.500 0.417 3.125
32.52**
29.98** 58.75** 8.3
.
三因素重复测量两因素的方差分析表(接上)
.
重复测量两个因素的三因素实验设计的平方和分解
SS被试间 df=np-1
SS总变异 df=npqr-1=31
SS被试内 df=np-1
SSA df=p-1
SS被试(A) df=p(n-1)
SSB df=q-1
SSAB
SSB×被试内(A )
df=(p-1)(q-1) df=p(p-1)(q-1)
SSC df=r-1
3:在一个被试间因素上,随机分配被试,每个被试接受 一个处理水平,在两个被试内因素上,每个被试接受所 有处理水平的结合。
.
重复测量两个因素的三因素实验设计的图解
b1
b1
b2
b2
b3
b3
c1
c2
c1
c2
c1
c2
s1
s1
s1
s1
s1
s1
a1 s2
s2
s2
实验心理学第五讲真实验(二)多因素实验设计1

典型的两因素实验设计
两因素完全随机实验设计 • 两个自变量都是被试间变量
两因素被试内实验设计 • 两个自变量都是被试内变量
两因素混合实验设计 • 一个自变量是被试内变量,一个是被试间变量
两因素完全随机(被试间)实验 设计
• • •
•
•
基本特点 两个自变量,每个自变量有两个或两个以上的 水平,如p×q个处理水平 两个自变量都是被试间变量 被试随机分配给各处理水平结合 每个被试只接受一个处理水平结合的处理 所需被试量:N=npq,n是接受同一实验条件 的被试的数量
•
SSBX被试(A)的实质 分别计算B因素在a1和a2水 平上的数据,可得到两个单 因素重复测量设计
SS残差(pooled)= SSBX被试(A) =60165.48+50105.12=110270.6 SSBX被试(A):相当于嵌套在a1和a2水平 内的两个单因
三因素实验设计
阅读反应时/ms
580 560 540 520 500 规则 不规则
高频 低频
简单效应检验(simple effect test)
多因素实验设计中,当交互作用显著时, 考察一个因素在另一个因素的每个水平 上的处理效应,以确定该因素的处理效 应在另一个因素的哪个水平上是显著的
可检验的假说
A因素在B的不同水平上可检验的假说 H0:aj(在b1水平) = 0 H0:aj(在b2水平) = 0 ………… B因素在A的不同水平上可检验的一组假说 H0:βk(在a1水平) = 0 H0:βk(在a2水平) = 0 …………
• •
•
基本特点 两个自变量,每个自变量有两个或两个 以上的水平,如p×q个处理水平 两个自变量一个是被试内变量,另一个 是被试间变量 所需被试量:N=np, n是接受同一实验 条件的被试的数量,p是被试间变量的水 平数
三因素实验设计

适用条件
研究中有三个自变量,A(P>=2)和B(Q>=2)和C (R>=2);研究者不仅关心各个自变量的单独效应,而且更 关心变量之间的交互作用。
设计方案
一.从总体中随机挑选出一部分被试,如果每种自变量 水平结合下安排n个被试,那么总共需要N*P*Q*R 个被试。
研究共有P×Q×R个处理水平的结合
研究者不仅关心各个自变量的单独效应,而且更关心变 量之间的交互作用
a1c1
a1c2
重复测量一个因素(混 合设计)被试分配方案
a2c1
a2c2
b1
b2
b3
S1
S1
S1
S2
S2
S2
S3
S3
S3
S4
S4
S4
S5
S5
S5
S6
S6
S6
S7
S7
S7
S8
S8
S8
S9
S9
S9
四.数据收集和分析
主效应 三因素交互效应 两因素交互效应 简单效应 简单简单效应 多重比较
#2022
总变异的分解:
AB
A×B×被试
01
AC
A×C×被试
02
BC
B×C×被试
03
ABC
A×B×C×被试
04
○ 关于简单交互作用和简单简单效应
轻工业耗能 重工业耗能
45 40 35 30 25 20 15 10
5 0
第一季度
第二季度
东部 西部
45 40 35 30 25 20 15 10
三因素重复测量设计

缺点: 当实验处理及水平较多时,每个被试重复 测量的次数大大增加,易产生疲劳效应和 顺序效应。 实验中的交互作用较多时,对结果的解释 更加复杂。
四、三因素被试内设计示意图
a1
b1 c1
a1
b1 c2
a1
b2 c1
a1
b2 c2
a2
b1 c1
a2
b1 c2
a2
b2 c1
a2
b2 c2
S1 S2 S3 S4
三、三因素被试内设计的优缺点
优点: 同被试间和混合设计相比,被试内设计选用的被 试数量少,带进被试间的个体差异也最少 被试内设计能够彻底分离由被试间的个体差异所 引起的误差,从而提高实验的敏感性 可以同时对多个实验处理的效应和交互作用进行 分析 实验中三个自变量都是被试内变量,且实验任务 较简单,每次施测不费时间时,是控制得最好的 设计。
SSBC*被试
SSABC
SSABC*被试
相关概念说明
主效应:实验中一个因素的不同水平引起的变异叫因素的主效应。 二重交互作用:当一个因素的水平在另外一个因素的不同水平上变化 趋势不一致时,称两个因素之间存在交互作用,而这 种交互作用就是二重交互作用。 简单效应:在因素实验中,一个因素的水平在另一个因素的某个水平 上的变异叫简单效应。 简单效应检验:把其中一个因素固定在某一个特定的水平上,考察另 一个因素对因变量的影响。
三重交互作用:当一个因素如何起作用受另外两个因素的影响时,称 三个因素之间存在交互作用,而这种交互作用称做三 重交互作用。 简单简单效应:一个因素的水平在另外两个因素的水平结合上的效应 简单简单效应检验:把两个因素都固定在各自的某一个特定的水平 上,考察第三个因素对因变量的影响。
实验心理学08-多因素的实验设计

导致假设越来越多等问题。
优点
灵活性 相对于析因设计有更高灵活性。
高效 不需要考虑贡献小的因素和水平
反馈
缺点
无交互作用 被试间设计
比较系列中不同实验的结果时 时间跨度长
需要在实验结果分析后才能做下次实验
总结
设计方法 2水平实验
多水平实验 析因实验
二.析因设计(Factorial Designs)
我们得到4×5×3×6×4×5设计 总共实验单元格是7200个
二.析因设计(Factorial Designs)
2.统计计算更困难。 3.高次交互作用有时很难解释。
有没有其他方法具有析因实验的优点而避开它的缺点呢?
三、会聚实验设计Converging-Series Designs
规则),四种处理水平的结合,字频是被试间变量,声旁 规则性是被试内变量 实验材料:160个汉字,每种处理水平40个汉字 被试:50名中学生,随机分成两组,每组25名,一组只阅 读高频字,包括高频-规则字和高频-不规则字,一组只阅 读低频字,包括低频-规则字和低频-不规则字 因变量:阅读汉字的反应时(每名被试阅读40个汉字的平 均反应时)
二.析因设计(Factorial Designs)
2×4 设计
2×3×4设计
二.析因设计(Factorial Designs)
优点 1、同时观察多个因 素的效应,提高了实 验效率; 2、能够分析各因素 间的交互作用;
解决问题的时间与领导的关系由组的大小决定
二.析因设计(Factorial Designs)
优点
决定一个变量是否有作用 结果易解释分析 对某些理论检验已充分 竞争理论
三因素实验设计

THANKS
实验条件限制
在某些情况下,实验条件的限制可能无法满 足三因素实验设计的要求,导致实验无法进 行或结果不准确。
07
三因素实验设计的未来发展 与展望
人工智能与机器学习在三因素实验设计中的应用
自动化实验流程
利用人工智能技术,实现实验流程的自动化管理,提高实验效率和 准确性。
数据挖掘与分析
通过机器学习算法对大量实验数据进行挖掘和分析,发现隐藏的规 律和趋势,为实验设计提供更准确的指导。
完全随机化法
定义
完全随机化法是一种将实验因素 完全随机分配到实验条件下的实 验设计方法。
特点
完全随机化法简单易行,能够减 少实验误差和偏差,但无法保证 实验因素在不同水平之间的均衡 分布。
应用场景
适用于多因素、多水平的情况, 尤其适用于因素间交互作用较小, 或因素间交互作用已知的情况。
04
三因素实验设计的步骤
灵活性
三因素实验设计允许研究者灵活地调整三个实验因素,以探究不同 因素组合下的实验结果,为实验提供了更大的灵活性。
高效性
相对于单因素或双因素实验设计,三因素实验设计能够更快速地得 出结论,提高了实验效率。
缺点
复杂性
三因素实验设计涉及的变量多,实验过程相 对复杂,需要更多的实验材料和时间。
误差控制
由于涉及三个因素的交互作用,三因素实验设计的 误差控制较为复杂,需要更多的数据分析和统计处 理。
03
三因素实验设计的方法
正交表法
1 3
定义
正交表法是一种基于正交表进行的实验设计方法,通过合理 安排实验因素和水平,实现实验的高效、经济和科学性。
特点
2
正交表具有均衡分散、整齐可比的特点,能够快速有效地筛
心理学多因素实验设计模版
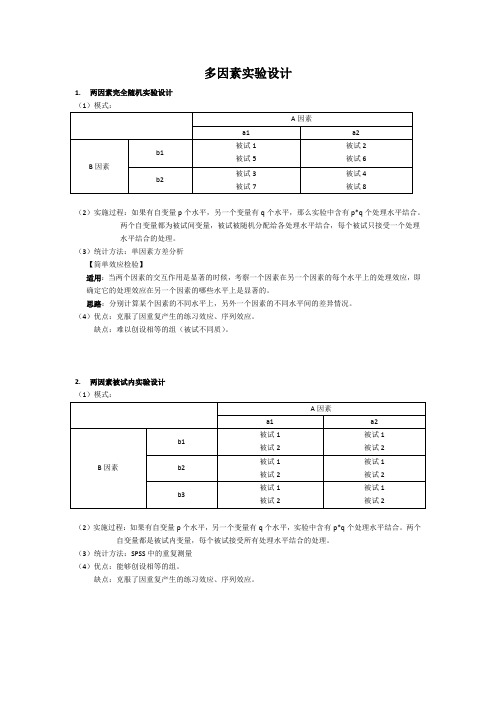
多因素实验设计
1.两因素完全随机实验设计
(1)模式:
(2)实施过程:如果有自变量p个水平,另一个变量有q个水平,那么实验中含有p*q个处理水平结合。
两个自变量都为被试间变量,被试被随机分配给各处理水平结合,每个被试只接受一个处理
水平结合的处理。
(3)统计方法:单因素方差分析
【简单效应检验】
适用:当两个因素的交互作用是显著的时候,考察一个因素在另一个因素的每个水平上的处理效应,即确定它的处理效应在另一个因素的哪些水平上是显著的。
思路:分别计算某个因素的不同水平上,另外一个因素的不同水平间的差异情况。
(4)优点:克服了因重复产生的练习效应、序列效应。
缺点:难以创设相等的组(被试不同质)。
2.两因素被试内实验设计
(1)模式:
(2)实施过程:如果有自变量p个水平,另一个变量有q个水平,实验中含有p*q个处理水平结合。
两个自变量都是被试内变量,每个被试接受所有处理水平结合的处理。
(3)统计方法:SPSS中的重复测量
(4)优点:能够创设相等的组。
缺点:克服了因重复产生的练习效应、序列效应。
3.两因素混合实验设计
(1)模式:
(2)实施过程:如果有自变量p个水平,另一个变量有q个水平,实验中含有p*q个处理水平结合。
两个变量中一个是被试内变量,另一个是被试间变量。
(3)统计方法:SPSS中的重复测量
(4)优点:有效的控制额外变量,更有利于揭示变量间的因果关系。
缺点:操作繁杂,费时费力。
重复两因素的三因素混合设计

重复测量两上因素的三因素实验设计:三因素混合设计一、重复测量两个因素的三因素实验设计的基本特点在有些研究中,需使用另外一种混合因素设计——重复测量两个因素的三因素的设计,它适合用于这样的研究条件:1.研究中有三个自变量,每个自变量有两个或多个水平,其中有一个自变量是被试间变量,两上自变量是被试内变量。
2.如果实验的三个自变量分别有p 、q 、r 个水平,则研究中共有p ×q ×r 个处理水平的结合。
重复测量两个因素的三因素设计的基本方法是,在一个被试间因素上,随机分配的被试,每个被试接受一个处理水平。
在两上被试内因素上,每个被试接受所有的处理水平的结合。
与上一节中介绍的实验设计的相比,重复测量两个因素的三因素设计同样具有重复测量一个因素的三因素设计的特点,不同的是它所需要的被试量时一步减少,例如,在同样的2×3×2实验中,需要的被试是N=np=8,每个被试接受6个实验处理。
重复测量两个因素的三因素设计可检验的假说与重复测量一个因素的三因素设主可检验的假说完全一致,我们就不在这里重述。
二、重复测量两个因素的三因素实验设计与计算举例(一)问题的提出实验设计当研究者希望更好地控制被试变异,或希望减少被试数量时,可将前一节研究中的两上因素,例如文章类型和平均句长,都作为被试内因素,仍保留生字密度做被试间因素。
这时,实验设计中只需8名被度,研究者首先将8名被试随机分为两组,分别在a 1、a 2两种情境中。
然后,每组中的每个被试阅读4篇文章,即一组中每个被试阅读4篇生字密度小的文章(a 1b 1c 1、a 1b1c 2、a 1b 2c 1和a 1b 2c 2),另一组中每个被试阅读4篇生字密度在的文章(a 2b 1c 1、a 2b 1c 2、a 2b 2c 1、和a 2b 1c 2)。
由于该研究中实验任务比较复杂,应采取有效措施克服疲劳和顺序效应。
例如,实验分四次实施,每个被试每次阅读一篇文章,阅读文章的先后顺序按拉丁方格平衡。
重复测量两个因素的三因素实验设计 多因素 心理实验案例 原创

当生词密度比较大(a1)时,学生对说明文与记叙 文的阅读成绩都比较差,且差异不显著;当生词密
度比较小(a2)时,学生对于说明文与记叙文的阅 读成绩显著提高,且记叙文的成绩显著好于说明文。
AB表
100
80
60Biblioteka b140b220
.0 a1 a2
两次交互作用和简单效应检验
当句子比较短时(c1), 文章类型对于学生的阅读理 解成绩的影响没有差异;当句子比较长时(c2), 记叙文的阅读成绩显著高于说明文的成绩,且 达到显著性水平。
(αβγ)jkl=0
重复测量两个因素的三因素实验设计不仅具有重复测量一 个因素的所有优点,而且可以节省更多的被试。
.
μ:总体平均数 αj:A因素水平j理效应 πi(j):嵌套在水平aj内的被试误差 βk:B因素水平k的处理效应 (αβ) jk:水平aj和βk的两次交互作用
(βπ)ki(j):水平βk和嵌套在aj内的被试πi的交互作用的残差
γl :C因素水平l的处理效应 (αγ )jl:水平αj和γl的两次交互作用 (γπ)li(j):γl水平和嵌套在aj内的被试的 交互作用的残差 (βγ)kl:水平βk和γl的两次交互作用 (αβγ)jkl:水平αj 、βk和γl的三次交互作用 (β的γπ残)kl差i(j): 水平βk 、γl水平和嵌套在aj内的被试πi的交互作用 ∈ijkl :指单元内误差
.
重复测量两个因素的三因素实验设计的平方和分解
SS被试间 df=np-1
SS总变异 df=npqr-1=31
SS被试内 df=np-1
SSA df=p-1
SS被试(A) df=p(n-1)
SSB df=q-1
SSAB
SSB×被试内(A )
重复测量两个因素的三因素实验设计 多因素 心理实验案例 原创

设计
——重复测量两个因素的三因素实验
精品课件
(一)重复测量两个因素的三因素实验设 计的特点
1:研究中有三个自变量,每个自变量有两个或多个水平 ,其中有一个自变量是被试间变量,两个自变量是被试 内变量。
2:如果实验中的三个自变量分别有p、q、r个水平,则研
究中共有p×q×r个处理水平的结合。
精品课件
(二)重复测量两个因素的三因素实验设计的假设
(1) A因素的处理效应为零H0:αj=0 (2) B因素的处理效应为零H0:βk=0 (3) C因素的处理效应为零H0:γl=0 (4) A和B两因素的交互作用为零H0: (αβ) jk=0 (5) A和C两因素的交互作用为零H0:(αγ)jl=0 (6)B和C两因素的交互作用为零H0:(βγ)kl=0 (7)A、 B、C三因素因素的交互作用为零H0:
3:在一个被试间因素上,随机分配被试,每个被试接受 一个处理水平,在两个被试内因素上,每个被试接受所 有处理水平的结合。
精品课件
重复测量两个因素的三因素实验设计的图解
精品课件
(三)设计模式
Yijkl =μ+αj+πi(j)+βk+ (αβ) jk+(βπ)ki(j)+ γ l+(αγ )jl+ (γπ)li(j) +(βγ)kl+(αβγ)jkl +(βγπ)kli(j) +∈ijkl
(αβγ)jkl=0
重复测量两个因素的三因素实验设计不仅具有重复测量 一个因素的所有优点,而且可以节省更多的被试。
精品课件
μ:总体平均数
αj:A因素水平j理效应
πi(j):嵌套在水平aj内的被试误差 βk:B因素水平k的处理效应
两因素重复测量实验设计

两因素重复测量实验设计引言:在科学研究中,为了验证研究对象的特定性质或现象,常常需要进行实验设计。
其中,重复测量实验设计是一种常见的方法,它能够减少误差因素对实验结果的影响,提高实验结果的可信度和可重复性。
本文将介绍两因素重复测量实验设计的基本原理、步骤和应用。
一、实验设计原理两因素重复测量实验设计是一种多因素实验设计方法,它通过对同一实验对象进行多次测量,以消除实验对象个体差异对实验结果的影响。
其中,两个因素分别称为主因素和副因素,主要通过重复测量和随机分组两种方式来进行实验。
二、实验设计步骤1. 确定研究目的和问题:明确实验的目的和需要验证的问题,确定主因素和副因素。
2. 设计实验方案:根据研究目的和问题,设计出合适的实验方案,包括实验对象、实验组和对照组的选择,实验条件的设置等。
3. 随机分组:根据实验方案,将实验对象随机分为不同的组别,以消除个体差异对实验结果的影响。
4. 重复测量:在实验过程中,对每个实验对象进行多次测量,以减少测量误差和提高实验结果的可靠性。
5. 数据分析与结果验证:通过对实验数据进行统计分析和假设检验,验证实验结果的可靠性和有效性。
三、实验设计应用1. 医学研究:在药物研究和治疗效果评估中,常常需要进行两因素重复测量实验设计,以确定药物的疗效和副作用。
2. 农业科学:在作物种植和农业生产中,通过两因素重复测量实验设计,可以评估不同种植条件和处理方式对作物产量和质量的影响。
3. 工程技术:在工程实践中,通过两因素重复测量实验设计,可以评估不同材料和工艺对产品性能和使用寿命的影响。
4. 教育研究:在教学实践和教育研究中,通过两因素重复测量实验设计,可以评估不同教学方法和教育资源对学生学习成绩和兴趣的影响。
结论:两因素重复测量实验设计是一种常用的实验设计方法,通过对同一实验对象进行多次测量和随机分组,可以减少个体差异对实验结果的影响,提高实验结果的可靠性和有效性。
在科学研究和应用领域中,该实验设计方法具有广泛的应用前景,对于验证和评估研究对象的特定性质和现象具有重要意义。
心理学与教育研究中的多因素实验设计

心理学与教育研究中的多因素实验设计——舒华第二章几种基本的实验设计第一节单因素完全随机实验设计一、基本特点适用于:研究中有一个自变量,自变量有两个或多于两个水平。
方法:把被试随机分配给自变量的各个水平,每个水平被试只接受一个水平的处理。
二、计算与举例(一)检验的问题与实验设计(二)实验数据及其计算第二节单因素随机区组实验设计一、基本特点适用于:研究中有一个变量,自变量有两个或多个水平(P≥2),研究中还有一个无关变量,也有两个或多个水平(n≥2);并且自变量的水平与无关变量的水平之间没有交互作用。
适合检验的假说:(1)处理水平的总体平均数相等或处理效应为零;(2)区组的总体平均数相等或区组效应为零。
二、计算三、优点:从实验中分离出了一个无关变量的效应,从而减少了实验误差。
第三节单因素拉丁方设计一、基本特点定义:是一个含P行、P列、把P个字母分配给方格的管理方案,其中每个字母在每行中只出现一次。
适用于:(1)研究中自变量与无关变量的水平平均≥2,一个无关变量的水平被分配给P行,另一个则给P列;(2)假定处理水平与无关变量水平之间没有交互作用,(3)随即分配处理水平给个方格单元,每个处理水平仅在每行,每列中出现一次。
无关变量C的四个水平无关变量B的四个水平自变量A的四个水平第四节单因素重复测量实验设计一、基本特点:(也叫被试内设计)基本方法:实验中每个被试接受所有的处理水平目的:利用被试自己做控制,使被试的各方面特点在所有的处理中保持恒定,以最大限度地控制由被试的个体差异带来的变异。
假设:当若干处理水平连续实施给同一被试时,被试接受前面的处理,对接受后面的处理没有长期的影响。
优点:从总变异中分离出了被试间变异,与完全随机实验相比,它提高了实验处理的F检验的敏感性。
第三章两因素完全随机和随机区组实验设计第一节两因素完全随机实验设计一、基本特点与单因素相比:可对两个或多个变量之间的交互作用进行估价不同:每个被试接受的是一个处理的结合,而不是一个处理水平二、举例第二节对交互作用的进一步检验一、交互作用图解二、简单效应检验(一)简单效应的基本特点及其作用分别检验一个因素在另一个因素的每个水平上的处理效应,以便具体地确定它的处理效应在另一个因素的哪个水平上是显著的,在哪些水平上是不显著的。
两因素重复测量实验的三线表

两因素重复测量实验的三线表一、引言两因素重复测量实验是一种常用的实验设计方法,用于研究两个或更多因素对实验结果的影响。
本文将以一份三线表为例,介绍如何使用该实验设计方法,并分析实验结果。
二、实验设计本次实验涉及两个因素:因素A和因素B,每个因素有三个水平,分别为A1、A2、A3和B1、B2、B3。
实验采用重复测量设计,每个水平下进行三次测量,共计27个观察值。
三、数据分析根据实验结果,我们可以绘制出如下的三线表:因素A因素B A1 A2 A3B1 X11 X12 X13B2 X21 X22 X23B3 X31 X32 X33其中,Xij表示在因素A的第i个水平和因素B的第j个水平下的观察值。
通过观察三线表,我们可以得到以下几个结论:1. 因素A对实验结果有显著影响:观察每一列的数据,可以发现在因素A不同水平下,观察值存在明显差异。
因此,我们可以得出结论:因素A对实验结果有显著影响。
2. 因素B对实验结果有显著影响:观察每一行的数据,可以发现在因素B不同水平下,观察值存在明显差异。
因此,我们可以得出结论:因素B对实验结果有显著影响。
3. 因素A和因素B之间存在交互作用:从整个三线表的数据来看,不同水平下的观察值存在交叉现象,即因素A和因素B之间存在交互作用。
具体来说,当因素A为A1时,因素B的影响程度可能与其他水平下不同。
四、结论与讨论通过两因素重复测量实验的三线表分析,我们得出了以下结论:1. 因素A对实验结果有显著影响;2. 因素B对实验结果有显著影响;3. 因素A和因素B之间存在交互作用。
这些结论为进一步深入研究和分析提供了重要线索。
在进行后续实验或研究时,可以重点关注因素A和因素B的影响机制,进一步探讨它们对实验结果的具体影响程度。
值得注意的是,本次实验只涉及两个因素,若研究对象更复杂,可以将两因素重复测量实验扩展为更高维度的实验设计,以获取更全面的数据和结论。
五、总结本文以一份三线表为例,介绍了两因素重复测量实验设计的基本原理和数据分析方法。
多因素实验设计案例

多因素实验设计案例实验设计是科学研究中非常重要的一部分,通过设计合理的实验,可以解决研究中的问题,并得出科学的结论。
多因素实验设计是一种考虑多个因素影响的实验设计方法。
下面将介绍一个多因素实验设计的案例。
假设我们想要研究不同养殖环境对鸡蛋孵化率的影响。
我们认为孵化率可能受到环境温度、湿度和光照强度等多个因素的影响。
我们选择了温度、湿度和光照强度作为研究因素,并设计了一个三因素二水平的实验。
首先,我们需要确定温度、湿度和光照强度的两个水平。
根据之前的研究和经验,我们选择了25°C和30°C作为温度的两个水平,60%和70%作为湿度的两个水平,5000 lx和7000 lx作为光照强度的两个水平。
接下来,我们需要确定实验的处理组合。
因为是一个三因素二水平的实验,所以总共有2^3=8个处理组合。
我们列出所有的处理组合如下:温度(A)湿度(B)光照强度(C)25°C 60% 5000 lx25°C 60% 7000 lx25°C 70% 5000 lx25°C 70% 7000 lx30°C 60% 5000 lx30°C 60% 7000 lx30°C 70% 5000 lx30°C 70% 7000 lx然后,我们需要随机分配实验单元到不同的处理组合中。
为了消除可能的混杂效应,我们可以采用随机化的方法。
将每个处理组合写在一张卡片上,然后将这些卡片放入一个袋子中,并在实验开始前适当搅拌袋子,然后取出一张卡片,即为一个处理组合。
在实验开始前,我们需要确定每个处理组合的重复次数。
根据实验资源的限制和统计学原则,我们选择每个处理组合的重复次数为3次。
也就是说,我们需要在每个处理组合中重复实验3次。
在实验进行过程中,我们需要记录每个处理组合的孵化率。
我们可以通过统计每个处理组合中鸡蛋的成功孵化数量并除以总的鸡蛋数量来得到孵化率。
多因素实验设计

(3) 2×3 混合设计:如果每各处理组合需要6 个被试,则需要 ?名被试 B(元认知水平,被试间变量)
b1 A
(题目类型,被 试内变量)
b2 a1b2 1- 6
b3 a1 b3 1- 6
a1
a1 b1 1- 6
a2
a2 b1 7- 12
a2b2 7- 12
a2 b3 7- 12
第二节 两因素完全随机和随机区组实验设计
生的部分文科教材和文学读物的编写提供心理学依据。
• 确定自变量:实验设计采用2 X 3(即:材料X呈
现方式)的两因素混合设计,其中材料(难、易)
是被试内设计,呈现方式(无插图、黑自插图、
彩色插图)是被试间设计。
• 确定因变量:阅读成绩、持续时间、注视次数、
眼跳距离、回视次数
• 确定被试:二年级大学生。如果每个处理用10名被试, 共需30名被试。
(1) 2×3 被试间设计:如果每个处理组合需要6个被试, 则共需 ?名被试
B(例如:年龄) b1 b2 b3
A
(材料类 型)
a1
a2
a1 b1 6名
a2 b1 6名
a1b2 6名
a2b2 6名
a1 b3 6名
a2 b3 6名
(2) 2×3重复测量设计:如果每个处理需要6个被试,
则需要 ?名被试
B(单词类型) b1 b2 b3
数划分区组。
随机区组2×3因素实验设计
区组
a1 b1 s1.1 s2.1 s3.1 s4.1
a1 b2 s1.2 s2.2 s3.2 s4.2
a1 b3 s1.3 s2.3 s3.3 s4.3
a2 b1 s1.4 s2.4 s3.4 s4.4
多因素实验设计案例

结果与分析
4.不同情境以及年龄对幼儿坚持性行为的影响
幼儿的4种典型行为的年龄差异均显著 随着年龄的增长,幼儿的溜号行为、求助行为、自言自语及
拾取方法的表现均有所变化。
结果与分析
4. 不同情境以及年龄对幼儿坚持性行为的影响
溜号行为的情境差异非常显著 其他典型行为受情境的影响不明显。
结果与分析
1.教师态度、言语指导和年龄对3~6岁幼儿坚持时间的影响
幼儿年龄主效应极为显著 教师态度主效应极为显著 教师言语指导主效应极为显著 年龄 × 言语指导方式的交互作用极为显著 言语指导 × 教师态度的交互作用极为显著 年龄 × 教师态度的交互作用不显著 年龄 × 言语指导 × 教师态度的交互作用不显著
2.被试同质性检验——《幼儿自我控制能力发展教师评定问卷》 3.实验材料——红豆、绿豆,两个盒子 4.实验设计与程序 4.1实验设计
3 × 2 × 2
(年龄×教师态度×言语指导方式)
研究方法
4.2实验程序
主试的选择——12名教师(工作年限2年以上) 记录员的选择——4名研究生
预实验——10人
发现不利因素,控制无关变量
恐惧型:重要他人启动&无重要他人启动——目标承诺得分 差异不显著(F(1,187)=0.57,p>0.05);
讨论
重要他人对目标追求的影响 依恋类型在重要他人影响目标追求过程中的调节作用
结论
1. 重要他人能显著地影响个体的目标追求; 2. 依恋关系在重要他人影响目标追求过程中起到调节作用;
控制组:自我信息回忆、描述 依恋类型量表 & 目标承诺量表
6.数据收集与统计分析
结果与分析——描述性统计结果
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重复测量两个因素的三因素实验设计的图解
b1
b1
b2
b2
b3
b3
c1
c2
c1
c2
c1
c2
s1
s1
s1
s1
s1
s1
a1 s2
s2
s2
s2
s2
s2
s3
s3
s3
s3
s3
s3
s4
s4
s4
s4
s4
s4
s5
s5
s5
s5
s5
s5
a2 s6
s6
s6
s6
s6
s6
s7
s7
s7
s7
s7
s7
s8
s8
s8
s8
s8
s8
(三)设计模式Βιβλιοθήκη 70BC表60
50
c1 c2 ∑
40
c1
30
c2
np=8
20
b1 48 43 91
10
b2 48 63 111
0 b1 b2
三次交互作用和简单简单效应检验
一般来说,如果三因素的交互作用显著,可以 进一步做简单简单效应检验。
本文中三因素ABC的交互作用显著,因此做 简单简单效应检验。本文的目的是检验生词密度 A在文章类型(B)与句长(C)的各个水平上的简单简 单效应。
Yijkl =μ+αj+πi(j)+βk+ (αβ) jk+(βπ)ki(j)+ γ l+(αγ )jl+ (γπ)li(j) +(βγ)kl+(αβγ)jkl
+(βγπ)kli(j) +∈ijkl
(二)重复测量两个因素的三因素实验设计的假设
(1) A因素的处理效应为零H0:αj=0 (2) B因素的处理效应为零H0:βk=0 (3) C因素的处理效应为零H0:γl=0 (4) A和B两因素的交互作用为零H0: (αβ) jk=0 (5) A和C两因素的交互作用为零H0:(αγ)jl=0 (6)B和C两因素的交互作用为零H0:(βγ)kl=0 ((7α)βγA)、jkl=B0、C三因素因素的交互作用为零H0:
181.375 153.125 28.250 87.500 12.500 24.500 2.500 3.125
np-1 P-1=1 p(n-1)=6 np(qr-1)=24 q-1=1 (p-1)(q-1)=1 p(n-1)(q-1)=6 r-1=1
153.125 4.708
12.500 24.500 0.417 3.125
下列为操作过程
谢谢观看! 2020
重复测量两个因素的三因素实验设计不仅具有重复测量一 个因素的所有优点,而且可以节省更多的被试。
μ:总体平均数 αj:A因素水平j理效应 πi(j):嵌套在水平aj内的被试误差 βk:B因素水平k的处理效应 (αβ) jk:水平aj和βk的两次交互作用
(βπ)ki(j):水平βk和嵌套在aj内的被试πi的交互作用的残差
∈ijkl :指单元内误差
重复测量两个因素的三因素实验设计的平方和分解
SS被试间 df=np-1
SS总变异 df=npqr-1=31
SS被试内 df=np-1
SSA df=p-1
SS被试(A) df=p(n-1)
SSB df=q-1
SSAB
SSB×被试内(A )
df=(p-1)(q-1) df=p(p-1)(q-1)
F
32.52**
29.98** 58.75** 8.3
三因素重复测量两因素的方差分析表(接上)
变异来源
平方和 自由度
均方 F
9.AC 10.C ×被(A)
1.125 (p-1)(r-1)=1 2.250 p(n-1)(r-1)=6
1.125 3.00 0.375
11.BC
12.500 (q-1)(r-1)=1
12.500 16.667**
12.ABC
24.500 (p-1)(q-1)(r-1)=1 24.500 32.667**
13.B ×C ×被试(A) 4.500 p(n-1)(q-1)(r-1)=1 0.750
14. 合计
268.875
npqr-1=31
两次交互作用和简单效应检验
当生词密度比较大(a1)时,学生对说明文与记叙 文的阅读成绩都比较差,且差异不显著;当生词密 度比较小(a2)时,学生对于说明文与记叙文的阅 读成绩显著提高,且记叙文的成绩显著好于说明文。
多因素实验设计
——重复测量两个因素的三因素实验设计
(一)重复测量两个因素的三因素实验设 计的特点
1:研究中有三个自变量,每个自变量有两个或多个水平, 其中有一个自变量是被试间变量,两个自变量是被试内 变量。
2:如果实验中的三个自变量分别有p、q、r个水平,则研
究中共有p×q×r个处理水平的结合。
3:在一个被试间因素上,随机分配被试,每个被试接受 一个处理水平,在两个被试内因素上,每个被试接受所 有处理水平的结合。
• 研究的问题与实验设计 • 例:探讨文章的生字密度、文章的类型和
文章的句子长度对学生阅读理解的影响。 • 生字密度5:1(a1)和20:1(a2),文章类型:
说明文(b1)和记叙文(b2),句子长度:平均 句长20个词(c1)和平均句长30个词(c2)。
实验数据
b1
b1
c1
c2
b2 b2 c1 c2
s1
a1 s2
s3
s4
s5
a2
s6
s7
s8
35 67 45 32 85 96 87 76
44 65 43 23 9 12 8 13 8 12 7 11
三因素重复测量两因素的方差分析表
变异来源
平方和 自由度
均方
1.被试间 2. A(生字密度) 3. 被试(A) 4. 被试内 5.B(文章类型) 6.AB 7B×被试(A) 8 C(句子长度)
γl :C因素水平l的处理效应 (αγ )jl:水平αj和γl的两次交互作用 (γπ)li(j):γl水平和嵌套在aj内的被试的 交互作用的残差 (βγ)kl:水平βk和γl的两次交互作用 (αβγ)jkl:水平αj 、βk和γl的三次交互作用 (β的γπ残)kl差i(j): 水平βk 、γl水平和嵌套在aj内的被试πi的交互作用
SSC df=r-1
SSAC SSC ×被试内(A) SSBC df=(p-1)(q-1) df=p(r-1)(n-1) df=(q-1)(r-1)
SSSABC df=(p-1)(q-1)
(r-1)
SSB×C ×被试内(A) df=p(q-1)(r-1)
(n-1)
(四)三因素重复测量两因素实验设计与计算举例
AB表
100
80
b1 b2 ∑
60
nr=8
40
b1 b2
a1 35 31 66
20
a2 56 80 136
0
a1 a2
两次交互作用和简单效应检验
当句子比较短时(c1), 文章类型对于学生的阅读理 解成绩的影响没有差异;当句子比较长时(c2), 记叙文的阅读成绩显著高于说明文的成绩,且 达到显著性水平。
