第五章 相图
第5章 相图

2.可逆与不可逆多晶转变
z 多晶转变相图 4个单相区
晶型II熔融曲线
晶型转变线 晶型I的升华曲线
熔体的蒸气压曲线
3相平衡点: 晶型II的升华曲线 晶型II、熔体和气相
3相平衡点: 晶型I、II和气相
z 多晶转变相图(介稳平衡态)
过热晶型I熔融曲线 过热晶型I的介稳单相区
过冷熔体的介稳单相区
硅钙石:不一致熔 各种高炉矿渣中
水泥熟料生产重要
9%体积效应
C2S:一致熔融化合物 具有复杂的多晶转变 C3S:不一致熔融化合物
2150℃ ~ 1250℃
IV. 三元系统相图
对于三元凝聚态系统, C=3,n=1(T)
相律:F = C-P + n = 4-P
Fmin = 0,Pmax = 4 Pmin = 1,Fmax = 3
z 自由度(F)
在温度、压力、组分浓度等可能影响系统平衡状态的变量中, 可以在一定范围内任意改变而不会引起旧相消失或新相产生的 独立变量数目.
z 组分及独立组分(C)
组分 系统中每个能独立分离出来,并能独立存在的化学纯物质. 独立组分 足以表示系统中各个相的组成所需的组分的最小数目.
C = 组分数-独立的化学反应数-独立的限制条件数
M’熔体的结晶路程
液相点
L M’
1
F=2
L→S F=1
3
L→S F=1
5
固相点
L→S 2
4 L→S
6S
M
⑦ 形成有限固溶体的二元相图
B在A中 形成的 固溶体
SA(B)的 溶解度 曲线
B在A中 的最大 固溶度
A在B中 的最大 固溶度
A在B中 形成的 固溶体
陶杰版材料科学基础--第5章 相图

90
10 20 30
40
II C% 50 60 70 80 90
90
80
70
60
50 ← A%
40
30
20
10
C
化学与化学工程系材料科学教研室
B 第五章 相图
课堂练习
1. 确定合金I、II、III、IV的成分 III 点:
70 80
90
10 20 30
A%=20% B%=20% C%=60%
60 B% 40 30 20 10
化学与化学工程系材料科学教研室
第五章 相图
意义
•
相图是反映物质在不同温度、成分和压力时,各种 相的平衡存在条件,以及相与相之间平衡关系的重要图 解,掌握相图对于了解物质在加热、冷却或压力改变时 的组织转变基本规律,以及物质的组织状态和预测物质 的性能,都具有重要意义。
•
研究多相系统的平衡在化学、化工的科研和生产中 有重要的意义,例如:溶解、蒸馏、重结晶、萃取、提 纯及金相分析等方面都要用到相平衡的知识
用一个温度坐标和一个压力坐标表示,这时的相图为一个二
维平面图。
化学与化学工程系材料科学教研室
第五章 相图
纯铁的相图
化学与化学工程系材料科学教研室
第五章 相图
二氧化碳相图示意图
B
p/Pa 固相
C
超临界 流体
临界点
液相
O
A
气相
T/K
纯净物质根据温度和压力的不同,会呈现出液体、气体、 固体等状态变化,如果 提高温度和压力,来观察状态的变化,那么会发现,如果达到特定的温度和压力,会 出现液体与气体界面消失的现象,该点被称为临界点。在临界点附近,会出现流体的 密度、粘度、溶解度、热容量、介电常数等所有流体的物性发生急剧变化的现象。 温度和压力均高于临界点时的流体,称为超临界流体。
第五章 三元相图
B
B%
C%
A
← A% C% →
C
b c
a
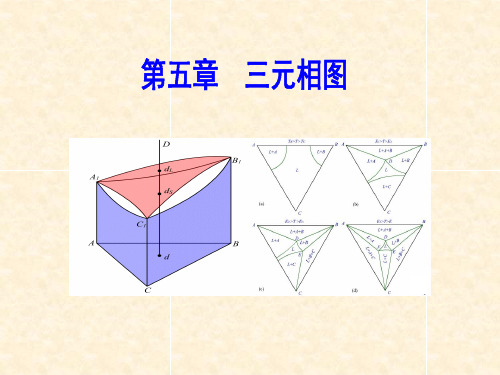
图 部分浓度三角形
§5.1.2 浓度三角形中具有特定意义的线
1)与某一边平行的直线
C
含对角组元浓度相等
A% d C% c
Bc C% 100% BC
A
B B% 图 平行于浓度三角形某一条边的直线
确定O点的成分 1)过O作A角对边的平行线 2)求平行线与A坐标的截距 得组元A的含量 3)同理求组元B、C的含量
三元系中如果任意两个组 元都可以无限互溶,那么它们 所组成的三元合金也可以形 成无限固溶体,这样的三元合 金相图,叫三元匀晶相图。
相图概况
[1] 特征点: ta, tb, tc- 三个纯组 元的熔点; [2]特征面:液相面、固相面; [3]相区:L, α, L+α。
图 三元匀晶相图
§5.3.1 相图分析
( A B )
Ax nE nA Ee
( A B C )
Ax ne nA Ee
§5.4.2 组元在固态下有限溶解,具有共晶转变的三 元相图
1.相图分析
从占有空间的角度看,固态有限互溶三元共晶相图比固态 完全不互溶三元共晶相图要多三个单相区(α、 β、 γ)和三个 固态两相区(α+β、 β+ γ、 α+ γ)。
图 过成分三角形顶点的变温截面图
图 平行于成分三角形一边的变温截面图
用垂直截面图可以分析合金的平衡结晶过程,了解合金在 平衡冷却过程中发生相变的临界温度,以及可以了解合金在 一定温度下所处的平衡状态。 但是,用垂直截面图不能了解合金在一定温度下的平衡相 成分和平衡相的重量。
图 变温截面图的应用
材料热力学第五章相图热力学

X
(2) 2 1
(5.13)
敞开系统的 d T V d P i d ni
i
dG SdT VdP i*dni RT ln X i dni RT ln i dni (5.14)
i i i
例氢 关气 系溶 如解 图度 和 所氢 示气 。压 力 的 平 方 根 的 比
5.2
含图 量 的总 变结 化说 对明 于了 氢在 气熔 溶融 解铁 度中 的合 影金 响元 。素
5.1
化学势定义为(2.40)
G i n i T , P , n j
引入活度,如式子(3.77), with
k
(5.23)
将 ei 的定义代入,当X0→1时, 根据3.84式的 定义 % i / X i 100 M i / M 0 得:
j
( j) i
230 M i ( j ) M 0 M j ei M0 M0
(5.24)
相应的5.13式也可以写成:
log
% i
e %j
( j) i j
ai lim i 1 X i 1 X i
如果溶质浓度由重量百分比来表示,上面的式子 可以表示为:(3.81)
a % i RT ln a & lim i 1 X 0 1 % i
i % i
% i
由 X 0 1(下标0表示溶剂)和温度以及压力可以 确定系统的状态 (此时 )。 X 1 0和 X 2 0
(5.25)
对于图5.1中所示的氢溶解在低浓度的铁合金中, 则5.25式可写成:
log
% H
第五章 相平衡和相图-Fe-FeC3相图131104

材料科学基础 第四节 Fe-C相图
三、 Fe- 石墨相图
1. 相图中的线和区 CD——从液相结晶出一次石墨GI; ES ——从奥氏体中析出二次石墨GII; PQ ——从铁素体中析出三次石墨GIII; ECF——共晶反应线,LC E + G PSK ——共析反应线, S P + G 2. Fe- 石墨结晶平衡组织
材料科学基础 第四节 Fe-C相图
二、 Fe- Fe3C
第五章 相平衡与相图
1. 组元和相
(1)Fe为同素异构体,在常压下从高温到低温,具有3个晶态: -Fe , -Fe, -Fe
(2)碳有两种晶态:
金刚石:金刚石结构;石墨:六方结构 (3)在Fe-Fe3C系中有4种晶体相:
• 铁素体( 或F):碳原子溶于-Fe形成的固溶体(体心立方结构);
第五章 相平衡与相图
• 0.09% <C < 0.17 % : L L+
• C = 0.17 %:L L+
• 0.17 % < C < 0.53 % :L L+ L • C > 0.53 %: L
• (固溶体同素异晶转变) 脱溶分解( +Fe3CIII)
脱溶分解( +Fe3CII)
+Fe3C)
共析转变(
• 室温平衡组织: Fe3CII + P +Ld ( Fe3CII + P + Fe3C共晶)
材料科学基础 第四节 Fe-C相图
(7)过共晶白口铁, 4.30%<C<6.69%; • L Fe3CI 共晶转变 L( + Fe3C)Ld
材料科学基础I 第五章 (相图)
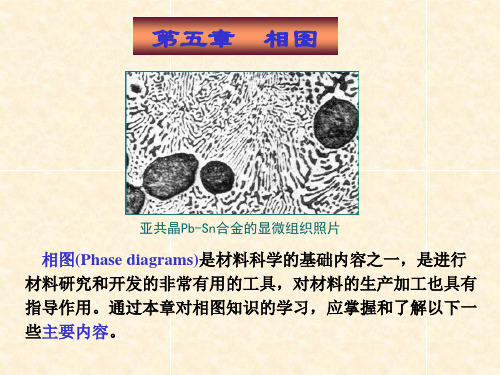
F = 0的含义是:在保持系统平衡状态不变的条件下,没有可以 的含义是:在保持系统平衡状态不变的条件下, 的含义是 独立变化的变量。 独立变化的变量。即,任何变量的变化都会造成系统平衡状态 的变化。 的变化。
纯水的PT相图: 纯水的 相图:在a点,水在 相图 点 水在1 大气压、 ℃ 条件下 保持液(水 条件下, 大气压、(0℃)条件下,保持液 水) –固(冰)二相平衡。温度升高,冰 二相平衡。 固 冰 二相平衡 温度升高, 溶化成水;温度降低, 溶化成水;温度降低,水结晶成 也就是说,此时水的液-固平 冰。也就是说,此时水的液 固平 衡转变是在恒温(0℃ 下进行的 下进行的。 衡转变是在恒温 ℃)下进行的。 b点是气 液二相平衡点,意义与 点是气–液二相平衡点 点是气 液二相平衡点,意义与a 点相似。 之间(0℃ 点相似。在a、b之间 ℃~100℃), 、 之间 ℃, 水是单一的液相(P =1),此时F =1, 水是单一的液相 ,此时 , 这说明在此范围内温度的变化不 会引起状态的改变。 会引起状态的改变。
二、相图的建立
建立相图的方法有两种: 建立相图的方法有两种: 利用已有的热力学参数,通过热力学计算和分析建立相图; 利用已有的热力学参数,通过热力学计算和分析建立相图; 依靠实验的方法建立相图。 依靠实验的方法建立相图。 目前计算法还在发展之中,实际使用的相图都是实验法建立的。 目前计算法还在发展之中,实际使用的相图都是实验法建立的。 实验法建立相图的原理和步骤: 实验法建立相图的原理和步骤: 二元合金相图的建立为例。 以A-B二元合金相图的建立为例。 二元合金相图的建立为例 首先, 首先,将A-B二元合金系分成 二元合金系分成 若干种不同成分的合金。 若干种不同成分的合金。 1) 合金成分间隔越小,合金数目 合金成分间隔越小, 越多,测得的相图越精确; 越多,测得的相图越精确; 2) 合金成分间隔不需要相等。 合金成分间隔不需要相等。
第五章 相图

相图
(2)∵150/500<70.0%∴当温度由共沸点刚有上升趋势时,系统处于气(G)与液(L1)两 相平衡设 L1 的质量为 x 则 x(150/500-0.087)=(500-x)(0.70-150/500) 解得 x=326g 气相质量为 174g。 6-10 为了将含非挥发性杂质的甲苯提纯,在 86.0kPa 压下用水蒸气蒸馏。已知:在此压力 下该系统的共沸点为 80℃,80℃时水的饱和蒸气压为 47.3kPa。试求: (1)气相组成(含甲苯的摩尔分数) ; (2)欲蒸出 100g 纯甲苯,需要消耗水蒸气多少千克? 86.0 47.3 100 / 92.140 解: y甲 0.45 y甲 解得 x=23.9kg 86.0 100 / 92.140 x / 18.02 6-14 低温时固态部分互溶、 高温时固态完全互溶且具有最低熔点的 A-B l 二组分凝聚系统相图如附图。指出各相区的相平衡关系及各条线所代表 T l+ 的意义。 解:上面的线为液相线或凝固点曲线;中间的线为固相线或熔点线;下 面的线为固相溶解度曲线 1+
A(l)+B(l) x(y) B
液态部分互溶
液态不互溶
5.常见的二组分固液相图(上述的气液相图中将气态变为液态,液态变为固态也是常 见的固液相图)
T
T l+A(s) l+B(s) A(s)+B(s) A x B l
T l l+s
T
l
l l+s ssl+s s源自x BAx
B
A
A
x
B
固态不互溶
固态完全互溶
54.22 0.4588 0.2523 98.54 p* x' (2) y’ y' A * ' A A * ' A=xA p A x A p B x B
第五章_铁碳相图

第五章铁碳相图定义:分析研究铁碳合金在平衡条件下合金的成分、温度、合金相之间关系的图解。
一、铁碳合金的基本组织与性能根据铁与碳组元的作用不同,铁碳合金的基本组织有:铁素体、奥氏体、渗碳体、珠光体和莱氏体。
1、铁素体铁素体F:碳溶入α-Fe中形成的间隙固溶体铁素体性能:σb=180-280MPa,δ=30%-50%,硬度≈80HBS。
2、奥氏体奥氏体(A):碳溶入γ-Fe中形成的间隙固溶体。
奥氏体性能:σb=400MPa,δ=40%-50%,硬度=160-200HBS。
3、渗碳体渗碳体(Fe3C):铁与碳形成的具有复杂晶体结构的间隙化合物。
渗碳体性能:熔点高约1227℃,硬度≈800HBW,δ≈0,脆性大。
Fe3C是钢中的强化相,它的形态、大小、数量与分布对铁碳合金性能产生非常大的影响。
4、珠光体珠光体(P):铁素体和渗碳体组成的两相复合物。
其性能介于F和Fe3C之间即:σb=770MPa,δ=20%-30%,硬度≈180HBS,A KV=24-32J。
5、莱氏体(Ld或Ld′)莱氏体:奥氏体和Fe3C组成的两相复合物。
在1148℃时称为高温莱氏体(Ld′),溶碳量为ωC=4.3%;在727℃时,由P和Fe3C组成的两相复合物,称为低温莱氏体(Ld)。
其性能与Fe3C相似,又硬又脆。
二、铁碳合金相图在铁碳合金中,铁与碳可形成Fe3C、Fe2C、FeC等一系列化合物。
而稳定的化合物可作为一个独立的组元。
因此,整个Fe-C相图可视为由Fe-Fe3C、Fe3C-Fe2C等一系列二元相图构成。
但因铁碳合金中当ωC>5%时,性能很脆,无实用价值,故铁碳合金相图中仅研究Fe-Fe3C相图。
简化后的Fe-Fe3C相图如图5-1所示。
1、相图分析Fe -Fe 3C 相图分为上、下两部分。
二元共晶相图(前面以讲)和二元共析相图。
⑴Fe -Fe 3C 相图中的特征点 P 点:碳在F 中的最大溶解度。
G 点:Fe Fe -⇔γα-的同素异晶转变点。
第五章相图(冶金物理化学)

重庆科技学院
冶金与材料工程学院
第五章 相图
水的相图
p-T图 —— 根据实验数据绘制 - 图
Kp =
2 pH 2 O 2 pH 2 pO 2
冶金与材料工程学院
第五章 相图
③自由度或独立变量
自由度:指体系可变因素( 、 自由度:指体系可变因素(T、P 、C…)的数目,这些 )的数目, 因素在一定程度内变动时新相不产生,旧相不消失。 因素在一定程度内变动时新相不产生,旧相不消失。 表示。 自由度数=独立变量数 用符号 f 表示。 自由度数 独立变量数 f=K-φ+2 相律的数学式
重庆科技学院
第五章 相图
(2)有化合物的二元系相图
② 不稳定化合物(异分化合物) 不稳定化合物(异分化合物)
化合物的熔点测不到, 化合物的熔点测不到,不到熔点化合物就分解 特点:在相图上出现 字形 特点:在相图上出现T字形
物液相线; 物液相线 Tf,*A P :A物液相线;
Tf,*B E :B物液相线; 物液相线; 物液相线
Au
s
960.5℃ ℃
Ag
重庆科技学院
冶金与材料工程学院
第五章 相图
(3) 完全互溶型
重庆科技学院
冶金与材料工程学院
第五章 相图
二元系相图 步冷曲线各 段 f=?
T
T 纯A ①
②
③
④
⑤ 纯B
τ→ 纯物质:均匀降温→液态凝固 不变) 均匀降温 液态凝固(T不变 纯物质:均匀降温 液态凝固 不变 →均匀降温 合金:均匀降温→有固体析出 降温变缓)→两种固体 有固体析出(降温变缓 合金:均匀降温 有固体析出 降温变缓 两种固体 同时析出(T不变 不变) 均匀降温 同时析出 不变 →均匀降温
材料科学基础 第五章 5.1-5.4相图

5.2.3 杠杆定律
设成份为 X的合金的总重量为1,液相的相对重量为 QL,其 成份为 X1,固相相对重量为Qα,其成份为X2,则 :
5.2.4 相图的类型和结构 根据组元的多少,可分为单元系、二元系、三元 系 …. 相图。
二元系相图的类型有:
① 液态无限溶解,固态无限溶解 -匀晶相图; ②液态无限溶解,固态有限溶解 -共晶相图和包晶
共晶组织:共晶转变产物。(是两相混合物)
共晶合金的特殊性质: ①比纯组元熔点低,简化了熔化和铸造的操作; ②共晶合金比纯金属有更好的流动性,其在凝固之 中防止了阻碍液体流动的枝晶形成,从而改善铸造 性能; ③恒温转变(无凝固温度范围)减少了铸造缺陷, 例如偏聚和缩孔; ④共晶凝固可获得多种形态的显微组织,尤其是规 则排列的层状或杆状共晶组织可能成为优异性能的 原位复合材料(in-situ composite )。
5.2.2 相律
相律(phase rule)是表示在平衡条件下,系统的自 由度数、组元数和相数之间的关系,是系统的平 衡条件的数学表达式。 相律数学表达式:f = C – P + 2 式中 P—平衡相数 C—体系的组元数 f—体系自由度(degrees of freedom) 数 2-温度和压力 自由度数 f:是指不影响体系平衡状态的独立可 变参数(温度、压力、浓度等)的数目。 在恒压下,相律表达式: f = C – P + 1
相律的应用
① 利用它可以确定系统中可能存在的最多平衡相数 单元系,因f ≥0,故 P≤1-0+1=2,平衡相最大为二个。 注意:这并不是说,单元系中能够出现的相数不能超过二 个,而是说,某一固定 T下,单元系中不同的相只能有两 个同时存在,而其它相则在别的条件下存在。
第五章:铁碳合金相图

第一节 Fe - C相图的基础知识
1.铁与碳可以形成 Fe3C、Fe2C、FeC 等一系列化合物。
2.稳定的化合物可以作为一个独的组 元。 3.Fe – C 二元相图。
Fe – C 二元相图
温 度
Fe
Fe3C Fe2C (6.69%C)
FeC
C
Mg – Si 合金相图
第二节 形成Fe - Fe3C 相图组元 和基本组织的结构与性能
2.优质碳素结构钢
* 45 --- Wc = 45%00 * 较高锰质量分数的优质碳素结构钢 45Mn --- Wc = 45%00 ; WMn = 0.7%~1.0%
3.碳素工具钢
T 12 A
高级优质
Wc = 12%0
碳素工具钢
4.铸造碳钢
ZG 200 - 400
σb ≥ 400MPa σs≥ 200MPa
1495℃
AJ
2.共晶转变反应式:
LC
1148℃
( AE + Fe3C )
Le
3.共析转变反应式:
AS
727℃
( FP + Fe3C )
P
三.典型铁碳合金的结晶过程分析
工业纯铁
( ingot iron ) 共析钢 ( eutectoid steel ) 亚共析钢 ( hypoeutectoid steel ) 过共析钢 ( hypereutectoid steel ) 共晶白口铁 ( eutectoid white iron ) 亚共晶白口铁( hypoeutectoid white iron ) 过共晶白口铁( hypereutectoid white iron )
Si — 有很强的固溶强化作用,能脱
第5章 相 图

200 α 100
tB
Pb
10
20
30
40
50
60
70
80
90
500 400 tA 300 327.5℃ 231.9℃ M α +L 183℃ 19 α +β F Pb 10 20 30 40 50 60 70 80 90 G Sn E 61.9 L+β N β 97.5 L
200 α 100
tB
例:根据下列已知条件画出一个A-B二元系相 图。已知组元A和B的熔点分别是900℃和 700℃,含B量为30%的合金在500 ℃完全凝 固后的平衡组织由80%的先共晶(或初晶)α 相和20%的( α +β)共晶体组成,而含B量 为55%的合金在500 ℃完全凝固后的平衡组 织由50%的α相和50%的β相两相组成;且含 B量为70%的合金在500 ℃平衡凝固后可得到 100%的(α+β)共晶体。
A
W(B)/%
A
W(B)/%
B
5.2.2固溶体的平衡凝固
L
1452 L+S
1083
S
Cu 0
10 20
30
40
50 60 WNi/%
70
Ni 80 90 100
问题1 单元系凝固过程与固溶体凝固过程差异
(1) 固溶体的凝固是在一个温度范围内完成的,
而纯金属的凝固是在恒温下完成的。 (2) 固溶体凝固时所形成的固相成分与液相不同, 所以形核时除需要结构起伏和能量起伏外,还需 要一定的成分起伏(液相中成分不均匀的现象即 称为成分起伏)。 (3) 固溶体凝固过程中,为了满足不同温度下两 相平衡共存的成分要求,液、固两相的成分必须 随温度下降而不断地发生变化,这种成分的变化 必然依赖于两组元原子的扩散来完成。
第五章 相 图

第五章 相 图相图中的一些基本概念:(1) 相(p )——相是指系统中具有相同物理性质和化学性质的均匀部分。
(2) 组份——系统中每一个能单独分离出来并独立存在的化学纯物质。
(3) 独立组份(c)——构成平衡物系所有各相组成所需要的最少组分数。
(4) 自由度(f)——即在温度、压力、组分浓度等可能影响系统平衡状态的变量中,可以在一定范围内任意改变而不会引起旧相消失或新相产生的独立变量的数目。
(5) 相律——n p c f +-=式中n 为外界的影响因素数。
对于凝聚系统而言,压力这一平衡因素可以忽略(如同电场、磁场对一般热力学体系相图的影响可以忽略一样),加以通常我们是在常压下研究体系和应用相图的,因而相律在凝聚系统中具有如下形式:1+-=p c f水型物质相图的特点:在水的相图上值得一提的是冰的熔点曲线oc 向左倾斜,斜率为负值。
这意味着压力增大,冰的熔点下降。
这是由于冰熔化成水时体积收缩而造成的。
oc 的斜率可以根据克劳修斯-克拉贝隆方程计算:V T H dT dP ∆∆=。
冰熔化成水时吸热△H >0,而体积收缩△V <0,因而造成dTdP <0。
像冰这样熔融时体积收缩的物质统称为水型物质,但这些物质并不多,铋、镓、锗、三氯化铁等少数物质属于水型物质。
可逆和不可逆多晶转变的单元相图:具有可逆多晶转变单元相图,其特点是晶型转变温度低于二个晶相的熔点,而且晶型转变温度点处在稳定相区之内。
即在一定的温度范围内都存在一个稳定的晶相,在晶型转变温度时二相可以互相转变,故称为可逆转变。
这种转变关系可表示为:熔体晶型晶型⇔-⇔-αβ。
具有不可逆多晶转变的单元相图,其特点是晶型转变温度高于二个晶相的熔点,并且晶型转变温度点处在稳定相区之内。
当系统温度低于晶型转变温度时,α相总有转变为β相的自发趋势,α相是不稳定的。
当熔体慢慢冷却时,不能析出α相,而是析出β相;只有当熔体快速冷却时,方能得到介稳的α相。
所以在一般情况下,α相可以转变为β相,但β相不能直接转变为α相,即是不可逆转变过程。
5 《材料科学基础》第五章 相平衡和相图

( p -T 图)
自由
一、水的相图
冰的熔融曲线 水的饱和蒸汽压曲线(蒸发曲线)
3个相区:
p=1, f=2 ,双变量系统(T、P) 3条界线: p=2 , f= 1,单变量系统(T或P) 1个无变量点(三相点):
T
p=3 , f=0 ,无变量系统
冰的饱和蒸汽压曲线(升华曲线)
??
注意:
•冰点和三相点O
第五章
第五章
§5.1
相平衡和相图
基本知识
§5.2
§5.3
单元系统
二元系统
§5.4
三元系统
§5.1
相平衡与相图的基本知识
一、相平衡的基本概念 二、相律 三、相平衡的研究方法
一、相平衡的基本概念
相平衡:是研究一个多组分(或单组分)多相系统中相的平
衡问题,即多相系统的平衡状态(包括相的个数、各相的状态、
二、二元凝聚系统相图的基本类型
三、复杂二元相图的分析步骤
四、二元系统专业相图
要求
一、二元系统相图的表示方法及杠杆规则
1、作为特种陶瓷的重要原料
由于7%~9%的体积效应,常加适量CaO或Y2O3稳定剂。
在>1500℃以上与四方型ZrO2形成立方晶型固溶体,称稳定
化立方ZrO2 。
2、熔点高(2680℃),作耐火材料 3、利用导氧导电性能,作氧敏传感器元件 4、利用体积效应,对陶瓷材料进行相变增韧。
增韧机理: 微裂纹增韧
实线部分: 四个单相区: 五条界线:
两个无变量点:
晶体的升华曲线(或延长线)与液体的蒸发曲线(或延长线) 的交点是该晶体的熔点。 两种晶型的升华曲线(或延长线)的交点是两种晶型的晶型转 变点。
材料科学基础_第5章_二元相图

Cu
18 20
30 40
66 60 80
Ni 相对质量为1/4。溶体合金的平衡凝固及组织
➢ 平衡凝固是指凝固过程中每个阶段都能达到平衡,因此 平衡凝固是在极其缓慢的冷速下实现的。现以30%Ni和 70%Cu的铜镍合金为例来说明固溶体的平衡冷却过程及其 组织的。
11
冷却曲线 t Ⅱ
23
X2合金结晶过程分析
L
(共晶合金)
T,C
183
L
L+
L+
c
d
e
+
T,C
(+ )
围内凝固,具有变温凝固的特征 ②还需要成分起伏
15
5.3.2 二元共晶相图 两组元在液态无限互溶,固态有限溶解,通过共晶反
应形成两相机械混合物的二元合金称为二元共晶相图。共 晶反应是液相在冷却过程中同时结晶出两个结构不同的固
相的过程。 L
16
Ta,tb分别是Pb,Sn的熔点 M:锡在铅中的最大溶解度。N:铅在锡中的最大溶解度 E:为共晶点,具有该点成分的合金在恒温183℃发生共 晶转变LE→aM+ΒN,共晶转变是具有一定成分的液相在恒 温下同时转变为两个具有一定成分和结构的固相的过程。 F:室温时锡在铅中的溶解度;G:室温时铅在锡中的溶 解度
之间一定是由这两个相组成的两相区。如铁区(线)区(
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三节 二元共晶相图及合金凝固
(2)共晶合金(分析要点) ① 凝固过程(冷却曲线、相变、组织示意图)。 ② 共晶线上两相的相对量计算。 ③ 室温组织(α+β)及其相对量计算。
2h
图4-28 Pb-Sn共晶合金平衡凝固过程示意图
1) 在液体中α 和β 同时具有析出条件,都可以析出。
2) 由于α 和β 析出过程在成分上可以互相补充和促进, 共同析出。
二元匀晶相图
一、匀晶相图及其分析 (1)匀晶转变:由液相直接结晶出单相固溶体的 转变。 (2)匀晶相图:具有匀晶转变特征的相图。 Cu-
Ni、 Cu-Au、 Au-Ag、Fe-Cr等
(3)相图分析(以Cu-Ni相图为例) 两点:纯组元的熔点; 两线:L, S相线; 三区:L, α, L+α。
固溶体合金的平衡结晶
金相法
膨胀法 电阻法
热分析法(以Cu-Ni系相图为例):
配制一系列成分不同的Cu-Ni合金; 测定上述合金的冷却曲线 找出各合金的临界点 以温度为纵坐标、以成分为横坐标的图中,将各临 界点连接起来即得到Cu-Ni合金相图
二.相图的建立
名称 晶格类型 熔点 合金1 合金2 合金3 …….. 合金9 合金10 合金11 A金属 fcc 高 100% 90% 80% …….. 20% 10% 0% B金属 fcc 低 0% 10% 20% ……. 80% 90% 100%
二、包晶体转变
过程
成分为P点合金的凝固 β 相的形核在α 相晶体和液体 的边界处,由于β 相的成分介于 液体和α 相之间,所以它是靠消 耗部分已有的α 相和部分液体来 实现。 β 相的生长在液体和α 相的交 界面处最有利,沿边界同时消耗 液体和α 相来长大,形成的β 相 包围在α 相外围,将α 相与液体 分隔开,所以把这种转变称为包 晶转变。
第二节 二元匀晶相图
(3)与纯金属结晶的比较 不同点:合金在一个温度范围内结晶; (可能性:相律分析;必要性: 成分均匀化。) 合金结晶是选分结晶:需成 分起伏。
第二节 二元匀晶相图
三、固溶体的不平衡结晶
固溶体的不平衡结晶
(1)原因:冷速快(假设液相成分均匀、固相成 分不均匀)。 (2)结晶过程特点:固相成分按平均成分线变 化(但每一时刻符合相图); 结晶的温度范围增大; 组织多为树枝状。
(成分在CE之间)L
β II)+(α +β )共 在到达TE温度前转变同固溶体的转变,在TE温度下剩余的 液体转变同共晶成分E(合金Ⅳ)的转变。 组织组成物:一般将显微组织中能清晰分辨的独立组成 部分,称为 亚共晶合金室温组织: α 初+ β II+(α +β )共 相组成物: α +β
→ L+α → α
地区性
系统的自由度数,就是平衡系统的独立可变因 素(如温度、压力、浓度等)的数目。这些因素 可在一定范围内任意独立地改变而不会影响到 原有的共存相数和状态,即不会影响原有的平 衡状态。值不能为负 压力一定时,f=c-p+1 分析不同的组元数,最多可以平衡共存的相 数
二、相图的建立
第二节。二元相图及其类型 一、相图的基本知识
1、有关相图的基本概念 相图:是描述系统的状态、 温度、压力及成分之间 关系的图解,利用相图 可以知道不同成分的材 料在不同温度下存在哪 些相、各相的相对量、 成分及温度变化时所可 能发生的变化。
地区性
相图是铸造、锻造、焊接、热处理和冶金 等专业的重要理论工具。 仅在热力学平衡条件下成立,不 能确定相结构、分布状态和具体形貌。
第四节 二元包晶相图
二、包晶体转变
二、一元系相图地区性
图5-3 纯铁的相图 a)温度和压力都变动的情况 b)只有温度变动的情况
[例] 图4-3为Bi-Sb二元合金相图,求 40%Sb的Bi-Sb合金在450℃时的组成。
图4-3 Bi-Sb相图
WL
DE 77 40 100 % 80.4% ; W 100 % Wl 19.6% CE 77 31
3) 凝固过程可以在恒温下进行到结束。
4) 最终得到两相交替的混合组织。
结论:合金(成分在E点附近) L →α +β 转变发生在TE 温度,得到的两项交替分布的组织称为共晶体。
第三节 二元共晶相图
图4-29 Pb-Sn合金系中亚共晶合金的平衡凝固
(3)亚共晶合金(要点) ① 凝固过程(冷却曲线、相变、组织示意图)。 ② 共晶线上两相的相对量计算。 ③ 室温组织(α+βⅡ+(α+β))及其相对量计算。
第四节 二元包晶相图
二、包晶体转变
过程
成分为P点合金的凝固 在略低于TP的温度下,进一步 的生长过程,伴随A组元从α 相穿过 β 相到达液体界面,液体转变为β 相,同时多余的B组元穿过β 相到达 α 相界面,α 相中A组元的减少使部 分α 相转变为β 相以保证α 相要求 的成分。即β 相长大的过程是A组元 穿过β 相向液体处扩散,B组元穿过 β 相向α 相处扩散,同时消耗液相 和α 相。
相与相之间的转变称为相变。 如果系统中各相经历很长时间而不互相转化, 则是处于平衡状态。实际上相平衡是一种动态 平衡,从系统内部来看,分子或原子仍在相界 处不停地转换,只不过同一时间内各相之间的 转化速度相同。 合金可以根据其所含的相的数目来分类,如果 合金仅由一个相组成,称为单相合金如果合金 由二个或二个以上的不同相所构成,则称为多 相合金。
第三节 二元共晶相图
三、不平衡结晶及其组织 (1)伪共晶 ① 伪共晶:由非共晶成分的合金所得到的完全共晶组织。 ② 形成原因:不平衡结晶;成分位于共晶点附近。 ③ 不平衡组织 由非共晶成分的合金得到的完全共晶组织。 共晶成分的合金得到的亚、过共晶组织。(伪共晶区偏移)
第三节 二元共晶相图
三、 不平衡结晶及其组织 (2)不平衡共晶 ①不平衡共晶:位于共晶线以外成分的合金发生共晶反 应而形成的组织。 ② 原因:不平衡结晶。成分位于共晶线以外端点附件。
4)在两相区内,成分一定、温度一定时,两相的
质量比是一定的,如在温度T1时,两相的质量比可 用杠杆表达
图4-3 Bi-Sb相图
第三节 二元共晶相图
共晶转变:由一定成分的液相同时结晶 出两个一定成分固相的转变。 共晶相图:具有共晶转变特征的相图。 (液态无限互溶、固态有限互溶或完全不 溶 , 且 发 生 共 晶 反 应 。 Al-Si、Pb-Sb、 Pb-Sn、Ag-Cu 共晶组织:共晶转变产物。(是两相混 合物)
热 分 析 法
二.相图的建立
温 度 温 度 温 度
时间
A 90 70 50
30
B B
温 度
L L +
a
S
S
A
ab : 液相线 ab : 固相线 L : 液相区 S : 固相区 L+S:液固共存区
b
B
温 度
L
a
TL Tn TS
S
A
b a c b
B
温 度
L
杠杆定理 QS + QL = 1 aQS + bQL = c QL=(ac/ab) 100% QS=(bc/ab) 100%
19 97.5
第三节 二元共晶相图
一、 相图分析(相图三要素) (1)点:纯组元熔点;最大溶解 度点;共晶点 (是亚共晶、过共晶成分分 界点)等。 (2)线:结晶开始、结束线;溶 解度曲线; 共晶线等。 (3)区:3个单相区;3个两相区; 1个三相区。 (4)共晶反应特点、反应式、温 度、相区间的接触关系
第三节 二元共晶相图
三、 不平衡结晶及其组织 (3)离异共晶 ① 离异共晶:两相分离的共晶组织。 ② 形成原因 平衡条件下,成分位于共晶线上两端点附近。 不平衡条件下,成分位于共晶线外两端点附。 ③ 消除:扩散退火。
第四节 二元包晶相图
包晶转变:由一个特定成分的固相和 液相生成另一个特定成分固相的转变。 包晶相图:具有包晶转变特征的相图。
脱溶过程:由固溶体中析出另一相的过 程;即过饱和固溶体的分解过程,也称 二次结晶(次生相、二次相βⅡ )
L → L+α → α → α +β II 在到ac线之前同固溶体, 到Cf线之下,α 相中溶剂B组元的量为过饱和,从中 将有β 相析出。一般从固态α 析出的β 相在的内部 成点状分布。值得指出的是β 量少时往往先在α 的 晶界处,此外,固态析出转变原子迁移和β 形核较 困难,当过饱和度不大时,这个析出往往不发生。
a
TL Tn TS
S
Qs A QL
b a c b
B
相图的建立
第一节 相图的基本知识
三、 杠杆定律 (1)平衡相成分的确定(根据相律,若温度一定, 则自由度为0,平衡相成分随之确定。) (2)数值确定:直接测量计算或投影到成分轴测 量计算。 (3)注意:只适用于两相区; 并且只能在平衡状态下 使用.三点(支点和端点)要选准。
包晶转变
L+α → β
第四节 二元包晶相图
二、包晶体转变
过程
成分为P点合金的凝固 在液相区为液体的冷却,进入 两相区,发生与固溶体凝固相同的 凝固转变,到达P点,液体的成分为 C,固体的成分为D。 从L+β 相区可知也满足液体和β 相的平衡,与C成分液体平衡还有P 成分的固体β 相。
第四节 二元包晶相图
初+(L+α
+β )→ (α
初+
第三节 二元共晶相图
(4)过共晶合金 位于共晶点右边, 成分在 de之间的合金为过共晶合 金(例如图中的合金Ⅳ),结晶过程与亚共晶合金相似,室 温组织为初生 β+ 二次α + (α+β) 。
