人教版九年级数学下册反比例函数测试习题及答案

合集下载

人教版九年级数学下册反比例函数全章测试含答案

初三数学反比例函数全章测试（60分钟，满分100分）一．填空题：（每题6分，共48分）1．函数13--=x y 的自变量的取值范围是 . 2．反比例函数xy 6=当自变量2-=x 时，函数值是 .3．图象经过点)4,2(--A 的反比例函数的解析式为 . 4．当0<x 时，反比例函数xy 3-=中，变量y 随x 的增大而 . 5．函数2||)1(--=k x k y 是y 关于x 反比例函数，则它的图象不经过的象限.6．反比例函数x ky =与一次函数2+=x y 图象的交于点),1(a A -，则=k . 7．反比例函数xk y 1+=的图象经过),(11y x A ，),(22y x B 两点，其中021<<x x 且21y y >，则k 的范围是 .8．已知：点A 在反比例函数图象上，B x AB 轴于点⊥，点C （0，1），且AB C ∆的面积是3，如图，则反比例函数的解析式为 .二．选择题：（每题5分，共35分）9．下列函数中，变量y 是x 的反比例函数的是（）.A ． 21x y =B ．1--=x y C ．32+=x y D ．11-=x y10．在物理学中压力F ，压强p 与受力面积S 的关系是：SFp =则下列描述中正确的是（）.A 当压力F 一定时，压强p 是受力面积S 的正比例函数B 当压强p 一定时，压力F 是受力面积S 的反比例函数C 当受力面积S 一定时，压强p 是压力F 的反比例函数D 当压力F 一定时，压强p 是受力面积S 的反比例函数11．反比例函数xy 6=与一次函数1+=x y 的图象交于点)3,2(A ，利用图象的对称性可知它们的另一个交点是（）.A )2,3(B )2,3(--C )3.2(--D )3,2(-12．若r 为圆柱底面的半径，h 为圆柱的高．当圆柱的侧面积一定时，则h 与r 之间函数关系的图象大致是（）.13．某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P(kPa)是气体体积V(m 3)的反比例函数，其图象如图所示. 当气球内的气压大于140kPa 时，气球将爆炸，为了安全起见，气体体积应（）. (13题图)h r O h r O h r O h r O A ． B ． C ． D ．A ．不大于3m 3524；B ．不小于3m 3524；C ．不大于3m 3724；D ．不小于3m 372414xk 1-的图象不可能是．．．．（）.A B C D15．正方形ABCD 的顶点A （2，2）,B(-2,2)C(-2,-2),反比例函数x y 2=与xy 2-=的图象均与正方形ABCD 的边相交,如图，则图中的阴影部分的面积是( ) . A 、2 B 、4 C 、8 D 、6三．解答题：（16题5分，17、18、19题每题4分，共17分）16．你吃过拉面吗？实际上在做拉面的过程中就渗透着数学知识：一定体积的面团做成拉面时，面条的总长度y （m ）是面条的粗细(横截面积)S （mm 2）的反比例函数，其图象如图所示．⑴写出y （m ）与S （mm 2）的函数关系式；⑵求当面条粗1.6 mm 2时，面条的总长度是多少米？x O yxOyxO yxOyS y(m)(mm 2)O P(4,32)100806040205432117．如图，正方形ABCD 的边长是2，E ，F 分别在BC ，CD 两边上，且E ，F 与BC ，CD 两边的端点不重合，AEF ∆的面积是1，设BE=x ，DF=y.(1)求y 关于x 函数的解析式；(2) 判断在（1）中，y 关于x 的函数是什么函数？（3）写出此函数自变量x 的范围.18．已知：反比例函数的图象经过)2,1(a a A )1,12(aaa a B ---两点，〈1〉求反比例函数解析式；〈2〉若点C )1,(m 在此函数图象上,则ABC ∆的面积是 .（填空）19．如图，已知直线m x y +=1与x 轴，y 轴分别交于点A 、B ，与双曲线xky =2（x <0）分别交于点C 、D ，且点C 的坐标为（-1，2）． ⑴ 分别求出直线及双曲线的解析式；⑵利用图象直接写出，当x 在什么范围内取值时，21y y >．答案1．1≠x ；2．3-=y ；3．xy 8=；4．增大；5．第一、三象限；6． ,1- 7．1->k 8．xy 6=；9．B ；10．D ；11．B ；12．B ；13．B ；14．D ；15．C 16．（1） x y 128= （2）80m ；17．（1）3+=x y xy 2-=（2）12-<<-x18．<1>x y 2=,<2> 3 19．(1)xy 2=(2)反比例函数(3)20<≤xxyD C BAO专项训练二概率初步一、选择题1．(徐州中考)下列事件中的不可能事件是( )A．通常加热到100℃时，水沸腾 B．抛掷2枚正方体骰子，都是6点朝上C．经过有交通信号灯的路口，遇到红灯 D．任意画一个三角形，其内角和是360°2．小张抛一枚质地均匀的硬币，出现正面朝上的可能性是( )A．25% B．50% C．75% D．85%3．(2016·贵阳中考)2016年5月，为保证“中国大数据产业峰会及中国电子商务创新发展峰会”在贵阳顺利召开，组委会决定从“神州专车”中抽调200辆车作为服务用车，其中帕萨特60辆、狮跑40辆、君越80辆、迈腾20辆，现随机从这200辆车中抽取1辆作为开幕式用车，则抽中帕萨特的概率是( )A.110B.15C.310D.254．(金华中考)小明和小华参加社会实践活动，随机选择“打扫社区卫生”和“参加社会调查”其中一项，那么两人同时选择“参加社会调查”的概率为( )A.14B.13C.12D.345．在一个不透明的袋中装着3个红球和1个黄球，它们只有颜色上的区别，随机从袋中摸出2个小球，两球恰好是一个黄球和一个红球的概率为( )A.12B.13C.14D.166．现有两枚质地均匀的正方体骰子，每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子，以朝上一面所标的数字为掷得的结果，那么所得结果之和为9的概率是( )A.13B.16C.19D.1127．分别转动图中两个转盘一次，当转盘停止转动时，两个指针分别落在某个数所表示的区域，则两个数的和是2的倍数或3的倍数的概率等于( )A.316B.38C.58D.1316第7题图第8题图8．(2016·呼和浩特中考)如图，△ABC是一块绿化带，将阴影部分修建为花圃，已知AB＝15，AC＝9，BC＝12，阴影部分是△ABC 的内切圆，一只自由飞翔的小鸟将随机落在这块绿化带上，则小鸟落在花圃上的概率为( )A.16B.π6C.π8D.π5二、填空题9．已知四个点的坐标分别是(－1，1)，(2，2)，⎝ ⎛⎭⎪⎫23，32，⎝ ⎛⎭⎪⎫－5，－15，从中随机选取一个点，在反比例函数y ＝1x 图象上的概率是________．10．(黄石中考)如图所示，一只蚂蚁从A 点出发到D ，E ，F 处寻觅食物．假定蚂蚁在每个岔路口都可能随机选择一条向左下或右下的路径(比如A 岔路口可以向左下到达B 处，也可以向右下到达C 处，其中A ，B ，C 都是岔路口)．那么，蚂蚁从A 出发到达E 处的概率是________．11．(贵阳中考)现有50张大小、质地及背面图案均相同的《西游记》任务卡片，正面朝下放置在桌面上，从中随机抽取一张并记下卡片正面所绘人物的名字后原样放回，洗匀后再抽．通过多次试验后，发现抽到绘有孙悟空这个人物卡片的频率约为0.3.估计这些卡片中绘有孙悟空这个人物的卡片张数约为________．12．(荆门中考)荆楚学校为了了解九年级学生“一分钟内跳绳次数”的情况，随机选取了3名女生和2名男生，则从这5名学生中，选取2名同时跳绳，恰好选中一男一女的概率是________．13．(重庆中考)点P 的坐标是(a ，b )，从－2，－1，0，1，2这五个数中任取一个数作为a 的值，再从余下的四个数中任取一个数作为b 的值，则点P (a ，b )在平面直角坐标系中第二象限内的概率是________．14．★从－1，1，2这三个数字中，随机抽取一个数记为a ，那么，使关于x 的一次函数y ＝2x ＋a 的图象与x 轴、y 轴围成的三角形的面积为14，且使关于x 的不等式组⎩⎨⎧x ＋2≤a ，1－x ≤2a有解的概率为________．三、解答题15．(南昌中考)在一个不透明的袋子中装有仅颜色不同的10个小球，其中红球4个，黑球6个．(1)先从袋子中取出m (m ＞1)个红球，再从袋子中随机摸出1个球，将“摸出黑球”记为事件A ，请完成下列表格：(2)先从袋子中取出m 个红球，再放入m 个一样的黑球并摇匀，随机摸出1个黑球的概率等于45，求m 的值．16．(菏泽中考)锐锐参加我市电视台组织的“牡丹杯”智力竞答节目，答对最后两道单选题就顺利通关，第一道单选题有3个选项，第二道单选题有4个选项，这两道题锐锐都不会，不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项)．(1)如果锐锐两次“求助”都在第一道题中使用，那么锐锐通关的概率是________；(2)如果锐锐两次“求助”都在第二道题中使用，那么锐锐通关的概率是________；(3)如果锐锐将每道题各用一次“求助”，请用树状图或者列表来分析他顺利通关的概率．17．(丹东中考)甲、乙两人进行摸牌游戏．现有三张形状大小完全相同的牌，正面分别标有数字2，3，5.将三张牌背面朝上，洗匀后放在桌子上．(1)甲从中随机抽取一张牌，记录数字后放回洗匀，乙再随机抽取一张．请用列表法或画树状图的方法，求两人抽取相同数字的概率；(2)若两人抽取的数字之和为2的倍数，则甲获胜；若抽取的数字之和为5的倍数，则乙获胜．这个游戏公平吗？请用概率的知识加以解释．18．一只不透明的袋子中装有4个质地、大小均相同的小球，这些小球分别标有数字3，3，5，x，甲、乙两人每次同时从袋中各随机摸出1个球，并计算摸出的这2个球上数字之和，记录后将小球放回袋中搅匀，进行重复实验．实验数据如下表：(1)如果实验继续进行下去，根据上表数据，出现“和为8”的频率稳定在它的概率附近，估计出现“和为8”的概率是________；(2)如果摸出的这两个小球上数字之和为9的概率是13，那么x的值可以取4吗？请用列表法或画树状图法说明理由；如果x的值不可以取4，请写出一个符合要求的x的值．参考答案与解析1．D 2.B 3.C 4.A 5.A 6.C 7.C8．B 解析：∵AB ＝15，BC ＝12，AC ＝9，∴AB 2＝BC 2＋AC 2，∴△ABC 为直角三角形，∴△ABC 的内切圆半径为12＋9－152＝3，∴S △ABC ＝12AC ·BC ＝12×12×9＝54，S 圆＝9π，∴小鸟落在花圃上的概率为9π54＝π6. 9.12 10.12 11.15 12.35 13.15 14.1315．解：(1)4 2或3(2)根据题意得6＋m 10＝45，解得m ＝2，所以m 的值为2. 16．解：(1)14 解析：第一道肯定能对，第二道对的概率为14，所以锐锐通关的概率为14； (2)16 解析：锐锐两次“求助”都在第二道题中使用，则第一道题对的概率为13，第二道题对的概率为12，所以锐锐能通关的概率为12×13＝16； (3)锐锐将每道题各用一次“求助”，分别用A ，B 表示剩下的第一道单选题的2个选项，a ，b ，c 表示剩下的第二道单选题的3个选项，树状图如图所示．共有6种等可能的结果，锐锐顺利通关的只有1种情况，∴锐锐顺利通关的概率为16.17．解：(1)所有可能出现的结果如下表，从表格可以看出，总共有9种结果，每种结果出现的可能性相同，其中两人抽取相同数字的结果有3种，所以两人抽取相同数字的概率为13； (2)不公平．从表格可以看出，两人抽取数字之和为2的倍数有5种，两人抽取数字之和为5的倍数有3种，所以甲获胜的概率为59，乙获胜的概率为13.∵59＞13，∴甲获胜的概率大，游戏不公平．2 3 5 22 23 2 5 2 32 3 3 3 5 3 52 53 5 5 518．解：(1)0.33(2)图略，当x 为4时，数字和为9的概率为212＝16≠13，所以x 不能取4；当x ＝6时，摸出的两个小球上数字之和为9的概率是13.。

人教版九年级数学下册反比例函数测试习题及答案.docx

专项训练四反比例函数一、选择题1．(哈尔滨中考 )点 (2，－ 4)在反比例函数 y ＝ kx 的图象上，则下列各点在此函数图象上的是( )A ． (2， 4)B ． (－ 1，－ 8)C ． (－2，－ 4)D ． (4，－ 2)2．对于双曲线y ＝ 1－m ，当 x ＞ 0 时， y 随 x 的增大而减小，则 m 的取值范围为 ()x A ． m ＞ 0B ． m ＞1C ．m ＜ 0D ． m ＜1k3．(新疆中考 )已知 A(x 1，y 1)，B(x 2，y 2 )是反比例函数 y ＝ x (k ≠ 0)图象上的两个点，当 x 1＜ x 2 ＜0时， y 1＞ y 2，那么一次函数 y ＝ kx － k 的图象不经过 ( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限4． (聊城中考 )二次函数 y ＝ ax 2＋ bx ＋c(a ， b ，c 为常数且 a ≠ 0)的图象如图所示，则一次函数y＝ ax ＋b 与反比例函数 y ＝cx 的图象可能是 ()5．在同一直角坐标系中，若正比例函数1k 2的图象没有公共点，y ＝ k x 的图象与反比例函数y ＝ x则 ()A ． k 1＋ k 2<0B ．k 1＋k 2>0C ． k 1k 2<0D ． k 1k 2>06．已知点 P(a ，b)是反比例函数1图象上异于点(－ 1，－ 1)的一个动点，则1 ＋1的值y ＝ x1＋ a 1＋ b为 ( )31A ． 2B ． 1C.21D. 2的图象相交于 A 、 B 两点， BC ⊥ x 轴于点 C ，则7．如图，正比例函数 y ＝ x 与反比例函数 y ＝ x△ ABC 的面积为 ( )35 A ． 1B ．2C.2D.2k8． (昆明中考 )如图，直线 y ＝－ x ＋ 3 与 y 轴交于点 A ，与反比例函数 y ＝ x (k ≠ 0)的图象交于点C ，过点 C 作 CB ⊥ x 轴于点 B ， AO ＝ 3BO ，则反比例函数的解析式为 ( )4 4 22 A ． y ＝ x B ． y ＝－ x C ． y ＝ x D ． y ＝－ x二、填空题9． (上海中考)已知反比例函数ky ＝ x(k ≠ 0)，如果在个函数象所在的每一个象限内，y 的随着x 的增大而减小，那么k 的取范是________ ．k10． (淮安中考)若点A(－ 2，3)、 B(m ，－ 6)都在反比例函数y ＝ x(k ≠ 0)的象上，m 的是________．k11． ( 坊中考 )已知反比例函数y ＝ x (k ≠ 0)的象点 (3，－ 1)，当 1＜ y ＜ 3 ，自量 x的取范是 __________．12．某合路中，源的定，流I(A) 与阻 R( Ω)成反比例．如表示的是路中流 I 与阻 R 之函数关系的象，当阻R 6Ω ，流 I ________A.第 12 第 13 第 1413． ( 口中考 )如，四形 ABCD 正方形，点 A 、B 在 y 上，点 C 的坐 (－ 3，1)，反比例函数 y ＝ k的象点 D ， k 的 ________．x414．★ ( 水中考 )如，一次函数 y ＝－ x ＋ b 与反比例函数y ＝ x (x ＞ 0)的象交于 A ， B 两点，与 x 、 y 分交于 C ，D 两点，接 OA ，OB ， A 作 AE ⊥x 于点 E ，交 OB 于点 F ，点 A 的横坐 m.(1)b ＝ ________(用含 m 的代数式表示 )；(2)若 S △ OAF ＋ S 四边形 EFBC ＝4 ， m 的是 ________．三、解答k15． (西宁中考 )如，一次函数y ＝ x ＋m 的象与反比例函数y ＝x 的象交于 A ， B 两点，且与 x 交于点 C ，点 A 的坐 (2， 1)．(1)求 m 及 k 的；0＜ x ＋ m ≤ k的解集．(2)求点 C 的坐，并合象写出不等式x16．某数学外活小在做气体，得 p(Pa)与体 V(cm 3)之有下列数据：p(Pa)⋯ 1 2 3 4 5 ⋯ V(cm 3)⋯6321.51.2⋯根据表中提供的信息，回答下列：(1)猜想 p 与 V 之的关系，并求出函数关系式； (2)当气体的体是12cm 3 ，是多少？k 17． ( 阳中考 )如，在平面直角坐系中，菱形 OBCD 的 OB 在 x 上，反比例函数y ＝ x(x ＞ 0)的象菱形角的交点 A ，且与 BC 交于点 F ，点 A 的坐 (4， 2)．(1)求反比例函数的表达式；(2)求点 F 的坐．k ＋ 118．★如，已知直 y ＝ x ＋ k 和双曲 y ＝ x (k 正整数 )交于 A ， B 两点．(1)当 k ＝1 ，求 A ， B 两点的坐；(2)当 k ＝2 ，求△ AOB 的面；2 ，△ OAB 的面 S ⋯依此推，当k ＝n(3)当 k ＝1 ，△ OAB 的面 S ，当 k ＝12，△ OAB 的面S n ，若 S 1＋ S 2＋⋯＋ S n ＝1332，求 n 的．参考答案1． D 2.D3.B4.C5.C1图象上异于点 (－1，－ 1)的一个动点，∴ ab ＝ 1，6． B 解析：∵点 P(a ， b)是反比例函数 y ＝ x∴ 1＋ 1＝ 1＋ b ＋ 1＋ a ＝ 2＋a ＋ b ＝2＋ a ＋ b ＝ 1.1＋ a 1＋ b （ 1＋ a ）（ 1＋ b ）（ 1＋ a ）（ 1＋ b ） 1＋ a ＋b ＋ ab 2＋ a ＋b7． A 解析：∵正比例函数1的图象相交于A 、B 两点，∴点 A 与点 By ＝ x 与反比例函数 y ＝ x关于原点对称，∴ S △ AOC ＝ S △ BOC .∵ BC ⊥ x 轴，∴ S △ ABC ＝ 2S △ BOC ＝ 2× 1× |1|＝1.2 8． B 解析：∵直线 y ＝－ x ＋3 与 y 轴交于点 A ，∴点 A 的坐标为 (0， 3)，即 OA ＝ 3.∵AO ＝ 3BO ，∴ OB ＝ 1，∴点 C 的横坐标为－ 1.∵点 C 在直线 y ＝－ x ＋ 3 上，∴点 C 的坐标为 (－ 1， 4)， ∴反比例函数的解析式为y ＝－ 4.x9． k ＞ 0 10.1 11.－ 3＜x ＜－ 1 12.1 13.614． (1)m ＋ 4 (2)2 解析： (1) ∵点 A 在反比例函数 4m y ＝ (x ＞ 0)的图象上，且点 A 的横坐标4 4 x为 m ，∴点 A 的纵坐标为 m ，即点 A 的坐标为 m ， m .令一次函数 y ＝－ x ＋ b 中 x ＝ m ，则 y ＝－ m ＋ b ，∴－ m ＋ b ＝ 4，即 b ＝ m ＋ 4.mm(2)作 AM ⊥OD 于 M ，BN ⊥ OC 于 N.∵反比例函数4，一次函数 y ＝－ x ＋ b 都是关于直线 yy ＝ x＝ x 对称，∴ AD ＝ BC ，OD ＝ OC ，DM ＝ AM ＝ BN ＝ CN.记△ AOF 的面积为 S ，则△ OEF 的面积为 2－ S ，四边形 EFBC 的面积为 4－ S ，△ OBC 和△ OAD 的面积都是 6－ 2S ，△ ADM 的面积为 6－2S－ 2＝ 4－ 2S ＝ 2(2－S)，∴ S △ADM ＝ 2S △ OEF ，∴ DM ＝ 2EF ，∴ EF ＝1BN ，∴ OE ＝ 1ON ，∴点 B 的横坐2 2 2标为 2m.点 B 的坐标为 2m ，，代入直线 y ＝－ x ＋m ＋ 4 ，得 2＝－ 2m ＋ m ＋ 4，整理得 m 2＝ 2.∵ mm mm m ＞ 0，∴ m ＝ 2.15．解： (1) ∵点 A(2，1) 在一次函数 y ＝ x ＋m 的图象上，∴ 2＋m ＝ 1，∴ m ＝－ 1.∵点 A(2， 1) 在反比例函数 y ＝kx 的图象上，∴ k2＝ 1，∴ k ＝ 2；(2)∵一次函数解析式为 y ＝x － 1，令 y ＝ 0，得 x ＝ 1，∴点 C 的坐标是 (1，0)．由图象可知不等式组 0＜ x ＋ m ≤ kx 的解集为 1＜ x ≤ 2.616．解： (1) p 与 V 成反比例， p ＝V ；(2)当 V ＝ 12cm 3 时， p ＝ 0.5Pa.k17．解： (1) ∵反比例函数 y ＝ x 的图象经过点 A ，点 A 的坐标为 (4，2)，∴ k ＝ 2× 4＝ 8，∴反比8例函数的解析式为y ＝；(2)过点 A 作 AM ⊥ x 轴于点 M ，过点 C 作 CN ⊥ x 轴于点 N ，由题意可知CN ＝ 2AM ＝ 4，ON ＝2OM ＝ 8，∴点 C 的坐标为 (8 ，4)．设 OB ＝x ，则 BC ＝ x ，BN ＝ 8－ x.在 Rt △ CNB 中， x 2－ (8－ x)2＝ 42，解得 x ＝5，∴点 B 的坐标为 (5，0)．设直线 BC 的函数表达式为 y ＝ ax ＋ b ，∴ 5a ＋ b ＝ 0，解4 4 20 8a ＋ b ＝ 4， a ＝ 3， y ＝ 4 x － 20.根据题意得方程组 y ＝ 3x － 3 ，得 ∴直线 BC 的解析式为解此方程组得20， 3 3 8，b ＝－ 3 y ＝ x x ＝ 6， x ＝－ 1， 44 或∵点 F 在第一象限，∴点 F 的坐标为 F 6， 3 .y ＝ 3y ＝－ 8.18．解：(1) 当 k ＝ 1 ，直 y ＝ x ＋ k 和双曲 y ＝k ＋1化 y ＝ x ＋ 1 和 y ＝2，解方程 y ＝ x ＋1，2xxy ＝ xx ＝－ 2， x ＝ 1，得∴A 点的坐 (1， 2)， B 点的坐 (－ 2，－ 1) ；y ＝－ 1， y ＝2，，直 y ＝ x ＋ k 和双曲 y ＝k ＋ 1化 y ＝ x ＋2 和 y ＝3，解方程y ＝ x ＋ 2，(2)当 k ＝23得xxy ＝ xx ＝－ 3， x ＝ 1，∴ A 点的坐 (1 ，3)， B 点的坐 (－ 3，－ 1)．又∵直 AB( y ＝ x ＋ 2)与 yy ＝－ 1， y ＝ 3，11的交点 (0， 2)，∴ S △ AOB ＝ 2× 2× 1＋ 2× 2× 3＝ 4；(3)当 k ＝1 ， S 1＝ 1× 1× (1＋2) ＝3，当 k ＝ 2 ， S 2＝1× 2× (1＋ 3)＝ 4，⋯当 k ＝ n ， S n ＝12 2 22n(1＋ n ＋ 1)＝1n 2＋ n.∵ S 1＋ S 2＋⋯＋ S n ＝ 133，∴ 1× (12＋ 22＋ 32＋⋯＋ n 2)＋(1＋ 2＋ 3＋⋯＋ n)＝ 133，2 2 22 整理得 1× n （ n ＋1）（ 2n ＋ 1）＋ n （n ＋ 1）＝133，解得 n ＝ 6.2 6 22。

人教新版九年级数学下册《反比例函数》单元测试及答案

人教版九下第二十六章《反比例函数》单元测试及答案【2】一、选择题（本题共10小题，每小题3分，共30分．每小题给出的4 个选项中只有一个是符合题目要求的。

）1、下列函数中，反比例函数是（）（A ） 1)1(=-y x （B ） 11+=x y （C ） 21xy = （D ） x y 31= 2、某村的粮食总产量为a （a 为常数）吨，设该村的人均粮食产量为y 吨，人口数为x ，则y 与x 之间的函数关系式的大致图像应为（）3、若y 与－3x 成反比例，x 与z4成反比例，则y 是z 的（）（A ）正比例函数（B ）反比例函数（C ）一次函数（D ）不能确定 4、若反比例函数22)12(--=m x m y 的图像在第二、四象限，则m 的值是（）（A ）－1或1 （B ）小于21的任意实数（C ）－1 （Ｄ）不能确定 5、已知反比例函数的图像经过点（a ，b ），则它的图像一定也经过（）（A ）(－a ,－b ) （B ）(a ,－b ) （C ）(－a ，b ) （D ）（0，0） 6、若M(12-,1y )、N(14-,2y )、P(12,3y )三点都在函数k y x =（k>0）的图象上，则1y 、2y 、3y 的大小关系是（）（A ）132y y y >> （B ）312y y y >> （C ） 213y y y >> （D ）123y y y >> 7、如图，A 为反比例函数ky x=图象上一点，AB 垂直x 轴于B 点。

若AOB S ∆＝5，则k 的值为（）（A ）10 （B ）10-（C ）5- （D ）25-8、在同一直角坐标系中，函数y=kx-k 与(0)ky k x=≠的图像大致是（）9、如图是三个反比例函数312,,k k ky y y x x x===，在x 轴上方的图像，由此观察得到k l 、k 2、k 3的大小关系为（）（A ）k 1>k 2>k 3 （B ）k 3>k 1>k 2 （C ）k 2>k 3>k 1 （D ）k 3>k 2>k 110、在同一直角坐标平面内，如果直线1y x k =与双曲线2k y x=没有交点，那么1k 和2k 的关系一定是（）(A) 1k 、2k 异号 (B) 1k 、2k 同号 (C) 1k >0， 2k <0 (D) 1k <0， 2k >0二、填空题（本大题共6小题，每小题3分，共18分．请把下列各题的正确答实填写在横线上） 11、已知22)1(--=a xa y 是反比例函数，则a=____ ．12、在函数y=25x -+13x -中自变量x 的取值范围是_________． 13、在反比例函数xk y 1+=的图象上有两点11()x y ，和22()x y ，，若120x x <<时，210y y >>，则k 的取值范围是．14、已知圆柱的侧面积是π102cm ，若圆柱底面半径为r cm ，高为h cm ，则h 与r 的函数关系式是。

九年级数学下册《第二十六章反比例函数》单元测试卷附答案解析-人教版

九年级数学下册《第二十六章反比例函数》单元测试卷附答案解析-人教版班级:___________姓名：___________考号：____________一、单选题1．如果反比例函数的图象经过点P （﹣3，﹣1），那么这个反比例函数的表达式为（） A ．y ＝3xB ．y ＝﹣3xC ．y ＝13xD ．y ＝﹣13x2．若反比例函数2y x=的图像经过(),n n ，则n 的值是（）A ．2±B ．CD ．3．如图，点A 在x 轴正半轴上，B （5，4）．四边形AOCB 为平行四边形，反比例函数y =8x的图象经过点C和AB 边的中点D ，则点D 的坐标为（）A ．（2，4）B ．（4，2）C ．（83，3）D ．（3，83）4．对于反比例函数4y x=，下列说法错误的是（） A ．它的图象与坐标轴永远不相交 B ．它的图象绕原点旋转180°能和本身重合 C ．它的图象关于直线y x =±对称D ．它的图象与直线y x =-有两个交点5．如图是同一直角坐标系中函数12y x =和22y x=的图象．观察图象可得不等式22x x >的解集为（）A ．11x -<<B ．1x <-或1x >C ．1x <-或01x <<D ．10x -<<或1x >6．如图，在平面直角坐标系中直线y mx =（0m ≠，m 为常数）与双曲线ky x=（0k ≠，k 为常数）交于点A ，B ，若()1,A a -和(),3B b -，过点A 作AM x ⊥轴，垂足为M ，连接BM ，则ABM ∆的面积是（）A ．2B ．1m -C ．3D ．67．如图，在平面直角坐标系中函数()0ky x x=>的图象经过点P 、Q 、R ，分别过这个三个点作x 轴、y 轴的平行线，阴影部分图形的面积从左到右依次为若OE ED DC ==，1310S S +=则k 的值为（）A ．6B ．12C ．18D ．24二、填空题8．平面直角坐标系xOy 中已知点(,6),(3,2),(3,2)--A m m B m n C m n 是函数(0)ky k x =≠图象上的三点.若2ABC S =△，则k 的值为___________．9．如图，△AOB 中AO ＝AB ，OB 在x 轴上C ，D 分别为AB ，OB 的中点，连接CD ，E 为CD 上任意一点，连接AE ，OE ，反比例函数y k x＝（x ＞0）的图象经过点A ．若△AOE 的面积为2，则k 的值是___．10．在平面直角坐标系xOy 中过一点分别作坐标轴的垂线，若垂线与坐标轴围成矩形的周长的值与面积的值相等，则这个点叫做“和谐点”．已知直线y ＝﹣2x ＋k 1与y 轴交于点A ，与反比例函数y 2k x＝的图象交于点P （52-，m ），且点P 是“和谐点”，则△OAP 的面积为___．11．不透明的袋子里装有除标号外完全一样的四个小球，小球上分别标有－1，2，3，4四个数，从袋子中随机抽取一个小球，记标号为k ，不放回，将袋子摇匀，再随机抽取一个小球，记标号为b ，两次抽取完毕后，则直线y kx =与反比例函数by x=的图象经过的象限相同的概率为______． 12．如图，点()2,A m ，B 分别在双曲线()60y x x =>和()0ky x x=>上，AB x ∥轴，作AC x ⊥轴于点C ，交OB 于点D ．若2OD BD =，则k 的值是______．13．如图所示，过y 轴正半轴上的任意一点P ，作x 轴的平行线，分别与反比例函数y ＝﹣6x（x ＜0）和y＝8x（x ＞0）的图象交于点A 和点B ，若点C 是x 轴上任意一点，连接AC 、BC ，则△ABC 的面积为__．14．一定质量的二氧化碳，其密度()3kg /m ρ=是体积()3m V 的反比例函数，请你根据图中的已知条件，写出反比例函数的关系式___________，当33m V =时，则ρ=_______3kg /m ．三、解答题15．如图1，反比例函数()0my x x=>的图象过点()4,3M ．(1)求反比例函数my x=的表达式，判断点()2,8在不在该函数图象上，并说明理由； (2)反比例函数()16my x x=≤≤的图象向左平移2个单位长度，平移过程中图象所扫过的面积是______； (3)如图2，直线:8l y x =-+与x 轴、y 轴分别交于点A 、点B ，点P 是直线l 下方反比例函数my x=图象上一个动点，过点P 分别作PC x ∥轴交直线l 于点C ，作PD y ∥轴交直线l 于点D ，请判断AC BD ⋅的值是否发生变化，并说明理由，如果不变化，求出这个值． 16．阅读下列材料定义运算min ,a b ，当a b ≥时，则min ,a b b =；当a b <时，则min ,a b a =．例如：min 1,31-=-与min 1,22--=-．完成下列任务(1)①()0min 3,2-= _________；②min 4--=_________ (2)如图，已知反比例函数1ky x=和一次函数22y x b =-+的图像交于A 、B 两点．当20x -<<时，则()()2min,213kx b x x x x-+=+--．求这两个函数的解析式． 17．在如图平面直角坐标系中矩形OABC 的顶点B 的坐标为（4，2），OA 、OC 分别落在x 轴和y 轴上，OB 是矩形的对角线．将△OAB 绕点O 逆时针旋转，使点B 落在y 轴上，得到△ODE ，OD 与CB 相交于点F ，反比例函数y ＝kx（x ＞0）的图象经过点F ，交AB 于点G ．（1）求k 的值和点G 的坐标；（2）连接FG ，则图中是否存在与△BFG 相似的三角形？若存在，请把它们一一找出来，并选其中一种进行证明；若不存在，请说明理由；（3）在线段OA 上存在这样的点P ，使得△PFG 是等腰三角形．请直接写出点P 的坐标．18．我们不妨约定：在平面直角坐标系中若某函数图象上至少存在不同的两点关于直线x n =（n 为常数）对称，则把该函数称之为“()X n 函数”．(1)在下列关于x 的函数中是“()X n 函数”的是________（填序号）； ①6y x=，②4y x =，③225y x x =-- (2)若关于x 的函数y x h =-（h 为常数）是“()3X 函数”，与my x=（m 为常数，0m >）相交于A （A x ，A y ）、B （B x ，B y ）两点，A 在B 的左边，5B A x x -=，求m 的值；(3)若关于x 的“()X n 函数”24y ax bx =++（a ，b 为常数）经过点（1-，1），且1n =，当1t x t -≤≤时，则函数的最大值为1y ，最小值为2y ，且1212y y -=，求t 的值． 19．如图，在平面直角坐标系中四边形ABCD 为正方形，已知点A (0，﹣6)、D (﹣3，﹣7)，点B 、C 在第三象限内．(1)求点B 的坐标；(2)在y 轴上是否存在一点P ，使ABP 是AB 为腰的等腰三角形？若存在，求点P 的坐标；若不存在，请说明理由．(3)将正方形ABCD 沿y 轴向上平移，若存在某一位置，使在第二象限内点B 、D 两点的对应点B '、D 正好落在某反比例函数的图象上，求该反比例函数的解析式．参考答案与解析1．【答案】A【分析】根据点P 的坐标，利用待定系数法即可得．【详解】解：设这个反比例函数的表达式为(0)ky k x =≠ 由题意，将点(3,1)P --代入得：3(1)3k =-⨯-= 则这个反比例函数的表达式为3y x =故选：A ．【点睛】本题考查了求反比例函数的解析式，熟练掌握待定系数法是解题关键． 2．【答案】B【分析】将(),n n 代入解析式中即可求出n 的值. 【详解】解：将(),n n 代入2y x =中得2n n=解得：n =故选B.【点睛】此题考查的是根据点所在的图像求点的坐标，将点的坐标代入解析式求点的坐标是解决此题的关键.3．【答案】B【分析】作CE ⊥OA 于E ，依据反比例函数系数k 的几何意义求得OE ，即可求得C 的坐标，从而求得点A 坐标，再根据中点坐标公式即可求得D 的坐标．【详解】解：作CE ⊥OA 于E ，如图∵B（5，4），四边形AOCB为平行四边形∴CE=4∵反比例函数y=8x的图象经过点C∴S△COE=12OE•CE=12×8∵CE=4∴OE=2∴C（2，4），OA=BC=5-2=3 ∴A（3，0）∵点D是AB的中点∴点D的坐标为（3+50+422，），即D（4，2）故选：B．【点睛】本题考查了平行四边形的性质，反比例函数系数k的几何意义等，求得点C和点A的坐标是解题的关键．4．【答案】D【分析】当k＞0，双曲线的两支分别位于第一、第三象限，在每一象限内y随x的增大而减小，根据反比例函数的性质对四个选项进行逐一分析即可．【详解】解：A.∵反比例函数4yx=中4＞0，∴此函数图象在一、三象限，故本选项正确；B.∵反比例函数4yx=的图象双曲线关于原点对称，故本选项正确；C.反比例函数的图象可知，图象关于直线y x=±对称，故本选项正确；D.∵反比例函数4yx=的图象位于第一、三象限，直线y x=-经过第二、四象限，所以直线y x=-与双曲线4yx=无交点，故本选项错误；故选D．【点睛】本题考查了反比例函数的性质，熟知反比例函数的增减性是解答此题的关键． 5．D【分析】根据图象进行分析即可得结果；【详解】解：∵22x x> ∴12y y >由图象可知，函数12y x=和22y x =分别在一、三象限有一个交点，交点的横坐标分别为11x x ==-，由图象可以看出当10x -<<或1x >时，则函数12y x=在22y x =上方，即12y y >故选：D ．【点睛】本题主要考查一次函数和反比例函数的应用，掌握一次函数和反比例函数图象的性质是解本题的关键． 6．【答案】C【分析】根据直线y mx =与双曲线k y x =都经过点A ，得出1a mk a =-⎧⎪⎨=⎪⎩-，进而得到k m =，再由直线y mx =与双曲线k y x =都经过点B ，得到33k b bm ⎧-=⎪⎨⎪-=⎩，进而得到2b m k =，进而求出b 的值，得到点A 的坐标，即可得到答案．【详解】由题，直线y mx =与双曲线ky x=都经过点A ∴1a m k a =-⎧⎪⎨=⎪⎩- ，得：k m =直线y mx =与双曲线ky x=都经过点B 33bm k b -=⎧⎪∴⎨-=⎪⎩，得：2b m k = 21b ∴=0b >1b ∴=13B ∴-（，）将点B 代入y mx =，得：3m -=3y x ∴=-13A ∴-（，）111313322ABM S ∆∴=⨯⨯+⨯⨯=故选：C【点睛】本题考查一次函数与反比例函数的图像问题，根据两者的交点结合解析式求出点的坐标是解题关键．7．【答案】B【分析】设未知数，表示出点P 、Q 、R 的坐标，进而表示S 1、S 2、S 3，由S 1+S 3＝10列方程求解即可．【详解】解：设OE ＝ED ＝DC ＝a ∵函数ykx =（x ＞0）的图象经过点P 、Q 、R∴点P （3k a ，3a ），Q （2k a ，2a ），R （ka ，a ）∴OF 3k a =，OG 2k a =，OA k a =∴S 1＝OF •CD 3k a =⨯a 3k =S 3＝AG •OE ＝（2k k a a -）×a 2k =又∵S 1+S 3＝10 ∴32k k +=10 解得k ＝12 故选：B ．【点睛】本题考查反比例函数系数k 的几何意义以及反比例函数图象上点的坐标特征，用坐标表示线段的长是解决问题的关键． 8．【答案】34##0.75 【分析】由点A 、B 、C 的坐标可知260k m =>，m ＝n ，点B 、C 关于原点对称，求出直线BC 的解析式，不妨设m ＞0，如图，过点A 作x 轴的垂线交BC 于D ，根据2ABC S =△列式求出2m ，进而可得k 的值．【详解】解：∵点(,6),(3,2),(3,2)--A m m B m n C m n 是函数(0)ky k x=≠图象上的三点 ∴260k m => 6k mn = ∴m ＝n∴(3,2)B m m (3,2)C m m -- ∴点B 、C 关于原点对称∴设直线BC 的解析式为()0y kx k =≠ 代入(3,2)B m m 得：23m mk = 解得：23k =∴直线BC 的解析式为23y x =不妨设m ＞0，如图，过点A 作x 轴的垂线交BC 于D 把x ＝m 代入23y x =得：23y m =∴D （m ，23m ）∴AD ＝216633m m m -=∴()11633223ABCSm m m =⨯⋅+= ∴218m =∴2136684k m ==⨯=而当m ＜0时，则同样可得34k =故答案为：34【点睛】本题考查了反比例函数与几何综合，中心对称的性质，待定系数法求函数解析式，熟练掌握反比例函数的图象和性质，学会利用数形结合的数学思想解答是解题的关键．9．【答案】4【分析】根据等腰△AOB，中位线CD得出AD⊥OB，S△AOE＝S△AOD＝2，应用|k|的几何意义求k．【详解】解：如图：连接AD△AOB中AO＝AB，OB在x轴上，C、D分别为AB，OB的中点∴AD⊥OB，AO∥CD∴S△AOE＝S△AOD＝2∴k＝4．故答案为：4．【点睛】本题考查了反比例函数图象、等腰三角形以及中位线的性质、三角形面积，解题的关键是灵活运用等腰三角形的性质．10．【答案】254或754【分析】先根据“和谐点”的定义求出m的值，进而可求出点A的坐标，根据三角形的面积可求出△OAP的面积．【详解】解：∵点P（52-，m）是“和谐点”∴5+2|m|52=|m|，解得m＝±10当m＝10时，则P（52-，10）把点P的坐标代入一次函数和反比例的解析式得：k1＝5，k2＝﹣25∴A（0，5）∴S△OAP15255224=⨯⨯=．当m ＝﹣10时，则P （52-，﹣10）∴k 1＝﹣15，k 2＝25 ∴A （0，﹣15） ∴S △OAP 12=⨯1557524⨯=．故答案为：254或754．【点睛】本题考查反比例函数系数k 的几何意义，过双曲线上的任意一点分别向两条坐标轴作垂线，与坐标轴围成的矩形面积就等于|k |，读懂题意，明确和谐点的定义是解题的关键． 11．【答案】12【分析】画树状图，共有12个等可能的结果，直线y kx =与反比例函数by x=的图象经过的象限相同的结果有6个，再由概率公式求解即可．【详解】解：画树状图如图：∵从袋子中随机抽取一个小球，记标号为k ，不放回后将袋子摇匀，再随机抽取一个小球，记标号为b ，共有12个数组∴直线y kx =与反比例函数by x=的图象经过的象限相同的数组有（2，3），（2，4），（3，2），（3，4），（4，2），（4，3），共有6组∴k ，b 直线y kx =与反比例函数b y x=的图象经过的象限相同的概率为61122=．故答案为：12【点睛】此题考查了用列表法或树状图法求概率及一次函数与反比例函数的性质，熟练掌握利用列表法或树状图列出所有等可能的结果以及一次函数与反比例函数的性质是解题的关键． 12．【答案】9【分析】先求解A 的坐标，再表示B 的坐标，再证明,ABD COD ∽利用相似三角形的性质列方程求解即可．【详解】解：点()2,A m ，B 分别在双曲线()60y x x =>和()0ky x x=>上，AB x ∥轴 63,,3,23kmB2,3,AAC x ⊥轴2,0,CAB x ∥轴,ABD COD ∽,ABBDOC OD而2OD BD = 213,22k 解得：9,k = 故答案为：9【点睛】本题考查的是反比例函数的性质，相似三角形的判定与性质，掌握“反比例函数的图像与性质”是解本题的关键． 13．【答案】7【分析】连接OA ，OB ，利用同底等高的两三角形面积相等得到三角形AOB 面积等于三角形ACB 面积，再利用反比例函数k 的几何意义求出三角形AOP 面积与三角形BOP 面积，即可得到结果．【详解】解：如图，连接OA ，OB∵△AOB 与△ACB 同底等高 ∴S △AOB ＝S △ACB ∵AB ∥x 轴∴AB ⊥y 轴∵A 、B 分别在反比例函数y ＝﹣6x （x ＜0）和y ＝8x （x ＞0）的图象上∴S △AOP ＝3，S △BOP ＝4∴S △ABC ＝S △AOB ＝S △AOP ＋S △BOP ＝3＋4＝7．故答案为：7．【点睛】本题考查的是反比例函数系数k 的几何意义，即在反比例函数y =kx的图象上任意一点向坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是12|k |，且保持不变．也考查了三角形的面积． 14．【答案】10V ρ=103【分析】由函数图像信息可得反比例函数过点(5,2)，根据待定系数法求解析式；将3V =代入即可求得ρ．【详解】反比例函数过点(5,2) 设反比例函数解析式为kVρ= 则10k =∴反比例函数解析式为10Vρ=当3V =时，则103ρ= 故答案为：10V ρ=103【点睛】本题考查了反比例函数的应用，待定系数法求反比例函数的解析式，根据解析式求函数值，从图像获取信息是解题的关键．15．【答案】(1)不在，理由见解析 (2)20 (3)不变化，24【分析】对于（1），利用待定系数法求出函数关系式，再代入判断即可；对于（2），设点E 的横坐标和点F 的横坐标，再分别表示出点E ，F ，G ，H 的坐标，进而得出线段的长度，再根据平行四边形面积公式得出答案；对于（3），设点P 的横坐标为t ，分别表示点C ，点D 的坐标，再根据两点之间的距离公式得出AC 和BD 的长，进而得出答案．（1）将点()4,3M 代入m y x =得34m= 12m =∴12y x=；当2x =时，则6y = ∵68≠∴点()2,8不在函数图象上；（2）设点E 的横坐标是1，点F 的横坐标是6，点G ，H 分别对应点E ，F ，如图所示.图形扫过的面积即为平行四边形EFHG 的面积．令12y x=中1x =，则12y = 所以(112)E ， -1,12G （）令12y x=中6x =，则2y = 所以(62)F ，，(4,2)H ．因为EG FH ∥，且EM FH = 所以四边形EGHF 为平行四边形所以=()2(122)20E F S EG y y ⋅-=⨯-=．故答案为：20；（3）不变化，理由如下：因为直线l ：8y x =-+与x 轴，y 轴分别交于点A ，点B 所以点A （8，0），B （0，8）．设点P 的横坐标是t 所以12(,)P t t．因为PC x ∥轴交直线l 于点C ，PD y ∥轴交直线l 于点D 所以1212(8,)C tt-+ (,8)D t t -+所以AC =BD =即24AC BD ⋅=⋅=所以AC BD ⋅为定值，为24.．【点睛】本题主要考查了反比例函数图象上点的坐标特征，待定系数法求函数关系式，求平行四边形面积等，掌握数形结合思想是解题的关键．16．【答案】(1)①1；②4- (2)12y x=- 223y x =--【分析】（1）根据材料中的定义进行计算，即可求出答案；（2）由函数图像可知当20x -<<时，则2kx bx ，则min ,22k x b x b x-+=-+，结合已知可得()()2213x b x x x -+=+--，即可求出b ，得到一次函数解析式，求出点A 的坐标，再利用待定系数法求出反比例函数解析式．（1）解：根据题意∵min ,a b ，当a b ≥时，则min ,a b b =；当a b <时，则min ,a b a = ∴①()0min 3,21-=；∵4-∴②min 44-=-；故答案为：①1；②4-；（2）解：由函数图像可知当20x -<<时，则2k x bx∴min,22kx b x b x-+=-+ 又∵()()2min,213kx b x x x x-+=+-- ∴()()2213x b x x x -+=+-- ∴3b =-∴一次函数223y x =-- 当x ＝－2时21y = ∴A （－2，1）将A （－2，1）代入1ky x=得212k =-⨯=-∴反比例函数12y x=-．【点睛】本题考查了新定义的运算法则，零次幂，反比例函数与一次函数的综合问题，解题的关键是掌握题意，正确的运用数形结合的思想求解．17．【答案】（1）k ＝2，点G 的坐标为（4，12）；（2）△COF ∽△BFG ；△AOB ∽△BFG ；△ODE ∽△BFG ；△CBO ∽△BFG ，证明详见解析；（3）点P 的坐标为（40）或（158，00）．【分析】（1）证明△COF ∽△AOB ，则CF OCAB OA=，求得：点F 的坐标为（1，2），即可求解；（2）△COF ∽△BFG ；△AOB ∽△BFG ；△ODE ∽△BFG ；△CBO ∽△BFG ．证△OAB ∽△BFG ：43AO BF = 24332AB BG ==即可求解．（3）分GF ＝PF 、PF ＝PG 、GF ＝PG 三种情况，分别求解即可．【详解】解：（1）∵四边形OABC 为矩形，点B 的坐标为（4，2） ∴∠OCB ＝∠OAB ＝∠ABC ＝90°，OC ＝AB ＝2，OA ＝BC ＝4 ∵△ODE 是△OAB 旋转得到的，即：△ODE ≌△OAB ∴∠COF ＝∠AOB ，∴△COF ∽△AOB ∴CF OC AB OA =，∴2CF ＝24，∴CF ＝1∴点F 的坐标为（1，2） ∵y ＝kx（x ＞0）的图象经过点F∴2＝1k ，得k ＝2 ∵点G 在AB 上 ∴点G 的横坐标为4对于y ＝2x ，当x ＝4，得y ＝12∴点G 的坐标为（4，12）；（2）△COF ∽△BFG ；△AOB ∽△BFG ；△ODE ∽△BFG ；△CBO ∽△BFG ．下面对△OAB ∽△BFG 进行证明： ∵点G 的坐标为（4，12），∴AG ＝12 ∵BC ＝OA ＝4，CF ＝1，AB ＝2∴BF＝BC﹣CF＝3BG＝AB﹣AG＝32．∴43AOBF=24332ABBG==∴AO AB BF BG=∵∠OAB＝∠FBG＝90°∴△OAB∽△FBG．（3）设点P（m，0），而点F（1，2）、点G（4，12）则FG2＝9+94＝454，PF2＝（m﹣1）2+4，PG2＝（m﹣4）2+14当GF＝PF时，则即454＝（m﹣1）2+4，解得：m；当PF＝PG时，则同理可得：m＝158；当GF＝PG时，则同理可得：m＝4综上，点P的坐标为（40）或（158，00）．【点睛】本题考查的是反比例函数综合运用，涉及到旋转的性质、三角形相似、等腰三角形的性质等，其中（3），要注意分类求解，避免遗漏．18．【答案】(1)②③( 2)4 (3)t＝2或t＝1【分析】（1）根据定义分析判断即可；（2）作出图形，y＝x﹣3与x轴交于C点，与y轴交于D点，作AM⊥x轴交于M点，BN⊥x轴交于N点，由xB﹣xA＝5，设CN＝x，则MC＝5﹣x，则B（3+x，x），A（x﹣2，5﹣x），根据轴对称的性质以及反比例函数的性质可得（3+x）x+（x﹣2）（5﹣x）＝0，继而求得x的值，即可求得B的坐标，根据反比例函数的意义即可求得m的值；（3）根据题意以及二次函数的性质，待定系数求二次函数解析式，进而分类讨论，根据121 2y y-=，即可求得t的值．（1）解：根据定义，函数关于直线x n=（n为常数）对称，即该函数图象是轴对称图形①6yx=的图象是中心对称图象，不符合题意；②4y x=，③225y x x=--的图象是轴对称图形，符合题意故答案为：②③（2）∵y＝|x-h|是“X（3）”函数∴h＝3如图，y＝x﹣3与x轴交于C点，与y轴交于D点，作AM⊥x轴交于M点，BN⊥x轴交于N点∴C（3，0），D（0，﹣3）∴∠BCN＝∠OCD＝45°由对称性可知，∠ACM＝∠OCD＝45°∴AM＝CM，BN＝CN∵xB﹣xA＝5∴MN＝5设CN＝x，则MC＝5﹣x∴B（3+x，x），A（x﹣2，5﹣x）∴（3+x）x+（x﹣2）（5﹣x）＝0∴x＝1∴B（4，1）∴m＝4；（3）由题意得4112a bba-+=⎧⎪⎨-=⎪⎩解得12 ab=-⎧⎨=⎩∴此“X（n）函数”为y＝﹣x2+2x+4①当t＜1时x＝t时，则y1＝﹣t2+2t+4x＝t﹣1时，则y2＝﹣（t﹣1）2十2（t﹣1）+4y1﹣y2＝（﹣t2+2t+4）﹣[﹣（t﹣1）2+2（t﹣1）+4]＝﹣2t+3＝12∴t＝54（舍）；②当t﹣1≥1，即t≥2时x＝t﹣1时，则y1＝﹣（t﹣1）2十2（t﹣1）+4x＝t时，则y2＝﹣t2+2t+4y1-y2＝﹣（t﹣1）2+2（t﹣1）+4﹣（﹣t2+2t+4）＝2t﹣3＝12∴t＝74（舍）；③当1≤t＜32时x＝1时，则y1＝5x＝t﹣1时，则y2＝﹣（t﹣1）2十2（t﹣1）+4y1﹣y2＝5﹣[﹣（t﹣1）2+2（t﹣1）+4]＝t2﹣4t+4＝12∴t＝2±，又因为1≤t＜3 2∴t＝2-④32≤t＜2时x＝1时，则y1＝5x＝t时，则y2＝﹣t2十2t+4y1﹣y2＝5﹣（﹣t2+2t+4）＝t2﹣4t+4＝12∴t＝1，又因为32≤t＜2∴t＝1综上所述：t＝2-t＝1【点睛】本题考查了新定义，一次函数的性质，反比例函数的性质，二次函数的性质，根据新定义以及轴对称的性质求解是解题的关键．19．【答案】(1)B (-1，-3)(2)存在，(06-，或(06-，或()00，(3)6y x =-【分析】（1）过点B 作BE ⊥y 轴于点E ，过点D 作DF ⊥y 轴于点F ，证明ADF BAE ≅得出BE 与OE 的长度便可求得B 点坐标；（2）先求出AB 的值，再根据题意可得分类讨论，分为当AB =AP 时有两种情况和当AB =BP 时有一种情况进行求解即可；（3）先设向上平移了m 表示B '和D 的坐标，再根据B 、D 两点的对应点B '、D 正好落在某反比例函数的图象上得B '和D 点的横、纵坐标的积相等，列出关于m 的方程即可求解．（1）过点B 作BE ⊥y 轴于点E ，过点D 作DF ⊥y 轴于点F ，如下图则90AFD AEB ∠=∠=︒∵点A (0，-6)，D (-3，-7)∴DF =3，AF =1∵四边形ABCD 是正方形∴AB =AD 90BAD ∠=︒∴90DAF BAE DAF ADF ∠+∠=∠+∠=︒∴ADF BAE =∠∠∵ADF BAE F EAD BA ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ADF BAE ≅∴DF =AE =3，AF =BE =1∴OE=OA-AE=6-3=3∴B(-1，-3)．（2）存在3种情况由（1）得ADF BAE≅且在Rt AFD中AB=AD①当AB=AP时的等腰三角形，如图则AP∵A为(0，-6)∴P点的坐标为(0，)；②当AB=AP时，则如下图则AP∵A 为(0，-6)∴P 点的坐标为(0，)；③当AB =BP 时，则如下图则BP ，且过B 作BE ⊥AP 于点E∵AB BP BE AP =⊥，∴3PE AE ==∴P 点在原点上则P 为(0，0)．综上所述点P 的坐标为(06-，或(06-，或()00，．（3）设向上平移了m 可得B '为(-1，-3+m )，D 为(-3，-7+m ) 反比例函数关系式为k y x=()0k ≠ ∴()()1337k m m =-⨯-+=-⨯-+解得m =9∴k =()13166m -⨯-+=-⨯=- ∴反比例函数解析式为：6y x=- 【点睛】此题是反比例函数与正方形结合的综合体，主要考查了反比例函数的性质、待定系数法、全等三角形的性质和判定和等腰三角形的性质和判定，解决本题的关键是证明全等三角形和分类讨论．。

人教版初中数学九年级数学下册第一单元《反比例函数》测试(答案解析)

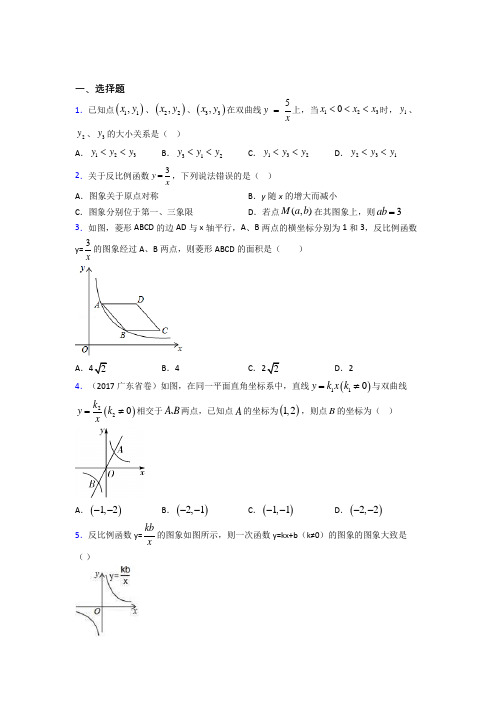
一、选择题1．已知点()11,x y 、()22,x y 、()33,x y 在双曲线5y x=上，当1230x x x <<<时，1y 、2y 、3y 的大小关系是（）A ．123y y y <<B ．312y y y <<C ．132y y y <<D ．231y y y <<2．关于反比例函数3y x=，下列说法错误的是（） A ．图象关于原点对称B ．y 随x 的增大而减小C ．图象分别位于第一、三象限D ．若点(,)M a b 在其图象上，则3ab =3．如图，菱形ABCD 的边AD 与x 轴平行，A 、B 两点的横坐标分别为1和3，反比例函数y=3x的图象经过A 、B 两点，则菱形ABCD 的面积是（）A ．42B ．4C ．22D ．24．（2017广东省卷）如图，在同一平面直角坐标系中，直线()110y k x k =≠与双曲线()220k y k x=≠相交于A B 、两点，已知点A 的坐标为()1,2，则点B 的坐标为（）A ．()1,2--B ．()2,1--C ．()1,1--D ．()2,2--5．反比例函数y=kbx的图象如图所示，则一次函数y=kx+b （k≠0）的图象的图象大致是（）A ．B ．C ．D ．6．如图，曲线表示温度T （℃）与时间t （h ）之间的函数关系，它是一个反比例函数的图像的一支．当温度T ≤2℃时，时间t 应（）A ．不小于23h B ．不大于23h C ．不小于32h D ．不大于32h 7．下列函数中图象不经过第三象限的是（） A ．y ＝﹣3x ﹣2B ．y ＝2xC ．y ＝﹣2x +1D ．y ＝3x +28．已知反比例函数y=21k x +的图上象有三个点（2，1y ）, (3, 2y ),(1-, 3y ),则1y ，2y ，3y 的大小关系是（）A ．1y ＞2y ＞3yB ．2y ＞1y ＞3yC ．3y ＞1y ＞2yD ．3y ＞2y ＞1y9．如图，在平面直角坐标系中，平行四边形OABC 的顶点A 在反比例函数1k y x=（x>0）的图像上，顶点B 在反比例函数2k y x=（x>0)的图像上，点C 在x 轴的正半轴上.若平行四边形OABC 的面积为8，则k 2-k 1的值为（）A ．4B ．8C ．12D ．1610．如图，点A 是反比例函数2(0)y x x=>的图象上任意一点，AB x 轴交反比例函数3y x =-的图象于点B ，以AB 为边作ABCD ，其中C 、D 在x 轴上，则ABCDS为（）A ．2.5B ．3.5C ．4D ．511．给出下列函数：①y ＝﹣3x +2：②y ＝3x ；③y ＝﹣5x：④y ＝3x ，上述函数中符合条件“当x ＞1时，函数值y 随自变量x 增大而增大”的是（） A ．①③ B ．③④ C ．②④ D ．②③12．如图， O 为坐标原点，点B 在x 轴的正半轴上，四边形OBCA 是平行四边形，45sin AOB ∠=，反比例函数()0m y m x=>在第一象限内的图像经过点A ，与BC 交于点F ，若点F 为BC 的中点，且AOF 的面积为12，则m 的值为（）A ．16B ．24C ．36D ．48二、填空题13．双曲线y ＝kx经过点A （a ，﹣2a ），B （﹣2，m ），C （﹣3，n ），则m _____n （＞，＝，＜）．14．如图，反比例函数y ＝kx（x ＞0）经过A ，B 两点，过点A 作AC ⊥y 轴于点C ，过点B 作BD ⊥y 轴于点D ，过点B 作轴BE ⊥x 于点E ，连接AD ，已知AC ＝2，BE ＝2，S 矩形BEOD ＝16，则S △ACD ＝_____．15．调查显示，某商场一款运动鞋的售价是销量的反比例函数（调查获得的部分数据如下表）．售价x （元/双） 200 240 250 400销售量y （双）30 252415已知该运动鞋的进价为180元/双，要使该款运动鞋每天的销售利润达到2400元，则其售价应定为_______元．16．近视眼镜的度数y （度）与镜片焦距x （米）成反比例，已知400度近视眼镜镜片的焦距为0.25米，则眼镜度数y 与镜片焦距x 之间的函数关系式为________．（无需确定x 的取值范围）17．如果反比例函数y 2mx-=的图象在第一、三象限，那么m 的取值范围是____． 18．如图，过x 轴正半轴上任意一点P 作x 轴的垂线，分别与反比例函数24y x=和12y x =的图象交于点A 和点B .若点C 是y 轴上任意一点，则ABC 的面积为______________．19．如图，直线y ＝34-x +6与反比例函数y ＝kx（k ＞0）的图象交于点M 、N ，与x 轴、y 轴分别交于点B 、A ，作ME ⊥x 轴于点E ，NF ⊥x 轴于点F ，过点E 、F 分别作EG ∥AB ，FH ∥AB ，分别交y 轴于点G 、H ，ME 交HF 于点K ，若四边形MKFN 和四边形HGEK 的面积和为12，则k 的值为_____．20．如图，菱形ABCD 顶点A 在函数y=4x（x>0）的图像上，函数y=kx （k>4，x>0）的图象关于直线AC 对称，且经过点B 、D 两点，若AB=4，∠ADC=150°，则k=______。

第26章反比例函数单元测试(含答案)2024-2025学年数学人教版九年级下册

第26章反比例函数一、选择题：本题共10小题，每小题3分，共30分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.如图是反比例函数的图象，它的函数表达式是( ).A. y=5xB. y=2x C. y=−1xD. y=−2x2.对于反比例函数y=−5x，下列说法错误的是( )A. 图象经过点(1,−5)B. 图象位于第二、四象限C. 当x<0时，y随x的增大而减小D. 当x>0时，y随x的增大而增大3.如图，点A在双曲线y=kx上，B在y轴上，且AO=AB.若△ABO的面积为6，则k的值为 ( )A. 6B. −6C. 12D. −124.如图，直线y1=kx+1与反比例函数y2=2x的图象在第一象限交于点P(1,t)，与x轴、y轴分别交于A，B 两点，则下列结论错误的是 ( )A. t=2B. △AOB是等腰直角三角形C. k=1D. 当x>1时，y2>y15.当x<0时，函数y=(k−1)x与y=2−k的y值都随x的增大而增大，则k的取值范围是( ).3xA. k>1B. 1<k<2C. k>2D. k<16.函数y=k和y=−kx+2(k≠0)在同一平面直角坐标系中的大致图象可能是( )xA. B.C. D.7.若点A(−3,y1)，B(−1,y2)，C(2,y3)都在反比例函数y=k(k<0)的图象上，则y1，y2，y3的大小关系是( )xA. y3<y1<y2B. y2<y1<y3C. y1<y2<y3D. y3<y2<y18.在大棚中栽培新品种的蘑菇，在18℃的条件下生长最快，因此用装有恒温系统的大棚栽培，如图是某天恒温系统从开启升温到保持恒温及关闭，大棚内温度y(℃)随时间x(时)变化的函数图象，其中BC段是函数(k>0)图象的一部分．若该蘑菇适宜生长的温度不低于12℃，则这y=kx天该品种蘑菇适宜生长的时间为( )A. 18小时B. 17.5小时C. 12小时D. 10小时9.设A，B，C，D是反比例函数y=k图象上的任意四点，现有以下结论：x①四边形ABCD可以是平行四边形；②四边形ABCD可以是菱形；③四边形ABCD不可能是矩形；④四边形ABCD不可能是正方形．其中正确的是( ).A. ①②B. ①④C. ②③D. ③④10.如图，点P、Q是反比例函数y=k(k≠0)图象上的两点，PA⊥y轴于点A，QN⊥x轴于点N，作PM⊥xx轴于点M，QB⊥y轴于点B，连接PB、QM.记SΔABP=S1，SΔQMN=S2，则S1与S2的大小关系为 ( )A. S1>S2B. S1<S2C. S1=S2D. 无法判断二、填空题：本题共6小题，每小题3分，共18分。

人教版九年级下数学第二十六章反比例函数单元检测卷含答案

第二十六章检测卷(120分钟150分)一、选择题(本大题共1.已知反比例函数y=的图象过点A(1,-2),则k的值为A.1B.2C.-2D.-12.若反比例函数y=经过点(a,2a),a≠0,则此反比例函数的图象在A.第一、三象限B.第一、二象限C.第二、三象限D.第二、四象限3.对于反比例函数y=-,下列说法不正确的是A.图象分布在第二、四象限B.当x>0时,y随x的增大而增大C.图象经过点(1,-2)D.若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则y1<y24.已知一个矩形的面积为24 cm2,其长为y cm,宽为x cm,则y与x之间的函数关系的图象大致在A.第一、三象限,且y随x的增大而减小B.第一象限,且y随x的增大而减小C.第二、四象限,且y随x的增大而增大D.第二象限,且y随x的增大而增大5.在下列选项中,是反比例函数关系的为A.在直角三角形中,30°角所对的直角边y与斜边x之间的关系B.在等腰三角形中,顶角y与底角x之间的关系C.圆的面积S与它的直径d之间的关系D.面积为20的菱形,其中一条对角线y与另一条对角线x之间的关系6.若a≠0,则函数y=与y=-ax2+a在同一平面直角坐标系中的大致图象可能是7.某人对地面的压强与他和地面接触面积的函数关系如图所示.若某一沼泽地地面能承受的压强不超过300 N/m2,那么为了不至于下陷,此人需要站立在木板上,则该木板的面积为(木板的重量忽略不计)A.至少2 m2B.至多2 m2C.2 m2D.无法确定8.如图,是反比例函数y1=和一次函数y2=mx+n的图象,若y1<y2,则相应的x的取值范围是A.1<x<6B.x<1C.x<6D.x>19.如图,A是反比例函数y=(x<0)的图象上的一点,过点A作平行四边形ABCD,使点B,C在x轴上,点D在y 轴上,则平行四边形ABCD的面积为A.1B.3C.6D.1210.在同一平面直角坐标系中,二次函数y=x2与反比例函数y=(x>0)的图象如图所示,若两个函数图象上有三个不同的点A(x1,m),B(x2,m),C(x3,m),其中m为常数,令ω=x1+x2+x3,则ω的值为A.1B.mC.m2D.二、填空题(本大题共4小题,每小题5分,满分20分)11.若反比例函数y=k-在各自象限内y随x的增大而增大,则k的值为-.12.点A(a,b)是一次函数y=x-1与反比例函数y=的交点,则a2b-ab2=4.13.已知A,B两点分别在反比例函数y=(m≠0)和y=-的图象上,若点A与点B关于x轴对称,则m的值为1.14.设双曲线y=(k>0)与直线y=x交于A,B两点(点A在第三象限),将双曲线在第一象限的一支沿射线BA 的方向平移,使其经过点A,将双曲线在第三象限的一支沿射线AB的方向平移,使其经过点B,平移后的两条曲线相交于P,Q两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,PQ为双曲线的“眸径”,当双曲线y=(k>0)的眸径为6时,k的值为.三、(本大题共2小题,每小题8分,满分16分)15.如果函数y=x2m-1为反比例函数,求m的值.:16.学校食堂用1200元购买大米,写出购买的大米质量y(kg)与单价x(元)之间的函数解析式,y是x的反比例函数吗?四、(本大题共2小题,每小题8分,满分16分)17.已知点A(2,-3),P,Q(-5,b)都在反比例函数的图象上.(1)求此反比例函数的解析式;(2)求a+的值.18.如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴的正半轴上,反比例函数y=的图象经过点C(3,m).(1)求菱形OABC的周长;(2)求点B的坐标.五、(本大题共2小题,每小题10分,满分20分)19.如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标为(-1,1),点B在x轴正半轴上,点D在第三象限的双曲线y=上,过点C作CE∥x轴交双曲线于点E,连接BE,求△BCE的面积.20.已知反比例函数y=(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.(1)求这个反比函数的解析式;(2)求△ACD的面积.六、(本题满分12分)21.已知反比例函数的图象经过三个点A(-4,-3),B(2m,y1),C(6m,y2),其中m>0.(1)当y1-y2=4时,求m的值;(2)如图,过点B,C分别作x轴、y轴的垂线,两垂线相交于点D,点P在x轴上,若三角形PBD的面积是8,请写出点P坐标.(不需要写解答过程)七、(本题满分12分)22.:观察表中数据,发现可以用反比例函数刻画这种海产品的每天销售量y(千克)与销售价格x(元/千克)之间的关系.现假定在这批海产品的销售中,每天的销售量y(千克)与销售价格x(元/千克)之间都满足这一关系.(1)写出这个反比例函数的解析式,并补全表格;(2)在试销8天后,公司决定将这种海产品的销售价格定为150元/千克,并且每天都按这个价格销售,那么余下的这些海产品预计再用多少天可以全部售出?(3)在按(2)中定价继续销售15天后,公司发现剩余的这些海产品必须在不超过2天内全部售出,此时需要重新确定一个销售价格,使后面两天都按新的价格销售,那么新确定的价格最高不超过每千克多少元才能完成销售任务?八、(本题满分14分)23.我们可以把一个假分数写成一个整数加上一个真分数的形式,如=3+.同样的,我们也可以把某些分式写成类似的形式,如----=3+-.这种方法我们称为“分离常数法”.(1)如果-=1+,求常数a的值;(2)利用分离常数法,解决下面的问题:当m取哪些整数时,分式--的值是整数?(3)我们知道一次函数y=x-1的图象可以看成是由正比例函数y=x的图象向下平移1个单位长度得到,函数y=的图象可以看成是由反比例函数y=的图象向左平移1个单位长度得到.那么请你分析说明函数y=--的图象是由哪个反比例函数的图象经过怎样的变换得到?第二十六章检测卷(120分钟150分)一、选择题(本大题共10小题,每小题4分,满分40分)1.已知反比例函数y=的图象过点A(1,-2),则k的值为A.1B.2C.-2D.-12.若反比例函数y=经过点(a,2a),a≠0,则此反比例函数的图象在A.第一、三象限B.第一、二象限C.第二、三象限D.第二、四象限3.对于反比例函数y=-,下列说法不正确的是A.图象分布在第二、四象限B.当x>0时,y随x的增大而增大C.图象经过点(1,-2)D.若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则y1<y24.已知一个矩形的面积为24 cm2,其长为y cm,宽为x cm,则y与x之间的函数关系的图象大致在A.第一、三象限,且y随x的增大而减小B.第一象限,且y随x的增大而减小C.第二、四象限,且y随x的增大而增大D.第二象限,且y随x的增大而增大5.在下列选项中,是反比例函数关系的为A.在直角三角形中,30°角所对的直角边y与斜边x之间的关系B.在等腰三角形中,顶角y与底角x之间的关系C.圆的面积S与它的直径d之间的关系D.面积为20的菱形,其中一条对角线y与另一条对角线x之间的关系6.若a≠0,则函数y=与y=-ax2+a在同一平面直角坐标系中的大致图象可能是7.某人对地面的压强与他和地面接触面积的函数关系如图所示.若某一沼泽地地面能承受的压强不超过300 N/m2,那么为了不至于下陷,此人需要站立在木板上,则该木板的面积为(木板的重量忽略不计)A.至少2 m2B.至多2 m2C.2 m2D.无法确定8.如图,是反比例函数y1=和一次函数y2=mx+n的图象,若y1<y2,则相应的x的取值范围是A.1<x<6B.x<1C.x<6D.x>19.如图,A是反比例函数y=(x<0)的图象上的一点,过点A作平行四边形ABCD,使点B,C在x轴上,点D在y轴上,则平行四边形ABCD的面积为A.1B.3C.6D.1210.在同一平面直角坐标系中,二次函数y=x2与反比例函数y=(x>0)的图象如图所示,若两个函数图象上有三个不同的点A(x1,m),B(x2,m),C(x3,m),其中m为常数,令ω=x1+x2+x3,则ω的值为A.1B.mC.m2D.二、填空题(本大题共4小题,每小题5分,满分20分)11.若反比例函数y=k-在各自象限内y随x的增大而增大,则k的值为-.12.点A(a,b)是一次函数y=x-1与反比例函数y=的交点,则a2b-ab2=4.13.已知A,B两点分别在反比例函数y=(m≠0)和y=-的图象上,若点A与点B关于x轴对称,则m的值为1.14.设双曲线y=(k>0)与直线y=x交于A,B两点(点A在第三象限),将双曲线在第一象限的一支沿射线BA的方向平移,使其经过点A,将双曲线在第三象限的一支沿射线AB的方向平移,使其经过点B,平移后的两条曲线相交于P,Q两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,PQ为双曲线的“眸径”,当双曲线y=(k>0)的眸径为6时,k的值为.三、(本大题共2小题,每小题8分,满分16分)15.如果函数y=x2m-1为反比例函数,求m的值.解:∵y=x2m-1是反比例函数,∴2m-1=-1,解得m=0.16.学校食堂用1200元购买大米,写出购买的大米质量y(kg)与单价x(元)之间的函数解析式,y是x的反比例函数吗?解:∵由题意得xy=1200,∴y=,∴y是x的反比例函数.四、(本大题共2小题,每小题8分,满分16分)17.已知点A(2,-3),P,Q(-5,b)都在反比例函数的图象上.(1)求此反比例函数的解析式;(2)求a+的值.解:(1)设反比例函数解析式为y=,把A点坐标(2,-3)代入得k=2×(-3)=-6,所以反比例函数的解析式为y=-.(2)把P点坐标代入y=-,得3×=-6,解得a=-4,把Q点坐标(-5,b)代入y=-,得-5b=-6,解得b=,所以a+=-4+=-4+1=-3.18.如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴的正半轴上,反比例函数y=的图象经过点C(3,m).(1)求菱形OABC的周长;(2)求点B的坐标.解:(1)∵反比例函数y=的图象经过点C(3,m),∴m=4.作CD⊥x轴于点D,由勾股定理,得OC==5,∴菱形OABC的周长为20.(2)作BE⊥x轴于点E,∵BC=OA=5,OD=3,∴OE=8.又∵BC∥OA,∴BE=CD=4,∴B(8,4).五、(本大题共2小题,每小题10分,满分20分)19.如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标为(-1,1),点B在x轴正半轴上,点D在第三象限的双曲线y=上,过点C作CE∥x轴交双曲线于点E,连接BE,求△BCE的面积.解:如图,过D点作GH⊥x轴,过A点作AG⊥GH,过B点作BM⊥HC于点M.设D点坐标为,∵四边形ABCD是正方形,∴AD=CD=BC,∠ADC=∠DCB=90°,易得△AGD≌△DHC≌△CMB,∴AG=DH=-x-1,∴DG=BM,∴1-=-x-1-,x=-2,∴D点坐标为(-2,-3),CH=DG=BM=1-=4,-∵AG=DH=-1-x=1,∴点E的纵坐标为-4,当y=-4时,x=-,∴E点坐标为--,∴EH=2-,∴CE=CH-HE=4-,∴S△CEB=CE·BM=×4=7.20.已知反比例函数y=(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.(1)求这个反比函数的解析式;(2)求△ACD的面积.解:(1)将B点坐标代入函数解析式,得=2,解得k=6,∴反比例函数的解析式为y=.(2)∵B(3,2),点B与点C关于原点O对称,∴C点坐标(-3,-2).∵BA⊥x轴于点A,CD⊥x轴于点D,∴A点坐标(3,0),D点坐标(-3,0).∴S△ACD=AD·CD=×[3-(-3)]×|-2|=6.六、(本题满分12分)21.已知反比例函数的图象经过三个点A(-4,-3),B(2m,y1),C(6m,y2),其中m>0.(1)当y1-y2=4时,求m的值;(2)如图,过点B,C分别作x轴、y轴的垂线,两垂线相交于点D,点P在x轴上,若三角形PBD的面积是8,请写出点P坐标.(不需要写解答过程)解:(1)设反比例函数的解析式为y=,∵反比例函数的图象经过点A(-4,-3),∴k=-4×(-3)=12,∴反比例函数的解析式为y=,∵反比例函数的图象经过点B(2m,y1),点C(6m,y2),∴y1=,y2=,∵y1-y2=4,∴=4,∴m=1.(2)设BD与x轴交于点E.∵点B,点C,∴D点坐标为,BD=.∵三角形PBD的面积是8,∴BD·PE=8,∴·PE=8,∴PE=4m,∵E点坐标为(2m,0),点P在x轴上,∴点P的坐标为(-2m,0)或(6m,0).七、(本题满分12分)22.:观察表中数据,发现可以用反比例函数刻画这种海产品的每天销售量y(千克)与销售价格x(元/千克)之间的关系.现假定在这批海产品的销售中,每天的销售量y(千克)与销售价格x(元/千克)之间都满足这一关系.(1)写出这个反比例函数的解析式,并补全表格;(2)在试销8天后,公司决定将这种海产品的销售价格定为150元/千克,并且每天都按这个价格销售,那么余下的这些海产品预计再用多少天可以全部售出?(3)在按(2)中定价继续销售15天后,公司发现剩余的这些海产品必须在不超过2天内全部售出,此时需要重新确定一个销售价格,使后面两天都按新的价格销售,那么新确定的价格最高不超过每千克多少元才能完成销售任务?解:(1)函数解析式为y=.表格中数从左至右:300,50.(2)2104-(30+40+48+50+60+80+96+100)=1600.当x=150时,y==80.1600÷80=20(天).答:余下的这些海产品预计再用20天可以全部售出.(3)1600-80×15=400(千克).400÷2=200(千克).即如果正好用2天售完,那么每天需要售出200千克.当y=200时,x==60.答:新确定的价格最高不超过60元/千克才能完成销售任务.八、(本题满分14分)23.我们可以把一个假分数写成一个整数加上一个真分数的形式,如=3+.同样的,我们也可以把某些分式写成类似的形式,如----=3+-.这种方法我们称为“分离常数法”.(1)如果-=1+,求常数a的值;(2)利用分离常数法,解决下面的问题:当m取哪些整数时,分式--的值是整数?(3)我们知道一次函数y=x-1的图象可以看成是由正比例函数y=x的图象向下平移1个单位长度得到,函数y=的图象可以看成是由反比例函数y=的图象向左平移1个单位长度得到.那么请你分析说明函数y=--的图象是由哪个反比例函数的图象经过怎样的变换得到?解:(1)∵--=1+-,∴a=-4.(2)---------=-3--,∴当m-1=3或-3或1或-1时,分式的值为整数,解得m=4或m=-2或m=2或m=0.(3)y=------=3+-,∴将y=的图象向右移动2个单位长度得到y=-的图象,再向上移动3个单位长度得到y-3=-,即y=--.。

人教版九年级下册数学第二十六章反比例函数含答案

人教版九年级下册数学第二十六章反比例函数含答案一、单选题(共15题，共计45分)1、已知反比例函数y＝，当1＜y＜3时，x的取值范围是（）A.0＜x＜1B.1＜x＜2C.2＜x＜6D.x＞62、近视眼镜的度数y（度）与镜片焦距x（m）成反比例，已知400度近视眼镜镜片的焦距为0.25m，则y与x的函数关系式为（）A. B. C. D.y=3、如图，在平面直角坐标系中，矩形ABCD的顶点A，B在x轴的正半轴上，反比例函数的图象经过顶点D，分别与对角线AC，边BC交于点E，F，连接EF，AF.若点E为AC的中点，的面积为1，则k的值为（）A. B. C.2 D.34、下列图形中，阴影部分面积最大的是（）A. B. C. D.5、如图，点A是反比例函数y=是图象上一点，AB⊥y轴于点B，则△AOB的面积是（）A.1B.2C.3D.46、若反比例函数的图象经过点（1，4），则它的图象也一定经过的点是（）A.（﹣1，﹣4）B.（1，﹣4）C.（4，﹣1）D.（﹣1，4）7、若y=2x m-5为反比例函数，则m=（）A.-4B.-5C.4D.58、若点（3，4）是反比例函数图象上一点，则此函数图象必须经过点（）A.（3，﹣4）B.（2，﹣6）C.（4，﹣3）D.（2，6）9、点A（﹣1，1）是反比例函数y=的图象上一点，则m的值为（）A.﹣1B.﹣2C.0D.110、如图，点A是反比例函数y=(x<0)的图象上的一点，过点A作平行四边形ABCD，使点B、C在x轴上，点D在y轴上已知平行四边形ABCD的面积为6，则k的值为( )A.6B.-6C.3D.-311、若M(－4,y1)、N(－2，y2)、P(2，y3)三点都在反比例函数y＝(k＜0)的图象上，则y1、y2、y3的大小关系为（）A.y2＞y3＞y1B.y2＞y1＞y3C.y3＞y1＞y2D.y3＞y2＞y112、下列函数中，y随x的增大而减小的是（）A.y=-3xB.y=3x－4C.y=－D.y=13、函数y= （k≠0）的图象如图所示，那么函数y=kx-k图象大致是（）A. B. C. D.14、已知反比例函数y＝－，当x＞0时，它的图象在（）A.第一象限B.第二象限C.第三象限D.第四象限15、如果等腰三角形的底边长为x，底边上的高为y，则它的面积为定植S时，则x与y的函数关系式为（）A.y=B.y=C.y=D.y=二、填空题(共10题，共计30分)16、普通投影仪灯泡的使用寿命约为1500小时，它的可使用天数y与平均每天使用的小时数x之间的函数关系式为________ ．17、点（a﹣1，y1）、（a+1，y2）在反比例函数y=（k＞0）的图象上，若y1＜y2，则a的范围是________18、如图，在平面直角坐标系中，等边和菱形的边都在轴上，点在边上，，反比例函数的图象经过点，则的值为________.19、如图，点A是双曲线y= 在第一象限上的一动点，连接AO并延长交另一分支于点B，以AB为斜边作等腰Rt△ABC，点C在第二象限，随着点A的运动，点C的位置也不断的变化，但始终在一函数图象上运动，则这个函数的解析式为________．20、如图，曲线C2是双曲线C1：y= （x＞0）绕原点O逆时针旋转45°得到的图形，P是曲线C2上任意一点，点A在直线l：y=x上，且PA=PO，则△POA 的面积等于________.21、已知函数y=（m﹣1）的图象是双曲线，则m=________ ．22、若点A（﹣2，3）、B（m，﹣6）都在反比例函数y= （k≠0）的图象上，则m的值是________．23、已知一个函数的图象与y= 的图象关于y轴成轴对称，则该函数的解析式为________．24、如图，已知：点A是双曲线y= 在第一象限的分支上的一个动点，连结AO并延长交另一分支于点B，以AB为边作等边△ABC，点C在第四象限．随着点A的运动，点C的位置也不断变化，但点C始终在双曲线y= （x＞0）上运动，则k的值是________．25、如果函数y= 的图象在每个象限内，当自变量x的值逐渐增大时，y 的值随着逐渐增大，那么m的取值范围是________．三、解答题(共5题，共计25分)26、已知, 与成正比例, 与成反比例，且当时,; 时, .试求当时, 的值.27、当m取何值时，下列函数是反比例函数？（1）y=；（2）y=（3﹣m）；（3）y=．28、已知反比例函数y=的图象经过点P（1，6）．（1）求k的值；（2）若点M（﹣2，m），N（﹣1，n）都在该反比例函数的图象上，试比较m，n的大小．29、反比例函数y=（m-2）x2m+1的函数值为3时，求自变量x的值.30、已知点M(2，a)在反比例函数y＝（k≠0）的图象上，点M关于原点中心对称的点N在一次函数y＝﹣2x+8的图象上，求此反比例函数的解析式．参考答案一、单选题(共15题，共计45分)1、C2、C3、D4、C5、B6、A7、C8、D9、B10、B11、B12、A13、C14、D二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)27、28、29、。

人教版数学九年级下册第二十六章《反比例函数》测试卷(含答案)

人教版数学九年级下册第二十六章《反比例函数》测试卷[时间：100分钟满分：120分]一、选择题(每小题3分，共30分)1. 下列函数中，y是x的反比例函数的是()A. y=－12xB. y=－29xC. y=86xD. y=1－6x2．反比例函数y＝5nx的图象经过点(2，3)，则n的值是()A. －2B. －1C. 0D. 13. 反比例函数y＝kx的图象经过点P(－1，2)，则这个函数的图象位于()A. 第二、三象限B. 第一、三象限C. 第三、四象限D. 第二、四象限4．已知反比例函数y＝3x，下列结论中不正确的是()A. 图象经过点(－1，－3)B. 图象在第一、三象限C. 当x＞1时，0＜y＜3D. 当x＜0时，y随着x的增大而增大5. 已知反比例函数y=－10x的图象上有两点P1(x1，y1)，P2(x2，y2)，若x1<0<x2，则下列结论正确的是()A. y1<y2<0B. y1<0<y2C. y1>y2>0D. y1>0>y26．如图所示，直线y＝x＋2与双曲线y＝kx相交于点A，点A的纵坐标为3，则k的值为()A. 1B. 2C. 3D. 4第6题第7题7．已知二次函数y＝－(x－a)2－b的图象如图所示，则反比例函数y＝abx与一次函数y＝ax＋b的图象可能是()A B C D8. 在一个可以改变体积的密闭容器内装有一定质量的二氧化碳，当改变容器的体积时，气体的密度也会随之改变，密度ρ(单位：kg/m 3)是体积V (单位：m 3)的反比例函数，它的图象如图所示，当V =10 m 3时，气体的密度是( )A. 1 kg/m 3B. 2 kg/m 3C. 100 kg/m 3D. 5 kg/m 3第8题第9题9．如图，A ，B 两点在反比例函数y ＝1k x 的图象上，C ，D 两点在反比例函数y ＝2kx的图象上，AC ⊥x 轴于点E ，BD ⊥x 轴于点F ，AC ＝2，BD ＝3，EF ＝103，则k 2－k 1的值为( )A. 4B.143 C. 163D. 6 10. 某医药研究所开发一种新药，成年人按规定的剂量限用，服药后每毫升血液中的含药量y (毫克)与时间t (小时)之间的函数关系近似满足如图所示曲线，当每毫升血液中的含药量不少于0.25毫克时治疗有效，则服药一次治疗疾病有效的时间为( )A. 16小时B. 1578小时C. 151516小时 D. 17小时二、填空题(每小题3分，共24分)11．请写出一个图象在第二、四象限的反比例函数的解析式：．12. 若反比例函数y=(m－1)x|m|－2，则m的值是.13．若函数y＝2mx的图象在每个象限内y的值随x值的增大而增大，则m的取值范围为．14. 如图，Rt△ABC的两个锐角顶点A，B在函数y=kx(x>0)的图象上，AC∥x轴，AC=2.若点A的坐标为(2，2)，则点B的坐标为.15．已知反比例函数y＝4x，当函数值y≥－2时，自变量x的取值范围是________．16．若变量y与x成反比例，且当x＝3时，y＝－3，则y与x之间的函数关系式是________，在每个象限内函数值y随x的增大而________．17．某闭合电路，电源的电压为定值，电流I(A)与电阻R(Ω)成反比例．如图表示的是该电路中电流I与电阻R之间的函数关系的图象，当电阻R为6 Ω时，电流I为________A.第17题第18题18. 如图，四边形OABC是矩形，ADEF是正方形，点A，D在x轴的正半轴上，点C在y轴的正半轴上，点F在AB上，点B，E在反比例函数y＝kx的图象上，OA＝1，OC＝6，则正方形ADEF的边长为________．三、解答题(共66分)19. (8分)已知y与x－1成反比例，且当x＝－5时，y＝2.(1)求y与x的函数关系式；(2)当x＝5时，求y的值．20. (8分)你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识：一定体积的面团做成拉面，面条的总长度y(m)是面条的粗细(横截面积)S(mm2)的反比例函数，其图象如图所示.(1)写出y与S的函数关系式；(2)当面条粗为1.6 mm2时，求面条总长度.21. (12分)已知反比例函数y＝4 x .(1)若该反比例函数的图象与直线y＝kx＋4(k≠0)只有一个公共点，求k的值；(2)如图，反比例函数y＝4x(1≤x≤4)的图象记为曲线C1，将C1向左平移2个单位长度，得曲线C2，请在图中画出C2，并直接写出C1平移到C2处所扫过的面积．22. (12分)如图，一次函数y=kx＋b的图象分别与反比例函数y=ax的图象在第一象限交于点A(4，3)，与y轴的负半轴交于点B，且OA=OB.(1)求函数y=kx＋b和y=ax的表达式；(2)已知点C(0，5)，试在该一次函数图象上确定一点M，使得MB=MC，求此时点M的坐标.23. (12分)如图，在平面直角坐标系xOy中，直线y＝x－2与y轴相交于点A，与反比例函数y＝kx在第一象限内的图象相交于点B(m，2)．(1)求该反比例函数的关系式；(2)若直线y＝x－2向上平移后与反比例函数y＝kx在第一象限内的图象相交于点C，且△ABC的面积为18，求平移后的直线对应的函数关系式．24. (14分)为了预防流行性感冒，某学校对教室采用药熏消毒法进行消毒.已知药物燃烧时室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例；药物燃烧后，y与x成反比例(如图所示).请根据图中提供的信息，解答下列问题：(1)药物燃烧后y与x的函数关系式为；(2)当空气中每立方米的含药量低于1.6毫克时学生方可进教室，那么从消毒开始，至少需要经过几分钟后，学生才能回到教室；(3)当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时，才能有效杀灭空气中的病菌，那么此次消毒是否有效?为什么?。

人教版九年级数学下册数学反比例函数综合检测题(含答案)

人教版九年级数学下册数学反比例函数综合检测题(含答案)一﹨选择题（每小题3分，共30分） 1﹨反比例函数y ＝xn 5图象经过点（2，3），则n 的值是（）． A ﹨－2 B ﹨－1 C ﹨0 D ﹨1 2﹨若反比例函数y ＝xk（k ≠0）的图象经过点（－1，2），则这个函数的图象一定经过点（）．A ﹨（2，－1）B ﹨（－21，2） C ﹨（－2，－1） D ﹨（21，2） 3﹨(08双柏县)已知甲﹨乙两地相距s （km ），汽车从甲地匀速行驶到乙地，则汽车行驶的时间t （h ）与行驶速度v （km/h ）的函数关系图象大致是（）4﹨若y 与x 成正比例，x 与z 成反比例，则y 与z 之间的关系是（）．A ﹨成正比例B ﹨成反比例C ﹨不成正比例也不成反比例D ﹨无法确定 5﹨一次函数y ＝kx －k ，y 随x 的增大而减小，那么反比例函数y ＝xk满足（）． A ﹨当x ＞0时，y ＞0 B ﹨在每个象限内，y 随x 的增大而减小 C ﹨图象分布在第一﹨三象限 D ﹨图象分布在第二﹨四象限6﹨如图，点P 是x 轴正半轴上一个动点，过点P 作x 轴的垂线PQ 交双曲线y ＝x1于点Q ，连结OQ ，点P 沿x 轴正方向运动时，Rt △QOP 的面积（）． A ﹨逐渐增大 B ﹨逐渐减小 C ﹨保持不变 D ﹨无法确定7﹨在一个可以改变容积的密闭容器内，装有一定质量m 的某种气体，当改变容积V 时，气体的密度ρ也随之改变．ρ与V 在一定范围内满足ρ＝Vm，它的图象如图所示，则该气体的质量m为（）．A ﹨1.4kgB ﹨5kgC ﹨6.4kgD ﹨7kg8﹨若A （－3，y 1），B （－2，y 2），C （－1，y 3）三点都在函数y ＝－x1的图象上，则y 1，y 2，y 3的大小关系是（）．A ﹨y 1＞y 2＞y 3B ﹨y 1＜y 2＜y 3C ﹨y 1＝y 2＝y 3D ﹨y 1＜y 3＜y 2Q pxyot /h Ot /h O t /hO t /h v /(km/h) O A ． B ． C ．．9﹨已知反比例函数y ＝xm21-的图象上有A （x 1，y 1）﹨B （x 2，y 2）两点，当x 1＜x 2＜0时，y 1＜y 2，则m 的取值范围是（）． A ﹨m ＜0 B ﹨m ＞0 C ﹨m ＜21 D ﹨m ＞21 10﹨如图，一次函数与反比例函数的图象相交于A ﹨B 两点，则图中使反比例函数的值小于一次函数的值的x 的取值范围是（）． A ﹨x ＜－1 B ﹨x ＞2C ﹨－1＜x ＜0或x ＞2D ﹨x ＜－1或0＜x ＜2 二﹨填空题（每小题3分，共30分）11.某种灯的使用寿命为1000小时，它的可使用天数y 与平均每天使用的小时数x 之间的函数关系式为 . 12﹨已知反比例函数xky =的图象分布在第二﹨四象限，则在一次函数b kx y +=中，y 随x 的增大而（填“增大”或“减小”或“不变”）．13﹨若反比例函数y ＝xb 3-和一次函数y ＝3x ＋b 的图象有两个交点，且有一个交点的纵坐标为6，则b ＝．14﹨反比例函数y ＝（m ＋2）x m2－10的图象分布在第二﹨四象限内，则m 的值为．15﹨有一面积为S 的梯形，其上底是下底长的31，若下底长为x ，高为y ，则y 与x 的函数关系是． 16﹨如图，点M 是反比例函数y ＝xa（a ≠0）的图象上一点，过M 点作x 轴﹨y 轴的平行线，若S 阴影＝5，则此反比例函数解析式为． 17﹨使函数y ＝（2m 2－7m －9）x m2－9m ＋19是反比例函数，且图象在每个象限内y 随x 的增大而减小，则可列方程（不等式组）为．18﹨过双曲线y ＝xk（k ≠0）上任意一点引x 轴和y 轴的垂线，所得长方形的面积为______． 19. 如图，直线y ＝kx(k ＞0)与双曲线xy 4=交于A （x 1，y 1）， B （x 2，y 2）两点，则2x 1y 2－7x 2y 1＝___________．20﹨如图，长方形AOCB 的两边OC ﹨OA 分别位于x 轴﹨y 轴上，点B 的坐标为 B （－320，5），D 是AB 边上的一点，将△ADO 沿直线OD 翻折，使A 点恰好落在对角线OB 上的点E 处，若点E 在一反比例函数的图象上，那么该函数的解析式是．三﹨解答题（共60分）21﹨（8分）如图，P 是反比例函数图象上的一点，且点P 到x 轴的距离为3，到y 轴的距离为2，求这个反比例函数的解析式．22﹨（9分）请你举出一个生活中能用反比例函数关系描述的实例，写出其函数表达式，并画出函数图象．举例：函数表达式：23﹨（10分）如图，已知A （x 1，y 1），B （x 2，y 2）是双曲线y ＝xk在第一象限内的分支上的两点，连结OA ﹨OB ．（1）试说明y 1＜OA ＜y 1＋1y k ；（2）过B 作BC ⊥x 轴于C ，当m ＝4时，求△BOC 的面积．24﹨（10分）如图，已知反比例函数y ＝－x8与一次函数y ＝kx ＋b 的图象交于A ﹨B 两点，且点A 的横坐标和点B 的纵坐标都是－2．求：（1）一次函数的解析式；（2）△AOB 的面积．25﹨（11分）如图，一次函数y ＝ax ＋b 的图象与反比例函数y ＝xk的图象交于M ﹨N 两点．（1）求反比例函数与一次函数的解析式；（2）根据图象写出使反比例函数的值大于一次函数的值的x 的取值范围．26﹨（12分）如图，已知反比例函数y ＝xk的图象与一次函数y ＝a x ＋b 的图象交于 M （2，m ）和N （－1，－4）两点．（1）求这两个函数的解析式；（2）求△MON 的面积；（3）请判断点P （4，1）是否在这个反比例函数的图象上，并说明理由．参考答案:一﹨选择题1﹨D ； 2﹨A ； 3﹨C ； 4﹨B ； 5﹨D ； 6﹨C 7﹨D ； 8﹨B ； 9﹨D ； 10﹨D ．二﹨填空题11﹨y ＝x 1000； 12﹨减小； 13﹨5 ； 14﹨－3 ；15﹨y ＝xs23 ； 16﹨y ＝－x 5； 17﹨⎩⎨⎧---=+-0972119922＞m m m m ； 18﹨|k|； 19﹨ 20； 20﹨y ＝－x 12．三﹨解答题 21﹨y ＝－x6． 22﹨举例：要编织一块面积为2米2的矩形地毯，地毯的长x （米）与宽y （米）间函数关系式为y ＝x2（x ＞0）． x (2)1 1 232 …y…4234 1…（只要是生活中符合反比例函数关系的实例均可）画函数图象如右图所示．23﹨（1）过点A 作AD ⊥x 轴于D ，则OD ＝x 1，AD ＝y 1，因为点A （x 1，y 1）在双曲线y ＝xk上，故x 1＝1y k ，又在Rt △OAD 中，AD ＜OA ＜AD ＋OD ，所以y 1＜OA ＜y 1＋1y k ；（2）△BOC 的面积为2．24﹨（1）由已知易得A （－2，4），B （4，－2），代入y ＝kx ＋b 中，求得y ＝－x ＋2；（2）当y ＝0时，x ＝2，则y ＝－x ＋2与x 轴的交点M （2，0），即|OM|＝2，于是S △AOB ＝S △AOM ＋S △BOM ＝21|OM|·|y A |＋21|OM|·|y B |＝21×2×4＋21×2×2＝6．25﹨（1）将N （－1，－4）代入y ＝xk ，得k ＝4．∴反比例函数的解析式为y ＝x 4．将M（2，m ）代入y ＝x 4，得m ＝2．将M （2，2），N （－1，－4）代入y ＝ax ＋b ，得⎩⎨⎧-=+-=+.b a ,b a 422解得⎩⎨⎧-==.b ,a 22∴一次函数的解析式为y ＝2x －2．（2）由图象可知，当x ＜－1或0＜x ＜2时，反比例函数的值大于一次函数的值． 26﹨解（1）由已知，得－4＝1-k ，k ＝4，∴y ＝x 4．又∵图象过M （2，m ）点，∴m ＝24＝2，∵y ＝a x ＋b 图象经过M ﹨N 两点，∴,422⎩⎨⎧-=+-=+b a b a 解之得,22⎩⎨⎧-==b a ∴y ＝2x －2．（2）如图，对于y ＝2x －2，y ＝0时，x ＝1，∴A （1，0），OA ＝1，∴S △MON ＝S △MOA ＋S △NOA ＝21OA ·MC ＋21OA ·ND ＝21×1×2＋21×1×4＝3．（3）将点P （4，1）的坐标代入y ＝x4，知两边相等，∴P 点在反比例函数图象上．。

人教版九年级数学下册《反比例函数》单元测试及答案

.
7、如图，面积为 3 的矩形 OABC的一个顶点 B 在反比例函数 y k x
的图象上，另三点在坐标轴上，则 k =
。
k 8、反比例函数 y 与一次函数 y kx m 的图象有一个交点是
x
（ -2 ， 1），则它们的另一个交点的坐标是
。
9．收音机刻度盘的波长 λ 和频率 f 分别用米（ m ）的千赫兹（ kHz ）为单位标刻的。波
-6-
16. 某商场出售一批进价为 2 元的贺卡，在市场营销中发现此商品的日销售单价
销售量 y 个之间有如下关系：（ 10
）
x( 元 )
3
y（个） 20
4
5
6
15
12
10
x 元与日
（ 1）根据表中数据，在直角坐标系中描出实数对（ x,y ）的对应点；（ 2）猜测并确定 y 与 x 之间的函数关系式，并画出图象；（ 3）设经营此贺卡的销售利润为 W元，试求出 W与 x 之间的函数关系式，若物价局规定此贺卡的销售价最高不能超过 10 元，请你求出当日销售单价 x 定为多少元时，才能使获利润最大？
药物燃烧后， y 关于 x 的函数关系式为
（２）研究表明，当空气中每立方米的含药量低于
1.6
毫克时学生方可进教室，那么从消毒开始，至少需要经过
分钟后，学生才能回到教室：
（３）研究表明，当空气中每立方米的含药量不低于３
毫克且持续时间不低于１０分钟，才能有效杀灭空气中的病
毒，那么此次消毒有效吗？为什么？
六．解：（ 1）设轮船上的货物总量为 k 吨，则根据已知条件有
240 k 30 8 240 ∴ v 与 t 的函数式为 v
t
（ 2）把 t

人教版数学九年级下26.1《反比例函数》基础测试题(含答案及解析)

人教版数学九年级下26.1《反比例函数》基础测试题（含答案及解析）反比例函数基础测试题时间：60分钟总分：100题号一二三总分得分一、选择题（本大题共10小题，共30.0分）1.下列函数中，是反比例函数的是()A. y=kxB. 3x+2y=0C. xy−√2=0 D. y=2x+12.下列式子中，y是x的反比例函数的是()A. y=1x2B. y=x2 C.y=xx+1 D.xy=13.反比例函数y=−32x中常数k为()A. −3B. 2C. −12D. −324.下列函数关系式中属于反比例函数的是()A. y=3xB. y=−2xC. y=x2+3D. x+y=55.下列关系式中：①y=2x；②yx=5；③y=−7x ；④y=5x+1；⑤y=x2−1；⑥y=1x2；⑦xy=11，y是x的反比例函数的共有()A. 4个B. 3个C. 2个D. 1个C. 矩形的长为a，宽为20，其面积S与a的关系D. 矩形的面积为40，长a与宽b之间的关系6.下列四个关系式中，y是x的反比例函数的是()A. y=4xB. y=13xC. y=1x2D. y=1x+1二、填空题（本大题共10小题，共30.0分）7.若y=(m−3)x m2−2m−4是反比例函数，则m=______ ．8.反比例函数y=(2m−1)x m2−2，在每个象限内，y随x的增大而增大，则m的值是______ ．9.函数y=(m+1)x m2−2m−4是y关于x的反比例函数，则m=______．10.若反比例函数y=(2k−1)x3k2−2k−1经过第一、三象限，则k=______11.已知函数y=(k−3)x 8−k2为反比例函数，则k=______ ．12.如果函数y=kx2k2+k−2是反比例函数，那么k=______ ．13.反比例函数y=(m+2)x m2−10的图象分布在第二、四象限内，则m的值为______ ．14.若函数y=(m−1)x m2−2是反比例函数，则m的值等于______ ．15.若函数y=(3+m)x8−m2是反比例函数，则m=______ ．16.若函数y=(m+1)x m2+3m+1是y关于x的反比例函数，则m的值为______ ．三、解答题（本大题共5小题，共40.0分）17.函数y=(m−1)x m2−m−1是反比例函数．(1)求m的值；(2)指出该函数图象所在的象限，在每个象限内，y随x的增大如何变化？,2)是否在这个函数的图象上．(3)判断点(1218.已知y是x的反比例函数，且当x=2时，y=−3，请你确定该反比例函数的解析式，并求当y=6时，自变量x的值．19.若函数y=(m+1)x m2+3m+1是反比例函数，求m的值．20.已知函数y=(m2+2m−3)x|m|−2．(1)若它是正比例函数，则m=______ ；(2)若它是反比例函数，则m=______ ．21.当k为何值时，y=(k−1)x k2−2是反比例函数？答案和解析【答案】1. C2. D3. D4. B5. C6. D7. C8. A9. D10. B11. −112. −113. 314. 2 315. −316. −1或1 217. −318. −119. 320. −221. 解：(1)由题意：{m2−m−1=−1m−1≠0，解得m=0．(2)∵反比例函数的解析式为y=−1x，∴函数图象在二四象限，在每个象限内，y随x 的增大而增大．(3)当x=12时，y=−2≠2，∴点(12,2)不在这个函数的图象上．22. 解：设反比例函数y=kx(k≠0)，∵当x=2时，y=−3，∴k=xy=2×(−3)=−6，∴y与x之间的函数关系式y=−6x．把y=6代入y=−6x，则x=−1．23. 解：由函数y=(m+3)x m2+3m+1为反比例函数可知m2+3m+1=−1，且m+1≠0解得m=−1(舍去)，m=−2，m的值是−2．24. 3；−125. 解：y=(k−1)x k2−2是反比例函数，得{k2−2=−1k−1≠0，解得k=−1，当k=−1时，y=(k−1)x k2−2是反比例函数．【解析】1. 解：A、不是反比例函数，故此选项错误；B、不是反比例函数，故此选项错误；C、是反比例函数，故此选项正确；D、不是反比例函数，故此选项错误；故选：C．根据反比例函数的概念形如y=kx(k为常数，k≠0)的函数称为反比例函数进行分析即可．此题主要考查了反比例函数的概念，判断一个函数是否是反比例函数，首先看看两个变量是否具有反比例关系，然后根据反比例函数的意义去判断，其形式为y=kx(k为常数，k≠0)或y=kx−1(k为常数，k≠0)．2. 【分析】本题考查了反比例函数，利用反比例函数的定义是解题关键.根据反比例函数的意义，可得答案．【解答】解：y=1x，y=x−1，yx=1是反比例函数．故选D．3. 解：反比例函数y=−32x中常数k为−32，故选D．找出反比例函数解析式中k的值即可．此题考查了反比例函数的定义，熟练掌握反比例函数解析式的一般形式是解本题的关键．4. 解：A、该函数是正比例函数，故本选项错误；B、该函数符合反比例函数的定义，故本选项正确；C、该函数是二次函数，故本选项错误；D、该函数是一次函数，故本选项错误；故选：B．根据反比例函数的定义进行判断．本题考查了反比例函数的定义，反比例函数的(k≠0)．一般形式是y=kx5. 解：①y=2x是正比例函数；=5可化为y=5x，不是反比例函数；②yx③y=−7符合反比例函数的定义，是反比例x函数；④y=5x+1是一次函数；⑤y=x2−1是二次函数；⑥y=1不是反比例函数；x2⑦xy=11可化为y=11，符合反比例函数的x定义，是反比例函数．故选C．分别根据反比例函数、二次函数及一次函数的定义对各小题进行逐一分析即可．本题考查的是反比例函数的定义，熟知形如y=kx(k为常数，k≠0)的函数称为反比例函数是解答此题的关键．6. 解：根据题意得2m+1=−1，解得m=−1．故选D．根据反比例函数的定义.即y=kx(k≠0)，只需令2m+1=−1即可．本题考查了反比例函数的定义，重点是将一般式y=kx(k≠0)转化为y=kx−1(k≠0)的形式．7. 解：(1)由题意可得：m=346.2n，是反比例函数关系；(2)由题意可得：I=UR，是反比例函数关系；(3)设腰长为x，底边长为y，由题意可得：x= C−y2，不是反比例函数关系；(4)设底边长为x，底边上的高为h，根据题意可得：x=5h，是反比例函数关系．故选：C．根据题意分别得出两变量的关系式，进而利用反比例函数的定义得出答案．此题主要考查了反比例函数的定义，正确得出各函数关系是解题关键．8. 解：根据题意，得2πrL=4，则L=42πr =2πr．所以这个圆柱的母线长L和底面半径r之间的函数关系是反比例函数．故选A．根据题意，由等量关系“矩形的面积=底面周长×母线长”列出函数表达式再判断它们的关系则可．本题考查了反比例函数的定义和圆柱侧面积的求法，涉及的知识面比较广．9. 解：A、根据题意，得S=a2，所以正方形的面积S与边长a的关系是二次函数关系；故本选项错误；B、根据题意，得l=4a，所以正方形的周长l与边长a的关系是正比例函数关系；故本选项错误；C、根据题意，得S=20a，所以正方形的面积S与边长a的关系是正比例函数关系；故本选项错误；D、根据题意，得b=40a，所以正方形的面积S与边长a的关系是反比例函数关系；故本选项正确．故选D．根据每一个选项的题意，列出方程，然后由反比例函数的定义进行一一验证即可．本题考查了反比例函数的定义.反比例函数的一般形式是y=kx(k≠0)．10. 解：y=13x=13x是反比例函数，故选：B．根据反比例函数的定义，可得答案．本题考查了反比例函数的定义，利用反比例函数的定义是解题关键．11. 解：由函数y=(m−3)x m2−2m−4是反比例函数，可知m2−2m−4=−1，m−3≠0，解得：m=−1．故答案为：−1．根据反比例函数的定义可知m2−2m−4=−1，m−3≠0，继而求出m的值．本题考查了反比例函数的定义，属于基础题，(k≠0)转化为y=重点是将一般式y=kxkx−1(k≠0)的形式．m2−2=−1，12. 解：根据题意得：{2m−1<0解得：m=−1．故答案为−1．根据反比例函数的定义列出方程求解，再根据它的性质决定解的取舍．本题考查了反比例函数的性质.对于反比例函，当k>0时，在每一个象限内，函数数y=kx值y随自变量x的增大而减小；当k<0时，在每一个象限内，函数值y随自变量x的增大而增大．13. 解：∵函数y=(m+1)x m2−2m−4是y关于x的反比例函数，∴m2−2m−4=−1且m+1≠0，解得m=3．故答案是：3．根据反比例函数的一般形式得到m2−2m−4=−1且m+1≠0，由此来求m的值即可．本题考查了反比例函数的定义，反比例函数的(k≠0)．一般形式是y=kx14. 解：∵是反比例函数，∴3k2−2k−1=−1，，解得k=0，或k=23∵反比例函数y=(2k−1)x3k2−2k−1经过第一、三象限，∴2k−1>0，解答k>0.5，∴k=2．3．故答案为：23让反比例函数中x的指数为−1，系数大于0列式求值即可．考查反比例函数的定义及反比例函数图象的性质；用到的知识点为：反比例函数的一般形式为y=kx−1(k≠0)；反比例函数中的比例系数大于0，图象的两个分支在一、三象限．15. 解：∵函数y=(k−3)x 8−k2为反比例函数，∴8−k2=−1且k−3≠0．解得k=−3．故答案是：−3．根据反比例函数的定义得到8−k2=−1且k−3≠0．本题考查了反比例函数的定义，反比例函数的一般形式是y =k x (k ≠0)．16. 解：根据题意得{2k 2+k −2=−1k ≠0，解得k =−1或12．一般地，如果两个变量x 、y 之间的关系可以表示成y =k x 或写成y =kx −1(k 为常数，k ≠0)的形式，那么称y 是x 的反比例函数． (1)将反比例函数解析式的一般式y =k x (k ≠0)，转化为y =kx −1(k ≠0)的形式，根据反比例函数的定义条件可以求出k 的值； (2)特别注意不要忽略k ≠0这个条件． 17. 解：根据题意得，m 2−10=−1且m +2<0，解得m 1=3，m 2=−3且m <−2，所以m =−3．故答案为：−3．根据反比例函数的定义可得m 2−10=−1，根据函数图象分布在第二、四象限内，可得m +2<0，然后求解即可．本题考查了反比例函数的定义，反比例函数的性质，对于反比例函数y =k x (k ≠0)，(1)k >0，反比例函数图象在一、三象限；(2)k<0，反比例函数图象在第二、四象限内．18. 解：∵y=(m−1)x m2−2是反比例函数，∴m2−2=−1，m−1≠0，∴m=−1．故答案为−1．根据反比例函数的定义先求出m的值，再根据系数不为0进行取舍．本题考查了反比例函数的定义，重点是将一般式y=kx(k≠0)转化为y=kx−1(k≠0)的形式．19. 解：根据题意得：{8−m2=−1 3+m≠0，解得：m=3．故答案是：3．根据反比例函数的一般形式：x的次数是−1，且系数不等于0，即可求解．本题考查了反比例函数的定义，重点是将一般式y=kx(k≠0)转化为y=kx−1(k≠0)的形式．20. 解：∵函数y=(m+1)x m2+3m+1是y关于x 的反比例函数，∴{m+1≠0m2+3m+1=−1，解得m=−2．故答案为：−2．根据反比例函数的定义列出关于m的不等式组，求出m的值即可．本题考查的是反比例函数的定义，熟知形如y=kx(k为常数，k≠0)的函数称为反比例函数是解答此题的关键．21. (1)根据反比例函数的定义可得{m2−m−1=−1m−1≠0，解得m=0．(2)利用反比例函数的性质即可解决问题；(3)利用待定系数法即可解决问题；本题考查反比例函数图象上的点的特征，反比例函数的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．22. 由题意y是x的反比例函数，可设y=kx(k≠0)，然后利用待定系数法进行求解；把y=6代入函数解析式求得相应的x的值即可．此题主要考查利用待定系数法求函数的解析式，是一道基础题，比较简单．23. 根据反比例函数的定义先求出m的值．本题考查了反比例函数的定义，重点是将一般式y=kx(k≠0)转化为y=kx−1(k≠0)的形式．24. 解：(1)y=(m2+2m−3)x|m|−2是正比例函数，m2+2m−3≠0，|m|−2=1m=3，(2)y=(m2+2m−3)x|m|−2是反比例函数，m2+2m−3≠0，|m|−2=−1，m=−1，故答案为：3，−1．(1)根据y=kx(k是常数，k≠0)是正比例函数，可得m的值；(2)根据y=k(k是常数，k≠0)是反比例函x数，可得m的值．本题考查了反比例函数，注意k不能为0．25. 根据反比例函数的定义，可得答案．本题考查了反比例函数的定义，重点是将一般(k≠0)转化为y=kx−1(k≠0)的形式y=kx式．。

人教版九年级数学下册《第二十六章反比例函数》测试卷-含参考答案

人教版九年级数学下册《第二十六章反比例函数》测试卷-含参考答案一、选择题1．下列关系式中，y 是x 反比例函数的是（） A ．y= 13 xB ．y=- 3xC ．y=3x 2D ．y=6x+12．函数 y =(m +1)x m 2+m−1是反比例函数，则m 的值为（）A ．0B ．﹣1C ．0或﹣1D ．0或13．若点A(x 1，−5)，B(x 2，2)，C(x 3，5)都在反比例函数y =m 2+1x的图象上，则x 1，x 2，x 3的大小关系是（） A ．x 1<x 2<x 3B ．x 2<x 3<x 1C ．x 1<x 3<x 2D ．x 3<x 1<x 24．函数y =x −a 与y =ax (a ≠0)在同一坐标系内的图象可以是（）A ．B ．C ．D ．5．反比例函数y =2−3k x的图象经过点(−2，5)，则k 的值为（）A ．10B ．-10C ．4D ．-43⎛⎫2⎛⎫2⎛⎫7．验光师测得一组关于近视眼镜的度数y （度）与镜片焦距x （米）的对应数据如下表.根据表中数据，可得y 关于x 的函数表达式为（）A．y=100x B．y=x100C．y=400xD．y=x4008．如图，菱形OABC的顶点C的坐标为(3，4)，顶点A在x轴的正半轴上.反比例函数y=kx(x>0)的图象经过顶点B，则k的值为（）A．12 B．16 C．20 D．32二、填空题9．反比例函数y=m−5x，其图象分别位于第一、第三象限，则m的取值范围是．10．已知点P位于第三象限内，且点P到两坐标轴的距离分别为3和4，若反比例函数图象经过点P，则该反比例函数的解析式为．11．在平面直角坐标系xOy中，直线y=−2x与双曲线y=mx交于A，B两点，若点A，B的纵坐标分别为y1，y2，则−3y1−3y2的值为.12．如图，一次函数y1=k1x+b与反比例函数y2=k2x的图象相交于A，B两点，点A的横坐标为2，点B的横坐标为−1，则不等式k1x+b<k2x的解集是.13．如图所示，点A是反比例函数y＝kx（x＜0）的图象上一点，过点A作AB⊥y轴于点P，点P在x轴上，若△ABP的面积是2，则k＝．三、解答题14．已知道y=y 1+y 2，y 1与x 2成正比例，y 2与x+3成反比例．并且x=0时，y=2，x=1时，y=0．试求函数y 的解析式，并指出自变量的取值范围．15．如图，双曲线y 1＝kx （k 为常数，且k ≠0）与直线y 2＝﹣13x+b 交于点A （﹣2，a ）和B （3c ，2﹣c ）.（1）求k ，b 的值；（2）求直线与x 轴的交点坐标.17．某单位为响应政府发出的全民健身的号召,打算在长和宽分别为20m 和11m 的矩形大厅内修建一个60m2的矩形健身房ABCD. 该健身房的四面墙壁中有两侧沿用大厅的旧墙壁(如图为平面示意图),已知装修旧墙壁的费用为20元/m 2,新建(含装修)墙壁的费用为80元/m 2.设健身房的高为3m,一面旧墙壁AB 的长为xm,修建健身房墙壁的总投入为y 元. (1)求y 与x 的函数关系式;(2)为了合理利用大厅,要求自变量x 必须满足条件:8≤x ≤12, 当投入的资金为4800元时,问利用旧墙壁的总长度为多少?18．如图，已知一次函数y =ax +b(a,b 为常数，a ≠0)的图象与x 轴，y 轴分别交于点A ，B ，且与反比例函数y =kx (k 为常数，k ≠0)的图象在第二象限内交于点C ，作CD ⊥x 轴于D ，若OA =OD =34OB =3．(1)求一次函数与反比例函数的解析式；(2)观察图象直接写出不等式0<ax +b ≤kx的解集；(3)在y 轴上是否存在点P ，使得△PBC 是以BC 为一腰的等腰三角形？如果存在，请直接写出P 点的坐标；如果不存在，请简要说明理由．11m20mDCB A参考答案 1．B 2．A 3．C 4．D 5．C 6．A 7．A 8．D 9．m ＞5 10．y =12x11．012．-1＜x ＜0或x ＞2 13．-414．解：∵y 1与x 2成正比例，y 2与x+3成反比例．∴y 1=k 1x 2，y 2= k2x+3∵y=y 1+y 2 ∴y=k 1x 2+k 2x+3∵x=0时，y=2，x=1时，y=0． ∴{k 23=2k 1+k 24=0解得k 1=﹣ 32 ，k 2=6∴y=﹣ 32 x 2+ 6x+3 （x ≠﹣3）15．（1）解：∵点B （3c ，2﹣c ）在直线y 2＝﹣13x+b 的图象上 ∴−13×3c +b =2−c 解得：b =2∴直线解析式为y 2＝﹣13x+2∵点A （﹣2，a ）在直线y 2＝﹣13x+2的图象上∴a =−13×(−2)+2=83 ∴点A 坐标为（-2，83） ∵点A （-2，83）在y 1＝k x 图象上 ∴83=k −2解得：k =−163.（2）解：∵直线解析式为y 2＝﹣13x+2 ∴当y 2=0时，x=6∴直线与x 轴的交点坐标为（6，0）. 16．（1）∵点A 、B 是反比例函数ky x=的图象上一点，AC x ⊥轴，BC y ⊥轴()3,4C - ∴3,3k A ⎛⎫ ⎪⎝⎭(),44kB --∵AB 经过原点∴A 、B 两点关于原点对称 ∴34k =∴12k =∴()3,4A ()3,4B -- ∴8AC = 6BC = ∴Rt ACB △的面积11862422AC BC =⋅=⨯⨯=；（2）∵()3,4A∴将()3,4A 代入y k x '=得43k '= 解得43k '=∴经过AB 两点的直线43y x =；由图象可得当30x -<<或3x >时k k x x'>． 17．解:(1)根据题意,AB=x,AB ·BC=60,所以BC=60x。

人教版九年级下1反比例函数含答案

人教版九年级下反比例函数含答案一、选择题1．已知y是x的反比例函数，且当x＝2时，y＝3，则该函数的解析式是( )A．y＝6x B．y＝16xC．y＝6xD．y＝x16—2．若y＝(a＋1)xa2－2是关于x的反比例函数，则a的值为( )A．1 B．－1C．±1 D．任意实数3．若一个矩形的面积为10，则这个矩形的长与宽之间的函数关系是( ) A．正比例函数关系B．反比例函数关系C．一次函数关系D．不能确定4．下列函数是反比例函数的是( )A．y＝3x B．y＝6x－2C．y＝－8xD．y＝8x25．设每名工人一天能做x个某种型号的工艺品，若某工艺品厂每天生产这种工艺品60个，则需要工人y名，则y关于x的函数解析式为( )A ．y ＝60xB ．y ＝160xC ．y ＝60xD ．y ＝60＋x6．已知y 与x 2成反比例，且当x ＝－2时，y ＝2，那么当x ＝4时，y 的值为( )链接听课例2归纳总结 A ．－2 B ．2 C.12 D ．－4二、填空题7．在y ＝－35x，y ＝12x －1，y ＝1x＋1，y ＝a ＋1x(a ≠－1)四个函数中，是反比例函数的有____________________________.8．小华看一部300页的小说所需的天数y 与平均每天看的页数x 成________比例，解析式为________．9．若函数y ＝m －1x ||m 是反比例函数，则m ＝________．10．将x 1＝23代入反比例函数y ＝－1x 中，所得的函数值记为y 1，将x 2＝y 1＋1代入反比例函数y ＝－1x中，所得的函数值记为y 2，再将x 3＝y 2＋1代入函数y ＝－1x中，所得的函数值记为y 3，…，如此继续下去，则在2019个函数值y 1，y2，…，y2019中，值为2的情况共出现了________次．三、解答题11．如图K－1－1，请指出哪些图中的y与x成反比例关系.图K－1－112．已知反比例函数y＝－3 2x .(1)写出这个函数的比例系数；(2)求当x＝－10时，函数y的值；(3)求当y＝6时，自变量x的值．13.已知变量y与变量x之间的部分对应值如下表：试求出变量y与x之间的函数解析式．14．某工人打算用不锈钢条加工一个面积为0.8平方米的矩形模具．假设模具的长与宽分别为x米和y米．(1)你能写出y与x之间的函数解析式吗？(2)变量y与x是什么函数关系？(3)已知这种不锈钢条每米6元，若想使模具的长比宽多1.6米，则加工这个模具共需花多少钱？15．已知关于x的函数y＝(5m－3)x2－n＋(m＋n)．(1)当m，n为何值时，此函数为一次函数？(2)当m，n为何值时，此函数为正比例函数？(3)当m，n为何值时，此函数为反比例函数？16．转化思想如果y是z的反比例函数，z是x的反比例函数，那么y是x的反比例函数吗？请说明理由．17．转化思想已知y＝y1＋y2，y1与x2成正比例，y2与x成反比例，且当x＝1时，y＝3；当x＝－1时，y＝1.求当x＝－12时，y的值．详解详析1．[解析] C 设y ＝k x ，把x ＝2，y ＝3代入y ＝kx ，得k ＝6，所以该函数的解析式是y ＝6x.故选C.2．A3．[解析] B 题目中的等量关系为：长×宽＝矩形面积，所以长×宽＝10，即长＝10宽，所以长与宽是反比例函数关系．故选B.4．C5．[解析] C ∵每名工人一天能做x 个这种型号的工艺品，某工艺品厂每天生产这种工艺品60个，需要工人y 名，∴xy ＝60，∴y ＝60x.故选C.6．[解析] C ∵y 与x 2成反比例，∴设y ＝kx2.∵当x ＝－2时，y ＝2，∴2＝k（－2）2，解得k ＝8.将x ＝4代入y ＝8x 2，得y ＝842＝12.故选C.7．y ＝－35x，y ＝12x －1，y ＝a ＋1x(a ≠－1) 8．[答案] 反 y ＝300x[解析] ∵总页数300是一定的，∴所需的天数y 与平均每天看的页数x 成反比例，解析式为y ＝300x.9．[答案] －1[解析] ∵y ＝m －1x ||m是反比例函数，∴|m|＝1，且m －1≠0，解得m ＝－1.10．[答案] 673[解析] y 1＝－123＝－32，把x 2＝－32＋1＝－12代入反比例函数y ＝－1x中，得y 2＝－1－12＝2；把x 3＝2＋1＝3代入反比例函数y ＝－1x 中，得y 3＝－13；把x 4＝－13＋1＝23代入反比例函数y ＝－1x 中，得y 4＝－32；…；如此继续下去，每3个数一循环．∵2019÷3＝673，∴值为2的情况共出现了673次．11．解：图中的函数解析式分别是： ①y ＝vx(v 表示速度)，y 是x 的正比例函数；②y ＝sx(s 表示路程)，y 是x 的反比例函数；③y ＝ml x(m 为物体的质量，l 为物体到支点的距离)，y 是x 的反比例函数；④y ＝kx(k 为底面直径一定时单位高度水的质量)，y 是x 的正比例函数；⑤y ＝Vx(V 表示水的体积)，y 是x 的反比例函数；⑥y ＝4Vπx 2(V 表示水的体积)，y 是x 2的反比例函数，不是x 的反比例函数．∴图②、图③、图⑤中的y 与x 成反比例关系． 12．解：(1)－32.(2)当x ＝－10时，y ＝－32×（－10）＝320.(3)当y ＝6时，x ＝－32×6＝－14. 13．解：观察表格可知，每一对x ，y 的对应值的积都是常数6，因而xy ＝6，即y ＝6x.故变量y 与x 之间的函数解析式为y ＝6x.14．解：(1)由题意，得xy ＝0.8，则y ＝0.8x (x ＞0)．(2)变量y 与x 是反比例函数关系．(3)已知模具的长为x 米，则宽为(x －1.6)米．根据题意，得x(x －1.6)＝0.8，解得x 1＝2，x 2＝－0.4(不合题意，舍去)，则模具的长为2米，宽为0.4米，故矩形模具的周长为2×(2＋0.4)＝4.8(米)，故加工这个模具共需花费4.8×6＝28.8(元)．15．解：(1)当关于x 的函数y ＝(5m －3)x 2－n ＋(m ＋n)为一次函数时，且5m －3≠0，2－n ＝1，解得m ≠35，n ＝1. (2)当关于x 的函数y ＝(5m －3)x 2－n ＋(m ＋n)为正比例函数时，⎩⎪⎨⎪⎧2－n ＝1，m ＋n ＝0，5m －3≠0，解得m ＝－1，n ＝1.(3)当关于x 的函数y ＝(5m －3)x 2－n ＋(m ＋n)为反比例函数时，⎩⎪⎨⎪⎧2－n ＝－1，m ＋n ＝0，5m －3≠0，解得m ＝－3，n ＝3.[素养提升]16．解：y 不是x 的反比例函数．理由如下：∵y 是z 的反比例函数，z 是x 的反比例函数，∴设y ＝m z ，z ＝n x，(其中m ，n 是常数，且mn ≠0) ∴y ＝m n x，即y ＝m nx ， ∴y 是x 的正比例函数，不是x 的反比例函数．17．解：因为y 1与x 2成正比例，y 2与x 成反比例，故设y 1＝k 1x 2(k 1≠0)，y 2＝k 2x (k 2≠0)，则y ＝k 1x 2＋k 2x. 把x ＝1，y ＝3；x ＝－1，y ＝1分别代入上式，得⎩⎪⎨⎪⎧3＝k 1＋k 2，1＝k 1－k 2，解得⎩⎪⎨⎪⎧k 1＝2，k 2＝1，故y ＝2x 2＋1x. 当x ＝－12时， y ＝2×⎝ ⎛⎭⎪⎪⎫－122＋1－12＝12－2＝－32.。