运筹学—网络模型
运筹学(第6章 图与网络分析)

(v2)钱
a2 a3 a4 a14 a15
a8 a9
a7 (v4) 李
(v3)孙
a5 (v5) 周 a6 a10 (v6)吴
图6-3
a12 a11 a13
(v7)陈
定义: 图中的点用v表示,边用e表示。对每条边可用它
所连接的点表示,记作:e1=[v1,v1]; e2=[v1,v2];
树是图论中结构最简单但又十分重要的图。在自然和社会领 域应用极为广泛。 例6.2 乒乓求单打比赛抽签后,可用图来表示相遇情况,如 下图所示。
运动员 A
B C
D
E
F G
H
例6.3 某企业的组织机构图也可用树图表示。
厂长
人事科
财务科
总工 程师
生产副 厂长
经营副 厂长
开发科
技术科
生产科
设备科
供应科
动力科
e2
(v1) 赵
e1
e3
e4 孙(v3) 李(v4)
周(v5)
图6-2
e5 吴(v6) 陈(v7)
(v2)钱
如果我们把上面例子中的“相互认识”关系改为“认识” 的关系,那么只用两点之间的联线就很难刻画他们之间的关 系了,这是我们引入一个带箭头的联线,称为弧。图6-3就是 一个反映这七人“认识”关系的图。相互认识用两条反向的 弧表示。
端点,关联边,相邻 若有边e可表示为e=[vi,vj],称vi和
e2 v2 e6 e1 e4 v1 e3 v3 e8
vj是边e的端点,反之称边e为点vi
或vj的关联边。若点vi、vj与同一条 边关联,称点vi和vj相邻;若边ei和
e5
e7
《运筹学》复习资料整理总结

《运筹学》复习资料整理总结1. 建立线性规划模型的步骤。
确定决策变量 确定目标函数 确定约束条件方程2. 线性规划问题的特征。
都有一个追求的目标,这个目标可表示为一组变量的线性函数,按照问题的不同,追求的目标可以为最大,也可以为最小。
问题中有若干个约束条件,用来表示问题中的限制或要求,这些约束条件可以用线性等式或线性不等式表示。
问题中用一组决策变量来表示一种方案。
3. 线性规划问题标准型的特征。
4. 化标准型的方法。
123123123123min z 2+223-8340,0,x x x x x x x x x x x x =+-+=⎧⎪-+-≤⎨⎪≤≥⎩为自由变量123123123123min z 2+223-634,0,x x x x x x x x x x x x =+-+=⎧⎪-+-≥⎨⎪≥⎩为自由变量5. 基本解:令其余的变量取值为0,则得到Ax=b 的一个解y,称此解为线性规划问题的基本解。
6. 基本可行解:若基本解y 满足y ≥0,则称这个解为基本可行解。
7. 可行解:满足约束条件的解x=(x1、x2、……xn )T 称为线性规划问题的可行解。
8. 最优解:函数达到最优的可行解叫做最优解。
9.图解法适合于变量个数为2个的线性规划问题。
10.单纯形法解线性规划问题如何确定初始基本可行解。
(1)约束条件为≤,先加入松弛变量x1、x2……xm后变为等式,取松弛变量为基本变量(2)约束条件为=,先加入人工变量xm+1、xm+2……xm+n,人工变量价值系数为m(3)约束条件为≥,先加入多于变量xn+1、xn+2……xm+n后变为等式,在添加人工变量xn+m+111.单纯形法最优解的检验准则。
(1)若基本可行解x’对应的典式的目标函数中非基变量的系数全部满足cN-cBB-1Pj≤0,则基本可行解x’为原问题的最优解。
(2)若基本可行解x’对应的典式的目标函数中所有非基变量的系数满足cN-cBB-1Pj≤0,且有一非基变量的系数满足Ck-Zk=0,则原问题有无穷多组最优解12.对目标函数为极小(min)型的线性规划问题,用单纯形法解的三种处理方法。
运筹学第六章网络计划

工序(i,j)的总时差=(j)最迟开始时间-t(i,j) -(i)最早开始时间
工序(i,j)的自由时差=(j)最早开始时间- (i)最早完成时间
所有时间参数
例3(P136)某项课题研究工作分解的作业表如下。根据此表绘制此项科研工作的网络图,计算时间参数,并确定关键路线。
工序代号
工序
紧前工序
工序时间
(3)按照工作的新工时,重新计算网络计划的关键 路线及关键工序。
(4)再比较关键工序的直接费用率与间接费用率。
不断重复,直到使总费用上升为止。 (直接费用率>间接费用率)
注:若压缩引起出现多于一条新的关键路线时,需同时压缩各关键路线.
(因为不同时压,则工期不能缩短, 工期=关键工序上工时之和)
表示相邻工序时间分界点,称为事 项,
用 表示
(3)相邻弧:
表示工序的前后衔接关系,称为紧前 (或紧后)关系。
如
A
B
A是B的紧前工序,B是A的紧后工序。
A
(4)虚工序(虚箭线)
为表示工序前后衔接关系的需要而增加的。
6.1 网络计划图的绘制 6.2 时间参数计算与关键路线确定 6.3 网络图的调整及优化
CLICK HERE TO ADD A TITLE
1.问题的一般提法:
设有一项工程,可分为若干道工序,已知各工序间 的先后关系以及各工序所需时间t。
问:
(1)工程完工期T?
(2)工程的关键工序有哪些?
若再各压缩1天
则应压缩B、C(同时压)
此时的直接费用率将是3+4=7>5
故最低成本工期为10天。
注:
(1)有时资料未给可压缩时间,但给了正常工作时间及最短工作时间。则压缩时间=正常工作时间-最短工作时间。
运筹学6(图与网络分析)

定义7:子图、生成子图(支撑子图)
图G1={V1、E1}和图G2={V2,E2}如果 V1 V2和E1 E2 称G1是G2的一个子图。
若有 V1=V2,E1 E2 则称 G1是G2的一 个支撑子图(部分图)。
图8-2(a)是图 6-1的一个子图,图8-2 (b)是图 8-1的支撑子图,注意支撑子图 也是子图,子图不一定是支撑子图。 e1
v2 ▲如果链中所有的顶点v0,v1,…,vk也不相
e1 e2 e4 v1 e3
v3 e5
同,这样的链称初等链(或路)。
e6
▲如果链中各边e1,e2…,ek互不相同称为简单链。
e7
e8
▲当v0与vk重合时称为回路(或圈),如果边不 v4
v5
重复称为简单回路,如果边不重复点也不重复
则称为初等回路。
图8-1中, μ1={v5,e8,v3,e3,v1,e2,v2,e4,v3,e7,v5}是一条链,μ1中因顶 点v3重复出现,不能称作路。
e1
e2 e4 v1 e3
v2
v3
e5
e6
e7
e8
v4
v5
定理1 任何图中,顶点次数的总和等于边数的2倍。
v1
v3
v2
定理2 任何图中,次为奇数的顶点必为偶数个。
e1
e2 e4 v1 e3
v2
v3
e5
e6
e7
e8
v4
v5
定义4 有向图: 如果图的每条边都有一个方向则称为有向图
定义5 混合图: 如何图G中部分边有方向则称为混合图 ② ⑤ ④
定理4 有向连通图G是欧拉图,当且仅当G中每个顶点的出 次等于入次。
② 15
9 10
第七讲 运筹学建模

2
7.1 运输问题模型
1.运输问题模型概述
运输问题是一类特殊的线性规划模型,该模型的建立最 初用于解决一个部门的运输网络所要求的最经济的运输路线
和产品的调配问题,并取得了成功.然而,在实际问题的应
用中,除运输问题外,许多非运输问题的实际问题一样可以 建立其相应的运输问题模型,并由此而求出其最优解.下面
们将列举一些模型范例,以说明这个事实.
27
0—1型整数规划的数学模型为:
m a x (m in ) z c 1 x 1 c 2 x 2
a 1 1 x1 a 1 2 x 2 a x a 22 x 2 21 1 s.t. a x a x m2 2 m1 1 x1 , x 2 ,
x ij 1 0
ij
( i , j 1, 2 ,..., n )
,
指派第 i 人完成第 不指派第
j 项任务 j 项任务
i 人完成第
数学模型为:
min Z
n
c ij x ij
x ij 1 i 1 n s .t . x ij 1 j 1 x 0或 1 ij
25
4.整数规划的求解方法 (1)分枝定界法-可求纯或混合整数线性规划。 (2)割平面法-可求纯或混合整数线性规划 (3)隐枚举法-求解“0-1”整数规划:①过滤隐枚举法 ;②分枝隐枚举法。 (4)匈牙利法-解决指派问题(“0-1”规划特殊情形) (5)蒙特卡洛法-求解各种类型规划。 这里不一一介绍,感兴趣的同学再去查找相关资料。
8
m
n
(7.1.1)
m
当然,在实际问题的应用中,常出现产销不平衡的情 形,此时,需要把产销不平衡问题转化为产销平衡问题来进
运筹学第六章图与网络分析

S
2
4
7
2 A
0 5
S
5 45 B
98
14
5
13
D
T
C
E
4
4
4
7
最短路线:S AB E D T
最短距离:Lmin=13
2.求任意两点间最短距离的矩阵算法
⑴ 构造任意两点间直接到达的最短距离矩阵D(0)= dij(0)
S A B D(0)= C D E T
SABCDET 0 25 4 2 02 7 5 20 1 5 3 4 1 0 4 75 0 15 3 41 0 7 5 7 0
e1 v1
e5
v0 e2
e3
v2
e4
e6 e7
v3
v4
(4)简单图:无环、无多重边的图称为简单图。
(5)链:点和边的交替序列,其中点可重复,但边不能 重复。
(6)路:点和边的交替序列,但点和边均不能重复。
(7)圈:始点和终点重合的链。
(8)回路:始点和终点重合的路。
(9)连通图:若一个图中,任意两点之间至少存在一条 链,称这样的图为连通图。 (10)子图,部分图:设图G1={V1,E1}, G2={V2,E2}, 如果有V1V2,E1E2,则称G1是G2的一个子图;若 V1=V2,E1E2,则称G1是G2的一个部分图。 (11)次:某点的关联边的个数称为该点的次,以d(vi)表示。
步骤:
1. 两两连接所有的奇点,使之均成为偶点;
2. 检查重复走的路线长度,是否不超过其所在 回路总长的一半,若超过,则调整连线,改 走另一半。
v1
4
v4
4
1
4
v2
v5
5
运筹学第6章 图与网络

也就是说| V1 |必为偶数。
定理6.2有学者也称作定理6.1的推论。根据定理6.2,握手定理也可以 表述为,在任何集体聚会中,握过奇次手的人数一定是偶数个。
12 该课件的所有权属于熊义杰
另外,现实中不存在面数为奇数且每个面的边数也是奇数的多面 体,如表面为正三角形的多面体有4个面,表面为正五边形的多面体有 12个面等等,也可以用这一定理予以证明。因为在任意的一个多面体 中, 当且仅当两个面有公共边时,相应的两顶点间才会有一条边,即 任意多面体中的一个边总关联着两个面。所以,以多面体的面数为顶
v j V2
(m为G中的边数)
因式中 2m 是偶数, d (v j ) 是偶数,所以 d (vi ) 也必为偶数
v j V2
vi V1
( 两个同奇同偶数的和差必为偶数 ), 同时,由于 d (vi ) 中的每个加数 d (vi )
均为奇数,因而 d (vi ) 为偶数就表明, d (vi ) 必然是偶数个加数的和 ,
图论、算法图论、极值图论、网络图论、代数图论、随机图论、 模糊图论、超图论等等。由于现代科技尤其是大型计算机的迅 猛发展,使图论的用武之地大大拓展,无论是数学、物理、化 学、天文、地理、生物等基础科学,还是信息、交通、战争、 经济乃至社会科学的众多问题.都可以应用图论方法子以解决。
1976年,世界上发生了不少大事,其中一件是美国数学家 Appel和Haken在Koch的协作之下,用计算机证明了图论难题— —四色猜想(4CC):任何地图,用四种颜色,可以把每国领土染 上一种颜色,并使相邻国家异色。4CC的提法和内容十分简朴, 以至于可以随便向一个人(哪怕他目不识丁)在几分钟之内讲清 楚。1852年英国的一个大学生格思里(Guthrie)向他的老师德·摩 根(De Morgan)请教这个问题,德·摩根是当时十分有名的数学家, 他不能判断这个猜想是否成立,于是这个问题很快有数学界流 传开来。1879年伦敦数学会会员Kemple声称,证明了4CC成立, 且发表了论文。10年后,Heawood指出了Kemple的证明中
运筹学第3版熊伟编著习题答案

运筹学(第3版)习题答案第1章线性规划 P36第2章线性规划的对偶理论 P74 第3章整数规划 P88 第4章目标规划 P105第5章运输与指派问题P142 第6章网络模型 P173 第7章网络计划 P195 第8章动态规划 P218 第9章排队论 P248 第10章存储论P277 第11章决策论P304第12章 多属性决策品P343 第13章博弈论P371 全书420页第1章 线性规划1.1工厂每月生产A 、B 、C 三种产品 ,单件产品的原材料消耗量、设备台时的消耗量、资源限量及单件产品利润如表1-23所示.表1-23产品 资源 A B C 资源限量 材料(kg) 1.5 1.2 4 2500 设备(台时) 3 1.6 1.2 1400 利润(元/件)101412根据市场需求,预测三种产品最低月需求量分别是150、260和120,最高月需求是250、310和130.试建立该问题的数学模型,使每月利润最大.【解】设x 1、x 2、x 3分别为产品A 、B 、C 的产量,则数学模型为123123123123123max 1014121.5 1.2425003 1.6 1.21400150250260310120130,,0Z x x x x x x x x x x x x x x x =++++≤⎧⎪++≤⎪⎪≤≤⎪⎨≤≤⎪⎪≤≤⎪≥⎪⎩ 1.2建筑公司需要用5m 长的塑钢材料制作A 、B 两种型号的窗架.两种窗架所需材料规格及数量如表1-24所示:表1-24 窗架所需材料规格及数量型号A 型号B 每套窗架需要材料长度(m ) 数量(根)长度(m) 数量(根)A 1:2 2B 1:2.5 2 A 2:1.53 B 2:23需要量(套)300400问怎样下料使得(1)用料最少;(2)余料最少. 【解】 第一步:求下料方案,见下表。
方案 一 二 三 四 五 六 七 八 九 十 需要量 B1 2.5 2 1 1 1 0 0 0 0 0 0 800 B2 2 0 1 0 0 2 1 1 0 0 0 1200 A1 2 0 0 1 0 0 1 0 2 1 0 600 A21.5120 2 3 900 余料(m) 0 0.5 0.5 1 1 1 010.5第二步:建立线性规划数学模型设x j (j =1,2,…,10)为第j 种方案使用原材料的根数,则 (1)用料最少数学模型为10112342567368947910min 28002120026002239000,1,2,,10jj j Z x x x x x x x x x x x x x x x x x x j ==⎧+++≥⎪+++≥⎪⎪+++≥⎨⎪+++≥⎪⎪≥=⎩∑ (2)余料最少数学模型为2345681012342567368947910min 0.50.50.52800212002*********0,1,2,,10j Z x x x x x x x x x x x x x x x x x x x x x x x x j =++++++⎧+++≥⎪+++≥⎪⎪+++≥⎨⎪+++≥⎪⎪≥=⎩1.3某企业需要制定1~6月份产品A 的生产与销售计划。
第7章:网络计划《运筹学》

min
i jk
LS j,k
t
i,
j
TLi
式中k是工序(i,j)的紧后工序的箭头节点。
⑷工序最迟必须完工时间(LF)
工序最迟必须完工时间是指为保证工程按期完工的最迟必须 完成的时间。工序最迟必须完成时间就等于该工序的箭头事件 的最迟必须发生时间,用公式表示即为:
LFi, j LS i, j t i, j
t(θ,i)的时间。
⑵工序最早完工时间(EF) 工序最早完工时间等于该工序的最早开始时间与工序所需时 间之和,用公式表示为:
EFi, j ESi, j t i, j
⑶工序最迟必须开始时间(LS)
工序最迟必须开始时间是指为保证不影响紧后工序按期开工, 本工序最迟必须开始的时间。用公式表示为:
LSi, j
1
2 12 3
4
(市场调研)
如增加人力分为三组同时进行,可画为许多图:
3
4
1
24
5
6
注意:
4 4
虚工序问题
——仅用于表明平行工序间的逻辑关系;
——虚工序越少越好。
两件或两件以上的工作交叉进行,称为交叉工作。如工作A 与工作B 分别为挖沟和埋管子,那么它们的关系可以是挖一段埋
一段,不必等沟全部挖好再埋。可用下图表示。
f
a
m
bt
t a 4m b 6
2 b a 2
6
2. 总网络图与多级网络图
⑴总网络图。总网络图画的比较概括、综合,反映任务的主 要组成部分之间的组织联系。
⑵分级网络图。分级网络图可细分为一级网络图、二级网络 图等,分别供不同的管理层次使用。
第二节 网络图的时间参数计算
计算网络图有关的时间参数,主要目的是找出关键线路(由于 网络图中每道工序上表示的都是工时数,所以关键线路是指网络 图中需时最长的线路—总起点事项到总终点事项),为网络计划 的优化、调整和执行提供明确的时间概念。
运筹学教材习题答案详解

B1:2.0
3
需要量(套)
200
150
问怎样下料使得(1)用料最少;(2)余料最少.
【解】第一步:求下料方案,见下表。
方案
一
二
三
四
五
六
七
八
九
十
十一
十二
十三
十四
需要量
B1:2.7m
2
1
1
1
0
0
0
0
0
0
0
0
0
0
300
B2:2m
0
1
0
0
3
2
2
1
1
1
0
0
0
0
450
A1:1.7m
0
0
1
0
0
1
0
2
1
0
3
2
1
0
(2)
【解】最优解X=(3/4,7/2);最优值Z=-45/4
(3)
【解】最优解X=(4,1);最优值Z=-10
(4)
【解】最优解X=(3/2,1/4);最优值Z=7/4
(5) 【解】最优解X=(3,0);最优值Z=3
(6)
【解】无界解。
(7)
【解】无可行解。
(8)
【解】最优解X=(2,4);最优值Z=13
【解】设x1、x2、x3分别为产品A、B、C的产量,则数学模型为
1.3建筑公司需要用6m长的塑钢材料制作A、B两种型号的窗架.两种窗架所需材料规格及数量如表1-23所示:
表1-23窗架所需材料规格及数量
型号A
型号B
每套窗架需要材料
长度(m)
运筹学-第7章-图与网络优化

20/139
连通图、子图、支撑子图、基础图
• 连通图 图G中,若任何两个点之间,至少有一条链,称为连通图。否 则称为不连通图。
• 奇点 次为奇数的点, 如 v5
18/139
链,圈,初等链,初等圈,简单链(圈)
• 链: 由两两相邻的点及其相关联的边构成的点边 序列, 如:
(v0 ,e1 ,v1 ,e2 ,v2 ,e3 ,v3 ,…,vn-1 ,en , vn ); 其中v0 ,vn分别为链的起点和终点, v1 ,v2 ,…,vn-1称 为中间点 ; • 圈: 起点与终点重合的链; • 简单链(圈):链(圈)中所含的边均不相同; • 初等链(圈):链(圈)中所含的点均不相同,也 称通路;
v2
a8
v5
a10
a4 a6
a9
a7
a5
v4
v7 a11 v6
•路 • 初等路 • 回路
(v1, a2 , v3 , a4 , v4 , a7 , v6 )是从v1到v6的路。也是一条初等路。 在上图中,(v3 , a3 , v2 , a5 , v4 , a6 , v5 , a8 , v3 )是一个回路。
vV1
vV2
vV
2m为偶数,且偶点的次之和 d(v)也为偶数,所以 d(v) 必为偶
数,即奇数点的个数必为偶数vV。2
vV1
27/139
第二节 树
本节主要内容: • 树的概念 • 构造生成树的方法 • 最小生成树问题
第六章物流运筹学——图与网络分析.

( vi ,v j )
l
ij
最小的 。
Dijkstra算法
算法的基本步骤: (1)给 v s 以 P 标号, P(vs ) 0 ,其余各点均给 T 标号, T (vi ) 。 (2)若 vi 点为刚得到 P 标号的点,考虑这样的点 v j: (vi , v j ) E ,且 v j 为 T 标号,对 v j 的 T 标号进行如下的更改:
v2
(4,3)
v4
(3,3)
(5,3) (1,1) (1,1) (3,0)
vs
(5,1)
vt
(2,1)
v1
(2,2)
v3
图 6-14
运输线路图
第四节 最小费用最大流问题
在容量网络 G (V , E, C ) ,每一条边 (vi , v j ) E 上,除了已 给容量 cij 外,还给了一个单位流量的费用 bij 0 ,记此时的容 量网络为 G (V , E, C , B) 。 所谓最小费用最大流问题就是要求一个最大流 f ,使流的 总运输费用 b( f )
定理 6-1 任何图中顶点次数的总和等于边数的 2 倍。 推论 6-1 任何图中,次为奇数的顶点必有偶数个。 图 G (V , E ) 和图 H (V , E ) ,若 V V且E E ,则 称 H 是 G 的子图,记作: H G ;特别的,当 V V 时, 称 H 为 G 的生成子图。
容量网络g若?为网络中从sv到tv的一条链给?定向为从sv到tv?上的边凡与?同向称为前向边凡与?反向称为后向边其集合分别用??和??表示??ijff?是一个可行流如果满足??????0ijijijijiijjffcvv??????????c???0ijijijfvv????则称?为从sv到tv的关于f的可增广链
运筹学—网络模型

连通的赋权图称为网络图,记为 G={V,E,W}
6.1 最小(支撑)树问题
Minimal (Spanning)Tree Problem
6.1 最小树问题 Minimal tree problem
6.1.1树的概念
一个无圈并且连通的无向图称为树图或简称树(Tree)。组织机 构、家谱、学科分支、因特网络、通讯网络及高压线路网络等 都能表达成一个树图 。
14
13
15
6
14
12
0
表6-3计算示例:
L
( i
3 j
)
等于表6-2中第i行与第j列对应元素相加取最小值。例如,
2
87
【解】 (1)依据图6-14,写出 任意两点间一步到达距离 4
④ 9⑤
16
表L1。见表6.1所示。本例
12
n=8,lg 7 2.807 ,因此计 算到L3lg 2
⑥
2
3 10
6
⑦ 12 ⑧
图6-14
6.2 最短路问题 Shortest Path Problem
表6-1 最短距离表 L1
v1
m in Z
cij xij
( i , j ) E
x12 x13 x14 1
(
i
,
j
)
E
xij
( k ,i )E
xki
0
i 2,3,
,6
x57 xij
x67 0或
1 1,(i,
j)
E
6.2 最短路问题 Shortest Path Problem
数学建模运筹学模型(一)汇总

数学建模运筹学模型(⼀)汇总运筹学模型(⼀)本章重点:线性规划基础模型、⽬标规划模型、运输模型及其应⽤、图论模型、最⼩树问题、最短路问题复习要求:1. 进⼀步理解基本建模过程,掌握类⽐法、图⽰法以及问题分析、合理假设的内涵.2. 进⼀步理解数学模型的作⽤与特点.本章复习重点是线性规划基础模型、运输问题模型和⽬标规划模型. 具体说来,要求⼤家会建⽴简单的线性规划模型,把实际问题转化为线性规划模型的⽅法要掌握,当然⽐较简单. 运输问题模型主要要求善于将⾮线性规划模型转化为运输规化模型,这种转化后求解相当简单. 你⾄少把⼀个很实际的问题转化为⽤表格形式写出的模型,⾄于求解是另外⼀回事,⼀般不要求. ⽬标模型⼀般是⽐较简单的线性规模模型在提出新的要求之后转化为⽬标规划模型. 另外,关于图论模型的问题涉及到最短路问题,具体说来⽤双标号法来求解⼀个最短路模型. 这之前恐怕要善于将⼀个实际问题转化为图论模型. 还有⼀个最⼩数的问题,该如何把⼀个⽹络中的最⼩数找到. 另外在个别场合可能会涉及⼀笔划问题.1. 营养配餐问题的数学模型m i Z n =C 1x 1+C 2x + C n x na 11x 1+a 12x 2+ +a 1n x n ≥b 1, a 21x 1+a 22x 2+ +a 2n x n ≥b 2, s ta x +a x + +a x ≥b , m 22mn n m m 11x j ≥0(j =1, 2, , n或更简洁地表为m i Z n =∑C x jj =1n jn ∑a ij x j ≥b i j =1s tx ≥0(i =1, 2, , m j j =1, 2, , n其中的常数C j 表⽰第j 种⾷品的市场价格,a ij 表⽰第j 种⾷品含第i 种营养的数量,b i 表⽰⼈或动物对第i 种营养的最低需求量.2. 合理配料问题的数学模型有m 种资源B 1,B 2,…,B m ,可⽤于⽣产n 种代号为A 1,A 2,…,A n 的产品. 单位产品A j 需⽤资源B i 的数量为a ij ,获利为C j 单位,第i 种资源可供给总量为b i 个单位. 问如何安排⽣产,使总利润达到最⼤?设⽣产第j 种产品x j 个单位(j =1,2,…,n ),则有m a Z x =C 1x 1+C 2x 2+ +C n x na 11x 1+a 12x 2+ +a 1n x n ≤b 1, a 21x 1+a 22x 2+ +a 2n x n ≤b l , s ta x +a x + +a x ≤b , m 22mn n m m 11x j ≥0(j =1, 2, , n或更简单地写为m a z x =∑Cj =1n j x jn ∑a ij x j ≤b i j =1 s t i =1, 2, , m x ≥0 j =1, 2, , n j3. 运输问题模型运输问题也是⼀种线性规划问题,只是决策变量设置为双下标变量. 假如问题具有m 个产地和n 个销地,第i 个产地⽤A i 表⽰,其产量为a i (i =1,2,…,m ),第j 个销地⽤B j 表⽰,其销量为b j (j =1,2,…,n ),从A i 运往B j 的运价为c ij ,⽽写成为∑a i =1m i =∑b j =1n j 表⽰产销平衡. 那么产销平衡运输问题的⼀般模型可以min Z =∑∑c ij x iji =1j =1m nn ∑x ij =a i j =1m s t ∑x ij =b j i =1i =1, 2, , m x ij ≥0 j =1, 2, , n4. ⽬标规划模型某⼯⼚⽣产代号为Ⅰ、Ⅱ的两种产品,这两种产品都要经甲、⼄两个车间加⼯,并经检验与销售两部门处理. 已知甲、⼄两车间每⽉可⽤⽣产⼯时分别为120⼩时和150⼩时,每⼩时费⽤分别为80元和20元,其它数据如下表表4-1⼯⼚领导希望给出⼀个可⾏性⽣产⽅案,使⽣产销售及检验等⽅⾯都能达标.问题分析与模型假设经与⼯⼚总经理交谈,确定下列⼏条:p 1:检验和销售费每⽉不超过4600元;p 2:每⽉售出产品I 不少于50件;p 3:两车间的⽣产⼯时充分利⽤(重要性权系数按两车间每⼩时费⽤⽐确定);p 4:甲车间加班不超过20⼩时;p 5:每⽉售出产品Ⅱ不少于80件;p 6:两车间加班总时数要有控制(对权系数分配参照第三优先级).模型建⽴设x 1,x 2分别为产品Ⅰ和Ⅱ的⽉产量,先建⽴⼀般约束条件组,依题设50x 1+30x 2≤4600x 1≥50 售出量x 2≥80 2x 1+x 2≤120 两车间总⼯时x 1+3x 2≤150+ 设d 1表检验销售费偏差,则希望d 1达最⼩,有p 1d 1+, 相应的⽬标约束为 5x 1+30x 2+d 1--d 1+ = 4600; --达最⼩,有p 2d 2, 相应的⽬标约束 d 2表产品I 售量偏差,则希望d 2-+x 1+d 2-d 2=50,以d 3、d 4表两车间⽣产⼯时偏差,则由于充分利⽤,故希望d 320=4:1,有--p 3(4d 3+d 4 . 相应的⽬标约束应为 --达最⼩,考虑到费⽤⽐例为80:, d 4-+-+=150, -d 42x 1+x 2+d 3-d 3=120和x 1+3x 2+d 4以d 5表甲车间加班偏差,则有+-+d 3+d 5-d 5=20, p 4d 5+, 相应⽬标约束为以d 6表产品Ⅱ售量偏差,则希望d 6达最⼩,有相应约束为-+x 2+d 6-d 6=80.++++表⽰,考虑到权系数,有p6(4d 3+d 4, 其⽬标约束由于利⽤超⽣+d 4- 最后优先级p 6可利⽤d 3产⼯时,已在⼯时限制中体现,于是得到该问题的⽬标规划模型为---+-++m i z n =p 1d 1++p 2d 2+p 3(4d 3+d 4 +p 4d 5+p 5d 6+p 6(4d 3+d 4 ?50x 1+30x 2+d 1--d 1+?-+x 1+d 2-d 2??-+2x +x +d -d 1233??-+s ?t ??x 1+3x 2+d 4-d 4?+-+d +d -d 355??x 2+d 6--d 6+?-+??x 1, x 2≥0, d l , d l≥0=4600=50=120=150=20=80(l =1, 2, , 65. 最⼩树问题⼀个图中若有⼏个顶点及其边的交替序列形成闭回路,我们就说这个图有圈;若图中所有连顶点间都有边相接,就称该图是连通的;若两个顶点间有不⽌⼀条边连接,则称该图具有多重边. ⼀个图被称为是树意味着该图是连通的⽆圈的简单图. .在具有相同顶点的树中,总赋权数最⼩的树称为最⼩树.最⼩树的求法有两种,⼀种称为“避圈法”,⼀种是“破圈法”,两法各具优缺点,它们具有共同的特征——去掉图中的圈并且每次都是去掉圈中边权较⼤的边.6. 最短路问题的数学模型最短路问题⼀般描述如下:在⼀个图(或者说⽹络)中,给定⼀个始点v s 和⼀个终点v t ,求v s 到v t 的⼀条路,使路长最短(即路的各边权数之和最⼩).狄克斯屈(E.D.Dijkstra )双标号法该法亦称双标号法,适⽤于所有权数均为⾮负(即⼀切w ij ≥0 w ij 表⽰顶点v i 与v j 的边的权数)的⽹络,能够求出⽹络的任⼀点v s 到其它各点的最短路,为⽬前求这类⽹络最短路的最好算法.该法在施⾏中,对每⼀个点v j 都要赋予⼀个标号,并分为固定标号P (v j )和临时标号T (v j )两种,其含义如下:P (v j )——从始点v s 到v j 的最短路长;T (v j )——从始点v s 到v j 的最短路长上界.⼀个点v j 的标号只能是上述两种标号之⼀. 若为T 标号,则需视情况修改,⽽⼀旦成为P 标号,就固定不变了.开始先给始点v s 标上P 标号0,然后检查点v s ,对其⼀切关联边(v s ,vj )的终点v j ,给出v j 的T 标号w ij ;再在⽹络的已有T 标号中选取最⼩者,把它改为P 标号. 以后每次都检查刚得到P 标号那点,按⼀定规则修改其⼀切关联边终点的T 标号,再在⽹络的所有T 标号中选取最⼩者并把它改为P 标号. 这样,每次都把⼀个T 标号点改为P 标号点,因为⽹络中总共有n 个结点,故最多只需n -1次就能把终点v t 改为P 标号. 这意味着已求得了v s 到v t 的最短路.狄克斯屈标号法的计算步骤如下:1°令S ={v s }为固定标号点集,=V \{v s }为临时标号点集,再令P (v i =0,v t ∈S ; 2°检查点v i ,对其⼀切关联边(v i , vj )的终点v j∈,计算并令 min{T (v j , P (v i +w ij }?T (v j3°从⼀切v j∈中选取并令 min{T (v j }=T (v r ?T (v r 选取相应的弧(v i , vr ). 再令 S {v r }?S , \{v r }?=?,则停⽌,P (v j 即v s 到v j 的最短路长,特别P (v t 即v s 到v t 的最短路长,⽽已选出 4°若的弧即给出v s 到各点的最短路;否则令v r ?v i ,返2°. 注意:若只要求v s 到某⼀点v t 的最短路,⽽没要求v s 到其他各点的最短路,则上述步骤4°可改为 4°若r = t 则结束,P (v r 即为所求最短路长;否则令v r ?v i ,返2°.。
运筹学经典模型

X13 1.000000 0.000000 X21 13.000000 0.000000 X24 12.000000 0.000000 X33 21.000000 0.000000 ROW SLACK OR SURPLUS DUAL PRICES 3) 0.000000 2.000000 4) 0.000000 5.000000 5) 0.000000 -6.000000 6) 0.000000 -2.000000 7) 0.000000 -6.000000 8) 0.000000 -5.000000 NO. ITERATIONS= 6
事实上,我们关心更多的是那些非零变量,因此, 可选择LINDO中的命令,只列出非零变量.
OBJECTIVE FUNCTION VALUE 1) 161.0000 VARIABLE VALUE REDUCED COST X11 2.000000 0.000000 X12 17.000000 0.000000
8
! The supply constraints 2) x11 + x12 + x13 + x14 <= 30 3) x21 + x22 + x23 + x24 <= 25 4) x31 + x32 + x33 + x34 <= 21 ! The demand constraints 5) x11 + x21 + x31 = 15 6) x12 + x22 + x32 = 17 7) x13 + x23 + x33 = 22 8) x14 + x24 + x34 = 12 end
一、运输问题
返 回 导 航
运筹学-最大流- 案例
案例BMZ公司的最大流问题背景BMZ 公司是欧洲一家生产豪华汽车的制造商。
它因为提供优质的服务而获得很好的声誉,保持这个声誉一个很重要的秘诀就是它有着充裕的汽车配件供应,从而能够随时供货给公司众多的经销商合授权维修店。
这些供应件主要存放在公司的配送中心里,这样一有需求就可以立即送货。
卡尔(BMZ 公司的供应链的经理)优先考虑的是改进这些配送中心的不足之处。
该公司在美国有几个配送中心。
但是,离洛杉机中心最近的一个配送中心却坐落离洛杉机1000 多英里的西雅图。
保证洛杉机中心良好的供应是尤为重要的。
因此,现在那里的供应不断减少的现状成为了公司高层管理真正关心的问题。
大部分的汽车配件以及新车是在该公司坐落于德国的斯图加特的总厂和新车一起生产的。
也就是这家工厂向洛杉机中心供应汽车配件。
每月有超过300000 立方英尺的配件需要运到.现在,下个月需要多得多的数量以补充正在减少的库存。
问题卡尔需要尽快制定一个方案,使得下个月从总厂运送到洛杉机配送中心的供应件尽可能多。
他认识到了这是个最大流的问题——一个使得从总厂运送到洛杉机配送中心的配件流最大的问题。
因为总厂生产的配件量远远要大于能够运送到配送中心的量,所以,可以运送多少配件的限制条件就是公司配送网络的容量。
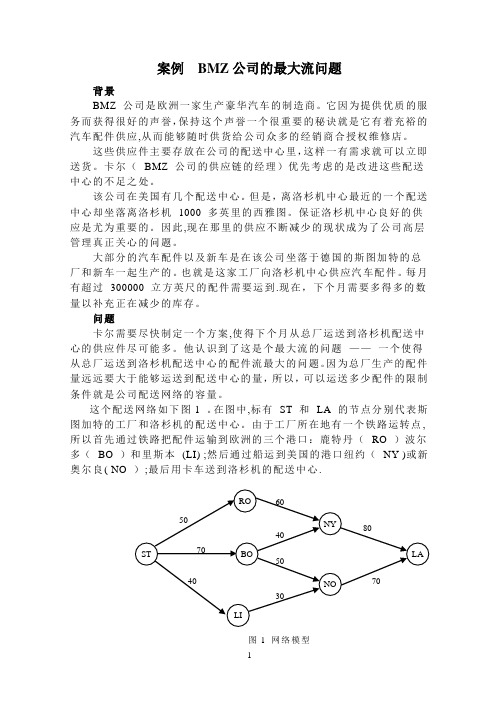
这个配送网络如下图1 。
在图中,标有ST 和LA 的节点分别代表斯图加特的工厂和洛杉机的配送中心。
由于工厂所在地有一个铁路运转点,所以首先通过铁路把配件运输到欧洲的三个港口:鹿特丹(RO )波尔多(BO )和里斯本(LI) ;然后通过船运到美国的港口纽约(NY )或新奥尔良( NO );最后用卡车送到洛杉机的配送中心.图1 网络模型经营这些铁路、船舶和卡车的组织是独立所有的公司,这些公司为很多的公司运输货物。
由于对这些老主顾原有的承诺,这些公司不可以在短时间内为任何一个客户大量增加运输空间配额。
因此,BMZ公司只能够保证获得下个月每条运输航线有限的运输空间.图1已经给出可以获得的空间数量,以100立方米为1个单位(由于每100立方米比3500立方英尺大一点,所以,需要运送的这批货物体积是很大的)。
数学建模 运筹学模型(一)汇总

运筹学模型(一)本章重点:线性规划基础模型、目标规划模型、运输模型及其应用、图论模型、最小树问题、最短路问题复习要求:1. 进一步理解基本建模过程,掌握类比法、图示法以及问题分析、合理假设的内涵.2. 进一步理解数学模型的作用与特点.本章复习重点是线性规划基础模型、运输问题模型和目标规划模型. 具体说来,要求大家会建立简单的线性规划模型,把实际问题转化为线性规划模型的方法要掌握,当然比较简单. 运输问题模型主要要求善于将非线性规划模型转化为运输规化模型,这种转化后求解相当简单. 你至少把一个很实际的问题转化为用表格形式写出的模型,至于求解是另外一回事,一般不要求. 目标模型一般是比较简单的线性规模模型在提出新的要求之后转化为目标规划模型. 另外,关于图论模型的问题涉及到最短路问题,具体说来用双标号法来求解一个最短路模型. 这之前恐怕要善于将一个实际问题转化为图论模型. 还有一个最小数的问题,该如何把一个网络中的最小数找到. 另外在个别场合可能会涉及一笔划问题.1. 营养配餐问题的数学模型m i Z n =C 1x 1+C 2x + C n x n⎧a 11x 1+a 12x 2+ +a 1n x n ≥b 1, ⎪⎪a 21x 1+a 22x 2+ +a 2n x n ≥b 2, ⎪ s ⋅t⋅⎨⎪a x +a x + +a x ≥b , m 22mn n m ⎪m 11⎪⎩x j ≥0(j =1, 2, , n或更简洁地表为m i Z n =∑C x jj =1n j⎧n ⎪∑a ij x j ≥b i ⎪j =1s ⋅t ⋅⎨⎪x ≥0(i =1, 2, , m j ⎪j =1, 2, , n ⎩其中的常数C j 表示第j 种食品的市场价格,a ij 表示第j 种食品含第i 种营养的数量,b i 表示人或动物对第i 种营养的最低需求量.2. 合理配料问题的数学模型有m 种资源B 1,B 2,…,B m ,可用于生产n 种代号为A 1,A 2,…,A n 的产品. 单位产品A j 需用资源B i 的数量为a ij ,获利为C j 单位,第i 种资源可供给总量为b i 个单位. 问如何安排生产,使总利润达到最大?设生产第j 种产品x j 个单位(j =1,2,…,n ),则有m a Z x =C 1x 1+C 2x 2+ +C n x n⎧a 11x 1+a 12x 2+ +a 1n x n ≤b 1, ⎪⎪a 21x 1+a 22x 2+ +a 2n x n ≤b l , ⎪ s ⋅t⋅⎨⎪a x +a x + +a x ≤b , m 22mn n m ⎪m 11⎪⎩x j ≥0(j =1, 2, , n或更简单地写为m a z x =∑Cj =1n j x j⎧n ⎪∑a ij x j ≤b i ⎪j =1 s ⋅t ⋅⎨i =1, 2, , m ⎛⎫⎪x ≥0 j =1, 2, , n ⎪⎪⎪j ⎝⎭⎩3. 运输问题模型运输问题也是一种线性规划问题,只是决策变量设置为双下标变量. 假如问题具有m 个产地和n 个销地,第i 个产地用A i 表示,其产量为a i (i =1,2,…,m ),第j 个销地用B j 表示,其销量为b j (j =1,2,…,n ),从A i 运往B j 的运价为c ij ,而写成为∑a i =1m i =∑b j =1n j 表示产销平衡. 那么产销平衡运输问题的一般模型可以min Z =∑∑c ij x iji =1j =1m n⎧n ⎪∑x ij =a i ⎪j =1⎪⎪m s ⋅t ⋅⎨∑x ij =b j ⎪i =1⎪⎛i =1, 2, , m ⎫⎪x ij ≥0 j =1, 2, , n ⎪⎪⎪⎝⎭⎩4. 目标规划模型某工厂生产代号为Ⅰ、Ⅱ的两种产品,这两种产品都要经甲、乙两个车间加工,并经检验与销售两部门处理. 已知甲、乙两车间每月可用生产工时分别为120小时和150小时,每小时费用分别为80元和20元,其它数据如下表表4-1工厂领导希望给出一个可行性生产方案,使生产销售及检验等方面都能达标.问题分析与模型假设经与工厂总经理交谈,确定下列几条:p 1:检验和销售费每月不超过4600元;p 2:每月售出产品I 不少于50件;p 3:两车间的生产工时充分利用(重要性权系数按两车间每小时费用比确定);p 4:甲车间加班不超过20小时;p 5:每月售出产品Ⅱ不少于80件;p 6:两车间加班总时数要有控制(对权系数分配参照第三优先级).模型建立设x 1,x 2分别为产品Ⅰ和Ⅱ的月产量,先建立一般约束条件组,依题设50x 1+30x 2≤4600x 1≥50 售出量x 2≥80 2x 1+x 2≤120 两车间总工时x 1+3x 2≤150+ 设d 1表检验销售费偏差,则希望d 1达最小,有p 1d 1+, 相应的目标约束为 5x 1+30x 2+d 1--d 1+ = 4600; --达最小,有p 2d 2, 相应的目标约束 d 2表产品I 售量偏差,则希望d 2-+x 1+d 2-d 2=50,以d 3、d 4表两车间生产工时偏差,则由于充分利用,故希望d 320=4:1,有--p 3(4d 3+d 4 . 相应的目标约束应为 --达最小,考虑到费用比例为80:, d 4-+-+=150, -d 42x 1+x 2+d 3-d 3=120和x 1+3x 2+d 4以d 5表甲车间加班偏差,则有+-+d 3+d 5-d 5=20, p 4d 5+, 相应目标约束为以d 6表产品Ⅱ售量偏差,则希望d 6达最小,有相应约束为-+x 2+d 6-d 6=80.++++表示,考虑到权系数,有p6(4d 3+d 4, 其目标约束由于利用超生+d 4- 最后优先级p 6可利用d 3产工时,已在工时限制中体现,于是得到该问题的目标规划模型为---+-++m i z n =p 1d 1++p 2d 2+p 3(4d 3+d 4 +p 4d 5+p 5d 6+p 6(4d 3+d 4 ⎧50x 1+30x 2+d 1--d 1+⎪-+x 1+d 2-d 2⎪⎪-+2x +x +d -d 1233⎪⎪-+s ⋅t ⋅⎨x 1+3x 2+d 4-d 4⎪+-+d +d -d 355⎪⎪x 2+d 6--d 6+⎪-+⎪⎩x 1, x 2≥0, d l , d l≥0=4600=50=120=150=20=80(l =1, 2, , 65. 最小树问题一个图中若有几个顶点及其边的交替序列形成闭回路,我们就说这个图有圈;若图中所有连顶点间都有边相接,就称该图是连通的;若两个顶点间有不止一条边连接,则称该图具有多重边. 一个图被称为是树意味着该图是连通的无圈的简单图. .在具有相同顶点的树中,总赋权数最小的树称为最小树.最小树的求法有两种,一种称为“避圈法”,一种是“破圈法”,两法各具优缺点,它们具有共同的特征——去掉图中的圈并且每次都是去掉圈中边权较大的边.6. 最短路问题的数学模型最短路问题一般描述如下:在一个图(或者说网络)中,给定一个始点v s 和一个终点v t ,求v s 到v t 的一条路,使路长最短(即路的各边权数之和最小).狄克斯屈(E.D.Dijkstra )双标号法该法亦称双标号法,适用于所有权数均为非负(即一切w ij ≥0 w ij 表示顶点v i 与v j 的边的权数)的网络,能够求出网络的任一点v s 到其它各点的最短路,为目前求这类网络最短路的最好算法.该法在施行中,对每一个点v j 都要赋予一个标号,并分为固定标号P (v j )和临时标号T (v j )两种,其含义如下:P (v j )——从始点v s 到v j 的最短路长;T (v j )——从始点v s 到v j 的最短路长上界.一个点v j 的标号只能是上述两种标号之一. 若为T 标号,则需视情况修改,而一旦成为P 标号,就固定不变了.开始先给始点v s 标上P 标号0,然后检查点v s ,对其一切关联边(v s ,vj )的终点v j ,给出v j 的T 标号w ij ;再在网络的已有T 标号中选取最小者,把它改为P 标号. 以后每次都检查刚得到P 标号那点,按一定规则修改其一切关联边终点的T 标号,再在网络的所有T 标号中选取最小者并把它改为P 标号. 这样,每次都把一个T 标号点改为P 标号点,因为网络中总共有n 个结点,故最多只需n -1次就能把终点v t 改为P 标号. 这意味着已求得了v s 到v t 的最短路.狄克斯屈标号法的计算步骤如下:1°令S ={v s }为固定标号点集,=V \{v s }为临时标号点集,再令P (v i =0,v t ∈S ; 2°检查点v i ,对其一切关联边(v i , vj )的终点v j∈,计算并令 min{T (v j , P (v i +w ij }⇒T (v j3°从一切v j∈中选取并令 min{T (v j }=T (v r ⇒T (v r 选取相应的弧(v i , vr ). 再令 S {v r }⇒S , \{v r }⇒=∅,则停止,P (v j 即v s 到v j 的最短路长,特别P (v t 即v s 到v t 的最短路长,而已选出 4°若的弧即给出v s 到各点的最短路;否则令v r ⇒v i ,返2°. 注意:若只要求v s 到某一点v t 的最短路,而没要求v s 到其他各点的最短路,则上述步骤4°可改为 4°若r = t 则结束,P (v r 即为所求最短路长;否则令v r ⇒v i ,返2°.。
运筹学图与网络分析(高级课堂)

E
I
A
2 C
2
4
G
5
1S
2
3
3K
B2
2 F 2 26 J
D
H
高等课堂
26
[例]今有煤气站A,将给一居民区供应煤气,居民区各 用户所在位置如图所示,铺设各用户点的煤气管道所需 的费用(单位:万元)如图边上的数字所示。要求设计 一个最经济的煤气管道路线,并求所需的总费用。
E
I
A
2 C
2
4
G
5
1S
2
3
3K
例 : G1为不连通图, G2为连通图
G1
高等课堂
G2
8
5、支撑子图
图G=(V,E)和G'=(V ' ,E '),若V =V ' 且E ' E ,
则称G' 为G的支撑子图。
例 :G2为G1的支撑子图
v5
v5
v1
v4 v1
v4
v2
v3
v2
v3
G1
G2
高等课堂
9
例 : G2 是G1 的子图;
v2
e1 v1
H
高等课堂
24
[例]今有煤气站A,将给一居民区供应煤气,居民区各 用户所在位置如图所示,铺设各用户点的煤气管道所需 的费用(单位:万元)如图边上的数字所示。要求设计 一个最经济的煤气管道路线,并求所需的总费用。
E
I
A 3.5
2
C
2
4
G
5
1S
2
3
3K
B2
2 F 2 26 J
D
H
高等课堂
25
运筹学图与网络模型以及最小费用最大流

最短路问题
(P233)例1 求下图中v1到v6的最短路 v2
7
3
v6
v1
5 2 v4 5
21
31
5
v3
v5
解:采用Dijkstra算法,可解得最短路径为v1 v3 v4 v6
v1
v2
v3
v4
v5
v6
把所有弧的权数计算如下表:
1
2
3
4
5
6
1
16
22
30
41
59
2
16
22
30
41
3Leabharlann 172331
4
17
23
5
18
6
最短路问题
(继上页) 把权数赋到图中,再用Dijkstra算法求最短路。
59
22
30 41
23
v1
16
v2 16 v3 17 v4 17 v5 18
v6
22
23
31
v2 v1
v4 v3
v5
最短路问题
最短路的Dijkstra算法(双标号法)的步骤:
1.给出点V1以标号(0,s) 2.找出已标号的点的集合I,没标号的点的集合J以及弧的集合
{(vi , v j ) | vi I , v j J}
3. 如果上述弧的集合是空集,则计算结束。如果vt已标号(lt,kt), 则 vs到vt的距离为lt,而从 vs到vt的最短路径,则可以从kt 反向 追踪到起点vs 而得到。如果vt 未标号,则可以断言不存在从 vs 到vt的有向路。如果上述的弧的集合不是空集,则转下一步。
