第3讲多元回归分析
多元回归分析概述

一、多元回归分析概述在处理测量数据时,经常要研究变量与变量之间的关系。
变量之间的关系一般分为两种。
一种是完全确定关系,即函数关系;一种是相关关系,即变量之间既存在着密切联系,但又不能由一个或多个变量的值求出另一个变量的值。
例如,学生对于高等数学、概率与统计、普通物理的学习,会对统计物理的学习产生影响,它们虽然存在着密切的关系,但很难从前几门功课的学习成绩来精确地求出统计物理的学习成绩。
但是,对于彼此联系比较紧密的变量,人们总希望建立一定的公式,以便变量之间互相推测。
回归分析的任务就是用数学表达式来描述相关变量之间的关系。
回归分析基本原理:(一)回归分析的数学模型相关变量之间的关系可以是线性的,也可以是非线性的。
这里只讨论多元线性回归。
设x1,x2,…,x p是p个可以精确测量或可控制的变量。
如果变量y与x1,x2,…,x p之间的内在联系是线性的,那么进行n次试验,则可得n组数据:(y i, x i1 ,x i2 , … , x ip), i= 1,2,…,n 它们之间的关系可表示为:y1 = b0 + b1x11 + b2x12 + …+ b p x1p +ε1y2 = b0 + b1x21 + b2x22 + …+ b p x2p +ε2…… …… ……y n = b0 + b1x n1 + b2x n2 + …+ b p x np +εn其中,b0,b1,b2,…,b p是p+l个待估参数,εi表示第i次试验中的随机因素对y i的影响。
为简便起见,将此n个方程表示成矩阵形式:Y = XB+ε其中Y=(y1,y2, …,y n)'B=(b0,b1, …,b p)'ε=(ε1,ε2, …,εn)'上式便是p元线性回归的数学模型。
(二)参数B的最小M乘估计为了求出多元线性回归模型中的参数b0,b1,b2,…,b p,可采用最小二乘法,即在其数学模型所属的函数类中找一个近似的函数,使得这个近似函数在已知的对应数据上尽可能和真实函数接近。
多元回归分析方法

多元回归分析方法一、简介多元回归分析是一种经济学和统计学中常用的分析方法,它可以用来研究多个自变量对一个因变量的影响关系。
在实际问题中,我们往往需要考虑多个因素对某个现象的影响,多元回归分析可以帮助我们揭示这种复杂关系。
二、回归模型回归分析基于回归模型,常见的多元回归模型可以表示为:Y = β0 + β1X1 + β2X2 + ... + βkXk + ε,其中Y是因变量,Xi是自变量,βi是对应的回归系数,ε是随机误差项。
回归系数反映了自变量对因变量的影响程度,通过对样本数据进行估计,我们可以得到回归系数的估计值。
三、数据收集与准备在进行多元回归分析之前,我们需要收集和准备相关的数据。
这包括确定因变量和自变量的测量指标,选择合适的样本规模,保证数据的有效性和可靠性。
同时,对于因变量和自变量之间可能存在的非线性关系,我们需要进行适当的变量转换或添加高阶项,以确保模型的拟合程度。
四、回归模型的选择在进行多元回归分析时,我们需要选择合适的回归模型。
这可以通过观察数据的分布情况、变量之间的关系以及领域知识来进行判断。
常见的回归模型包括线性回归、多项式回归和逻辑回归等。
选择合适的模型能够提高分析的准确性和可解释性。
五、模型拟合与评估在得到回归模型的估计值后,我们需要评估模型的拟合程度和预测能力。
常见的评估指标包括均方误差(MSE)、决定系数(R-squared)和F统计量等。
通过这些指标,我们可以判断模型的拟合优度和自变量的显著性,进而确定模型是否可靠以及变量是否具有统计显著性。
六、多重共线性检验多元回归分析中存在一个重要的问题,即多重共线性。
当自变量之间存在强相关关系时,容易导致模型估计结果的不稳定和不可靠。
因此,在进行多元回归分析之前,必须对自变量进行多重共线性的检验。
常用的方法包括方差膨胀因子(VIF)和特征值分解等。
七、模型解释与应用通过对多元回归模型的估计和评估,我们可以得到自变量对因变量的影响程度和方向,并进行合理的解释。
多元回归分析原理及例子

多元回归分析原理回归分析是一种处理变量的统计相关关系的一种数理统计方法。
回归分析的基本思想是: 虽然自变量和因变量之间没有严格的、确定性的函数关系, 但可以设法找出最能代表它们之间关系的数学表达形式。
回归分析主要解决以下几个方面的问题:(1) 确定几个特定的变量之间是否存在相关关系, 如果存在的话, 找出它们之间合适的数学表达式; (2) 根据一个或几个变量的值, 预测或控制另一个变量的取值, 并且可以知道这种预测或控制能达到什么样的精确度;(3) 进行因素分析。
例如在对于共同影响一个变量的许多变量(因素)之间, 找出哪些是重要因素, 哪些是次要因素, 这些因素之间又有什么关系等等。
回归分析有很广泛的应用, 例如实验数据的一般处理, 经验公式的求得, 因素分析, 产品质量的控制, 气象及地震预报, 自动控制中数学模型的制定等等。
多元回归分析是研究多个变量之间关系的回归分析方法, 按因变量和自变量的数量对应关系可划分为一个因变量对多个自变量的回归分析(简称为“一对多”回归分析)及多个因变量对多个自变量的回归分析(简称为“多对多”回归分析), 按回归模型类型可划分为线性回归分析和非线性回归分析。
本“多元回归分析原理”是针对均匀设计3.00软件的使用而编制的, 它不是多元回归分析的全面内容, 欲了解多元回归分析的其他内容请参阅回归分析方面的书籍。
本部分内容分七个部分, §1~§4介绍“一对多”线性回归分析, 包括数学模型、回归系数估计、回归方程及回归系数的显著性检验、逐步回归分析方法。
“一对多”线性回归分析是多元回归分析的基础, “多对多”回归分析的内容与“一对多”的相应内容类似, §5介绍“多对多”线性回归的数学模型,§6介绍“多对多”回归的双重筛选逐步回归法。
§7简要介绍非线性回归分析。
§1 一对多线性回归分析的数学模型§2 回归系数的最小二乘估计§3 回归方程及回归系数的显著性检验§4 逐步回归分析§5 多对多线性回归数学模型§6 双重筛选逐步回归§7 非线性回归模型§1 一对多线性回归分析的数学模型设随机变量与个自变量存在线性关系:, (1.1)(1.1)式称为回归方程, 式中为回归系数,为随机误差。
多元回归分析范文

多元回归分析范文多元回归分析是一种统计分析方法,用于探究多个自变量与一个因变量之间的关系。
它是简单回归分析的扩展,可以更准确地预测因变量的值,并提供对自变量的影响程度的评估。
在本文中,将介绍多元回归分析的原理、步骤和应用,并将其与其他相关的统计分析方法进行比较。
Y=β0+β1X1+β2X2+β3X3+…+βnXn+ε其中,β0为常数项,β1,β2,β3为自变量的系数,ε为误差项。
多元回归分析的目标是通过估计自变量的系数,找到一个最佳的拟合线来预测因变量的值。
1.数据收集:收集包括因变量和自变量在内的相关数据。
2.数据预处理:处理缺失值、异常值等数据,进行变量转换和标准化等操作。
3.模型拟合:使用最小二乘法估计自变量的系数,并通过显著性检验确定哪些自变量对因变量有显著影响。
4.模型评价:通过诸如回归系数、拟合优度等指标评价模型的拟合效果。
5.模型预测:利用拟合好的模型进行因变量的预测。
多元回归分析的应用非常广泛。
在社会科学领域,可以用于预测人们的投票行为、消费行为等。
在经济学中,可以用于分析商品价格与销量之间的关系,以及其他经济因素对市场产生的影响。
在医学领域,可以用于分析多个因素对疾病发生的影响。
在工程领域,可以用于预测产品性能与各个因素之间的关系。
与其他统计分析方法相比,多元回归分析的优点在于可以同时考虑多个自变量对因变量的影响,提供更全面的预测能力。
它可以揭示多个自变量之间的相互作用效应和各自的独立影响,并通过系数的大小提供对各个自变量的相对重要性的评估。
此外,多元回归分析还可以控制其他变量,剔除掉与因变量无关的影响。
然而,多元回归分析也存在一些局限性,如对线性假设的依赖、需要满足一些基本假设(如线性无关性、同方差性等)等。
总之,多元回归分析是一种重要的统计分析方法,可应用于多个领域。
通过分析多个自变量与一个因变量之间的关系,可以提供更准确的预测和深入的解释。
然而,在应用多元回归分析时,需要注意对数据的收集和预处理,并且验证模型的拟合优度和假设的合理性。
第三讲_多元线性回归模型检验及stata软件应用
F检验的思想来自于总离差平方和的分解式: TSS=ESS+RSS
2 ˆ ESS y 由 于 回 归 平 方 和 解 释 变 量 X 的 联 合 体 对 被 解 i 是
释 变 量 Y 的 线 性 作 用 的 结 果 , 考 虑 比 值
2 ˆ ESS /RSS y i 2 e i
如果这个比值较大,则X的联合体对Y的解释程度 高,可认为总体存在线性关系,反之总体上可能不存 在线性关系。 因此,可通过该比值的大小对总体线性关系进行推 断。
**关于P值:以t统计量的观测值作为临界值,并计算该检 验的响应显著水平,这就是P值。
P值检验法(p-value test)
p 值的概念: 为了方便,将 t 统计量的值记为
பைடு நூலகம்t0
Se
j j
计算 称为p
p=P{|t|>t 0}
值(p-value )
通常的计量经济学软件都可自动计算出p 值
Excel格式数据的读取
直接拷贝,粘贴到stata中
使用Stat
transfer把其它格式的数据转成 stata格式的数据 读入ASCII格式数据文件:比较麻烦
常见数据格式
格式:dta 文本格式:txt Excel格式:xls 其它格式:sas、spss、gauss等
Stata
检验统计量2250nntn???????当用正态已知时当未知时也可用正态n用分布很小1t变量iiiibtbsb???其中1ixxsbs???12iiiixxbn????2t检验统计量给定显著性水平??可得到临界值t??2nk由样本求出统计量t的数值通过t??t??2nk或t??t??2nk来拒绝或不能拒绝原假设h0从而判定对应的解释变量是否应包括在模型中
心理学研究方法多元回归分析PPT课件

save ——distance –勾上Cook’s和leverage 值
Plots-histogram 和 normal probability plot勾
上-把ZPRED放入Y,把ZRESID放入X轴——
.
12
OK
原始回归方程Y=0.0498X+0.441
标准化回归方程Zy=0.881Zx
β = (δy/ δx)*r =(0.41989/7.426)*0.881=0.04981
.
29
步骤同一元回归
补充步骤 在statistic勾上R square change,part and partial correlation(半偏 相关和偏相关), conlinerarity diagnostics (共线性判断)
.
30
分层回归方法
Enter:强制进入 Forward:前向选择法 Backward:反向删除法 Stepwise:逐步回归,最常用 把需要控制的变量用这种方法强制enter法
.
39
对强影响点的诊断和处理
同一元线性回归
.
40
多重共线性(conlinerarity diagnostics)
判断方法
✓ 相关系数矩阵:当相关系数>0.8,代表共线性 越大。
✓ 容忍度(tolerance):最大值为1。当值越小, 代表共线性越大。
✓ 特征值(eigenvalue):表示该因子所解释变 量的方差。如果很多变量的特征值<1,表示共 线性。
残差是否独立:用durbin-watson进行分析(取值 0<d<4)。如果独立,则d约等于2。如果相邻两点的 残差为正相关,d<2。当相邻两点的残差为负相关时, d>2。
多元回归分析

Multi Regression
22
Adjusted R2
在迴歸分析中,如果自變項的個數很多,有時 候就要用調整後的判定係數代替原先的判定係 數,因為增加新的自變項後,均會使R2變大。
「Adjusted R2」為調整後的判定係數:
SSE 2 2 n k 1 1 n 1 (1 R 2 ) Adjusted R R a 1 SST n k 1 n 1
平均平方和MS SSR MSR k SSE MSE n k 1
F F MSR MSE
ˆ Note: 殘差 ei yi yi ,i 1, 2,, n
K為預測變數個數(不含β0)
Multi Regression 18
模式檢定(1)
迴歸分析之假說檢定包括總檢定與邊際檢定兩種。 總檢定: – 目的在探討迴歸模式中的所有斜率係數是否全部 為0。 – 當斜率係數不全為0時,Y與(X1,X2,…,XK)才具有 某種程度的函數關係 。 – 總檢定之虛無假說與對立假說可列示如下: H0: j=0,對所有j H1: j0,對某些j (j=1,2,…,K) – 檢定統計量: F=MSR/MSE
2 iid
或
Y1 1 X11 X1k 0 1 Y2 1 X21 X2k 1 2 Yn 1 Xn1 Xnk k n
Yn1 Xn(k1)β(k1)1 ε n1
Multi Regression
17
迴歸分析 ―變異數分析表
變異來源 迴歸 隨機 總和 平方和SS
ˆ ˆ SSR y 2 (Y Y ) 2
SSE e 2 (Y Y ) 2
多元回归分析法的介绍及具体应用

多元回归分析法的介绍及具体应用在数量分析中,经常会看到变量与变量之间存在着一定的联系。
要了解变量之间如何发生相互影响的,就需要利用相关分析和回归分析。
回归分析的主要类型:一元线性回归分析、多元线性回归分析、非线性回归分析、曲线估计、时间序列的曲线估计、含虚拟自变量的回归分析以及逻辑回归分析等。
这里主要讲的是多元线性回归分析法。
1. 多元线性回归的定义说到多元线性回归分析前,首先介绍下医院回归线性分析,一元线性回归分析是在排除其他影响因素或假定其他影响因素确定的条件下,分析某一个因素(自变量)是如何影响另一事物(因变量)的过程,所进行的分析是比较理想化的。
其实,在现实社会生活中,任何一个事物(因变量)总是受到其他多种事物(多个自变量)的影响。
元线性回归分析讨论的回归问题只涉及了一个自变量,但在实际问题中,影响因变量的因素往往有多个。
例如,商品的需求除了受自身价格的影响外, 要受到消费者收入、其他商品的价格、消费者偏好等因素的影响;影响水果产量的外界因素有平均气温、平均日照时数、平均湿度等。
因此,在许多场合,仅仅考虑单个变量是不够的,还需要就一个因变量与多个自变量的联系来进行考察, 才能获得比较满意的结果。
这就产生了测定多因素之间相关关系的问题。
研究在线性相关条件下, 两个或两个以上自变量对一个因变量的数量变化关系,称为多元线性回归分析, 表现这一数量关系的数学公式,称为多元线性回归模型。
多元线性回归模型是一元线性回归模型的扩展,其基本原理与一元线性回归模型类似,只是在计算上更为复杂,一般需借助计算机来完成。
2. 多元回归线性分析的运用具体地说,多元线性回归分析主要解决以下几方面的问题。
(1)、确定几个特定的变量之间是否存在相关关系,如果存在的话,找出它y n = 3。
中 ^Xn ^ 卩2X n2 十"+ 3 p X np 十 %们之间合适的数学表达式;(2)、根据一个或几个变量的值,预测或控制另一个变量的取值,并且可以知道这种预测或控制能达到什么样的精确度;(3)、进行因素分析。
多元回归分析 ppt课件

ppt课件
3
汽车销售
若公司管理人员要预测来年该公 司的汽车销售额y时,影响销 售额的因素---广告宣传费x1
还有个人可 支配收入x2, 价格x3
ppt课件
4
研究地区经济增长GDP,受劳动力投入人数 x1影响!
还有:资本要素X2,科 技水平X3的影响
ppt课件
5
多元回归应用
25.96732 2.85478 0.01449
Lower 95% 57.58835 -48.57626 17.55303
Upper 95%
555.46404 -12.237392
130.70888
多元回归方程
Sales 306.526- 24.975(Prci e) 74.131(Advertising)
Sales 306.526- 24.975(Prci e) 74.131(Advertising) 306.526- 24.975(5.50) 74.131(3.5) 428.62
预测销量为 428.62 pies
ppt课件
注意:单位百元,$350 意味 X2 = 3.5
24
模型的F检验 系数的T检验 拟合度检验--决定系数
描述因变量 y 依赖于自变量 x1 , x2 ,…, xk 和误差项 的方程,称为多元回归模型
y 0 1x1 2 x2 k xk
β0 ,β1,β2 ,,βk是参数
是被称为误差项的随机变量
包含在y里面但不能被k个自变量的线性关系所解释
的变异性
价格 Price
($) 5.50 7.50 8.00 8.00 6.80 7.50 4.50 6.40 7.00 5.00 7.20 7.90 5.90 5.00 7.00
多元回归分析

多元回归分析引言多元回归分析是一种统计方法,用于探究自变量对因变量的影响程度。
它通过建立一个数学模型,分析多个自变量与一个因变量之间的关系,以预测因变量的变化。
本文将介绍多元回归分析的基本原理、应用场景和步骤。
基本原理多元回归分析建立了一个包含多个自变量的线性回归方程,如下所示:Y = β0 + β1X1 + β2X2 + ... + βnXn + ε其中,Y为因变量,X1、X2、…、Xn为自变量,β0、β1、β2、…、βn为回归系数,ε为误差项。
回归系数表示自变量对因变量的影响程度。
多元回归分析可以通过最小二乘法估计回归系数,即找到使误差项平方和最小的系数值。
在得到回归系数后,可以通过对自变量的设定值,预测因变量的值。
应用场景多元回归分析广泛应用于各个领域,例如经济学、社会科学和工程学等。
以下是一些常见的应用场景:1.经济学:多元回归分析可以用于预测经济指标,如国内生产总值(GDP)和通货膨胀率。
通过分析多个自变量,可以了解各个因素对经济发展的影响程度。
2.社会科学:多元回归分析可以用于研究社会现象,如教育水平和收入水平之间的关系。
通过分析多个自变量,可以找出对收入水平影响最大的因素。
3.工程学:多元回归分析可以用于预测产品质量,如汽车的油耗和引擎功率之间的关系。
通过分析多个自变量,可以找到影响产品质量的关键因素。
分析步骤进行多元回归分析时,以下是一般的步骤:1.收集数据:收集自变量和因变量的数据,并确保数据的可靠性和有效性。
2.数据预处理:对数据进行清洗和转换,以消除异常值和缺失值的影响。
3.变量选择:根据实际问题和领域知识,选择合适的自变量。
可以使用相关性分析、变量逐步回归等方法来确定自变量。
4.拟合模型:使用最小二乘法估计回归系数,建立多元回归模型。
5.模型评估:通过检验残差分布、解释变量的显著性和模型的拟合程度等指标,评估多元回归模型的质量。
6.预测分析:使用已建立的多元回归模型,对新的自变量进行预测,得到因变量的预测值。
《数学多元回归》课件

7. 总结
1
回归分析的优缺点
总结回归分析的优点和局限性。
2
多元回归分析的应用领域
讨论多元回归分析在不同领域的应用。
3
未来发展展望
探讨未来回归分析方法的发展趋势和研究方向。
2
最小二乘法
解释多元回归分析中的最小二乘法。
3
模型评价方法
讨论如何评估多元回归模型的拟合度和预测能力。
4. 变量选择方法
向前选择法
描述向前选择法在多元回归 分析中的应用,以选择最重 要的自变量。
向后删除法
介绍向后删除法的原理和步 骤,在多元回归分析中剔除 不重要的自变量。
逐步回归
解释逐步回归算法,它是一 种综合了向前选择法和向后 删除法的方法。
5. 非线性回归分析
多项式回归
介绍多项式回归分析,可以更好地拟合非线性数据。
指数回归
讨论指数回归分析,可用于描述变量之间的指数关系。
6. 应用案例分析
房价预测
消费者购物行为分析
使用多元回归分析来预测房价, 并了解影响房价的因素。
通过多元回归分析,了解消费 者购物行为中的关键因素。
薪资预测
应用多元回归分析方法来预测 个体的薪资水平。
《数学多元回归》PPT课 件
这个《数学多元回归》的PPT课件将帮助你深入了解回归分析的概念和多元 回归分析的方法。通过简单线性回归分析、多元回归分析、变量选择方法和 非线性回归分析的介绍,以及应用案 简介
1 回归分析的概念
介绍回归分析的基本概念和用途。
2 多元回归分析的概念
解释多元回归分析是如何扩展到多个自变量的。
2. 简单线性回归分析
1
简单线性回归模型
解释简单线性回归模型的原理和公式。
多元回归分析

多元回归分析在经济学、社会学、心理学、医学等领域的实证研究中,多元回归分析是一种重要的统计方法。
它能够帮助研究者建立模型,估计各个变量的影响力,并对研究问题作出预测。
本文将介绍多元回归分析的概念、基本假设、模型建立、参数估计、模型诊断和解释结果等方面。
一、概念多元回归分析是一种用来研究因变量与多个自变量之间关系的统计方法。
在多元回归分析中,我们以因变量为被解释变量,以自变量为解释变量,建立一个多元线性回归模型,然后用样本数据估计各个系数,进而对总体进行推断。
通常,我们所研究的因变量与自变量之间是存在着某种联系的。
这种联系可以是线性关系,也可以是非线性关系。
我们可以通过多元回归模型来表达和解释完整的联系。
二、基本假设在进行多元回归分析时,我们需要基于以下三个基本假设:1.线性假设:多元回归模型中,因变量与自变量之间的关系是线性的。
2.独立假设:所有观测量之间都是相互独立的。
3.常态假设:模型的误差项服从正态分布。
三、模型建立建立一个多元回归模型通常有以下几个步骤:1.选择自变量:确定那些自变量对目标变量具有影响。
2.确定函数形式:使用线性函数或者非线性函数建立多元回归模型。
3.估计参数:使用样本数据来估计函数中的系数。
4.模型检验:验证模型是否可以拟合样本数据以及是否可以推广到总体。
五、参数估计在确定自变量和函数形式之后,我们需要使用已有数据来估计模型中的系数。
在多元线性回归中,一般采用最小二乘法对模型中的系数进行估计。
最小二乘法会尝试选择一组系数,使得用这组系数确定的模型与观测值之间的残差平方和最小。
残差平方和表示由于模型和观测值之间的差异而产生的差异的度量。
六、模型诊断模型的诊断是一个非常重要的步骤,用于检查多元回归模型的各种假设是否得到满足。
模型诊断的两个步骤:1.检查多元回归模型的基本假设是否得到满足。
这包括线性假设、独立假设和常态假设。
2.分析模型的残差以检查模型是否存在某种偏差。
如果存在偏差,可能会导致模型不准确,预测不可信。
多元回归分析

多元回归分析多元回归分析是一种常用的统计方法,用于研究多个自变量对一个因变量的影响。
该方法可以帮助研究人员理解不同自变量对因变量的相对重要性,并建立预测模型。
本文将介绍多元回归分析的基本原理和应用,并通过一个实例来说明其实际应用价值。
多元回归分析的基本原理是基于线性回归模型。
线性回归模型的基本形式是:Y = β0 + β1X1 + β2X2 + ... + βnXn + ε其中,Y表示因变量,X1至Xn表示自变量,β0至βn表示回归系数,ε表示误差项。
多元回归分析通过求解最小二乘法来估计回归系数,以找到最佳拟合线。
回归系数的估计结果可以反映不同自变量对因变量的影响。
多元回归分析的应用十分广泛,特别是在社会科学、经济学以及市场营销等领域。
例如,研究人员可以使用多元回归分析来探索广告投资对销售额的影响,或者研究不同因素对消费者购买行为的影响。
为了更好地理解多元回归分析的应用,我们以市场营销领域的一个案例为例。
假设某公司希望了解其产品销售额与广告投资、价格和竞争公司销售额之间的关系。
研究人员首先收集了一段时间内的数据,包括广告投资、产品价格和竞争公司销售额的信息。
在进行多元回归分析之前,研究人员需要对数据进行预处理,包括数据清洗、变量选择和变量转换等。
然后,他们可以根据以上模型构建一个方程,以评估广告投资、价格和竞争公司销售额对销售额的影响。
通过对数据进行多元回归分析,研究人员可以得到各自变量的回归系数。
这些系数可以告诉他们不同自变量对销售额的相对重要性。
例如,如果广告投资的回归系数较大,则说明广告投资对销售额的影响较大;反之,如果竞争公司销售额的回归系数较大,则说明竞争对销售额的影响较大。
通过多元回归分析的结果,研究人员可以得出一些结论,并提出相应的建议。
例如,如果广告投资对销售额的影响较大,公司可以考虑增加广告投资以提高销售额。
如果价格对销售额的影响较大,公司可以考虑调整产品价格以更好地满足消费者需求。
计量经济学第三章第3节多元线性回归模型的显著性检验

人均国内生 产总值 1602.3 1727.2 1949.8 2187.9 2436.1
1983
1984 1985
572.8
635.6 716
931.4
1059.2 1185.2
1995
1996 1997
1213.1
1322.8 1380.9
2663.7
2889.1 3111.9
1986 1987
1988 1989
(2) 当k =0时,即只有截距项式时,R = R (3) 当k 0时,R R
2 2 2 2 2
2 k (4) R 会出现负值,当R < 时,会出现 R <0的情况 n-1 2
此时,将理解为R =0
2
(5)对调整后拟合优度的补充说明:
RSS n k 1 n 1 RSS R 1 1 TSS n 1 n k 1 TSS
第三节 显著性检验及预测
一、拟合优度检验
二、变量的显著性检验 三、回归方程的显著性检验
四、利用方程进行预测
一、多元线性回归模型的统计检验
<一> 拟合优度
• 类似一元回归,多元回归同样可以用拟合优度R2度量样本 回归方程拟合样本观察值的程度。R2越接近1,拟合的越好。
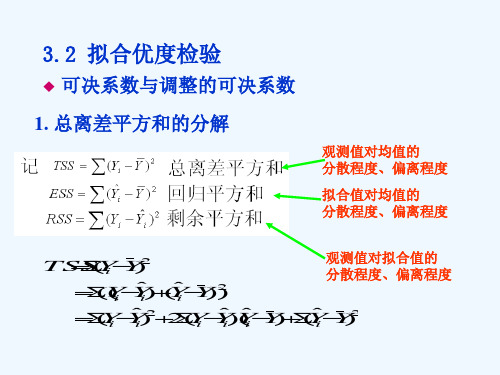
(1)总离差平方和分解 设多元线性回归模型为:
(6) 修正的拟合优度总结
• 解释变量的增加,有可能导致样本回归方程与 样本观察值拟合程度的提高,也会由于变量的个数 的增加导致拟合优度虚假的提高。 • 调整后的拟合优度,是剔除由于解释变量个数 增加导致拟合数值虚假提高,而拟合程度并没有实 际提高的部分。 由此可见,修正的拟合优度 R 比一般意义的拟合 优度 R 2 更准确的反映了解释变量对被解释变量的影响 程度。因此在一般情况下修正拟合优度 R 比 R 应用 更广。
多元回归分析估计PPT课件

yˆi y2 explained sumof squaresSSE 解释平方和
uˆi2 residualsumof squaresSSR 残差平方和
25
第25页/共85页
拟合优度(续)
我们怎样衡量我们的样本回归线拟合样本数 据有多好呢? 可以计算总平方和(SST)中被模型解释的 部分,称此为回归R2
一个拟合yˆ值i 或ˆ0预测ˆ1x值i1 ,ˆ对2xi观2 测点 iˆ,k xik其拟
合值就是
uˆi yi yˆi
• 第i个观测的残差第为12页:/共85页
12
OLS拟合值和残差的性质
• 残差项的均值为零
uˆ i
0
• 每个自变量和OLS协残差之间的样本协方差
为零。
uˆi xk 0
uˆ i
• 其中,i 表示观测次数,j=1,…,k代表第j
个回归元(变量序第号32页) /共85页
32
假定MLR.3 (不存在完全共线性)
• 在样本(因而在总体)中,没有一个自变量是常 数,自变量之间也不存在严格的线性关系。
• 如果方程中一个自变量是其它自变量的一个 线性组合时,我们说此模型遇到完全共线性 (perfect collinearity)问题,此时不能用OLS估计 参数。
• 统计性质是估计量在随机抽样不断重复时的 性质。我们并不关心在某一特定样本中估计 量如何。
30
第30页/共85页
假定 MLR.1(线性于参数)
• 总体模型可写成
y= 0+ 1x1+ 2x2+ …+kxk+u
多元回归分析

基本介绍
Hale Waihona Puke 通常影响因变量的因素有多个,这种多个自变量影响一个因变量的问题可以通过多元回归分析来解决。例如, 经济学知识告诉我们,商品需求量Q除了与商品价格P有关外,还受到替代品的价格、互补品的价格,和消费者收 入等因素,甚至还包括商品品牌Brand这一品质变量(品质变量不能用数字来衡量,需要在模型中引入虚拟变量) 的影响。多元回归分析应用的范围更加广泛。由于线性回归分析比较简单和普遍,下面首先介绍多元线性回归, 在线性分析基础上,逐步引入虚拟变量回归和一类能够变换成线性回归的曲线回归模型 。
多元回归分析
数理统计方法
目录
01 基本介绍
03 引进虚拟变量
02 多元回归模型 04 曲线回归
多元回归分析(Multiple Regression Analysis)是指在相关变量中将一个变量视为因变量,其他一个或 多个变量视为自变量,建立多个变量之间线性或非线性数学模型数量关系式并利用样本数据进行分析的统计分析 方法。另外也有讨论多个自变量与多个因变量的线性依赖关系的多元回归分析,称为多元多重回归分析模型(或 简称多对多回归)。
感谢观看
当虚拟变量的引入形式只影响回归方程的截距,我们称为加法模型。引入虚拟变量的另外一种形式是乘法模 型,这时引入虚拟变量后并不影响模型的截距,而是影响了斜率。当然,在模型设定时也可能同时引入加法和乘 法,同时改变模型的截距和斜率。
曲线回归
前面我们在模型中都假定Y和之间是线性关系,从广义的线性角度来讲,下面所讲的曲线模型是通过变量替换 而转化成线性的模型。表1列出了常用的可以通过变量替换而转化成线性的曲线模型 。
多元回归模型
多元回归模型的数学形式 设因变量为Y,影响因变量的k个自变量分别为,假设每一个自变量对因变量Y的影响都是线性的,也就是说, 在其他自变量不变的情况下,Y的均值随着自变量的变化均匀变化,这时我们把 称为总体回归模型,把称为回归参数。回归分析的基本任务是: 任务1:利用样本数据对模型参数作出估计。 任务2:对模型参数进行假设检验。 任务3:应用回归模型对因变量(被解释变量)作出预测。 模型的基本假定 为了保证多元回归分析的参数估计、统计检验以及置信区间估计的有效性,与一元线性回归分析类似,我们 需要对总体回归模型及数据作一些基本假定。 假定1:随机误差项的概率分布具有零均值,即。 假定2:随机误差项的概率分布对于不同的自变量表现值而言,具有同方差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
525 .28253286
Number of obs =
F( 1, 524) =
Prob > F
=
R-squared
=
Adj R-squared =
Root MSE
=
526 119.58 0.0000 0.1858 0.1843 .48008
lwage
educ _cons
Coef.
.0827444 .5837727
t
12.10 7.89
-6.16 1.21
P>|t|
0.000 0.000 0.000 0.227
[95% Conf. Interval]
.0756948 .0308002 -.000941 -.0801085
.1050368 .0512175 -.0004861 .3361035
工作经历的二次项系数显著为负,模型本身的拟合程度也有所
其随机表达式:
Yi ˆ0 ˆ1X1i ˆ2 X 2i ˆk X ki ei , i 1,2, , n 即:Y Xˆ e
其中:
ˆ
ˆ0 ˆ1 , ˆk
e
e1 e2 en
Q
0
ˆ
2
Q
0
ˆ k
Q
0
n
n
其中: Q ei2 (Yi Yˆi ) 2
i 1
i 1
n
2
(Yi (ˆ0 ˆ1 X 1i ˆ2 X 2i ˆk X ki ))
i 1
于是得到关于待估参数估计值的正规方程组:
其中: i 1,2,, n, 表示第i次观测值; k表示解释变量的数目;
j称为回归参数
这个式子也被称为总体回归函数的随机表达形式,他的非随机 表达式为:
E(Yi | X1i , X 2i , X ki ) 0 1 X1i 2 X 2i k X ki
总的说来,相对于简单回归分析而言,多元回归分 析具备以下优势:
多元回归分析控制了除关键解释变量之外的更多变量,更适合 于其他条件不变情况下的分析。 多元回归分析能够容纳更多解释变量,因而在推断变量之间的 因果关系、对被解释变量进行预测时的效果会更好。 多元回归分析可以表现为更一般的函数形式。 多元回归分析是经验分析中最广泛使用的工具。
二、使用多元回归的动因
在实证工作中使用简单回归模型的主要缺陷是:在其它条件 不变情况假定下我们估计出的x对y的影响值是否可信依赖,完全 取决于零条件均值假设是否现实。而在仅含有一个解释变量的情 况下,误差项和解释变量不相关的假设很难实现,因此要得到在 其它条件不变的情况下 x对y的影响非常困难。
而多元回归分析允许我们明确地控制许多其它也同时影响因 变量的因素,因而更适合于其它条件不变情况下的分析。
所以,保持 x2 ,, xk 不变意味着: yˆ ˆ1x1
也就是说,每个偏回归系数 都有一个局部效应,或
者其他情况不变效应解释。
具体而言,ˆ1表示其他条件不变时, x1 每增加一个
单位, yˆ 平均增加 ˆ1 个单位;ˆ j 表示其他条件不 变时, x j每增加一个单位, yˆ 平均增加 ˆ j 个单位。
例3.1:大学GPA的决定因素(GPA1.RAW)
colGPA:大学平均成绩;hsGPA : 高中平均成绩;
ACT :大学能力测验分数 见教材P74
Source
SS
df
MS
Model Residual
3.42365506
2 1.71182753
15.9824444 138 .115814814
Total
ˆ0 ˆ1
ˆ k
1 X 11 X k1
1 X 12 Xk2
1 Y1
X 1n Y2
Xk
n
பைடு நூலகம்
Yn
即:
(XX)βˆ XY
由于X’X满秩,故有:
βˆ (XX)1 XY
19.4060994 140 .138614996
Number of obs =
F( 2, 138) =
Prob > F
=
R-squared
=
Adj R-squared =
Root MSE
=
141 14.78 0.0000 0.1764 0.1645 .34032
(ˆ0 ˆ1 X 1i ˆ2 X 2i ˆ k X ki ) X ki Yi X ki
这个方程组通常被称为OLS一阶条件,解该(K+1)个方
程组成的线性代数方程组,即可得到(K+1)个待估参
数的估计值
ˆ j , j 0,1,2,, k
在估计之后,我们得到OLS回归线,或称为样本回归方
2
二、参数估计的方法
普通最小二乘估计(OLS) 极大似然估计(ML)
三、如何得到OLS估计值
对于随机抽取的n组观测值 (Yi , X ji ), i 1,2, , n, j 0,1,2, k
根据最小二乘原理,参数估计值应该是下列方程组的
解
:
ˆ
0
Q
0
ˆ1
k Xk2
2
Yn 0 1 X1n 2 X 2n k X kn n
写成矩阵形式为:
Y1 1 X11 X 21
Y2 Yn n1
1 1
X 12 X 1n
X 22 X 2n
Root MSE
=
526 74.67 0.0000 0.3003 0.2963 .44591
lwage
educ exper expersq _cons
Coef.
.0903658 .0410089 -.0007136 .1279975
Std. Err.
.007468 .0051965 .0001158 .1059323
Prob > F
=
R-squared
=
Adj R-squared =
Root MSE
=
526 86.86 0.0000 0.2493 0.2465 .46141
lwage
educ exper _cons
Coef.
.0979356 .0103469 .2168544
Std. Err.
.0076224 .0015551
((ˆˆ00(ˆ0ˆˆ11XX1ˆ1i1i X1ˆiˆ22i XXˆ222ii
X 2i ˆk ˆk X ki ˆk X ki
X ki ) ) X 1i ) X 2i
Yi Yi X 1i Yi X 2i
著变大,说明工作经历还和受教育程度可能反向变动的关系。受教
育年限的系数意味着在工作年限相同的情况下,多接受一年教育可
以带来收入增加9.79%。模型的拟合程度也有提高,说明控制工作
经历之后,模型对个人收入变动有更强的解释力。
多元线性回归中,变量之间存在非线性关系并不少见,
上例中引入工作经历的二次项:
或者说j给出了Xj的单位变化对Y均值的“直
接”或“净”(不含其他变量)影响。
yi 0 1x1i 2 x2i k xki ui
等价于: Y1 0 1 X11 2 X 21 k X k1 1
Y2
0
1 X12 2 X 22
上升,但此时工作经验的系数不能再解释为“受教育程度相同”以
及“工作经历平方项相同”时,工作经历增加一年对收入水平的影
响,那么在这样的模型中,各参数应该怎么解释?
第二节 OLS的操作和解释
一、参数估计的任务
1、 2、
求出ˆ j ( j 0,1,2, , k) 求出随机干扰项的方差估计ˆ
.108595
t
12.85 6.65 2.00
P>|t|
0.000 0.000 0.046
[95% Conf. Interval]
.0829613 .0072919 .0035183
.1129099 .013402
.4301904
很显然,控制工作经历之后,工作经历的系数显著为正,这说
明工作经历对个人收入确实存在正向影响;且受教育年限的系数显
.控re制g l工wag作e e经duc历exp之er 后:
Source
SS
df
MS
Model Residual
36.9850396
2 18.4925198
111.344712 523 .212896199
Total 148.329751 525 .28253286
Number of obs =
F( 2, 523) =
总体回归函数的非随机表达式:
E(Yi | X1i , X 2i , X ki ) 0 1 X1i 2 X 2i k X ki
方程表示:各变量X值固定时Y的平均响应。
j也被称为偏回归系数,表示在其他解释变量
保持不变的情况下,Xj每变化1个单位时,Y的 均值E(Y)的变化;
即:Y X
X k1 Xk2 X kn
n(k
1)
0
1
2
k
(
k
1)1
1 2 n n1
