求三角形内最大内接正方形面积
人教版九年级数学上册 第二十四章 圆 填空题—2019年中考真题汇编(一)(解析版)

第二十四章圆填空题—2019年中考真题汇编(一)1.(2019•辽阳)如图,A,B,C,D是⊙O上的四点,且点B是的中点,BD交OC于点E,∠AOC =100°,∠OCD=35°,那么∠OED=.2.(2019•鄂尔多斯)如图,△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC于点F.若AB=6,∠CDF=15°,则阴影部分的面积是.3.(2019•青海)如图在正方形ABCD中,点E是以AB为直径的半圆与对角线AC的交点,若圆的半径等于1,则图中阴影部分的面积为.4.(2019•鞍山)如图,AC是⊙O的直径,B,D是⊙O上的点,若⊙O的半径为3,∠ADB=30°,则的长为.5.(2019•营口)圆锥侧面展开图的圆心角的度数为216°,母线长为5,该圆锥的底面半径为.6.(2019•铁岭)如图,点A,B,C在⊙O上,∠A=60°,∠C=70°,OB=9,则的长为.7.(2019•盘锦)如图,△ABC内接于⊙O,BC是⊙O的直径,OD⊥AC于点D,连接BD,半径OE⊥BC,连接EA,EA⊥BD于点F.若OD=2,则BC=.8.(2019•莱芜区)用一块圆心角为120°的扇形铁皮,围成一个底面直径为10cm的圆锥形工件的侧面,那么这个圆锥的高是cm.9.(2019•锦州)如图,正六边形ABCDEF内接于⊙O,边长AB=2,则扇形AOB的面积为.10.(2019•湘潭)《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积=(弦×矢+矢2).孤田是由圆弧和其所对的弦围成(如图中的阴影部分),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,运用垂径定理(当半径OC ⊥弦AB时,OC平分AB)可以求解.现已知弦AB=8米,半径等于5米的弧田,按照上述公式计算出弧田的面积为平方米.11.(2019•铜仁市)如图,四边形ABCD为⊙O的内接四边形,∠A=100°,则∠DCE的度数为;12.(2019•内江)如图,在平行四边形ABCD中,AB<AD,∠A=150°,CD=4,以CD为直径的⊙O交AD于点E,则图中阴影部分的面积为.13.(2019•陕西)若正六边形的边长为3,则其较长的一条对角线长为.14.(2019•娄底)如图,C、D两点在以AB为直径的圆上,AB=2,∠ACD=30°,则AD=.15.(2019•雅安)如图,△ABC内接于⊙O,BD是⊙O的直径,∠CBD=21°,则∠A的度数为.16.(2019•吉林)如图,在扇形OAB中,∠AOB=90°.D,E分别是半径OA,OB上的点,以OD,OE为邻边的▱ODCE的顶点C在上.若OD=8,OE=6,则阴影部分图形的面积是(结果保留π).17.(2019•包头)如图,BD是⊙O的直径,A是⊙O外一点,点C在⊙O上,AC与⊙O相切于点C,∠CAB=90°,若BD=6,AB=4,∠ABC=∠CBD,则弦BC的长为.18.(2019•柳州)在半径为5的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为.19.(2019•梧州)如图,已知半径为1的⊙O上有三点A、B、C,OC与AB交于点D,∠ADO=85°,∠CAB=20°,则阴影部分的扇形OAC面积是.20.(2019•贵阳)如图,用等分圆的方法,在半径为OA的圆中,画出了如图所示的四叶幸运草,若OA =2,则四叶幸运草的周长是.21.(2019•绥化)半径为5的⊙O是锐角三角形ABC的外接圆,AB=AC,连接OB、OC,延长CO交弦AB于点D.若△OBD是直角三角形,则弦BC的长为.22.(2019•鸡西)如图,在⊙O中,半径OA垂直于弦BC,点D在圆上且∠ADC=30°,则∠AOB的度数为.23.(2019•贵港)如图,在扇形OAB中,半径OA与OB的夹角为120°,点A与点B的距离为2,若扇形OAB恰好是一个圆锥的侧面展开图,则该圆锥的底面半径为.24.(2019•河池)如图,P A,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P=°.25.(2019•广西)《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为1寸,锯道AB=1尺(1尺=10寸),则该圆材的直径为寸.26.(2019•烟台)如图,分别以边长为2的等边三角形ABC的三个顶点为圆心,以边长为半径作弧,三段弧所围成的图形是一个曲边三角形,已知⊙O是△ABC的内切圆,则阴影部分面积为.27.(2019•贺州)已知圆锥的底面半径是1,高是,则该圆锥的侧面展开图的圆心角是度.28.(2019•绥化)用一个圆心角为120°的扇形作一个圆锥的侧面,若这个圆锥的底面半径恰好等于4,则这个圆锥的母线长为.29.(2019•齐齐哈尔)将圆心角为216°,半径为5cm的扇形围成一个圆锥的侧面,那么围成的这个圆锥的高为cm.30.(2019•鸡西)若一个圆锥的底面圆的周长是5πcm,母线长是6cm,则该圆锥的侧面展开图的圆心角度数是.31.(2019•哈尔滨)一个扇形的弧长是11πcm,半径是18cm,则此扇形的圆心角是度.32.(2019•海南)如图,⊙O与正五边形ABCDE的边AB、DE分别相切于点B、D,则劣弧所对的圆心角∠BOD的大小为度.33.(2019•荆州)如图,AB为⊙O的直径,C为⊙O上一点,过B点的切线交AC的延长线于点D,E 为弦AC的中点,AD=10,BD=6,若点P为直径AB上的一个动点,连接EP,当△AEP是直角三角形时,AP的长为.34.(2019•十堰)如图,AB为半圆的直径,且AB=6,将半圆绕点A顺时针旋转60°,点B旋转到点C 的位置,则图中阴影部分的面积为.35.(2019•广元)如图,△ABC是⊙O的内接三角形,且AB是⊙O的直径,点P为⊙O上的动点,且∠BPC=60°,⊙O的半径为6,则点P到AC距离的最大值是.36.(2019•荆门)如图,等边三角形ABC的边长为2,以A为圆心,1为半径作圆分别交AB,AC边于D,E,再以点C为圆心,CD长为半径作圆交BC边于F,连接E,F,那么图中阴影部分的面积为.37.(2019•福建)如图,边长为2的正方形ABCD中心与半径为2的⊙O的圆心重合,E、F分别是AD、BA的延长线与⊙O的交点,则图中阴影部分的面积是.(结果保留π)38.(2019•咸宁)如图,半圆的直径AB=6,点C在半圆上,∠BAC=30°,则阴影部分的面积为(结果保留π).39.(2019•河南)如图,在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥OA.若OA=2,则阴影部分的面积为.第二十四章圆填空题—2019年中考真题汇编(一)参考答案与试题解析1.【分析】连接OB,求出∠D,利用三角形的外角的性质解决问题即可.【解答】解:连接OB.∵=,∴∠AOB=∠BOC=50°,∴∠BDC=∠BOC=25°,∵∠OED=∠ECD+∠CDB,∠ECD=35°,∴∠OED=60°,故答案为60°.【点评】本题考查圆周角定理,圆心角,弧,弦之间的关系等知识,解题的关键是学会添加常用辅助线,属于中考常考题型.2.【分析】根据S阴影部分=S扇形OAE﹣S△OAE即可求解.【解答】解:连接OE,∵∠CDF=15°,∠C=75°,∴∠OAE=30°=∠OEA,∴∠AOE=120°,S△OAE=AE×OE sin∠OEA=×2×OE×cos∠OEA×OE sin∠OEA=,S阴影部分=S扇形OAE﹣S△OAE=×π×32﹣=3π﹣.故答案3π﹣.【点评】本题考查扇形的面积公式,等腰三角形的性质,三角形的面积等知识,解题的关键是学会用分割法求阴影部分的面积.3.【分析】直接利用正方形的性质结合转化思想得出阴影部分面积=S△CEB,进而得出答案.【解答】解:如图所示:连接BE,可得,AE=BE,∠AEB=90°,且阴影部分面积=S△CEB=S△ABC=S正方形ABCD=×2×2=1故答案为1【点评】本题考查正方形的性质,扇形的面积等知识,解题的关键是学会把不规则图形转化为规则图形,属于中考常考题型.4.【分析】根据圆周角定理求出∠AOB,得到∠BOC的度数,根据弧长公式计算即可.【解答】解:由圆周角定理得,∠AOB=2∠ADB=60°,∴∠BOC=180°﹣60°=120°,∴的长==2π,故答案为:2π.【点评】本题考查的是圆周角定理、弧长的计算,掌握圆周角定理、弧长公式是解题的关键.5.【分析】设该圆锥的底面半径为r,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到2πr=,然后解关于r的方程即可.【解答】解:设该圆锥的底面半径为r,根据题意得2πr=,解得r=3.故答案为3.【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.6.【分析】连接OA,根据等腰三角形的性质求出∠OAC,根据题意和三角形内角和定理求出∠AOB,代入弧长公式计算,得到答案.【解答】解:连接OA,∵OA=OC,∴∠OAC=∠C=70°,∴∠OAB=∠OAC﹣∠BAC=70°﹣60°=10°,∵OA=OB,∴∠OBA=∠OAB=10°,∴∠AOB=180°﹣10°﹣10°=160°,则的长==8π,故答案为:8π.【点评】本题考查的是弧长的计算、圆周角定理,掌握弧长公式是解题的关键.7.【分析】根据垂径定理得到AD=DC,由等腰三角形的性质得到AB=2OD=2×2=4,得到∠BAE=∠CAE=∠BAC=90°=45°,求得∠ABD=∠ADB=45°,求得AD=AB=4,于是得到DC=AD=4,根据勾股定理即可得到结论.【解答】解:∵OD⊥AC,∴AD=DC,∵BO=CO,∴AB=2OD=2×2=4,∵BC是⊙O的直径,∴∠BAC=90°,∵OE⊥BC,∴∠BOE=∠COE=90°,∴=,∴∠BAE=∠CAE=∠BAC=90°=45°,∵EA⊥BD,∴∠ABD=∠ADB=45°,∴AD=AB=4,∴DC=AD=4,∴AC=8,∴BC===4.故答案为:4.【点评】本题考查了三角形的外接圆与外心,圆周角定理,垂径定理,勾股定理,正确的识别图形是解题的关键.8.【分析】求得圆锥的母线的长利用勾股定理求得圆锥的高即可.【解答】解:设圆锥的母线长为l,则=10π,解得:l=15,∴圆锥的高为:=10,故答案为:10【点评】考查了圆锥的计算,解题的关键是了解圆锥的底面周长等于圆锥的侧面扇形的弧长,难度不大.9.【分析】根据已知条件得到∠AOB=60°,推出△AOB是等边三角形,得到OA=OB=AB=2,根据扇形的面积公式即可得到结论.【解答】解:∵正六边形ABCDEF内接于⊙O,∵OA=OB,∴△AOB是等边三角形,∴OA=OB=AB=2,∴扇形AOB的面积==,故答案为:.【点评】本题考查了正多边形与圆及扇形的面积的计算,解题的关键是熟练掌握扇形的面积公式.10.【分析】根据垂径定理得到AD=4,由勾股定理得到OD==3,求得OA﹣OD=2,根据弧田面积=(弦×矢+矢2)即可得到结论.【解答】解:∵弦AB=8米,半径OC⊥弦AB,∴AD=4,∴OD==3,∴OA﹣OD=2,∴弧田面积=(弦×矢+矢2)=×(8×2+22)=10,故答案为:10.【点评】此题考查垂径定理的应用,关键是根据垂径定理和扇形面积解答.11.【分析】直接利用圆内接四边形的性质:外角等于它的内对角得出答案.【解答】解:∵四边形ABCD为⊙O的内接四边形,∴∠DCE=∠A=100°,故答案为:100°【点评】考查圆内接四边形的外角等于它的内对角.12.【分析】连接OE,作OF⊥DE,先求出∠COE=2∠D=60°、OF=OD=1,DF=OD cos∠ODF=,DE=2DF=2,再根据阴影部分面积是扇形与三角形的面积和求解可得.【解答】解:如图,连接OE,作OF⊥DE于点F,∵四边形ABCD是平行四边形,且∠A=150°,则∠COE=2∠D=60°,∵CD=4,∴CO=DO=2,∴OF=OD=1,DF=OD cos∠ODF=2×=,∴DE=2DF=2,∴图中阴影部分的面积为+×2×1=+,故答案为:+.【点评】本题考查的是扇形面积计算、平行四边形的性质,掌握扇形面积公式:S=是解题的关键.13.【分析】根据正六边形的性质即可得到结论.【解答】解:如图所示为正六边形最长的三条对角线,由正六边形性质可知,△AOB,△COD为两个边长相等的等边三角形,∴AD=2AB=6,故答案为6.【点评】该题主要考查了正多边形和圆的性质及其应用问题;解题的关键是灵活运用正多边形和圆的性质来分析、判断、解答.14.【分析】利用圆周角定理得到∠ADB=90°,∠B=∠ACD=30°,然后根据含30度的直角三角形三边的关系求求AD的长.【解答】解:∵AB为直径,∴∠ADB=90°,∵∠B=∠ACD=30°,∴AD=AB=×2=1.故答案为1.【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.15.【分析】直接利用圆周角定理得出∠BCD=90°,进而得出答案.【解答】解:∵△ABC内接于⊙O,BD是⊙O的直径,∴∠BCD=90°,∵∠CBD=21°,∴∠A=∠D=90°﹣21°=69°.故答案为:69°【点评】此题主要考查了三角形的外接圆与外心,正确掌握圆周角定理是解题关键.16.【分析】连接OC,根据同样只统计得到▱ODCE是矩形,由矩形的性质得到∠ODC=90°.根据勾股定理得到OC=10,根据扇形的面积公式和矩形的面积公式即可得到结论.【解答】解:连接OC,∵∠AOB=90°,四边形ODCE是平行四边形,∴▱ODCE是矩形,∴∠ODC=90°.∵OD=8,OE=6,∴OC=10,∴阴影部分图形的面积=﹣8×6=25π﹣48.故答案为:25π﹣48.【点评】本题考查了扇形的面积的计算,矩形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.17.【分析】连接CD,由圆周角定理得出∠BCD=90°=∠CAB,证明△ABC∽△CBD,得出=,即可得出结果.【解答】解:连接CD,如图:∵BD是⊙O的直径,∴∠BCD=90°=∠CAB,∵∠ABC=∠CBD,∴△ABC∽△CBD,∴=,∴BC2=AB×BD=4×6=24,∴BC==2;故答案为:2.【点评】本题考查了圆周角定理、相似三角形的判定与性质;熟练掌握圆周角定理,证明三角形相似是解题的关键.18.【分析】先根据题意画出图形,再连接OB、OC,过O作OE⊥BC,设此正方形的边长为a,由垂径定理及正方形的性质得出OE=BE=,再由勾股定理即可求解.【解答】解:如图所示,连接OB、OC,过O作OE⊥BC,设此正方形的边长为a,∵OE⊥BC,∴OE=BE=,即a=5.故答案为:5.【点评】本题考查的是正多边形和圆,解答此类问题的关键是根据题意画出图形,利用数形结合求解.19.【分析】根据三角形外角的性质得到∠C=∠ADO﹣∠CAB=65°,根据等腰三角形的性质得到∠AOC =50°,由扇形的面积公式即可得到结论.【解答】解:∵∠ADO=85°,∠CAB=20°,∴∠C=∠ADO﹣∠CAB=65°,∵OA=OC,∴∠OAC=∠C=65°,∴∠AOC=50°,∴阴影部分的扇形OAC面积==,故答案为:.【点评】本题考查了扇形面积的计算,由等腰三角形的性质和三角形的内角和求出∠AOC是解题的关键.20.【分析】由题意得出:四叶幸运草的周长为4个半圆的弧长=2个圆的周长,求出圆的半径,由圆的周长公式即可得出结果.【解答】解:由题意得:四叶幸运草的周长为4个半圆的弧长=2个圆的周长,连接AB、BC、CD、AD,则四边形ABCD是正方形,连接OB,如图所示:则正方形ABCD的对角线=2OA=4,OA⊥OB,OA=OB=2,∴AB=2,过点O作ON⊥AB于N,则NA=AB=,∴圆的半径为,∴四叶幸运草的周长=2×2π×=4π;故答案为:4π.【点评】本题考查了正多边形和圆、正方形的性质以及圆周长公式;由题意得出四叶幸运草的周长=2个圆的周长是解题的关键.21.【分析】如图1,当∠ODB=90°时,推出△ABC是等边三角形,解直角三角形得到BC=AB=5,如图2,当∠DOB=90°,推出△BOC是等腰直角三角形,于是得到BC=OB=5.【解答】解:如图1,当∠ODB=90°时,即CD⊥AB,∴AD=BD,∴AC=BC,∵AB=AC,∴△ABC是等边三角形,∴∠DBO=30°,∵OB=5,∴BD=OB=,∴BC=AB=5,如图2,当∠DOB=90°,∴∠BOC=90°,∴△BOC是等腰直角三角形,∴BC=OB=5,综上所述:若△OBD是直角三角形,则弦BC的长为5或5,故答案为:5或5.【点评】本题考查了三角形的外接圆与外心,等边三角形的判定和性质,等腰直角三角形的性质,正确的作出图形是解题的关键.22.【分析】利用圆周角与圆心角的关系即可求解.【解答】解:∵OA⊥BC,∴=,∴∠AOB=2∠ADC,∵∠ADC=30°,∴∠AOB=60°,故答案为60°.【点评】此题考查了圆周角与圆心角定理,熟练掌握圆周角与圆心角的关系是解题关键.23.【分析】利用弧长=圆锥的底面周长这一等量关系可求解.【解答】解:连接AB,过O作OM⊥AB于M,∵∠AOB=120°,OA=OB,∴∠BAO=30°,AM=,∴OA=2,∵=2πr,∴r=故答案是:【点评】本题运用了弧长公式和圆的周长公式,建立准确的等量关系是解题的关键.24.【分析】由切线的性质得出P A=PB,P A⊥OA,得出∠P AB=∠PBA,∠OAP=90°,由已知得出∠PBA=∠P AB=90°﹣∠OAB=52°,再由三角形内角和定理即可得出结果.【解答】解:∵P A,PB是⊙O的切线,∴P A=PB,P A⊥OA,∴∠P AB=∠PBA,∠OAP=90°,∴∠PBA=∠P AB=90°﹣∠OAB=90°﹣38°=52°,∴∠P=180°﹣52°﹣52°=76°;故答案为:76.【点评】本题考查了切线的性质、直角三角形的性质、等腰三角形的性质以及三角形内角和定理;利用切线的性质来解答问题时,解此类问题的一般思路是利用直角来解决问题.25.【分析】设⊙O的半径为r.在Rt△ADO中,AD=5,OD=r﹣1,OA=r,则有r2=52+(r﹣1)2,解方程即可.【解答】解:设⊙O的半径为r.在Rt△ADO中,AD=5,OD=r﹣1,OA=r,则有r2=52+(r﹣1)2,解得r=13,∴⊙O的直径为26寸,故答案为:26.【点评】本题考查垂径定理、勾股定理等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.26.【分析】连接OB,作OH⊥BC于H,如图,利用等边三角形的性质得AB=BC=AC=2,∠ABC=60°,再根据三角形内切圆的性质得OH为⊙O的半径,∠OBH=30°,再计算出BH=CH=1,OH=BH =,然后根据扇形的面积公式,利用阴影部分面积=3S弓形AB+S△ABC﹣S⊙O=3(S扇形ACB﹣S△ABC)+S△ABC﹣S⊙O进行计算.【解答】解:连接OB,作OH⊥BC于H,如图,∵△ABC为等边三角形,∴AB=BC=AC=2,∠ABC=60°,∵⊙O是△ABC的内切圆,∴OH为⊙O的半径,∠OBH=30°,∵O点为等边三角形的外心,∴BH=CH=1,在Rt△OBH中,OH=BH=,∵S弓形AB=S扇形ACB﹣S△ABC,∴阴影部分面积=3S弓形AB+S△ABC﹣S⊙O=3(S扇形ACB﹣S△ABC)+S△ABC﹣S⊙O=3S扇形ACB﹣2S△ABC﹣S⊙O =3×﹣2××22﹣π×()2=π﹣2.故答案为π﹣2.【点评】本题考查了三角形的内切圆与内心:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.也考查了等边三角形的性质和扇形面积公式.27.【分析】先根据勾股定理求出圆锥的母线为4,进而求得展开图的弧长,然后根据弧长公式即可求解.【解答】解:设圆锥的母线为a,根据勾股定理得,a=4,设圆锥的侧面展开图的圆心角度数为n°,根据题意得2π•1=,解得n=90,即圆锥的侧面展开图的圆心角度数为90°.故答案为:90.【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.28.【分析】根据底面周长等于圆锥的侧面展开扇形的弧长列式计算即可.【解答】解:设圆锥的母线长为l,根据题意得:=2π×4,解得:l=12,故答案为:12.【点评】考查了扇形的弧长公式;圆的周长公式;用到的知识点为:圆锥的弧长等于底面周长.29.【分析】圆锥的底面圆的半径为r,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到2πr=,解得r=3,然后根据勾股定理计算出圆锥的高.【解答】解:设圆锥的底面圆的半径为r,根据题意得2πr=,解得r=3,所以圆锥的高==4(cm).故答案为4.【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.30.【分析】利用圆锥的底面周长和母线长求得圆锥的侧面积,然后再利用圆锥的面积的计算方法求得侧面展开扇形的圆心角的度数即可.【解答】解:∵圆锥的底面圆的周长是5πcm,∴圆锥的侧面展开扇形的弧长为5πcm,∴=5π,解得:n=150故答案为150°.【点评】本题考查了圆锥的计算,解题的关键是根据圆锥的侧面展开扇形的弧长等于圆锥的底面周长来求出弧长.31.【分析】直接利用弧长公式l=即可求出n的值,计算即可.【解答】解:根据l===11π,解得:n=110,故答案为:110.【点评】本题考查了扇形弧长公式计算,注意公式的灵活运用是解题关键.32.【分析】根据正多边形内角和公式可求出∠E、∠D,根据切线的性质可求出∠OAE、∠OCD,从而可求出∠AOC,然后根据圆弧长公式即可解决问题.【解答】解:∵五边形ABCDE是正五边形,∴∠E=∠A==108°.∵AB、DE与⊙O相切,∴∠OBA=∠ODE=90°,∴∠BOD=(5﹣2)×180°﹣90°﹣108°﹣108°﹣90°=144°,故答案为:144.【点评】本题主要考查了切线的性质、正五边形的性质、多边形的内角和公式、熟练掌握切线的性质是解决本题的关键.33.【分析】根据切线的性质得出△ABD是直角三角形,DB2=CD•AD,根据勾股定理求得AB,即可求得AE,然后分两种情况求得AP的长即可.【解答】解:∵过B点的切线交AC的延长线于点D,∴AB⊥BD,∴AB===8,当∠AEP=90°时,∵AE=EC,∴EP经过圆心O,∴AP=AO=4;当∠APE=90°时,则EP∥BD,∴=,∵DB2=CD•AD,∴CD===3.6,∴AC=10﹣3.6=6.4,∴AE=3.2,∴=,∴AP=2.56.综上AP的长为4和2.56.故答案为4和2.56.【点评】本题考查了切线的性质,勾股定理的应用,垂径定理的应用,平行线的判定和性质,分类讨论是解题的关键.34.【分析】根据图形可知,阴影部分的面积是半圆的面积与扇形ABC的面积之和减去半圆的面积.【解答】解:由图可得,图中阴影部分的面积为:=6π,故答案为:6π.【点评】本题考查扇形面积的计算、旋转的性质,解答本题的关键是明确题意,利用数形结合的思想解答.35.【分析】过O作OM⊥AC于M,延长MO交⊙O于P,则此时,点P到AC距离的最大,且点P到AC距离的最大值=PM,解直角三角形即可得到结论.【解答】解:过O作OM⊥AC于M,延长MO交⊙O于P,则此时,点P到AC的距离最大,且点P到AC距离的最大值=PM,∵OM⊥AC,∠A=∠BPC=60°,⊙O的半径为6,∴OP=OA=6,∴OM=OA=×6=3,∴PM=OP+OM=6+3,∴则点P到AC距离的最大值是6+3,故答案为:6+3.【点评】本题考查了三角形的外接圆与外心,圆周角定理,解直角三角形,正确的作出辅助线是解题的关键.36.【分析】过A作AM⊥BC于M,EN⊥BC于N,根据等边三角形的性质得到AM=BC=×2=,求得EN=AM=,根据三角形的面积和扇形的面积公式即可得到结论.【解答】解:过A作AM⊥BC于M,EN⊥BC于N,∵等边三角形ABC的边长为2,∠BAC=∠B=∠ACB=60°,∴AM=BC=×2=,∵AD=AE=1,∴AD=BD,AE=CE,∴EN=AM=,∴图中阴影部分的面积=S△ABC﹣S扇形ADE﹣S△CEF﹣(S△BCD﹣S扇形DCF)=×2×﹣﹣×﹣(×﹣)=+﹣,故答案为:+﹣.【点评】本题考查了扇形的面积的计算,等边三角形的性质,正确的作出辅助线是解题的关键.37.【分析】延长DC,CB交⊙O于M,N,根据圆和正方形的面积公式即可得到结论.【解答】解:延长DC,CB交⊙O于M,N,则图中阴影部分的面积=×(S圆O﹣S正方形ABCD)=×(4π﹣4)=π﹣1,故答案为:π﹣1.【点评】本题考查了扇形面积的计算,正方形的性质,正确的识别图形是解题的关键.38.【分析】根据题意,作出合适的辅助线,即可求得CD和∠COB的度数,即可得到阴影部分的面积是半圆的面积减去△AOC和扇形BOC的面积.【解答】解:连接OC、BC,作CD⊥AB于点D,∵直径AB=6,点C在半圆上,∠BAC=30°,∴∠ACB=90°,∠COB=60°,∴AC=3,∵∠CDA=90°,∴CD=,∴阴影部分的面积是:=3π﹣,故答案为:3π﹣.【点评】本题考查扇形面积的计算、圆周角定理,解答本题的关键是明确题意,利用数形结合的思想解答.39.【分析】根据题意,作出合适的辅助线,然后根据图形可知阴影部分的面积是△AOD的面积与扇形OBC的面积之和再减去△BDO的面积,本题得以解决.【解答】解:作OE⊥AB于点F,∵在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥OA.OA=2,∴∠AOD=90°,∠BOC=30°,OA=OB,∴∠OAB=∠OBA=30°,∴OD=OA•tan30°=×=2,AD=4,AB=2AF=2×2×=6,OF=,∴BD=2,∴阴影部分的面积是:S△AOD+S扇形OBC﹣S△BDO==+π,故答案为:+π.【点评】本题考查扇形面积的计算,解答本题的关键是明确题意,利用数形结合的思想解答.。
六年级上册数学素材-【六暑】尖端班讲义第四讲直线型计算综合(一)(无答案) 全国通用

第4讲 直线型计算综合(一)知识点回顾一、等积变形等底等高的两个三角形面积相等,这就是说两个三角形的形状可以不同,但只要底与高分别相等,它们的面积就相等。
第一类:两个三角形有一个公共顶点,而这个公共顶点所对的边在一条直线上且相等。
第二类:两个三角形有一条公共的底边,而这条底边上的高相等,即这条底边所对的顶点在一条与底边平行的直线上。
二、比例模型两个三角形的高相等,面积比等于它们的底边之比 两个三角形的的底相等,面积之比等于它们的高之比三、鸟头模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上), 则:():()ABC ADE S S AB AC AD AE =⨯⨯△△图⑴ 图⑵EDCBAEDCB A四、蝴蝶模型任意四边形中的比例关系(“蝶形定理”或“蝴蝶模型”): ①1243::S S S S =或者1324S S S S ⨯=⨯ ②()()1243::AO OC S S S S =++蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径。
通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
本讲重点1. 等积变形2. 三角形内接正方形3. 鸟头模型4. 蝴蝶模型A BCDO ba S 3S 2S 1S 4热身小练习1.如下图,在三角形ABC中,DC=2BD,CE=3AE,阴影部分的面积是20平方厘米,三角形ABC的面积是平方厘米。
2.图中两个正方形的边长分别是5cm和3cm,阴影部分的面积是2cm。
3.下图的三角形ABC 中,AD:DC=2:3,AE=EB,则甲乙两个图形面积的比是。
典型例题例1:如图,正方形ABCD的边长为12,P是AB边上任意一点,点M,N,I,H分别是边BC,AD的三等分点,点E,F,G是边CD的四等分点,求图中阴影部分面积。
三角形内接矩形的关系式及其应用

三角形内接矩形的关系式及其应用作者:沐文中来源:《中学数学杂志(初中版)》2013年第02期如果矩形有四个顶点都在三角形的边上,那么这个矩形称为此三角形的内接矩形.三角形及其内接矩形有一个应用广泛的关系式,现介绍如下:命题如图1,矩形EFGH的两个顶点E、H在BC上,另外两个顶点F、G分别在AB、AC上,若BC=a,BC边上的高AD=h,EF=Y,FG=x,则xa+yh=1.证明因为FG∥BC,所以△AFG∽△ABC,所以FGBC=AKAD,即xa=h-yh,所以xa+yh=1.这一关系或在课标入教版,北师大版,华师大版等教材中均有所介绍.下面就举例说明此关系式在中考中的应用.例1 (2012年山东日照)如图2,在Rt△ABC内有矩形PQMN,P、N分别在直角边AB、AC上,Q、M在斜边BC上,已知AB=3,AC=4,内接矩形PQMN的面积等于53,求BQ和MC的长.解因为AB=3,AC=4,所以BC=32+42=5.作AD⊥BC于D,则由AD·BC=AB·AC=2S△ABC得AD=3×45=125.设PQ=y,PN=x,则由关系式,得x5+y125=1. ①又xy=53(已知)②故解①、②得y=2或y=25.因为Rt△CMN∽Rt△CAB,所以CMMN=CAAB即CM=43y,所以CM=83或CM=815.同理可得BQ=34y,故BQ=32或BQ=310.点评本题借助三角形内接矩形的关系式和矩形面积公式列出二元一次方程组,简捷明快地先求得了PQ和PN的长度,然后再通过相似三角形求得BQ和MC的长度,使问题由繁变简,从而使复杂的问题简单化了.例2 (2012年辽宁大连)如图3,在Rt△ABC的斜边AB上任取一点P,过P点作AC、BC的平行线分别交BC、AC于N、M,则△APM和△PBN的面积之和不小于矩形MPNC的面积,试证明之.证明设AC=b,BC=a,PM=x,PN=y,S矩形MPNC=S1,S△APM+S△PBN=S由关系式点评本题应用上述关系式和面积公式,通过变形化简求得xa与yb的积与和,利用韦达定理的逆定理,构造出一元二次方程,再运用根的判别式得证.这种解题思路充分体现了构造法解题的科学性,符合新课程的理念要求,它能使抽象或隐含的条件清晰地显示出来,能把复杂的问题转化为简单的问题,因而解题时,就能化繁为简,变难为易.例3 (2012年云南大理)一张等腰三角形纸片,底边长15cm,底边上的高长225cm,现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条,如图4所示.已知剪得的纸条中有一张是正方形,则这张正方形纸条是第几张?所以这张正方形的纸条是第6张.点评本题是一道创新中考试题,通过六次运用本文的关系式,最后求得JK的长为3厘米,从而使实际问题得到了解决,如果不用三角形内接矩形的上述性质求解,将会使思路陷入困境.例4 (2012年山西大同)已知△ABC和内接矩形EFGH(如图5),问:在什么条件下,矩形EFGH的面积最大?解如图5,作AC边上的高BI,交EF于J,设BI=h,AC=b,则由题设条件,可设EH=x,所以由关系式得EFb+xh=1,故EF=bh(h-x),所以矩形EFGH的面积S=f(x)=EF·EH=bh(h-x)x=-bhx2+bx.因为-bh〈0,所以二次函数f(x)有最大值.故当x=--b2·bh=h2时,f(x)max=0-b24-bh=bh4=12S△ABC,这时,EF=bh(h-h2)=b2,所以,当内接矩形的长、宽分别等于三角形的底边和底边上的高的一半时,其面积最大.点评本题是运用本文的关系式和矩形面积公式先求得二次函数解析式,再运用二次函数求最大值的方法,求得矩形面积的最大值,方法新,过程简,易理解,要重视.综上述可知,应用本文关系式解中考问题,其关键在于要从问题的实际出发,根据题设去灵活应用.通过教学实践,笔者认为:注意对学生进行联系课本内容的专题讲座的训练,利于帮助学生理解课本内容提高学习数学的兴趣,利于拓宽学生的视野,提高解题水平,利于启迪学生思维,调动学习的积极性.因此在今后的教学过程中,注意对学生进行这类专题内容的探索与研究,是很有必要的.。
相似三角形内接正方形问题例析

证: P Q : = P D’ Q G . 分析 : ( 1 )根 据 同角的余 角相 等 即可证 得
AA D E =/ - - - B , 然后根 据有 两个 角对应 相等的 三
图 5
角 形 相 似 即 可证 得 ; ( 2 ) 设正方形 D E F G 的边 长 是 , 根 据 AC D G一 △ B, 相 似 三 角 形 对 应 边
一
图 3
图 4
由三 角形 面积 公 式得 :
、
求 边 长
-  ̄ - - A B × A c ÷B C X A M ,
‘ . ‘
例 1 已知正方形 D E F G 内接 于 △A B C 中, 且 E、 F 在B C上 , 点 D、 G分别在 A B . AC上.
B=4, A C=3, BC=5 . AM =2 . 4,
・
.
‘
四边形 D EF G是 正 方形 ,
.
DG =G F = E F - = DE= MN : , DG/ / BC,
AADG∽ AABC, DG AN
,
・
. .
.
‘
旦 : 5 2 . 4
6U
’
5 加=1 , S △ 肋E =3, S△ m产 1 ,
。
‘
.
・ . .
a , A N = b ,根据 三 角形的 面积公 式求 出 B E = 3 b ,
0 6 = 1 , 船 ‘ n 3 , } ‘ 。 = 1 ,
BE=3 b, CF= -b,
‘
C F = b , a b = 2 ,推 出 6 = ① ,根 据 S
j /
;
叶老师五年级ABC试卷秋04图形问题(2)
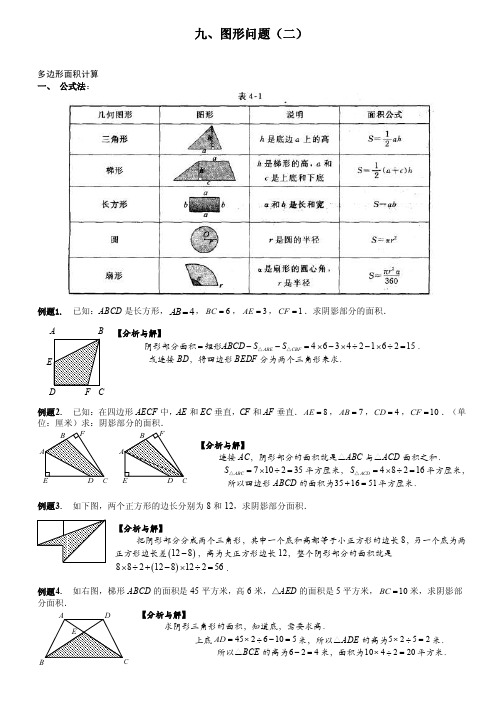
九、图形问题(二)多边形面积计算 一、 公式法:例题1. 已知:ABCD 是长方形,4AB =,6BC =,3AE =,1CF =.求阴影部分的面积.【分析与解】 阴影部分面积4634216215ABE CBF ABCD S S =--=⨯-⨯÷-⨯÷=△△矩形.或连接BD ,将四边形BEDF 分为两个三角形来求.例题2. 已知:在四边形AECF 中,AE 和EC 垂直,CF 和AF 垂直.8AE =,7AB =,4CD =,10CF =.(单位:厘米)求:阴影部分的面积.【分析与解】连接AC ,阴影部分的面积就是△ABC 与△ACD 面积之和.710235ABC S =⨯÷=△平方厘米,48216ACD S =⨯÷=△平方厘米,所以四边形ABCD 的面积为351651+=平方厘米.例题3. 如下图,两个正方形的边长分别为8和12,求阴影部分面积.【分析与解】把阴影部分分成两个三角形,其中一个底和高都等于小正方形的边长8,另一个底为两正方形边长差()128-,高为大正方形边长12,整个阴影部分的面积就是()88212812256⨯÷+-⨯÷=.例题4. 如右图,梯形ABCD 的面积是45平方米,高6米,△AED 的面积是5平方米,10BC =米,求阴影部分面积.【分析与解】 求阴影三角形的面积,知道底,需要求高.上底4526105AD =⨯÷-=米,所以△ADE 的高为5252⨯÷=米.所以△BCE 的高为624-=米,面积为104220⨯÷=平方米.A B C DF二、 割补法: 通过添加辅助线,把不规则图形变成可计算图形; 例题1. 大小两个正方形,大正方形的边长比小正方形的边长多4厘米,大正方形的面积比小正方形的面积多136平方厘米。
大正方形的边长是多少厘米?【分析与解】 大正方形的边长是()1364424419-⨯÷÷+=厘米;例题2. 长方形ABCD 的周长是20厘米,在它的每条边上各画一个以该边为边长的正方形(如下图)。
专题10 面积计算(组合图形的面积)(原卷)

2022-2023学年小学六年级思维拓展举一反三精编讲义专题10 面积计算(组合图形的面积)对于一些比较复杂的组合图形,有时直接分解有一定的困难,这时,可以通过把其中的部分图形进行平移、翻折或旋转,化难为易。
有些图形可以根据“容斥问题“的原理来解答。
在圆的半径r用小学知识无法求出时,可以把“r2”整体地代入面积公式求面积。
【典例分析01】如图20-1所示,求图中阴影部分的面积。
【思路导航】解法一:阴影部分的一半,可以看做是扇形中减去一个等腰直角三角形(如图20-2),等腰直角三角形的斜边等于圆的半径,斜边上的高等于斜边的一半,圆的半径为20÷2=10厘米【3.14×102×14-10×(10÷2)】×2=107(平方厘米)答:阴影部分的面积是107平方厘米。
解法二:以等腰三角形底的中点为中心点。
把图的右半部分向下旋转90度后,阴影部分的面积就变为从半径为10厘米的半圆面积中,减去两直角边为10厘米的等腰直角三角形的面积所得的差。
(20÷2)2×12-(20÷2)2×12=107(平方厘米)知识精讲典例分析【典例分析02】如图20-6所示,求图中阴影部分的面积(单位:厘米)。
【思路导航】解法一:先用长方形的面积减去小扇形的面积,得空白部分(a )的面积,再用大扇形的面积减去空白部分(a )的面积。
如图20-7所示。
3.14×62×14 -(6×4-3.14×42×14 )=16.82(平方厘米)解法二:把阴影部分看作(1)和(2)两部分如图20-8所示。
把大、小两个扇形面积相加,刚好多计算了空白部分和阴影(1)的面积,即长方形的面积。
3.14×42×14 +3.14×62×14 -4×6=16.28(平方厘米) 答:阴影部分的面积是16.82平方厘米。
小专题11 三角形内接特殊四边形问题

专题讲解 |单元自测|滚动学习 | 科学高效
第四章 图形的相似 小专题11 三角形内接特殊四边形问题 ——教材P122复习题T21的变式与应用
可编辑PPT
请双击文本框弹出对象, 便可编辑修改哦!!
【教材母题】 (教材 P122 复习题 T21)一块直角三角形木板的面积为 1.5 m2,一条直角边 AB 为 1.5 m,怎样才能把它加工成一个无拼接的 面积最大的正方形桌面?甲、乙两位木匠的加工方法如图所示,请你 用学过的知识说明哪位木匠的方法符合要求(加工损耗忽略不计,计算 结果中的分数可保留).
则1x20=808-02x, 解得 x=30,∴2x=60. ∴长为 60 mm,宽为 30 mm.
②PN 为宽,PQ 为长,
则122x0=808-0 x, 解得 x=2470,∴2x=4780. ∴长为4780 mm,宽为2740 mm. 答:矩形的长为 60 mm,宽为 30 mm 或长为4870mm,宽为2470mm.
设甲设计的桌面边长为 x m, ∵DE∥AC,∴∠BDE=∠C,∠BED=∠A. ∴△BDE∽△BCA. ∴BBHP=ADCE,即1.12.-2 x=2x.5,解得 x=3370. 在图乙中,设正方形的边长为 y m, ∵DE∥AB,∴∠CDE=∠B,∠CED=∠A. ∴△CDE∽△CBA. ∴CCDB=AEDB,即2-2 y=1y.5,解得 y=3305. ∵y>x,∴图乙中的正方形面积较大. ∴乙木匠的方法符合要求.
解:由 AB=1.5 m,S△ABC=1.5 m2,可得 BC=2 m,在图甲中,过点 B 作 Rt△ ABC 斜边 AC 上的高,BH 交 DE 于点 P,交 AC 于点 H.由 AB=1.5 m,BC=2 m,得 AC= AB2+BC2=2.5(m), 由 AC·BH=AB·BC 可得 BH=ABA·CBC=1.2(m).
三角形内接正方形的一个关系式及其应用

三角形内接正方形的一个关系式及其应用-权威资料本文档格式为WORD,若不是word文档,则说明不是原文档。
最新最全的学术论文期刊文献年终总结年终报告工作总结个人总结述职报告实习报告单位总结如果正方形的四个顶点都在三角形的边上,那么这个正方形称为此三角形的内接正方形.关于三角形的内接正方形问题,有一个应用广泛的关系式:若三角形的一边长为a,这边上的高为h,则立在这边上的内接正方形的边长为aha+h.证明如图1,设△ABC的内接正方形边长为x,BC=a,AD=h,则因为OR∥BC,所以△AOR∽△ABC,所以ORBC=AFAD,即xa=h-xh,所以x=aha+h.这一关系式即为北师大版义务教育课程标准实验教科书《数学》八年级下册第147页的例题.利用这个关系式,可以解答三角形的内接正方形的有关问题,现以部分竞赛题为例说明如下.例1 (1991年全国初中数学联赛试题)如图1,正方形OPQR内接于△ABC,已知△AOR、△BOP和△CRQ的面积分别是S1=1、S2=3和S3=1,那么,正方形OPQR的边长是()A.2B.3C.2D.3解作AD⊥BC于D,交OR于F,设正方形OPQR的边长为x,则1=S1=12x·AF,从而有AF=2x,同理可得BP=6x,QC=2x,于是BC=x+8x,AD=x+2x.所以由上述关系式得x=(x+8x)(x+2x)x+8x+x+2x,化简整理得x4=16,因为x为正,所以x=2,故选C.点评本题通过设内接正方形的边长为x,先利用三角形的面积公式,求得AF、BP、QC用x表示的分式,再运用三角形内接正方形的关系式列出一个分式方程,最后求得x,由于运用代数方法解决了几何问题,因而数形结合,问题也由繁变简了.例2 (第五届美国数学邀请赛试题)如图2,△ABC (∠C=Rt∠)的两个内接正方形DFCE、PQMN的面积分别是S1=441、S2=440,求AC+BC的值.解令BC=a,AC=b,AB=C,斜边上的高为h,则由上述关系式得S1=aba+b,S2=chc+h.注意到ab=ch,a2+b2=c2,即有S1=c2h2c2+2ch,而有c2+2ch=c2h2S1,于是S2=c2h2c2+2ch+h2=c2h2c2h2S1+h2=c2S1c2+S1,由此解得c2=S1S2S1-S2.再注意到ad=S1(a+b),即有c2=a2+b2=(a+b)2-2ab=(a+b)2-2S1(a+b),从而有c2+S1=(a+b-S1)2,于是S1S2S1-S2+S1=(a+b-S1)2,由此可解得ab=S1+S1S1-S2.将S1=441,S2=440代入上式即得a+b=462,即AC+BC的值为462.点评本题比较复杂,如用常规方法求解,将很困难.然而两次运用了三角形内接正方形的关系式,结合三角形面积化简轻松求得结果.本题又是一道代数与几何融为一体的综合题,解题关键是通过数形结合方法直观解题,因而有明显的选拔功能和考查功能.例3 (1986年美国第四届数学邀请赛试题)证明边长为2的正方形必不能被三边分别为3、4、5的三角形所覆盖.证明令△ABC的边AC=3,BC=4,AB=5,则∠ACB=Rt∠,如图3可知,正方形DECF为内接于Rt△ABC的最大正方形,设CE=x,由上述关系式得x=3×43+4=127.因为127<2,所以边长为2的正方形必不能被三边分别为3、4、5的三角形所覆盖.点评本题设计比较新颖,难度不太大,只要运用三角形内接正方形的关系式求得正方形边长127,再通过与已知正方形边长2比较就可以了.例4 如图4,在锐角△ABC中内接一正方形PQMN,试证明这正方形的面积不超过三角形ABC面积之半,(1978年广东省中学生数学竞赛题).证明设△ABC的底边BC=a,高AD=h,正方形边长为x,由三角形的内接正方形的关系式得xa+xh=1. ①又SPQMN=x2,即xa·xh=SPQMNah②所以由①、②知xa、xh是方程z2-z+SPQMNah=0的两个实数根.所以Δ≥0,即(-1)2-4×1×SQPMNah≥0.从而得SPQMN≤ah4=12.12ah=12S△ABC,即SPQMN≤12S△ABC.点评本题是一道几何与韦达定理,一元二次方程根的判别式构成的综合题.解题关键是先利用三角形内接正方形的关系式求得x=aha+h推出xa+xh=1①,再由SPQMN=x2推出xa·xh=SPQMNah②,然后利用韦达定理的逆定理,利用①、②构造出一元二次方程z2-z+SPQMNah=0,最后应用根的判别式Δ≥0得证,这种解题主法充分体现了构造法解题的科学性,符合新课程的理念要求,利于激发学生的学习数学的积极性,利于培养学生的创新和探索精神.例5 如图5,正方形EFGH内接于△ABC,设BC=ab(这是一个两位数),EF=C,三角形的高AD=d,已知a,b,c,d 恰好是从小到大的四个连续正整数,试求△ABC的面积,(1997年安徽省部分地区初中数学竞赛题)解由上述关系式得 1d+ 1 ab=1c,依题意有b=a+1,c=a+2,d=a+3,则ab=10a+b=11a+1,所以1a+3+111a+1=1a+2.化简得(a-3)2=4,所以a-3=±2,a1=1,a2=5.当a=1时,S△ABC=12·ab·d=12×12×4=24;当a=5时,S△ABC=12·ab·d=12×56×8=224.点评本题是一道几何与代数相结合的综合题,解题关键是先利用关系式写出1d+1ab=1c再结合b=a+1,c=a+2,d=a+3,通过化简变形求得a的值,最后求得S△A BC.这是一道创新的竞赛题,由于数形结合,因而符合新课程改革的理念要求.综上所述可知,应用本文中的关系式解竞赛问题,其关键在于要从问题的实际出发,根据题设去灵活运用,通过教学实践,笔者认为,注意对学生进行课本内容的探究应用的研究,有利于培养学生的思维品质,有利于调动学生学习的积极性,有利于提高学生的专题总结水平,有利于融会贯通所学过的几何代数知识,有利于培养学生研究数学的兴趣,有利于提高教与学的质量.阅读相关文档:140例口腔颌面部恶性肿瘤临床病理分析国内职教动态信息若干则厄贝沙坦氢氯噻嗪治疗原发性高血压疗效观察颅脑外伤术后应激性溃疡护理研究结合Illustrator教学实例探讨直接教学模式中职项目Access数据库的有效教学实践藏药涂抹药的应用前景研究白内障术前术后护理体会《数控系统数据备份与恢复》单元教学设计案例研究 50例脑梗塞并肺部感染致气道阻塞病人的护理体会电视节目低俗化的深层反思截瘫患者临床护理体会 1例骨盆肿瘤切除及人工骨盆重建术的护理体会浅谈胃切除患者手术后早期经口饮食的护理对32例妊娠高血压患者的综合护理分析护理干预配合临床中西医*本文若侵犯了您的权益,请留言。
几个常见几何图形内接正方形的作图方法及其应用

几个常见几何图形内接正方形的作图方法及其应用本文从网络收集而来,上传到平台为了帮到更多的人,如果您需要使用本文档,请点击下载按钮下载本文档(有偿下载),另外祝您生活愉快,工作顺利,万事如意!几何是中学数学课程里的传统主要内容之一,不仅仅是因为它对培养人的逻辑思维能力、推理论证能力具有重要教育价值,更是在现代科技中也有重要的地位,因此学习几何和几何教育受到了全世界的广泛关注,然而几何的教育在我国的中学生身上总存在很多困难,畏惧几何。
由于数学向来有着枯燥乏味的坏名声,它的高度抽象和概括性,严谨的逻辑思维让一部分人在小学就开始觉得它晦涩难懂,在中学的几何更是严格的逻辑要求使学生觉得学习几何太难太抽象了。
现在的学生缺乏学习的主动钻研和创新精神,动手能力差,都习惯与一步一步的跟着老师的套路学习,不会画图、不会看图,同时书上的图形没有进行研究和利用,反而成了学习的障碍,不善于与周围的实际生活联想,解决问题的意识淡薄,还停留在只会做现成题的水平,思维和眼界狭隘。
本为主要通过对一些中学里常见的几何图形的内接正方形的作图方法及其应用的整理和研究,从而使之成为几何学习有趣的一个例子,在学习几何不仅仅是书本上的东西,每个有兴趣的同学可以通过自己的看法和想法去研究相关的东西,这与我们想要的创新有着密切的联系,达到激发更多的人喜爱和研究几何这门学科,希望给读者以启发。
1几何学的起源及其发展几何是数学的一门分科,在古代埃及为兴建尼罗河水利工程,曾经进行过测地工作,使它逐渐发展成为几何学。
公元前约三百年,,古希腊数学家欧几里德把前人生产实践中长期积累的几何学的研究加以整理总结为演绎体系,写成了《几何原本》。
我国对几何学的研究也有悠久的历史。
早在上古时期,我国劳动人民就已利用规矩来制作方圆。
秦汉五百年成书的《周髀算经》和《九章算术》中,对图形面积的计算已有记载,刘徽、祖冲之、王孝通等对几何学都有重大贡献。
十七世纪欧洲工业迅速发展起来,以前所用的几何方法不能满足实际需要,这就使笛卡尔利用代数方法研究几何问题,建立了解析几何。
三角形内接正方形的解法

三角形内接正方形的解法■杨光雄北师大版义务教育课程标准试验教科书《数学》八年级下册第147 页的例题图1如图1,A D是△A B C的高,点P、Q在B C边上,点R在A C边上,点S在A B边上,B C=60c m,A D=40 c m,四边形P QRS是正方形.(1)△A SR与△A B C相似吗?为什么?( 2)求正方形PQRS 的边长.思考与探究: 由正方形PQRS 可知SR∥ BC,故△A SR∽△A B C,依此有形的一边落在三角形的一边上,其余两个顶点分别在三角形的另外两边上,则这样的正方形叫做三角形的内接正方形.图2( 1) 如图2,在△ABC 中,B C=a,B C边上的高A D=h a,E F G H是△A B C的内接正方形,设正方形EFGH 的边长是x,求证: x =a h a; (2)在Rt△A B C中,A B=4,A C=3,∠B A C= a + haSR= ASBC AB同理△BPS ∽ △BDA,Ⓒ图3 图490°、请在图3、图4 中分别画出可能的内接正方形,并根据计算回答哪个内接正方形的面积大.又得SPAD= SBABⒸ解析: (1) 依本文结论( B) ,有1 =x1 +1 =a ha根据上述探讨,我们有:⑴Ⓒ+Ⓒ,得SRBCSPAD= a + h aaha,所以x =ah a.a + ha1;( A)(2)如果SR=S P,则( A)式变为1+1=BC AD 1( 2) 可能的内接正方形分别如图3、图4 中的E F G H、E F G H.在图3中作A D⊥B C于点D,易知B C=( B) .SR至此,例题中的两个小题可轻松方便地解答完毕.不仅如此,我们还顺便得到了( A) ( B) 两个优美漂亮5,据三角形的面积公式,有1×3×4=2所以A D=12.51 ×5 × AD,2的结论,它们的应用较为广泛,特别是在解答某些较难的问题时作用更大,常化难为易化繁为简,收到出奇制胜的效果.兹以部分中考与竞赛试题为例说明如下,供大家参考.例1 ( 2004 年广东佛山市中考试题) 如果正方对图3、图4 分别运用本文结论( B),得1 =1 +HG BC1 =1 +1 = 37;1 =1 +1 =1 +1 =7AD 5 12 /5 60 HE AB AC 4 3 12 =35.所以1>1,H G>H E.所以在直角三角形中,60 HG HE作者简介: 杨光雄,中学高级教师,主要从事初中数学教学研究+内接正方形的一边落在直角边上时,正方形的面积最大.例 2 ( 1991 年全国初中数学联赛试题) 如图 5, 正方形 O P Q R 内接于 △A B C . 已知 △A O R、△BO P 和 周长的值在什么情况下是有理数? 在什么情况下是无理数?解析: 设 B C = a ,A D = h ,S R = p ,S P = q . 由本文结论( A ) ,得图 7△C RQ 的面积分别是 S 1 = 1、S 2 = 3 和 S 3 = 1. 那么,p + q = 1 Ⓒ; 由 已 知 1 ah =正方形 OPQ R 的边长是()a h 2( A) ( B) ( C) 2 ( D) 3 3pq ,有 p • q 1 pq = 2 1 pq=2 = 1Ⓒ. 解析: 作A D ⊥ B C 于D ,交O R 于F . 设O R = O P =P Q = Q R = x ,则1 = S = 1 x •A F ,所以 A F = 2; 同a h 1 ah2 p 3pqp 6 1 p q 2 xⒸ2- 4 × Ⓒ 得 ( a - ) 2 = h 3 ,即 a - h = 理 B P = 6 ,Q C = 2 . 所以 B C = x + 8 ,A D = x + 2. x x xx± 槡3 ,Ⓒ 把 Ⓒ 与 Ⓒ 分别相加、减可解得: p = 1 ( 1 ± 据本文结论( B) ,有 1 = x1 + 8 3 1 ,注意 x2 321 3 x + x x + x槡) a ,q = 3 ( 1 槡) h . 2 3> 0,解得 x = 2,故正确答案应选( C ) .图 5 图 6例 3 ( 1997 年安徽省初中数学竞赛试题) 如图 6,正方形 E F G H 内接于△A B C ,设 B C = a b ( 这是一个两位数) ,E F = c ,三角形的高 A D = d . 已知 a 、b 、c 、d 恰好是从小到大的四个连续正整数. 试求 △ABC 的面积.解析: 由本文结论( B) ,有1 = 1 + 1依题意设 b 于是,矩形 PQ RS 的周长值为: 2p + 2q = a + h ± 槡3 ( a - h ) . 当 a = h 时,矩形 PQ RS 的周长值为有理 3数; 当 a ≠ h 时,矩形 PQ RS 的周长值为无理数.例 5 ( 1997 年安徽省部分地区初中数学竞赛试题) 在一块锐角三角形的斜料上,加工成正方形零件, 使正方形的四个顶点都在三角形的边上. 若三角形的 三边长分别为 a 、b 、c ,且 a > b > c . 问正方形的两个顶点放在哪条边上可使得加工出来的正方形零件面积最大?c d ab= a + 1,c = a + 2,d = a + 3,则a b = 10a + b = 11a+ 1. 所以 1 = 1 + 1 ,化简得( a - 3) 2=a + 2 a + 3 11a + 1 4,所以 a - 3 = ± 2,a 1 = 1,a 2 = 5. 1 1图 8图 9解析: 由面积关系式 1 a •AD = 1c •CG = S当 a = 1 时,S △ABC = 2 •ab •d = 2 × 12 × 4 = 2 2△ABC11= S ,有 1 = a ,1 = c( 如 图 8 与 图 9)24; 当a = 5 时,S △A B C = 2 •ab •d = 2 × 56 × 8 = 224.AD 2S CG 2S例 4 ( 1985 年广州、武汉、福州初中数学联赛试 依本文结论( B) 得 1= 1 + 1 = 1 + a ,Ⓒ 题) 如图7,△ABC 的面积是它内接矩形 PQ RS 面积的 3倍,且边 BC 和高 AD 的值是有理数. 问矩形 PQ RS 的1 1 1 MN = c + CG = PS a AD a 2S 1 cc + 2S Ⓒ•8•槡2 槡3 1槡S 1 - S 2槡S 1 - S 2 1 •9•11 ( a - c ) ( ac - 2S )1 1 11 a2 + b 2+ 2abⒸ - Ⓒ 得PS- MN=2acSⒸ= c + h ,所以 S= a 2 b 2=所以 c = A B > A D =2S,所以 a c > 2S ,a c - 2S > ac 2+ 2ch 2 2,c h0,由 a - c > 0,故由 Ⓒ 知 1 - 1> 0,1c 2 + 2ch + h 21 h 211PS MN= c 2h 2= S + c 2 h 2 = S+ 2 , c所以 P S < M N ,即 S 正方形P Q RS < S 正方形M N K L . 由于 a > b > c ,所以边 A B 上的内接正方形面积最大.所 以 c 2=S 1 S 2ⒸS 1 - S 2例 6 ( 1997 年第 19 届江苏省初中数学竞赛试 由 Ⓒ 有 ab = 槡S 1 ( a + b ) , 题) 设 △ABC 三边上的三个内接正方形( 有一边在三 角形的一边上,另两个顶点在另两边上) 的面积相等. 证明: △ABC 为正三角形.从而 c 2= a 2+ b 2= ( a + b ) 2- 2ab = ( a + b ) 2- 2 槡S 1 ( a + b ) + S 1 - S 1 = ( a + b - 槡S 1 ) 2- S 1 Ⓒ S S 证明 : 由例 5 中的 Ⓒ 式可知 S 正方形PQ RS = S 正方形M N K L a = c . 因为 △A B C 三边上的三个内接正方 结合 Ⓒ 与Ⓒ,得1 2 S 1 - S 2= ( a + b - 槡S 1 ) 2 - S 1 ,S 2 形的面积相等,所以 △ABC 为正三角形.例 7 ( 第五届美国数学邀请赛试题) 如图 10, △ABC ( ∠C = Rt ∠) 的两个内接正方形DFCE 、PQMN 所以( a + b -S 1,槡S 1 ) 2= 1 ,a + b - S 1 - S 2槡S 1 = 的面积是 S 1 = 441,S 2 = 440,求 A C + B C 的值.S 1故 a + b =+ 槡S 1 .图 10解析: 设 B C = a ,A C = b ,A B = c ,斜边 A B 上的高为 h . 注意到 a b = c h ( 由面积关系式可得) ,a 2+ b 2= 把 S 1 = 441,S 2 = 440 代入上式即得 a + b = 462, 即 A C + B C = 462.[云南省曲靖市会泽县大井一中 ( 654222) ]c 2 ,依本文结论( B) ,有 1 = 1 + 1 Ⓒ槡S 1a b槡S 2 1 S 21。
同圆的内接正三角形与内接正方形的面积-概述说明以及解释

同圆的内接正三角形与内接正方形的面积-概述说明以及解释1.引言1.1 概述概述部分的内容可以从以下几个方面进行展开:概述部分是整篇文章的开场白,主要是对文章的主题进行简要介绍,并引起读者的兴趣。
首先,可以简要介绍同圆的内接正三角形和内接正方形的概念及其性质。
同圆的内接正三角形指的是一个三角形的三个顶点都位于同一个圆的圆周上,并且三个顶点所对应的圆心角都为60的特殊三角形。
内接正方形指的是一个正方形的四个顶点都位于同一个圆的圆周上的特殊方形。
这两种几何形体具有独特的性质,对于解决某些几何问题有着重要的作用。
其次,可以提及本文的目的和意义。
研究同圆的内接正三角形和内接正方形的面积,旨在探究它们之间的数学关系和几何特性。
通过分析和比较它们的面积计算方法,可以深入理解几何形体的性质和几何学的基本原理。
这对于提升数学思维、加深对几何学的理解以及应用数学知识解决实际问题具有重要意义。
最后,可以简要介绍文章的结构和内容安排。
本文将分为引言、正文和结论三部分。
其中,引言部分介绍了同圆的内接正三角形和内接正方形的概念、目的和意义。
正文部分将详细探讨同圆的内接正三角形和内接正方形的定义、性质、构造方法以及面积计算等内容。
结论部分将对文章进行总结,并提出一些讨论和思考的问题。
通过以上的概述,读者可以对本文的主题和内容有一个初步的了解,为接下来的阅读打下基础。
接下来,我们将进入正文部分,详细介绍同圆的内接正三角形和内接正方形的相关知识点。
文章结构(Article Structure)本文将从引言、正文和结论三个部分来探讨同圆的内接正三角形与内接正方形的面积。
以下是各部分的详细内容:1. 引言(Introduction)1.1 概述:在这一部分,我们将介绍同圆的内接正三角形和内接正方形,并强调它们在几何学中的重要性。
1.2 文章结构:这一小节将详细说明本文的结构和各个部分的内容,以帮助读者更好地理解文章的整体框架。
1.3 目的:在这一段,我们将明确本文的目标和研究问题,即探讨同圆的内接正三角形和内接正方形的面积计算方法。
九年级巧解三角形内接正方形

巧解三角形内接正方形北师版八年级下册第147页的例题:如图,AD 是△ABC 的高,点P 、Q 在BC 边上, 点R 在AC 边上,点S 在AB 边上,BC =60cm ,AD=40 cm ,四边形PQRS 是正方形。
(1)△ASR 与△ABC 相似吗?为什么? (2)求正方形PQRS 的边长。
思考与探究:由正方形PQRS 可知SR ∥BC ,于是△ASR ∽△ABC ,依此有SR AS BC AB =①; 同理△BPS ∽△BDA ,又得SP SB AD AB=②. 由①+②,得SR SP 1BC AD+=(*). 又SR=SP ,则(*)式变为111BC AD SR +=. 至此,例题中的两个小题可轻松方便地解答完毕。
不仅如此,我们还顺便得到了两个优美漂亮的结论,它们的应用较为广泛,特别是在解答某些较难的问题时作用更大,常化难为易化繁为简,收到出奇制胜的效果,以部分中考与竞赛试题为例说明如下:例1(广东佛山中考题)如果正方形的一边落在三角形的一边上,其余两个顶点分别在三角形的另外两边上,则这样的正方形叫做三角形的内接正方形。
(1)如图1,在△ABC 中,BC=a ,BC 边上的高AD=h a ,EFGH 是△ABC 的内接正方形,设正方形EFGH 的边长是x ,求证:a aah x a h =+;(2)在Rt △ABC 中,AB=4,AC=3,∠BAC=90º,请在图2、图3中分别画出可能的内接正方形,并根据计算回答哪个内接正方形的面积大。
解析:(1)依本文结论,有111a a a a h x a h ah +=+=,a a ah x a h ∴=+。
(2)可能的内接正方形分别如图2、图3中的EFGH 、EGAH.在图2中作AD ⊥BC 于点D ,易知BC=5.据三角形的面积公式,有AD 5214321⨯⨯=⨯⨯,∴512AD =. 对图2、图3分别运用本文结论,得603712551AD 1BC 1HG 1=+=+=,60351273141AC 1AB 1HE 1==+=+=. ∴HG 1>HE1,HG <HE . ∴在直角三角形中,内接正方形的一边落在直角边上时,正方形的面积最大。
三角形内接正方形

三角形内接正方形一、概念三角形的内接正方形是指正方形四个顶点都在三角形边上的正方形,正方形有4个顶点,而三角形只有3条边,所以,正方形一定有两个顶点在同一条边上,即正方形一定有一条边落在三角形的边上.二、个数分情况讨论:1.在锐角三角形中:(1)如果三角形为等边三角形,则它的内接正方形只有一个.(正方形的边无论落在哪一条边上,根据对称性可知,都是在同一位置).(2)如果三角形为等腰三角形(底与腰不等),则它的内接正方形有2个.一个是正方形的边落在等腰三角形底边上;另一种是正方形的边落在腰上(无论哪个腰,位置是相同的);(3)如果三角形为不等边三角形(三边两两不等),则它的内接正方形有3个.2.在直角三角形中:内接正方形有2个:一个是正方形的边落在斜边上;另一个是正方形的边落在直角边上.3.在钝角三角形中:内接正方形只有1个:即正方形一条边落在斜边上.三、画法1.计算法通过计算,求出三角形内接正方形的边长a,然后在某一边上作三角形的高h,在h上截取一段长度为a 的线段,记下截点,通过截点作这边上的平行线,交另两边于两点,最后通过这两点作h的平行线即可. 2.尺规法利用位似图形的原理,选择一个位似中心和再作出一个正方形便可作出三角形内接最大正方形.方法一:先作个小正方形,再利用位似作出所求的内接正方形。
方法二:1)以△ABC的一边BC为一边,向下作正方形BCYX; 2)连接AX.BY与BC交于E,F.3)分别过E,F作ED,FG分别交AB,AC于D,G. 4)连结DG四边形EFGD便是所求图形由此便探索出了三角形内接最大正方形的一种尺规作法,我们是选顶点A作为位似中心,那么点B,点C可不可以做位似中心呢?答案是肯定的。
一共是四种做法。
四、教材衔接1.如图,四边形EFGH是△ABC内接正方形,BC=27cm,高AD=21cm,求内接正方形EFGH的面积.解:设正方形EFGH的边长为x,设AD与GH的交点为I,∵HG∥BC,∴△AHG∽△ABC,∴AI:AD=GH:BC,正方形EFGH的边长为xcm.∵BC=27,AD=21,∴(21-x):21=x:27,即可求解.点评:本题主要考查正方形的面积、相似三角形的判定与性质,关键在于通过求证△AHG∽△ABC,推出正方形的边长.2. 如图,Rt△ABC(∠C=90°)中有三个内接正方形,DF=9厘米,GK=6厘米,猜想第三个正方形的边长PQ 的长.解:GF=EF-EG=9-6=3,设PQ=x,∵GK∥PQ,∴∠FKG=∠KQP.又∵∠FGK=∠KPQ=90°,∴△FGK∽△KPQ.∴ FGKP=GKPQ.∴ 36-x=6x.解得x=4.答:第三个正方形的边长为4厘米.点评:本题利用了平行线的性质,相似三角形的判定和性质求解.3. 如图所示,四边形EFGH是三角形ABC的内接矩形,AD⊥BC,垂足为D,BC=21cm,AD=14cm,EF:FG=1:2,求矩形EFGH的面积.解:如图,设矩形的边长EF=x,则FG=2x,∵四边形EFGH是三角形ABC的内接矩形,∴EH∥BC,EH=FG,∴△AEH∽△ABC,又∵AD⊥BC,则ID=x,AI=AD-ID,∴ EHBC= AIAD,BC=21cm,AD=14cm,∴ 2x21= 14-x14,解得,x=6cm,即2x=12cm,∴S矩形EFGH=EF×FG=6×12=72cm2.答:矩形EFGH的面积为72cm2.点评:本题主要考查了矩形的性质和相似三角形的判定与性质,知道相似三角形的对应高之比就等于对应边之比,即相识比.五、中考应用(几何综合题,规律型)1.2.把边长为40厘米的正方形ABCD 沿对角线AC 截成两个三角形,在两个三角形内如图所示剪下两个内接正方形M 、N ,则M 、N 的的面积的差是4009平方厘米. 解:正方形M 的面积=20cm ×20cm=400cm 2,设:正方形N 的边长为x ,则存在:x2+ 12×x2+ 12×x2+ 12× 12×x2= 40×402,解得:x2= 32009cm 2,故M 、N 的面积的差为(400- 32009)cm2= 4009cm 2,故答案为 4009cm 2.点评:本题考查了正方形,等腰三角形面积的计算方法,考查了正方形四边相等,各内角均为直角的性质,解本题的关键是正方形N 的面积的计算.3.如图1,在△ABC 中,∠C=90°,AC=4,BC=3,四边形DEFG 为△ABC 的内接正方形,若设正方形的边长为x ,容易算出x 的长为 60/37.探究与计算:(1)如图2,若三角形内有并排的两个全等的正方形,它们组成的矩形内接于△ABC ,则正方形的边长为 60/49;(2)如图3,若三角形内有并排的三个全等的正方形,它们组成的矩形内接于△ABC ,则正方形的边长为 60/61;(3)如图4,若三角形内有并排的n 个全等的正方形,它们组成的矩形内接于△ABC ,请你猜想正方形的边长是多少?并对你的猜想进行证明.解:(1) 6049;(2分) (2) 6061;(2分)(3)若三角形内有并排的n 个全等的正方形,它们组成的矩形内接于△ABC ,正方形的边长是 6025+12n . 证明,如图,过点C 作CN ⊥AB ,垂足为N ,交GF 于点M ,设小正方形的边长为x ,∵四边形GDEF 为矩形,∴GF ∥AB ,CM ⊥GF ,易算出CN= 125,∴ CMCN=GFAB ,即 125-x125=nx5, ∴x= 6025+12n .即小正方形的边长是 6025+12n .(4分)点评:主要考查了正方形,矩形的性质和相似三角形的性质.会利用三角形相似中的相似比来得到相关的线段之间的等量关系是解题的关键. 4. (2009•湘西州)如图,等腰直角△ABC 腰长为a ,现分别按图1,图2方式在△ABC 内内接一个正方形ADFE 和正方形PMNQ .设△ABC 的面积为S ,正方形ADFE 的面积为S1,正方形PMNQ 的面积为S2. (1)在图1中,求AD :AB 的值;在图2中,求AP :AB 的值; (2)比较S1+S2与S 的大小.。
相似三角形性质1应用三角形内接矩形问题
挑战一下吧!
在△ABC中,有一个内接正三角形DEF, 点D、E、F分别在AB、CA、BC上,DE//BC, 已知BC=6cm,BC上的高为AH=3cm.求DE的 长.
如果正方形的一边落在三角形的一边上,其余两个顶点 分别在三角形的另外两条边上,则这样的正方形叫做三 角形的内接正方形. (1)如图①,在△ABC中,BC=a,BC边上的高AD=ha, EFGH是△ABC的内接正方(2)在Rt△ABC中,AB=4,AC=3,∠BAC=90度.请在 图②,图③中分别画出可能的内接正方形,并根据计算 回答哪个内接正方形的面积最大;
(3)在锐角△ABC中,BC=a,AC=b,AB=c,且a<b<c. 请问这个三角形的内接正方形中哪个面积最大?并说明 理由.
人教版初三数学下册三角形内接正方形

解得:x=48
B
G
答:这个正方形的边长为48mm.
A F
K DH C
方法二
解:设正方形的边长为x,依题得
x2x(8 0 x)x(12 x)012 800
2
2
2
解得:x=48mm A
答:这个正方形的边长为48mm.
E
F
K
面积法
B
G
DH C
归纳总结:
1.本题考查相似三角形的应用,在章节复 习中链接了相似三角形的判定和性质知识 点的联系,有助于学生构建知识框架,引 导学生探索数学问题的解题方法。
EF AE BC AB
难点突破
E/F B / C
AEF∽ ABC
EF
AADK-KD
B1C20 A8D0
1E2F0 AD80E F设EF=x
80mm
K
D
方法一
解: 正方形EGHF的边GH在BC上
EF//BC
AEF∽ ABC
EF AK BC AD
设EF=xmm ,则EF=FH=KD=xmm E
x2=____________, 按如此方法继续作正方形,第 x n 个正
方形的边长 =____________.
A
意图:学生在了解原题的解法后,通 过观察、猜想和验证,探索其中的规 律,这是对原题方法的总结和提升, 发展学生推理解题的思维能力。 B
I
N
E
F
J KM
G
DH C
图1
变式二:现把△ABC按照图2加工成三个相同大 小的正方形零件(边长为x),△ABC的边BC与高 AD需要满足一定的数量关系.则这一数量关系是 :_______________.
第七讲 最大内接与最小覆盖(教师版)

典题精练1问题探究答案解析问题解决如图,将()中的翻折得到四边形,对角线、相交于点,请以点为位似中心作正方形,使得点、、、在四边形的各边上.要求:图(3)求出正方形的面积.1写出作法,证明四边形是正方形.2画图见解析.(1).(2)证明见解析.1证明见解析.2(3)如图,(1)图连并延长交于,过作交于,过作交于,过作交于,即为所求.如图,图在上截取,上截取,使,以为边作正方形,连并延长交于连并延长交于以为边作正方形,∵,∴,∴,,∵,∴,∴,∴正方形.(2)设,则,∵,∴,∵,∴,∴,,∴,1(3)标注综合类问题>新定义>题型:与四边形有关的新定义∴,∴,∴正方形.如图,图在上截取,上截取,使,以为边作矩形,使,连并延长交于点,连并延长交于点,过作交于点,过作交于点,连接,四边形即为所求正方形,由线束定理得:,,∴,∵,,,∴于,与都关于对称,∴,,∴,∵,∴四边形为正方形.2田总的那道题目例题22我们将能完全覆盖某平面图形的最小正方形称为该平面图形的最小覆盖正方形.例如圆的最小覆3问题探究:答案在图的半径为的半圆内(含弧),画出一边落在直径上的面积最大的正方形,并求出这个正方形的面积.(2)如图,现有一块半径的半圆形钢板,是否可以裁出一边落在上的面积最大的矩形?若存在,请说明理由,并求出这个矩形的面积;若不存在,说明理由.(3)如图,在以为直径的半圆内,,有两个正方形、,点、分别在半圆上,、、在直径上,求两个正方形的面积和.(4)如图,在以为直径的半圆内,,有两个扇、,点、分别在半圆上,、、在直径上,且、,求两个扇形的面积和.(5),画图见解析.(1),画图见解析.(2)4阅读理解:实践探索:(1)若,如图①②正方形为扇形的内接正方形,则图①正方形的边长,图②正方形的边长为.图图联系拓展:(2)若,在扇形中是否存在内接正(示意图),使?若存在,请分别指出此时点、点所在的位置,并求出该正的边长,若不存在,请说明理由.综合应用:(3)现需要用扇形余料裁剪出一块最大的正方形,已知扇形的半径为,,请在图中画出最大的正方形(保留画图痕迹),并求出最大正方形的面积(用含的代数式表示).备用图备用图答案解析1.2.(1)存在,边长为.(2).(3)略.(1)设边长为,作,则,在中,,,得:,此时与重合,故存在,边长为.(2)①,∴,∴,∴;②作,则,,∴,,,∴方案①面积最大.(3)5我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段。
正方形中最大内接正三角形证明

正方形中最大内接正三角形证明在一个阳光明媚的下午,我们来聊聊一个有趣的几何问题——在正方形里面,能放进多大的正三角形。
听上去有点枯燥,但别急,咱们慢慢来,搞清楚这其中的奥妙。
想象一下,一个正方形,四个边,四个角,方方正正的,简直就像个小盒子。
然后,在这个小盒子里,我们要放进一个正三角形,咱们可得让它尽量大,让它在方方正正的正方形中优雅地舞动,像个小明星一样。
想象一下正方形的样子。
四条边都一样长,四个角都是九十度,简直是几何的天花板。
咱们来找找这个正方形的中心。
把正方形分成四份,就像切蛋糕一样。
中间的位置就是正方形的中心。
然后,咱们来试试把正三角形放进这个正方形里。
正三角形,有三个边,三个角,边也要一样长,角也得是六十度。
这不,就像三个好朋友一起去旅行,想要找到一个舒适的地方住下。
现在,咱们要把这个正三角形放得又稳又好。
可以想象,正三角形的一个顶点正好放在正方形的顶点上,其他两个顶点得恰好落在正方形的边上。
咱们先把正三角形的一个顶点放在正方形的上顶点,这样一来,另外两个顶点就要在正方形的左边和右边各找到一个地方。
听起来简单,可实际上要做到这一点,还得动动脑筋。
对了,咱们可以用简单的公式来看看正方形和正三角形的关系。
假设正方形的边长是a,那正三角形的边长要怎么计算呢?这个正三角形的边长其实是正方形的边长乘以一个神奇的数字,叫做根号3除以2。
用个简单的算式,算出来,正三角形的边长是 a * √3 / 2。
这个小公式就像是给正三角形量身定做的衣服,刚刚好,特别合身。
咱们也可以通过画图来理解这个过程。
画个正方形,然后在正方形的中心画个正三角形。
看到没有?这个正三角形的边缘正好触碰正方形的边。
是不是特别美?像是正方形和正三角形在跳舞,一边旋转一边微笑,彼此间的距离刚刚好,不远不近,简直是天作之合。
我们再来想象一下,假如我们把正三角形的每个顶点都放在正方形的边上,这个正三角形的面积该有多大啊!计算面积的时候,咱们可以用边长的平方来表示。
三角形内接正方形(专题)

三角形内接正方形一、概念三角形的内接正方形是指正方形四个顶点都在三角形边上的正方形,正方形有4个顶点,而三角形只有3条边,所以,正方形一定有两个顶点在同一条边上,即正方形一定有一条边落在三角形的边上.二、个数分情况讨论:1.在锐角三角形中:(1)如果三角形为等边三角形,则它的内接正方形只有一个.(正方形的边无论落在哪一条边上,根据对称性可知,都是在同一位置).(2)如果三角形为等腰三角形(底与腰不等),则它的内接正方形有2个.一个是正方形的边落在等腰三角形底边上;另一种是正方形的边落在腰上(无论哪个腰,位置是相同的);(3)如果三角形为不等边三角形(三边两两不等),则它的内接正方形有3个.2.在直角三角形中:内接正方形有2个:一个是正方形的边落在斜边上;另一个是正方形的边落在直角边上.3.在钝角三角形中:内接正方形只有1个:即正方形一条边落在斜边上.三、画法1.计算法通过计算,求出三角形内接正方形的边长a,然后在某一边上作三角形的高h,在h上截取一段长度为a 的线段,记下截点,通过截点作这边上的平行线,交另两边于两点,最后通过这两点作h的平行线即可. 2.尺规法利用位似图形的原理,选择一个位似中心和再作出一个正方形便可作出三角形内接最大正方形.方法一:先作个小正方形,再利用位似作出所求的内接正方形。
方法二:1)以△ABC的一边BC为一边,向下作正方形BCYX; 2)连接AX.BY与BC交于E,F.3)分别过E,F作ED,FG分别交AB,AC于D,G. 4)连结DG四边形EFGD便是所求图形由此便探索出了三角形内接最大正方形的一种尺规作法,我们是选顶点A作为位似中心,那么点B,点C可不可以做位似中心呢?答案是肯定的。
一共是四种做法。
四、教材衔接1.如图,四边形EFGH是△ABC内接正方形,BC=27cm,高AD=21cm,求内接正方形EFGH的面积.解:设正方形EFGH的边长为x,设AD与GH的交点为I,∵HG∥BC,∴△AHG∽△ABC,∴AI:AD=GH:BC,正方形EFGH的边长为xcm.∵BC=27,AD=21,∴(21-x):21=x:27,即可求解.点评:本题主要考查正方形的面积、相似三角形的判定与性质,关键在于通过求证△AHG∽△ABC,推出正方形的边长.2. 如图,Rt△ABC(∠C=90°)中有三个内接正方形,DF=9厘米,GK=6厘米,猜想第三个正方形的边长PQ 的长.解:GF=EF-EG=9-6=3,设PQ=x,∵GK∥PQ,∴∠FKG=∠KQP.又∵∠FGK=∠KPQ=90°,∴△FGK∽△KPQ.∴ FGKP=GKPQ.∴ 36-x=6x.解得x=4.答:第三个正方形的边长为4厘米.点评:本题利用了平行线的性质,相似三角形的判定和性质求解.3. 如图所示,四边形EFGH是三角形ABC的内接矩形,AD⊥BC,垂足为D,BC=21cm,AD=14cm,EF:FG=1:2,求矩形EFGH的面积.解:如图,设矩形的边长EF=x,则FG=2x,∵四边形EFGH是三角形ABC的内接矩形,∴EH∥BC,EH=FG,∴△AEH∽△ABC,又∵AD⊥BC,则ID=x,AI=AD-ID,∴ EHBC= AIAD,BC=21cm,AD=14cm,∴ 2x21= 14-x14,解得,x=6cm,即2x=12cm,∴S矩形EFGH=EF×FG=6×12=72cm2.答:矩形EFGH的面积为72cm2.点评:本题主要考查了矩形的性质和相似三角形的判定与性质,知道相似三角形的对应高之比就等于对应边之比,即相识比.五、中考应用(几何综合题,规律型)1.2.把边长为40厘米的正方形ABCD 沿对角线AC 截成两个三角形,在两个三角形内如图所示剪下两个内接正方形M 、N ,则M 、N 的的面积的差是4009平方厘米. 解:正方形M 的面积=20cm ×20cm=400cm 2,设:正方形N 的边长为x ,则存在:x2+ 12×x2+ 12×x2+ 12× 12×x2= 40×402,解得:x2= 32009cm 2,故M 、N 的面积的差为(400- 32009)cm2= 4009cm 2,故答案为 4009cm 2.点评:本题考查了正方形,等腰三角形面积的计算方法,考查了正方形四边相等,各内角均为直角的性质,解本题的关键是正方形N 的面积的计算.3.如图1,在△ABC 中,∠C=90°,AC=4,BC=3,四边形DEFG 为△ABC 的内接正方形,若设正方形的边长为x ,容易算出x 的长为 60/37.探究与计算:(1)如图2,若三角形内有并排的两个全等的正方形,它们组成的矩形内接于△ABC ,则正方形的边长为 60/49;(2)如图3,若三角形内有并排的三个全等的正方形,它们组成的矩形内接于△ABC ,则正方形的边长为 60/61;(3)如图4,若三角形内有并排的n 个全等的正方形,它们组成的矩形内接于△ABC ,请你猜想正方形的边长是多少?并对你的猜想进行证明.解:(1) 6049;(2分) (2) 6061;(2分)(3)若三角形内有并排的n 个全等的正方形,它们组成的矩形内接于△ABC ,正方形的边长是 6025+12n . 证明,如图,过点C 作CN ⊥AB ,垂足为N ,交GF 于点M ,设小正方形的边长为x ,∵四边形GDEF 为矩形,∴GF ∥AB ,CM ⊥GF ,易算出CN= 125,∴ CMCN=GFAB ,即 125-x125=nx5, ∴x= 6025+12n .即小正方形的边长是 6025+12n .(4分)点评:主要考查了正方形,矩形的性质和相似三角形的性质.会利用三角形相似中的相似比来得到相关的线段之间的等量关系是解题的关键. 4. (2009•湘西州)如图,等腰直角△ABC 腰长为a ,现分别按图1,图2方式在△ABC 内内接一个正方形ADFE 和正方形PMNQ .设△ABC 的面积为S ,正方形ADFE 的面积为S1,正方形PMNQ 的面积为S2. (1)在图1中,求AD :AB 的值;在图2中,求AP :AB 的值; (2)比较S1+S2与S 的大小.。
求三角形内最大内接正方形面积

思路:假设△ABC是已知三角形,如果内接正方形EFGH有两顶点E、F在BC 上,此时设BC=a,AC=b,AB=c,BC边上的高AD=h1,设正方形EFGH的边长是x,(又假设AC、AB边上的高分别为h2、h3)1)并且设△ABC是任意锐角三角形,并且a>b>c由△ABC∽△AHG,所以高的比等于相似比即:x/a=(h1-x)/h1,所以内接正方形边长x=ah1/(a+h1)如果有两顶点在AB、AC边上时也同样可以得:边长为:bh2/(b+h2),ch3/(c+h3)要使内接正方形面积最大,则边长应最大,下面比较ah1/(a+h1)、bh2/(b+h2),ch3/(c+h3)的大小即可因为△ABC的面积S=ah1/2=bh2/2=ch3/2,即 ah1=bh2=ch3所以分子相同,分母越小,分数越大比较a+h1、b+h2、c+h3由(a+h1)-(b+h2)=(a-b)+(h1-h2)=(a-b)+(2S/a-2s/b)=(a-b)+2S(1/a-1/b)=(a-b)(1-2S/ab)=(a-b)(ab-2s)/ab (S是△ABC的面积)由垂线段最短,知b大于高h1,即ab>ah1,而ah1=2S,所以(a-b)(ab-2s)/ab >0所以 a+h1>b+h2 ,即如果内接正方形有两个顶点在BC边上时,边长较小,面积也较小同理,如果有两顶点在AC边上时其面积比两点在AB边上小因此得结论:当内接正方形有两个顶点在最小边上时,其面积最大此时内接正方形的边长是:ch3/(c+h3)(设最小边是c,这边上的高是h3)面积就是其平方了。
2)直角三角形其内接正方形面积最大应为一顶点与直角顶点重合,三边上各有一顶点。
其边长为:两直角边之积/两直角边之和。
3)类似方法讨论,任意钝角三角形,内接正方形的两个顶点在钝角所对的边上时面积最大,其边长为:最大边与这边上的高的积/最大边与这边上高的和。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
思路:假设△ABC是已知三角形,如果内接正方形EFGH有两顶点E、F在BC 上,此时设BC=a,AC=b,AB=c,BC边上的高AD=h1,设正方形EFGH的边长是x,
(又假设AC、AB边上的高分别为h2、h3)
1)并且设△ABC是任意锐角三角形,并且a>b>c
由△ABC∽△AHG,所以高的比等于相似比
即:x/a=(h1-x)/h1,所以内接正方形边长x=ah1/(a+h1)
如果有两顶点在AB、AC边上时也同样可以得:边长为:bh2/(b+h2),ch3/(c+h3)
要使内接正方形面积最大,则边长应最大,
下面比较ah1/(a+h1)、bh2/(b+h2),ch3/(c+h3)的大小即可
因为△ABC的面积S=ah1/2=bh2/2=ch3/2,即 ah1=bh2=ch3
所以分子相同,分母越小,分数越大
比较a+h1、b+h2、c+h3
由(a+h1)-(b+h2)=(a-b)+(h1-h2)=(a-b)+(2S/a-2s/b)=(a-b)+2S(1/a-1/b)=(a-b)(1-2S/ab)
=(a-b)(ab-2s)/ab (S是△ABC的面积)由垂线段最短,知b大于高h1,即ab>ah1,而ah1=2S,
所以(a-b)(ab-2s)/ab >0
所以 a+h1>b+h2 ,即如果内接正方形有两个顶点在BC边上时,边长较小,面积也较小
同理,如果有两顶点在AC边上时其面积比两点在AB边上小
因此得结论:当内接正方形有两个顶点在最小边上时,其面积最大此时内接正方形的边长是:ch3/(c+h3)(设最小边是c,这边上的高是h3)面积就是其平方了。
2)直角三角形其内接正方形面积最大应为一顶点与直角顶点重合,三边上各有一顶点。
其边长为:两直角边之积/两直角边之和。
3)类似方法讨论,任意钝角三角形,内接正方形的两个顶点在钝角所对的边上时面积最大,其边长为:最大边与这边上的高的积/最大边与这边上高的和。
