勾股定理五种证明方法

勾股定理16种经典证明方法

勾股定理16种经典证明方法ab c ab b a 214214222⨯+=⨯++【证法1】（课本的证明）做8个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c ，再做三个边长分别为a 、b 、c 的正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形的边长都是a + b ，所以面积相等. 即整理得 .【证法2】（邹元治证明）以a 、b 为直角边，以c 为斜边做四个全等的直角三角形，则每个直角三角形的面积等于. 把这四个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上，B 、F 、C 三点在一条直线上，C 、G 、D 三点在一条直线上.∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF.222c b a =+ab 21∵ ∠AEH + ∠AHE = 90º,∴ ∠AEH + ∠BEF = 90º.∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的正方形. 它的面积等于c 2. ∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA.∵ ∠HGD + ∠GHD = 90º,∴ ∠EHA + ∠GHD = 90º.又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形，它的面积等于.∴ . ∴ .【证法3】（赵爽证明）以a 、b 为直角边（b>a ），以c 为斜边作四个全等的直角三角形，则每个直角三角形的面积等于. 把这四个直角三角形拼成如图所示形状.∵ Rt ΔDAH ≌ Rt ΔABE, ∴ ∠HDA = ∠EAB.∵ ∠HAD + ∠HAD = 90º，∴ ∠EAB + ∠HAD = 90º，∴ ABCD 是一个边长为c 的正方形，它的面积等于c 2.∵ EF = FG =GH =HE = b ―a ,∠HEF = 90º.()2b a +()22214c ab b a +⨯=+222c b a =+ab 21∴ EFGH 是一个边长为b ―a 的正方形，它的面积等于.∴ .∴ .【证法4】（1876年美国总统Garfield 证明）以a 、b 为直角边，以c 为斜边作两个全等的直角三角形，则每个直角三角形的面积等于. 把这两个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE, ∴ ∠ADE = ∠BEC.∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º. ∴ ∠DEC = 180º―90º= 90º.∴ ΔDEC 是一个等腰直角三角形，它的面积等于.又∵ ∠DAE = 90º, ∠EBC = 90º,∴ AD ∥BC.∴ ABCD 是一个直角梯形，它的面积等于.∴ .∴ .【证法5】（梅文鼎证明）做四个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c. 把它们拼成如图那样的一个多边形，使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P.∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD,∴ ∠EGF = ∠BED ，()2a b -()22214c a b ab =-+⨯222c b a =+ab 21221c ()221b a +()222121221c ab b a +⨯=+222c b a =+∵ ∠EGF + ∠GEF = 90°，∴ ∠BED + ∠GEF = 90°，∴ ∠BEG =180º―90º= 90º.又∵ AB = BE = EG = GA = c ，∴ ABEG 是一个边长为c 的正方形. ∴ ∠ABC + ∠CBE = 90º.∵ Rt ΔABC ≌ Rt ΔEBD,∴ ∠ABC = ∠EBD.∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º.又∵ ∠BDE = 90º，∠BCP = 90º，BC = BD = a.∴ BDPC 是一个边长为a 的正方形.同理，HPFG 是一个边长为b 的正方形.设多边形GHCBE 的面积为S ，则, ∴ .【证法6】（项明达证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ），斜边长为c. 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形，使E 、A 、C 三点在一条直线上.过点Q 作QP ∥BC ，交AC 于点P. 过点B 作BM ⊥PQ ，垂足为M ；再过点F 作FN ⊥PQ ，垂足为N.∵ ∠BCA = 90º，QP ∥BC ，,21222ab S b a ⨯+=+abS c 2122⨯+=222c b a =+∴ ∠MPC = 90º，∵ BM ⊥PQ ，∴ ∠BMP = 90º，∴ BCPM 是一个矩形，即∠MBC = 90º.∵ ∠QBM + ∠MBA = ∠QBA = 90º，∠ABC + ∠MBA = ∠MBC = 90º，∴ ∠QBM = ∠ABC ，又∵ ∠BMP = 90º，∠BCA = 90º，BQ = BA = c ，∴ Rt ΔBMQ ≌ Rt ΔBCA.同理可证Rt ΔQNF ≌ Rt ΔAEF.从而将问题转化为【证法4】（梅文鼎证明）.【证法7】（欧几里得证明）做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使H 、C 、B 三点在一条直线上，连结BF 、CD. 过C 作CL ⊥DE ，交AB 于点M ，交DE 于点L.∵ AF = AC ，AB = AD ，∠FAB = ∠GAD ，∴ ΔFAB ≌ ΔGAD ，∵ ΔFAB 的面积等于，ΔGAD 的面积等于矩形ADLM 的面积的一半，∴ 矩形ADLM 的面积 =.同理可证，矩形MLEB 的面积 =.∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积221a 2a 2b∴ ，即 .【证法8】（利用相似三角形性质证明）如图，在Rt ΔABCa 、b ，斜边AB 的长为c ，过点C 作在ΔADC 和ΔACB 中，∵ ∠ADC = ∠ACB = 90∠CAD = ∠BAC ，∴ ΔADC ∽ ΔACB.AD ∶AC = AC ∶AB ，即 .同理可证，ΔCDB ∽ ΔACB ，从而有 .∴ ，即 .【证法9】（杨作玫证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ），斜边长为c. 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ，AF 交GT 于F ，AF 交DT 于R. 过B 作BP ⊥AF ，垂足为P. 过D 作DE 与CB 的延长线垂直，垂足为E ，DE 交AF 于H.∵ ∠BAD = 90º，∠PAC = 90º，∴ ∠DAH = ∠BAC.又∵ ∠DHA = 90º，∠BCA = 90º，AD = AB = c ，∴ Rt ΔDHA ≌ Rt ΔBCA.∴ DH = BC = a ，AH = AC = b.由作法可知， PBCA 是一个矩形，所以 Rt ΔAPB ≌ Rt ΔBCA. 即PB = CA = b ，AP= a ，从而PH = b ―a.222b ac +=222c b a =+AB AD AC ∙=2AB BD BC ∙=2()222AB AB DB AD BC AC =∙+=+222c b a =+∵ Rt ΔDGT ≌ Rt ΔBCA ,Rt ΔDHA ≌ Rt ΔBCA.∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ，∠GDT = ∠HDA . 又∵ ∠DGT = 90º，∠DHF = 90º，∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º，∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF ，TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形，上底TF=b ―a ，下底BP= b ，高FP=a +（b ―a ）.用数字表示面积的编号（如图），则以c 为边长的正方形的面积为①∵=，，∴ = . ②把②代入①，得= = .∴ .【证法10】（李锐证明）设直角三角形两直角边的长分别为a 、b （b>a ），斜边的长为c. 做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使A 、E 、G 三点在一条直线上. 用数字表示面积的编号（如图）.543212S S S S S c ++++=()[]()[]a b a a b b S S S -+∙-+=++21438abb 212-985S S S +=824321S ab b S S --=+812S S b --98812212S S S S b S S c ++--++=922S S b ++22a b +222c b a =+∵ ∠TBE = ∠ABH = 90º，∴ ∠TBH = ∠ABE.又∵ ∠BTH = ∠BEA = 90º，BT = BE = b ，∴ Rt ΔHBT ≌ Rt ΔABE.∴ HT = AE = a.∴ GH = GT ―HT = b ―a.又∵ ∠GHF + ∠BHT = 90º，∠DBC + ∠BHT = ∠TBH + ∠BHT = 90º，∴ ∠GHF = ∠DBC.∵ DB = EB ―ED = b ―a ，∠HGF = ∠BDC = 90º，∴ Rt ΔHGF ≌ Rt ΔBDC. 即 .过Q 作QM ⊥AG ，垂足是M. 由∠BAQ = ∠BEA = 90º，可知 ∠ABE= ∠QAM ，而AB = AQ = c ，所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌Rt ΔABE. 所以Rt ΔHBT ≌ Rt ΔQAM . 即 .由Rt ΔABE ≌ Rt ΔQAM ，又得QM = AE = a ，∠AQM = ∠BAE.∵ ∠AQM + ∠FQM = 90º，∠BAE + ∠CAR = 90º，∠AQM = ∠BAE ，∴ ∠FQM = ∠CAR.又∵ ∠QMF = ∠ARC = 90º，QM = AR = a ，∴ Rt ΔQMF ≌ Rt ΔARC. 即.∵ ，，，又∵ ，，，27S S =58S S =64S S =543212S S S S S c ++++=612S S a +=8732S S S b ++=27S S =58S S =64S S =∴ ==，即 .【证法11】（利用切割线定理证明）在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c. 如图，以B 为圆心a 为半径作圆，交AB 及AB 的延长线分别于D 、E ，则BD = BE = BC = a. 因为∠BCA = 90º，点C 在⊙B 上，所以AC 是⊙B 的切线. 由切割线定理，得=== ，即，∴ .【证法12】（利用多列米定理证明）在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c （如图）. 过点A 作AD ∥CB ，过点B 作BD ∥CA ，则ACBD 为矩形，矩形ACBD 内接于一个圆. 根据多列米定理，圆内接四边形对角线的乘积等于两对边乘积之和，有，∵ AB = DC = c ，AC = BD = b ，∴ ，即 8736122S S S S S b a++++=+52341S S S S S ++++2c 222c b a =+ADAE AC ∙=2()()BD AB BE AB -+()()a c a c -+22a c -222a cb -=222c b a =+BD AC BC AD DC AB ∙+∙=∙222AC BC AB +=22b ac +=a b aa B ACD c∴ .【证法13】（作直角三角形的内切圆证明）在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c. 作Rt ΔABC 的内切圆⊙O ，切点分别为D 、E 、F （如图），设⊙O 的半径为r.∵ AE = AF ，BF = BD ，CD = CE ，∴ = = r + r = 2r,即，∴ .∴ ，即，∵ ，∴ ，又∵ = = == ，∴ ，∴ ，∴ ， ∴ .【证法14】（利用反证法证明）如图，在Rt ΔABC 中，设直角边AC 、BC 的长度分别为a 、b ，斜边AB 的长为c ，过点C 作CD ⊥AB ，垂足是D.假设，即假设，则由==可知，或者 . 即 AD ：AC ≠AC ：AB ，或者 BD ：222c b a =+()()()BF AF CD BD CE AE AB BC AC +-+++=-+CD CE +r c b a 2=-+c r b a +=+2()()222c r b a +=+()222242c rc r ab b a ++=++ab S ABC 21=∆ABC S ab ∆=42AOC BOC AOB ABC S S S S ∆∆∆∆++=br ar cr 212121++()r c b a ++21()r c c r ++221rc r +2()ABC S rc r ∆=+442()ab rc r 242=+22222c ab ab b a +=++222c b a =+222c b a ≠+222AB BC AC ≠+AB AB AB ∙=2()BD AD AB +BDAB AD AB ∙+∙AD AB AC ∙≠2BD AB BC ∙≠2c b a r r r O F D B ABC ≠BC ：AB.在ΔADC 和ΔACB 中，∵ ∠A = ∠A ，∴ 若 AD ：AC ≠AC ：∠ADC ≠∠ACB.在ΔCDB 和ΔACB ∵ ∠B = ∠B ，∴ 若BD ：BC ≠BC ：AB ，则∠CDB ≠∠ACB.又∵ ∠ACB = 90º，∴ ∠ADC ≠90º，∠CDB ≠90º.这与作法CD ⊥AB 矛盾.所以，的假设不能成立.∴ .【证法15】（辛卜松证明）222AB BC AC ≠+222c b a =+ab 21ab 21ab 21ab 212c2b 2a B C b a b a b a b a b ac c c cb ab ab b a b a设直角三角形两直角边的长分别为a 、b ，斜边的长为c. 作边长是a+b 的正方形ABCD. 把正方形ABCD 划分成上方左图所示的几个部分，则正方形ABCD 的面积为；把正方形ABCD 划分成上方右图所示的几个部分，则正方形ABCD 的面积为 =.∴ ,∴ .【证法16】（陈杰证明）设直角三角形两直角边的长分别为a 、b （b>a ），斜边的长为c. 做两个边长分别为a 、b 的正方形（b>a ），把它们拼成如图所示形状，使E 、H 、M 三点在一条直线上. 用数字表示面积的编号（如图）.在EH = b 上截取ED = a ，连结DA 、DC ，则 AD = c.∵ EM = EH + HM = b + a , ED = a ，∴ DM = EM ―ED = ―a = b.又∵ ∠CMD = 90º，CM = a ，∠AED = 90º， AE = b ，∴ Rt ΔAED ≌ Rt ΔDMC.∴ ∠EAD = ∠MDC ，DC = AD = c.∵ ∠ADE + ∠ADC+ ∠MDC =180º，∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º，∴ ∠ADC = 90º.∴ 作AB ∥DC ，CB ∥DA ，则ABCD 是一个边长为c 的正方形.∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º，∴ ∠BAF=∠DAE.连结FB ，在ΔABF 和ΔADE 中，()ab b a b a 2222++=+()22214c ab b a +⨯=+22c ab +22222c ab ab b a +=++222c b a =+()a b +∵ AB =AD = c ，AE = AF = b ，∠BAF=∠DAE ，∴ ΔABF ≌ ΔADE.∴ ∠AFB = ∠AED = 90º，BF = DE = a.∴ 点B 、F 、G 、H 在一条直线上.在Rt ΔABF 和Rt ΔBCG 中，∵ AB = BC = c ，BF = CG = a ，∴ Rt ΔABF ≌ Rt ΔBCG.∵ ，，，，∴ ===∴ .54322S S S S c +++=6212S S S b ++=732S S a +=76451S S S S S +===6217322S S S S S b a ++++=+()76132S S S S S ++++5432S S S S +++2c 222c b a =+。

勾股定理五种证明方法

勾股定理五种证明方法
1. 代数证明：假设直角三角形的两条直角边分别为a和b，斜
边为c。

根据勾股定理，我们有a^2 + b^2 = c^2。

将三条边的
长度代入该等式，进行计算验证即可证明。

2. 几何证明：通过绘制直角三角形，并利用几何原理证明。

例如，可以画一个正方形，然后在其两条相对边上各画一个相等的直角三角形，再使用平行四边形的性质可以得出a^2 + b^2
= c^2。

3. 相似三角形证明：假设两个直角三角形，已知其斜边比例为m:n，利用相似三角形的性质可以得出直角边的比例也是m:n，进而得到a^2 + b^2 = c^2。

4. 平行四边形法证明：利用平行四边形的性质，可通过画出一个具有相等对边的平行四边形来证明勾股定理。

通过平行四边形的性质可以得出a^2 + b^2 = c^2。

5. 微积分证明：利用微积分的知识可以证明勾股定理。

通过对直角三角形边长进行微分，并进行适当的运算，可以得到a^2 + b^2 = c^2。

这种证明方法比较复杂，需要较高的数学知识和
技巧。

勾股定理的6种最常用证明方法

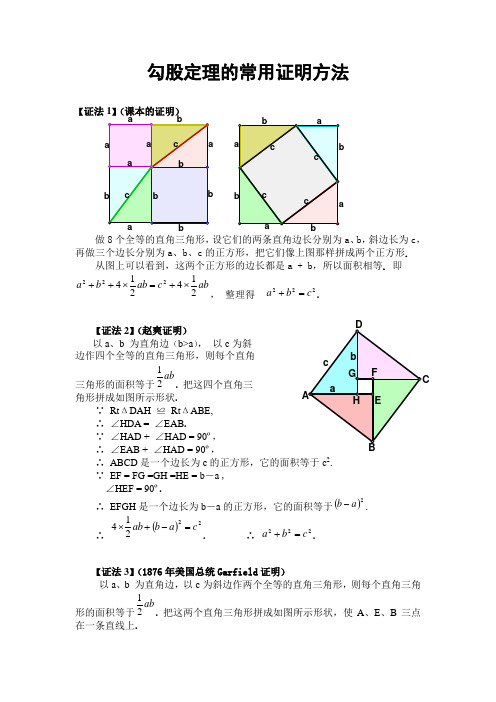
勾股定理的常用证明方法【证法1】（课本的证明）做8个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c ，再做三个边长分别为a 、b 、c 的正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形的边长都是a + b ，所以面积相等. 即abc ab b a 214214222⨯+=⨯++，整理得 222c b a =+.【证法2】（赵爽证明）以a 、b 为直角边（b>a ），以c 为斜边作四个全等的直角三角形，则每个直角三角形的面积等于ab21. 把这四个直角三角形拼成如图所示形状. ∵ Rt ΔDAH ≌ Rt ΔABE, ∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º，∴ ∠EAB + ∠HAD = 90º，∴ ABCD 是一个边长为c 的正方形，它的面积等于c 2. ∵ EF = FG =GH =HE = b ―a , ∠HEF = 90º.∴ EFGH 是一个边长为b ―a 的正方形，它的面积等于()2a b -.∴ ()22214c a b ab =-+⨯. ∴ 222c b a =+.【证法3】（1876年美国总统Garfield 证明）以a 、b 为直角边，以c 为斜边作两个全等的直角三角形，则每个直角三角形的面积等于ab 21. 把这两个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上.∵RtΔEAD ≌RtΔCBE, ∴∠ADE = ∠BEC.∵∠AED + ∠ADE = 90º,∴∠AED + ∠BEC = 90º.∴∠D EC = 180º―90º= 90º.∴ΔDEC是一个等腰直角三角形，它的面积等于2 21c.又∵∠DAE = 90º, ∠EBC = 90º, ∴AD∥BC.∴ABCD是一个直角梯形，它的面积等于()2 21b a+.∴()222121221cabba+⨯=+. ∴222cba=+.【证法4】（邹元治证明）以a、b为直角边，以c为斜边做四个全等的直角三角形，则每个直角三角形的面积等于ab21.把这四个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上，B、F、C三点在一条直线上，C、G、D三点在一条直线上.∵RtΔHAE ≌RtΔEBF,∴∠AHE = ∠BEF.∵∠AEH + ∠AHE = 90º,∴∠AEH + ∠BEF = 90º.∴∠HEF = 180º―90º= 90º.∴四边形EFGH是一个边长为c的正方形. 它的面积等于c2.∵RtΔGDH ≌RtΔHAE,∴∠HGD = ∠EHA.∵∠HGD + ∠GHD = 90º,∴∠EHA + ∠GHD = 90º.又∵∠GHE = 90º,∴∠DHA = 90º+ 90º= 180º.∴ABCD是一个边长为a + b的正方形，它的面积等于()2b a+.∴()22214cabba+⨯=+. ∴222cba=+.【证法5】（欧几里得证明）做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使H 、C 、B 三点在一条直线上，连结 BF 、CD . 过C 作CL ⊥DE ，交AB 于点M ，交DE 于点L .∵ AF = AC ，AB = AD ， ∠FAB = ∠GAD ， ∴ ΔFAB ≌ ΔGAD ，∵ ΔFAB 的面积等于221a ， ΔGAD 的面积等于矩形ADLM 的面积的一半，∴ 矩形ADLM 的面积 =2a . 同理可证，矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴ 222b a c += ，即 222c b a =+.【证法6】（辛卜松证明）设直角三角形两直角边的长分别为a 、b ，斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分，则正方形ABCD的面积为()ab b a b a 2222++=+；把正方形ABCD 划分成上方右图所示的几个部分，则正方形ABCD 的面积为 ()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+.D。

几种简单证明勾股定理的方法

几种简单证明勾股定理的方法勾股定理是一个著名的数学定理，它描述了直角三角形三条边的长度之间的关系。

下面是几种简单证明勾股定理的方法：方法一：特例验证法对于任意一个直角三角形，我们可以列出它的两条直角边的长度的平方和，以及斜边的长度的平方，验证它们是否相等。

例如，对于一个直角边分别为3和4的直角三角形，我们可以计算出它的斜边的长度为5，然后验证3²+4²=5²。

这种方法虽然简单，但是只适用于特例，不能推广到一般情况。

方法二：几何构造法将两个大小相同的直角三角形放在同一直线上，使得它们的斜边成为一条直线。

这时，我们可以证明两个三角形的面积之和等于底边长度之和的两倍。

由于两个三角形面积相等，因此可以得出底边长度之和等于斜边长度。

例如，对于两个直角边分别为a和b的直角三角形，它们的斜边长度分别为c，将它们放在同一直线上，使得它们的斜边成为一条直线。

可以证明两个三角形的面积之和等于底边长度之和的两倍，即ab/2+ab/2=c²/2。

因此，可以得出a²+b²=c²。

方法三：代数推导法通过代入特殊值的方式，可以得到勾股定理的公式。

例如，当直角三角形的两条直角边分别为3和4时，可以得出斜边的长度为5，然后代入公式3²+4²=5²得到验证。

这种方法虽然简单，但是只适用于已知直角三角形两条直角边长度的特殊情况。

方法四：平方法通过平方法证明勾股定理的思路是：将直角三角形的一条直角边平移到斜边所在的直线上方，与斜边重合。

这时，可以将直角三角形的一条直角边看作是斜边减去一条直角边的长度所得的差，因此可以得出斜边的平方等于两条直角边的平方和。

例如，对于一个直角边分别为a和b的直角三角形，可以将其一条直角边平移到斜边所在的直线上方，与斜边重合。

这时，可以将直角三角形的一条直角边看作是斜边减去一条直角边的长度所得的差，即a²+b²=c²。

证明勾股定理的多种方法

证明勾股定理的多种方法1. 几何证明：假设有一个直角三角形，其中两条边长分别为a和b，斜边长为c。

根据直角三角形的定义，可以得知两条直角边构成一条直角。

根据勾股定理，a^2 + b^2 = c^2，即通过几何构造证明了勾股定理。

2. 代数证明：假设有一个直角三角形，其中两条边长分别为a和b，斜边长为c。

根据勾股定理，a^2 + b^2 = c^2。

就是要证明等式成立。

我们可以假设a = m^2 - n^2，b = 2mn，c = m^2+ n^2，其中m和n为任意正整数。

将a、b、c代入勾股定理的等式中，可以得到(m^2 - n^2)^2 + (2mn)^2 = (m^2 + n^2)^2。

将等式展开后，可以得到m^4 - 2m^2n^2 + n^4 + 4m^2n^2 =m^4 + 2m^2n^2 + n^4。

整理后，可以看出等式两边相等，证明了勾股定理。

3. 数学归纳法证明：假设存在一个正整数n，使得勾股定理对所有小于n的正整数都成立。

我们要证明勾股定理对n+1也成立。

假设有三个正整数a、b和c，使得a^2 + b^2 = c^2。

在等式两边同时乘以k，可以得到(k*a)^2 + (k*b)^2 = (k*c)^2。

由于a、b和c都是正整数，所以k*a、k*b和k*c也都是正整数。

因此，勾股定理对于所有小于n+1的正整数也成立。

据此可以得出，勾股定理对于所有正整数都成立。

以上是勾股定理的三种常见证明方法，每一种方法都能够清晰地证明勾股定理的正确性。

勾股定理几种证明方法

勾股定理几种证明方法勾股定理的证明【证法1】（课本的证明）做8个全等的直角三角形，设它们的两条直角边长分别为a、b，斜边长为c，再做三个边长分别为a、b、c的正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形的边长都是a+b，所以面积相等.即11a2+b2+4×ab=c2+4×ab22，整理得a2+b2=c2.【证法2】（邹元治证明）以a、b为直角边，以c为斜边做四个全等的直角三角形，则每个直角三角形的面积1ab2等于.把这四个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上，B、F、C三点在一条直线上，C、G、D三点在一条直线上.∵RtΔHAE≌RtΔEBF,∴∠AHE=∠BEF.∵∠AEH+∠AHE=90º,∴∠AEH+∠BEF=90º.∴∠HEF=180º―90º=90º.∴四边形EFGH是一个边长为c的正方形.它的面积等于c2.∵RtΔGDH≌RtΔHAE,∴∠HGD=∠EHA.∵∠HGD+∠GHD=90º,∴∠EHA+∠GHD=90º.又∵∠GHE=90º,∴∠DHA=90º+90º=180º.2∴.∴a+b=c.【证法3】（赵爽证明）以a、b为直角边（b>a），以c为斜边作四个全等的直角三角形，则每个直角(a+∴ABCD是一个边长为a+b的正方形，它的面积等于(a+b)2=4×1ab+c22221ab2三角形的面积等于.把这四个直角三角形拼成如图所示形状.∵RtΔDAH≌RtΔABE,∴∠HDA=∠EAB.∵∠HAD+∠HAD=90º，∴∠EAB+∠HAD=90º，2∴ABCD是一个边长为c的正方形，它的面积等于c.∵EF=FG=GH=HE=b―a,∠HEF=90º. 2(b−a)∴EFGH是一个边长为b―a的正方形，它的面积等于.14×ab+(b−a)2=c22∴.222∴a+b=c.【证法4】（1876年美国总统Garfield证明）以a、b为直角边，以c为斜边作两个全等的直角三角形，则每个直角三角形的面1ab2积等于.把这两个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上.∵∴∵∴∴∴RtΔEAD≌RtΔCBE,∠ADE=∠BEC.∠AED+∠ADE=90º,∠AED+∠BEC=90º.∠DEC=180º―90º=90º.ΔDEC是一个等腰直角三角形，12c2它的面积等于.又∵∠DAE=90º,∠EBC=90º,∴AD∥BC.1(a+b)2∴ABCD是一个直角梯形，它的面积等于2.1(a+b)2=2×1ab+1c222.∴2∴a+b=c.【证法5】（梅文鼎证明）做四个全等的直角三角形，设它们的两条直角边长分别为a、b，斜边长为c.把它们拼成如图那样的一个多边形，使D、E、F在一条直线上.过C作AC的延长线交DF于点P.∵D、E、F在一条直线上,且RtΔGEF≌RtΔEBD,∴∠EGF=∠BED，∵∠EGF+∠GEF=90°，222∴∴又∵∴∴∵∴∴即又∵∠BED+∠GEF=90°，∠BEG=180º―90º=90º.AB=BE=EG=GA=c，ABEG是一个边长为c的正方形.∠ABC+∠CBE=90º.RtΔABC≌RtΔEBD,∠ABC=∠EBD.∠EBD+∠CBE=90º.∠CBD=90º.∠BDE=90º，∠BCP=90º，BC=BD=a.∴BDPC是一个边长为a的正方形.同理，HPFG是一个边长为b的正方形.设多边形GHCBE的面积为S，则1a2+b2=S+2×ab,21c2=S+2×ab2,∴a2+b2=c2.【证法6】（项明达证明）做两个全等的直角三角形，设它们的两条直角边长分别为a、b（b>a），斜边长为c.再做一个边长为c的正方形.把它们拼成如图所示的多边形，使E、A、C三点在一条直线上.过点Q作QP∥BC，交AC于点P.过点B作BM⊥PQ，垂足为M；再过点F作FN⊥PQ，垂足为N.∵∠BCA=90º，QP∥BC，∴∠MPC=90º，∵BM⊥PQ，∴∠BMP=90º，∴BCPM是一个矩形，即∠MBC=∵∠QBM+∠MBA=∠QBA=90º，∠ABC+∠MBA=∠MBC=90º，∴∠QBM=∠ABC，又∵∠BMP=90º，∠BCA=90º，BQ=BA=c，∴RtΔBMQ≌RtΔBCA.同理可证RtΔQNF≌RtΔAEF.从而将问题转化为【证法4】（梅文鼎证明）.【证法7】（欧几里得证明）做三个边长分别为a、b、c的正方形，把它们拼成如图所示形状，使H、C、B三点在一条直线上，连结BF、CD.过C作CL⊥DE，交AB于点M，交DE于点L.∵AF=AC，AB=AD，∠FAB=∠GAD，∴ΔFAB≌ΔGAD，12a∵ΔFAB的面积等于2ΔGAD的面积等于矩形ADLM的面积的一半，2∴矩形ADLM的面积=a.2b同理可证，矩形MLEB的面积=.∵正方形ADEB的面积=矩形ADLM的面积+矩形MLEB的面积222222∴c=a+b，即a+b=c.【证法8】（杨作玫证明）做两个全等的直角三角形，设它们的两条直角边长分别为a、b（b>a），斜边长为c.再做一个边长为c的正方形.把它们拼成如图所示的多边形.过A作AF⊥AC，AF交GT于F，AF交DT于R.过B作BP⊥AF，垂足为P.过D作DE与CB的延长线垂直，垂足为E，DE交AF于H.∵∠BAD=90º，∠PAC=90º，∴∠DAH=∠BAC.又∵∠DHA=90º，∠BCA=90º，AD=AB=c，∴RtΔDHA≌RtΔBCA.∴DH=BC=a，AH=AC=b.由作法可知，PBCA是一个矩形，所以RtΔAPB≌RtΔBCA.即PB=CA=b，AP=a，从而PH=b―a.∵RtΔDGT≌RtΔBCA,RtΔDHA≌RtΔBCA.∴RtΔDGT≌RtΔDHA.∴DH=DG=a，∠GDT=∠HDA.又∵∠DGT=90º，∠DHF=90º，∠GDH=∠GDT+∠TDH=∠HDA+∠TDH=90º，∴DGFH是一个边长为a的正方形.∴GF=FH=a.TF⊥AF，TF=GT―GF=b―a.∴TFPB是一个直角梯形，上底TF=b―a，下底BP=b，高FP=a+（b―a）.用数字表示面积的编号（如图），则以c为边长的正方形的面积为c2=S1+S2+S3+S4+S5①∵S8+S3+S4=1[b+(b−a)]•[a+(b−a)]b2−1ab22，=S5=S8+S9，1S3+S4=b2−ab−S8b2−S−S18.2∴=②把②代入①，得c2=S1+S2+b2−S1−S8+S8+S92b+S2+S9=b2+a2.=222∴a+b=c.【证法9】（李锐证明）设直角三角形两直角边的长分别为a、b（b>a），斜边的长为c.做三个边长分别为a、b、c的正方形，把它们拼成如图所示形状，使A、E、G三点在一条直线上.用数字表示面积的编号（如图）.∵∠TBE=∠ABH=90º，∴∠TBH=∠ABE.又∵∠BTH=∠BEA=90º，BT=BE=b，∴RtΔHBT≌RtΔABE.∴HT=AE=a.∴GH=GT―HT=b―a.又∵∠GHF+∠BHT=90º，∠DBC+∠BHT=∠TBH+∴∠GHF=∠DBC.∵DB=EB―ED=b―a，∠HGF=∠BDC=90º，∴RtΔHGF≌RtΔBDC.即S7=S2.过Q作QM⊥AG，垂足是M.由∠BAQ=∠BEA=90º，可知∠ABE=∠QAM，而AB=AQ=c，所以RtΔABE≌RtΔQAM.又RtΔHBT≌RtΔABE.所以RtΔHBT≌RtΔQAM.即S8=S5.由RtΔABE≌RtΔQAM，又得QM=AE=a，∠AQM=∠BAE.∵∠AQM+∠FQM=90º，∠BAE+∠CAR=90º，∠AQM=∠BAE，∴∠FQM=∠CAR.又∵∠QMF=∠ARC=90º，QM=AR=a，∴RtΔQMF≌RtΔARC.即S4=S6.222c=S+S+S+S+Sa=S+Sb1234516∵，，=S3+S7+S8，又∵S7=S2，S8=S5，S4=S6，22a+b=S1+S6+S3+S7+S8∴=S1+S4+S3+S2+S5=c，222即a+b=c.【证法10】（利用反证法证明）如图，在RtΔABC中，设直角边AC、BC的长度分别为a、b，斜边AB的长为c，过点C作CD⊥AB，垂足是D.222222假设a+b≠c，即假设AC+BC≠AB，则由AB2=AB•AB=AB(AD+BD)=AB•AD+AB•BD22可知AC≠AB•AD，或者BC≠AB•BD.即AD：AC≠AC：AB，或者BD：BC≠BC：AB.在ΔADC和ΔACB中，∵∠A=∠A，∴若AD：AC≠A C：AB，则∠ADC≠∠ACB.在ΔCDB和ΔACB中，∵∠B=∠B，∴若BD：BC≠BC：AB，则∠CDB≠∠ACB.又∵∠ACB=90º，∴∠ADC≠90º，∠CDB≠90º.222AC+BC≠AB这与作法CD⊥AB矛盾.所以，的假设不能成立.222∴a+b=c.【证法15】（辛卜松证明）DD2设直角三角形两直角边的长分别为a、b，斜边的长为c.作边长是a+b的正方形ABCD.把正方形ABCD划分成上方左图所示的几个部分，则正方形ABCD的面积为(a+b)2=a2+b2+2ab；把正方形ABCD划分成上方右图所示的几个部分，则正方形ABCD 的面积为∴∴(a+b)21=4×ab+c222=2ab+c.a2+b2+2ab=2ab+c2,【证法11】（陈杰证明）设直角三角形两直角边的长分别为a、b（b>a），斜边的长为c.做两个边长分别为a、b的正方形（b>a），把它们拼成如图所示形状，使E、H、M三点在一条直线上.用数字表示面积的编号（如图）.在EH=b上截取ED=a，连结则AD=c.∵EM=EH+HM=b+a,ED=∴DM=EM―ED=(b+a)―a=b.又∵∠CMD=90º，CM=a，∠AED=90º，AE=b，∴RtΔAED≌RtΔDMC.∴∠EAD=∠MDC，DC=AD=c.∵∠ADE+∠ADC+∠MDC=180º，∠ADE+∠MDC=∠ADE+∠EAD=90º，∴∠ADC=90º.∴作AB∥DC，CB∥DA，则ABCD是一个边长为c的正方形.∵∠BAF+∠FAD=∠DAE+∠FAD=90º，∴∠BAF=∠DAE.连结FB，在ΔABF和ΔADE中，∵AB=AD=c，AE=AF=b，∠BAF=∠DAE，∴ΔABF≌ΔADE.∴∠AFB=∠AED=90º，BF=DE=a.∴点B、F、G、H在一条直线上.在RtΔABF和RtΔBCG 中，∵AB=BC=c，BF=CG=a，∴RtΔABF≌RtΔBCG.2c=S2+S3+S4+S5，∵S1=S5=S4=S6+S7，b2=S1+S2+S6，a2=S3+S7，22a+b=S3+S7+S1+S2+S6∴=S2+S3+S1+(S6+S7)∴=S2+S3+S4+S52=c。

勾股定理的证明方法5种

勾股定理的证明方法5种勾股定理是几何学中最为经典的定理之一，它揭示了直角三角形中直角边与斜边的关系。

勾股定理有多种不同的证明方法，下面我们将依次介绍其中五种不同的证明方法。

方法一：几何法证明这种证明方法是最为直观的，它通过几何形状的变换来证明勾股定理。

首先，我们先画出一个直角三角形ABC，然后作出辅助线AD ⊥BC，将三角形ABC分成两个小三角形ΔABD和ΔADC。

根据相似三角形的性质，我们可以得到BD/AB=AB/AC，即BD*AC=AB^2。

同理，我们可以得到CD*AB=AC^2。

将这两个式子相加起来，我们就可以得到BD*AC+CD*AB=AB^2+AC^2，根据平行四边形的性质，我们可以得到BC*AD=AB^2+AC^2，而BC*AD就是直角三角形ABC的斜边的平方AC^2。

因此，通过几何法证明，我们可以得到勾股定理成立。

方法二：代数法证明这种证明方法是使用代数运算来证明勾股定理。

我们可以用直角三角形的三条边的长度来表示三角形的面积。

假设直角三角形的三条边分别为a、b、c，其中c 为斜边，利用面积公式S=1/2*底*高，我们可以得到三角形面积的两种表达式：S=1/2* a*bS=1/2* c*h通过这两个表达式，我们可以得到c*h=a*b，即c^2=a^2+b^2。

方法三：相似三角形法证明这种证明方法利用相似三角形的性质来证明勾股定理。

我们可以在直角三角形ABC中找到一个与之全等的直角三角形DEF。

然后我们可以发现直角三角形ABC和DEF分别是直角三角形ACB和EDF的相似三角形。

由于相似三角形的对应边成比例，我们可以得到AB/DE=BC/EF=AC/DF。

利用这个性质，我们可以得到AB^2=DE^2+DF^2和AC^2=DE^2+EF^2。

将这两个式子相加起来，我们可以得到AB^2+AC^2=DE^2+DF^2+DE^2+EF^2，根据平行四边形的性质，我们可以得到AB^2+AC^2=2*DE^2+2*DF^2。

勾股定理16种经典证明方法

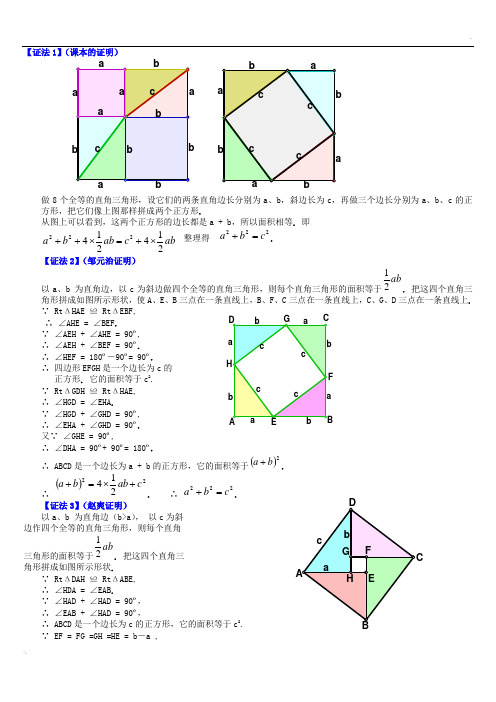
ab c ab b a 214214222⨯+=⨯++【证法1】（课本的证明）做8个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c ，再做三个边长分别为a 、b 、c 的正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形的边长都是a + b ，所以面积相等. 即整理得 222c b a =+.【证法2】（邹元治证明）以a 、b 为直角边，以c 为斜边做四个全等的直角三角形，则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上，B 、F 、C 三点在一条直线上，C 、G 、D 三点在一条直线上.∵ Rt ΔHAE ≌ Rt ΔEBF,∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º,∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的正方形. 它的面积等于c 2.∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA .∵ ∠HGD + ∠GHD = 90º,∴ ∠EHA + ∠GHD = 90º.又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形，它的面积等于()2b a +.∴ ()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法3】（赵爽证明）以a 、b 为直角边（b>a ），以c 为斜边作四个全等的直角三角形，则每个直角三角形的面积等于ab21. 把这四个直角三角形拼成如图所示形状.∵ Rt ΔDAH ≌ Rt ΔABE, ∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º， ∴ ∠EAB + ∠HAD = 90º，∴ ABCD 是一个边长为c 的正方形，它的面积等于c 2. ∵ EF = FG =GH =HE = b ―a ,∠HEF = 90º.∴ EFGH 是一个边长为b ―a 的正方形，它的面积等于()2a b -.∴ ()22214c a b ab =-+⨯.∴ 222c b a =+.【证法4】（1876年美国总统Garfield 证明）以a 、b 为直角边，以c 为斜边作两个全等的直角三角形，则每个直角三角形的面积等于ab 21. 把这两个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE, ∴ ∠ADE = ∠BEC .∵ ∠AED + ∠ADE = 90º, ∴ ∠AED + ∠BEC = 90º. ∴ ∠DEC = 180º―90º= 90º.∴ ΔDEC 是一个等腰直角三角形，它的面积等于221c.又∵ ∠DAE = 90º, ∠EBC = 90º, ∴ AD ∥BC .∴ ABCD 是一个直角梯形，它的面积等于()221b a +.∴ ()222121221c ab b a +⨯=+. ∴ 222c b a =+.【证法5】（梅文鼎证明）做四个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c . 把它们拼成如图那样的一个多边形，使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P .∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD, ∴ ∠EGF = ∠BED ，∵ ∠EGF + ∠GEF = 90°，∴ ∠BED + ∠GEF = 90°，∴ ∠BEG =180º―90º= 90º. 又∵ AB = BE = EG = GA = c ， ∴ ABEG 是一个边长为c 的正方形. ∴ ∠ABC + ∠CBE = 90º.∵ Rt ΔABC ≌ Rt ΔEBD, ∴ ∠ABC = ∠EBD . ∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º. 又∵ ∠BDE = 90º，∠BCP = 90º，BC = BD = a . ∴ BDPC 是一个边长为a 的正方形. 同理，HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ，则,21222ab S b a ⨯+=+ abS c 2122⨯+=,∴ 222c b a =+.【证法6】（项明达证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ），斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形，使E 、A 、C 三点在一条直线上.过点Q 作QP ∥BC ，交AC 于点P . 过点B 作BM ⊥PQ ，垂足为M ；再过点 F 作FN ⊥PQ ，垂足为N .∵ ∠BCA = 90º，QP ∥BC ，∴ ∠MPC = 90º，∵ BM ⊥PQ ，∴ ∠BMP = 90º，∴ BCPM 是一个矩形，即∠MBC = 90º.∵ ∠QBM + ∠MBA = ∠QBA = 90º， ∠ABC + ∠MBA = ∠MBC = 90º， ∴ ∠QBM = ∠ABC ，又∵ ∠BMP = 90º，∠BCA = 90º，BQ = BA = c ，∴ Rt ΔBMQ ≌ Rt ΔBCA . 同理可证Rt ΔQNF ≌ Rt ΔAEF . 从而将问题转化为【证法4】（梅文鼎证明）. 【证法7】（欧几里得证明）做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使H 、C 、B 三点在一条直线上，连结 BF 、CD . 过C 作CL ⊥DE ，交AB 于点M ，交DE 于点 L .∵ AF = AC ，AB = AD ， ∠FAB = ∠GAD ， ∴ ΔFAB ≌ ΔGAD ，∵ ΔFAB 的面积等于221a ，ΔGAD 的面积等于矩形ADLM的面积的一半，∴ 矩形ADLM 的面积 =2a .同理可证，矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB∴ 222b ac += ，即 222c b a =+【证法8】（利用相似三角形性质证明）如图，在Rt ΔABC 中，设直角边AC 、BC 的长度分别为a 、b ，斜边AB 的长为c ，过点C 作CD ⊥AB ，垂足是D .在ΔADC 和ΔACB 中，∵ ∠ADC = ∠ACB = 90º， ∠CAD = ∠BAC ， ∴ ΔADC ∽ ΔACB . AD ∶AC = AC ∶AB ，即 AB AD AC •=2.同理可证，ΔCDB ∽ ΔACB ，从而有 AB BD BC •=2.∴ ()222AB AB DB AD BC AC =•+=+，即 222c b a =+.【证法9】（杨作玫证明）做两个全等的直角三角形，设它们的两条直角边长分别为a 、b （b>a ），斜边长为c . 再做一个边长为c 的正方形.把它们拼成如图所示的多边形. 过A 作AF ⊥AC ，AF 交GT 于F ，AF 交DT 于R . 过B 作BP ⊥AF ，垂足为P . 过D 作DE 与CB 的延长线垂直，垂足为E ，DE 交AF 于H .∵ ∠BAD = 90º，∠PAC = 90º， ∴ ∠DAH = ∠BAC . 又∵ ∠DHA = 90º，∠BCA = 90º，AD = AB = c ， ∴ Rt ΔDHA ≌ Rt ΔBCA . ∴ DH = BC = a ，AH = AC = b .由作法可知， PBCA 是一个矩形，所以 Rt ΔAPB ≌ Rt ΔBCA . 即PB = CA = b ，AP= a ，从而PH = b ―a . ∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA .∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ，∠GDT = ∠HDA . 又∵ ∠DGT = 90º，∠DHF = 90º，∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º， ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF ，TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形，上底TF=b ―a ，下底BP= b ，高FP=a +（b ―a ）. 用数字表示面积的编号（如图），则以c 为边长的正方形的面积为543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+•-+=++21438 =ab b 212-， 985S S S +=，∴ 824321S ab b S S --=+=812SS b -- . ② 把②代入①，得98812212S S S S b S S c ++--++==922S S b ++ = 22a b +. ∴ 222c b a =+.【证法10】（李锐证明）设直角三角形两直角边的长分别为a 、b （b>a ），斜边的长为c . 做三个边长分别为a 、b 、c 的正方形，把它们拼成如图所示形状，使A 、E 、G 三点在一条直线上. 用数字表示面积的编号（如图）.∵ ∠TBE = ∠ABH = 90º， ∴ ∠TBH = ∠ABE .又∵ ∠BTH = ∠BEA = 90º， BT = BE = b ，∴ Rt ΔHBT ≌ Rt ΔABE . ∴ HT = AE = a .∴ GH = GT ―HT = b ―a .又∵ ∠GHF + ∠BHT = 90º，∠DBC + ∠BHT = ∠TBH + ∠BHT = 90º， ∴ ∠GHF = ∠DBC .∵ DB = EB ―ED = b ―a ， ∠HGF = ∠BDC = 90º， ∴ Rt ΔHGF ≌ Rt ΔBDC . 即 27SS =. 过Q 作QM ⊥AG ，垂足是M . 由∠BAQ = ∠BEA = 90º，可知 ∠ABE= ∠QAM ，而AB = AQ = c ，所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌Rt ΔABE . 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58SS =. 由Rt ΔABE ≌ Rt ΔQAM ，又得QM = AE = a ，∠AQM = ∠BAE .∵ ∠AQM + ∠FQM = 90º，∠BAE + ∠CAR = 90º，∠AQM = ∠BAE ， ∴ ∠FQM = ∠CAR .又∵ ∠QMF = ∠ARC = 90º，QM = AR = a ，∴ Rt ΔQMF ≌ Rt ΔARC . 即64S S =.∵ 543212S S S S S c ++++=，612S S a +=，8732S S S b ++=，又∵27S S =，58S S =，64S S =，∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c ，即 222c b a =+.【证法11】（利用切割线定理证明）在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c . 如图，以B 为圆心a 为半径作圆，交AB 及AB 的延长线分别于D 、E ，则BD = BE = BC = a . 因为∠BCA = 90º，点C 在⊙B 上，所以AC 是⊙B 的切线. 由切割线定理，得AD AE AC •=2=()()BD AB BE AB -+=()()a c a c -+ = 22a c -，即222a c b -=，∴ 222c b a =+.【证法12】（利用多列米定理证明）在Rt ΔABC 中，设直角边BC = a ，AC = bAD ∥CB ，过点B 作BD ∥CA ，则ACBD 为矩形，矩形ACBD 内接于一个圆. 根据多列米定理，圆内接四边形对角线的乘积等于两对边乘积之和，有BD AC BC ADDC AB •+•=•，∵ AB = DC = c ，AD = BC = a ， AC = BD = b ，∴ 222ACBC AB +=，即 222b a c +=，∴ 222c b a =+.【证法13】（作直角三角形的内切圆证明）在Rt ΔABC 中，设直角边BC = a ，AC = b ，斜边AB = c . 作Rt ΔABC 的内切圆⊙O ，切点分别为D 、E 、F （如图），设⊙O 的半径为r .∵ AE = AF ，BF = BD ，CD = CE ，∴ ()()()BF AF CD BD CE AE AB BC AC +-+++=-+= CD CE += r + r = 2r,即 r c b a 2=-+， ∴ c r b a +=+2.∴ ()()222c r b a +=+，即 ()222242c rc r ab b a ++=++，∵ ab S ABC 21=∆，∴ABC S ab ∆=42，又∵AOC BOCAOB ABC S S S S ∆∆∆∆++= = br ar cr 212121++ = ()r c b a ++21= ()r c c r ++221= rc r +2，∴()ABC S rc r ∆=+442， ∴ ()ab rc r242=+，∴ 22222c ab ab b a +=++， ∴ 222c b a =+.【证法14】（利用反证法证明）如图，在Rt ΔABC 中，设直角边AC 、BC 的长度分别为a 、b ，斜边AB 的长为c ，过点C 作CD ⊥AB ，垂足是D .假设222c b a ≠+，即假设 222AB BC AC ≠+，则由AB AB AB •=2=()BD AD AB +=BD AB AD AB •+• 可知 AD AB AC •≠2，或者 BD AB BC •≠2. 即 AD ：AC ≠AC ：AB ，或者 BD ：BC ≠BC ：AB .在ΔADC 和ΔACB 中， ∵ ∠A = ∠A ，∴ 若 AD ：AC ≠AC ：AB ，则 ∠ADC ≠∠ACB . 在ΔCDB 和ΔACB 中， ∵ ∠B = ∠B ，∴ 若BD ：BC ≠BC ：AB ，则 ∠CDB ≠∠ACB . 又∵ ∠ACB = 90º，∴ ∠ADC ≠90º，∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以，222AB BC AC ≠+的假设不能成立.∴ 222c b a =+.【证法15】（辛卜松证明）设直角三角形两直角边的长分别为a 、b ，斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分，则正方形ABCD 的面积为()ab b a b a 2222++=+；把正方形ABCD 划分成上方右图所示的几个部分，则正方形ABCD 的面积为()22214c ab b a +⨯=+ =22c ab +.D D∴ 22222c ab ab b a +=++,∴ 222c b a =+.【证法16】（陈杰证明）设直角三角形两直角边的长分别为a 、b （b>a ），斜边的长为c . 做两个边长分别为a 、b 的正方形（b>a ），把它们拼成如图所示形状，使E 、H 、M 三点在一条直线上. 用数字表示面积的编号（如图）.在EH = b 上截取ED = a ，连结DA 、DC ，则 AD = c .∵ EM = EH + HM = b + a , ED = a ， ∴ DM = EM ―ED = ()a b +―a = b . 又∵ ∠CMD = 90º，CM = a ，∠AED = 90º， AE = b ， ∴ Rt ΔAED ≌ Rt ΔDMC .∴ ∠EAD = ∠MDC ，DC = AD = c . ∵ ∠ADE + ∠ADC+ ∠MDC =180º，∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º， ∴ ∠ADC = 90º.∴ 作AB ∥DC ，CB ∥DA ，则ABCD 是一个边长为c 的正方形. ∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º， ∴ ∠BAF=∠DAE .连结FB ，在ΔABF 和ΔADE 中，∵ AB =AD = c ，AE = AF = b ，∠BAF=∠DAE ， ∴ ΔABF ≌ ΔADE .∴ ∠AFB = ∠AED = 90º，BF = DE = a . ∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中，∵ AB = BC = c ，BF = CG = a ， ∴ Rt ΔABF ≌ Rt ΔBCG .∵ 54322S S S S c +++=， 6212S S S b ++=，732S S a +=，76451S S S S S +===，∴6217322S S S S S b a ++++=+ =()76132S S S S S ++++ =5432S S S S +++=2c∴ 222c b a =+.。

勾股定理几种证明方法

勾股定理几种证明方法勾股定理的证明【证法1】（课本的证明）做8个全等的直角三角形，设它们的两条直角边长分别为a、b，斜边长为c，再做三个边长分别为a、b、c的正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形的边长都是a+b，所以面积相等.即11a2+b2+4×ab=c2+4×ab22，整理得a2+b2=c2.【证法2】（邹元治证明）以a、b为直角边，以c为斜边做四个全等的直角三角形，则每个直角三角形的面积1ab2等于.把这四个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上，B、F、C三点在一条直线上，C、G、D三点在一条直线上.∵RtΔHAE≌RtΔEBF,∴∠AHE=∠BEF.∵∠AEH+∠AHE=90º,∴∠AEH+∠BEF=90º.∴∠HEF=180º―90º=90º.∴四边形EFGH是一个边长为c的正方形.它的面积等于c2.∵RtΔGDH≌RtΔHAE,∴∠HGD=∠EHA.∵∠HGD+∠GHD=90º,∴∠EHA+∠GHD=90º.又∵∠GHE=90º,∴∠DHA=90º+90º=180º.2∴.∴a+b=c.【证法3】（赵爽证明）以a、b为直角边（b>a），以c为斜边作四个全等的直角三角形，则每个直角(a+∴ABCD是一个边长为a+b的正方形，它的面积等于(a+b)2=4×1ab+c22221ab2三角形的面积等于.把这四个直角三角形拼成如图所示形状.∵RtΔDAH≌RtΔABE,∴∠HDA=∠EAB.∵∠HAD+∠HAD=90º，∴∠EAB+∠HAD=90º，2∴ABCD是一个边长为c的正方形，它的面积等于c.∵EF=FG=GH=HE=b―a,∠HEF=90º. 2(b−a)∴EFGH是一个边长为b―a的正方形，它的面积等于.14×ab+(b−a)2=c22∴.222∴a+b=c.【证法4】（1876年美国总统Garfield证明）以a、b为直角边，以c为斜边作两个全等的直角三角形，则每个直角三角形的面1ab2积等于.把这两个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上.∵∴∵∴∴∴RtΔEAD≌RtΔCBE,∠ADE=∠BEC.∠AED+∠ADE=90º,∠AED+∠BEC=90º.∠DEC=180º―90º=90º.ΔDEC是一个等腰直角三角形，12c2它的面积等于.又∵∠DAE=90º,∠EBC=90º,∴AD∥BC.1(a+b)2∴ABCD是一个直角梯形，它的面积等于2.1(a+b)2=2×1ab+1c222.∴2∴a+b=c.【证法5】（梅文鼎证明）做四个全等的直角三角形，设它们的两条直角边长分别为a、b，斜边长为c.把它们拼成如图那样的一个多边形，使D、E、F在一条直线上.过C作AC的延长线交DF于点P.∵D、E、F在一条直线上,且RtΔGEF≌RtΔEBD,∴∠EGF=∠BED，∵∠EGF+∠GEF=90°，222∴∴又∵∴∴∵∴∴即又∵∠BED+∠GEF=90°，∠BEG=180º―90º=90º.AB=BE=EG=GA=c，ABEG是一个边长为c的正方形.∠ABC+∠CBE=90º.RtΔABC≌RtΔEBD,∠ABC=∠EBD.∠EBD+∠CBE=90º.∠CBD=90º.∠BDE=90º，∠BCP=90º，BC=BD=a.∴BDPC是一个边长为a的正方形.同理，HPFG是一个边长为b的正方形.设多边形GHCBE的面积为S，则1a2+b2=S+2×ab,21c2=S+2×ab2,∴a2+b2=c2.【证法6】（项明达证明）做两个全等的直角三角形，设它们的两条直角边长分别为a、b（b>a），斜边长为c.再做一个边长为c的正方形.把它们拼成如图所示的多边形，使E、A、C三点在一条直线上.过点Q作QP∥BC，交AC于点P.过点B作BM⊥PQ，垂足为M；再过点F作FN⊥PQ，垂足为N.∵∠BCA=90º，QP∥BC，∴∠MPC=90º，∵BM⊥PQ，∴∠BMP=90º，∴BCPM是一个矩形，即∠MBC=∵∠QBM+∠MBA=∠QBA=90º，∠ABC+∠MBA=∠MBC=90º，∴∠QBM=∠ABC，又∵∠BMP=90º，∠BCA=90º，BQ=BA=c，∴RtΔBMQ≌RtΔBCA.同理可证RtΔQNF≌RtΔAEF.从而将问题转化为【证法4】（梅文鼎证明）.【证法7】（欧几里得证明）做三个边长分别为a、b、c的正方形，把它们拼成如图所示形状，使H、C、B三点在一条直线上，连结BF、CD.过C作CL⊥DE，交AB于点M，交DE于点L.∵AF=AC，AB=AD，∠FAB=∠GAD，∴ΔFAB≌ΔGAD，12a∵ΔFAB的面积等于2ΔGAD的面积等于矩形ADLM的面积的一半，2∴矩形ADLM的面积=a.2b同理可证，矩形MLEB的面积=.∵正方形ADEB的面积=矩形ADLM的面积+矩形MLEB的面积222222∴c=a+b，即a+b=c.【证法8】（杨作玫证明）做两个全等的直角三角形，设它们的两条直角边长分别为a、b（b>a），斜边长为c.再做一个边长为c的正方形.把它们拼成如图所示的多边形.过A作AF⊥AC，AF交GT于F，AF交DT于R.过B作BP⊥AF，垂足为P.过D作DE与CB的延长线垂直，垂足为E，DE交AF于H.∵∠BAD=90º，∠PAC=90º，∴∠DAH=∠BAC.又∵∠DHA=90º，∠BCA=90º，AD=AB=c，∴RtΔDHA≌RtΔBCA.∴DH=BC=a，AH=AC=b.由作法可知，PBCA是一个矩形，所以RtΔAPB≌RtΔBCA.即PB=CA=b，AP=a，从而PH=b―a.∵RtΔDGT≌RtΔBCA,RtΔDHA≌RtΔBCA.∴RtΔDGT≌RtΔDHA.∴DH=DG=a，∠GDT=∠HDA.又∵∠DGT=90º，∠DHF=90º，∠GDH=∠GDT+∠TDH=∠HDA+∠TDH=90º，∴DGFH是一个边长为a的正方形.∴GF=FH=a.TF⊥AF，TF=GT―GF=b―a.∴TFPB是一个直角梯形，上底TF=b―a，下底BP=b，高FP=a+（b―a）.用数字表示面积的编号（如图），则以c为边长的正方形的面积为c2=S1+S2+S3+S4+S5①∵S8+S3+S4=1[b+(b−a)]•[a+(b−a)]b2−1ab22，=S5=S8+S9，1S3+S4=b2−ab−S8b2−S−S18.2∴=②把②代入①，得c2=S1+S2+b2−S1−S8+S8+S92b+S2+S9=b2+a2.=222∴a+b=c.【证法9】（李锐证明）设直角三角形两直角边的长分别为a、b（b>a），斜边的长为c.做三个边长分别为a、b、c的正方形，把它们拼成如图所示形状，使A、E、G三点在一条直线上.用数字表示面积的编号（如图）.∵∠TBE=∠ABH=90º，∴∠TBH=∠ABE.又∵∠BTH=∠BEA=90º，BT=BE=b，∴RtΔHBT≌RtΔABE.∴HT=AE=a.∴GH=GT―HT=b―a.又∵∠GHF+∠BHT=90º，∠DBC+∠BHT=∠TBH+∴∠GHF=∠DBC.∵DB=EB―ED=b―a，∠HGF=∠BDC=90º，∴RtΔHGF≌RtΔBDC.即S7=S2.过Q作QM⊥AG，垂足是M.由∠BAQ=∠BEA=90º，可知∠ABE=∠QAM，而AB=AQ=c，所以RtΔABE≌RtΔQAM.又RtΔHBT≌RtΔABE.所以RtΔHBT≌RtΔQAM.即S8=S5.由RtΔABE≌RtΔQAM，又得QM=AE=a，∠AQM=∠BAE.∵∠AQM+∠FQM=90º，∠BAE+∠CAR=90º，∠AQM=∠BAE，∴∠FQM=∠CAR.又∵∠QMF=∠ARC=90º，QM=AR=a，∴RtΔQMF≌RtΔARC.即S4=S6.222c=S+S+S+S+Sa=S+Sb1234516∵，，=S3+S7+S8，又∵S7=S2，S8=S5，S4=S6，22a+b=S1+S6+S3+S7+S8∴=S1+S4+S3+S2+S5=c，222即a+b=c.【证法10】（利用反证法证明）如图，在RtΔABC中，设直角边AC、BC的长度分别为a、b，斜边AB的长为c，过点C作CD⊥AB，垂足是D.222222假设a+b≠c，即假设AC+BC≠AB，则由AB2=AB•AB=AB(AD+BD)=AB•AD+AB•BD22可知AC≠AB•AD，或者BC≠AB•BD.即AD：AC≠AC：AB，或者BD：BC≠BC：AB.在ΔADC和ΔACB中，∵∠A=∠A，∴若AD：AC≠A C：AB，则∠ADC≠∠ACB.在ΔCDB和ΔACB中，∵∠B=∠B，∴若BD：BC≠BC：AB，则∠CDB≠∠ACB.又∵∠ACB=90º，∴∠ADC≠90º，∠CDB≠90º.222AC+BC≠AB这与作法CD⊥AB矛盾.所以，的假设不能成立.222∴a+b=c.【证法15】（辛卜松证明）DD2设直角三角形两直角边的长分别为a、b，斜边的长为c.作边长是a+b的正方形ABCD.把正方形ABCD划分成上方左图所示的几个部分，则正方形ABCD的面积为(a+b)2=a2+b2+2ab；把正方形ABCD划分成上方右图所示的几个部分，则正方形ABCD 的面积为∴∴(a+b)21=4×ab+c222=2ab+c.a2+b2+2ab=2ab+c2,【证法11】（陈杰证明）设直角三角形两直角边的长分别为a、b（b>a），斜边的长为c.做两个边长分别为a、b的正方形（b>a），把它们拼成如图所示形状，使E、H、M三点在一条直线上.用数字表示面积的编号（如图）.在EH=b上截取ED=a，连结则AD=c.∵EM=EH+HM=b+a,ED=∴DM=EM―ED=(b+a)―a=b.又∵∠CMD=90º，CM=a，∠AED=90º，AE=b，∴RtΔAED≌RtΔDMC.∴∠EAD=∠MDC，DC=AD=c.∵∠ADE+∠ADC+∠MDC=180º，∠ADE+∠MDC=∠ADE+∠EAD=90º，∴∠ADC=90º.∴作AB∥DC，CB∥DA，则ABCD是一个边长为c的正方形.∵∠BAF+∠FAD=∠DAE+∠FAD=90º，∴∠BAF=∠DAE.连结FB，在ΔABF和ΔADE中，∵AB=AD=c，AE=AF=b，∠BAF=∠DAE，∴ΔABF≌ΔADE.∴∠AFB=∠AED=90º，BF=DE=a.∴点B、F、G、H在一条直线上.在RtΔABF和RtΔBCG 中，∵AB=BC=c，BF=CG=a，∴RtΔABF≌RtΔBCG.2c=S2+S3+S4+S5，∵S1=S5=S4=S6+S7，b2=S1+S2+S6，a2=S3+S7，22a+b=S3+S7+S1+S2+S6∴=S2+S3+S1+(S6+S7)∴=S2+S3+S4+S52=c。

最好的勾股定理五种证明方法

勾股定理五种证明方法【证法1】做8个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c ，再做三个边长分别为a 、b 、c 的正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形的边长都是a + b ，所以面积相等. 即，整理得.以a、b 为直角边，以c为斜边做四个全等的直角三角形，则每个直角三角形的面积等于ab21.把这四个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上，B、F、C三点在一条直线上，C、G、D三点在一条直线上.∵RtΔHAE ≌RtΔEBF,∴∠AHE = ∠BEF.∵∠AEH + ∠AHE = 90º,∴∠AEH + ∠BEF = 90º.∴∠HEF = 180º―90º= 90º.∴四边形EFGH是一个边长为c的正方形. 它的面积等于c2.∵RtΔGDH ≌RtΔHAE,∴∠HGD = ∠EHA.∵∠HGD + ∠GHD = 90º,∴∠EHA + ∠GHD = 90º.又∵∠GHE = 90º,∴∠DHA = 90º+ 90º= 180º.∴ABCD是一个边长为a + b 的正方形，它的面积等于.∴.∴.做四个全等的直角三角形，设它们的两条直角边长分别为a、b ，斜边长为c. 把它们拼成如图那样的一个多边形，使D、E、F在一条直线上. 过C作AC 的延长线交DF于点P.∵D、E、F在一条直线上, 且RtΔGEF ≌RtΔEBD,∴∠EGF = ∠BED，∵∠EGF + ∠GEF = 90°，∴∠BED + ∠GEF = 90°，Array∴∠BEG =180º―90º= 90º.又∵AB = BE = EG = GA = c，∴ABEG是一个边长为c的正方形.∴∠ABC + ∠CBE = 90º.∵RtΔABC ≌RtΔEBD,∴∠ABC = ∠EBD.∴∠EBD + ∠CBE = 90º.即∠CBD= 90º.又∵∠BDE = 90º，∠BCP = 90º，BC = BD = a.∴BDPC是一个边长为a的正方形.同理，HPFG是一个边长为b的正方形.设多边形GHCBE的面积为S，则.以a 、b 为直角边，以c 为斜边作两个全等的直角三角形，则每个直角三角形的面积等于ab 21. 把这两个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE,∴ ∠ADE = ∠BEC .∵ ∠AED + ∠ADE = 90º, ∴ ∠AED + ∠BEC = 90º. ∴ ∠DEC = 180º―90º= 90º. ∴ ΔDEC 是一个等腰直角三角形，它的面积等于221c.又∵ ∠DAE = 90º, ∠EBC = 90º, ∴ AD ∥BC .∴ ABCD 是一个直角梯形，它的面积等于...设直角三角形两直角边的长分别为a 、b ，斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分，则正方形ABCD的面积为；把正方形ABCD 划分成上方右图所示的几个分，则正方形ABCD 的面积为.初二一班游彬ab21ab 21ab 21ab 212c 2b 2aA D BB ab a ba b b a c c ccb a ab abb a b a。

勾股定理的5种方式

勾股定理的五种证明方式1．画两个边长为(a+b)的正方形，如图，其中a、b为直角边，c为斜边。

这两个正方形全等，故面积相等。

左图与右图各有四个与原直角三角形全等的三角形，左右四个三角形面积之和必相等。

从左右两图中都把四个三角形去掉，图形剩下部分的面积必相等。

左图剩下两个正方形，分别以a、b为边。

右图剩下以c为边的正方形。

于是a2+b2=c2。

这就是我们几何教科书中所介绍的方法。

既直观又简单，任何人都看得懂。

2．直接在直角三角形三边上画正方形，如图。

容易看出，△ABA’ ≌△AA’’ C。

过C向A’’B’’引垂线，交AB于C’，交A’’B’’于C’’。

△ABA’与正方形ACDA’同底等高,前者面积为后者面积的一半，△AA’’C与矩形AA’’C’’C’同底等高，前者的面积也是后者的一半。

由△ABA’≌△AA’’C，知正方形ACDA’的面积等于矩形AA’’C’’C’的面积。

同理可得正方形BB’EC的面积等于矩形B’’BC’C’’的面积。

于是，S正方形AA’’B’’B=S正方形ACDA’+S正方形BB’EC，即a2+b2=c2。

3.将四个直角三角形涂上朱色，把中间小正方形涂上黄色，叫做中黄实，以弦为边的正方形称为弦实，然后经过拼补搭配，“令出入相补，各从其类”，他肯定了勾股弦三者的关系是符合勾股定理的。

即“勾股各自乘，并之为弦实，开方除之，即弦也”。

4.S梯形ABCD= (a+b)2 = (a2+2ab+b2)，①又S梯形ABCD=S△AED+S△EBC+S△CED = ab+ ba+ c2 = (2ab+c2)。

②比较以上二式，便得a2+b2=c25.在直角三角形中，斜边上的高把这个直角三角形所分成的两个直角三角形与原三角形相似。

Rt△ABC中，∠ACB=90°。

作CD⊥BC，垂足为D。

则△BCD∽△BAC，△CAD∽△BAC。

由△BCD∽△BAC可得BC2=BD • BA，①由△CAD∽△BAC可得AC2=AD • AB。

勾股定理五种证明方法

勾股定理五种证明方法1. 几何证明法勾股定理是数学中的基本定理之一，用于描述直角三角形的边长关系。

根据勾股定理，直角三角形的斜边的平方等于两个直角边的平方和。

几何证明法是最直观的证明方法之一。

我们可以通过绘制一个正方形来证明勾股定理。

假设直角三角形的两个直角边分别为a和b，斜边为c。

我们可以将这个三角形绘制在一个边长为a+b的正方形内。

将正方形分成四个小正方形，其中三个小正方形的边长分别为a，b和c。

通过计算小正方形的面积，我们可以得出结论：c^2 = a^2 + b^2。

2. 代数证明法代数证明法是另一种常用的证明勾股定理的方法。

这种方法使用代数运算和方程的性质来证明定理。

假设直角三角形的两个直角边分别为a和b，斜边为c。

我们可以通过使用平方的性质来证明勾股定理。

根据勾股定理，我们有：c^2 = a^2 + b^2。

我们可以将c^2展开为(a + b)2，即：c2 = (a + b)^2 = a^2 + 2ab + b^2。

通过对比等式两边的表达式，我们可以得出结论：2ab = 0。

由于直角三角形的边长必须为正数，因此我们可以得出结论：ab = 0。

这意味着a或b至少有一个为0。

如果a为0，那么直角三角形就变成了一个直角边长为b的直角三角形，此时勾股定理显然成立。

同样地，如果b为0，那么直角三角形就变成了一个直角边长为a的直角三角形，此时勾股定理也成立。

综上所述，勾股定理成立。

3. 数学归纳法证明数学归纳法是一种常用的证明数学命题的方法，它通常用于证明自然数的性质。

虽然勾股定理是针对直角三角形的，但我们可以通过数学归纳法证明勾股定理对于所有正整数的直角三角形都成立。

首先，我们证明当直角三角形的直角边长度为1时，勾股定理成立。

这是显而易见的，因为直角三角形的斜边长度必然大于1，所以直角边长度为1的直角三角形一定满足勾股定理。

然后，我们假设当直角三角形的直角边长度为k时，勾股定理成立。

即假设a^2 + b^2 = c^2，其中a和b分别为直角三角形的直角边，c为斜边。

勾股定理16种证明方法

【证法1】（课本的证明）做8个全等的直角三角形，设它们的两条直角边长分别为a、b，斜边长为c，再做三个边长分别为a、b、c的正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形的边长都是a + b，所以面积相等. 即a²+b²+4x1/2ab=c²+4x1/2ab，整理得a²+b²=c²。

1. 2【证法2】（邹元治证明）以a、b 为直角边，以c为斜边做四个全等的直角三角形，则每个直角三角1ab2形的面积等于. 把这四个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上，B、F、C三点在一条直线上，C、G、D三点在一条直线上. ∵RtΔHAE ≌RtΔEBF, ∴∠AHE = ∠BEF.∵∠AEH + ∠AHE = 90o, ∴∠AEH + ∠BEF = 90o. ∴∠HEF = 180o―90o= 90o.∴四边形EFGH是一个边长为c的正方形. 它的面积等于c2. ∵ RtΔGDH ≌ RtΔHAE,∴∠HGD = ∠EHA. ∵∠HGD + ∠GHD = 90o,∴∠EHA + ∠GHD = 90o.又∵∠GHE = 90o,∴∠DHA = 90o+ 90o= 180o.∴ ABCD是一个边长为a + b的正方形，它的面积等于(a+b)².∴(a+b)²=4x1/2ab+c²∴ a²+b²=c²。

2. 3【证法3】（赵爽证明）以a、b 为直角边（b>a），以c为斜边作四个全等的直角三角形，则每个直角 1ab2三角形的面积等于. 把这四个直角三角形拼成如图所示形状. ∵ RtΔDAH ≌ RtΔABE,∴∠HDA = ∠EAB.∵∠HAD + ∠HAD = 90o，∴∠EAB + ∠HAD = 90o， 2∴ ABCD是一个边长为c的正方形，它的面积等于c.∵ EF = FG =GH =HE = b―a ,∠HEF = 90o.∴ EFGH是一个边长为b―a的正方形，它的面积等于(b-a)².∴(b-a)²=4x1/2ab+c²∴ a²+b²=c²。