位置关系的相对性
【精品】人教版六年级数学上册第二单元位置与方向(二)思维导图(PDF高清版)

第二单元 位置与方向(二)
数
对 由
两个数组成,中间用逗号隔开,用括号括起
来。
括号里面的数由左至右为列数和行数,即“先
列后行”。
作
用:确定一个点的位置。
经度和纬度就是这个 原理。
确
定物体位置的方法 (1).先找观测点 (2).再定方向(看方向夹角的度数) (3).最后确定距离(看比例尺)
描绘路线图的关键是选好观测点,建立方向标, 确定方向和路程。
位
置关系的相对性 两地的位置具有相对性在叙述两地的位置关系
时,观测点例外,叙述的方向凑巧相反,而角度 和距离不变。
相
对位置 东--西
南--北
南偏东--北偏西。
位置的相对性 (3)-四(下)xguybf

当堂训练
你我位置描述
你在我的东偏南45° 的方向上,距离是1米。
45°
北 西 南 东
45°
你在我的西偏北 45°的方向上, 距离是 1 米。
当堂训练
1. 我们站在学校看小刚家, 小刚家在学校的什么方向 上?距离是多少米?
家校地图 小刚家
200米
小芳家
30°学校 21°小红家 27°Fra bibliotek45°
2. 我们站在小刚家看 学校,学校在小刚家的 什么方向上?距离是多 少米?
小刚家在学校的 东偏北45度的方向上, 距离是1000米。
小亮家
学校在小刚家的西 偏南45度的方向上, 距离是1000米。
当堂训练
抢答游戏
A在B的北偏东30°的方向上,距离是300米。 B在A的( 南)偏( 西)(30 )°的方向上,距离是 (300 )米。
说说你的方法:
方向相反;角度相同;距离相等。
人教版数学
四年级下册
位置的相对性
课前准备
北 200米
岛
看图回答: 西
40º 灯塔
东
岛在灯塔的( 东 )偏( 北 )( 40 )°方 向上,距离是( 1200 )米。
或者说:
岛在灯塔的( 北 )偏( 东 )( 50 )°方 向上,距离是( 1200 )米。
北
课前准备
小林家
300米
看图回答:
西
35°
学校
小林家在学校的( 西 )偏(北 )( 35)° 方向上,距离是( 300 )米。
或者说:
小林家在学校的(北 )偏(西 )(55)° 方向上,距离是( 300 )米。
小组讨论
认真阅读教材P22的例3,边看边思考: 1.找出北京和上海两个城市在地图上的位 置。 2.上海在北京的( )方向,北京在上海 的( )方向,分别是以谁为观测点? 两个城市的位置是什么关系?
空间关系知识点总结

空间关系知识点总结一、空间概念空间是指周围的环境由物质实体所构成的三维空间。
在这个空间中,物体可以相对移动,相对位置也会发生变化。
在空间中,我们可以观察到物体的位置、形状和大小等属性。
空间关系是指事物在空间中的相对位置关系。
空间关系有三种形式,即相对位置、方位和距离。
1.相对位置:相对位置是指两个物体在空间中的相对位置关系。
当我们描述一个事物所处的位置时,一定要以另一事物为基准来描述,这就是相对位置。
例如,A在B的左边,B在A的右边,这是相对位置的描述。
2.方位:方位是指事物在空间中的朝向关系。
方位由四个基本方向组成,即东、西、南、北。
在地理空间中还有东北、东南、西北、西南等方位。
方位是空间中非常重要的关系,能够帮助我们更准确地描述事物在空间中的位置。
3.距离:距离是指两个事物在空间中的间隔距离。
在空间中,物体可以通过距离来描述物体的相对远近。
距离是空间关系中很重要的一个方面,它可以通过度量直线距离、曲线距离来描述物体之间的相对远近。
二、空间语言描述空间关系可以通过语言来进行描述。
语言描述可以帮助我们更加准确地了解物体在空间中的位置、方位以及距离。
在语言描述中,要注意以下几点:1.使用准确的定位词语:在描述空间关系时,要使用准确的定位词语,如“上、下、左、右、前、后”等。
这些词语可以帮助我们更加准确地描述事物在空间中的位置。
2.使用准确的方向词语:在描述方位时,要使用准确的方向词语,如“东、西、南、北”等。
这些词语可以帮助我们更加准确地描述事物在空间中的朝向关系。
3.使用准确的距离词语:在描述距离时,要使用准确的距离词语,如“远、近、远离、靠近”等。
这些词语可以帮助我们更加准确地描述事物在空间中的相对远近关系。
三、空间关系的认知发展儿童对空间关系的认知发展是一个渐进的过程。
在儿童的认知过程中,从最初的“具体视觉参照”到“图形概念”再到“抽象概念”,儿童对空间关系的认知逐渐升级。
1.具体视觉参照:儿童最开始的认知是基于具体的物体进行的。
六年级数学重点内容及易错题(上册)

六年级数学重点内容及易错题(上册)第一单元分数乘法一、分数乘法(一)分数乘法的意义:1、分数乘整数与整数乘法的意义相同。
都是求几个相同加数的和的简便运算。
例如:65×5表示求5个65的和是多少? 1/3×5表示求5个1/3的和是多少?2、一个数乘分数的意义是求一个数的几分之几是多少。
例如:1/3×4/7表示求1/3的4/7是多少。
4×3/8表示求4的3/8是多少.(二)、分数乘法的计算法则:1、分数与整数相乘:分子与整数相乘的积做分子,分母不变。
(整数和分母约分)2、分数与分数相乘:用分子相乘的积做分子,分母相乘的积做分母。
注意:当带分数进行乘法计算时,要先把带分数化成假分数再进行计算。
3、为了计算简便,能约分的要先约分,再计算。
(尽量约分,不会约分的就不约,常考的质因数有11×11=121;13×13=169;17×17=289;19×19=361)4、小数乘分数,可以先把小数化为分数,也可以把分数化成小数再计算(建议把小数化分数再计算)。
(三)、乘法中比较大小的规律一个数(0除外)乘大于1的数,积大于这个数。
一个数(0除外)乘小于1的数(0除外),积小于这个数。
一个数(0除外)乘1,积等于这个数。
(四)、分数混合运算的运算顺序和整数的运算顺序相同。
整数乘法的交换律、结合律和分配律,对于分数乘法也同样适用。
乘法交换律: a × b = b × a乘法结合律:( a × b )×c = a × ( b × c )乘法分配律:( a + b )×c = a c + b c二、分数乘法的解决问题(已知单位“1”的量(用乘法),即求单位“1”的几分之几是多少)1、画线段图:(1)两个量的关系:画两条线段图,先画单位一的量,注意两条线段的左边要对齐。
(2)部分和整体的关系:画一条线段图。
位置与方向相对性

位置与方向相对性《位置的相对性》教学设计教学内容:新课标人教版第四册下第二单元《位置与方向》p22例3、做一做及p24练习四1、2题。
教学目标:知识与技能:使学生在学会确定任意方向的基础上,进一步体会位置关系的相对性过程与方法:并使学生在积极探索与交流的过程中进一步发展空间观念。
情感态度价值观:培养学生勇于探索、实践的学习精神。
教学重点:体会位置关系的相对性教学难点:现实生活中位置关系的相对性教学过程:一、自主学习1、同组同学互相说道:张三在李四的边,李四在张三的边。
教师:为什么同学们相互叙述对方的边线不一样?生:东和西、南和北的位置不是固定不变的,是相对而言的。
【设计意图】通过这一小游戏使学生自己辨认出:观测点出现了发生改变,对边线关系的叙述也随之发生改变了,这样的设计能够训练学生擅于从平时的生活中辨认出问题,并且自己谋求解决问题的方法和途径,培育积极探索精神。
通过游戏,同学们得出了左右相对而言的道理,那么我们这几天一直在研究的物体的位置会是什么样子的呢?2、写作并独立自主顺利完成教材p22基准3及搞一搞(1)上海在北京的南偏东约30°的方向上,距离约1067千米。
北京在上海的约°的方向上,距离约千米。
(2)做一做3、4、问题:(1)我们描述的沈阳和北京两个城市的位置关系和两位同学的位置关系为什么会出现两种不同的方式呢?(2)恳请同学们观测我们记录的两个城市之间的边线关系以及两位同学间的边线关系,你能够辨认出他们在方向、角度和距离上分别存有什么关系?二、交流展示1、小组内交流,合作自学,亲身经历解决问题的过程2、全班交流首先学生汇报自主学习2、3题的学习结果。
然后在些基础上交流第4题的结论。
在交流中引导学生明确:由于所选观测点不同,所在在描述两物体的位置关系时也存在着相对性;两物体的位置关系是“方向相对,偏角相同,距离相等”。
3、检验地图上两个城市之间的边线关系的相对性(1)请同学们,观察测量一下北京和沈阳之间的位置关系,它们之间的位置关系是不是也具有这样的性质?(2)辨认出了两物体之间边线关系的相对性,能够帮忙我们化解什么问题?生:我测量出了其中的一个,例如:北京在上海的北偏西约30°的方向上,利用相对性就得出了上海在北京的南偏东约30°的方向上师:除了谁也就是这么搞的?谁就是两个都测量出的?结果一样吗?三、测评反馈1、课本p24练习四第1题2、(1)小芳家在学校的偏约°的方向上,距离约米。
位置与方向相对性

《位置的相对性》教学设计教学内容:新课标人教版第四册下第二单元《位置与方向》P22例3、做一做及P24练习四1、2题。
教学目标:知识与技能:使学生在学会确定任意方向的基础上,进一步体会位置关系的相对性过程与方法:使学生在探索与交流的过程中进一步发展空间观念。
情感态度价值观:培养学生勇于探索、实践的学习精神。
教学重点:体会位置关系的相对性教学难点:现实生活中位置关系的相对性教学过程:一、自主学习1、同组同学互相说:张三在李四的边,李四在张三的边。
教师:为什么同学们相互描述对方的位置不一样?生:东和西、南和北的位置不是固定不变的,是相对而言的。
【设计意图】通过这一小游戏让学生自己发现:观测点发生了改变,对位置关系的描述也随之改变了,这样的设计能训练学生善于从平常的生活中发现问题,并且自己寻求解决问题的方法和途径,培养探索精神。
通过游戏,同学们得出了左右相对而言的道理,那么我们这几天一直在研究的物体的位置会是什么样子的呢?2、阅读并自主完成教材P22例3及做一做(1)上海在北京的南偏东约30°的方向上,距离约1067千米。
北京在上海的约°的方向上,距离约千米。
(2)做一做3、4、问题:(1)我们描述的沈阳和北京两个城市的位置关系和两位同学的位置关系为什么会出现两种不同的方式呢?(2)请同学们观察我们记录的两个城市之间的位置关系以及两位同学间的位置关系,你能发现他们在方向、角度和距离上分别有什么关系?二、交流展示1、小组内交流,合作学习,亲身经历解决问题的过程2、全班交流首先学生汇报自主学习2、3题的学习结果。
然后在些基础上交流第4题的结论。
在交流中引导学生明确:由于所选观测点不同,所在在描述两物体的位置关系时也存在着相对性;两物体的位置关系是“方向相对,偏角相同,距离相等”。
3、验证地图上两个城市之间的位置关系的相对性(1)请同学们,观察测量一下北京和沈阳之间的位置关系,它们之间的位置关系是不是也具有这样的性质?(2)发现了两物体之间位置关系的相对性,能帮我们解决什么问题?生:我测量出了其中的一个,例如:北京在上海的北偏西约30°的方向上,利用相对性就得出了上海在北京的南偏东约30°的方向上师:还有谁也是这么做的?谁是两个都测量出来的?结果一样吗?三、测评反馈1、课本P24练习四第1题2、(1)小芳家在学校的偏约°的方向上,距离约米。
位置关系的相对性
南
50米 米
豌豆在三叶草的 西 偏 的方向上, 的方向上,距离 北 25° 200 米。 三叶草在豌豆的 东 偏 南25° 的方向上, 的方向上,距离 200 米。
北 西 南 东
绿色圃中小学教育网
快速抢答
• • • • • • 小明在小东的南偏西25°,距离是3 米。 小东在小明的北偏东25° ,距离是3 米。 公园在房子的东偏南60°,距离是230米。 房子在公园的南偏东60° ,距离是230米。 熊在动物园的北偏西70°,距离是 50 米。 动物园在熊的西偏北70° ,距离是 50 米。
绿色圃中小学教育网
你能说出学校 距他们家的方 向和路程吗?
学校在小亮家的___偏 ___ ___的方向上,距离 约是___米。
绿色圃中小学教育网
你能说出学校 距他们家的方 向和路程吗?
学校在小刚家的___偏 ___ ___的方向上,距离 约是___米。
北 北京 东 南 北 上海 西
绿色圃中小学教育网
北京在上海的 _偏_约_的 方向上。 方向上。 上海在北京的 _偏_约_的 方向上。 方向上。
北
北京在上海的 北 _ 30° _偏西 约_的 30° 方向上。 方向上。 上海在北京的 南 _ 30° _偏东 约_的 30° 方向上。 方向上。
东 北京
30° 30°
南 北
30° 30°
西 上海
绿色圃中小学教育网
•观测点不同,同一个 观测点不同, 观测点不同 城市位置的说法也不 同。
绿色圃中小学教育网
北
相同: 相同:度数和距离
25° °
东
不同: 不同:方向Biblioteka 北 西北 东北 45° °
六年级下册数学知识点总结

六年级下册数学知识点总结 基础数学的知识与运⽤是个⼈与团体⽣活中不可或缺的⼀部分.其基本概念的精炼早在古埃及、美索不达⽶亚及古印度内的古代数学⽂本内便可观见。
下⾯店铺整理了⼀些关于六年级下册数学知识点总结,欢迎⼤家参考! 第⼀单元分数乘法 ⼀、分数乘法 (⼀)分数乘法的意义: 1、分数乘整数与整数乘法的意义相同。
都是求⼏个相同加数的和的简便运算。
例如:65×5表⽰求5个65的和是多少? 1/3×5表⽰求5个1/3的和是多少? 2、⼀个数乘分数的意义是求⼀个数的⼏分之⼏是多少。
例如:1/3×4/7表⽰求1/3的4/7是多少。
4×3/8表⽰求4的3/8是多少. (⼆)、分数乘法的计算法则: 1、分数与整数相乘:分⼦与整数相乘的积做分⼦,分母不变。
(整数和分母约分) 2、分数与分数相乘:⽤分⼦相乘的积做分⼦,分母相乘的积做分母。
注意:当带分数进⾏乘法计算时,要先把带分数化成假分数再进⾏计算。
3、为了计算简便,能约分的要先约分,再计算。
(尽量约分,不会约分的就不约,常考的质因数有11×11=121;13×13=169;17×17=289;19×19=361) 4、⼩数乘分数,可以先把⼩数化为分数,也可以把分数化成⼩数再计算(建议把⼩数化分数再计算)。
(三)、乘法中⽐较⼤⼩的规律 ⼀个数(0除外)乘⼤于1的数,积⼤于这个数。
⼀个数(0除外)乘⼩于1的数(0除外),积⼩于这个数。
⼀个数(0除外)乘1,积等于这个数。
(四)、分数混合运算的运算顺序和整数的运算顺序相同。
整数乘法的交换律、结合律和分配律,对于分数乘法也同样适⽤。
乘法交换律: a × b = b × a 乘法结合律: ( a × b )×c = a × ( b × c ) 乘法分配律: ( a + b )×c = a c + b c ⼆、分数乘法的解决问题(已知单位“1”的量(⽤乘法),即求单位“1”的⼏分之⼏是多少) 1、画线段图:(1)两个量的关系:画两条线段图,先画单位⼀的量,注意两条线段的左边要对齐。
位置的相对关系学会描述物体的位置关系

位置的相对关系学会描述物体的位置关系物体的位置关系是描述物体在空间中相对位置的一种方式,它能够准确传达物体之间的相对位置,为我们理解和描述环境中的事物提供了基础。
掌握位置的相对关系不仅在日常生活中有着广泛的应用,也是科学研究和技术应用的基础。
本文将介绍一些常见的描述物体位置关系的方法和技巧。
一、方位词描述位置关系方位词是描述物体位置关系最常用的工具之一。
方位词可以帮助我们准确地描述物体在空间中的位置,指明它们之间的相对关系。
常见的方位词有:上、下、左、右、前、后、内、外等。
例如,我们可以说:“杯子在桌子上。
”这句话用方位词“上”指明了杯子与桌子的位置关系。
同样,我们可以说:“书放在书架的左边。
”通过方位词“左边”,我们清楚地描述了书与书架之间的位置关系。
二、距离和方向描述位置关系除了方位词,距离和方向也是描述物体位置关系的重要因素。
距离可以用来表示物体之间的远近关系,而方向可以指示物体之间相对位置的朝向。
在描述距离时,我们可以使用数字、单位和比较级词语来量化。
例如,“这两个建筑物相距500米。
”或者“机场离市区比较远。
”在描述方向时,可以使用方位词、指示词和动词短语等。
例如,“从北向南走”或者“朝右边拐”。
三、图形和示意图描述位置关系图形和示意图是更直观地描述物体位置关系的方法。
通过绘制物体的简图或者示意图,我们可以更加清楚地展示物体之间的相对位置。
在图形和示意图上,可以使用箭头、线段和标记等来表示物体的位置和方向。
这种方法常用于地图、平面图、拓扑图等领域。
四、应用举例位置的相对关系在各行各业都有广泛的应用。
以下是一些实际应用举例:1. 导航系统:利用位置的相对关系,导航系统能够准确地指引我们的行进方向,并帮助我们到达目的地。
2. 建筑设计:在建筑设计中,需要准确描述建筑物之间的相对位置和布局,这样才能保证建筑物的合理布局和空间利用。
3. 调度管理:在物流和交通领域,位置的相对关系是调度管理的基础。
位置关系的相对性

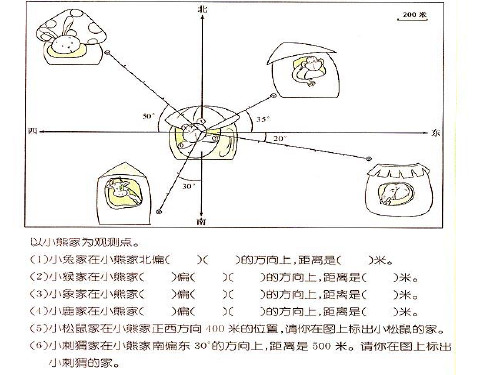
30° 1、以北京为观测点,上海在北京的( ) 偏( )约( )度方向上,距离是( )。 2、以上海为观测点,北京在上海的( ) 偏( )约( )度方向上,距离是( )。 3、观察一下我们记录的两个城市 北 之间的位置关系,你发现了什么?
西 上海
同样的两个城市,因为观测点不一样,所描述 的位置关系也就不一样,并且它们的方向正好 是相对的,由此看出两个城市的位置关系的相 对性。
西 北
45° 1
“东偏南45°” 也可以说是 “东南方向”。
• 东偏南45°或者南偏东45°称为 东南方向 • 东偏北45°或者北偏东45°称为 东北方向 西偏南45°或者南偏西45°称为 西南方向 西偏北45°或者北偏西45°称为 西北方向
超市在学校的北偏东30°的方向上,距离是300米。 学校在超市的(南)偏( 西 )(30 )°的方向上,距 离是(300 )米。
北
相同:度数和距离
25°
东
不同:方向
南
50米
豌豆在三叶草的 西 偏 的方向上,距离 北 25° 200 米。 三叶草在豌豆的 东 偏 南25° 的方向上,距离 200 米。
北 明在小东的南偏西25°,距离是3 米。 小东在小明的北偏东25° ,距离是3 米。 公园在房子的东偏南60°,距离是230米。 房子在公园的西偏北60° ,距离是230米。 熊在动物园的北偏西70°,距离是 50 米。 动物园在熊的南偏东70° ,距离是 50 米。
在学会确定任意方向的基础上,体会 位置关系的相对性。
北京和上海两 地相距大约 1067千米。
独学两分钟: 107 108 109 110 104 105 120 117 118 115 113 101 98 92 85 86 87 88 89 83 78 75 73 68 69 64 59 60 49 50 51 52 53 46 43 44 40 38 34 32 27 28 24 25 22 16 17 18 19 20 10 11 12 13 6 7 8 9 3 4 0 还剩 102 111 106 103 119 116 114 112 100 99 93 94 95 96 97 90 91 84 79 80 81 82 76 77 74 70 71 72 65 66 67 61 62 63 54 55 56 57 58 47 48 45 41 42 39 35 36 37 33 29 30 31 26 23 21 14 15 5 秒 1 2 群学两分钟: 107 108 109 110 104 105 120 117 118 115 113 101 98 92 85 86 87 88 89 83 78 75 73 68 69 64 59 60 49 50 51 52 53 46 43 44 40 38 34 32 27 28 24 25 22 16 17 18 19 20 10 11 12 13 6 7 8 9 3 4 0 还剩 102 111 106 103 119 116 114 112 100 99 93 94 95 96 97 90 91 84 79 80 81 82 76 77 74 70 71 72 65 66 67 61 62 63 54 55 56 57 58 47 48 45 41 42 39 35 36 37 33 29 30 31 26 23 21 14 15 5 秒 1 2 展示五分钟: 还剩 300 270 272 274 275 276 278 283 284 285 286 287 288 290 291 293 295 296 298 101 102 104 105 107 108 109 110 113 115 117 118 120 122 123 125 126 128 129 132 134 136 139 143 144 146 147 148 149 150 151 152 153 154 155 156 158 159 162 164 166 167 168 169 170 171 172 173 175 176 179 180 181 182 184 188 189 190 191 192 193 194 195 196 198 200 202 203 204 205 207 208 209 211 212 213 214 215 216 217 218 219 220 221 222 223 225 226 227 228 229 230 231 234 236 238 239 240 241 242 243 244 245 246 248 250 251 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 269 10 11 12 13 16 17 18 19 20 22 24 25 27 28 32 34 38 40 43 44 46 49 50 51 52 53 59 60 64 68 69 73 75 78 83 85 86 87 88 89 92 98 0 秒 3 4 6 7 8 9 271 273 277 279 280 281 282 289 292 294 297 299 100 103 106 111 112 114 116 119 121 124 127 130 131 133 135 137 138 140 141 142 145 157 160 161 163 165 174 177 178 183 185 186 187 197 199 201 206 210 224 232 233 235 237 247 249 252 268 14 15 21 23 26 29 30 31 33 35 36 37 39 41 42 45 47 48 54 55 56 57 58 61 62 63 65 66 67 70 71 72 74 76 77 79 80 81 82 84 90 91 93 94 95 96 97 99 1 2 5 北 北京
空间位置关系的认知与应用

空间位置关系的认知与应用一、介绍空间位置关系是人们认知世界的重要方式之一。
准确理解和应用空间位置关系不仅能够提高我们的生活效率,还能够帮助我们更好地理解和解决问题。
本文将探讨空间位置关系的认知与应用,旨在帮助读者更好地掌握和运用这一认知方式。
二、基本概念1. 方向:方向指物体或地点相对于参考点的相对位置。
包括前后、左右、上下等方向关系。
人们通常会以自身为参考点来认知和描述方向。
2. 相对位置:相对位置是指物体或地点之间的相对关系。
常见的相对位置关系包括靠近、远离、外部、内部等。
相对位置的认知有助于我们理解事物之间的关联性。
3. 绝对位置:绝对位置是指物体或地点在空间中的具体坐标位置。
使用地理坐标等工具可以准确确定物体或地点的绝对位置。
绝对位置的认知有助于我们进行地图导航等活动。
三、认知与应用1. 生活中的应用空间位置关系的认知在日常生活中有很多应用。
比如,当我们在陌生的城市中旅行时,我们可以通过准确理解方向来避免迷路;在购物时,了解物品的相对位置可以帮助我们更快地找到所需商品;在家居摆设或者装修中,了解房间中物体的相对位置可以使我们更好地进行布局设计。
2. 学习中的应用在学习过程中,空间位置关系的应用也非常广泛。
在数学学科中,几何和立体几何等内容都离不开空间位置关系的应用;在地理学科中,通过地图等工具的应用,我们可以更好地了解地球上各个地区之间的相对位置和绝对位置;在物理学等自然科学学科中,空间位置关系的应用可以帮助我们更好地理解物体之间的相互作用。
3. 技术领域的应用随着科技的不断进步,空间位置关系的应用也越来越广泛。
比如,全球定位系统(GPS)的应用使得人们可以更准确地确定自身的位置,进行导航等活动;在虚拟现实和增强现实技术中,空间位置关系的应用可以使得虚拟世界与现实世界更好地结合,提供更丰富的用户体验。
四、空间位置关系的认知发展1. 儿童期:儿童期是空间位置关系认知发展的重要阶段。
在此期间,孩子们逐渐学会使用前后、左右等基本方向词汇,并能够在日常生活中准确理解和应用相对位置关系。
位置关系的相对性课件

03
推动物理学理论的进 步
位置关系的相对性是物理学理论的重 要组成部分,对它的深入研究有助于 推动物理学理论的进步和发展。
对未来研究的展望
探索位置关系相对性的更深层次机制
尽管我们已经对位置关系的相对性有了基本的理解,但还有很多问题需要进一步研究,例如相对性在量子力学中的表 现和机制等。
探索位置关系相对性在现实生活中的应用
强调实验和观察
位置关系的相对性是一个抽象的概念,通过实验和观察可以帮 助学生更好地理解它。教育者应该强调实验和观察在理解位置
关系的相对性中的重要性。
培养学生的科学思维
通过教授位置关系的相对性,教育者可以培养学生的科学思维 ,例如如何从多个角度思考问题、如何进行科学的推理和判断
等。
促进跨学科的整合
位置关系的相对性不仅在物理学中有重要应用,在地理学、天 文学、工程学等领域也有应用,教育者可以促进跨学科的整合
通工具的航行轨迹和速度,确保安全和高效的交通流。
天文学中的位置关系
天体位置
天文学中,位置关系的相对性对于确定天体的位置和运动轨迹至关重要。通过比较不同时 间点上星星的位置,可以计算出地球的自转和公转轨迹。
天体距离
天文学家利用三角测量法等手段,通过观测不同天体之间的相对位置和角度,计算出天体 之间的距离。
相对位置的实例
地球上的经纬度系统
交通导航系统
经度和纬度是描述地球上任意一点相 对于地球中心的相对位置。
车载导航系统通过接收卫星信号,计 算车辆相对于卫星的位置,再结合地 图数据,提供准确的导航信息。
地图上的地理坐标
地图上的坐标系统也是基于相对位置 的概念,通过经纬度或平面坐标来描 述地物的位置。
02
根据人物关系之间的位置知识点总结

根据人物关系之间的位置知识点总结在故事或文章中,人物之间的位置关系是理解情节和发展的重要要素之一。
通过观察和理解人物在场景中的相对位置,我们可以推断他们之间的互动和关系。
以下是关于人物关系之间位置的知识点总结:1. 相对方位: 人物之间的相对方位指的是他们在场景中的位置关系。
这可以包括前后、左右、上下等方位。
观察人物之间的相对位置可以帮助我们理解他们之间的距离和关系。
相对方位: 人物之间的相对方位指的是他们在场景中的位置关系。
这可以包括前后、左右、上下等方位。
观察人物之间的相对位置可以帮助我们理解他们之间的距离和关系。
2. 距离: 人物之间的距离可以反映他们之间的情感和关系。
如果两个人物之间距离很近,可能表示他们之间的亲密关系或密切的互动。
相反,如果两个人物之间距离较远,可能表示他们之间存在隔阂或冷漠。
距离: 人物之间的距离可以反映他们之间的情感和关系。
如果两个人物之间距离很近,可能表示他们之间的亲密关系或密切的互动。
相反,如果两个人物之间距离较远,可能表示他们之间存在隔阂或冷漠。
3. 身体语言: 人物的身体语言可以揭示他们之间的关系。
例如,一个人面对另一个人,眼神接触和微笑可能表示友好或亲近的关系。
而背对着对方、避免眼神接触或者身体紧张可能表示紧张或冲突的关系。
身体语言: 人物的身体语言可以揭示他们之间的关系。
例如,一个人面对另一个人,眼神接触和微笑可能表示友好或亲近的关系。
而背对着对方、避免眼神接触或者身体紧张可能表示紧张或冲突的关系。
4. 场景环境: 场景环境也会对人物之间的位置关系产生影响。
例如,如果两个人物在同一个桌子上坐着,可能表示他们之间有共同的目标或合作的关系。
而如果一个人物位于高处,另一个人物位于低处,可能表示两者之间的权力关系。
场景环境: 场景环境也会对人物之间的位置关系产生影响。
例如,如果两个人物在同一个桌子上坐着,可能表示他们之间有共同的目标或合作的关系。
而如果一个人物位于高处,另一个人物位于低处,可能表示两者之间的权力关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北 西 南 东
45° °
当堂训练
家校地图 200米 小刚家
1. 我们站在学校看小刚 家,小刚家在学校的什么 方向上?距离是多少米? 方向上?距离是多少米?
小芳家 30°学校 21° 小红家 27° 45°
2. 我们站在小刚 家看学校, 家看学校,学校在 小刚家的什么方向 距离是多少米? 上?距离是多少米?
方向相反;角度相同;距离相等。 方向相反;角度相同;距离相等。 相反 相同 相等
同学们今天 学得很好, 学得很好,希望 大家回去好好 复习! 复习!
人教版数学
四年级下册
位置的相对性
课前准备
北 200米
岛
西
看图回答: 看图回答:
40º 灯塔
东
岛在灯塔的( 岛在灯塔的( 东 )偏( 北 )( 40 )°方 向上,距离是( 向上,距离是( 1200 )米。
或者说: 或者说:
岛在灯塔的( 岛在灯塔的( 北 )偏( 东 )( 50 )°方 向上,距离是( 向上,距离是( 1200 )米。
小组讨论
认真阅读教材P22的例3 边看边思考: 认真阅读教材P22的例3,边看边思考: P22的例 1.找出北京和上海两个城市在地图上的位 1.找出北京和上海两个城市在地图上的位 置。 2.上海在北京的 上海在北京的( 方向, 2.上海在北京的( )方向,北京在上海 方向,分别是以谁为观测点? 的( )方向,分别是以谁为观测点? 两个城市的位置是什么关系? 两个城市的位置是什么关系? 3.观察这两个城市的位置,你有什么发现? 3.观察这两个城市的位置,你有什么发现? 观察这两个城市的位置 同桌互说) (同桌互说)
小刚家在学校的东 偏 北 45 度 的 方 向 上 , 距离是1000米。 距离是 米
小亮家
学校在小刚家的西 偏 南 45 度 的 方 向 上 , 距离是1000米。 距离是 米
当堂训练
抢答游戏 A在B的北偏东 °的方向上,距离是 在 的北偏东 的北偏东30°的方向上,距离是300米。 米
30 B在A的(南 )偏(西 )( )°的方向上,距离是 在 的 的方向上, (300 米。 ) 说说你的方法: 说说你的方法
南
北
课前准备
小林家
300米 35°
西 看图回答: 看图回答:
学校
小林家在学校的( ) 小林家在学校的( 西 偏(北 )( 35)° 方向上,距离是( 方向上,距离是( 300 )米。
或者说: 或者说:
小林家在学校的( 小林家在学校的( 北)偏( 西)( 55)° 方向上,距离是( 方向上,距离是( 300 )米。
用量角器量一量, 用量角器量一量,说一说 北京与上海的位置关系。 北京与上海的位置关系。
你发现了 什么? 什么?
北 西
30°
位置关系的相对性
观测点 标准) (标准)
上海
位置的变化
北京在上海的北偏西 °方向上 北京在上海的北偏西30° 的北偏西
北京
上海在北京的南偏东 ° 上海在北京的南偏东30°方向上 的南偏东
观测点变了,所以位置就变了
小结
我的发现 两个城市的位置是相对对方来说的; 两个城市的位置是相对对方来说的; 物体位置关系的相对性
方向相反;角度相同;距离相等。 方向相反;角度相同;距离相等。 相反 相同 相等
当堂训练
你在我的东偏南45°的 方向上,距离是1米。
Байду номын сангаас
你我位置描述
45° °
你在我的西偏北 45°的 方向上,距离是 1 米。
